A Taxonomy and Theoretical Analysis of Collapse Phenomena in Unsupervised Representation Learning

Abstract

Unsupervised representation learning has emerged as a promising paradigm in machine learning, owing to its capacity to extract semantically meaningful features from unlabeled data. Despite recent progress, however, such methods remain vulnerable to collapse phenomena, wherein the expressiveness and diversity of learned representations are severely degraded. This phenomenon poses significant challenges to both model performance and generalizability. This paper presents a systematic investigation into two distinct forms of collapse: complete collapse and dimensional collapse. Complete collapse typically arises in non-contrastive frameworks, where all learned representations converge to trivial constants, thereby rendering the learned feature space non-informative. While contrastive learning has been introduced as a principled remedy, recent empirical findings indicate that it falls to prevent collapse entirely. In particular, contrastive methods are still susceptible to dimensional collapse, where representations are confined to a narrow subspace, thus restricting both the information content and effective dimensionality. To address these concerns, we conduct a comprehensive literature analysis encompassing theoretical definitions, underlying causes, and mitigation strategies for each collapse type. We further categorize recent approaches to collapse prevention, including feature decorrelation techniques, eigenvalue distribution regularization, and batch-level statistical constraints, and assess their effectiveness through a comparative framework. This work aims to establish a unified conceptual foundation for understanding collapse in unsupervised learning and to guide the design of more robust representation learning algorithms.

1. Introduction

Unsupervised representation learning has gained considerable interest across various domains of artificial intelligence (AI), including computer vision, natural language processing, and signal processing. This attention is largely due to its ability to extract generalizable features from large-scale unlabeled datasets [1,2,3,4,5,6]. Among these, self-supervised learning approaches have demonstrated performance on par with traditional supervised methods and have proven effective in transfer learning and a wide range of downstream tasks [7,8,9].

Despite these promising outcomes, unsupervised methods are fundamentally vulnerable to a phenomenon known as collapse, wherein the learned representations lose diversity and fail to capture meaningful distinctions among data instances. Such collapse severely undermines the discriminative power of representations, leading to degraded performance in downstream applications.

Prior research has primarily dealt with the so-called complete collapse, in which the learned representations degenerate into trivial solutions, such as converging to a constant vector or becoming confined to a severely limited subspace. Complete collapse can be quantitatively characterized through simple geometric statistics. In this scenario, all embedding vectors converge to a nearly identical direction in the feature space, regardless of input variability. This results in a cosine similarity matrix where most entries approach 1, which is not due to meaningful semantic similarity but because the representations have lost all structural diversity. Importantly, this differs from the desirable behavior in representation learning, where only semantically similar inputs yield high similarity. Furthermore, per-dimension variance across embeddings tends to vanish, indicating that the learned features occupy an extremely low-dimensional subspace.

In contrastive learning, contrastive loss functions have been leveraged to enforce representation dispersion, thereby mitigating such trivial solutions [10,11]. Meanwhile, non-contrastive approaches, such as bootstrap your own latent (BYOL) and simple Siamese network (SimSiam), have incorporated architectural innovations, namely, the predictor module and the stop-gradient mechanism, respectively, to maintain representation diversity without the need for explicit contrastive objectives [12,13].

However, recent findings indicate that collapse is not entirely eliminated even in contrastive settings. A more nuanced and often overlooked variant, termed dimensional collapse, has emerged [14]. In this scenario, although the representations do not converge to a single constant vector, they tend to disproportionately concentrate along a small number of principal components or within a low-dimensional subspace.

Unlike complete collapse, which can often be detected through metrics such as feature variance or cosine similarity, relying solely on these measures is insufficient for a reliable diagnosis. Dimensional collapse remains difficult to quantify consistently. Although widely used proxies, such as the singular value spectrum and participation ratio (PR), are often employed to assess it, these indicators lack standardized thresholds, vary across implementations, and strongly depend on task and architecture. As a result, no universally accepted quantitative definition of dimensional collapse has been established.

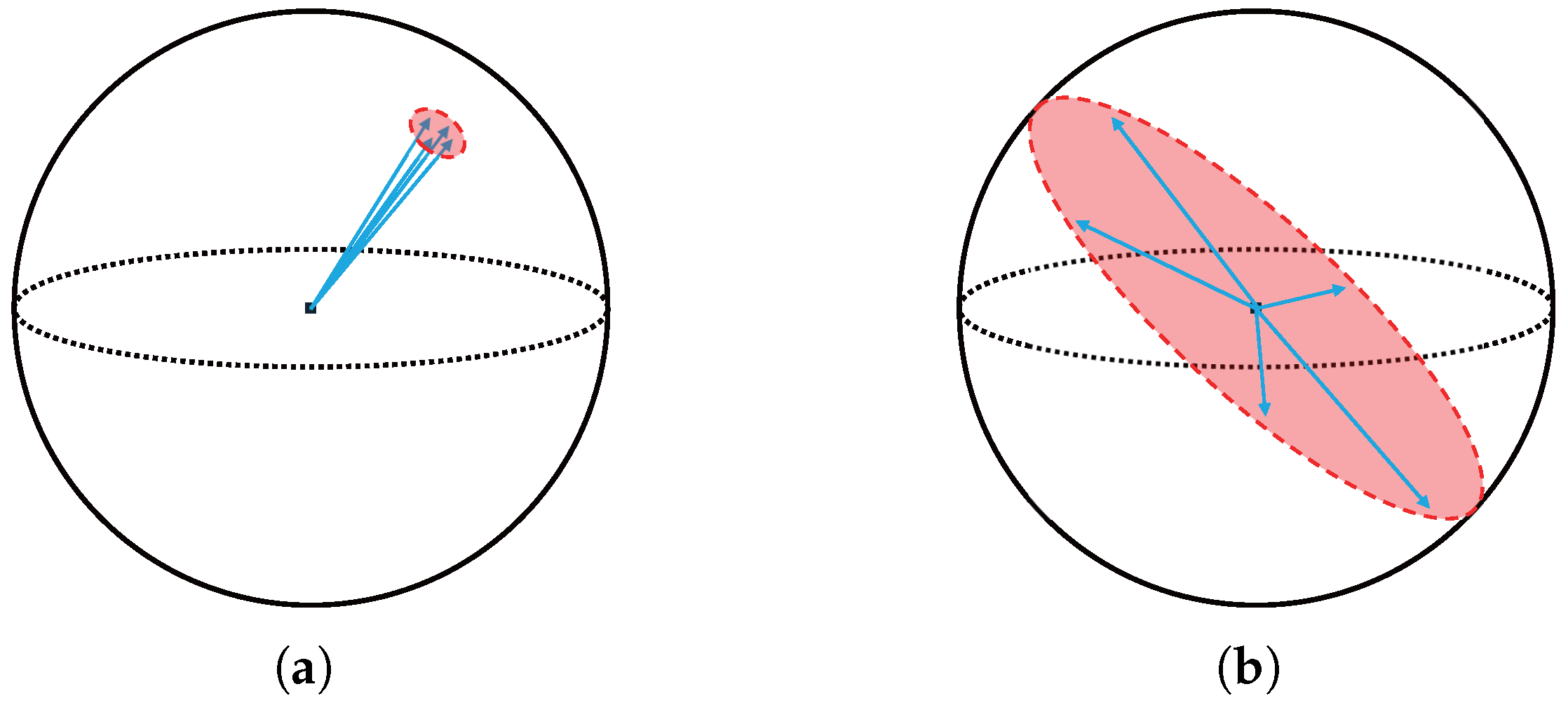
This phenomenon leads to a significant reduction in both the effective dimensionality and the diversity of the representations, thereby diminishing the overall information content of the learned features [15]. Compared to complete collapse, dimensional collapse is subtler and more difficult to detect, yet it poses equally serious limitations on the expressiveness of the learned representations and their performance in downstream tasks. An illustration of these two collapse categories is provided in Figure 1.

To address this issue, this paper provides a comprehensive investigation of the collapse phenomena in unsupervised representation learning. Specifically, we categorize collapse into complete and dimensional forms and systematically examine their theoretical foundations, causal mechanisms, and recent mitigation strategies (while this paper focuses on complete and dimensional collapse as the two most consistently studied categories in the current literature, other extensions such as mode collapse and semantic collapse have also been discussed in related contexts [16,17]. These are beyond the scope of this work and remain open for future investigation.) Through this analysis, we aim to offer a unified framework for understanding the structural limitations of unsupervised representation learning and to guide the development of more robust learning algorithms.

1.1. Related Work

1.1.1. Self-Supervised Learning

Self-supervised learning methods can be broadly categorized by the structural principles they adopt to learn useful representations from unlabeled data. One prominent family follows a Siamese architecture, where pairs of augmented views are processed through shared encoders to enforce representation consistency across transformations [18,19]. These methods typically rely on similarity-based objectives to encourage invariance while reducing redundancy. Another line of research emphasizes clustering-based learning, aiming to preserve group-level structures and induce semantically meaningful partitions in the learned space without explicit labels [20]. These approaches often involve online clustering mechanisms and promote consistency across different cluster assignments. A third direction explores adversarial frameworks, where discriminators are used to encourage feature diversity and prevent the overfitting of representations to specific views or augmentations [21]. By promoting distributional robustness or maximizing information retention, adversarial strategies contribute to better generalization under varying input conditions. Together, these structurally distinct perspectives represent complementary efforts to address the challenges of learning effective representations in the absence of supervision.

1.1.2. Visual Diagnosis and Interpretability in Self-Supervised Learning

As self-supervised learning models grow in complexity, there has been increasing interest in understanding what these models learn and how they attend to input data [22]. A significant line of research focuses on visualizing internal representations, with methods such as Class Activation Mapping (CAM), attention map visualization, and query-specific output highlighting [23,24,25]. These tools offer a means to inspect the spatial or semantic focus of the model across different layers or inputs.

Visualization techniques such as CAM and attention maps have been widely used across different types of neural networks to examine how models process input data. Regardless of whether a model is supervised or self-supervised, these tools help reveal what structural cues the model attends to, how features are spatially and semantically organized, and how internal representations evolve through layers. By exposing these mechanisms, such efforts contribute to the broader field of interpretable AI, which seeks not only high performance but also transparency and explainability. As self-supervised learning continues to gain traction, especially in high-stakes scenarios, the ability to visually interpret learned features is becoming an essential component of trustworthy model development.

1.1.3. Dimensional Analysis and Interpretability in Representation Learning

As representation learning advances, there is growing interest in analyzing the geometric and statistical properties of learned feature spaces, particularly their dimensional structure [26]. Recent research highlights the importance of factors such as effective dimensionality, variance distribution, and the concentration of information across dimensions, suggesting that these properties are closely linked to generalization and interpretability.

In supervised learning, efforts have focused on incorporating dimensionality reduction or normalization mechanisms to ensure that representations remain compact yet informative, thereby enhancing both efficiency and generalization [27]. In self-supervised learning, more attention is being paid to preventing excessive dimensional concentration or the collapse of useful axes, with methods aiming to preserve structural diversity across features to promote transferable representations [28].

In addition, multi-view and multimodal learning settings raise new challenges around aligning or balancing representations across modalities, where disentanglement and compositionality become increasingly important [29]. Collectively, these trends point toward a broader effort to establish more structured and theoretically grounded criteria for evaluating and designing learned representations.

1.2. Paper Organization

This paper is organized as follows. Section 2 defines collapse phenomena and presents a taxonomy for their classification. Section 3 delves into complete collapse, examining its causes, illustrative examples, and potential mitigation strategies. Section 4 turns to dimensional collapse, following a similar analytical framework. Broader discussion and future research directions are offered in Section 5, and this paper concludes with a summary in Section 6.

2. Definition and Taxonomy of Collapse Phenomena

In unsupervised representation learning, collapse refers to a degenerative phenomenon in which learned representations fail to capture meaningful structure and converge toward information-poor states. This typically occurs when the model generates restricted or nearly constant embeddings that inadequately reflect the intrinsic differences among input samples. Consequently, the discriminative capacity of the representations deteriorates, often resulting in degraded performance on downstream tasks. Notably, collapse is not necessarily a symptom of training failure, but it can also manifest in seemingly converged models whose representations remain uninformative despite stable loss values or training metrics.

Collapse may arise due to a variety of factors, including the design of the objective function, the loss function, or both, network architecture, and training dynamics. It is particularly prevalent in unsupervised or self-supervised settings, where the absence of explicit label supervision increases the risk of convergence to trivial or shortcut solutions that fail to preserve the diversity and informativeness of representations.

Rather than representing a singular failure mode, collapse is better understood as a spectrum of behaviors that vary in severity and structural characteristics. At one extreme, all inputs may be mapped to an identical output vector. More subtle instances involve the concentrations of representations along a single axis or within a narrow (i.e., low-dimensional) subspace. These nuanced behaviors indicate that collapse should not be characterized by a single diagnostic criterion, but rather by a texanomy grounded in the degree and nature of representational degeneration, particularly in terms of the loss of representational diversity.

Accordingly, this paper categorizes collapse into two principal types. The first is complete collapse, a well-known scenario in which representations degenerate to a constant vector. The second, which has received growing attention in recent literature, is dimensional collapse, wherein representations remain some variation but are restricted to a narrow (i.e., low-dimensional) subspace. These two types differ markedly in their underlying mechanisms, empirical signatures, and mitigation strategies, and thus merit separate, in-depth analysis in the subsequent sections.

2.1. Definition and Characteristics of Complete Collapse

Complete collapse represents the most prototypical and extreme form of degeneration in representation learning, wherein the learned representations converge to constant or highly restricted vectors that carry virtually no informational content. In such cases, the model produces identical or nearly identical embeddings for all inputs, regardless of their intrinsic variability. As a result, the representations lose their discriminative capacity and become ineffective for downstream tasks. When the outputs fail to reflect structural differences in the input data, the learning process is deemed unsuccessful.

This phenomenon is particularly prevalent in non-contrastive learning settings. In the absence of explicit constraints to enforce dissimilarity among representations, the model may converge to trivial solutions, such as outputting a constant vector for all inputs, as a shortcut for minimizing the loss function, as illustrated in Figure 1a. Complete collapse is especially common in reconstruction- or prediction-based self-supervised learning frameworks that lack sufficient architectural regularization or implicit variance-promoting mechanisms.

To mitigate this issue, contrastive learning introduces loss functions that explicitly promote representation dispersion. Methods such as SimCLR and MoCo utilize positive and negative sample pairs to enforce representational dissimilarity, thereby reducing the risk of collapse into a single or near-constant output.

However, while contrastive learning effectively prevents complete collapse, it does not ensure high effective dimensionality or sufficient informational richness of the learned representations. That is, the mere presence of representational dissimilarity does not guarantee that the features are diverse or expressive enough for complex downstream tasks. This limitation is closely related to the more nuanced phenomenon of dimensional collapse, which will be addressed in the following subsection.

2.2. Definition and Characteristics of Dimensional Collapse

Dimensional collapse refers to a more subtle and less conspicuous form of degeneration in unsupervised representation learning, in which learned vectors appear dispersed on the surface but are in fact excessively concentrated along a small number of dimensions or specific directions, as illustrated in Figure 1b [30]. While complete collapse involves convergence of all representations to a constant vector, dimensional collapse manifests as a partial degeneration that undermines both representational diversity and the effective utilization of the embedding space. Since loss functions may converge normally and pairwise similarities among representations may still appear meaningful, this phenomenon is often misinterpreted as successful learning

Dimensional collapse typically arises from inefficient use of the representational space, where variance is disproportionately allocated to a small subset of dimensions, leaving the remaining dimensions nearly inactive. This behavior can be diagnosed through spectral analysis of the covariance matrix or singular value decomposition, where the collapse is indicated by a small number of dominant eigenvalues and the rest approaching zero.

Unlike complete collapse, dimensional collapse can occur in both non-contrastive and contrastive learning frameworks [14]. Even when representations exhibit pairwise distances and the loss converges stably, excessive dimensional concentration implies that the model has failed to capture a diverse and informative feature space. Such structural bias poses a latent risk, as it can be mistaken for effective learning while in reality degrading representational expressiveness.

This form of dimensional collapse impairs the fundamental objectives of representation learning; namely, capturing diverse information and enabling generalization. As a result, performance in downstream tasks such as classification, clustering, and transfer learning can be significantly hindered. Accordingly, recent research has focused on developing quantitative metrics for early detection and diagnosis of collapse, along with designing loss functions and architectural constraints to prevent it. Within this context, dimensional collapse is increasingly recognized as a hidden bottleneck in self-supervised representation learning, and is emerging as a critical challenge for future investigation.

3. Complete Collapse: Causes, Examples, and Mitigation Strategies

3.1. Underlying Mechanisms

Complete collapse refers to a condition in unsupervised representation learning where learned features fail to reflect structural differences among inputs, instead collapsing to a single constant vector or a highly restricted set of representations. Although the training loss may decrease steadily and converge as expected, the model in fact maps all inputs to identical or nearly identical embeddings. This results in virtually zero mutual information across representations, indicating a clear failure of the learning process.

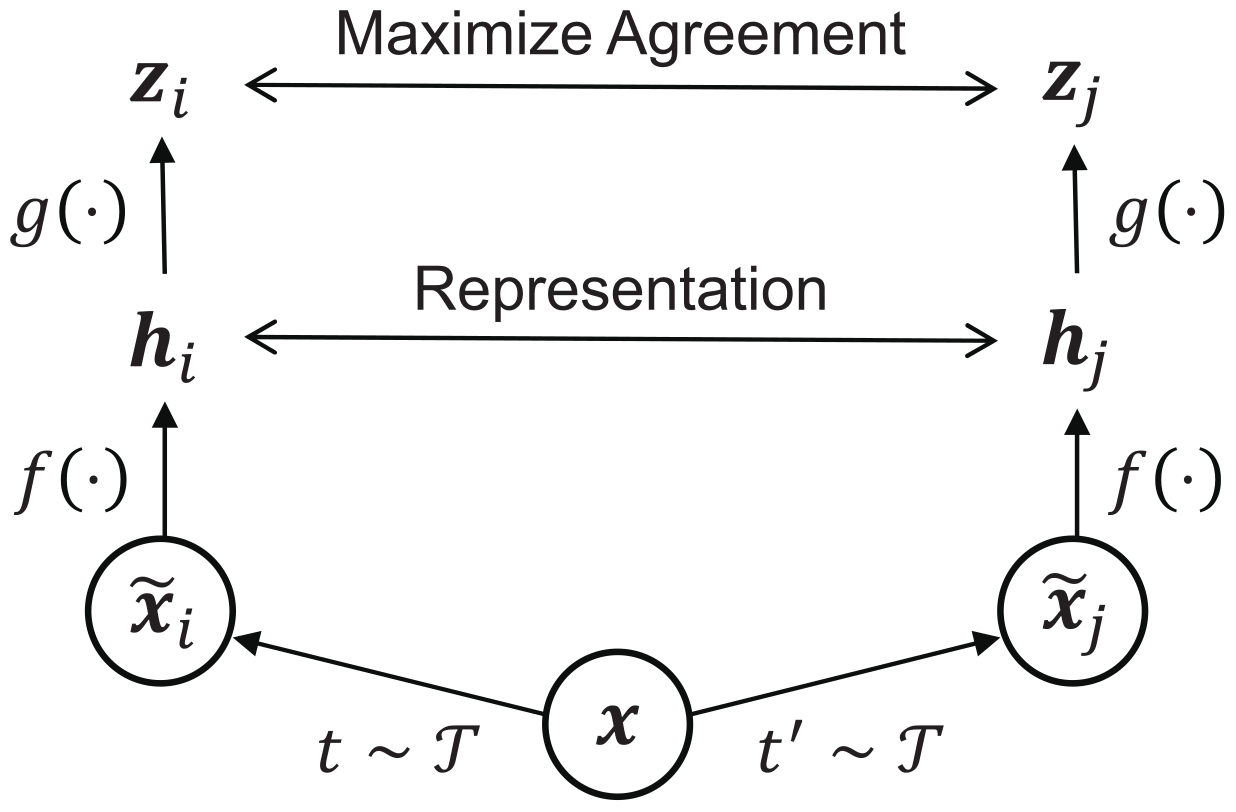
Such collapse commonly arises when the loss function can be minimized without explicit constraints that encourage dispersion or diversity in the learned representations. For example, in learning frameworks that aim to maximize the similarity between two augmented views of the same input, the most straightforward solution is to output the same vectors for all inputs [31]. Although this trivially minimizes the loss, the resulting embeddings carry no meaningful information.

The risk of collapse is particularly high in non-contrastive learning settings, where the training objective lacks any mechanism to enforce inter-sample dissimilarity. In the absence of constraints, either architectural or loss-based, the model is implicitly incentivized to converge toward trivial solutions. This reveals an inherent weakness in objective functions that focus solely on similarity maximization.

In this sense, complete collapse can be viewed as a trivial but locally optimal outcome of the optimization process: the loss function is minimized, yet the learned features are uninformative. This leads to the illusion of successful training while the representational space has, in fact, collapsed, a structural failure that undermines the core objective of representation learning.

This risk of collapse is not confined to any single framework but constitutes a general challenge across unsupervised learning, motivating diverse strategies for its prevention.

3.2. Contrastive Learning as a Defense Against Collapse

Contrastive learning is one of the most widely adopted paradigms in unsupervised representation learning and provides a principled framework for effectively mitigating complete collapse. Its core principle is to enforce the dispersion among representations of different data samples, thereby preserving diversity in the representation space and preventing convergence to trivial solutions.

This strategy is commonly implemented using a Siamese-like structure, in which two augmented views of the same input form a positive pair, and other instances in the batch are treated as negatives [31,32]. A widely used loss function in this setting is InfoNCE loss, which encourages positive pairs to be mapped closely in the embedding space while simultaneously pushing negative pairs apart [33,34,35]. This loss function inherently promotes dispersion and dissimilarity among representations, thus acting as a natural deterrent against collapse.

Mathematically, the contrastive loss for an anchor $z_i$ can be defined as follows:

$${\mathcal{L}}_{\mathrm{contrastive}}=-log{\displaystyle \frac{exp(\mathrm{sim}(z_i,z_j)/\tau )}{{\sum }_{k\in \mathcal{B}\left(i\right)}exp(\mathrm{sim}(z_i,z_k)/\tau )}}$$

(1)

where $z_j$ is the positive sample corresponding to $z_i$, $\mathcal{B}\left(i\right)$ is the set of contrastive samples (including one positive and multiple negatives), $\mathrm{sim}(·,·)$ denotes cosine similarity, and $\tau$ is a temperature scaling parameter [36]. This objective brings positive pairs closer while separating negatives, thereby promoting dispersion and reducing the risk of collapse. By explicitly regulating pairwise similarity, the formulation also serves as an effective regularization mechanism against representational degeneration.

Representative implementations include SimCLR and MoCo, both of which incorporate architectural components designed to promote diversity and prevent collapse. These frameworks employ techniques such as large batch sizes, memory banks, and momentum encoders, depending on their design.

3.2.1. SimCLR: A Representative Contrastive Learning Framework

SimCLR is a widely used framework for self-supervised representation learning, notable for its ability to learn high-quality representations through a relatively simple architecture [10]. As shown in Figure 2, SimCLR consists of three main components: an encoder $f(·)$, a projection head $g(·)$, and a contrastive loss function.

The framework generates two different augmented views of the same input image using independent augmentation strategies. These views are passed through the encoder to obtain representations $h_x$ and $h_y$, which are then mapped to the projection space as $z_i=g\left(h_x\right)$ and $z_j=g\left(h_y\right)$. SimCLR employs the normalized temperature-scaled cross entropy (NT-Xent) loss to train the model [33,36,37].

The loss is formulated as follows:

$${\mathcal{L}}_{i,j}=-log{\displaystyle \frac{exp\left(\mathrm{sim}(z_i,z_j)/\tau \right)}{{\sum }_{k=1}^{2N}{\mathbf{1}}_{[k\ne i]}exp\left(\mathrm{sim}(z_i,z_k)/\tau \right)}}$$

(2)

where N is the number of samples in the batch (yielding $2N$ augmented examples). This objective encourages high similarity between positive pairs while discouraging similarity with negative samples [38].

A key design decision in SimCLR is to apply the contrastive loss not in the representation space h, but in the projection space z. This design prevents the contrastive loss from directly over-regularizing the learned representations, thus preserving the semantic informativeness of h. Since only h is used for downstream tasks, this separation allows the model to benefit from contrastive learning while maintaining high-quality features.

Moreover, as illustrated in Figure 3, SimCLR incorporates a set of data augmentation strategies [1,39,40], including random cropping and resizing, color distortion, and Gaussian blur, to prevent the model from relying on low-level visual cues. These augmentations encourage the model to focus on semantic features, thereby enhancing both robustness and representation diversity.

In addition, SimCLR uses L2 normalization and large batch training to increase the effectiveness of contrastive loss and suppress convergence to trivial solutions. With these architectural and training strategies, SimCLR has demonstrated the ability to learn semantically meaningful representations without relying on memory banks or momentum encoders. Notably, the introduction of the projection head has proven to be a pivotal contribution, influencing the architecture of many subsequent self-supervised learning frameworks.

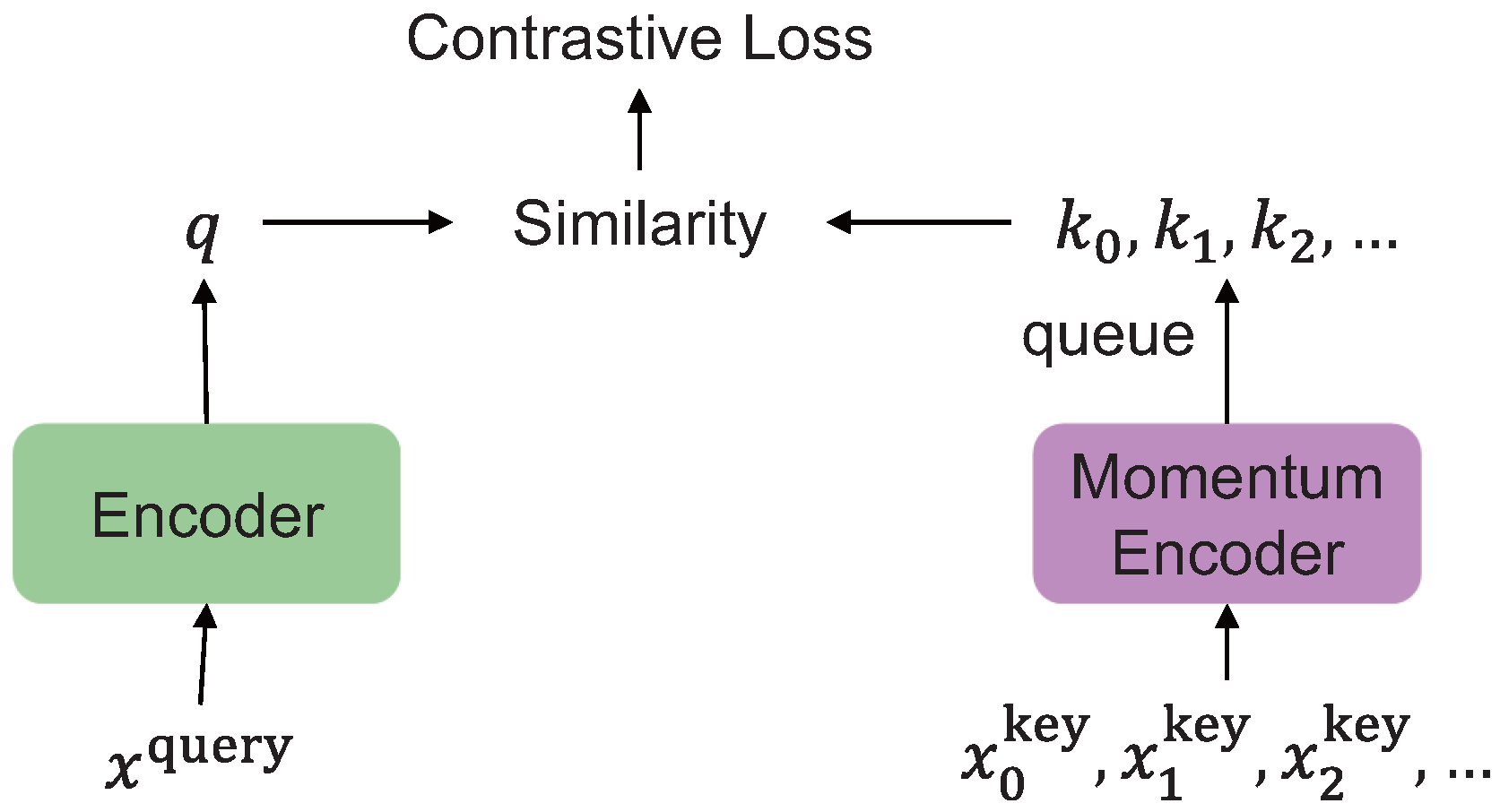
3.2.2. MoCo: Momentum-Based Contrastive Learning Framework

Momentum contrast (MoCo) is a self-supervised learning framework based on contrastive learning, designed to balance representational quality and transferability [11]. MoCo redefines contrastive learning as a dictionary lookup problem. Its architecture, depicted in Figure 4, illustrates how a query is matched against a dynamic queue of encoded keys maintained via a momentum encoder. This dictionary is implemented as a queue-based memory bank, and its contents are updated via a momentum encoder to ensure consistency over time [36].

The loss function used in MoCo is the InfoNCE loss [11], defined as follows:

$${\mathcal{L}}_{\mathrm{MoCo}}=-log{\displaystyle \frac{exp\left(\mathrm{sim}(q,k^{+})/\tau \right)}{{\sum }_{k\in \mathcal{K}}exp\left(\mathrm{sim}(q,k)/\tau \right)}}$$

(3)

where q is the query, $k^{+}$ is the positive key corresponding to the same input, and $\mathcal{K}$ denotes a dictionary of negative keys.

MoCo employs several architectural strategies to prevent complete collapse. First, by maintaining a queue-based dictionary, it provides a large and continually updated set of negative samples independent of the mini-batch size, which is crucial for preserving the discriminative power of the contrastive loss. Second, the key encoder is updated using a momentum-based moving average of the query encoder, ensuring temporal consistency among the stored key representations. This mechanism helps prevent convergence to trivial solutions.

A notable advantage of MoCo is its computational efficiency. The contrastive loss is computed only between the current query and its positive/negative keys, while older keys in the dictionary are reused without backpropagation. To address potential drift in the key encoder, MoCo uses a momentum encoder, where the key encoder is updated as a moving average of the query encoder parameters. This stabilizes training and encourages consistent alignment of representations in the dictionary, especially in early training stages where collapse is most likely.

3.2.3. Summary and Limitations of Contrastive Learning

Contrastive learning has demonstrated strong effectiveness in preventing complete collapse by structurally encouraging representational dispersion. However, this dispersion does not necessarily guarantee expressive or information-rich representations. For instance, if representations collapse into a subspace aligned with a few dominant components, or if semantic redundancy exists, downstream generalization performance may still suffer despite apparent dispersion [3].

Contrastive learning inherently requires large numbers of negative pairs, which significantly increases memory consumption and computational cost. These resource demands limit its scalability and practical deployment [12]. Furthermore, contrastive learning suffers from limitations such as reduced generalization performance, and restricted expressiveness of conventional distance metrics [41,42]. Such limitations have motivated the development of non-contrastive learning methods, leading to diversified strategies for collapse prevention and more efficient training paradigms.

3.3. Collapse Prevention in Non-Contrastive Learning

Non-contrastive learning has recently emerged as a promising paradigm in self-supervised representation learning, demonstrating that effective feature learning is possible even without contrastive loss or negative pairs. These approaches challenge the conventional belief that explicit sample-wise distance manipulation is required, and instead raise important questions regarding the underlying mechanisms that prevent collapse in such architectures.

Traditionally, it was assumed that learning without negative pairs would inevitably lead to complete collapse, wherein all representations converge to identical outputs [43]. However, models such as BYOL and SimSiam have empirically shown that it is possible to avoid collapse without using negative samples, provided that specific architectural and optimization dynamics are incorporated [12,13].

These models introduce asymmetry and gradient control mechanisms to implicitly maintain representational diversity. In BYOL, an asymmetric structure is created by employing an online encoder and a momentum encoder, both equipped with projection heads, but only the online branch includes a predictor network. This structural difference prevents trivial solutions by enforcing a directional representation alignment. Similarly, SimSiam employs a stop-gradient operation to break symmetry, computing the loss based only on one side of the architecture, thereby mitigating collapse.

Collectively, these findings suggest that in Non-Contrastive Learning, architectural design and learning dynamics, rather than the loss function itself, play a critical role in maintaining meaningful representations and preventing collapse.

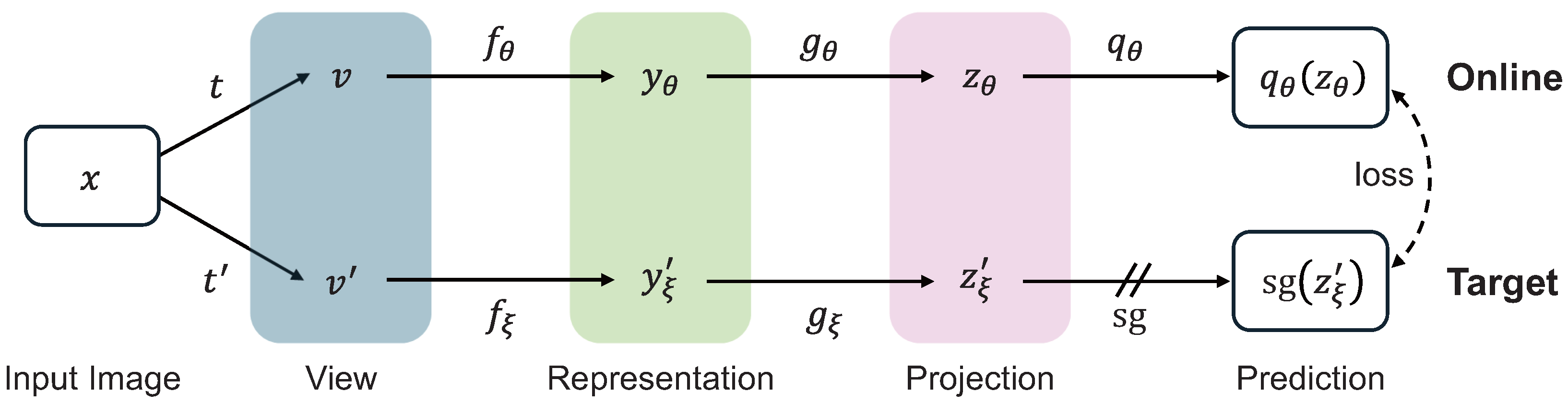
3.3.1. BYOL: Negative-Free Self-Supervised Representation Learning

BYOL is a self-supervised learning framework that demonstrates that effective representation learning is possible without negative samples [12]. Unlike traditional contrastive methods, which rely on pushing apart negative pairs while pulling together positive ones, BYOL learns representations by predicting one augmented view of an image from another, using a dual-network structure comprising an online network and a target network.

As illustrated in Figure 5, BYOL consists of three primary components: an encoder $f_{\theta }$, a projection head $g_{\theta }$, and a predictor $q_{\theta }$ in the online network, and a structurally identical target network updated via exponential moving average (EMA) of the online parameters. The training objective is for the online network to predict the representation output of the target network using cosine similarity. The loss function is formulated as follows:

$${\mathcal{L}}_{\mathrm{BYOL}}={∥norm\left(q_{\theta }\left(g_{\theta }\left(f_{\theta }\left(x\right)\right)\right)\right)-stopgrad\left(norm\left(g_{\xi }\left(f_{\xi }\left(x^{\prime }\right)\right)\right)\right)∥}_2^2$$

(4)

where $norm\left(v\right)$ denotes L2 normalization of vector v, $stopgrad(·)$ prevents gradients from flowing through the target network, x and $x^{\prime }$ are two augmentations of the same image, and $\xi$ represent parameters of the target network.

Despite the lack of negative samples, BYOL empirically avoids collapse and maintains representational diversity, due to the following architectural mechanisms:

• Predictor: The predictor $q_{\theta }$, exclusive to the online branch, introduces asymmetry and plays a critical role in preventing the convergence to trivial solutions.
• Slow-moving target network: The target network is updated as an EMA of the online network, providing stable targets that improve training stability and mitigate early collapse.
• Architectural asymmetry and stop-gradient: Although both networks share the same architecture, gradient flow is blocked in the target branch via the stop-gradient operation, introducing effective asymmetry.
• Loss symmetrization and normalization: The training objective includes bidirectional prediction and employs vector normalization, which prevents excessive alignment of representations.

Remarkably, BYOL achieves collapse-free training without incorporating any explicit collapse-avoidance terms in its loss function. The framework does not require large batch sizes or memory banks, making it more computationally efficient and robust to batch size variations. Additionally, BYOL exhibits greater tolerance to augmentation changes than contrastive methods, supporting its capacity to learn stable and transferable representations.

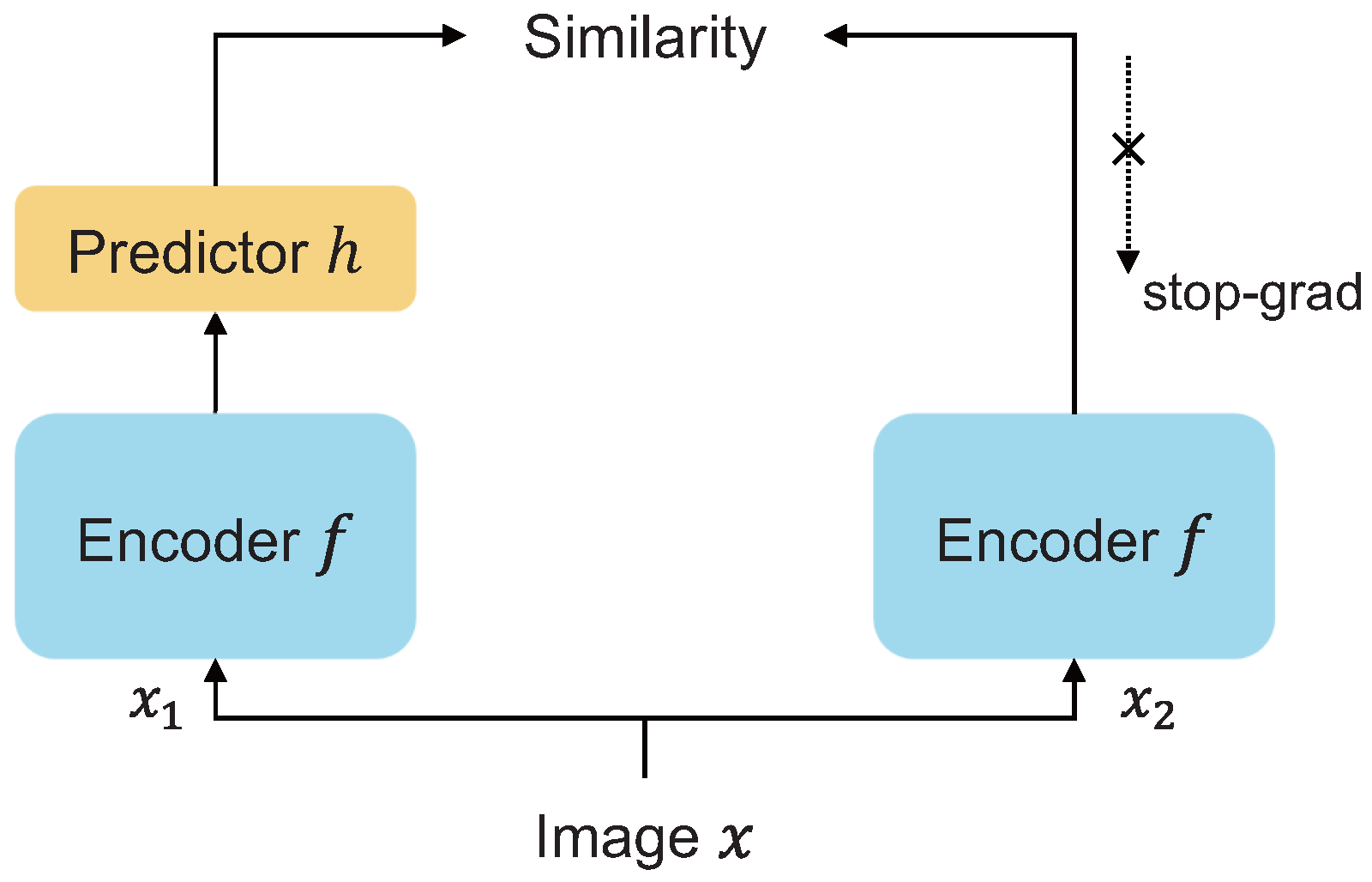
3.3.2. SimSiam: Minimalist Non-Contrastive Learning Framework

SimSiam presents a drastically simplified self-supervised learning framework that demonstrates the ability to learn meaningful representations without negative samples, momentum encoders, or large batch sizes, which have traditionally been considered essential components in contrastive or momentum-based learning [13].

SimSiam operates by applying two independent augmentations to a single input image, creating a pair of views that are processed through a shared encoder f and a projection MLP to produce feature vectors $z_1$ and $z_2$. The overall process is illustrated in Figure 6. A prediction MLP h is then applied to only one branch (typically the online branch) to predict the representation of the other. The stop-gradient operation, which blocks backpropagation on one branch, is the critical design element preventing collapse.

Although SimSiam does not explicitly enforce representational dispersion through negative samples, which could theoretically lead to complete collapse, empirical results show that the model avoids collapse and achieves stable training. This robustness arises from several architectural innovations:

• Stop-Gradient Operation: By preventing gradient flow in one branch, the optimizer is disincentivized from converging to trivial solutions. Removing this operation has been shown to cause the loss to rapidly decrease while the representations collapse to a constant vector.
• Presence of a Prediction MLP: Merely using an encoder and projection head is insufficient; the predictor h plays a crucial role in maintaining representational diversity. Removing or replacing it with a fixed random function leads to either collapse or failed learning.
• Symmetric Loss Structure with Bidirectional Alignment: SimSiam computes a symmetric loss between both views. The loss function is defined as follows:

  $${\mathcal{L}}_{\mathrm{SimSiam}}={\displaystyle \frac{1}{2}}D(p_1,\mathrm{stopgrad}\left(z_2\right))+{\displaystyle \frac{1}{2}}D(p_2,\mathrm{stopgrad}\left(z_1\right))$$

  (5)

  where $p_i$ denotes the predictor output, $z_i$ the projected representation, and D is typically the negative cosine similarity. This bidirectional alignment enhances learning stability and the quality of representations.

SimSiam operates robustly even with small batch sizes, unlike many contrastive methods, and incorporates L2 normalization to prevent directional collapse. Notably, SimSiam can be interpreted as BYOL without the momentum encoder, offering a minimal yet effective approach to non-contrastive self-supervised learning.

Its effectiveness in avoiding collapse without relying on loss regularization or external constraints underscores the central role of asymmetry in gradient flow and simple architectural design in preserving representational diversity.

3.3.3. SwAV: Clustering-Based Self-Supervised Learning

Swapping assignments between views (SwAV) is a self-supervised learning framework that demonstrates the possibility of learning meaningful representations without requiring negative pairs, positioning itself between contrastive and non-contrastive learning paradigms [44]. Instead of aligning instance-level representations, SwAV performs clustering-based assignments and trains the model to predict the cluster assignment of one view from another. This design enables structural separation among representations without pairwise comparison, effectively mitigating collapse.

As illustrated in Figure 7, SwAV applies two distinct augmentations to the same image, processes them through a shared encoder and projection head, and maps the resulting representations into a low-dimensional space. These embeddings are then soft-assigned to learnable prototype vectors, and each view is trained to predict the cluster assignment of its counterpart, a mechanism known as swapped prediction.

The soft assignments are computed using the Sinkhorn-Knopp normalization algorithm, which transforms the outputs into probability distributions over clusters [45]. The loss function typically takes the following form:

$${\mathcal{L}}_{\mathrm{SwAV}}=\sum _i{D}_{\mathrm{KL}}\left(P_i^{\left(a\right)}\Vert Q_i^{\left(b\right)}\right)+D_{\mathrm{KL}}\left(P_i^{\left(b\right)}\Vert Q_i^{\left(a\right)}\right)$$

(6)

where $P^{\left(a\right)}$ and $P^{\left(b\right)}$ are the soft assignments for each view, $Q^{\left(a\right)}$ and $Q^{\left(b\right)}$ are the predicted assignments for the other view, and $D_{\mathrm{KL}}$ denotes the Kullback–Leibler divergence.

SwAV prevents collapse through several architectural mechanisms:

• High-entropy assignments encourage the dispersion of representations across clusters, avoiding excessive concentration.
• Equipartition constraints ensure balanced usage of all prototypes, maintaining diversity across the representation space.
• Prototype-level alignment provides structural regularization that replaces the need for explicit negative sampling, preventing convergence to trivial solutions.

In particular, SwAV does not require memory banks, momentum encoders, or prediction heads, making it a computationally efficient and practical alternative to traditional contrastive learning. At the same time, its structure offers a quantifiable and stable method for controlling collapse, bridging the gap between the contrastive and non-contrastive self-supervised strategies.

3.3.4. Summary and Limitations of Non-Contrastive Learning

As reviewed in preceding sections, various non-contrastive learning models demonstrate distinct yet effective strategies for mitigating representation collapse, each leveraging one or more architectural mechanisms to maintain the integrity of the learned embedding space. These mechanisms extend beyond the design of the loss function itself and include techniques such as asymmetric learning pathways, implicit comparative structures, and selective gradient blocking, collectively illustrating the multifaceted nature of collapse prevention in non-contrastive settings [12,13,44,46,47].

Unlike contrastive methods, where the presence of explicit negative pairs serves as a primary mechanism for enforcing representational separation, non-contrastive frameworks rely heavily on indirect alignment structures and asymmetry in information flow. These elements play a critical role in sustaining representational diversity and structure, even in the absence of pairwise contrastive objectives.

The overall findings suggest that collapse is not solely a consequence of the presence or absence of contrastive loss. Instead, successful collapse prevention appears to result from the combined influence of several interacting factors: the goal orientation of the loss function, the interaction dynamics between network branches, the structural configuration of information propagation, the stability of training dynamics, and the type and intensity of regularization [48,49]. It is this synergistic combination of structural elements that constitutes the practical key to avoiding collapse and should be regarded as a central design consideration for future self-supervised learning frameworks.

3.4. Theoretical Understanding and Open Challenges of Complete Collapse

Despite significant empirical advances in mitigating complete collapse through various structural techniques and loss function designs, the theoretical understanding of why these methods work remains incomplete. Most collapse-prevention strategies are empirically observed to be effective, but lack the mathematical guarantees needed to generalize their stability and correctness.

3.4.1. Loss Function Perspective: Trivial Solution as a Global Minimum

Early theoretical efforts to analyze collapse have focused on the properties of the loss function. In self-alignment settings, trivial solutions, where all representations collapse to a constant vector, can minimize the loss, revealing that such solutions are often global minima of poorly constrained objectives.

For instance, the fact that the marginal likelihood used in deep kernel learning (DKL) can favor trivial representations is mathematically demonstrated [50]. This implies that collapse is not merely a training failure, but may be a theoretically inevitable outcome induced by the structure of the loss function.

Such results highlight the necessity of introducing explicit regularization terms or constraints to promote representation diversity and suggest the importance of deriving stability conditions to guide loss function design.

3.4.2. Architectural Asymmetry and the Lack of Formal Theoretical Justification

Models like BYOL and SimSiam have demonstrated strong empirical success in avoiding collapse without negative samples. However, the theoretical explanation for their effectiveness remains elusive [15,51].

In BYOL, it is hypothesized that the presence of a predictor and a momentum-updated target encoder introduces representation drift, thus preventing convergence to trivial solutions [12]. SimSiam is said to rely on stop-gradient operations to restrict optimization paths [13]. However, these interpretations are based primarily on intuitive reasoning and empirical behavior, and lack formal theoretical generalization or proof [52,53].

This reveals a significant gap: despite the practical success of non-contrastive methods, the underlying principles that guarantee collapse avoidance are not yet well understood. Future research should seek to generalize these empirical mechanisms and derive theoretical stability conditions to inform principled architectural and training choices.

3.4.3. Summary and Remaining Challenges

In summary, complete collapse refers to a failure mode in which self-supervised learning models converge to constant vectors, effectively reducing the information content of learned representations to near zero. While architectural innovations such as asymmetric pathways, stop-gradient operations, and predictors have empirically demonstrated success in avoiding this outcome, the theoretical basis for their efficacy remains underdeveloped.

This theoretical shortfall limits the interpretability, reproducibility, and generalizability of current methods. Although complete collapse is conceptually well-defined, there remains a lack of theoretical clarity regarding the exact conditions under which collapse occurs and how architectural elements interact to prevent it. Addressing these gaps will be critical for advancing the theoretical foundations of self-supervised representation learning.

4. Dimensional Collapse: Causes, Examples and Mitigation Strategies

4.1. Underlying Mechanisms

Dimensional collapse refers to a phenomenon in self-supervised representation learning wherein learned representations, though nominally situated in a high-dimensional space, are in fact concentrated within a narrow subspace, resulting in a sharp reduction in the effective dimensionality of the representation space [30,54]. This collapse undermines representational diversity and leads to degraded performance on downstream tasks [55].

The core objective of representation learning is to extract shared essential features from input data while discarding irrelevant details or noise. In practice, this involves removing variability introduced by background information, environmental noise, or data augmentations. However, if this compression is too aggressive or if the model lacks explicit constraints for preserving information, even semantically relevant dimensions may be erroneously eliminated, which can result in a collapse into a low-dimensional subspace.

This phenomenon can be quantitatively diagnosed through analysis of the singular value spectrum or eigenvalue distribution of the covariance matrix. In collapse scenarios, most of the variance becomes concentrated in a few leading dimensions, while the remaining singular values approach zero.

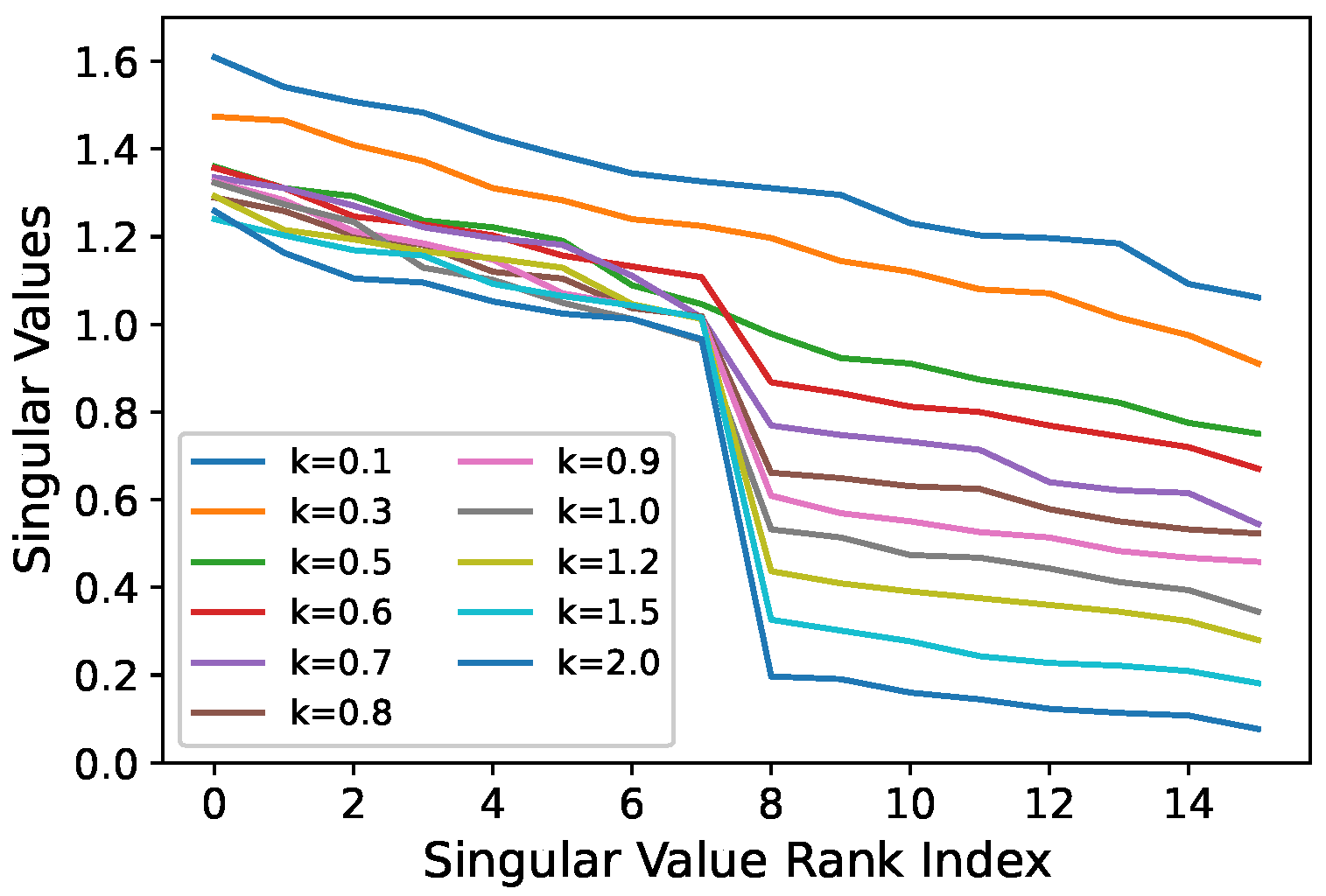
Recent findings further indicate that overly strong augmentations can induce collapse [14,56,57,58]. As shown in Figure 8, when the strength of augmentation increases, representations of different inputs may become indistinguishable in the embedding space, misleading the model into treating them as identical. This erodes the semantic resolution of the representation space, undermining the self-supervised learning objective of contrasting different views, and ultimately leads to collapse.

In such cases, the model effectively misinterprets important feature dimensions as noise, resulting in their removal. Therefore, dimensional collapse should not be seen merely as an optimization failure, but rather as a failure to balance information compression and retention, which is central to the stability and expressiveness of self-supervised learning.

4.2. Quantitative Metrics for Diagnosing Dimensional Collapse

Dimensional collapse reduces the effective dimensionality of representation spaces. To detect and analyze this phenomenon, it is important to measure the dispersion and utilization of embedding dimensions, with many metrics focusing on estimating the rank of the representations to quantitatively assess the severity of dimensional collapse [14,59,60,61]. This section introduces commonly used statistical metrics for such diagnostics.

4.2.1. Singular Value Spectrum

One of the most intuitive and widely used methods involves computing the covariance matrix of representation vectors and analyzing its eigenvalue spectrum. The magnitude of each eigenvalue reflects the variance along its corresponding axis [14].

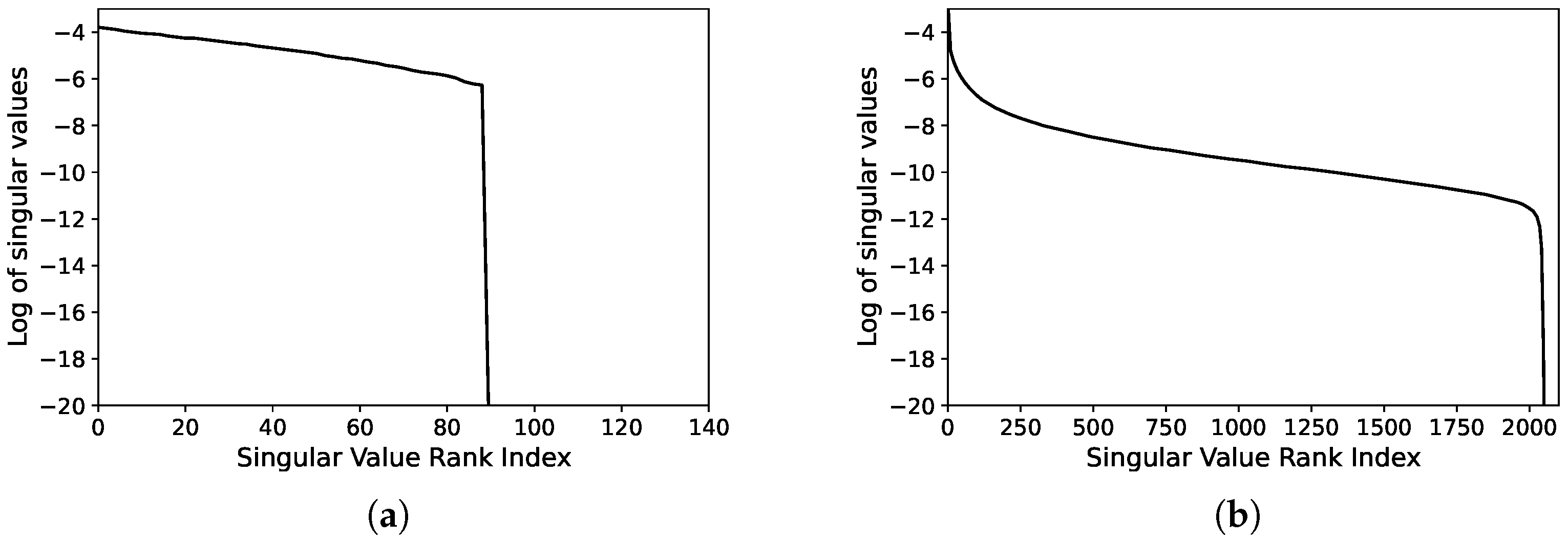
In cases of collapse, a few leading eigenvalues dominate the total variance, indicating that representations are concentrated in a low-dimensional subspace, as illustrated in Figure 9a. A sharp drop in the spectrum after a few components often signals that the model relies excessively on limited directions, implying dimensional collapse. In contrast, healthy representations show a relatively more gradual or flat eigenvalue decay, as shown in Figure 9b [61]. This pattern indicates that variance is more evenly distributed across dimensions, which in turn reflects a richer and more balanced representational geometry and helps maintain the expressive capacity of the learned embeddings.

Although this method is easily visualized via PCA or SVD, it is sensitive to subjective interpretation and may lack precise quantitative resolution [63].

4.2.2. Participation Ratio (PR)

The participation ratio (PR) estimates the number of effective dimensions used by the representations. It is computed from the eigenvalues ${\lambda }_i$ as follows [64,65]:

$$\mathrm{PR}={\displaystyle \frac{{\left({\sum }_i{\lambda }_i\right)}^2}{{\sum }_i{\lambda }_i^2}}.$$

(7)

A low PR indicates high variance concentration in a few dimensions (i.e., collapse), while a high PR implies dispersed information across multiple axes.

PR is particularly useful for cross-model comparison, representation evolution tracking, and collapse monitoring during training, thanks to its single-scalar output.

4.2.3. Effective Rank

Effective Rank measures the informational richness of the representation space based on the Shannon entropy of the normalized eigenvalue distribution [66]:

$$\mathrm{Effective}\mathrm{Rank}=exp\left(-\sum _i{p}_{i}log{p}_i\right),$$

(8)

where

$$p_i={\displaystyle \frac{{\lambda }_i}{{\sum }_j{\lambda }_j}}.$$

(9)

Uniform eigenvalue distributions lead to higher entropy and Effective Rank values, while concentration among few eigenvalues reduces both. This makes Effective Rank a robust indicator of dimensional usage and collapse resistance.

It is especially valuable for tracking structural changes in learned embeddings across different training stages.

4.2.4. Condition Number

The Condition Number is defined as the ratio of the largest to the smallest eigenvalue of the covariance matrix [67]:

$$\mathrm{Condition}\mathrm{Number}={\displaystyle \frac{{\lambda }_{\max }}{{\lambda }_{\min }}}.$$

(10)

Higher values suggest strong alignment along a principal axis, with minimal activation in other dimensions, which is a hallmark of dimensional collapse. Lower values indicate more balanced dispersion.

This metric reflects both numerical stability and representational balance, making it a practical tool for evaluating representation quality and collapse severity across learning conditions.

4.3. Structural Approaches to Preventing Dimensional Collapse

Dimensional collapse refers to the phenomenon in self-supervised representation learning where learned representations become excessively concentrated within a narrow subspace, leading to a sharp reduction in the effective dimensionality of the embedding space. This collapse compromises the expressiveness of the learned features and significantly impairs the model’s ability to generalize to downstream tasks.

Unlike complete collapse, dimensional collapse is more subtle and difficult to detect. Although the training loss converges to low values and the model may appear to produce diverse outputs, the representations often occupy only a small subset of the full embedding space. As a result, this latent degeneration can easily go unnoticed, despite having a considerable negative impact on model performance.

In response, recent studies have shifted their focus from merely diagnosing dimensional collapse to developing structural solutions and loss function designs aimed at preventing or mitigating it. These include the introduction of explicit or implicit constraints to preserve representational diversity and maintain effective dimensionality, establishing such mechanisms as core components for stable and generalizable representation learning.

4.3.1. VICReg: Loss-Level Structural Regularization Against Dimensional Collapse

Variance-invariance-covariance regularization (VICReg) is recognized as one of the earliest models to explicitly incorporate structural loss terms that preserve representational diversity in self-supervised learning [15]. By relying solely on loss function design without contrastive structures or asymmetric architectures, VICReg demonstrates that dimensional collapse can be mitigated through regularization alone.

As illustrated in Figure 10, VICReg takes two different augmented views of the same image, encodes them into representations $z_1$ and $z_2$, and applies a composite loss consisting of three components:

$${\mathcal{L}}_{\mathrm{VICReg}}={\lambda }_{\mathrm{inv}}{\mathcal{L}}_{\mathrm{inv}}+{\lambda }_{\mathrm{var}}{\mathcal{L}}_{\mathrm{var}}+{\lambda }_{\mathrm{cov}}{\mathcal{L}}_{\mathrm{cov}},$$

(11)

where ${\lambda }_{\mathrm{inv}}$ is the invariance loss, which enforces similarity between representations of different views, ${\lambda }_{\mathrm{var}}$ is the variance loss, encouraging each embedding dimension to maintain non-trivial variance and thereby preventing dimensional collapse, and ${\mathcal{L}}_{\mathrm{cov}}$ is the covariance loss, which minimizes cross-dimensional correlations to reduce redundancy across dimensions.

Empirical results show that VICReg achieves superior performance on Participation Ratio, Effective Rank, and spectrum flatness, outperforming previous methods. These results confirm that explicit regularization can maintain diversity and structural integrity in the representation space, offering an effective means of addressing dimensional collapse.

Importantly, VICReg has shifted the paradigm by demonstrating that contrastive loss is not a prerequisite for effective self-supervised representation learning. It has inspired a line of follow-up studies that seek to prevent collapse via carefully designed loss functions, highlighting the central role of regularization in stable and expressive feature learning.

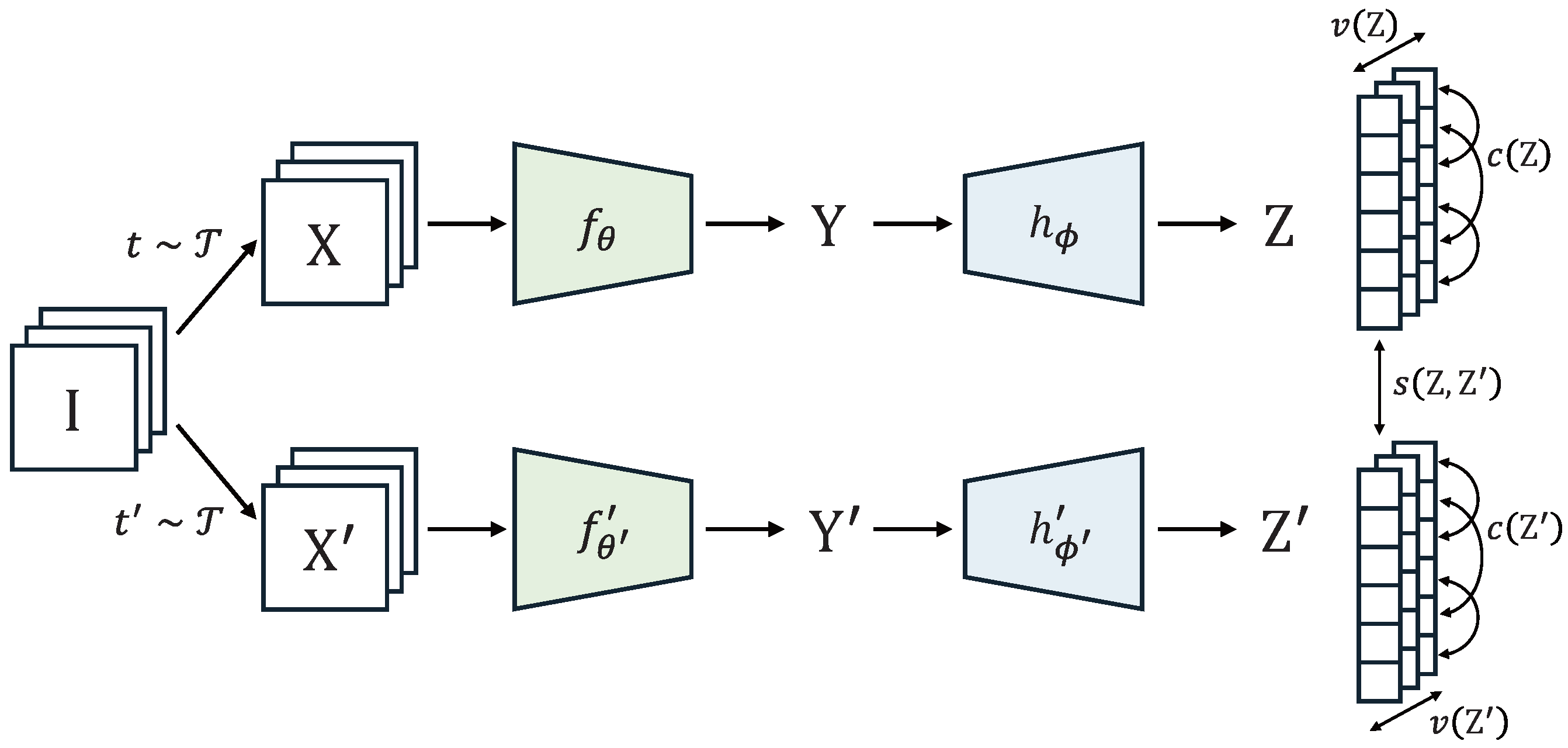
4.3.2. ADM: Controlling Dimensional Collapse via Statistical Independence

Adversarial dependence minimization (ADM) is a novel self-supervised representation learning framework that aims to reduce inter-dimensional redundancy and promote statistical independence among representation components, as illustrated in Figure 11 [68]. Traditional representation learning methods have primarily focused on removing linear correlations using techniques such as principal component analysis (PCA) or feature decorrelation. In contrast, ADM addresses more general forms of statistical dependence.

However, these approaches fall short in addressing nonlinear and higher-order dependencies that often persist among latent features. A classic example involves three random variables, $x_1$, $x_2$, and $x_3$, that are pairwise independent but jointly dependent, a structure that is invisible to conventional measures such as correlation coefficients or mutual information [69]. Figure 12 illustrates this phenomenon, showing that even when variables appear orthogonal in pairwise views, they may still exhibit nonlinear, multivariate dependence when jointly analyzed. This highlights the limitations of traditional dependency metrics and motivates more expressive mechanisms for dependency minimization. To address these limitations, ADM employs an adversarial training strategy between an encoder and a set of predictors, explicitly targeting nonlinear, multivariate dependencies that contribute to dimensional collapse through representational redundancy.

The ADM architecture consists of an encoder $f_{\theta }\left(x\right)$, which maps input data into low-dimensional representations z, and a set of lightweight MLP-based predictors $h_{{\varphi }_i}\left(z_{-i}\right)$, each trained to predict one dimension $z_i$ from the remaining dimensions $z_{-i}$. These two components engage in an adversarial game: while the predictors aim to exploit existing dependencies to minimize prediction error, the encoder learns to maximize this error by erasing dependencies, thus generating statistically independent latent features. This learning mechanism surpasses traditional linear decorrelation by minimizing the predictability between dimensions, which is a more robust proxy for statistical independence.

To ensure training stability and prevent loss escalation due to growing representation magnitudes, ADM applies per-dimension standardization, enforcing zero mean and unit variance for each component of z. Over the course of training, the predictors gradually converge to predicting only the mean zero, signaling the absence of exploitable dependencies in the learned features. Furthermore, recognizing that complete independence may not always be optimal, particularly in certain application scenarios, ADM supports an optional margin loss. This constraint limits the predictor’s reconstruction error to a maximum threshold, enabling a controlled trade-off between dependency reduction and information retention.

Experimental results demonstrate that ADM effectively suppresses representational redundancy, not only reducing statistical dependencies but also improving metrics such as participation ratio and effective rank, which reflect higher-dimensional feature utilization. These advantages make ADM particularly suitable for self-supervised learning regimes, where dimensional collapse is prevalent, positioning it as a structurally grounded approach for improving generalizability and interpretability in learned representations.

4.3.3. FeDi: Information-Theoretic Strategy for Preventing Dimensional Collapse

Feature disentanglement (FeDi) introduces an information-theoretic learning framework to mitigate inter-dimensional redundancy and collapse in self-supervised learning [70]. Unlike conventional contrastive or redundancy reduction approaches, FeDi explicitly addresses the collapse of individual embedding dimensions that occurs as the dimensionality of the representation increases.

To this end, FeDi jointly optimizes two key objectives: alignment and disentanglement. The overall loss function is defined as follows:

$${\mathcal{L}}_{\mathrm{FeDi}}={\mathcal{L}}_{\mathrm{align}}+\lambda {\mathcal{L}}_{\mathrm{dis}},$$

(12)

where ${\mathcal{L}}_{\mathrm{align}}$ enforces the similarity between the corresponding dimensions of two augmented views of the same image, encouraging them to remain close in the embedding space, and ${\mathcal{L}}_{\mathrm{dis}}$ reduces redundancy by minimizing the absolute sum of the off-diagonal elements in the cross-correlation matrix, thus approximating mutual information minimization between dimensions.

Instead of directly estimating mutual information, which can be computationally expensive, FeDi leverages a correlation-based proxy to efficiently promote feature disentanglement. To further improve the disentanglement process, a hardness-aware weighting strategy is applied. This mechanism assigns higher penalties to difficult negative samples, promoting separation among highly entangled dimensions and suppressing collapse-prone configurations.

FeDi maintains inter-dimensional independence even as the embedding dimensionality increases. This stability is quantitatively validated via the Disentanglement Score, defined as the sum of the absolute values of off-diagonal entries in the cross-correlation matrix. The score serves as a direct measure of statistical independence across embedding dimensions.

By carefully balancing the alignment and disentanglement objectives and incorporating hardness-aware regulation, FeDi provides a robust solution to the problem of dimensional collapse. Unlike previous methods that often degrade under high-dimensional conditions, FeDi scales effectively, preserving both the diversity and structural stability of learned representations.

In this way, FeDi constitutes a substantial advancement toward dimensionally resilient self-supervised learning, successfully addressing long-standing challenges associated with representation redundancy and collapse.

4.3.4. DirectCLR: Mitigating Collapse via Subvector-Based Contrastive Learning

DirectCLR introduces a contrastive learning strategy that circumvents the use of a projection head, aiming to maintain representational diversity without requiring architectural modifications [14]. In conventional contrastive frameworks, a projection head is typically appended to the encoder, and the contrastive loss is applied in the projected space. While this setup is effective in mitigating representational collapse, it also causes the loss to operate uniformly across the entire representation vector. This often results in gradient concentration and reduced feature diversity.

To address this issue, DirectCLR applies the contrastive loss only to a subset of the representation dimensions. This strategy is called subvector-based contrastive learning. As illustrated in Figure 13, this approach involves computing the InfoNCE loss using only a partial subvector. Given a representation $r\in {\mathbb{R}}^D$, only the first $d_0$ dimensions are utilized for the loss computation, while the remaining dimensions are excluded from this operation [33]. Despite this partial usage, the encoder is trained end-to-end. However, the gradient flow is localized to the selected subvector, thereby allowing the unused dimensions to evolve more freely and capture diverse features.

This design offers several advantages. First, it reduces gradient concentration across dimensions, promoting greater independence among features. Second, it encourages dispersion of information throughout the embedding space, thereby preventing uniform convergence. Third, it introduces algorithmic flexibility by enabling the selective application of contrastive loss to targeted subspaces of the representation.

In summary, DirectCLR presents a structurally minimal yet effective approach to collapse mitigation. By constraining the domain in which the contrastive loss operates, it provides fine-grained control over the learning dynamics without altering the encoder architecture.

4.4. Theoretical Understanding and Open Challenges of Dimensional Collapse

Dimensional collapse refers to the phenomenon in which learned embeddings become excessively concentrated within a low-dimensional subspace, leading to a sharp reduction in the effective dimensionality of the representation [14]. Although this behavior is widely observed in self-supervised learning, there currently exists no rigorous mathematical definition or universally accepted criterion for identifying such collapse.

Several studies have proposed using the eigenvalue distribution of the covariance matrix or the decline in effective rank as quantitative proxies for dimensional collapse [71,72]. However, such statistical metrics often fall short of capturing the structural or semantic quality of learned representations. For example, maximizing variance across dimensions may numerically increase the spread of embeddings, but it does not ensure that the resulting dimensions encode semantically meaningful or task-relevant information. This reveals a critical gap between statistical dispersion and representational utility, highlighting the absence of principled criteria for diagnosing or preventing collapse in a theoretically grounded manner.

In practice, many recent approaches aim to mitigate collapse by incorporating variance preservation or redundancy reduction terms into the loss function [15,73,74]. While these techniques have demonstrated empirical success, they often lack grounding in formal theoretical mechanisms. Rather than addressing the root cause of collapse, such methods typically seek to optimize surrogate numeric metrics. For example, enforcing a minimum standard deviation across dimensions may increase embedding spread, but it does not guarantee that the retained dimensions encode semantically meaningful or useful information.

Consequently, although these regularization strategies influence statistical properties, they fail to provide insight into the structural composition or semantic utility of the learned features. Most current analyses remain focused on optimization dynamics and loss-based formulations, with relatively little attention given to the geometric or information-theoretic nature of the representation space.

A particularly critical gap exists in the absence of a theoretical linkage between representational diversity and downstream utility. Namely, whether well-dispersed embeddings inherently correspond to more meaningful and generalizable features.

In summary, despite dimensional collapse being a central failure mode in self-supervised learning, our theoretical understanding of the phenomenon remains limited. Key challenges include the lack of a formal definition of collapse, the conceptual constraints of existing loss-based solutions, insufficient geometric and information-theoretic analysis, and the ambiguity in interpreting diagnostic metrics. Addressing these limitations requires a shift from heuristic prevention toward the development of foundational theoretical frameworks that can quantify and explain the structure, stability, and expressiveness of learned representations.

5. Discussion and Future Research Directions

This study categorizes representation collapse in self-supervised learning into two main types: complete collapse and dimensional collapse. For each, we analyze their causal mechanisms, representative factors, and structural/functional mitigation strategies, which are summarized in

Table 1. Summary of complete collapse and dimensional collapse in self-supervised learning.

Category	Complete Collapse	Dimensional Collapse
Definition	All representations (embedding vector) converge to a single point	Representations use only a subset of dimensions
Causes	• Encoder learns trivial solution • Lack of contrastive pairs • Strong augmentation	• Excessive invariance pressure • Loss functions ignoring isotropy/diversity • Representation redundancy
Indicator	• Near-zero variance across features	• Skewed Singular value spectrum • High Condition Number • Effective Rank ≪ Total Rank
Prevention	• Introduce negative samples • Asymmetry of the network architecture • Variance term	• Feature decorrelation • Variance regularization • Orthogonality constraints • Variance + Covariance term

. While the awareness of dimensional collapse is growing, its theoretical and empirical understanding remains limited. Therefore, this taxonomy and diagnostic framework provide a foundation for future research directions.

1.

Theoretical Definition of Collapse. Current approaches focus mainly on loss function design and optimization behavior, with limited attention to the geometric or statistical structure of the representation space [75]. Particularly in the case of dimensional collapse, training may appear successful despite informational distortion through subspace concentration.

While metrics such as Participation Ratio and Effective Rank are commonly used, there remains no consensus on what constitutes meaningful representational diversity. The lack of a theoretical framework connecting representational structure and utility is a critical gap.

Future research should aim to redefine collapse in terms of representational structure, effective information encoding, and geometric distribution. Especially in self-supervised settings targeting task-independent representations, formalizing the notion of representational quality is essential.

2.

Toward a Unified Framework for Collapse Mitigation. These strategies are summarized in

Table 2. Comparison of representation learning models and their strategies to prevent representation collapse.

Model	Type	Collapse Prevention Strategy	Loss Function	Architecture Feature	Notable Limitation
SimCLR	Contrastive	Positive/Negative pair discrimination	NT-Xent	Uses Projection Head	Requires large batch size
MoCo	Contrastive	Queue + Momentum encoder	InfoNCE	Memory bank structure	Structural complexity
BYOL	Non-Contrastive	Predictor + Stop-Gradient + EMA	Cosine Similarity based L2 Loss	Asymmetric + EMA target	No theoretical guarantee
SimSiam	Non-Contrastive	Predictor + Stop-Gradient	$\mathcal{L}=(D(p_1,\mathrm{stopgrad}\left(z_2\right))+D(p_2,\mathrm{stopgrad}\left(z_1\right)))/2$	Asymmetric + Stop Gradient	More vulnerable to collapse
SwAV	Non-Contrastive/Clustering	Clustering + Entropy maximization	Prototype-based Cross-Entropy Loss	Uses prototypes	Complex pre-training
VICReg	Non-Contrastive	Invariance + Variance + Covariance Regularization	$\mathcal{L}={\lambda }_{\mathrm{inv}}{\mathcal{L}}_{\mathrm{inv}}+{\lambda }_{\mathrm{var}}{\mathcal{L}}_{\mathrm{var}}+{\lambda }_{\mathrm{cov}}{\mathcal{L}}_{\mathrm{cov}}$	Three-branch regularization	Risk of over-regularization
ADM	Non-Contrastive	Adversarial dependence minimization	Adversarial Game-based Loss	Predictor vs Encoder game	Training instability with high dependency
FeDi	Info-Theoretic	Alignment + Disentanglement	Correlation-based alignment + disentanglement loss	MLP-based dual branches	Mutual info proxy needed
DirectCLR	Contrastive	Subvector-based contrastive learning	InfoNCE	Selective subvector gradient flow	Limited information dispersion

, which provides a comparative overview of representative models, their collapse prevention mechanisms, loss functions, architectural features, and notable limitations. Existing solutions, such as VICReg (variance preservation), FeDi (mutual information reduction), DirectCLR (subvector alignment), and ADM (adversarial independence), offer isolated, model-specific strategies. However, these remain fragmented, lacking a shared mathematical basis or unifying evaluation criteria.

This hinders the generalization or cross-comparison of collapse prevention mechanisms. A meta-framework grounded in representation theory or learning dynamics is required to consolidate these techniques and provide principled design criteria for future architectures.

3.

Modal Sensitivity of Collapse Phenomena. While both complete and dimensional collapse degrade learning, their sensitivity to data modality appears to differ significantly. Complete collapse leads to trivial representations regardless of modality, whereas dimensional collapse may manifest more readily in domains with inherently low-dimensional semantics (e.g., text or signal data). In contrast, high-dimensional modalities like images may be more resilient due to their richer feature diversity.

However, current studies focus predominantly on single-modality settings. Future research should conduct systematic, cross-modal analyses to better understand how modality influences the onset, severity, and impact of different collapse types.

4.

Linking Representational Diversity and Utility. Although preventing collapse often aims to maximize representational diversity, diversity alone does not guarantee usefulness. Even well-distributed embeddings may fail to encode signals that matter for downstream tasks.

Future research should investigate not only variance-based metrics, but also task alignment indicators. For instance, correlating diversity scores with performance on downstream tasks, or developing new metrics capturing the interplay between dispersion and utility, could lead to more actionable diagnostics.

5.

Reinterpreting Collapse: Intentional Feature Concentration. Lastly, it is worth questioning whether all forms of collapse are undesirable. In some cases, intentional collapse, where representations concentrate on task-relevant features, may enhance generalization.

From this perspective, collapse is not necessarily a failure, but rather a form of goal-oriented representation compression. Future work could aim to design systems that strategically balance information compression with structural diversity, treating collapse as a potentially beneficial phenomenon under specific conditions.

In conclusion, collapse is not merely a limitation but a lens through which the structural principles of representation learning can be re-examined. Collapse is not confined to contrastive learning but consistently emerges as a common challenge across diverse self-supervised frameworks, including non-contrastive, clustering-based, and adversarial approaches. This highlights collapse as a framework-agnostic limitation rather than a method-specific artifact. If future research can define and balance representation diversity and semantic utility, this will offer a foundation for more robust, interpretable, and generalizable self-supervised learning.

6. Conclusions

Unsupervised representation learning has emerged as a powerful paradigm for learning meaningful features without labels. However, it remains structurally vulnerable to representation collapse, wherein the learned features lose diversity and informativeness. This paper has addressed this issue by categorizing collapse into two primary types, complete collapse and dimensional collapse, and comprehensively analyzing their causal mechanisms, representative methods, mitigation strategies, and theoretical implications.

Complete collapse denotes the degeneration of representations into a single constant vector, a situation that has largely been alleviated in both contrastive and non-contrastive learning through architectural innovations. Dimensional collapse, on the other hand, emerges when representations become overly concentrated in a restricted low-dimensional subspace. While their manifestations differ, both cases ultimately signal the breakdown of meaningful representation learning. Consequently, direct empirical demonstrations of collapse causing degraded downstream performance remain scarce. Once collapse takes place, whether in its complete or dimensional form, the learned representations themselves lose validity, making further evaluation irrelevant. Our contribution is to address this fundamental limitation. Instead of waiting for collapse to appear as performance degradation in downstream tasks, we systematically identify the conditions under which collapse can occur and stress the importance of preventing it. By articulating these potential failure modes in advance and underscoring the necessity of their resolution, we aim to provide a substantive and enduring scholarly contribution.

Recent approaches following VICReg, such as variance regularization, whitening, adversarial disentanglement, and feature decorrelation, reflect a shift from avoiding collapse to explicitly structuring the representation space. These developments emphasize the need to understand and manipulate representation geometry directly, and they highlight the critical gap between statistical diversity and task-relevant utility.

Nevertheless, key challenges remain unresolved: the lack of a formal definition of collapse, the ambiguous interpretation of evaluation metrics, and the absence of a theoretical framework linking representational diversity to downstream usefulness. These limitations point to a deeper issue: the absence of a principled foundation for designing, interpreting, and measuring the structure of learned representations.

Future research should reposition representation collapse not merely as a peripheral technical failure but as a central and enduring theoretical challenge in representation learning. Despite the increasing awareness of collapse phenomena, current efforts remain largely empirical, lacking formal principles that define, prevent, or guarantee robustness against such failures. To address this, a more rigorous foundation is needed, one that integrates geometric, statistical, and task-aligned perspectives to better characterize the structure and function of learned representations.

In particular, it is crucial to move beyond heuristic or architecture-specific solutions, and toward the development of theoretical criteria for representational diversity. This includes defining meaningful diversity in a mathematically principled manner and deriving provable guarantees under which representation collapse can be avoided or bounded. Such theoretical guarantees would not only deepen our understanding of how information is encoded but also serve as a basis for building reliable and generalizable self-supervised systems across tasks, modalities, and learning conditions.

Ultimately, formalizing the principles that underlie collapse and connecting them to downstream utility will enable the field to transition from reactive diagnosis to proactive design, fostering more robust, interpretable, and theoretically grounded representation learning.

We hope this work serves as a foundational step toward a unified understanding of representation collapse and provides a theoretical grounding for future research in the design of more robust, expressive, and generalizable self-supervised learning systems.