Development of an Optimal Novel Cascaded 1+TDFλ/PIλDμ Controller for Frequency Management in a Triple-Area Power Grid Considering Nonlinearities and PV/Wind Integration
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.2.1. Power Grid Configurations
1.2.2. Controller Classification
1.2.3. Types of Optimization Approaches
1.3. Motivations
1.4. Primary Contributions and Paper Organization
- i.
- Developing a novel controller design called 1+TDFλ/PIλDμ for frequency and tie-line power regulation in a triple-area power system.
- ii.
- An evolutionary socio-economic optimization algorithm, known as the divine religions algorithm (DRA) [51], is employed for the first time to optimize the parameters of the proposed controller in the context of LFC.
- iii.
- iv.
- v.
- Validating the superiority of the proposed 1+TDFλ/PIλDμ controller over the other compared ones under realistic conditions involving system nonlinearities, stochastic load disturbances, and high-penetration stochastic RESs such as PV and wind power.
- vi.
- Validating the robustness of the presented 1+TDFλ/PIλDμ controller by testing its performance under significant variations in system parameters, demonstrating its adaptability to practical power system uncertainties.
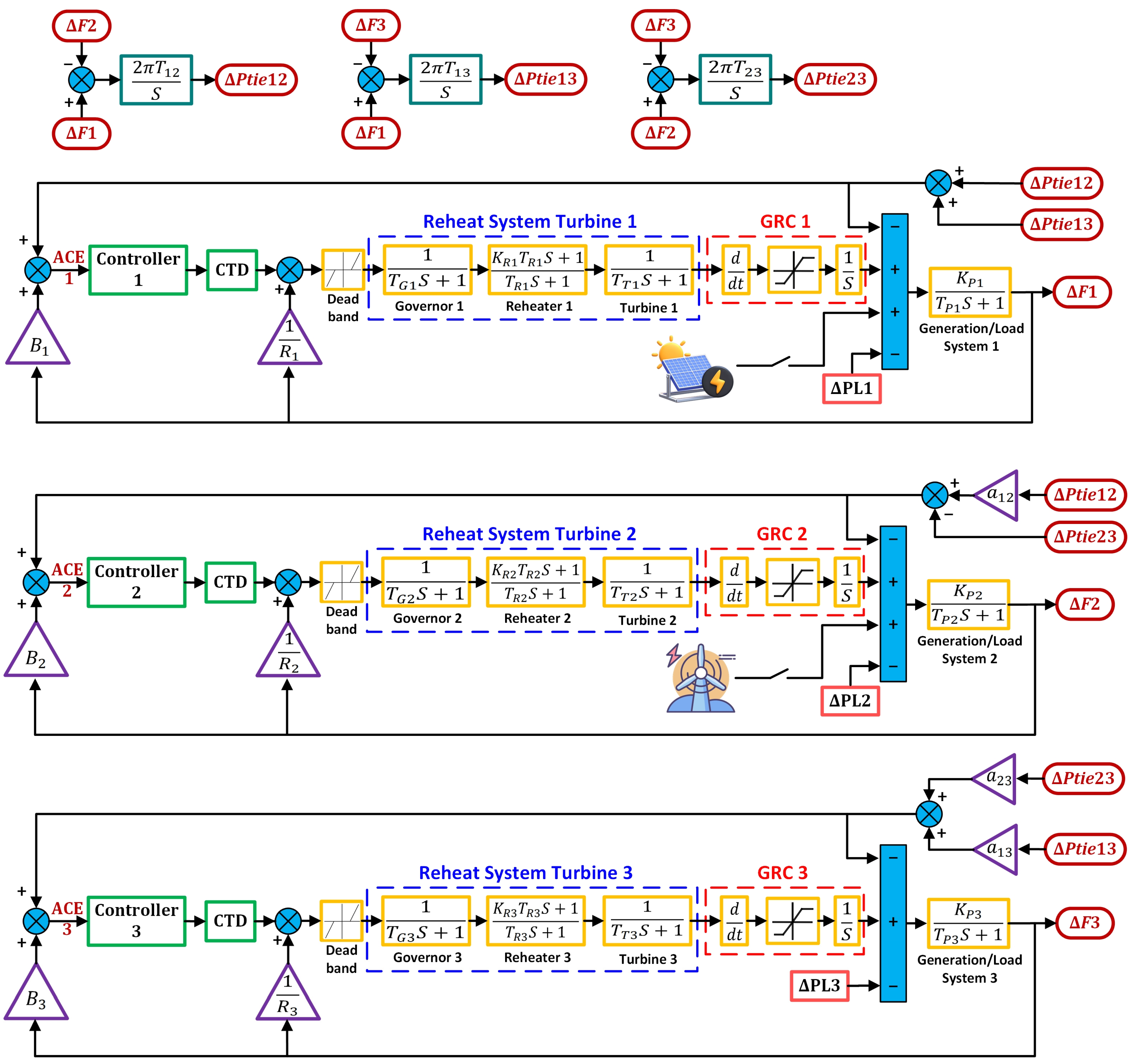
2. The Investigated Triple-Area System Model
- 1.
- Governor Dynamics: , , represent the time constants of the governors in Areas 1, 2, and 3, respectively. For this study, their values are taken as 0.08 s, 0.06 s, and 0.07 s.
- 2.
- Turbine Dynamics: , , denote the turbine time constants. The values used in this study are 0.4 s, 0.44 s, and 0.3 s, respectively.
- 3.
- Reheat Turbine Parameters: , , are the gains, and , , are the time constants of the reheat turbine components. The gains are set to 0.6, 0.7, and 0.5, while the corresponding time constants are 12 s, 14 s, and 10 s, respectively.
- 4.
- Generation and Load Dynamics: , , and , , are the time constants and gains associated with the generation-load subsystems in each area. The time constants are taken as 20 s, 22 s, and 24 s, while the gains are set to 105 Hz/P.U MW, 100 Hz/P.U MW, and 120 Hz/P.U MW, respectively.
- ➢
- Additional control and system interconnection parameters include the following:
- Frequency Bias Factors: , , , which influence the sensitivity of each area’s frequency control mechanism. Their values are taken as 0.3483 P.U MW/Hz, 0.3827 P.U MW/Hz, and 0.3692 P.U MW/Hz, respectively.
- Droop Settings: , , , which determine the governor response to frequency deviations. The respective values used are 3 Hz/P.U MW, 2.73 Hz/P.U MW, and 2.82 Hz/P.U MW.
- Tie-Line Synchronizing Coefficients: , , , representing the coupling strength between the areas through tie-lines. Their values are taken as 0.2 P.U MW/rad, 0.3 P.U MW/rad, and 0.44 P.U MW/rad, respectively.
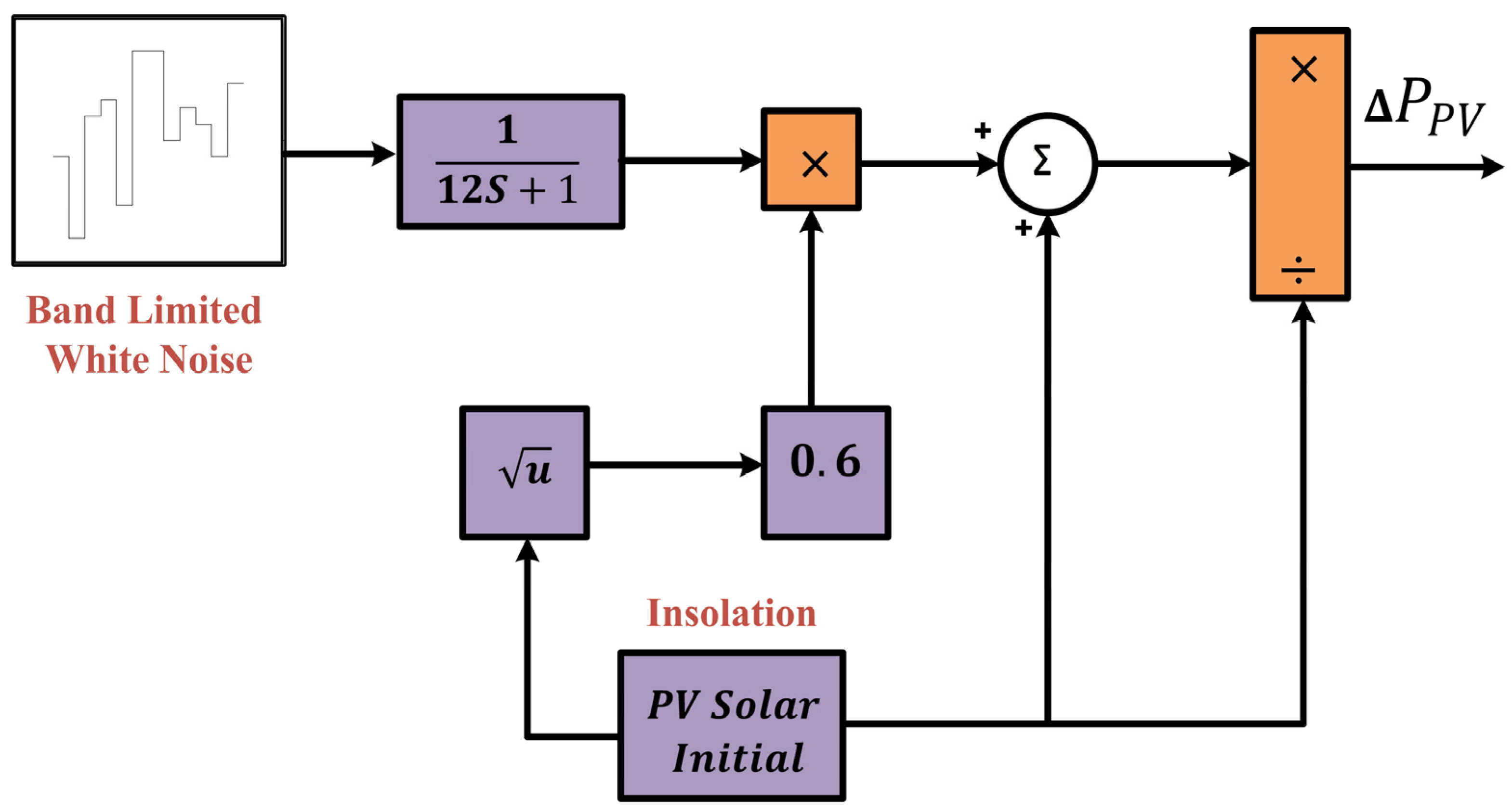
2.1. Modelling of PV Unit
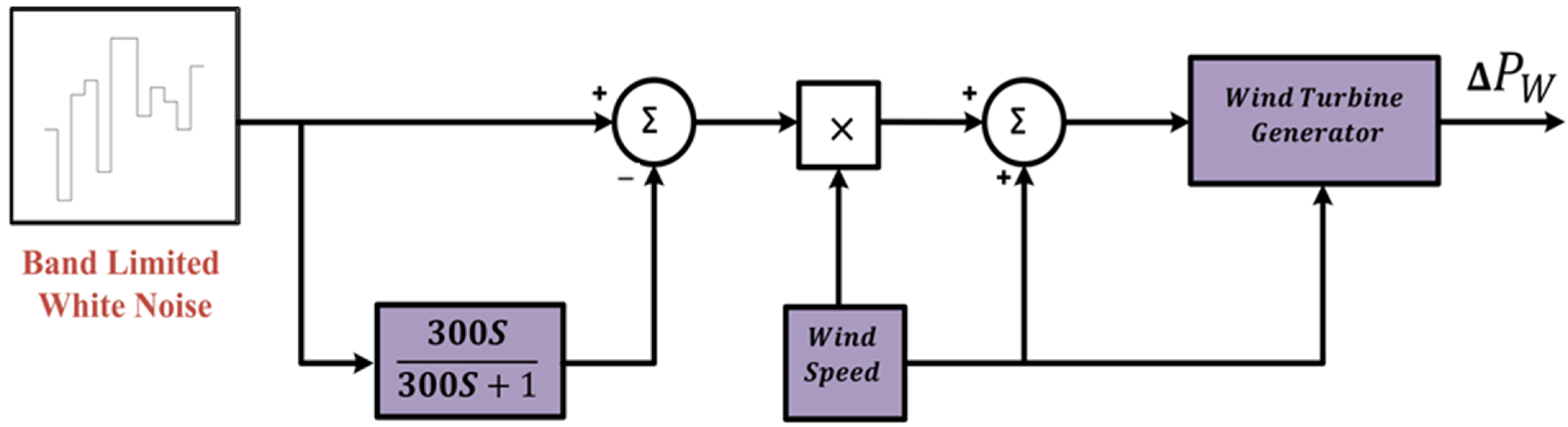
2.2. Modelling of Wind Unit
3. Problem Formulation and Mathematical Representations of Controllers and DRA
3.1. Explanation of the Fitness Function (FF)
3.2. The Examined Controllers’ Designs
3.2.1. PID Controller
3.2.2. FOPID Controller
3.2.3. 2 DOF-PID Controller
3.2.4. 2 DOF-TIDμ Controller
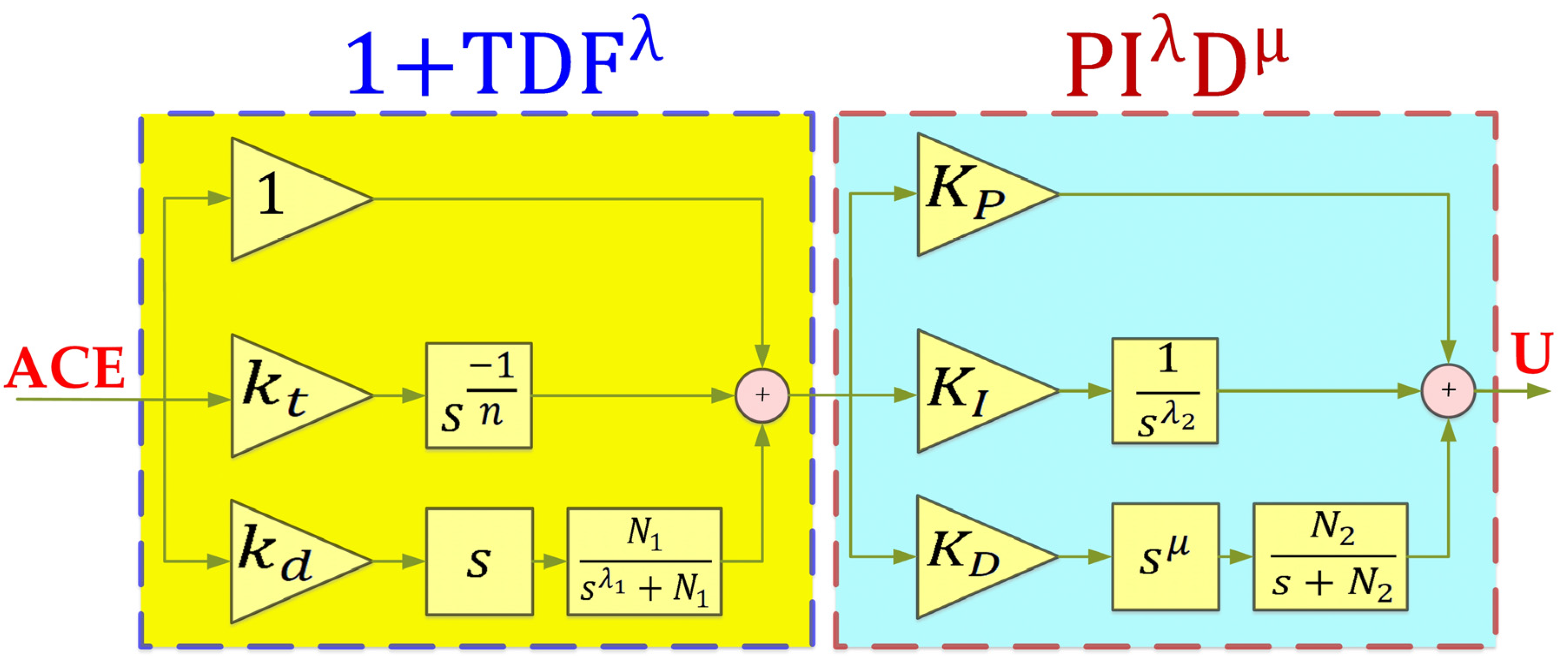
3.2.5. 1+TDFλ/PIλDμ Controller (Proposed)
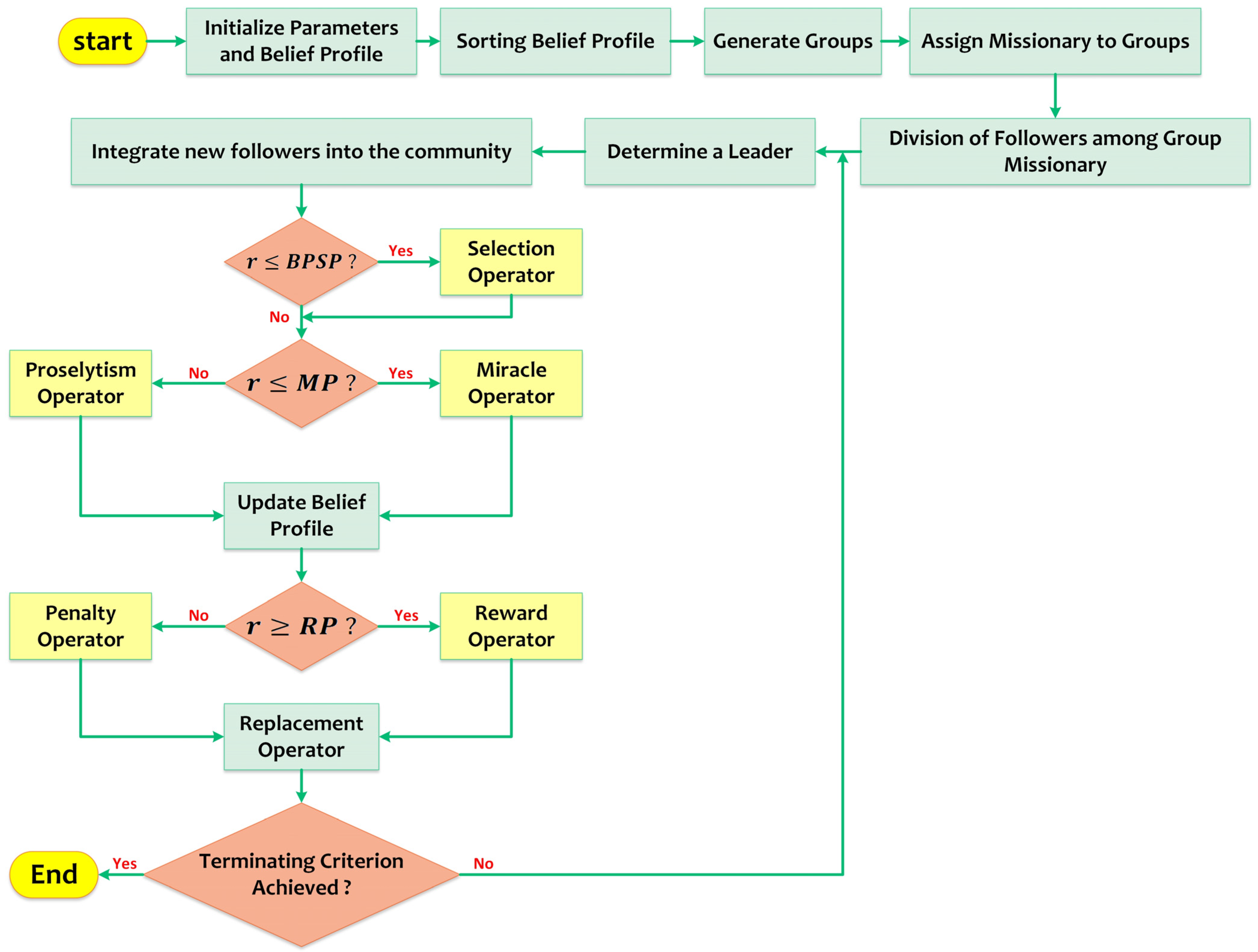
3.3. Divine Religions Algorithm (DRA)
3.4. DRA Procedure Modelling
3.5. Sending Believers to Different Populations
- BPSP: Belief Profile Selection Probability.
- MP: Miracle Probability.
- RP: Reward/Penalty Probability.
- NI: Number of Iterations.
3.6. Finding the Most Appreciated Follower
3.7. Inviting a Fresh Follower
- Selection Operator: A prominent follower in the same community is identified. One belief index is arbitrarily selected:
- Miracles Operator: With a probability governed by the miracle probability (MP), a new follower may be added with arbitrarily assigned beliefs to diversify the community and boost its overall performance.
- Proselytism Operator: This reflects a missionary’s influence, guiding new followers to align with existing beliefs. To facilitate this process, a randomly created value between zero and unity is compared with a predefined MP threshold. Based on this comparison, the selection of followers is determined using a specific evaluation formula for the miracles and proselytism mechanisms:
3.8. A Prospective Follower Fitness
3.9. Creating the Operator of Reward or Penalty
- If , the reward is applied.
- If , the penalty is applied.
3.10. Modifying a Follower’s Faith Status
3.11. Creating the Operator of Replacement
3.12. Terminating Criterion
| Algorithm 1. DRA Pseudocode |
| Inputs: |
| → Number of communities |
| → Total number of followers |
| → Set of all communities |
| → Set of all followers |
| → Number of belief attributes per follower |
| Output: |
| → Optimal belief vector of the society |
| Initialize: |
| → Iteration counter |
| Repeat |
| // Step 1: Distribute Followers into Communities |
| For ( to do |
| Initialize → Belief matrix of followers in community (Equation (20)) |
| Initialize → Fitness matrix of community (Equation (23)) |
| End For |
| // Step 2: Society-Wide Initialization |
| Initialize → Combined belief matrix of all communities (Equation (21)) |
| Initialize → Combined fitness matrix of all communities (Equation (24)) |
| // Step 3: Identify Most Prominent Follower |
| Find → Follower with the best fitness in society (Equation (26)) |
| Set → Community index of |
| Set → Belief profile of (Equation (27)) |
| // Step 4: Belief Update Based on Probability |
| Set → Random number in |
| If then |
| // Selection Operator |
| → Randomly selected attribute index (Equation (28)) |
| // Copy the -th belief from to (Equation (29)) |
| End If |
| If then |
| // Miracles Operator |
| → Integrate a fresh follower with arbitrary belief values into the community (Equation (26)) |
| // Proselytism Operator |
| Substitute one belief attribute in leader’s vector with that of an arbitrary follower (Equation (27)) |
| End If |
| // Step 5: Evaluate New Follower |
| Compute → Fitness of new follower (Equation (33)) |
| // Step 6: Reward Operator |
| Set → Random number in |
| If then |
| choose an attribute index () arbitrarily (Equation (34)) |
| End If |
| // Step 7: Update Weakest Follower |
| Set → Index of weakest follower in community (Equation (35)) |
| Set → Belief profile of weakest follower (Equation (36)) |
| If then |
| // Swap beliefs (Equation (37)) |
| End If |
| // Step 8: Replacement with the Most Prominent Follower |
| Set → Index of most prominent follower in (Equation (38)) |
| Set → Belief profile of (Equation (39)) |
| If then |
| // Swap beliefs (Equation (40)) |
| End If |
| Until |
| Return |
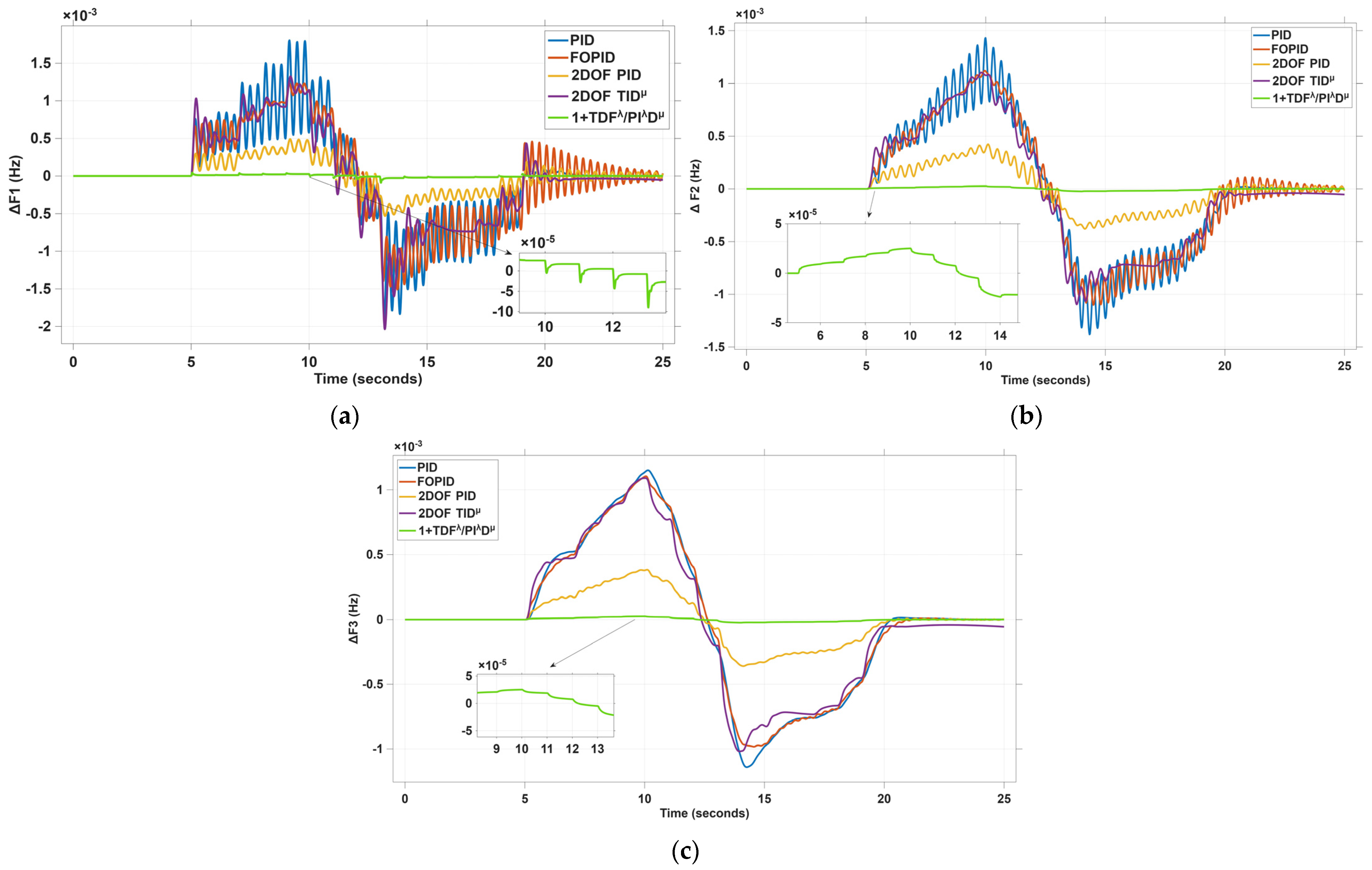
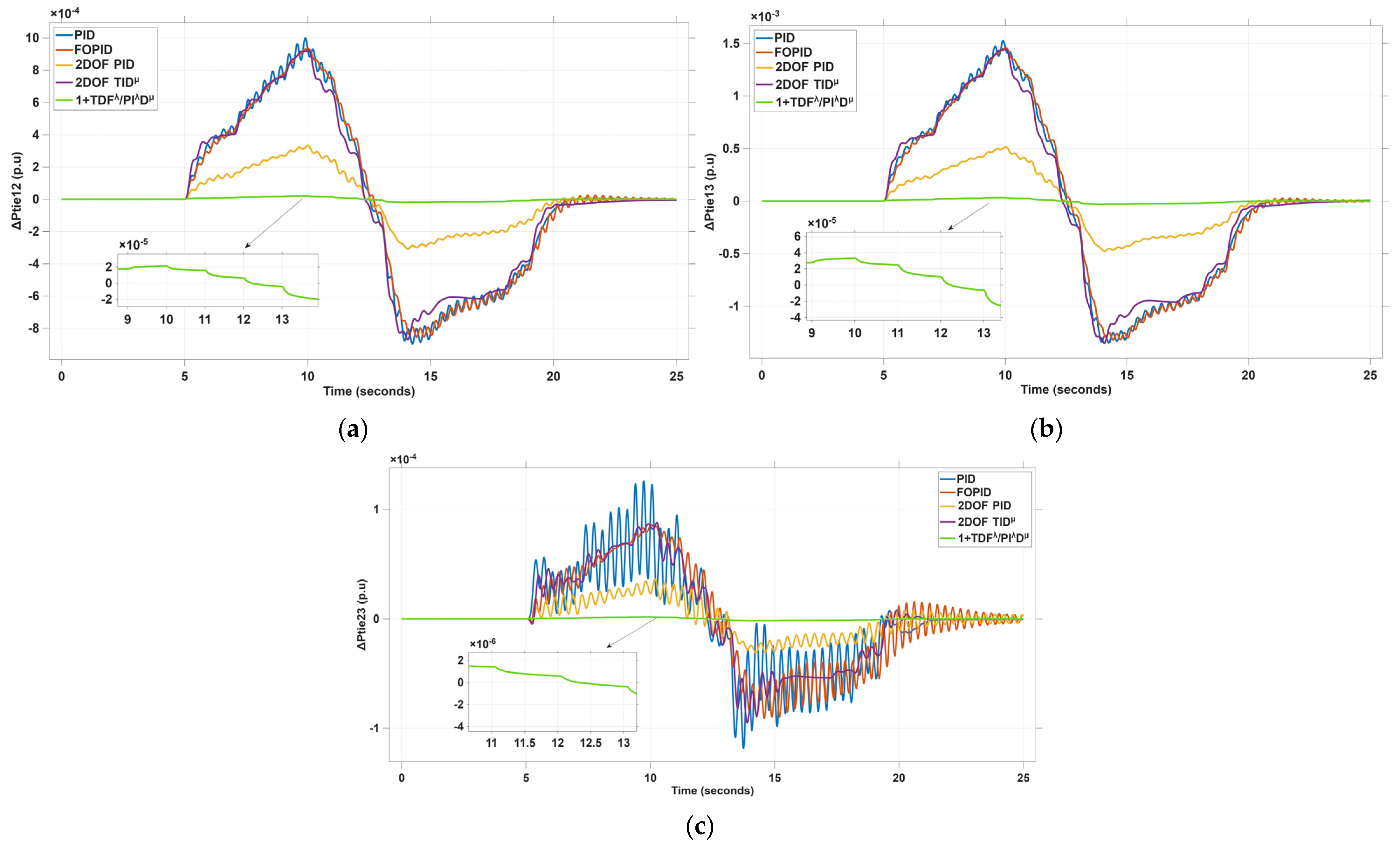
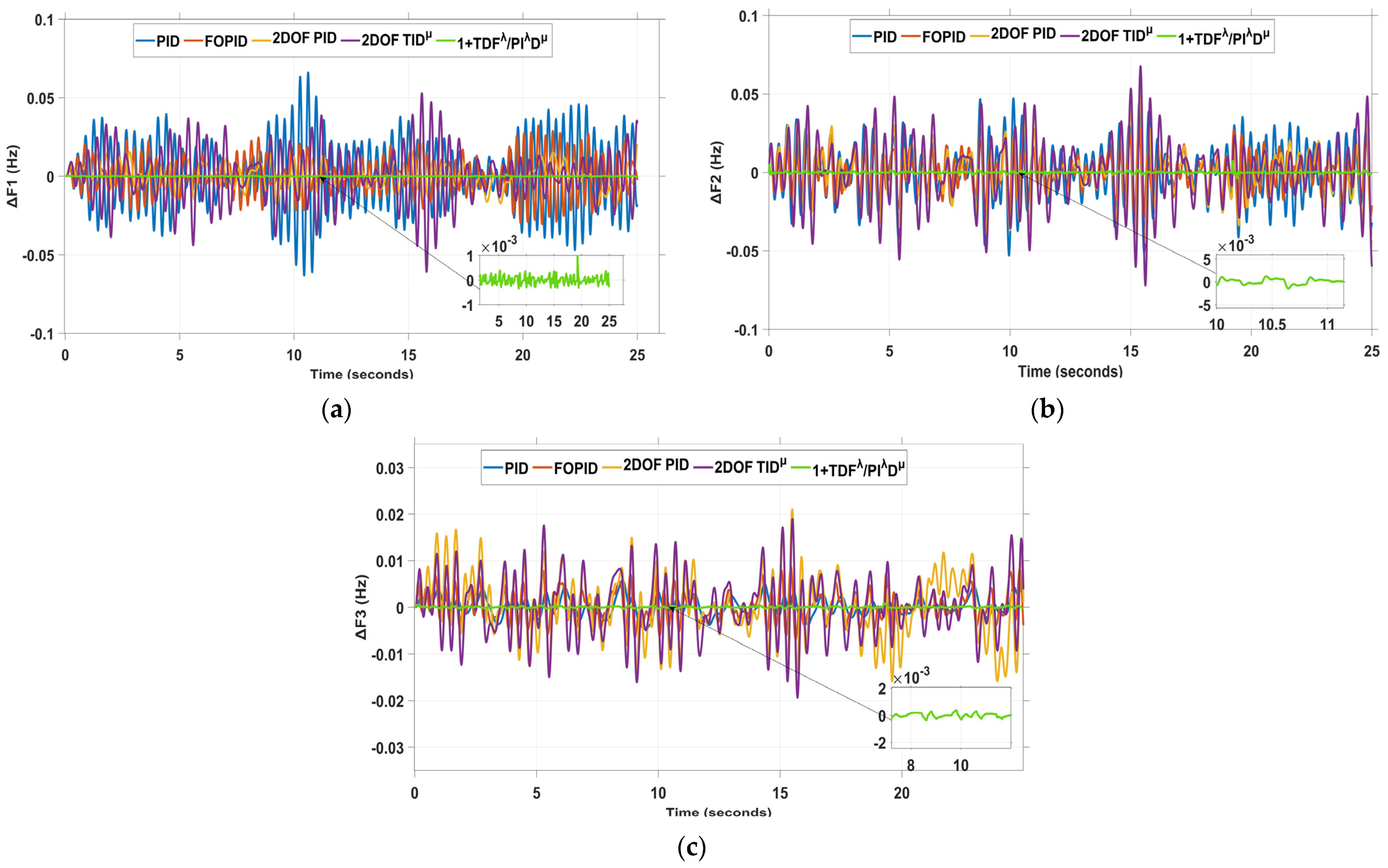
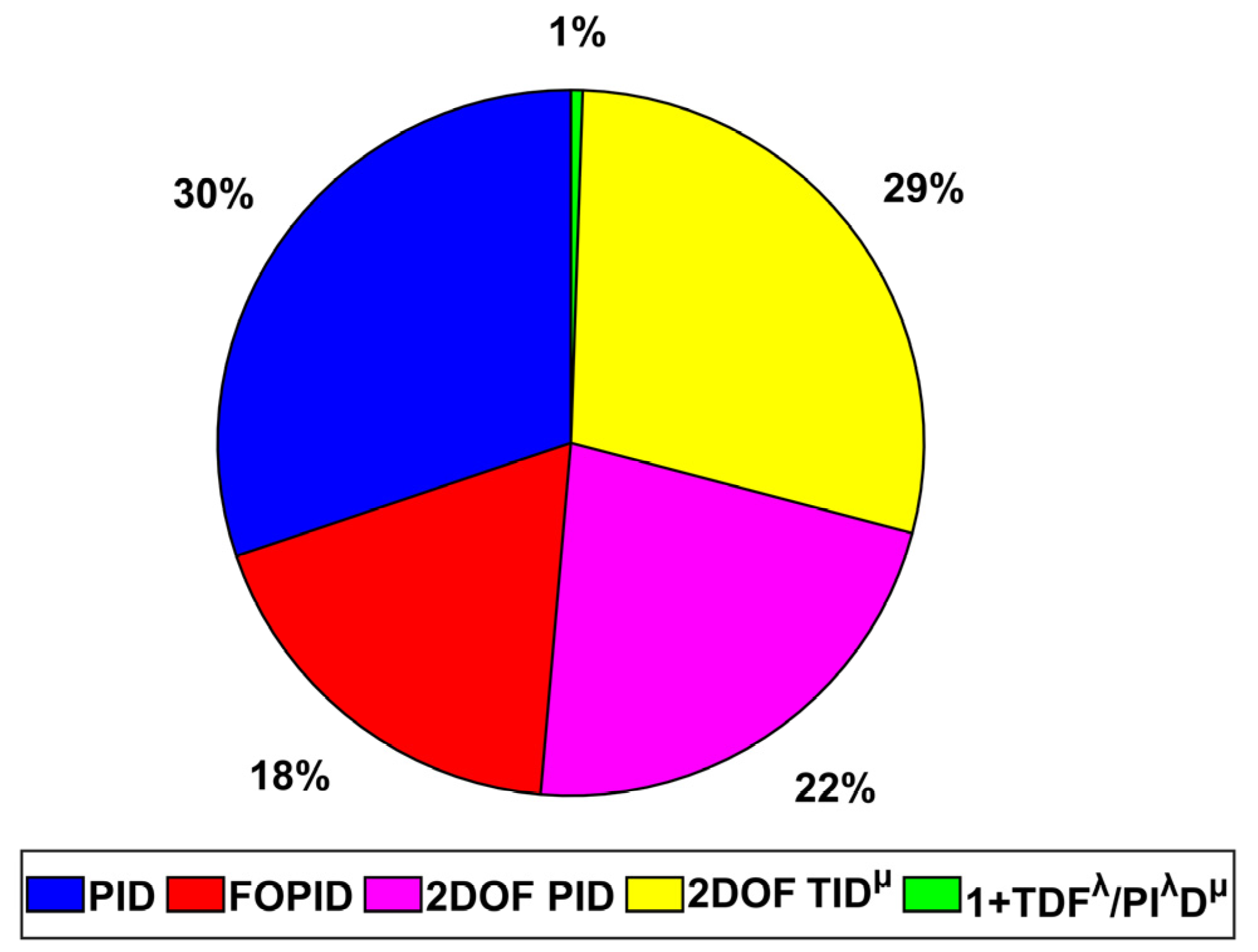
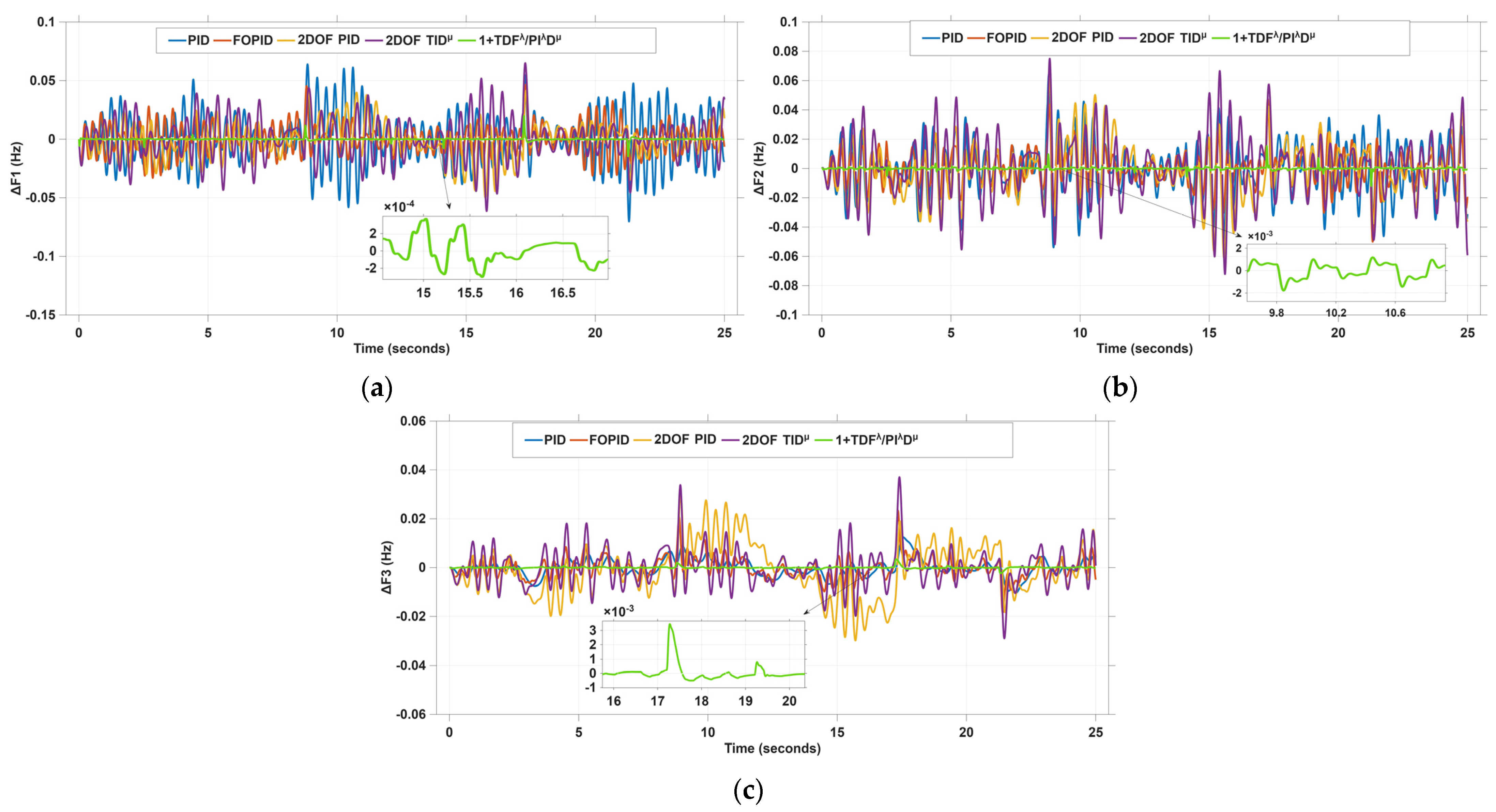
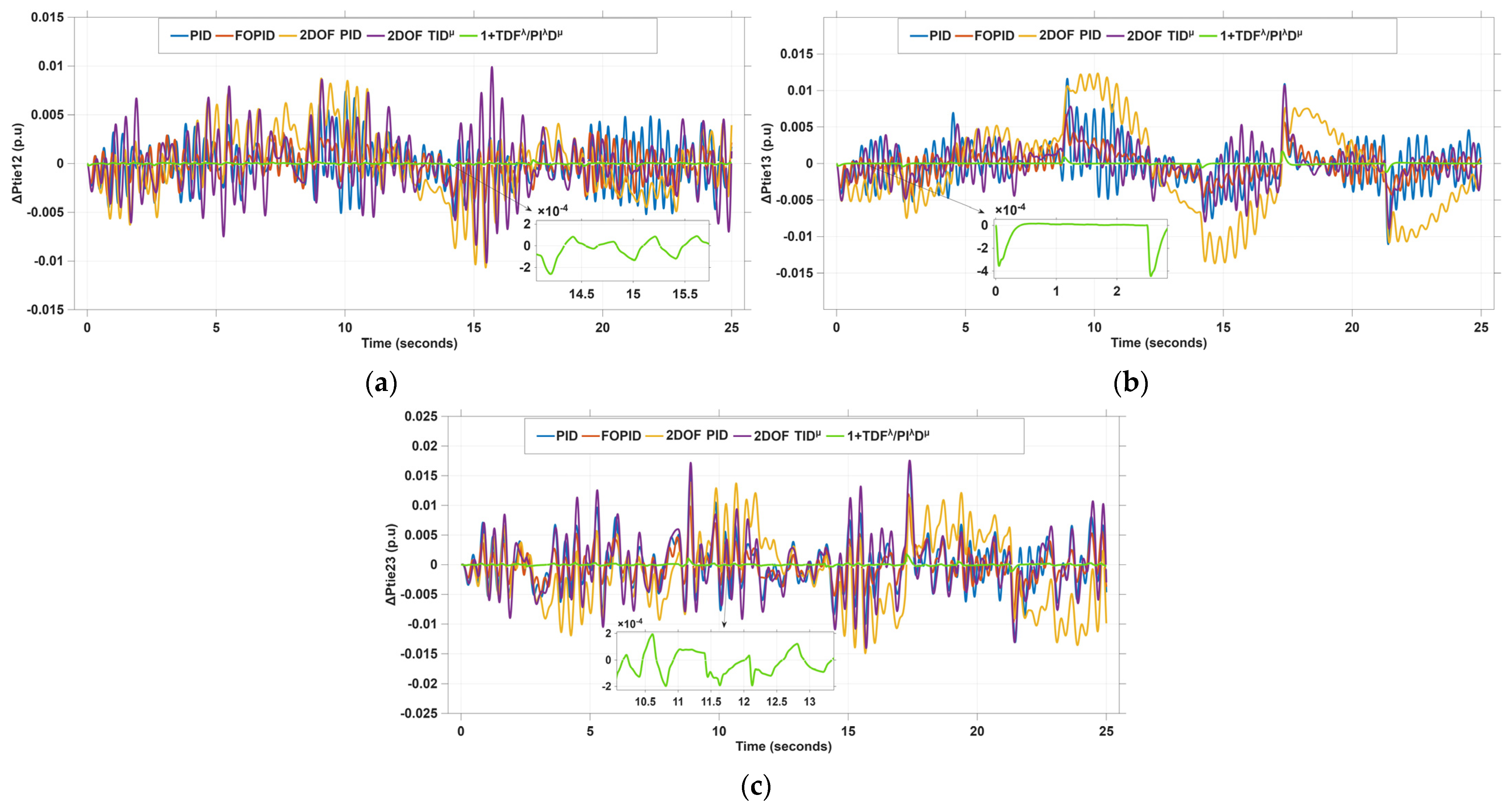
4. Simulation Results and Discussion
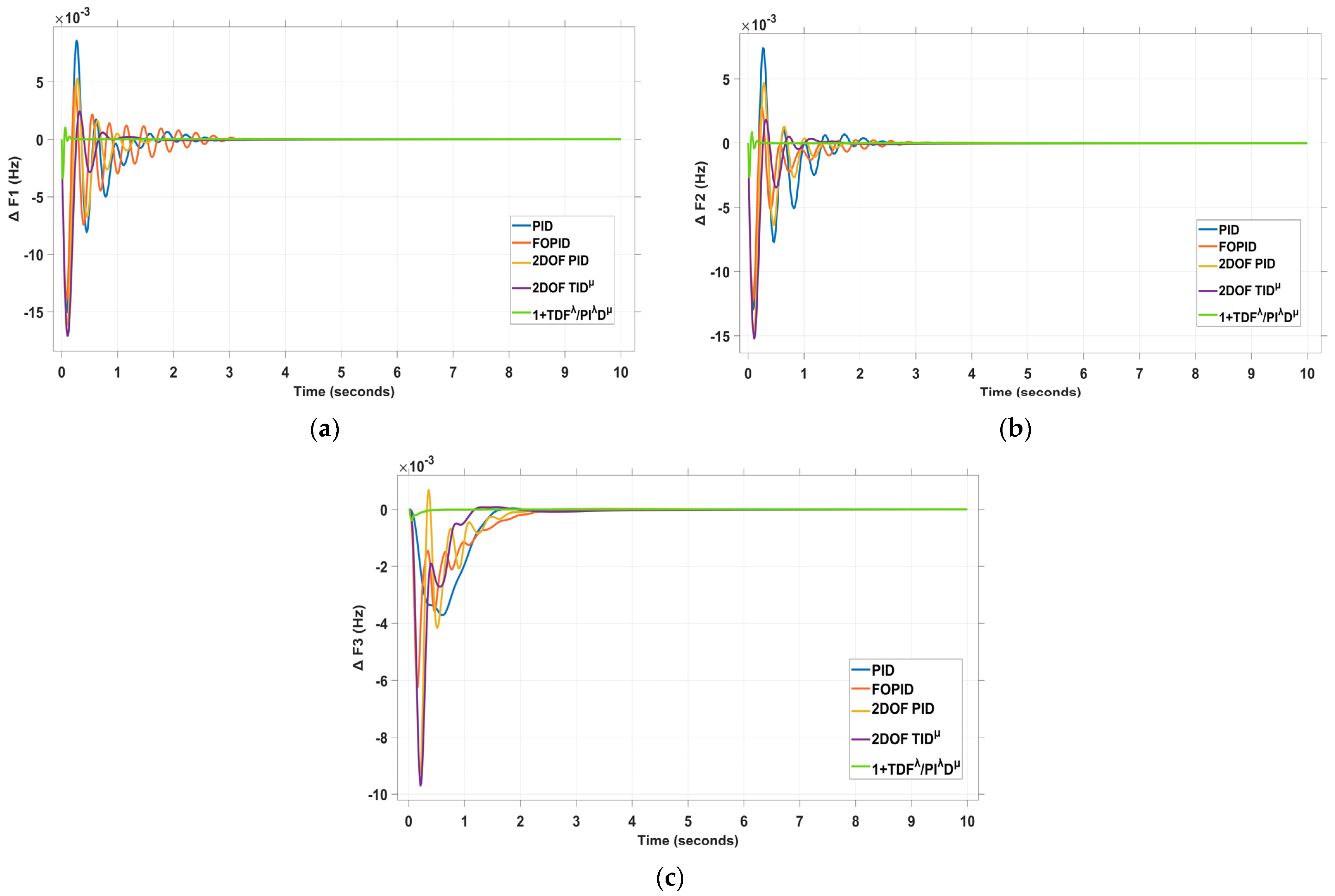
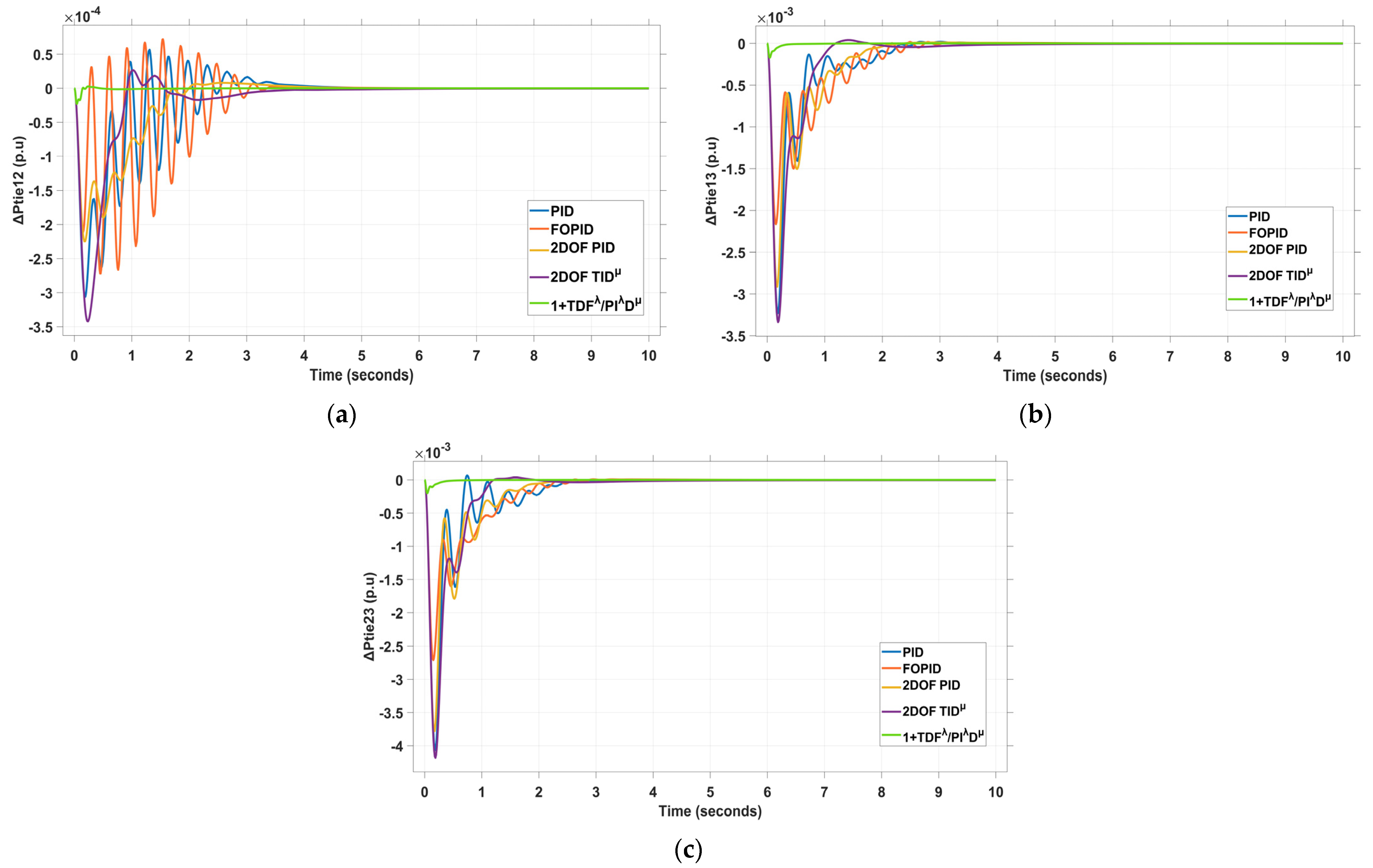
4.1. Scenario I: 5% Step Load Disturbance (SLD) in Area 1 and Area 2
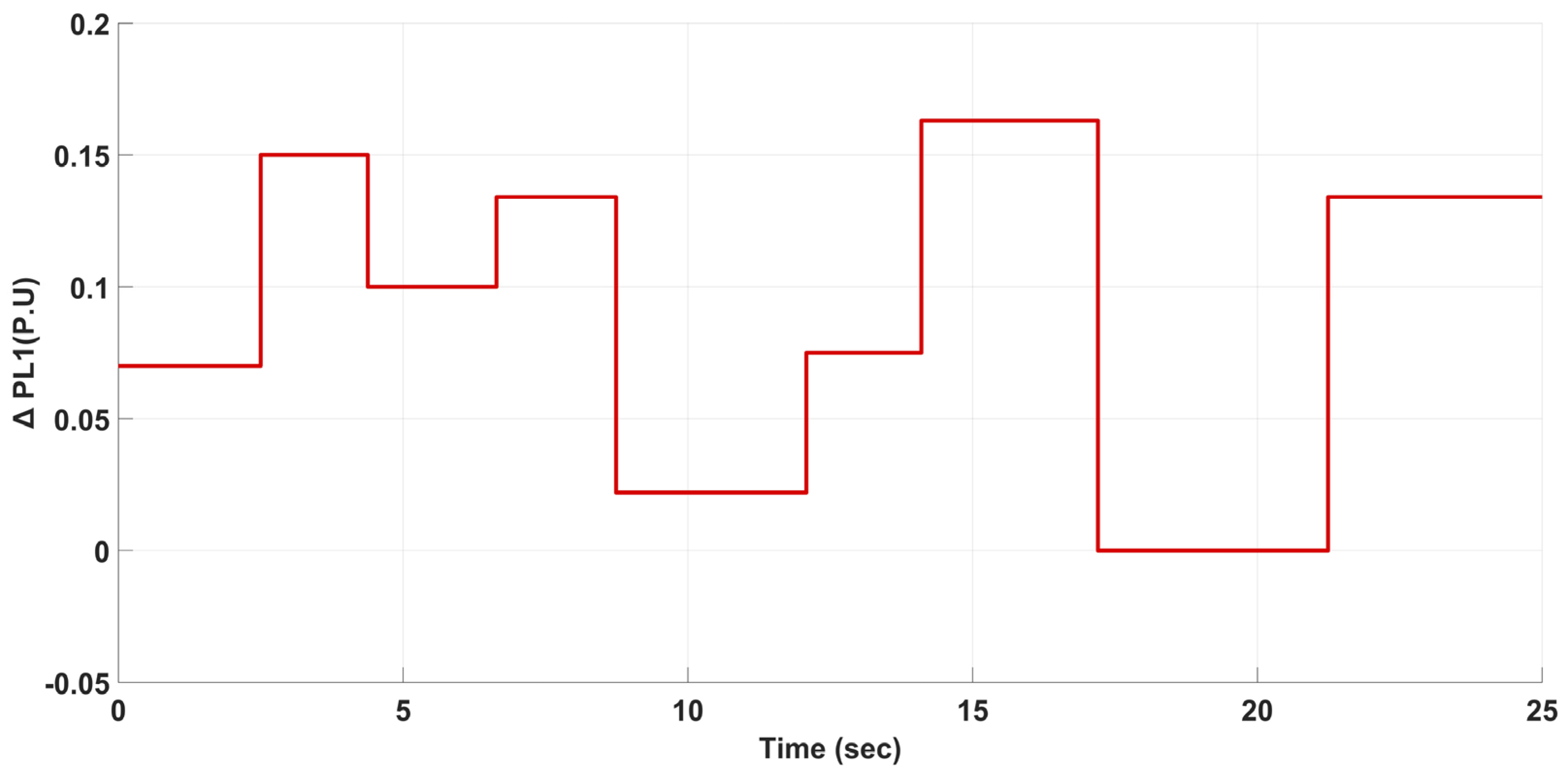
4.2. Scenario 2: A Multi-Step Load Disturbance (MSLD) in Area 1 and Area 2
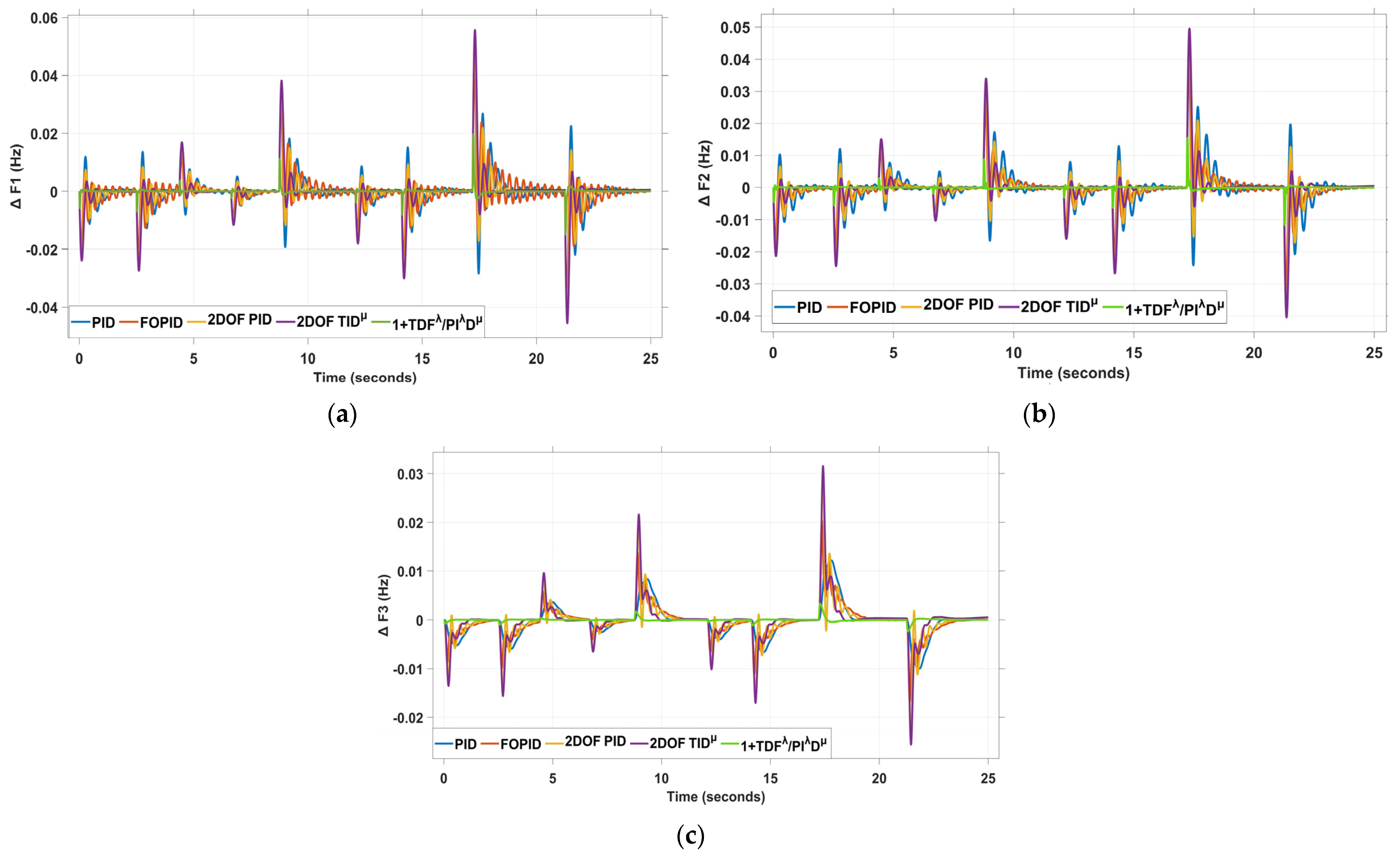
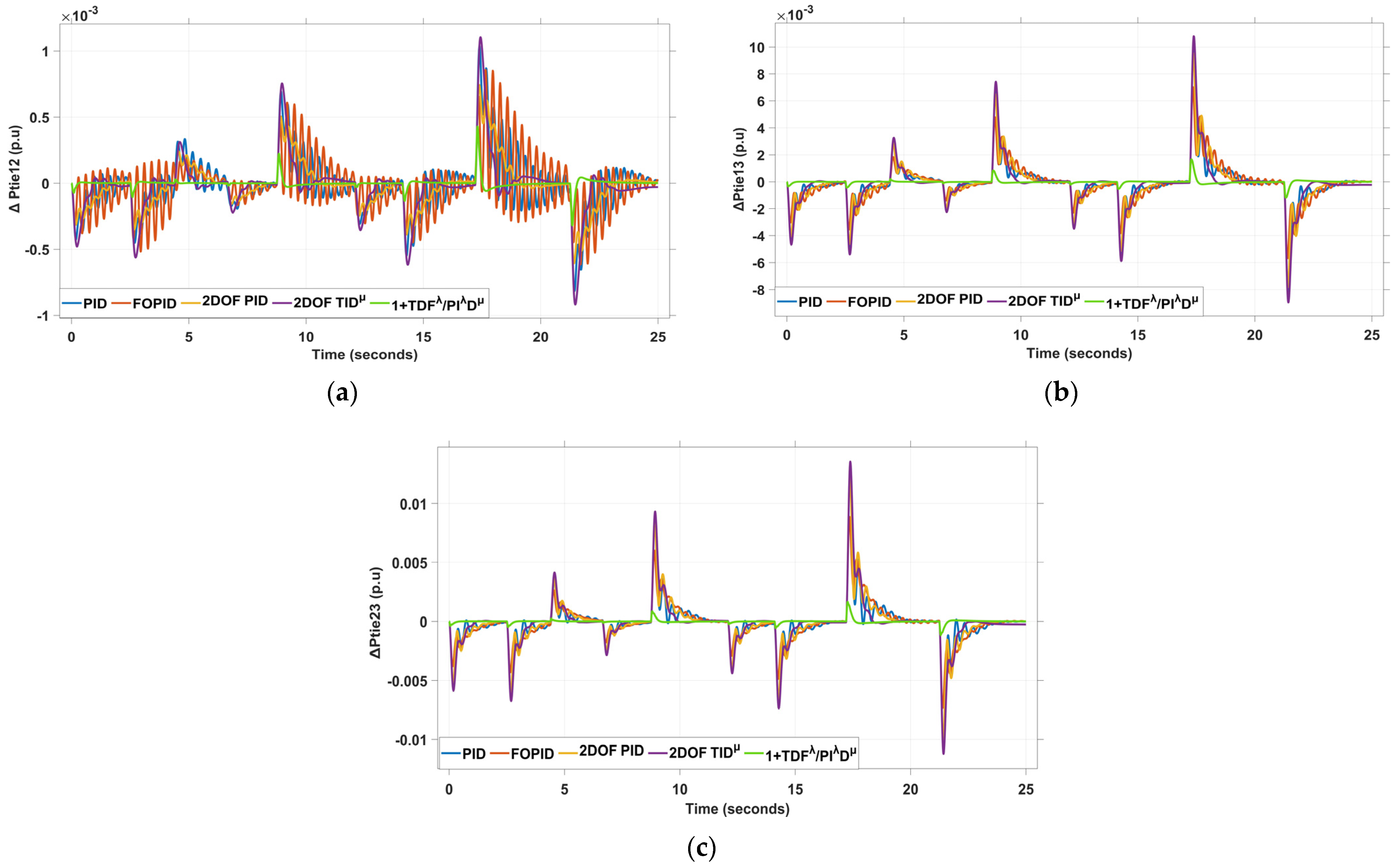
4.3. Scenario 3: Pulse Load Disturbance (PLD) in Area 1 and Area 2
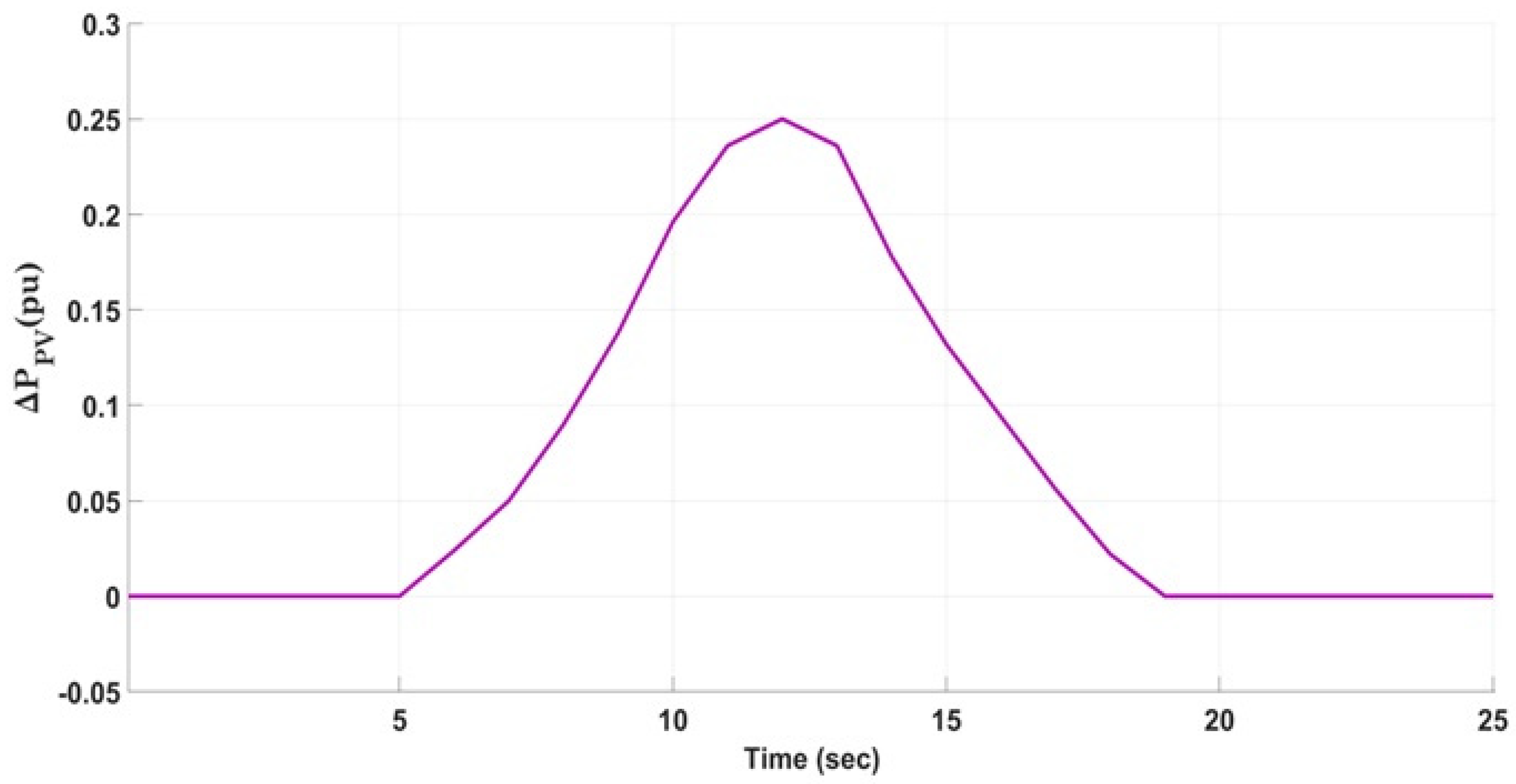
4.4. Scenario 4: PV Integration in Area 1
4.5. Scenario 5: Wind Integration in Area 2
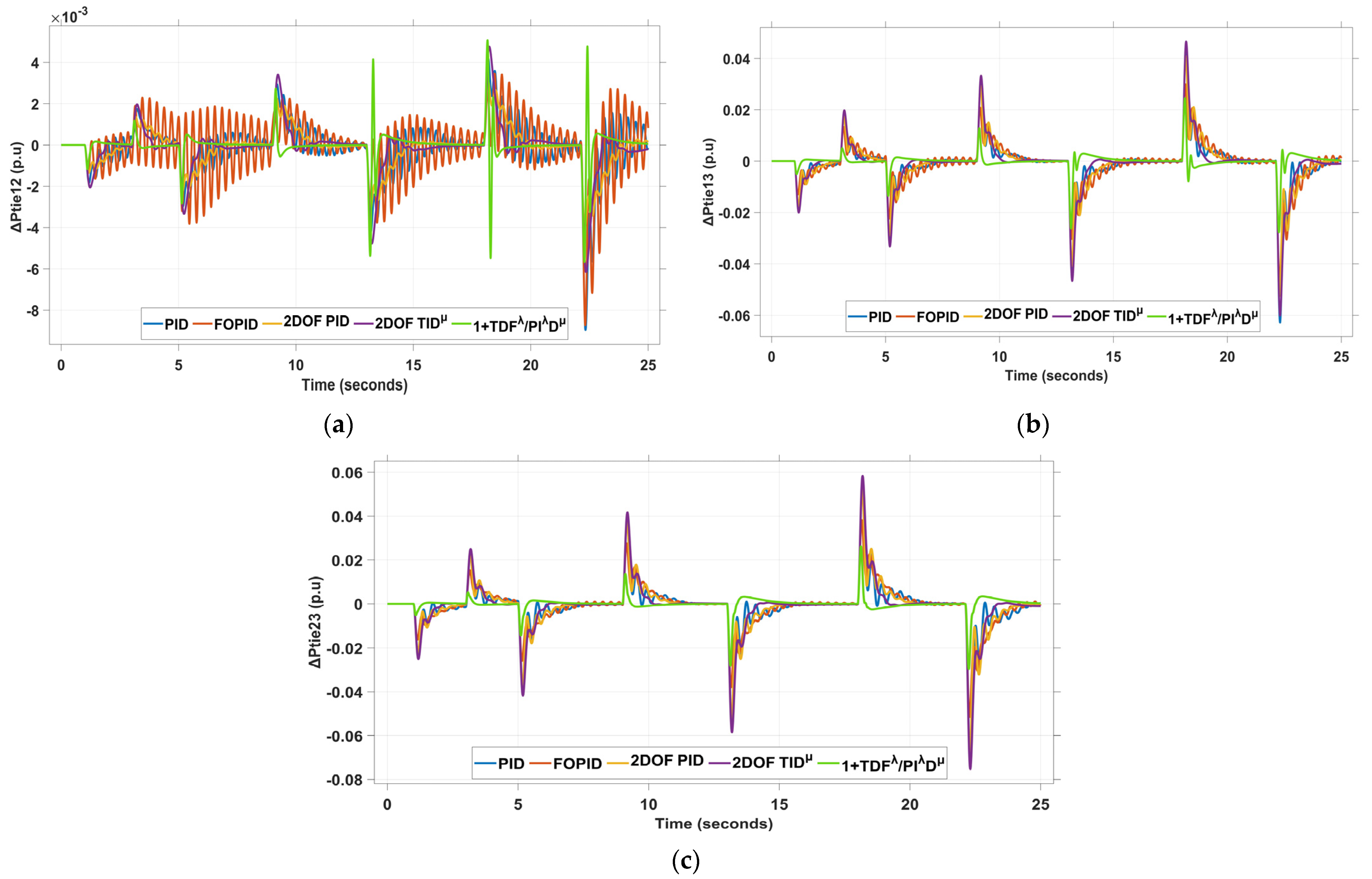
4.6. Scenario 6: PV/Wind Integration and MSLD in Area 1 and Area 2
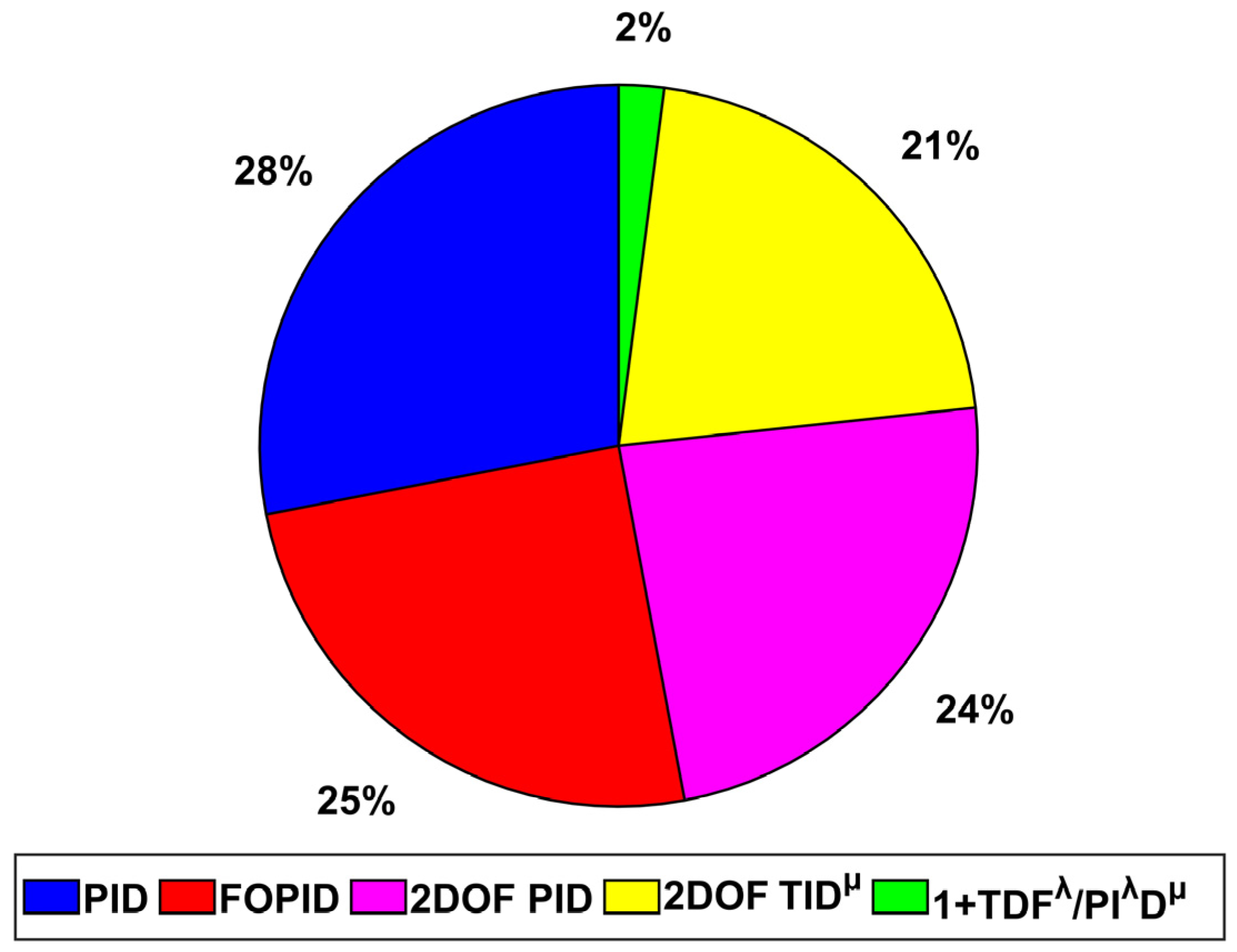
4.7. Scenario 7: Sensitivity Analysis
5. Conclusions
6. Challenges and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| Symbol | Description |
|---|---|
| The number of missionaries (number of religions) | |
| The number of all people in the society | |
| The set of all religions | |
| The set of individuals corresponding to a community | |
| The set of all individuals in the community | |
| -th religion in the society | |
| The maximum number of beliefs of each follower | |
| -th follower in society | |
| Belief vector of follower interested in community | |
| Belief matrix of all followers belonging to community | |
| Belief matrix of all followers in the society | |
| Fitness of follower who is a member of community | |
| Fitness values of attracted followers in community | |
| Fitness values of the entire society (consisting of religions) | |
| Optimal vector of belief attributes in the algorithm | |
| Community index of the most prominent follower | |
| Belief profile of the most prominent follower | |
| Belief profile of the most prominent follower in community | |
| Belief vector of follower hoping to join community | |
| Arbitrary number with a uniform distribution in the interval | |
| Identifier index of the weakest follower in community | |
| Belief profile of the weakest follower in community | |
| Most prominent follower of community | |
| Belief profile of the most prominent follower in community |
References
- Singh, S.P.; Prakash, T.; Singh, V.P.; Babu, M.G. Analytic hierarchy process based automatic generation control of multi-area interconnected power system using Jaya algorithm. Eng. Appl. Artif. Intell. 2017, 60, 35–44. [Google Scholar] [CrossRef]
- Gozde, H.; Taplamacioglu, M.C. Automatic generation control application with craziness based particle swarm optimization in a thermal power system. Int. J. Electr. Power Energy Syst. 2011, 33, 8–16. [Google Scholar] [CrossRef]
- Gozde, H.; Taplamacioglu, M.C.; Kocaarslan, I. Comparative performance analysis of Artificial Bee Colony algorithm in automatic generation control for interconnected reheat thermal power system. Int. J. Electr. Power Energy Syst. 2012, 42, 167–178. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control, 8th ed.; Tata McGraw-Hill: New Delhi, India, 2009. [Google Scholar]
- Tabak, A. Fractional order frequency proportional-integral-derivative control of microgrid consisting of renewable energy sources based on multi-objective grasshopper optimization algorithm. Trans. Inst. Meas. Control 2022, 44, 378–392. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Kriging based surrogate modeling for fractional order control of microgrids. IEEE Trans. Smart Grid 2015, 6, 36–44. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y.V. Fractional order PID controller for load frequency control. Energy Convers. Manag. 2014, 85, 343–353. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd-Elazim, S.M. Bacteria foraging optimization algorithm based load frequency controller for interconnected power system. Int. J. Electr. Power Energy Syst. 2011, 33, 633–638. [Google Scholar] [CrossRef]
- Rout, U.K.; Sahu, R.K.; Panda, S. Design and analysis of differential evolution algorithm based automatic generation control for interconnected power system. Ain Shams Eng. J. 2013, 4, 409–421. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Rout, U.K.; Sahoo, D.K. Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller. Int. J. Electr. Power Energy Syst. 2016, 77, 287–301. [Google Scholar] [CrossRef]
- Elmelegi, A.; Mohamed, E.A.; Aly, M.; Ahmed, E.M.; Mohamed, A.A.A.; Elbaksawi, O. Optimized tilt fractional order cooperative controllers for preserving frequency stability in renewable energy-based power systems. IEEE Access 2021, 9, 8261–8277. [Google Scholar] [CrossRef]
- Padhan, S.; Sahu, R.K.; Panda, S. Application of firefly algorithm for load frequency control of multi-area interconnected power system. Electr. Power Compon. Syst. 2014, 42, 1419–1430. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Sekhar, G.T.C. A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi-area interconnected power systems. Int. J. Electr. Power Energy Syst. 2015, 64, 880–893. [Google Scholar] [CrossRef]
- Mohanty, B.; Panda, S.; Hota, P.K. Differential evolution algorithm based automatic generation control for interconnected power systems with non-linearity. Alex. Eng. J. 2014, 53, 537–552. [Google Scholar] [CrossRef]
- Hasanien, H.M. Whale optimisation algorithm for automatic generation control of interconnected modern power systems including renewable energy sources. IET Gener. Transm. Distrib. 2018, 12, 607–614. [Google Scholar] [CrossRef]
- Khamari, D.; Sahu, R.K.; Gorripotu, T.S.; Panda, S. Automatic generation control of power system in deregulated environment using hybrid TLBO and pattern search technique. Ain Shams Eng. J. 2020, 11, 553–573. [Google Scholar] [CrossRef]
- Nandi, M.; Shiva, C.K.; Mukherjee, V. TCSC based automatic generation control of deregulated power system using quasi-oppositional harmony search algorithm. Eng. Sci. Technol. Int. J. 2017, 20, 1380–1395. [Google Scholar] [CrossRef]
- Gorripotu, T.S.; Sahu, R.K.; Panda, S. AGC of a multi-area power system under deregulated environment using redox flow batteries and interline power flow controller. Eng. Sci. Technol. Int. J. 2015, 18, 555–578. [Google Scholar] [CrossRef]
- AboRas, K.M.; Ragab, M.; Shouran, M.; Alghamdi, S.; Kotb, H. Voltage and frequency regulation in smart grids via a unique Fuzzy PIDD2 controller optimized by Gradient-Based Optimization algorithm. Energy Rep. 2023, 9, 1201–1235. [Google Scholar] [CrossRef]
- Kumar, N.K.; Gopi, R.S.; Kuppusamy, R.; Nikolovski, S.; Teekaraman, Y.; Vairavasundaram, I.; Venkateswarulu, S.V. Fuzzy logic-based load frequency control in an island hybrid power system model using artificial bee colony optimization. Energies 2022, 15, 2199. [Google Scholar] [CrossRef]
- Eshetu, W.; Sharma, P.; Sharma, C. ANFIS based load frequency control in an isolated micro-grid. In Proceedings of the IEEE International Conference on Industrial Technology, Lyon, France, 20–22 February 2018; pp. 1165–1170. [Google Scholar]
- Khuntia, S.R.; Panda, S. Simulation study for automatic generation control of a multi-area power system by ANFIS approach. Appl. Soft Comput. 2012, 12, 333–341. [Google Scholar] [CrossRef]
- Kumar, A.; Anwar, M.N.; Kumar, S. Sliding mode controller design for frequency regulation in an interconnected power system. Prot. Control Mod. Power Syst. 2021, 6, 6. [Google Scholar] [CrossRef]
- Tran, A.-T.; Huynh, V.V.; Shim, J.W.; Lim, C.P. Optimized sliding mode frequency controller for power systems integrated energy storage system with droop control. IEEE Access 2025, 13, 43749–43766. [Google Scholar] [CrossRef]
- Hakimuddin, N.; Nasiruddin, I.; Bhatti, T.S.; Arya, Y. Optimal automatic generation control with hydro, thermal, gas, and wind power plants in 2-area interconnected power system. Electr. Power Compon. Syst. 2020, 48, 558–571. [Google Scholar] [CrossRef]
- Shangguan, X.C.; Zhang, C.K.; He, Y.; Jin, L.; Jiang, L.; Spencer, J.W.; Wu, M. Robust load frequency control for power system considering transmission delay and sampling period. IEEE Trans. Ind. Inform. 2021, 17, 5292–5303. [Google Scholar] [CrossRef]
- Panda, S.; Yegireddy, N.K. Automatic generation control of multi-area power system using multi-objective non-dominated sorting genetic algorithm-II. Int. J. Electr. Power Energy Syst. 2013, 53, 54–63. [Google Scholar]
- Çelik, E. Incorporation of stochastic fractal search algorithm into efficient design of PID controller for an automatic voltage regulator system. Neural Comput. Appl. 2018, 30, 1991–2002. [Google Scholar] [CrossRef]
- Topno, P.N.; Chanana, S. Differential evolution algorithm based tilt integral derivative control for LFC problem of an interconnected hydro-thermal power system. J. Vib. Control 2017, 24, 3952–3973. [Google Scholar] [CrossRef]
- Bhuyan, M.; Das, D.C.; Barik, A.K. Proficient power control strategy for combined solar gas turbine-wind turbine generator-biodiesel generator based two-area interconnected microgrid employed with DC link using Harris’s hawk optimization optimised tilt-integral-derivative controller. Int. J. Numer. Model. Electron. Netw. Devices Fields 2022, 35, e2991. [Google Scholar] [CrossRef]
- Shukla, H.; Nikolovski, S.; Raju, M.; Rana, A.S.; Kumar, P. A particle swarm optimization technique tuned TID controller for frequency and voltage regulation with penetration of electric vehicles and distributed generations. Energies 2022, 15, 8225. [Google Scholar] [CrossRef]
- Fathy, A.; Yousri, D.; Rezk, H.; Thanikanti, S.B.; Hasanien, H.M. A robust fractional-order PID controller based load frequency control using modified hunger games search optimizer. Energies 2022, 15, 361. [Google Scholar] [CrossRef]
- Lamba, R.; Singla, S.K.; Sondhi, S. Design of fractional order PID controller for load frequency control in perturbed two-area interconnected system. Electr. Power Compon. Syst. 2019, 47, 998–1011. [Google Scholar] [CrossRef]
- Bayati, N.; Dadkhah, A.; Vahidi, B.; Hossein, S.; Sadeghi, H. FOPID design for load-frequency control using genetic algorithm. Sci. Int. 2015, 27, 3089–3094. [Google Scholar]
- Mohamed, E.A.; Ahmed, E.M.; Elmelegi, A.; Aly, M.; Elbaksawi, O.; Mohamed, A.A.A. An optimized hybrid fractional order controller for frequency regulation in multi-area power systems. IEEE Access 2020, 8, 213899–213915. [Google Scholar] [CrossRef]
- Sharma, M.; Prakash, S.; Saxena, S.; Dhundhara, S. Optimal fractional-order tilted-integral-derivative controller for frequency stabilization in hybrid power system using salp swarm algorithm. Electr. Power Compon. Syst. 2021, 48, 1912–1931. [Google Scholar] [CrossRef]
- Ahmed, M.; Magdy, G.; Khamies, M.; Kamel, S. Modified TID controller for load frequency control of a two-area interconnected diverse-unit power system. Int. J. Electr. Power Energy Syst. 2022, 135, 107528. [Google Scholar] [CrossRef]
- Alharbi, M.; Ragab, M.; AboRas, K.M.; Kotb, H.; Dashtdar, M.; Shouran, M.; Elgamli, E. Innovative AVR-LFC design for a multi-area power system using hybrid fractional-order PI and PIDD2 controllers based on dandelion optimizer. Mathematics 2023, 11, 1387. [Google Scholar] [CrossRef]
- Mohamed, E.A.; Aly, M.; Watanabe, M. New tilt fractional-order integral derivative with fractional filter (TFOIDFF) controller with artificial hummingbird optimizer for LFC in renewable energy power grids. Mathematics 2022, 10, 3006. [Google Scholar] [CrossRef]
- Das, S.; Saikia, L.C.; Datta, S. Maiden application of TIDN-(1 + PI) cascade controller in LFC of a multi-area hydro-thermal system incorporating EV–Archimedes wave energy-geothermal-wind generations under deregulated scenario. Int. Trans. Electr. Energy Syst. 2021, 31, e12907. [Google Scholar] [CrossRef]
- Bhuyan, M.; Das, D.C.; Barik, A.K.; Sahoo, S.C. Performance assessment of novel solar thermal-based dual hybrid microgrid system using CBOA optimized cascaded PI-TID controller. IETE J. Res. 2022, 69, 9076–9093. [Google Scholar] [CrossRef]
- Arya, Y. ICA assisted FTI λ DN controller for AGC performance enrichment of interconnected reheat thermal power systems. J. Ambient Intell. Humaniz. Comput. 2021, 14, 1919–1935. [Google Scholar] [CrossRef]
- Choudhary, R.; Rai, J.N.; Arya, Y. FOPTID + 1 controller with capacitive energy storage for AGC performance enrichment of multi-source electric power systems. Electr. Power Syst. Res. 2023, 221, 109450. [Google Scholar] [CrossRef]
- Hassan, A.; Aly, M.; Elmelegi, A.; Nasrat, L.; Watanabe, M.; Mohamed, E.A. Optimal frequency control of multi-area hybrid power system using new cascaded TID-PIλDμN controller incorporating electric vehicles. Fractal Fract. 2022, 6, 548. [Google Scholar] [CrossRef]
- Kihal, M.C.; Yahiou, A.; Kihal, M.; Azizi, H.; Sekki, D.; Chabout, M. TID-FOPIDN controller for frequency control using Lemur optimization in two-area power systems. Braz. J. Technol. 2024, 7, e74676. [Google Scholar] [CrossRef]
- Ahmad, R.; Arya, Y.; Ahmer, M.F.; Nasiruddin, I. Enhanced frequency/voltage control in multi-source power system using CES and SSA-optimized cascade TID-FOPTID controller. IETE J. Res. 2025, 71, 652–667. [Google Scholar] [CrossRef]
- Tabak, A.; Duman, S. Levy flight and fitness distance balance-based coyote optimization algorithm for effective automatic generation control of PV-based multi-area power systems. Arab J. Sci. Eng. 2022, 47, 14757–14788. [Google Scholar]
- Khudhair, M.; Ragab, M.; AboRas, K.M.; Abbasy, N.H. A newly resilient combination of PIDD2 and PD controllers to boost the frequency response in a two-area hybrid power system with nonlinearities using wild horse optimizer. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022; pp. 1–11. [Google Scholar]
- AboRas, K.M.; Sedik, A.M.A.; Hammad, M.R. Hybrid dual-area power grid frequency fluctuation effective control utilizing a maiden combination of MOA-based 1 + PIID and PDμFλ controllers. Sci. Prog. 2025, 108, 00368504251330521. [Google Scholar] [CrossRef] [PubMed]
- Raju, M.; Saikia, L.C.; Sinha, N. Automatic generation control of a multi-area system using ant lion optimizer algorithm based PID plus second order derivative controller. Int. J. Electr. Power Energy Syst. 2016, 80, 52–63. [Google Scholar] [CrossRef]
- Mozhdehi, A.T.; Khodadadi, N.; Aboutalebi, M.; El-kenawy, E.S.M.; Hussien, A.G.; Zhao, W.; Nadimi-Shahraki, M.H.; Mirjalili, S. Divine Religions Algorithm: A novel social-inspired metaheuristic algorithm for engineering and continuous optimization problems. Clust. Comput. 2025, 28, 253. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2022, 38, 3025–3056. [Google Scholar] [CrossRef]
- Sahu, R.K.; Chandra Sekhar, G.; Panda, S. DE optimized fuzzy PID controller with derivative filter for LFC of multi-source power system in deregulated environment. Ain Shams Eng. J. 2015, 6, 511–530. [Google Scholar] [CrossRef]
- Soni, V.; Parmar, G.; Kumar, M.; Panda, S. Hybrid Grey Wolf Optimization-Pattern Search (hGWO-PS) optimized 2DOF-PID controllers for load frequency control in interconnected thermal power plants. ICTACT J. Soft Comput. 2016, 6, 1244–1256. [Google Scholar]
- Moschos, I.; Parisses, C. Combined frequency and voltage control of two-area multi-source interconnected microgrids via the 2DOF-TIDμ controller. e-Prime Adv. Electr. Eng. Electron. Energy 2023, 5, 100268. [Google Scholar] [CrossRef]

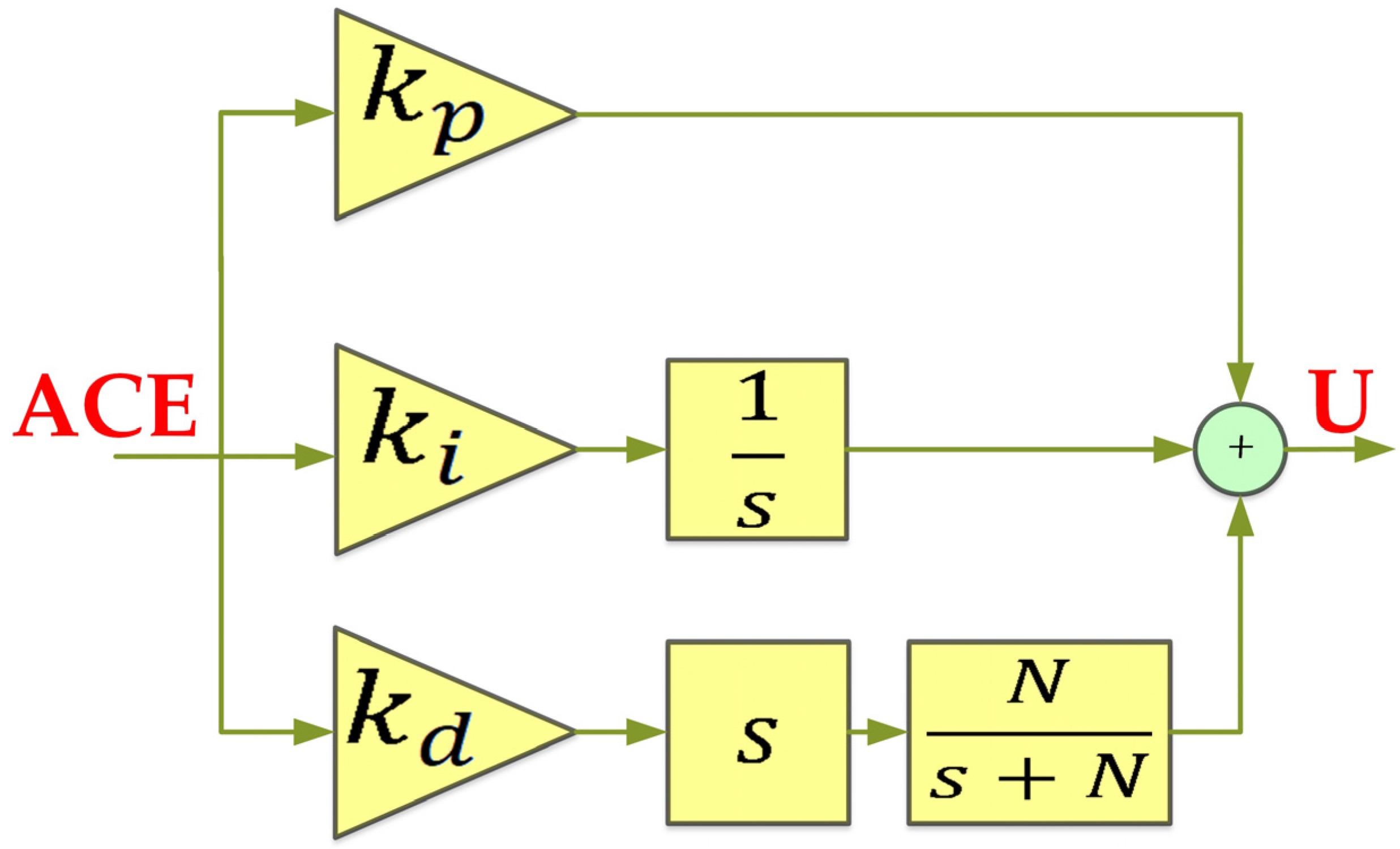
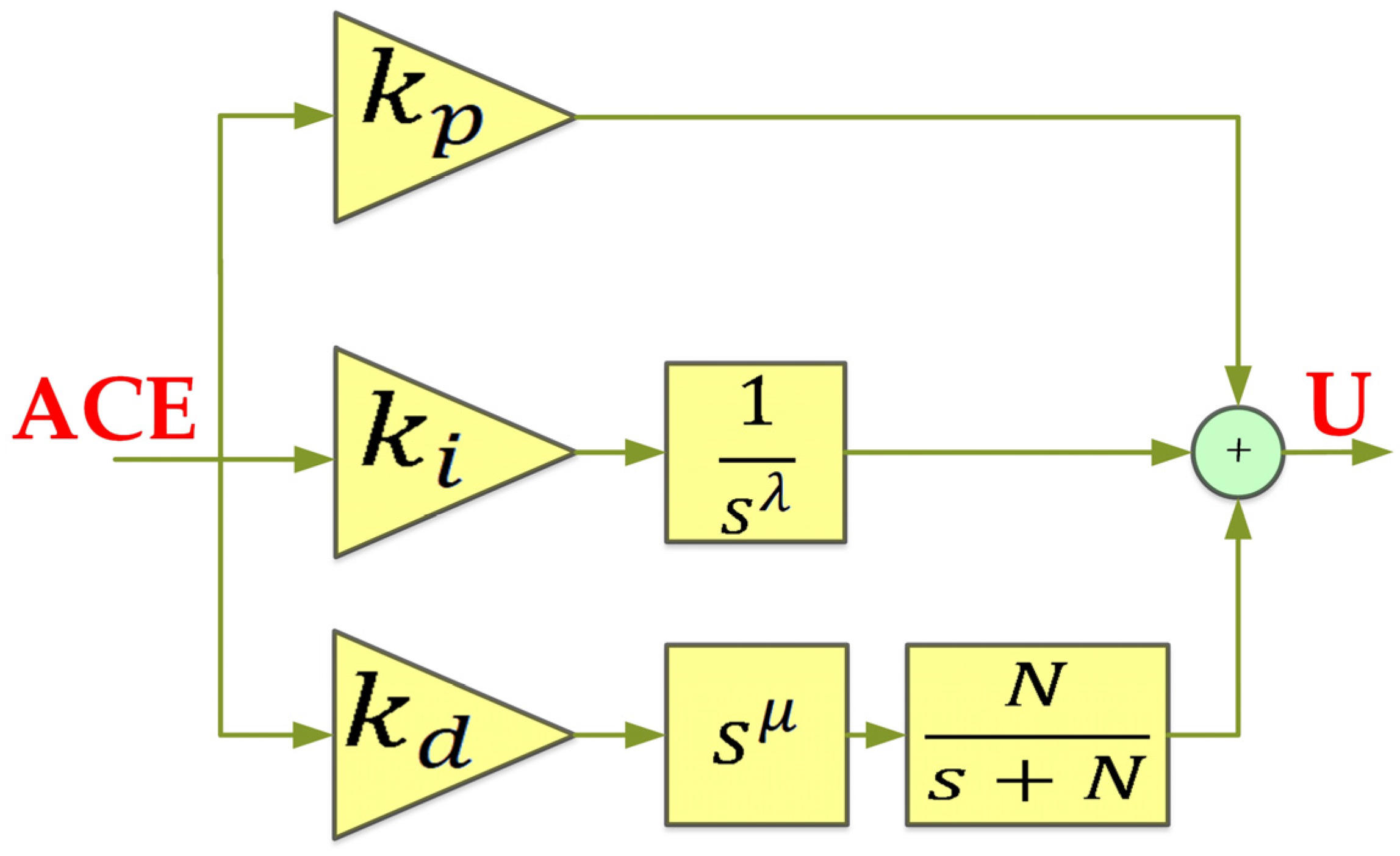
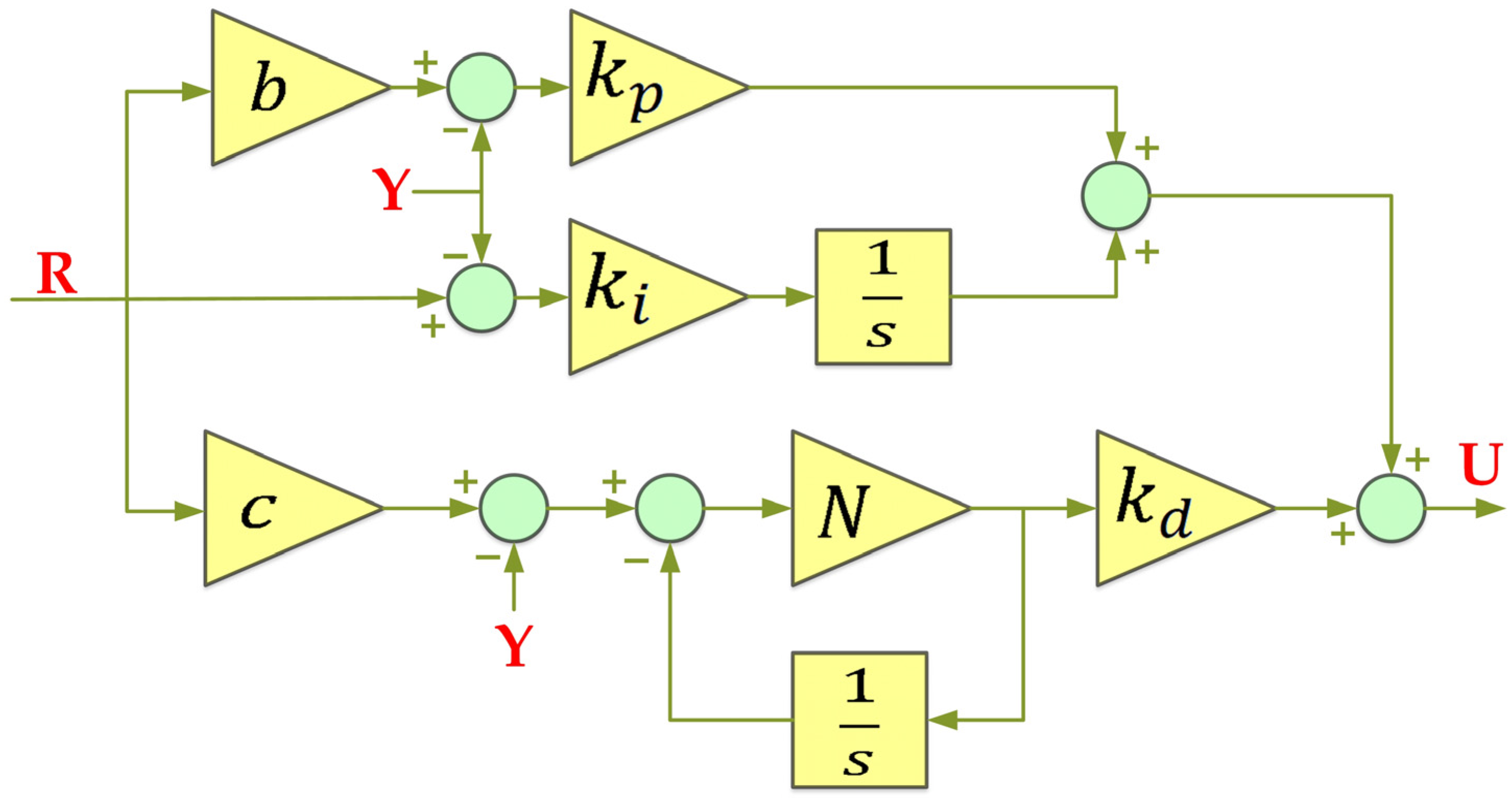
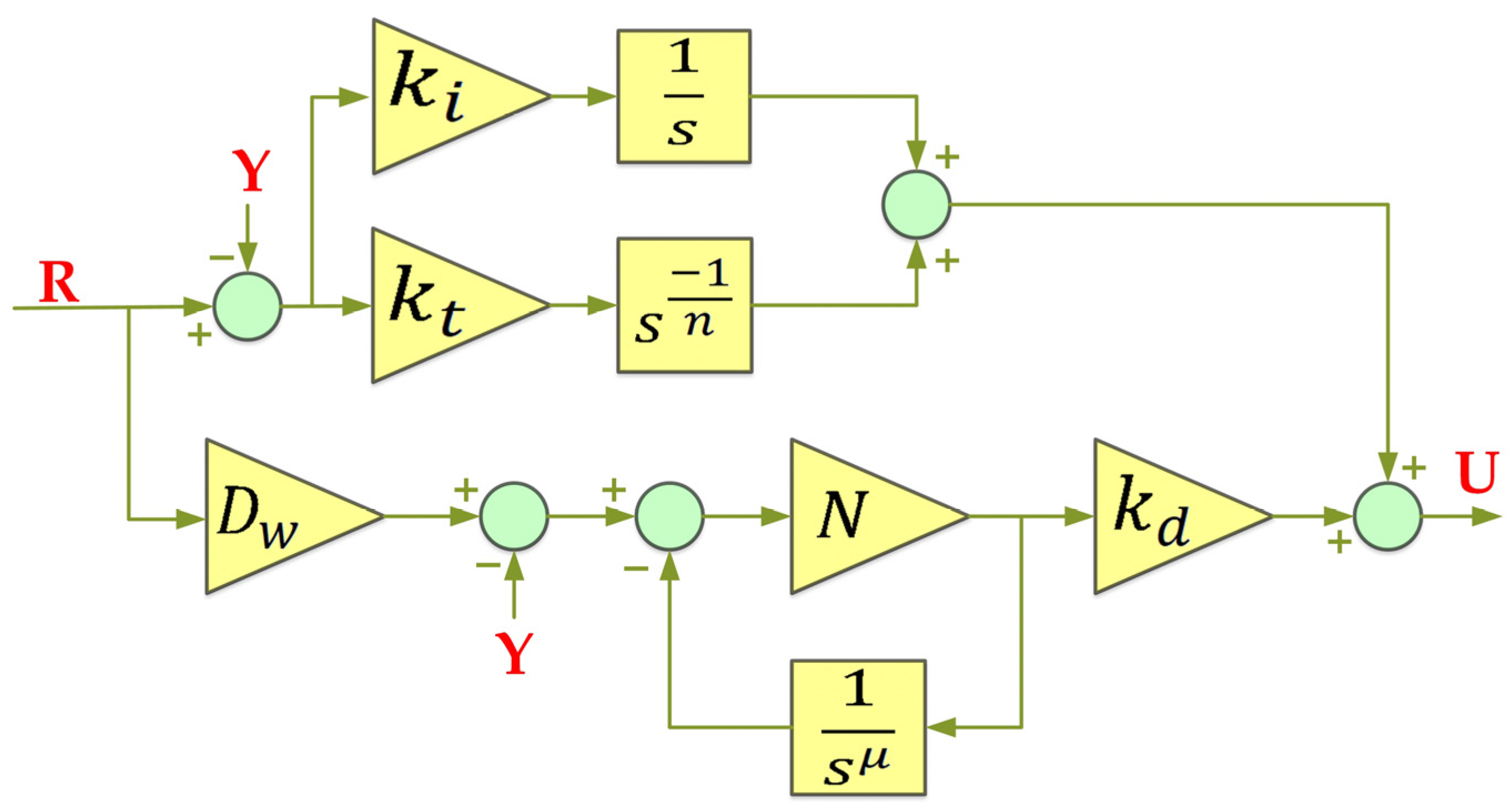

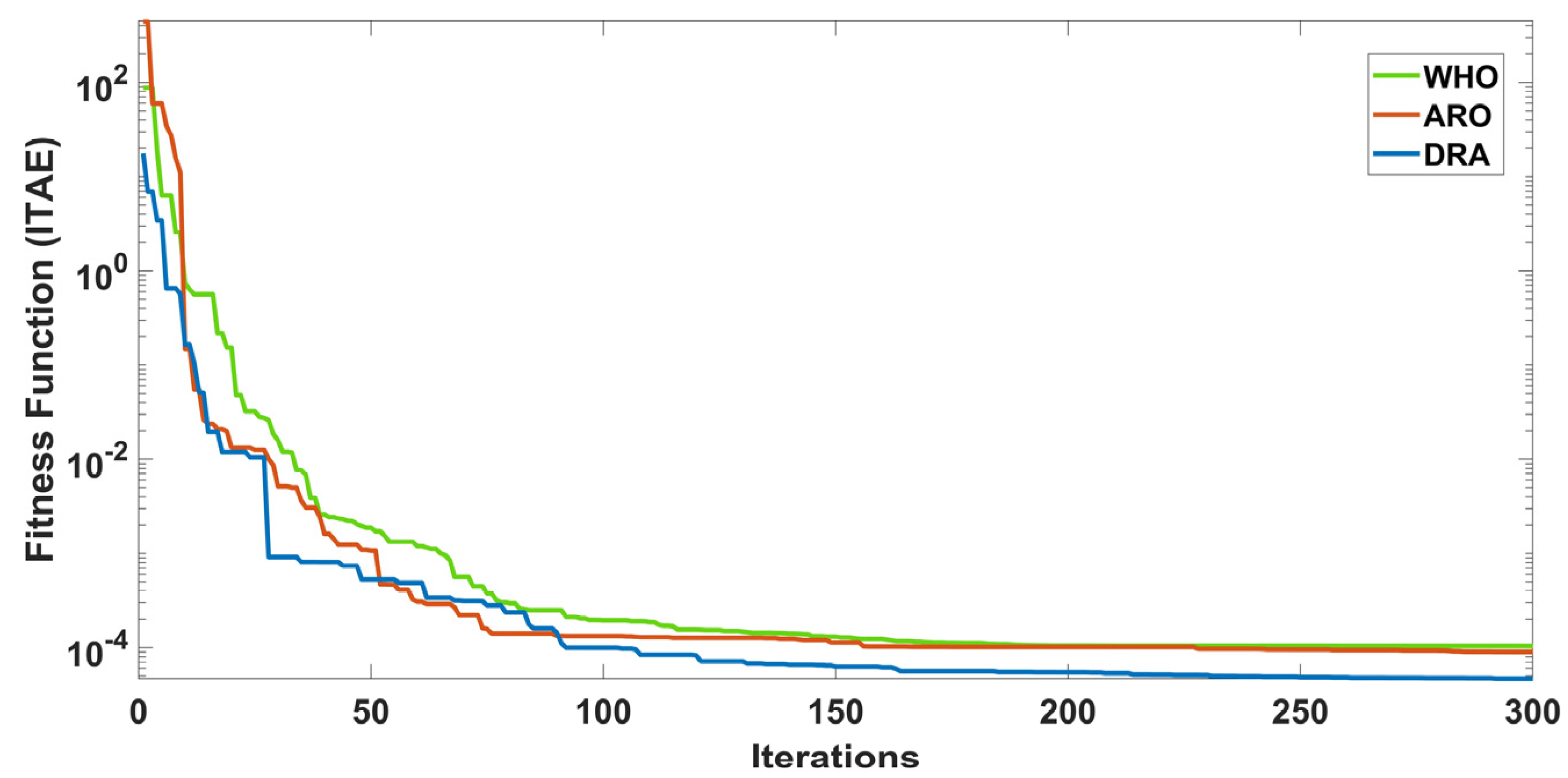

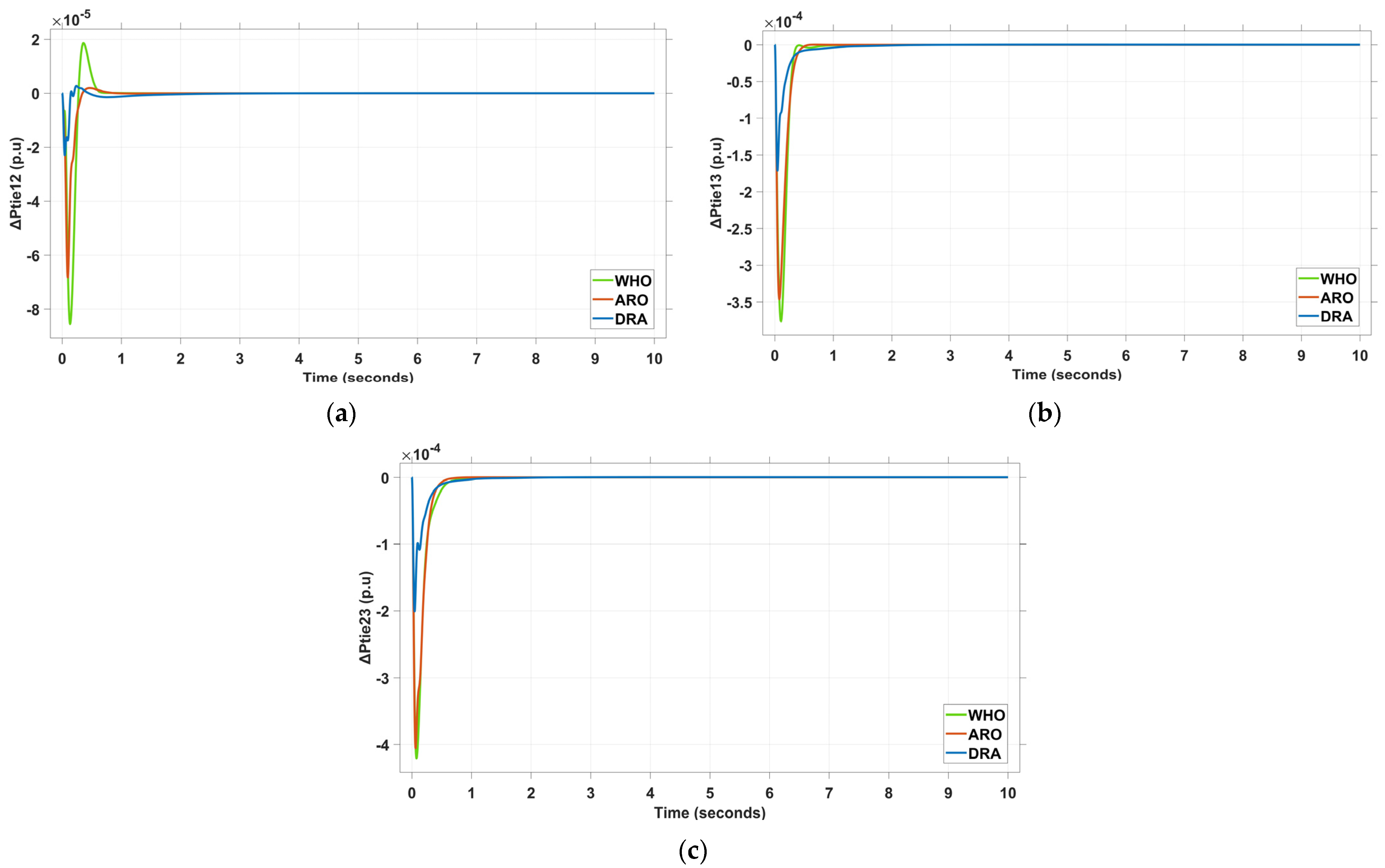





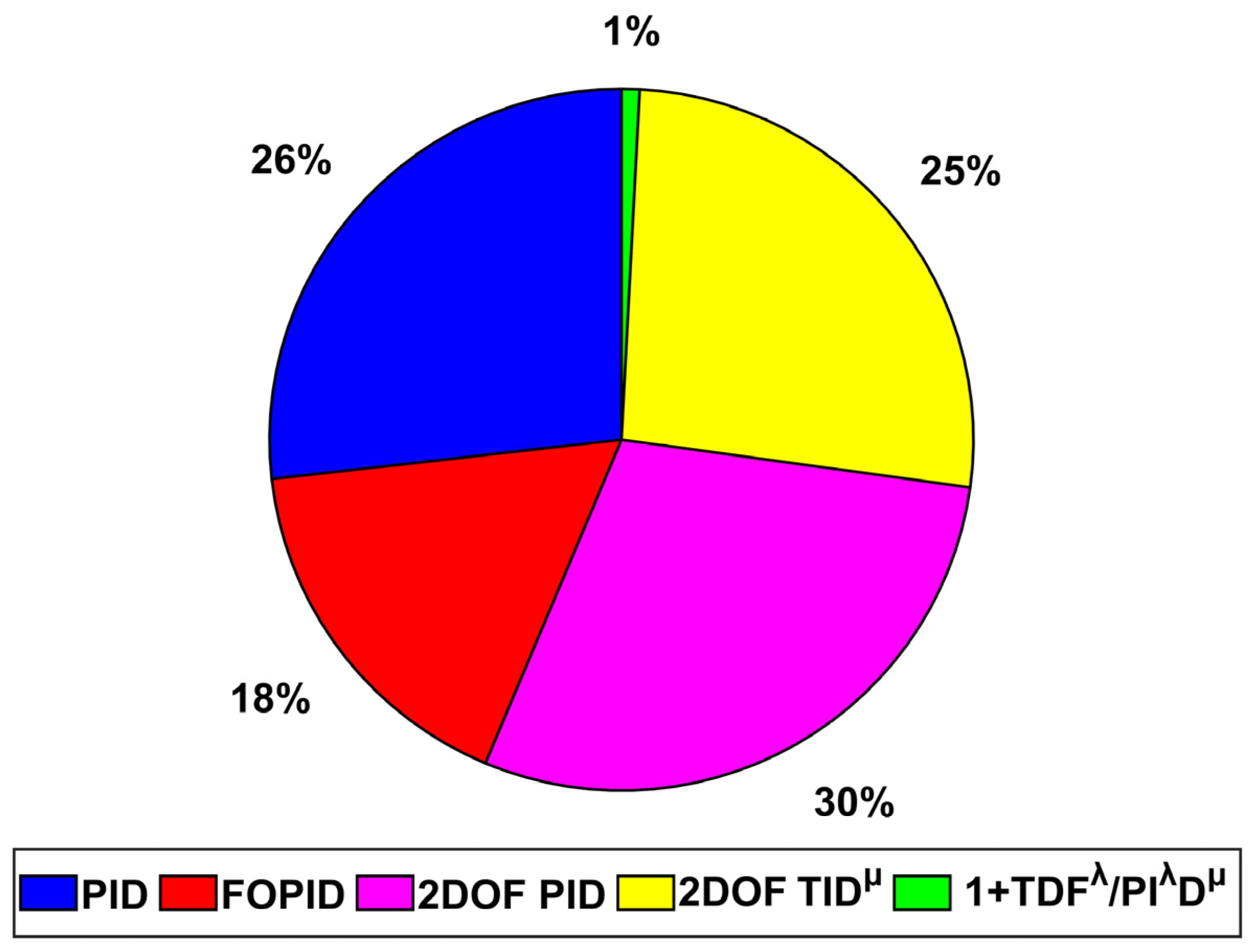
| Algorithm | Runtime (Hour) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WHO | 1.24 | |||||||||||
| Area 1 | 18.136 | 6.022 | 14.158 | 1.353 | 236 | 19.938 | 19.997 | 0.835 | 1.544 | 0.789 | 289 | |
| Area 2 | 19.122 | 1.021 | 13.142 | 1.781 | 140 | 11.795 | 19.986 | 1.722 | 1.402 | 1.478 | 488 | |
| Area 3 | 17.777 | 1 | 3.478 | 1.523 | 486 | 19.853 | 0.867 | 1.258 | 4.507 | 1.369 | 500 | |
| ARO | 1.25 | |||||||||||
| Area 1 | 16.451 | 1 | 4.982 | 1.792 | 223 | 20 | 19.991 | 0.751 | 9.472 | 1.257 | 190 | |
| Area 2 | 15.232 | 1.186 | 3.871 | 1.432 | 101 | 19.839 | 19.985 | 0.366 | 10.591 | 1.479 | 203 | |
| Area 3 | 19.639 | 1.683 | 7.417 | 1.401 | 101 | 0.322 | 0.176 | 1.002 | 1.390 | 1.893 | 101 | |
| DRA | 1.21 | |||||||||||
| Area 1 | 17.462 | 7.551 | 11.568 | 1.521 | 209 | 19.994 | 19.988 | 1.743 | 3.263 | 0.793 | 201 | |
| Area 2 | 12.153 | 9.913 | 14.298 | 1.743 | 478 | 19.853 | 18.366 | 1.258 | 2.325 | 1.743 | 319 | |
| Area 3 | 18.126 | 8.311 | 18.647 | 1.692 | 489 | 20 | 17.548 | 1.487 | 3.754 | 1.235 | 451 |
| Controller | Parameters | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PID | ||||||||||||||||||||||||
| Area 1 | 18.023 | 20 | 6.145 | 256 | ||||||||||||||||||||
| Area 2 | 19.149 | 19.681 | 6.059 | 348 | ||||||||||||||||||||
| Area 3 | 0.164 | 0.114 | 0.009 | 409 | ||||||||||||||||||||
| FOPID | ||||||||||||||||||||||||
| Area 1 | 19.997 | 20 | 7.175 | 0.761 | 0.573 | 489 | ||||||||||||||||||
| Area 2 | 20 | 19.981 | 6.885 | 0.493 | 0.373 | 426 | ||||||||||||||||||
| Area 3 | 18.323 | 19.928 | 16.997 | 0.831 | 0.664 | 500 | ||||||||||||||||||
| 2DOF-PID | ||||||||||||||||||||||||
| Area 1 | −17.204 | −19.996 | −5.223 | −1.755 | −1.998 | 499 | ||||||||||||||||||
| Area 2 | −17.988 | −20 | −4.976 | 0.118 | −1.973 | 173 | ||||||||||||||||||
| Area 3 | −19.998 | −8.425 | −7.889 | 2 | 2 | 271 | ||||||||||||||||||
| 2DOF-TIDμ | ||||||||||||||||||||||||
| Area 1 | 1.443 | −3.609 | −19.988 | 16.318 | 1.083 | 489 | 10 | |||||||||||||||||
| Area 2 | 19.496 | −4.094 | −19.998 | −16.191 | 1.021 | 498 | 9.998 | |||||||||||||||||
| Area 3 | 1.093 | −7.748 | 6.386 | −17.631 | 0.972 | 483 | 9.997 | |||||||||||||||||
| 1+TDFλ/PIλDμ | ||||||||||||||||||||||||
| Area 1 | 17.462 | 7.551 | 11.568 | 1.521 | 209 | 19.994 | 19.988 | 1.743 | 3.263 | 0.793 | 201 | |||||||||||||
| Area 2 | 12.153 | 9.913 | 14.298 | 1.743 | 478 | 19.853 | 18.366 | 1.258 | 2.325 | 1.743 | 319 | |||||||||||||
| Area 3 | 18.126 | 8.311 | 18.647 | 1.692 | 489 | 20 | 17.548 | 1.487 | 3.754 | 1.235 | 451 | |||||||||||||
| Controller | ΔF1 (Hz) | ΔF2 (Hz) | ΔF3 (Hz) | ΔPtie12 (P.U) | ΔPtie13 (P.U) | ΔPtie23 (P.U) | |
|---|---|---|---|---|---|---|---|
| PID | |||||||
| OS | 858.5 | 740.5 | 3.67 | 5.66 | 1.97 | 6.78 | |
| US | −15.05 | −12.96 | −3.719 | −0.306 | −3.233 | −4.068 | |
| ST (Sec.) | 2.5 | 1.8 | 1.8 | 2.55 | 2.6 | 2.4 | |
| FF | 29.91 | 30.24 | 24.09 | 2.117 | 10.27 | 8.988 | |
| FOPID | |||||||
| OS | 469.5 | 276.7 | 2.013 | 7.193 | 1.753 | 0.922 | |
| US | −13.96 | −12.24 | −6.248 | −0.272 | −2.165 | −2.71 | |
| ST (Sec.) | 2.2 | 1.6 | 1.6 | 2.4 | 2.45 | 2.25 | |
| FF | 38.27 | 21.04 | 21.4 | 2.848 | 10.86 | 9.948 | |
| 2DOF-PID | |||||||
| OS | 528.3 | 470.2 | 68.42 | 0.798 | 1.122 | 0.318 | |
| US | −16.16 | −14.66 | −9.277 | −0.225 | −2.914 | −3.779 | |
| ST (Sec.) | 1.5 | 1 | 1.4 | 2 | 2.2 | 1.6 | |
| FF | 15.53 | 16.11 | 17.2 | 1.468 | 8.517 | 7.788 | |
| 2DOF-TIDμ | |||||||
| OS | 243.2 | 181.8 | 8.022 | 2.648 | 3.988 | 3.476 | |
| US | −17.07 | −15.2 | −9.698 | −0.3421 | −3.338 | −4.183 | |
| ST (Sec.) | 0.7 | 0.6 | 1.2 | 1.6 | 1.8 | 1.2 | |
| FF | 26.74 | 27.05 | 28.26 | 1.161 | 10.67 | 8.991 | |
| 1+TDFλ/PIλDμ (Proposed) | |||||||
| OS | 102.1 | 84.31 | 0.065 | 0.271 | 0.027 | 0.0349 | |
| US | −3.373 | −2.661 | −0.389 | −0.023 | −0.1712 | −0.2007 | |
| ST (Sec.) | 0.1 | 0.14 | 0.3 | 0.2 | 0.1 | 0.1 | |
| FF | 0.0851 | 0.0805 | 0.1412 | 0.018 | 0.0681 | 0.0775 |
| Parameters | Percentage Change | Dynamic Features | ΔF1 (Hz) | ΔF2 (Hz) | ΔF3 (Hz) | ΔP12 (P.U) | ΔP13 (P.U) | ΔP23 (P.U) |
| Normal | OS | 102.1 | 84.31 | 0.065 | 0.271 | 0.027 | 0.0349 | |
| US | −3.373 | −2.661 | −0.389 | −0.023 | −0.171 | −0.201 | ||
| ST (Sec.) | 0.1 | 0.14 | 0.3 | 0.2 | 0.1 | 0.1 | ||
| OS | 194.1 | 157.9 | 0.08726 | 0.4296 | 0.02791 | 0.03454 | ||
| US | −4.011 | −3.125 | −0.6457 | −0.03669 | −0.2238 | −0.2498 | ||
| ST (Sec.) | 0.16 | 0.266 | 0.3 | 0.33 | 0.21 | 0.43 | ||
| OS | 24.68 | 25.09 | 0.01334 | 0.2225 | 0.05161 | 0.05813 | ||
| US | −3.531 | −2.786 | −0.3295 | −0.03635 | −0.1802 | −0.2132 | ||
| ST (Sec.) | 0.165 | 0.183 | 0.56 | 0.33 | 0.5 | 0.55 | ||
| OS | 93.67 | 84.57 | 0.0738 | 0.2175 | 0.03014 | 0.04033 | ||
| US | −3.625 | −2.887 | −0.4295 | −0.02534 | −0.189 | −0.2214 | ||
| ST (Sec.) | 0.12 | 0.2 | 0.41 | 0.37 | 0.33 | 0.5 | ||
| OS | 96.36 | 84.55 | 0.0739 | 0.221 | 0.03007 | 0.04004 | ||
| US | −3.65 | −2.889 | −0.4295 | −0.02533 | −0.1891 | −0.2216 | ||
| ST (Sec.) | 0.17 | 0.22 | 0.53 | 0.37 | 0.42 | 0.56 | ||
| OS | 47.2 | 27.52 | 0.07199 | 0.1216 | 0.0295 | 0.03902 | ||
| US | −3.198 | −2.502 | −0.3291 | −0.0204 | −0.144 | −0.1741 | ||
| ST (Sec.) | 0.213 | 0.125 | 0.5 | 0.466 | 0.418 | 0.52 | ||
| OS | 158.8 | 141.6 | 0.07559 | 0.4668 | 0.0307 | 0.04119 | ||
| US | −4.058 | −3.228 | −0.5264 | −0.03436 | 0.232 | −0.2682 | ||
| ST (Sec.) | 0.14 | 0.253 | 0.445 | 0.4 | 0.41 | 0.47 | ||
| OS | 73.54 | 47.16 | 0.06787 | 0.07678 | 0.02856 | 0.03597 | ||
| US | −3.172 | −2.472 | −0.3192 | −0.02015 | −0.1391 | −0.1646 | ||
| ST (Sec.) | 0.144 | 0.12 | 0.55 | 0.43 | 0.554 | 0.52 | ||
| OS | 94.11 | 63.13 | 0.1318 | 0.121 | 0.03491 | 0.0729 | ||
| US | −4.082 | −3.261 | −0.5379 | −0.0336 | −0.2395 | −0.2781 | ||
| ST (Sec.) | 0.145 | 0.157 | 0.4 | 0.44 | 0.35 | 0.4 | ||
| , | OS | 96.31 | 84.51 | 0.07636 | 0.2189 | 0.03003 | 0.04003 | |
| US | −3.649 | −2.889 | −0.4294 | −0.0253 | −0.189 | −0.2215 | ||
| ST (Sec.) | 0.19 | 0.14 | 0.5 | 0.37 | 0.43 | 0.42 | ||
| OS | 96.44 | 84.61 | 0.07391 | 0.2193 | 0.03006 | 0.04017 | ||
| US | −3.65 | −2.89 | −0.4296 | −0.02553 | −0.1891 | −0.2216 | ||
| ST (Sec.) | 0.12 | 0.14 | 0.42 | 0.35 | 0.5 | 0.5 | ||
| , , | OS | 80.05 | 71.25 | 0.0728 | 0.07651 | 0.02979 | 0.03951 | |
| US | −3.661 | −2.901 | −0.3359 | −0.01876 | −0.1469 | −0.1746 | ||
| ST (Sec.) | 0.12 | 0.14 | 0.43 | 0.23 | 0.4 | 0.4 | ||
| OS | 112.9 | 95.82 | 0.0745 | 0.3736 | 0.0303 | 0.0406 | ||
| US | −3.644 | −2.874 | −0.5172 | −0.0321 | −0.2286 | −0.2647 | ||
| ST (Sec.) | 0.13 | 0.094 | 0.36 | 0.206 | 0.35 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhazmi, A.H.; Megahed, A.I.; Elrashidi, A.; AboRas, K.M. Development of an Optimal Novel Cascaded 1+TDFλ/PIλDμ Controller for Frequency Management in a Triple-Area Power Grid Considering Nonlinearities and PV/Wind Integration. Mathematics 2025, 13, 2985. https://doi.org/10.3390/math13182985
Alhazmi AH, Megahed AI, Elrashidi A, AboRas KM. Development of an Optimal Novel Cascaded 1+TDFλ/PIλDμ Controller for Frequency Management in a Triple-Area Power Grid Considering Nonlinearities and PV/Wind Integration. Mathematics. 2025; 13(18):2985. https://doi.org/10.3390/math13182985
Chicago/Turabian StyleAlhazmi, Abdullah Hameed, Ashraf Ibrahim Megahed, Ali Elrashidi, and Kareem M. AboRas. 2025. "Development of an Optimal Novel Cascaded 1+TDFλ/PIλDμ Controller for Frequency Management in a Triple-Area Power Grid Considering Nonlinearities and PV/Wind Integration" Mathematics 13, no. 18: 2985. https://doi.org/10.3390/math13182985
APA StyleAlhazmi, A. H., Megahed, A. I., Elrashidi, A., & AboRas, K. M. (2025). Development of an Optimal Novel Cascaded 1+TDFλ/PIλDμ Controller for Frequency Management in a Triple-Area Power Grid Considering Nonlinearities and PV/Wind Integration. Mathematics, 13(18), 2985. https://doi.org/10.3390/math13182985





