Tail Conditional Expectation and Tail Variance for Extended Generalized Skew-Elliptical Distributions

Abstract

This study derives explicit expressions for the Tail Conditional Expectation (TCE) and Tail Variance (TV) within the framework of the extended generalized skew-elliptical (EGSE) distribution. The EGSE family generalizes the class of elliptical distributions by incorporating a selection method, thereby allowing simultaneous and flexible control over location, scale, skewness, and tail heaviness in a unified parametric setting. As notable special cases, our results encompass the extended skew-normal, extended skew-Student-t, extended skew-logistic, and extended skew-Laplace distributions. The derived formulas extend existing results for generalized skew-elliptical distributions and reduce, to a considerable extent, the reliance on numerical integration, thus enhancing their tractability for actuarial and financial risk assessment. The practical utility of the proposed framework is further illustrated through an empirical analysis based on real stock market data, highlighting its effectiveness in quantifying and contrasting the heterogeneous tail risk profiles of financial assets.

1. Introduction

Risk measurement constitutes a cornerstone of modern finance, insurance, and actuarial science, providing a quantitative foundation for capital allocation, regulatory compliance, and strategic decision-making. Among the most widely implemented measures is the Value-at-Risk (VaR), originally popularized in the banking industry through J.P. Morgan’s RiskMetrics framework [1]. For a loss random variable X with cumulative distribution function (cdf) $F_X\left(x\right)$ and confidence level $q\in (0,1)$, VaR is defined as

$$\begin{array}{c}\hfill {VaR}_q\left(X\right):=inf\{x\in \mathbb{R}\mid F_X\left(x\right)\ge q\},\end{array}$$

(1)

which represents the smallest loss threshold exceeded with probability $1-q$. Despite its computational simplicity, VaR fails to satisfy the coherence axioms of [2]—most notably subadditivity—and moreover conveys no information about the severity of losses beyond the designated quantile.

To address this limitation, the Tail Conditional Expectation (TCE), also referred to as the Conditional Tail Expectation (CTE) or Expected Shortfall (ES), is defined as

$$\begin{array}{c}\hfill {TCE}_q\left(X\right)=\mathbb{E}[X\mid X>{VaR}_q\left(X\right)],\end{array}$$

(2)

representing the expected loss conditional on exceeding the VaR level [3,4]. Unlike VaR, TCE is a coherent risk measure and provides particular advantages in capturing extreme outcomes in heavy-tailed distributions. As a complementary measure, the Tail Variance (TV), introduced by [5], quantifies the dispersion of losses beyond the VaR threshold:

$$\begin{array}{c}\hfill {TV}_q\left(X\right)=\mathbb{E}\left[{(X-{TCE}_q\left(X\right))}^2\mid X>{VaR}_q\left(X\right)\right],\end{array}$$

(3)

thereby measuring the variability of extreme losses [6]. Extensions to higher-order measures, such as tail skewness, tail kurtosis, and tail co-skewness, have also been proposed (see, e.g., [3,7,8]). Nevertheless, in practice, particularly in stress testing, solvency analysis, and capital adequacy assessment, VaR, TCE, and TV remain the predominant benchmarks for tail risk.

Most analytical results for these measures have been derived under elliptical distributional assumptions, such as the normal or Student-t families, which impose symmetry and afford closed-form tractability [3,9]. However, mounting empirical evidence highlights the inadequacy of symmetry for realistic risk modeling. Financial data frequently display marked asymmetry [10,11,12]. For example, negative skewness is a persistent feature of stock returns [13], closely linked to crash risk [14], and predictive of future bond and interest rate dynamics through biased market beliefs [15]. In actuarial applications, loss distributions such as rainfall-related insurance are often strongly right-skewed with heavy tails, which symmetric models fail to capture [16].

These empirical challenges have motivated the development of more flexible families. The seminal skew-normal distribution of [17], later extended to the multivariate setting [18], provided the foundation for a broad spectrum of skewed models, including the skew-Student-t, the generalized skew-elliptical (GSE), and the extended generalized skew-elliptical (EGSE) families [6,19,20]. Recent methodological advances further emphasize this necessity. For example, Zhang et al. [21] develop skew-elliptical link models for imbalanced correlated data, while generalized hyperbolic (GH) distributions provide additional flexibility for modeling both skewness and heavy tails [22,23]. Most of these frameworks introduce asymmetry via conditioning or selection mechanisms, thereby offering robust tools for capturing the complex distributional features observed in finance and insurance.

Within this broader class, the EGSE distribution [20] stands out as a particularly powerful and unifying framework. By applying a selection distribution H, the EGSE family simultaneously accommodates location, scale, skewness, and tail heaviness within a single parametric structure while preserving analytical tractability. It subsumes many widely used distributions as special cases. For instance, the extended skew-normal (ESN) distribution has resolved the long-standing ‘wrong skewness’ issue in stochastic frontier analysis [24], with its moment properties further exploited in risk management applications such as TCE computation [25]. Similarly, the extended skew-t (EST) distribution provides a versatile framework for complex multivariate data with censoring or missing observations, accommodating skewness and heavy tails simultaneously [26]. The preservation of analytical tractability across these subclasses renders the EGSE family an ideal vehicle for extending classical results on tail risk measures beyond the restrictive symmetric setting.

This paper investigates the derivation of the risk measures TCE and TV under the extended generalized skew-elliptical (EGSE) distribution and offers three main contributions. First, we derive explicit closed-form expressions for the TCE and TV of the EGSE distribution in a general case. These formulas extend existing results for the generalized skew-elliptical distribution [6,27], thereby enlarging the class of skewed and heavy-tailed models for which analytical tail risk measures are available. Second, we demonstrate that, through its selection distribution mechanism, the EGSE framework subsumes several important subclasses—namely, the extended skew-normal, extended skew-Student-t, extended skew-logistic, and extended skew-Laplace distributions—so that our formulas for TCE and TV apply uniformly across these models. Third, we present a numerical illustration based on real-world stock market data to highlight the practical relevance of our analytical results. Specifically, we model the annualized log-losses of four major stocks using the extended skew-normal distribution and apply the derived formulas to compute their TCE and TV. The empirical findings demonstrate how our tractable expressions can be directly implemented to quantify and compare the heterogeneous tail risk profiles of financial assets, thereby providing valuable insights for both financial and actuarial practice.

The remainder of the paper is organized as follows. Section 2 reviews the EGSE family and presents our preliminary results. Section 3 derives the TCE and TV for the univariate EGSE distribution. Section 4 provides explicit expressions for these measures in the four subclasses. Section 5 presents a numerical illustration using stock market data to assess tail risks. Section 6 concludes the paper.

2. Extended Generalized Skew-Elliptical Distributions

We begin by considering the class of elliptical distributions. Several equivalent formulations exist for defining random vectors within this class. In line with [28], we adopt the following definition, and all integrations discussed in this paper are tacitly assumed to exist.

Definition 1

(Multivariate elliptical distribution). A random vector $\mathit{X}={(X_1,\dots ,X_n)}^{\top }$ is said to follow a multivariate elliptical distribution, denoted by $\mathit{X}\sim E_n(\mathit{\mu },\mathbf{\Sigma },\psi )$, if its characteristic function takes the form

$${\phi }_{\mathit{X}}\left(\mathit{t}\right)=\mathbb{E}\left[exp\left(i{\mathit{t}}^{\top }\mathit{X}\right)\right]=exp\left(i{\mathit{t}}^{\top }\mathit{\mu }\right)\psi \left({\displaystyle \frac{1}{2}}{\mathit{t}}^{\top }\mathbf{\Sigma }\mathit{t}\right),$$

where μ is the location vector, Σ is an $n\times n$ scale matrix, and $\psi (·)$ is the characteristic generator function.

In general, if the density exists, it has the following form:

$$\begin{array}{c}\hfill f_{\mathit{X}}\left(x\right)={\displaystyle \frac{1}{\sqrt{|\mathbf{\Sigma }|}}}{g}^{\left(n\right)}\left({\displaystyle \frac{1}{2}}{(x-\mathit{\mu })}^{\top }{\mathbf{\Sigma }}^{-1}(x-\mathit{\mu })\right),\end{array}$$

where the the density generator function $g^{\left(n\right)}(·)$ satisfies the condition

$$\begin{array}{c}\hfill {\int }_0^{\infty }{x}^{n/2-1}{g}^{\left(n\right)}\left(x\right)dx<\infty .\end{array}$$

The family of skew-elliptical distributions encompasses a variety of constructions that have found extensive applications in statistics and related scientific fields. The seminal skew-normal distribution was first introduced by [17] and subsequently extended to the multivariate setting by [18]. Building on these developments, Branco and Dey [19] and Azzalini and Capitanio [29] proposed the broader class of skew-elliptical distributions, which includes prominent members such as the skew-normal, skew-Student-t, and skew-Pearson type II distributions. Alternative approaches have also been considered, for example, the truncation-based construction of [30] and the skew-symmetric framework studied by [31]. Further generalizations were introduced by [20], who investigated the extended generalized skew-elliptical (EGSE) family and derived explicit expressions for moments and covariance structures. Subsequent contributions have enriched this literature, including [32,33,34].

In this paper, we focus on the class of extended generalized skew-elliptical (EGSE) distributions. To present their definition in a rigorous manner, we begin with the following lemma, which plays a central role (see also [20] for further details).

Lemma 1.

Let $\mathit{X}\sim E_n(\mathit{\mu },\mathbf{\Sigma },g^{\left(n\right)})$, and let U be a symmetric random variable with distribution function $H\left(u\right)$ and density $h\left(u\right)$. Let $\gamma \in {\mathbb{R}}^n$ and $\beta \in \mathbb{R}$ be constants, where ${({\gamma }^{\top },\beta )}^{\top }$ is referred to as the vector of skewness parameters. Define $\varsigma =U-{\gamma }^{\top }\mathit{X}$ with density $f_{\varsigma }(·)$ and distribution function $F_{\varsigma }(·)$, which corresponds to the independent convolution of U and $-{\gamma }^{\top }\mathit{X}$. Then

$$\begin{array}{cc}\hfill \mathbb{E}\left[H\left({\gamma }^{\top }\mathit{X}+\beta \right)\right]& ={\displaystyle \frac{1}{{|\mathbf{\Sigma }|}^{1/2}}}{\int }_{{\mathbb{R}}^n}H({\gamma }^{\top }\mathit{x}+\beta )g^{\left(n\right)}\left({\displaystyle \frac{1}{2}}{(\mathit{x}-\mathit{\mu })}^{\top }{\mathbf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right)d\mathit{x}\hfill \\ \hfill & =F_{\varsigma }\left(\beta \right),\hfill \end{array}$$

(4)

and

$$\begin{array}{cc}\hfill \mathbb{E}\left[h\left({\gamma }^{\top }\mathit{X}+\beta \right)\right]& ={\displaystyle \frac{1}{{|\mathbf{\Sigma }|}^{1/2}}}{\int }_{{\mathbb{R}}^n}h({\gamma }^{\top }\mathit{x}+\beta )g^{\left(n\right)}\left({\displaystyle \frac{1}{2}}{(\mathit{x}-\mathit{\mu })}^{\top }{\mathbf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right)d\mathit{x}\hfill \\ \hfill & =f_{\varsigma }\left(\beta \right).\hfill \end{array}$$

(5)

Proof. 

See Appendix A. □

Remark 1.

Let $\mathit{X}\sim N_n(\mathit{\mu },\mathbf{\Sigma })$ and $U\sim N_1(0,1)$ be independent. Then $\varsigma =U-{\gamma }^{\top }\mathit{X}$ follows the univariate normal distribution

$$\varsigma \sim N_1\left(-{\gamma }^{\top }\mathit{\mu },1+{\gamma }^{\top }\mathbf{\Sigma }\gamma \right).$$

Consequently,

$$\begin{array}{cc}\hfill \mathbb{E}\left[\Phi \left({\gamma }^{\top }\mathit{X}+\beta \right)\right]& =\mathbb{P}\left(\varsigma \le \beta \right)\hfill \\ \hfill & =\mathbb{P}\left({\displaystyle \frac{\varsigma +{\gamma }^{\top }\mathit{\mu }}{\sqrt{1+{\gamma }^{\top }\mathbf{\Sigma }\gamma }}}\le {\displaystyle \frac{\beta +{\gamma }^{\top }\mathit{\mu }}{\sqrt{1+{\gamma }^{\top }\mathbf{\Sigma }\gamma }}}\right)\hfill \\ \hfill & =\Phi \left({\displaystyle \frac{\beta +{\gamma }^{\top }\mathit{\mu }}{\sqrt{1+{\gamma }^{\top }\mathbf{\Sigma }\gamma }}}\right),\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \mathbb{E}\left[\varphi \left({\gamma }^{\top }\mathit{X}+\beta \right)\right]={\displaystyle \frac{1}{\sqrt{1+{\gamma }^{\top }\mathbf{\Sigma }\gamma }}}\varphi \left({\displaystyle \frac{\beta +{\gamma }^{\top }\mathit{\mu }}{\sqrt{1+{\gamma }^{\top }\mathbf{\Sigma }\gamma }}}\right),\end{array}$$

where $\Phi (·)$ and $\varphi (·)$ denote the cdf and pdf of the standard normal distribution, respectively.

We now provide the formal definition of the EGSE distribution; additional details are available in [20].

Definition 2

(Multivariate EGSE distribution). Using the notations introduced in Lemma 1, we say that an n-variate random vector $\mathit{Y}$ follows an extended generalized skew-elliptical (EGSE) distribution, denoted by

$$\mathit{Y}\sim {EGSE}_n\left(\mathit{\mu },\mathbf{\Sigma },\gamma ,\beta ,g^{\left(n\right)},H\right),$$

where $\mathit{\mu }\in {\mathbb{R}}^n$ is the location vector, Σ is an $n\times n$ positive-definite scale matrix, $g^{\left(n\right)}$ is a density generator function that determines the elliptical family (e.g., normal, Student-t), H is a symmetric skewing distribution function, and $\gamma \in {\mathbb{R}}^n$ and $\beta \in \mathbb{R}$ are the skewness parameters. The probability density function is given by

$$\begin{array}{cc}\hfill f_{\mathit{Y}}\left(\mathit{y}\right)& ={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}{\displaystyle \frac{1}{{|\mathbf{\Sigma }|}^{1/2}}}{g}^{\left(n\right)}\left({\displaystyle \frac{1}{2}}{(\mathit{y}-\mathit{\mu })}^{\top }{\mathbf{\Sigma }}^{-1}(\mathit{y}-\mathit{\mu })\right)H\left({\gamma }^{\top }\mathit{y}+\beta \right),\hfill \end{array}$$

(6)

where $\varsigma =U-{\gamma }^{\top }\mathit{X}$.

Lemma 1 ensures the non-negativity and integrability conditions required for the above density function. Consequently, the univariate extended generalized skew-elliptical distribution, denoted by

$$Y\sim {\mathrm{EGSE}}_1(\mu ,{\sigma }^2,\gamma ,\beta ,g_1,H),$$

with density $f_Y\left(y\right)$, is well defined (see [20]):

$$f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}{g}_1\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)H(\gamma y+\beta ).$$

Remark 2.

Density (6) can also be derived by employing the selection method for random vectors, as proposed in [32]. Specifically, let $\mathit{Y}\stackrel{d}{=}(\mathit{V}\mid \mathit{X}\in \mathbb{S})$, where $\mathit{V}\in {\mathbb{R}}^n$ is a random vector, and $\mathbb{S}$ is a measurable subset of ${\mathbb{R}}^n$. Hence, the density of $\mathit{Y}$ is given by

$$f_{\mathit{Y}}\left(\mathit{y}\right)=f_{\mathit{X}}\left(\mathit{y}\right){\displaystyle \frac{\mathbb{P}(\mathit{X}\in \mathbb{S}\mid \mathit{V}=\mathit{y})}{\mathbb{P}(\mathit{X}\in \mathbb{S})}}.$$

In fact, if we define the selection variable $\mathit{Y}\stackrel{d}{=}(\mathit{X}\mid \varsigma \le \beta )$, then the pdf of $\mathit{Y}$ is given by (6).

As an extension of the generalized skew-elliptical (GSE) distribution, the EGSE distribution reduces to the GSE distribution under a specific parameter configuration.

Remark 3.

For $\mathit{Y}\sim {\mathrm{EGSE}}_n\left(\mathit{\mu },\mathbf{\Sigma },\gamma ,\beta ,g^{\left(n\right)},H\right)$, if we set ${\gamma }^{\top }={\overline{\gamma }}^{\top }{\overline{\mathbf{\Sigma }}}^{-1/2}$ and $\beta =-{\overline{\gamma }}^{\top }{\overline{\mathbf{\Sigma }}}^{-1/2}\mathit{\mu }$, then $\mathit{Y}$ reduces to the GSE distribution

$$\overline{\mathit{Y}}\sim {\mathrm{GSE}}_n\left(\mathit{\mu },\mathbf{\Sigma },\overline{\gamma },g^{\left(n\right)},H\right),$$

with the probability density function

$$\begin{array}{c}\hfill f_{\mathit{Y}}\left(\mathit{y}\right)={\displaystyle \frac{2}{{|\mathbf{\Sigma }|}^{1/2}}}{g}^{\left(n\right)}\left({\displaystyle \frac{1}{2}}{(\mathit{y}-\mathit{\mu })}^{\top }{\mathbf{\Sigma }}^{-1}(\mathit{y}-\mathit{\mu })\right)H\left({\overline{\gamma }}^{\top }{\mathbf{\Sigma }}^{-1/2}(\mathit{y}-\mathit{\mu })\right).\end{array}$$

For further details, see [6].

3. The TCE and TV for Univariate EGSE Distributions

Although extensive research has been devoted to the computation of classical risk measures under symmetric elliptical distributions, comparatively little attention has been paid to their counterparts within asymmetric families such as the EGSE. To address this gap, we extend the definitions of the Tail Conditional Expectation (TCE) and Tail Variance (TV) to the EGSE framework. In what follows, we concentrate on the univariate EGSE distribution in order to derive and analyze these risk measures.

In the univariate case, let $X\sim E_1(\mu ,{\sigma }^2,g_1)$. The standardized variable $Z=(X-\mu )/\sigma$ then follows a standard elliptical distribution (also referred to as a spherical distribution), i.e., $Z\sim E_1(0,1,g_1)$. Its distribution function is given by

$$\begin{array}{c}\hfill F_Z\left(z\right)={\int }_{-\infty }^z{g}_1\left({\displaystyle \frac{1}{2}}{u}^2\right)du,\end{array}$$

with mean 0 and variance

$$\begin{array}{c}\hfill {\sigma }_Z^2=2{\int }_0^{\infty }{u}^2{g}_1\left({\displaystyle \frac{1}{2}}{u}^2\right)du=-{\psi }^{\prime }\left(0\right),\end{array}$$

provided that the condition $|{\psi }^{\prime }\left(0\right)|<\infty$ holds. Moreover, when the generator of the elliptical family is chosen such that ${\psi }^{\prime }\left(0\right)=-1$, it follows that ${\sigma }_Z^2=1$.

To calculate the risk measures, following [20,35], we employ the cumulative tail generator associated with the elliptical family, defined by

$$\begin{array}{c}\hfill {\overline{G}}_1\left(x\right)={\int }_x^{\infty }{g}_1\left(u\right)du,\end{array}$$

(7)

and

$$\begin{array}{c}\hfill {\overline{\mathcal{G}}}_1\left(x\right)={\int }_x^{\infty }{\overline{G}}_1\left(u\right)du,\end{array}$$

(8)

with the convention ${\overline{G}}_1(\infty )={\overline{\mathcal{G}}}_1(\infty )=0$.

Let $Z^{*}\sim E_1(0,1,{\overline{G}}_1)$ and $Z^{**}\sim E_1(0,1,{\overline{\mathcal{G}}}_1)$ be two standardized random variables. Suppose the following variances are finite:

$$\begin{array}{cc}\hfill {\sigma }_Z^2& =2c_1{\int }_0^{\infty }{u}^2{g}_1\left(\frac{1}{2}{u}^2\right)du<\infty ,\hfill \\ \hfill {\sigma }_{Z^{*}}^2& =2{\int }_0^{\infty }{u}^2{\overline{G}}_1\left(\frac{1}{2}{u}^2\right)du=\sqrt{2}{\int }_0^{\infty }\sqrt{u}{\overline{G}}_1\left(u\right)du<\infty .\hfill \end{array}$$

Then, the probability density functions of $Z^{*}$ and $Z^{**}$ are given, respectively, by

$$\begin{array}{cc}\hfill f_{Z^{*}}\left(z\right)& ={\displaystyle \frac{1}{{\sigma }_Z^2}}{\overline{G}}_1\left(\frac{1}{2}{z}^2\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill f_{Z^{**}}\left(z\right)& ={\displaystyle \frac{1}{{\sigma }_{Z^{*}}^2}}{\overline{\mathcal{G}}}_1\left(\frac{1}{2}{z}^2\right),\hfill \end{array}$$

(10)

where both $Z^{*}$ and $Z^{**}$ are additional spherical random variables, referred to as the associated random variables of Z; see, for example, [3,27]. These associated random variables are theoretical constructs that arise naturally when calculating tail moments of elliptical distributions. Their densities, formed from the tail generator functions, serve as a mathematical tool to simplify the derivation of tail risk measures like TCE and TV.

Proposition 1 presents the expression for TCE of the EGSE distribution.

Proposition 1.

Let $Y\sim EGS{E}_1(\mu ,{\sigma }^2,\gamma ,\beta ,g_1,H)$, and let the TCE for a univariate EGSE distribution be given by

$${\mathit{TCE}}_q\left(Y\right)=\mu +{\Lambda }_{1,q}\sigma ,$$

(11)

where

$$\begin{array}{cc}\hfill {\Lambda }_{1,q}& ={\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\left(H(\gamma \sigma z_q+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)+\gamma \sigma \kappa \left(z_q\right)\right),\hfill \end{array}$$

(12)

and

$$\begin{array}{cc}\hfill z_q& ={\mathit{VaR}}_q\left(Z\right)={\displaystyle \frac{y_q-\mu }{\sigma }},\hfill \\ \hfill \kappa \left(z_q\right)& ={\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)h(\gamma \sigma z+\gamma \mu +\beta )dz.\hfill \end{array}$$

Proof. 

See Appendix B. □

Remark 4.

As noted in Remark 3, if we set $\gamma ={\displaystyle \frac{\overline{\gamma }}{\sigma }}$ and $\beta =-{\displaystyle \frac{\overline{\gamma }\mu }{\sigma }}$, the TCE expression reduces to that of the generalized skew-elliptical distribution $\overline{Y}\sim {GSE}_1(\mu ,{\sigma }^2,\overline{\gamma },g_1,H)$, namely,

$$\begin{array}{c}\hfill TC{E}_q\left(\overline{Y}\right)=\mu +{\overline{\Lambda }}_{1,q}\sigma ,\end{array}$$

where

$$\begin{array}{cc}\hfill {\overline{\Lambda }}_{1,q}& ={\displaystyle \frac{2}{1-q}}\left(H\left(\overline{\gamma }{z}_q\right){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)+\overline{\gamma }\overline{\kappa }\left(z_q\right)\right),\hfill \end{array}$$

(13)

with

$$\begin{array}{c}\hfill \overline{\kappa }\left(z_q\right)={\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)h\left(\overline{\gamma }z\right)dz,\end{array}$$

which coincides with the results derived in [6,36].

Remark 5.

When $q=0$, the expectation of Y can be obtained (cf. [20]) as follows:

$$\begin{array}{cc}\hfill \mathbb{E}\left[Y\right]=& \underset{q\to 0}{lim}{\mathit{TCE}}_q\left(Y\right)\hfill \\ \hfill =& \mu +\underset{q\to 0}{lim}{\displaystyle \frac{1}{1-q}}{\displaystyle \frac{\sigma }{F_{\varsigma }\left(\beta \right)}}\left(H(\gamma \sigma z_q+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)+\gamma \sigma \kappa \left(z_q\right)\right)\hfill \\ \hfill =& \mu +{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\gamma {\sigma }^2{\int }_{-\infty }^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)h(\gamma \sigma z+\gamma \mu +\beta )dz\hfill \\ \hfill =& \mu +{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\gamma {\sigma }^2{\sigma }_Z^2{\int }_{-\infty }^{\infty }{\displaystyle \frac{1}{{\sigma }_Z^2\sigma }}{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)h(\gamma y+\beta )dy\hfill \\ \hfill =& \mu +{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\gamma {\sigma }^2{\sigma }_Z^2{f}_{{\varsigma }^{*}}\left(\beta \right),\hfill \end{array}$$

where ${\varsigma }^{*}=U-\gamma X^{*}$, with U having distribution $H\left(u\right)$, and $X^{*}\sim E_1\left(\mu ,{\sigma }^2,{\displaystyle \frac{1}{{\sigma }_Z^2}}{\overline{G}}^{\left(1\right)}\right)$; see Lemma 4.

We now present the Tail Variance measure for the extended generalized skew-elliptical distributions.

Proposition 2.

For a univariate EGSE distribution, the TV is given by

$$\begin{array}{cc}\hfill {\mathit{TV}}_q\left(Y\right)=& {\displaystyle \frac{{\sigma }^2}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(z_q·H(\gamma \sigma z_q+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)+{\kappa }_1\left(z_q\right)\hfill \\ \hfill & +\gamma \sigma \left(h(\gamma \sigma z_q+\gamma \mu +\beta ){\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)+\gamma \sigma {\kappa }_2\left(z_q\right)\right))-{\left({\Lambda }_{1,q}\sigma \right)}^2.\hfill \end{array}$$

(14)

where ${\Lambda }_{1,q}$ is given by (12), and

$$\begin{array}{cc}\hfill {\kappa }_1\left(z_q\right)=& {\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)H(\gamma \sigma z+\gamma \mu +\beta )dz,\hfill \\ \hfill {\kappa }_2\left(z_q\right)=& {\int }_{z_q}^{\infty }{\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)h^{\prime }(\gamma \sigma z+\gamma \mu +\beta )dz.\hfill \end{array}$$

Proof. 

See Appendix C. □

Remark 6.

By setting $\gamma ={\displaystyle \frac{\overline{\gamma }}{\sigma }}$ and $\beta =-{\displaystyle \frac{\overline{\gamma }\mu }{\sigma }}$ in (14), the TV expression reduces to that of the generalized skew-elliptical distribution $\overline{Y}\sim {\mathrm{GSE}}_1(\mu ,{\sigma }^2,\overline{\gamma },g_1,H)$, namely,

$$\begin{array}{cc}\hfill {\mathit{TV}}_q\left(Y\right)=& {\displaystyle \frac{2{\sigma }^2}{1-q}}(z_q·H\left(\overline{\gamma }{z}_q\right){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)+{\overline{\kappa }}_1\left(z_q\right)\hfill \\ \hfill & +\overline{\gamma }\left(h\left(\overline{\gamma }{z}_q\right){\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)+\overline{\gamma }{\overline{\kappa }}_2\left(z_q\right)\right))-{\left({\overline{\Lambda }}_{1,q}\sigma \right)}^2.\hfill \end{array}$$

where ${\overline{\Lambda }}_{1,q}$ is given by (13), and

$$\begin{array}{cc}\hfill {\overline{\kappa }}_1\left(z_q\right)=& {\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)H\left(\overline{\gamma }{z}_q\right)dz,\hfill \\ \hfill {\overline{\kappa }}_2\left(z_q\right)=& {\int }_{z_q}^{\infty }{\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)h^{\prime }\left(\overline{\gamma }{z}_q\right)dz,\hfill \end{array}$$

which is consistent with the results in [6].

Remark 7.

When we take $q=0$, we can obtain the expectation of Y, c.f., [20], that is,

$$\begin{array}{cc}\hfill \mathit{Var}\left[Y\right]=& \underset{q\to 0}{lim}{\mathit{TV}}_q\left(Y\right)\hfill \\ \hfill =& {\sigma }^2{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\left(\underset{q\to 0}{lim}{\kappa }_1\left(z_q\right)+{\gamma }^2{\sigma }^2\underset{q\to 0}{lim}{\kappa }_2\left(z_q\right)\right)-{\left(\underset{q\to 0}{lim}{\Lambda }_{1,q}\sigma \right)}^2.\hfill \end{array}$$

In particular,

$$\begin{array}{cc}\hfill \underset{q\to 0}{lim}{\kappa }_1\left(z_q\right)=& {\int }_{-\infty }^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)H(\gamma \sigma z+\gamma \mu +\beta )dz\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }{\displaystyle \frac{1}{\sigma }}{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)H(\gamma y+\beta )dy\hfill \\ \hfill =& {\sigma }_Z^2{\int }_{-\infty }^{\infty }{\displaystyle \frac{1}{{\sigma }_Z^2\sigma }}{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)H(\gamma y+\beta )dy\hfill \\ \hfill =& {\sigma }_Z^2{F}_{{\varsigma }^{*}}\left(\beta \right),\hfill \end{array}$$

where ${\varsigma }^{*}=U-\gamma X^{*}$, U has distribution $H\left(u\right)$, and $X^{*}\sim E_1\left(\mu ,{\sigma }^2,{\displaystyle \frac{1}{{\sigma }_Z^2}}{\overline{G}}^{\left(1\right)}\right)$.

Similarly,

$$\begin{array}{cc}\hfill \underset{q\to 0}{lim}{\kappa }_2\left(z_q\right)=& {\int }_{-\infty }^{\infty }{\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)h^{\prime }(\gamma \sigma z+\gamma \mu +\beta )dz\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }{\displaystyle \frac{1}{\sigma }}{\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)h^{\prime }(\gamma y+\beta )dy\hfill \\ \hfill =& {\sigma }_{Z^{*}}^2{\int }_{-\infty }^{\infty }{\displaystyle \frac{1}{{\sigma }_{Z^{*}}^2\sigma }}{\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)h^{\prime }(\gamma y+\beta )dy\hfill \\ \hfill =& {\sigma }_{Z^{*}}^2{\displaystyle \frac{\partial }{\partial \beta }}{\int }_{-\infty }^{\infty }{\displaystyle \frac{1}{{\sigma }_{Z^{*}}^2\sigma }}{\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)h(\gamma y+\beta )dy\hfill \\ \hfill =& {\sigma }_{Z^{*}}^2{\displaystyle \frac{\partial }{\partial \beta }}{f}_{{\varsigma }^{**}}\left(\beta \right),\hfill \end{array}$$

where ${\varsigma }^{**}=U-\gamma X^{**}$, with $X^{**}\sim E_1(\mu ,{\sigma }^2,{\displaystyle \frac{1}{{\sigma }_{Z^{*}}^2}}{\overline{\mathcal{G}}}^{\left(1\right)})$.

Therefore, we obtain

$$\begin{array}{cc}\hfill \mathit{Var}\left[Y\right]=& {\sigma }^2{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\left({\sigma }_Z^2{F}_{{\varsigma }^{*}}\left(\beta \right)+{\gamma }^2{\sigma }^2{\sigma }_{Z^{*}}^2{\displaystyle \frac{\partial }{\partial \beta }}{f}_{{\varsigma }^{**}}\left(\beta \right)\right)\hfill \\ \hfill & -{\left({\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\gamma {\sigma }^2{\sigma }_Z^2{f}_{{\varsigma }^{*}}\left(\beta \right)\right)}^2,\hfill \end{array}$$

which is the same as the equation in [20].

4. Expressions for the Proposed TCE and TV

In this section, we derive the proposed TCE and TV measures for four well-known subclasses of the extended generalized skew-elliptical family, namely the extended skew-normal, extended skew-Student-t, extended skew-logistic, and extended skew-Laplace distributions.

4.1. Extended Generalized Skew-Normal Distribution

Assume that Y follows an extended generalized skew-normal distribution, i.e.,

$$Y\sim {EGSN}_1(\mu ,{\sigma }^2,\gamma ,\beta ,H),$$

with probability density function

$$\begin{array}{c}\hfill f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}\varphi \left({\displaystyle \frac{y-\mu }{\sigma }}\right)H\left(\gamma y+\beta \right),\end{array}$$

where $\varsigma =U-\gamma X$, $X\sim N(\mu ,{\sigma }^2)$, and $\varphi (·)$ denotes the standard normal density.

From (7) and (8), we obtain

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left(x\right)=& {\int }_x^{\infty }{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-u}du={\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-x},\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left(x\right)=& {\int }_x^{\infty }{\overline{G}}^{\left(1\right)}\left(u\right)du={\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-x}.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill {\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{x}^2\right)={\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{x}^2\right)=\varphi \left(x\right),\end{array}$$

and the corresponding TCE and TV of Y can be obtained directly from (11) and (14), respectively.

Extended Skew-Normal Distribution

We now consider a special case of the extended generalized skew-normal distribution, where $H=\Phi$ denotes the cumulative distribution function of the standard normal distribution. In this case, the probability density function of Y takes the form

$$\begin{array}{c}\hfill f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}\varphi \left({\displaystyle \frac{y-\mu }{\sigma }}\right)\Phi \left(\gamma y+\beta \right),\end{array}$$

where $\varsigma =U-\gamma X$, with $U\sim N(0,1)$ and $X\sim N(\mu ,{\sigma }^2)$ being independent random variables. It follows that $\varsigma \sim N\left(-\gamma \mu ,1+{\gamma }^2{\sigma }^2\right)$, and hence,

$$\begin{array}{cc}\hfill {\Lambda }_{1,q}=& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }\varphi \left(z\right)\varphi (\gamma \sigma z+\gamma \mu +\beta )dz)\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{z}^2}{\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{1}{2}}{(\gamma \sigma z+\gamma \mu +\beta )}^2}dz)\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +\gamma \sigma {\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{(\gamma \mu +\beta )}^2}{2(1+{\gamma }^2{\sigma }^2)}}}{\displaystyle \frac{1}{\sqrt{1+{\gamma }^2{\sigma }^2}}}\overline{\Phi }\left(\sqrt{1+{\gamma }^2{\sigma }^2}\left(z_q+{\displaystyle \frac{\gamma \sigma (\gamma \mu +\beta )}{1+{\gamma }^2{\sigma }^2}}\right)\right))\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{\Phi \left(\frac{\beta +\gamma \mu }{\sqrt{1+{\gamma }^2{\sigma }^2}}\right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +\gamma \sigma {\displaystyle \frac{1}{\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{(\gamma \mu +\beta )}^2}{2(1+{\gamma }^2{\sigma }^2)}}}{\displaystyle \frac{1}{\sqrt{1+{\gamma }^2{\sigma }^2}}}\overline{\Phi }\left(\sqrt{1+{\gamma }^2{\sigma }^2}\left(z_q+{\displaystyle \frac{\gamma \sigma (\gamma \mu +\beta )}{1+{\gamma }^2{\sigma }^2}}\right)\right)),\hfill \end{array}$$

where the third equality is derived by completing the square in the exponent of the product of the two normal pdfs, which results in a new normal survival function, and then

$$\begin{array}{c}\hfill {\mathrm{TCE}}_q\left(Y\right)=\mu +{\Lambda }_{1,q}\sigma .\end{array}$$

Furthermore, the corresponding Tail Variance is given by

$$\begin{array}{cc}\hfill {\mathrm{TV}}_q\left(Y\right)=& {\displaystyle \frac{{\sigma }^2}{1-q}}{\displaystyle \frac{1}{\Phi \left(\frac{\beta +\gamma \mu }{\sqrt{1+{\gamma }^2{\sigma }^2}}\right)}}(z_q·\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +{\int }_{z_q}^{\infty }\varphi \left(z\right)\Phi (\gamma \sigma z+\gamma \mu +\beta )dz+\gamma \sigma (\varphi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }\varphi \left(z\right){\varphi }^{\prime }(\gamma \sigma z+\gamma \mu +\beta )dz\left)\right)-{\left({\Lambda }_{1,q}\sigma \right)}^2\hfill \\ \hfill =& {\displaystyle \frac{{\sigma }^2}{1-q}}{\displaystyle \frac{1}{\Phi \left(\frac{\beta +\gamma \mu }{\sqrt{1+{\gamma }^2{\sigma }^2}}\right)}}(z_q·\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & +{\int }_{z_q}^{\infty }\varphi \left(z\right)\Phi (\gamma \sigma z+\gamma \mu +\beta )dz+\gamma \sigma (\varphi (\gamma \sigma z_q+\gamma \mu +\beta )\varphi \left(z_q\right)\hfill \\ \hfill & -\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{1}{2\pi }}(\gamma \sigma z+\gamma \mu +\beta )e^{-{\displaystyle \frac{1}{2}}{z}^2-{\displaystyle \frac{1}{2}}{\left(\gamma \sigma z+\gamma \mu +\beta \right)}^2}dz\left)\right)-{\left({\Lambda }_{1,q}\sigma \right)}^2.\hfill \end{array}$$

(15)

4.2. Extended Generalized Skew-Student-t Distribution

Assume that Y follows the extended generalized skew-Student-t distribution, denoted by

$$Y\sim EGSS{t}_1(\mu ,{\sigma }^2,\gamma ,\beta ,m,H),$$

with m degrees of freedom. The probability density function of Y is given by

$$f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}{t}_m\left({\displaystyle \frac{y-\mu }{\sigma }}\right)H\left(\gamma y+\beta \right),$$

where $\varsigma =U-\gamma X$, with $X\sim S{t}_1(\mu ,{\sigma }^2,m)$, and $t_m(·)$ denotes the pdf of the standardized Student-t distribution, i.e.,

$${\displaystyle \frac{X-\mu }{\sigma }}\sim S{t}_1(0,1,m),$$

with

$$t_m\left(x\right)={\displaystyle \frac{\Gamma \left(\frac{m+1}{2}\right)}{\sqrt{m\pi }\Gamma \left(\frac{m}{2}\right)}}{\left[1+{\displaystyle \frac{x^2}{m}}\right]}^{-{\displaystyle \frac{m+1}{2}}}.$$

The corresponding density generator is

$$g^{\left(1\right)}\left(u\right)={\displaystyle \frac{\Gamma \left(\frac{m+1}{2}\right)}{\sqrt{m\pi }\Gamma \left(\frac{m}{2}\right)}}{\left(1+{\displaystyle \frac{2u}{m}}\right)}^{-{\displaystyle \frac{m+1}{2}}}.$$

Therefore,

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left(x\right)=& {\int }_x^{\infty }{\displaystyle \frac{\Gamma \left(\frac{m+1}{2}\right)}{\sqrt{m\pi }\Gamma \left(\frac{m}{2}\right)}}{\left[1+{\displaystyle \frac{2u}{m}}\right]}^{-{\displaystyle \frac{m+1}{2}}}du\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}{\displaystyle \frac{m\Gamma \left(\frac{m-1}{2}\right)}{\sqrt{m\pi }\Gamma \left(\frac{m}{2}\right)}}{\left[1+{\displaystyle \frac{2x}{m}}\right]}^{-{\displaystyle \frac{m-1}{2}}},\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left(x\right)=& {\int }_x^{\infty }{\displaystyle \frac{1}{2}}{\displaystyle \frac{m\Gamma \left(\frac{m-1}{2}\right)}{\sqrt{m\pi }\Gamma \left(\frac{m}{2}\right)}}{\left[1+{\displaystyle \frac{2u}{m}}\right]}^{-{\displaystyle \frac{m-1}{2}}}du\hfill \\ \hfill =& {\displaystyle \frac{1}{4}}{\displaystyle \frac{m^2\Gamma \left(\frac{m-3}{2}\right)}{\sqrt{m\pi }\Gamma \left(\frac{m}{2}\right)}}{\left[1+{\displaystyle \frac{2x}{m}}\right]}^{-{\displaystyle \frac{m-3}{2}}}.\hfill \end{array}$$

In particular, for $m>4$, we have

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{x}^2\right)& =\sqrt{{\displaystyle \frac{m}{m-2}}}{t}_{m-2}\left(\sqrt{{\displaystyle \frac{m-2}{m}}}x\right),\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{x}^2\right)& ={\displaystyle \frac{m}{m-2}}\sqrt{{\displaystyle \frac{m}{m-4}}}{t}_{m-4}\left(\sqrt{{\displaystyle \frac{m-4}{m}}}x\right),\hfill \end{array}$$

where $t_k(·)$ denotes the pdf of the standard Student-t distribution with k degrees of freedom.

Extended Skew-Student-t Distribution

Consider a special case of a generalized skew-Student-t distribution with $H=T_m$, and where the cdf of the standard Student-t distribution has m degrees of freedom. In this case, the pdf of Y is

$$f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}{t}_m\left({\displaystyle \frac{y-\mu }{\sigma }}\right)T_m\left(\gamma y+\beta \right),$$

where $\varsigma =U-\gamma X$, with $U\sim S{t}_1(0,1,m)$ and $X\sim S{t}_1(\mu ,{\sigma }^2,m)$ being independent. The pdf of $\varsigma$ can be written as the convolutions

$$\begin{array}{cc}\hfill f_{\varsigma }\left(x\right)=& {\int }_{-\infty }^{\infty }{f}_U\left(u\right)f_{-\gamma X}(x-u)du\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }{t}_m\left(u\right){\displaystyle \frac{1}{\left|\gamma \right|\sigma }}{t}_m\left({\displaystyle \frac{x-u+\gamma \mu }{\left|\gamma \right|\sigma }}\right)du,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill F_{\varsigma }\left(\beta \right)=& {\int }_{-\infty }^{\beta }{f}_{\varsigma }\left(x\right)dx\hfill \\ \hfill =& {\int }_{-\infty }^{\beta }{\int }_{-\infty }^{\infty }{t}_m\left(u\right){\displaystyle \frac{1}{\left|\gamma \right|\sigma }}{t}_m\left({\displaystyle \frac{x-u+\gamma \mu }{\left|\gamma \right|\sigma }}\right)dudx.\hfill \end{array}$$

Then, we can obtain ${\Lambda }_{1,q}$

$$\begin{array}{cc}\hfill {\Lambda }_{1,q}=& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(T_m\left(\gamma \sigma z_q+\gamma \mu +\beta \right){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)t_m\left(\gamma \sigma z+\gamma \mu +\beta \right)dz)\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(T_m\left(\gamma \sigma z_q+\gamma \mu +\beta \right)\sqrt{{\displaystyle \frac{m}{m-2}}}{t}_{m-2}\left(\sqrt{{\displaystyle \frac{m-2}{m}}}{z}_q\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }\sqrt{{\displaystyle \frac{m}{m-2}}}{t}_{m-2}\left(\sqrt{{\displaystyle \frac{m-2}{m}}}z\right)t_m\left(\gamma \sigma z+\gamma \mu +\beta \right)dz)\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}\left(T_m\right(\gamma \sigma z_q+\gamma \mu +\beta ){\displaystyle \frac{\Gamma \left(\right(m-1)/2)}{\sqrt{m\pi }\Gamma (m/2)}}{\left[1+{\displaystyle \frac{z_q^2}{m}}\right]}^{-{\displaystyle \frac{m-1}{2}}}\hfill \\ \hfill & +\gamma \sigma {\displaystyle \frac{\Gamma \left(\right(m+1)/2)\Gamma \left(\right(m-1)/2)}{2\pi \Gamma {(m/2)}^2}}{\int }_{z_q}^{\infty }{\left[1+{\displaystyle \frac{z^2}{m}}\right]}^{-{\displaystyle \frac{m-1}{2}}}{\left[1+{\displaystyle \frac{{(\gamma \sigma z+\gamma \mu +\beta )}^2}{m}}\right]}^{-{\displaystyle \frac{m+1}{2}}}dz),\hfill \end{array}$$

and hence,

$$TC{E}_q\left(Y\right)=\mu +{\Lambda }_{1,q}\sigma .$$

For $m>4$, using (14), the TV measure is given by

$$\begin{array}{cc}\hfill {\mathrm{TV}}_q\left(Y\right)=& {\displaystyle \frac{{\sigma }^2}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(z_q{T}_m(\gamma \sigma z_q+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)\hfill \\ \hfill & +{\int }_{z_q}^{\infty }{T}_m(\gamma \sigma z+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)dz\hfill \\ \hfill & +\gamma \sigma t_m(\gamma \sigma z_q+\gamma \mu +\beta ){\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{d}{dz}}\left(t_m(\gamma \sigma z+\gamma \mu +\beta )\right){\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)dz)-{\left(\sigma {\Lambda }_{1,q}\right)}^2\hfill \\ \hfill =& {\displaystyle \frac{{\sigma }^2}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(z_q{T}_m(\gamma \sigma z_q+\gamma \mu +\beta )\sqrt{{\displaystyle \frac{m}{m-2}}}{t}_{m-2}\left(\sqrt{{\displaystyle \frac{m-2}{m}}}{z}_q\right)\hfill \\ \hfill & +{\int }_{z_q}^{\infty }{T}_m(\gamma \sigma z+\gamma \mu +\beta )\sqrt{{\displaystyle \frac{m}{m-2}}}{t}_{m-2}\left(\sqrt{{\displaystyle \frac{m-2}{m}}}z\right)dz\hfill \\ \hfill & +\gamma \sigma t_m(\gamma \sigma z_q+\gamma \mu +\beta ){\displaystyle \frac{m}{m-2}}\sqrt{{\displaystyle \frac{m}{m-4}}}{t}_{m-4}\left(\sqrt{{\displaystyle \frac{m-4}{m}}}{z}_q\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{d}{dz}}\left(t_m(\gamma \sigma z+\gamma \mu +\beta )\right){\displaystyle \frac{m}{m-2}}\sqrt{{\displaystyle \frac{m}{m-4}}}{t}_{m-4}\left(\sqrt{{\displaystyle \frac{m-4}{m}}}z\right)dz)-{\left(\sigma {\Lambda }_{1,q}\right)}^2.\hfill \end{array}$$

4.3. Extended Generalized Skew-Logistic Distribution

Suppose that Y follows the extended generalized skew-logistic distribution, denoted by $Y\sim EGS{L}_1(\mu ,{\sigma }^2,\gamma ,\beta ,H)$, with probability density function

$$f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}{g}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{y-\mu }{\sigma }}\right)}^2\right)H(\gamma y+\beta ),$$

where $g^{\left(1\right)}\left(u\right)={\displaystyle \frac{1}{2}}{\displaystyle \frac{e^{-u}}{{(1+e^{-u})}^2}}$ is the generator of logistic distribution, and H denotes a symmetric cdf about 0. Moreover, let $\varsigma =U-\gamma X$, where $X\sim L{o}_1(\mu ,{\sigma }^2)$ has the pdf

$$f\left(x\right)={\displaystyle \frac{1}{2\sigma }}{\displaystyle \frac{e^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}}{{\left(1+e^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}\right)}^2}},$$

(see, for example [3]). Then we have

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left(u\right)=& {\displaystyle \frac{1}{2}}{\int }_u^{\infty }{\displaystyle \frac{e^{-x}}{{(1+e^{-x})}^2}}dx={\displaystyle \frac{1}{2}}{\displaystyle \frac{e^{-u}}{1+e^{-u}}},\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left(u\right)=& {\displaystyle \frac{1}{2}}{\int }_u^{\infty }{\displaystyle \frac{1}{1+e^x}}dx={\displaystyle \frac{1}{2}}ln(1+e^{-u}),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)& ={\displaystyle \frac{1}{2}}{\displaystyle \frac{e^{-\frac{1}{2}{z}_q^2}}{1+e^{-\frac{1}{2}{z}_q^2}}}\hfill \\ & ={\displaystyle \frac{1}{2}}{\displaystyle \frac{\varphi \left(z_q\right)}{{\left(\sqrt{2\pi }\right)}^{-1}+\varphi \left(z_q\right)}},\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)& ={\displaystyle \frac{1}{2}}ln(1+e^{-{\displaystyle \frac{1}{2}}{z}_q^2})\hfill \\ & ={\displaystyle \frac{1}{2}}ln(1+\sqrt{2\pi }\varphi \left(z_q\right)),\hfill \end{array}$$

where $\varphi (·)$ denotes the standard normal pdf.

Extended Skew-Logistic-Normal Distribution

Consider a special case in which H is the cdf of the standard normal distribution. In this case, the pdf of Y is given by

$$f_Y\left(y\right)={\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)\sigma }}{g}^{\left(1\right)}\left({\displaystyle \frac{y-\mu }{\sigma }}\right)\Phi (\gamma y+\beta ),$$

where $\varsigma =U-\gamma X$, with $U\sim N_1(0,1)$ and $X\sim L{o}_1(\mu ,{\sigma }^2)$ being independent random variables.The pdf of $\varsigma$ can be expressed as

$$\begin{array}{cc}\hfill f_{\varsigma }\left(x\right)=& {\int }_{-\infty }^{\infty }{f}_U\left(u\right)f_{-\gamma X}(x-u)du\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }\varphi \left(u\right){\displaystyle \frac{1}{2\left|\gamma \right|\sigma }}{\displaystyle \frac{e^{-\frac{1}{2}{\left(\frac{x-u+\gamma \mu }{\gamma \sigma }\right)}^2}}{{\left(1+e^{-\frac{1}{2}{\left(\frac{x-u+\gamma \mu }{\gamma \sigma }\right)}^2}\right)}^2}}du,\hfill \end{array}$$

and its cdf is

$$\begin{array}{cc}\hfill F_{\varsigma }\left(\beta \right)=& {\int }_{-\infty }^{\beta }{f}_{\varsigma }\left(x\right)dx\hfill \\ \hfill =& {\int }_{-\infty }^{\beta }{\int }_{-\infty }^{\infty }\varphi \left(u\right){\displaystyle \frac{1}{2\left|\gamma \right|\sigma }}{\displaystyle \frac{e^{-\frac{1}{2}{\left(\frac{x-u+\gamma \mu }{\gamma \sigma }\right)}^2}}{{\left(1+e^{-\frac{1}{2}{\left(\frac{x-u+\gamma \mu }{\gamma \sigma }\right)}^2}\right)}^2}}dudx.\hfill \end{array}$$

Hence, ${\Lambda }_{1,q}$ is given by

$$\begin{array}{cc}\hfill {\Lambda }_{1,q}=& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)\varphi \left(\gamma \sigma z+\gamma \mu +\beta \right)dz)\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{\varphi \left(z_q\right)}{{\left(\sqrt{2\pi }\right)}^{-1}+\varphi \left(z_q\right)}}\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }\varphi \left(\gamma \sigma z+\gamma \mu +\beta \right)\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{\varphi \left(z\right)}{{\left(\sqrt{2\pi }\right)}^{-1}+\varphi \left(z\right)}}\right)dz),\hfill \end{array}$$

and thus,

$$\begin{array}{c}\hfill TC{E}_q\left(Y\right)=\mu +{\Lambda }_{1,q}\sigma .\end{array}$$

Using (14), the TV is represented as

$$\begin{array}{cc}\hfill {\mathrm{TV}}_q\left(Y\right)=& {\displaystyle \frac{{\sigma }^2}{(1-q)}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(z_q\Phi (\gamma \sigma z_q+\gamma \mu +\beta )\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{\varphi \left(z_q\right)}{{\left(\sqrt{2\pi }\right)}^{-1}+\varphi \left(z_q\right)}}\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }\Phi \left(\gamma \sigma z+\gamma \mu +\beta \right)\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{\varphi \left(z\right)}{{\left(\sqrt{2\pi }\right)}^{-1}+\varphi \left(z\right)}}\right)dz\hfill \\ \hfill & +\gamma \sigma \varphi \left(\gamma \sigma z+\gamma \mu +\beta \right)\left({\displaystyle \frac{1}{2}}ln(1+\sqrt{2\pi }\varphi \left(z_q\right))\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{d}{dz}}\left(\varphi (\gamma \sigma z+\gamma \mu +\beta )\right)\left({\displaystyle \frac{1}{2}}ln(1+\sqrt{2\pi }\varphi \left(z\right))\right)dz)-{\left(\sigma {\Lambda }_{1,q}\right)}^2.\hfill \end{array}$$

4.4. Extended Generalized Skew-Laplace Distribution

Suppose that Y follows the extended generalized skew-Laplace distribution, denoted by $Y\sim EGSL{a}_1(\mu ,{\sigma }^2,\gamma ,\beta )$, with the pdf

$$f_Y\left(y\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2\sigma }}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}{e}^{{\displaystyle \frac{y-\mu }{\sigma }}}H(\gamma y+\beta ),\hfill & \hfill {\displaystyle \frac{y-\mu }{\sigma }}<0,\\ {\displaystyle \frac{1}{2\sigma }}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}{e}^{-{\displaystyle \frac{y-\mu }{\sigma }}}H(\gamma y+\beta ),\hfill & \hfill {\displaystyle \frac{y-\mu }{\sigma }}\ge 0,\end{array}\right.$$

where $\varsigma =U-\gamma X$, with $X\sim L{a}_1(\mu ,{\sigma }^2)$. The pdf of X is given by

$$f\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2\sigma }}{e}^{{\displaystyle \frac{x-\mu }{\sigma }}},\hfill & \hfill {\displaystyle \frac{x-\mu }{\sigma }}<0,\\ {\displaystyle \frac{1}{2\sigma }}{e}^{-{\displaystyle \frac{x-\mu }{\sigma }}},\hfill & \hfill {\displaystyle \frac{x-\mu }{\sigma }}\ge 0.\end{array}\right.$$

The corresponding density generator is $g^{\left(1\right)}\left(u\right)={\displaystyle \frac{1}{2}}{e}^{-\sqrt{2u}}$, and hence,

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left(u\right)=& {\int }_u^{\infty }{\displaystyle \frac{1}{2}}{e}^{-\sqrt{2x}}dx={\displaystyle \frac{1}{2}}(1+\sqrt{2u})e^{-\sqrt{2u}},\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left(u\right)=& {\int }_u^{\infty }{\displaystyle \frac{1}{2}}(1+\sqrt{2x})e^{-\sqrt{2x}}dx={\displaystyle \frac{1}{2}}(3+2u+3\sqrt{2u})e^{-\sqrt{2u}},\hfill \end{array}$$

(see, for example, [37]).

For $z_q\ge 0$, we have

$$\begin{array}{cc}\hfill {\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)=& {\displaystyle \frac{1}{2}}(1+z_q)e^{-z_q}\hfill \\ \hfill {\overline{\mathcal{G}}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}_q^2\right)=& {\displaystyle \frac{1}{2}}(3+z_q^2+3z_q)e^{-z_q}.\hfill \end{array}$$

Extended Skew-Laplace-Normal Distribution

Consider a special case where H is the cdf of the standard normal distribution. In this case, the pdf of Y is given by

$$f_Y\left(y\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2\sigma }}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}{e}^{{\displaystyle \frac{y-\mu }{\sigma }}}\Phi (\gamma y+\beta ),\hfill & \hfill {\displaystyle \frac{y-\mu }{\sigma }}<0,\\ {\displaystyle \frac{1}{2\sigma }}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}{e}^{-{\displaystyle \frac{y-\mu }{\sigma }}}\Phi (\gamma y+\beta ),\hfill & \hfill {\displaystyle \frac{y-\mu }{\sigma }}\ge 0,\end{array}\right.$$

where $\varsigma =U-\gamma X$, with $U\sim N_1(0,1)$ and $X\sim L{a}_1(\mu ,{\sigma }^2)$ being independent random variables. The pdf of $\varsigma$ can be expressed as

$$\begin{array}{cc}\hfill f_{\varsigma }\left(x\right)=& {\int }_{-\infty }^{\infty }{f}_U\left(u\right)f_{-\gamma X}(x-u)du\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }\varphi \left(u\right){\displaystyle \frac{1}{2\left|\gamma \right|\sigma }}{e}^{-\left|{\displaystyle \frac{x-u+\gamma \mu }{\left|\gamma \right|\sigma }}\right|}du,\hfill \end{array}$$

and thus,

$$\begin{array}{cc}\hfill F_{\varsigma }\left(\beta \right)=& {\int }_{-\infty }^{\beta }{f}_{\varsigma }\left(x\right)dx\hfill \\ \hfill =& {\int }_{-\infty }^{\beta }{\int }_{-\infty }^{\infty }\varphi \left(u\right){\displaystyle \frac{1}{2\left|\gamma \right|\sigma }}{e}^{-\left|{\displaystyle \frac{x-u+\gamma \mu }{\left|\gamma \right|\sigma }}\right|}dudx.\hfill \end{array}$$

The quantity ${\Lambda }_{1,q}$ is then given by

$$\begin{array}{cc}\hfill {\Lambda }_{1,q}=& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta ){\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z_q}^2\right)\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\overline{G}}^{\left(1\right)}\left({\displaystyle \frac{1}{2}}{z}^2\right)\varphi (\gamma \sigma z+\gamma \mu +\beta )dz)\hfill \\ \hfill =& {\displaystyle \frac{1}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(\Phi (\gamma \sigma z_q+\gamma \mu +\beta )·{\displaystyle \frac{1}{2}}(1+z_q)e^{-z_q}\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{1}{2}}(1+z)e^{-z}\varphi (\gamma \sigma z+\gamma \mu +\beta )dz).\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill TC{E}_q\left(Y\right)=\mu +{\Lambda }_{1,q}\sigma .\end{array}$$

Using equation (14), the Tail Variance is given by

$$\begin{array}{cc}\hfill {\mathrm{TV}}_q\left(Y\right)=& {\displaystyle \frac{{\sigma }^2}{1-q}}{\displaystyle \frac{1}{F_{\varsigma }\left(\beta \right)}}(z_q\Phi (\gamma \sigma z_q+\gamma \mu +\beta )·{\displaystyle \frac{1}{2}}(1+z_q)e^{-z_q}\hfill \\ \hfill & +{\int }_{z_q}^{\infty }\Phi (\gamma \sigma z+\gamma \mu +\beta )·{\displaystyle \frac{1}{2}}(1+z)e^{-z}dz\hfill \\ \hfill & +\gamma \sigma \varphi (\gamma \sigma z_q+\gamma \mu +\beta )·{\displaystyle \frac{1}{2}}(3+z_q^2+3z_q)e^{-z_q}\hfill \\ \hfill & +\gamma \sigma {\int }_{z_q}^{\infty }{\displaystyle \frac{d}{dz}}\left(\varphi (\gamma \sigma z+\gamma \mu +\beta )\right)·{\displaystyle \frac{1}{2}}(3+3z+z^2)e^{-z}dz)-{\left(\sigma {\Lambda }_{1,q}\right)}^2.\hfill \end{array}$$

5. Numerical Illustration

In this section, we provide a numerical illustration based on real stock market data to demonstrate the application of the EGSE distribution and the derived analytical formulas in risk assessment. Specifically, we analyze the annualized log-losses of four stocks over the period August 2021 to August 2025 (The dataset covers 1004 trading days and is publicly available at https://finance.yahoo.com/): Apple Inc. (AAPL), Alphabet Inc. (GOOGL), Microsoft Corporation (MSFT), and NVIDIA Corporation (NVDA). Descriptive statistics, including the mean, variance, skewness, and kurtosis of the annualized losses, are reported in

Table 1. Descriptive statistics of the financial assets’ annualized log losses.

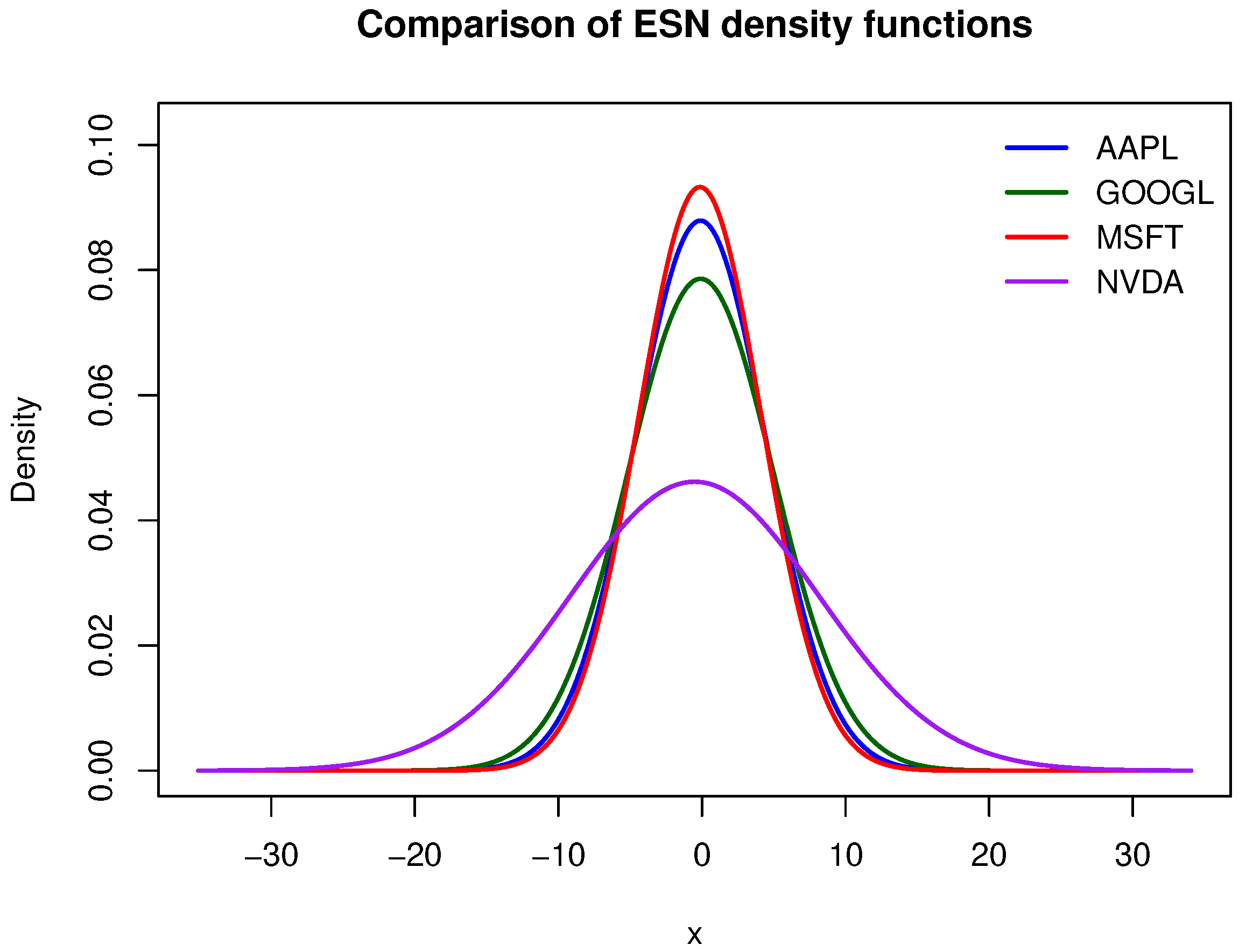
Stock	Mean	Variance	Minimum	Median	Maximum	Skewness	Kurtosis
AAPL	−0.1103	20.6282	−35.9396	−0.2757	24.4474	−0.2896	6.0404
GOOGL	−0.0972	25.7890	−24.5316	−0.2871	25.1809	0.1527	2.9529
MSFT	−0.1384	18.3213	−24.3242	−0.1709	20.2344	−0.1123	2.9616
NVDA	−0.5211	74.7393	−54.9581	−0.7576	46.8584	−0.2557	3.5786

. The results indicate that the data exhibit noticeable skewness, and for certain stocks, the kurtosis substantially exceeds 3 (the benchmark value for a normal distribution), thereby suggesting pronounced peakedness and heavy-tailed behavior.

To capture these empirical features, we model the data using the extended skew-normal (ESN) distribution (see Section 4.1). In contrast to elliptical families such as the normal or Student-t, the ESN distribution provides greater flexibility in accommodating both skewness and heavy-tailed behavior. The model parameters for each stock are estimated by maximum likelihood. Estimation of the EGSE distribution is computationally demanding, as it requires careful initialization to avoid convergence to local maxima; to this end, we adopt a grid search strategy. To highlight the distributional characteristics of the individual stocks, Figure 1 compares their fitted probability density functions.

The estimated ESN density functions reveal marked differences in the risk profiles of the four stocks. NVDA exhibits the heaviest tails and the lowest peak, indicating both a higher probability of extreme outcomes and pronounced downside asymmetry. By contrast, MSFT displays the sharpest peak with relatively thin tails, suggesting greater stability and a concentration of losses around the mean. AAPL and GOOGL fall between these two extremes, with moderately heavy tails and relatively symmetric distributions. Overall, this comparison highlights NVDA’s elevated tail risk and asymmetric loss potential, whereas MSFT appears comparatively less exposed to extreme outcomes.

Table 2. Risk measures at different confidence levels for the four stocks.

Stock	Confidence	VaR	TCE	TV
AAPL	70%	2.2703	5.1509	5.4514
	75%	2.9516	5.6600	4.9794
	80%	3.7103	6.2442	4.5057
	85%	4.5947	6.9459	4.0162
	90%	5.7074	7.8565	3.4858
GOOGL	70%	2.5643	5.7852	6.8155
	75%	3.3261	6.3544	6.2254
	80%	4.1744	7.0076	5.6331
	85%	5.1632	7.7922	5.0210
	90%	6.4074	8.8103	4.3582
MSFT	70%	2.1049	4.8197	4.8419
	75%	2.7470	5.2994	4.4226
	80%	3.4620	5.8500	4.0019
	85%	4.2955	6.5114	3.5672
	90%	5.3441	7.3695	3.0961
NVDA	70%	4.0103	9.4933	19.7490
	75%	5.3072	10.4622	18.0388
	80%	6.7513	11.5742	16.3223
	85%	8.4346	12.9099	14.5484
	90%	10.5525	14.6431	12.6247

reports the risk measures of the four stocks, computed using the analytical formulas developed in this paper. The evaluation of TCE and TV for a generic EGSE distribution necessarily involves the numerical computation of one-dimensional integrals; see, for example, (15). Since these integrals can be computed with high efficiency, all results in Table 2 were obtained within only $0.180$ s on an Apple M1 Pro CPU. These results enable a quantitative assessment and comparison of the risk exposures across assets.

The reported measures provide further evidence of the heterogeneity in the loss distributions and are consistent with the density estimates in Figure 1. NVDA clearly stands out with the largest VaR and TCE values at all confidence levels. For instance, at the 90% level, NVDA’s VaR reaches 10.55 and its TCE exceeds 14.64, both more than double those of the other stocks. This confirms the heavy-tailed nature and pronounced volatility of NVDA’s loss distribution, as reflected in its relatively flat density peak and thick tails in Figure 1.

By contrast, MSFT consistently records the lowest VaR and TCE values across the full confidence range. This aligns with its sharply peaked density and thinner tails, indicating that MSFT is comparatively less exposed to extreme downside risk. AAPL and GOOGL fall between these two extremes: their risk measures rise moderately with the confidence level, and their values are relatively close, reflecting distributions with moderate tail thickness but less asymmetry than NVDA.

The TV results further highlight differences in the dispersion of extreme losses. NVDA not only exhibits the largest Expected Shortfall but also the greatest variability in the tail, with TV values substantially higher—by nearly an order of magnitude—than those of the other stocks (e.g., 19.75 at the 70% level). This indicates that NVDA’s extreme losses are both more severe on average and considerably more volatile. In contrast, MSFT displays the smallest TV values (below 3.1 at the 90% level), suggesting markedly greater stability in its tail risk. AAPL and GOOGL exhibit intermediate patterns: both incur moderate expected losses beyond the VaR threshold, though GOOGL shows higher TV at lower confidence levels, suggesting more dispersed tail outcomes, whereas AAPL’s TV declines more rapidly with the confidence level, indicating faster convergence of its tail risk.

Taken together, these results underscore the distinct risk profiles of the assets. NVDA is characterized by substantial tail risk and instability in its extreme losses, making it the riskiest asset among the four. MSFT appears the most stable and least exposed to extreme outcomes, while AAPL and GOOGL present broadly comparable but intermediate levels of risk.

Beyond the financial risk domain, the EGSE framework also resonates with recent advances in environmental and survival risk modeling. For example, Cheng et al. [38] employ block maxima sub-sampling to quantify environmental extremes such as earthquakes and climate-related risks, while [39] investigate competing risks under Dagum distributions with progressive censoring in survival analysis. These studies underscore the wide applicability of heavy-tailed and skewed distributional models in practical risk-management contexts and suggest promising directions for extending EGSE-based tail risk measures to environmental, actuarial, and reliability settings.

6. Conclusions

In this paper, we derive explicit closed-form expressions for the Tail Conditional Expectation and Tail Variance under the extended generalized skew-elliptical (EGSE) distribution. These results generalize existing findings for symmetric and GSE distributions and apply uniformly to several important subclasses, including the extended skew-normal and extended skew-Student-t families, thereby establishing a tractable analytical framework for a broad class of asymmetric and heavy-tailed models. To illustrate the practical relevance of the theoretical results, we conduct a numerical study based on real stock market data, demonstrating how the proposed formulas can be directly implemented to quantify and compare the tail risk profiles of financial assets. While the primary focus of this paper is the derivation of univariate tail risk measures, the framework also suggests several promising directions for future research. In particular, it can be extended to multivariate settings to construct new tail risk measures. Further investigations may also explore applications of this flexible distribution family to other domains, such as environmental risk modeling or competing risks analysis in actuarial science, and the development of more efficient parameter estimation algorithms.