Abstract
The bond market serves dual roles in fiscal and financial spheres, playing a crucial role in coordinating monetary policy. This paper investigates the impact of quantitative and price-based monetary policies on the liquidity level of China’s bond market. A comprehensive index measuring the liquidity of the local bond market is constructed using a combination weighting method that integrates the entropy method and the coefficient of variation. Employing the time-varying stochastic volatility structure vector autoregression (TVP-SV-SVAR) model on data spanning from 2013 to 2021, this study empirically compares the impulse response of local bond market liquidity to monetary policy shocks. The findings reveal that both types of monetary policy operations exhibit asymmetric, nonlinear, and time-varying impacts on bond market liquidity. Quantitative monetary instruments induce deeper impulse responses, with longer-lasting effects. These conclusions offer insights for monetary policy reforms and bond market development in China.
Keywords:
local government bond market; liquidity; monetary policy; TVP-SV-SVAR model; time-varying impulse response MSC:
62P20; 91B64
1. Introduction
Local government bonds in China have been pivotal in raising government funds. With the rapid expansion of the local government bond market, various risks have emerged, especially the significant issue of insufficient liquidity. Misjudgments and improper management of the bond market’s liquidity by investment entities are key factors contributing to sudden liquidity shortages. Underlying this issue is the strategic interplay between the monetary authorities and financial institutions regarding the future direction of monetary policy. Amihud and Mendelson (1988) [1] pointed out that “liquidity is everything in the market”. Only a market with robust liquidity can be deemed efficient and competitive. A properly performing and efficient bond market is widely considered to be important for the smooth functioning of trading systems in general. An important feature of the bond market for investors is its liquidity [2]. Therefore, strengthening liquidity management and maintaining sufficient liquidity is of paramount importance for promoting the long-term and healthy development of both China and the global bond market in the future.
As China’s economy transitions to a new normal, monetary policy becomes a vital tool for macroeconomic regulation, requiring a balance between total quantity optimization and structural adjustment. Among the current mixed monetary policy rules, the “quantity price parallel” rule aligns best with China’s macroeconomic regulation needs. China continually innovates in policy tools and ideas, introducing a series of structural monetary tools to achieve these goals.
Since 2021, digital finance in China has exhibited characteristics of integration, scenario-based applications, intelligence, greening, and standardization. This is evident in the ongoing maturity of digital payment models, such as the dual advancements in the scale and field of the pilot of the digital yuan, and the emergence of industrial digital finance as a critical direction. The innovative development of digital finance is driving rapid and profound changes in the financial industry, enhancing service quality and efficiency while providing robust support for the implementation of monetary policy. Therefore, in the context of these rapid changes, studying the impact of monetary policy on the liquidity of local government bonds in China holds significant practical importance.
This article measures the liquidity of the local bond market through multiple dimensions, including transaction immediacy, depth, width, and elasticity, while considering factors such as transaction activity and transaction price. A comprehensive liquidity indicator for the local bond market is constructed using a combination weighting method of the entropy method and the coefficient of variation method. This approach expands upon the existing qualitative research on local bond market liquidity by providing a quantitative analysis. The TVP-SV-SVAR model is utilized to explore the impact of two types of monetary policies, price-based and quantity-based, on the liquidity of the local bond market.
This study makes three significant contributions to the literature on monetary policy and bond market liquidity. First, we develop a novel liquidity composite index for China’s local government bond market by innovatively combining entropy and coefficient of variation weighting methods, which dynamically captures regime shifts in market conditions. Second, we are the first to apply the TVP-SV-SVAR model to analyze China’s bond market, revealing how the effects of price-based versus quantity-based monetary tools have evolved through key policy transitions (2015 interest rate liberalization, 2017 financial deleveraging, and 2020 pandemic response). Third, we identify a unique ‘policy tool asymmetry’ in China’s context—where quantity tools dominate during crises but price tools are more effective in normal periods—challenging the conventional wisdom from developed markets.
The remainder of this paper is organized as follows: Section 2 establishes the theoretical framework, reviewing the seminal studies on monetary policy transmission and liquidity dynamics, while highlighting gaps in analyzing China’s bond market; Section 3 details our methodology, including the construction of liquidity index and the TVP-SV-SVAR model’s adaptation to China’s institutional context; Section 4 presents the empirical results, with subsections analyzing time-varying impulse responses and robustness checks; Section 5 discusses the main findings and policy implications, and concludes with recommendations for regulators and future research directions.
2. Theoretical Framework
2.1. Literature Review
As a macroeconomic stabilizer, monetary policy mainly acts on the financial market by adjusting interest rates, asset prices, balance sheets, bank lending, market expectations, and signals (Borio, 2006 [3]; Klingelhofer and Sun, 2019 [4]; Martinez-Miera and Repullo, 2019 [5]; Demirer et al., 2021 [6]; Parker and Semmler, 2024 [7]; Wu et al., 2024 [8]; Salimi et al., 2025 [9]). Scholars have extensively researched the impact of monetary policy on bond market liquidity. Goyenko and Ukhov (2009) found that contractionary monetary policy negatively affects bond market liquidity [10]. Pasquariello et al. (2012) pointed out that permanent open market operations (POMOs) would reduce the bid-ask spread in the bond market, thereby narrowing liquidity [11]. The findings of Fernández-Amador et al. (2013) indicated that the expansionary monetary policy of the European Central Bank increases overall stock market liquidity in Germany, France, and Italy [12]. Lee et al. (2016) found that central bank communication plays an important role in reducing liquidity damage by improving the predictability of policy actions and reducing information asymmetry [13]. Albagli et al. (2019) analyzed the impact of US monetary policy on the international bond market after the financial crisis, finding that international bond market liquidity was more significantly influenced by spillover effects after the crisis [14]. Christensen and Gillan (2022) found that the adoption of quantitative easing policies (QE) by the government can increase bond market liquidity, evidenced by the Federal Reserve’s quantitative easing program [15]. Cohen and Furman (2024) demonstrated that the pre-pandemic QE of ECB shored up the liquidity of eligible bonds [16].
Harris (1990) proposed four dimensions of liquidity: width, depth, immediacy, and elasticity [17]. Liquidity measurement indicators are typically analyzed at three levels: liquidity width, liquidity depth, and liquidity immediacy. To characterize liquidity width, transaction costs are commonly used, with the bid-ask spread model proposed by Demsetz [18] and later used by Amihud and Mendelson [19] being the most representative. The difference between buy and sell prices is inversely proportional to the market popularity—the larger the bid-ask spread, the lower the market liquidity. Depth characterizing liquidity mainly measures the trading influence of the securities market. For example, the greater the price change caused by a certain number of exchanges, the smaller the liquidity. Main measurement indicators include the Amivest liquidity index proposed by Dubofsky and Groth [20], the Hui Heubel liquidity index obtained by modifying the Amivest liquidity index by Hui and Heubel [21], and the non-liquidity index constructed by Amihud [22]. Describing the size of liquidity from the perspective of immediacy mainly involves the speed of recovery, with representative models such as the Garbade–Silber model [23]. Pan (2023) [24] adopted the quote depth and the bid-ask spread, which are intuitive and heuristic measures of direct transaction costs [25], as liquidity proxies.
In terms of model selection, Primiceri (2005) set the intercept, coefficient, and variance in a simple VAR model as time-varying parameters, establishing a time-varying parameter model with random fluctuations that can capture time-varying characteristics well [26]. Nakajima suggested that the TVP-SV-VAR nonlinear model outperforms other fixed parameter VAR models [27]. Boufateh and Saadaoui (2021) used the TVP-SVAR-SV model to study the time-varying effects of oil price shocks as transmission channels on financial intermediaries (credit markets) and inflation [28]. Ding et al. (2021) employed a random volatility (TVP-SVAR-SV) model to explore the financial and geopolitical uncertainties in commodity markets [29]. Jiménez et al. (2023) estimated hybrid TVP-VAR-SV models to identify and quantify the impact of fiscal shocks on GDP growth [30]. Lyu and Hu (2024) used the TVP-SVAR-SV model to examine the dynamic impact of monetary policy on stock market liquidity in the short, medium, and long run and the asymmetry of the impact in bull and bear markets [31].
While seminal papers by Amihud (2002) [22] and Goyenko and Ukhov (2009) [10] laid the foundation for liquidity measurement and policy impact analysis, their frameworks exhibit critical limitations in addressing dynamic market environments. Amihud’s illiquidity ratio, though instrumental for static markets, fails to capture time-varying volatility in emerging economies like China—where digital finance integration accelerates market shifts. Similarly, Goyenko and Ukhov’s findings on monetary policy effects primarily reflect developed markets (e.g., US Treasury bonds), overlooking structural heterogeneities in China’s local government bond market, such as regional fragmentation and regulatory interventions. Recent studies, including Pasquariello et al. (2011) [11] and Fernández-Amador et al. (2013) [12], rely on fixed-parameter models (e.g., standard VAR), which cannot quantify the asymmetric and nonlinear responses of liquidity to different policy tools—specifically, the distinct impacts of quantitative (M0) versus price-based (IBO001) instruments. This gap is pronounced in China’s context, where the transition from high-speed to high-quality development in monetary policy necessitates dynamic analysis.
This study bridges these voids by (1) leveraging the TVP-SV-SVAR model to explicitly quantify time-varying impulse responses, a dimension absent in prior work; (2) focusing on China’s local bond market, addressing spatial–temporal gaps; and (3) integrating digital finance evolution to re-evaluate policy transmission mechanisms. By doing so, we resolve the consensus deficit on monetary policy mechanisms and provide a replicable framework for emerging economies undergoing financial digitization.
In summary, there is currently no consensus on the mechanism by which monetary policy affects the liquidity of the bond market. This may be, on the one hand, due to the changing economic and market environments during research periods, as well as significant variations in research subjects and data. On the other hand, some research methods have limitations, particularly the lack of analysis of the impact of different monetary policy tools on bond market liquidity from a time-varying and dynamic perspective. As China’s economy transitions from high-speed growth to high-quality development and the bond market becomes increasingly refined, the process, path, and effects of monetary policy on bond market liquidity are not static but exhibit characteristics of dynamism and time-variability.
2.2. Theoretical Analysis
From the perspective of price channels, interest rates, as the primary indicator of price-based monetary policy, are crucial in determining bond prices and yields. Changes in bond prices directly affect the investors’ decisions and behaviors, thereby affecting the liquidity of the bond market. Interest rate changes also directly reflect the tightness of the market’s money supply. An increase in interest rates indicates a tightening of the money supply, prompting financial institutions to sell bonds and to reduce bond purchases to retrieve funds. A rise in interest rates can easily lead to expectations of deflation and, as bonds are assets with higher security, their value preservation function becomes prominent. Investors may choose to continue holding bonds, further reducing their liquidity. In other words, various policy interest rates affect the money market interest rates and, consequently, the liquidity and status of the bond market through channels such as the supply and demand of funds, bond price levels, social inflation expectations, and investor decisions.
From the perspective of money supply, the money supply is the product of currency base and the money multiplier. The central bank can adjust the money supply by conducting open market operations and changing the reserve requirement ratio, to directly influence the amount of funds available to financial institutions and financial markets. On the one hand, the central bank can alter the supply of the currency base through open market operations, thereby affecting the money supply. On the other hand, changes in the statutory reserve requirement ratio and excess reserve requirement ratio have an impact on the money supply by acting on the money multiplier. In other words, the money supply adjusts the funding situation of financial institutions and the debt side of the market, affects the inflation expectations of investors, alters their decision-making, and ultimately affects the liquidity of the bond market. The transmission mechanism is represented in Figure 1.
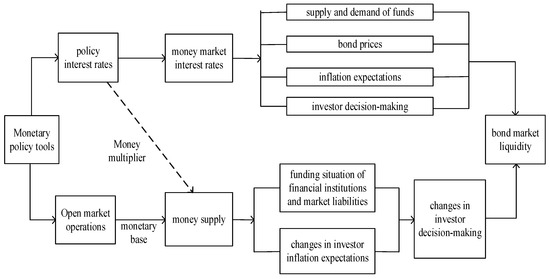
Figure 1.
Dual-Pathway Transmission Framework for Monetary Policy Effects on Bond Liquidity.
From Figure 1, two research questions for this paper can be derived:
Quantitative monetary policy mainly affects the liquidity level and state of the bond market by changing the pressure on the liability side of financial institutions and the market, altering inflation expectations, causing an imbalance between the liability and asset sides, and modifying the decision-making behavior of investment entities.
Price-based monetary policy can affect the liquidity level and state of the bond market by influencing the bond prices, the supply and demand of funds in the bond market, inflation expectations, and the decision-making behavior of investors, with the pathways and effects being more direct and rapid.
2.3. Model Selection Justification
Traditional VAR and SVAR models assume fixed parameters over time, which may fail to capture the dynamic and nonlinear effects of monetary policy on bond market liquidity (Primiceri, 2005) [26]. However, China’s monetary policy framework has undergone significant changes, including interest rate liberalization and the shift to a “dual-pillar” regulatory system. These structural breaks necessitate models with time-varying parameters (TVP) and stochastic volatility (SV) to accurately capture evolving policy transmission mechanisms.
The TVP-SV-SVAR model overcomes these shortcomings through three key features. First, its time-varying coefficients allow the transmission of monetary policy to evolve across business cycles—for instance, the post-2015 interest-rate reforms versus the COVID-19 stimulus packages. Second, stochastic volatility captures the pronounced heteroskedasticity observed in financial markets, such as the liquidity squeezes in 2013 and 2020, an empirical regularity that fixed-parameter models necessarily overlook. Third, the framework accommodates nonlinearities: quantitative easing and policy-rate reductions exert asymmetric effects on market liquidity, a pattern documented for the U.S. Treasury market by Christensen and Gillan (2022) [15].
By contrast, alternative models suffer from pronounced limitations. The GARCH-type specifications can reproduce volatility clustering—persistent high volatility during crises—yet they cannot detect structural shifts in policy regimes, such as China’s regulatory overhaul of 2017. The DSGE models, constrained by rigid micro-foundations and calibrated to low-frequency data, are ill-suited for real-time policy evaluation with high-frequency financial indicators (e.g., monthly liquidity metrics). Integrating time-varying mechanisms with stochastic volatility, the TVP-SV-SVAR model provides an indispensable methodological foundation for analyzing the transmission of China’s monetary policy in the era of digital finance.
3. Model Construction
3.1. Indicator Construction
This paper selects the year-on-year growth rate of money supply (M0) as the proxy variable for quantitative monetary instruments, and the overnight interbank offered rate (IBO001) as the proxy variable for price-based monetary policy for subsequent research and analysis.
The Chinese interbank bond market has formed a dual characteristic of both on-exchange and off-exchange markets. Therefore, both market research paradigms should be considered when analyzing liquidity. This paper innovatively adopts the method of instruction-driven markets and focuses on transaction data for research, diverging from the traditional approach of using market-making quotes as price indicators.
The selection of liquidity measurement indicators considers both trading volume and price information. On the one hand, a positive indicator, the turnover rate capturing changes in market trading volume, is selected. The monthly turnover rate (T) is represented by the ratio of total trading volume to the stock of the month, where the stock is the average of the stock at the beginning and end of the month. On the other hand, negative indicators, such as price deviation (D) and Amihud non-liquidity indicators (A), are selected to measure the price shock caused by changes in trading volume.
The calculation method for price deviation is as follows:
The Amihud Ratio refers to the following equation:
where is the number of trading days of the k th bond in month i, is the yield of the k th bond on d day of month i, and is the transaction amount of the k th bond on day d of month i. The calculation for average liquidity level of the market is as follows:
where is the number of bonds participating in the calculation of the average market liquidity for the month i.
To measure liquidity, this paper constructs a comprehensive measurement index, and the weight setting combines the entropy method [32] and the coefficient of variation weighting method. Compared to the subjective weighting method, the information entropy principle adopted by the global entropy method in the weight determination process can effectively avoid the disadvantage of randomness, making the weight setting more scientific and objective, and to some extent, avoiding information overlap between the selected economic variables. The coefficient of variation method can also simultaneously resolve the weight equalization phenomenon generated by the entropy method. The calculation are formed using the following steps.
Step 1, Indicator selection and simplification. Indicator selection is grounded in market-microstructure theory. The price-deviation ratio captures the deviations of transaction prices (the breadth dimension), reflecting information asymmetry; turnover gauges trading intensity (the depth dimension), linking to market efficiency; and the Amihud Ratio quantifies price impact (the immediacy dimension), corresponding to liquidity resilience. Collectively, these three dimensions span Harris’s (1990) [18] liquidity taxonomy, ensuring comprehensive coverage of the index. Dimensionless normalization (e.g., formulas for positive/negative indicators) removes scale effects, renders the metrics comparable, and prevents the amplification of market noise.
Assuming there are three single indicators (primary indicators) and m months (secondary indicators), is the th indicator of month i, where . The second level indicator is dimensionless. The formula is as follows:
Step 2, use the entropy method to calculate the weight of the second indicator. The entropy method is rooted in information economics: liquidity is ultimately an expression of informational efficiency. Entropy quantifies the uncertainty embedded in each indicator—the Amihud Ratio, for instance, displays elevated entropy during policy-tightening episodes, reflecting greater volatility. Assigning higher weight to such high-entropy indicators renders the composite index more responsive to monetary-policy shocks, as illustrated by the 2017 liquidity deterioration triggered by stringent regulation. This data-driven weighting eliminates subjective bias and aligns with the pronounced heterogeneity of China’s bond market, including its regional fragmentation. This is calculated as follows:
where is the entropy value of the indicator, as follows:
Step 3, use the coefficient of variation method to calculate the weight of the th indicator: , where is the mean square deviation of the th indicator and is the mean of the th indicator. The coefficient-of-variation method adds a temporal dimension: indicators exhibiting high coefficients—such as turnover that spikes during crises—signal heightened market responsiveness and are therefore assigned greater weight.
Step 4, calculate the total weight of the th indicator: . Relying solely on entropy weighting collapses when all bonds exhibit synchronized monthly turnover fluctuations—entropy approaches a value of 1 and the weighting scheme breaks down. Conversely, an exclusive use of the coefficient-of-variation method, being sensitive to outliers, can overreact to a single bond whose price deviation spikes abnormally. A composite weighting scheme reconciles structure with dynamics: the entropy method anchors the fundamental dimension (e.g., the persistent importance of trading immediacy), while the coefficient-of-variation layer captures cyclical swings (e.g., the post-COVID rebound in turnover). This hybrid approach mirrors the market participants’ adaptive expectations and underpins China’s “price-and-quantity” monetary-policy rule.
Under the combination of the entropy method and the coefficient of variation weighting method, the comprehensive liquidity index of the local bond market is represented as follows:
where , , and represent the turnover rate, standardized price deviation, and the Amihud indicators, respectively, and , , and are the weights calculated by the combination weighting method.
The variables used in this paper are summarized in Table 1.

Table 1.
The Variables Involved in the TVP-SV-SVAR model.
3.2. TVP-SV-SVAR Model
Compared to traditional VAR and SVAR models, the TVP-SV-SVAR model can flexibly and accurately capture the time-varying characteristics of bond market liquidity, quantity-based monetary instruments, and price-based monetary instruments. It can describe the asymmetric, nonlinear, and time-varying characteristics, and characterize the dynamic impact relationship.
Compared to the GARCH and DSGE models, the TVP-SV-SVAR model [33] includes time-varying parameters and stochastic volatility, which allows it to better capture the dynamic relationships between economic variables, especially when these relationships change over time. GARCH typically assumes that conditional variance is a function of past squared errors, which may limit its ability to capture dynamic changes. The DSGE model, on the other hand, requires the construction of a more complex economic system model, necessitating the collection and processing of a large amount of macroeconomic and microeconomic data, which poses significant challenges in data acquisition and processing.
Therefore, this paper uses the TVP-SV-SVAR model to test the time-varying characteristics of the pulse response of bond market liquidity under the impact of central bank price and quantity monetary policies. Unlike traditional SVAR models, this model extends static parameters to time-varying or dynamic parameters as follows:
In the model, we have expressed in matrix form above the properties of vectors, and the related matrices are listed as follows: is the vector of endogenous variables at time t, wherein 3 denotes the number of variables in Table 1: the overnight interbank rate (IBO001) as the price-based monetary policy proxy, the year-on-year growth rate of money supply (M0) representing quantitative policy, and the composite liquidity index (LIQ) of local bonds. is a stacked vector of lagged endogenous variables, the symbol represents the Kronecker product, is a third-order identity matrix, and is the number of lag periods, which can be determined by the information criteria. is the time-varying parameter matrix, whose elements evolve over time. Each row of bt represents the dynamic response of a variable to its own and other variables past values. is used to model stochastic volatility in these relationships, and the coefficient matrix is a lower triangular matrix, which is calculated as follows:
Let be the stacked vector of the lower triangular elements , and capture the dynamic responses of LIQ to monetary shocks, is the logarithmic random volatility matrix, and .
Assume that all estimated parameters in the model follow the random walk process shown in Formula (11):
where . The variance and covariance of time-varying parameters in the equation are determined by and , respectively. and are positive definite diagonal matrices. The synchronous relationships of different equations are independent of each other. This matrix and dimensional structure provide a comprehensive framework for analyzing time-varying relationships within the model.
The model’s time-varying impulse responses align with market microstructure theory. Regarding price-based policy IBO001, higher interbank rates tighten funding liquidity, which in turn increases bond market illiquidity, as measured by the Amihud (2002) [23] metric. The time-varying parameter (TVP) feature of the model specifically captures how this effect intensified after 2015 following interest rate liberalization. For quantitative policy M0, before 2015, M0 growth boosted liquidity primarily through traditional bank lending channels; however, post-2015, the impact reversed due to financial innovations and regulatory arbitrage, particularly the crackdown on shadow banking. The stochastic volatility (SV) component in the model effectively reflects the pronounced volatility spikes occurring during these structural transitions.
4. Empirical Analysis
4.1. Data Sources and Descriptive Statistics
The variables data are sourced from the Wind and Choice databases. The data for the liquidity measurement indicators span from 1 January 2013 to 31 December 2021. The total transaction volume of local government bonds used to calculate the turnover rate is provided as monthly data, while the rest of the variables are in daily data format. Based on the method described in Section 3.2, this paper converts the three individual liquidity indicators into monthly data and then calculates the comprehensive liquidity proxy variable.
To avoid the curse of dimensionality, monthly data of monetary policy proxy variables were selected for empirical analysis, while reducing the loss of sample information. The sample covers the period from January 2013 to December 2021, with a total of 108 sets of data sourced from the Choice and Wind databases. The descriptive statistics of the three variables are presented in Table 2.

Table 2.
Descriptive Statistics of Three Variables.
From Table 2, the standard deviation of IBO001 is 0.675, indicating that the overnight lending rate fluctuates significantly, suggesting that the market’s short-term supply and demand for funds may change frequently. The mean of M0 is 6.073, which implies that during the sample period, the central bank was implementing or maintaining an accommodative monetary policy to stimulate economic growth and to reduce borrowing costs. The average liquidity level in the bond market during the selected sample period is relatively low, with a standard deviation of 0.204, indicating relatively small fluctuations in bond market liquidity and a relatively stable market. The skewness is 0.851, showing a right skew in the distribution, which means that there are relatively fewer instances of good liquidity. Additionally, all three variables exhibit a peaked and thick-tailed pattern, indicating they do not follow a normal distribution. Figure 2 shows the trend of three variables over time.
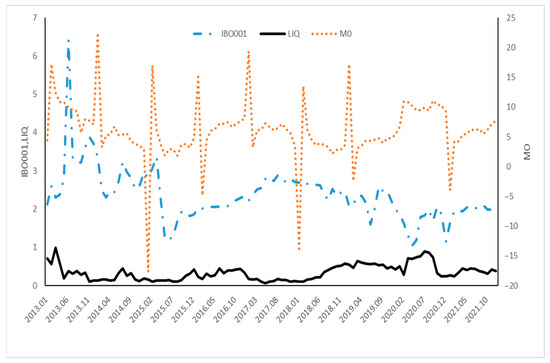
Figure 2.
Temporal Evolution of Key Variables. Notes: IBO001 is the price-based monetary policy proxy variable, LIQ is the comprehensive liquidity index of the local bond market, and M0 is the quantitative monetary instrument proxy variable.
As shown in Figure 2, due to the “money shortage” in June 2013 and the continuous reduction of the reserve requirement ratio by the People’s Bank of China since March 2015, IBO001 exhibited significant fluctuations before May 2015. The peak occurred in June 2013, corresponding to the “money crunch” event in the market. Afterwards, IBO001 tended to stabilize and steadily increase until June 2018, when it began to steadily decline. Subsequently, under the influence of the central bank’s loose monetary policy during the COVID-19 pandemic, the overnight lending rate declined sharply, reaching its lowest level in the sample period around April 2020.
The overall year-on-year growth rate of money supply M0 shows a fluctuating downward trend. Affected by the demand for cash withdrawals during the Spring Festival, there is a cyclical surge from January to February each year, followed by cash inflows after the holiday, forming liquidity replenishment.
The liquidity of the local bond market has continued to strengthen against the backdrop of explosive growth in the local bond secondary market since 2016. In 2017, the liquidity of the local bond market experienced a brief decline due to the strong regulatory policy environment of the banking industry, but then continued to rise and maintain a high level. At the beginning of 2020, the liquidity of China’s local bond market experienced a brief decline and quickly rebounded, reaching its highest level in recent years around July of that year.
Overall, the comprehensive liquidity indicators of the local bond market and the price-based monetary policy proxy variable IBO001 have exhibited similar trends for most periods, moving in roughly the same direction. However, there is a divergence in the trend of year-on-year growth rate with the quantitative monetary policy proxy variable M0.
4.2. Time-Varying Pulse Response and Comparative Analysis
4.2.1. Parameter Estimation and Model Validation
The principle of stationarity testing is primarily to determine whether a time series possesses the characteristic of stationarity; that is, whether its statistical properties remain stable over different time periods. Stationarity in a time series means that the mean, variance, and autocorrelation structure do not change over time. If a time series is non-stationary, it may exhibit trends, seasonality, or other forms of systematic variation that could affect the validity of statistical analyses or models that assume stationarity.
In this paper, the augmented Dickey–Fuller (ADF) method is used to perform stationarity tests on variables such as IBO001, M0, and LIQ, with the lag order determined by the Schwarz information criterion (SIC). The test results are shown in Table 3.

Table 3.
Results of Stationarity Test for Three Variables.
From Table 3, the ADF statistical values of each variable are all below the critical value at the 5% significance level. Therefore, the null hypothesis of the existence of unit roots can be rejected; that is, the original data of each variable is stationary. This result indicates that these variables have stable statistical characteristics, which can be used for forecasting, modeling, and economic analysis, thereby providing valuable insights and recommendations.
Based on information criteria, such as the likelihood ratio (LR), the final prediction error (FPE), the Akaike information criterion (AIC), the Schwarz criterion (SC), and the Hannan–Quinn criterion (HQ), the optimal lag order of the model is determined. The test results of each criterion are shown in Table 4.

Table 4.
Selection of Model Lag Order.
According to the LR criterion, the optimal lag order is 6, while the FPE, AIC, SC, and HQ criteria all point to an optimal lag order of 1. Considering the lag significance between the variables, the optimal lag order of the model is set to 1. This means that the value of s in Formula (1) is 1.
The Markov chain Monte Carlo (MCMC) estimation method under the Bayesian framework was selected for the time-varying parameters of the TVP-SV-SVAR model. The number of model iterations was set to 10,000. Considering that the initial value would affect the stability of model estimation, the first 1000 pre-burned samples were discarded. The estimation results are shown in Table 5.

Table 5.
Sample Autocorrelation Coefficient Estimation Results.
The Geweke diagnostic values and ineffective factors are used to test the convergence and effectiveness of the TVP-SV-SVAR model, which are important indicators for evaluating the effectiveness of the MCMC method. According to Table 5, the Geweke diagnostic values of the model parameters are all less than the critical value of 1.96, and the null hypothesis cannot be rejected at the 5% significance level. The Geweke diagnostics significantly converge to the posterior distribution, showing that the parameters of the model significantly converge to the posterior distribution, indicating good convergence of the selected sample in this study. Ineffective factors are mainly responsible for testing effectiveness, with smaller values indicating better sampling efficiency. In Table 5, the values of ineffective factors corresponding to each parameter remain at a relatively low level, with a maximum value of 44.89, indicating that we can obtain at least 223 unrelated sample observations in this state. There is a lot of sample information contained in the observation period, allowing for effective estimation. Therefore, the samples extracted through the MCMC method are effective.
Based on the estimation results, Figure 3 shows the trend of autocorrelation coefficient changes of the estimated variables in the TVP-SV-SVAR model. The sample path of MCMC sampling is shown in Figure 4, and the posterior distribution of the MCMC simulated parameter samples is shown in Figure 5.
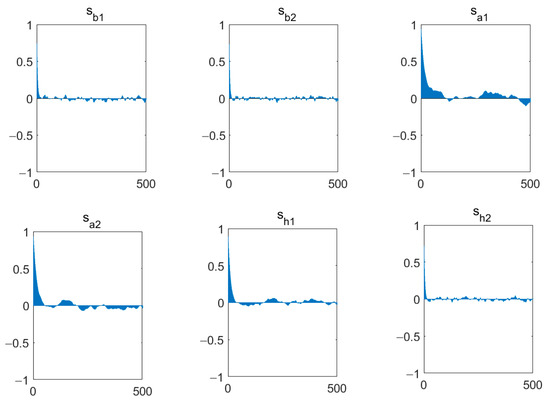
Figure 3.
Autocorrelation Functions for Model Parameters.
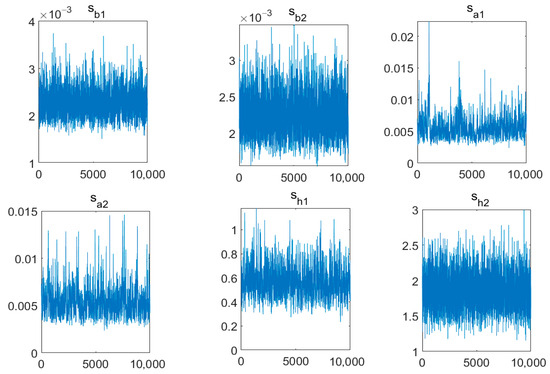
Figure 4.
Markov chain Monte Carlo (MCMC) Convergence Diagnostics.
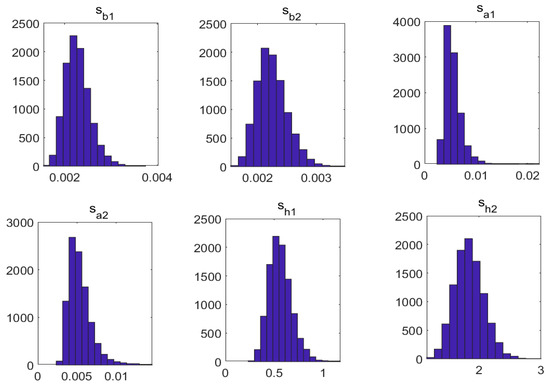
Figure 5.
Posterior Distributions of Estimated Parameters.
From Figure 3, the estimated parameter autocorrelation coefficient gradually decreases, and after 500 rounds of the MCMC, the fluctuation values tend to zero, indicating that the sampling is stable, and the preset initial values of each parameter make the sampling effective. Figure 4 shows that, as the number of samples increases, the estimated variable exhibits a significant mean recovery characteristic, indicating that the estimation results of the variable become more robust. The posterior distribution density map in Figure 5 shows that, after 10,000 MCMC sampling estimates, the parameter results have good convergence and clustering characteristics, indicating the effectiveness of the model simulation results. Therefore, the TVP-SV-SVAR model is highly effective for impact analysis.
4.2.2. Analysis of Time-Varying Random Fluctuations
The time-varying stochastic volatility analysis results of price and quantity based monetary policy proxy variables and local bond market liquidity comprehensive indicators are shown in Figure 6.
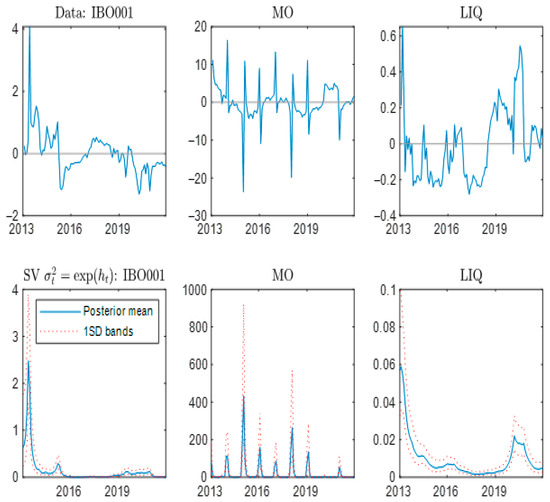
Figure 6.
Time-Varying Stochastic Volatility of Key Variables.
As shown in Figure 6, the price-based monetary policy proxy variable IBO001 exhibits a positive random fluctuation characteristic, with significant differences in volatility before and after 2016. Specifically, the fluctuation range of random volatility was relatively large before 2016, but the random volatility remained relatively stable and eventually tended to zero after 2016. This change can be attributed to the facts that the central bank lifted the upper limit of deposit interest rate control in October 2015, and the degree of marketization of interbank lending rates gradually increased. The random volatility of the year-on-year growth rate of the quantitative policy proxy variable M0 quickly converges to 0 after a brief cyclical peak.
4.2.3. Analysis of Time-Varying Pulse Response
Based on the estimation results of the TVP-SV-SVAR model, this paper analyzes two types of impulse response functions: the first is the equidistant impulse response function, which reflects the impact of a positive impact of one standard deviation shock on the liquidity of the local bond market at the same time interval under different lead times when monetary policy variables experience a positive impact; the second type is the time point impulse response function, which reflects the impact on the liquidity of local bond markets at different time points when a positive one standard deviation shock occurs in monetary policy variables.
Figure 7 and Figure 8 show the impulse response effects of local bond market liquidity on two types of monetary policy shocks under different lead times. Among them, three periods, six periods, and twelve periods in advance correspond to the short-term, medium-term, and long-term time states, respectively.
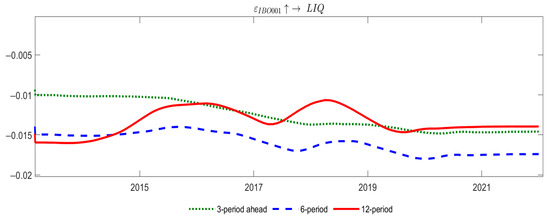
Figure 7.
Impulse Responses of Liquidity to IBO001 Shocks Across Horizons.
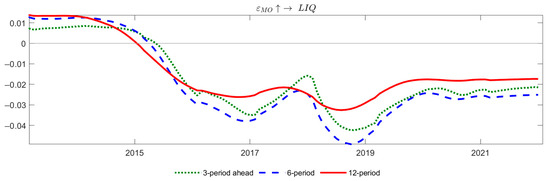
Figure 8.
Impulse Responses of Liquidity to M0 Shocks Across Horizons.
From Figure 7, we can observe that the pulse response of local bond market liquidity to price-based monetary policy is consistently negative, indicating that an increase in overnight interbank lending rates promotes a decrease in liquidity in the local bond market across the short, medium, and long terms.
The index’s negative response to IBO001—peaking at the medium horizons—captures the economic mechanism whereby higher policy rates, transmitted through the price channel, sap trading willingness and erode liquidity breadth. Entropy weights amplify this effect by assigning the dimension a high, data-driven loading. During the 2020 loan-pricing reform, the strongest index reaction illustrates how the composite weights dynamically adapt to policy transitions such as interest-rate liberalization: the coefficient-of-variation component rapidly registers the heightened sensitivity of turnover, furnishing the PBOC with an on-the-fly risk signal.
With the extension of the lag period, the pulse response intensity shows a trend of increasing and then decreasing. The response value with a lag of six periods is the highest, indicating that the medium-term impact of price-based monetary policy on the liquidity of local bond markets is the strongest, though its sustainability is not strong. The fluctuation amplitude of pulse response shows a gradually increasing trend, with more obvious time-varying characteristics. The fluctuation amplitude with a lag of 12 periods is the largest, indicating that the impact of price-based monetary policy is relatively stable in the short and medium term, and liquidity is more sensitive to its impact in the long term. As revealed by Goyenko and Ukhov [10], the influence of monetary policy on the bond market is significant and lasts for a considerable duration.
From a market-microstructure perspective, the hump-shaped impulse response of local-government bond liquidity to an IBO001 hike—first intensifying, then fading—mirrors a two-stage adjustment. Immediately, the higher policy rate raises interbank funding costs, inflating the dealers’ inventory risk and prompting an abrupt narrowing of bid–ask spreads, and the response curve plunges. Over the medium term, institutional investors rebalance portfolios. Because local bonds are relatively illiquid, these trades generate sizeable price-impact costs, driving the impulse to its peak. In the long run, the market completes its repricing, and the PBOC may offset the shock through open-market operations, so the response gradually subsides.
Figure 8 illustrates the pulse response of liquidity in the local bond market to quantitative monetary policy. There is a notable shift in the response around 2015. Before 2015, the pulse response was positive, indicating that an increase in M0 had a positive effect on the liquidity of local bonds. This is consistent with Iwatsubo and Taishi (2018) [34] and Christensen and Gillan (2019) [15], who found that quantitative and qualitative monetary easing (QQE) policies adopted by the government significantly enhanced the liquidity of the bond market. From the perspective of Japan’s policy adjustments, increasing the frequency of purchases, reducing the amount of each transaction, and lowering the variability of the purchase volume have significantly improved market liquidity. After 2015, the pulse response turned negative, indicating that an increase in M0 would lead to a decrease in liquidity in the local bond market.
The sign-reversal of M0’s impact on the index around 2015 is rooted in the evolving weighting scheme. Before 2015, the entropy method highlighted the informational content of price deviations, so looser policy reduced information costs and lifted the index. After 2015, the coefficient-of-variation method assigned greater weight to the Amihud Ratio, causing quantitative expansions to translate into heavier price-impact penalties and a negative impulse. This micro-foundation aligns with, and helps interpret, the TVP-SV-SVAR model’s time-varying estimates. During the 2017 local-debt clampdown, the pronounced negative response cautioned policymakers to calibrate quantity tools carefully to avert market dysfunction.
Similar to price-based policy, with the extension of the hysteresis period, the pulse response intensity increases and the decreases with the lag period, with the greatest impact observed in the mid-term. The fluctuation amplitude of pulse response is the largest with a lag of 12 periods, indicating that the long-term impact is relatively stable, meaning that, in the long run, the sensitivity of local bond market liquidity to changes in money supply is relatively low.
The structural shift before and after 2015 mirrors a deeper transformation of China’s financial architecture. In the pre-2015 regime, an M0 increase worked through a “credit expansion—LGFV borrowing surge—rising demand for local bonds” pipeline, delivering a positive liquidity impulse. After 2015, the same expansion flips sign: higher M0 stokes inflation expectations, prompting investors to offload long-duration local bonds faster than new demand emerges; meanwhile, abundant liquidity is parked in highly liquid safe assets rather than channeled into the local bond market, reflecting heightened credit-risk aversion. The lesson for policymakers is clear—when clamping down on local-debt growth, quantitative easing must be paired with targeted risk-mitigation tools to prevent stimulus from “idling” outside the bond market.
In summary, both price-based and quantity-based monetary policies have significant time-varying impacts on the liquidity of the local bond market. The relationship between impulse response and lag period shows nonlinear characteristics, with the medium-term impact being the most significant. Overall, the impact of quantitative monetary policy on the liquidity of local bond markets is greater than that of price-based monetary policy.
The asymmetry and time-varying nature of impulse responses carry immediate policy implications. A negative response to price-based shocks (IBO001) shows that rate hikes curb market activity through the price channel: higher funding costs lead investors to scale back bond trading, eroding liquidity breadth (wider bid–ask spreads) and depth (lower turnover). This mechanism was starkly visible during the 2017 clampdown on local-government debt, where the peak response at a lag of six periods coincided with regulatory tightening—a reminder that overlapping measures can tip the market toward dysfunction. Likewise, the sign reversal in quantitative-policy shocks (M0) around 2015 signals a structural break: pre-2015 expansions in M0 boosted liquidity by lowering information costs, whereas post-2015 expansions dampened it as the rise of digital finance amplified the price impact. Policymakers should therefore prioritize quantitative tools for day-to-day liquidity management and avoid clustering rate adjustments, particularly during episodes of interest-rate liberalization (e.g., the 2020 loan-pricing reform) to safeguard market stability.
To analyze the effect in more details, several specific time points are selected for the time-point pulse response analysis. We have selected three points that reflect the process of China’s financial market transitioning from a regulated to a market-oriented system. Each step has had a profound impact on the efficiency, stability, and competitiveness of the financial market.
In October 2015, the restrictions on the fluctuation of deposit and loan interest rates in China were basically lifted, and the market-oriented reform of interest rates entered a new stage. The formation mechanism and regulatory mechanism of market-oriented interest rates were at the core. This marks a significant turning point in China’s financial market. The marketization of interest rates helps to improve the efficiency of the financial market, to promote the rational allocation of resources, and to enhance the competitiveness and risk management capabilities of banks. This reform also lays the foundation for subsequent innovation in financial products and the deepening of the financial market.
In July 2017, the National Financial Work Conference made important arrangements for local debt, including proposing to strictly control its scale, further promoting deleveraging, resolutely implementing a prudent monetary policy, and emphasizing the local government’s responsibility for risk disposal. This conference indicated that the government is aware of the risks associated with local debt and has taken measures to prevent and to resolve these risks. This policy adjustment helps to maintain macroeconomic stability and to promote sustainable economic development.
The third time period is January 2020, and new loans will no longer be priced based on the benchmark loan interest rate starting from that day. This change signifies that China’s loan market interest rates are becoming more market-oriented. This reform helps to enhance the flexibility and sensitivity of loan interest rates, enabling them to reflect more accurately the market supply and demand relationship and the level of risk.
Based on the selected time point, the pulse response of local bond market liquidity to two types of monetary policies is shown in Figure 9 and Figure 10.
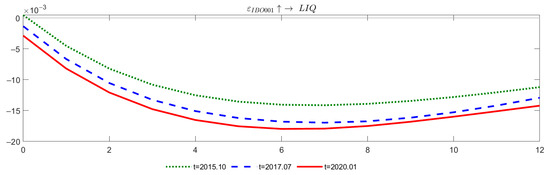
Figure 9.
Impulse Responses of Liquidity to IBO001 Shocks at Different Time Points.
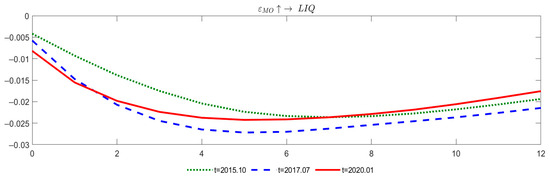
Figure 10.
Impulse Responses of Liquidity to M0 Shocks at Different Time Points.
Figure 9 shows that, at three time points, the pulse response pattern of liquidity in the local bond market to price-based monetary policy shocks is consistent, all of which have a sustained negative effect and produce relatively weak responses in the current period. The degree of response increases and then weakens, ultimately exceeding the initial level, and reaches its maximum value between the sixth and seventh periods. The difference lies in the response intensity and duration. In the event of “new loans no longer being priced based on loan benchmark interest rates” in January 2020, the impact of price-based monetary policy on liquidity was the greatest and the duration was the longest. The impact on the liquidity of the local bond market was minimal and the duration was the shortest during the “basic lifting of floating restrictions on deposit and loan interest rates” event in October 2015.
Figure 9 illustrates how price-based monetary policy transmits to local-government bond liquidity at three pivotal junctures. In October 2015, shortly after the formal completion of interest-rate liberalization, the impulse response is modest, reflecting China’s lingering “dual-track” interest-rate regime. Although the deposit-rate ceiling had been abolished, the banks’ liability costs adjusted sluggishly, blunting the pass-through of policy rates to the bond market. By July 2017, under the banner of “strictly controlling local-debt expansion” issued at the National Financial Work Conference, the response intensifies sharply. The tightening narrative heightened institutional sensitivity to rate hikes. Tighter interbank funding (IBO001 surged) coincided with a flight from local bonds, prompting market-makers to scale back quotes and turnover to fall. The liquidity shock exceeded that of 2015 but remained below the 2020 peak. After the LPR reform in 2020, the impulse response reaches its apex. The synchronized liberalization of loan and deposit pricing generated a policy synergy that markedly improved transmission efficiency. These contrasting episodes demonstrate that the dividends of interest-rate liberalization materialize only when sequenced and coordinated with broader financial reforms.
From Figure 10, at three time points, quantitative monetary policy also has a sustained negative effect on the liquidity of the local bond market. With the extension of time, there is a crossover in the pulse response at the three time points. However, under the “strict control of local government debt increment” event in July 2017, the degree of pulse response is the highest.
In summary, the pulse response of liquidity in the local bond market to both quantity and price-based monetary policy shocks exhibits asymmetric, nonlinear, and time-varying characteristics. The impact differences caused by quantitative monetary policy at three time points are greater, including the fluctuation amplitude of the impulse response function, the position of the maximum value, and the response form, indicating that liquidity has a more significant time-varying impulse response to quantitative monetary policy shocks. In addition, the pulse response value of liquidity to quantitative monetary policy is larger, indicating that quantitative monetary policy has a deeper impact on the liquidity of local bond markets.
Figure 10 disentangles the heterogeneous impact of quantity-based monetary policy on local-bond liquidity at three critical junctures. In 2015, an expansion of M0 produced only a mild adverse reaction, as the market’s pricing flexibility absorbed the extra base money without major disruption. By July 2017, however, an identical increase in M0 coincided with a sharp deterioration in liquidity. The “tight supervision–loose money” mix of that episode induced banks to hoard liquidity rather than redeploy it; excess reserves piled up in the interbank market while risk-asset allocations were slashed, creating a textbook case of “liquidity hoarding”. After the LPR reform in 2020, the policy shifted emphasis toward price signals, muting the marginal impact of M0 growth. The impulse-response curves diverge markedly from the sixth month onward, underscoring three lessons: quantity measures are hostage to the regulatory backdrop—2017’s intensified oversight lengthened the transmission lag; they hinge on market expectations—stable sentiment during the 2020 pandemic shortened it; and they depend on the policy mix—targeted instruments proved decisive in restoring efficiency.
These point-in-time responses (Figure 9 and Figure 10) yield granular operational guidance. At the October 2015 milestone of interest-rate liberalization, the muted reaction to an IBO001 shock (≈−0.02) reflected pre-emptive duration adjustments; regulators can exploit such “policy windows” to deepen reforms without replicating the heightened sensitivity observed in 2020 (≈−0.08). The six-period lag to peak response calls for coupling policy moves with forward guidance (Lee et al., 2016) [13] to smooth expectations. When M0 expansion coincides with a digital-finance boom—as in January 2020—tightening maturity-mismatch limits on wealth-management products can force banks to reduce the share of long bonds funded by short liabilities, cushioning price shocks. Conversely, when M0 is being drained amid a debt clampdown—as in July 2017—activating the Standing Lending Facility to inject emergency liquidity can stabilize bid–ask spreads (the breadth dimension) and avert market seizures.
4.3. Robustness Check
Robustness testing involves two aspects of work. The first case chooses turnover rate as a liquidity proxy indicator. The second method uses the overnight collateral repo rate R001 and the open market net placement PO as new proxy variables for price and quantity monetary policies. The ADF test results of turnover rate, R001 and PO show that they are both first-order stationary variables. Therefore, the TVP-SV-SAR models were established for two combinations, IBO001, M0, and turnover rate, R001, PO, and LIQ, with the same parameter settings as before, respectively. Figure 11 and Figure 12, respectively, show the pulse response results of local bond market liquidity to two types of monetary policy shocks at different lead times and time points.
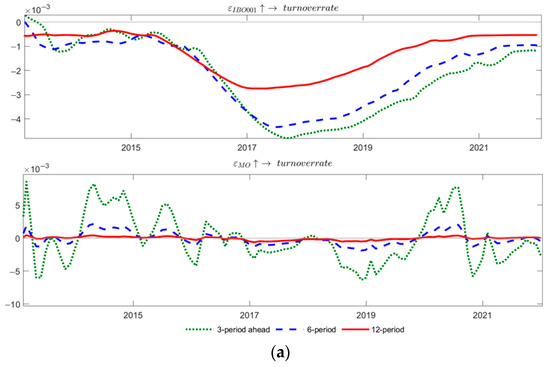
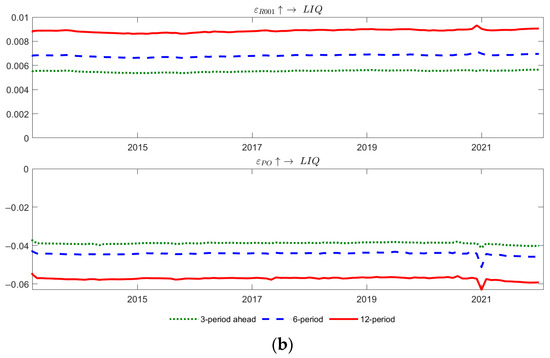
Figure 11.
Robustness Checks: Impulse Responses of Liquidity Across Horizons: (a) IBO001, M0, and turnover rate; (b) R001, PO, and LIQ.
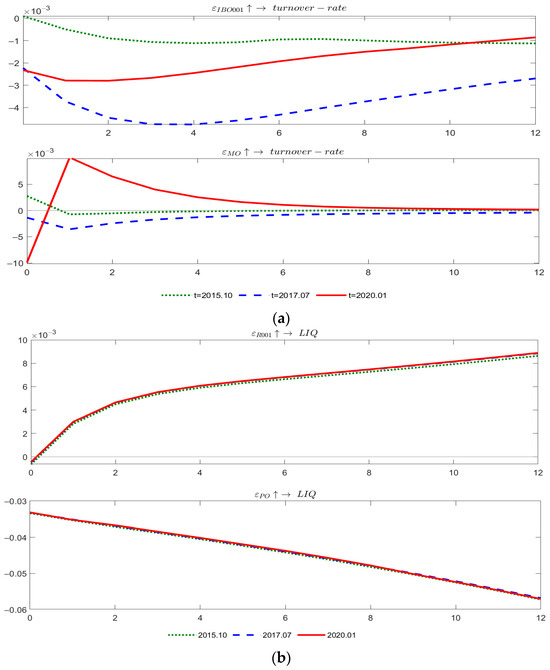
Figure 12.
Robustness Checks: Impulse Responses of Liquidity at Different Time Points: (a) IBO001, M0, and turnover rate; (b) R001, PO, and LIQ.
From Figure 11 and Figure 12, the pulse response of liquidity in the local bond market to both types of monetary policy shocks exhibits asymmetric, nonlinear, and time-varying characteristics. Quantitative monetary policies notably exhibit larger pulse response values, indicating a deeper impact on the local bond market liquidity compared to price-based monetary policies. Therefore, the conclusions drawn from empirical research are robust.
5. Discussion
5.1. Main Findings
This paper constructs a comprehensive index to measure the development and changes in the liquidity of China’s local government bond market. The novelty of the composite-weighting scheme lies in its economic foundations: the entropy method leverages information entropy to curb model risk—such as subjective-bias errors—while the coefficient-of-variation term embeds market heterogeneity, yielding a more robust index. Compared with traditional single metrics, this approach is able, in the era of digital finance, to incorporate new liquidity traits, such as the immediacy of algorithmic trading, thereby furnishing the central bank with a high-frequency monitoring tool.
This paper empirically analyzes the impulse response of local bond market liquidity to two types of monetary policy shocks using the TVP-SV-SVAR model. Regardless of the different lead times or different time points, the liquidity of the bond market during the sample period exhibits significant asymmetric, nonlinear, and time-varying characteristics in impulse response to price and quantity based monetary instruments. This variability is attributed to the evolving diversity of bond types and market participants in the expanding bond market. On the one hand, due to the significant heterogeneity among various participants, the impact of monetary policy on each entity varies greatly. On the other hand, the interlinking relationships and information transmission between the different bond market segments further complicate the mechanism of influence.
The impact differences observed across three time points for quantitative monetary policy are more pronounced, evidenced by the fluctuations in the amplitude of the impulse response function, the position of the maximum value, and the response form, indicating that liquidity has a more significant temporal variability in the impulse response of quantitative monetary policy. In addition, comparing the absolute values of response values under the two policies, it was found that quantitative monetary policies have a stronger impact on liquidity. The economic rationale underpinning the index translates directly into actionable guidance. The entropy method identifies information efficiency as the core of liquidity, while the coefficient-of-variation layer stresses dynamic management, adjusting weights during crises. Together they quantify the “price-and-quantity” rule. The sharp rebound of the index in 2020 (COVID-19 peak) and its shifting weights captured the confidence lift from policy easing, steering the PBOC away from over-reliance on any single instrument.
The larger response to quantitative shocks (M0) is most valuable for risk pricing. As M0 expands, the balance-sheet pressure on financial institutions forces investors to liquidate bonds and withdraw funds, amplifying liquidity shocks. Policymakers can exploit the TVP-SV-SVAR model’s time-varying results—such as the crossing points of impulse responses—to design buffer mechanisms. For example, during the 2015 interest-rate-liberalization transition, structural instruments were phased in to released liquidity gradually, preventing a single operation from overshooting the market.
This paper verifies the robustness of the empirical results by replacing proxy variables for liquidity indicators and monetary policies. The results affirm that the impact of both types of monetary policy on the liquidity of the local bond market exhibits obvious characteristics of asymmetry, nonlinearity, and time-varying nature. Moreover, the quantitative monetary policy has a deeper impact, further reinforcing the conclusions drawn in the previous text.
5.2. Implications of Research
Based on the above results, this paper proposes the following suggestions.
First, this paper constructs a comprehensive index to measure the development and changes in the liquidity of China’s local government bond market. The analysis of the results reveals that the liquidity of the local bond market is highly volatile and susceptible to the influence of economic events in the market. The product types of local government bonds in China are relatively singular, lacking in short-term bonds of less than one year or long-term bonds of more than ten years. The diversified investment needs are not fully met, preventing the local bond market from fully absorbing idle social capital. Therefore, a more diverse product system should be established to attract investors from various sectors, thereby optimizing the structure of investors. Efforts should continue to cultivate and develop institutional investors, to improve the market maker system, and to institute effective incentives for market makers to play their role in regulating and stabilizing bond market liquidity.
Second, both types of monetary policies can cause changes in the liquidity of local government bonds, but quantitative monetary policies have a greater impact. Therefore, when regulating the liquidity of the local government bond market, quantitative tools can be prioritized. To enhance the regulatory role of price-based policy tools, the central bank can innovate the interest rate transmission mechanism on the existing basis, leverage the interest rate corridor mechanism, and use some policy tools, such as mortgage supplementary loans and medium-term lending convenience, among other tools, to guide the money market interest rates more accurately and effectively. The central bank should avoid making concentrated adjustments to the reserve requirement ratio and should opt for gradual and moderate monetary policy tools, such as open market operations. Attention should be paid to the combination of two types of monetary policy tools to reduce excessive shocks to bond market liquidity. The management of bond market liquidity should be from a time-varying and dynamic perspective, to clear the transmission mechanism of monetary policy, and to pay timely attention to the heterogeneous impact of “quantitative” and “price” types of monetary policy on bond market liquidity, especially the lag and memory of the two types of monetary policy.
Third, the approach of using monetary policy to affect market liquidity has reference significance for other economies in regulating economic cycles and financial market fluctuations. Strengthen the coordination of monetary policy with financial regulatory policy to promote the stable operation of the bond market. At present, with the continuous development of financial innovation, the connection between monetary policy and the bond market is becoming more closely linked. The formulation and implementation of monetary policy must consider the micro-foundation of its transmission, fully consider the impact of the interbank asset allocation structure of commercial banks on bond market liquidity, and strengthen the coordination between monetary policy and regulatory policy to ensure the efficiency of policy transmission and the stable operation of the bond market.
This study delivers policymakers with an integrated dashboard: the Liquidity Index (LIQ) fuses entropy weights that lock in structural importance with coefficient-of-variation weights that track dynamic swings, enabling the real-time surveillance of market heterogeneity amid regional fragmentation or crisis turbulence. The COVID-19 rebound of 2020 illustrates the tool in action—weights migrated toward high-volatility components as stimulus revived confidence, a signal that should now be embedded in the macro-prudential toolkit and coupled with the TVP-SV-SVAR model for forward-looking liquidity analytics. Operationally, when LIQ shows that quantitative easing is eliciting an outsized response, the PBOC should lean on open-market operations to avert concentrated shocks; over the medium term, interest-rate liberalization must reinforce the price channel by widening the policy-rate corridor and weaving digital-finance instruments into the transmission architecture; and, as the index’s 2017 spike following local-debt shocks attests, monetary and regulatory levers must be calibrated in tandem to pre-empt regional liquidity droughts.
6. Conclusions and Limitations
6.1. Conclusions
This study provides a comprehensive analysis of how monetary policy impacts liquidity in China’s local government bond market, leveraging an innovative TVP-SV-SVAR framework to capture asymmetric and time-varying effects. By examining quantitative tools (M0) and price-based tools (IBO001), we reveal that monetary operations exhibit distinct nonlinear dynamics across critical economic events, such as the 2015 interest-rate liberalization and the 2020 pandemic response. Notably, quantitative easing initially boosted liquidity, but suppressed it post-2015 due to regulatory shifts, highlighting the importance of adaptive policy calibration in emerging markets. Our entropy-CV-weighted composite liquidity index (LIQ) dynamically quantifies these responses, demonstrating heightened sensitivity during crises like the 2017 deleveraging episode.
The research makes three pivotal contributions to financial economics. First, the TVP-SV-SVAR model overcomes the limitations of static approaches (e.g., standard VAR) by quantifying the evolving policy transmission channels, offering a robust tool for capturing stochastic volatility in bond markets. Second, we identify a unique asymmetry: quantitative tools dominate price-based tools in driving liquidity changes—a finding that challenges conventional paradigms from developed markets and urges tailored instrument strategies. For instance, M0 shocks induce deeper and longer-lasting impacts, with effects persisting beyond 12 months. Third, the LIQ index provides a replicable methodology for emerging markets navigating digital finance integration, enabling real-time liquidity monitoring.
In summary, this research redefines monetary policy efficacy for bond market stability, emphasizing data-driven regulation. By integrating dynamic modeling with empirical rigor, it equips policymakers to balance quantitative and price-based tools in volatile environments, fostering resilient financial systems in China and beyond.
6.2. Limitations and Perspectives
There are still the following limitations in this paper, which are worthy of further discussion in future research.
First, this paper selected two representative tools from the monetary instruments, namely the interbank lending rate IBO001 and the year-on-year growth rate of the money supply M0, to act as proxy variables for the two types of policies. However, there are many monetary tools under the central bank system in China, and the selection of a certain proxy variable may cause some bias in the research results. In future research, the selection range of monetary tools can be expanded, and other tools can be added to the model for a comprehensive comparison to obtain more comprehensive and accurate results.
Second, this paper only studied the impulse response of the local government bond market to the impact of monetary policy shocks. Follow-up research can expand the scope of research from two aspects: breadth and depth. It can further explore the impulse response of liquidity in other important sub-markets of bonds on the impact of monetary policy shocks based on the local debt market; it can also divide the local debt market into regions to study the regional heterogeneity of the impact of monetary policy on the local debt market, to better regulate the liquidity of the bond market comprehensively through monetary policy, and thus to prevent the occurrence of financial risks.
Third, our research has opened a door for further research. According to the Keynesian view, the ultimate impact of monetary policy on bond market liquidity depends on the relative attractiveness of other asset markets (i.e., the stock market). For example, the tightening of monetary policy will make bonds more attractive than stocks, and part of the impact of monetary policy on bond liquidity will be transmitted through the stock market. It is worth noting that the existing literature supports this conclusion, as shown by Goyenko and Ukhov (2009) [10]. In this regard, it should be noted that this effect does not change the direction of the causal relationship observed in our research (from monetary policy to bond liquidity), but only involves the transmission mechanism of the impact of monetary policy shocks on the bond market (which may also pass through the stock market).
Author Contributions
Software, X.L. and F.L.; formal analysis, Y.H.; writing—original draft preparation, X.L., Y.H. and F.L.; writing—review and editing, X.L. and R.Z.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Youth Research Special Project of NCUT (No. 2025NCUTYRSP039), the Research Initiation Fund Project of the North China University of Technology (110051360002), and the Yuxiu Innovation Project of NCUT (2024NCUTYXCX114).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Thanks to Xinyu Wang for the literature review and for proofreading this paper.
Conflicts of Interest
Author Fang Liu was employed by the company Jinan City Construction Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Amihud, Y.; Mendelson, H. Liquidity and Asset Prices: Financial Management Implications. Financ. Manag. 1988, 3, 5–15. [Google Scholar] [CrossRef]
- Alaminos, D.; Salas, M.B.; Fernández-Gámez, M.A. High-Frequency Trading in Bond Returns: A Comparison Across Alternative Methods and Fixed-Income Markets. Comput. Econ. 2024, 64, 2263–2354. [Google Scholar] [CrossRef]
- Borio, C. Monetary and financial stability: Here to stay? J. Bank. Financ. 2006, 30, 3407–3414. [Google Scholar] [CrossRef]
- Klingelhofer, J.; Sun, R. Macroprudential policy, central banks and financial stability: Evidence from China. J. Int. Money Financ. 1993, 20, 19–41. [Google Scholar] [CrossRef]
- Martinez-Miera, D.; Repullo, R. Monetary policy, macroprudential policy, and financial stability. Annu. Rev. Econ. 2019, 11, 809–832. [Google Scholar] [CrossRef]
- Demirer, R.; Gabauer, D.; Gupta, R.; Ji, Q. Monetary policy and speculative spillovers in financial markets. Res. Int. Bus. Financ. 2021, 56, 101373. [Google Scholar] [CrossRef]
- Parker, D.N.; Semmler, W. Monetary Policy and the Evolution of Wealth Disparity: An assessment using US survey of consumer finance data. Comput. Econ. 2024, 64, 3509–3541. [Google Scholar] [CrossRef]
- Wu, N.; Zhang, Z.; Lin, B. Responses of financial stress and monetary policy to global warming: Evidence from China. Int. Rev. Financ. Anal. 2024, 92, 103092. [Google Scholar] [CrossRef]
- Salimi, S.; Kazinczy, E.; Tatay, T.; Amini, M. Evaluating Fiscal and Monetary Policy Coordination Using a Nash Equilibrium: A Case Study of Hungary. Mathematics 2025, 13, 1427. [Google Scholar] [CrossRef]
- Goyenko, R.Y.; Ukhov, A.D. Stock and Bond Market Liquidity: A Long-Run Empirical Analysis. J. Financ. Quant. Anal. 2009, 44, 189–212. [Google Scholar] [CrossRef]
- Pasquariello, P.; Roush, J.; Vega, C. Government Intervention and Strategic Trading in the U.S. Treasury Market. J. Financ. Quant. Anal. 2012, 55, 117–157. [Google Scholar] [CrossRef]
- Fernández-Amador, O.; Gächter, M.; Larch, M.; Peter, G. Does monetary policy determine stock market liquidity? New evidence from the euro zone. J. Empir. Financ. 2013, 21, 54–68. [Google Scholar] [CrossRef]
- Lee, J.; Ryu, D.; Kutan, A.M. Monetary Policy Announcements, Communication, and Stock Market Liquidity. Aust. Econ. Pap. 2016, 55, 227–250. [Google Scholar] [CrossRef]
- Albagli, E.; Ceballos, L.; Claro, S.; Romero, D. Channels of US monetary policy spillovers to international bond markets. J. Financ. Econ. 2019, 134, 447–473. [Google Scholar] [CrossRef]
- Christensen, J.H.E.; Gillan, J.M. Does quantitative easing affect market liquidity? J. Bank. Financ. 2022, 134, 106349. [Google Scholar] [CrossRef]
- Cohen, L.; Furman, I. The impact of the ECB’s PEPP project on the COVID-19-Induced crisis in the corporate bond market. Econ. Lett. 2024, 235, 111563. [Google Scholar] [CrossRef]
- Harris, M. Liquidity, Trading Rules, and Electronic Trading System; Monogragh Series of Finance and Economics; NYU Salomon Center: New York, NY, USA, 1990; Volume 4. [Google Scholar]
- Demsetz, H. The Cost of Transacting; The Quarterly Journal of Economics; Oxford University Press: Oxford, UK, 1968; Volume 82, pp. 33–53. [Google Scholar]
- Amihud, Y.; Mendelson, H. Asset Pricing and the Bid-ask Spread. J. Financ. Econ. 1986, 17, 223–249. [Google Scholar] [CrossRef]
- Dubofsky, D.A.; Growth, J.C. Exchange Listing and Stock Liquidity. J. Financ. Res. 1984, 7, 291–302. [Google Scholar] [CrossRef]
- Hui, B.; Heubel, B. Comparative Liquidity Advantages Among Major US Stock Markets; DRI Financial Information Group Study Series; Data Resources, Inc.: Columbia, CA, USA, 1984. [Google Scholar]
- Amihud, Y. Illiquidity and Stock Returns: Cross-section and Time-series Effect. J. Financ. Mark. 2002, 5, 31–56. [Google Scholar] [CrossRef]
- Garbade, K.D.; Silber, W.L. Price Movements and Price Discovery in Futures and Cash Markets. Rev. Econ. Stat. 1983, 65, 289–297. [Google Scholar] [CrossRef]
- Pan, B. The asymmetric dynamics of stock–bond liquidity correlation in China: The role of macro-financial determinants. Econ. Model. 2023, 124, 106295. [Google Scholar] [CrossRef]
- Liao, C.; Luo, Q.; Tang, G. Aggregate liquidity premium and cross-sectional returns: Evidence from China. Econ. Model. 2021, 104, 105645. [Google Scholar] [CrossRef]
- Primiceri, G.E. Time varying structural vector autoregressions and monetary policy. Rev. Econ. Stud. 2005, 72, 821–852. [Google Scholar] [CrossRef]
- Nakajima, J. Time-Varying Parameter VAR Model with Stochastic Volatility: An Overview of Methodology and Empirical Applications; Bank of Japan: Tokyo, Japan, 2011. [Google Scholar]
- Boufateh, T.; Saadaoui, Z. The time-varying responses of financial intermediation and inflation to oil supply and demand shocks in the US: Evidence from Bayesian TVP-SVAR-SV approach. Energy Econ. 2021, 102, 105535. [Google Scholar] [CrossRef]
- Ding, Q.; Huang, J.B.; Zhang, H.W. The time-varying effects of financial and geopolitical uncertainties on commodity market dynamics: A TVP-SVAR-SV analysis. Resour. Policy 2021, 72, 102079. [Google Scholar] [CrossRef]
- Jiménez, A.; Rodríguez, G.; Arellano, M.A. Time-varying impact of fiscal shocks over GDP growth in Peru: An empirical application using hybrid TVP-VAR-SV models. Struct. Change Econ. Dyn. 2023, 64, 314–332. [Google Scholar] [CrossRef]
- Lyu, X.; Hu, H. The dynamic impact of monetary policy on stock market liquidity. Econ. Anal. Policy 2024, 81, 388–405. [Google Scholar] [CrossRef]
- Heng, Y.; Sheng, C.; Hu, Y. Assessment and governance of industrial internet maturity in the building materials industry using the entropy weight method and factor analysis. Heliyon 2023, 9, 18650. [Google Scholar] [CrossRef]
- Ari, Y.; Kurt, H.; Uçak, H. Volatility Spillovers Among EAGLE Economies: Insights from Frequency-Based TVP-VAR Connectedness. Mathematics 2025, 13, 1256. [Google Scholar] [CrossRef]
- Iwatsubo, K.; Taishi, T. Quantitative Easing and Liquidity in the Japanese Government Bond Market. Int. Rev. Financ. 2018, 18, 463–475. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).