A Vertex Separator Problem for Power Graphs of Groups

Abstract

Given a graph G, an st-connected vertex separator (CVS) problem refers to the search for a minimum connected component in G whose removal leaves the pair of nodes s and t in two disjoint components. We investigate this specific problem on certain types of graphs—so-called power graphs associated with groups. We present a mathematical model and an algorithm to solve this problem in a reasonable time. Finally, numerical tests show that the algorithm runs considerably fast even on graphs of high orders.

1. Introduction

The graph separation problem concerns with the search for good separators in graphs, for example, the problem of finding the minimum set of vertices disconnecting two specific vertices in a graph. Currently, in applied and computational mathematics, it is often inevitable to have to deal with difficult algorithms that require considerable a amount of time and memory, for example, with large matrices as input. Indeed, if a given problem has many variables in play, the associated matrix becomes very large in size. One possible approach to simplify such a problem is to partition the input (i.e., to subdivide the matrix into sub-matrices) and then run simpler algorithms for each part individually. Often, an effective way for doing this is to associate, with to the given matrix, a graph which represents it, and then try to partition the graph via the so-called separation graph problem. In this context, one looks for small-sized sets of edges (or vertices) which separate the graph into several connected components. These minimal sets of vertices or edges, called vertex separators and edge separators, are important concepts in graph theory, and they have drawn the attention of many mathematicians and computer scientists in recent years.

A connected vertex separator (abbreviated CVS) is one of the possible vertex separators which are connected, and these specific separators have been extensively studied over the years; see, for instance [1,2,3]. In particular, the connected vertex separation problem deals with the issue of finding the minimum connected component whose removal disconnects the graph.

Analogously, given the two vertices s and t of a connected graph G, the st-CVS problem focuses on finding the minimum subset S of vertices in G such that the removal of S leaves the vertices s and t in two disjointed connected components.

Some natural examples of separation problems include, for example, the problem of finding the minimum number of vertices disconnecting the vertices of a given set from each other, as well as the problem of finding the minimum number of vertices disconnecting multiple specified pairs of vertices. However, it turns out that these problems are computationally difficult to deal with in the classical setting, and, in order to make them more tractable, one often changes the computational point of view.

More precisely, let us consider a computational problem with a parameter k in the input. Its complexity can be measured as a function of this parameter. If k is fixed, then the problem is called a parametrized problem. When such a problem can be solved by an algorithm whose solution can be obtained in $f\left(k\right)·n^{O\left(1\right)}$ time, where f is some computable function depending only on the parameter k, then the problem is said to belong to the class FTP (which means Fixed Parameter Tractable).

It has been proved by Marx et al. [4] that the st-CVS problem is NP-hard and belongs to the category of FPT algorithms. On the other hand, for graphs of chordality 4, an algorithm running in polynomial time was presented to solve the st-CVS problem by Narayanaswamy and Sadagopan [5]. However, they also showed that the same problem on graphs of chordality 5 (or more) is NP-complete. Recently, this same problem was investigated from the perspective of complexity of polyhedra; see [6]. Finally, in [7,8], the first author presented some inequalities and three programming formulations to solve a similar related problem.

In the present paper, we will address the problem of finding st-connected separators for a special class of graphs associated to groups, called power graphs (to be defined in the next sections), and we will define a fast algorithm solving this specific problem.

2. The $\mathit{st}-$Connected Separator

Let G be a finite simple undirected graph with vertex set V and edge set E. The open neighborhood of a vertex $v\in V$, denoted by $N\left(v\right)$, is the set of all vertices that are adjacent to v. The closed neighborhood of v, denoted by $N\left[v\right]$, is just $N\left(v\right)\cup \left\{v\right\}$. The set of all incident edges to v is denoted by $\delta \left(v\right)$. Given a subset S of the vertex set V, the subgraph induced by S, denoted by $G\left[S\right]$, is simply defined as the subgraph obtained after deleting all the vertices of the set $V-S$ from the graph G. Using $P_{uv}$, we will denote a path joining u to v, while we will write $P_{uv}^{\prime }$ for the internal path obtained from $P_{uv}$ by excluding the extremal vertices u and v. The family of all such paths connecting u to v will be denoted by ${\Gamma }_{uv}$, while ${\beta }_{uv}$ will indicate the maximum number of disjoint paths between u and v.

Definition  1.

Let G be a connected graph and $s,t$ be a pair of non-adjacent vertices. An $st$-connected separator is defined as a subset S of the vertex set V of G satisfying the following conditions:

1. 

$s,t\notin S$;

2. 

S induces a connected subgraph (that is, $G\left[S\right]$ is connected);

3. 

$G\left[G\setminus S\right]$ is disconnected.

From the definition, any connected graph has a st-connected separator since one can put the non-adjacent vertices s and t in two sets A and B, respectively, and all other vertices make the connected separator S. The st-connected problem asks for the smallest subset of vertices $S\subseteq V$, where S is a connected separator.

For an $st$-connected separator S of a finite graph G with vertex set $V=\{v_1,v_2,\dots ,v_n\}$, let a be a positive integer such that $\left|S\right|\le a$, and $\sigma :V\to (0,\infty )$ is a real positive function. Let $Y_S\in {\mathbb{R}}^n$ be the incidence vector $(y_1,y_2,\dots y_n)$, defined as follows:

$$y_i=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{v}_i\in S,\hfill \\ 0\hfill & \mathrm{if}{v}_i\notin S.\hfill \end{array}\right.$$

Let $Pol{y}_{st}\left(G\right)$ denote the $(s,t)$-vertex separator polyhedron associated with $(G,s,t)$, namely, the convex hull over all incidence vectors corresponding to all the st-separators in G. In a more mathematical language, this can be defined as follows:

$$Pol{y}_{st}\left(G\right)=\mathrm{conv}\{Y_S:S\mathrm{is}\mathrm{an}\mathrm{st-connected}\mathrm{separator}\mathrm{of}G\}.$$

The problem above is equivalent to the following linear program:

$$min\left\{\sum _{v\in V}{\sigma }_v{y}_v:Y\in Pol{y}_{st}\left(G\right)\right\},$$

and hence finding a solution for this linear program gives the following solution to our main problem: $Pol{y}_{st}\left(G\right)=\mathrm{conv}\{Y_S:S\mathrm{is}\mathrm{an}\mathrm{st-connected}\mathrm{separator}\mathrm{of}G\}$. Moreover, by taking $\sigma \left(v\right)=1$ for all $v\in V$, we can rewrite the problem as

$$min\left\{\sum _{v\in V}{y}_v:Y\in Pol{y}_{st}\left(G\right)\right\}$$

subject to the following conditions:

$$\begin{array}{cc}|P_{st}^{\prime }|\ge 1\hfill & \hfill \forall P_{st}\in {\Gamma }_{st}\end{array}$$

(1)

$$\begin{array}{cc}\left|N\left(U\right)\right|\ge y_u+y_v-1\hfill & \hfill \forall u\in U,v\notin U\cup N\left(u\right)\end{array}$$

(2)

Remark 1.

The inequality (1) guarantees the existence of at least one vertex of S that is also an internal vertex of $P_{st}$, while the inequality (2) ensures that the subgraph induced by S is connected.

3. An Algorithm

The aim of this section is to introduce an algorithm that runs in polynomial time to solve the following problem, denoted $\mathcal{P}$ for simplicity:

$$\mathcal{P}=min\left\{\sum _{v\in V}{y}_v\right\}$$

for which, in addition to the conditions (1) and (2) from above, the following conditions are also needed:

$$\begin{array}{c}{y}_s=0,y_t=0\hfill \end{array}$$

(3)

$$\begin{array}{cc}{y}_v+y_u\le 1\hfill & \hfill \forall v,u\in V\end{array}$$

(4)

$$\begin{array}{c}{\displaystyle \sum _{v\in V}(y_v+y_u)=n-{\beta }_{st}}\hfill \end{array}$$

(5)

$$\begin{array}{cc}{y}_v,y_u\in \{0,1\}\hfill & \hfill \forall v,u\in V\end{array}$$

(6)

where ${\beta }_{st}$ denotes the maximum number of disjoint paths between s and t.

The problem $\mathcal{P}$ from above is called mixed-integer problem and, obviously, a solution for it produces a set of vertices. Now, let L be a subset of V obtained by solving $\mathcal{P}$. Also, let $S_L$ be the set obtained by L together with its corresponding neighborhoods, that is, $S_L=L\cup N\left(L\right)$ where $N\left(L\right)={\bigcup }_{u\in L}N\left(u\right)$. The neighborhoods of the vertices of L will play a crucial role in the algorithm we will define. Roughly speaking, the algorithm will consist of two stages: The first finds a separator L by solving the problem $\mathcal{P}$. The second one runs a check on whether $S_L$ induced a connected subgraph.

In other words, our first algorithm, denoted by Algorithm 1, solves the problem and finds a set L, and then creates two new sets $S_L$ and $S^{\prime }$, where $S_L$ contains all the vertices of L and their neighborhoods, while, for the moment, $S^{\prime }$ is empty. Now, since our purpose is to empty both sets $S_L$ and $S^{\prime }$, the process continues by taking, in some (degree) order, vertices from L, adding them to $S^{\prime }$, and removing them from $S_L$, until when $S_L$ will be empty. At this point, the algorithm analyses a “new” $S_L$, namely $N\left(S^{\prime }\right)$, and a “new” L, namely $L-S^{\prime }$, and repeats the process until one empties both $S_L$ and $S^{\prime }$.

Algorithm 1  mixed-integer

1: Find $L=\{v_1,\dots ,v_k\}$ by solving $\mathcal{P}$. 2: Initiate $S_L={\cup }_{m=1}^{k}N\left[v_m\right]$ and $S^{\prime }=\varnothing$. 3: Pick a vertex from L with the highest degree (say $v_i$). Then add it to $S^{\prime }$ and remove it from $S_L$. 4: Add the vertices of L, which are neighbors of $v_i$ to $S^{\prime }$, and remove them from $S_L$. 5: Else, whenever $v_j\in L$ is not a neighbor of $v_i$, then add its neighbors to $S^{\prime }$ if they are also neighbors of $v_i$ and remove them from $S_L$. 6: Terminate the process and return $S^{\prime }$ as the solution if $S_L=\varnothing$. 7: Else, set $S_L=N\left[S^{\prime }\right]$ and $L=L-S^{\prime }$ and return to step 3.

4. The Power Graph

In graph theory, there are several notions of graphs that are constructed from semigroups and groups such as the intersection graphs of subsemigroups and subgroups; see, for instance, [9,10]. Such constructions share a common property in which the vertex set is the whole semigroup $\mathcal{S}$ or the whole group $\mathcal{G}$.

Kelarev and Quinn [11,12] presented a class of graphs associated with semigroups called directed power graphs, for which, if $g,h\in \mathcal{S}$, a directed edge exists from g to h if $g=h^k$ for some $k\in \mathbb{N}$. Chakrabarty et al. [13] later provided a comprehensive analysis of the undirected power graph of semigroups. They also offered partial insights for the case of groups by studying the Hamiltonicity and planarity of the undirected power graph of the groups of units. Moreover, they proved several interesting results on this topic by proving, for instance, that the power graph of a group is complete if and only if the group has order 1 or $p^m$ for some prime p.

Then, Cameron and Ghosh in [14] investigated the undirected power graph of finite groups and proved an important result, stating that two finite abelian groups are isomorphic if their power graphs are isomorphic. They also conjectured that two finite groups have the same number of elements of each order if their power graphs are isomorphic. This conjecture was proved later by Cameron [15].

The study of graphs defined on algebraic structures such as power graphs is an active area of research in graph and group theory. We refer the reader to [16,17,18,19,20,21,22,23,24] for some recent works on these topics.

Definition 2.

Given a group $\mathcal{G}$, the undirected power graph $P\left(\mathcal{G}\right)$ of $\mathcal{G}$ is the graph whose vertex set is the group itself, and two distinct vertices in $P\left(\mathcal{G}\right)$ are adjacent if one is a power of the other (in the group).

In the following, we will always use the term “power graph” to indicate “undirected power graph”. Now, we consider two interesting spanning subgraphs of the undirected power graphs of groups. We define $P_1\left(\mathcal{G}\right)$ to be the spanning subgraph of $P\left(\mathcal{G}\right)$ in which g is adjacent to h if $g=h^k$ and $h=g^m$ for some $k,m\in \mathbb{N}$. The second subgraph $P_2\left(\mathcal{G}\right)$ is then defined as the spanning subgraph whose edges are those of $P\left(\mathcal{G}\right)$ without the edges of $P_1\left(\mathcal{G}\right)$. In this way, the two subgraphs $P_1\left(\mathcal{G}\right)$ and $P_2\left(\mathcal{G}\right)$ are then edge-disjointed and their union is $P\left(\mathcal{G}\right)$ itself.

The problem of searching the minimum connected separator for the spanning subgraph $P_2\left(\mathcal{G}\right)$ will be addressed in the following sections.

Example 1.

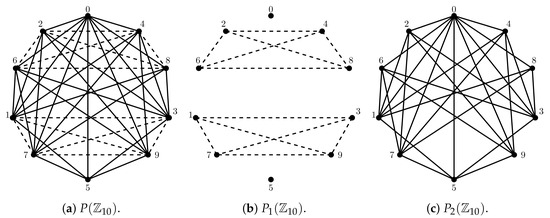
Let ${\mathbb{Z}}_{10}$ be the additive group of integers modulo 10. The power graph of ${\mathbb{Z}}_{10}$ and its spanning subgraphs of interest are shown in Figure 1.

The additive group ${\mathbb{Z}}_{10}$ is a cyclic group of order 10. Thus, the subgroups of ${\mathbb{Z}}_{10}$ are of orders $1,2,5$ and 10. Since the elements of the set $\{1,3,7,9\}$ generate ${\mathbb{Z}}_{10}$ itself, the corresponding vertices will be adjacent to the rest of vertices in $P_2\left({\mathbb{Z}}_{10}\right)$, while they form a clique in $P_1\left({\mathbb{Z}}_{10}\right)$. Similarly, the vertices $\{2,4,6,8\}$ form a clique in $P_1\left({\mathbb{Z}}_{10}\right)$, while each one of them is adjacent to 0 in $P_2\left({\mathbb{Z}}_{10}\right)$. Finally, 0 and 5 are adjacent in $P_2\left({\mathbb{Z}}_{10}\right)$.

Proposition 1.

The subgraph $P_2\left(\mathcal{G}\right)$ is connected whenever $\mathcal{G}$ is finite.

Proof. 

This is clear, since $g^k=e$ for every element $g\in \mathcal{G}$.    □

Theorem 1.

Let $\mathcal{G}$ be a finite group and $g,h\in \mathcal{G}$. Then,

(a) 

g and h are adjacent in $P_1\left(\mathcal{G}\right)$ if and only if $\langle g\rangle =\langle h\rangle$.

(b) 

g and h are adjacent in $P_2\left(\mathcal{G}\right)$ if and only if either one of $\langle g\rangle$ and $\langle h\rangle$ is a proper subgroup of the other.

Proof. 

Let $g,h$ be two distinct elements of a finite group $\mathcal{G}$.

(a)

Assume that g and h are adjacent in $P_1\left(\mathcal{G}\right)$, then there exists $k,m\in \mathbb{N}$, such that $g=h^k$ and $h=g^m$. Hence, each one of them belongs to the subgroup generated by the other one. Also,

$$\left|g\right|=|h^k|\le |h\left|and\right|h|=|g^m|\le |g|.$$

That is, g and h have the same order. Consequently, g and h generate the same cyclic group. So, $\langle g\rangle =\langle h\rangle$.

The converse is obvious, since, if $\langle g\rangle =\langle h\rangle$, we obtain that $g=h^k$ and $h=g^m$ for some $k,n\in \mathbb{N}$.

(b)

Let g and h be adjacent in $P_2\left(\mathcal{G}\right)$. Then, without loss of generality, we can suppose that there exists $k\in \mathbb{N}$, such that $g=h^k$ and $h\ne g^m$ for all $m\in \mathbb{N}$. Thus, $\left|g\right|\le \left|h\right|$ and $g\in \langle h\rangle$.

Conversely, suppose that $\langle g\rangle$ is a proper subgroup of $\langle h\rangle$. Then $g=h^k$ for some $k\in \mathbb{N}$ and $g^m\ne h$ for all $m\in \mathbb{N}$.    □

Corollary 1.

Let $\mathcal{G}$ be a finite cyclic group of order n. Then $P_2\left(\mathcal{G}\right)$ is k-partite.

Proof. 

Let $D=\{d_1,d_2,\dots ,d_k\}$ be the divisors of n. According to the fundamental theorem of cyclic groups, for each $d_i\in D$, there exists a unique subgroup of order $d_i$. That is, every element of $\mathcal{G}$ generates one of those k distinct subgroups. Thus, the elements of $\mathcal{G}$ can be partitioned into k partitions in which the elements of each partition generate the same unique subgroup. Theorem 1 asserts that each partition is actually independent. Also, any pair of partitions together form a complete bipartite if a vertex of each one is adjacent. The connectivity is satisfied by Proposition 1 in which every partition forms a complete bipartite with the partition that only contains the identity e. This shows that $P_2\left(\mathcal{G}\right)$ is k-partite.    □

5. Computations

Corollary 1 suggests separating the technique for separating the vertices of $P_2\left(\mathcal{G}\right)$ into three sets, A, B, and C, in which C is a minimum connected component and A and B are not linked by any edges. This is exactly the connected vertex separator problem in a graph. Actually, Algorithm 2 applied to $P_2\left(\mathcal{G}\right)$, aims to split its vertex set into three disjoint sets of vertices, where C induces a connected subgraph and the vertices in A are not adjacent to the vertices in B. That is, C works as a connected separator, and the goal of Algorithm 2 is just to find such minimum set.

Algorithm 2 separates the elements of G into k independent sets. Then, the vertices of each independent set are distributed into A, B, or C based on their corresponding orders, as shown in Algorithm 2.

Note that, in some cases, Algorithm 2 does not produce the best outcome regarding the minimality of C. However, in such cases, the next Algorithm 3 comes into play to overcome the situation. For instance, when Algorithm 2 produces a connected separator, Algorithm 3 checks whether there is another separator with less elements. If so, Algorithm 3 produces the one with less elements. In fact, it simply checks whether the number of vertices of the independent set $S_1$ (the set of elements of the group G with order n) is greater than the total number of the rest of the vertices. If this is the case, Algorithm 3 splits the set $S_1$ into two halves. One half becomes A, while the other half becomes B. The rest of the vertices are then distributed in C.

Remark 2.

It is worth pointing out that, based on our observations of Algorithms 2 and 3, the lower bound for C is $min\{n-\varphi (n),\varphi (n)+1\}$ where $\varphi \left(n\right)$ is Euler’s totient function (the function that counts all the positive integers up to n, which are relatively prime to n).

The Python 3.11 (64-bit) language was used to test, numerically, the algorithm on a Dell laptop with an Intel Core i7-5500U CPU, 2.40 GHz, and 8 GB of RAM.

Table 1. Specified choices of n.

$\left|\mathit{V}\right|$	$\left|\mathit{A}\right|$	$\left|\mathit{B}\right|$	$\left|\mathit{C}\right|$	Time
100	40	10	50	0.000
101	50	50	1	0.000
102	64	2	36	0.000
103	51	51	1	0.000
104	48	4	52	0.000
105	42	8	55	0.000
106	52	1	53	0.000
107	53	53	1	0.016
108	36	18	54	0.000
109	54	54	1	0.000
1000	400	100	500	0.016
1001	360	360	281	0.000
1002	664	2	336	0.016
1003	464	464	75	0.000
1004	500	2	502	0.016
1005	264	264	477	0.000
1006	502	1	503	0.000
1007	468	468	71	0.016
1008	576	48	384	0.031
1009	504	504	1	0.000
10,000	4000	1000	5000	0.312
10,001	4896	4896	209	0.053
10,002	6664	2	3336	0.078
10,003	4284	4284	1435	0.047
10,004	5040	80	4884	0.141
10,005	2464	2464	5077	0.196
10,006	5002	1	5003	0.031
10,007	5003	5003	1	0.016
10,008	6624	24	3360	0.281
10,009	5004	5004	1	0.016

illustrates the data obtained for specified choices of n, whereas

Table 2. Random choices of n.

V	$\left|\mathit{A}\right|$	$\left|\mathit{B}\right|$	$\left|\mathit{C}\right|$	Time
160	64	16	80	0.000
352	160	16	176	0.017
381	126	126	129	0.000
619	309	309	1	0.000
665	216	216	233	0.000
819	216	216	387	0.016
995	396	396	203	0.016
1391	636	636	119	0.001
1510	900	4	606	0.017
1689	562	562	565	0.000
1974	1380	12	582	0.052
3560	2112	16	1432	0.165
5596	2796	2	2798	0.034
5732	2864	2	2866	0.048
7808	3840	64	3904	0.174
8251	3996	3996	259	0.038
8867	4433	4433	1	0.016
10,428	7176	40	3212	0.315
17,284	8880	56	8348	0.250
17,346	12,180	84	5082	0.508
18,866	9432	1	9433	0.078
38,838	25,888	2	12,948	0.341
56,942	28,800	70	28,072	0.532
60,646	30,322	1	30,323	0.228
81,311	38,256	38,256	4799	0.353
87,607	38,544	38,544	10,519	0.863
108,679	53,960	53,960	759	0.487
111,891	32,400	32,400	47,091	2.314
132,613	60,600	60,600	11,413	0.984
133,566	88,984	224	44,358	2.598

shows the results of random choices of n between $n=100$ and $n=$ 200,000.

Algorithm 2  $separator\left(n\right)$

Ensure:  Sets of vertices $\mathbf{A},\mathbf{B},\mathbf{C}$, where $\mathbf{C}$ is adjacent to the non-adjacent sets $\mathbf{A}$ and $\mathbf{B}$. 1: Initialize $\mathbf{A}=\varnothing$                                                                                            ▹ Empty set 2: Initialize $\mathbf{B}=\varnothing$                                                                                             ▹ Empty set 3: Initialize $\mathbf{C}=\varnothing$                                                                                             ▹ Empty set 4: Define $\mathbf{P}=\{m\in \mathbb{N}:\mathit{m\; is\; prime\; and }$m|n}                                ▹ The set of prime divisors 5: Define $\mathbf{D}=\{m\in \mathbb{N}:\mathit{m\; is\; composite\; and }$m|n}                   ▹The set of composite divisors 6: Define ${\mathbf{S}}_k=\{m\in \mathbb{N}:m\le nandgcd(m,n)=k\}$ 7: for  $k\in \mathbf{P}$  do 8:     if $k=1$ then 9:         Add the elements of ${\mathbf{S}}_k$ to $\mathbf{C}$ 10:     else if $k=max\left(\mathbf{P}\right)$ then 11:         Add the elements of ${\mathbf{S}}_k$ to $\mathbf{B}$ 12:     else 13:         Add the elements of ${\mathbf{S}}_k$ to $\mathbf{A}$ 14:     end if 15: end for 16: for  $m\in \mathbf{D}$  do 17:     if $m=n$ then 18:         Add the elements of ${\mathbf{S}}_{\mathbf{m}}$ to $\mathbf{C}$ 19:     else if $m\nmid t$ for all ${\mathbf{S}}_{\mathbf{t}}$ in $\mathbf{B}$ then 20:         Add the elements of ${\mathbf{S}}_{\mathbf{m}}$ to $\mathbf{B}$ 21:     else if $m\nmid t$ for all ${\mathbf{S}}_{\mathbf{t}}$ in $\mathbf{A}$ then 22:         Add the elements of ${\mathbf{S}}_{\mathbf{m}}$ to $\mathbf{B}$ 23:     else 24:         Add the elements of ${\mathbf{S}}_{\mathbf{m}}$ to $\mathbf{C}$ 25:     end if 26: end for

Algorithm 3  $Separator(n,\mathbf{A},\mathbf{B},\mathbf{C})$

Ensure:  Sets of vertices $\mathbf{A},\mathbf{B},\mathbf{C}$ where $\mathbf{C}$ is of minimum order adjacent to the non-adjacent sets  $\mathbf{A}$ and $\mathbf{B}$. 1: if  $\left|\mathbf{A}\right|+\left|\mathbf{B}\right|+1\ge |{\mathbf{S}}_{\mathbf{1}}|$  then 2:     Return $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ 3: else: 4:     Clear $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ 5:     for $i\in \mathbf{P}\cup \mathbf{D}$ do 6:         if $i=1$ then 7:            Split ${\mathbf{S}}_{\mathbf{i}}$ into two non empty sets ${\mathbf{S}}_{\mathbf{ff}}$ and ${\mathbf{S}}_{\mathbf{fi}}$ 8:            Add the elements of ${\mathbf{S}}_{\mathbf{ff}}$ to $\mathbf{A}$ and the elements of ${\mathbf{S}}_{\mathbf{fi}}$ to $\mathbf{B}$ 9:         else: 10:            Add the elements of ${\mathbf{S}}_{\mathbf{i}}$ to $\mathbf{C}$ 11:         end if 12:     end for 13: end if

6. An Example

Let $G={\mathbb{Z}}_{33}$ and suppose we want to find three sets, A, B, and a connected separator C, in the graph ${\mathcal{P}}_2\left({\mathbb{Z}}_{33}\right)$. The possible divisors of 33 are 1, 3, 11, and 33. We can define then, for each $s\in \{1,3,11,33\}$, the sets $A_s=\{k\in {\mathbb{Z}}_{33}|gcd(k,33)=s\}$.

That is,

• $A_1=\{1,2,4,5,7,8,10,13,14,16,17,19,20,23,25,26,28,29,31,32\}$;
• $A_3=\{3,6,9,12,15,18,21,24,27,30\}$;
• $A_{11}=\{11,22\}$;
• $A_{33}=\left\{0\right\}$.

Notice that the elements of each set $A_s$ have the same order. For instance, the set $A_1$ contains the element of order 33.

In general, if $A_{\alpha }$ and $A_{\beta }$ are two sets defined in this way, then every element in $A_{\alpha }$ is adjacent to every element in $A_{\beta }$ whenever $\alpha |\beta$.

Our Algorithm 2 works as follows:

• Add the elements of $A_1$ and $A_{33}$ to C;
• Add the elements of $A_3$ to A;
• Add the elements of $A_{11}$ to B.

The output for Algorithm 2 in this example is then

• $A=A_3$, which implies that $\left|A\right|=10$;
• $B=A_{11}$, which implies that $\left|B\right|=2$;
• $C=A_1\cup A_{33}$, which implies that $\left|C\right|=21$.

Now, the question is why the algorithm initially adds the elements of $A_1$ and $A_{33}$ to C. If we add the elements of $A_1$ to A, then B should be empty, since the elements of $A_1$ are adjacent to all other vertices; similarly for $A_{33}$. In other words, no vertex which is put in A can have a neighbor in B, and vice versa.

Finally, Algorithm 3 checks if C is minimal. In fact, the process works in the following way:

• Input the output of Algorithm 2: A, B, and C;
• If $|A_1|\le |A_3|+|A_{11}|+|A_{33}|$, then return the same A, B, and C.
• Otherwise, split $A_1$ into two halves as follows, and make one half as a new A and the other as a new B.

In our case, since $|A_1|$ is greater than $|A_3|+|A_{11}|+|A_{33}|$, then the new A is its first half and B the second one is

$$A=\{1,2,4,5,7,8,10,13,14,16,17\}\Rightarrow \left|A\right|=11$$

$$B=\{19,20,23,25,26,28,29,31,32\}\Rightarrow \left|B\right|=10$$

$$C=A_3\cup A_{11}\cup A_{33},\Rightarrow \left|C\right|=13.$$

7. Conclusions

In this research, we have considered the problem of an st-connected separator on power graphs. Also, a mathematical model, an algorithm, and a heuristic were presented to solve the problem on such graphs in a short time. For future developments of this work, we will try to solve this problem by using the concepts Branch and Cut. Furthermore, one could study the same problem for some particular classes of graphs, such as Halin graphs or Free graphs.