Abstract
Heart Rate Variability (HRV) analysis allows for assessing autonomic control from the beat-by-beat dynamics of the time series of cardiac intervals. However, some HRV indices may strongly correlate with the mean heart rate, possibly flawed by the interpretation of HRV changes in terms of autonomic control. Therefore, this study aims to (1) investigate how HRV indices of fluctuation amplitude and multiscale complex dynamics of cardiac time series faithfully describe the autonomic control at different heart rates through a mathematical model of the generation of cardiac action potentials driven by realistically synthesized autonomic modulations; and (2) propose an alternative procedure of HRV analysis less sensitive to the mean heart rate. Results on the synthesized series confirm a strong dependency of amplitude indices of HRV on the mean heart rate due to a nonlinearity in the model, which can be removed by our procedure. Application of our procedure to real cardiac intervals recorded in different postures suggests that the dependency of these indices on the heart rate may importantly affect the physiological interpretation of HRV. By contrast, multiscale complexity indices do not substantially depend on the heart rate provided that multiscale analyses are defined on a time- rather than a beat-basis.
Keywords:
detrended fluctuation analysis; multiscale entropy; self-similarity; power spectrum; supine; sitting; sympathetic; vagal tone; cardiac pacemaker; membrane potential MSC:
92.08; 92C30; 92.C55; 93A30
1. Introduction
In physiology and medicine, the term “Heart Rate Variability” (HRV) refers to the methods for assessing the spontaneous fluctuations of time intervals between successive heartbeats [1]. Although widely used in the scientific literature, this term is somewhat misleading because the variability components studied with HRV methods are those of the time series of cycle length (CL) of the cardiac beats, in seconds, and not of the heart-rate (HR) series, in beats/min. The distinction is not irrelevant because of the nonlinear relationship between the two quantities: CL = 60/HR. Nonetheless, in keeping with the literature on the topic, here we will use the acronym HRV to indicate CL variability. Furthermore, it should be considered that the way the beat-by-beat CL series are generated gives them a peculiar nature, being time series sampled unevenly at the sampling rate of the instantaneous HR. For this reason, the literature on HRV analysis introduced specific procedures, such as interpolation and evenly resampling for frequency-domain analyses or mapping the beat-domain into the temporal domain for complexity-based analyses.
When the heart is in sinus rhythm, the two branches of the autonomic nervous system modulate the HR in opposite ways, the sympathetic outflow accelerating and the vagal outflow decelerating it. Previous works have shown that any shift of the sympathovagal balance toward sympathetic prevalence reduces the amplitude of HRV fluctuations and vice versa. Therefore, quantification of HRV by “time-domain” or “frequency-domain” indices is widely used to noninvasively derive information on the sympathovagal balance [2,3], its adaptations to different environmental conditions, and alterations in diseases [4]. Following the observation that altered HRV correlates with higher morbidity and mortality even in the general population [5,6], HRV indices have also been proposed for risk stratification [7,8,9].
However, a major problem in interpreting HRV studies lies in the intrinsic dependency of the amplitude of the CL fluctuations on mean HR. Indeed, an analysis of sinoatrial pacemaker modulation at the myocyte level [10] disclosed a mechanism, independent of autonomic balance, that “numerically” links changes in HRV to changes in mean CL. This mechanism is based on the nonlinear relationship between the diastolic depolarization rate of the sinoatrial node, DDR, the factor directly modulated by autonomic signals, and CL. This implies that, unless balanced out by other factors, any increase in mean CL (that is, any decrease in mean HR) is bound to increase the amplitude of HRV fluctuations, and vice versa [11]. The significance of this concept has been demonstrated in vivo by direct neural recordings [12] and reported by independent groups [13]. Nevertheless, the numerical relationship between HRV and mean HR is overlooked in the interpretation of autonomic cardiac control, for instance, when studying inflammatory processes, which increase mean HR [14] and decrease HRV [15], or aging, which alters HRV [16] and decreases mean HR [17].
This concept particularly applies to conditions in which changes in intrinsic properties of the sinoatrial node (e.g., blockers of pacemaker currents [18], sinus node remodeling [19]) may account for CL changes. It may even have clinical consequences, for instance, when monitoring rehabilitation programs in cardiac patients. Therapeutic options and lifestyle changes aimed at decreasing the energy needs of the myocardium in chronic heart failure patients by lowering the mean HR might alter the quantification of HRV improvements, precluding a correct assessment of cardiac autonomic control. Similarly, exercise interventions in rehabilitation programs aimed at improving cardiovascular fitness may functionally remodel the sinus node to induce bradycardia, independently of the autonomic nervous system [19]; this can influence the interpretation of HRV indices in terms of improvements in neurovegetative regulation.
A possible solution for this problem is provided by more recent studies investigating the HRV complex dynamics [20,21,22]. Complexity-based indices assessing fractal or entropy structures rather than the amplitude of HRV fluctuations demonstrated a potential value in the assessment of autonomic balance [23,24,25]. It is unknown, however, whether the interpretation of HRV complex dynamics in terms of autonomic cardiac modulations may also be flawed by a possible dependency of the complexity indices on mean HR.
This work aims to (1) investigate whether the HRV indices of complex dynamics are biased by an intrinsic dependency on mean HR; (2) develop an algorithm to derive the beat-by-beat series of DDR from the CL ones, thus allowing to apply HRV analysis to a parameter linearly dependent on autonomic input; and (3) test the sensitivity of the HRV methods by applying them to CL series recorded under postural changes, likely to induce an autonomic response and a change in mean HR.
2. Materials and Methods
Dependency of HRV indices on mean HR was tested on the synthesized CL series and their derived DDR series generated by a numerical model of the sinoatrial pacemaking myocytes [10,11]. Indeed, the use of synthesized series provides the only way to quantify HRV changes when the mean HR varies over a wide range of values without concomitantly inducing changes in autonomic modulations. Furthermore, the sensitivity of HRV indices in detecting autonomic changes was tested on real CL series recorded in volunteers switching from the supine to the sitting position. This section illustrates the following: Section 2.1, the model generating the CL series; Section 2.2, the synthesized autonomic perturbations of the DDR series, input of the model; Section 2.3, the HRV methods to analyze the CL series; Section 2.4, the procedure, based on the proposed model, to derive DDR series from the CL one; and Section 2.5, the experimental recording of the real CL series.
2.1. Generation of Synthesized CL Series
We used the model of cardiac pacemaker activity previously validated on rabbit sinoatrial myocytes, to which the reader is referred [10,11]. For practicality, the model is detailed in Appendix A. Fitting some model parameters to human data (see Appendix A) the model provides the following nonlinear relation between the beat-by-beat series of cycle length, CL(n), in seconds, and the corresponding beat-to-beat series of diastolic depolarization rate, DDR(n), in mV/s, where the index n identifies the n-th beat:
DDR directly reflects net transmembrane current flowing during diastole (see the Appendix A); hence, it is the cycle component modulated directly by autonomic agonists. If the diastolic depolarization rate were constant, i.e., DDR(n) = DDR0, the cycle length would also be constant, CL(n) = CL0, and linked to DDR0 by a hyperbolic relationship:
Thus, the impact of any DDR perturbation on CL depends strongly on the baseline DDR0, being greater at lower DDR0. This implies an intrinsic dependency of CL variability (i.e., HRV) on the mean CL (or mean HR), as previously predicted for some indices of the amplitude of HR fluctuations (see Figure 3 in [11]).
2.2. Autonomic Modulation of Synthesized CL Series
Autonomic agonists modulate CL(n) by acting on ionic currents that contribute to the net transmembrane current flowing during diastole. Therefore, the cycle parameter suitable to reflect autonomic modulation is largely DDR(n) [10]. In the original model, HRV was generated by intrinsic stochastic variability (as observed experimentally [10]) with a superimposed autonomic input simulated by a sum of sinusoids reflecting fluctuations at low and high frequency (see Appendix A in [11]). To focus on autonomic modulations of HRV, in the present work, DDR variability was entirely attributed to the autonomic input, and DDR(n) was modeled as the sum of a constant component and a variable autonomic contribution, DDRA(n):
To reproduce all the variability components of potential relevance to autonomic modulation, we generated DDRA(n) series characterized by a broadband “1/f” trend, Mayer waves with a period around 10 s, and a fast respiratory sinus arrhythmia, as described in the HRV literature [1,2]. These components are generally indicated as very-low-frequency (VLF, <0.04 Hz), low-frequency (LF, between 0.04 and 0.15 Hz), and high-frequency (HF, between 0.15 and 0.40 Hz) spectral components, respectively.
To generate physiologically realistic “1/f” components, as in [26], we calculated the Fast Fourier Transform (FFT) of white Gaussian noise and rescaled the FFT so that the log-power spectrum decreased linearly with the log frequency, the slope of the linear decrease being −β. We set the β-slope equal to 1 to generate a “1/f” trend. Then, we calculated the Inverse FFT, obtaining a pink-noise series, u(n). We filtered the pink noise with an autoregressive model of order 1 and low-pass cut-off frequency :
where
and CL0 is the mean cycle length. We set Hz to obtain x(n) series with β-slope equal to 1 at scales longer than 10 s and greater than 1 at shorter scales, as observed in HRV studies [26,27]. The synthesized series were rescaled to ±2.8 mV/s: this value was empirically selected to generate CL series in a physiological range of cardiac intervals.
The Mayer waves m(n) are hypothesized to be generated by a resonant frequency in the baroreceptor reflex that amplifies broadband stochastic fluctuations [28]. Thus, we bandpass-filtered , the broadband fractal component of DDRA(n), to generate the Mayer waves. We used a fourth-order Butterworth filter with a frequency band defined by the cut-off frequencies of 0.07 and 0.12 Hz, and we got m(n) as the output of the filter whose input was x(n).
We reproduced the respiratory component r(n), i.e., DDRA(n) oscillations synchronous with respiration, with a 0.25 Hz sinusoid. This sinusoid represents the respiratory arrhythmia during paced breathing at 15 breaths per minute. To obtain realistic components, the sinusoid amplitude was set at 10−3 mV/s, and we multiplied the Mayer waves by the scaling factor K = 3.6 to reproduce a physiological LF/HF powers ratio close to 2. The synthesized DDRA(n) was the sum of the respiratory oscillation, the Mayer waves, and the broadband fractal component:
DDRA(n) = r(n) + m(n) + x(n).
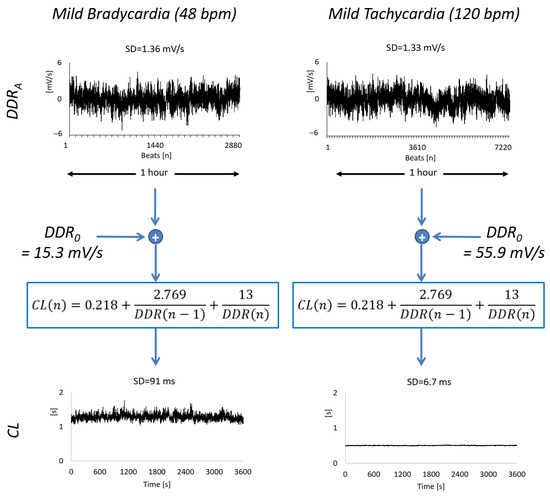
Figure 1.
Example of synthesized series of beat-by-beat autonomic perturbations of diastolic depolarization rate, DDRA, and the corresponding series of cardiac cycle length, CL, of 1-h duration. The DDRA series are generated at mild bradycardia (HR0 = 48 bpm, corresponding to CL0 = 1.25 s, DDR0 = 15.3 mV/s in Equation (2), and 2880 samples) and mild tachycardia (HR0 = 120 bpm, CL0 = 0.5 s, DDR0 = 55.9 mV/s and 7200 samples). While the DDRA series have similar overall variability as quantified by their standard deviation, SD, the overall variability of the CL series differs by an order of magnitude.
As for mean HR, HR0, we considered 68.6 bpm as the reference value, representing a typical adult resting normocardia. Then we generated six additional mean HR starting from the cycle length CL0 = 1.5 s (corresponding to HR0 = 40 bpm) and decreasing CL0 at steps of 250 ms up to CL0 = 0.25 s (HR0 = 240 bpm), simulating three conditions decreasing towards severe bradycardia and three increasing toward severe tachycardia from the reference normocardia (Table 1). In this way, the CL0 of normocardia (i.e., 0.875 s) is the average of the six additional conditions. We generated a series of 1 h duration, meaning that their size ranged from a minimum of 40 × 60 = 2400 samples, in case of severe bradycardia, to a maximum of 240 × 60 = 14,400 samples, in case of severe tachycardia. We repeated these steps 10 times, starting with different random seeds, and generated 70 DDR(n) and 70 CL(n) series.

Table 1.
Mean HR levels, HR0, used to synthesize seven CL(n) series for each DDRA(n) driving input of the sinus-node firing model; CL0 and DDR0 are the corresponding mean cycle lengths and mean diastolic depolarization rates.
2.3. HRV Measures
First, we quantified the HRV with two classical time-domain indices: the standard deviation, SDNN, reflecting the overall variability, and the root-mean-square of successive increments, RMSSD, reflecting its faster components [1,2].
As to the frequency-domain indices, we performed power spectral analysis with the broadband approach to set an optimal trade-off between frequency resolution and consistency of the estimate [29]. First, cubic splines interpolated the beat-by-beat series evenly at 5 Hz. The Welch periodogram was calculated over 90% overlapped, Hann data windows of 600-s length. The periodogram was smoothed by a moving average filter of order ma(f), a function of the frequency f. The order increased linearly with log f from ma = 3 to ma = 33 between 0.003 < f ≤ 0.04 Hz to preserve the frequency resolution at the lower frequencies, where it is more required, and consistently reduce the estimation variance at the higher frequencies, where it is particularly relevant. We calculated spectral indices as defined by international guidelines [2]: the HF, LF, and VLF powers; the total power, the LF/HF powers ratio; the normalized LF and HF powers, LFnu and HFnu (ratio between the LF or HF power and the difference between total and VLF power); and the β-slope from the regression line between the log-power spectrum and the log-frequency over the VLF band.
Complexity-domain indices are based on assessing the time-series unpredictability by entropy methods and fractal dynamics by self-similarity assessments. Entropy analysis was performed, calculating the Sample Entropy (SE) and the Multiscale Sample Entropy (MSE). SE quantifies the time-series unpredictability from the conditional probability that any two segments of m consecutive beats that are similar remain similar when their length increases by one beat [30]. Each segment is represented as a point in an m-dimensional space, and two segments are similar if their distance is lower than a given tolerance r. We calculated SE setting m = 1 and r = 20% the standard deviation of the series. Multiscale estimates can be obtained by calculating SE after coarse-graining the beat-by-beat series, as originally indicated in [31], or through a repeated filtering and sub-sampling procedure as in [32]. This provides SE measures at different scales τn, expressed in the number of beats. Following the latter approach, we calculated indices proposed in the HRV literature to concisely describe the SE profile at τn ≥ 1: the short-term complexity index defined as the area of SE estimates over the scale range 1 ≤ τn ≤ 5 beats (CIS); the long-term complexity index defined as the SE area over 6 ≤ τn ≤ 20 beats (CIL); and SE at τn = 5 beats (SE5), which is the scale separating the short- from the long-term range [33]. We also calculated MSE expressing the scale as τ in seconds rather than τn in number of beats, where τ = τn × CL0, with CL0 the mean cycle length, in seconds, as in [34]. MSE(τ) was concisely quantified by the average over the scales included in the HF band, i.e., 2.5 ≤ τ < 7 s (MSEHF), and the LF band, i.e., 7 < τ < 25 s (MSELF); and by the MSE(τ) value at the scale τ = 7 s separating the two bands (MSE7).
We assessed the fractal dynamics by calculating the self-similarity structure of the time series with the detrended fluctuation analysis (DFA) method [27]. This method splits the cumulative sum of the series into blocks of n beats and calculates Fd(n), the root mean square of the deviations of the cumulative sum from a polynomial trend. For fractal series, Fd(n) increases with the block size n following a power law, Fd(n)~nα, and α is estimated as the slope of the regression line between Fd(n) and n on a log-log plot (α is equal to the Hurst’s exponent H for fractional Gaussian noises and to H + 1 for fractional Brownian motions [35]). The α coefficient can be estimated separately for faster and slower fractal dynamics [23], and typically, the short-term coefficient, α1, is estimated over blocks of size between 4 and 16 beats, and the long-term coefficient, α2, over block sizes in the range 16 < n ≤ 64 beats [36]. However, the same block size, in number of beats n, corresponds to different temporal scales τ in seconds, if conditions with different heart rates are compared. Therefore, it has been proposed to estimate a temporal spectrum of DFA exponents, α(τ), by calculating the derivative of log Fd(n) vs. log n and mapping the block size n into the temporal scale τ = n × CL0, with CL0 the mean cycle length, in seconds [37]. Following this approach, we calculated α(τ) and estimated the short-term exponent, αS, and the long-term exponent, αL, as the slope of the regression lines over 4 ≤ τ ≤ 16 s and over 16 < τ ≤ 64 s.
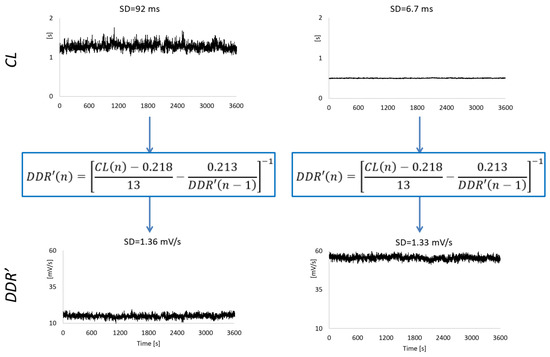
2.4. From CL(n) to DDR(n) Series
Equation (1) indicates how to estimate the diastolic depolarization rate, DDR′(n), from measured CL(n) series. Moving DDR(n) to the left side of Equation (1), we have
The recursive Equation (7) holds for n > 1 because DDR′(n) is not defined for n = 0. To obtain the first value of the estimated DDR(n) series and start the recursion, we set DDR′(0) = DDR′(1) in Equation (7), obtaining the initial value of the series as
Examples of the DDR′(n) series estimated from CL(n) are shown in Figure 2. We estimated the DDR′(n) series for all the synthesized CL series and calculated their HRV indices.
2.5. Real Heart Rate Series
The postural shift from lying to sitting has been associated with a shift toward higher sympathovagal balance, e.g., as quantified by a greater LF/HF powers ratio [38,39]. The purpose of analyzing real HRV data is to illustrate how our model helps better interpret posture-induced sympathovagal changes. We recorded the electrocardiogram at 200 Hz in 30 healthy volunteers (15 males and 15 females between 18 and 27 years) for 8 min at rest twice: first in the supine and then in the sitting posture. We discarded the first 2 min of each recording to remove any possible present postural transient and analyse steady-state conditions only. Therefore, all HRV indices were calculated on 6 min beat-to-beat series segments. The interval between consecutive R peaks of the electrocardiogram is a more practical way to measure CL. Thus, we derived the series of R-R intervals, RRI(n), by applying a derivative-and-threshold algorithm to the electrocardiogram [40]. For each RRI(n) series, we estimated the diastolic depolarization rates, DDR′(n), with Equations (6) and (7). We calculated spectral indices by broadband analysis (Welch periodogram with 90% overlapped Hann windows of 180 s length) for both the RRI(n) and DDR′(n) series, in supine and sitting postures. We also calculated the multiscale entropy, evaluating MSE(τ) for 2 ≤ τ ≤ 32 s as in [34], and the temporal spectrum of DFA exponents, evaluating α(τ) for 8 ≤ τ ≤ 112 s as in [37]. No outlier detection/removal procedures were applied. We statistically compared the two postures for each HRV index by the Wilcoxon Signed Rank test, using the Statistics Calculator provided by Statistics Kingdom (2017), available online from: http://www.statskingdom.com (accessed on 1 March 2025); p values < 0.05 were considered statistically significant and <0.15 as indicative of trends. Effect sizes were computed based on the rank-biserial correlation statistics, r [41]. Following the proposal in [42], we interpreted the effect size as small if 0.1 ≤ |r| < 0.3, medium if 0.3 ≤ |r| < 0.5, and large if |r| ≥ 0.5. The study was approved by the University of Insubria Ethics Committee (number 0086422, 23 July 2024), and participants signed informed consent.
3. Results
3.1. Synthesized Series
Figure 3 shows the power spectra of the autonomic perturbation of the diastolic depolarization rate, DDRA, and the corresponding CL series, output of the model of Equation (1), separately for the seven mean HR defined in Table 1. Power spectra of the DDRA series are characterized by the respiratory peak at 0.25 Hz, Mayer waves around 0.1 Hz, and a 1/f trend with a greater slope above 0.1 Hz. Interestingly, while at f < 0.1 Hz the DDRA spectra generated at the seven mean HR are identical, at f > 0.1 Hz the respiratory peak tends to decrease as the mean HR decreases, with higher harmonics appearing during mild and severe bradycardia. At each mean HR, the shapes of the CL spectra are remarkably similar to the shapes of DDRA spectra, including the presence of harmonics higher than the respiratory peak during mild or severe bradycardia. Unlike the DDRA spectra, however, the CL spectra dramatically differ among the seven mean HR levels, decreasing from bradycardia to tachycardia.
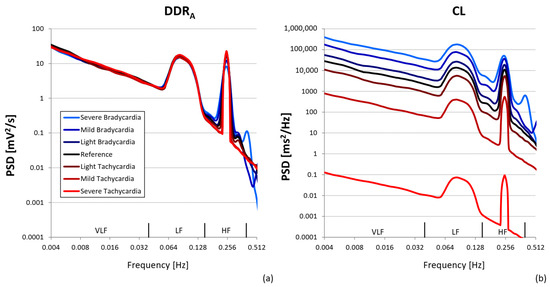
Figure 3.
Power spectra of synthesized series. The series were generated using the seven mean HR levels from Table 1 and the resulting spectra are plotted with colored lines, where each color refers to a different mean HR: the spectra at the reference heart rate are plotted by black lines; spectra at HR reproducing conditions of light, mild, and severe bradycardia by dark blue, blue, and light blue lines; and spectra at HR reproducing conditions of light, mild, and severe tachycardia by dark red, red, and bright red lines. (a) refers to spectra of autonomic perturbations of diastolic depolarization rate, DDRA, series; (b) to spectra of corresponding CL series, output of the model of Equation (1).
Table 2 summarizes the differences in HRV indices among the 7 HR0 levels. It reports the mean value of each index and, in squared brackets, the ratio of the mean value to the reference mean, this latter to quantify the sensitivity to HR0 among indices (interested readers find the corresponding effect sizes in Table A1 of Appendix B).

Table 2.
HRV indices for synthesized CL series at the reference heart rate (resting normocardia) and in conditions of light, mild, and severe bradycardia or tachycardia: values as the mean of 10 synthesized series and, in square brackets, the ratio with the corresponding reference value.
The time-domain indices decrease dramatically as mean HR increases. Compared to the reference normocardia condition (HR0 = 68.6 bpm), SDNN and RMSSD are more than three times greater in severe bradycardia and much smaller, less than 1%, in severe tachycardia. Similar trends appear in spectral powers, much greater in bradycardia and much lower in tachycardia. Despite these differences, the LF/HF powers ratio and the normalized powers are relatively independent of mean HR, even if in severe bradycardia, HFnu is substantially lower (−30%) and the LF/HF powers ratio substantially greater (+70%) than the reference. The β-slope is virtually the same at all mean HRs.
Figure 4 aims to show whether the metrics used in HRV analysis to quantify the unpredictability of a time series, i.e., the multiscale entropy, MSE(τ), or its self-similarity, i.e., the temporal spectrum of DFA coefficients, α(τ), produce different results when applied on the synthesized autonomic modulation series, DDRA, or on the corresponding CL series, output from the model of Equation (1). Figure 4 shows that both MSE(τ) and α(τ) do not depend on mean HR and have the same shape for CL and DDRA. This is confirmed by the αS, αL, MSEHF, MSE7, and MSELF values in Table 2, remarkably stable among mean HRs. However, Table 2 also points out that the fractal indices defined on block sizes (i.e., α1 and α2) and the entropy indices defined on the beat scales (i.e., SE, SE5, CIS, and CIL) are more sensitive to mean HR than fractal (αS and αL) and entropy indices (MSE7, MSEHF, and MSELF) defined on the temporal scale.
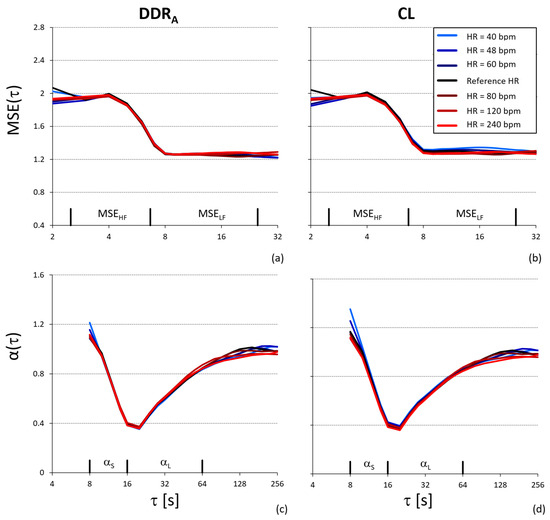
Figure 4.
Multiscale entropy, MSE(τ), and temporal spectrum of DFA scale coefficients, α(τ), at the reference heart rate and conditions of light, mild, and severe bradycardia or tachycardia. (a) MSE(τ) of DDRA series; (b) MSE(τ) of the corresponding CL series; the axes show the scales where MSEHF and MSELF are estimated. (c) α(τ) of DDRA series; (d) α(τ) of the corresponding CL series; the axes show the scales over which αS and αL are estimated.
Table 3 reports the HRV indices for the DDR′ series estimated by Equations (7) and (8) from the CL series (Table A2 of Appendix B reports the corresponding effect sizes). SDNN remains stable from severe bradycardia to severe tachycardia while RMSSD shows a residual trend, being still greater in bradycardia and lower in tachycardia. Total, VLF, and LF powers also appear stable among the seven HR0 levels. The HF power, however, is 20% lower in severe bradycardia compared with the reference condition. Powers ratios and normalized spectral powers are less sensitive to HR0 when assessed on the DDRA series. Spectral slopes of the “1/f” trend, entropy, and fractal indices have values and sensitivity to HR0 similar to the corresponding CL series of Table 2.

Table 3.
HRV indices for DDR′ series estimated from the synthesized CL series: in square brackets, the ratio with the corresponding reference value.
3.2. Real Series
The HR median value [IQR] over the group of volunteers increased from 63 [10] bpm in the supine position to 71 [11] bpm in the sitting position. Figure 5 shows that the RRI and DDR′ power spectra are characterized by a 1/f trend in the VLF band, Mayer waves in the LF band, and a smoothed respiratory component in the HF band, resulting from the superposition of individual respiratory peaks during spontaneous breathing. However, even if RRI and DDR′ spectra have similar shapes, they respond differently to the posture change. As to RRI, the change of posture from supine to sitting produces small variations of opposite sign in the VLF-LF band on one side and in the HF band on the other side, while in the DDR′ spectra it produces a clear increase in the VLF-LF band with overlapping powers in the HF band.
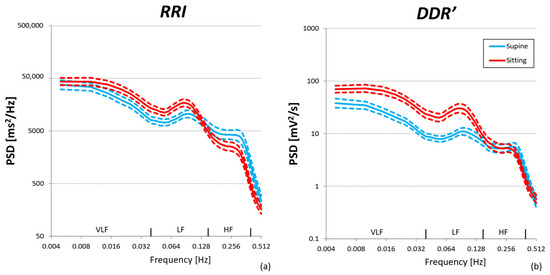
Figure 5.
Power spectra in supine and sitting postures over N = 30 participants: geometric mean (solid line) ± geometric standard error of the mean (dashed lines). (a) RRI series; (b) DDR′ series estimated from RRI.
Table 4 compares the two postures for the time- and frequency-domain indices of RRI and DDR′ separately. Changing posture from supine to sitting shortens the mean RRI and increases the mean DDR′ with similarly large effect sizes. Furthermore, it increases the LF/HF powers ratio and LFnu of both RRI and DDR′ with similarly large effect sizes.

Table 4.
Time- and frequency-domain indices of HRV over 30 participants in supine and sitting postures for RRI and DDR′: median [IQR] with significance p and effect size r of the difference between postures.
By contrast, the posture shift changes the time-domain indices differently for the RRI and DDR′ series. SDNN, the index of overall variability, increases significantly, with a large effect size, for DDR′ only; and RMSSD, the index of the faster components of variability, decreases significantly, with a large effect size, for RRI only. Important discrepancies also concern the spectral powers. As to DDR′, VLF and LF powers increase significantly with a large effect size, while the HF power does not change. By contrast, VLF and LF powers of RRI do not change significantly, while the HF power of RRI decreases significantly with a large effect size.
Finally, Figure 6 shows the results of the complexity analysis. As for α(τ), the self-similarity coefficients of RRI are greater in sitting than supine position at the shorter scales, and lower in sitting than supine position at the larger scales. The same trend characterizes the self-similarity coefficients of DDR′, being α(τ) of the RRI and DDR′ series identical. MSE(τ) is greater in sitting than supine posture at all the scales, with the same trend for RRI and DDR′, being the entropy profiles of RRI and DDR′ very similar in both postures.
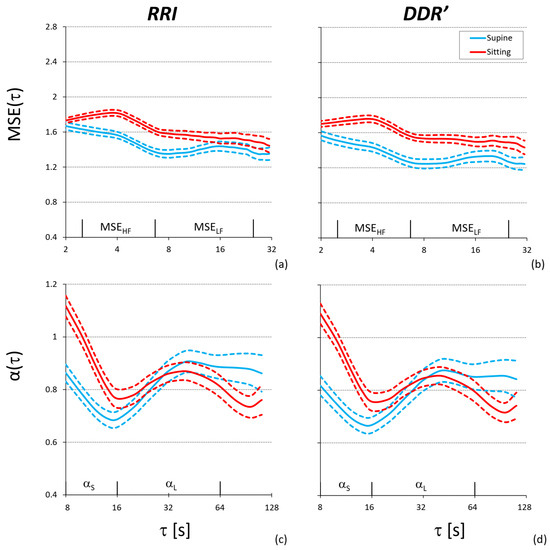
Figure 6.
Complexity analysis in the supine and sitting posture over 30 participants: mean (solid line) ± standard error of the mean (dashed line). Multiscale entropy of RRI (a) and RRI-derived DDR′ (b); temporal spectrum of DFA scale coefficients of RRI (c) and RRI-derived DDR′ (d).
4. Discussion
The HRV literature reported associations between HRV indices and mean HR. For instance, analyzing the large cohort of the Framingham study, it has been concluded that, irrespective of age, indices of the amplitude of HRV fluctuations, like LF and HF powers or SDNN, are inversely related to mean HR [43]. This has been widely interpreted in terms of shifts in autonomic balance: a decrease in cardiac vagal outflow is expected to increase mean HR and simultaneously decrease its vagal fluctuations. However, once considered that DDR, as opposed to CL, is the actual target of modulation by neurohumors [10], such an association may also have a mathematical origin, being accounted for by the nonlinear relation between CL and DDR [11]. In other words, as confirmed in the present study and by other groups [13], HRV indices reflecting the amplitude of HRV fluctuations depend on mean HR and might not properly reflect the autonomic cardiac control [12].
Previous attempts to remove the relationship between HR and HRV (hypothesized to depend on the inverse relationship between HR and CL [44]) led to the suggestion of normalizing the CL series by the mean CL [45] or dividing the HF power by the fifth power of the mean CL [46]. Furthermore, the observation of an exponential decay of SDNN with HR led to the proposal to correct SDNN by an exponential function of mean HR [13]. However, empirical approaches, based on fitting population data, also remove the effects of any true physiological mechanism affecting both the mean HR and HRV. Furthermore, the question of how to correct other HRV indices in the time-, frequency-, and complexity- domains remains unresolved, as it remains unresolved the question of whether other mechanisms of a mathematical and non-physiological nature, in addition to the considered nonlinearity in the sinus node, play a role in associating HRV with mean HR.
This work employed a simple model of the sinus node pacemaking [11] driven by autonomic currents of known dynamics to synthesize realistic CL series. This not only confirmed the previously reported dependency of time- and frequency-domain HRV indices on mean HR [11,13] but also allowed us to quantify changes in complexity-domain indices of HRV self-similarity and unpredictability when mean HR changes in the absence of any modulation in the autonomic outflows. Furthermore, we showed that the beat-by-beat DDR series (that, unlike CL, is linearly related to the autonomic currents) can be estimated from the CL series. This provides us with a powerful tool to assess the cardiac autonomic control from HRV. Moreover, after removing the effect of the model nonlinearity by back-computation of the DDR series, we highlighted residual dependencies due to other mathematical causes. A more detailed analysis follows.
Time domain indices. We confirm the previously observed strong dependency of SDNN on mean HR [11,13]. In particular, our analysis indicates that SDNN may increase or decrease by 40% just by shifting mean HR from normocardia to light bradycardia or tachycardia, in the absence of any change in autonomic perturbations (Table 2). The SDNN variation range considered in our simulations is not unrealistic, and the literature on HRV reports similarly large variations in SDNN associated with large changes in mean HR comparing rest with maximal exercise [47]. We also highlight an even more pronounced dependency for RMSSD. Assessing SDNN on the DDR series back-calculated from the CL ones removes the dependency on mean HR completely (Table 3). This was possible over the very wide range of mean HR considered, corresponding to depolarization rates between 12.3 and 492.8 mV/s (Table 1), a result that suggests the applicability of the reverse modeling approach in all real applications. As to RMSSD, a residual dependency remains, the RMSSD of DDR being greater by +50% in severe bradycardia and lower by −70% in severe tachycardia compared to the normocardic level of 68.6 bpm. This residual dependency is explained by a mathematical mechanism beyond the DDR-CL nonlinearity. RMSSD quantifies the magnitude of changes between consecutive beats, and the time interval between beats is 6 times longer in severe bradycardia (1.5 s) than in tachycardia (0.25 s). Stationary RRI series show positive autocorrelation at short lags, which decays rapidly as the lag increases [48], suggesting that the autocorrelation function of the modulating autonomic perturbations decreases similarly. This may make the absolute difference between consecutive DDR values (relevant to the RMSSD calculation) to increase as RRI increases, causing the inverse relation between RMSSD of the DDR series and mean HR we observed in Table 3.
Frequency domain indices. The presence of realistic “1/f” trends, Mayer waves, and respiratory oscillations in the power spectra of Figure 3b and the substantial similarity between the spectra of synthesized CL and real RRI series (see Figure 5a) validate our procedure for generating realistic spectral components of the autonomic modulations. With our analysis, we also confirm the dependency of the absolute HRV powers on mean HR [11]. The dependency can be extremely strong: for instance, the LF power, a combined measure of sympathetic and vagal cardiac modulations, almost doubles when the mean HR shifts from normocardia to light bradycardia (Table 2). This dependency is almost completely removed if spectral powers are calculated on the DDR series (Table 3). Nonetheless, the HF power of DDR is slightly underestimated in severe bradycardia. Also, Figure 3a shows multiple respiratory peaks in the DDRA spectra at the lower mean HR, and the DDRA spectral peaks cannot be attributed to nonlinearities of the sinus-node model. A possible explanation involves the interpolation procedure to calculate the periodogram. The Fourier Transform needs to interpolate the beat-to-beat series evenly, and cubic spline functions are popular interpolants, used in widespread commercial software [36]. The spline functions interpolate consecutive beats with a cubic polynomial that, at the lower heart rates, may slightly alter the real profile of the respiratory fluctuation (a sinusoid in our synthesized series), generating higher harmonics that spread the power of the respiratory oscillation over multiple peaks. The higher harmonics may fall outside the HF band, thus decreasing the HF power.
Complexity domain indices. Complexity analysis of the synthesized series showed MSE(τ) values greater in the HF than the LF band, as in sleeping subjects [34], and that the α(τ) profile decreases from values characteristic of fractional Brownian motions at τ = 8 s to a minimum around τ = 16 s, reaching a plateau at larger scales, as in healthy subjects [49] (Figure 4). These similarities with real measures support our procedure for synthesizing realistic DDRA series.
As to the entropy measures, SE shows an inverse relation with mean HR, being SE lower in mild/severe tachycardia for both the CL (Table 2) and DDR (Table 3) series. To understand this dependency, we should consider that SE for a given embedding dimension m measures how likely it is that similar segments of m consecutive beats remain similar when their length increases to m + 1 beats. The autocorrelation function of the RRI series decays very rapidly [48]; thus, it is more likely that similar sequences remain similar when their length increases by one beat if the time lag separating the new beat from the previous ones is small (as in severe tachycardia, where CL0 = 0.25 s) rather than long (as in severe bradycardia, where CL0 = 1.5 s). This would explain the lower SE values at the higher mean HR in our synthesized series and the inverse association between SE and mean HR previously observed in human and animal data [50].
By contrast, the MSE(τ) of the CL series (Figure 4b) and its derived indices (MSEHF, MSELF, and MSE7 in Table 2) are remarkably insensitive to mean HR and similar to the MSE(τ) indices of DDR (Table 3). This strongly suggests that measures of unpredictability based on MSE(τ) are not affected by mean HR. Nonetheless, if indices of multiscale entropy are defined on the beat scale rather than the temporal scale (SE5, CIS, and CIL in Table 2 and Table 3), dependency on mean HR emerges. The explanation is that at different mean HR, the same scale in beats corresponds to different time scales in seconds. For instance, SE5 (Sample Entropy at the scale of five beats) corresponds to the entropy value calculated at τ = 1.25 s in severe tachycardia and τ = 7.5 s in severe bradycardia.
Similarly, whereas fractal indices assessed on temporal scales too are insensitive to mean HR (Figure 4c,d; αS and αL in Table 2), fractal indices assessed on scales defined by block sizes (α1 and α2 in Table 2) show substantial HR dependency. The explanation is again that the same block size (in number of beats) corresponds to different time scales (in seconds) at different mean HR, thus affecting the α1 and α2 estimates substantially.
Physiological interpretations of HRV changes. Our work may help improve the understanding of HRV changes in relation to the changes in cardiac autonomic control. In the real series, once a steady state was reached, mean HR increased from 63 bpm in the supine position to 71 bpm in the sitting position, roughly corresponding to a shift from light bradycardia to the reference HR (Table 1). Under this condition, the SDNN of RRI did not change in our participants. Because it was estimated over six-minute recording periods, this overall variability index primarily reflects the faster modulations associated with autonomic control. Therefore, according to the usual interpretation of this index of overall variability, it should be concluded that the postural shift did not change the overall variability of autonomic modulations. However, the SDNN of DDR increased from supine to sitting (Table 4). In the synthesized series, shifting from light bradycardia to the reference HR decreased SDNN of RRI by 40% (Table 2)—such a decrease might have masked a true increase in autonomically induced variability in response to the change of posture. Therefore, the alternative interpretation suggested by our analysis is that the overall variability of the autonomic input to the sinus node increased from supine to sitting. Similarly, from supine to sitting, RMSSD decreased significantly for RRI only, not for DDR (Table 4). This might be mostly explained by the dependency of RMSSD of RRI on changes in mean HR (Table 2) rather than by decreased vagal input. This evidence may radically affect the current interpretation of time-domain HRV indices when comparing conditions characterized by even modest differences in mean HR.
Let us now consider the spectral indices of sympathovagal balance, i.e., the LF/HF powers ratio and LFnu. These indices increased from supine to sitting, independent of being calculated from the RRI or DDR series. Accordingly, we can conclude that the postural change shifted the sympathovagal balance in favor of sympathetic tone. However, is this due to an increase in the sympathetic drive only, a decrease in the vagal drive only, or both? Let’s look at the HF power, classically considered an index of vagal modulations, not affected by the slower effects of sympathetic modulations. From supine to sitting, the HF power decreased significantly for RRI (−46% in Table 4), but it did not change for DDR. The analysis of synthesized data showed that the corresponding shift in mean HR, from light bradycardia to the reference HR, decreased the HF power of RRI (−47% in Table 2) without affecting the HF power of DDR (Table 3). As DDR and not RRI is linearly related to the autonomic input, this would suggest that the decreased HF power of RRI reflects the increase in mean HR and not lower cardiac vagal modulations in sitting. On the other hand, the increased LF power of DDR from supine to sitting can be interpreted as a genuine increase in sympathetic input (vagal contributions may be excluded because the HF power of DDR did not change). Such an increase was undetected in the RRI time series, likely because counterbalanced by the concomitant effect of the higher mean HR while sitting.
Therefore, while the traditional analysis, based on HRV indices calculated directly on the RRI series, would have suggested that the sympathovagal balance increased because of a decreased vagal input in the sitting posture, the alternative analysis of HRV indices calculated on the derived DDR series suggests a substantially different interpretation. Accordingly, the sympathovagal balance increased not because of a vagal withdrawal but because of an increased LF variability attributable to the sympathetic drive. These findings suggest substantial changes when interpreting frequency-domain indices in terms of autonomic balance, if conditions with different mean HR are compared.
Finally, as predicted by the results on the synthesized series, the complexity-domain indices of HRV assessing self-similarity or irregularity provide a very similar picture of the effects of changing posture, regardless of whether they are calculated on the RRI or DDR series. Thus, the physiological interpretation of changes in the entropy profile or fractal structure of HRV does not appear to be influenced by the nonlinear link between autonomic input and CL output in the sinus node pacemaker.
Limitations and Future Perspective. We synthesized the CL series, making use of a simple mathematical model of the sinus node [10,11]. The model parameters in Appendix A were estimated from data collected on a population of healthy controls during an incremental exercise involving shifts in autonomic balance to obtain a wide range of CL values [51]. Data collection on larger populations might help to better adjust the model parameters to the subject characteristics, for instance, by stratifying the results by gender and age. Some cardiomyopathies may be responsible for an increased duration of the action potential [52], and collecting similar data in patients will allow a further generalization of the model. In any case, these limitations are not relevant when comparing experimental conditions in the same group of subjects, as in our analysis of posture change. We also hypothesized that the threshold of the membrane potential that triggers an action potential, ΔVm, remains constant. Even if ΔVm appears relatively stable over time [10], the possible effects of its long-term changes on HRV indices deserve to be quantified in future studies.
5. Conclusions
While confirming that HRV indices of the amplitude of RRI fluctuations, as spectral powers or time-domain measures of overall and short-term variability, depend strongly on the mean HR, we also showed that complexity-domain indices are mostly insensitive to mean HR. To mitigate the strong dependency of frequency- and time-domain indices of HRV, we proposed a procedure that almost completely eliminates this dependency, based on the estimation of DDR series from directly measured RRI series. This procedure removes the nonlinear link between the autonomic input and the DDR output of the sinus node pacemaker. Therefore, even if based on a few quantitative assumptions, estimating DDR from the measured cardiac intervals is highly advisable in HRV studies involving groups or conditions with different mean HR.
Author Contributions
Conceptualization, P.C., A.Z. and A.F.; methodology, P.C. and A.F.; software, A.F.; validation, P.C. and A.F.; formal analysis, P.C., A.Z. and A.F.; investigation, P.C., G.M. and A.F.; resources, P.C., G.M. and A.F.; data curation, P.C., G.M. and A.F.; writing—original draft preparation, P.C. and A.F.; writing—review and editing, P.C., A.Z., G.M. and A.F.; visualization, P.C.; supervision, P.C.; project administration, P.C., A.Z., G.M. and A.F.; funding acquisition, P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The synthesized data generated in the study are openly available in Zenodo at https://doi.org/10.5281/zenodo.16810869. The real data collected from volunteers have been uploaded to Zenodo at https://doi.org/10.5281/zenodo.16911630 with access granted on justified request to researchers who meet the criteria for access to confidential data, due to the restrictions requested for approval by the local ethical committee.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
We used the model of the cardiac pacemaker activity previously validated on rabbit sinoatrial myocytes [10]. The model considered that the cycle length of the n-th beat, CL(n), is the sum of the corresponding action potential duration, APD(n), and diastolic interval, DI(n):
A new action potential is generated when the membrane potential, , exceeds a given threshold. Therefore, the automatic activity of the sinus node is determined by the depolarization rate of the membrane potential during DI(n). The depolarization rate is proportional to the total (net) ionic currents flowing inward the cell, I(t)
with Cm the membrane capacitance (constant for the present purpose). As shown experimentally [10], the sinoatrial membrane depolarizes linearly during most of DI, thus reflecting I(t) to be close to constant in this phase. This implies that Vm increases linearly by the amount ΔVm, from the more negative value at the end of the action potential up to the threshold value that triggers the next action potential. Let’s indicate DDR(n), in mV/s, the depolarization rate describing the linear increase of Vm in DI(n) (see Figure 1 in [10]). Since DDR(n) produces a ΔVm increase in the DI(n) interval, we can express it with the ratio:
As per Equation (A1), APD(n) also contributes to CL(n). It has been shown that APD(n) depends on the preceding diastolic interval and that within a small range, the dependence can be modeled linearly [10]:
where a and b are species-specific constants. By combining Equations (A1) and (A4) we have
and combining Equation (A5) with (A3) we obtain
In this model, we set ΔVm = 13 mV, the value measured in rabbit sinoatrial myocytes [10] (no data from the human sinoatrial myocytes are available). As to the a and b coefficients in humans, APD is closely related to the QT interval of the electrocardiogram (e.g., see Figure 2 in [53]), and we set a = 0.218 s and b = 0.213 by fitting the relationship between QT intervals and cardiac intervals in humans [51]. This finally leads to the relation
Nonlinearity of the CL/DDR relationship implies nonlinearity between CL and perturbations of the net transmembrane currents and translates into steep dependency of some time-domain HRV parameters from the mean HR (see Figure 3 in [11]).
Appendix B
This appendix reports the effect sizes of the paired comparisons in Table 2 and Table 3 between the reference HR and each HR level for HRV indices calculated on the synthesized CL series (Table A1) and the corresponding DDR′ series (Table A2). Effect sizes are calculated as the ratio between the mean difference and the standard deviation of paired differences.

Table A1.
Effect sizes for the comparison of HRV indices reported in Table 2.
Table A1.
Effect sizes for the comparison of HRV indices reported in Table 2.
| Severe | Mild | Light | Reference | Light | Mild | Severe | |
|---|---|---|---|---|---|---|---|
| Bradycardia | Normocardia | Tachycardia | |||||
| SDNN | 13 | 15 | 15 | N/A | −6 | −16 | −20 |
| RMSSD | 14 | 21 | 23 | N/A | −16 | −49 | −56 |
| Spectral Indices | |||||||
| Total | 20 | 20 | 31 | N/A | −5 | −24 | −20 |
| VLF | 12 | 14 | 15 | N/A | −3 | −15 | −56 |
| LF | 21 | 15 | 18 | N/A | −4 | −17 | −77 |
| HF | 17 | 23 | 24 | N/A | −19 | −83 | −51 |
| LF/HF | 4 | 2 | 1.0 | N/A | −0.7 | −1.5 | −43 |
| LFnu | 3 | 2 | 1.0 | N/A | −0.7 | −1.5 | −388 |
| HFnu | −7 | −2 | −1.0 | N/A | 0.7 | 1.5 | −0.8 |
| β-slope | 0.6 | 0.4 | −0.1 | N/A | −0.2 | −0.1 | −0.8 |
| Entropy Indices (Beat Scales) | |||||||
| SE | 4 | 5 | 7 | N/A | −2 | −8 | −19 |
| SE5 | −10 | −8 | −3 | N/A | 1 | −2 | 3 |
| CIS | −5 | −6 | −3 | N/A | −3 | −5 | −11 |
| CIL | −1 | −2 | −2 | N/A | 1 | 4 | 7 |
| Entropy Indices (Temporal Scales) | |||||||
| MSE7 | 0.5 | 0.7 | 0.7 | N/A | −0.8 | −0.1 | −0.4 |
| MSEHF | 0.0 | −0.4 | 0.2 | N/A | −0.6 | −0.8 | −0.4 |
| MSELF | 0.9 | 0.4 | 1.2 | N/A | −0.4 | −0.1 | −0.1 |
| Fractal Indices (Beat Scales) | |||||||
| α1 | −25 | −12 | −4 | N/A | 0.1 | 1 | 28 |
| α2 | 7 | 5 | 4 | N/A | −3 | 1 | 5 |
| Fractal Indices (Temporal Scale) | |||||||
| αS | 1 | 0.6 | 0.4 | N/A | −0.9 | −0.9 | −0.9 |
| αL | 0.9 | 0.5 | 0.8 | N/A | 0.2 | 0.2 | −0.1 |
N/A = not available; see Table 2 for abbreviations.

Table A2.
Effect sizes for the comparison of HRV indices reported in Table 3.
Table A2.
Effect sizes for the comparison of HRV indices reported in Table 3.
| Severe | Mild | Light | Reference | Light | Mild | Severe | |
|---|---|---|---|---|---|---|---|
| Bradycardia | Normocardia | Tachycardia | |||||
| SDNN | −0.6 | −0.3 | −1.6 | N/A | −0.4 | −0.7 | −0.1 |
| RMSSD | 20 | 20 | 21 | N/A | −7 | −32 | −59 |
| Spectral Indices | |||||||
| Total | −1.4 | −0.8 | −2.0 | N/A | −0.3 | −0.6 | −0.1 |
| VLF | −0.5 | −0.3 | −0.4 | N/A | −0.3 | −0.5 | −0.4 |
| LF | −1.0 | −0.6 | −2.0 | N/A | −0.3 | −0.7 | 0.0 |
| HF | −12 | −8 | −0.4 | N/A | 0.8 | 0.8 | 0.7 |
| LF/HF | 1.3 | 0.1 | −1.8 | N/A | −0.4 | −0.8 | 0.0 |
| LFnu | 1.2 | 0.1 | −1.7 | N/A | −0.4 | −0.8 | −0.1 |
| HFnu | −1.3 | −0.1 | 1.8 | N/A | 0.4 | 0.8 | 0.1 |
| β-slope | 0.8 | 0.5 | −0.1 | N/A | −0.2 | −0.1 | −0.2 |
| Entropy Indices (Beat Scales) | |||||||
| SE | 10 | 9 | 7 | N/A | −2 | −10 | −23 |
| SE5 | −11 | −9 | −4 | N/A | 1 | −2 | 4 |
| CIS | −9 | −7 | −3 | N/A | −3 | −9 | −15 |
| CIL | −3 | −3 | −2 | N/A | 1 | 4 | 7 |
| Entropy Indices (Temporal Scales) | |||||||
| MSE7 | 0.1 | 0.3 | 0.3 | N/A | −0.7 | 0.1 | 0.0 |
| MSEHF | −0.4 | −0.7 | 0.0 | N/A | −0.4 | −0.4 | 0.0 |
| MSELF | 0.2 | −0.1 | 0.6 | N/A | −0.2 | 0.2 | 0.4 |
| Fractal Indices (Beat Scales) | |||||||
| α1 | −27 | −13 | −5 | N/A | 0.2 | 2 | 30 |
| α2 | 6 | 6 | 4 | N/A | −3 | 1 | 5 |
| Fractal Indices (Temporal Scale) | |||||||
| αS | −0.5 | −0.4 | 0 | N/A | −0.6 | −0.4 | −0.2 |
| αL | −0.3 | 0 | 0.6 | N/A | 0.5 | 0.4 | 0.1 |
N/A = not available; see Table 2 for abbreviations.
References
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Malik, M. Task Force of the European Society of Cardiology; The North American Society of Pacing Electrophysiology. Heart Rate Variability: Standards of Measurement, Physiological Interpretation, and Clinical Use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef]
- Billman, G.E. Heart Rate Variability—A Historical Perspective. Front. Physiol. 2011, 2, 86. [Google Scholar] [CrossRef] [PubMed]
- Mccraty, R.; Shaffer, F. Heart Rate Variability: New Perspectives on Physiological Mechanisms, Assessment of Self-Regulatory Capacity, and Health Risk. Glob. Adv. Health Med. 2015, 4, 46–61. [Google Scholar] [CrossRef] [PubMed]
- Dekker, J.M.; Schouten, E.G.; Klootwijk, P.; Pool, J.; Swenne, C.A.; Kromhout, D. Heart Rate Variability from Short Electrocardiographic Recordings Predicts Mortality from All Causes in Middle-Aged and Elderly Men: The Zutphen Study. Am. J. Epidemiol. 1997, 145, 899–908. [Google Scholar] [CrossRef]
- Jarczok, M.N.; Weimer, K.; Braun, C.; Williams, D.P.; Thayer, J.F.; Gündel, H.O.; Balint, E.M. Heart Rate Variability in the Prediction of Mortality: A Systematic Review and Meta-Analysis of Healthy and Patient Populations. Neurosci. Biobehav. Rev. 2022, 143, 104907. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Md Imam, H.; Al-Aubaidy, H.; Khandoker, A.H. Association of Cardiovascular Risk Using Non-Linear Heart Rate Variability Measures with the Framingham Risk Score in a Rural Population. Front. Physiol. 2013, 4, 52475. [Google Scholar] [CrossRef]
- Huikuri, H.V.; Stein, P.K. Heart Rate Variability in Risk Stratification of Cardiac Patients. Prog. Cardiovasc. Dis. 2013, 56, 153–159. [Google Scholar] [CrossRef]
- Voss, A.; Schroeder, R.; Vallverdú, M.; Schulz, S.; Cygankiewicz, I.; Vázquez, R.; Bayés De Luna, A.; Caminal, P. Short-Term vs. Long-Term Heart Rate Variability in Ischemic Cardiomyopathy Risk Stratification. Front. Physiol. 2013, 4, 364. [Google Scholar] [CrossRef]
- Rocchetti, M.; Malfatto, G.; Lombardi, F.; Zaza, A. Role of the Input/Output Relation of Sinoatrial Myocytes in Cholinergic Modulation of Heart Rate Variability. J. Cardiovasc. Electrophysiol. 2000, 11, 522–530. [Google Scholar] [CrossRef]
- Zaza, A.; Lombardi, F. Autonomic Indexes Based on the Analysis of Heart Rate Variability: A View from the Sinus Node. Cardiovasc. Res. 2001, 50, 434–442. [Google Scholar] [CrossRef] [PubMed]
- Dias Da Silva, V.J.; Tobaldini, E.; Rocchetti, M.; Wu, M.A.; Malfatto, G.; Montano, N.; Zaza, A. Modulation of Sympathetic Activity and Heart Rate Variability by Ivabradine. Cardiovasc. Res. 2015, 108, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Monfredi, O.; Lyashkov, A.E.; Johnsen, A.-B.; Inada, S.; Schneider, H.; Wang, R.; Nirmalan, M.; Wisloff, U.; Maltsev, V.A.; Lakatta, E.G.; et al. Biophysical Characterization of the Underappreciated and Important Relationship Between Heart Rate Variability and Heart Rate. Hypertension 2014, 64, 1334–1343. [Google Scholar] [CrossRef] [PubMed]
- Whelton, S.P.; Narla, V.; Blaha, M.J.; Nasir, K.; Blumenthal, R.S.; Jenny, N.S.; Al-Mallah, M.H.; Michos, E.D. Association Between Resting Heart Rate and Inflammatory Biomarkers (High-Sensitivity C-Reactive Protein, Interleukin-6, and Fibrinogen) (from the Multi-Ethnic Study of Atherosclerosis). Am. J. Cardiol. 2014, 113, 644–649. [Google Scholar] [CrossRef]
- Cooper, T.M.; McKinley, P.S.; Seeman, T.E.; Choo, T.-H.; Lee, S.; Sloan, R.P. Heart Rate Variability Predicts Levels of Inflammatory Markers: Evidence for the Vagal Anti-Inflammatory Pathway. Brain Behav. Immun. 2015, 49, 94–100. [Google Scholar] [CrossRef]
- Olivieri, F.; Biscetti, L.; Pimpini, L.; Pelliccioni, G.; Sabbatinelli, J.; Giunta, S. Heart Rate Variability and Autonomic Nervous System Imbalance: Potential Biomarkers and Detectable Hallmarks of Aging and Inflammaging. Ageing Res. Rev. 2024, 101, 102521. [Google Scholar] [CrossRef]
- Santos, M.A.A.; Sousa, A.C.S.; Reis, F.P.; Santos, T.R.; Lima, S.O.; Barreto-Filho, J.A. Does the Aging Process Significantly Modify the Mean Heart Rate? Arq. Bras. Cardiol. 2013, 101, 388–398. [Google Scholar] [CrossRef]
- Krüger, C. The Bradycardic Agent Zatebradine Enhances Baroreflex Sensitivity and Heart Rate Variability in Rats Early after Myocardial Infarction. Cardiovasc. Res. 2000, 45, 900–912. [Google Scholar] [CrossRef][Green Version]
- D’Souza, A.; Bucchi, A.; Johnsen, A.B.; Logantha, S.J.R.J.; Monfredi, O.; Yanni, J.; Prehar, S.; Hart, G.; Cartwright, E.; Wisloff, U.; et al. Exercise Training Reduces Resting Heart Rate via Downregulation of the Funny Channel HCN4. Nat. Commun. 2014, 5, 3775. [Google Scholar] [CrossRef]
- Sen, J.; McGill, D. Fractal Analysis of Heart Rate Variability as a Predictor of Mortality: A Systematic Review and Meta-Analysis. Chaos: Interdiscip. J. Nonlinear Sci. 2018, 28, 072101. [Google Scholar] [CrossRef]
- Hu, M.; Liang, H. Multiscale Entropy: Recent Advances. In Complexity and Nonlinearity in Cardiovascular Signals; Barbieri, R., Scilingo, E.P., Valenza, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 115–138. ISBN 978-3-319-58708-0. [Google Scholar] [CrossRef]
- Henriques, T.; Ribeiro, M.; Teixeira, A.; Castro, L.; Antunes, L.; Costa-Santos, C. Nonlinear Methods Most Applied to Heart-Rate Time Series: A Review. Entropy 2020, 22, 309. [Google Scholar] [CrossRef] [PubMed]
- Huikuri, H.V.; Perkiömäki, J.S.; Maestri, R.; Pinna, G.D. Clinical Impact of Evaluation of Cardiovascular Control by Novel Methods of Heart Rate Dynamics. Philos. Transact. A Math. Phys. Eng. Sci. 2009, 367, 1223–1238. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Schulz, S.; Schroeder, R.; Baumert, M.; Caminal, P. Methods Derived from Nonlinear Dynamics for Analysing Heart Rate Variability. Phil. Trans. R. Soc. A. 2009, 367, 277–296. [Google Scholar] [CrossRef] [PubMed]
- Sassi, R.; Cerutti, S.; Lombardi, F.; Malik, M.; Huikuri, H.V.; Peng, C.K.; Schmidt, G.; Yamamoto, Y. Advances in Heart Rate Variability Signal Analysis: Joint Position Statement by the e-Cardiology ESC Working Group and the European Heart Rhythm Association Co-Endorsed by the Asia Pacific Heart Rhythm Society. Europace 2015, 17, 1341–1353. [Google Scholar] [CrossRef]
- Kobayashi, M.; Musha, T. 1/f Fluctuation of Heartbeat Period. IEEE Trans. Biomed. Eng. 1982, 29, 456–457. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Hausdorff, J.M.; Mietus, J.E.; Stanley, H.E.; Goldberger, A.L. Fractal Mechanisms and Heart Rate Dynamics. Long-Range Correlations and Their Breakdown with Disease. J. Electrocardiol. 1995, 28 (Suppl. S1), 59–65. [Google Scholar] [CrossRef]
- Julien, C. The Enigma of Mayer Waves: Facts and Models. Cardiovasc. Res. 2006, 70, 12–21. [Google Scholar] [CrossRef]
- Di Rienzo, M.; Castiglioni, P.; Parati, G.; Mancia, G.; Pedotti, A. Effects of Sino-Aortic Denervation on Spectral Characteristics of Blood Pressure and Pulse Interval Variability: A Wide-Band Approach. Med. Biol. Eng. Comput. 1996, 34, 133–141. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined Multiscale Entropy: Application to 24-h Holter Recordings of Heart Period Variability in Healthy and Aortic Stenosis Subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef]
- Tang, S.-Y.; Ma, H.-P.; Lin, C.; Lo, M.-T.; Lin, L.-Y.; Chen, T.-Y.; Wu, C.-K.; Chiang, J.-Y.; Lee, J.-K.; Hung, C.-S.; et al. Heart Rhythm Complexity Analysis in Patients with Inferior ST-Elevation Myocardial Infarction. Sci. Rep. 2023, 13, 20861. [Google Scholar] [CrossRef] [PubMed]
- Faini, A.; Caravita, S.; Parati, G.; Castiglioni, P. Alterations of Cardiovascular Complexity during Acute Exposure to High Altitude: A Multiscale Entropy Approach. Entropy 2019, 21, 1224. [Google Scholar] [CrossRef]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal Characterization of Complexity in Temporal Physiological Signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, M.P.; Niskanen, J.P.; Lipponen, J.A.; Ranta-Aho, P.O.; Karjalainen, P.A. Kubios HRV—Heart Rate Variability Analysis Software. Comput. Methods Programs Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef]
- Castiglioni, P.; Parati, G.; Di Rienzo, M.; Carabalona, R.; Cividjian, A.; Quintin, L. Scale Exponents of Blood Pressure and Heart Rate during Autonomic Blockade as Assessed by Detrended Fluctuation Analysis. J. Physiol. 2011, 589, 355–369. [Google Scholar] [CrossRef]
- Watanabe, N.; Reece, J.; Polus, B.I. Effects of Body Position on Autonomic Regulation of Cardiovascular Function in Young, Healthy Adults. Chiropr. Man. Ther. 2007, 15, 19. [Google Scholar] [CrossRef]
- Zuttin, R.S.; Moreno, M.A.; César, M.C.; Martins, L.E.B.; Catai, A.M. Evaluation of Autonomic Heart Rate Modulation among Sedentary Uoung Men, in Sitting and Supine Postures. Rev. Bras. Fisioter. 2008, 12, 7–12. [Google Scholar]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Kerby, D.S. The Simple Difference Formula: An Approach to Teaching Nonparametric Correlation. Compr. Psychol. 2014, 3, 11.IT.3.1. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988; ISBN 978-1-134-74270-7. [Google Scholar]
- Tsuji, H.; Venditti, F.J.; Manders, E.S.; Evans, J.C.; Larson, M.G.; Feldman, C.L.; Levy, D. Determinants of Heart Rate Variability. J. Am. Coll. Cardiol. 1996, 28, 1539–1546. [Google Scholar] [CrossRef] [PubMed]
- Sacha, J. Why Should One Normalize Heart Rate Variability with Respect to Average Heart Rate. Front. Physiol. 2013, 4, 68271. [Google Scholar] [CrossRef] [PubMed]
- Sacha, J.; Pluta, W. Alterations of an Average Heart Rate Change Heart Rate Variability Due to Mathematical Reasons. Int. J. Cardiol. 2008, 128, 444–447. [Google Scholar] [CrossRef] [PubMed]
- Sacha, J.; Sobon, J.; Sacha, K.; Barabach, S. Heart Rate Impact on the Reproducibility of Heart Rate Variability Analysis. Int. J. Cardiol. 2013, 168, 4257–4259. [Google Scholar] [CrossRef]
- Poehling, C.P. The Effects of Submaximal and Maximal Exercise on Heart Rate Variability. Int. J. Exerc. Sci. 2019, 12, 9–14. [Google Scholar] [CrossRef]
- Leite, A.S.; Rocha, A.P.; Silva, M.E.; Costa, O. Modelling Long-Term Heart Rate Variability: An ARFIMA Approach. Biomed. Technol./Biomed. Eng. 2006, 51, 215–219. [Google Scholar] [CrossRef]
- Castiglioni, P.; Parati, G.; Lombardi, C.; Quintin, L.; Di Rienzo, M. Assessing the Fractal Structure of Heart Rate by the Temporal Spectrum of Scale Exponents: A New Approach for Detrended Fluctuation Analysis of Heart Rate Variability. Biomed. Technol. 2011, 56, 175–183. [Google Scholar] [CrossRef]
- Kazmi, S.Z.H.; Zhang, H.; Aziz, W.; Monfredi, O.; Abbas, S.A.; Shah, S.A.; Kazmi, S.S.H.; Butt, W.H. Inverse Correlation between Heart Rate Variability and Heart Rate Demonstrated by Linear and Nonlinear Analysis. PLoS ONE 2016, 11, e0157557. [Google Scholar] [CrossRef]
- Malfatto, G.; Rocchetti, M.; Zaza, A. The Role of the Autonomic System in Rate-Dependent Repolarization Changes. Heart Rhythm. 2010, 7, 1700–1703. [Google Scholar] [CrossRef]
- Li, G.-R.; Lau, C.-P.; Leung, T.-K.; Nattel, S. Ionic Current Abnormalities Associated with Prolonged Action Potentials in Cardiomyocytes from Diseased Human Right Ventricles. Heart Rhythm. 2004, 1, 460–468. [Google Scholar] [CrossRef]
- Pollard, C.E.; Abi Gerges, N.; Bridgland-Taylor, M.H.; Easter, A.; Hammond, T.G.; Valentin, J.-P. An Introduction to QT Interval Prolongation and Non-Clinical Approaches to Assessing and Reducing Risk. Br. J. Pharmacol. 2010, 159, 12–21. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).