The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams
Abstract
1. Introduction
2. Adsorption Model Development
2.1. Quantitative Characterization Model for CH4 Isothermal Adsorption Characteristics in Coal
2.2. Simplification of the Quantitative Characterization Model
2.3. CH4 Adsorption Parameters of Quantitative Characterization Model
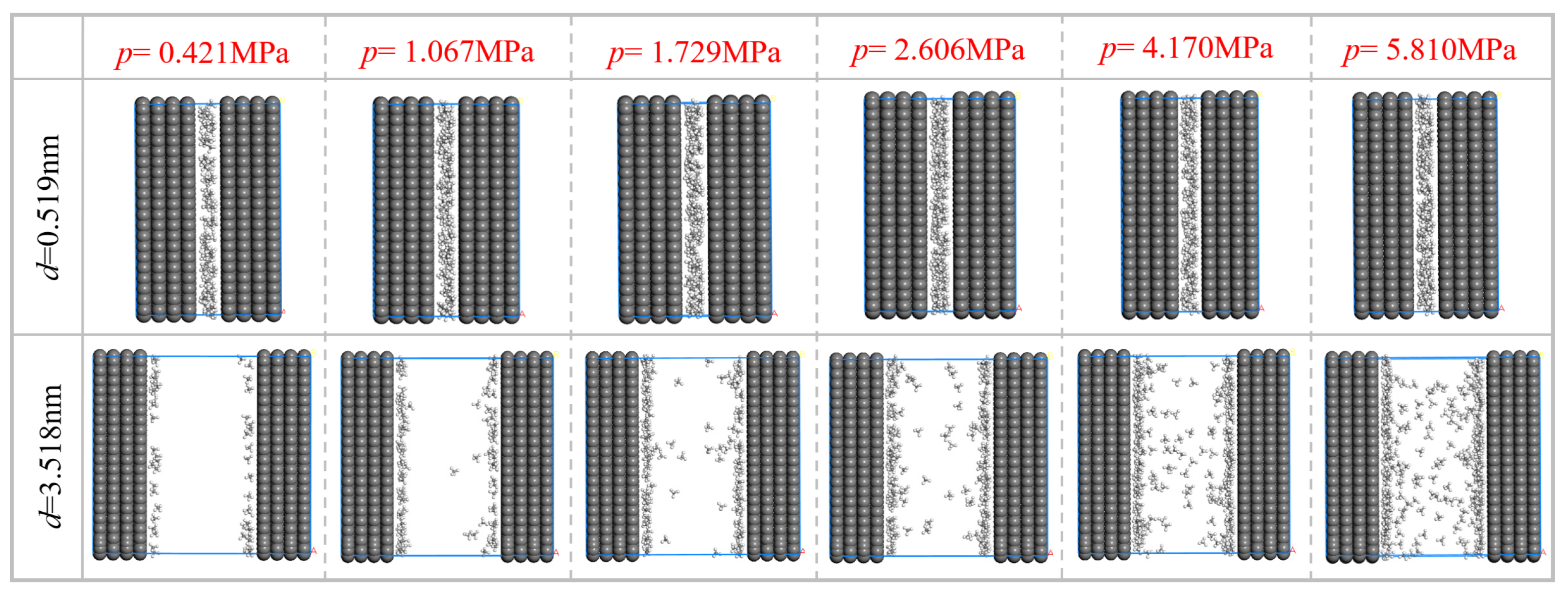
2.3.1. Construction of Pore Structures of Different Sizes and Simulation of CH4 Adsorption
2.3.2. CH4 Adsorption Parameters of Pore Structures of Different Sizes
3. Experimental
3.1. Sample Preparation
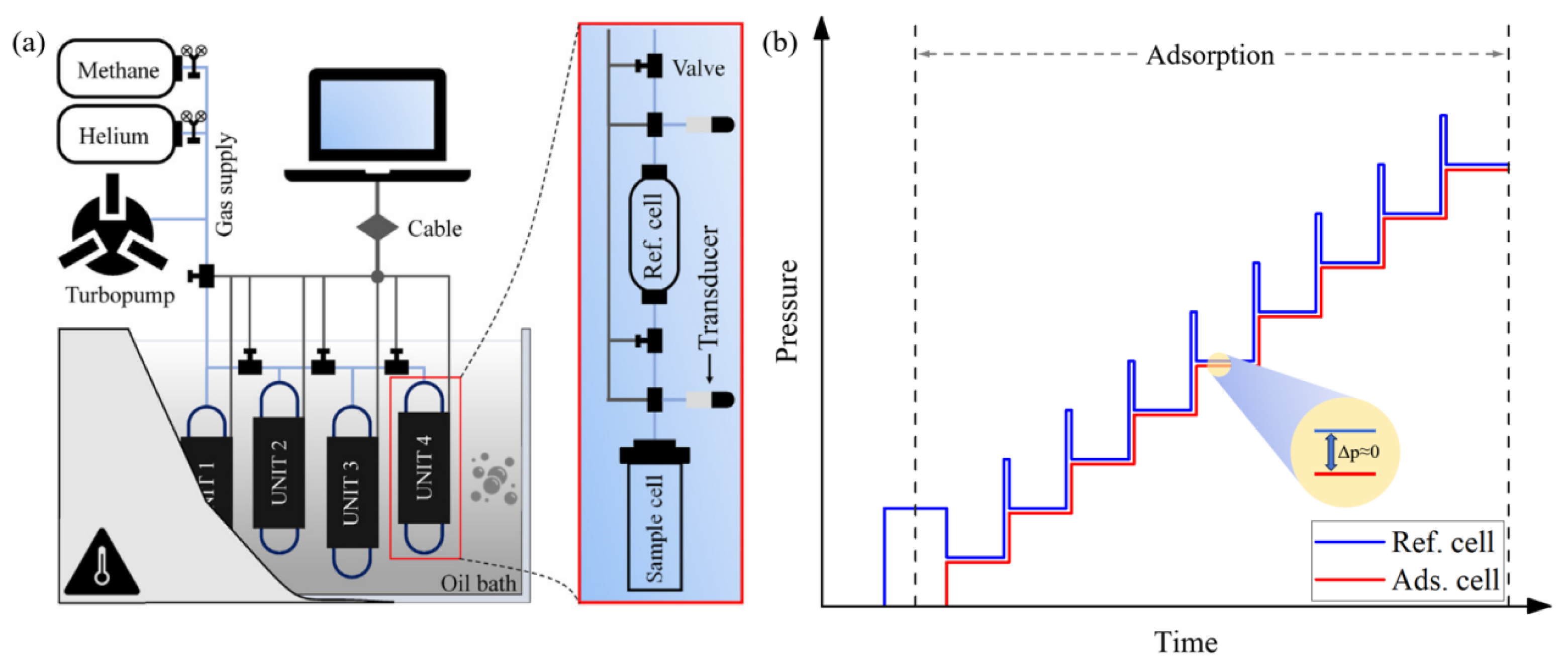
3.2. Testing Methods
4. Results and Discussion
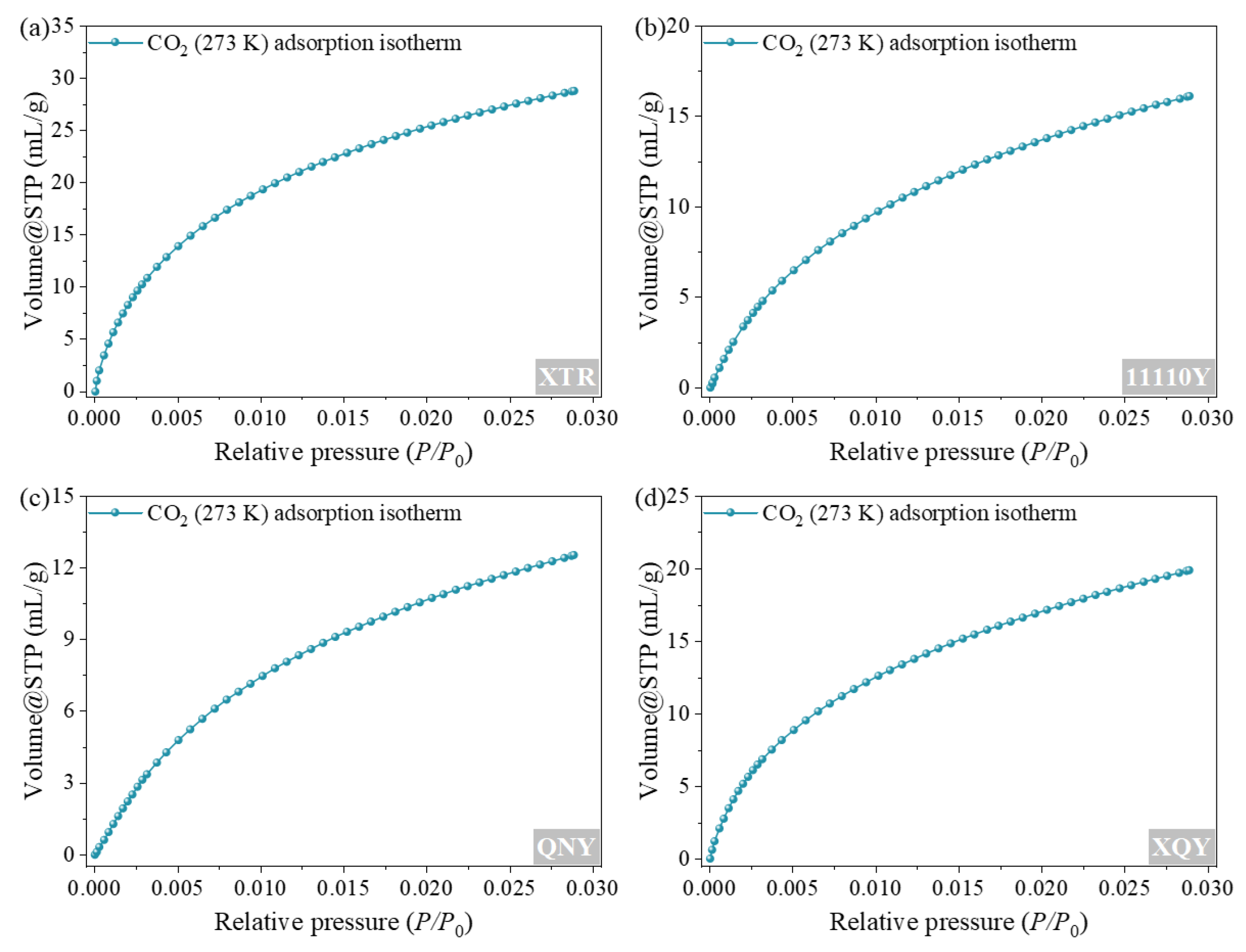
4.1. Pore Size Distribution in Coal Samples
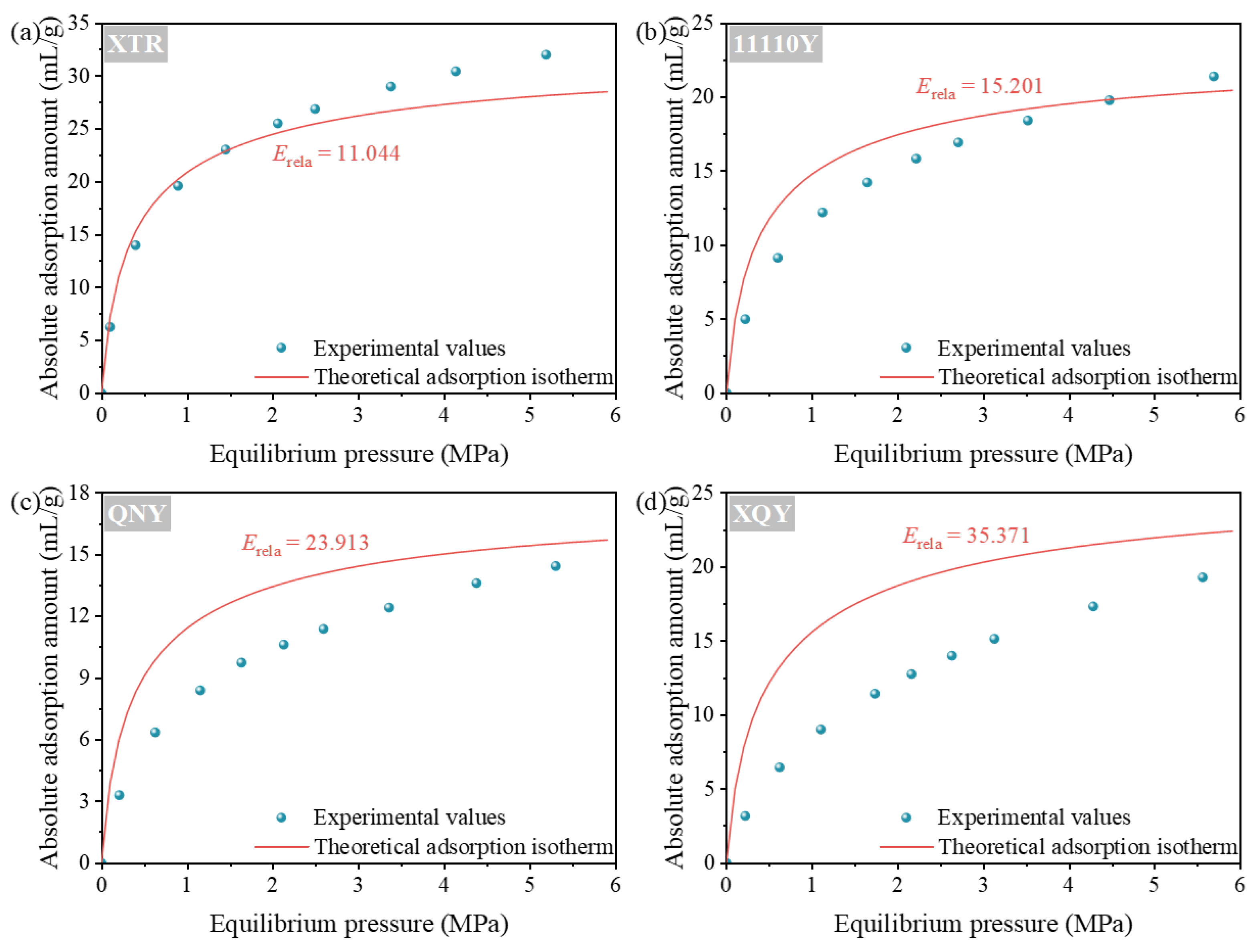
4.2. Validation of the Theoretical CH4 Adsorption Isotherms
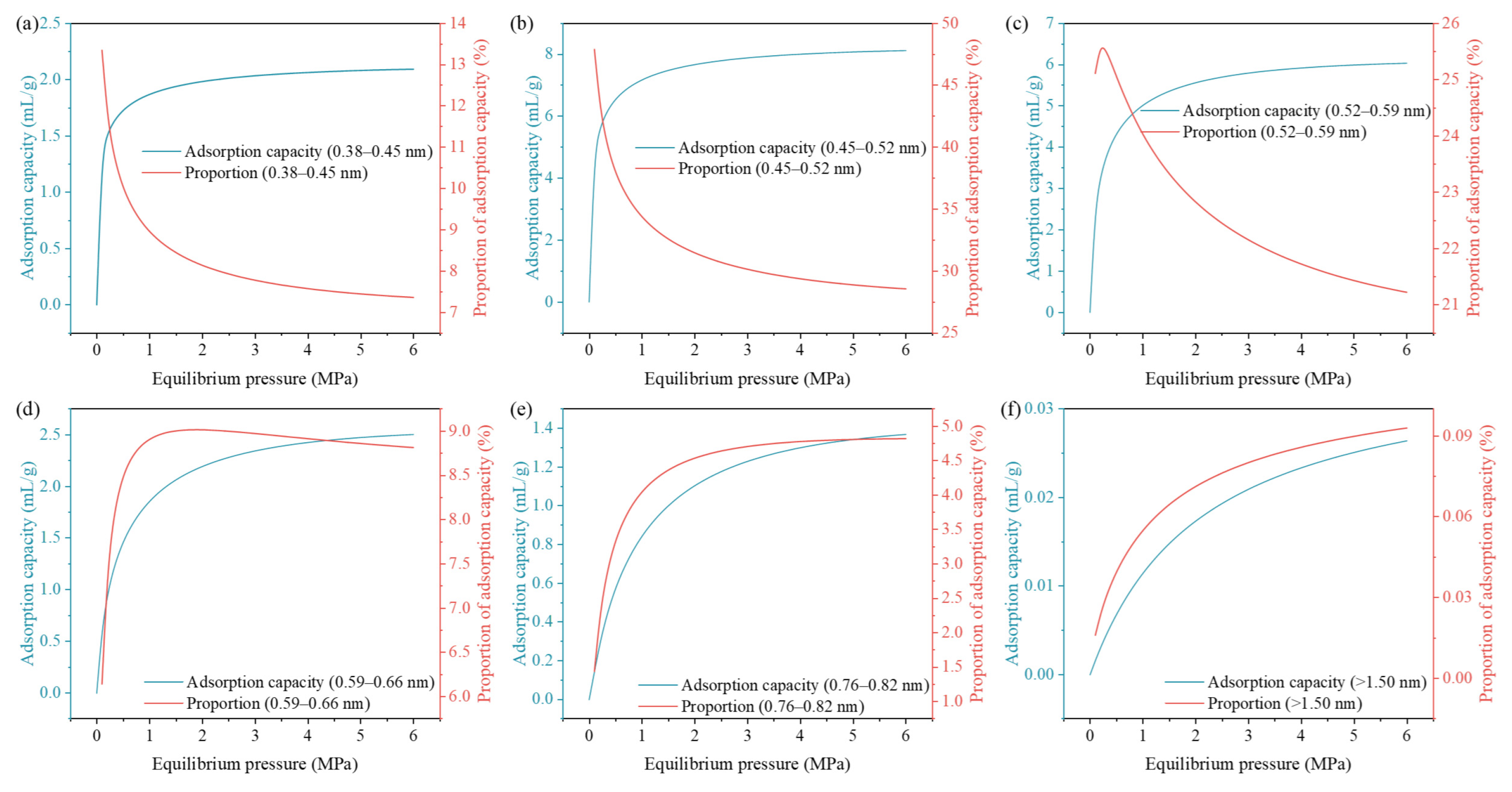
4.3. Distribution Characteristics of Adsorbed CH4
4.4. Limitations and Future Perspectives
- (1)
- The analysis in this study was conducted isothermally at 30 °C. However, in situ reservoir temperatures can vary significantly with depth. To extend the model’s applicability, future work should involve performing GCMC simulations across a range of geologically relevant temperatures. This would enable the establishment of temperature-dependent thermodynamic parameters, which in turn allows the model to predict gas distribution under diverse geothermal gradients—a capability crucial for deep coalbed methane (CBM) exploration.
- (2)
- The experimental validation and simulations in this study were limited to a maximum pressure of 6 MPa, constrained by our experimental setup. While this pressure range is sufficient for many conventional CBM scenarios, deep coal seams typically exhibit much higher pressures. Future studies should aim to acquire high-pressure experimental data to validate and potentially refine the model’s predictive behavior in the supercritical region—this will ensure the model’s robustness for deep reservoir conditions.
- (3)
- It should be noted that the GCMC simulations in this study employed a simplified slit-pore geometry. Although coal contains various pore morphologies, such as ink-bottle, wedge-shaped, and irregular pores, previous research has shown that slit pores are the most frequent type in the coal matrix [44,73]. They provide a large specific surface area and significantly influence methane adsorption capacity. Furthermore, GCMC studies have demonstrated that experimentally measured isotherms align more closely with slit-pore model predictions, whereas circular and square pore models tend to underestimate actual adsorption [46]. Therefore, the slit-pore model was adopted to simulate methane adsorption behavior, ensuring comparability and reducing computational complexity. However, it may overlook the effects of complex pore connectivity and geometric features. Future research will incorporate more realistic pore geometries to improve predictive accuracy.
5. Conclusions
- (1)
- Micropores (0.38–1.5 nm) dominate the pore structure of the studied coals. They account for 95.10–95.75% of the total pore volume. Within this range, ultra-micropores (0.38–0.76 nm) contribute 58.23–66.33%, serving as the principal adsorption sites for CH4 storage.
- (2)
- CH4 adsorption behavior strongly depends on pore size. Smaller pores require lower pressure to reach CH4 saturation and exhibit higher adsorption potential energy. In slit pores from 0.419 to 1.466 nm, the characteristic parameter νmi,r decreases irregularly overall (from 500.7 to 278.5 cm3/cm3), Kr increases significantly (from 0.018 to 0.255, 14 times), and nr initially rises (from 2.044 to 2.366) and then declines (to 1.607). For larger slit pores (1.619–4.040 nm), VL gradually decreases (from 0.211 to 0.198 cm3/m2), while PL remains almost constant. This suggests similar CH4 adsorption behavior in these pores.
- (3)
- The proposed thermodynamic model is based on GCMC-derived adsorption behavior. It shows good agreement with experimental CH4 adsorption isotherms, especially for high-rank coals. As coal rank increases, the mean relative deviation between theoretical and measured CH4 adsorption isotherms drops sharply from 35.371% to 11.044%. This supports the model’s applicability to coals with graphite-like molecular structures.
- (4)
- Adsorbed CH4 distribution analysis reveals dynamic pressure-dependent pore contributions: pores <0.52 nm dominate at low pressures but saturate rapidly, reducing their relative share. Pores in the range of 0.52–0.76 nm show a peak contribution at intermediate pressures. Pores larger than 0.92 nm continue to increase their contribution as pressure rises, highlighting their importance for high-pressure CH4 storage.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, W.; Zhao, D.; Wang, K.; Fan, L.; Zhao, Z.; Dong, H.; Shu, L. Will Greenhouse Gas Emissions Increase with Mining Depth in Coal Mines? An Analysis of Gas Occurrence under Varying in-Situ Stress Conditions. Sci. Total Environ. 2024, 945, 173957. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, B. Main occurrence form of methane in coal: Micropore filling. J. China Coal Soc. 2021, 46, 2933–2948. [Google Scholar] [CrossRef]
- Zhao, W.; Dong, H.; Yan, Z.; Wang, K.; Shu, L.; Feng, Z.; Lu, S.; Hu, K. Hierarchical occurrence law of gas content in deep coal seams and its relationship with outburst prevention. J. China Coal Soc. 2025, 50, 1555–1568. [Google Scholar] [CrossRef]
- Qin, Y.; Shen, J.; Shi, R. Strategic value and choice on construction of large CMG industry in China. J. China Coal Soc. 2022, 47, 371–387. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, C.; Wang, R. Monitoring Technologies for CO2 Storage in Coal Seams and Enhanced Coalbed Methane Recovery: A Review of Field Applications. Fuel Process. Technol. 2025, 276, 108274. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.; Liu, H.; Hong, Y.; Zou, Q.; Lu, J.; Mou, J. Gas-Flow Microchannels in Coal Due to Microwave-LN2 Cycles: Adsorption/Desorption Behavior and Nanoscale Surface Morphology. Energy Fuels 2025, 39, 5349–5363. [Google Scholar] [CrossRef]
- Xue, H.; Wang, G.; Gong, H.; Li, X.; Du, F. Effect of CO2 Sinusoidal, Step-Flow Injection on Coalbed CH4 Desorption-Diffusion Mechanisms. Energy Fuels 2024, 38, 16756–16771. [Google Scholar] [CrossRef]
- Chai, H.; Wu, J.; Zhang, L.; Zhao, Y.; Cai, K. Research on an Equivalent Algorithm for Predicting Gas Content in Deep Coal Seams. Appl. Sci. 2024, 14, 9601. [Google Scholar] [CrossRef]
- Zhao, B.; Wen, G.; Ma, Q.; Sun, H.; Yan, F.; Nian, J. Distribution Characteristics of Pulverized Coal and Stress–Gas Pressure–Temperature Response Laws in Coal and Gas Outburst under Deep Mining Conditions. Energy Sci. Eng. 2022, 10, 2205–2223. [Google Scholar] [CrossRef]
- Chen, D.; Qu, B.; Zhang, J.; Long, Q.; Sun, R. Methods and Techniques for Determining the Gas Content of Coal Seams in China: A Mini-Review. Fuel Process. Technol. 2025, 275, 108257. [Google Scholar] [CrossRef]
- Yang, D.; Cui, G.; Elsworth, D.; Wang, C.; Cheng, W.; Yang, C.; Chen, T. Damage-Based Microscale Model Explains Observed Two-Stage Shale Gas Depletion Profiles at Reservoir Scale. Energy Fuels 2025, 39, 13488–13504. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Sang, S.; Yang, W.; Liu, T.; Liu, S.; Zheng, S.; Wang, T. Control Mechanisms of Macromolecular Compositions and Structures of Coals on the Evolution of Nanopores during Coalification. Energy Fuels 2024, 38, 13002–13018. [Google Scholar] [CrossRef]
- Yang, T.; Tang, H.; Hou, Y.; He, Y.; Liu, B.; Wang, P.; Peng, X.; Zhang, M.; Wang, Z.; Wang, M. Pore Structure Evolution in Long-Term Water-Flooding Unconsolidated Sandstone Reservoirs. Energy Fuels 2025, 39, 12860–12874. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Bustin, R.M. The Effect of Pore Structure and Gas Pressure upon the Transport Properties of Coal: A Laboratory and Modeling Study. 2. Adsorption Rate Modeling. Fuel 1999, 78, 1345–1362. [Google Scholar] [CrossRef]
- Nie, B.; Liu, X.; Yang, L.; Meng, J.; Li, X. Pore Structure Characterization of Different Rank Coals Using Gas Adsorption and Scanning Electron Microscopy. Fuel 2015, 158, 908–917. [Google Scholar] [CrossRef]
- Lu, J.; Wang, X.; Li, H.; Shi, S.; Yang, W.; Lu, Y.; Shao, S.; Ye, Q. Molecular Insights into the Methane Adsorption Capacity of Coal under Microwave Irradiation Based on Solid-State 13C-NMR and XPS. Fuel 2023, 339, 127484. [Google Scholar] [CrossRef]
- Liu, D.; Yao, Y.; Chang, Y. Measurement of Adsorption Phase Densities with Respect to Different Pressure: Potential Application for Determination of Free and Adsorbed Methane in Coalbed Methane Reservoir. Chem. Eng. J. 2022, 446, 137103. [Google Scholar] [CrossRef]
- Moore, T.A. Coalbed Methane: A Review. Int. J. Coal Geol. 2012, 101, 36–81. [Google Scholar] [CrossRef]
- Bustin, R.M.; Clarkson, C.R. Geological Controls on Coalbed Methane Reservoir Capacity and Gas Content. Int. J. Coal Geol. 1998, 38, 3–26. [Google Scholar] [CrossRef]
- An, F.-H.; Cheng, Y.-P.; Wu, D.-M.; Wang, L. The Effect of Small Micropores on Methane Adsorption of Coals from Northern China. Adsorption 2013, 19, 83–90. [Google Scholar] [CrossRef]
- Tao, S.; Chen, S.; Tang, D.; Zhao, X.; Xu, H.; Li, S. Material Composition, Pore Structure and Adsorption Capacity of Low-Rank Coals around the First Coalification Jump: A Case of Eastern Junggar Basin, China. Fuel 2018, 211, 804–815. [Google Scholar] [CrossRef]
- Byamba-Ochir, N.; Shim, W.G.; Balathanigaimani, M.S.; Moon, H. High Density Mongolian Anthracite Based Porous Carbon Monoliths for Methane Storage by Adsorption. Appl. Energy 2017, 190, 257–265. [Google Scholar] [CrossRef]
- Juntgen, H. Research for Future in Situ Conversion of Coal. Fuel 1987, 66, 443–453. [Google Scholar] [CrossRef]
- Busch, A.; Gensterblum, Y. CBM and CO2-ECBM Related Sorption Processes in Coal: A Review. Int. J. Coal Geol. 2011, 87, 49–71. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Y.; Liu, S.; Zhang, R. Pore Characterization and Its Impact on Methane Adsorption Capacity for Organic-Rich Marine Shales. Fuel 2016, 181, 227–237. [Google Scholar] [CrossRef]
- Lozano-Castelló, D.; Cazorla-Amorós, D.; Linares-Solano, A. Powdered Activated Carbons and Activated Carbon Fibers for Methane Storage: A Comparative Study. Energy Fuels 2002, 16, 1321–1328. [Google Scholar] [CrossRef]
- Jin, K.; Cheng, Y.; Liu, Q.; Zhao, W.; Wang, L.; Wang, F.; Wu, D. Experimental Investigation of Pore Structure Damage in Pulverized Coal: Implications for Methane Adsorption and Diffusion Characteristics. Energy Fuels 2016, 30, 10383–10395. [Google Scholar] [CrossRef]
- Li, C.; Qin, Y.; Guo, T.; Shen, J.; Yang, Y. Supercritical Methane Adsorption in Coal and Implications for the Occurrence of Deep Coalbed Methane Based on Dual Adsorption Modes. Chem. Eng. J. 2023, 474, 145931. [Google Scholar] [CrossRef]
- He, X.; Zhang, R.; Elsworth, D.; He, L.; Liu, S. Beyond Liquid Density Assumptions: A Novel SANS-Based Approach to Quantify Adsorbed Methane and Adsorption-Induced Coal Microstructure Alterations. Chem. Eng. J. 2025, 518, 164725. [Google Scholar] [CrossRef]
- Hu, B.; Ren, Z.; Li, S.; He, X.; Lin, H.; Bai, Y.; Yan, D.; Luo, R. A New Quantitative Characterization Method of Absolute Methane Adsorption Isotherm in Coal. Chem. Eng. J. 2025, 522, 167551. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, Y.; He, X.; Wang, Z.; Jiang, Z.; Wang, C.; Li, W.; Wang, L. New Insights into the CH4 Adsorption Capacity of Coal Based on Microscopic Pore Properties. Fuel 2020, 262, 116675. [Google Scholar] [CrossRef]
- Jia, T.; Zhang, S.; Tang, S.; Xin, D.; Zhang, S.; Wang, B.; Zhang, Q.; Zhang, K.; Lin, D.; Yang, W. Density and Volume of Adsorbed Methane in Key Applications for In-Situ Gas Content: Insights from Molecular Simulation. Chem. Eng. J. 2024, 490, 151809. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, Y.; Pan, Z. Classification Methods of Pore Structures in Coal: A Review and New Insight. Gas Sci. Eng. 2023, 110, 204876. [Google Scholar] [CrossRef]
- Zhang, K.; Xing, X.; Wang, L.; Yang, B.; Li, J.; Zhang, H. Micro-CT Image-Based Characterization of Microstructure Complexity in Coal: From the Perspective of Fractal Geometrical Theory. Nat. Resour. Res. 2025. [Google Scholar] [CrossRef]
- Dubinin, M.M. The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces. Chem. Rev. 1960, 60, 235–241. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Dubinin, M.M.; Astakhov, V.A. Description of Adsorption Equilibria of Vapors on Zeolites over Wide Ranges of Temperature and Pressure. In Advances in Chemistry; American Chemical Society: Washington, DC, USA, 1971; Volume 102, pp. 69–85. [Google Scholar] [CrossRef]
- Dubinin, M.M. Adsorption in Micropores. J. Colloid Interface Sci. 1967, 23, 487–499. [Google Scholar] [CrossRef]
- Hao, S.; Chu, W.; Jiang, Q.; Yu, X. Methane Adsorption Characteristics on Coal Surface above Critical Temperature through Dubinin–Astakhov Model and Langmuir Model. Colloids Surf. Physicochem. Eng. Asp. 2014, 444, 104–113. [Google Scholar] [CrossRef]
- Charoensuppanimit, P.; Mohammad, S.A.; Robinson, R.L.; Gasem, K.A.M. Modeling the Temperature Dependence of Supercritical Gas Adsorption on Activated Carbons, Coals and Shales. Int. J. Coal Geol. 2015, 138, 113–126. [Google Scholar] [CrossRef]
- Yelash, L.V.; Kraska, T. A Generic Equation of State for the Hard-Sphere Fluid Incorporating the High Density Limit. Phys. Chem. Chem. Phys. 2001, 3, 3114–3118. [Google Scholar] [CrossRef]
- Hu, B. Methane Adsorption Behavior Characteristics of Multi-Scale Pore Structure in Coal and its Microscopic Influencing Mechanism. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2022. [Google Scholar] [CrossRef]
- Mosher, K.; He, J.; Liu, Y.; Rupp, E.; Wilcox, J. Molecular Simulation of Methane Adsorption in Micro- and Mesoporous Carbons with Applications to Coal and Gas Shale Systems. Int. J. Coal Geol. 2013, 109, 36–44. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Liu, S.; Li, W.; Tang, X. Temperature Effect on Gas Adsorption Capacity in Different Sized Pores of Coal: Experiment and Numerical Modeling. J. Pet. Sci. Eng. 2018, 165, 821–830. [Google Scholar] [CrossRef]
- Song, W.; Yao, J.; Ma, J.; Li, A.; Li, Y.; Sun, H.; Zhang, L. Grand Canonical Monte Carlo Simulations of Pore Structure Influence on Methane Adsorption in Micro-Porous Carbons with Applications to Coal and Shale Systems. Fuel 2018, 215, 196–203. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties, Version 9.1; NIST: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Ortiz, L.; Kuchta, B.; Firlej, L.; Roth, M.W.; Wexler, C. Methane Adsorption in Nanoporous Carbon: The Numerical Estimation of Optimal Storage Conditions. Mater. Res. Express 2016, 3, 55011. [Google Scholar] [CrossRef]
- Heffelfinger, G.S.; Tan, Z.; Gubbins, K.E.; Marini Bettolo Marconi, U.; Van Swol, F. Fluid Mixtures in Narrow Cylindrical Pores: Computer Simulation and Theory. Int. J. Thermophys. 1988, 9, 1051–1060. [Google Scholar] [CrossRef]
- Song, W.; Yao, B.; Yao, J.; Li, Y.; Sun, H.; Yang, Y.; Zhang, L. Methane Surface Diffusion Capacity in Carbon-Based Capillary with Application to Organic-Rich Shale Gas Reservoir. Chem. Eng. J. 2018, 352, 644–654. [Google Scholar] [CrossRef]
- GB/T 19222-2003; Sampling of Coal Petrology. Standard Press of China: Beijing, China, 2003.
- GB/T 212-2008; Proximate Analysis of Coal. Standard Press of China: Beijing, China, 2008.
- GB/T 21650.2-2008; Pore Size Distribution and Porosity of Solid Materials by Mercury Porosimetry and Gas Adsorption—Part 2: Analysis of Mesopores and Macropores by Gas Adsorption. Standard Press of China: Beijing, China, 2008.
- GB/T 21650.3-2011; Pore Size Distribution and Porosity of Solid Materials by Mercury Porosimetry and Gas Adsorption—Part3: Analysis of Micropores by Gas Adsorption. Standard Press of China: Beijing, China, 2011.
- Hu, B.; Cheng, Y.; Wang, Z.; He, X.; Jiang, Z.; Yi, M.; Li, W.; Wang, L. Effect of Pulverization on the Microporous and Ultramicroporous Structures of Coal Using Low-Pressure CO2 Adsorption. Energy Fuels 2019, 33, 10611–10621. [Google Scholar] [CrossRef]
- He, X.; Cheng, Y.; Hu, B.; Wang, Z.; Wang, C.; Yi, M.; Wang, L. Effects of Coal Pore Structure on Methane-coal Sorption Hysteresis: An Experimental Investigation Based on Fractal Analysis and Hysteresis Evaluation. Fuel 2020, 269, 117438. [Google Scholar] [CrossRef]
- GB/T 19560-2008; Experimental Method of High-Pressure Isothermal Adsorption to Coal. Standard Press of China: Beijing, China, 2008.
- Hu, B.; Cheng, Y.; Wang, L.; Zhang, K.; He, X.; Yi, M. Experimental Study on Influence of Adsorption Equilibrium Time on Methane Adsorption Isotherm and Langmuir Parameter. Adv. Powder Technol. 2021, 32, 4110–4119. [Google Scholar] [CrossRef]
- Ekundayo, J.M.; Rezaee, R. Effect of Equation of States on High-Pressure Volumetric Measurements of Methane–Coal Sorption Isotherms—Part 1: Volumes of Free Space and Methane Adsorption Isotherms. Energy Fuels 2019, 33, 1029–1036. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of Gases, with Special Reference to the Evaluation of Surface Area and Pore Size Distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Landers, J.; Gor, G.Y.; Neimark, A.V. Density Functional Theory Methods for Characterization of Porous Materials. Colloids Surf. A 2013, 437, 3–32. [Google Scholar] [CrossRef]
- Thommes, M.; Cychosz, K.A. Physical Adsorption Characterization of Nanoporous Materials: Progress and Challenges. Adsorption 2014, 20, 233–250. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, D.; Pan, Z.; Yao, Y.; Li, J.; Qiu, Y. Pore Structure and Its Impact on CH4 Adsorption Capacity and Flow Capability of Bituminous and Subbituminous Coals from Northeast China. Fuel 2013, 103, 258–268. [Google Scholar] [CrossRef]
- Guo, H.; Cheng, Y.; Wang, L.; Lu, S.; Jin, K. Experimental Study on the Effect of Moisture on Low-Rank Coal Adsorption Characteristics. J. Nat. Gas Sci. Eng. 2015, 24, 245–251. [Google Scholar] [CrossRef]
- Sing, K.S.W. Reporting Physisorption Data for Gas/Solid Systems with Special Reference to the Determination of Surface Area and Porosity (Recommendations 1984). Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Brunauer, S.; Deming, L.S.; Deming, W.E.; Teller, E. On a Theory of the van Der Waals Adsorption of Gases. J. Am. Chem. Soc. 1940, 62, 1723–1732. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, Y.; He, X.; Wang, Z.; Jiang, Z.; Yi, M.; Li, W.; Wang, L. Effects of Equilibrium Time and Adsorption Models on the Characterization of Coal Pore Structures Based on Statistical Analysis of Adsorption Equilibrium and Disequilibrium Data. Fuel 2020, 281, 118770. [Google Scholar] [CrossRef]
- Neimark, A.V.; Ravikovitch, P.I.; Grün, M.; Schüth, F.; Unger, K.K. Pore Size Analysis of MCM-41 Type Adsorbents by Means of Nitrogen and Argon Adsorption. J. Colloid Interface Sci. 1998, 207, 159–169. [Google Scholar] [CrossRef]
- Monson, P.A. Understanding Adsorption/Desorption Hysteresis for Fluids in Mesoporous Materials Using Simple Molecular Models and Classical Density Functional Theory. Microporous Mesoporous Mater. 2012, 160, 47–66. [Google Scholar] [CrossRef]
- Li, K.; Liu, Q.; Cheng, H.; Hu, M.; Zhang, S. Classification and Carbon Structural Transformation from Anthracite to Natural Coaly Graphite by XRD, Raman Spectroscopy, and HRTEM. Spectrochim. Acta. A. Mol. Biomol. Spectrosc. 2021, 249, 119286. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Liang, W.; Wei, C.; Wu, D.; Gao, X.; Hu, G. Mineral Composition and Graphitization Structure Characteristics of Contact Thermally Altered Coal. Molecules 2022, 27, 3810. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Li, H.; Lu, J.; Lu, Y.; Shi, S.; Ye, Q.; Li, M.; Wang, Z. An Investigation into the Modification of Microwave-Assisted Oxidation in the Macromolecular Structure of Coal via XRD and Raman Spectroscopy. Fuel 2023, 338, 127192. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Li, W.; Xiang, J.; Wang, Y.; Li, J.; Zeng, F. Molecular Simulation of Methane Adsorption in Shale Based on Grand Canonical Monte Carlo Method and Pore Size Distribution. J. Nat. Gas Sci. Eng. 2016, 30, 119–126. [Google Scholar] [CrossRef]


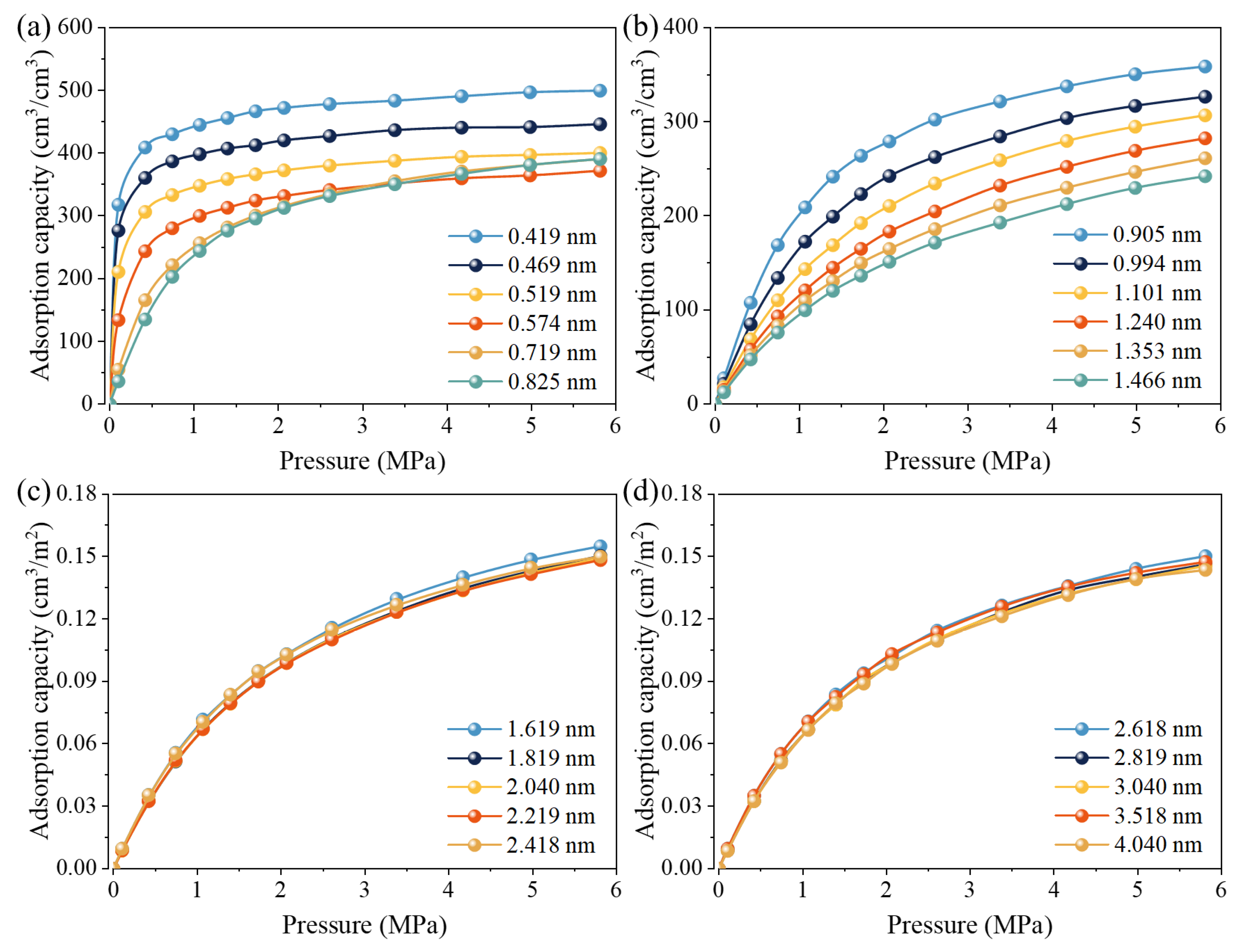

| r (nm) | νmi,r (cm3/cm3) | Kr | nr | R2 | r (nm) | νmo,r (cm3/m2) | PL,r (MPa) | R2 |
|---|---|---|---|---|---|---|---|---|
| 0.419 | 500.7 | 0.019 | 2.044 | 0.9971 | 1.619 | 0.211 | 2.107 | 0.9997 |
| 0.469 | 447 | 0.018 | 2.124 | 0.9977 | 1.819 | 0.209 | 2.275 | 0.9999 |
| 0.519 | 400.2 | 0.018 | 2.281 | 0.998 | 2.04 | 0.207 | 2.252 | 0.9997 |
| 0.574 | 368.4 | 0.026 | 2.366 | 0.9982 | 2.219 | 0.205 | 2.216 | 0.9998 |
| 0.719 | 393.6 | 0.061 | 2.238 | 0.9994 | 2.418 | 0.202 | 1.977 | 0.9998 |
| 0.825 | 396.6 | 0.066 | 2.309 | 0.9997 | 2.618 | 0.201 | 1.989 | 0.9999 |
| 0.905 | 373.3 | 0.088 | 2.182 | 0.9996 | 2.819 | 0.202 | 2.176 | 0.9997 |
| 0.994 | 348.8 | 0.128 | 1.984 | 0.9996 | 3.04 | 0.2 | 2.139 | 0.9997 |
| 1.101 | 339.9 | 0.184 | 1.785 | 0.9997 | 3.518 | 0.198 | 1.933 | 0.9998 |
| 1.24 | 321.1 | 0.23 | 1.665 | 0.9998 | 4.04 | 0.198 | 2.137 | 0.9984 |
| 1.353 | 297.6 | 0.242 | 1.637 | 0.9998 | — | — | — | — |
| 1.466 | 278.5 | 0.255 | 1.607 | 0.9998 | — | — | — | — |
| Sample Number | Sampling Location | Industrial Analysis | |||
|---|---|---|---|---|---|
| Mad (%) | Ad (%) | Vdaf (%) | FCad (%) | ||
| XTR | Xintian coal mine 4 coal seam | 0.84 | 8.33 | 4.96 | 86.39 |
| 11110Y | Pingmei 13th mine 15–17 coal seams | 0.51 | 10.77 | 16.31 | 74.29 |
| QNY | Qinan coal mine 10 coal seam | 0.55 | 7.64 | 33.61 | 60.98 |
| XQY | Qingqing coal mine 7 coal seam | 1.49 | 6.29 | 37.26 | 57.92 |
| Coal Sample Serial Number | Segmental Pore Volume (×10−3 cm3/g) | |||
|---|---|---|---|---|
| XTR | 11110Y | QNY | XQY | |
| 0.38–0.45 | 12.433 | 1.319 | 0.993 | 7.650 |
| 0.45–0.52 | 4.164 | 4.650 | 2.377 | 2.794 |
| 0.52–0.59 | 18.837 | 10.874 | 9.274 | 11.860 |
| 0.59–0.66 | 15.948 | 10.361 | 8.973 | 10.910 |
| 0.66–0.76 | 6.689 | 4.817 | 4.222 | 5.292 |
| 0.76–0.82 | 3.279 | 2.958 | 1.749 | 2.956 |
| 0.82~0.92 | 3.528 | 2.745 | 2.193 | 3.715 |
| 0.92–1.03 | 4.339 | 3.815 | 2.655 | 3.913 |
| 1.03–1.14 | 3.880 | 2.978 | 2.165 | 3.026 |
| 1.14–1.26 | 3.668 | 2.724 | 1.998 | 2.853 |
| 1.26–1.37 | 3.566 | 2.567 | 1.920 | 2.899 |
| 1.37–1.50 | 3.504 | 2.487 | 1.880 | 2.679 |
| >1.50 | 3.717 | 2.692 | 1.994 | 3.102 |
| Pore Size (nm) | DA Adsorption Model | Pore Size (nm) | Langmuir Adsorption Model | |||
|---|---|---|---|---|---|---|
| V0 (cm3/cm3) | K | n | VL (cm3/m2) | PL (MPa) | ||
| 0.415 | 505.110 | 0.019 | 2.038 | 1.619 | 0.211 | 2.107 |
| 0.485 | 432.081 | 0.018 | 2.174 | 1.819 | 0.209 | 2.275 |
| 0.555 | 379.544 | 0.023 | 2.336 | 2.040 | 0.207 | 2.252 |
| 0.625 | 377.234 | 0.038 | 2.321 | 2.219 | 0.205 | 2.216 |
| 0.710 | 392.030 | 0.058 | 2.246 | 2.418 | 0.202 | 1.977 |
| 0.789 | 395.564 | 0.064 | 2.285 | 2.618 | 0.201 | 1.989 |
| 0.868 | 383.998 | 0.078 | 2.240 | 2.819 | 0.202 | 2.176 |
| 0.972 | 354.831 | 0.118 | 2.032 | 3.040 | 0.200 | 2.139 |
| 1.084 | 341.351 | 0.175 | 1.817 | 3.518 | 0.198 | 1.933 |
| 1.198 | 326.751 | 0.216 | 1.701 | 4.040 | 0.198 | 2.137 |
| 1.315 | 305.512 | 0.238 | 1.646 | — | — | — |
| 1.437 | 283.404 | 0.251 | 1.615 | — | — | — |
| 1.500 | 216.615 | 0.242 | 1.634 | — | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Ren, Z.; Li, S.; He, X.; Long, H.; Cheng, L.; Luo, R. The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams. Mathematics 2025, 13, 2931. https://doi.org/10.3390/math13182931
Hu B, Ren Z, Li S, He X, Long H, Cheng L, Luo R. The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams. Mathematics. 2025; 13(18):2931. https://doi.org/10.3390/math13182931
Chicago/Turabian StyleHu, Biao, Zeyu Ren, Shugang Li, Xinxin He, Hang Long, Liang Cheng, and Rongwei Luo. 2025. "The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams" Mathematics 13, no. 18: 2931. https://doi.org/10.3390/math13182931
APA StyleHu, B., Ren, Z., Li, S., He, X., Long, H., Cheng, L., & Luo, R. (2025). The Distribution Characteristics of Adsorbed CH4 in Various-Sized Pore Structures of Coal Seams. Mathematics, 13(18), 2931. https://doi.org/10.3390/math13182931






