2.1. Biometric Template Protection Setting with Homomorphic Encryption
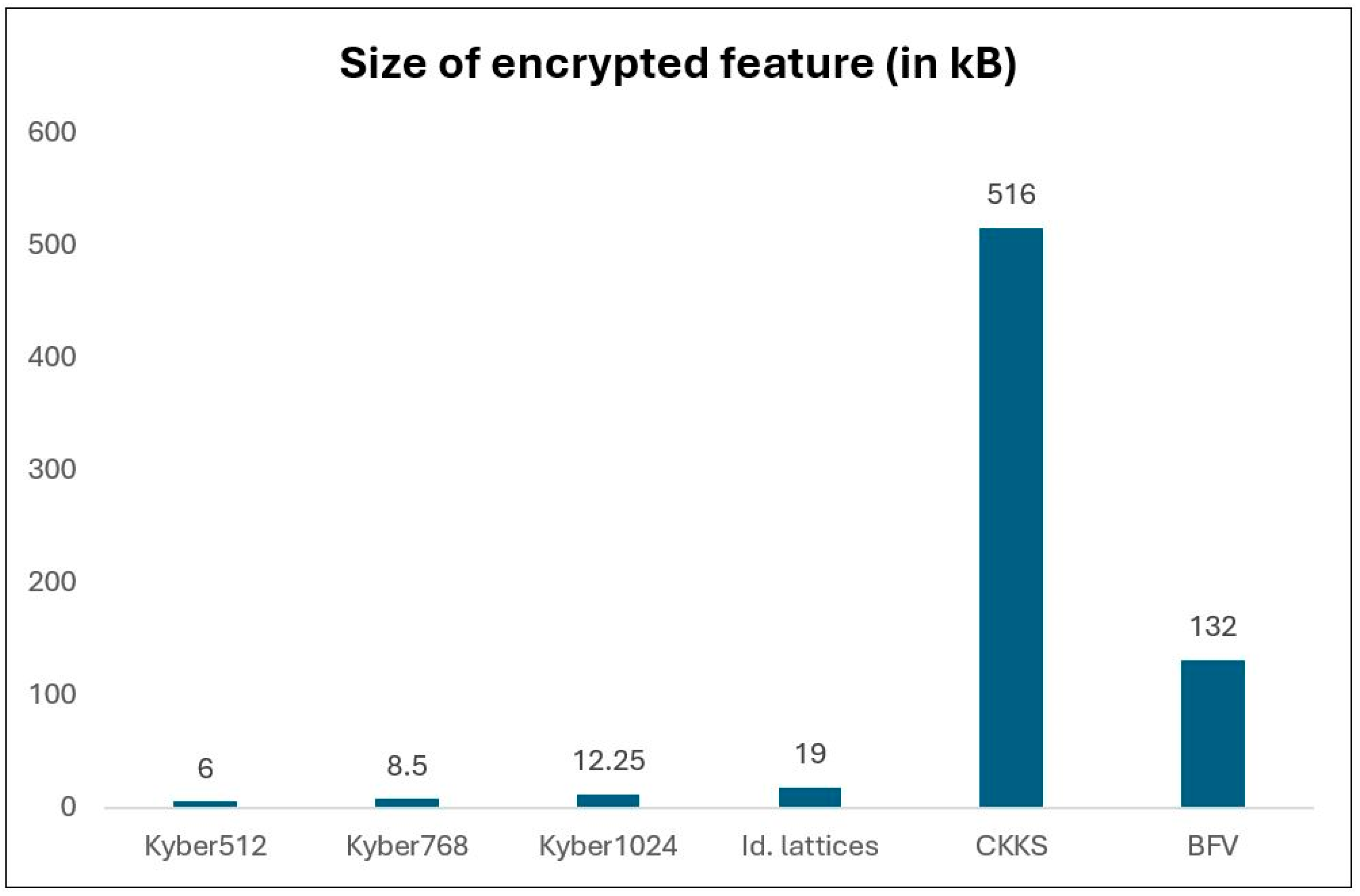
We consider the biometric template protection of features in binary form that are compared using the Hamming distance, i.e., addition modulo 2. An example is the iris features. We use the scheme in [
30,
31] as references of homomorphic encryption-based settings, although they employ non-standardized post-quantum cryptography (among others, CKKS and BFV in the case of [
30], and ideal lattices in the case of [
31]).
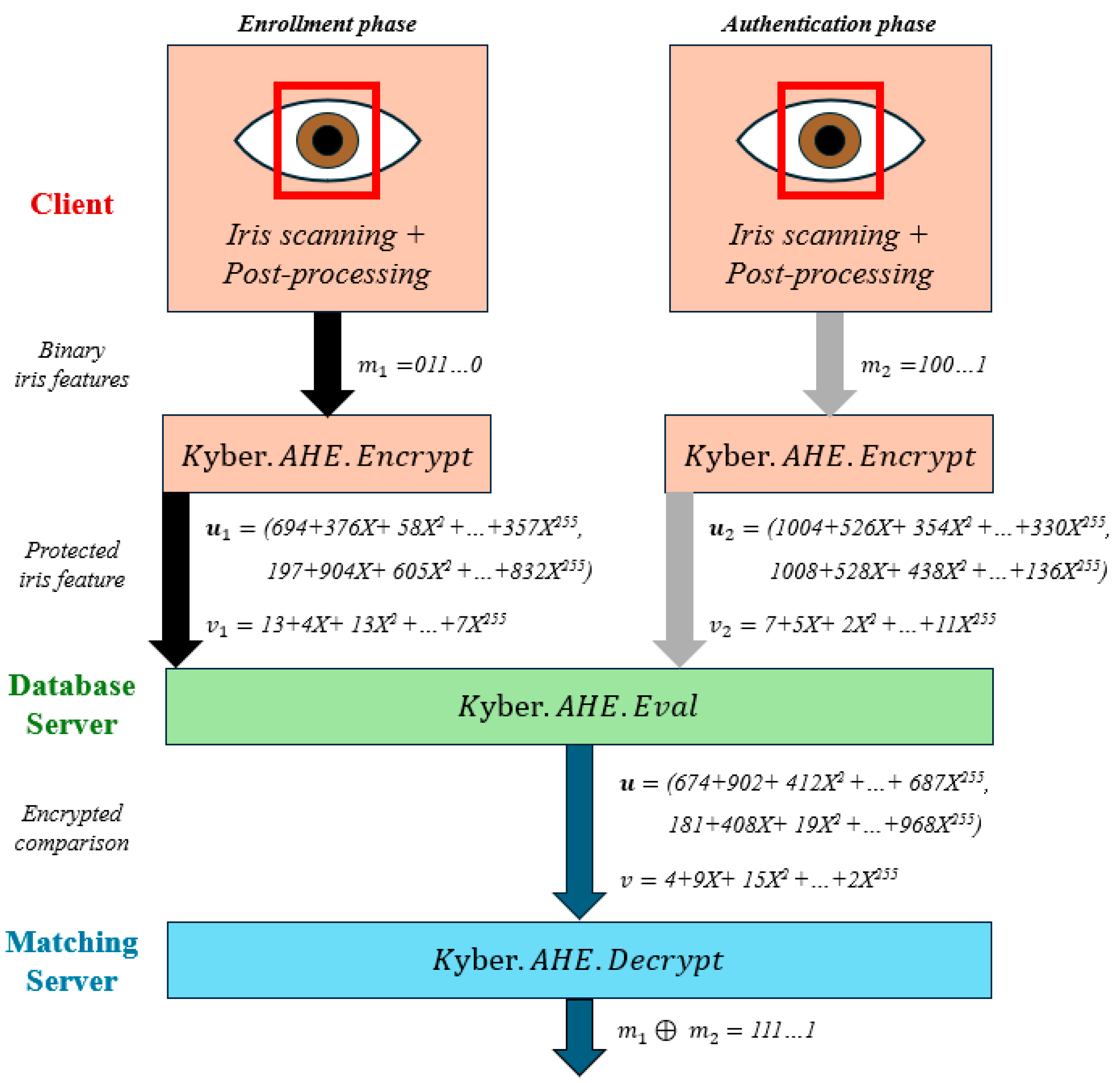
We assume three parties, the Client, the Database Server, and the Matching Server. It is assumed a
passive honest-but-curious model where the servers will not deviate from the defined protocol but will attempt to learn all possible information from legitimately received messages. Also, the servers cannot collude, that is, exchange information outside the protocol. This is often assumed in biometric template protection schemes based on homomorphic encryption [
7,
30]. If the non-collusion assumption is not met, the database server can send the user’s encrypted biometric feature to the matching server. This allows them to know the biometric feature without deviating from the protocol. This could affect the user’s security and privacy in two ways. First, if an attacker gains access to one of the servers and learns the user’s biometric features, s/he can impersonate the user in other applications. This is a major concern since biometric features are linked to individuals and cannot be changed. Second, if the database server knows the biometric feature in clear text, the user can be traced if different enrollments have been performed in more than one matching server. Thus, the user privacy is affected. Of course, if they collaborate, the matching servers could also trace the user.
It is assumed that the communication between the entities is secure. KEMTLS, a quantum-safe upgrade of TLS 1.3, and Kyber KEM can be used to establish secure and authenticated channels [
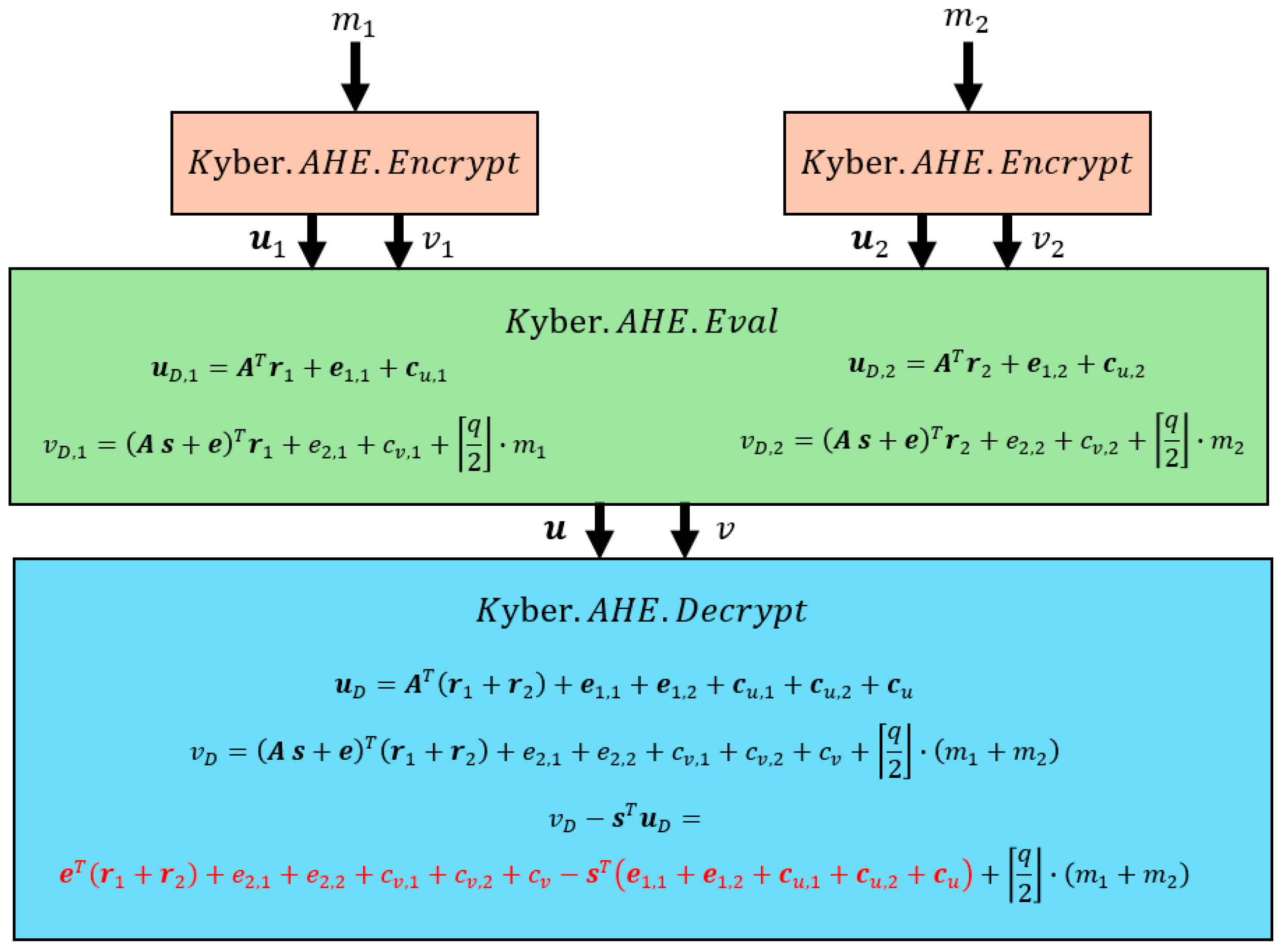
26]. First, in an enrollment phase, a reference biometric template is stored in an encrypted way with Kyber AHE (with the algorithm denoted as Kyber.AHE.Encrypt) in the Database Server. In an authentication phase, shown in
Figure 1, the user sends a fresh biometric query encrypted with Kyber AHE to the Database Server, and the Database Server then runs the Kyber AHE evaluation algorithm (denoted as Kyber.AHE.Eval) on the enrolled ciphertext and the fresh ciphertext. Finally, the resulting ciphertext is sent to the Matching Server and decrypted (with the algorithm denoted as Kyber.AHE.Decrypt) to obtain the Hamming distance between the biometric features. The algorithms of Kyber AHE are detailed in
Section 3.
Note that, with this scheme, the matching server knows more than just the Hamming distance because it knows the XOR between two biometric responses. This is an issue already reported in the literature [
32]. It has been stated that the XOR of an individual’s biometric responses can reveal information about the reliability of those responses and that this information could be used to track the individual. However, several solutions have been proposed that could use the proposed scheme while circumventing this issue. One solution is to use Biohashing and cancellable biometrics to erase the link between the template and the individual [
32]. Promising results have been found for face templates [
33]. Another solution is the use of multi-party computation (MPC) and garbled circuits [
34].
2.2. Applications of Additive Homomorphic Encryption Beyond Biometric Template Protection
Masking against side-channel attacks. Side-channel attacks are a major concern for lattice-based cryptographic schemes, including Kyber [
35]. To address this issue, new masking techniques are being developed to protect specific implementations. One interesting masking scheme for ring-LWE decryption is presented in [
36]. The main idea is that an additive homomorphism in the encryption scheme can introduce randomness into the decryption procedure. Suppose we want to decrypt the ciphertext
, where
is the message that we want to decrypt. First, an internal random message
is generated. Then,
is encrypted using the secret key
to obtain
. Later, the resulting ciphertext
is homomorphically added to
, resulting in
. Finally,
is decrypted to obtain
, which, XOR-ed with
, is used to obtain the message
. The mentioned work applies the idea to the LPR (Lyubashevsky, Peikert, and Regev) encryption scheme.
The aforementioned approach is easy to implement because it does not require a masked decoder. However, the experimental results show that the failure rate is too high, making the solution impractical. For example, it cannot be used with CCA-secure schemes [
37]. In this paper, we demonstrate that the parameters used with Kyber AHE provide low failure probabilities. Thus, this work opens the door to new masking techniques for Kyber PKE or Kyber KEM.
Other schemes that use non-uniform and unreliable secrets. Additive homomorphic encryption can be applied in scenarios where a string that is neither completely uniform nor reliable is used to identify an entity. Device authentication using Physically Unclonable Functions (PUFs) is a good example. PUFs measure the effects of random process variations during the manufacturing of integrated circuits. These variations result in a binary string that can be used as an identifier. Thus, PUF data is similar to biometric data, and the same approach used to compute the XOR of a reference and a fresh response in the encrypted domain can be applied [
38,
39].
2.3. Notation
Rings and vectors. Let denote the ring of integers and denote the ring of integers modulo an integer . and denote the rings and , respectively, where such that is the -th cyclotomic polynomial. Throughout this paper, the values of , , and are 256, 9, and 3329, respectively, as considered in the specifications of CRYSTALS-Kyber. The notation employed is that regular font letters denote elements in or (which includes elements in and ), bold lower-case letters represent vectors with components in or , and bold upper-case letters are matrices. All vectors are column vectors. For a vector (or matrix ), we denote its transpose by (or ).
Modulo reduction. For an even positive integer , we define to be the unique element in the range such that . For an odd positive integer , we define to be the unique element in the range such that . For any positive integer , we define to be the unique element in the range such that . If the exact representation is not important, we will use the expression .
Rounding. For an element we denote by the rounding of to the closest integer with ties being rounded up. As example that will appear in this paper, if is a prime number greater than two, then .
Size of elements and norms. For an element , we write to mean . For a polynomial of degree , we define the norm for as . Similarly, for a vector of polynomials , we define it as .
Sets and distributions. For a set , we write to denote that is chosen uniformly at random from . If is a probability distribution, then this denotes that is chosen according to the distribution .
Let be an extendable output function (XOF), that is, a function on bit strings where the output can be extended to any length. If we want to take as input and then produce a value that is distributed according to a given distribution (or uniformly over a set ), we write .
We define the output of a centered binomial distribution for some positive integer as given the samples .
If is an element of , we write to mean that is generated from a distribution where each of its coefficients is generated according to . Similarly, a -dimensional vector of polynomials can be generated according to the distribution .
Compression and decompression functions. For an element
and two positive integers
and
, with
, the functions
and
are defined as
and
. An important property (demonstrated in Appendix X.C in [
40]) is that if
, then the following is met:
When or is used with (and ), the procedure is applied to each coefficient individually (and each polynomial individually).
2.5. Kyber Public Key Encryption
The Kyber Public Key Encryption (PKE) scheme is defined by a message space and a triple of probabilistic algorithms, which are key generation (), encryption (), and decryption () algorithms. The key generation algorithm returns a pair consisting of a public key and a secret key, respectively. The encryption algorithm takes a public key and a message to produce a ciphertext . Finally, the decryption algorithm takes a secret key and a ciphertext and returns a message .
In the
algorithm, defined as Algorithm 1, two seeds,
and
, are sampled from a uniform random distribution. These seeds are used to sample coefficients from a uniform random distribution for polynomials in the matrix
and from a binomial central distribution (
) for polynomials in
and
, where η is a positive integer. A XOF is used.
is computed as
. Note that the result is not compressed because a problem was found in the security proof for the indistinguishability under chosen plaintext attack (IND-CPA) [
41]. The seed
is also stored with
to form the public key
and
is stored as the secret key
.
| Algorithm 1. |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
The
algorithm, defined as Algorithm 2, takes, as input, a message
, with message space
, and the public key
. Every message
can be viewed as a polynomial in
with coefficients in
. First, a seed
is sampled from a uniform random distribution. Then, the matrix
is retrieved from the seed
as in the
algorithm. The seed
is used for sampling coefficients from a binomial central distribution
for polynomials in
and
and the polynomial
. Then, two parts of the ciphertext are computed, from
and
. The two parts are compressed with
, resulting in
and
. The ciphertext
is formed by
and
.
| Algorithm 2. |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
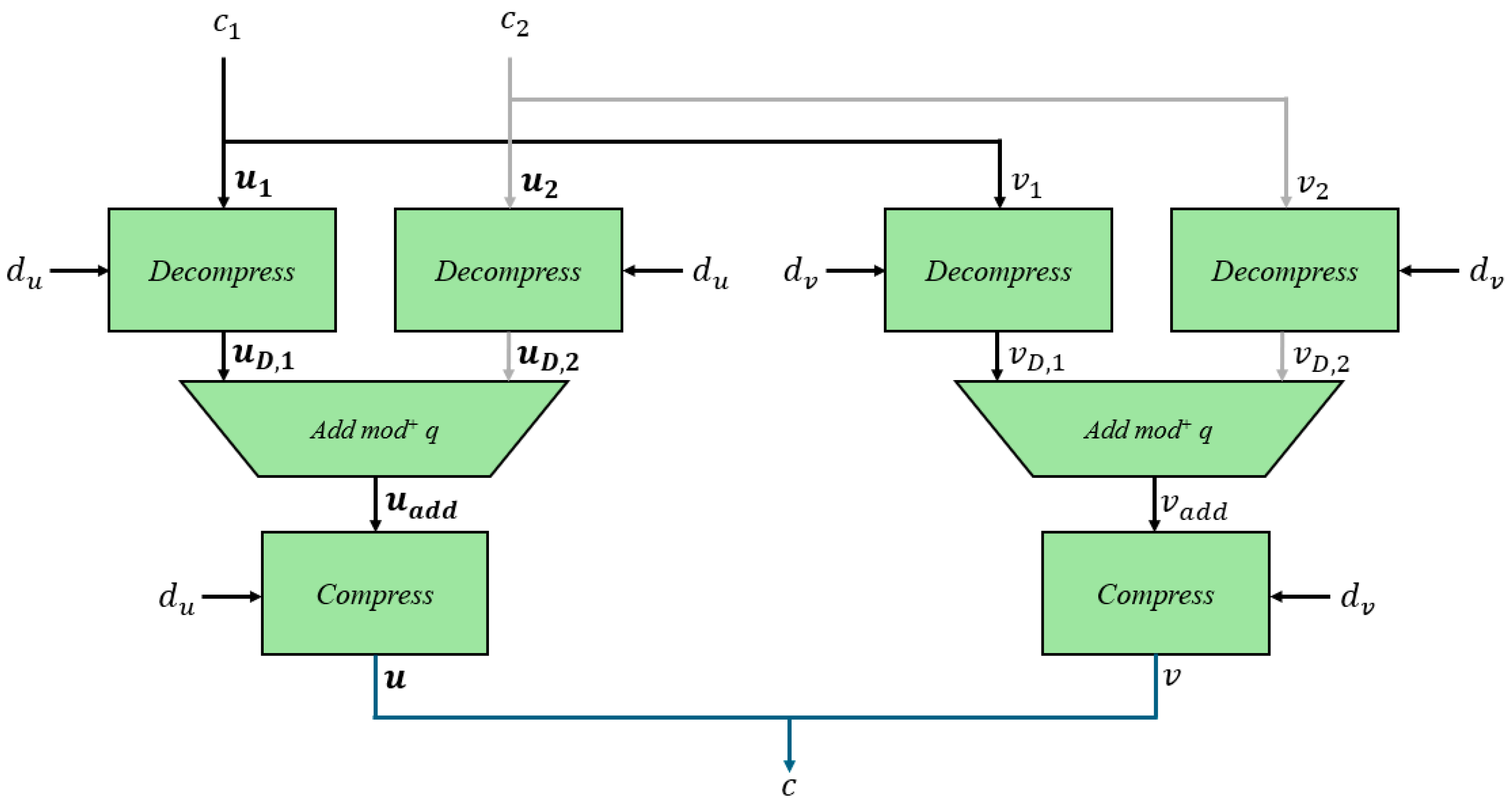
In the
algorithm, defined as Algorithm 3, the ciphertext
and the secret key
are taken as inputs. First, the parts of the ciphertext
and
are decompressed using
, resulting in
and
. Then, the value
is computed. The
function is used to decrypt to a 1 if
is closer to
than to 0 and decrypt it to a 0 otherwise.
| Algorithm 3. |
| 1: |
| 2: |
| 3: |