Prediction of Sulfur Dioxide Emissions in China Using Novel CSLDDBO-Optimized PGM(1, N) Model
Abstract
1. Introduction
- Multiple: linear regression prediction models: Long et al. [1] conducted dimensionality reduction and collinearity analysis on SO2 emission data variables based on the analysis of the sulfur metabolism mechanism in the sintering process. They derived a statistical regression prediction model for SO2 emissions from sintering based on the principle of multiple linear regression. However, this model is sensitive to the linearity assumption of the data, while SO2 emissions from sintering flue gas are influenced by the nonlinear coupling of multiple factors, such as the sulfur contents in raw materials, the air volume, and temperature. Zheng et al. [2] established a regression model for SO2 emissions from coal combustion using multiple linear regression analysis and variance analysis and applied it to predict SO2 emissions from thermal power plants in Shandong Province. This method did not consider the impact of accident slurry ponds in the flue gas desulfurization system and thus failed to effectively prevent environmental pollution.
- Machine learning: In 2018, Xue et al. [3] established a flue gas SO2 emission prediction model based on support vector machines (SVMs) for the nonlinear characteristics of flue gas SO2 objects in circulating fluidized bed boiler control systems. The model parameters were determined using a univariate parameter search combined with grid optimization, overcoming the various shortcomings of previous methods that directly used grid search to determine the parameters of SVM regression models, thereby achieving good prediction results. However, this method requires frequent parameter tuning, resulting in high maintenance costs. When facing circulating fluidized bed systems with strong real-time requirements and high data noise, the model accuracy is easily limited. In 2021, Vitor Miguel Ribeiro [4] used economic-related theories combined with machine learning models to predict SO2 emissions near a thermal power plant in Portugal. According to the final results, the performance of machine learning models is superior to that of traditional methods, but the prediction accuracy of this method will significantly decrease when facing local emission data policy adjustments and monitoring equipment anomalies.
- Statistical models: In 2023, Ghosh and Verma [5] applied an aerosol field and estimated the constrained emissions of SO2 in India based on relevant data. They first constrained the scattering of absorbing aerosols, and they then used this constraint method to obtain the constrained SO2 emissions. They concluded that the annual emission rate of SO2 in the Indian restricted-emission database was lower than the emission rate reported by China. However, if this method underestimates hotspot pollution sources or overestimates emission reduction effects, it may exacerbate the environmental governance risks in the Indian region. Fu et al. [6] used the LEAP model and emission factor method to predict the SO2 emissions in some eastern regions of China and studied future emission trends. However, this method did not consider the transmission of pollutants between urban agglomerations and the drastic changes in energy structures caused by industrial upgrading in the eastern region, which made it difficult for traditional linear prediction models to capture the dynamic impact of emerging high-energy-consuming industries.
- The gray prediction model selected in this article has carried out the differential definition and optimization of the order of variables, solving the disadvantage of different variables with the same order in the gray model, and combining the idea of parameter combination optimization to enhance the modeling capabilities of gray models.
- An improved Dung Beetle Optimization (CSLDDBO) algorithm is proposed, which introduces three strategies and the idea of differential evolution to enhance the performance of the original algorithm. The effectiveness of this algorithm was verified by testing it on the CEC2022 test set.
- To predict SO2 emissions, a PGM(1, N) model optimized with CSLDDBO parameters was used for predicting SO2 emissions in China.
2. PGM(1, N)
2.1. Related Concepts
2.1.1. The Order of Gray Generative Operators
2.1.2. Smooth Generation Operator
2.2. Model Definition and Parameter Estimation
- If and , then ;
- If and , then ;
- If and , then .
2.3. Solution of the Model
3. Overview of Dung Beetle Optimization Algorithms
3.1. Ball-Rolling Dung Beetles
3.2. Producing Dung Beetles
3.3. Larvae
3.4. Thief Dung Beetle
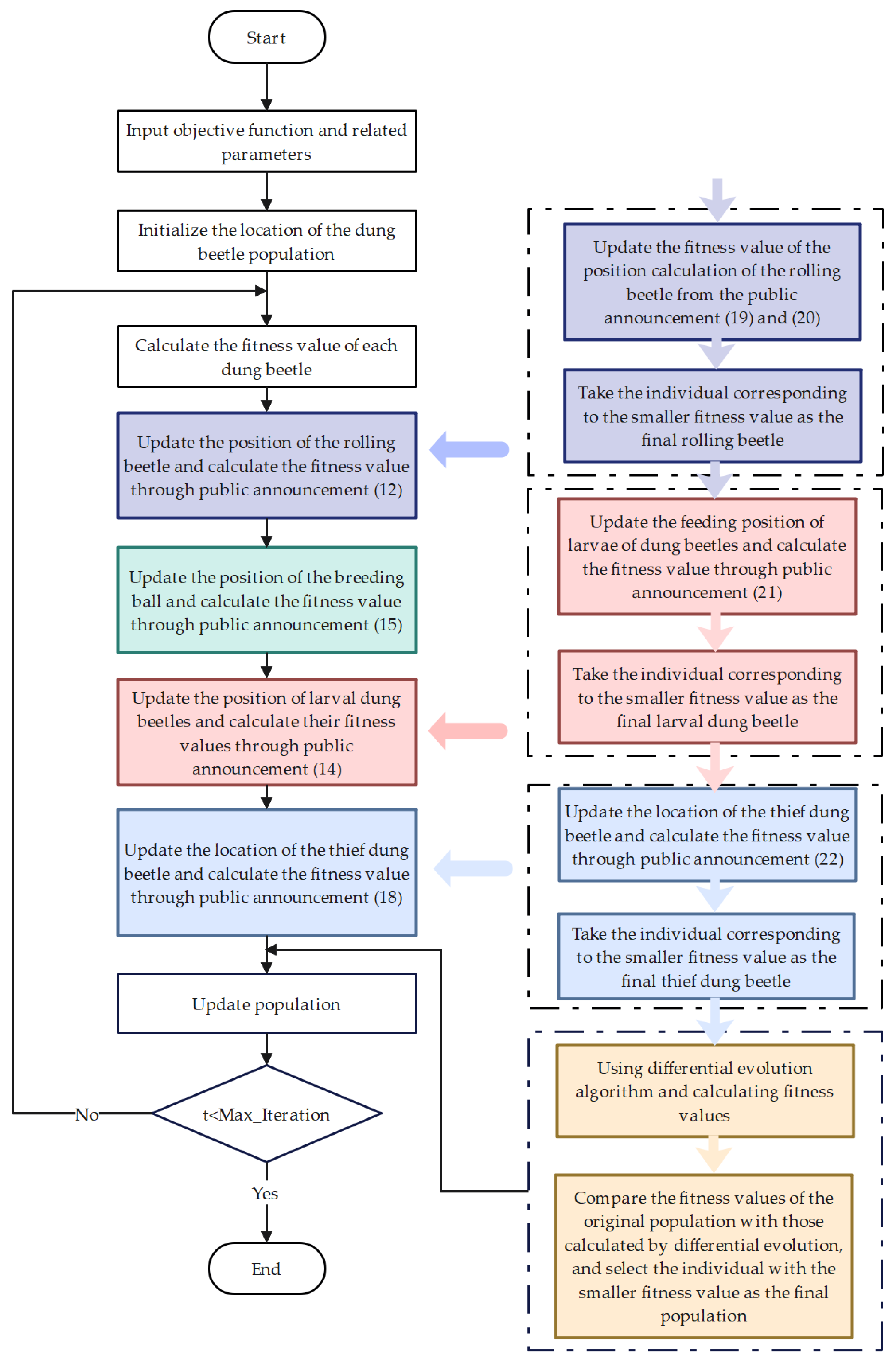
4. CSLDDBO Algorithm
4.1. Chain Foraging Strategy
4.2. Somersault Foraging Strategy
4.3. Learning Strategy
4.4. Differential Evolution
- 1.
- Initial population
- 2.
- Mutation
- 3.
- Cross operation
- 4.
- Select action
| Algorithm 1: Pseudocode for CSLDDBO algorithm |
  |
4.5. Time Complexity
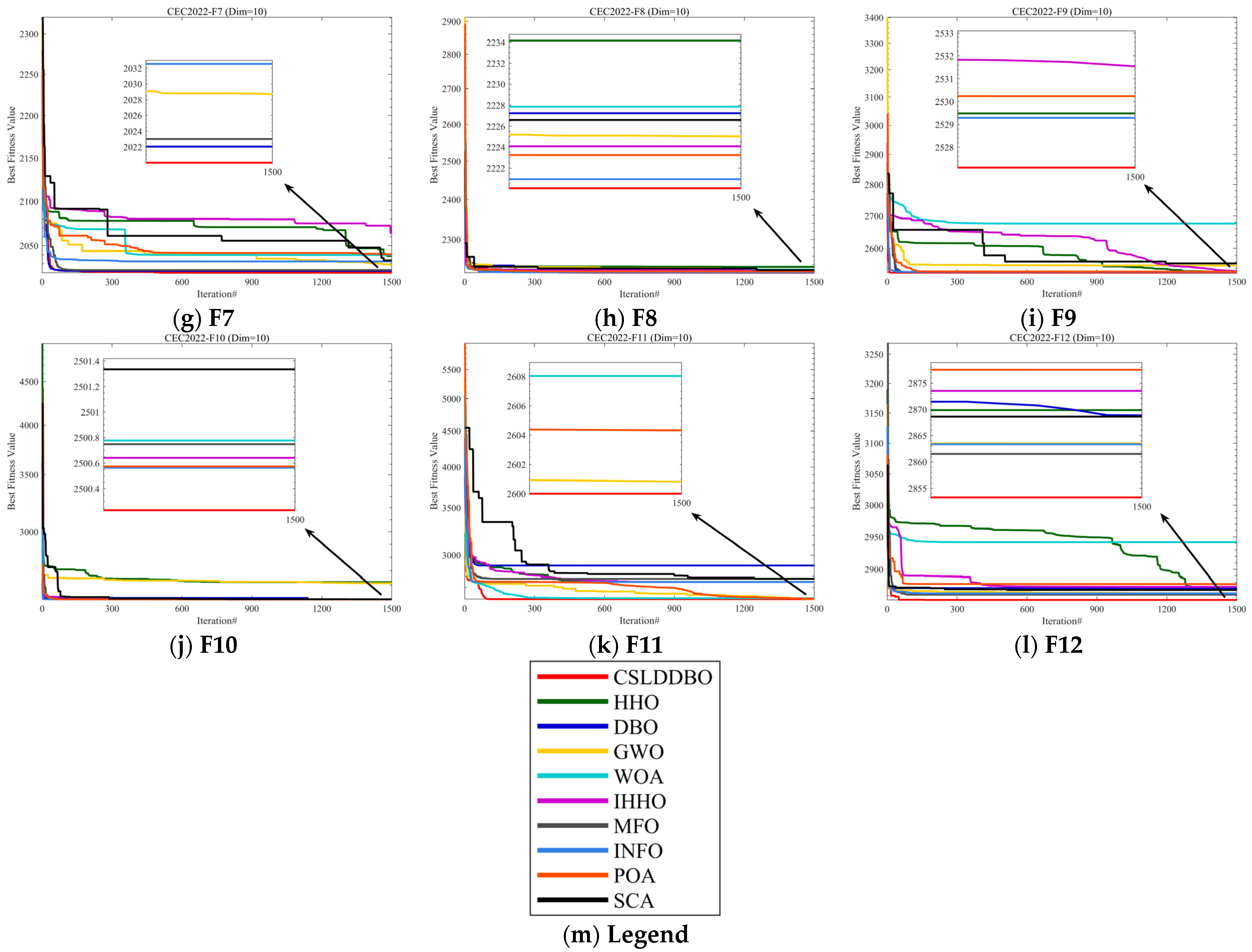
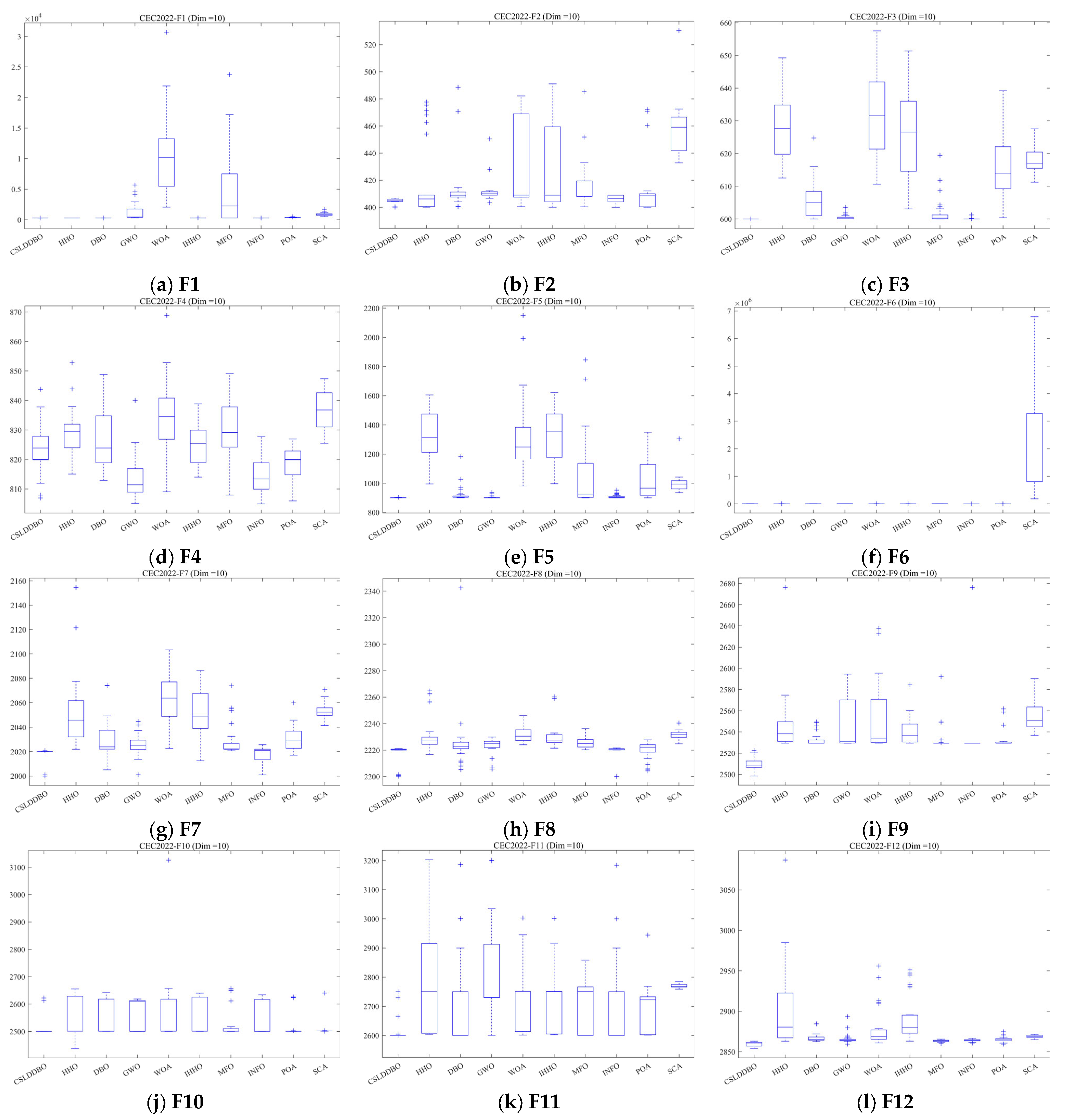
5. Numerical Experiment and Discussion
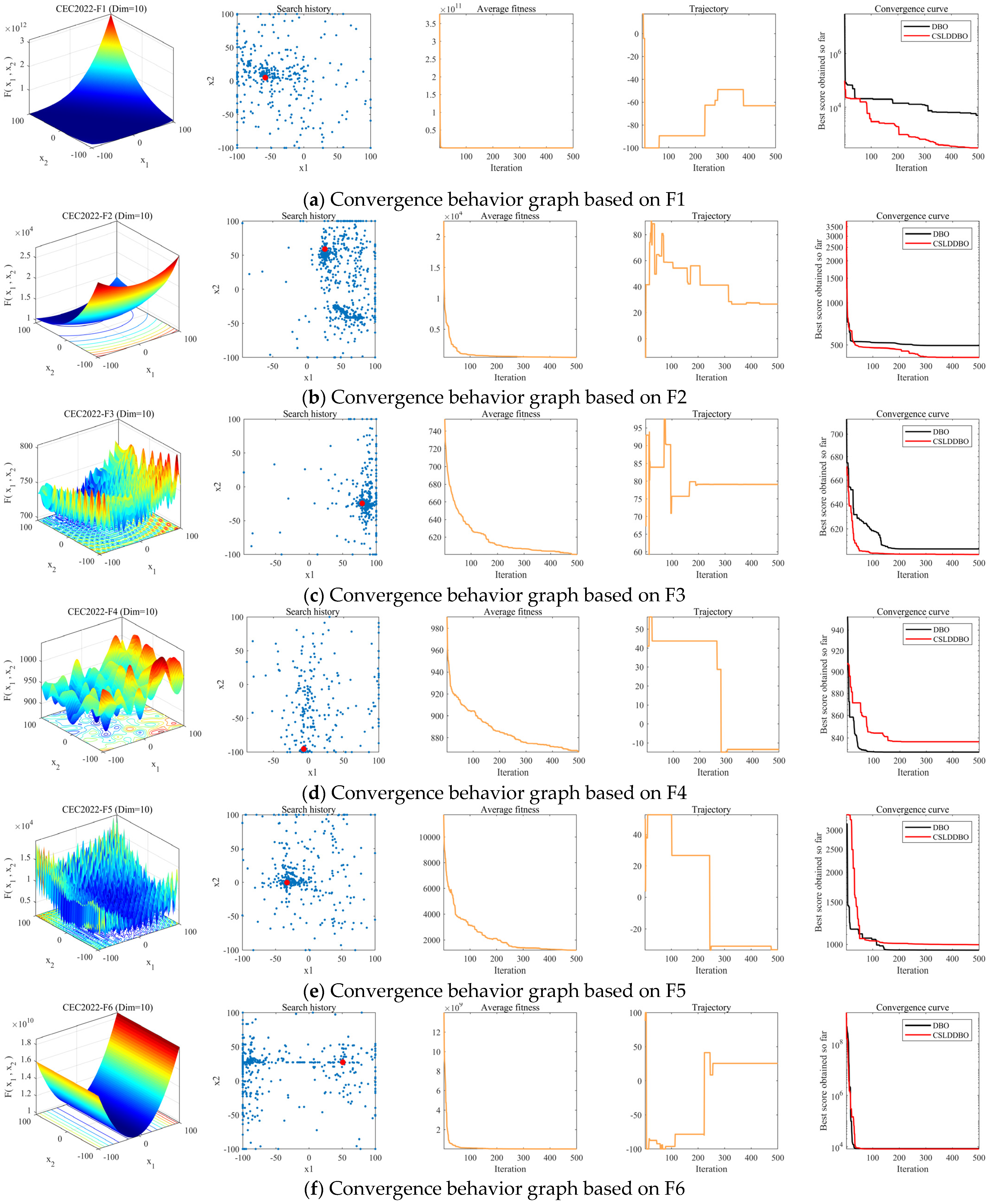
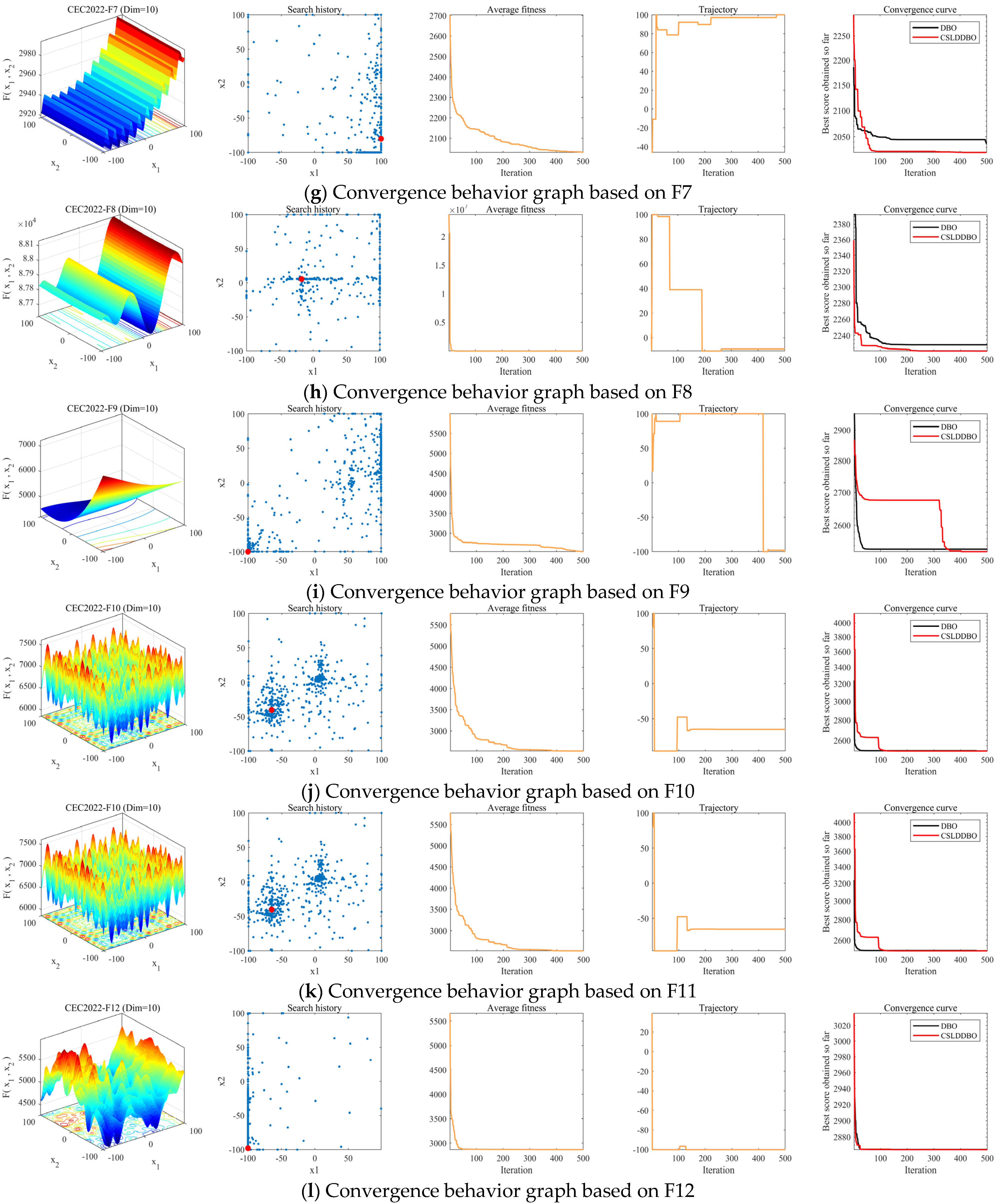
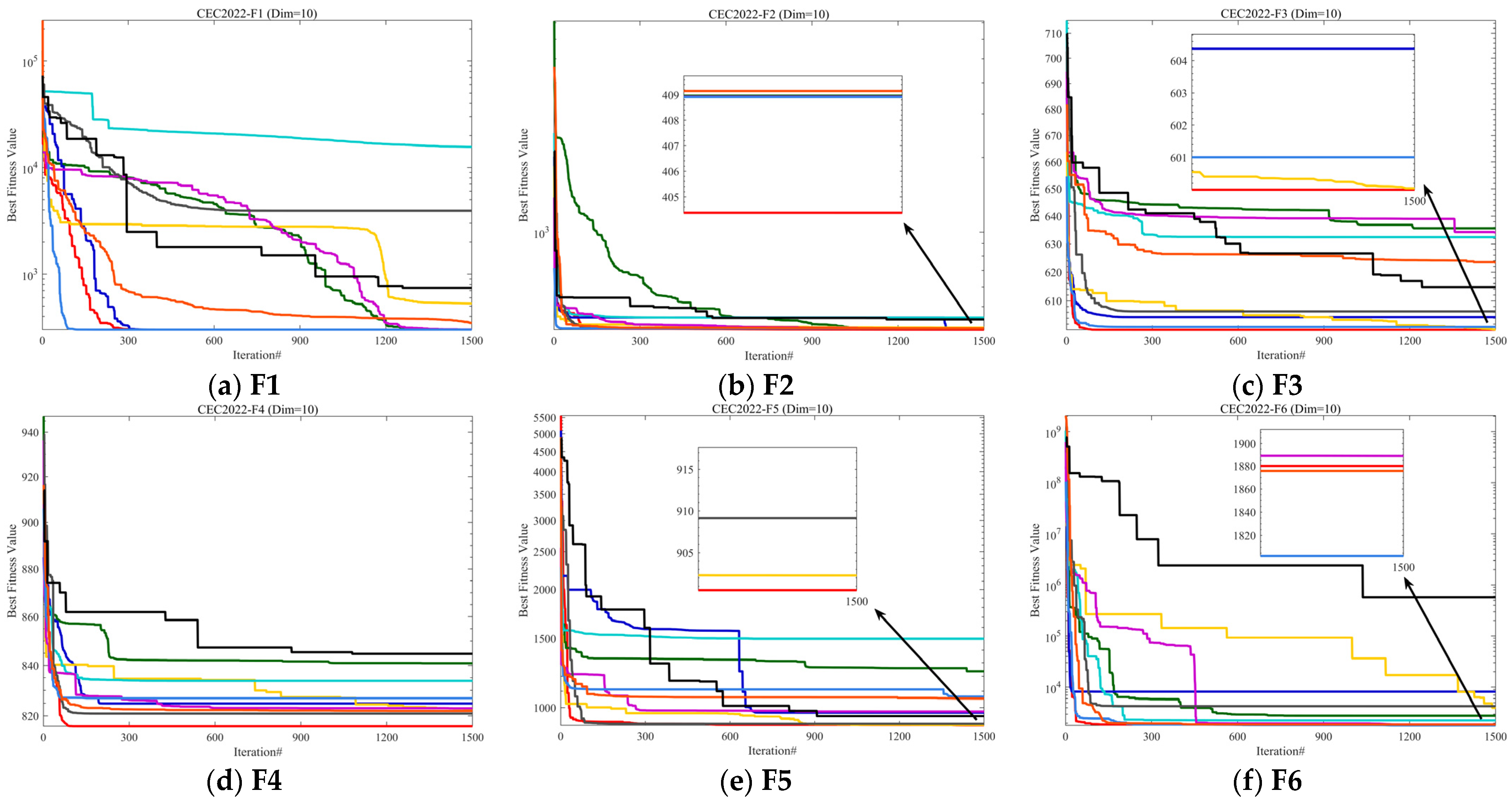
5.1. Convergence Behavior Analysis
- Search History
- 2.
- Average fitness
- 3.
- Search trajectory
- 4.
- Convergence curve
5.2. Sensitivity of Parameters
5.3. Experimental Results
6. Prediction of SO2 Emissions in China
6.1. Preparation of SO2 Emission Data
6.1.1. Data Sources and Preprocessing
- The sample proportion meets industrial standards
- 2.
- Completeness of feature space coverage
- 3.
- Error stability and industrial benchmarking
- 4.
- Robustness verification with small samples
6.1.2. Data Analysis
6.2. Establishment of SO2 Emission Model
6.2.1. Data Classification
- Data from 2012 to 2018 were used as the training data.
- Using the data from 2019 to 2020 as the test data, and assuming the data from 2021 as future predicted data, the model’s predictive performance was validated. The specific data were as follows:
6.2.2. Parameter Estimation and Model Construction
6.2.3. Error Solving and Performance Evaluation
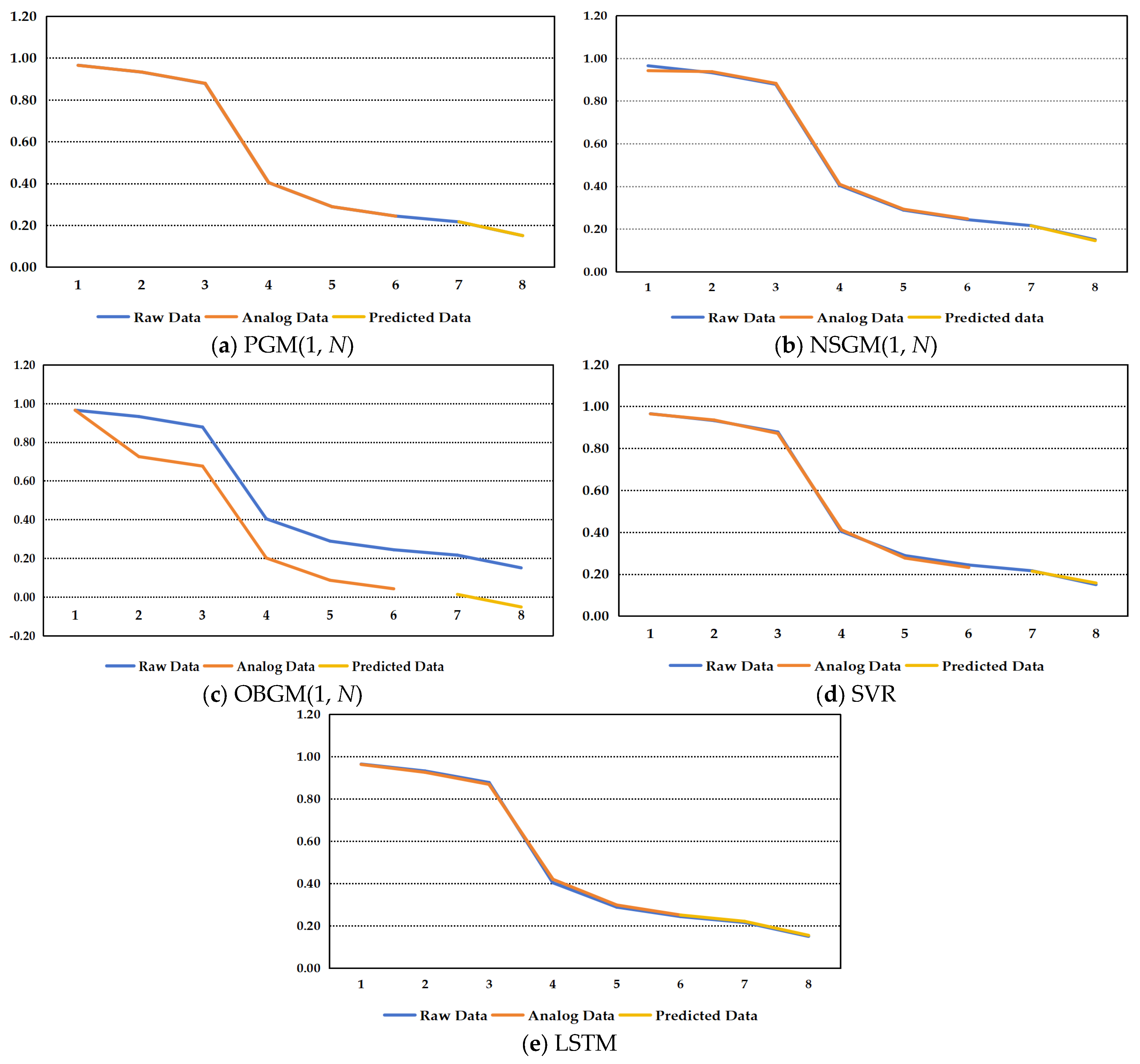
- Analyzing the simulation process in Figure 7, the simulated values of PGM(1, N) are closest to the original values. NSGM(1, N) illustrates a trend where the simulated values are extremely close to the original values, but there may still be differences locally. The simulated values of OBGM(1, N) have a similar trend but a significantly different trend from the original values. And PGM(1, N) shows the predicted value closest to the original value.
- Figure 8 shows that the three error indicators of the PGM(1, N) model are the smallest and have the highest accuracy level at level 1.
6.3. Prediction of Future SO2 Emissions
- Increase the development of the desulfurization industry and improve innovation in desulfurization technology. Encourage the invention of SO2 desulfurization technology, combine traditional flue gas desulfurization with emerging desulfurization technologies, improve the desulfurization efficiency, and reduce desulfurization energy consumption. For example, using catalytic reduction technology to convert waste into valuable solid sulfur or elemental sulfur can reduce SO2 pollution due to its sustainability, space requirements, and low water consumption.
- Strengthen monitoring of the coal-fired industry and control coal use. Set restrictions on the mining of industrial coal in various regions, upgrade the equipment and technology of coal-fired plants, encourage the research and development of coal gasification gas combined with other new energy power generation technologies, and allow the emissions of SO2 and sulfur in industrial emissions only after reaching the standard.
- Promote social policy guidance and improve SO2 control policies. Adjust the current electricity price mechanism, improve various social systems, increase the treatment and emission reduction fees for SO2, and allocate the pollution discharge fees to the environmental treatment of SO2.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LOO-CV | Leave-One-Out Cross-Validation |
Appendix A
GM(1, N)
- 1.
- The solution of the whitening equation (Equation (A7)) is as follows:
- 2.
- When the change in is ignored without timing, is taken as the gray constant. The time response expression is as follows:
- 3.
- The differential simulation formula for the GM(1, N) model is as follows:
References
- Gong, Y.F. Establishment and validation of a linear regression prediction model for SO2 emissions from sintering flue gas. Angang Technol. 2017, 3, 32–38. [Google Scholar]
- Zheng, Y.L.; Li, F.L. Regression Calculation Model for Sulfur Dioxide Emissions from Coal Combustion. Energy Environ. Prot. 2009, 23, 47–50. [Google Scholar]
- Xue, M.S.; Wang, X.; Ji, R.Y. A Predictive Model for Sulfur Dioxide Emissions from Flue Gas Based on Support Vector Machine. Comput. Syst. Appl. 2018, 27, 186–191. [Google Scholar]
- Ribeiro, V.M. Sulfur dioxide emissions in Portugal: Prediction, estimation and air quality regulation using machine learning. J. Clean. Prod. 2021, 317, 128358. [Google Scholar] [CrossRef]
- Ghosh, S.; Verma, S. Estimates of spatially and temporally resolved constrained organic matter and sulfur dioxide emissions over the Indian region through the strategic source constraints modelling. Atmos. Res. 2023, 282, 106504. [Google Scholar] [CrossRef]
- Fu, L.X.; Hao, J.M.; Zhou, X.L. Prediction of Energy Consumption and SO2 Emission Trends in Eastern China. China Environ. Sci. 1997, 4, 62–65. [Google Scholar]
- Deng, J.L. The Control problem of grey systems. Syst. Control Letter. 1982, 1, 288–294. [Google Scholar]
- Deng, J.L. Fundamentals of Grey Theory; Huazhong University of Science and Technology Press: Wuhan, China, 2022. [Google Scholar]
- Deng, J.L. Grey control system. J. Huazhong Inst. Technol. 1982, 3, 9–18. [Google Scholar]
- Li, S.Z.; Chen, Y.Z.; Dong, R. A novel optimized grey model with quadratic polynomials term and its application. Chaos Solitons Fractals X 2022, 8, 100074. [Google Scholar] [CrossRef]
- He, X.B.; Wang, Y.; Zhang, Y.Y.; Ma, X.; Wu, W.Q.; Zhang, L. A novel structure adaptive new information priority discrete grey prediction model and its application in renewable energy generation forecasting. Appl. Energy 2022, 325, 119854. [Google Scholar] [CrossRef]
- Wang, Z.X.; Jv, Y.Q. A novel grey prediction model based on quantile regression. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105617. [Google Scholar] [CrossRef]
- Zeng, B.; Zhou, M.; Liu, X.Z.; Zhang, Z.W. Application of a new grey prediction model and grey average weakening buffer operator to forecast China’s shale gas output. Energy Rep. 2020, 6, 1608–1618. [Google Scholar] [CrossRef]
- Duan, H.M.; Pang, X.Y. A multivariate grey prediction model based on energy logistic equation and its application in energy prediction in China. Energy 2021, 229, 120716. [Google Scholar] [CrossRef]
- Duan, H.M.; Luo, X.L. A novel multivariable grey prediction model and its application in forecasting coal consumption. ISA Trans. 2022, 120, 110–127. [Google Scholar] [CrossRef]
- Ye, J.; Li, Y.; Ma, Z.Z.; Xiong, P.P. Novel weight-adaptive fusion grey prediction model based on interval sequences and its applications. Appl. Math. Model. 2023, 115, 803–818. [Google Scholar] [CrossRef]
- Yin, F.F.; Bo, Z.; Yu, L.; Wang, J.Z. Prediction of carbon dioxide emissions in China using a novel grey model with multi-parameter combination optimization. J. Clean. Prod. 2023, 404, 136889. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar] [CrossRef]
- Han, H.G.; Lu, W.; Hou, Y.; Qiao, J.F. An adaptive-PSO-based self-organizing RBF neural network. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 104–117. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Hu, G.; Cheng, M.; Houssein, E.H.; Hussien, A.G.; Abualigah, L. SDO: A novel sled dog-inspired optimizer for solving engineering problems. Adv. Eng. Inform. 2024, 62, 102783. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Li, S.M.; Chen, H.L.; Wang, M.J.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Jafari, M.; Salajegheh, E.; Salajegheh, J. Elephant clan optimization: A nature-inspired metaheuristic algorithm for the optimal design of structures. Appl. Soft Comput. 2021, 113, 107892. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X.F.; Wei, G. An enhanced black widow optimization algorithm for feature selection. Knowl.-Based Syst. 2022, 235, 107638. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.Y.; Wei, G. SaCHBA_PDN: Modified honey badger algorithm with multi-strategy for UAV path planning. Expert Syst. Appl. 2023, 223, 119941. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Wei, G.; Chang, C.T. DTCSMO: An efficient hybrid starling murmuration optimizer for engineering applications. Comput. Methods Appl. Mech. Engrg. 2023, 405, 115878. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J.; Li, M.; Hussien, A.G.; Abbas, M. EJS: Multi-strategy enhanced jellyfish search algorithm for engineering applications. Mathematics 2023, 11, 851. [Google Scholar] [CrossRef]
- Hu, G.; Gong, C.S.; Li, X.X.; Xu, Z.Q. CGKOA: An enhanced Kepler optimization algorithm for multi-domain optimization problems. Comput. Methods Appl. Mech. Eng. 2024, 425, 116964. [Google Scholar] [CrossRef]
- Hu, G.; Song, K.K.; Abdel, S.M. Sub-population evolutionary particle swarm optimization with dynamic fitness-distance balance and elite reverse learning for engineering design problems. Adv. Eng. Softw. 2025, 202, 103866. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Dacke, M.; Baird, E.; El, J.B.; Warrant, E.J.; Byrne, M. How dung beetles steer straight. Annu. Rev. Entomol. 2021, 66, 243–256. [Google Scholar] [CrossRef] [PubMed]
- Byrne, M.; Dacke, M.; Nordström, P.; Scholtz, C.; Warrant, E. Visual cues used by ball-rolling dung beetles for orientation. J. Comp. Physiol. A 2003, 189, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Dacke, M.; Nilsson, D.E.; Scholtz, C.H.; Byrne, M.; Warrant, E.J. Insect orientation to polarized moonlight. Nature 2003, 424, 33. [Google Scholar] [CrossRef]
- Zeng, B.; Li, S.L.; Meng, W. Grey Prediction Theory and Its Applications; Science Press: Beijing, China, 2020; pp. 89–146. [Google Scholar]
- Meng, W.; Zeng, B. Research on Fractional Order Operators and Grey Prediction Model; Science Press: Beijing, China, 2015; pp. 18–78. [Google Scholar]
- Li, H.; Zeng, B.; Zhou, W. Forecasting domestic waste clearing and transporting volume by employing a new grey parameter combination optimization model. Chin. J. Manag. Sci. 2022, 30, 96–107. [Google Scholar] [CrossRef]
- Zhao, W.G.; Zhang, Z.X.; Wang, L.Y. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.J.; Li, A.L. Harris Hawk Optimization Algorithm Integrating Normal Cloud and Dynamic Disturbance. Mini-Micro Syst. 2022, 44, 1–11. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S. INFO: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Liu, S.F. Grey System Theory and Its Application; Science Press: Beijing, China, 2021; pp. 35–78. [Google Scholar]
- Chen, D.L.; Wang, X.Z.; Wang, C.C. Analysis and prediction of mechanical properties of RTSF/PVA slag concrete after high temperature based on NSGM (1, N) model. J. Disaster Prev. Mitig. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Zhang, S.L.; Yao, Q. Measurement and Prediction of Time Series of SF6 Decomposition Products in High Voltage Composite Electrical Appliances by Combining NDIR Technology and Grey System OBGM (1, N) Model. Power Grid Technol. 2020, 44, 2770–2777. [Google Scholar] [CrossRef]


| Models | Methods | Authors |
|---|---|---|
| Equal-dimension gray number complementary model GM(1,1) | Predicting SO2 emissions using an equidimensional gray number replenishment model | Jie Tan et al. |
| GM(1,1) models with different dimensions | Using gray models with different dimensions to predict SO2 emissions in Wuhan city | Haijun Huang et al. |
| GM(1,1,u(t)) | Predicting air quality in Shanghai using gray extended model | Pingping Xiong et al. |
| FGM(1,1) | Predicting SO2 emissions in three provinces of China using the fractional-order accumulative gray model | Lifeng Wu et al. |
| NLDGM(1,1r, t) | Predicting SO2 emissions in the power industry using a nonlinear gray direct model | Yuelin Xiang |
| GNNM(1,1) | Predicting the emissions of air pollutants such as SO2 using a gray neural network model | Wenqiang Bai |
| GIFM | Predicting the concentration and emissions of SO2 in a capital city using a gray interval forecast model | Bo Zeng |
| F | Index | |||||
|---|---|---|---|---|---|---|
| F1 | Mean | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 |
| Std. | 2.5856 × 10−14 | 2.9856 × 10−14 | 2.7927 × 10−14 | 2.3603 × 10 | 2.9856 × 10−14 | |
| Rank | 2 | 4 | 3 | 1 | 5 | |
| F2 | Mean | 4.0565 × 102 | 4.0488 × 102 | 4.0494 × 102 | 4.0510 × 102 | 4.0491 × 102 |
| Std. | 6.5041 × 10−1 | 1.4507 × 100 | 1.8062 × 100 | 1.2583 × 100 | 1.3784 × 100 | |
| Rank | 5 | 2 | 4 | 3 | 1 | |
| F3 | Mean | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 |
| Std. | 1.2253 × 10−3 | 1.0804 × 10−3 | 5.8368 × 10−3 | 1.2469 × 10−3 | 1.4698 × 10−3 | |
| Rank | 4 | 2 | 3 | 1 | 5 | |
| F4 | Mean | 8.2733 × 102 | 8.2893 × 102 | 8.2406 × 102 | 8.2415 × 102 | 8.2241 × 102 |
| Std. | 1.0922 × 101 | 9.8191 × 100 | 9.0324 × 100 | 8.6112 × 100 | 8.6088 × 100 | |
| Rank | 3 | 5 | 4 | 2 | 1 | |
| F5 | Mean | 9.0159 × 102 | 9.0335 × 102 | 9.0798 × 102 | 9.0528 × 102 | 9.0428 × 102 |
| Std. | 1.1590 × 100 | 4.3363 × 100 | 1.2568 × 101 | 7.6271 × 100 | 6.6092 × 100 | |
| Rank | 2 | 4 | 5 | 3 | 1 | |
| F6 | Mean | 5.1886 × 103 | 5.3654 × 103 | 4.7569 × 103 | 4.8279 × 103 | 4.7332 × 103 |
| Std. | 2.0818 × 103 | 2.3782 × 103 | 2.3555 × 103 | 2.3019 × 103 | 2.1325 × 103 | |
| Rank | 4 | 5 | 2 | 1 | 3 | |
| F7 | Mean | 2.0174 × 103 | 2.0173 × 103 | 2.0156 × 103 | 2.0163 × 103 | 2.0181 × 103 |
| Std. | 6.8560 × 100 | 6.7762 × 100 | 8.2303 × 100 | 7.6728 × 100 | 6.0097 × 100 | |
| Rank | 3 | 2 | 4 | 1 | 5 | |
| F8 | Mean | 2.2187 × 103 | 2.2184 × 103 | 2.2166 × 103 | 2.2163 × 103 | 2.2192 × 103 |
| Std. | 6.0069 × 100 | 6.4178 × 100 | 8.1253 × 100 | 7.8750 × 100 | 5.0877 × 100 | |
| Rank | 3 | 5 | 2 | 1 | 4 | |
| F9 | Mean | 2.5024 × 103 | 2.5025 × 103 | 2.5005 × 103 | 2.5025 × 103 | 2.5019 × 103 |
| Std. | 5.8785 × 100 | 6.3623 × 100 | 4.7273 × 100 | 5.5257 × 100 | 4.5194 × 100 | |
| Rank | 3 | 2 | 1 | 5 | 4 | |
| F10 | Mean | 2.5016 × 103 | 2.5048 × 103 | 2.5004 × 103 | 2.5040 × 103 | 2.5004 × 103 |
| Std. | 2.8183 × 101 | 3.5398 × 101 | 9.5712 × 10−2 | 1.9961 × 101 | 1.6101 × 10−1 | |
| Rank | 5 | 3 | 4 | 2 | 1 | |
| F11 | Mean | 2.6270 × 103 | 2.6212 × 103 | 2.6492 × 103 | 2.6354 × 103 | 2.6427 × 103 |
| Std. | 5.6483 × 101 | 4.6717 × 101 | 6.6460 × 101 | 6.0552 × 101 | 5.6935 × 101 | |
| Rank | 2 | 1 | 4 | 3 | 5 | |
| F12 | Mean | 2.8542 × 103 | 2.8547 × 103 | 2.8554 × 103 | 2.8545 × 103 | 2.8558 × 103 |
| Std. | 1.9441 × 100 | 1.8005 × 100 | 2.4041 × 100 | 2.6550 × 100 | 2.6017 × 100 | |
| Rank | 1 | 3 | 4 | 2 | 5 | |
| Mean Rank | 3.08 | 3.17 | 3.33 | 2.08 | 3.33 | |
| Result | 2 | 3 | 4 | 1 | 4 | |
| F | Index | ||||||
|---|---|---|---|---|---|---|---|
| F1 | Mean | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0000 × 102 |
| Std. | 2.7927 × 10−14 | 3.5009 × 10−14 | 3.1667 × 10−14 | 3.1667 × 10−14 | 2.5856 × 10−14 | 2.3603 × 10−14 | |
| Rank | 3 | 6 | 4 | 5 | 2 | 1 | |
| F2 | Mean | 4.0547 × 102 | 4.0515 × 102 | 4.0495 × 102 | 4.0488 × 102 | 4.0553 × 102 | 4.0513 × 102 |
| Std. | 1.2084 × 100 | 1.7468 × 100 | 1.0827 × 100 | 1.4707 × 100 | 1.5629 × 100 | 1.1028 × 100 | |
| Rank | 4 | 5 | 2 | 1 | 6 | 3 | |
| F3 | Mean | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 | 6.0000 × 102 |
| Std. | 3.3057 × 10−4 | 3.2125 × 10−3 | 7.9021 × 10−4 | 7.8667 × 10−4 | 6.6565 × 10−3 | 2.2567 × 10−3 | |
| Rank | 1 | 4 | 3 | 2 | 6 | 5 | |
| F4 | Mean | 8.2569 × 102 | 8.2238 × 102 | 8.2512 × 102 | 8.2345 × 102 | 8.2410 × 102 | 8.2589 × 102 |
| Std. | 7.9754 × 100 | 8.2391 × 100 | 1.0405 × 101 | 1.0276 × 101 | 9.2398 × 100 | 9.9054 × 100 | |
| Rank | 5 | 2 | 4 | 3 | 1 | 6 | |
| F5 | Mean | 9.0197 × 102 | 9.0689 × 102 | 9.0596 × 102 | 9.0184 × 102 | 9.0112 × 102 | 9.0309 × 102 |
| Std. | 3.4169 × 100 | 1.5632 × 101 | 8.5332 × 100 | 2.4193 × 100 | 1.2816 × 100 | 5.7967 × 100 | |
| Rank | 3 | 6 | 5 | 1 | 2 | 4 | |
| F6 | Mean | 4.5076 × 103 | 4.4476 × 103 | 4.2687 × 103 | 4.1147 × 103 | 4.0999 × 103 | 4.3517 × 103 |
| Std. | 2.2630 × 103 | 2.0903 × 103 | 2.0140 × 103 | 2.0094 × 103 | 2.0058 × 103 | 2.1164 × 103 | |
| Rank | 6 | 4 | 5 | 1 | 2 | 3 | |
| F7 | Mean | 2.0130 × 103 | 2.0176 × 103 | 2.0185 × 103 | 2.0163 × 103 | 2.0171 × 103 | 2.0163 × 103 |
| Std. | 9.5358 × 100 | 6.5162 × 100 | 5.1413 × 100 | 8.1505 × 100 | 7.1656 × 100 | 7.7639 × 100 | |
| Rank | 1 | 5 | 3 | 4 | 6 | 2 | |
| F8 | Mean | 2.2178 × 103 | 2.2180 × 103 | 2.2177 × 103 | 2.2166 × 103 | 2.2150 × 103 | 2.2159 × 103 |
| Std. | 6.5593 × 100 | 6.5969 × 100 | 7.1240 × 100 | 7.7401 × 100 | 8.9153 × 100 | 8.1584 × 10+00 | |
| Rank | 2 | 3 | 6 | 4 | 1 | 5 | |
| F9 | Mean | 2.5081 × 103 | 2.5027 × 103 | 2.5009 × 103 | 2.5123 × 103 | 2.5061 × 103 | 2.5035 × 103 |
| Std. | 4.0310 × 100 | 7.0478 × 100 | 4.8576 × 100 | 4.6156 × 100 | 8.3110 × 100 | 6.7890 × 100 | |
| Rank | 5 | 2 | 1 | 6 | 4 | 3 | |
| F10 | Mean | 2.4972 × 103 | 2.5242 × 103 | 2.5046 × 103 | 2.5163 × 103 | 2.5044 × 103 | 2.5165 × 103 |
| Std. | 1.7657 × 101 | 4.8467 × 101 | 2.2985 × 101 | 4.1522 × 101 | 2.1825 × 101 | 4.1856 × 101 | |
| Rank | 2 | 4 | 5 | 3 | 1 | 6 | |
| F11 | Mean | 2.6231 × 103 | 2.6183 × 103 | 2.6299 × 103 | 2.6002 × 103 | 2.6249 × 103 | 2.6110 × 103 |
| Std. | 4.8031 × 101 | 4.6247 × 101 | 5.3975 × 101 | 9.0182 × 10−1 | 5.6633 × 101 | 3.4876 × 101 | |
| Rank | 6 | 4 | 5 | 1 | 3 | 2 | |
| F12 | Mean | 2.8573 × 103 | 2.8564 × 103 | 2.8553 × 103 | 2.8585 × 103 | 2.8562 × 103 | 2.8557 × 103 |
| Std. | 3.0571 × 100 | 4.0336 × 100 | 2.6506 × 100 | 2.8718 × 100 | 2.7627 × 100 | 2.5544 × 100 | |
| Rank | 5 | 3 | 1 | 6 | 4 | 2 | |
| Mean Rank | 3.58 | 4.00 | 3.67 | 3.08 | 3.17 | 3.50 | |
| Result | 4 | 6 | 5 | 1 | 2 | 3 | |
| Algorithm | Parameter Value |
|---|---|
| DBO | is or , and decreases from . |
| HHO | E0 is a random value in . |
| GWO | Parameter decreases from 2 to 0. |
| WOA | decreases from to , . |
| IHHO | . |
| MFO | |
| INFO | |
| POA | is a random integer of 1 or 2, and is ditto. |
| SCA |
| F | Index | CSLDDBO | HHO | DBO | GWO | WOA | IHHO | MFO | INFO | POA | SCA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Median | 3.0000 × 102 | 3.0085 × 102 | 3.0000 × 102 | 4.4900 × 102 | 1.0209 × 104 | 3.0078 × 102 | 2.2642 × 103 | 3.0000 × 102 | 3.4132 × 102 | 8.7713 × 102 |
| IQR | 0.0000 × 100 | 6.8210 × 10−1 | 1.6200 × 10−11 | 1.3426 × 10+3 | 7.8154 × 10+3 | 3.8360 × 10−1 | 7.2122 × 10+3 | 6.0000 × 10−14 | 5.8045 × 101 | 2.6696 × 102 | |
| Best | 3.0000 × 10+02 | 3.0034 × 102 | 3.0000 × 102 | 3.0549 × 102 | 2.0623 × 103 | 3.0027 × 102 | 3.0000 × 102 | 3.0000 × 102 | 3.0060 × 102 | 5.2351 × 102 | |
| Mean | 3.0000 × 10+02 | 3.0096 × 102 | 3.0086 × 102 | 1.3082 × 103 | 1.0407 × 104 | 3.0089 × 102 | 4.9682 × 103 | 3.0000 × 102 | 3.5235 × 102 | 9.0036 × 102 | |
| Std. | 2.3603 × 10−14 | 3.9220 × 10−1 | 2.7061 × 100 | 1.4553 × 103 | 6.4672 × 103 | 3.8540 × 10−1 | 6.5894 × 103 | 6.1549 × 10−14 | 4.9754 × 101 | 2.4679 × 102 | |
| Rank | 1 | 4 | 3 | 8 | 10 | 5 | 6 | 2 | 7 | 9 | |
| 2 | Median | 4.0485 × 102 | 4.0618 × 102 | 4.0892 × 102 | 4.1046 × 102 | 4.0900 × 102 | 4.0894 × 102 | 4.0824 × 102 | 4.0645 × 102 | 4.0848 × 102 | 4.5906 × 102 |
| IQR | 1.6845 × 100 | 8.4757 × 100 | 3.7468 × 100 | 2.6369 × 100 | 6.1524 × 101 | 5.5403 × 101 | 1.1459 × 101 | 4.9295 × 100 | 9.6228 × 100 | 2.4575 × 101 | |
| Best | 4.0010 × 102 | 4.0006 × 102 | 4.0039 × 102 | 4.0342 × 102 | 4.0044 × 102 | 4.0005 × 102 | 4.0036 × 102 | 4.0000 × 102 | 4.0003 × 102 | 4.3286 × 102 | |
| Mean | 4.0463 × 102 | 4.1684 × 102 | 4.1576 × 102 | 4.1310 × 102 | 4.2822 × 102 | 4.2426 × 102 | 4.1525 × 102 | 4.0592 × 102 | 4.1181 × 102 | 4.5667 × 102 | |
| Std. | 1.9071 × 100 | 2.6610 × 101 | 2.3028 × 101 | 1.0876 × 101 | 3.0941 × 101 | 3.0186 × 101 | 1.6810 × 101 | 3.3008 × 100 | 1.9535 × 101 | 1.9242 × 101 | |
| Rank | 1 | 4 | 5 | 9 | 8 | 6 | 7 | 2 | 3 | 10 | |
| 3 | Median | 6.0000 × 102 | 6.2766 × 102 | 6.0500 × 102 | 6.0008 × 102 | 6.3157 × 102 | 6.2655 × 102 | 6.0025 × 102 | 6.0000 × 102 | 6.1399 × 102 | 6.1690 × 102 |
| IQR | 8.0608 × 10−4 | 1.5026 × 101 | 7.3713 × 100 | 4.8650 × 10−1 | 2.0503 × 101 | 2.1439 × 101 | 1.2363 × 100 | 3.1654 × 10−3 | 1.2778 × 101 | 4.9650 × 100 | |
| Best | 6.0000 × 102 | 6.1253 × 102 | 6.0000 × 102 | 6.0003 × 102 | 6.1061 × 102 | 6.0305 × 102 | 6.0000 × 102 | 6.0000 × 102 | 6.0038 × 102 | 6.1123 × 102 | |
| Mean | 6.0000 × 102 | 6.2819 × 102 | 6.0595 × 102 | 6.0043 × 102 | 6.3215 × 102 | 6.2567 × 102 | 6.0199 × 102 | 6.0005 × 102 | 6.1563 × 102 | 6.1770 × 102 | |
| Std. | 2.2269 × 10−3 | 1.0102 × 101 | 5.8179 × 100 | 7.5521 × 10−1 | 1.3540 × 101 | 1.3196 × 101 | 4.2576 × 100 | 2.2846 × 10−1 | 9.4222 × 100 | 3.4901 × 100 | |
| Rank | 1 | 9 | 5 | 4 | 10 | 8 | 3 | 2 | 6 | 7 | |
| 4 | Median | 8.2388 × 102 | 8.2941 × 102 | 8.2389 × 102 | 8.1144 × 102 | 8.3454 × 102 | 8.2547 × 102 | 8.2912 × 102 | 8.1343 × 102 | 8.1990 × 102 | 8.3678 × 102 |
| IQR | 7.9596 × 100 | 7.9585 × 100 | 1.5919 × 101 | 7.9585 × 100 | 1.3930 × 101 | 1.0915 × 101 | 1.3631 × 101 | 8.9546 × 100 | 8.0450 × 100 | 1.1563 × 101 | |
| Best | 8.0696 × 102 | 8.1506 × 102 | 8.1293 × 102 | 8.0514 × 102 | 8.0908 × 102 | 8.1404 × 102 | 8.0796 × 102 | 8.0497 × 102 | 8.0597 × 102 | 8.2550 × 102 | |
| Mean | 8.2346 × 102 | 8.2911 × 102 | 8.2681 × 102 | 8.1376 × 102 | 8.3366 × 102 | 8.2514 × 102 | 8.3044 × 102 | 8.1474 × 102 | 8.1880 × 102 | 8.3660 × 102 | |
| Std. | 8.4639 × 100 | 7.7850 × 100 | 9.2693 × 100 | 7.3020 × 100 | 1.2251 × 101 | 6.5477 × 100 | 1.0575 × 101 | 6.2407 × 100 | 5.6236 × 100 | 6.3956 × 100 | |
| Rank | 4 | 7 | 5 | 1 | 9 | 6 | 8 | 2 | 3 | 10 | |
| 5 | Median | 9.0094 × 102 | 1.3140 × 103 | 9.0615 × 102 | 9.0107 × 102 | 1.2480 × 103 | 1.3565 × 103 | 9.2602 × 102 | 9.0212 × 102 | 9.6627 × 102 | 9.9405 × 102 |
| IQR | 1.2191 × 100 | 2.6284 × 102 | 9.0716 × 100 | 1.3354 × 100 | 2.1871 × 102 | 2.9792 × 102 | 2.3447 × 102 | 9.0840 × 100 | 2.1163 × 102 | 5.5847 × 101 | |
| Best | 9.0000 × 102 | 9.9517 × 102 | 9.0054 × 102 | 9.0002 × 102 | 9.7925 × 102 | 9.9674 × 102 | 9.0000 × 102 | 9.0000 × 102 | 9.0009 × 102 | 9.3528 × 102 | |
| Mean | 9.0120 × 102 | 1.3373 × 103 | 9.2430 × 102 | 9.0413 × 102 | 1.3112 × 103 | 1.3267 × 103 | 1.0385 × 103 | 9.0807 × 102 | 1.0335 × 103 | 1.0001 × 103 | |
| Std. | 1.0815 × 100 | 1.6194 × 102 | 5.5428 × 101 | 9.0135 × 100 | 2.6945 × 102 | 1.7934 × 102 | 2.4208 × 102 | 1.2889 × 101 | 1.3724 × 102 | 6.6067 × 101 | |
| Rank | 1 | 10 | 4 | 2 | 8 | 9 | 5 | 3 | 6 | 7 | |
| 6 | Median | 3.9270 × 103 | 2.5004 × 103 | 5.1824 × 103 | 5.1725 × 103 | 2.5907 × 103 | 2.8218 × 103 | 5.2374 × 103 | 1.8157 × 103 | 1.9279 × 103 | 1.6204 × 106 |
| IQR | 2.9407 × 103 | 1.6873 × 103 | 2.8432 × 103 | 4.4973 × 103 | 1.8697 × 103 | 1.9660 × 103 | 4.2366 × 103 | 1.5222 × 101 | 7.5852 × 101 | −2.4739 × 106 | |
| Best | 1.8066 × 103 | 1.9298 × 103 | 1.8296 × 103 | 1.9193 × 103 | 1.9112 × 103 | 1.8930 × 103 | 1.9348 × 103 | 1.8014 × 103 | 1.8641 × 103 | 1.8332 × 105 | |
| Mean | 4.3012 × 103 | 3.4123 × 103 | 4.9202 × 103 | 5.3927 × 103 | 3.4725 × 103 | 3.2129 × 103 | 5.1222 × 103 | 1.8214 × 103 | 2.1683 × 103 | 2.1617 × 106 | |
| Std. | 2.2671 × 103 | 2.0031 × 103 | 1.9291 × 103 | 2.1304 × 103 | 1.9434 × 103 | 1.3321 × 103 | 2.1036 × 103 | 1.8006 × 101 | 9.0500 × 102 | 1.7356 × 106 | |
| Rank | 6 | 4 | 7 | 9 | 5 | 3 | 8 | 1 | 2 | 10 | |
| 7 | Median | 2.0200 × 103 | 2.0457 × 103 | 2.0239 × 103 | 2.0251 × 103 | 2.0639 × 103 | 2.0490 × 103 | 2.0223 × 103 | 2.0210 × 103 | 2.0287 × 103 | 2.0524 × 103 |
| IQR | 5.8328 × 10−2 | 2.9625 × 101 | 1.5339 × 101 | 7.6266 × 100 | 2.8280 × 101 | 2.8730 × 101 | 4.7552 × 100 | 8.6236 × 100 | 1.3976 × 101 | 6.2804 × 100 | |
| Best | 2.0000 × 103 | 2.0220 × 103 | 2.0050 × 103 | 2.0011 × 103 | 2.0226 × 103 | 2.0126 × 103 | 2.0207 × 103 | 2.0010 × 103 | 2.0170 × 103 | 2.0414 × 103 | |
| Mean | 2.0182 × 103 | 2.0512 × 103 | 2.0304 × 103 | 2.0262 × 103 | 2.0637 × 103 | 2.0516 × 103 | 2.0286 × 103 | 2.0174 × 103 | 2.0300 × 103 | 2.0535 × 103 | |
| Std. | 5.9385 × 100 | 2.8783 × 101 | 1.5330 × 101 | 8.7531 × 100 | 2.2986 × 101 | 1.9674 × 101 | 1.3518 × 101 | 8.2565 × 100 | 9.2051 × 100 | 6.5623 × 100 | |
| Rank | 1 | 7 | 5 | 3 | 10 | 8 | 4 | 2 | 6 | 9 | |
| 8 | Median | 2.2205 × 103 | 2.2269 × 103 | 2.2226 × 103 | 2.2250 × 103 | 2.2305 × 103 | 2.2276 × 103 | 2.2249 × 103 | 2.2207 × 103 | 2.2221 × 103 | 2.2317 × 103 |
| IQR | 7.1478 × 10−1 | 5.5596 × 100 | 4.6460 × 100 | 4.6333 × 100 | 7.9595 × 100 | 6.0778 × 100 | 5.6920 × 100 | 9.7991 × 10−1 | 5.5605 × 100 | 3.6522 × 100 | |
| Best | 2.2003 × 103 | 2.2167 × 103 | 2.2052 × 103 | 2.2056 × 103 | 2.2240 × 103 | 2.2215 × 103 | 2.2203 × 103 | 2.2001 × 103 | 2.2043 × 103 | 2.2247 × 103 | |
| Mean | 2.2166 × 103 | 2.2309 × 103 | 2.2258 × 103 | 2.2235 × 103 | 2.2317 × 103 | 2.2299 × 103 | 2.2258 × 103 | 2.2200 × 103 | 2.2203 × 103 | 2.2316 × 103 | |
| Std. | 8.0300 × 100 | 1.2210 × 101 | 2.3157 × 101 | 5.6982 × 100 | 5.7404 × 100 | 8.6614 × 100 | 3.9086 × 100 | 3.7897 × 100 | 6.5349 × 100 | 2.8369 × 100 | |
| Rank | 1 | 7 | 4 | 5 | 9 | 8 | 6 | 2 | 3 | 10 | |
| 9 | Median | 2.5080 × 103 | 2.5384 × 103 | 2.5293 × 103 | 2.5308 × 103 | 2.5343 × 103 | 2.5366 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5506 × 103 |
| IQR | 6.0732 × 100 | 1.8622 × 101 | 3.1477 × 100 | 4.0773 × 101 | 4.0988 × 101 | 1.7089 × 101 | 0.0000 × 100 | 0.0000 × 100 | 9.6768 × 10−1 | 1.8647 × 101 | |
| Best | 2.4986 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5293 × 103 | 2.5368 × 103 | |
| Mean | 2.5099 × 103 | 2.5457 × 103 | 2.5323 × 103 | 2.5480 × 103 | 2.5519 × 103 | 2.5408 × 103 | 2.5324 × 103 | 2.5342 × 103 | 2.5322 × 103 | 2.5540 × 103 | |
| Std. | 5.2546 × 100 | 2.7209 × 101 | 6.0187 × 100 | 2.2461 × 101 | 3.1301 × 101 | 1.2935 × 101 | 1.1868 × 101 | 2.6826 × 101 | 8.2775 × 100 | 1.3193 × 101 | |
| Rank | 1 | 8 | 4 | 7 | 9 | 6 | 3 | 2 | 5 | 10 | |
| 10 | Median | 2.5003 × 103 | 2.5010 × 103 | 2.5009 × 103 | 2.6094 × 103 | 2.5011 × 103 | 2.5010 × 103 | 2.5008 × 103 | 2.5005 × 103 | 2.5006 × 103 | 2.5016 × 103 |
| IQR | 8.0465 × 10−2 | 1.2778 × 102 | 1.1765 × 102 | 1.1129 × 103 | 1.1173 × 103 | 1.2472 × 102 | 9.6906 × 100 | 1.1657 × 102 | 4.4324 × 10−1 | 4.2404 × 10−1 | |
| Best | 2.5002 × 103 | 2.4375 × 103 | 2.5004 × 103 | 2.5003 × 103 | 2.5003 × 103 | 2.5004 × 103 | 2.5003 × 103 | 2.5003 × 103 | 2.5003 × 103 | 2.5007 × 103 | |
| Mean | 2.5082 × 103 | 2.5516 × 103 | 2.5392 × 103 | 2.5642 × 103 | 2.5607 × 103 | 2.5437 × 103 | 2.5215 × 103 | 2.5482 × 103 | 2.5173 × 103 | 2.5062 × 103 | |
| Std. | 2.9838 × 101 | 6.8928 × 101 | 5.9878 × 101 | 5.6803 × 101 | 1.2277 × 102 | 6.1766 × 101 | 4.8907 × 101 | 5.9698 × 101 | 4.3059 × 101 | 2.5316 × 101 | |
| Rank | 1 | 9 | 6 | 4 | 7 | 8 | 5 | 3 | 2 | 10 | |
| 11 | Median | 2.6000 × 103 | 2.7506 × 103 | 2.6000 × 103 | 2.7309 × 103 | 2.7511 × 103 | 2.7506 × 103 | 2.7508 × 103 | 2.6000 × 103 | 2.7228 × 103 | 2.7688 × 103 |
| IQR | 4.8133 × 10−4 | 3.0780 × 102 | 1.5047 × 102 | 1.8278 × 102 | 1.3772 × 102 | 1.4603 × 102 | 1.6677 × 102 | 1.5043 × 102 | 1.2992 × 102 | 9.6115 × 100 | |
| Best | 2.6000 × 103 | 2.6040 × 103 | 2.6000 × 103 | 2.6006 × 103 | 2.6014 × 103 | 2.6030 × 103 | 2.6000 × 103 | 2.6000 × 103 | 2.6013 × 103 | 2.7590 × 103 | |
| Mean | 2.6169 × 10+3 | 2.7864 × 103 | 2.7018 × 103 | 2.7834 × 103 | 2.7483 × 103 | 2.7135 × 103 | 2.7079 × 103 | 2.6879 × 103 | 2.6825 × 103 | 2.7705 × 103 | |
| Std. | 4.4697 × 101 | 1.6599 × 102 | 1.4794 × 102 | 1.5621 × 102 | 1.1319 × 102 | 1.2748 × 102 | 8.5734 × 101 | 1.4996 × 102 | 8.3664 × 101 | 6.5652 × 100 | |
| Rank | 1 | 9 | 3 | 7 | 8 | 6 | 5 | 2 | 4 | 10 | |
| 12 | Median | 2.8597 × 103 | 2.8805 × 103 | 2.8654 × 103 | 2.8642 × 103 | 2.8687 × 103 | 2.8799 × 103 | 2.8635 × 103 | 2.8641 × 103 | 2.8649 × 103 | 2.8688 × 103 |
| IQR | 4.6049 × 100 | 5.5301 × 101 | 3.9591 × 100 | 1.7836 × 100 | 1.1572 × 101 | 2.2354 × 101 | 1.5751 × 100 | 1.4963 × 100 | 2.7423 × 100 | 2.9024 × 100 | |
| Best | 2.8540 × 103 | 2.8630 × 103 | 2.8626 × 103 | 2.8594 × 103 | 2.8609 × 103 | 2.8631 × 103 | 2.8600 × 103 | 2.8607 × 103 | 2.8594 × 103 | 2.8650 × 103 | |
| Mean | 2.8592 × 103 | 2.8998 × 103 | 2.8669 × 103 | 2.8659 × 103 | 2.8782 × 103 | 2.8902 × 103 | 2.8634 × 103 | 2.8639 × 103 | 2.8653 × 103 | 2.8688 × 103 | |
| Std. | 2.8103 × 100 | 5.0029 × 101 | 4.1838 × 100 | 6.1777 × 100 | 2.3730 × 101 | 2.6922 × 101 | 1.2255 × 100 | 1.3995 × 100 | 3.1091 × 100 | 1.7218 × 100 | |
| Rank | 1 | 9 | 6 | 5 | 7 | 10 | 2 | 3 | 4 | 8 | |
| Mean Rank | 1.67 | 7.25 | 4.75 | 5.33 | 8.33 | 6.92 | 5.17 | 2.17 | 4.25 | 9.17 | |
| Result | 1 | 8 | 4 | 6 | 9 | 7 | 5 | 2 | 3 | 10 | |
| F | HHO | DBO | GWO | WOA | IHHO | MFO | INFO | POA | SCA |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.1436 × 10−12 + | 1.2193 × 10−5 + | 5.1436 × 10−12 + | 5.1436 × 10−12 + | 5.1436 × 10−12 + | 3.8376 × 10−4 + | 7.6743 × 10−5 + | 5.1436 × 10−12 + | 5.1436 × 10−12 + |
| 2 | 4.0354 × 10−1 + | 1.2491 × 10−7 + | 4.1997 × 10−10 + | 4.1178 × 10−6 + | 2.2658 × 10−3 + | 2.1391 × 10−9 + | 5.1802 × 10−1 = | 9.6263 × 10−2 = | 3.0199 × 10−11 + |
| 3 | 2.9897 × 10−11 + | 1.0834 × 10−10 + | 2.9897 × 10−11 + | 2.9897 × 10−11 + | 2.9897 × 10−11 + | 1.4041 × 10−6 + | 1.3603 × 10−4 + | 2.9897 × 10−11 + | 2.9897 × 10−11 + |
| 4 | 4.8554 × 10−3 + | 3.5543 × 10−1 + | 1.5288 × 10−5 − | 2.5301 × 10−4 + | 3.0417 × 10−1 + | 5.8261 × 10−3 + | 7.8612 × 10−5 − | 3.6436 × 10−2 − | 1.2536 × 10−7 + |
| 5 | 3.0161 × 10−11 + | 6.2560 × 10−8 + | 6.4141 × 10−1 = | 3.0161 × 10−11 + | 3.0161 × 10−11 + | 2.5196 × 10−4 + | 1.1877 × 10−1 = | 3.4936 × 10−9 + | 3.0161 × 10−11 + |
| 6 | 1.9073 × 10−1 − | 1.3345 × 10−1 = | 2.0681 × 10−2 + | 2.3399 × 10−1 − | 8.5000 × 10−2 = | 3.9167 × 10−2 + | 7.3803 × 10−10 − | 4.7445 × 10−6 − | 3.0199 × 10−11 + |
| 7 | 3.0199 × 10−11 + | 4.1997 × 10−10 + | 6.5277 × 10−8 + | 3.0199 × 10−11 + | 4.1997 × 10−10 + | 3.3384 × 10−11 + | 1.1228 × 10−2 + | 8.8910 × 10−10 + | 3.0199 × 10−11 + |
| 8 | 3.1589 × 10−10 + | 8.2919 × 10−6 + | 2.3897 × 10−8 + | 3.0199 × 10−11 + | 3.0199 × 10−11 + | 7.3803 × 10−10 + | 2.9205 × 10−2 + | 2.1265 × 10−4 + | 3.0199 × 10−11 + |
| 9 | 3.0199 × 10−11 + | 2.3967 × 10−11 + | 3.0199 × 10−11 + | 3.0199 × 10−11 + | 3.0199 × 10−11 + | 7.8511 × 10−12 + | 1.7203 × 10−12 + | 3.0199 × 10−11 + | 3.0199 × 10−11 + |
| 10 | 1.4294 × 10−8 + | 2.4386 × 10−9 + | 5.8737 × 10−4 + | 8.4848 × 10−9 + | 2.4386 × 10−9 + | 3.3520 × 10−8 + | 8.8829 × 10−6 + | 3.3242 × 10−6 + | 7.1186 × 10−9 + |
| 11 | 5.6856 × 10−10 + | 7.5825 × 10−5 + | 6.2445 × 10−9 + | 1.0997 × 10−9 + | 9.7341 × 10−9 + | 2.4243 × 10−2 + | 1.9100 × 10−1 = | 1.7245 × 10−7 + | 1.7883 × 10−11 + |
| 12 | 3.0199 × 10−11 + | 4.9691 × 10−11 + | 5.0723 × 10−10 + | 3.8202 × 10−10 + | 3.0199 × 10−11 + | 1.3014 × 10−8 + | 3.4763 × 10−9 + | 2.6695 × 10−9 + | 3.0199 × 10−11 + |
| +/=/− | 12/0/0 | 11/1/0 | 10/1/1 | 11/0/1 | 11/1/0 | 12/0/0 | 8/2/2 | 9/1/2 | 12/0/0 |
| F | CSLDDBO | HHO | DBO | GWO | WOA | IHHO | MFO | INFO | POA | SCA |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 24.6407 | 10.7344 | 7.2813 | 5.0313 | 2.9219 | 22.8283 | 4.9375 | 16.3751 | 8.5938 | 4.7969 |
| 2 | 33.0312 | 15.0000 | 9.6094 | 6.4688 | 4.2031 | 30.5314 | 6.2188 | 21.9688 | 12.2187 | 6.3594 |
| 3 | 25.4843 | 12.2969 | 6.8594 | 5.4688 | 4.0313 | 26.9219 | 5.2812 | 12.9375 | 9.3752 | 5.0781 |
| 4 | 13.0938 | 5.6719 | 3.4219 | 2.5000 | 1.6718 | 12.0937 | 2.5469 | 7.6563 | 4.0781 | 2.5469 |
| 5 | 17.6563 | 8.2032 | 4.9063 | 3.5625 | 2.4218 | 18.0468 | 3.7813 | 10.4219 | 5.9219 | 3.3750 |
| 6 | 27.1563 | 12.5313 | 7.9844 | 5.2344 | 3.1875 | 25.8438 | 5.5781 | 17.3750 | 9.0469 | 5.0312 |
| 7 | 26.0469 | 12.1251 | 6.4375 | 5.1719 | 4.0313 | 27.5002 | 5.1875 | 12.0782 | 9.6876 | 5.1719 |
| 8 | 29.7190 | 13.6406 | 6.8906 | 5.39066 | 3.9219 | 29.1408 | 5.4375 | 12.7813 | 10.5625 | 5.7969 |
| 9 | 28.1876 | 12.7813 | 7.9219 | 5.9688 | 4.2188 | 29.3126 | 5.5938 | 12.5939 | 9.6095 | 5.5781 |
| 10 | 29.9689 | 15.1876 | 8.7031 | 6.4531 | 4.7187 | 33.9533 | 6.2969 | 16.3595 | 11.6875 | 6.0156 |
| 11 | 34.8128 | 16.9844 | 8.7500 | 7.0312 | 5.5000 | 38.0471 | 7.1094 | 15.3593 | 12.9376 | 6.8438 |
| 12 | 25.0784 | 11.2500 | 6.5313 | 4.87506 | 4.2344 | 25.9378 | 5.5157 | 10.6563 | 8.64065 | 5.1407 |
| Mean Time | 26.2396 | 12.2002 | 7.1080 | 5.2630 | 3.7552 | 26.6798 | 5.2903 | 13.8802 | 9.3633 | 5.1445 |
| Time | SO2 Emissions/Ten Thousand Tons | Proportion of Industrial Output Value in Total Domestic Production/% | Energy Consumption GDP/t/Ten Thousand CNY | Industrial SO2 Emission Intensity/t/Ten Thousand CNY | Proportion of Non-Clean Energy Consumption/% |
|---|---|---|---|---|---|
| 2012 | 2118 | 45.42 | 0.75 | 0.0087 | 85.5 |
| 2013 | 2043.9 | 44.18 | 0.7 | 0.0078 | 84.5 |
| 2014 | 1974.4 | 43.09 | 0.67 | 0.0071 | 83 |
| 2015 | 1859.1 | 40.84 | 0.63 | 0.0066 | 82 |
| 2016 | 854.89 | 39.58 | 0.59 | 0.0029 | 80.3 |
| 2017 | 610.84 | 39.85 | 0.55 | 0.0018 | 79.5 |
| 2018 | 516.12 | 39.69 | 0.51 | 0.0014 | 77.9 |
| 2019 | 457.29 | 38.59 | 0.49 | 0.0012 | 76.7 |
| 2020 | 318.22 | 37.84 | 0.49 | 0.0008 | 75.7 |
| 2021 | 274.78 | 39.43 | 0.46 | 0.0006 | 74.5 |
| Evaluation Dimensions | Training Set Range | Test Set Scope | Coverage Results |
|---|---|---|---|
| The proportion of industrial output value in GDP/% | 39.58–45.42 | 37.84–38.59 | Complete coverage |
| Energy consumption per unit of GDP/t/10,000 CNY | 0.51–0.75 | 0.49 | Boundary coverage |
| Industrial SO2 emission intensity/t/10,000 CNY | 0.0014–0.0087 | 0.0008–0.0012 | Complete coverage |
| Proportion of non-renewable energy consumption/% | 77.9–85.5 | 75.7–76.7 | Complete coverage |
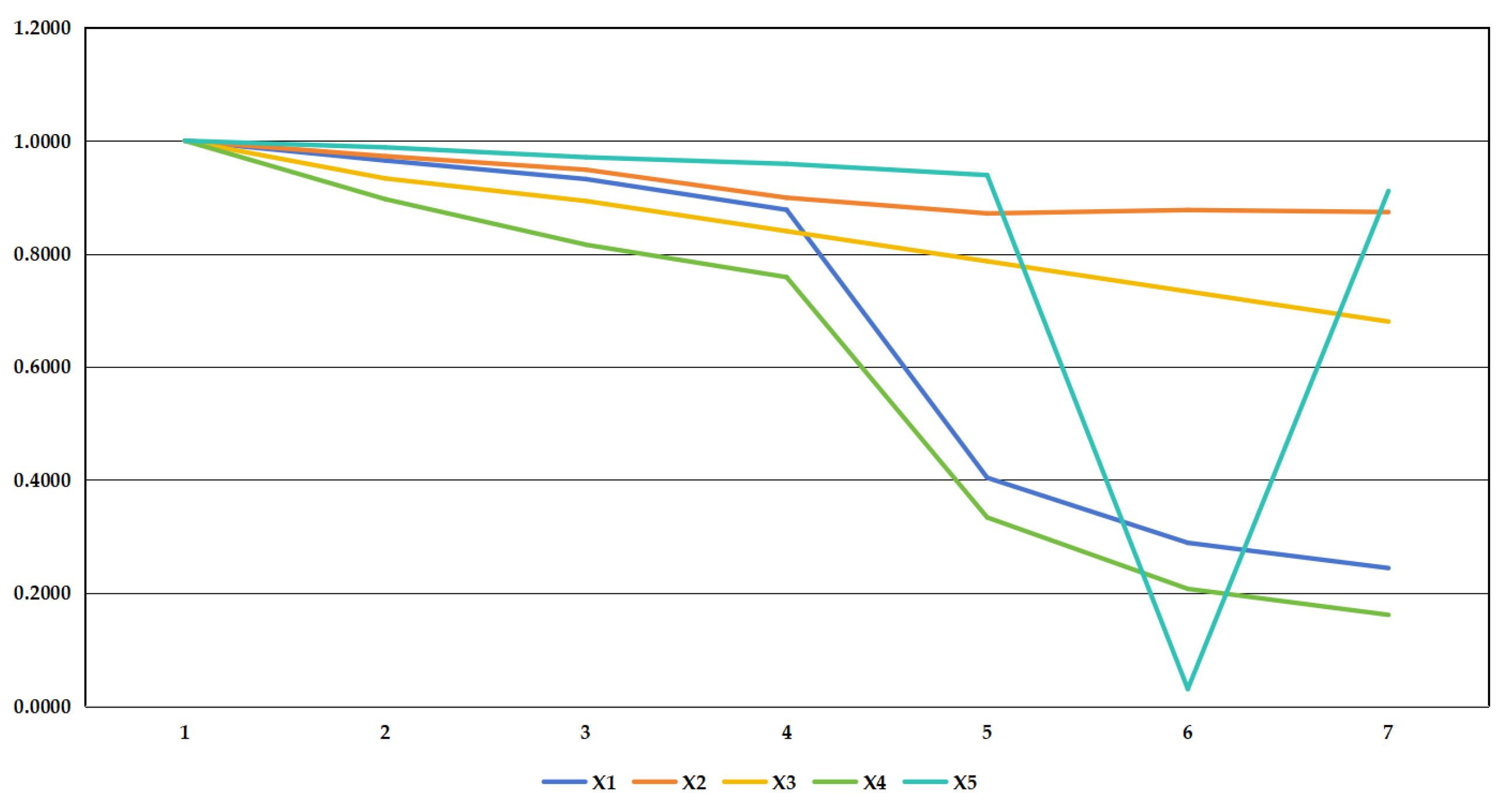
| Time | X1 | X2 | X3 | X4 | X5 |
|---|---|---|---|---|---|
| 2012 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2013 | 0.9650 | 0.9727 | 0.9333 | 0.8966 | 0.9883 |
| 2014 | 0.9322 | 0.9487 | 0.8933 | 0.8160 | 0.9708 |
| 2015 | 0.8778 | 0.8992 | 0.8400 | 0.7586 | 0.9591 |
| 2016 | 0.4036 | 0.8714 | 0.7867 | 0.3333 | 0.9392 |
| 2017 | 0.2884 | 0.8774 | 0.7333 | 0.2069 | 0.9298 |
| 2018 | 0.2437 | 0.8738 | 0.6800 | 0.1609 | 0.9111 |
| 2019 | 0.2159 | 0.8496 | 0.6533 | 0.1379 | 0.8971 |
| 2020 | 0.1502 | 0.8331 | 0.6533 | 0.0920 | 0.8854 |
| 2021 | 0.1297 | 0.8681 | 0.6133 | 0.0690 | 0.8713 |
| Index | ||||
|---|---|---|---|---|
| Value | 0.648 | 0.739 | 0.937 | 0.612 |
| Index | |||||
|---|---|---|---|---|---|
| Value | −0.9979 | 2.6046 | 35.0000 | 35.0000 | −12.7324 |
| Index | |||||
| Value | 1 | 1 | 1 | 1 | 0.8714 |
| Level | I | II | III | IV |
|---|---|---|---|---|
| Error | 0.01 | 0.05 | 0.10 | 0.20 |
| Index | Meaning | Data/Calculation Method |
|---|---|---|
| Raw data (RD) | Statistical data | |
| Simulated or predicted data (SPD) | The final recovery expression of the model | |
| Residual | ||
| Relative squared (RSPE) | ||
| Mean relative simulated percentage error (MRSPE) | ||
| (RPPE) | ||
| Mean relative prediction percentage error (MRPPE) | ||
| Comprehensive mean relative percentage error (CMRPE) |
| Model | Parameter | Value |
|---|---|---|
| NSGM(1, N) | : Development coefficient | |
| : Driving coefficient | ||
| : Gray action | ||
| OBGM(1, N) | : Resolution | |
| : Gray relational degree threshold | ||
| : Background value coefficient | ||
| SVR | Kernel function | Radial basis function (RBF) |
| : RBF kernel coefficient | ||
| : Penalty factor | ||
| : Insensitive loss band width | ||
| LSTM | : Hidden unit | |
| : Number of layers | ||
| : Batch size | ||
| : Learning rate |
| NSGM(1, N) | OBGM(1, N) | PGM(1, N) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.9650 | 0.9420 | −0.0229 | 2.3779 | 0.9650 | 0.0000 | 0.0000 | 0.9645 | −0.0004 | 0.0494 |
| 3 | 0.9322 | 0.9374 | 0.0052 | 0.5583 | 0.7250 | −0.2070 | 22.2060 | 0.9327 | 0.0005 | 0.0549 |
| 4 | 0.8778 | 0.8826 | 0.0048 | 0.5506 | 0.6760 | −0.2020 | 23.0120 | 0.8788 | 0.0010 | 0.1156 |
| 5 | 0.4036 | 0.4096 | 0.0060 | 1.5017 | 0.2010 | −0.2030 | 50.2970 | 0.4040 | 0.0004 | 0.1013 |
| 6 | 0.2884 | 0.2929 | 0.0045 | 1.5746 | 0.0860 | −0.2020 | 70.0420 | 0.2887 | 0.0003 | 0.1208 |
| 7 | 0.2437 | 0.2478 | 0.0041 | 1.6903 | 0.0420 | −0.2020 | 82.8890 | 0.2435 | −0.0001 | 0.0686 |
| Mean relative simulated percentage error () | 1.3756% | 59.6197% | 0.0851% | |||||||
| NSGM(1, N) | OBGM(1, N) | PGM(1, N) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 0.2159 | 0.2153 | −0.0005 | 0.2484 | 0.0130 | −0.2030 | 94.0250 | 0.2164 | 0.0005 | 0.2471 |
| 9 | 0.1502 | 0.1452 | −0.0049 | 3.3017 | −0.0520 | −0.2020 | 134.4870 | 0.1505 | 0.0003 | 0.2471 |
| Mean relative prediction percentage error () | 1.7751% | 119.2394% | 0.2471% | |||||||
| Comprehensive mean relative percentage error () | 1.3115% | 79.4930% | 0.1117% | |||||||
| NSGM(1, N) | OBGM(1, N) | PGM(1, N) | |||
|---|---|---|---|---|---|
| 10 | 0.1297 | ||||
| Actual predicted value | 0.129071 | 0.133271 | 0.129720 | ||
| SVR | LSTM | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 0.9650 | 0.9640 | −0.0010 | 0.1000 | 0.9631 | −0.0019 | 0.1942 |
| 3 | 0.9322 | 0.9350 | 0.0028 | 0.3040 | 0.9260 | −0.0062 | 0.6200 |
| 4 | 0.8778 | 0.8711 | −0.0067 | 0.7298 | 0.8692 | −0.0086 | 0.9821 |
| 5 | 0.4036 | 0.4112 | 0.0076 | 1.4820 | 0.4200 | 0.0164 | 4.1010 |
| 6 | 0.2884 | 0.2766 | −0.0118 | 4.0048 | 0.2983 | 0.0099 | 3.3247 |
| 7 | 0.2437 | 0.2317 | −0.0120 | 4.0908 | 0.2509 | 0.0072 | 2.8331 |
| Average relative prediction percentage error () | 1.7852% | 2.0091% | |||||
| SVR | LSTM | ||||||
|---|---|---|---|---|---|---|---|
| 8 | 0.2159 | 0.2142 | −0.0017 | 0.7474 | 0.2213 | 0.0054 | 2.3075 |
| 9 | 0.1502 | 0.1578 | 0.0076 | 5.0010 | 0.1550 | 0.0048 | 3.1020 |
| Average relative prediction percentage error () | 2.8742% | 1.5510% | |||||
| Comprehensive average relative percentage error () | 2.0574% | 1.8945% | |||||
| SVR | LSTM | ||
|---|---|---|---|
| 10 | 0.1297 | ||
| Actual predicted value | 0.128715 | 0.129983 |
| Index | Error | PGM(1, N) | NSGM(1, N) | OBGM(1, N) | SVR | LSTM |
|---|---|---|---|---|---|---|
| MRSPE | Maximum error | 0.1208% | 2.3779% | 82.8890% | 4.0908% | 4.1010% |
| Minimum error | 0.0494% | 0.5506% | 0.0000% | 0.100% | 0.1942% | |
| Error range | 0.0714% | 1.8273% | 82.8890% | 3.9908% | 3.9068% | |
| MRPPE | Maximum error | 0.2471% | 3.3017% | 134.4870% | 5.0010% | 3.1020% |
| Minimum error | 0.2471% | 0.2484% | 94.0250% | 0.7474% | 2.3075% | |
| Error range | 0.0000% | 3.0533% | 40.4620% | 4.2536% | 0.7945% |
| 11 | 0.8597 | 0.5958 | 0.0481 | 0.8692 |
| 12 | 0.8476 | 0.5745 | 0.0179 | 0.8511 |
| 13 | 0.8385 | 0.5445 | 0.0083 | 0.8493 |
| 14 | 0.8492 | 0.5106 | 0.0034 | 0.8337 |
| 15 | 0.8269 | 0.4769 | 0.0010 | 0.8299 |
| Time | 2022 | 2023 | 2024 | 2025 | 2026 |
|---|---|---|---|---|---|
| Predictive value | 238.0632 | 185.5368 | 85.1436 | 15.8850 | 10.4720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, L.; Hu, G.; Hussien, A.G. Prediction of Sulfur Dioxide Emissions in China Using Novel CSLDDBO-Optimized PGM(1, N) Model. Mathematics 2025, 13, 2846. https://doi.org/10.3390/math13172846
Cui L, Hu G, Hussien AG. Prediction of Sulfur Dioxide Emissions in China Using Novel CSLDDBO-Optimized PGM(1, N) Model. Mathematics. 2025; 13(17):2846. https://doi.org/10.3390/math13172846
Chicago/Turabian StyleCui, Lele, Gang Hu, and Abdelazim G. Hussien. 2025. "Prediction of Sulfur Dioxide Emissions in China Using Novel CSLDDBO-Optimized PGM(1, N) Model" Mathematics 13, no. 17: 2846. https://doi.org/10.3390/math13172846
APA StyleCui, L., Hu, G., & Hussien, A. G. (2025). Prediction of Sulfur Dioxide Emissions in China Using Novel CSLDDBO-Optimized PGM(1, N) Model. Mathematics, 13(17), 2846. https://doi.org/10.3390/math13172846







