Studies on Poisson–Nernst–Planck Systems with Large Permanent Charges Under Relaxed Neutral Boundary Conditions

Abstract

Modeling ion transport through membrane channels is crucial for understanding cellular processes, and Poisson–Nernst–Planck (PNP) equations provide a fundamental continuum framework for such ionic fluxes. We investigate a quasi-one-dimensional steady-state PNP system for two oppositely charged ion species, focusing on how large permanent charges within the channel and realistic boundary conditions impact ion transport. In contrast to classical models that impose ideal electroneutrality at the channel ends (a simplification that eliminates boundary layers near the membrane interfaces), we adopt relaxed neutral boundary conditions that allow small charge imbalances at the boundaries. Using asymptotic analysis treating the large permanent charge as a singular perturbation, we derive explicit first-order expansions for each ionic flux, incorporating boundary layer parameters $(\sigma ,\rho )$ to quantify slight deviations from electroneutrality. This analysis enables a qualitative characterization of individual cation and anion flux behaviors. Notably, we identify two critical transmembrane potentials, $V_{1c}$ and $V_{2c}$, at which the cation and anion fluxes, respectively, vanish, signifying flux-reversal thresholds that delineate distinct monotonic regimes in the flux-voltage response; these critical values depend on the permanent charge magnitude and the boundary layer parameters. We further show that both ionic fluxes exhibit saturation: as the applied voltage becomes extreme, each flux approaches a finite limiting value, with the saturation level modulated by the degree of boundary charge imbalance. Moreover, allowing even small boundary charge deviations reveals non-intuitive discrepancies in flux behavior relative to the ideal electroneutral case. For example, in certain parameter regimes, a large permanent charge that enhances an ionic current under strict electroneutral conditions will instead suppress that current under relaxed-neutral conditions (and vice versa). This new analytical framework exposes subtle yet essential nonlinear dynamics that classical electroneutral assumptions would otherwise obscure. It provides deeper insight into the interplay between large fixed charges and boundary-layer effects, emphasizing the importance of incorporating such realistic boundary conditions to ensure accurate modeling of ion transport through membrane channels. Numerical simulations are performed to provide more intuitive illustrations of our analytical results.

1. Introduction

The cell is the constitutional and functional unit for organisms. The cell membrane defines the cell from the outside environment. There are various types of substance exchange between the cell and surroundings. Ion channels, which are the huge proteins embedded in the cell membrane, determine which specific ion can go through the cell membrane. Thereby, ion channels play a significant role in the smooth running of the cell and, furthermore, in the normal functioning of the organism. For example, several types of calcium ion channels locate on fungi’s mitochondria. They control the synthesis of ATP, the transportation of calcium, and the cell apoptosis cycle [1,2,3]. For human beings, sodium and potassium channels on the neurons are responsible for the induction of action potential and resting potential alternatively [4,5]. A group of channels on muscle cells cooperate to trigger muscle contraction [6,7]. Conversely, the malfunctioning ion channels are testified to cause many diseases, such as cholera and Alzheimer [8,9,10,11,12]. Getting the knowledge of the structural characteristics and the working mechanism of an open ion channel would not only help one to manufacture artificial ion channels in the industrial field but also benefit for the pharmacological treatment of diseases related to ion channels.

Thanks to the development of many advanced observation techniques, such as cryo-electron microscopy awarded the 2017 Nobel Prize, biophysical scientists are capable of studying the structure of an ion channel by its images in different status at atomic resolution [1,2,3]. For an open channel with a given structure, the main interest is on the study of its electrodiffusion property. The main difficulty in examining properties of ionic flows through ion channels lies in the characterization of the nonlinear interplays among specific physical parameters involved in the system, such as the boundary ion concentrations, boundary potentials, permanent charges, channel geometry, finite ion sizes, and diffusion coefficients. However, all present experimental measurements about ionic flow are of the input–output type [13]; that is, the internal dynamics within the channel cannot be measured with the current technology. Mathematical analysis plays important and unique roles for generalizing and understanding the principles that allow control of electrodiffusion, explaining mechanics of observed biological phenomena and for discovering new ones, assuming a more or less explicit solution of the associated mathematical model can be obtained.

The results obtained in current work demonstrate that accounting for boundary layer charges leads to new and sometimes counter-intuitive transport phenomena. We identify critical potentials (denoted $V_{1c},V_{2c}$) where the cation or anion flux undergoes a qualitative change (such as a sign reversal or slope change), sensitively depending on the permanent charge strength and the boundary layer parameters. Furthermore, we prove that both ionic fluxes saturate (tend to constant magnitudes) as the transmembrane potential V grows extremely large, but these saturation levels are shifted by deviations from perfect boundary neutrality. Notably, the comparison between relaxed-neutral and electroneutral cases uncovers non-intuitive flux behaviors: in certain regimes, a large fixed charge can enhance an ionic current under one boundary condition but suppress it under the other. Such discrepancies highlight that assuming strict electroneutrality can overlook important qualitative features of ionic transport.

This work’s main contributions include developing an analytical PNP framework with relaxed boundary neutrality and revealing how even slight boundary charge imbalances can dramatically alter flux characteristics. By bridging the gap between idealized PNP models and physiologically realistic conditions, the study provides insights into how permanent channel charges act as regulatory filters (flux modifiers). Its theoretical predictions−for example, explicit flux bounds at extreme voltages−align with observed current saturation in experiments. Overall, the results underscore the importance of including boundary layer effects in ion transport models and pave the way for more accurate descriptions of ionic flows in biological channels, with implications for future experimental validation and more complex multi-species PNP analyses.

1.1. One-Dimensional Poisson–Nernst–Planck Models

The Poisson–Nernst–Planck (PNP) equations provide a fundamental continuum model for ionic flow through channels, capturing the coupled electrodiffusion of multiple ion species [14,15,16,17,18]. The PNP framework consists of Poisson’s equation for the electrostatic potential and Nernst–Planck equations for ionic transport, and it can be derived from more microscopic descriptions, such as molecular dynamics or Boltzmann transport equations [19,20], and from variational principles [21,22,23,24]. Owing to its solid physical basis and relative simplicity, the PNP model has been extensively used to analyze ion channel behavior both analytically (see [25,26,27,28,29,30] for example) and numerically ([31,32,33,34,35,36,37,38,39] and the references therein). In its classical form, however, the PNP model assumes point-like ions and neglects ion–ion interactions beyond mean-field electrostatics. This classical PNP (cPNP) approximation often fails to capture important features such as ionic saturation and selectivity that arise from the finite size of ions and their interactions in confined geometries. For example, two cations with the same valence (e.g., ${\mathrm{Na}}^{+}$ vs. ${\mathrm{K}}^{+}$) can exhibit very different permeation behavior in a narrow channel due to their difference in ionic radius. Thus, finite ion size effects are critical for accurately modeling selectivity and saturating behavior in ionic flows. To account for finite ion sizes, modified PNP models include an excess chemical potential term (often modeled by hard-sphere repulsion) in each ion species’ transport equation [30,40,41,42,43,44,45,46,47,48,49]. This steric term introduces a highly nonlinear coupling between ion concentrations, effectively imposing a limit on how densely ions can pack in the channel pore.

In this work, we consider the quasi-one-dimensional steady-state PNP model (the same as that adopted in [50,51]), which was first proposed in [52]. For an ion channel containing n distinct types of ion species, the quasi-one-dimensional steady-state PNP model reads

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{1}{A\left(X\right)}}{\displaystyle \frac{d}{dX}}\left({\epsilon }_r\left(X\right){\epsilon }_{0}A\left(X\right){\displaystyle \frac{d\mathsf{\Phi }}{dX}}\right)=-e_0\left(\sum _{i=1}^n{z}_i{C}_i\left(X\right)+\mathcal{Q}\left(X\right)\right),\hfill \\ \hfill & {\displaystyle \frac{d{\mathcal{J}}_i}{dX}}=0,-{\mathcal{J}}_i={\displaystyle \frac{1}{k_{B}T}}{\mathcal{D}}_i\left(X\right)A\left(X\right)C_i\left(X\right){\displaystyle \frac{d{\mu }_i}{dX}},i=1,2,\cdots ,n,\hfill \end{array}\end{array}$$

(1)

where $e_0$ is the elementary charge, $k_B$ is the Boltzmann constant, T is the absolute temperature, $X\in [a_0,b_0]$ is the position variable along the longitudinal axis of an ion channel with two boundaries, $A\left(X\right)$ represents the cross sectional area of the ion channel over the point X, ${\epsilon }_r\left(X\right)$ is the relative dielectric coefficient, ${\epsilon }_0\left(X\right)$ is the local dielectric coefficient, $\mathsf{\Phi }\left(X\right)$ is the electric potential, and $\mathcal{Q}\left(X\right)$ is the permanent charge density of the channel. For the ith ion species, $z_i$ is the ion valence, $C_i\left(X\right)$ is the ion concentration, ${\mathcal{J}}_i$ is the flux density, ${\mathcal{D}}_i\left(X\right)$ is the diffusion coefficient, and ${\mu }_i\left(X\right)$ is the electrochemical potential.

The boundary conditions are (see [53] for detailed explanations) for $i=1,2,\cdots ,n$

$$\mathsf{\Phi }\left(a_0\right)=\mathcal{V},C_i\left(a_0\right)={\mathcal{L}}_i>0;\mathsf{\Phi }\left(b_0\right)=0,C_i\left(b_0\right)={\mathcal{R}}_i>0.$$

(2)

We point out that the system (1) being called a quasi-one-dimensional is due to the fact that $A\left(X\right)$, the area of the cross section of the ion channel over the point X, varies along the longitudinal axis.

1.2. Permanent Charges

In the system (1), $\mathcal{Q}\left(X\right)$ is the permanent charge density that is generated by the side chain of amino acid distributed along the channel wall, whose acidic side chains contribute negative charges while its basic side chains carry positive charges [54]. $\mathcal{Q}\left(X\right)$ reflects the location of amino acids along the ion channel, which varies among different types of ion channels. Therefore, $\mathcal{Q}\left(X\right)$ plays a significant role in studying the selectivity property of ion channels [55].

Mathematically, the following piecewise model is utilized to characterize the essential information of permanent charges. For a partition $X_0=a_0<X_1<\cdots <X_{n-1}<X_n=b_0$ on $[a_0,b_0]$, $\mathcal{Q}\left(X\right)={\mathcal{Q}}_m$ for $X\in (X_{m-1},X_m)$ where ${\mathcal{Q}}_m$s are constants with ${\mathcal{Q}}_1={\mathcal{Q}}_n=0$. In particular, the following setup for $\mathcal{Q}\left(x\right)$

$$\mathcal{Q}\left(X\right)=\left\{\begin{array}{c}0,X\in [a_0,X_1)\cup (X_2,b_0]\hfill \\ 2{\mathcal{Q}}_0,X\in (X_1,X_2).\hfill \end{array}\right.$$

(3)

has been adopted in many works, such as [50,51,53,56,57,58,59]. Viewing $|{\mathcal{Q}}_0|$ as a small (compared to boundary concentrations) regular parameter, the authors in [56,57,58,59] employed regular perturbation analysis to characterize the effects on ionic flows from small permanent charges. Many interesting and non-intuitive phenomena have been observed. In particular, it shows that, to optimize the effect of permanent charges, a short and narrow filter, within which the permanent charge is confined, is expected, which is consistent with the typical structure of an ion channel. Recently, the authors in [50,51] studied the case for permanent charges with large magnitude, both of which are discussed under electroneutrality boundary conditions. We would like to point out that the dynamics of ionic flows for small permanent charges and large permanent charges are quite different. For example, large positive permanent charge inhibits the flux of cations (see Proposition $3.1$ in [51]), while the small positive permanent charge does not (see Corollary $3.2$ in [58]). For more details, one can refer to [58] for PNP system with small permanent charges and [51] for PNP system with large permanent charges.

1.3. Electrochemical Potentials

Electrochemical potential ${\mu }_i$ consists of ideal component ${\mu }_i^{id}\left(X\right)$ and excess component ${\mu }_i^{ex}\left(X\right)$, where the ideal component reads

$${\mu }_i^{id}\left(X\right)=z_i{e}_0\mathsf{\Phi }\left(X\right)+k_{B}Tln{\displaystyle \frac{C_i\left(X\right)}{C_0}}$$

(4)

with some characteristic number density $C_0$. The ideal component regards ions as point charges without ion sizes and describes electrochemical potential as outcome generated by electric part $\mathsf{\Phi }\left(X\right)$ with chemical part $C_i\left(X\right)$. The classical PNP model only takes ideal component to approximate ${\mu }_i$ ([27,28,51,58,60], etc.). The excess component accounts for ion size effects, which is the complement of ideal component (see [47] for more details). In this work, we only take the ideal component ${\mu }_i^{id}\left(X\right)$.

1.4. Electroneutrality Boundary Conditions and Boundary Layers

In the study of PNP system, very often, the electroneutrality boundary condition is introduced to the system, which is formulated by

$$\begin{array}{c}\hfill \sum _{i=1}^n{z}_i{\mathcal{L}}_i=\sum _{i=1}^n{z}_i{\mathcal{R}}_i=0.\end{array}$$

(5)

The electroneutrality boundary condition reflects the relation between each ion concentration from two boundaries. Precisely, it indicates that there is no net charge on two boundaries. The experiments also showed that ion concentrations on two boundaries of ion channels are very closed to this condition [61,62]. Many results have been obtained under electroneutrality boundary conditions ([27,40,58] and references therein). However, once substituting this condition into the system, the boundary layers of the system disappear (see Section 1.3 in [57] for more details). The effects from boundary layers on ionic flows cannot be analyzed, which is critical for some ionic flow properties (see [63] for more details). On the other hand, boundary layers will remarkably influence the behaviors of ionic flows from distant regions of ion channels ([53]). Richer phenomenon are observed by some recent works with boundary layers ([60,64]). In this work, we use the following relaxed neutral boundary conditions to modify the electroneutrality boundary conditions (5) and characterize the ionic flow properties with boundary layers.

$$\begin{array}{c}\hfill \sum _{i=1}^k{z}_i{\mathcal{L}}_i=\sigma ·\left(-\sum _{i=k+1}^n{z}_i{\mathcal{L}}_i\right)\mathrm{a}\mathrm{n}\mathrm{d}\sum _{i=1}^k{z}_i{\mathcal{R}}_i=\rho ·\left(-\sum _{i=k+1}^n{z}_i{\mathcal{R}}_i\right),\end{array}$$

(6)

where $z_i>0$ for $i=1,2,\dots ,k$, while $z_i<0$ as $i=k+1,\dots ,n$ and $(\sigma ,\rho )\to (1,1)$. Note that when $(\sigma ,\rho )=(1,1)$, the condition (6) degenerates to electroneutrality boundary conditions (5). For convenience, we name $\sigma$ and $\rho$ as boundary layer parameters.

As mentioned above, in [50,51], the authors examine large (positive) permanent charge effects on ionic flows under electroneutrality boundary conditions. Many interesting properties of ionic flows are observed. To further understand the mechanism of ionic flows through membrane channels under more realistic setups–relaxed neutral boundary conditions in concentrations, particularly, the nonlinear interactions between different physical parameters, in the current work, as a first step, we would like to

(i)

Investigate the large permanent charge effects on individual fluxes under the relaxed neutral conditions;

(ii)

Examine the effects on ionic flows from the boundary layers due to the relaxation of the neutral boundary conditions.

The rest of this paper is organized as follows. We set up our problem in Section 2. Our results are provided in Section 3, which consists of three subsections. Section 3.1 deals with large permanent charge effects on individual fluxes with boundary layers; Section 3.2 focuses on boundary layer effects on ionic flows, while Section 3.3 provides more intuitive illustrations of our analytical results by performing numerical simulations to the underlying PNP system. In Section 4, we further discuss our results including potential extensions of current work. Finally, a conclusion section is provided in Section 5.

2. Problem Formulation

2.1. Assumptions

We take the same assumptions as those in [50,51], except the last one in our following analysis.

• Two types of ion species ($n=2$) with $z_1=-z_2=1$ are included in system;
• Distribution of the large positive permanent charge (3) is employed to characterize $\mathcal{Q}\left(X\right)$;
• Ideal component ${\mu }_i^{id}\left(X\right)$ in (4) is used to approximate the electrochemical potential ${\mu }_i\left(X\right)$;
• Relaxed neutral conditions with $n=2$ in (6):

  $$\begin{array}{c}\hfill z_1{L}_1=\sigma ·(-z_2{L}_2),z_1{R}_1=\rho ·(-z_2{R}_2)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}(\sigma ,\rho )\to (1,1).\end{array}$$

  (7)

2.2. Dimensionless Form of the Quasi-One-Dimensional PNP Model

Taking the above assumptions into consideration, we rescale the system (1) and (2) to get a dimensionless form. To be specific, let $C_0$ be a characteristic concentration of the ionic solution and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\epsilon }^2={\displaystyle \frac{{\epsilon }_r{\epsilon }_0{k}_{B}T}{e_0^2{(b_0-a_0)}^2{C}_0}},x={\displaystyle \frac{X-a_0}{b_0-a_0}},h\left(x\right)={\displaystyle \frac{A\left(X\right)}{{(b_0-a_0)}^2}},Q\left(x\right)={\displaystyle \frac{\mathcal{Q}\left(X\right)}{C_0}},\hfill \\ \hfill & D\left(x\right)=\mathcal{D}\left(X\right),\varphi \left(x\right)={\displaystyle \frac{e_0}{k_{B}T}}\mathsf{\Phi }\left(X\right),c_i\left(x\right)={\displaystyle \frac{C_i\left(X\right)}{C_0}},J_i={\displaystyle \frac{{\mathcal{J}}_i}{(b_0-a_0)C_0{\mathcal{D}}_i}},\hfill \\ \hfill & {\overline{\mu }}_i\left(x\right)={\displaystyle \frac{1}{k_{B}T}}{\mu }_i\left(X\right)=z_i\varphi \left(x\right)+ln{c}_i\left(x\right).\hfill \end{array}\end{array}$$

(8)

Correspondingly, the permanent charge profile in (3) rescales to the dimensionless form

$$Q\left(x\right)=\left\{\begin{array}{c}0,x\in [0,a)\cup (b,1]\hfill \\ 2Q_0,x\in (a,b),\hfill \end{array}\right.$$

(9)

where $Q_0={\displaystyle \frac{{\mathcal{Q}}_0}{C_0}},a={\displaystyle \frac{X_1-a_0}{b_0-a_0}},\mathrm{and}b={\displaystyle \frac{X_2-a_0}{b_0-a_0}}.$

In terms of the new variables in (8), the boundary value problem (1) and (2) becomes

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{{\epsilon }^2}{h\left(x\right)}}{\displaystyle \frac{d}{dx}}\left(h\left(x\right){\displaystyle \frac{d\varphi }{dx}}\right)=-c_1+c_2-Q\left(x\right),{\displaystyle \frac{d{J}_i}{dx}}=0,-J_i=D_i\left(x\right)h\left(x\right)c_i{\displaystyle \frac{d{\overline{\mu }}_i}{dx}}\hfill \end{array}\end{array}$$

(10)

with boundary conditions at $x=0$ and $x=1$ given by

$$\varphi \left(0\right)=V,c_i\left(0\right)=L_i;\varphi \left(1\right)=0,c_i\left(1\right)=R_i,$$

(11)

where $V={\displaystyle \frac{e_0}{k_{B}T}}\mathcal{V},L_i={\displaystyle \frac{{\mathcal{L}}_i}{C_0}}\mathrm{a}\mathrm{n}\mathrm{d}{R}_i={\displaystyle \frac{{\mathcal{R}}_i}{C_0}}.$

2.3. Existing Results

Since the nonzero permanent charge $Q_0$ is large compared to the boundary concentrations, its reciprocal $\nu =1/Q_0$ is a small parameter. One can employ regular perturbation analysis to the individual fluxes $J_k$ along $\nu =0$, that is,

$$\begin{array}{c}\hfill J_1=J_{10}+J_{11}\nu +o\left(\nu \right),J_2=J_{20}+J_{21}\nu +o\left(\nu \right).\end{array}$$

(12)

Under the assumption of electroneutrality boundary conditions, the authors in [51] obtained

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & J_{10}=0,J_{20}={\displaystyle \frac{2\sqrt{L_1{R}_1}\left(\sqrt{L_2}-\sqrt{e^V{R}_2}\right)}{H\left(1\right)(1-\beta )(\sqrt{e^V{L}_1}+\alpha \sqrt{R_1})}},\hfill \\ \hfill & J_{11}={\displaystyle \frac{e^V{L}_1-R_1}{2H\left(1\right)(\beta -\alpha )}}{\left({\displaystyle \frac{(1-\beta )L+\alpha R}{(1-\beta )\sqrt{e^V{L}_1}+\alpha \sqrt{R_1}}}\right)}^2,\hfill \\ \hfill & J_{21}=-{\displaystyle \frac{(\beta -\alpha )e^V{L}_1{R}_1\left((1-\beta )L+\alpha R\right)\left(\sqrt{e^{-V}{L}_2}-\sqrt{R_2}\right)}{H\left(1\right){\left((1-\beta )\sqrt{e^V{L}_1}+\alpha \sqrt{R_1}\right)}^3}}\hfill \\ \hfill & +{\displaystyle \frac{(e^V{L}_1-R_1)(-V+ln{L}_2-ln{R}_2){\left((1-\beta )L+\alpha R\right)}^3}{4(\beta -\alpha )H\left(1\right)\left(\sqrt{e^{-V}{L}_2}-\sqrt{R_2}\right){\left((1-\beta )\sqrt{e^V{L}_1}+\alpha \sqrt{R_1}\right)}^3}}\hfill \\ \hfill & -{\displaystyle \frac{e^V{L}_1-R_1}{2(\beta -\alpha )H\left(1\right)}}{\left({\displaystyle \frac{(1-\beta )L+\alpha R}{(1-\beta )\sqrt{e^V{L}_1}+\alpha \sqrt{R_1}}}\right)}^2,\hfill \end{array}\end{array}$$

(13)

where

$$\begin{array}{c}\hfill L^2=L_1{L}_2,R^2=R_1{R}_2,H\left(x\right)={\int }_0^x{\displaystyle \frac{1}{D\left(s\right)h\left(s\right)}}ds,\alpha ={\displaystyle \frac{H\left(a\right)}{H\left(1\right)}},\beta ={\displaystyle \frac{H\left(b\right)}{H\left(1\right)}}.\end{array}$$

(14)

This is the starting point of our studies on ionic flow properties with large permanent charges under relaxed neutral boundary conditions.

3. Results

As mentioned above, our main interest is to analyze the large permanent charge effects on ionic flows in terms of the individual fluxes under relaxed electroneutrality boundary conditions. More precisely, we study the qualitative properties of ionic flows at the state that is not neutral but close to; mathematically, we require that $(\sigma ,\rho )\to (1,1)$ but not equal to $(1,1)$ simultaneously (see (7) for the setup).

To get started, we expand $J_{11},J_{20}$, and $J_{21}$ along $(\sigma ,\rho )=(1,1)$ up to the first order and neglect higher-order terms. Careful calculation leads to

$$\begin{array}{cc}\hfill J_{11}(V;\sigma ,\rho )=& J_{11}(V;1,1)+{\displaystyle \frac{\partial J_{11}(V;1,1)}{\partial \sigma }}(\sigma -1)+{\displaystyle \frac{\partial J_{11}(V;1,1)}{\partial \rho }}(\rho -1),\hfill \\ \hfill J_{20}(V;\sigma ,\rho )=& J_{20}(V;1,1)+{\displaystyle \frac{\partial J_{20}(V;1,1)}{\partial \sigma }}(\sigma -1)+{\displaystyle \frac{\partial J_{20}(V;1,1)}{\partial \rho }}(\rho -1),\hfill \\ \hfill J_{21}(V;\sigma ,\rho )=& J_{21}(V;1,1)+{\displaystyle \frac{\partial J_{21}(V;1,1)}{\partial \sigma }}(\sigma -1)+{\displaystyle \frac{\partial J_{21}(V;1,1)}{\partial \rho }}(\rho -1),\hfill \end{array}$$

where with $w_1=(1-\beta )L_2+\alpha R_2,w_2=(1-\beta )\sqrt{e^V{L}_2}+\alpha \sqrt{R_2},w_3=\sqrt{e^{-V}{L}_2}-\sqrt{R_2},w_4=e^V{L}_2-R_2$, and $w_5=ln{L}_2-ln{R}_2-V$,

$$\begin{array}{cc}\hfill J_{11}(V;1,1)& ={\displaystyle \frac{w_1^2{w}_4}{2H\left(1\right)(\beta -\alpha )w_2^2}},\hfill \\ \hfill {\displaystyle \frac{\partial J_{11}(V;1,1)}{\partial \sigma }}& ={\displaystyle \frac{w_1}{2H\left(1\right)(\beta -\alpha )w_2^3}}[{(1-\beta )}^2{L}_2^{{\displaystyle \frac{5}{2}}}{e}^{{\displaystyle \frac{3}{2}}V}+2\alpha (1-\beta )L_2^2{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V+{\alpha }^2{L}_2{R}_2^{{\displaystyle \frac{3}{2}}}{e}^V\hfill \\ & +\alpha (1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V}-\alpha (1-\beta )L_2{R}_2^{{\displaystyle \frac{3}{2}}}],\hfill \\ \hfill {\displaystyle \frac{\partial J_{11}(V;1,1)}{\partial \rho }}& ={\displaystyle \frac{w_1}{2H\left(1\right)(\beta -\alpha )w_2^3}}[\alpha (1-\beta )L_2^{{\displaystyle \frac{3}{2}}}{R}_2{e}^{{\displaystyle \frac{3}{2}}V}-\alpha (1-\beta )L_2^2{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V\hfill \\ & -2\alpha (1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V}-{(1-\beta )}^2{L}_2^{{\displaystyle \frac{3}{2}}}{R}_2{e}^{{\displaystyle \frac{1}{2}}V}-{\alpha }^2{R}_2^{{\displaystyle \frac{5}{2}}}],\hfill \\ \hfill J_{20}(V;1,1)& ={\displaystyle \frac{2\sqrt{L_2{R}_2}{e}^{\frac{1}{2}V}{w}_3}{H\left(1\right)w_2}},{\displaystyle \frac{\partial J_{20}(V;1,1)}{\partial \sigma }}={\displaystyle \frac{\alpha \sqrt{L_2}{R}_2{e}^{\frac{1}{2}V}{w}_3}{H\left(1\right)w_2^2}},\hfill \\ \hfill {\displaystyle \frac{\partial J_{20}(V;1,1)}{\partial \rho }}& ={\displaystyle \frac{(1-\beta )L_2\sqrt{R_2}{e}^V{w}_3}{H\left(1\right)w_2^2}},\hfill \\ \hfill J_{21}(V;1,1)& =-{\displaystyle \frac{w_1^2{w}_4}{2H\left(1\right)(\beta -\alpha )w_2^2}}-{\displaystyle \frac{(\beta -\alpha )e^V{L}_2{R}_2{w}_1{w}_3}{H\left(1\right)w_2^3}}+{\displaystyle \frac{w_1^3{w}_4{w}_5}{4(\beta -\alpha )H\left(1\right)w_2^3{w}_3}},\hfill \\ \hfill {\displaystyle \frac{\partial J_{21}(V;1,1)}{\partial \sigma }}& =-{\displaystyle \frac{(\beta -\alpha )e^V{L}_2{R}_2{w}_3}{H\left(1\right)w_2^3}}\left(w_1+{\displaystyle \frac{(1-\beta )L_2}{2}}-{\displaystyle \frac{3(1-\beta )\sqrt{e^V{L}_2}{w}_1}{2w_2}}\right)\hfill \\ \hfill & +{\displaystyle \frac{w_1^2{w}_5{e}^V{L}_2}{4(\beta -\alpha )H\left(1\right)w_2^3{w}_3}}\left(w_1+{\displaystyle \frac{3(1-\beta )L_2{w}_4}{2}}-{\displaystyle \frac{3(1-\beta )\sqrt{e^V{L}_2}{w}_1{w}_4}{2w_2}}\right)\hfill \\ & -{\displaystyle \frac{e^V{L}_2{w}_1}{2H\left(1\right)(\beta -\alpha )w_2^2}}\left(w_1+(1-\beta )L_2{w}_4-{\displaystyle \frac{(1-\beta )\sqrt{e^V{L}_2}{w}_1{w}_4}{w_2}}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial J_{21}(V;1,1)}{\partial \rho }}& =-{\displaystyle \frac{(\beta -\alpha )e^V{L}_2{R}_2{w}_3}{H\left(1\right)w_2^3}}\left(w_1+{\displaystyle \frac{\alpha R_2}{2}}-{\displaystyle \frac{3\alpha \sqrt{R_2}{w}_1}{2w_2}}\right)\hfill \\ \hfill & +{\displaystyle \frac{w_1^2{w}_5}{4(\beta -\alpha )H\left(1\right)w_2^3{w}_3}}\left(-R_2{w}_1+{\displaystyle \frac{3\alpha R_2{w}_4}{2}}-{\displaystyle \frac{3\alpha \sqrt{R_2}{w}_1{w}_4}{2w_2}}\right)\hfill \\ & -{\displaystyle \frac{w_1}{2H\left(1\right)(\beta -\alpha )w_2^2}}\left(-R_2{w}_1+\alpha R_2{w}_4-{\displaystyle \frac{\alpha \sqrt{R_2}{w}_1{w}_4}{w_2}}\right).\hfill \end{array}$$

For convenience, in our following discussion, we rewrite $J_{11},J_{20}$, and $J_{21}$ as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& J_{11}={\displaystyle \frac{w_1}{2H\left(1\right)(\beta -\alpha )w_2^3}}\left[\right(2\alpha (1-\beta )L_2^2{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V+{(1-\beta )}^2{L}_2^{{\displaystyle \frac{5}{2}}}{e}^{{\displaystyle \frac{3}{2}}V}+{\alpha }^2{L}_2{R}_2^{{\displaystyle \frac{3}{2}}}{e}^V-\hfill \\ & \alpha (1-\beta )L_2{R}_2^{{\displaystyle \frac{3}{2}}}+\alpha (1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V})\sigma +(-2\alpha (1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V}\hfill \\ & -{(1-\beta )}^2{L}_2^{{\displaystyle \frac{3}{2}}}{R}_2{e}^{{\displaystyle \frac{1}{2}}V}-{\alpha }^2{R}_2^{{\displaystyle \frac{5}{2}}}+\alpha (1-\beta )L_2^{{\displaystyle \frac{3}{2}}}{R}_2{e}^{{\displaystyle \frac{3}{2}}V}-\alpha (1-\beta )L_2^2{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V\left)\rho \right],\hfill \\ & J_{20}={\displaystyle \frac{\sqrt{L_2{R}_2}(\sqrt{L_2}-\sqrt{e^V{R}_2})}{H\left(1\right)w_2^2}}\left[\alpha \sqrt{R_2}(\sigma +1)+(1-\beta )\sqrt{e^V{L}_2}(\rho +1)\right],\hfill \\ & J_{21}={\displaystyle \frac{(\beta -\alpha )L_2{e}^V{R}_2{w}_1{w}_3(1-\sigma -\rho )}{H\left(1\right)w_2^3}}+{\displaystyle \frac{w_1^2(e^V{L}_2\sigma -R_2\rho )}{2(\beta -\alpha )H\left(1\right)w_2^2}}\left({\displaystyle \frac{w_1{w}_5}{2w_2{w}_3}}-1\right)\hfill \\ & +{\displaystyle \frac{[(1-\beta )L_2(1-\sigma )+\alpha R_2(1-\rho )]}{2H\left(1\right)w_2^2}}({\displaystyle \frac{(\beta -\alpha )L_2{R}_2{e}^V{w}_3}{(1-\beta )\sqrt{e^V{L}_2}+\alpha \sqrt{R_2}}}\hfill \\ & +{\displaystyle \frac{w_2(e^V{L}_2-R_2)}{\beta -\alpha }}-{\displaystyle \frac{3w_1^2{w}_4{w}_5}{4(\beta -\alpha )w_2{w}_3}})\hfill \\ & +{\displaystyle \frac{w_1[(1-\beta )\sqrt{e^V{L}_2}(\sigma -1)+\alpha \sqrt{R_2}(\rho -1)]}{2H\left(1\right)w_2^3}}\hfill \\ & \times \left({\displaystyle \frac{3(\beta -\alpha )L_2{R}_2{e}^V{w}_3}{w_2}}+{\displaystyle \frac{w_1{w}_4}{\beta -\alpha }}-{\displaystyle \frac{3w_1^2{w}_4{w}_5}{4(\beta -\alpha )w_2{w}_3}}\right).\hfill \end{array}\end{array}$$

(15)

3.1. Analysis of Individual Fluxes with Boundary Layers

We first examine the large permanent charge effects on the individual fluxes with boundary layers due to the relaxation of boundary neutral conditions. To get started, we consider the monotonicity of $J_{11}$ and $J_{20}$ in (15) with respect to the electric potential V, which is critical for our discussion of the large permanent charge effects on ionic flows.

Lemma 1.

Assume that $(\sigma ,\rho )\to (1,1)$. For the leading terms of the counterion flow $J_2$ and the co-ion flow $J_1$, one has ${\partial }_V{J}_{20}<0$ and ${\partial }_V{J}_{11}>0.$

Proof. 

Direct calculation gives

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{\partial J_{11}}{\partial V}}={\displaystyle \frac{w_1}{2H\left(1\right)(\beta -\alpha )w_2^4}}(L_2{R}_2{e}^V[{\alpha }^3{R}_2\sigma +{(1-\beta )}^3{L}_2\rho ]\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\alpha {(1-\beta )}^2{L}_2^{{\displaystyle \frac{5}{2}}}{R}_2^{{\displaystyle \frac{1}{2}}}{e}^{{\displaystyle \frac{3}{2}}V}(\sigma +\rho )+{\displaystyle \frac{1}{2}}{\alpha }^2(1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^{{\displaystyle \frac{5}{2}}}{e}^{{\displaystyle \frac{1}{2}}V}(\sigma +\rho )\hfill \\ \hfill & +{\alpha }^2(1-\beta )L_2^2{R}_2{e}^V(2\sigma -\rho )+\alpha {(1-\beta )}^2{L}_2{R}_2^2{e}^V(2\rho -\sigma )\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\alpha {(1-\beta )}^2{L}_2^{{\displaystyle \frac{3}{2}}}{R}_2^{{\displaystyle \frac{3}{2}}}{e}^{{\displaystyle \frac{1}{2}}V}(3\sigma -\rho )+{\displaystyle \frac{1}{2}}{\alpha }^2(1-\beta )L_2^{{\displaystyle \frac{3}{2}}}{R}_2^{{\displaystyle \frac{3}{2}}}{e}^{{\displaystyle \frac{3}{2}}V}(3\rho -\sigma )),\hfill \\ \hfill & {\displaystyle \frac{\partial J_{20}}{\partial V}}={\displaystyle \frac{\alpha (1-\beta )L_2{R}_2{e}^V}{2H\left(1\right)w_2^3}}\left(-\sqrt{L_2{e}^{-V}}(2\sigma -\rho +1)+\sqrt{R_2}(\sigma -2\rho -1)\right).\hfill \end{array}\end{array}$$

Note that $(\sigma ,\rho )\to (1,1)$ and $0<\alpha <\beta <1.$ Together with the fact that $L_2>0$ and $R_2>0$, one has ${\displaystyle \frac{\partial J_{11}}{\partial V}}>0$ directly. As for ${\displaystyle \frac{\partial J_{20}}{\partial V}}$, the sign is determined by the term

$$-\sqrt{L_2{e}^{-V}}(2\sigma -\rho +1)+\sqrt{R_2}(\sigma -2\rho -1),$$

which is clearly negative with $(\sigma ,\rho )\to (1,1).$ This completes the proof.

□

Note that

$$\begin{array}{cc}\hfill & \underset{V\to -\infty }{lim}{J}_{11}=-{\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){\alpha }^2}}[(1-\beta )L_2\sigma +\alpha R_2\rho ]<0,\hfill \\ \hfill & \underset{V\to \infty }{lim}{J}_{11}={\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){(1-\beta )}^2}}[(1-\beta )L_2\sigma +\alpha R_2\rho ]>0.\hfill \end{array}$$

Together with Lemma 1, we have the following definition.

Definition 1.

We define two critical potentials $V_{1c}$ and $V_{2c}$ by

$$J_{11}\left(V_{1c}\right)=0\mathit{and}{J}_{20}\left(V_{2c}\right)=0.$$

We are now ready to establish one of our main results.

Theorem 1.

Assume $\epsilon >0$ small and $\nu >0$ small.

(i)

Small parameter ν enhances $J_1$ if $V>V_{1c}$ while reducing it if $V<V_{1c}$. That is, $J_{11}(V;\sigma ,\rho ;\nu )>0$ (resp. $J_{11}(V;\sigma ,\rho ;\nu )<0$) if $V>V_{1c}$ (resp. $V<V_{1c}$). Equivalently, the large permanent charge reduces cation’s flux $J_1$ if $V>V_{1c}$ while enhancing it if $V<V_{1c}$.

(ii)

The large permanent charge strengthens anion’s flow $J_2$ if $V<V_{2c}$ while weakening it if $V>V_{2c}$. That is, $J_{20}(V;\sigma ,\rho )>0$ (resp. $J_{20}(V;\sigma ,\rho )<0$) if $V<V_{2c}$ (resp. $V>V_{2c}$).

Proof. 

The proof is straightforward and we skip it here. □

We now consider the concavity of the leading terms $J_{20}$ and $J_{11}$ with respect to the electric potential V.

Lemma 2.

Assume that $(\sigma ,\rho )\to (1,1)$.

(i)

There exists a unique critical potential $V_{1\ast }$ such that ${\partial }_V^2{J}_{11}>0$ for $V<V_{1\ast }$ and ${\partial }_V^2{J}_{11}<0$ for $V>V_{1\ast }$.

(ii)

${\partial }_V^2{J}_{20}>0$ as $V>ln{\displaystyle \frac{4R_2{\alpha }^2}{L_2{(1-\beta )}^2}}$ and ${\partial }_V^2{J}_{20}<0$ as $V<ln{\displaystyle \frac{R_2{\alpha }^2}{4L_2{(1-\beta )}^2}}$.

Proof. 

From (15), direct calculation gives

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\displaystyle \frac{{\partial }^2{J}_{11}}{\partial V^2}}={\displaystyle \frac{[(1-\beta )L_2+\alpha R_2]\sqrt{e^V}}{2H\left(1\right)(\beta -\alpha ){\left[(1-\beta )\sqrt{e^V{L}_2}+\alpha \sqrt{R_2}\right]}^5}}{f}_1\left(V\right),\hfill \\ \hfill & {\displaystyle \frac{{\partial }^2{J}_{20}}{\partial V^2}}={\displaystyle \frac{L_2{R}_2\alpha (1-\beta )e^V}{4H\left(1\right){\left[(1-\beta )\sqrt{e^V{L}_2}+\alpha \sqrt{R_2}\right]}^4}}[\left(2L_2(1-\beta )-\sqrt{{\displaystyle \frac{L_2{R}_2}{e^V}}}\alpha \right)(2\sigma -\rho +1)\hfill \\ \hfill & +\left(2R_2\alpha -\sqrt{L_2{R}_2{e}^V}(1-\beta )\right)(\sigma -2\rho -1)],\hfill \end{array}\end{array}$$

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & f_1\left(V\right)=-{\displaystyle \frac{1}{2}}{(1-\beta )}^2{L}_2^2{e}^{{\displaystyle \frac{3}{2}}V}[(1-\beta )L_2\sigma +\alpha R_2\rho ]+\alpha {(1-\beta )}^2{L}_2^{{\displaystyle \frac{5}{2}}}{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V\left(-{\displaystyle \frac{1}{2}}\sigma +\rho \right)\hfill \\ \hfill & +{\alpha }^2(1-\beta )L_2^{{\displaystyle \frac{3}{2}}}{R}_2^{{\displaystyle \frac{3}{2}}}{e}^V\left({\displaystyle \frac{3}{2}}\rho -\sigma \right)+\alpha {(1-\beta )}^2{L}_2^{{\displaystyle \frac{3}{2}}}{R}_2^{{\displaystyle \frac{3}{2}}}\left(2\sigma -{\displaystyle \frac{1}{2}}\rho \right)\hfill \\ \hfill & +{\alpha }^2(1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^{{\displaystyle \frac{5}{2}}}\left({\displaystyle \frac{1}{2}}\sigma +\rho \right)+\alpha {(1-\beta )}^2{L}_2{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V}\left(3\rho -{\displaystyle \frac{3}{2}}\sigma \right)\hfill \\ \hfill & +{\alpha }^2(1-\beta )L_2^2{R}_2{e}^{{\displaystyle \frac{1}{2}}V}(2\sigma -\rho )+L_2{R}_2{e}^{{\displaystyle \frac{1}{2}}V}\left[{\alpha }^3{R}_2\sigma +{\displaystyle \frac{3}{2}}{(1-\beta )}^3{L}_2\rho \right].\hfill \end{array}\end{array}$$

Taking the derivative of $f_1$ with respect to V and further letting $t=e^{{\displaystyle \frac{1}{2}}V}$, one has $f_1^{\prime }\left(t\right)=t·g_1\left(t\right)$, where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & g_1\left(t\right)=-{\displaystyle \frac{3}{4}}{(1-\beta )}^2{L}_2^2[(1-\beta )L_2\sigma +\alpha R_2\rho ]t^2+\alpha (1-\beta )L_2^{{\displaystyle \frac{3}{2}}}{R}_2^{{\displaystyle \frac{1}{2}}}[(1-\beta )L_2\left(-{\displaystyle \frac{1}{2}}\sigma +\rho \right)\hfill \\ & +\alpha R_2\left({\displaystyle \frac{3}{2}}\rho -\sigma \right)]t+{\displaystyle \frac{1}{2}}\alpha {(1-\beta )}^2{L}_2{R}_2^2\left(3\rho -{\displaystyle \frac{3}{2}}\sigma \right)+{\displaystyle \frac{1}{2}}{\alpha }^2(1-\beta )L_2^2{R}_2(2\sigma -\rho )\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{L}_2{R}_2\left[{\alpha }^3{R}_2\sigma +{\displaystyle \frac{3}{2}}{(1-\beta )}^3{L}_2\rho \right].\hfill \end{array}\end{array}$$

Note that $g_1\left(t\right)$ is a quadratic function and concave down. Note also that

$$t^c={\displaystyle \frac{2\alpha R_2^{\frac{1}{2}}}{3(1-\beta )L_2^{\frac{1}{2}}}}\left((1-\beta )L_2\left(\rho -{\displaystyle \frac{1}{2}}\sigma \right)+\alpha R_2\left({\displaystyle \frac{3}{2}}\rho -\sigma \right)\right)>0$$

is the unique critical point. Together with $g_1\left(0\right)>0$, one concludes that there exists a root of $g_1\left(t\right)$, say $t_{\ast }>t^c$, such that $g_1\left(t\right)>0$ as $0<t<t_{\ast }$, while $g_1\left(t\right)<0$ as $t>t_{\ast }$. Since $f_1^{\prime }\left(t\right)=t·g_1\left(t\right)$ and $t=e^{{\displaystyle \frac{1}{2}}V}$, one has $f_1$ is increasing (resp. decreasing) as $V<V_{\ast }$ (resp. $V>V_{\ast }$) where $V_{\ast }=2ln{t}_{\ast }$, and together with

$$\begin{array}{cc}\hfill & \underset{V\to -\infty }{lim}{f}_1\left(V\right)=\alpha {(1-\beta )}^2{L}_2^{{\displaystyle \frac{3}{2}}}{R}_2^{{\displaystyle \frac{3}{2}}}\left(2\sigma -{\displaystyle \frac{1}{2}}\rho \right)+{\alpha }^2(1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^{{\displaystyle \frac{5}{2}}}\left({\displaystyle \frac{1}{2}}\sigma +\rho \right)>0,\hfill \\ \hfill & \underset{V\to \infty }{lim}{f}_1\left(V\right)=\underset{V\to \infty }{lim}-{\displaystyle \frac{1}{2}}{(1-\beta )}^2{L}_2^2{e}^{{\displaystyle \frac{3}{2}}V}[(1-\beta )L_2\sigma +\alpha R_2\rho ]=-\infty ,\hfill \end{array}$$

we can conclude that there exists one unique root $V_{1\ast }$ of $f_1\left(V\right)$ such that $f_1\left(V\right)>0$ for $V<V_{1\ast }$ and $f_1\left(V\right)<0$ for $V>V_{1\ast }$. Note that ${\partial }_V^2{J}_{11}$ has the same sign as $f_1\left(V\right)$. The statement (i) follows. The discussion for the second statement is similar, and we omit it here. □

We are now able to discuss the saturation properties for the individual fluxes and the total current, which reflect the behaviors of ionic flows as $\left|V\right|$ goes to a large quantity. From Lemmas 1 and 2, the following result can be established.

Corollary 1.

[Saturation Property] For large permanent charge $Q_0$ (small $\nu =1/Q_0$), up to the leading terms in ν, the individual fluxes $J_1$ and $J_2$ saturate in $\left|V\right|$. Furthermore, $|J_{11}|$ and $|J_{20}|$ are uniformly bounded in V, which can be determined by

$$\begin{array}{cc}\hfill \underset{V\to -\infty }{lim}{J}_{11}& =-{\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){\alpha }^2}}[(1-\beta )L_2\sigma +\alpha R_2\rho ],\hfill \\ \hfill \underset{V\to \infty }{lim}{J}_{11}& ={\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){(1-\beta )}^2}}[(1-\beta )L_2\sigma +\alpha R_2\rho ],\hfill \\ \hfill \underset{V\to -\infty }{lim}{J}_{20}& ={\displaystyle \frac{L_2}{H\left(1\right)\alpha }}(\sigma +1),\underset{V\to \infty }{lim}{J}_{20}=-{\displaystyle \frac{R_2}{H\left(1\right)(1-\beta )}}(\rho +1).\hfill \end{array}$$

3.2. Boundary Layer Effects on Ionic Flows

In this section, we further investigate the boundary layer effects on the qualitative properties of ionic flows with large permanent charges. To get started, we introduce two critical potentials $V_{1c}^{EN}$ and $V_{2c}^{EN}$ with the up-script $EN$ indicating that they are obtained under electroneutrality conditions.

Definition 2.

We define two critical potentials $V_{1c}^{EN}$ and $V_{2c}^{EN}$, such that

$$J_{11}^{EN}\left(V_{1c}^{EN}\right)=0and{J}_{20}^{EN}\left(V_{2c}^{EN}\right)=0,$$

where $-V_{1c}^{EN}=V_{2c}^{EN}=ln{\displaystyle \frac{L_2}{R_2}}$.

Comparing with the critical potentials in definition 1, one has $V_{2c}^{EN}=V_{2c}$. As for the order of $V_{1c}^{EN}$ and $V_{1c}$, the following result can be established.

Lemma 3.

One has $V_{1c}>V_{1c}^{EN}$ if $\sigma <\rho$ and $V_{1c}<V_{1c}^{EN}$ if $\sigma >\rho$.

Proof. 

From (15),

$$\begin{array}{cc}\hfill J_{11}=& {\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){\left[(1-\beta )\sqrt{e^V{L}_2}+\alpha \sqrt{R_2}\right]}^3}}{f}_2\left(V\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill f_2\left(V\right)=& \left[\right(2\alpha (1-\beta )L_2^2{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V+{(1-\beta )}^2{L}_2^{{\displaystyle \frac{5}{2}}}{e}^{{\displaystyle \frac{3}{2}}V}+{\alpha }^2{L}_2{R}_2^{{\displaystyle \frac{3}{2}}}{e}^V-\alpha (1-\beta )L_2{R}_2^{{\displaystyle \frac{3}{2}}}\hfill \\ & +\alpha (1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V})\sigma +(-2\alpha (1-\beta )L_2^{{\displaystyle \frac{1}{2}}}{R}_2^2{e}^{{\displaystyle \frac{1}{2}}V}-{(1-\beta )}^2{L}_2^{{\displaystyle \frac{3}{2}}}{R}_2{e}^{{\displaystyle \frac{1}{2}}V}\hfill \\ & -{\alpha }^2{R}_2^{{\displaystyle \frac{5}{2}}}+\alpha (1-\beta )L_2^{{\displaystyle \frac{3}{2}}}{R}_2{e}^{{\displaystyle \frac{3}{2}}V}-\alpha (1-\beta )L_2^2{R}_2^{{\displaystyle \frac{1}{2}}}{e}^V\left)\rho \right].\hfill \end{array}$$

Note that ${\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){\left[(1-\beta )\sqrt{e^V{L}_2}+\alpha \sqrt{R_2}\right]}^3}}$ is positive. Evaluating $f_2\left(V\right)$ at $V=V_{1c}^{EN}$, one has

$$\begin{array}{c}\hfill f_2\left(V_{1c}^{EN}\right)=R_2^{{\displaystyle \frac{3}{2}}}\left[{\alpha }^2{R}_2+{(1-\beta )}^2{L}_2\right](\sigma -\rho )+\alpha (1-\beta )R_2^{{\displaystyle \frac{3}{2}}}(L_2+R_2)(\sigma -\rho ).\end{array}$$

It is easy to verify that $f_2\left(V_{1c}^{EN}\right)$ is positive (resp. negative) if $\sigma >\rho$ (resp. $\sigma <\rho$). Recall that ${\partial }_V{J}_{11}\left(V\right)>0$ and $f_2\left(V_{1c}\right)=0$, we obtain $V_{1c}<V_{1c}^{EN}$ (resp. $V_{1c}>V_{1c}^{EN}$) if $\sigma >\rho$ (resp. $\sigma <\rho$). This completes the proof. □

From Lemmas 1 and 3, together with the description of $J_{11}\left(V\right)$ in Lemma 1 and $J_{11}^{EN}\left(V\right)$ in Corollary 3.2 of [50], it allows us to further characterize the boundary layer effects on ionic flows in terms of $J_{11}$.

Theorem 2.

Assume that $(\sigma ,\rho )\to (1,1,)$. For small $\epsilon >0$ and small $\nu >0$, one has

(i)

For $\sigma >\rho$,

(i1)

$J_1(V;\sigma ,\rho ;\nu )<0$ and $J_1^{EN}(V;1,1;\nu )<0$ over $(-\infty ,V_{1c})$. That is, the small parameter ν reduces cation’s fluxes $J_1$ and $J_1^{EN}$, equivalently, and the large permanent charge $Q_0$ enhances both $J_1$ and $J_1^{EN}$.

(i2)

$J_1(V;\sigma ,\rho ;\nu )>0$ but $J_1^{EN}(V;1,1;\nu )<0$ over $(V_{1c},V_{1c}^{EN})$. That is, the small parameter ν enhances $J_1$ while reducing $J_1^{EN}$, equivalently, the large permanent charge $Q_0$ reduces $J_1$ while enhancing $J_1^{EN}$.

(i3)

$J_1(V;\sigma ,\rho ;\nu )>0$ and $J_1^{EN}(V;1,1;\nu )>0$ over $(V_{1c}^{EN},\infty )$. That is, the small parameter ν enhances cation’s fluxes $J_1$ and $J_1^{EN}$, equivalently, and the large permanent charge $Q_0$ reduces both $J_1$ and $J_1^{EN}$.

(ii)

For $\sigma <\rho$,

(ii1)

$J_1(V;\sigma ,\rho ;\nu )<0$ and $J_1^{EN}(V;1,1;\nu )<0$ over $(-\infty ,V_{1c}^{EN})$. That is, the small parameter ν reduces cation’s fluxes $J_1$ and $J_1^{EN}$, equivalently, and the large permanent charge $Q_0$ enhances both $J_1$ and $J_1^{EN}$.

(ii2)

$J_1(V;\sigma ,\rho ;\nu )<0$ but $J_1^{EN}(V;1,1;\nu )>0$ over $(V_{1c}^{EN},V_{1c})$. That is, the small parameter ν reduces $J_1$ while enhancing $J_1^{EN}$, equivalently, and the large permanent charge $Q_0$ enhances $J_1$ while reducing $J_1^{EN}$.

(ii3)

$J_1(V;\sigma ,\rho ;\nu )>0$ and $J_1^{EN}(V;1,1;\nu )>0$ over $(V_{1c},\infty )$. That is, the large permanent charge enhances cation’s fluxes $J_1$ and $J_1^{EN}$, equivalently, and the large permanent charge $Q_0$ reduces both $J_1$ and $J_1^{EN}$.

Proof. 

We will just provide a detailed proof for statement (i1); others can be discussed similarly. From Theorem 1, one has $J_{11}(V;\sigma ,\rho ;\nu )<0$ for $V<V_{1c}$. From Corollary $3.2$ in [50], $J_{11}^{EN}(V;1,1;\nu )<0$ for $V<V_{1c}^{EN}$. In Lemma 3, we have shown that $V_{1c}<V_{1c}^{EN}$ as $\sigma >\rho$. Recall that $J_1=J_{11}\nu +o\left(\nu \right)$. Correspondingly, with $\sigma >\rho$ and $V<V_{1c}$, one has $J_1(V;\sigma ,\rho ;\nu )<0$ and $J_1^{EN}(V;1,1;\nu )<0$. That is, the small parameter $\nu$ reduces both $J_1$ and $J_1^{EN}$ over this region, equivalently, and the large permanent charge $Q_0$ enhances both $J_1$ and $J_1^{EN}$ for $\sigma >\rho$ and $V<V_{1c}$. This completes the proof of the statement (i1). □

Remark 1.

From the above theorem, we observe that over some specific potential subregion, the large permanent charge plays opposite roles in the cation flux $J_1$ under different boundary conditions. To be specific, as shown in the case (i2), with $\sigma >\rho$, the large permanent charge reduces $J_1$, while under electroneutrality boundary conditions, the large permanent charge enhances $J_1^{EN}$ over the same potential region $(V_{1c},V_{1c}^{EN})$. One can also find this discrepancy on $(V_{1c}^{EN},V_{1c})$ with $\sigma <\rho$ (see case (ii2) for details). Those discrepancies indicate that the ionic flow properties are sensitive to the boundary layers, and this observation could be critical for future numerical and even experimental studies. We also demonstrate that those various and nonintuitive behaviors between $J_{11}$ and $J_1^{EN}$ depend on the nonlinear interaction among the boundary layer parameters $(\sigma ,\rho )$, large permanent charges $Q_0$, boundary potential V, boundary concentrations $(L_1,L_2;R_1,R_2)$, and channel geometry in terms of $(\alpha ,\beta )$.

To further examine the effects from boundary layers, we next consider the magnitudes of each individual flux at saturation state.

Theorem 3.

Assume $(\sigma ,\rho )\to (1,1)$, for the magnitudes of cation’s flux $J_{11}$ at the saturation state, one has

(i)

$\left|J_{11}\right|<|J_{11}^{EN}|$ as $\left|V\right|\to \infty$ if one of the following conditions holds

(i1)

$\sigma \to 1^{-}$, $\rho \to 1^{-}$;

(i2)

$\sigma \to 1^{+}$, $\rho \to 1^{-}$, ${\displaystyle \frac{L_2(1-\beta )}{R_2\alpha }}<{\displaystyle \frac{\rho -1}{1-\sigma }}$.

(ii)

$\left|J_{11}\right|>|J_{11}^{EN}|$ as $\left|V\right|\to \infty$ if one of the following conditions holds

(ii1)

$\sigma \to 1^{+}$, $\rho \to 1^{+}$;

(ii2)

$\sigma \to 1^{-}$, $\rho \to 1^{+}$, ${\displaystyle \frac{L_2(1-\beta )}{R_2\alpha }}<{\displaystyle \frac{\rho -1}{1-\sigma }}$.

(iii)

$\left|J_{11}\right|<|J_{11}^{EN}|$ as $V\to -\infty$, while $\left|J_{11}\right|>|J_{11}^{EN}|$ as $V\to \infty$ if $\sigma \to 1^{-}$, $\rho \to 1^{+}$, ${\displaystyle \frac{L_2(1-\beta )}{R_2\alpha }}>{\displaystyle \frac{\rho -1}{1-\sigma }}$.

(iv)

$\left|J_{11}\right|>\left|J_{11}^{EN}\right|$ as $V\to -\infty$, while $\left|J_{11}\right|<\left|J_{11}^{EN}\right|$ as $V\to \infty$ if $\sigma \to 1^{+}$, $\rho \to 1^{-}$, ${\displaystyle \frac{L_2(1-\beta )}{R_2\alpha }}>{\displaystyle \frac{\rho -1}{1-\sigma }}$.

Proof. 

From Corollary 3.2 in [50], one has

$$\begin{array}{cc}\hfill \underset{V\to -\infty }{lim}{J}_{11}^{EN}& =-{\displaystyle \frac{{\left[(1-\beta )L_2+\alpha R_2\right]}^2}{2H\left(1\right)(\beta -\alpha ){\alpha }^2}},\underset{V\to \infty }{lim}{J}_{11}^{EN}={\displaystyle \frac{{\left[(1-\beta )L_2+\alpha R_2\right]}^2}{2H\left(1\right)(\beta -\alpha ){(1-\beta )}^2}}.\hfill \end{array}$$

Using the limits of $J_{11}$ in Corollary 1 and those for $J_{11}^{EN}$, one can calculate that

$$\begin{array}{cc}\hfill \underset{V\to -\infty }{lim}\left(J_{11}-J_{11}^{EN}\right)& =-{\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){\alpha }^2}}\left[(1-\beta )L_2(\sigma -1)+\alpha R_2(\rho -1)\right],\hfill \\ \hfill \underset{V\to \infty }{lim}\left(J_{11}-J_{11}^{EN}\right)& ={\displaystyle \frac{(1-\beta )L_2+\alpha R_2}{2H\left(1\right)(\beta -\alpha ){(1-\beta )}^2}}\left[(1-\beta )L_2(\sigma -1)+\alpha R_2(\rho -1)\right].\hfill \end{array}$$

Therefore, as $(\sigma ,\rho )\to (1^{-},1^{-})$, one has

$$\underset{V\to -\infty }{lim}\left(J_{11}-J_{11}^{EN}\right)>0,\mathrm{w}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{e}\underset{V\to \infty }{lim}\left(J_{11}-J_{11}^{EN}\right)<0.$$

On the other hand, we have $\underset{V\to -\infty }{lim}{J}_{11}<0$, $\underset{V\to -\infty }{lim}{J}_{11}^{EN}<0$ and $\underset{V\to \infty }{lim}{J}_{11}>0$, $\underset{V\to \infty }{lim}{J}_{11}^{EN}>0$. It then follows that $\left|J_{11}\right|<|J_{11}^{EN}|$ as $\left|V\right|\to \infty$ with $(\sigma ,\rho )\to (1^{-},1^{-})$, which is depicted in case (i1). Other cases can be discussed similarly. □

Similar arguments lead to the following results for the anion’s flux $J_{20}$.

Theorem 4.

Assume $(\sigma ,\rho )\to (1,1)$, for the magnitude of anion’s flux $J_{20}$ at the saturation state, one has

(i)

$\left|J_{20}\right|<\left|J_{20}^{EN}\right|$ as $\left|V\right|\to \infty$ if $\sigma \to 1^{-}$, $\rho \to 1^{-}$.

(ii)

$\left|J_{20}\right|>\left|J_{20}^{EN}\right|$ as $\left|V\right|\to \infty$ if $\sigma \to 1^{+}$, $\rho \to 1^{+}$.

(iii)

$\left|J_{20}\right|<\left|J_{20}^{EN}\right|$ as $V\to -\infty$, while $\left|J_{20}\right|>\left|J_{20}^{EN}\right|$ as $V\to \infty$ if $\sigma \to 1^{-}$, $\rho \to 1^{+}$.

(iv)

$\left|J_{20}\right|>\left|J_{20}^{EN}\right|$ as $V\to -\infty$, while $\left|J_{20}\right|<\left|J_{20}^{EN}\right|$ as $V\to \infty$ if $\sigma \to 1^{+}$, $\rho \to 1^{-}$.

3.3. Numerical Simulations

To provide more intuitive illustrations for some analytical results, we perform numerical simulations to the following system by letting $u=\epsilon {\displaystyle \frac{d\varphi }{dx}}$ in (10),

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \epsilon {\displaystyle \frac{d\varphi }{dx}}=& u,{\displaystyle \frac{\epsilon }{h\left(x\right)}}{\displaystyle \frac{d}{dx}}\left(h\left(x\right)u\right)=-c_1+c_2-Q\left(x\right),\hfill \\ \hfill \epsilon {\displaystyle \frac{d{c}_1}{dx}}=& -c_{1}u-\epsilon {\displaystyle \frac{J_1}{h\left(x\right)}},\epsilon {\displaystyle \frac{d{c}_2}{dx}}=c_{2}u-\epsilon {\displaystyle \frac{J_2}{h\left(x\right)}},{\displaystyle \frac{d{J}_1}{dx}}={\displaystyle \frac{d{J}_2}{dx}}=0,\hfill \end{array}\end{array}$$

(16)

with boundary conditions

$$\varphi \left(0\right)=V,c_i\left(0\right)=L_i;\varphi \left(1\right)=0,c_i\left(1\right)=R_i,i=1,2.$$

(17)

Our numerical study consists of two directions:

(i)

Numerically verify the saturation properties of $J_{11}\left(V\right)$ and $J_{20}\left(V\right)$ under different setups (see Figure 1 and Figure 2).

(ii)

Numerically identify the two critical potentials $V_{1c}$ and $V_{1c}^{EN}$ under different setups for the boundary layer parameters $(\sigma ,\rho )$ and illustrate our analytical results stated in Theorem 2 (see Figure 3).

In our numerical simulation, we take

$$\epsilon =0.008,a={\displaystyle \frac{1}{3}},b={\displaystyle \frac{1}{2}},r_0=0.5,\nu =0.01,L_2=0.5,R_2={10}^{-5}$$

and

$$h\left(x\right)=\left\{\begin{array}{cc}\pi {(-x+r_0+a)}^2\hfill & \mathrm{if}x\in (0,a)\hfill \\ \pi r_0^2\hfill & \mathrm{if}x\in (a,b)\hfill \\ \pi {(x+r_0-b)}^2\hfill & \mathrm{if}x\in (b,1).\hfill \end{array}\right.$$

Correspondingly, one has

$$\alpha =0.3243243\mathrm{a}\mathrm{n}\mathrm{d}\beta =0.594595.$$

We demonstrate that, with $\nu =0.01,$ one has $Q_0=100$, which is large compared to the boundary concentrations $L_2=0.5$ and $R_2={10}^{-5}$.

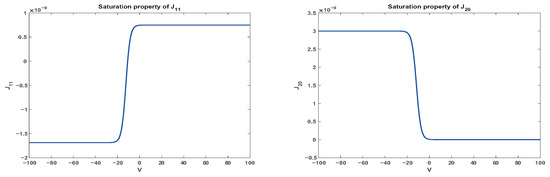
Figure 1. Saturation properties for individual fluxes $J_{11}$ and $J_{20}$.

Figure 1. Saturation properties for individual fluxes $J_{11}$ and $J_{20}$.

For the first numerical task, five different pairs of values for the boundary layer parameters $(\sigma ,\rho )$ are taken. More precisely, we choose $(\sigma ,\rho )=(1,1)$ corresponding to electroneutrality boundary conditions, while $({\sigma }_1,{\rho }_1)=(0.9998,0.9999)$, $({\sigma }_2,{\rho }_2)=(0.9999,1.0001)$, $({\sigma }_3,{\rho }_3)=(1.0001,0.9999)$, and (${\sigma }_4,{\rho }_4)=(1.0001,1.0002)$ indicate the existence of boundary layers. However, due to the fact that all those values of $({\sigma }_k,{\rho }_k),k=1,2,3,4$ are close to $(1,1)$, curves generated under different values of $\sigma$ and $\rho$ are very close to each other; for this, we provide the zoom-in version (Figure 2) to tell the difference and observe the boundary layer effects.

The numerical result shown in Figure 2 is consistent with our analytical results stated in Theorems 3 and 4. We next take the first column graphs for $J_{11}$ in Figure 2 for example (others can be checked similarly) to connect with our analytical results. Note that the top two graphs are for $V<0$, while the bottom two ones are for $V>0$. The red curve represents $J_{11}$ with $\sigma =0.9998<\rho =0.9999$. When the potential V is negative and gets smaller, the red curve is above the black one that stands for $J_{11}^{EN}$, the one under electroneutrality boundary conditions (that is, $(\sigma ,\rho )=(1,1)$). Directly, one has $\left|J_{11}\right|<\left|J_{11}^{EN}\right|$ as $V\to -\infty$. From the bottom two graphs with $V>0$, the red curve now is below the black one, and we have $\left|J_{11}\right|<\left|J_{11}^{EN}\right|$ as $V\to \infty$. Either way, we have $\left|J_{11}\right|<\left|J_{11}^{EN}\right|$ as $\left|V\right|\to \infty$ and $(\sigma ,\rho )\to (1^{-},1^{-})$ with $\sigma <\rho$. This is stated in case (i1) of Theorem 3.

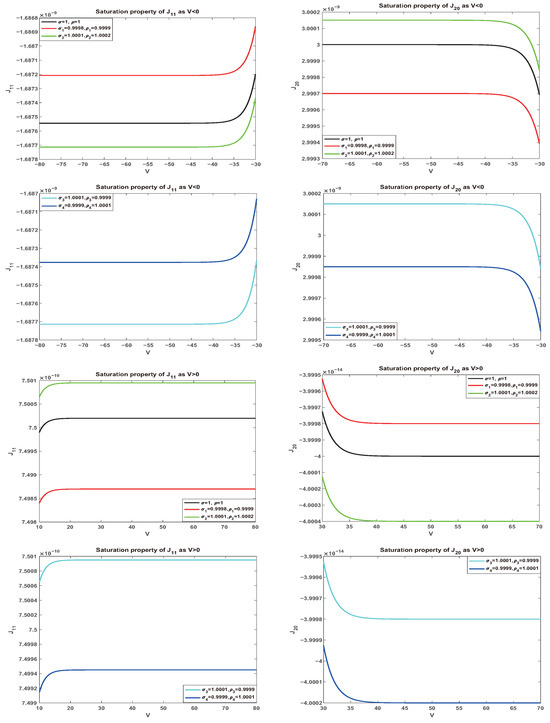
Figure 2. Zoom-in version of the saturation properties for $J_{11}$ and $J_{20}$ with different values for $\sigma$ and $\beta$.

Figure 2. Zoom-in version of the saturation properties for $J_{11}$ and $J_{20}$ with different values for $\sigma$ and $\beta$.

Our second numerical task is to identify the two critical potentials $V_{1c}$ and $V_{1c}^{EN}$ for two cases: (i) $\sigma >1>\rho$ and (ii) $\sigma <1<\rho$. From Figure 3 (the left one), it is clear that, taking the case with $\sigma >1>\rho$ for example, one has $V_{1c}<V_{1c}^{EN}$. Furthermore, both $J_{11}\left(V\right)$ and $J_{11}^{EN}\left(V\right)$ are negative for $V\in (-\infty ,V_{1c})$; $J_{11}\left(V\right)$ is positive, while $J_{11}^{EN}\left(V\right)$ is negative for $V\in (V_{1c},V_{1c}^{EN})$; and both $J_{11}\left(V\right)$ and $J_{11}^{EN}\left(V\right)$ are positive for $V\in (V_{1c}^{EN},\infty )$. This is consistent with the result (i) stated in Theorem 2 since the large permanent charge inhibits the cation.

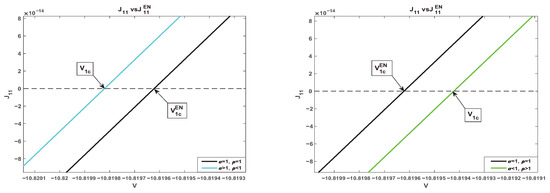
Figure 3. The graph of $J_{11}^{EN}(V;1,1)$ under electroneutrality boundary conditions and $J_{11}(V;\sigma ,\rho )$ with boundary layers.

Figure 3. The graph of $J_{11}^{EN}(V;1,1)$ under electroneutrality boundary conditions and $J_{11}(V;\sigma ,\rho )$ with boundary layers.

To end this section, we point out that “bvp4c” in Matlab [65] is employed as the solver for the boundary value problem (16) and (17). Our main focus is to examine the effects on ionic flows from boundary layers due to the relaxation of the electroneutrality boundary concentrations. There may have different ways to add and deal with the boundary conditions, such as the one described in [66] that could replace the complex, thin electric double layer near a charged surface. However, this is beyond the goal of the current work, and we would like to consider it in our future work.

4. Discussion

The present study provides a detailed asymptotic and qualitative analysis of ionic flows in quasi-one-dimensional Poisson–Nernst–Planck systems with large permanent charges under relaxed neutral boundary conditions. Building upon the framework established in [7,11], where electroneutrality boundary conditions were assumed, our investigation explicitly incorporates boundary layer effects arising from deviations from perfect electroneutrality. A key observation is the identification of critical boundary potentials $V_{1c}$ and $V_{2c}$, which delineate distinct regimes in the behavior of cation and anion fluxes. The established monotonicity and concavity properties of $J_{11}$ and $J_{20}$ with respect to boundary potential V reveal nonlinear dependencies induced by both large permanent charges and boundary layer parameters $(\sigma ,\rho )$. Notably, the existence of critical potentials $V_1^{\ast }$ and $V_2^{\ast }$ indicates nontrivial saturation behavior, confirming and extending the saturation phenomena previously reported under stricter boundary assumptions. The comparison between fluxes $J_{11}$ and $J_{20}$ under relaxed neutral boundary conditions and their counterparts $J_{11}^{EN}$ and $J_{20}^{EN}$ under electroneutrality reveals several non-intuitive effects. For instance, Theorems 2–4 demonstrate parameter regimes where large permanent charges exert opposite influences on ionic fluxes depending on the presence or absence of boundary layers. Specifically, we observed that in certain potential intervals, relaxing the neutral condition alters not only the magnitude but even the direction of flux modulation by large permanent charges. From a modeling perspective, these results emphasize that assuming electroneutrality boundary conditions may overlook essential qualitative features of ionic transport, especially in systems where boundary ion concentrations deviate slightly from neutrality—a realistic scenario in physiological and experimental settings. The findings suggest that boundary layers, despite being localized phenomena, can exert global influences on flux characteristics due to the nonlinear coupling inherent in PNP systems. Furthermore, the saturation bounds derived for $|J_{11}|$ and $|J_{20}|$ as $\left|V\right|\to \infty$ provide explicit estimates on ionic fluxes under extreme conditions. These bounds may inform experimental interpretations where current saturation is observed and are consistent with the physical intuition that permanent charges act as regulatory filters in ion channels. In conclusion, this work bridges a critical gap between idealized PNP modeling and more physically realistic boundary setups. The analytical insights obtained here pave the way for future numerical simulations and experimental validations. Potential extensions include incorporating finite ion size effects and multi-species ionic systems beyond two components, as well as exploring geometric singular perturbation approaches for systematically analyzing more complex PNP structures under relaxed boundary conditions.

5. Conclusions

In this work, we have conducted a comprehensive analytical study on quasi-one-dimensional Poisson–Nernst–Planck systems with large permanent charges under relaxed neutral boundary conditions. By systematically comparing the individual ionic fluxes $J_1$ and $J_2$ with those obtained under classical electroneutrality boundary conditions, we have uncovered several new qualitative behaviors influenced by boundary layer effects. Our main contributions can be summarized as follows:

• We derived explicit asymptotic expansions for individual fluxes up to first-order terms in the small parameter $\nu ={\displaystyle \frac{1}{Q_0}}$, incorporating the boundary layer parameters $(\sigma ,\rho )$ as perturbations from electroneutrality.
• We identified critical potentials $V_{1c}$ and $V_{2c}$, characterizing sign changes and monotonicity properties of fluxes, which are sensitive to both large permanent charge magnitudes and boundary layer parameters.
• We established rigorous saturation results showing that both cation and anion fluxes saturate as the transmembrane potential V tends to infinity, with their magnitudes influenced by deviations from boundary neutrality.
• Most notably, we demonstrated non-intuitive discrepancies in flux behaviors between relaxed neutral and electroneutral boundary conditions. Specifically, in certain parameter regimes, large permanent charges can enhance or reduce ionic fluxes in opposite directions under these two boundary setups.

These findings highlight the importance of considering boundary layer effects in the mathematical modeling of ionic flows through membrane channels, particularly in biophysical contexts where strict electroneutrality is not guaranteed. The results also provide theoretical insights that may guide future experimental designs and numerical simulations aimed at validating boundary layer-induced phenomena in ion channel studies.

Looking forward, several open questions remain. Extending this framework to multi-species systems with asymmetric valences and incorporating finite ion size effects would provide a more complete picture. Moreover, exploring dynamical (time-dependent) PNP systems under similar relaxed boundary conditions represents another promising direction. Such efforts would further enhance the applicability and predictive power of PNP-type models in real-world biological and engineering contexts.