A Novel Optimization Method and Its Application for Hazardous Materials Vehicle Routing Problem Under Different Road Conditions
Abstract
1. Introduction
1.1. A Literature Review
1.2. Research Innovations
- (1)
- According to the road conditions in parks, the vehicle transport segments are divided into straight and curved segments. Among them, the curved segments refer to the segments where vehicles travel when making a turn (not limited to specific intersections). This responds to the lack of targeted analysis for different geometric road types in hazmat routing studies;
- (2)
- The geometric modeling of accident exposure areas, with parameters obtained from expert knowledge and accident records, provides a more realistic quantification of transportation risk than conventional circular or Euclidean approximations;
- (3)
- The proposed TSACO algorithm integrates improved node probability selection, pheromone updating with dynamic evaporation rate, and Dijkstra-based preprocessing of actual road geometry, overcoming limitations of conventional ACO in handling both bi-objective optimization and complex road networks.
2. Materials and Methods
2.1. Problem Description and Symbol Definition
- (1)
- The locations and quantities of the depot and customer nodes are predetermined, with goods transported from a single depot to multiple customers;
- (2)
- The nodes in the road network are interconnected, and all road segments permit bidirectional travel;
- (3)
- Throughout the delivery process, each vehicle starts and ends its route at the depot;
- (4)
- The vehicle types and their respective load capacities at the depot are known a priori;
- (5)
- The numbers of intersections and traversable road segments are fully specified;
- (6)
- The demand of each customer node is given and deterministic;
- (7)
- Each vehicle serves at least one customer node;
- (8)
- Each customer node is only serviced when the vehicle visits for the first time. In all other cases, it is merely passed by;
- (9)
- The available travel distance of each vehicle is sufficient to complete its assigned delivery tasks;
- (10)
- The load on the front and rear axles is evenly distributed when the vehicle turns.
2.2. Model Construction
- (1)
- Cost quantification process
- (2)
- Risk quantification process
3. Solution Approach
3.1. Ant Colony Algorithm
| Algorithm 1 The pseudo-code of the ACO algorithm | |
| Algorithm: Ant Colony Optimization (ACO) | |
| 1: | Input: |
| 2: | Number of ants (); |
| 3: | Number of iterations (); |
| 4: | Pheromone evaporation rate; |
| 5: | Pheromone influence factor; |
| 6: | Initial pheromone level (); |
| 7: | Number of objectives (); |
| 8: | Output: |
| 9: | Best solution. |
| 10: | Begin: |
| 11: | Initialize: |
| 12: | Set pheromone levels for all edges ; |
| 13: | Initialize Pareto archive ; |
| 14: | Set ; |
| 15: | For to : |
| 16: | For each ant to : |
| 17: | Put ant on the starting node; |
| 18: | While the ant has not visited all nodes: |
| 19: | Choose the next node j from unvisited nodes with probability; |
| 20: | Move ant to node ; |
| 21: | Mark node as visited; |
| 22: | Evaluate the solution on the distance; |
| 23: | Update pheromone levels; |
| 24: | Update the global optimal solution; |
| 25: | Return Best solution. |
| 26: | End Begin |
3.2. Improved Node Probability Selection
3.3. Improved Pheromone Update Strategy
3.4. Algorithm Implementation Process
4. Application Example
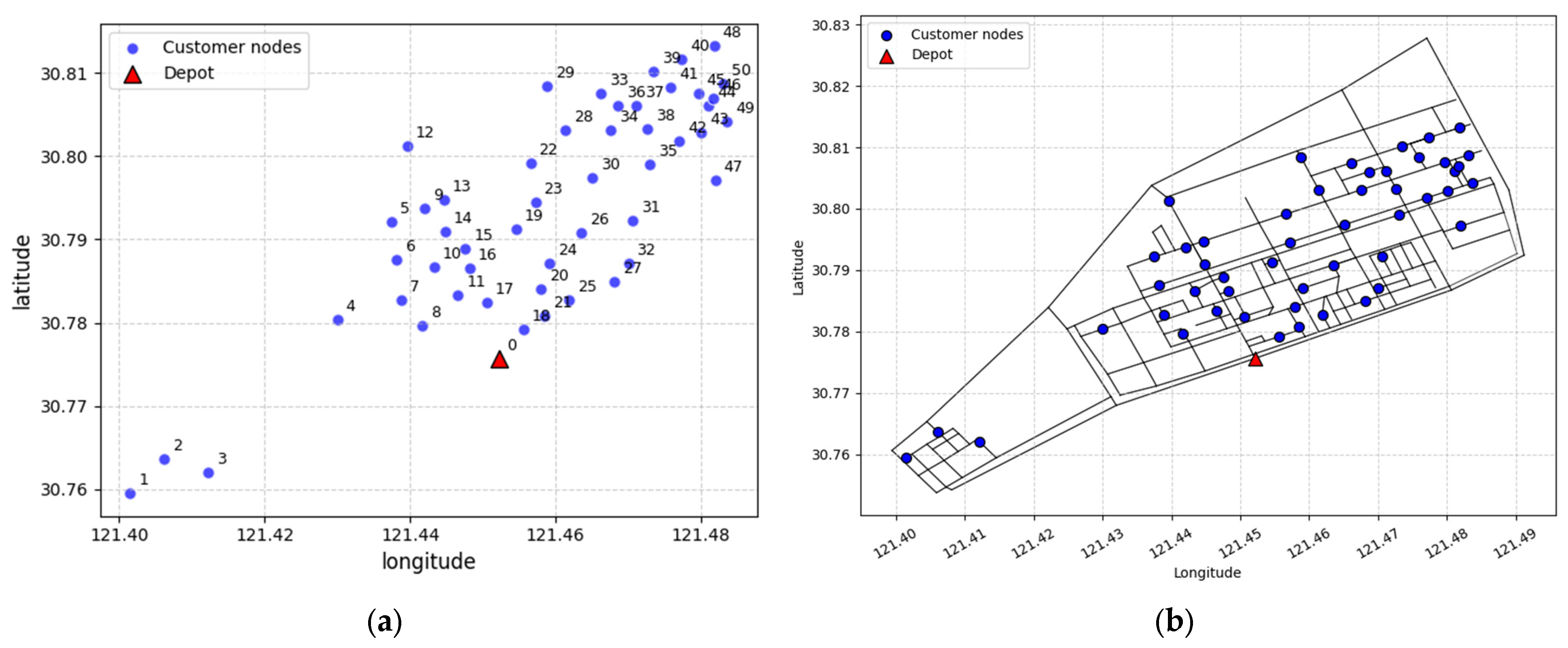
4.1. Data Collection
4.2. Calculation and Analysis
- (1)
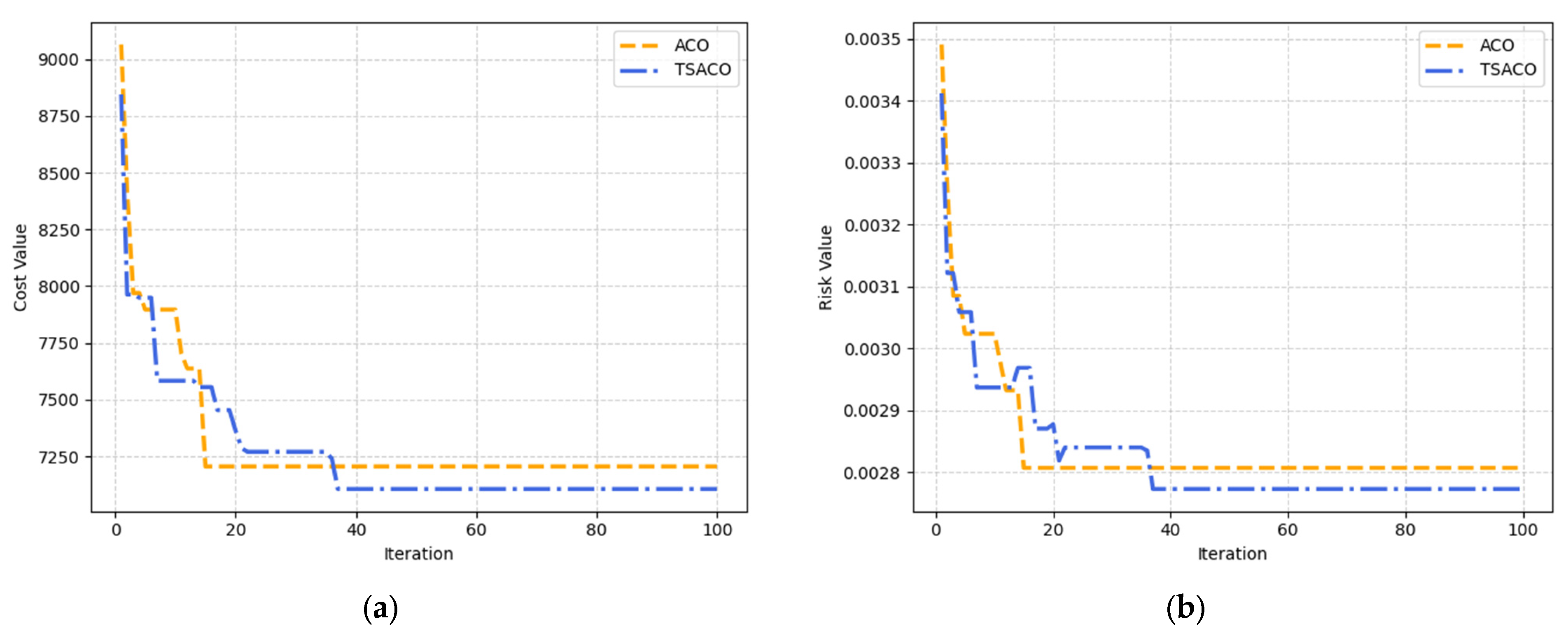
- Figure 5 reveals that during the early stages (iterations 1–20), the ACO algorithm demonstrates faster convergence rates. However, its performance plateaus upon reaching a certain threshold. In contrast, the TSACO algorithm exhibits initial fluctuations in objective values but ultimately achieves superior solutions through continued iterations. These results indicate that while the ACO algorithm shows rapid initial optimization, it becomes trapped in local optima.
- (2)
- Table 3 presents the detailed data obtained by the two algorithms, including the number of vehicles, total cost, total risk, and the running time of the algorithms. Additionally, the discrepancy between the objective values of these feasible solutions is quantified using a formulated calculation method, i.e., . The results demonstrate significant quality improvements in both total transportation cost (1.38%) and total risk (1.21%) metrics for the optimized solutions, obtained by using the proposed model. It is noteworthy that the modified algorithm requires more computational time compared to the conventional ACO due to its additional calculation steps. This temporal overhead represents a trade-off between solution quality and computational efficiency, which is common in metaheuristic algorithm improvements. However, as the computational complexity decreases, the running times of the two models show a convergence trend. The 12 examples proposed in Section 4.4. to verify this regulation.
4.3. Sensitivity Analysis
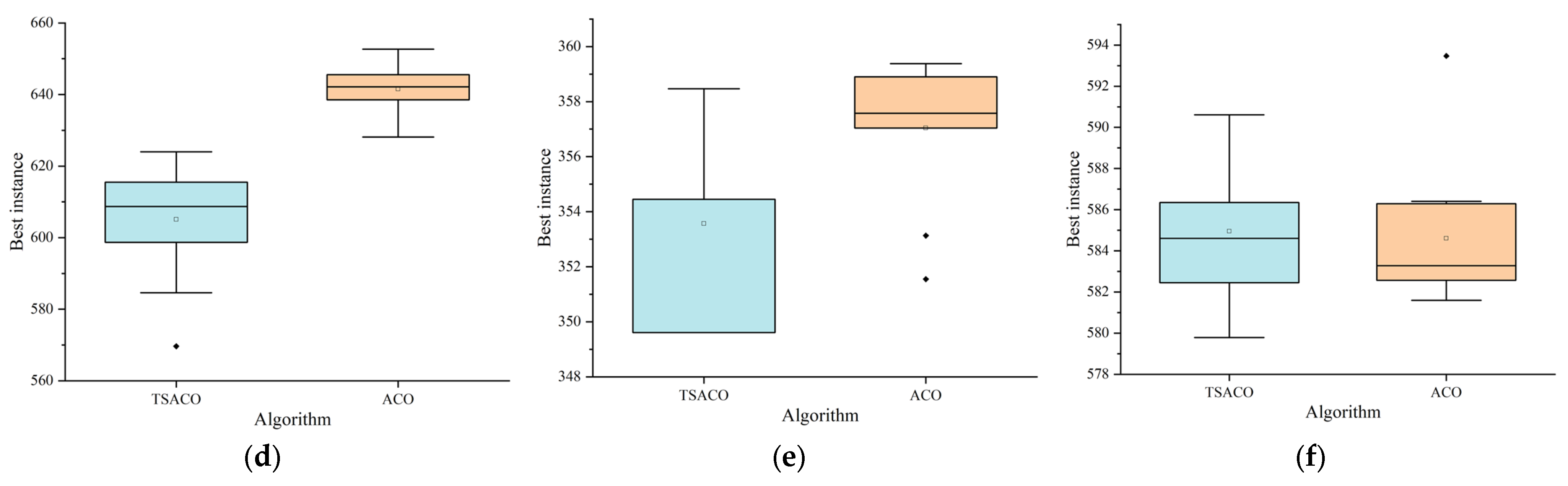
4.4. Algorithm Validation
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lyu, S.; Zhang, S.H.; Huang, X.M.; Peng, S.N.; Li, J. Investigation and modeling of the LPG tank truck accident in Wenling, China. Process Saf. Environ. Prot. 2022, 157, 493–508. [Google Scholar] [CrossRef]
- Oyugi, B.; Kamara, I.F.; Nuwagira, I.; Musoke, R.; Lakoh, S.; Jalloh, A.; Kamara, R.F.; Relan, P.; Lajolo, C.; Ndiaye, R.A.M.; et al. A review of the response and the emergency medical team (EMT) deployment following a tanker explosion in Freetown, Sierra Leone. Confl. Health 2024, 18, 63. [Google Scholar] [CrossRef] [PubMed]
- Elvik, R. The more (sharp) curves, the lower the risk. Accid. Anal. Prev. 2019, 133, 105322. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.K.; Wang, H.K. Risk assessment and hybrid algorithm transportation path optimization model for road transport of dangerous goods. IATSS Res. 2025, 49, 72–80. [Google Scholar] [CrossRef]
- Shankar, V.; Mannering, F.; Barfield, W. Effect of roadway geometrics and environmental factors on rural freeway accident frequencies. Accid. Anal. Prev. 1995, 27, 371–389. [Google Scholar] [CrossRef]
- Maji, S.; Maity, S.; Giri, D.; Nielsen, I.; Maiti, M. Multi-objective multi-path COVID-19 medical waste collection problem with type-2 fuzzy logic based risk using partial opposition-based weighted genetic algorithm. Eng. Appl. Artif. Intell. 2025, 143, 109916. [Google Scholar] [CrossRef]
- Zhai, C.L.; Li, P.L.; Zhao, R.H.; Jing, N.N. Selection and planning of hazardous materials transportation routes based on explosion accident risks. J. Loss Prev. Process Ind. 2024, 92, 105440. [Google Scholar] [CrossRef]
- Xie, L.; Cao, C.X. Multi-modal and multi-route transportation problem for hazardous materials under uncertainty. Eng. Optim. 2020, 53, 2180–2200. [Google Scholar] [CrossRef]
- Zandieh, F.; Ghannadpour, S.F. A comprehensive risk assessment view on interval type-2 fuzzy controller for a time-dependent hazmat routing problem. Eur. J. Oper. Res. 2023, 305, 685–707. [Google Scholar] [CrossRef]
- Wang, J.P.; Bai, X.J.; Liu, Y.K. Building sustainable hazardous products supply chain against ambiguous risk with accelerated Benders decomposition algorithm. Transport. Res. E-Log. 2025, 194, 103941. [Google Scholar] [CrossRef]
- Kang, D.; Zhao, J.X.; Dick, C.T.; Liu, X.; Bian, Z.Y.; Kirkpatrick, S.W.; Lin, C.Y. Probabilistic risk analysis of unit trains versus manifest trains for transporting hazardous materials. Accid. Anal. Prev. 2023, 181, 106950. [Google Scholar] [CrossRef]
- Li, G.Q.; Pu, G.; Yang, J.X.; Jiang, X.G. A multidimensional quantitative risk assessment framework for dense areas of stay points for urban hazmat vehicles. Reliab. Eng. Syst. Saf. 2024, 241, 109637. [Google Scholar] [CrossRef]
- Chiou, S.W. A learning optimization for resilience enhancement of risk-informed traffic control system with hazardous materials transportation under uncertainty. Reliab. Eng. Syst. Saf. 2024, 252, 110425. [Google Scholar] [CrossRef]
- Zhan, H.F.; Wang, G.; Shan, X.; Liu, Y.H. Risk-aware lane-change trajectory planning with rollover prevention for autonomous light trucks on curved roads. Mech. Syst. Signal Proc. 2024, 211, 111126. [Google Scholar] [CrossRef]
- Zheng, X.L.; Yu, L.J.; Ren, Y.Y.; Li, X.S.; Liang, B.; Xi, J.F. Modeling of tank vehicle rollover risk assessment on curved-slope combination sections for sustainable transportation safety. Sustainability 2025, 17, 906. [Google Scholar] [CrossRef]
- Wang, T.; Ge, Y.E.; Wang, Y.J.; Chen, W.Q.; Qian, F.; Niu, Y.C. A novel model for real-time risk evaluation of vehicle–pedestrian interactions at intersections. Accid. Anal. Prev. 2024, 206, 107727. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.Z.; Qian, C.; Li, L.H.; Qu, X.; Ran, B. Risk quantification based Adaptive Cruise control and its application in approaching behavior at signalized intersections. Accid. Anal. Prev. 2025, 212, 107939. [Google Scholar] [CrossRef]
- Zhai, C.L.; Wu, A.Z. Probabilistic risk analysis and characterization of hazardous material road transportation routes under explosion accidents. J. Loss Prev. Process Ind. 2024, 88, 105265. [Google Scholar] [CrossRef]
- Yang, J.G.; Zhuang, Y.B. An improved ant colony optimization algorithm for solving a complex combinatorial optimization problem. Appl. Soft Comput. 2010, 10, 653–660. [Google Scholar] [CrossRef]
- Zhou, X.S.; Gui, W.Y.; Heidari, A.A.; Cai, Z.N.; Liang, G.X.; Chen, H.L. Random following ant colony optimization: Continuous and binary variants for global optimization and feature selection. Appl. Soft Comput. 2023, 144, 110513. [Google Scholar] [CrossRef]
- Wang, T.C.; Wang, L.; Li, D.D.; Cai, J.C.; Wang, Y.X. Monte Carlo-based improved ant colony optimization for path planning of welding robot. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101603. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Y.C.; Zhang, L.Y.; Yuan, X.M. Application of improved genetic algorithm to vehicle routing problem considering the environmental self-regulation of the freight companies. Expert Syst. Appl. 2025, 274, 127010. [Google Scholar] [CrossRef]
- Sarbijan, M.S.; Behnamian, J. Multi-fleet feeder vehicle routing problem using hybrid metaheuristic. Comput. Oper. Res. 2022, 141, 105696. [Google Scholar] [CrossRef]
- Shi, X.W.; Yao, H.D.; Liang, Z.H.; Li, X.P. An empirical study on fuel consumption of commercial automated vehicles. Transp. Res. Part D Transp. Environ. 2022, 106, 103253. [Google Scholar] [CrossRef]
- Gao, C.; Xu, J.L.; Jia, M.; Sun, Z.H. Correlation between carbon emissions, fuel consumption of vehicles and speed limit on expressway. J. Traffic Transp. Eng. 2024, 11, 631–642. [Google Scholar] [CrossRef]
- Li, T.T.; Deng, S.J.; Lu, C.Y.; Wang, Y.; Liao, H.J. Optimization of Green Vehicle Paths Considering the Impact of Carbon Emissions: A Case Study of Municipal Solid Waste Collection and Transportation. Sustainability 2023, 15, 16128. [Google Scholar] [CrossRef]
- Ma, T.M.; Wang, Z.; Yang, J.L.; Huang, C.Y.; Liu, L.J.; Chen, X.F. Real-time risk assessment model for hazmat release accident involving tank truck. J. Loss Prev. Process Ind. 2022, 77, 104759. [Google Scholar] [CrossRef]
- Chakrabarti, U.K.; Parikh, J.K. Route evaluation for hazmat transportation based on total risk–a case of Indian state highways. J. Loss Prev. Process Ind. 2011, 24, 524–530. [Google Scholar] [CrossRef]
- Bejleri, I.; Xu, X.J.; Silva, K.R.; Srinivasan, S. Safety performance analysis of horizontal curves in urban areas. Accid. Anal. Prev. 2024, 195, 107402. [Google Scholar] [CrossRef]
- Liu, C.; Wu, L.; Xiao, W.S.; Li, G.X.; Xu, D.P.; Guo, J.J.; Li, W.T. An improved heuristic mechanism ant colony optimization algorithm for solving path planning. Knowl.-Based Syst. 2023, 271, 110540. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]

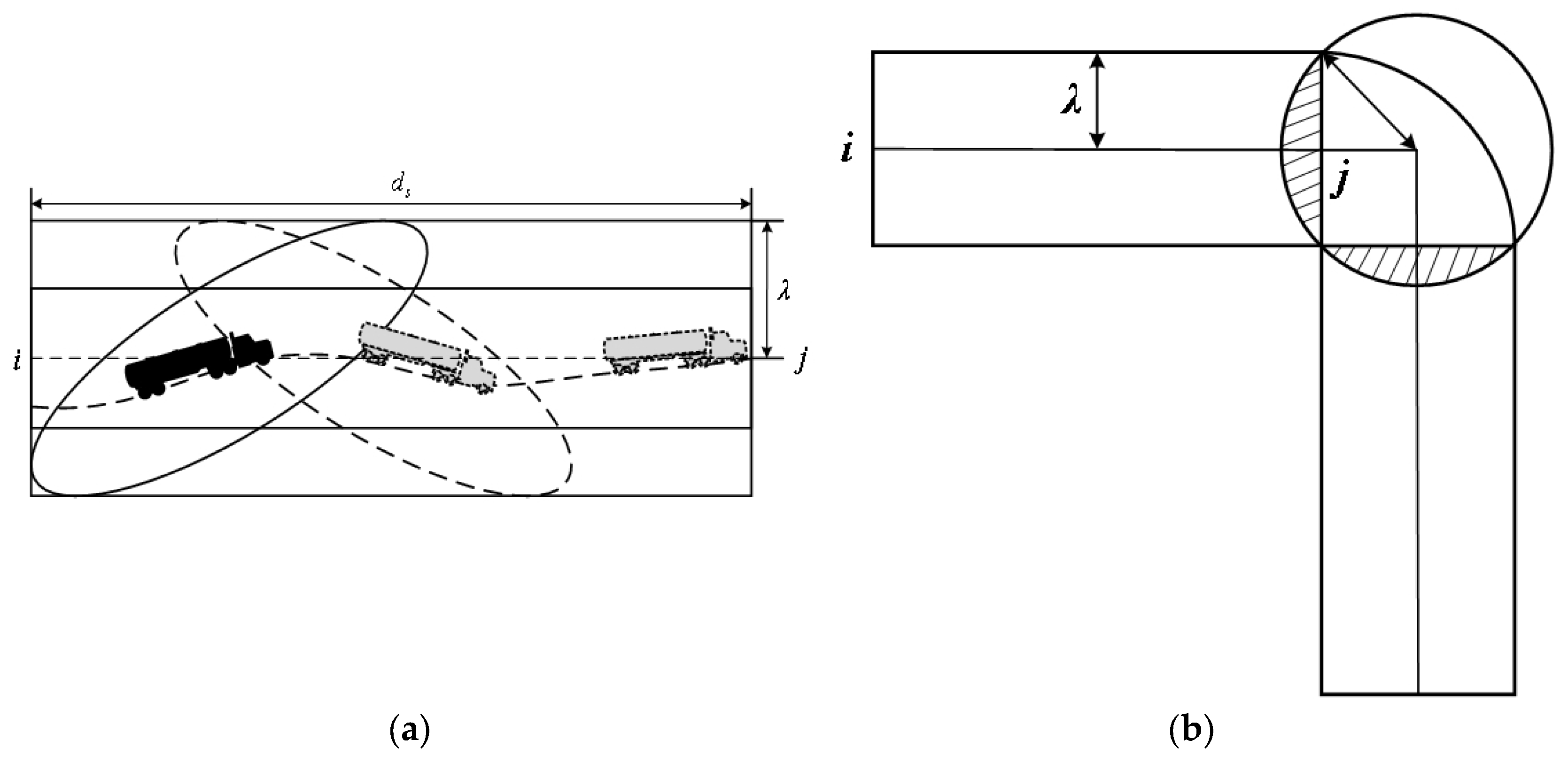



| Symbol | Definition |
|---|---|
| N | Set of all nodes in the studied road network |
| The depot within the port-based chemical industrial park | |
| S | |
| C | |
| K | |
| Q | Vehicle rated load capacity |
| Vehicle empty load capacity | |
| Actual vehicle load capacity | |
| The demand of customer node n | |
| R | |
| Fuel consumption rate of the vehicle when it is empty (L/h) | |
| Vehicle steering angle (°) | |
| The average speed of the vehicle when traveling on straight road | |
| The average speed of the vehicle when traveling on curved road | |
| Carbon emission factor | |
| Population density on road segment s | |
| Population density on road segment c | |
| Vehicle rental cost | |
| Vehicle maintenance cost | |
| Vehicle insurance cost | |
| Fixed salary for drivers | |
| Diesel prices (L/USD) | |
| Carbon tax (L/USD) | |
| Binary decision variable, which is 1 if vehicle k passes through a straight road segment s of route r, and 0 otherwise | |
| Binary decision variable, which is 1 if vehicle k passes through a curve road segment c of route r, and 0 otherwise |
| Parameters | Description | Numerical Value |
|---|---|---|
| Iterations | 100 | |
| Number of ants | 50 | |
| Evaporation coefficient of pheromone | 0.3 | |
| Pheromone importance parameter | 1 | |
| Heuristic function importance parameter | 4 | |
| Pheromone increment parameter | 1 | |
| Vehicle rental cost | 30 | |
| Vehicle maintenance cost | 10 | |
| Vehicle insurance cost | 20 | |
| Fixed salary for drivers | 25 | |
| Diesel prices | 1.5 | |
| Carbon tax | 50 | |
| Carbon emission factor | 2.68 | |
| Fuel consumption rate at empty | 0.1 | |
| The multiple of the curved segment | 3 | |
| Compensation factor | 0.003, 0.1 | |
| Driving speed on the straight | 10 | |
| Driving speed on the curve | 5 | |
| Accident probability | 0.11 × 10−6 |
| Algorithm | Vehicle Number | Total Cost | Total Risk | Runtime |
|---|---|---|---|---|
| ACO | 4 | 7205.43 | 0.0028073 | 16.34 |
| TSACO | 4 | 7105.75 | 0.0027732 | 24.55 |
| Vehicle Number | Route * |
|---|---|
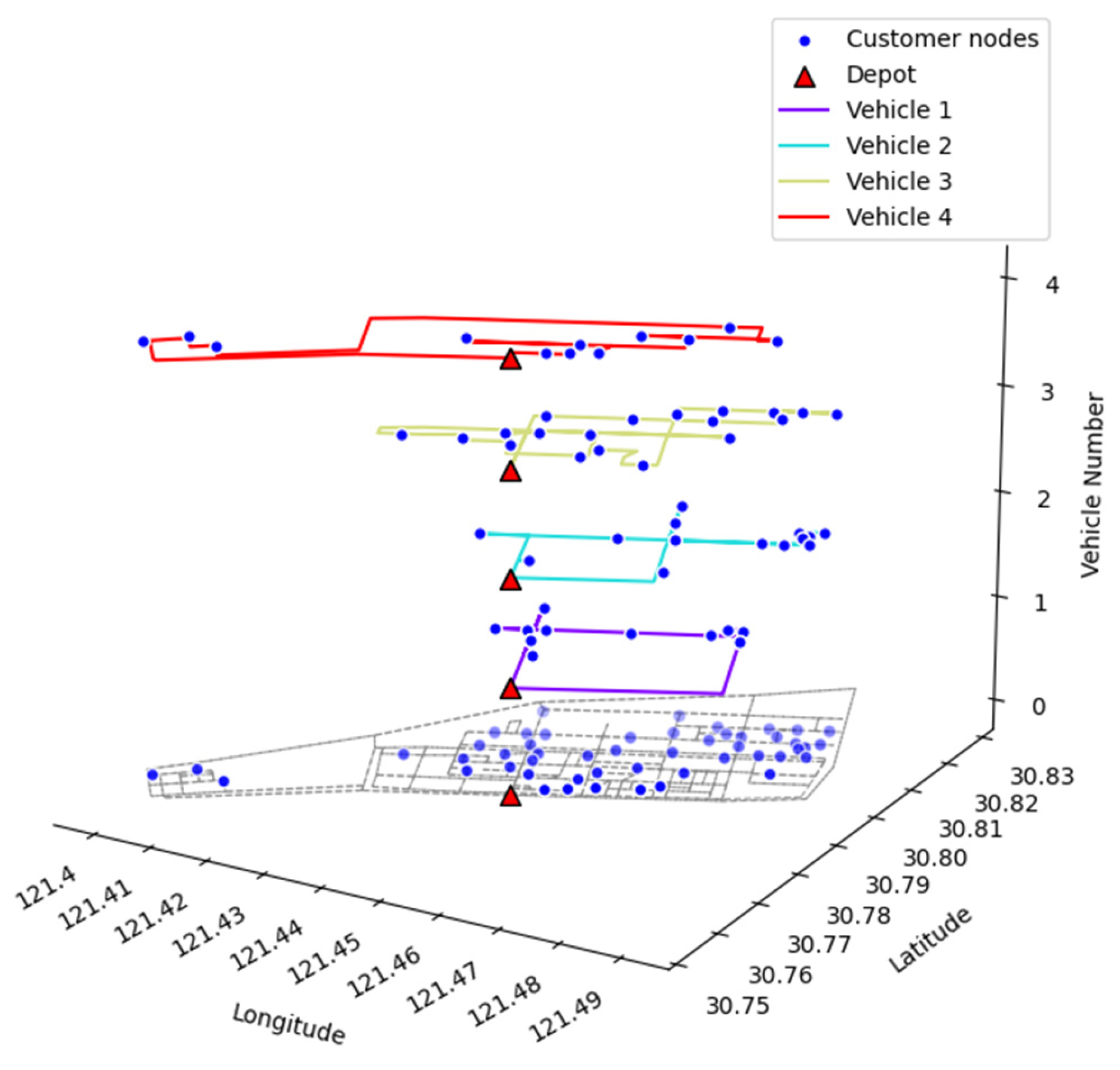
| 1 | [1000, 74, 73, 72, 71, 70, 69, 68, 67, 66, 65, 64, 63, 1014, 62, 1012, 62, 1014, 63, 64, 65, 66, 1016, 66, 67, 68, 69, 70, 71, 72, 73, 80, 1018, 90, 1021, 89, 1020, 89, 85, 70, 59, 44, 1008, 44, 59, 70, 85, 89, 1020, 100, 102, 1025, 102, 100, 1020, 89, 85, 70, 59, 58, 1011, 57, 56, 50, 42, 1007, 41, 37, 31, 1004, 31, 32, 33, 46, 74, 1000] |
| 2 | [1000, 74, 73, 72, 71, 70, 69, 68, 67, 66, 65, 1010, 65, 1015, 76, 81, 86, 95, 118, 1035, 118, 117, 116, 1028, 115, 1029, 115, 1028, 116, 117, 118, 119, 120, 121, 122, 123, 1027, 123, 128, 127, 1032, 122, 121, 120, 119, 118, 117, 116, 1028, 115, 130, 1033, 149, 1039, 1040, 162, 169, 1048, 169, 162, 1041, 163, 151, 1034, 132, 116, 1022, 93, 1013, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 1000] |
| 3 | [1000, 74, 73, 72, 71, 70, 69, 1017, 69, 68, 67, 66, 65, 64, 63, 1014, 62, 1009, 62, 1013, 62, 1009, 53, 48, 1005, 48, 53, 1009, 62, 1013, 93, 1022, 116, 132, 1034, 151, 1038, 151, 1037, 150, 1036, 150, 149, 148, 147, 60, 22, 13, 1002, 14, 9, 5, 1001, 5, 9, 14, 17, 18, 19, 20, 1003, 21, 24, 25, 1000] |
| 4 | [1000, 74, 73, 72, 71, 70, 69, 68, 67, 66, 65, 64, 63, 1006, 63, 94, 1023, 117, 1030, 152, 1042, 1043, 165, 167, 1049, 167, 165, 1044, 164, 1045, 166, 1050, 166, 1046, 167, 1049, 177, 178, 173, 1047, 160, 159, 154, 140, 133, 120, 1026, 120, 133, 134, 1031, 134, 133, 120, 107, 98, 97, 96, 1019, 96, 97, 98, 99, 1024, 99, 100, 101, 91, 74, 1000] |
| Instance | ACO | TSACO | Deviation (%) | ||||
|---|---|---|---|---|---|---|---|
| VN * | BD * | Runtime | VN | BD | Runtime | ||
| C101-25 | 3 | 202.64 | 0.71 | 3 | 198.19 | 0.69 | −2.20 |
| C101-50 | 5 | 410.69 | 2.32 | 5 | 396.01 | 2.33 | −3.57 |
| C201-25 | 1 | 201.15 | 0.68 | 1 | 201.86 | 0.67 | 0.35 |
| C201-50 | 2 | 363.73 | 2.30 | 2 | 361.71 | 2.49 | −0.56 |
| R101-25 | 2 | 335.27 | 0.69 | 2 | 335.27 | 0.65 | 0.00 |
| R101-50 | 4 | 628.15 | 2.25 | 4 | 569.64 | 2.28 | −9.31 |
| R201-25 | 1 | 315.7 | 0.70 | 1 | 313.34 | 0.77 | −0.75 |
| R201-50 | 1 | 482.42 | 2.29 | 1 | 465.31 | 2.39 | −3.55 |
| RC101-25 | 3 | 351.55 | 0.67 | 3 | 349.61 | 0.67 | −0.55 |
| RC101-50 | 5 | 581.6 | 2.40 | 5 | 579.79 | 2.35 | −0.31 |
| RC201-25 | 1 | 227.02 | 0.64 | 1 | 227.02 | 0.74 | 0.00 |
| RC201-50 | 1 | 374.66 | 2.31 | 1 | 374.66 | 2.44 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Ding, L.; Jiang, J.; Kong, F.; Liu, X. A Novel Optimization Method and Its Application for Hazardous Materials Vehicle Routing Problem Under Different Road Conditions. Mathematics 2025, 13, 2690. https://doi.org/10.3390/math13162690
Zhang F, Ding L, Jiang J, Kong F, Liu X. A Novel Optimization Method and Its Application for Hazardous Materials Vehicle Routing Problem Under Different Road Conditions. Mathematics. 2025; 13(16):2690. https://doi.org/10.3390/math13162690
Chicago/Turabian StyleZhang, Fangwei, Lu Ding, Jun Jiang, Fanyi Kong, and Xiaoyu Liu. 2025. "A Novel Optimization Method and Its Application for Hazardous Materials Vehicle Routing Problem Under Different Road Conditions" Mathematics 13, no. 16: 2690. https://doi.org/10.3390/math13162690
APA StyleZhang, F., Ding, L., Jiang, J., Kong, F., & Liu, X. (2025). A Novel Optimization Method and Its Application for Hazardous Materials Vehicle Routing Problem Under Different Road Conditions. Mathematics, 13(16), 2690. https://doi.org/10.3390/math13162690





