Abstract
Life testing of products often requires extended observation periods. To shorten the duration of these tests, products can be subjected to more extreme conditions than those encountered in normal use; an approach known as accelerated life testing (ALT) is considered. This study investigates the estimation of unknown parameters and the acceleration factor for the modified Fréchet-Lomax exponential distribution (MFLED), utilizing Type II progressively first-failure censored (PFFC) samples obtained under the framework of constant-stress partially accelerated life testing (CSPALT). Maximum likelihood (ML) estimation is employed to obtain point estimates for the model parameters and the acceleration factor, while the Fisher information matrix is used to construct asymptotic confidence intervals (ACIs) for these estimates. To improve the precision of inference, two parametric bootstrap methods are also implemented. In the Bayesian context, a method for eliciting prior hyperparameters is proposed, and Bayesian estimates are obtained using the Markov Chain Monte Carlo (MCMC) method. These estimates are evaluated under both symmetric and asymmetric loss functions, and the corresponding credible intervals (CRIs) are computed. A comprehensive simulation study is conducted to compare the performance of ML, bootstrap, and Bayesian estimators in terms of mean squared error and coverage probabilities of confidence intervals. Finally, real-world failure time data of light-emitting diodes (LEDs) are analyzed to demonstrate the applicability and efficiency of the proposed methods in practical reliability studies, highlighting their value in modeling the lifetime behavior of electronic components.
Keywords:
constant-stress; partially accelerated life test; modified Fréchet-Lomax exponential distribution; bootstrap methods; asymptotic confidence intervals; Bayesian estimation MSC:
60E05; 62F15; 62F10; 62N01; 62N02; 62N05
1. Introduction
It is well established that all devices and equipment used in daily life have a limited operating life. Understanding and modeling this useful life span is essential to improve product design, reliability, and maintenance strategies. However, obtaining lifetime data through standard testing procedures can be both time-consuming and prohibitively expensive, especially when failures occur infrequently under normal usage conditions. To overcome this limitation, accelerated life tests (ALTs) have become a widely adopted solution, particularly in manufacturing and engineering applications. ALTs involve subjecting test items to higher-than-normal stress levels, such as elevated temperatures, pressures, or voltages, to induce early failures. This approach enables researchers to gather failure data more quickly, which can then be extrapolated using appropriate statistical models to estimate product lifetime under normal operating conditions. Accelerated life testing (ALT) is an essential methodology in reliability engineering aimed at obtaining failure data more quickly by subjecting test items to elevated stress levels compared to normal operating conditions. Depending on the availability of information on the relationship between stress and life expectancy, ALTs are generally classified into two main types: fully accelerated life tests (Fully ALTs) and partially accelerated life tests (PALTs). In Fully ALTs, it is assumed that the functional relationship between stress and product lifetime is known in advance. This assumption facilitates simpler modeling and allows for efficient planning of the reliability experiment. Among the commonly employed strategies in this context is the constant-stress ALT, where each test item is subjected to a fixed elevated stress level throughout the experiment. This method has been thoroughly discussed in the works of Meeker and Escobar [1], Dey and Nassar [2], Nelson [3], Lin et al. [4], and Haj Ahmad et al. [5]. Another notable approach is the step-stress ALT, in which the stress level is increased in stages at predetermined intervals if failure does not occur, allowing earlier detection of failures. Studies by Hakamipour [6] and Wang [7] have contributed to understanding and modeling of this type. Progressive stress ALT, on the contrary, involves a constantly increasing stress level over time and is particularly useful to simulate realistic degradation processes, as illustrated by Mahto et al. [8] and Abdel-Hamid and Al-Hussaini [9]. Haj Ahmad et al. [10,11] applied a simple step-stress life testing and considered multiple causes of failure. On the other hand, PALTs are employed when the exact relationship between stress and life expectancy is unknown or cannot be easily modeled. These tests serve as valuable alternatives for estimating the acceleration factor, which is used to extrapolate failure information from accelerated conditions to normal usage environments. One common form is the constant-stress PALT (CSPALT), where items are tested under both normal and accelerated fixed stress levels. This form has been explored under different censoring schemes by Hassan et al. [12] and Nassar et al. [13]. Another approach is the step-stress PALT, which begins with a period of normal stress followed by a transition to a higher stress level if the item does not fail, effectively dividing the test duration into two distinct phases. This method has been examined in the works of Gouno et al. [14], Wu et al. [15], and Bai and Chung [16]. Progressive-stress PALTs, where stress is gradually increased over time, offer a more continuous transition from normal use to failure and are discussed in studies such as those by Fan et al. [17] and Ismail and Al-Babtain [18]. These classifications reflect the diversity and adaptability of the ALT frameworks, each of which provides specific advantages depending on the product characteristics and testing objectives. Understanding the nature and structure of the ALT and PALT designs is vital to select the appropriate statistical methods and ensuring meaningful reliability inferences. In life testing experiments, it is often impossible to obtain complete data on failure times for all test items, leading to a phenomenon known as censoring. The data collected from these tests are referred to as censored data. The Type-I and Type-II censoring are the most common types of censoring. In Type-I censoring, the units are tested simultaneously for a predetermined duration. If not all test units fail within this period, the surviving units are removed once the period ends; see Algarni et al. [19]. In contrast, Type-II censoring involves running the units simultaneously until a specified number of items fail, at which point the remaining items are removed, see Kundu and Howlader [20]. In both of these types, there is limited flexibility in withdrawing test items during the testing process. To address this limitation, a more general approach known as a Type-II progressive censoring scheme has been proposed. In this censoring approach, after each observed failure, a predetermined number of surviving units are randomly withdrawn from the test. This process continues sequentially, with removals occurring at each failure time, until a fixed number of failures has been observed; the remaining surviving items are also withdrawn, as illustrated in studies by Wu and Gui [21] and EL-Sagheer [22]. To reduce both testing time and cost, the most flexible censoring scheme is the Progressive First Failure Censoring (PFFC) scheme, proposed by Wu and Kuş [23]. This method is specifically designed to preserve the maximum number of test units by progressively withdrawing surviving items before they fail. Its efficiency and practicality have made it a popular subject of study under various lifetime distributions. Notable contributions in this area include the work of Xie and Gui [24] and Lin et al. [25]. A detailed discussion of the PFFC scheme will be presented in the following section. In the field of probability theory, it has become commonplace in recent years to adjust classical probability distributions to enhance the flexibility of existing models. These adjustments are informed by various techniques, including the incorporation of additional parameters and the implementation of transformations of the original distribution. The motivation behind recent modifications of classical lifetime models is to improve their flexibility and adaptability to various types of data. In this context, Ahmed et al. [26] introduced a new distribution derived from the Lomax exponential distribution, originally proposed by Ijaz et al. [27], demonstrating enhanced flexibility compared to several existing generalized models. This newly proposed distribution was constructed using the modified Fréchet-G (MF-G) family, as described by Khalil et al. [28], and is, therefore, referred to as the modified Fréchet-Lomax exponential distribution (MFLED) [26]. The MFLED is adopted in the current study due to its superior adaptability and modeling capacity relative to other generalized forms of the Lomax distribution. The cumulative distribution function (CDF) and the probability density function (PDF) of MFLED can be written, respectively, as follows
where is a scale parameter that controls the horizontal direction of the distribution. Hence, increasing spreads the distribution over a wider range. The shape parameter affects the skewness and thickness of the tail for the distribution, while is another shape parameter that influences the peak and sharpness of the distribution near its mode. The SF and FRF of MFLED can be expressed, respectively, as follows:
where The increasing complexity and performance requirements of modern electronic and industrial systems have intensified the demand for flexible and robust statistical models capable of accurately describing lifetime data. In response to this need, the MFLED has recently emerged as a promising model due to its capacity to accommodate a wide range of hazard rate shapes, such as increasing, decreasing, and bathtub forms, making it well-suited for modeling various types of failure mechanisms. This flexibility enhances its applicability in practical reliability studies across different industries. Despite its modeling advantages, the statistical inference procedures for the MFLED, particularly under advanced censoring schemes, remain relatively underdeveloped. This study addresses that gap by investigating point and interval estimation for the MFLED parameters and the associated acceleration factor within the framework of constant-stress partially accelerated life testing (CSPALT), incorporating the progressive first-failure censoring (PFFC) scheme. This censoring structure is especially relevant to real-world reliability experiments, where observing full lifetimes is often impractical, and accelerated conditions are required to elicit failure information in a feasible time frame. To achieve this, the study employs both classical and Bayesian statistical approaches. Maximum likelihood estimation (MLE) is used alongside the asymptotic confidence intervals, while Bayesian estimation is conducted via Markov Chain Monte Carlo (MCMC) techniques under different loss functions to capture uncertainty more comprehensively. Furthermore, two parametric bootstrap methods are utilized to evaluate the stability and precision of the estimators and to construct alternative confidence bounds. The practical value of the proposed methodology is demonstrated through a real-life application involving failure time data from light-emitting diodes (LEDs), a component widely used in modern electronics. This application underscores not only the modeling power of the MFLED but also the effectiveness of the CSPALT-PFFC framework in handling realistic reliability testing scenarios, thereby bridging theoretical development with industrial needs. The remainder of this paper is structured as follows. Section 2 provides a detailed description of the constant-stress partially accelerated life testing (CSPALT) scheme under the progressive first-failure censoring (PFFC) framework. Section 3 presents the derivation of the maximum likelihood estimates (MLEs) along with the observed Fisher information matrix (FIM). In Section 4, two bootstrap approaches—the percentile bootstrap-p (B-p) and the bootstrap-t (B-t) methods—are introduced and discussed. Section 5 focuses on Bayesian estimation, utilizing both the linear exponential (LINX) and squared error (SQE) loss functions. Section 6 reports the findings of a Monte Carlo simulation study conducted to evaluate the performance of the proposed estimators. A real-world engineering application involving lifetime data of light-emitting diodes (LEDs) is analyzed in Section 7. Finally, Section 8 concludes the paper with a summary of the main findings.
2. Characterization of the Model
2.1. Test Methodology
Consider a scenario in which a total of d test elements are divided into two groups based on a specified proportion r. A fraction r is randomly selected for testing under standard use conditions, and the remaining fraction items are subjected to accelerated life tests. The implementation of the PFFC scheme is as follows:
- i.
- The test items subjected to both standard and accelerated conditions are classified into multiple groups, denoted by , where , with each group comprising the same number of items , for .
- ii.
- Suppose represent two PFFC samples with censoring schemes , where and , derived from MFLED.
- iii.
- Upon the occurrence of the first failure item in a group, that group, along with the groups, is randomly withdrawn from the groups. Similarly, when the second failure item occurs in a group, the group containing this failure item, along with the groups, is randomly withdrawn from the remaining groups. This process continues until the -th failure item occurs in a group, at which point the group that contains this failure item, along with the remaining groups, is withdrawn and the test is terminated. In our study, it is noteworthy that < and the groups are predetermined
- iv.
- The constant-stress partially accelerated life test (CSPALT) plan, as discussed in Meeker and Escobar [3], provides a practical balance between cost and efficiency by subjecting only a portion of test units to higher stress levels, while retaining others at normal conditions, under the CSPALT model and given the censoring schemes , the joint PDF of the < < …< can be derived using the principles of PFFC order statistics aswhere .
In particular, Equation (5) can deteriorate into complete sample, first failure censoring, Type-II censoring, and progressive Type-II censoring.
2.2. Assumptions
In this context, it is assumed that the items’ lifetimes under normal conditions follow the MFLED, as described by Equations (1)–(4). The lifetimes of the items under accelerated conditions decrease, as the hazard rate of the tested item is raised to where and is called the acceleration factor. The failure rate function under accelerated conditions can be written as follows:
where and . Also, the survival function under accelerated conditions can be expressed as follows
In practical terms, the survival function under accelerated conditions is derived by scaling the baseline cumulative hazard function by the acceleration factor . This implies that failure occurs more quickly under stress conditions. The greater the value of , the steeper the decline in , reflecting increased risk and shorter lifetime due to the accelerated environment. This approach is widely adopted in accelerated life testing, where stressors such as temperature, pressure, or load accelerate the degradation process. Moreover, from Equation (7), the survival function under accelerated conditions is given by , where for . Since the exponential function is strictly monotonic, it follows that for any two values , we have . Therefore, different values of yield distinct survival functions, ensuring that is identifiable. Consequently, the CDF and PDF of MFLED under accelerated conditions can be written as
and
where and . Notice that the items’ lifetimes , are identically distributed and statistically independent.
3. Maximum Likelihood Estimation
In this section, we focus on producing ML estimators of the parameters based on the data , where and , collected under the PFFC scheme with CSPALT. Also, some abbreviations are introduced in this section to simplify the form of equations, such as as and as . The likelihood function, without the inclusion of the normalizing constant, can be expressed as follows
where By taking the natural logarithm of Equation (10), the log-likelihood function ℓ, can be expressed as
Differentiating the log-likelihood function ℓ with respect to the parameters , and and equating the results to zero yields the following normal equations.
and
Unfortunately, the integral involved does not admit a closed-form solution and must be evaluated using numerical techniques. Due to the complexity of solving Equations (12)–(15), non-linear optimization algorithms such as the Newton–Raphson method are used to obtain parameter estimates for , and . The Newton–Raphson algorithm is widely regarded as an efficient and powerful root-finding method, particularly when the function’s derivatives are analytically tractable and a good initial approximation is available. Nevertheless, this method has limitations, such as sensitivity to initial values and the potential for divergence, especially in cases involving complex or ill-behaved likelihood surfaces. To address these challenges, hybrid approaches or alternative optimization strategies may be required to ensure reliable convergence. In this study, the convergence of the Newton–Raphson algorithm is shown to be highly dependent on the careful selection of initial parameter values, emphasizing the need for thoughtful initialization.
Asymptotic Confidence Bounds
Utilizing the asymptotic normality of the MLE, the asymptotic confidence intervals (ACIs) for the parameters can be constructed using the asymptotic variances obtained from the inverse of the FIM, see [29]. This can be determined in accordance with the likelihood equations, as expressed in the following form:
At times, the FIM will be utilized without computing the expectation, as it can be challenging to determine a precise expression for Equation (16). Consequently, the inverse of the FIM, also known as the asymptotic variance-covariance matrix, is given by the following expression:
It is important to note that the derivation of confidence intervals based on the inverse of the Fisher information matrix, as shown in Equation (17), relies on the asymptotic normality of the MLEs. Although rigorous verification of all regularity conditions is analytically challenging due to the complex form of the MFLED and the structure of the PFFC scheme, the fundamental requirements, such as parameter identifiability, differentiability of the log-likelihood function, and the openness of the parameter space, are satisfied. Furthermore, our simulation study confirms that MLEs exhibit desirable asymptotic properties, including consistency and approximate normality, particularly for moderate to large sample sizes. These empirical findings support the use of asymptotic theory in the construction of confidence intervals within the proposed framework. The asymptotic variances for , and can be derived from the matrix (17). Therefore, it follows that (), and this allows for the determination of , two-sided ACIs for as follows:
where represents the top percentile of the standard normal distribution. In certain cases, despite the inherent non-negativity of the model parameters, the asymptotic confidence intervals (ACIs) may yield negative lower bounds, which are not interpretable in a practical context. To address this issue, we employed a logarithmic transformation approach as proposed by Ren and Gui [30], in conjunction with the delta method introduced by Greene [31]. This transformation allows for the construction of more appropriate confidence intervals based on the asymptotic distribution of log.
where denotes distribution convergence and . Therefore, the log-transformed ML estimates-based ACIs are
When the sample size is too small, the normal approximation of ML estimates may become less accurate and efficient. To get over the problem of creating ACIs of the parameters when sample sizes are minimal, a resampling technique is presented in the following section.
4. Bootstrap Confidence Intervals
Small sample sizes are one of the difficulties with traditional statistical methods, which can lead to insufficient confidence intervals CIs based on asymptotic results. This challenge can be solved by using the parametric bootstrap method where the estimated parametric distribution of the data serves as the foundation for this method, enabling the generation of numerous resamples. This approach provides an effective way to approximate the sampling distribution of a statistic, particularly when analytical solutions are complex or unavailable. Confidence intervals constructed using the parametric bootstrap are generally more accurate and dependable, especially in small-sample scenarios. In this study, two techniques for implementing the parametric bootstrap are explored: Bootstrap-p (B-p), proposed by Efron [32], and Bootstrap-t (B-t), introduced by Hall [33].
4.1. Parametric Bootstrap-p Confidence Interval
- 1.
- From the original dataset determine , and by using Equations (11)–(14).
- 2.
- Use the censoring strategy (, , , ) along with to produce a PFFC bootstrap sample .
- 3.
- Calculate the bootstrap estimates of the PFFC bootstrap sample generated from the previous step, represented as , where ℘ corresponds to , and .
- 4.
- Repeat steps (2) and (3) for a total of (N) times to derive , i = 1, 2…, N.
- 5.
- Organize , i = 1, 2 …N ascendingly as , i = 1, 2…, N.
Let = P be the CDF of . Define = For a given z. The approximate 100(1)% 1 Boot-p CI of is given by
4.2. Parametric Bootstrap-t Confidence Interval
Consider the first three steps in Boot-p are the same here and continue as follows:
- 4.
- Calculate utilizing the asymptotic variance-covariance matrix specified in (17).
- 5.
- Determine the statistic .
- 6.
- Steps 1–5 should be repeated for ( iterations in order to get .
- 7.
- Arrange the values of in ascending order to get 1, 2 …Nboot.
The cumulative distribution function (or CDF) of is defined as = P . If z is a given value, define he approximate 100(1)% Boot-t CI of is given by
5. Bayes Estimation
The Bayesian approach is distinguished from the classical method by its capacity to incorporate prior subjective information about life parameters, an aspect that is particularly valuable and effective in reliability analysis. Additionally, the Bayesian method typically requires smaller sample sizes, making it especially suitable for costly life-testing experiments. To proceed with the Bayesian framework, it is necessary to specify prior distributions for the unknown parameters. We assume that the parameters , , , and follow independent gamma prior distributions, due to the flexibility of the gamma distribution in capturing a wide range of prior beliefs. In the absence of prior information regarding the acceleration factor , its corresponding hyperparameters are set to zero. Consequently, the prior probability density functions (PDFs) of the gamma distributions can be defined as follows:
We chose the hyperparameters to represent prior information regarding the unknown parameters. So, we mentioned a method for eliciting the values of the hyperparameters in Section 5.3. The joint prior density can be expressed as:
Thus, the joint posterior density can be expressed as:
In the Bayesian framework, the estimate of a particular function is typically derived by minimizing the expected loss under a chosen loss function, which reflects the cost associated with estimation errors.
5.1. Loss Functions
In Bayesian theory, the loss function plays a crucial role in quantifying the deviation between an estimated value and the true parameter. The central goal often involves minimizing the expected loss while accounting for uncertainty in the parameter estimation. Let denote an estimate of the true parameter . The loss function, expressed as , is a real-valued function that satisfies the condition for all possible estimates , and all values of . This condition reflects the idea that the loss function measures the penalty or discrepancy associated with using as an estimate when the actual value is . Loss functions are typically categorized into two types: symmetric and asymmetric, depending on whether they penalize overestimation and underestimation equally.
5.1.1. Symmetric Loss Function
In practice, symmetric loss functions are favored, when the losses arising from overestimation and underestimation are equally significant. One of the well-known symmetric loss functions is the squared error (SQE) loss function due to its useful mathematical properties, which can be defined as follows:
The Bayesian estimate of with respect to the SQE loss function is written as:
Therefore, the Bayesian estimate for a specified function under the SQE loss function can be written as:
5.1.2. Asymmetric Loss Function
In certain scenarios, asymmetric loss functions are preferred to improve the practical applicability of the Bayesian framework. This preference arises from the fact that both overestimation and underestimation may result in significantly different consequences, potentially leading to substantial losses. In such contexts, symmetric loss functions may fail to adequately capture the cost of estimation errors, making them less suitable. An example of an asymmetric loss function is the linear exponential (LINEX) loss function, which is defined as follows:
The orientation and degree of asymmetry are reflected by the sign and magnitude of c, respectively. When c > 0, the implications of overestimating are more pronounced than those of underestimating, whereas the reverse is true for c < 0. When c approaches zero, the LINEX loss function approximates the properties of the SE loss function, resulting in a nearly symmetric behavior; for further information, see [34]. The Bayesian estimate for under the LINX loss function is given as:
Therefore, the Bayesian estimate for a specified function under the LINX loss function can be written as:
The Bayesian estimates associated with the previously discussed loss functions involve four integrals and cannot be expressed in closed form. Consequently, the Markov Chain Monte Carlo (MCMC) method will be used to derive these estimates.
5.2. MCMC Method
To address the challenges posed by complex or analytically intractable equations in Bayesian computations, various algorithms have been developed based on Markov Chain Monte Carlo (MCMC) methodologies. Among these, the Gibbs sampling algorithm, introduced by Geman and Geman [35], is one of the most widely adopted techniques due to its conceptual simplicity and ease of implementation. The core idea behind Gibbs sampling is to iteratively draw samples from the full conditional distributions of individual parameters. A more general and flexible alternative to Gibbs sampling is the Metropolis–Hastings (M-H) algorithm, originally proposed by Metropolis et al. [36] and later generalized by Hastings [37]. This algorithm allows for sampling from complex distributions utilizing both conditional densities and proposal distributions tailored to each parameter of interest. The generated samples can then be used to compute Bayesian estimates and construct credible intervals. As shown in Equation (25), the joint posterior distribution can be reformulated as follows:
where Consequently, the conditional densities may be articulated as follows.
and
It is clear that Equations (33)–(36) do not match known distributions. Because of this, the Gibbs sampler is not appropriate for sample generation; instead, the Metropolis–Hastings (M-H) algorithm is used to apply the Markov Chain Monte Carlo (MCMC) methodology. In order to integrate Gibbs sampling with the M-H algorithm, the hybrid technique will go through the following steps:
- (1)
- Put MLEs () as initial estimate ().
- (2)
- Set
- (3)
- Generate and from , , and with the normal proposal distributions using the M-H technique outlined below.
- (4)
- Produce a proposal from from from and from .
- (5)
- Set .
- (6)
- Repeat Steps N times and get
- (7)
- To compute the credible intervals of , , , and arrange , as and Then, the credible intervals of , , , and denoted such that (ß1, ß2, ß3, become .
To achieve convergence and remove the impact of starting value selection, the first M simulated alternatives are deleted. The chosen samples are for N. The computed Bayes estimate under SEL function for is provided by
The estimated Bayes estimates under LINEX loss function for is given by
5.3. Method for Hyperparameter Elicitation
In Bayesian inference, prior distributions are typically categorized as either informative or non-informative, based on the specification of their hyperparameters. Non-informative priors are designed to exert minimal influence on the posterior distribution. This is often achieved by assigning hyperparameter values that are either exactly zero or approach zero, thereby reflecting a state of prior ignorance or neutrality. On the other hand, informative priors are used to incorporate existing knowledge, empirical evidence, or expert opinion into the analysis. The hyperparameters of such priors are determined through a structured elicitation process, which may involve expert judgment, historical data, or domain-specific considerations, as outlined below:
- 1.
- Collect a number of samples (n) from MFLED under both normal and accelerated conditions.
- 2.
- Compute the corresponding maximum likelihood estimates (, , ) for .
- 3.
- Determine the mean and variance of (, , ) for as:where represents , , and .
- 4.
- Determine the mean and variance of the specified priors, which in this paper are the gamma priors
- 5.
- The estimated hyperparameters can be derived by equating the mean and variance of for with the mean and variance of the gamma priors, and solving the equations as follows:
For more information on this method, one may refer to Dey et al. [38].
6. Simulations
To assess the efficacy of the suggested methods, Monte Carlo simulation experiments are performed using Mathematica (version 11.3). Following the algorithm, which incorporates the distribution function and introduced by Balakrishnan and Sandhu [39], 1000 PFFC samples are generated under normal and accelerated conditions from the MFLED, when the parameters , , and = 4. Using the maximum likelihood estimation, two parametric bootstrap techniques, and the MCMC method, are used to derive point and interval estimates for the parameters , , , and . For point estimates, the mean estimates (MEs) and the mean square error (MSE) are evaluated, while for interval estimates, the mean of width (MOW) is evaluated. To carry out this study, we consider distinct combinations of (s: group size) . We consider distinct combinations of group size and different values of (n: the number of groups) while the observed data are , where . This analysis is conducted under several censoring schemes (CSCHs) , where . For clarity, we focus on three distinct types of CSs: SCH I: SCH II: SCH III: , where * in the above schemes represents the number of repetitions of zero failures. In this simulation analysis, informative priors are used with hyperparameters chosen based on the approach detailed in Section 5.3. Specifically, the values selected are and , which are utilized to compute the necessary estimates. Additionally, the MCMC procedure is repeated 11,000 times, with the first 1000 times eliminated as a sufficient burn-in period to reduce the impact of the initial values. Table 1, Table 2, Table 3, and Table 4 display the simulation results of MEs and MSEs when . Table 5, Table 6, Table 7, and Table 8 display the simulation results of MOW when .

Table 1.
MEs and MSEs of the estimates of and when n = 100, , and .

Table 2.
MEs, MSEs of the estimates of and when n = 100, , and .

Table 3.
MEs, MSEs of the estimates of and when n = 100, , and .

Table 4.
MEs and MSEs of the estimates of and when n = 100, , and .

Table 5.
MOW of the estimates of and when n = 100, , and .

Table 6.
MOW of the estimates of and when n = 100, , and .

Table 7.
MOW of the estimates of and when n = 100, , and .

Table 8.
MOW of the estimates of and when n = 100, , and .
7. Applications
In this section, we illustrate the performance of the proposed inferential methods utilizing the failure times of light-emitting diodes (LEDs); see Cheng and Wang [40], who implemented this dataset with the Burr XII distribution. Table 9 provides comprehensive observed failure data records under standard and accelerated testing conditions. The goodness-of-fit between MFLED and the LEDs lifetimes is performed using the Kolmogorov–Smirnov (K–S) test statistic, and the results are shown in Table 10. For the assessment of robustness and efficacy, we compare the proposed MFLED model with the Burr XII distribution for normal and accelerated conditions. The obtained statistics and p-values infer that the MFLED offers a statistically significant and reliable fit to the observed data, providing strong evidence to support the adequacy of the MFLED model in capturing the behavior of the failure data under both normal and accelerated conditions. The observed p-values exceed conventional significance thresholds (e.g., 0.05), indicating that there is no significant difference between the empirical distribution of the data and the theoretical MFLED distribution. Moreover, when compared with the Burr XII distribution, the MFLED shows comparable or superior goodness-of-fit, thereby affirming its flexibility and suitability for modeling lifetime data across varying stress levels. Figure 1 illustrates the differences in PDFs between the normal and accelerated scenarios. The procedure described in Section 2 was applied to the failure times of LEDs data presented in Table 9, with a group size of one, resulting in the acquisition of PFFC samples. A comprehensive overview of the CSPALT framework is provided in Table 11. The point estimates for ML, B-p, and B-t, along with their respective CIs, have been derived. Additionally, we utilize the methodology outlined in Section 5.3 in the Bayesian estimation process to select the hyperparameters of the informative priors as follows: and . Furthermore, the Markov chain has been executed for a total of 55,000 iterations, with the first 5000 values discarded to remove the effect of initial values, Bayesian point estimates are obtained using both SQE and LINX loss functions. Table 12 and Table 13 present the results of point and interval estimates based on various values of the parameter , along with the corresponding 95% CRIs. Figure 2 illustrates the SF of MFLED under a normal scenario with the normal failure times of LEDs, while Figure 3 illustrates the SF of MFLED under a stress scenario with the accelerated failure times of LEDs.

Table 9.
The failure times of LEDs.

Table 10.
The MLEs under normal and accelerated use conditions with k-s and p-value.
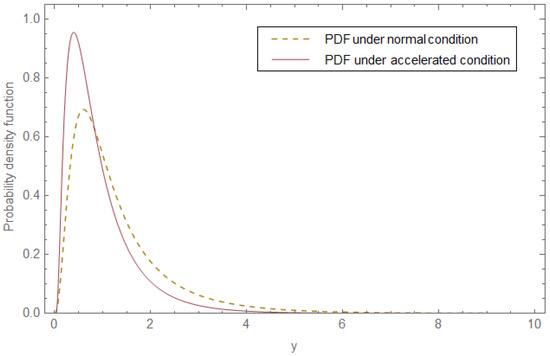
Figure 1.
PDFs of the failure times of LEDs under normal and accelerated scenarios.

Table 11.
The failure times of LEDs under CSPALT framework.

Table 12.
MLEs, B-pEs, B-tEs, and the Bayesian estimates of and .

Table 13.
Length of the confidence intervals of and .
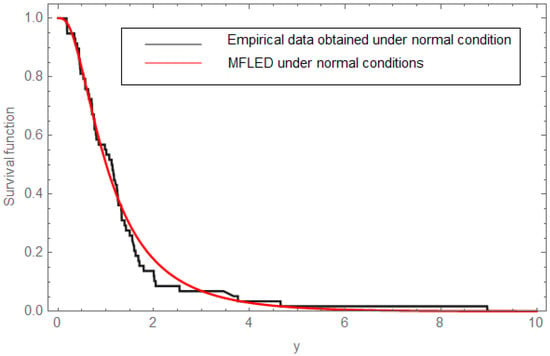
Figure 2.
Empirical normal LEDs with the SF of MFLED.
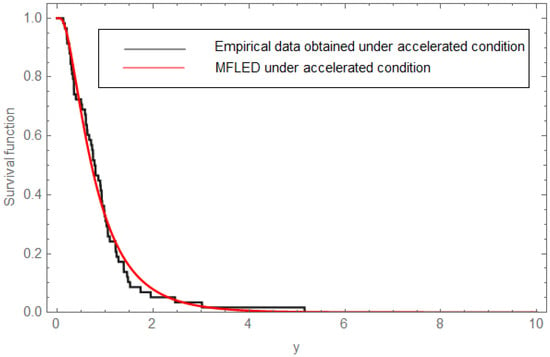
Figure 3.
Empirical stress LEDs with the SF of MFLED.
Table 12 gives the estimates of the parameters of the MFLED when , for LEDs data.
Table 13 gives the length of the confidence intervals of the MFLED estimates when for LED data. The Bayesian results in Table 11 and Table 12 can be seen in Figure 4, which shows the values , , , and for 50,000 simulated variables, after excluding the first 5000 simulated variables, for the MFLED parameters. The decision to select a group size of one is intended to facilitate a comparison between the estimator values, when the failure data are omitted (the elements failed) and when there are no omitted failure data. The K-S and p-values are calculated as explored in Table 14. Choosing a group size of one was intended to make it easier to compare the estimated values when failure data are omitted (i.e., only failed items are considered) and when no data are omitted. This helps in understanding how the removal of failure data affects the accuracy of the estimates. Table 14 shows that the MFLED model still provides a good fit. This confirms the model’s stability and reliability, even when some failure data are missing. This is considered a good result, as it is close to the results obtained when , and the size of groups are equal to 1, as in Table 15 for the complete LEDs. The close agreement between the current findings and those based on the complete LED data highlights the robustness of the MFLED model. Furthermore, when compared to the Burr XII distribution, the MFLED consistently demonstrates a comparable or better fit across both complete and grouped data settings. This suggests that MFLED maintains its flexibility and reliability even under different data configurations, offering a more stable modeling alternative in accelerated life testing scenarios.
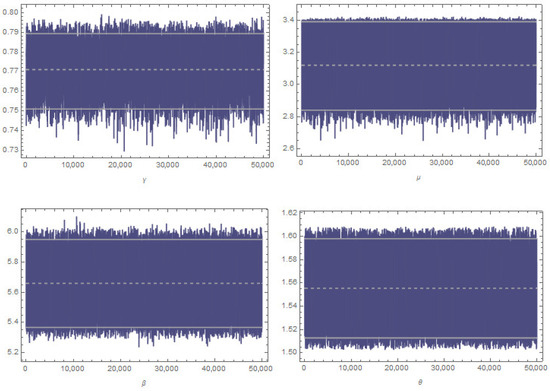
Figure 4.
The figure shows the values , , , and for 50,000 simulated variables, excluding the first 5000 simulated variables, for MFLED.

Table 14.
The MLEs under normal and accelerated use conditions with K-s and p-value.

Table 15.
The MLEs under normal and accelerated use conditions with K-s and p-value.
8. Conclusions
In this study, statistical inference for MFLED has been investigated under CSPALT within the PFFC framework. The motivation behind this work lies in its practical relevance to industrial applications, where reductions in testing time, number of units, and associated costs are increasingly important. Parameter estimation for MFLED has been conducted using various techniques. Classical estimation is performed using the ML method, and the corresponding ACIs are constructed based on the FIM. Additionally, for point and interval estimation, the two parametric bootstrap methods (B-p and B-t) are proposed. Also, the MCMC technique has been employed to obtain Bayesian point and interval estimates, due to the intractability of the Bayesian estimates in closed forms. A simulation study has been conducted to evaluate the behavior of the model parameters under varying sample sizes and experimental conditions, including both normal and stress environments across different testing schemes. The analysis demonstrates that increasing the number of failed units from 60 to 90 leads to a reduction in both the overall MSE and the MOW across all estimation methods. Bayesian methods outperform classical likelihood estimation when the group size is greater than one, while B-p, B-t, and ML methods show better performance when the group size is one. Based on these findings, it is recommended that Bayesian estimation can be used when group sizes exceed one, as it offers robustness against data loss due to group deletion. For a real application, a group size of one is applied to the LED data. It is worth noting that while the simulation study shows that the MLEs yield less mean squared errors comparable to those of the bootstrap and Bayesian approaches, the real-data application reveals a noticeable increase in the confidence interval lengths associated with the MLEs. This discrepancy may be attributed to the greater complexity and variability inherent in the real dataset, such as smaller sample sizes, stronger censoring effects, or the presence of outliers, which are not fully captured in the idealized simulation scenarios. In controlled simulations, data are generated under assumed model conditions that ensure identifiability and regularity, whereas real data may violate these assumptions to some extent. Therefore, the observed difference highlights the importance of complementing simulation studies with robust real-data analyses when evaluating estimator performance. The results demonstrate that the MFLED provides a reliable and flexible fit to failure data under both complete and grouped conditions. Compared with the Burr XII distribution, MFLED showed comparable or better performance in terms of goodness of fit. Selecting a group size of one enables effective comparison between full and partial data scenarios, and the model remained stable even when failure data were omitted. Overall, MFLED proves to be a robust choice for lifetime data modeling, particularly under censoring and acceleration settings. For future work, we plan to explore Bayesian estimation using non-informative priors. Furthermore, the investigation of alternative censoring schemes will be considered to enhance the flexibility and applicability of the proposed inference methods.
Author Contributions
Conceptualization, A.T.F., D.A.R. and B.S.E.-D.; methodology, A.T.F., D.A.R. and B.S.E.-D.; software, D.A.R.; validation, A.T.F. and H.H.A.; formal analysis, D.A.R. and B.S.E.-D.; investigation, H.H.A. and B.S.E.-D.; resources, A.T.F.; data curation, D.A.R.; writing—original draft preparation, A.T.F.; writing—review & editing, D.A.R. and H.H.A.; visualization, H.H.A.; supervision, B.S.E.-D.; project administration, D.A.R. and H.H.A.; funding acquisition, H.H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [GRANT No. KFU252867].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| ALTs | Accelerated life tests |
| ACIs | Asymptotic confidence intervals |
| B-p | Bootstrap-p |
| B-t | Bootstrap-t |
| B-pEs | Bootstrap-p estimates |
| B-tEs | Bootstrap-t estimates |
| B-p CIs | Bootstrap-p confidence intervals |
| B-t CIs | Bootstrap-ts confidence intervals |
| FRF | Failure rate function |
| SCH | Scheme |
| CSCH | Censoring scheme |
| CSPALT | Constant-stress partially accelerated life test |
| CRIs | Credible intervals |
| CIs | Confidence intervals |
| PALTs | Partially accelerated life tests |
| PFFC | Progressive first-failure censoring |
| FIM | Fisher information matrix |
| LINX | Linear exponential |
| LEDs | Light-emitting diodes |
| MCMC | Markov chain Monte Carlo |
| MEs | Mean Estimates |
| MFLED | Modified Fréchet-Lomax exponential distribution |
| MSEs | Mean squared errors |
| MW | Mean of width |
| ML | Maximum likelihood |
| MLEs | Maximum likelihood estimates |
| P | Parameters |
| K-S | Kolmogorov–Smirnov |
| SF | Survival function |
| SQE | Squared error |
References
- Nelson, W.B. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Dey, S.; Nassar, M. Generalized inverted exponential distribution under constant stress accelerated life test: Different estimation methods with application. Qual. Reliab. Eng. Int. 2020, 36, 1296–1312. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Lin, C.T.; Hsu, Y.Y.; Lee, S.Y.; Balakrishnan, N. Inference on constant stress accelerated life tests for log-location-scale lifetime distributions with type-I hybrid censoring. J. Stat. Simul. 2019, 89, 720–749. [Google Scholar] [CrossRef]
- Haj Ahmad, H.; Almetwally, E.M.; Ramadan, D.A. A comparative inference on reliability estimation for a multi-component stress-strength model under power Lomax distribution with applications. AIMS Math. 2022, 7, 18050–18079. [Google Scholar] [CrossRef]
- Hakamipour, N. Comparison between constant-stress and step-stress accelerated life tests under a cost constraint for progressive type I censoring. Seq. Anal. 2021, 40, 17–31. [Google Scholar] [CrossRef]
- Wang, B. Unbiased estimations for the exponential distribution based on step-stress accelerated life-testing data. Appl. Math. Comput. 2006, 173, 1227–1237. [Google Scholar] [CrossRef]
- Mahto, A.K.; Tripathi, Y.M.; Wu, S.J. Statistical inference based on progressively type-II censored data from the Burr X distribution under progressive-stress accelerated life test. J. Stat. Comput. Simul. 2021, 91, 368–382. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.H.; Al-Hussaini, E.K. Progressive stress accelerated life tests under finite mixture models. Metrika 2007, 66, 213–231. [Google Scholar] [CrossRef]
- Ahmad, H.H.; Ramadan, D.A.; Almetwally, E.M. Tampered Random Variable Analysis in Step-Stress Testing: Modeling, Inference, and Applications. Mathematics 2024, 12, 1248. [Google Scholar] [CrossRef]
- Haj Ahmad, H.; Almetwally, E.M.; Ramadan, D.A. Competing Risks in Accelerated Life Testing: A Study on Step-Stress Models with Tampered Random Variables. Axioms 2025, 14, 32. [Google Scholar] [CrossRef]
- Hassan, A.S.; Nassr, S.G.; Pramanik, S.; Maiti, S.S. Estimation in constant stress partially accelerated life tests for Weibull distribution based on censored competing risks data. Ann. Data Sci. 2020, 7, 45–62. [Google Scholar] [CrossRef]
- Nassar, M.; Alam, F.M.A. Analysis of modified Kies exponential distribution with constant stress partially accelerated life tests under type-II censoring. Mathematics 2022, 10, 819. [Google Scholar] [CrossRef]
- Gouno, E.; Sen, A.; Balakrishnan, N. Optimal step-stress test under progressive Type-I censoring. IEEE Trans. Reliab. 2004, 53, 388–393. [Google Scholar] [CrossRef]
- Wu, S.J.; Lin, Y.P.; Chen, S.T. Optimal step-stress test under type I progressive group-censoring with random removals. J. Stat. Plan. Inference 2008, 138, 817–826. [Google Scholar] [CrossRef]
- Bai, D.S.; Chung, S.W. Optimal design of partially accelerated life tests for the exponential distribution under type-I censoring. IEEE Trans. Reliab. 1992, 7, 400–406. [Google Scholar] [CrossRef]
- Fan, T.H.; Wang, W.L.; Balakrishnan, N. Exponential progressive step-stress life-testing with link function based on Box–Cox transformation. J. Stat. Plan. Inference 2008, 138, 2340–2354. [Google Scholar] [CrossRef]
- Ismail, A.A.; Al-Babtain, A.A. On Studying Partially Accelerated Life Tests Under Progressive Stress. J. Testing Eval. 2015, 43, 897–905. [Google Scholar] [CrossRef]
- Algarni, A.; Almarashi, A.M.; Okasha, H.; Ng, H.K.T. E-bayesian estimation of chen distribution based on type-I censoring scheme. Entropy 2020, 22, 636. [Google Scholar] [CrossRef]
- Kundu, D.; Howlader, H. Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data. Comput. Stat. Data Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
- Wu, M.; Gui, W. Estimation and prediction for Nadarajah-Haghighi distribution under progressive type-II censoring. Symmetry 2021, 13, 999. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M. Estimation of parameters of Weibull–Gamma distribution based on progressively censored data. Stat. Pap. 2018, 59, 725–757. [Google Scholar] [CrossRef]
- Wu, S.J.; Kuş, C. On estimation based on progressive first-failure-censored sampling. Comput. Stat. Data Anal. 2009, 53, 3659–3670. [Google Scholar] [CrossRef]
- Xie, Y.; Gui, W. Statistical inference of the lifetime performance index with the log-logistic distribution based on progressive first-failure-censored data. Symmetry 2020, 12, 937. [Google Scholar] [CrossRef]
- Lin, H.; Wang, L.; Lio, Y.; Dey, S. Estimation of Matusita measure between generalized inverted exponential distributions under progressive first-failure censored data. J. Comput. Applied Math. 2023, 421, 114836. [Google Scholar] [CrossRef]
- Farhat, A.T.; Ramadan, D.A.; El-Desouky, B.S. Application of Modified Fréchet-Lomax Exponential Distribution to COVID-19 with some Characteristics. Mans. J. Math. 2025, 41, 24–40. [Google Scholar]
- Ijaz, M.; Asim, S.M.; Alamgir. Lomax exponential distribution with an application to real-life data. PLoS ONE 2019, 14, e0225827. [Google Scholar] [CrossRef]
- Khalil, A.; Ahmadini, A.A.H.; Ali, M.; Mashwani, W.K.; Alshqaq, S.S.; Salleh, Z. A novel method for developing efficient probability distributions with applications to engineering and life science data. J. Math. 2021, 2021, 4479270. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ren, J.; Gui, W. Inference and optimal censoring scheme for progressively Type-II censored competing risks model for generalized Rayleigh distribution. Comput. Stat. 2021, 36, 479–513. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2000; pp. 201–215. [Google Scholar]
- Efron, B. The Jackknife, the Bootstrap and Other Resampling Plans; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1982. [Google Scholar]
- Hall, P. Theoretical comparison of bootstrap confidence intervals. Ann. Stat. 1988, 16, 927–953. [Google Scholar] [CrossRef]
- Zellner, A. Bayesian estimation and prediction using asymmetric loss functions. J. Am. Stat. Assoc. 1986, 81, 446–451. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Dey, S.; Singh, S.; Tripathi, Y.M.; Asgharzadeh, A. Estimation and prediction for a progressively censored generalized inverted exponential distribution. Stat. Methodol. 2016, 32, 185–202. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. A simple simulational algorithm for generating progressive Type-II censored samples. Am. Stat. 1995, 49, 229–230. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Wang, F.K. Estimating the Burr XII parameters in constant-stress partially accelerated life tests under multiple censored data. Commun.-Stat.-Simul. Comput. 2012, 41, 1711–1727. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).