Privacy-Aware Table Data Generation by Adversarial Gradient Boosting Decision Tree

Abstract

Privacy preservation poses significant challenges in third-party data sharing, particularly when handling table data containing personal information such as demographic and behavioral records. Synthetic table data generation has emerged as a promising solution to enable data analysis while mitigating privacy risks. While Generative Adversarial Networks (GANs) are widely used for this purpose, they exhibit limitations in modeling table data due to challenges in handling mixed data types (numerical/categorical), non-Gaussian distributions, and imbalanced variables. To address these limitations, this study proposes a novel adversarial learning framework integrating gradient boosting trees for synthesizing table data, called Adversarial Gradient Boosting Decision Tree (AGBDT). Experimental evaluations on several datasets demonstrate that our method outperforms representative baseline models regarding statistical similarity and machine learning utility. Furthermore, we introduce a privacy-aware adaptation of the framework by incorporating k-anonymization constraints, effectively reducing overfitting to source data while maintaining practical usability. The results validate the balance between data utility and privacy preservation achieved by our approach.

1. Introduction

The rapid advancement of information technology has enabled large-scale data collection across sectors such as healthcare, finance, and public administration. While the rise of deep learning has significantly improved data-driven decision-making, most applications remain confined within organizational boundaries. Expanding data sharing with external parties holds great promise for value creation but introduces serious privacy risks.

Many real-world datasets contain Personally Identifiable Information (PII) such as names, genders, ages, and locations [1]. Even after removing direct identifiers, quasi-identifiers (e.g., age, gender, zip code) can still enable re-identification. For instance, Sweeney demonstrated that anonymized medical records could be cross-linked with voter registrations to re-identify individuals [2], while Narayanan and Shmatikov showed that movie ratings can be deanonymized via statistical matching [3]. These privacy risks have prompted strict legal regulations such as the EU’s General Data Protection Regulation (GDPR) (https://gdpr-info.eu/, accessed on 20 July 2025) and the California Consumer Privacy Act (CCPA) (https://oag.ca.gov/privacy/ccpa, accessed on 20 July 2025).

Traditional anonymization techniques like k-anonymity [2], l-diversity [4], and t-closeness [5] offer some protection but often sacrifice data utility [6]. Synthetic data generation has emerged as an alternative, aiming to generate artificial datasets that retain statistical fidelity without linking to real individuals. Recent research [7] extended and evaluated synthetic data generation for longitudinal cohorts using statistical methods grounded in k-anonymity and l-diversity, ensuring privacy protection and analytical reproducibility. Generative Adversarial Networks (GANs) [8] have shown promise in synthetic data generation by training a generator–discriminator pair adversarially [9,10]. However, applying GANs to tabular data introduces several challenges, such as mixed data types, imbalanced variables, and non-Gaussian distributions.

To address these challenges, deep learning-based methods such as Table-GAN [11], CTGAN [12], and TVAE [12] have been proposed. These models incorporate innovations like mode-specific normalization and stratified sampling to capture tabular structures better. CTAB-GAN+ [13] further introduces downstream task alignment and differential privacy, while federated methods like FedEqGAN [14] integrate encryption to address cross-source heterogeneity. In addition, for privacy-aware synthesis, DP-CTGAN [15] embeds rigorous $(ϵ,\delta )$-differential privacy into Conditional Tabular GANs through gradient clipping and Gaussian noise injection, preserves higher statistical fidelity and downstream predictive accuracy than prior private baselines.

In parallel, tree-based machine learning approaches have also gained traction for tabular data synthesis. ARF [16] uses ensembles of random forests to model local feature distributions, while Generative Trees (GTs) [17] mimic the partition logic of decision trees to synthesize data along learned splits. A recent study by Emam et al. [18] utilized a sequential synthesis framework based on gradient-boosted decision trees (GBDT) to assess the replicability of health data analyses, showing high consistency between synthetic and real datasets. While efficient, these models struggle to capture global feature dependencies or provide substantial privacy enhancement.

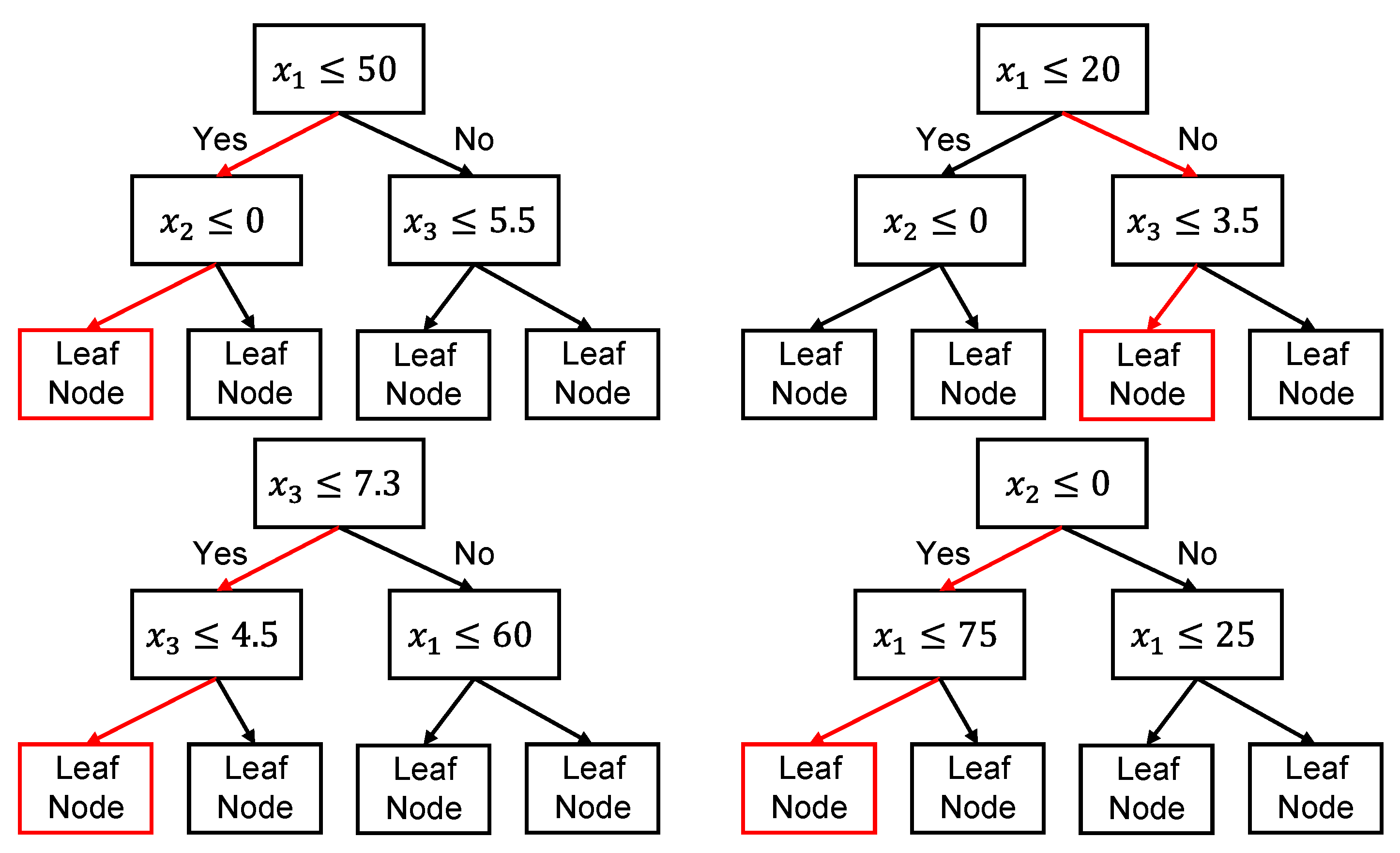
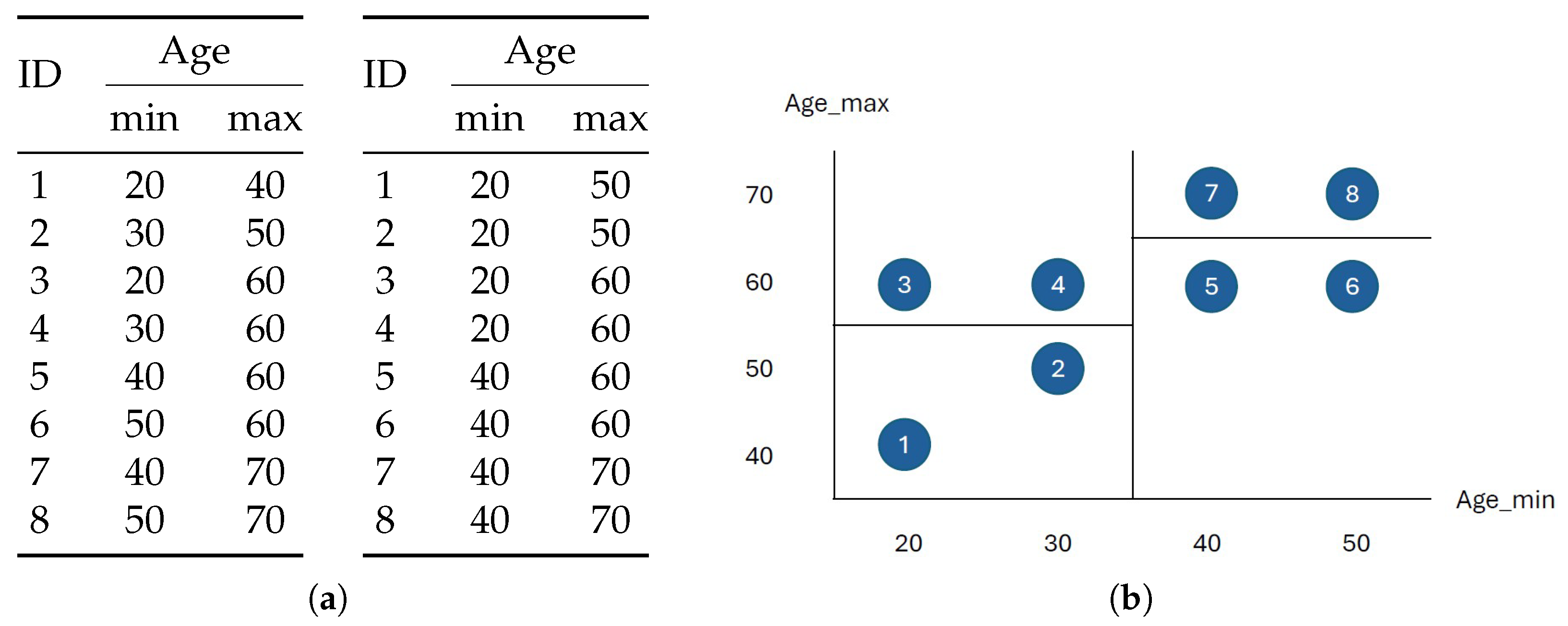
Building on this line of work, we propose a novel method called Adversarial Gradient Boosting Decision Tree (AGBDT). It integrates Gradient Boosting Decision Tree ensembles with adversarial training to generate high-quality tabular data while ensuring privacy. Our method iteratively updates data generation domains through discriminator feedback, then employs a k-anonymity Mondrian sampling strategy to generate privacy-aware synthetic records. To further enhance protection, we extend our framework to support l-diversity and t-closeness constraints.

Our main contributions include the following:

• A novel hybrid framework combining gradient boosting and adversarial learning for tabular data synthesis.
• A domain update mechanism guided by decision path logic, enabling privacy-preserving generation with controlled fidelity.
• Empirical evaluation on five datasets against several baselines, with ablation studies on k-anonymity constraints.

2. Methods

2.1. Adversarial Gradient Boosting Framework

The proposed methodology, Adversarial Gradient Boosting Decision Tree (AGBDT), integrates gradient boosting trees into an adversarial learning framework to address the limitations of existing table data generation approaches. As illustrated in Figure 1, the system comprises three core components: (1) a generator that synthesizes privacy-preserving synthetic data, (2) a discriminator that distinguishes real from synthetic records using gradient boosting decision trees, and (3) a range table that dynamically constrains attribute value ranges to prevent overfitting.

2.1.1. Core Mechanism

The workflow begins with initial synthetic data generation, where a range table (Table (b) in Figure 2) is constructed by extracting minimum and maximum values for each attribute from the original dataset (Table (a) in Figure 2). Synthetic records are generated by uniformly sampling values within these ranges (Table (c) in Figure 2). For example, an integer-type attribute $x_1$ with a range of [0, 100] would produce synthetic values randomly drawn from this interval.

A gradient boosting tree classifier learns to distinguish real and synthetic data during discriminator training through iterative 5-fold cross-validation. The discriminator’s decision paths are then used to guide the generator adaptation. Inspired by GTs [17], the proposed method augments each boosting round with a “range table” that records split conditions across all features. The generator retrains its gradient boosting trees using discriminator-predicted labels, updating the range table by narrowing attribute value boundaries according to the discriminator’s splitting criteria. For example, as illustrated in Figure 3, record $ID=1$ in Figure 2 traverses eight split predicates to reach a leaf node, at which point the generator uses these predicates to tighten its intervals to $20<x_1\le 50$, $x_2\le 0$, and $x_3<3.5$; the updated range table is shown in Table (d) in Figure 2. Such training processes of gradient boosting tree classifiers for the discriminator and generator are iterated until the discriminator’s classification accuracy falls below a predefined threshold, ensuring synthetic data convergence toward the real data distribution.

For details, in AGBDT, each real record $x_i\in \mathbb{R}$ is associated with a feature-wise domain ${\mathbb{D}}_i$, which represents the feasible sampling interval for generating synthetic data. This domain is iteratively refined using the decision paths of the gradient boosting classifier. Let ${\mathbb{D}}_{i,f}^{\left(j\right)}$ denote the domain of feature f for record $x_i$ after the j-th decision tree in the ensemble. Each internal node of the decision tree defines a binary split of the form $x^f\le \theta$, where $\theta$ is the split threshold. We update the domain ${\mathbb{D}}_{i,f}^{\left(j\right)}$ based on whether the path of $x_i$ goes left or right at each node:

$${\mathbb{D}}_{i,f}^{\left(j\right)}=\left\{\begin{array}{cc}\left[{\mathbb{D}}_{i,f}^{(j-1)}\left[0\right],min\left({\mathbb{D}}_{i,f}^{(j-1)}\left[1\right],\theta \right)\right]\hfill & \mathrm{if}{x}_i^f\le \theta ,\hfill \\ \left[max\left({\mathbb{D}}_{i,f}^{(j-1)}\left[0\right],\theta \right),{\mathbb{D}}_{i,f}^{(j-1)}\left[1\right]\right]\hfill & \mathrm{if}{x}_i^f>\theta .\hfill \end{array}\right.$$

(1)

The final domain after traversing all M trees is the intersection of all intermediate updates:

$${\mathbb{D}}_i^{(*)}=\bigcap _{j=1}^M{\mathbb{D}}_i^{\left(j\right)}.$$

(2)

This iterative domain shrinking ensures that synthetic samples generated from ${\mathbb{D}}_i^{(*)}$ follow the same logical constraints as the real data under the ensemble classifier, thereby improving fidelity while maintaining diversity. See Line 4–14 in Algorithm 1.

2.1.2. Parameter Tuning

Key hyperparameters include the tree depth to limit model complexity, the number of trees to balance computational efficiency and learning capacity, and a range update ratio to control the granularity of attribute range adjustments. These settings prevent excessive overfitting while maintaining synthesis fidelity.

2.2. Privacy Enhancement via k-Anonymity

To address the risk of privacy leakage caused by overfitting during synthetic data generation, the proposed method incorporates k-anonymization into the range table using the Mondrian k-anonymity algorithm [19]. Although alternative privacy-preserving methods such as k-concealment [20] or differential privacy [21] could also be considered, we select the Mondrian k-anonymity approach due to its natural compatibility with the decision path partitioning logic of gradient boosting trees. The range table stores the minimum and maximum values of each attribute for all records, and is treated as a $2d$-dimensional space (where d is the number of attributes).

For example, in Figure 4a, the original range table contains age ranges such as $[20,40]$ for $ID=1$ and $[30,50]$ for $ID=2$. The Mondrian algorithm recursively partitions this space by selecting a random dimension (e.g., minimal value of age (Age_min) or maximum value of age (Age_max)) and splitting it at the median value until each partition contains at least k records. As shown in Figure 4b, IDs $\{1,2\}$ are merged into a single partition after splitting the Age_min dimension at 35 and the Age_max dimension at 50. The generalized range for these IDs becomes $[20,50]$, replacing their original ranges $[20,40]$ and $[30,50]$. This process ensures that any synthetic record generated from the anonymized range table cannot be uniquely linked to fewer than k original records, thereby satisfying k-anonymity. The final anonymized range table (Figure 4a) guarantees that each generalized range corresponds to at least k original records. Synthetic data is then regenerated within these generalized ranges, balancing privacy protection with statistical utility.

To formally define k-anonymity, let $\mathcal{D}=r_1,r_2,\dots ,r_n$ denote the original dataset, where each record $r_i$ contains a set of quasi-identifiers $\mathrm{QI}\left(r_i\right)=a_{i1},a_{i2},\dots ,a_{id}$. A dataset ${\mathcal{D}}^{\prime }$ satisfies k-anonymity if every combination of quasi-identifier values in ${\mathcal{D}}^{\prime }$ appears in at least k distinct records. Mathematically,

$$\forall r_i\in {\mathcal{D}}^{\prime },\left|\left\{r_j\in {\mathcal{D}}^{\prime }\mid \mathrm{QI}\left(r_j\right)=\mathrm{QI}\left(r_i\right)\right\}\right|\ge k$$

(3)

In our framework, each record $r_i$ is associated with an interval-based domain $\mathbb{D}i=[li1,u_{i1}],[l_{i2},u_{i2}],\dots ,[l_{id},u_{id}]$, where $[l_{ij},u_{ij}]$ denotes the valid range of attribute j for record i. After applying Mondrian partitioning, records are grouped into equivalence classes ${\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_m$, each satisfying $\left|{\mathcal{P}}_k\right|\ge k$. Within each class, all records are generalized to share the same domain:

$$\forall r_i,r_j\in \mathcal{P}k,\mathbb{D}i=\mathbb{D}j=\left[\min r\in \mathcal{P}karj,maxr\in \mathcal{P}karj\right]{j=1}^d$$

(4)

This ensures that any synthetic record generated from the generalized domain cannot be uniquely traced back to fewer than k original records, thereby mitigating re-identification risks. See Line 15–26 in Algorithm 1.

Algorithm 1: AGBDT: Adversarial Gradient Boosting for Tabular Data Synthesis

3. Experiments

3.1. Datasets

The experiments utilized five table datasets: Adult, Census, Credit, Covtype, and Intrusion. The Adult, Census, Credit, and Covtype datasets were sourced from SDV [22], and the Intrusion dataset was sourced from UCI KDD Archive [23].

Table 1. Overview of benchmark datasets used for evaluation.

	Classes	Train Size	Test Size	Numeric Cols	Categorical Cols
Adult	2	22,792	9769	6	9
Census	2	45,000	5000	7	34
Credit	2	40,000	10,000	29	1
Covtype	7	45,000	5000	10	45
Intrusion	5	45,000	5000	32	10

represents classification tasks with varying characteristics. To address computational constraints, Census, Credit, Covtype, and Intrusion were subsampled to 50,000 records each, stratified by their target variables.

3.2. Synthetic Data Generation

The proposed method AGBDT was compared against four baselines: CTGAN [12], TVAE [12], CTAB-GAN+ [13], DP-CTGAN [15,24], and ARF [16]. All models were configured using parameters specified in their original publications. For AGBDT, three variants were tested: baseline (without k-anonymization), $k=2$, and $k=5$ (with Mondrian-based k-anonymization applied to the range table). The gradient boosting trees in AGBDT were trained using scikit-learn’s GradientBoostingClassifier with fixed hyperparameters: the maximum tree depth is set to 3; the number of trees is set to 50; the discriminator’s classification accuracy threshold for early stopping is set to $0.52$; and the maximum number of rounds is set to 100. For a discussion on parameter selection and computational cost, see the Discussion section. Each synthesis experiment was repeated five times per dataset to ensure statistical reliability.

3.3. Results

3.3.1. Statistical Similarity

Synthetic data fidelity was evaluated using Wasserstein Distance (WD) for numerical attributes, Jensen–Shannon Divergence (JSD) for categorical attributes, and Difference in Correlation Matrices (Diff. Corr). The lower the value, the better, indicating that the synthetic data is closer to the original data. It will be marked in bold in

Table 2. Average statistical similarity metrics across all datasets.

	WD	JSD	DiffCorr
Model
CTGAN	0.103	0.132	3.201
TVAE	0.241	0.121	1.612
CTAB-GAN+	0.088	0.068	1.769
DP-CTGAN	0.148	0.156	4.046
ARF	0.195	0.003	0.598
AGBDT	0.005	0.008	0.485
AGBDT ($k=2$)	0.153	0.003	3.287
AGBDT ($k=5$)	0.152	0.004	3.285

and

Table A1. Average statistical similarity evaluation index.

Dataset	Model	WD	JSD	Diff. Corr
Adult	CTGAN	0.066	0.084	0.386
	TVAE	0.307	0.260	0.251
	CTAB-GAN+	0.047	0.078	0.267
	DP-CTGAN	0.103	0.272	0.828
	ARF	0.203	0.007	0.046
	AGBDT	0.002	0.014	0.042
	AGBDT ($k=2$)	0.155	0.006	0.571
	AGBDT ($k=5$)	0.158	0.006	0.494
Census	CTGAN	0.087	0.109	2.947
	TVAE	0.205	0.183	1.133
	CTAB-GAN+	0.143	0.166	2.198
	DP-CTGAN	0.264	0.294	3.875
	ARF	0.195	0.005	0.303
	AGBDT	0.001	0.015	0.066
	AGBDT ($k=2$)	0.150	0.005	3.003
	AGBDT ($k=5$)	0.150	0.005	2.982
Credit	CTGAN	0.214	0.327	2.508
	TVAE	0.513	0.024	1.019
	CTAB-GAN+	0.137	0.005	3.353
	DP-CTGAN	0.065	0.020	2.491
	ARF	0.117	0.001	1.481
	AGBDT	0.018	0.003	1.376
	AGBDT ($k=2$)	0.242	0.002	3.151
	AGBDT ($k=5$)	0.227	0.002	3.031
Covtype	CTGAN	0.050	0.044	2.210
	TVAE	0.065	0.063	1.052
	CTAB-GAN+	0.023	0.021	1.259
	DP-CTGAN	0.152	0.077	3.066
	ARF	0.150	0.001	0.445
	AGBDT	0.002	0.002	0.052
	AGBDT ($k=2$)	0.067	0.001	1.926
	AGBDT ($k=5$)	0.076	0.001	2.087
Intrusion	CTGAN	0.096	0.097	7.956
	TVAE	0.115	0.077	4.604
	CTAB-GAN+	-	-	-
	DP-CTGAN	0.156	0.115	9.969
	ARF	0.310	0.003	0.713
	AGBDT	0.002	0.006	0.887
	AGBDT ($k=2$)	0.149	0.003	7.786
	AGBDT ($k=5$)	0.150	0.004	7.830

.

Table 2 shows that AGBDT achieves the best overall performance across all datasets in terms of average results. Specifically, AGBDT attains optimal values in WD and Diff. Corr metrics, while its JSD value ranks second-best and remains within the same order of magnitude as the leading method. After applying k-anonymity, JSD improves to the best result, whereas WD experiences a noticeable increase. This observation suggests that synthetic data, which is highly similar to real data, will be excluded due to privacy enforcement. Moreover, Diff. Corr significantly rises to a level comparable with DP-CTGAN, likely indicating insufficient data meeting privacy-preservation criteria, leading to substantial duplication of certain records. For details, as shown in Appendix A Table A1, the model applying k-anonymity exhibits a substantial increase in magnitude for the Census and Intrusion datasets, which contain numerous categorical columns. This suggests that after applying k-anonymity, only a few decision trees satisfy the required conditions, significantly reducing synthetic data per iteration. Consequently, repeated iterations of data synthesis lead to a notable increase in redundancy. However, due to our mechanism controlling the anonymity parameter k, the extent of this increase remains lower than DP-CTGAN, thus validating the effectiveness of our method.

3.3.2. Machine Learning Utility

We evaluated the utility of synthetic data in machine learning by comparing two scenarios: (1) results from training and testing entirely on original data, and (2) results from training on synthetic data and testing on original data. Closer alignment between these outcomes indicates higher substitutability of original training data with synthetic data, i.e., greater machine learning utility. Best results will be marked in bold in

Table 3. Model-averaged machine learning usefulness evaluation.

	AUC	F1-Score	Accuracy
Model
Oracle	0.909	0.809	0.859
CTGAN	0.718	0.604	0.718
TVAE	0.784	0.670	0.648
CTAB-GAN+	0.810	0.683	0.767
DP-CTGAN	0.528	0.525	0.586
ARF	0.891	0.757	0.805
AGBDT	0.898	0.792	0.846
AGBDT ($k=2$)	0.496	0.524	0.599
AGBDT ($k=5$)	0.504	0.532	0.600

and

Table A2. Average machine learning usefulness evaluation index.

Dataset	Model	AUC	F1-Score	Accuracy
Adult	Oracle	0.891	0.769	0.845
	CTGAN	0.563	0.439	0.748
	TVAE	0.757	0.561	0.754
	CTAB-GAN+	0.851	0.723	0.814
	DP-CTGAN	0.532	0.466	0.692
	ARF	0.878	0.749	0.836
	AGBDT	0.884	0.767	0.841
	AGBDT ($k=2$)	0.488	0.440	0.748
	AGBDT ($k=5$)	0.499	0.440	0.754
Census	Oracle	0.920	0.714	0.948
	CTGAN	0.630	0.490	0.937
	TVAE	0.718	0.498	0.935
	CTAB-GAN+	0.677	0.670	0.934
	DP-CTGAN	0.544	0.476	0.902
	ARF	0.889	0.615	0.944
	AGBDT	0.914	0.708	0.947
	AGBDT ($k=2$)	0.514	0.486	0.936
	AGBDT ($k=5$)	0.479	0.491	0.929
Credit	Oracle	0.882	0.799	0.999
	CTGAN	0.987	0.612	0.977
	TVAE	-	-	-
	CTAB-GAN+	0.886	0.726	0.997
	DP-CTGAN	0.550	0.502	0.998
	ARF	0.886	0.742	0.999
	AGBDT	0.861	0.750	0.999
	AGBDT ($k=2$)	0.462	0.497	0.989
	AGBDT ($k=5$)	0.540	0.496	0.984
Covtype	Oracle	0.943	0.768	0.635
	CTGAN	0.693	0.500	0.189
	TVAE	-	0.637	0.273
	CTAB-GAN+	0.824	0.614	0.322
	DP-CTGAN	0.485	0.420	0.102
	ARF	0.909	0.683	0.434
	AGBDT	0.934	0.739	0.583
	AGBDT ($k=2$)	0.518	0.471	0.108
	AGBDT ($k=5$)	0.496	0.469	0.107
Intrusion	Oracle	-	0.995	0.870
	CTGAN	-	0.977	0.738
	TVAE	0.877	0.984	0.629
	CTAB-GAN+	-	-	-
	DP-CTGAN	-	0.759	0.235
	ARF	-	0.994	0.813
	AGBDT	-	0.995	0.862
	AGBDT ($k=2$)	-	0.728	0.216
	AGBDT ($k=5$)	-	0.766	0.226

.

Here, four classifiers—Decision Tree Classifier (DTC), Logistic Regression (LR), Multilayer Perceptron (MLP), and Random Forest (RF)—were trained on synthetic data and evaluated using AUC, F1-score, and Accuracy. Label encoding was applied for DTC and RF for categorical variable preprocessing, while one-hot encoding was used for LR and MLP. Numerical variables were normalized exclusively for MLP. Machine learning models were implemented using scikit-learn without hyperparameter tuning. The average evaluation metrics for each combination of generative model and dataset are shown in Table 3. Each value represents the average of 20 trials (5 synthetic datasets × 4 machine learning models). The Oracle row represents results from training and testing entirely on original data, where closer alignment indicates higher synthetic data utility.

For details in Table A2, for the Credit and Covtype dataset, TVAE failed to generate the minority class of the target variable, which is marked as ‘-’. For the Intrusion dataset, stratified sampling resulted in the absence of the least frequent class in the test data, rendering AUC calculation infeasible (also marked as ‘-’). The AGBDT achieved the best results on three out of five datasets. Thus, AGBDT is validated to generate synthetic data with superior utility for machine learning tasks. After applying k-anonymization to the range table, the model struggles to accurately capture data distribution characteristics due to privacy protection constraints, resulting in a decline in performance metrics similar to DP-CTGAN, which also prioritizes privacy. However, the proposed method exhibits smaller reductions in the F1-score and Accuracy compared to DP-CTGAN, demonstrating that our model provides greater utility relative to the state-of-the-art privacy-preserving method.

3.3.3. Privacy Evaluation

We adopt the NewRowSynthesis metric [22], which evaluates the proportion of synthetic records that exactly match records in the original data (i.e., $1-m/t$, where m is the number of matching synthetic records with the original data and t is the number of total synthetic records). The metric ranges from 0 (all synthetic records exist in the original data) to 1 (all synthetic records are novel).

Table A3. Privacy evaluation metrics.

Dataset	Model	NewRowSynthesis		DCR	NNDR
		Average	Worst
Adult	CTGAN	1.0	1.0	0.340	0.320
	TVAE	1.0	1.0	0.513	0.101
	CTAB-GAN+	1.0	1.0	0.199	0.203
	DP-CTGAN	1.0	1.0	0.975	0.438
	ARF	1.0	1.0	0.352	0.434
	AGBDT	0.999+	0.999+	0.085	0.062
	AGBDT ($k=2$)	1.0	1.0	0.958	0.679
	AGBDT ($k=5$)	1.0	1.0	1.013	0.701
Census	CTGAN	1.0	1.0	0.791	0.561
	TVAE	0.986	0.978	1.225	0.416
	CTAB-GAN+	0.997	0.990	0.480	0.368
	DP-CTGAN	1.0	1.0	9.200	0.760
	ARF	1.0	1.0	0.700	0.757
	AGBDT	0.642	0.595	0	0
	AGBDT ($k=2$)	1.0	1.0	1.158	0.659
	AGBDT ($k=5$)	1.0	1.0	1.165	0.661
Credit	CTGAN	0.999	0.998	0.886	0.878
	TVAE	0.002	0.001	0	0
	CTAB-GAN+	0.999+	0.999	0.992	0.902
	DP-CTGAN	0.999+	0.999+	1.545	0.849
	ARF	0.999	0.998	0.696	0.838
	AGBDT	0.622	0.577	0	0
	AGBDT ($k=2$)	0.999+	0.999+	1.165	0.926
	AGBDT ($k=5$)	1.0	1.0	1.162	0.926
Covtype	CTGAN	1.0	1.0	0.883	0.886
	TVAE	1.0	1.0	0.862	0.821
	CTAB-GAN+	1.0	1.0	0.794	0.845
	DP-CTGAN	1.0	1.0	1.700	0.905
	ARF	1.0	1.0	0.665	0.783
	AGBDT	1.0	1.0	0.283	0.234
	AGBDT ($k=2$)	1.0	1.0	0.915	0.878
	AGBDT ($k=5$)	1.0	1.0	0.918	0.889
Intrusion	CTGAN	1.0	1.0	1.568	0.870
	TVAE	1.0	1.0	1.263	0.715
	CTAB-GAN+	0.992	0.971	-	-
	DP-CTGAN	1.0	1.0	11.719	0.942
	ARF	0.995	0.994	0.712	0.808
	AGBDT	0.423	0.411	0	0
	AGBDT ($k=2$)	0.999	0.995	1.597	0.731
	AGBDT ($k=5$)	0.999	0.996	1.601	0.731

reports the average and worst-case values across five trials, rounded to four decimal places. Best results will be marked in bold. Without k-anonymization, AGBDT generated the lowest proportion of novel records (highest privacy risk). However, applying $k=2$ anonymization reduced the overlap with original records, achieving parity with baseline models on almost all datasets.

In addition, referring to [25,26,27], we use Distance to Closest Records (DCR) to measure Euclidean distance between any synthetic data record and its closest corresponding real neighbour; the higher the DCR, the lesser the risk of privacy breach. In addition, we also use Nearest Neighbor Distance Ratio (NNDR) to calculate the ratio of the distance between the closest synthetic record, the second closest synthetic record, and the closest record in the original data. Higher values indicate better privacy. These metrics’ 5^th percentile is computed to provide a robust estimate of the privacy risk. At the same time, we calculate these Euclidean distance-based metrics only on numeric columns to eliminate inaccuracies in distance calculations. The results are shown in Table A3 and

Table 4. Average privacy evaluation metrics.

	DCR	NNDR
Model
CTGAN	0.894	0.703
TVAE	0.773	0.411
CTAB-GAN+	0.616	0.580
DP-CTGAN	5.028	0.779
ARF	0.625	0.724
AGBDT	0.074	0.059
AGBDT ($k=2$)	1.159	0.775
AGBDT ($k=5$)	1.172	0.782

. Best results will be marked in bold.

Across all three datasets, the proposed AGBDT method without k-anonymity yielded DCR and NNDR values of 0 on Census, Credit, and Intrusion, suggesting that some synthetic records are overly similar to real ones, thus risking privacy leakage. In contrast, incorporating k-anonymity (with $k=2$ or $k=5$) significantly improved both metrics, with DCR scores exceeding 1.0 and NNDR values approaching or exceeding 0.8 on most datasets. These results demonstrate that AGBDT with k-anonymity provides enhanced privacy compared to baseline generative models such as CTGAN, TVAE, and CTAB-GAN+, highlighting the effectiveness of anonymity-aware sampling in mitigating memorization and improving synthetic data privacy. It is worth mentioning that compared with the differential privacy version of CTGAN (DP-CTGAN), AGBDT has a lower DCR value, indicating that even in the most extreme case, the distance of the generated data is farther than the real data, proving the effectiveness of the differential privacy method for privacy protection. However, regarding the NNDR indicator, the AGBDT with k-anonymization is better than DP-CTGAN, which also proves the effectiveness of our method.

In addition, Figure 5 illustrates the density distributions of each record of Distance to Closest Record (DCR) and Nearest Neighbor Distance Ratio (NNDR), respectively, across different generative models and datasets. These metrics assess privacy risks in synthetic data by quantifying proximity and indistinguishability concerning real records. In the DCR plots (Figure 5a), a higher concentration of synthetic samples with large DCR values indicates improved privacy, as the generated records are farther from the closest real instances. It can be seen that most of the DCR of ARF falls around 1.0, while the DCR of the proposed model is more evenly distributed, and the peak values of the proposed models are all greater than 1.0, which proves that the synthesized data by the proposed model is far from the real data and has good privacy protection. While in the NNDR plots (Figure 5b), distributions with mass closer to 1.0 reflect better privacy preservation, as the synthetic samples have similar distances to multiple real neighbors, making linkage attacks more difficult. The NNDR of most models falls around 1.0, proving that both the proposed model and the baseline can synthesize data that is different from the real data. In the Adult and Covtype datasets, the proposed model with $k=5$ can surpass the SOTA model DP-CTGAN, proving the effectiveness of the proposed model.

4. Discussion

Based on our experimental results and observations, several critical points merit discussion to guide future research and practical applications clearly:

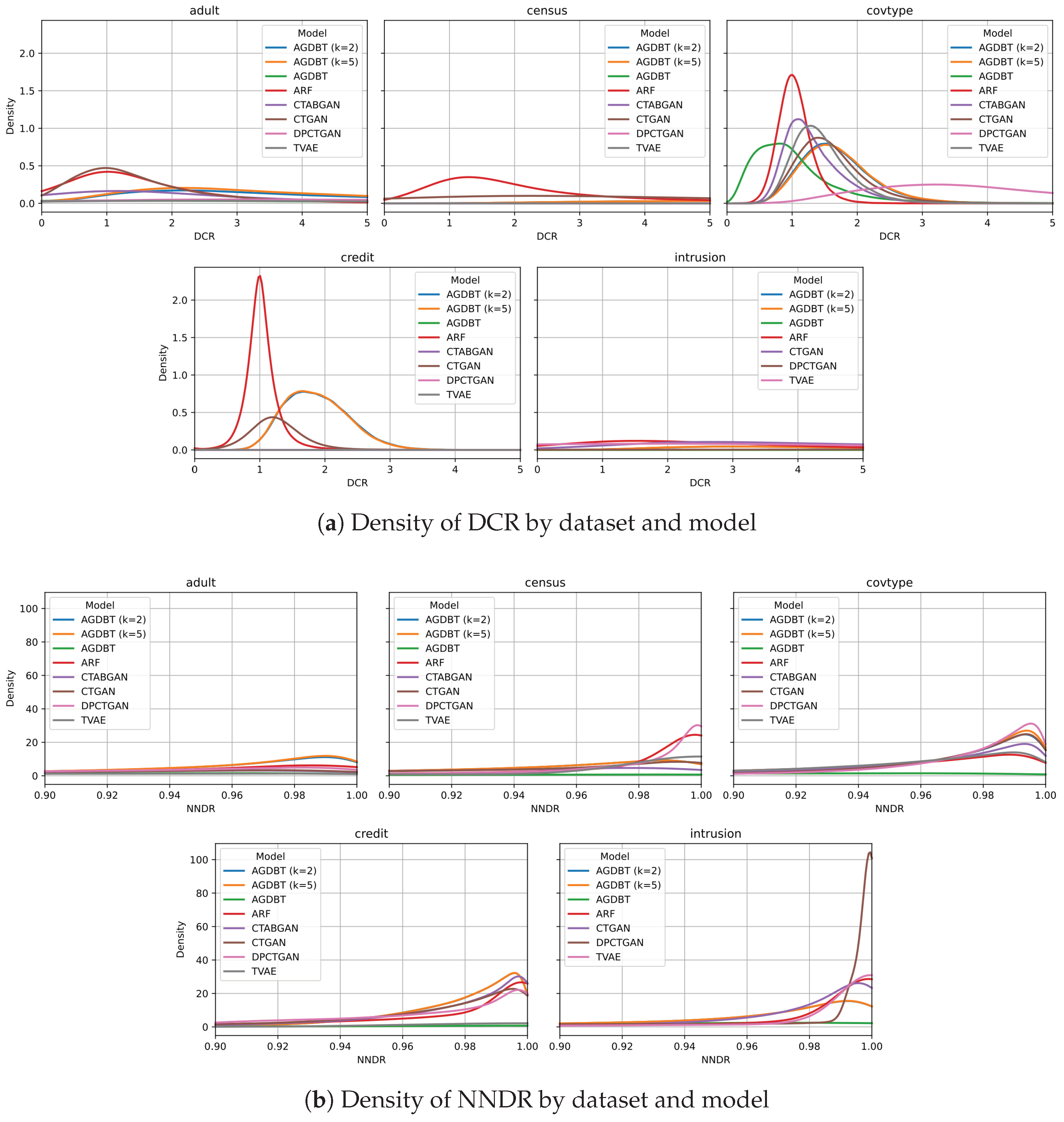
• Utility vs. Privacy Tradeoff: The proposed AGBDT model demonstrated superior or competitive performance across multiple datasets regarding statistical similarity and machine learning utility, confirming its strong capability for generating analytically valuable synthetic data. However, without explicit privacy constraints, the method showed relatively low novelty and potential privacy risks. Introducing k-anonymity effectively mitigated these risks while maintaining acceptable utility degradation.
• Handling Severe Class Imbalance: Our method showed limitations in replicating severely imbalanced datasets, notably the Credit dataset. In such cases, alternative generative models (e.g., CTAB-GAN+ or ARF), which better manage minority class distributions, may offer improved synthetic data quality. Enhancing our framework to better capture imbalanced class structures will be a priority in future work.
• Alternative Privacy Protection Approaches: Although Mondrian k-anonymity aligns naturally with gradient boosting tree logic, it can lead to information loss and reduced data diversity. Exploring alternatives such as k-concealment or differential privacy for more rigorous privacy guarantees, possibly through hybrid methods, will be valuable in future developments.
• Missing Data Handling: All datasets in this study were complete, but real-world data frequently contain missing values. Integrating advanced imputation techniques (e.g., median/mode imputation, predictive models, or surrogate splits in tree structures) into the AGBDT framework would significantly enhance its applicability and robustness to common practical scenarios.
• Sensitivity to Hyperparameters: The parameter analysis (see

  Table A4. Fitting time and distance indicators under different parameter designs. The best results for WD and JSD are in bold.

  Dataset	Max Depth	Estimators	Fitting Time/s	WD	JSD	Diff. Corr
  Census	2	30	0.698	0.003	0.014	0.042
  	2	50	1.198	0.001	0.014	0.030
  	2	70	1.586	0.002	0.009	0.040
  	3	30	0.963	0.001	0.017	0.057
  	3	50	1.578	0.001	0.014	0.086
  	3	70	2.281	0.003	0.001	0.054
  	4	30	1.266	0.003	0.002	0.047
  	4	50	2.051	0.025	0.010	2.090
  	4	70	2.880	0.021	0.002	1.676
  	5	30	1.505	0.016	0.003	0.830
  	5	50	2.402	0.002	0.005	1.681
  	5	70	3.333	0.001	0.004	0.588
  Credit	2	30	0.505	0.002	0.017	0.032
  	2	50	0.817	0.002	0.009	0.031
  	2	70	1.100	0.002	0.024	0.073
  	3	30	0.652	0.001	0.017	0.083
  	3	50	1.071	0.001	0.012	0.058
  	3	70	1.453	0.003	0.001	0.060
  	4	30	0.830	0.003	0.001	0.038
  	4	50	1.380	0.026	0.003	2.198
  	4	70	1.885	0.021	0.000	0.906
  	5	30	1.015	0.002	0.007	1.370
  	5	50	1.754	0.002	0.004	0.724
  	5	70	2.304	0.001	0.003	0.575
  Covtype	2	30	0.864	0.003	0.017	0.032
  	2	50	1.391	0.002	0.011	0.049
  	2	70	1.949	0.003	0.025	0.057
  	3	30	1.314	0.001	0.015	0.083
  	3	50	1.984	0.001	0.009	0.053
  	3	70	2.847	0.003	0.001	0.069
  	4	30	1.626	0.002	0.001	0.043
  	4	50	2.532	0.026	0.005	2.052
  	4	70	3.578	0.022	0.002	1.486
  	5	30	1.863	0.014	0.002	1.085
  	5	50	3.190	0.002	0.006	0.683
  	5	70	4.298	0.002	0.004	0.821

  ) demonstrated that moderate complexity (tree depth = 3, estimators = 50) provided optimal balance between data quality and computational efficiency in most datasets. With higher depths and estimators, data quality deteriorated significantly, indicating increased risks of overfitting and decreased generalizability. Future research should investigate automated hyperparameter tuning strategies, such as Bayesian optimization or validation-driven dynamic adjustment, to improve model adaptability across diverse datasets.

In summary, AGBDT effectively balances data utility and privacy under general scenarios. However, further improvements addressing its limitations—including handling severe class imbalance, integrating formal privacy guarantees, dealing with missing data, and optimizing parameter sensitivity—will significantly enhance its generalizability and practical applicability.

5. Conclusions

In this study, we proposed an Adversarial Gradient Boosting Decision Tree (AGBDT) framework for synthesizing privacy-aware tabular data by integrating adversarial training with gradient boosting trees. Empirical evaluations on five diverse datasets demonstrated that AGBDT achieved superior or highly competitive results in statistical similarity and machine learning utility compared to state-of-the-art baseline models.

Key findings indicated that our approach effectively balanced data fidelity and privacy risks, particularly in datasets with moderate diversity and class balance. Nevertheless, we observed performance degradation in datasets characterized by severe class imbalance, highlighting a limitation regarding the current model’s sensitivity to minority class distributions. Additionally, our application of k-anonymity provided intuitive privacy protection, but lacks formal probabilistic privacy guarantees available through differential privacy.

Practical implications of our study suggest that while AGBDT effectively synthesizes highly usable tabular data suitable for typical analytical tasks, careful consideration should be given when dealing with severely imbalanced datasets or stringent formal privacy constraints. Future research directions include exploring differential privacy integration for formal guarantees, improving methods for handling missing values common in real-world data, and conducting comprehensive sensitivity analyses to enhance the robustness and generalizability of the proposed framework.