Abstract
This research is concerned with design optimization of control systems. Our case study deals with magnetic levitation, in which an essential part is a solenoid. Its dimensions, along with controller parameters, form the optimization variables. We present a novel way of writing the explicit expression of the solenoid’s force acting on a magnetic dipole, as well as its first derivatives. Numerical tests using non-gradient search algorithms show the difference in optimal designs provided by these methods. Since such optimization depends on output signals, a comparison of step response analysis methods is presented.
MSC:
65Y15; 68W50; 90C26; 90C56; 90C59; 93B51; 93-04; 93C80
1. Introduction
Nonsmooth optimization algorithms do not rely on estimating the derivatives of the objective function. Although finding a global minimum for nonlinear nonconvex optimization problems is not guaranteed, these methods can be applied to a much larger pool of tasks than classic gradient search methods [1,2,3]. Gradient-based design methods may be ineffective in the case of highly nonlinear design spaces. Heuristic optimization techniques can lead to nonintuitive designs being found. Such routines have the ability to search the parameter space in areas that were previously considered irrelevant to the search.
Nonsmooth minimum search algorithms may be applied to optimization problems where the objective or constraint functions are continuous, discontinuous or stochastic. These functions may not have derivatives, may include simulations or may be black box functions. For problems with multiple objectives, one can identify a Pareto front. These methods often provide the ability to use custom data types to represent problems that cannot be easily expressed with standard data formats. Antenna designs with strict constraints on the size and bandwidth profile can be acquired using genetic algorithms, particle swarm optimization and specially crafted algorithms [4,5,6,7,8]. Very large-scale integration chip design has to place millions of transistors efficiently and is based on nonsmooth optimization methods [9,10]. Originally, it was simulated annealing that proved to be a robust algorithm. By treating the task as an energy minimization problem and accepting suboptimal moves, the algorithm enabled the miniaturization of integrated circuits. Nonsmooth optimization is frequently employed in structural engineering concerning problems with friction and optimal material layouts [11,12,13]. Objective functions are usually not smooth and include constraints on stresses or displacements.
Optimization of magnetic coils or solenoids is often concerned with improving homogeneity of the produced magnetic field. The authors of [14] optimized the radius, length and number of turns while addressing the relation between field homogeneity and practical constraints, like size or power consumption. A notable mention is the Loney’s solenoid, which is sometimes used as a benchmark for optimization algorithms [15,16,17]. A primary solenoid is supplemented by two smaller correcting coils placed along the central axis. The goal is to determine the optimal size and spacing of these correcting coils in order for the system to produce a highly uniform magnetic field.
The solenoid’s inductance and self-capacitance depend on its dimensions, including length, internal and external radii, and cross-sectional area. In [18], analytical formulas for inductance and capacitance of coaxial inductors with rectangular cross sections are presented. These formulas are valid for two types of windings and address possible practical imperfections. Explicit expressions of magnetic fields of coaxial electromagnetic coils and some shapes of permanent magnets can be found in various sources [19,20,21,22,23,24]. Field-free points in space are a requirement for magnetic particle imaging. The authors of [21] analyzed a few possibilities to achieve such conditions using solenoids and permanent magnets. A standard magnetic resonance setup produces a single homogeneous field volume where the analysis is performed. Chou et al. explored the idea of having multiple homogeneous field volumes along the axis and inside the main coil [22]. A multilayered solenoid coil is a key component of optical polarimetry based on Faraday modulation. Bashar et al. studied the dependence of different geometrical and electromagnetic parameters on the optimal design of such solenoids [23].
Magnetic levitation is a phenomenon that is often used in control system studies. The key component of this process is a solenoid. This phenomenon has a variety of applications, like active magnetic bearings [25] or high-speed train transportation [26]. Quite often, the goal is to move or keep the levitated object at a desired height. Magnetic levitation is often used to validate various modern control strategies. Peng et al. created a nonlinear control strategy based on real-time deep learning [27]. Using a concept called long short-term memory, their procedure deduces a locally linearized model without the need for a Taylor expansion. Magnetic levitation systems are subject to vibration due to changes in the operating point. The authors of [28] were able to produce a nonlinear control strategy to decrease the vibration period and vertical displacement by 40 and 27% for a magnetic levitation decoupling platform. Multi-objective optimization procedures have proven to be useful for controller tuning. The authors of [29] considered a class of uncertain control systems and used the Kharitonov theorem to obtain regions of stability as the search space for their multi-objective algorithm. There are studies indicating that magnetic levitation can be controlled with fractional-order control strategies. The authors of [30] applied a fractional-order linear quadratic regulator to a current-controlled attractive force magnetic levitation system using a constructed state observer.
Recent years have seen an increase in interest in new coil designs as a result of the wide usage of electrical motors and other solenoid applications. These designs may be heuristic, empirical or created with extensive numerical simulations. The authors of [31] designed a low-field unilateral magnet for a magnetic resonance scanner by creating unique split gradient coils. The coil patterns were obtained by solving an optimization problem. Anatomy-specific radio-frequency-receiving coil arrays are part of magnetic resonance imaging (MRI). However, they are commonly burdened by their bulky configurations, which may be inappropriate in certain situations. Wu et al. developed the concept of using coaxial cables to design wireless and lightweight passive detuning MRI coils that achieve a high signal-to-noise ratio [32]. Novel winding, in addition to special auxiliary solenoids, with a gradually changing diameter on each side of a regular solenoid was introduced in [33]. Optimization of different parameters of the auxiliary solenoids improved the magnetic field uniformity by more than five times, which is important for high-precision electromagnetic sensing applications.
This work deals with a multi-objective design optimization problem, where the objective function depends on step response characteristics. Our previous work [34,35] was concerned with fast means of step response analysis, for which we have created an algorithmic procedure. The numerical tests in [35] showed the advantage of this method in terms of computational time for integer-order systems. That work also introduced an extension of the mentioned algorithm to fractional-order systems since various physical processes are described by fractional calculus, including processes in porous media, capacitance theory, and fluid dynamics. Here we apply these results to the design of a magnetic levitation system and present a comparative study of several nonsmooth optimization algorithms. The structure of the paper is as follows: Section 2 formulates the optimization problem and describes the challenges of accurately modeling the interaction between a solenoid and a magnetic dipole. This is followed by an explicit solution of the differential equations governing this process. Section 3 presents a solution of the optimization problem using several nonsmooth search algorithms and showcases the advantage of the step response analysis technique developed in [34,35].
2. Materials and Methods
This section presents an optimization problem for the control system design. Our case study deals with magnetic levitation in which an essential part is a solenoid. It has four main dimensions that, along with controller parameters, form seven optimization variables. We present a novel form of writing the explicit expression of the solenoid’s force acting on a magnetic dipole, as well as its first derivatives. We show how the coil’s self-capacitance and inductance affect the performance of magnetic levitation. This allows us to perform proper linearization and get an explicit solution of the differential equations governing this process. Formulation of the optimization problem and a discussion of nonsmooth search methods conclude this section.
2.1. Magnetic Levitation
The control system used to formulate the optimization problem and to apply the algorithm developed in [35] is a magnetic levitation setup. The goal of this system is to move or maintain the levitated object at a desired height. We start by analyzing the force F acting upon a permanent magnet in a magnetic field of a solenoid.
A permanent magnet can be modeled as a collection of microscopic currents or magnetic dipoles. The net effect of these loops is a surface current which is called the Amperian current [36]. Let the current loop (magnetic dipole) have a magnetic moment of and be in a uniform magnetic field The torque acting on such a loop is expressed as [37]
The force acting on a magnetic dipole in this field is the gradient of the potential energy associated with this torque:
As the magnetic dipole moment only has a constant vertical component we can express the vertical component of the force as
Now we need an explicit expression of the coil’s magnetic field. A solenoid has 4 main dimensions: length or height L, external radius internal radius and diameter of the wire
Solenoids have a symmetry axis along the coaxial line. Let us introduce a function where . Since then . Then the magnetic flux density of a coil described in Figure 1 along the Z-axis is [20,23]
where H/m is the magnetic permeability of vacuum and is the permanent magnet’s vertical component of the magnetic moment. The force from the coil acting on a permanent magnet is expressed as the first partial derivative of (4):
where
and
are the auxiliary functions.
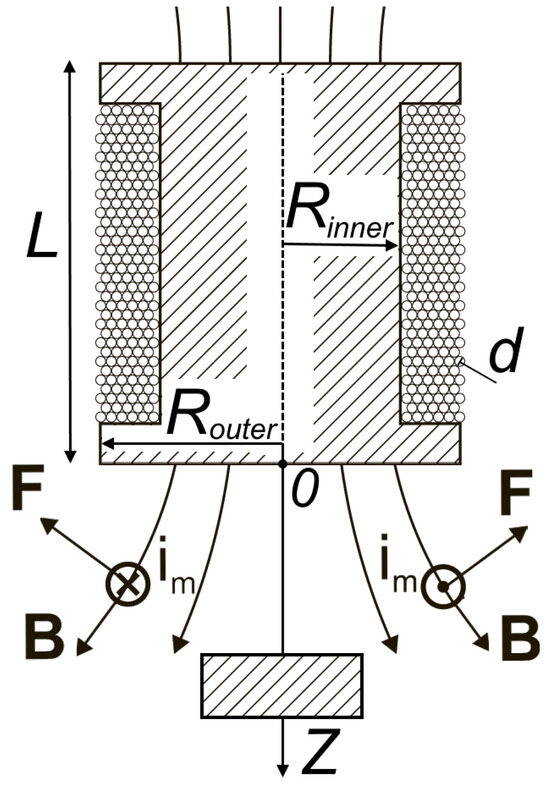
Figure 1.
Scheme of a magnetic levitation system with a solenoid and a permanent magnet as the levitated object. The four dimensions of the coil are among the optimization variables. The crossed circle symbol represents the direction of the resulting magnetic dipole surface current away from the observer, while the circled dot points towards the observer. The small circles are the wires of the winding, whereas the dashed lines represent solid matter.
As for the derivatives of the force, first we note that
where the derivative is left in the numerator intentionally. For example, when and when Then,
The derivatives of the auxiliary functions and are
where
and
where
Therefore, we have acquired explicit expressions of the magnetic force and its derivatives.
The expressions (5) to (14) represent a novel compact form of the explicit expression of the magnetic force acting from a multilayered coil on a permanent magnet. While a significant amount of research has been devoted to magnetic levitation, a lot of the time, much shorter expressions are used, like
where A, B, c and C are constant values [28,38,39]. The accuracy of modeling is affected by this, which we have showcased in [34] by curve-fitting experimental data. We hope that our effort here to highlight that such a magnetic force can be expressed easier using special substitutions like and in (12) and (14) will be noticed by other researchers.
2.2. Inductance and Self-Capacitance
During the optimization process, the dimensions of the coil change; thus, its properties like the number of turns, resistance, inductance and self-capacitance also change. We take this into account in our model. A typical double thickness of the isolation of a wire is mm, so is the full diameter. Let be the number of wire turns vertically or along the coil’s height. It depends on the thickness of the wire as The number of turns or layers of wire in the space between and is
where N is the total number of turns in a solenoid.
The diameter of the wire has a number of practical effects. The strength of a solenoid’s magnetic field is determined by its ampere-turns, which is a product of the current I and number of turns N. The diameter of the wire introduces a critical trade-off in this relationship [18]. On the one hand, a thicker wire means that fewer turns of wire can be accommodated, but a higher current is possible. On the other hand, a thinner wire allows for a greater number of turns, but restricts the amount of current that can be safely passed through it. Another concern is heat generation due to the electrical current flowing through the coil. A thicker wire has a lower electrical resistance, leading to less heat generation for a given current. Their larger surface area also provides for better heat dissipation. Therefore, solenoids wound with thinner wire are often limited to low-power applications.
The passive resistance of the coil depends on the length of the wire. By introducing the medium radius this length can be estimated as . With the cross-section of the wire without isolation being the total resistance is
where is the resistivity of copper in Ohms per meter.
For the coil’s inductance (in micro Henries), we are going to use the following [18] expression:
Every solenoid has self-capacitance. Here we implement a model for self-capacitance mentioned in [24] and introduced in [18]. Electrical permittivity of air is farads per mm, while for the polyvinyl chloride insulation, it is a dimensionless quantity The authors of [18] introduced a factor of where the so-called azimuth filling factor (a value in mm) equals zero if we have a tightly wound coil. Another factor is the axial filling factor , which is a value in mm and may be negative. As a result, the self-capacitance of a multi-layered solenoid coil is equal to
2.3. Control System Modeling
The designed system consists of two main parts—the electrical circuit and the electro-mechanical relationship between the coil and the levitated permanent magnet. We start with creating the model of the circuit, the input of which is the voltage on the coil , while the output is the current . Consider the electrical circuit in Figure 2.
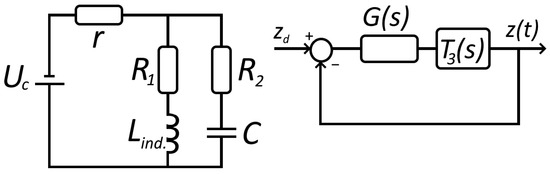
Figure 2.
Scheme of the electrical circuit with the coil and the block diagram of a modeled feedback control system.
An experimental realization of this design can be found in [34]. Let r be the total resistance of the electronic components that lead to the solenoid. Let and be the resistances associated with the coil itself. Here we would like to consider the self-capacitance of the wound wires as well. Let us create a transfer function in the general case shown in Figure 2. Later for the optimization process, we are going to assume and One can show that the transfer function of such circuit is
If we neglect the viscous resistive forces of air, the movement along the Z-axis is described by Newton’s second law:
where m is the mass of the magnet, g is the gravitational acceleration constant and the force is given by expression (5). Let be the relative change in coordinate z from an operating point :
Then, a zero initial value satisfies the differentiation rule of originals for the Laplace transform [40].
Let be the relative change in current from operating point If operating point is selected as the equilibrium state , then the initial current is expressed through (5) as
with the initial voltage being
We expand in a Taylor series at the point , where and . Then, Equation (21) becomes
where the values of partial derivatives of the force are given by expressions (9) and (10). The Laplace transform of (24) is
Note, that with this system and the direction of the Z-axis, The transfer function of equation (24) is, therefore,
Combined with expression (20), the resulting transfer function of the uncontrolled magnetic levitation system is
Let represent the system’s controller. If we use a proportional–integral–derivative (PID) controller in a parallel form, its Laplace image is equal to
For a unity feedback loop, the transfer function of the closed-loop system is
where is the Laplace image of the desired position of the permanent magnet and the Laplace image of its actual position. Therefore the input signal of the controlled system is the voltage on the coil and the output signal is the position of the magnet . In order to obtain a step response of this system, one should multiply by and then perform the inverse Laplace transformation.
Transfer functions of linear time invariant dynamic systems have a form of
Let be the roots of the denominator If there are no equal roots then the inverse Laplace transform of (30) is given by a partial fraction expansion [40]:
where
If there are identical roots in the denominator, then the partial fraction expansion is different [41]. Let
where are the root multiplicities. Let be a polynomial whose degree k is less than Then the inverse Laplace transform of (30) is given by the expression
where
The ability to acquire explicit expressions of the inverse Laplace transform was utilized in [34,35] for additional computational speed.
2.4. Design Optimization: Problem Statement
Consider an engineering system under design [35] (see Figure 3). We denote the input internal parameters of the system as ; the input controller parameters vector as ; and the vector of output characteristics as where and are feasible sets. The optimization problem is to minimize an objective function that depends on the signal output characteristics Since depends on and , one may formulate the optimization problem as
where is a chosen optimization algorithm formulated as a set of rules. In control theory the input to includes a vector of output signal characteristics , while the rules of may consider the values of and as well during iterations. The output of can be expressed as a unified vector
which is called the optimization variables vector. The choice of depends on various factors and is a subject of research [42,43,44].
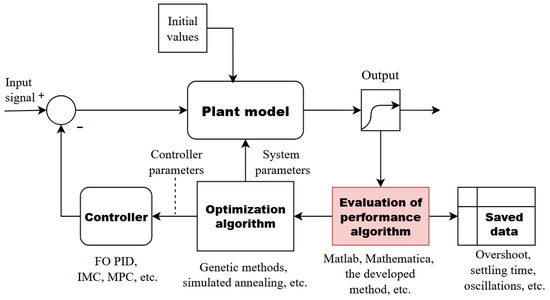
Figure 3.
The scheme of optimization problem (36). The red part represents the focus of our research in [35]. Obtaining the output characteristics is an important part of the optimization process.
In [35] we focused on obtaining the vector for the case when design optimization is combined with step response analysis. Figure 3 shows that improving the calculations in this part speeds up the solution of the entire optimization problem. In [35] it was shown that it is possible to increase the computational speed of obtaining step response characteristics over standard methods. For that we have created an algorithmic procedure that was compared with existing methods using numerical tests. It is notable that the algorithm developed in [35] is also applicable to fractional-order [45] dynamic systems.
2.5. Formulation of the Optimization Problem for a Magnetic Levitation System
Let us define all the necessary components of optimization problem (36). The design process of the magnetic levitation system is concerned with seven optimization variables. The input internal parameters vector consists of the solenoid’s four dimensions:
while the feasible set X is
We shall refer to and as the lower and upper bound vectors. The input controller parameters vector is
while the feasible set is
Here we also introduce the lower and upper bound vectors and
The vector of output characteristics of optimization problem definition (36) can be written as
If there are no right-half plane roots (if no real parts of the roots are greater than zero) in the denominator in (29), the system is stable and the feasible set H can be written as
Let , and be constant real values. For numerical tests we have chosen
as the objective function takes into account the four output characteristics that we acquire with step response analysis. Evaluating a magnetic levitation system’s performance is a multi-objective problem. Modeling of this phenomenon is based on linearization and it is performed near an operating point, which is usually the desired position of the levitated object. Therefore, the most important step response characteristic is overshoot. A large overshoot or a large distance from the levitated object to the operating point creates inaccuracies.
In dynamic system modeling, determination of step response characteristics (vector ) is usually performed with major mathematical software like Matlab (current version is 2025a), Mathematica (current version is 14.2.1) or Maple (current version is 2025.1). One of the most notable is Matlab’s Control System Toolbox, which provides built-in functions for design and tuning of control systems [46]. It has means for working with both the frequency and time domains.
Although step response analysis is one of the foundations of control theory, its applications in practical systems depend heavily on the nature of the process. For example, classic control theory relies heavily on the second-order approximation. This provides explicit formulas for step response characteristics, such as the overshoot or settling time. Step response analysis is based on the assumption that the system is linear and time-invariant, so its behavior does not change with the operating point. Meanwhile, almost all real systems are nonlinear to some extent. Among the examples are valves, actuators and chemical reactions. For example, an industrial robot moves by sending step responses to its individual joints, which requires both speed and precision [47]. Each joint has a sensor called a rotary encoder that reports its angular position. Since payloads may be different, modern robotic systems use adaptive control to continuously update their parameters, ensuring an optimal step response regardless of the task. This is performed inside the robot controller, which is essentially a computer that sends commands and reads high-frequency feedback from the joint’s encoder. The timestamps and joint positions are processed using software to perform a step response analysis like Matlab/Simulink (current version is 2025a), Python (current version is 3.13.3) scripts using robotics libraries or the software provided by the robot manufacturer. Therefore, algorithmic procedures within these programs influence the effectiveness of the entire operation.
If optimization problem (36) depends on step response characteristics, the process of acquiring them is critical, as can be seen in Figure 3. The standard approach is to process the entire output signal with equal time steps. In [35] we developed a novel step response analysis algorithm with a variable time step. Numerical tests showed that this approach provides additional computational speed for integer- and fractional-order dynamical systems.
2.6. Nonsmooth Optimization Search Algorithms
Here we describe the five nonsmooth search algorithms that we are going to compare. First, let us define what a nonsmooth optimization algorithm is. A function is smooth if it is differentiable and the derivatives are continuous. Classical or smooth optimization algorithms, like the gradient descent or Newton’s method, rely on the existence and continuity of the objective function’s gradient. It is used as the main criterion to determine a search direction that guarantees a decrease in the function’s value. For a nonsmooth optimization problem, the gradient may not exist while various nonlinear constraints may be present. Nonsmooth optimization algorithms are search techniques developed to compensate for the absence of differentiability [48]. They may use a generalized notion of a derivative or do not use any derivative information. These algorithms usually have different convergence properties that do not necessarily require the objective function’s value to decrease at every step.
Pattern search is a deterministic non-gradient method of searching the optimization variable space in criss-cross patterns [49,50]. The sides of the cross or the steps are called pattern vectors. The algorithm starts with selecting a random (or user-defined) point in the search space called a poll point. Function evaluations along the pattern vector from this poll point are conducted along all four sides. In the next iteration, starting from the smallest poll point, the cross expands out twice as much as in the previous step, and three new points are added. If the search runs out of permissible boundaries, the cross compresses. This process continues until the minimum is found or the maximum number of attempts is exceeded.
Genetic algorithms are heuristic minimum search methods inspired by natural selection and evolution [51]. They are population-based, non-gradient search algorithms with stochastic iterates. The starting population is random or chosen by the user. This method can run in parallel and allows for an easy implementation of integer constraints. Genetic algorithms can converge to a global optimum under certain conditions [52].
Particle swarm optimization (PSO) is a population-based stochastic algorithm inspired by the movement of large groups of animals. A particle is an element of the search vector space; in our case, part of . After each iteration a swarm of particles is updated. Simple rules tell each particle to move in a direction that depends on the previous best positions among all of the particles in the swarm [53]. Much like with genetic algorithms, asymptotic convergence is proven under certain assumptions [54].
Surrogate optimization is a stochastic strategy used to solve computationally expensive optimization problems [55]. It evaluates the objective function at a small number of points and fits a surrogate model using these samples. To save time, it evaluates this approximation model of the real objective function. Surrogate optimization requires bound constraints while also accepting linear or nonlinear inequality constraints. This method has proven convergence to the global optimum for bounded problems. Bayesian optimization is one of the most popular frameworks for surrogate optimization, particularly with Gaussian process models [56].
Simulated annealing is a stochastic search technique based on the analogy of the metal annealing process, which involves the formation of a minimum-energy crystal structure upon cooling [57,58]. Despite the various applications, the speed of convergence has still been fairly little studied. One of the main advantages of simulated annealing is its ability to escape local minima. At the time of its appearance, gradient methods were dominant, so the idea of a search method that accepts changes in optimization variables that decrease the objective function’s value was unique. This is based on the so-called temperature—a numerical characteristic of the modeled process. The higher this temperature is, larger increases in the objective function’s value are allowed with higher probability. Simulated annealing stands out since convergence proofs have been successfully established under certain conditions. It is a population-free heuristic technique that has a proven global convergence in a general optimization setting [59].
3. Results and Discussion
The first aim of the numerical tests is to try and compare the discussed nonsmooth optimization algorithms on the problem of solenoid design and controller tuning. The performance criteria of the magnetic levitation system are step response characteristics. The second aim of the numerical tests is to compare two methods of step response analysis—the algorithm developed in [35] and the built-in Matlab functions. We begin by setting up lower and upper bound vectors:
where the values of are in centimeters. As for the controller parameter bounds,
Some of the implemented algorithms support linear constraints. We need them in order to provide for the condition, where is the required difference in the radius. For the optimization variables vector , the linear constraints are usually set in a format where A is a matrix and is a vector of fitting dimensions. In our case cm and
As for the mentioned constants in objective function (44), we have chosen the following values: , and This selection was based on observing the various step responses.
The permanent magnet was chosen to have the form of a cylinder with a 4 mm radius and 5 mm height with a weight of g. For a neodymium magnet of such dimensions, the vertical component of the magnetic moment in Formulas (5) and (10) can be estimated to have a value of . This was also confirmed by curve fitting experimental data in [34].
The initial conditions vector needed for some of the search algorithms was chosen to be
PSO and the genetic algorithm scan the search space not at a single point, but rather in a population of size Instead of vector , these two techniques require a starting population matrix of size consisting of random values within the chosen bounds.
The search algorithms were tested using Matlab’s Global Optimization Toolbox [60]. Optimization ends if the relative change in the objective function is less than a defined function tolerance or if the maximum number of function evaluations is exceeded. For the pattern search, surrogate optimization and simulated annealing, this number can be defined by the user. While scanning the search space in a population of size , PSO and the genetic algorithm also have a number of generations For these two methods
Each of the five nonsmooth search algorithms requires certain information as the input. Table 1 shows what each algorithm accepts at the start of the optimization.

Table 1.
Prerequisites for the chosen nonsmooth search algorithms.
Table 2 shows the results of the optimization for for the genetic algorithm and PSO, which corresponds to for the remaining three search methods. The results of the search in Table 2 are illustrated in Figure 4. Based on the values of the objective function in Table 2, the best results were achieved by PSO, the genetic algorithm and surrogate optimization. Let us see what choices of the optimization variables vector values led to this outcome.

Table 2.
A comparison of performance of several nonsmooth search algorithms for and for the PSO and the genetic algorithm and for the other three search methods. Rows 2 to 8 represent the optimization variables vector .
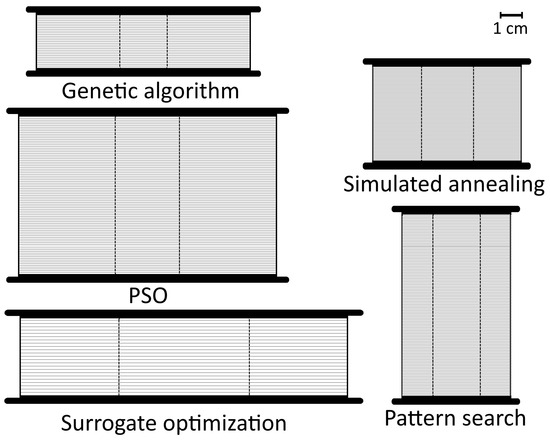
Figure 4.
A visual representation of the optimal coil designs from Table 2. Each of the nonsmooth search algorithms went for a different solenoid geometry.
The first and most noticeable dimension of the solenoid is its height. Figure 4 shows that the pattern search and PSO went for a taller coil, while the genetic algorithm and surrogate optimization chose a more flat geometry. Therefore, for L and , there are values close to both the upper and lower boundaries. However, the majority of the algorithms stayed closer to the lower boundary for In applications of air-filled coils, the inner radius exists mostly for mounting reasons and structural rigidity. This shows that for the magnetic levitation process, a narrower inner coil radius is preferable. As for the diameter of the wire, all of the nonsmooth search methods, except surrogate optimization, have chosen to be around the mm value. The coil’s resistance and self-capacitance depend on this parameter, as shown in (17) and (19).
The choice of solenoid dimensions, along with the PID controller parameters, has led to the optimal step responses being found (see Figure 5). The percentage overshoot is one of the most important output values for a magnetic levitation system. A large overshoot is undesirable since the permanent magnet travels too far away from the operational point, which may lead to instability. The simulated annealing and pattern search yielded step responses with the largest overshoot values. At the same time, the pattern search showed the largest settling time.
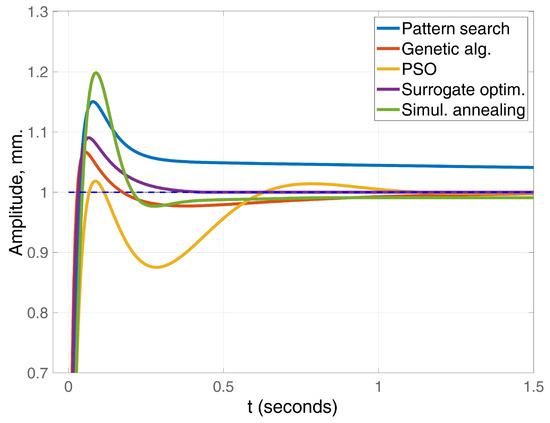
Figure 5.
A comparison of step responses with lowest values of the objective function. The blue dashed line represents the steady-state value.
Step responses with the lowest values of overshoot were acquired by the PSO, the genetic algorithm and surrogate optimization. While the values acquired by the genetic algorithm and surrogate optimization are very similar, the value acquired by PSO has the lowest overshoot. However, this is achieved by a dive under the settling value or an undershoot. Due to the same reason of potential instability of the whole system, this is undesirable. We have defined as the difference between the actual and desired distances of the levitated object to the operating point. In the case of a feedback controller, the input signal will depend on this value. Linear constraints cannot be easily met when using the Laplace transform. In an actual maglev system, there are physical limitations, like the maximum voltage on the coil , which we have discussed in our previous work [34]. A large downstroke in the numerical solution or the actual process may result in exceeding these limitations. In the real world a controller is usually protected with electronics to prevent this from happening. Therefore, with the described boundaries (45) and (46), the linear inequality constraint (47) and maximum number of function evaluations, the genetic algorithm acquired the best step response out of the nonsmooth search methods implemented.
During the optimization process, the acquisition of the output vector was achieved using two distinct methods. The first was Matlab’s Control System Toolbox built-in stepinfo function. The second was the step response analysis algorithm that we developed in [35]. In short, it is a special type of rapid analysis of simulated transient responses. Numerical tests yielded improvements of this method in terms of the computational time.
First, we defined the values needed for comparison. Let N be the total number of function evaluations performed by one of the five search algorithms and . In each iteration, a search algorithm produces a transfer function of the designed magnetic levitation system (29). By we denote the time it takes to analyze the i-th transfer function and its step response using one of the two approaches. Let be the time of the method based on [34,35] and be the time it took to do the same analysis but with Matlab’s built-in method as described before. The total time for each method would be and Let 100% represent the percentage time difference. The value of is positive if Let and be the mean and maximum values of over Let be the full time of the optimization performed by one of the five search algorithms.
Table 3 shows that the step response analysis occupied a considerable part of the computations needed for the optimization process. All of the five nonsmooth search methods yielded the advantage in computational time from using the approach from [35]. While the value of peaked at for the genetic algorithm, the values of all exceeded , peaking at 69.5% for PSO and the genetic algorithm. These results represent the advantage of processing the output signals of dynamical systems that can be represented in the form of (30). This is a new result compared with the numerical tests in [35] since we only compared transfer functions in the form of a constant divided by a polynomial. For design processes where the evaluation of output signals takes up more time, this approach becomes more valuable. Therefore, the algorithm developed in [35] is useful for solving optimization problems that rely on step response characteristics.

Table 3.
Comparison of computational times of the chosen nonsmooth search algorithms.
4. Conclusions
In this work, we have formulated and solved an optimization design problem for a magnetic levitation system. The optimization variables were the solenoid’s dimensions, as well as the feedback controller parameters. Notable results include the following:
- Obtaining a novel way of writing the analytical formulas for the interaction force of a multilayered solenoid with a magnetic dipole, as well as its first derivatives. The influence of the coil’s dimensions on its inductance, resistance, and self-capacitance was addressed. This allowed us to create an accurate model of a magnetic levitation system capable of high-precision calculations.
- A numerical solution to the problem was proposed using five nonsmooth search algorithms. Based on the values of the objective function, the best results were achieved by PSO, the genetic algorithm and surrogate optimization. The test results show that a smaller inner radius is beneficial for the step response performance of a magnetic levitation system.
- The step response output characteristics were chosen as the basis for optimization. Numerical tests showed that step response analysis takes up a considerable amount of computation time during the optimization process. Unlike our previous work, here we were able to compare the computational times for transfer functions of the form (30). All of the five nonsmooth search methods yielded the advantage in computational time from using the approach developed in [35]. With this method of step response analysis, we were able to achieve an up to 69% reduction in the signal processing time. Therefore, the optimization process described in this work is useful for solving problems that rely on step response characteristics.
Author Contributions
Conceptualization, I.R., P.P. and A.P.; methodology, I.R., P.P. and A.P.; software, I.R.; validation, I.R., P.P. and A.P.; formal analysis, I.R.; investigation, I.R.; resources, I.R., P.P. and A.P.; data curation, I.R., P.P. and A.P.; writing—original draft preparation, I.R.; writing—review and editing, I.R., P.P. and A.P.; visualization, I.R., P.P. and A.P.; supervision, P.P. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was co-funded by ARIS—Slovenian Research and Innovation Agency, grants P2-0270 and P1-0222.
Data Availability Statement
The data used in this research are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; The MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Arora, J. Introduction to Optimum Design, 3rd ed.; Academic Press: Waltham, MA, USA, 2012. [Google Scholar]
- Belegundu, A.D.; Chandrupatla, T.R. Optimization Concepts and Applications in Engineering, 2nd ed.; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- Boeringer, D.W.; Werner, D.H. Particle swarm optimization versus genetic algorithms for phased array synthesis. IEEE Trans. Antennas Propag. 2004, 52, 771–779. [Google Scholar] [CrossRef]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Geng, J.; Jin, R. Design UWB antenna by binary coding optimization method. In Antenna Optimization and Design Based on Binary Coding; Modern Antenna; Springer: Singapore, 2022; Chapter 7. [Google Scholar] [CrossRef]
- Rolla, J.; Reynolds, B.; Weiler, J.; Connolly, A.; Debolt, R.; Machtay, A.; Sipe, B.; Wells, D. Design of 3D antenna geometries using genetic algorithms. Interplanet. Netw. Prog. Rep. 2023, 42–234, 1–26. [Google Scholar]
- Zang, T.; Xiao, G. Synthesis of shaped-beam radiation patterns with efficient optimization algorithm. IEEE Open J. Antennas Propag. 2025, 6, 694–704. [Google Scholar] [CrossRef]
- Jiménez, A.; Muñoz, A. Very-large-scale integration (VLSI) implementation and performance comparison of multiplier topologies for fixed- and floating-point numbers. Appl. Sci. 2025, 15, 4621. [Google Scholar] [CrossRef]
- Ślot, K.; Łuczak, P.; Kapusta, P.; Hausman, S.; Rantala, A.; Flak, J. Very-large-scale integration-friendly method for vital activity detection with frequency-modulated continuous wave radars. Sensors 2025, 25, 2151. [Google Scholar] [CrossRef]
- Zozulya, V. Nonsmooth optimization algorithms in some problems of fracture dynamics. Intell. Inf. Manag. 2010, 2, 637–646. [Google Scholar] [CrossRef]
- Su, R.; Tangaramvong, S.; Van, T.H.; Chaiwongnoi, A.; Song, C. Binary comprehensive learning particle swarm optimization approach for optimal design of nonlinear steel structures with standard sizes. Buildings 2023, 13, 1988. [Google Scholar] [CrossRef]
- Pillay, T.L.; Saha, A.K. A review of metaheuristic optimization techniques for effective energy conservation in buildings. Energies 2024, 17, 1547. [Google Scholar] [CrossRef]
- Aiello, G.; Alfonzetti, S.; Dilettoso, E.; Salerno, N. Improving the accuracy of the integral equation in the hybrid FEM-DBCI method for open boundary electrostatic problems. IEEE Trans. Magn. 2006, 42, 579–582. [Google Scholar] [CrossRef]
- Borghi, C.A.; Fabbri, M.; Di Barba, P.; Savini, A. Loney’s solenoid multi-objective optimization problem. IEEE Trans. Magn. 1999, 35, 1706–1709. [Google Scholar] [CrossRef]
- Borghi, C.A.; Fabbri, M.; Di Barba, P.; Savini, A. A comparative study of Loney’s solenoid by different techniques of global optimization. Int. J. Appl. Electromagn. Mech. 1999, 10, 417–423. [Google Scholar] [CrossRef]
- Coelho, L.D.S.; Alotto, P. Tribes optimization algorithm applied to the Loney’s solenoid. IEEE Trans. Magn. 2009, 45, 1526–1529. [Google Scholar] [CrossRef]
- Martinez, J.; Babic, S.; Akyel, C. On evaluation of inductance, DC resistance, and capacitance of coaxial inductors at low frequencies. IEEE Trans. Magn. 2014, 50, 1–12. [Google Scholar] [CrossRef]
- Grover, F.W. Inductance Calculations: Working Formulas and Tables; D. Van Nostrand: Princeton, NJ, USA, 2004; Available online: https://books.google.si/books?id=K3KHi9lIltsC (accessed on 11 June 2025).
- Duffy, R.M.; Netterfield, R.P. Design of Faraday rotators and modulators. Rev. Sci. Instrum. 1984, 55, 743. [Google Scholar] [CrossRef]
- Irfan, M.; Dogan, O.M.; Dogan, N.; Bingolbali, A. Selection field generation using permanent magnets and electromagnets for a magnetic particle imaging scanner. Alex. Eng. J. 2022, 61, 7685–7696. [Google Scholar] [CrossRef]
- Chou, C.-Y.; Ferrage, F.; Aubert, G.; Sakellariou, D. Simple method for the generation of multiple homogeneous field volumes inside the bore of superconducting magnets. Sci. Rep. 2015, 5, 12200. [Google Scholar] [CrossRef] [PubMed]
- Basharat, M.; Ding, M.; Cai, H.; Li, Y.; Fang, J. Design and analysis of multilayer solenoid coil for Faraday modulator. MATEC Web Conf. 2017, 114, 04004. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, X.; Liu, X.; He, C. An Analytical Model for Predicting the Self-Capacitance of Multi-Layer Circular-Section Induction Coils. IEEE Trans. Magn. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Kamath, K.P.; Vijay, G.S.; Bekinal, S.I.; Doddamani, M. Power amplifiers and their feedback mechanisms for AMB—A comprehensive review. IEEE Access 2023, 11, 132893–132915. [Google Scholar] [CrossRef]
- Sotelo, G.G.; De Oliveira, R.A.H.; Costa, F.S.; Dias, D.H.N.; De Andrade, R.; Stephan, R.M. A full scale superconducting magnetic levitation (MagLev) vehicle operational line. IEEE Trans. Appl. Supercond. 2014, 25, 1–5. [Google Scholar] [CrossRef]
- Peng, T.; Peng, H.; Li, R. Deep learning based model predictive controller on a magnetic levitation ball system. ISA Trans. 2024, 149, 348–364. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Li, C.; Zhou, J.; Wei, W.; Wu, Z. Vibration suppression control and anti-eccentric load correction mechanism of magnetic levitation decoupling platform. Mech. Syst. Signal Process. 2025, 225, 112314. [Google Scholar] [CrossRef]
- Kagami, R.M.; Freire, R.Z.; Reynoso-Meza, G. Multiobjective robust PI synthesis in plants with uncertain poles. IFAC-PapersOnLine 2024, 58–7, 174–179. [Google Scholar] [CrossRef]
- Yoneda, R.; Moriguchi, Y.; Kuroda, M.; Kawaguchi, N. Servo control of a current-controlled attractive-force-type magnetic levitation system using fractional-order LQR control. Fractal Fract. 2024, 8, 458. [Google Scholar] [CrossRef]
- Grandinetti, J.; Zhong, Y.; Peng, Y.; Jia, X. Design and construction of gradient coils for an MRI-guided small animal radiation platform. Heliyon 2024, 10, e26251. [Google Scholar] [CrossRef]
- Wu, K.; Zhu, X.; Anderson, S.W.; Zhang, X. Wireless, customizable coaxially shielded coils for magnetic resonance imaging. Sci. Adv. 2024, 10, eadn5195. [Google Scholar] [CrossRef]
- Zhu, X.; Xing, M.; Ye, J.; Liu, X.; Ren, Z. Design and optimization of a novel solenoid with high magnetic uniformity. Sci. Rep. 2024, 14, 24650. [Google Scholar] [CrossRef]
- Reznichenko, I.; Podržaj, P. Design methodology for a magnetic levitation system based on a new multi-objective optimization algorithm. Sensors 2023, 23, 979. [Google Scholar] [CrossRef]
- Reznichenko, I.; Podržaj, P.; Peperko, A. Variable time step algorithm for transient response analysis for control and optimization. Fractal Fract. 2024, 8, 710. [Google Scholar] [CrossRef]
- Tipler, P.A.; Mosca, G. Physics for Scientists and Engineers, 6th ed.; W.H. Freeman and Company: New York, NY, USA, 2008. [Google Scholar]
- Serway, R.A.; Jewett, J.W. Physics for Scientists and Engineers with Modern Physics, 9th ed.; Brooks/Cole: Boston, MA, USA, 2014. [Google Scholar]
- Maheedhar, M.; Deepa, T. Design and performance analysis of a nonlinear magnetic levitation system using PID controller optimized with COOT algorithm. IEEE Access 2023, 11, 104606–104621. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, Z.; Yin, S.; Long, Z. Real-time performance optimization of electromagnetic levitation systems and the experimental validation. IEEE Trans. Ind. Electron. 2023, 70, 3035–3044. [Google Scholar] [CrossRef]
- Doetsch, G. Introduction to the Theory and Application of the Laplace Transformation; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Bateman, H.; Erdelyi, A. Tables of Integral Transforms; McGraw-Hill Book Company: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization, 7th ed.; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Wilde, D.J. Principles of Optimal Design; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Arora, R.K. Optimization: Algorithms and Applications; Taylor and Francis/CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- MathWorks. Control System Toolbox User’s Guide; MathWorks: Natick, MA, USA, 2018; Available online: https://www.mathworks.com/help/control/ (accessed on 6 June 2025).
- Siciliano, B.; Khatib, O. (Eds.) Springer Handbook of Robotics; Springer: Berlin, Germany, 2008; Available online: https://books.google.si/books?id=Xpgi5gSuBxsC (accessed on 17 May 2025).
- Rockafeller, T. Nonsmooth optimization. In Mathematical Programming: State of the Art; Birge, J.R., Murty, K.G., Eds.; University of Michigan Press: Ann Arbor, MI, USA, 1994; pp. 248–258. Available online: https://sites.math.washington.edu/~rtr/papers/rtr153-NonsmoothOptimization.pdf (accessed on 12 June 2025).
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by direct search: New perspectives on some classical and modern methods. SIAM Rev. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Gardeux, V.; Omran, M.G.H.; Chelouah, R.; Siarry, P.; Glover, F. Adaptive pattern search for large-scale optimization. Appl. Intell. 2017, 47, 319–330. [Google Scholar] [CrossRef]
- Meza, J.C.; Judson, R.S.; Faulkner, T.R.; Treasurywala, A.M. A comparison of a direct search method and a genetic algorithm for conformational searching. J. Comput. Chem. 1996, 17, 1142–1151. [Google Scholar] [CrossRef]
- Rudolph, G. Convergence analysis of canonical genetic algorithms. IEEE Trans. Neural Netw. 1994, 5, 96–101. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle swarm optimization: A survey of historical and recent developments with hybridization perspectives. Mach. Learn. Knowl. Extr. 2018, 1, 157–191. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sobester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Hajek, B. Cooling schedules for optimal annealing. Math. Oper. Res. 1988, 13, 311–329. Available online: https://www.jstor.org/stable/3689827 (accessed on 20 April 2025). [CrossRef]
- MathWorks. Global Optimization Toolbox User’s Guide; MathWorks: Natick, MA, USA, 2024; Available online: https://www.mathworks.com/help/gads/index.html (accessed on 2 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).