A Novel Bio-Inspired Optimization Algorithm Based on Mantis Shrimp Survival Tactics

Abstract

This paper presents a novel meta-heuristic algorithm inspired by the visual capabilities of the mantis shrimp (Gonodactylus smithii), which can detect linearly and circularly polarized light signals to determine information regarding the polarized light source emitter. Inspired by these unique visual characteristics, the Mantis Shrimp Optimization Algorithm (MShOA) mathematically covers three visual strategies based on the detected signals: random navigation foraging, strike dynamics in prey engagement, and decision-making for defense or retreat from the burrow. These strategies balance exploitation and exploration procedures for local and global search over the solution space. MShOA’s performance was tested with 20 testbench functions and compared against 14 other optimization algorithms. Additionally, it was tested on 10 real-world optimization problems taken from the IEEE CEC2020 competition. Moreover, MShOA was applied to solve three studied cases related to the optimal power flow problem in an IEEE 30-bus system. Wilcoxon and Friedman’s statistical tests were performed to demonstrate that MShOA offered competitive, efficient solutions in benchmark tests and real-world applications.

1. Introduction

Metaheuristics are methods that can be implemented to solve optimization problems to obtain an optimal solution (near-to-optimal), including non-linear problems with non-linear constraints [1]; real-world engineering applications [2,3,4,5], such as optimization problems in power electronics [6]; or even those that traditional methods cannot solve [7]. However, as described in [8,9], there is no method capable of solving every optimization problem, as some of these approaches might perform better than others. Metaheuristics involve exploring the local and global solution search space efficiently [10]. The local exploration strategy refers to a search focused on a promising area of space or domain, whereas global exploration focuses on searching for new areas within the problem domain. A good balance between global and local searches can improve the metaheuristic performance.

Metaheuristics can be categorized as evolutionary-based, trajectory-based, and nature-inspired; see Figure 1. A short description of these metaheuristic types can be summarized as follows. The process of biological evolution inspires evolutionary algorithms [11,12,13,14,15]. Nature-inspired algorithms include swarm algorithms, which are metaheuristics based on the collective behavior of biological systems [16,17,18,19,20,21,22,23,24,25,26,27,28]. They also include physics-inspired algorithms that use physical principles for optimization [29,30,31,32,33,34], and algorithms inspired by human behavior [35,36,37,38]. Moreover, trajectory-based metaheuristics follow a trajectory through the solution space, aiming to improve the solution found at each step. Unlike population-based algorithms, which work with multiple solutions simultaneously, trajectory-based metaheuristics focus on a single solution that evolves and improves iteratively. A more extensive metaheuristic classification can be found in [39,40].

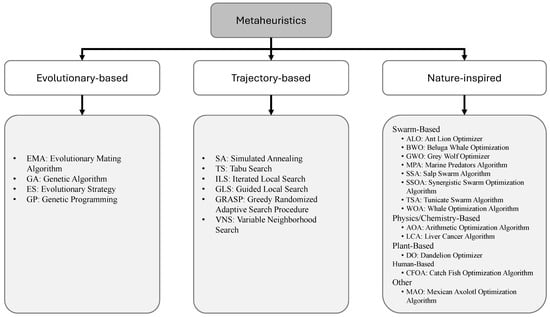
Figure 1. Metaheuristic classification.

A schematic representation of a metaheuristic algorithm is shown in Figure 2. In the first stage, a set of vectors, also named as search agents, is randomly generated. The size of the vector represents the number of variables of the problem, where its value represents a possible solution.

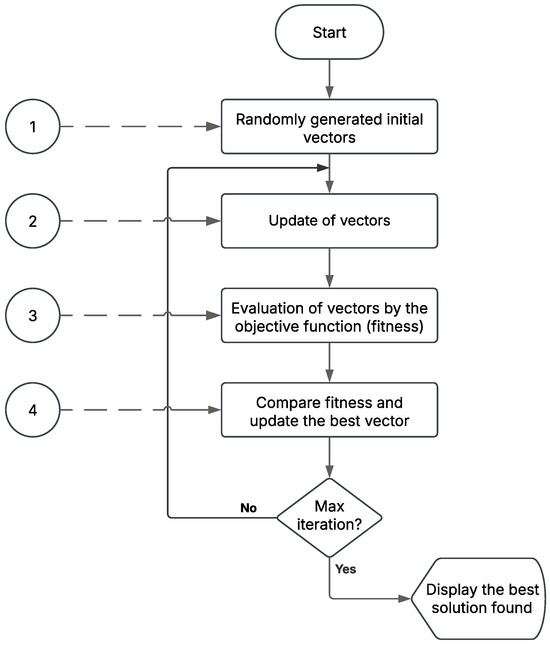
Figure 2. Schematic representation of a metaheuristic algorithm.

In the second stage, vectors are updated by functions representing living organisms’ behavior or physical and chemical phenomena as bio-inspired models. These vector modifications present an additional opportunity to investigate novel regions within the solution search space.

In the third stage, vectors are evaluated by the objective function, where the calculated value is referred to as the fitness. In minimization, the ideal fitness vector is the minimum within the population.

In the fourth stage, during each iteration, the vector exhibiting the best fitness is thereafter compared with the fitness of the previously recombined vectors.

This process is repeated until the stop criterion is reached, either the number of interactions or the number of objective function evaluations is satisfied, and then the best achievable solution is found.

The contributions of this work are the following:

• A novel bio-inspired optimization algorithm named MShOA, which is based on the mantis shrimp’s visual ability to detect polarized light, is proposed. Once the polarization state is determined, these detection capabilities allow the mantis shrimp to decide whether to search for food, hit predators, defend itself, or escape from its burrow.
• The performance of MShOA was evaluated with a set of 20 unimodal and multimodal functions reported in the literature. Furthermore, it was implemented in 10 real-world constraint optimization applications from CEC2020 and 3 study cases of an electrical engineering optimal power flow problem.
• In the Wilcoxon and Friedman statistical tests, MShOA outperformed 14 algorithms taken from the state of the art.
• MShOA’s source code is available for the scientific community.

This paper is structured as follows: Section 2 shows the MShOA bio-inspiration, outlines the mathematical model, provides the pseudocode, and includes the general flowchart of the algorithm. Section 3 shows the performance of MShOA compared with 14 recent bio-inspired algorithms. Section 4 presents the results and discusses the algorithm. Section 5 describes the application of MShOA to real-world optimization problems. Finally, Section 6 summarizes the conclusions and future work.

2. Mantis Shrimp Optimization Algorithm (MShOA)

2.1. Biological Fundamentals

The purple-spotted mantis shrimp (Gonodactylus smithii) is a stomatopod crustacean that primarily inhabits shallow tropical marine waters worldwide. They are sedentary animals that spend most of the day hidden in burrows on the seabed. However, they make forays to feed, exhibiting a remarkable ability to return to their burrows [41]. During these outings, they behave in a cautious and observant manner, using their complex visual systems to detect dangers and opportunities, especially when searching for food [42]. They have the most complex eyes in the animal kingdom, with up to 12 types of photoreceptors that allow them to discriminate linearly and circularly polarized light [43,44,45]. Their eyes are also extremely mobile, capable of performing proactive torsional rotations of up to 90 degrees. These movements can be coordinated or independent during visual scanning, allowing them to individually adjust the orientation of each eye in response to specific stimuli, such as polarized light signals [46]. Mantis shrimps use these specific polarization signals, both linear and circular, in critical social contexts, such as mating and territorial defense [47,48]. This adaptation enables them to accurately orient themselves in their surroundings to detect objects, predators, prey, and communicate visually with other mantis shrimp, optimizing their visual perception and behavior in their environment [49]. Additionally, they are also characterized by their fierce competition for their burrows, which are highly valuable resources due to their multifunctional use. They use their acute vision to determine the size of the opponent and their fighting ability. The opponent’s fighting ability is decisive in deciding whether to fight for the burrow or avoid the confrontation [50]. Figure 3 summarizes most of the aforementioned mantis shrimps’ behaviors. Figure 3a illustrates how shrimp hide in their shelter to increase their chances of staying safe. The shrimp’s eyes gaze in multiple directions at once for further decision-making, which may include strike, defense or shelter, burrow, or cautiously forage, as seen in Figure 3b. Figure 3c shows a lateral view of a red mantis shrimp. Additionally, Figure 3d illustrates the impact of a mantis shrimp’s strike on a prey shell.

Figure 3. (a) The shrimp inside its shelter. Photograph (published under a CC BY license). Author unknown. (b) The shrimp observing in different directions simultaneously. Photograph (published under a CC BY-SA license). Author unknown. (c) The purple-spotted mantis shrimp (Gonodactylus smithii). Photograph by Roy L. Caldwell (published under a CC BY-SA license). (d) Strike of a mantis shrimp. Photograph (published under a CC BY license). Author unknown.

Overall, when observing its surroundings, the mantis shrimp can see independently with both eyes. In this way, each eye detects a predominant type of polarization (vertical, horizontal, or circular) within its field of view, which allows it to identify prey, a threat, or a potential mate. Subsequently, the shrimp compares the information captured by both eyes and selects the detected signal that is the most predominant, which then guides its subsequent behavior. Based on this process, this study considered that the mantis shrimp engages in foraging when vertical polarization dominates; attacks when horizontal polarization is more intense; and burrows, defends, or shelters when circular polarization is detected, as depicted in Figure 4.

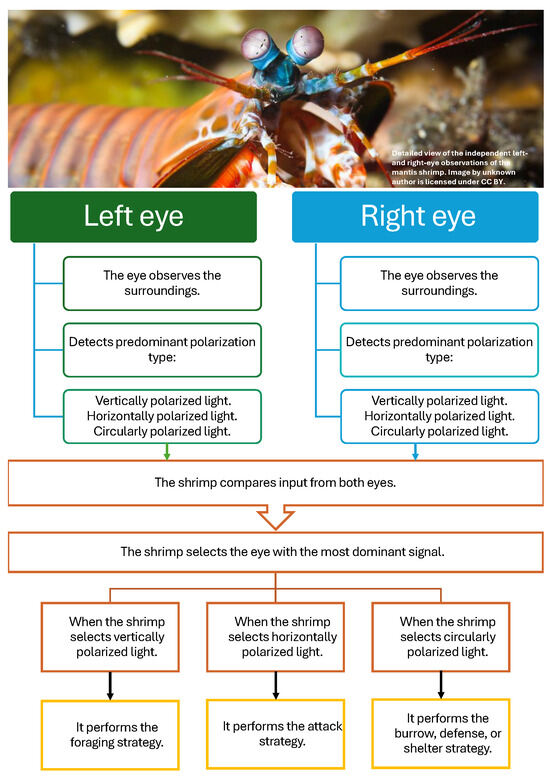
Figure 4. Shrimp strategies based on detected polarized light.

2.2. Initialization

The algorithm’s initialization consists of two phases to obtain the initial values. As seen in Equation (1), a set of multidimensional solutions representing the initial population is randomly generated in the first phase:

$$X_{i,j}=l{b}_{1,j}+{\mathrm{rand}}_{i,j}·(u{b}_{1,j}-l{b}_{1,j}),\mathrm{for}i=1,2,\dots ,N\mathrm{and}j=1,2,\dots ,dim$$

(1)

where $X_{i,j}$ is the initial population, N is defined as the number of search agents, and $dim$ represents the dimension of the problem (number of variables). Figure 5a presents a graphical representation of the initial population X. Finally, $lb$ and $ub$ represent the lower and upper bounds of the search space, respectively. As described in Equation (2), a vector is randomly generated in the second phase to represent the detected polarization’s Polarization Type Indicator (PTI):

$$PTI=round\left[\right(1+2\ast rand\left)\right]$$

(2)

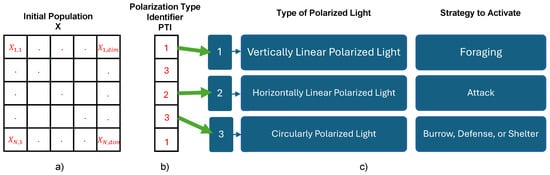
Figure 5. (a) Schematic representation of the initial population, where $dim$ stands for the vector size; (b) Polarization Type Identifier (PTI) vector representation; (c) strategy activated by the type of polarized light detected.

In both phases, the rand function is assumed to follow a uniform distribution in the range $[0,1]$. The round function restricts the $PTI$ value to 1, 2, or 3, as seen in Figure 5b. These values represent the reference angle set at ($\pi /2$), (0 or $\pi$), or ($\pi /4$ or $3\pi /4$), which are related to vertical linearly, horizontal linearly, and circularly polarized light, respectively. Each of these polarization states is based on the visual capabilities of the mantis shrimp. In addition, a $PTI$ value of 1 activates the mantis shrimp’s foraging strategy, while a $PTI$ value of 2 activates the attack strategy. The final strategy, burrow, defense, or shelter, is triggered by a $PTI$ of 3. Figure 5c illustrates the correlation of the PTI value and the type of polarized light detected, as well as its relationship with the forage; attack; or burrow, defense, or shelter strategies.

2.3. Polarization Type Identifier (PTI) Vector Update Process

The following steps outline how the PTI vector is updated. The whole process is summarized in Figure 6.

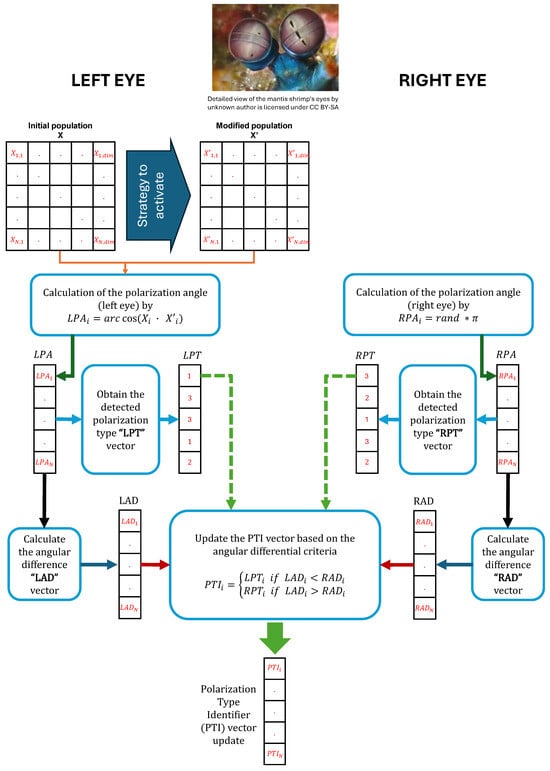
Figure 6. Schematic diagram of the Polarization Type Identifier ($PTI$) vector update process.

• The calculation of the polarization angle was inspired by the visual system of the mantis shrimp, where each eye performs independent perception. The left eye employs vectors from both the initial (X) and updated population ($X^{\prime }$) to compute the Left Polarization Angle ($LPA$), as described in Equation (3). In contrast, the Right Polarization Angle ($RPA$) is determined through Equation (4).

  $$\begin{array}{cc}\hfill & LPA=arc\cos (X_i·X_i^{\prime })\hfill \end{array}$$

  (3)

  $$\begin{array}{cc}\hfill & RPA=rand\ast \pi \hfill \end{array}$$

  (4)
  Furthermore, the angular difference between $LPA$ and $RPA$ is computed for subsequent consideration in the PTI update process.
• Before the PTI value is updated, the detected left- and right-eye polarization types should be calculated. The Left Polarization Type ($LPT$) vector and the Right Polarization Type ($RPT$) vector are determined by the criteria described in Equation (5):

  $$\begin{gathered} \begin{array}{ccc}\mathrm{Left} \mathrm{eye}LPT=\hfill & \left\{\begin{array}{c}1,\mathrm{if}{\displaystyle \frac{3\pi }{8}}\le LPA\le {\displaystyle \frac{5\pi }{8}}\hfill \\ 2,\mathrm{if}0\le LPA\le {\displaystyle \frac{\pi }{8}}\mathrm{or}{\displaystyle \frac{7\pi }{8}}\le LPA\le \pi \hfill \\ 3,\mathrm{if}{\displaystyle \frac{\pi }{8}}<LPA<{\displaystyle \frac{3\pi }{8}}\mathrm{or}{\displaystyle \frac{5\pi }{8}}<LPA<{\displaystyle \frac{7\pi }{8}}\hfill \end{array}\right.& \\ \end{array} \\ \mathrm{Right} \mathrm{eye}RPT=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{\displaystyle \frac{3\pi }{8}}\le RPA\le {\displaystyle \frac{5\pi }{8}}\hfill \\ 2,\hfill & \mathrm{if}0\le RPA\le {\displaystyle \frac{\pi }{8}}\mathrm{or}{\displaystyle \frac{7\pi }{8}}\le RPA\le \pi \hfill \\ 3,\hfill & \mathrm{if}{\displaystyle \frac{\pi }{8}}<RPA<{\displaystyle \frac{3\pi }{8}}\mathrm{or}{\displaystyle \frac{5\pi }{8}}<RPA<{\displaystyle \frac{7\pi }{8}}\hfill \end{array}\right. \end{gathered}$$

  (5)
• The Left-Eye Angular Difference ($LAD$) between the Left Polarization Angle ($LPA$) and the reference angles of the polarized light is calculated using Equation (6). Similarly, the Right-Eye Angular Difference ($RAD$) is calculated with the Right Polarization Angle ($RPA$).

  $$\begin{gathered} \begin{array}{ccc}LAD=\hfill & \left\{\begin{array}{cc}LPA,\hfill & \mathrm{if}0\le LPA\le {\displaystyle \frac{\pi }{8}}\hfill \\ \pi -LPA,\hfill & \mathrm{if}{\displaystyle \frac{7\pi }{8}}\le LPA\le \pi \hfill \\ \left|{\displaystyle \frac{\pi }{2}}-LPA\right|,\hfill & \mathrm{if}{\displaystyle \frac{3\pi }{8}}\le LPA\le {\displaystyle \frac{5\pi }{8}}\hfill \\ \left|{\displaystyle \frac{\pi }{4}}-LPA\right|,\hfill & \mathrm{if}{\displaystyle \frac{\pi }{8}}<LPA<{\displaystyle \frac{3\pi }{8}}\hfill \\ \left|{\displaystyle \frac{3\pi }{4}}-LPA\right|,\hfill & \mathrm{if}{\displaystyle \frac{5\pi }{8}}<LPA<{\displaystyle \frac{7\pi }{8}}\hfill \end{array}\right.& \\ \end{array} \\ RAD=\left\{\begin{array}{cc}RPA,\hfill & \mathrm{if}0\le RPA\le {\displaystyle \frac{\pi }{8}}\hfill \\ \pi -RPA,\hfill & \mathrm{if}{\displaystyle \frac{7\pi }{8}}\le RPA\le \pi \hfill \\ \left|{\displaystyle \frac{\pi }{2}}-RPA\right|,\hfill & \mathrm{if}{\displaystyle \frac{3\pi }{8}}\le RPA\le {\displaystyle \frac{5\pi }{8}}\hfill \\ \left|{\displaystyle \frac{\pi }{4}}-RPA\right|,\hfill & \mathrm{if}{\displaystyle \frac{\pi }{8}}<RPA<{\displaystyle \frac{3\pi }{8}}\hfill \\ \left|{\displaystyle \frac{3\pi }{4}}-RPA\right|,\hfill & \mathrm{if}{\displaystyle \frac{5\pi }{8}}<RPA<{\displaystyle \frac{7\pi }{8}}\hfill \end{array}\right. \end{gathered}$$

  (6)
• Finally, by Equation (7), the PTI value is calculated. The pseudocode for the previously discussed polarization type identifier vector update process (PTI) is described in Algorithm 1 and in Figure 7.

  $$PT{I}_i=\left\{\begin{array}{cc}LP{T}_i\hfill & \mathrm{if}LA{D}_i<RA{D}_i\hfill \\ RP{T}_i\hfill & \mathrm{if}LA{D}_i>RA{D}_i\hfill \end{array}\right.$$

  (7)
  

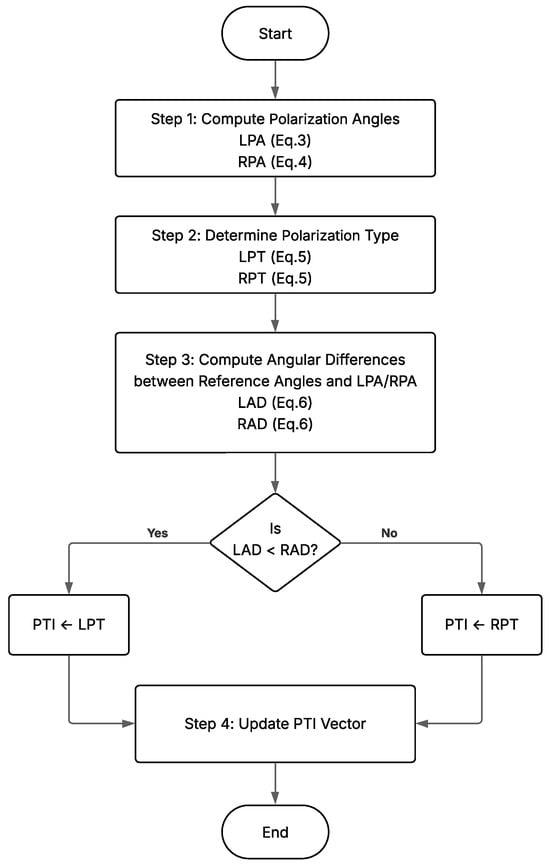  Figure 7. Algorithm 1’s Polarization Type Identifier (PTI) vector update process—flowchart.

Algorithm 1 Polarization Type Identifier (PTI) Vector Update Process

1: procedure  PTI_Vector_Update   2:     Step 1: compute polarization angles.   3:     Left-Eye Polarization Angle ($LPA$) calculated by Equation (3).   4:     Right-Eye Polarization Angle ($RPA$) calculated by Equation (4).   5:     Step 2: determine polarization type.   6:     Left-Eye Polarization Type ($LPT$) calculated by Equation (5).   7:     Right-Eye Polarization Type ($RPT$) calculated by Equation (5).   8:     Step 3: compute angular differences.   9:     Left-Eye Angular Difference ($LAD$) calculated by Equation (6). 10:     Right-Eye Angular Difference ($RAD$) calculated by Equation (6). 11:     Step 4: update PTI vector. 12:     if $LAD<RAD$ then 13:         $PT{I}_i\leftarrow LP{T}_i$ 14:     else 15:         $PT{I}_i\leftarrow RP{T}_i$ 16:     end if 17:     Output: updated PTI vector. 18: end procedure

2.4. Mathematical Model and Optimization Algorithm

Overall, the mantis shrimp’s behavior is characterized by foraging trips, in which it remains cautious and observant to detect prey or predators. In its burrow, it remains vigilant for any danger or opportunity for food. As previously described, it performs all these activities thanks to its eye’s independent movement skills, making it capable of perceiving linearly horizontal, linearly vertical, and circularly polarized light. This study used the polarized light detection signal capabilities of the mantis shrimp to determine the crustacean’s movement strategy, whether it is a forage; attack; or burrow, defense, or shelter survival tactic.

A mathematical model that simulates each eye’s rotational and independent movements is introduced to explore the mantis shrimp’s polarized light detection skills. Each eye of the mantis shrimp is considered a polarizing filter. The left eye is set to observe a known environment, while the right eye randomly explores an area, searching for new interactions within the environment. The intensity of the polarized light detected by each eye is meticulously compared, and then, the final decision is based on the signal with the highest intensity, which is directly related to the proximity of the polarization angle. Table 1 summarizes the polarized light detection capabilities of the mantis shrimp and their relationships with their behavioral strategies.

Table 1. Behavioral strategies of the mantis shrimp based on detected polarized light.

Type of Detected Light by Mantis Shrimp	Action to Take
Vertical linearly polarized light	Foraging
Horizontal linearly polarized light	Attack
Circularly polarized light	Burrow, defense, or shelter

2.5. Strategy 1: Foraging

The characteristic movement of the mantis shrimp when searching for food can be described as Brownian motion. Therefore, we can analyze this behavior starting with the generalized Langevin equation. This equation describes the motion of a particle without external forces, known as a free Brownian particle [51]. The dynamics of this particle are described by Equation (8). In this case, by assuming that no external forces are acting on the particle, $W\left(q\right)$ is set to 0, which simplifies Equation (8) to Equation (9). This represents the equilibrium between friction (${\zeta }_0$) and the noise term $R\left(t\right)$. A detailed explanation of this simplification process can be found in [51].

$$\mu \ddot{q}=-{\displaystyle \frac{dW}{dq}}-{\int }_0^t{q}^{\prime }\left(\tau \right)\zeta (t-\tau )d\tau +R\left(t\right).$$

(8)

$$\mu \ddot{q}=-{\zeta }_0\dot{q}+R\left(t\right)$$

(9)

Given that only $\ddot{q}$ and $\dot{q}$ appear in the equation of motion, Equation (9) can be rewritten in terms of the velocity $v=\dot{q}$ to obtain Equation (10), where the quantity $\zeta \left(t\right)$ in the Langevin equation is called the dynamic friction kernel, while $R\left(t\right)$ is known as a random force. In Equation (11), a diffusion constant D, which allows the random component of the model to be scaled, is then incorporated:

$$\mu \dot{v}=-{\zeta }_{0}v+R\left(t\right)$$

(10)

$$\mu \dot{v}=-{\zeta }_{0}v+D·R\left(t\right)$$

(11)

Moreover, the current position is updated by adding the random movement defined by the Langevin equation. For this work, the value of $\zeta \left(t\right)$ is proposed to be 1; thus, the equation can be rewritten as

$$\begin{array}{c}{x}_i(t+1)=x_{best}-v+D·R\left(t\right);\hfill \\ v=x_i\left(t\right)-x_{best};\hfill \\ R\left(t\right)=x_r\left(t\right)-x_i\left(t\right)\hfill \end{array}$$

(12)

where $x_i(t+1)$ represents the new position of the mantis shrimp in the ($t+1$)-th iteration; $x_{best}$ represents the best position found for the mantis shrimp; v is defined by the difference between the current position $x_i\left(t\right)$ and the best position $x_{best}$; $R\left(t\right)$ represents the difference between $x_r\left(t\right)$ and the current vector $x_i\left(t\right)$, where $r\in [1, \mathrm{population} \mathrm{size}]$, $r\ne i$; and D is a random diffusion value set within $[-1,1]$. The foraging strategy is summarized in Figure 8.

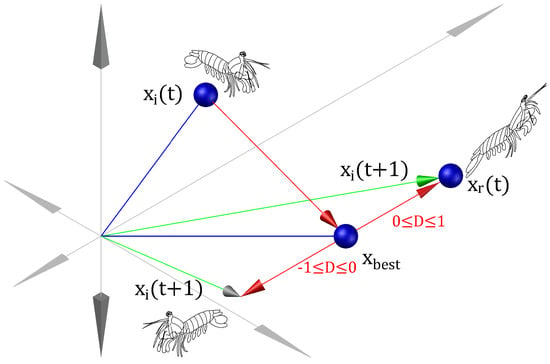
Figure 8. Foraging strategy.

2.6. Strategy 2: Attack

The mantis shrimp’s strike is renowned in biology for its capacity to fracture hard shells, comparable to the impact of a bullet [52,53,54,55]. Equation (13) shows how this hit can be represented by a circular motion parametric equation in a two-dimensional plane:

$$x_t=r\ast \cos \theta$$

(13)

where the vector r represent the mantis shrimp’s front appendages and $\theta$ is the angular strike motion.

Finally, the mantis shrimp’s attack can be expressed as follows:

$$x_i(t+1)=x_{best}\ast \cos \theta$$

(14)

where $x_i(t+1)$ represents the new position of the mantis shrimp in the ($t+1$)-th iteration, $x_{best}$ represents the best position found for the mantis shrimp, and $\theta$ is randomly generated with $\theta \in [\pi ,2\pi ]$. The graphical representation of the attack strategy is shown in Figure 9.

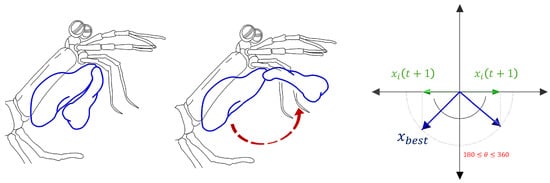
Figure 9. Mantis shrimp’s attack strike.

2.7. Strategy 3: Burrow, Defense, or Shelter

The mantis shrimp bases its decision-making strategy regarding defending, sheltering, or burrowing on its exceptional visual ability to assess an opponent’s threat. Using their keen vision, they determine whether the opponent is significantly larger and likely stronger, choosing to flee, or if similar in size or smaller, they aggressively decide to defend or shelter in their territory [56,57,58,59,60]. These animals hide in their shelters to increase the chance of staying safe [61]. Equation (15) is used to describe the mantis shrimp’s defense or shelter strategy:

$$\begin{gathered} \begin{array}{c}\mathrm{Defense}:x_i(t+1)=x_{best}+k\ast \left(x_{best}\right),k\in [0,0.3]\hfill \end{array} \\ \mathrm{Shelter}:x_i(t+1)=x_{best}-k\ast \left(x_{best}\right),k\in [0,0.3] \end{gathered}$$

(15)

where $x_i(t+1)$ represents the new position of the mantis shrimp in the ($t+1$)-th iteration, $x_{best}$ represents the best position found for the mantis shrimp, and k is a scaling factor randomly generated between 0 and $0.3$. The graphic representation of the burrow, defense, or shelter strategy is shown in Figure 10.   

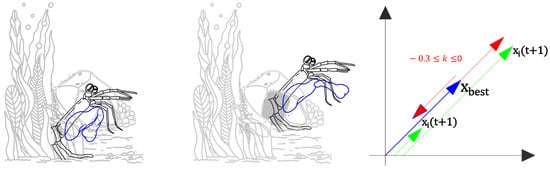
Figure 10. Burrow, defense, or shelter strategy.

Sensitivity Analysis of k Parameter

The third strategy introduces a scaling parameter k fixed at 0.3. To evaluate the algorithm’s sensitivity to this parameter, nine different values of k running from 0.1 to 0.9 in increments of 0.1 were studied. The analysis included 10 unimodal and 10 multimodal benchmark functions; see Table A1 and Table A2. Each test was executed independently 30 times, with a population size of 30 and 200 iterations. The statistical results of this sensitivity analysis are presented in Table 2, Table 3, Table 4, Table 5 and Table 6. Figure 11 illustrates the behavior of MShOA when using different values of k, as tested on one representative unimodal function and one multimodal function.

Table 2. Comparative performances of MShOA with $k=0.1$ to $0.9$ on benchmark functions.

K Value			K = 0.1			K = 0.2
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	0	0	0	0	0	0
F2	0	0	0	0	0	0	0
F3	0	0	$3.84\times {10}^{-279}$	0	0	$1.08\times {10}^{-283}$	0
F4	0	0	$2.15\times {10}^{-290}$	0	0	$1.05\times {10}^{-289}$	0
F5	0	0	$8.90\times {10}^{-285}$	0	0	$5.42\times {10}^{-287}$	0
F6	0	0	0	0	0	0	0
F7	0	0	0	0	0	0	0
F8	0	0	0	0	0	0	0
F9	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0
F10	0	0	0	0	0	0	0
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0
F12	−4.59	$-4.59\times {10}^{+00}$	$-2.89\times {10}^{+00}$	$1.65\times {10}^{+00}$	$-4.59\times {10}^{+00}$	$-2.85\times {10}^{+00}$	$1.60\times {10}^{+00}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$
F14	0	$4.22\times {10}^{-06}$	$1.72\times {10}^{-04}$	$1.42\times {10}^{-04}$	$1.63\times {10}^{-05}$	$2.36\times {10}^{-04}$	$2.02\times {10}^{-04}$
F15	0	0	0	0	0	0	0
F16	0	$2.90\times {10}^{+01}$	$2.90\times {10}^{+01}$	$8.43\times {10}^{-03}$	$2.89\times {10}^{+01}$	$2.90\times {10}^{+01}$	$2.63\times {10}^{-02}$
F17	0	0	0	0	0	0	0
F18	0	$1.02\times {10}^{-161}$	$3.43\times {10}^{-33}$	$1.88\times {10}^{-32}$	$1.59\times {10}^{-169}$	$4.68\times {10}^{-13}$	$1.96\times {10}^{-12}$
F19	0	$7.51\times {10}^{-08}$	$1.17\times {10}^{-05}$	$2.59\times {10}^{-05}$	$8.19\times {10}^{-08}$	$6.22\times {10}^{-06}$	$1.20\times {10}^{-05}$
F20	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0

Table 3. Continuation of comparative performances of MShOA with $k=0.1$ to $0.9$ on benchmark functions.

K Value			K = 0.3			K = 0.4
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	0	0	0	0	0	0
F2	0	0	0	0	0	0	0
F3	0	0	$1.99\times {10}^{-283}$	0	0	$2.44\times {10}^{-281}$	0
F4	0	0	$3.83\times {10}^{-285}$	0	0	$1.92\times {10}^{-286}$	0
F5	0	0	$5.36\times {10}^{-285}$	0	0	$9.14\times {10}^{-287}$	0
F6	0	0	0	0	0	0	0
F7	0	0	0	0	0	0	0
F8	0	0	0	0	0	0	0
F9	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0
F10	0	0	0	0	0	0	0
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0
F12	−4.59	$-4.59\times {10}^{+00}$	$-3.39\times {10}^{+00}$	$1.22\times {10}^{+00}$	$-4.59\times {10}^{+00}$	$-2.72\times {10}^{+00}$	$1.61\times {10}^{+00}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$
F14	0	$7.37\times {10}^{-06}$	$1.23\times {10}^{-04}$	$1.33\times {10}^{-04}$	$7.17\times {10}^{-06}$	$1.55\times {10}^{-04}$	$1.61\times {10}^{-04}$
F15	0	0	0	0	0	0	0
F16	0	$2.90\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.16\times {10}^{-02}$	$2.89\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.77\times {10}^{-02}$
F17	0	0	0	0	0	0	0
F18	0	$3.41\times {10}^{-170}$	$2.45\times {10}^{-24}$	$1.31\times {10}^{-23}$	$5.08\times {10}^{-174}$	$4.79\times {10}^{-34}$	$2.62\times {10}^{-33}$
F19	0	$5.96\times {10}^{-08}$	$7.01\times {10}^{-06}$	$8.81\times {10}^{-06}$	$2.10\times {10}^{-238}$	$1.99\times {10}^{-05}$	$5.03\times {10}^{-05}$
F20	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0

Table 4. Continuation of comparative performances of MShOA with $k=0.1$ to $0.9$ on benchmark functions.

K Value			K = 0.5			K = 0.6
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	0	0	0	0	0	0
F2	0	0	0	0	0	0	0
F3	0	0	$5.68\times {10}^{-286}$	0	0	$6.66\times {10}^{-284}$	0
F4	0	0	$1.35\times {10}^{-286}$	0	0	$5.04\times {10}^{-285}$	0
F5	0	0	$7.30\times {10}^{-281}$	0	0	$1.52\times {10}^{-285}$	0
F6	0	0	0	0	0	0	0
F7	0	0	0	0	0	0	0
F8	0	0	0	0	0	0	0
F9	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0
F10	0	0	0	0	0	0	0
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0
F12	−4.59	$-4.59\times {10}^{+00}$	$-2.48\times {10}^{+00}$	$1.61\times {10}^{+00}$	$-4.59\times {10}^{+00}$	$-3.18\times {10}^{+00}$	$1.49\times {10}^{+00}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$
F14	0	$4.95\times {10}^{-06}$	$1.87\times {10}^{-04}$	$1.89\times {10}^{-04}$	$1.09\times {10}^{-06}$	$1.69\times {10}^{-04}$	$1.37\times {10}^{-04}$
F15	0	0	0	0	0	0	0
F16	0	$2.89\times {10}^{+01}$	$2.90\times {10}^{+01}$	$2.02\times {10}^{-02}$	$2.89\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.69\times {10}^{-02}$
F17	0	0	0	0	0	0	0
F18	0	$2.35\times {10}^{-157}$	$1.69\times {10}^{-37}$	$9.26\times {10}^{-37}$	$9.64\times {10}^{-158}$	$1.53\times {10}^{-07}$	$8.35\times {10}^{-07}$
F19	0	$1.87\times {10}^{-07}$	$9.20\times {10}^{-06}$	$1.16\times {10}^{-05}$	$3.15\times {10}^{-07}$	$1.85\times {10}^{-05}$	$2.58\times {10}^{-05}$
F20	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0

Table 5. Continuation of comparative performances of MShOA with $k=0.1$ to $0.9$ on benchmark functions.

K Value			K = 0.7			K = 0.8
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	0	0	0	0	0	0
F2	0	0	0	0	0	0	0
F3	0	0	$9.43\times {10}^{-284}$	0	0	$5.55\times {10}^{-290}$	0
F4	0	0	$1.55\times {10}^{-279}$	0	0	$6.40\times {10}^{-286}$	0
F5	0	0	$9.67\times {10}^{-291}$	0	0	$5.62\times {10}^{-293}$	0
F6	0	0	0	0	0	0	0
F7	0	0	0	0	0	0	0
F8	0	0	0	0	0	0	0
F9	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0
F10	0	0	0	0	0	0	0
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0
F12	−4.59	$-4.59\times {10}^{+00}$	$-3.19\times {10}^{+00}$	$1.28\times {10}^{+00}$	$-4.58\times {10}^{+00}$	$-2.91\times {10}^{+00}$	$1.47\times {10}^{+00}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$
F14	0	$5.75\times {10}^{-06}$	$1.78\times {10}^{-04}$	$1.76\times {10}^{-04}$	$5.16\times {10}^{-06}$	$1.34\times {10}^{-04}$	$1.54\times {10}^{-04}$
F15	0	0	0	0	0	0	0
F16	0	$2.89\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.80\times {10}^{-02}$	$2.90\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.19\times {10}^{-02}$
F17	0	0	0	0	0	0	0
F18	0	$8.57\times {10}^{-166}$	$1.04\times {10}^{-23}$	$5.67\times {10}^{-23}$	$4.63\times {10}^{-152}$	$4.56\times {10}^{-11}$	$2.50\times {10}^{-10}$
F19	0	$3.55\times {10}^{-07}$	$2.48\times {10}^{-05}$	$5.23\times {10}^{-05}$	$9.23\times {10}^{-08}$	$1.00\times {10}^{-05}$	$1.41\times {10}^{-05}$
F20	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0

Table 6. Continuation of comparative performances of MShOA with $k=0.1$ to $0.9$ on benchmark functions.

K Value			K = 0.9
F	$\mathit{f\; min}$	Best	Ave	Std
F1	0	0	0	0
F2	0	0	0	0
F3	0	0	$8.01\times {10}^{-289}$	0
F4	0	0	$5.30\times {10}^{-291}$	0
F5	0	0	$7.29\times {10}^{-290}$	0
F6	0	0	0	0
F7	0	0	0	0
F8	0	0	0	0
F9	−1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0
F10	0	0	0	0
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0
F12	−4.59	$-4.59\times {10}^{+00}$	$-2.77\times {10}^{+00}$	$1.66\times {10}^{+00}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$
F14	0	$1.71\times {10}^{-06}$	$1.51\times {10}^{-04}$	$1.31\times {10}^{-04}$
F15	0	0	0	0
F16	0	$2.90\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.11\times {10}^{-02}$
F17	0	0	0	0
F18	0	$2.01\times {10}^{-165}$	$3.79\times {10}^{-14}$	$2.07\times {10}^{-13}$
F19	0	$4.03\times {10}^{-08}$	$6.07\times {10}^{-06}$	$7.16\times {10}^{-06}$
F20	− 1	$-1.00\times {10}^{+00}$	$-1.00\times {10}^{+00}$	0

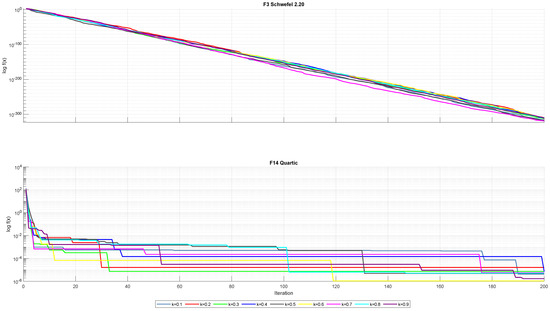
Figure 11. Convergence performances of unimodal function F3 and multimodal function F14.

Subsequently, the nonparametric Wilcoxon signed-rank test was applied to determine whether any alternative value of k led to statistically significant performance differences when compared with $k=0.3$. The results of this test, as summarized in Table 7, indicate that no statistically significant differences were observed at the 5% significance level.

Table 7. Statistical analysis of the Wilcoxon signed-rank test that compared different values of the parameter k in MShOA for 10 unimodal and 10 multimodal functions using a 5% significance level.

k = 0.3 vs. k = 0.1		k = 0.3 vs. k = 0.2		k = 0.3 vs. k = 0.4
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(5/13/2)	$1.76\times {10}^{-01}$	(3/13/4)	$6.12\times {10}^{-01}$	(4/13/3)	$2.37\times {10}^{-01}$
k = 0.3 vs. k = 0.5		k = 0.3 vs. k = 0.6		k = 0.3 vs. k = 0.7
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(4/13/3)	$2.37\times {10}^{-01}$	(5/13/2)	$1.28\times {10}^{-01}$	(5/13/2)	$6.30\times {10}^{-02}$
k = 0.3 vs. k = 0.8		k = 0.3 vs. k = 0.9
(+/=/−)	p-Value	(+/=/−)	p-Value
(4/13/3)	$1.76\times {10}^{-01}$	(3/13/4)	$6.12\times {10}^{-01}$

2.8. Pseudocode for MShOA

The pseudocode and flowchart of MShOA are described in Algorithm 2 and Figure 12, respectively.

Algorithm 2 Optimization Algorithm of the Mantis Shrimp

1: Procedure MShOA   2: Initialization of parameters. Specify the number of search agents, population size, and maximum number of iterations.   3: Randomly generate the initial population.   4: Randomly generate the Polarization Type Indicator (PTI).   5: while iteration < max number of iterations do   6:     if $PT{I}_i=1$ then                   % vertical linearly polarized light   7:         Strategy 1: foraging (Equation (12)).   8:     else if $PT{I}_i=2$ then             % horizontal linearly polarized light   9:         Strategy 2: attack (Equation (14)). 10:     else if $PT{I}_i=3$ then             % circularly polarized light 11:         Strategy 3: burrow, defense, or shelter (Equation (15)). 12:     end if 13:     Update the Polarization Type Identifier (PTI) vector (Algorithm 1). 14:     Update the population. 15:     Calculate the fitness value from the new population. 16:     Update the fitness and the best solution found. 17:     $iteration$ = $iteration+1$. 18: end while 19: Display the best solution found. 20: end procedure

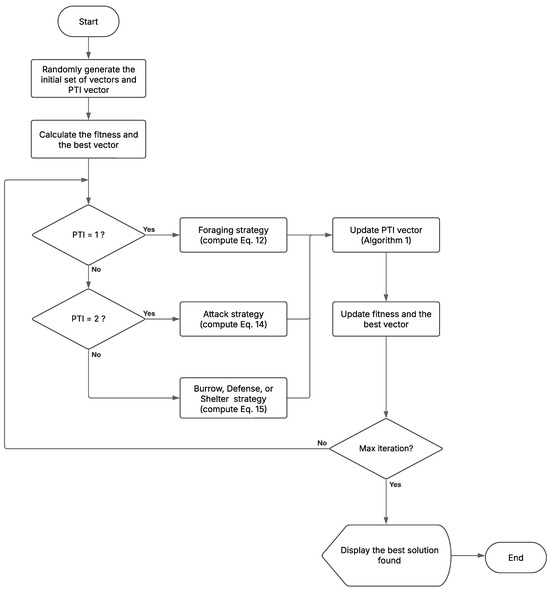
Figure 12. MShOA flowchart.

MShOA’s Time Complexity

The computational complexity of an optimization method is characterized by a function that relates the method’s runtime to the size of the problem’s input. Big-O notation functions as a widely accepted representation. The time complexity of MShOA is described as follows:

$$\begin{array}{cc}\hfill O\left(\mathrm{MShOA}\right)=& O\left(\mathrm{Initial}\mathrm{population}\right)+O\left(\mathrm{Generate}\mathrm{Polarization}\mathrm{Type}\mathrm{Indicator}\right)\hfill \\ \hfill & +O\left(\mathrm{Strategy}1\right)+O\left(\mathrm{Strategy}2\right)+O\left(\mathrm{Strategy}3\right)\hfill \\ & +O\left(\mathrm{Update}\mathrm{Polarization}\mathrm{Type}\mathrm{Indicator}\mathrm{by}\mathrm{Algorithm}1\right)\hfill \\ \hfill & +O\left(\mathrm{Update}\mathrm{population}\right)+O\left(\mathrm{Update}\mathrm{fitness}\right)\hfill \end{array}$$

(16)

In addition to Equation (16), the time complexity of MShOA depends on the number of iterations ($MaxIter$), the population size of mantis shrimps (nMS), the dimensionality of the problem (dim), and the cost of the objective function (f). Table 8 describes each part of Equation (16).

Table 8. Description of the MShA algorithm’s computational complexity.

Instruction	Big-O Notation	Observation
Initial population	$O(nMS\ast dim)$	No loop is related.
Polarization Type Indicator	$O(dim\ast 1)$	No loop is related.
Strategy 1: foraging (Equation (12))	$O(MaxIter\ast 1)$	Consists of a sequence of constant operations. It does not depend on the input size or iterable data structures, and the loop is related to $MaxIter$.
Strategy 2: attack (Equation (14))	$O(MaxIter\ast 1)$	Consists of a sequence of constant operations. It does not depend on the input size or iterable data structures, and the loop is related to $MaxIter$.
Strategy 3: burrow, defense, or shelter (Equation (15))	$O(MaxIter\ast 1)$	Consists of a sequence of constant operations. It does not depend on the input size or iterable data structures, and the loop is related to $MaxIter$.
Update Polarization Type Indicator (PTI) by Algorithm 1	$O(MaxIter\ast 1)$	Algorithm 1 consists of a sequence of constant operations. It does not depend on the input size or iterable data structures, and the loop is related to $MaxIter$.
Update population	$O(MaxIter\ast nMS)$	The loop is related to $MaxIter$.
Update fitness	$O(MaxIter\ast nMS\ast dim\ast f)$	The loop is related to $MaxIter$.

Therefore, the overall time complexity of MshOA can be computed as follows:

$$\begin{array}{cc}\hfill O\left(\mathrm{MShOA}\right)=& O(nMS\ast \mathit{dim})+O(\mathit{dim}\ast 1)+O(MaxIter\ast 1)+O(MaxIter\ast 1)\hfill \\ \hfill & +O(MaxIter\ast 1)+O(MaxIter\ast 1)+O(MaxIter\ast nMS)\hfill \\ \hfill & +O(MaxIter\ast nMS\ast \mathit{dim}\ast f)\hfill \end{array}$$

(17)

In O notation, when we add several terms, the fastest-growing one dominates. Hence, the time complexity of MShOA can be expressed as follows:

$$O\left(\mathrm{MShOA}\right)=O(MaxIter\ast nMS\ast \mathit{dim}\ast f)$$

(18)

3. Experimental Setup

The efficiency and stability of MShOA were evaluated by solving 20 optimization functions from the literature; see Appendix A. MShOA was compared with the 14 bio-inspired algorithms described below:

• Ant Lion Optimizer (ALO): The algorithm presents the predatory behavior of the ant lion in nature and mathematically models five stages: random movement, building traps, entrapment of ants in traps, catching prey, and rebuilding traps [21].
• Arithmetic Optimization Algorithm (AOA): This algorithm takes advantage of the distribution behavior of fundamental arithmetic operations in mathematics, including multiplication (M), division (D), subtraction (S), and addition (A) [62].
• Beluga Whale Optimization (BWO): This algorithm was inspired by the natural behaviors of beluga whales and mathematically models their behavior in pair swimming, preying, and whale fall [63].
• Dandelion Optimizer (DO): This algorithm simulates the long-distance flight of dandelion seeds relying on the wind and is divided into three stages: the rising stage, the descending stage, and the landing stage [64].
• Evolutionary Mating Algorithm (EMA): the evolutionary algorithm is based on a random mating concept from the Hardy–Weinberg equilibrium [65].
• Grey Wolf Optimizer (GWO): This algorithm is inspired by grey wolves (Canis lupus) and mimics their leadership hierarchy and hunting mechanisms in nature [22].
• Liver Cancer Algorithm (LCA): This algorithm mimics liver tumor’s growth and takeover processes and mathematically models their ability to replicate and spread to other organs [66].
• Mexican Axolotl Optimization Algorithm (MAO): This algorithm was inspired by the way axolotls live in their aquatic environment and is modeled after their processes of regeneration, reproduction, and tissue restoration [67].
• Marine Predators Algorithm (MPA): This algorithm is inspired by the interactions between predators and prey in marine ecosystems and models the widespread foraging strategies and optimal encounter rate policies [68].
• Salp Swarm Algorithm (SSA): This algorithm is inspired by the behavior of salps in nature and primarily models their swarming behavior when navigating and foraging in oceans [17].
• Synergistic Swarm Optimization Algorithm (SSOA): This algorithm combines swarm intelligence with synergistic cooperation to find optimal solutions. It mathematically models a cooperation mechanism, where particles exchange information and learn from one another, enhancing their search behaviors and improving the overall performance [69].
• Tunicate Swarm Algorithm (TSA): this algorithm imitates the behavior of tunicates and models their use of jet propulsion and collective movements while navigating and searching for food [70].
• Whale Optimization Algorithm (WOA): this algorithm imitates the social behavior of humpback whales in nature and mathematically models their bubble-net hunting strategy [18].
• Catch Fish Optimization Algorithm (CFOA): this algorithm is inspired by traditional rural fishing practices and models the strategic process of fish capture through two main phases: an exploration phase combining individual intuition and group collaboration, and an exploitation phase based on coordinated collective action [71].

Each algorithm was executed independently 30 times, with a population size of 30 and 200 iterations. The initial configuration parameters of all the employed algorithms are detailed in Table 9. The Wilcoxon test was applied to compare the performances of the algorithms. The four best-ranked algorithms, as computed using the Friedman test, were selected for further evaluation on 10 optimization problems taken from the CEC2020 benchmark suite detailed in Table 24. Moreover, three engineering study cases based on the optimal power flow optimization problem were also studied.

Table 9. Initial parameters for each algorithm.

Algorithm	Parameters	Value
For all algorithms	Population size for all problems	30
	Maximum iterations for testbench functions and real-world problems	200
	Number of repetition for testbench functions	30
MShOA	Does not use additional parameters	-
ALO	I ratio	10
	w	2.0–0.6
AOA	$\alpha$	5.0
	$\mu$	0.5
BWO	$W_f$	[0.1, 0.05]
DO	$\alpha$	[0, 1]
	k	[0, 1]
EMA	r	[0, 0.2]
	$Cr$	[0, 1]
GWO	$\alpha$	2.0–0.0
LCA	f	1
MAO	$dp$	0.5
	$rp$	0.1
	k	3
	$\lambda$	0.5
MPA	P	0.5
	$FADs$	0.2
SSA	v	0.0
SSOA	w	0.7
	$C1$	2.0
	$C2$	2.0
	k	0.5
TSA	$P_{min}$	1
	$P_{max}$	4
WOA	$\alpha$	2.0–0.0
	b	2.0
CFOA	Does not use additional parameters	−

All experiments were conducted on a standard desktop with the following specifications: Intel Core i9-13900K 5.8 GHz processor, 192 GB RAM, Linux Ubuntu 24.04 LTS operating system, and MATLAB R2024a compiler.

4. Results and Discussion

The computational results of MShOA, GWO, BWO, DO, WOA, MPA, LCA, SSA, EMA, ALO, MAO, AOA, SSOA, TSA, and CFOA on 20 benchmark test functions are presented in Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16 and Table 17, where the average, standard deviation, and best values are provided for comparison measurements.

Table 10. Comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			MShOA			GWO
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	0	0	0	$1.12\times {10}^{-12}$	$1.51\times {10}^{-11}$	$1.39\times {10}^{-11}$
F2	0	0	0	0	$1.07\times {10}^{-09}$	$1.08\times {10}^{-02}$	$1.54\times {10}^{-02}$
F3	0	0	$1.16\times {10}^{-286}$	0	$2.14\times {10}^{-05}$	$4.62\times {10}^{-05}$	$1.73\times {10}^{-05}$
F4	0	0	$1.21\times {10}^{-288}$	0	$4.92\times {10}^{-03}$	$3.08\times {10}^{-02}$	$1.86\times {10}^{-02}$
F5	0	0	$5.63\times {10}^{-284}$	0	$3.26\times {10}^{-05}$	$8.29\times {10}^{-05}$	$3.22\times {10}^{-05}$
F6	0	0	0	0	$1.43\times {10}^{-39}$	$2.07\times {10}^{-31}$	$9.76\times {10}^{-31}$
F7	0	0	0	0	$4.10\times {10}^{-13}$	$1.95\times {10}^{-11}$	$2.26\times {10}^{-11}$
F8	0	0	0	0	$1.97\times {10}^{-10}$	$1.22\times {10}^{-09}$	$1.51\times {10}^{-09}$
F9	−1	−1.00	−1.00	0	$9.96\times {10}^{-01}$	$9.97\times {10}^{-01}$	$2.53\times {10}^{-04}$
F10	0	0	0	0	$1.73\times {10}^{-02}$	$3.47\times {10}^{-01}$	$3.22\times {10}^{-01}$
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$6.44\times {10}^{-06}$	$1.67\times {10}^{-05}$	$7.44\times {10}^{-06}$
F12	−4.59	−4.59	$-2.79$	$1.36$	−4.59	−4.59	$1.73\times {10}^{-06}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$1.19$	$2.36$	$1.95$
F14	0	$3.68\times {10}^{-07}$	$1.51\times {10}^{-04}$	$1.46\times {10}^{-04}$	$2.39\times {10}^{-03}$	$7.00\times {10}^{-03}$	$4.16\times {10}^{-03}$
F15	0	0	0	0	$4.43$	$1.62\times {10}^{+01}$	$8.43$
F16	0	$2.89\times {10}^{+01}$	$2.90\times {10}^{+01}$	$1.58\times {10}^{-02}$	$2.61\times {10}^{+01}$	$2.73\times {10}^{+01}$	$7.56\times {10}^{-01}$
F17	0	0	0	0	$2.00\times {10}^{-01}$	$2.98\times {10}^{-01}$	$5.61\times {10}^{-02}$
F18	0	$2.75\times {10}^{-162}$	$1.33\times {10}^{-27}$	$7.27\times {10}^{-27}$	$1.40\times {10}^{-16}$	$9.98\times {10}^{-06}$	$5.46\times {10}^{-05}$
F19	0	$4.34\times {10}^{-07}$	$1.54\times {10}^{-05}$	$2.70\times {10}^{-05}$	$1.67\times {10}^{-10}$	$1.27\times {10}^{-07}$	$2.58\times {10}^{-07}$
F20	−1	−1.00	−1.00	0	$3.56\times {10}^{-15}$	$7.86\times {10}^{-15}$	$3.17\times {10}^{-15}$

Table 11. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			BWO			DO
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	$9.60\times {10}^{-117}$	$7.51\times {10}^{-107}$	$2.97\times {10}^{-106}$	$1.18\times {10}^{-05}$	$9.70\times {10}^{-05}$	$5.74\times {10}^{-05}$
F2	0	0	0	0	$1.25\times {10}^{-02}$	$6.76\times {10}^{-02}$	$4.38\times {10}^{-02}$
F3	0	$1.97\times {10}^{-56}$	$4.47\times {10}^{-52}$	$1.09\times {10}^{-51}$	$2.29\times {10}^{-01}$	$4.54\times {10}^{-01}$	$1.57\times {10}^{-01}$
F4	0	$4.29\times {10}^{-55}$	$5.33\times {10}^{-52}$	$1.00\times {10}^{-51}$	$2.71$	$1.09\times {10}^{+01}$	$5.30$
F5	0	$2.07\times {10}^{-56}$	$1.95\times {10}^{-52}$	$4.28\times {10}^{-52}$	$1.77\times {10}^{-01}$	$8.69$	$4.33\times {10}^{+01}$
F6	0	0	0	0	$5.34\times {10}^{-16}$	$1.34\times {10}^{-09}$	$5.13\times {10}^{-09}$
F7	0	$5.11\times {10}^{-118}$	$7.58\times {10}^{-106}$	$3.97\times {10}^{-105}$	$1.57\times {10}^{-05}$	$5.59\times {10}^{-05}$	$4.28\times {10}^{-05}$
F8	0	$1.01\times {10}^{-112}$	$9.62\times {10}^{-103}$	$5.19\times {10}^{-102}$	$1.22\times {10}^{-03}$	$3.74\times {10}^{-03}$	$2.10\times {10}^{-03}$
F9	−1	−1.00	−1.00	0	$9.95\times {10}^{-01}$	$9.96\times {10}^{-01}$	$3.48\times {10}^{-04}$
F10	0	$1.47\times {10}^{-101}$	$3.55\times {10}^{-93}$	$8.37\times {10}^{-93}$	$1.77$	$8.49$	$6.83$
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$1.02\times {10}^{-02}$	$3.83\times {10}^{-01}$	$6.86\times {10}^{-01}$
F12	−4.59	−4.59	$-4.58$	$1.53\times {10}^{-02}$	−4.59	−4.59	$1.35\times {10}^{-10}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$1.03$	$1.13$	$7.30\times {10}^{-02}$
F14	0	$1.24\times {10}^{-06}$	$2.76\times {10}^{-04}$	$2.13\times {10}^{-04}$	$2.20\times {10}^{-02}$	$6.61\times {10}^{-02}$	$3.19\times {10}^{-02}$
F15	0	0	0	0	$5.38$	$4.29\times {10}^{+01}$	$2.29\times {10}^{+01}$
F16	0	$2.26\times {10}^{-04}$	$7.66\times {10}^{-03}$	$1.16\times {10}^{-02}$	$2.57\times {10}^{+01}$	$2.76\times {10}^{+01}$	$7.95\times {10}^{-01}$
F17	0	$6.65\times {10}^{-51}$	$5.03\times {10}^{-43}$	$1.72\times {10}^{-42}$	$7.00\times {10}^{-01}$	$1.08$	$2.25\times {10}^{-01}$
F18	0	$4.73\times {10}^{-36}$	$1.84\times {10}^{-17}$	$1.01\times {10}^{-16}$	$1.49\times {10}^{-05}$	$1.73\times {10}^{-01}$	$2.36\times {10}^{-01}$
F19	0	$3.51\times {10}^{-12}$	$3.69\times {10}^{-12}$	$7.63\times {10}^{-13}$	$3.04\times {10}^{-11}$	$1.26\times {10}^{-10}$	$1.07\times {10}^{-10}$
F20	−1	−1.00	−1.00	0	$1.20\times {10}^{-15}$	$3.28\times {10}^{-15}$	$1.44\times {10}^{-15}$

Table 12. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			WOA			MPA
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	$4.28\times {10}^{-38}$	$3.44\times {10}^{-31}$	$1.06\times {10}^{-30}$	$1.24\times {10}^{-10}$	$1.09\times {10}^{-09}$	$9.38\times {10}^{-10}$
F2	0	0	$3.68\times {10}^{-02}$	$1.41\times {10}^{-01}$	$1.83\times {10}^{-07}$	$1.15\times {10}^{-05}$	$4.85\times {10}^{-05}$
F3	0	$1.10\times {10}^{-23}$	$2.81\times {10}^{-18}$	$1.02\times {10}^{-17}$	$1.90\times {10}^{-04}$	$1.27\times {10}^{-03}$	$7.01\times {10}^{-04}$
F4	0	$6.78$	$5.70\times {10}^{+01}$	$2.16\times {10}^{+01}$	$2.03\times {10}^{-03}$	$4.22\times {10}^{-03}$	$1.16\times {10}^{-03}$
F5	0	$3.53\times {10}^{-22}$	$3.44\times {10}^{-17}$	$1.63\times {10}^{-16}$	$2.66\times {10}^{-04}$	$1.28\times {10}^{-03}$	$5.84\times {10}^{-04}$
F6	0	$1.65\times {10}^{-102}$	$4.46\times {10}^{-66}$	$1.96\times {10}^{-65}$	$7.15\times {10}^{-41}$	$3.13\times {10}^{-36}$	$1.40\times {10}^{-35}$
F7	0	$2.56\times {10}^{-38}$	$4.80\times {10}^{-27}$	$2.62\times {10}^{-26}$	$7.58\times {10}^{-11}$	$1.29\times {10}^{-09}$	$9.13\times {10}^{-10}$
F8	0	$5.50\times {10}^{-34}$	$2.96\times {10}^{-28}$	$1.24\times {10}^{-27}$	$2.71\times {10}^{-09}$	$6.67\times {10}^{-08}$	$5.53\times {10}^{-08}$
F9	−1	−1.00	−1.00	$1.09\times {10}^{-16}$	$-9.73\times {10}^{-01}$	$2.56\times {10}^{-01}$	$8.42\times {10}^{-01}$
F10	0	$3.47\times {10}^{+02}$	$5.08\times {10}^{+02}$	$1.02\times {10}^{+02}$	$4.35\times {10}^{-01}$	$1.39$	$6.78\times {10}^{-01}$
F11	0	$3.11\times {10}^{-15}$	$2.23\times {10}^{-14}$	$1.81\times {10}^{-14}$	$6.58\times {10}^{-05}$	$1.57\times {10}^{-04}$	$6.56\times {10}^{-05}$
F12	−4.59	−4.59	−4.59	$2.17\times {10}^{-05}$	−4.59	−4.59	$2.08\times {10}^{-13}$
F13	$0.9$	$9.00\times {10}^{-01}$	$1.41$	$6.32\times {10}^{-01}$	$1.01$	$1.14$	$1.00\times {10}^{-01}$
F14	0	$6.84\times {10}^{-04}$	$1.08\times {10}^{-02}$	$8.88\times {10}^{-03}$	$1.44\times {10}^{-03}$	$3.89\times {10}^{-03}$	$1.89\times {10}^{-03}$
F15	0	0	$1.33\times {10}^{-14}$	$3.23\times {10}^{-14}$	$4.65\times {10}^{-07}$	$1.30\times {10}^{-02}$	$3.78\times {10}^{-02}$
F16	0	$2.76\times {10}^{+01}$	$2.85\times {10}^{+01}$	$2.97\times {10}^{-01}$	$2.62\times {10}^{+01}$	$2.69\times {10}^{+01}$	$4.03\times {10}^{-01}$
F17	0	$9.89\times {10}^{-12}$	$1.30\times {10}^{-01}$	$6.51\times {10}^{-02}$	$2.00\times {10}^{-01}$	$2.07\times {10}^{-01}$	$2.54\times {10}^{-02}$
F18	0	$6.80\times {10}^{-16}$	$6.75\times {10}^{+03}$	$3.70\times {10}^{+04}$	$6.95\times {10}^{-16}$	$1.11\times {10}^{-08}$	$3.87\times {10}^{-08}$
F19	0	$3.51\times {10}^{-12}$	$5.63\times {10}^{-12}$	$3.42\times {10}^{-12}$	$3.51\times {10}^{-12}$	$8.06\times {10}^{-12}$	$4.12\times {10}^{-12}$
F20	−1	−1.00	$-1.67\times {10}^{-01}$	$3.79\times {10}^{-01}$	$1.47\times {10}^{-14}$	$1.46\times {10}^{-13}$	$1.01\times {10}^{-13}$

Table 13. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			LCA			SSA
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	$1.22\times {10}^{-06}$	$7.62\times {10}^{-04}$	$1.10\times {10}^{-03}$	$3.82\times {10}^{-02}$	$2.85$	$4.62$
F2	0	$5.22\times {10}^{-03}$	$3.62\times {10}^{-01}$	$3.26\times {10}^{-01}$	$1.08$	$1.45$	$4.03\times {10}^{-01}$
F3	0	$1.39\times {10}^{-01}$	$2.13$	$1.59$	$2.75\times {10}^{+01}$	$8.03\times {10}^{+01}$	$2.92\times {10}^{+01}$
F4	0	$1.72\times {10}^{-03}$	$8.44\times {10}^{-02}$	$6.41\times {10}^{-02}$	$1.00\times {10}^{+01}$	$1.70\times {10}^{+01}$	$4.35$
F5	0	$2.93\times {10}^{-01}$	$1.98$	$1.45$	$4.20\times {10}^{+03}$	$1.17\times {10}^{+19}$	$4.18\times {10}^{+19}$
F6	0	$4.60\times {10}^{-35}$	$1.66\times {10}^{-16}$	$8.89\times {10}^{-16}$	$1.01\times {10}^{-03}$	$1.67\times {10}^{+01}$	$2.80\times {10}^{+01}$
F7	0	$2.22\times {10}^{-05}$	$7.77\times {10}^{-04}$	$1.47\times {10}^{-03}$	$2.29\times {10}^{-02}$	$1.32\times {10}^{-01}$	$8.38\times {10}^{-02}$
F8	0	$5.85\times {10}^{-05}$	$5.90\times {10}^{-02}$	$1.51\times {10}^{-01}$	$7.19$	$3.18\times {10}^{+01}$	$2.17\times {10}^{+01}$
F9	−1	−1.00	$-9.97\times {10}^{-01}$	$4.25\times {10}^{-03}$	$9.96\times {10}^{-01}$	$9.96\times {10}^{-01}$	$1.61\times {10}^{-04}$
F10	0	$1.09\times {10}^{-02}$	$7.77$	$1.25\times {10}^{+01}$	$1.34\times {10}^{+02}$	$2.39\times {10}^{+02}$	$7.25\times {10}^{+01}$
F11	0	$2.96\times {10}^{-03}$	$1.57\times {10}^{-01}$	$1.70\times {10}^{-01}$	$2.90$	$5.38$	$1.41$
F12	−4.59	$-4.56$	$-3.62$	$9.77\times {10}^{-01}$	−4.59	−4.59	$7.94\times {10}^{-12}$
F13	$0.9$	$9.00\times {10}^{-01}$	$5.48$	$4.76$	$1.01$	$1.16$	$1.51\times {10}^{-01}$
F14	0	$9.68\times {10}^{-05}$	$1.73\times {10}^{-03}$	$1.54\times {10}^{-03}$	$1.38\times {10}^{-01}$	$3.52\times {10}^{-01}$	$1.58\times {10}^{-01}$
F15	0	$6.90\times {10}^{-04}$	$1.53\times {10}^{-01}$	$2.86\times {10}^{-01}$	$2.43\times {10}^{+01}$	$5.58\times {10}^{+01}$	$2.03\times {10}^{+01}$
F16	0	$2.54\times {10}^{-03}$	$1.34\times {10}^{-01}$	$1.32\times {10}^{-01}$	$4.63\times {10}^{+01}$	$1.18\times {10}^{+02}$	$4.82\times {10}^{+01}$
F17	0	$1.01\times {10}^{-01}$	$2.23\times {10}^{-01}$	$1.18\times {10}^{-01}$	$2.90$	$4.59$	$7.56\times {10}^{-01}$
F18	0	$9.52\times {10}^{-06}$	$1.15\times {10}^{-04}$	$1.08\times {10}^{-04}$	$8.17\times {10}^{-02}$	$8.98\times {10}^{+01}$	$2.71\times {10}^{+02}$
F19	0	$3.51\times {10}^{-12}$	$3.52\times {10}^{-12}$	$1.27\times {10}^{-14}$	$1.70\times {10}^{-11}$	$1.40\times {10}^{-10}$	$1.87\times {10}^{-10}$
F20	−1	$-9.66\times {10}^{-01}$	$-8.06\times {10}^{-01}$	$1.43\times {10}^{-01}$	$8.25\times {10}^{-14}$	$4.88\times {10}^{-13}$	$2.67\times {10}^{-13}$

Table 14. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			EMA			ALO
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	$1.16\times {10}^{-04}$	$1.50\times {10}^{-03}$	$1.26\times {10}^{-03}$	$1.21\times {10}^{-05}$	$2.72\times {10}^{-02}$	$5.38\times {10}^{-02}$
F2	0	$4.72\times {10}^{-02}$	$5.24\times {10}^{-01}$	$2.43\times {10}^{-01}$	$1.17$	$9.93$	$6.33$
F3	0	$2.87\times {10}^{-02}$	$2.64\times {10}^{-01}$	$1.82\times {10}^{-01}$	$1.73\times {10}^{+02}$	$2.19\times {10}^{+02}$	$3.65\times {10}^{+01}$
F4	0	$3.06\times {10}^{+01}$	$6.15\times {10}^{+01}$	$1.70\times {10}^{+01}$	$1.47\times {10}^{+01}$	$2.30\times {10}^{+01}$	$5.59$
F5	0	$1.40\times {10}^{-02}$	$2.77\times {10}^{-01}$	$1.90\times {10}^{-01}$	$4.80\times {10}^{+02}$	$3.42\times {10}^{+24}$	$1.54\times {10}^{+25}$
F6	0	$9.16\times {10}^{-06}$	$6.04\times {10}^{+01}$	$2.20\times {10}^{+02}$	$8.06\times {10}^{-01}$	$3.01\times {10}^{+03}$	$1.12\times {10}^{+04}$
F7	0	$2.10\times {10}^{-04}$	$6.44\times {10}^{-03}$	$9.76\times {10}^{-03}$	$1.06\times {10}^{-01}$	$2.52$	$1.76$
F8	0	$6.14\times {10}^{-03}$	$9.74\times {10}^{-02}$	$9.60\times {10}^{-02}$	$1.34\times {10}^{+01}$	$1.11\times {10}^{+02}$	$5.17\times {10}^{+01}$
F9	−1	$9.95\times {10}^{-01}$	$9.95\times {10}^{-01}$	$5.22\times {10}^{-16}$	−1.00	$-9.83\times {10}^{-01}$	$2.85\times {10}^{-02}$
F10	0	$2.93\times {10}^{+02}$	$4.40\times {10}^{+02}$	$8.74\times {10}^{+01}$	$1.74\times {10}^{+02}$	$3.85\times {10}^{+02}$	$9.94\times {10}^{+01}$
F11	0	$1.81\times {10}^{-02}$	$1.12\times {10}^{-01}$	$7.69\times {10}^{-02}$	$7.97$	$1.24\times {10}^{+01}$	$2.09$
F12	−4.59	−4.59	$-4.53$	$2.23\times {10}^{-01}$	−4.59	−4.59	$2.61\times {10}^{-11}$
F13	$0.9$	$2.51$	$3.37$	$6.31\times {10}^{-01}$	$9.40\times {10}^{-01}$	$1.07$	$5.54\times {10}^{-02}$
F14	0	$4.97\times {10}^{-02}$	$1.45\times {10}^{-01}$	$7.41\times {10}^{-02}$	$4.80\times {10}^{-01}$	$1.04$	$5.72\times {10}^{-01}$
F15	0	$1.29\times {10}^{-01}$	$1.58\times {10}^{+01}$	$2.08\times {10}^{+01}$	$3.81\times {10}^{+01}$	$8.90\times {10}^{+01}$	$2.55\times {10}^{+01}$
F16	0	$2.88\times {10}^{+01}$	$3.53\times {10}^{+01}$	$7.84$	$8.56\times {10}^{+01}$	$3.69\times {10}^{+02}$	$2.39\times {10}^{+02}$
F17	0	$8.03\times {10}^{-01}$	$1.15$	$2.30\times {10}^{-01}$	$5.30$	$7.89$	$1.49$
F18	0	$1.03\times {10}^{-06}$	$4.35\times {10}^{-02}$	$8.95\times {10}^{-02}$	$6.14\times {10}^{+03}$	$3.37\times {10}^{+09}$	$7.40\times {10}^{+09}$
F19	0	$2.07\times {10}^{-11}$	$2.51\times {10}^{-11}$	$1.88\times {10}^{-12}$	0	$3.27\times {10}^{-12}$	$6.66\times {10}^{-12}$
F20	−1	$3.27\times {10}^{-13}$	$9.86\times {10}^{-13}$	$4.08\times {10}^{-13}$	$1.02\times {10}^{-14}$	$6.56\times {10}^{-13}$	$2.72\times {10}^{-12}$

Table 15. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			MAO			AOA
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	$9.33\times {10}^{+01}$	$2.68\times {10}^{+02}$	$1.47\times {10}^{+02}$	$2.27$	$6.62$	$8.88$
F2	0	$3.40\times {10}^{+01}$	$6.16\times {10}^{+01}$	$1.45\times {10}^{+01}$	$9.00\times {10}^{-03}$	$3.99\times {10}^{-01}$	$2.05\times {10}^{-01}$
F3	0	$2.78\times {10}^{+02}$	$3.57\times {10}^{+02}$	$4.38\times {10}^{+01}$	$2.03\times {10}^{-35}$	$3.33\times {10}^{-10}$	$1.82\times {10}^{-09}$
F4	0	$2.59\times {10}^{+01}$	$3.59\times {10}^{+01}$	$4.45$	$1.11\times {10}^{-17}$	$2.80\times {10}^{-02}$	$2.15\times {10}^{-02}$
F5	0	$4.35\times {10}^{+20}$	$8.75\times {10}^{+25}$	$2.39\times {10}^{+26}$	$7.48\times {10}^{-46}$	$6.62\times {10}^{-08}$	$3.62\times {10}^{-07}$
F6	0	$1.26\times {10}^{+05}$	$7.67\times {10}^{+05}$	$6.73\times {10}^{+05}$	0	0	0
F7	0	$1.27\times {10}^{+01}$	$1.86\times {10}^{+01}$	$3.71$	0	0	0
F8	0	$5.66\times {10}^{+02}$	$9.44\times {10}^{+02}$	$2.35\times {10}^{+02}$	0	$2.62\times {10}^{-240}$	0
F9	−1	$9.99\times {10}^{-01}$	$9.99\times {10}^{-01}$	$1.01\times {10}^{-04}$	−1.00	$-7.34\times {10}^{-01}$	$6.91\times {10}^{-01}$
F10	0	$1.36\times {10}^{+02}$	$7.07\times {10}^{+05}$	$2.25\times {10}^{+06}$	$2.52\times {10}^{+02}$	$3.98\times {10}^{+02}$	$6.68\times {10}^{+01}$
F11	0	$1.29\times {10}^{+01}$	$1.44\times {10}^{+01}$	$8.01\times {10}^{-01}$	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0
F12	−4.59	−4.59	$-3.96$	$5.87\times {10}^{-01}$	−4.59	−4.59	$1.14\times {10}^{-05}$
F13	$0.9$	$6.83$	$8.54$	$8.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$
F14	0	$1.00$	$2.31$	$7.98\times {10}^{-01}$	$1.19\times {10}^{-07}$	$1.44\times {10}^{-04}$	$1.31\times {10}^{-04}$
F15	0	$2.00\times {10}^{+02}$	$2.38\times {10}^{+02}$	$1.49\times {10}^{+01}$	0	0	0
F16	0	$2.18\times {10}^{+03}$	$3.90\times {10}^{+03}$	$1.23\times {10}^{+03}$	$2.87\times {10}^{+01}$	$2.88\times {10}^{+01}$	$4.70\times {10}^{-02}$
F17	0	$6.91$	$8.86$	$9.47\times {10}^{-01}$	$9.99\times {10}^{-02}$	$9.99\times {10}^{-02}$	$6.56\times {10}^{-08}$
F18	0	$2.75\times {10}^{+01}$	$2.25\times {10}^{+05}$	$1.09\times {10}^{+06}$	0	0	0
F19	0	$2.06\times {10}^{-07}$	$3.66\times {10}^{-06}$	$4.38\times {10}^{-06}$	$6.21\times {10}^{-08}$	$4.46\times {10}^{-05}$	$1.16\times {10}^{-04}$
F20	−1	$1.65\times {10}^{-11}$	$8.97\times {10}^{-11}$	$7.30\times {10}^{-11}$	$1.13\times {10}^{-08}$	$9.19\times {10}^{-08}$	$6.28\times {10}^{-08}$

Table 16. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			SSOA			TSA
F	$\mathit{f\; min}$	Best	Ave	Std	Best	Ave	Std
F1	0	$1.45\times {10}^{-170}$	$7.68\times {10}^{-155}$	$4.18\times {10}^{-154}$	$4.61\times {10}^{-79}$	$4.25\times {10}^{-76}$	$6.57\times {10}^{-76}$
F2	0	0	0	0	0	$3.11\times {10}^{-03}$	$5.48\times {10}^{-03}$
F3	0	$6.92\times {10}^{-84}$	$6.63\times {10}^{-78}$	$3.31\times {10}^{-77}$	$3.38\times {10}^{-40}$	$2.07\times {10}^{-38}$	$2.36\times {10}^{-38}$
F4	0	$7.10\times {10}^{-82}$	$3.21\times {10}^{-76}$	$9.69\times {10}^{-76}$	$3.94\times {10}^{-37}$	$4.64\times {10}^{-36}$	$5.72\times {10}^{-36}$
F5	0	$6.86\times {10}^{-83}$	$2.68\times {10}^{-78}$	$9.53\times {10}^{-78}$	$7.84\times {10}^{-41}$	$2.26\times {10}^{-38}$	$2.74\times {10}^{-38}$
F6	0	0	0	0	0	0	0
F7	0	$2.75\times {10}^{-168}$	$1.05\times {10}^{-156}$	$5.72\times {10}^{-156}$	$3.56\times {10}^{-82}$	$8.62\times {10}^{-78}$	$2.69\times {10}^{-77}$
F8	0	$6.39\times {10}^{-167}$	$9.21\times {10}^{-157}$	$3.74\times {10}^{-156}$	$9.46\times {10}^{-82}$	$3.99\times {10}^{-76}$	$1.62\times {10}^{-75}$
F9	−1	$9.98\times {10}^{-01}$	$9.99\times {10}^{-01}$	$1.69\times {10}^{-04}$	$9.97\times {10}^{-01}$	$9.98\times {10}^{-01}$	$2.59\times {10}^{-04}$
F10	0	$1.39\times {10}^{-104}$	$8.76\times {10}^{-92}$	$2.42\times {10}^{-91}$	$2.31\times {10}^{-74}$	$3.94\times {10}^{-71}$	$9.39\times {10}^{-71}$
F11	0	$-4.44\times {10}^{-16}$	$-4.44\times {10}^{-16}$	0	$3.11\times {10}^{-15}$	$3.35\times {10}^{-15}$	$9.01\times {10}^{-16}$
F12	−4.59	−4.59	$-4.46$	$1.77\times {10}^{-01}$	−4.59	$-4.32$	$4.11\times {10}^{-01}$
F13	$0.9$	$9.00\times {10}^{-01}$	$9.00\times {10}^{-01}$	$4.52\times {10}^{-16}$	$4.00$	$7.48$	$1.33$
F14	0	$4.57\times {10}^{-06}$	$2.09\times {10}^{-04}$	$2.25\times {10}^{-04}$	$2.62\times {10}^{-05}$	$2.90\times {10}^{-04}$	$2.01\times {10}^{-04}$
F15	0	0	0	0	0	$1.58\times {10}^{+01}$	$4.69\times {10}^{+01}$
F16	0	$2.88\times {10}^{+01}$	$2.89\times {10}^{+01}$	$7.06\times {10}^{-02}$	$2.79\times {10}^{+01}$	$2.87\times {10}^{+01}$	$3.02\times {10}^{-01}$
F17	0	$3.20\times {10}^{-69}$	$8.63\times {10}^{-02}$	$3.96\times {10}^{-02}$	$9.99\times {10}^{-02}$	$1.10\times {10}^{-01}$	$3.05\times {10}^{-02}$
F18	0	$3.37\times {10}^{-75}$	$1.24\times {10}^{-31}$	$6.82\times {10}^{-31}$	$7.70\times {10}^{-23}$	$4.18\times {10}^{-07}$	$1.64\times {10}^{-06}$
F19	0	$1.56\times {10}^{-07}$	$2.28\times {10}^{-05}$	$2.25\times {10}^{-05}$	$2.80\times {10}^{-08}$	$7.30\times {10}^{-06}$	$1.82\times {10}^{-05}$
F20	−1	$3.99\times {10}^{-10}$	$1.84\times {10}^{-09}$	$1.24\times {10}^{-09}$	$1.99\times {10}^{-11}$	$1.18\times {10}^{-10}$	$1.34\times {10}^{-10}$

Table 17. Continuation of comparative performances of MShOA and 14 algorithms on benchmark functions.

Algorithms			CFOA
F	$\mathit{f\; min}$	Best	Ave	Std
F1	0	$2.45\times {10}^{+02}$	$3.89\times {10}^{+04}$	$1.33\times {10}^{+05}$
F2	0	$6.35\times {10}^{+01}$	$1.23\times {10}^{+02}$	$5.28\times {10}^{+01}$
F3	0	$3.15\times {10}^{+02}$	$4.98\times {10}^{+02}$	$1.06\times {10}^{+02}$
F4	0	$2.92\times {10}^{+01}$	$4.77\times {10}^{+01}$	$9.91\times {10}^{+00}$
F5	0	$5.05\times {10}^{+24}$	$6.42\times {10}^{+33}$	$2.83\times {10}^{+34}$
F6	0	$2.35\times {10}^{+05}$	$5.12\times {10}^{+07}$	$1.21\times {10}^{+08}$
F7	0	$8.95\times {10}^{+00}$	$3.36\times {10}^{+01}$	$1.45\times {10}^{+01}$
F8	0	$6.66\times {10}^{+02}$	$1.64\times {10}^{+03}$	$7.98\times {10}^{+02}$
F9	−1	$9.95\times {10}^{-01}$	$9.96\times {10}^{-01}$	$5.13\times {10}^{-04}$
F10	0	$2.73\times {10}^{+02}$	$1.01\times {10}^{+05}$	$5.46\times {10}^{+05}$
F11	0	$1.16\times {10}^{+01}$	$1.57\times {10}^{+01}$	$1.46\times {10}^{+00}$
F12	−4.59	$-4.59\times {10}^{+00}$	$-3.36\times {10}^{+00}$	$1.16\times {10}^{+00}$
F13	$0.9$	$6.40\times {10}^{+00}$	$8.54\times {10}^{+00}$	$1.23\times {10}^{+00}$
F14	0	$1.41\times {10}^{+00}$	$7.13\times {10}^{+00}$	$5.45\times {10}^{+00}$
F15	0	$1.87\times {10}^{+02}$	$2.65\times {10}^{+02}$	$4.74\times {10}^{+01}$
F16	0	$2.85\times {10}^{+03}$	$1.31\times {10}^{+04}$	$9.58\times {10}^{+03}$
F17	0	$7.40\times {10}^{+00}$	$1.20\times {10}^{+01}$	$2.76\times {10}^{+00}$
F18	0	$3.40\times {10}^{+01}$	$5.11\times {10}^{+09}$	$2.06\times {10}^{+10}$
F19	0	$1.60\times {10}^{-09}$	$3.38\times {10}^{-07}$	$6.10\times {10}^{-07}$
F20	−1	$5.66\times {10}^{-11}$	$5.60\times {10}^{-10}$	$8.06\times {10}^{-10}$

Three stages of nonparametric Wilcoxon signed-rank tests, at a 5% significance level, and Friedman tests determined the algorithms’ performances. In stage 1, 10 unimodal functions were analyzed, whereas in stage 2, 10 multimodal functions were studied. The unimodal and multimodal functions evaluated the algorithms’ capabilities in exploitation and exploration in the solution space, respectively. In stage 3, the set of 20 previously used functions—unimodal and multimodal—was analyzed with the Wilcoxon and Friedman statistical tests; see Table A1 and Table A2. The Wilcoxon test assessed whether MShOA exhibited statistically superior performance; a p-value below 0.05 signified that MShOA outperformed the algorithm under comparison. The Friedman test evaluated algorithms by ranking them according to their average performance and benchmark scores.

In stage 1, according to the Wilcoxon test (see Table 18), the MShOA algorithm was better than all the others in local searches. The results of the Friedman test (see Table 19) show that MShOA ranked first among the analyzed algorithms. Figure 13 presents the convergence curves for each unimodal function.

Table 18. Statistical analysis of the Wilcoxon signed-rank test comparing MShOA with other algorithms for 10 unimodal functions using a 5% significance level.

MShOA–GWO		MShOA–BWO		MShOA–DO
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$	(7/3/0)	$\mathbf{1}.\mathbf{80}\times {\mathbf{10}}^{-\mathbf{02}}$	(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$
MShOA–WOA		MShOA–MPA		MShOA–LCA
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(9/1/0)	$\mathbf{7}.\mathbf{69}\times {\mathbf{10}}^{-\mathbf{03}}$	(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$	(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$
MShOA–SSA		MShOA–EMA		MShOA–ALO
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$	(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$	(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$
MShOA–MAO		MShOA–AOA		MShOA–SSOA
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$	(8/2/0)	$\mathbf{1}.\mathbf{17}\times {\mathbf{10}}^{-\mathbf{02}}$	(8/2/0)	$\mathbf{1}.\mathbf{17}\times {\mathbf{10}}^{-\mathbf{02}}$
		MShOA–TSA		MShOA–CFOA
		(+/=/−)	p-Value	(+/=/−)	p-Value
		(9/1/0)	$\mathbf{7}.\mathbf{69}\times {\mathbf{10}}^{-\mathbf{03}}$	(10/0/0)	$\mathbf{5}.\mathbf{06}\times {\mathbf{10}}^{-\mathbf{03}}$

The bold numbers in this table indicate a significant difference between the two compared algorithms, where MShOA demonstrated a superior performance.

Table 19. Performance comparison on 10 unimodal functions by Friedman test.

Algorithm	MShOA	GWO	BWO	DO	WOA
Mean of ranks	$\mathbf{1}.\mathbf{45}$	$7.20$	$\mathbf{2}.\mathbf{90}$	$9.15$	$6.90$
Global ranking	$\mathbf{1}$	8	$\mathbf{2}$	10	7
Algorithm	MPA	LCA	SSA	EMA	ALO
Mean of ranks	$6.80$	$8.70$	$11.15$	$10.80$	$11.50$
Global ranking	6	9	12	11	13
Algorithm	MAO	AOA	SSOA	TSA	CFOA
Mean of ranks	$13.95$	$6.45$	$\mathbf{3}.\mathbf{65}$	$\mathbf{5}.\mathbf{10}$	$14.30$
Global ranking	14	5	$\mathbf{3}$	$\mathbf{4}$	15

The five algorithms with the best overall performance according to the Friedman test are highlighted in bold.

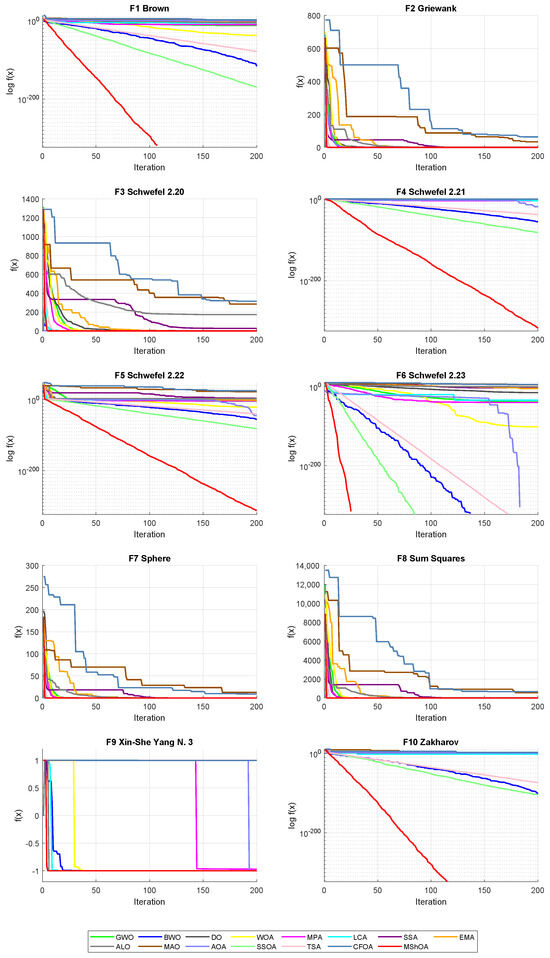
Figure 13. Convergence curves of 10 unimodal functions.

In stage 2, the algorithms’ performances were evaluated with 10 multimodal functions; see Table A1. The Wilcoxon test results (see Table 20) indicate that MShOA outperformed SSA, EMA, ALO, MAO, and CFOA; meanwhile, they also demonstrate competitive results compared with GWO, BWO, DO, WOA, MPA, LCA, AOA, SSOA, and TSA. The Friedman test results (see Table 21) indicate that the BWO algorithm ranked first. In the global search, MShOA demonstrated a competitive performance by ranking in second place. Figure 14 presents the convergence curves for each multimodal function.

Table 20. Statistical analysis of the Wilcoxon signed-rank test comparing MShOA with other algorithms for 10 multimodal functions using a 5% significance level.

MShOA–GWO		MShOA–BWO		MShOA–DO
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(7/0/3)	$3.86\times {10}^{-01}$	(3/4/3)	$4.63\times {10}^{-01}$	(7/0/3)	$3.33\times {10}^{-01}$
MShOA–WOA		MShOA–MPA		MShOA–LCA
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(7/0/3)	$3.33\times {10}^{-01}$	(7/0/3)	$5.08\times {10}^{-01}$	(7/0/3)	$3.86\times {10}^{-01}$
MShOA–SSA		MShOA–EMA		MShOA–ALO
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(8/0/2)	$\mathbf{2}.\mathbf{84}\times {\mathbf{10}}^{-\mathbf{02}}$	(8/0/2)	$\mathbf{4}.\mathbf{69}\times {\mathbf{10}}^{-\mathbf{02}}$	(8/0/2)	$\mathbf{2}.\mathbf{84}\times {\mathbf{10}}^{-\mathbf{02}}$
MShOA–MAO		MShOA–AOA		MShOA–SSOA
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(8/0/2)	$\mathbf{1}.\mathbf{66}\times {\mathbf{10}}^{-\mathbf{02}}$	(3/3/4)	$8.66\times {10}^{-01}$	(4/3/3)	$8.66\times {10}^{-01}$
		MShOA–TSA		MShOA–CFOA
		(+/=/−)	p-Value	(+/=/−)	p-Value
		(7/0/3)	$2.85\times {10}^{-01}$	(8/0/2)	$\mathbf{1}.\mathbf{25}\times {\mathbf{10}}^{-\mathbf{02}}$

The bold numbers in this table indicate a significant difference between the two compared algorithms, where MShOA demonstrated a superior performance.

Table 21. Performance comparison on 10 multimodal functions by Friedman test.

Algorithm	MShOA	GWO	BWO	DO	WOA
Mean of ranks	$\mathbf{5}.\mathbf{30}$	$7.40$	$\mathbf{3}.\mathbf{10}$	$7.90$	$6.50$
Global ranking	$\mathbf{2}$	8	$\mathbf{1}$	9	6
Algorithm	MPA	LCA	SSA	EMA	ALO
Mean of ranks	$\mathbf{5}.\mathbf{90}$	$7.10$	$9.90$	$9.55$	$9.80$
Global ranking	$\mathbf{4}$	7	13	11	12
Algorithm	MAO	AOA	SSOA	TSA	CFOA
Mean of ranks	$13.20$	$\mathbf{5}.\mathbf{55}$	$6.25$	$8.45$	$14.10$
Global ranking	14	$\mathbf{3}$	5	10	15

The four algorithms with the best overall performance according to the Friedman test are highlighted in bold.

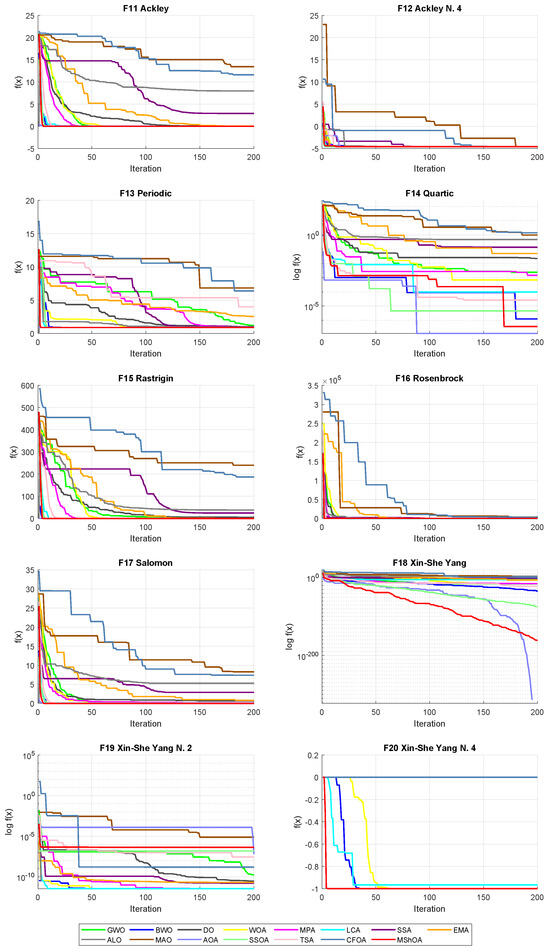
Figure 14. Convergence curves of 10 multimodal functions.

In stage 3, the set of 20 previously used functions—unimodal and multimodal—was analyzed with the Wilcoxon and Friedman statistical tests; see Table A1. The Wilcoxon test results, shown in Table 22, indicate that MShOA outperformed the following optimization algorithms: ALO, DO, EMA, GWO, LCA, MAO, MPA, SSA, TSA, and WOA. However, no significant differences were observed with BWO, AOA, and SSOA. The Friedman test analysis (see Table 23) shows that BWO ranked first, MShOA ranked second, and SSOA and AOA ranked third and fourth, respectively.

Table 22. Statistical analysis of the Wilcoxon signed-rank test comparing MShOA with other algorithms for 20 functions using a 5% significance level.

MShOA–GWO		MShOA–BWO		MShOA–DO
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(17/0/3)	$\mathbf{1}.\mathbf{69}\times {\mathbf{10}}^{-\mathbf{02}}$	(10/7/3)	$4.63\times {10}^{-01}$	(17/0/3)	$\mathbf{5}.\mathbf{73}\times {\mathbf{10}}^{-\mathbf{03}}$
MShOA–WOA		MShOA–MPA		MShOA–LCA
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(16/1/3)	$\mathbf{2}.\mathbf{18}\times {\mathbf{10}}^{-\mathbf{02}}$	(17/0/3)	$\mathbf{2}.\mathbf{76}\times {\mathbf{10}}^{-\mathbf{02}}$	(17/0/3)	$\mathbf{1}.\mathbf{11}\times {\mathbf{10}}^{-\mathbf{02}}$
MShOA–SSA		MShOA–EMA		MShOA–ALO
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(18/0/2)	$\mathbf{2}.\mathbf{93}\times {\mathbf{10}}^{-\mathbf{04}}$	(18/0/2)	$\mathbf{6}.\mathbf{81}\times {\mathbf{10}}^{-\mathbf{04}}$	(18/0/2)	$\mathbf{2}.\mathbf{93}\times {\mathbf{10}}^{-\mathbf{04}}$
MShOA–MAO		MShOA–AOA		MShOA–SSOA
(+/=/−)	p-Value	(+/=/−)	p-Value	(+/=/−)	p-Value
(18/0/2)	$\mathbf{1}.\mathbf{63}\times {\mathbf{10}}^{-\mathbf{04}}$	(11/5/4)	$7.83\times {10}^{-02}$	(12/5/3)	$1.40\times {10}^{-01}$
		MShOA–TSA		MShOA–TSA
		(+/=/−)	p-Value	(+/=/−)	p-Value
		(16/1/3)	$\mathbf{2}.\mathbf{69}\times {\mathbf{10}}^{-\mathbf{02}}$	(18/0/2)	$\mathbf{1}.\mathbf{40}\times {\mathbf{10}}^{-\mathbf{04}}$

The bold values in this table indicate a significant difference between the two compared algorithms, where MShOA demonstrated a superior performance.

Table 23. Performance comparison of algorithms on 20 unimodal and multimodal functions by Friedman test.

Algorithm	MShOA	GWO	BWO	DO	WOA
Mean of ranks	$\mathbf{3}.\mathbf{38}$	$7.30$	$\mathbf{3}.\mathbf{00}$	$8.53$	$6.70$
Global ranking	$\mathbf{2}$	8	$\mathbf{1}$	10	6
Algorithm	MPA	LCA	SSA	EMA	ALO
Mean of ranks	$6.35$	$7.90$	$10.53$	$10.18$	$10.65$
Global ranking	5	9	12	11	13
Algorithm	MAO	AOA	SSOA	TSA	CFOA
Mean of ranks	$13.58$	$\mathbf{6}.\mathbf{00}$	$\mathbf{4}.\mathbf{95}$	$6.78$	$14.20$
Global ranking	14	$\mathbf{4}$	$\mathbf{3}$	7	15

The four algorithms with the best overall performance according to the Friedman test are highlighted in bold.

5. Real-World Applications

The performance of MShOA was evaluated by solving 10 optimization problems from CEC 2020 [72]. These problems are presented in Table 24 and described in Section 5.2, Section 5.3, Section 5.4, Section 5.5, Section 5.6, Section 5.7, Section 5.8, Section 5.9, Section 5.10 and Section 5.11. In addition, MShOA was tested on three different cases of the optimal power flow problem for the IEEE bus 30 configuration. These cases were fuel cost, active power, and reactive power. The results for each of these engineering problems were obtained with MShOA and the top three algorithms ranked according to the Friedman test: BWO, SSOA, and AOA; see Table 23. The results for each real-world optimization problem described in Table 24 are summarized in table form to include the decision variables and the feasible objective function value found, as can be seen in Table 25, Table 26, Table 27, Table 28, Table 29, Table 30, Table 31, Table 32, Table 33 and Table 34. The constraint-handling method used on each of the real-world optimization problems is described in Section 5.1.

Table 24. Real-world optimization problems from the CEC2020 benchmark, where D is the problem dimension, g is the number of inequality constraints, h is the number of equality constraints, and f(${\overline{x}}^{*}$) is the best-known feasible objective function value.

Prob	Name	D	g	h	f(${\overline{\mathit{x}}}^{*}$)
CEC20-RC08	Process synthesis problem	2	2	0	$2.0000000000$
CEC20-RC09	Process synthesis and design problem	3	1	1	$2.5576545740$
CEC20-RC10	Process flow sheeting problem	3	3	0	$1.0765430833$
CEC20-RC15	Weight minimization of a speed reducer	7	11	0	$2.9944244658\times {10}^{+03}$
CEC20-RC17	Tension/compression spring design (case 1)	3	3	0	$1.2665232788\times {10}^{-02}$
CEC20-RC19	Welded beam design	4	5	0	$1.6702177263$
CEC20-RC21	Multiple disk clutch brake design problem	5	8	0	$2.3524245790\times {10}^{-01}$
CEC20-RC22	Planetary gear train design optimization problem	9	10	1	$5.2576870748\times {10}^{-01}$
CEC20-RC30	Tension/compression spring design (case 2)	3	8	0	$2.6138840583$
CEC20-RC32	Himmelblau’s function	5	6	0	$-3.0665538672\times {10}^{+04}$

Table 25. Results of the process synthesis problem.

Algorithms	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{f}}_{\mathit{min}}$
BWO	$5.00\times {10}^{-01}$	$0.149\times {10}^{-01}$	$0.200\times {10}^{-01}$
MShOA	$5.00\times {10}^{-01}$	$9.37\times {10}^{-01}$	$\mathbf{0}.\mathbf{200}\times {\mathbf{10}}^{-\mathbf{01}}$
SSOA	0	$8.94\times {10}^{-01}$	$0.201\times {10}^{-01}$ *
AOA	$4.98\times {10}^{-01}$	$9.24\times {10}^{-01}$	$0.200\times {10}^{-01}$ *

* This solution does not satisfy one or more constraints.

Table 26. Comparison results of the process synthesis and design problem.

Algorithms	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{f}}_{\mathit{min}}$
BWO	$8.60\times {10}^{-01}$	$8.44\times {10}^{-01}$	$-1.09\times {10}^{-01}$	$0.257\times {10}^{-01}$ *
MShOA	$8.53\times {10}^{-01}$	$8.52\times {10}^{-01}$	$-8.45\times {10}^{-02}$	$\mathbf{0}.\mathbf{256}\times {\mathbf{10}}^{-\mathbf{01}}$
SSOA	$9.03\times {10}^{-01}$	$7.93\times {10}^{-01}$	$-3.65\times {10}^{-01}$	$0.261\times {10}^{-01}$ *
AOA	$8.62\times {10}^{-01}$	$8.41\times {10}^{-01}$	$-2.95\times {10}^{-04}$	$0.257\times {10}^{-01}$ *

* This solution does not satisfy one or more constraints.

Table 27. Comparison results of the process flow sheeting problem.

Algorithms	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{f}}_{\mathit{min}}$
BWO	$9.48\times {10}^{-01}$	$-0.209\times {10}^{-01}$	$6.11\times {10}^{-01}$	$0.118\times {10}^{-01}$ *
MShOA	$9.43\times {10}^{-01}$	$-0.210\times {10}^{-01}$	$8.50\times {10}^{-01}$	$\mathbf{0}.\mathbf{108}\times {\mathbf{10}}^{-\mathbf{01}}$
SSOA	$9.67\times {10}^{-01}$	$-0.211\times {10}^{-01}$	$0.142\times {10}^{-01}$	$0.119\times {10}^{-01}$
AOA	$9.38\times {10}^{-01}$	$-0.209\times {10}^{-01}$	$0.149\times {10}^{-01}$	$0.114\times {10}^{-01}$ *

* This solution does not satisfy one or more constraints.

Table 28. Comparison results of the weight minimization of a speed reducer.

Parameters	BWO	MShOA	SSOA	AOA
$x_1$	$0.354\times {10}^{-01}$	$0.350\times {10}^{-01}$	$0.358\times {10}^{-01}$	$0.360\times {10}^{-01}$
$x_2$	$7.00\times {10}^{-01}$	$7.00\times {10}^{-01}$	$7.13\times {10}^{-01}$	$7.00\times {10}^{-01}$
$x_3$	$1.70\times {10}^{+01}$	$1.72\times {10}^{+01}$	$2.56\times {10}^{+01}$	$1.70\times {10}^{+01}$
$x_4$	$0.790\times {10}^{-01}$	$0.734\times {10}^{-01}$	$0.766\times {10}^{-01}$	$0.730\times {10}^{-01}$
$x_5$	$0.815\times {10}^{-01}$	$0.796\times {10}^{-01}$	$0.777\times {10}^{-01}$	$0.830\times {10}^{-01}$
$x_6$	$0.340\times {10}^{-01}$	$0.339\times {10}^{-01}$	$0.385\times {10}^{-01}$	$0.350\times {10}^{-01}$
$x_7$	$0.529\times {10}^{-01}$	$0.534\times {10}^{-01}$	$0.532\times {10}^{-01}$	$0.531\times {10}^{-01}$
$f_{min}$	$\mathbf{3}.\mathbf{04}\times {\mathbf{10}}^{+\mathbf{03}}$	$3.08\times {10}^{+03}$	$6.04\times {10}^{+03}$ *	$3.10\times {10}^{+03}$

* This solution does not satisfy one or more constraints.

Table 29. Comparison results of the tension/compression spring design (case 1).

Algorithms	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{f}}_{\mathit{min}}$
BWO	$5.00\times {10}^{-02}$	$3.17\times {10}^{-01}$	$1.41\times {10}^{+01}$	$\mathbf{1}.\mathbf{27}\times {\mathbf{10}}^{-\mathbf{02}}$
MShOA	$5.43\times {10}^{-02}$	$4.23\times {10}^{-01}$	$0.827\times {10}^{-01}$	$1.28\times {10}^{-02}$
SSOA	$6.17\times {10}^{-02}$	$7.09\times {10}^{-01}$	$0.351\times {10}^{-01}$	$2.68\times {10}^{-02}$ *
AOA	$5.00\times {10}^{-02}$	$3.11\times {10}^{-01}$	$1.50\times {10}^{+01}$	$1.32\times {10}^{-02}$

* This solution does not satisfy one or more constraints.

Table 30. Comparison results of the welded beam design.

Algorithms	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{f}}_{\mathit{min}}$
BWO	$2.40\times {10}^{-01}$	$0.280\times {10}^{-01}$	$0.959\times {10}^{-01}$	$2.00\times {10}^{-01}$	$0.178\times {10}^{-01}$ *
MShOA	$1.89\times {10}^{-01}$	$0.394\times {10}^{-01}$	$0.917\times {10}^{-01}$	$2.00\times {10}^{-01}$	$\mathbf{0}.\mathbf{174}\times {\mathbf{10}}^{-\mathbf{01}}$
SSOA	$2.58\times {10}^{-01}$	$0.383\times {10}^{-01}$	$0.763\times {10}^{-01}$	$3.74\times {10}^{-01}$	$0.273\times {10}^{-01}$ *
AOA	$1.25\times {10}^{-01}$	$0.604\times {10}^{-01}$	$1.00\times {10}^{+01}$	$1.96\times {10}^{-01}$	$0.199\times {10}^{-01}$

* This solution does not satisfy one or more constraints.

Table 31. Comparison results of the multiple disk clutch brake design problem.

Variables	BWO	MShOA	SSOA	AOA
$x_1$	$7.00\times {10}^{+01}$	$7.01\times {10}^{+01}$	$6.61\times {10}^{+01}$	$7.00\times {10}^{+01}$
$x_2$	$9.00\times {10}^{+01}$	$9.01\times {10}^{+01}$	$9.00\times {10}^{+01}$	$9.00\times {10}^{+01}$
$x_3$	$0.10\times {10}^{-01}$	$0.10\times {10}^{-01}$	$0.10\times {10}^{-01}$	$0.10\times {10}^{-01}$
$x_4$	$7.71\times {10}^{+01}$	$2.04\times {10}^{+02}$	$0.415\times {10}^{-01}$	$1.00\times {10}^{+03}$
$x_5$	$0.20\times {10}^{-01}$	$0.20\times {10}^{-01}$	$0.20\times {10}^{-01}$	$0.20\times {10}^{-01}$
$f_{min}$	$\mathbf{2}.\mathbf{35}\times {\mathbf{10}}^{-\mathbf{01}}$ *	$2.36\times {10}^{-01}$	$2.74\times {10}^{-01}$ *	$2.35\times {10}^{-01}$ *

* This solution does not satisfy one or more constraints.

Table 32. Comparison results of the planetary gear train design optimization problem (transposed).

Variables	BWO	MShOA	SSOA	AOA
$x_1$	$2.44\times {10}^{+01}$	$4.53\times {10}^{+01}$	$2.40\times {10}^{+01}$	$2.27\times {10}^{+01}$
$x_2$	$1.35\times {10}^{+01}$	$3.05\times {10}^{+01}$	$1.35\times {10}^{+01}$	$1.35\times {10}^{+01}$
$x_3$	$1.35\times {10}^{+01}$	$2.42\times {10}^{+01}$	$1.35\times {10}^{+01}$	$1.35\times {10}^{+01}$
$x_4$	$1.65\times {10}^{+01}$	$2.48\times {10}^{+01}$	$1.65\times {10}^{+01}$	$1.65\times {10}^{+01}$
$x_5$	$1.35\times {10}^{+01}$	$1.82\times {10}^{+01}$	$1.35\times {10}^{+01}$	$1.35\times {10}^{+01}$
$x_6$	$5.57\times {10}^{+01}$	$9.11\times {10}^{+01}$	$5.87\times {10}^{+01}$	$5.81\times {10}^{+01}$
$x_7$	$5.10\times {10}^{-01}$	$9.06\times {10}^{-01}$	$5.10\times {10}^{-01}$	$0.105\times {10}^{-01}$
$x_8$	$0.207\times {10}^{-01}$	$0.101\times {10}^{-01}$	$5.10\times {10}^{-01}$	$0.649\times {10}^{-01}$
$x_9$	$5.10\times {10}^{-01}$	$0.164\times {10}^{-01}$	$6.15\times {10}^{-01}$	$0.371\times {10}^{-01}$
$f_{min}$	$7.77\times {10}^{-01}$	$\mathbf{5}.\mathbf{30}\times {\mathbf{10}}^{-\mathbf{01}}$	$8.70\times {10}^{-01}$ *	$6.66\times {10}^{-01}$ *

* This solution does not satisfy one or more constraints.

Table 33. Comparison results of the tension/compression spring design (case 2).

Algorithms	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{f}}_{\mathit{min}}$
BWO	$1.05\times {10}^{+01}$	$0.116\times {10}^{-01}$	$3.55\times {10}^{+01}$	$0.299\times {10}^{-01}$
MShOA	$0.548\times {10}^{-01}$	$0.166\times {10}^{-01}$	$3.69\times {10}^{+01}$	$\mathbf{0}.\mathbf{270}\times {\mathbf{10}}^{-\mathbf{01}}$
SSOA	$0.631\times {10}^{-01}$	$0.163\times {10}^{-01}$	$3.73\times {10}^{+01}$	$0.304\times {10}^{-01}$
AOA	$1.72\times {10}^{+01}$	$8.98\times {10}^{-01}$	$3.45\times {10}^{+01}$	$0.291\times {10}^{-01}$

Table 34. Comparison results of Himmelblau’s function.

Variables	BWO	MShOA	SSOA	AOA
$x_1$	$7.80\times {10}^{+01}$	$7.87\times {10}^{+01}$	$8.33\times {10}^{+01}$	$7.80\times {10}^{+01}$
$x_2$	$3.30\times {10}^{+01}$	$3.44\times {10}^{+01}$	$3.67\times {10}^{+01}$	$3.36\times {10}^{+01}$
$x_3$	$3.01\times {10}^{+01}$	$3.08\times {10}^{+01}$	$3.25\times {10}^{+01}$	$3.07\times {10}^{+01}$
$x_4$	$4.50\times {10}^{+01}$	$4.40\times {10}^{+01}$	$3.79\times {10}^{+01}$	$4.50\times {10}^{+01}$
$x_5$	$3.65\times {10}^{+01}$	$3.50\times {10}^{+01}$	$3.43\times {10}^{+01}$	$3.42\times {10}^{+01}$
$f_{min}$	$-\mathbf{3}.\mathbf{06}\times {\mathbf{10}}^{+\mathbf{04}}$ *	$-3.05\times {10}^{+04}$	$-2.96\times {10}^{+04}$ *	$-3.02\times {10}^{+04}$ *

* This solution does not satisfy one or more constraints.

5.1. Constraint Handling

The penalization method taken from [39], which is applied to engineering problems with constraints, is presented in Equation (19):

$$F\left(\overrightarrow{x}\right)=\left\{\begin{array}{ccc}f\left(\overrightarrow{x}\right),& if& MCV\left(\overrightarrow{x}\right)\le 0\\ f_{\max }+MCV\left(\overrightarrow{x}\right),& & otherwise.\end{array}\right.$$

(19)

where $f\left(\overrightarrow{x}\right)$ is the fitness function value of a viable solution (i.e., a solution that satisfies all the constraints). In other matters, $f_{max}$ represents the fitness function value of the worst solution in the population, and $MCV\left(\overrightarrow{x}\right)$ is the Mean Constraint Violation [39] represented in Equation (20):

$$MCV\left(\overrightarrow{x}\right)={\displaystyle \frac{{\displaystyle \sum _{i=1}^p}{G}_i\left(\overrightarrow{x}\right)+{\displaystyle \sum _{j=1}^m}{H}_j\left(\overrightarrow{x}\right)}{p+m}}$$

(20)

In this case, $MCV\left(\overrightarrow{x}\right)$ represents the average sum of the inequality constraints ($G_i\left(\overrightarrow{x}\right)$) and the equality constraints ($H_j\left(\overrightarrow{x}\right)$), as shown in Equations (21) and (22), respectively. It is important to note that the inequality constraints $g_i\left(\overrightarrow{x}\right)$ and the equality constraints $h_j\left(\overrightarrow{x}\right)$ only have single value, which is the penalty applied when the constraint is violated.

$$G_i\left(\overrightarrow{x}\right)=\left\{\begin{array}{ccc}0,& if& g_i\left(\overrightarrow{x}\right)\le 0\\ g_i\left(\overrightarrow{x}\right),& & otherwise.\end{array}\right.$$

(21)

$$H_j\left(\overrightarrow{x}\right)=\left\{\begin{array}{cc}0,\hfill & if|h_j\left(\overrightarrow{x}\right)|-\delta \le 0\hfill \\ \left|h_j\left(\overrightarrow{x}\right)\right|,\hfill & otherwise\hfill \end{array}\right.$$

(22)

5.2. Process Synthesis Problem

The process synthesis problem includes two decision variables and two inequality constraints. The mathematical representation of the problem is shown in Equation (23). The best-known feasible objective value taken from Table 24 is 2.

$$\begin{array}{cc}Minimize\hfill & f\left(\overline{x}\right)=x_2+2x_1\hfill \\ \\ Subject\mathrm{to}\hfill & g_1\left(\overline{x}\right)=-x_1^2-x_2+1.25\le 0\hfill \\ & g_2\left(\overline{x}\right)=x_1+x_2\le 1.6\hfill \\ \\ with\mathrm{bounds}:\hfill & 0\le x_1\le 1.6\hfill \\ & x_2\in \{0,1\}\hfill \end{array}$$

(23)

Table 25 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, SSOA and AOA did not satisfy one or more problem constraints. MShOA’s difference from the best-known feasible objective function value was $7.2546608720\times {10}^{-09}$. The convergence graph is shown in Figure 15.

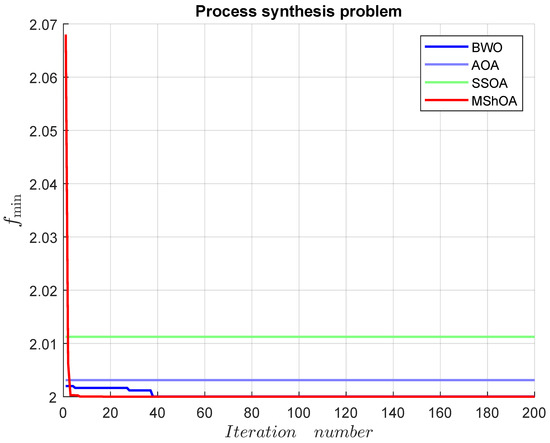
Figure 15. Convergence graph of the process synthesis problem.

5.3. Process Synthesis and Design Problem

The process synthesis and design problem included three decision variables, one inequality, and one equality constraint. The mathematical representation of the problem is shown in Equation (24). The best-known feasible objective value taken from Table 24 is $2.5576545740$.

$$\begin{array}{cc}Minimize\hfill & f\left(\overline{x}\right)=-x_3+x_2+2x_1\hfill \\ \\ Subject\mathrm{to}:\hfill & h_1\left(\overline{x}\right)=-2\exp (-x_2)+x_1=0\hfill \\ & g_1\left(\overline{x}\right)=x_2-x_1+x_3\le 0\hfill \\ \\ with\mathrm{bounds}:\hfill & 0.5\le x_1,x_2\le 1.4\hfill \\ & x_3\in \{0,1\}\hfill \end{array}$$

(24)

Table 26 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. However, only the results of MShOA did not violate any problem constraints. MShOA’s difference from the best-known feasible objective function value was $1.8912987813\times {10}^{-04}$. The convergence graph is shown in Figure 16.

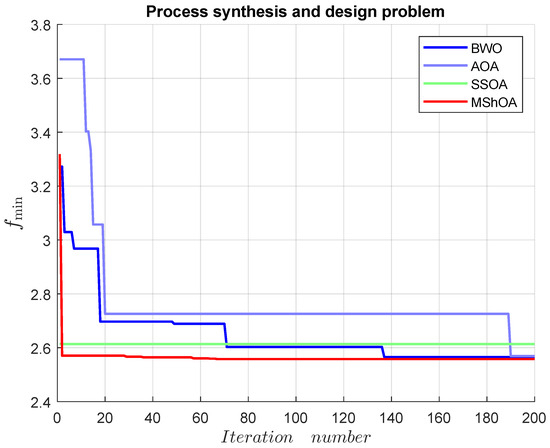
Figure 16. Convergence graph of the process synthesis and design problem.

5.4. Process Flow Sheeting Problem

The process flow sheeting problem includes three decision variables and three inequality constraints. The mathematical representation of the problem is shown in Equation (25). The best-known feasible objective value from Table 24 is $1.0765430833$.

$$\begin{array}{cc}Minimize\hfill & f\left(\overline{x}\right)=-0.7x_3+0.8+5{(0.5-x_1)}^2\hfill \\ \\ Subject\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=-\exp (x_1-0.2)-x_2\le 0\hfill \\ & g_2\left(\overline{x}\right)=x_2+1.1x_3\le -1.0\hfill \\ & g_3\left(\overline{x}\right)=x_1-x_3\le 0.2\hfill \\ \\ with\mathrm{bounds}:\hfill & -2.22554\le x_2\le -1\hfill \\ & 0.2\le x_1\le 1\hfill \\ & x_3\in \{0,1\}\hfill \end{array}$$

(25)

Table 27 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, BWO and AOA did not satisfy one or more problem constraints. MShOA’s difference from the best-known feasible objective function value was $3.4569167\times {10}^{-03}$. The convergence graph is shown in Figure 17.

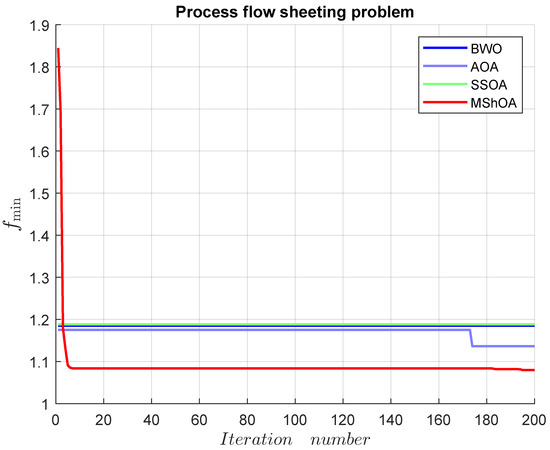
Figure 17. Convergence graph of the process flow sheeting problem.

5.5. Weight Minimization of a Speed Reducer

The weight minimization of a speed reducer includes seven decision variables and eleven inequality constraints. The mathematical representation of the problem is shown in Equation (26). The best-known feasible objective value taken from Table 24 is $2.9944244658\times {10}^{+03}$.

$$\begin{array}{cc}Minimize\hfill & f\left(\overline{x}\right)=0.7854x_2^2{x}_1\left(14.9334x_3-43.0934+3.3333x_3^2\right)\hfill \\ & +0.7854(x_5{x}_7^2+x_4{x}_6^2)-1.508x_1(x_7^2+x_8^2)+7.477(x_7^3+x_6^3)\hfill \\ \\ Subject\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=-x_1{x}_2^2{x}_3+27\le 0\hfill \\ & g_2\left(\overline{x}\right)=-x_1{x}_2^2{x}_3^2+397.5\le 0\hfill \\ & g_3\left(\overline{x}\right)=-x_2{x}_6^4{x}_3{x}_4^{-3}+1.93\le 0\hfill \\ & g_4\left(\overline{x}\right)=-x_2{x}_7^4{x}_3{x}_5^{-3}+1.93\le 0\hfill \\ & g_5\left(\overline{x}\right)=10x_6^{-3}\sqrt{16.91\times {10}^6+{\left(745x_4{x}_2^{-1}{x}_3^{-1}\right)}^2}-1100\le 0\hfill \\ & g_6\left(\overline{x}\right)=10x_7^{-3}\sqrt{157.5\times {10}^6+{\left(745x_5{x}_2^{-1}{x}_3^{-1}\right)}^2}-850\le 0\hfill \\ & g_7\left(\overline{x}\right)=x_2{x}_3-40\le 0\hfill \\ & g_8\left(\overline{x}\right)=-x_1{x}_2^{-1}+5\le 0\hfill \\ & g_9\left(\overline{x}\right)=x_1{x}_2^{-1}-12\le 0\hfill \\ & g_{10}\left(\overline{x}\right)=1.5x_6-x_4+1.9\le 0\hfill \\ & g_{11}\left(\overline{x}\right)=1.1x_7-x_5+1.9\le 0\hfill \\ \\ with\mathrm{bounds}:\hfill & 0.7\le x_2\le 0.8,17\le x_3\le 28,2.6\le x_1\le 3.6,\hfill \\ & 5\le x_7\le 5.5,7.3\le x_5,x_4\le 8.3,2.9\le x_6\le 3.9.\hfill \end{array}$$

(26)

Table 28 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, SSOA did not satisfy one or more problem constraints. MShOA’s difference from the best-known feasible objective function value was $8.3485313744\times {10}^{+1}$. The convergence graph is shown in Figure 18.

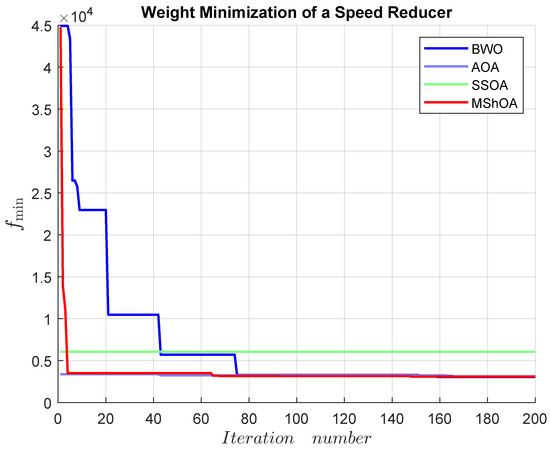
Figure 18. Convergence graph of the weight minimization of a speed reducer.

5.6. Tension/Compression Spring Design (Case 1)

The tension/compression spring design (case 1) problem includes three decision variables and four inequality constraints. The mathematical representation of the problem is shown in Equation (27). The best-known feasible objective value taken from Table 24 is $1.2665232788\times {10}^{-02}$.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & f\left(\overline{x}\right)=x_1^2{x}_2(2+x_3)\hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=1-{\displaystyle \frac{x_2^3{x}_3}{71785x_1^4}}\le 0,\hfill \\ \hfill & g_2\left(\overline{x}\right)={\displaystyle \frac{4x_2^2-x_1{x}_2}{12566(x_2{x}_1^3-x_1^4)}}+{\displaystyle \frac{1}{5108x_1^2}}-1\le 0,\hfill \\ \hfill & g_3\left(\overline{x}\right)=1-{\displaystyle \frac{140.45x_1}{x_2{x}_3}}\le 0,\hfill \\ \hfill & g_4\left(\overline{x}\right)={\displaystyle \frac{x_1+x_2}{1.5}}-1\le 0,\hfill \\ \\ \mathrm{With}\mathrm{bounds}:\hfill & 0.05\le x_1\le 2.00,\hfill \\ \hfill & 0.25\le x_2\le 1.30,\hfill \\ \hfill & 2.00\le x_3\le 15.00.\hfill \end{array}$$

(27)

Table 29 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, SSOA did not satisfy one or more problem constraints. MShOA’s difference from the best-known feasible objective function value was $1.3085251562\times {10}^{-04}$. The convergence graph is shown in Figure 19.

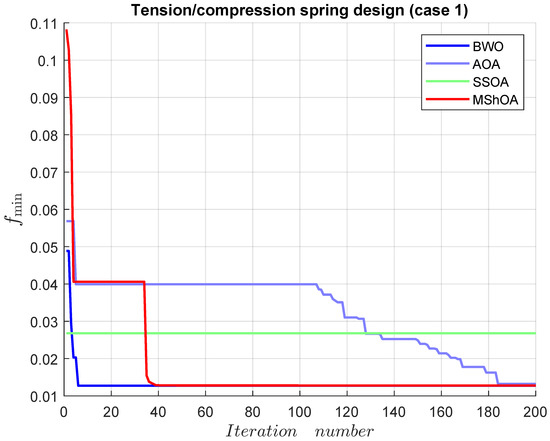
Figure 19. Convergence graph of the tension/compression spring design (case 1).

5.7. Welded Beam Design

The welded beam design includes four decision variables and five inequality constraints. The mathematical representation of the problem is shown in Equation (28). The best-known feasible objective value from Table 24 is $1.6702177263$.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & f\left(\overline{x}\right)=0.04811x_3{x}_4(x_2+14)+1.10471x_1^2{x}_2,\hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=x_1-x_4\le 0\hfill \\ \hfill & g_2\left(\overline{x}\right)=\delta \left(\overline{x}\right)-{\delta }_{\max }\le 0\hfill \\ \hfill & g_3\left(\overline{x}\right)=P\le P_c\left(\overline{x}\right)\hfill \\ \hfill & g_4\left(\overline{x}\right)={\tau }_{\max }\ge \tau \left(\overline{x}\right)\hfill \\ \hfill & g_5\left(\overline{x}\right)=\sigma \left(\overline{x}\right)-{\sigma }_{\max }\le 0\hfill \\ \\ \mathrm{Where}:\hfill & \tau =\sqrt{{\tau }^{\prime 2}+{\tau }^{″2}+2{\tau }^{\prime }{\tau }^{″}{\displaystyle \frac{x_2}{2R}}},{\tau }^{″}={\displaystyle \frac{RM}{J}},{\tau }^{\prime }={\displaystyle \frac{P}{\sqrt{2}{x}_2{x}_1}},\hfill \\ \hfill & M=P\left({\displaystyle \frac{x_2}{2}}+L\right),R=\sqrt{{\displaystyle \frac{x_2^2}{4}}+{\left({\displaystyle \frac{x_1+x_3}{2}}\right)}^2},J=2\left(\left({\displaystyle \frac{x_2^2}{4}}+{\left({\displaystyle \frac{x_1+x_3}{2}}\right)}^2\right)\sqrt{2}{x}_1{x}_2\right),\hfill \\ \hfill & \sigma \left(\overline{x}\right)={\displaystyle \frac{6PL}{x_4{x}_3^2}},\delta \left(\overline{x}\right)={\displaystyle \frac{6P{L}^3}{E{x}_3^2{x}_4}},P_c\left(\overline{x}\right)={\displaystyle \frac{4.013E{x}_3{x}_4^3}{6L^2}}\left(1-{\displaystyle \frac{x_3}{2L}}\sqrt{{\displaystyle \frac{E}{4G}}}\right),\hfill \\ \\ \mathrm{Constants}:\hfill & L=14\mathrm{in},P=6000\mathrm{lb},E=30\times {10}^6\mathrm{psi},{\sigma }_{\max }=30,000\mathrm{psi},\hfill \\ \hfill & {\tau }_{\max }=13,600\mathrm{psi},G=12.10\times {10}^6\mathrm{psi},{\delta }_{\max }=0.25\mathrm{in},\hfill \\ \\ \mathrm{With}\mathrm{bounds}:\hfill & 0.125\le x_1\le 2,\hfill \\ \hfill & 0.1\le x_2,x_3\le 10,\hfill \\ \hfill & 0.1\le x_4\le 2.\hfill \end{array}$$

(28)

Table 30 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, BWO and SSOA did not satisfy one or more problem constraints. MShOA’s difference from the best-known feasible objective function value was $6.7148143232\times {10}^{-02}$. The convergence graph is shown in Figure 20.

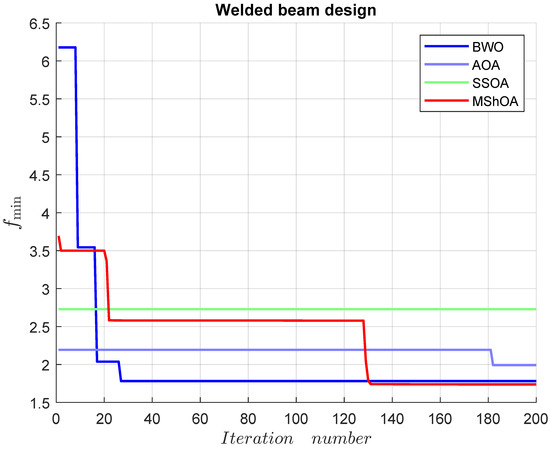
Figure 20. Convergence graph of the welded beam design.

5.8. Multiple Disk Clutch Brake Design Problem

The multiple disk clutch brake design problem includes five decision variables and eight inequality constraints. The mathematical representation of the problem is shown in Equation (29). The best-known feasible objective value taken from Table 24 is $2.3524245790\times {10}^{-01}$.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & f\left(\overline{x}\right)=\pi \left(x_2^2-x_1^2\right)x_3(x_5+1)\rho \hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=-p_{\max }+p_{\mathrm{tr}}\le 0,\hfill \\ \hfill & g_2\left(\overline{x}\right)=p_{\mathrm{rz}}{V}_{\mathrm{sr}}-V_{\mathrm{sr},\max }{p}_{\max }\le 0,\hfill \\ \hfill & g_3\left(\overline{x}\right)=▵R+x_1-x_2\le 0,\hfill \\ \hfill & g_4\left(\overline{x}\right)=-L_{\max }+(x_5+1)(x_3+\delta )\le 0,\hfill \\ \hfill & g_5\left(\overline{x}\right)=s{M}_s-M_h\le 0,\hfill \\ \hfill & g_6\left(\overline{x}\right)=T\ge 0,\hfill \\ \hfill & g_7\left(\overline{x}\right)=-V_{\mathrm{sr},\max }+V_{\mathrm{sr}}\le 0,\hfill \\ \hfill & g_8\left(\overline{x}\right)=T-T_{\max }\le 0.\hfill \\ \\ \mathrm{Where}:\hfill & M_h={\displaystyle \frac{2}{3}}\mu x_4{x}_5{\displaystyle \frac{x_2^3-x_1^3}{x_2^2-x_1^2}}\mathrm{N}.\mathrm{mm},\hfill \\ \hfill & \omega ={\displaystyle \frac{\pi n}{30}}\mathrm{rad}/\mathrm{s},\hfill \\ \hfill & A=\pi (x_2^2-x_1^2){\mathrm{mm}}^2,\hfill \\ \hfill & p_{\mathrm{rz}}={\displaystyle \frac{x_4}{A}}{\mathrm{N}/\mathrm{mm}}^2,\hfill \\ \hfill & V_{\mathrm{sr}}={\displaystyle \frac{\pi R_{\mathrm{sr}}n}{30}}\mathrm{mm}/\mathrm{s},\hfill \\ \hfill & R_{\mathrm{sr}}={\displaystyle \frac{2}{3}}{\displaystyle \frac{x_2^3-x_1^3}{x_2^2-x_1^2}}\mathrm{mm},\hfill \\ \hfill & T={\displaystyle \frac{I_z\omega }{M_h+M_f}},\hfill \\ \\ \mathrm{Constants}:\hfill & ▵R=20\mathrm{mm},L_{max}=30\mathrm{mm},\mu =0.6,\hfill \\ \hfill & V_{sr,max}=10\mathrm{m}/\mathrm{s},\delta =0.5\mathrm{mm},s=1.5,\hfill \\ \hfill & T_{max}=15\mathrm{s},n=250rpm,I_z=55{\mathrm{kg}.\mathrm{m}}^2.\hfill \\ \hfill & M_s=40\mathrm{Nm},M_f=3\mathrm{Nm},and{p}_{max}=1\hfill \\ \\ \mathrm{With}\mathrm{bounds}:\hfill & 60\le x_1\le 80,90\le x_2\le 110,1\le x_3\le 3\hfill \\ \hfill & 0\le x_4\le 1000,2\le x_5\le 9\hfill \end{array}$$

(29)

Table 31 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, BWO, SSOA, and AOA did not satisfy one or more problem constraints. MShOA’s difference from the best-known feasible objective function value was $3.8493744275\times {10}^{-04}$. The convergence graph is shown in Figure 21.

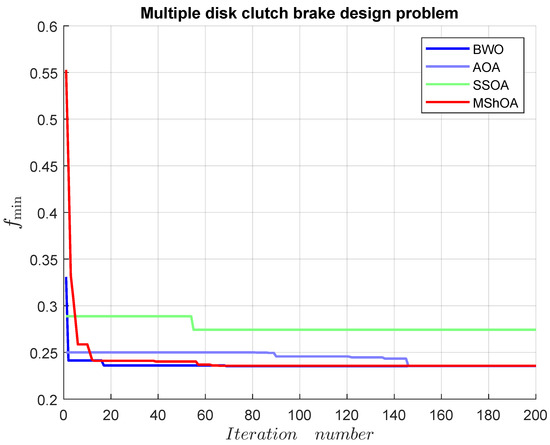
Figure 21. Convergence graph of the multiple disk clutch brake design problem.

5.9. Planetary Gear Train Design Optimization Problem

The planetary gear train design optimization problem includes six decision variables and eleven inequality constraints. The mathematical representation of the problem is shown in Equation (30). The best-known feasible objective value from Table 24 is $5.2576870748\times {10}^{-01}$.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & f\left(\overline{x}\right)=\max |i_k-i_{0k}|,k=\{1,2,\cdots ,R\}\hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=m_3\left(N_6+2.5\right)-D_{\max }\le 0,\hfill \\ \hfill & g_2\left(\overline{x}\right)=m_1\left(N_1+N_2\right)+m_1\left(N_2+2\right)-D_{\max }\le 0,\hfill \\ \hfill & g_3\left(\overline{x}\right)=m_3\left(N_4+N_5\right)+m_3\left(N_5+2\right)-D_{\max }\le 0,\hfill \\ \hfill & g_4\left(\overline{x}\right)=\left|m_1\left(N_1+N_2\right)-m_3\left(N_6-N_3\right)\right|-m_1-m_3\le 0,\hfill \\ \hfill & g_5\left(\overline{x}\right)=-\left(N_1+N_2\right)\sin (\pi /p)+N_2+2+{\delta }_{22}\le 0,\hfill \\ \hfill & g_6\left(\overline{x}\right)=-\left(N_6-N_3\right)\sin (\pi /p)+N_3+2+{\delta }_{33}\le 0,\hfill \\ \hfill & g_7\left(\overline{x}\right)=-\left(N_4+N_5\right)\sin (\pi /p)+N_5+2+{\delta }_{55}\le 0,\hfill \\ \hfill & g_8\left(\overline{x}\right)={\left(N_3+N_5+2+{\delta }_{35}\right)}^2-{\left(N_6-N_3\right)}^2-{\left(N_4+N_5\right)}^2\hfill \\ \hfill & +2\left(N_6-N_3\right)\left(N_4+N_5\right)\cos \left({\displaystyle \frac{2\pi }{p}}-\beta \right)\le 0,\hfill \\ \hfill & g_9\left(\overline{x}\right)=N_4-N_6+2N_5+2{\delta }_{56}+4\le 0,\hfill \\ \hfill & g_{10}\left(\overline{x}\right)=2N_3-N_6+N_4+2{\delta }_{34}+4\le 0,\hfill \\ \hfill & h_1\left(\overline{x}\right)={\displaystyle \frac{N_6-N_4}{p}}=integer,\hfill \\ \\ \mathrm{Where}:\hfill & i_1={\displaystyle \frac{N_6}{N_4}},i_{01}=3.11,i_2={\displaystyle \frac{N_6\left(N_1{N}_3+N_2{N}_4\right)}{N_1{N}_3\left(N_6-N_4\right)}},i_{0R}=-3.11,\hfill \\ \hfill & I_R=-{\displaystyle \frac{N_2{N}_6}{N_1{N}_3}},i_{02}=1.84,\overline{x}=\left(p,N_6,N_5,N_4,N_3,N_2,N_1,m_2,m_1\right)\hfill \\ \hfill & {\delta }_{22}={\delta }_{33}={\delta }_{55}={\delta }_{35}={\delta }_{56}=0.5.\hfill \\ \hfill & \beta ={\displaystyle \frac{{\cos }^{-1}\left({\left(N_4+N_5\right)}^2+{\left(N_6-N_3\right)}^2-{\left(N_3+N_5\right)}^2\right)}{2\left(N_6-N_3\right)\left(N_4+N_5\right)}},D_{\max }=220,\hfill \\ \\ \mathrm{With}\mathrm{bounds}:\hfill & p=(3,4,5),\hfill \\ \hfill & m_1=(1.75,2.0,2.25,2.5,2.75,3.0),\hfill \\ \hfill & m_3=(1.75,2.0,2.25,2.5,2.75,3.0),\hfill \\ \hfill & 17\le N_1\le 96,14\le N_2\le 54,14\le N_3\le 51\hfill \\ \hfill & 17\le N_4\le 46,14\le N_5\le 51,48\le N_6\le 124,\hfill \\ \hfill & and{N}_i=integer.\hfill \end{array}$$

(30)

Table 32 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, SSOA and AOA did not satisfy one or more problem constraints. MShOA’s difference with the best-known feasible objective function value was $4.2312925200\times {10}^{-03}$. The convergence graph is shown in Figure 22.

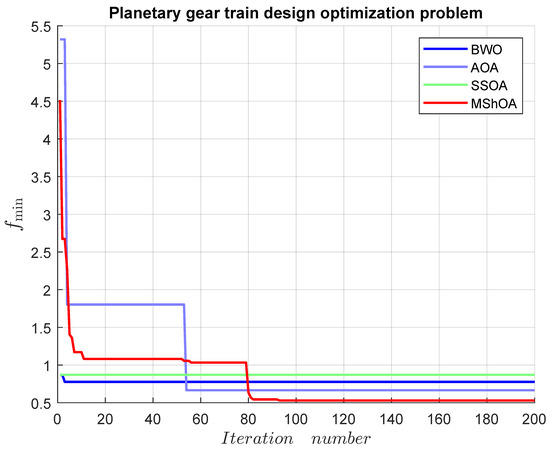
Figure 22. Convergence graph of the planetary gear train design optimization problem.

5.10. Tension/Compression Spring Design (Case 2)

The tension/compression spring design (case 2) problem includes three decision variables and eight inequality constraints. The mathematical representation of the problem is shown in Equation (31). The best-known feasible objective value taken from Table 24 is $2.6138840583$.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & f\left(\overline{x}\right)={\displaystyle \frac{{\pi }^2{x}_2{x}_3^2\left(x_1+2\right)}{4}}\hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g_1\left(\overline{x}\right)={\displaystyle \frac{8000C_f{x}_2}{\pi x_3^3}}-189000\le 0,\hfill \\ \hfill & g_2\left(\overline{x}\right)=l_f-14\le 0,\hfill \\ \hfill & g_3\left(\overline{x}\right)=0.2-x_3\le 0,\hfill \\ \hfill & g_4\left(\overline{x}\right)=x_2-3\le 0,\hfill \\ \hfill & g_5\left(\overline{x}\right)=3-{\displaystyle \frac{x_2}{x_3}}\le 0,\hfill \\ \hfill & g_6\left(\overline{x}\right)={\sigma }_p-6\le 0,\hfill \\ \hfill & g_7\left(\overline{x}\right)={\sigma }_p+{\displaystyle \frac{700}{K}}+1.05\left(x_1+2\right)x_3-l_f\le 0,\hfill \\ \hfill & g_8\left(\overline{x}\right)=1.25-{\displaystyle \frac{700}{K}}\le 0,\hfill \\ \\ \mathrm{Where}:\hfill & C_f={\displaystyle \frac{4\frac{x_2}{x_3}-1}{4\frac{x_2}{x_3}-4}}+{\displaystyle \frac{0.615x_3}{x_2}},K={\displaystyle \frac{11.5\times {10}^6{x}_3^4}{8x_1{x}_2^3}},{\sigma }_p={\displaystyle \frac{300}{K}},\hfill \\ \hfill & l_f={\displaystyle \frac{1000}{K}}+1.05\left(x_1+2\right)x_3\hfill \\ \\ \mathrm{With}\mathrm{bounds}:\hfill & 1\le x_1\left(integer\right)\le 70,\hfill \\ \hfill & x_3\left(discreate\right)\in \{0.009,0.0095,0.0104,0.0118,0.0128,\hfill \\ \hfill & 0.0132,0.014,0.015,0.0162,0.0173,0.018,0.020,0.023,\hfill \\ \hfill & 0.025,0.028,0.032,0.035,0.041,0.047,0.054,0.063,0.072,\hfill \\ \hfill & 0.080,0.092,0.0105,0.120,0.135,0.148,0.162,0.177,0.192,\hfill \\ \hfill & 0.207,0.225,0.244,0.263,0.283,0.307,0.0331,0.362,0.394,\hfill \\ \hfill & 0.4375,0.500\}\hfill \\ \hfill & 0.6\le x_2\left(continuous\right)\le 3.\hfill \end{array}$$

(31)

Table 33 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. MShOA’s difference from the best-known feasible objective function value was $8.5610383350\times {10}^{-02}$. The convergence graph is shown in Figure 23.

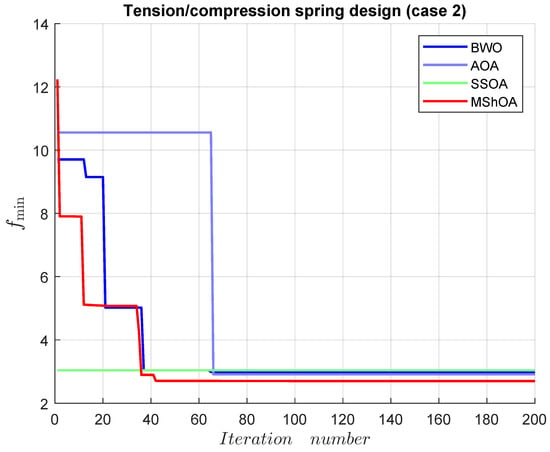
Figure 23. Convergence graph of the tension/compression spring design (case 2).

5.11. Himmelblau’s Function

The Himmelblau’s function problem includes five decision variables and six inequality constraints. The mathematical representation of the problem is shown in Equation (32). The best-known feasible objective value taken from Table 24 is $-3.0665538672\times {10}^{+04}$.

$$\begin{array}{cc}\mathrm{Minimize}\hfill & f\left(\overline{x}\right)=5.3578547x_3^2+0.8356891x_1{x}_5+\hfill \\ & 37.293239x_1-40792.141\hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g_1\left(\overline{x}\right)=-G1\le 0,\hfill \\ \hfill & g_2\left(\overline{x}\right)=G1-92\le 0,\hfill \\ \hfill & g_3\left(\overline{x}\right)=90-G2\le 0,\hfill \\ \hfill & g_4\left(\overline{x}\right)=G2-110\le 0,\hfill \\ \hfill & g_5\left(\overline{x}\right)=20-G3\le 0,\hfill \\ \hfill & g_6\left(\overline{x}\right)=G3-25\le 0,\hfill \\ \\ \mathrm{Where}:\hfill & G1=85.334407+0.0056858x_2{x}_5+\hfill \\ & 0.0006262x_1{x}_4-0.0022053x_3{x}_5,\hfill \\ \hfill & G2=80.51249+0.{0071317}_2{x}_5+\hfill \\ & 0.0029955x_1{x}_2+0.0021813x_3^2,\hfill \\ \hfill & G3=9.300961+0.0047026x_3{x}_5+\hfill \\ & 0.00125447x_1{x}_3+0.0019085x_3{x}_4\hfill \\ \mathrm{With}\mathrm{bounds}:\hfill & 78\le x_1\le 102,\hfill \\ \hfill & 33\le x_2\le 45,\hfill \\ \hfill & 27\le x_3\le 45,\hfill \\ \hfill & 27\le x_4\le 45,\hfill \\ \hfill & 27\le x_5\le 45.\hfill \end{array}$$

(32)

Table 34 compares MShOA, BWO, AOA, and SSOA, all of which provided effective and competitive solutions. Nonetheless, BWO, SSOA, and AOA did not satisfy one or more problem constraints. MShOA’s difference with the best-known feasible objective function value was $1.9624794082\times {10}^{+02}$. The convergence graph is shown in Figure 24.

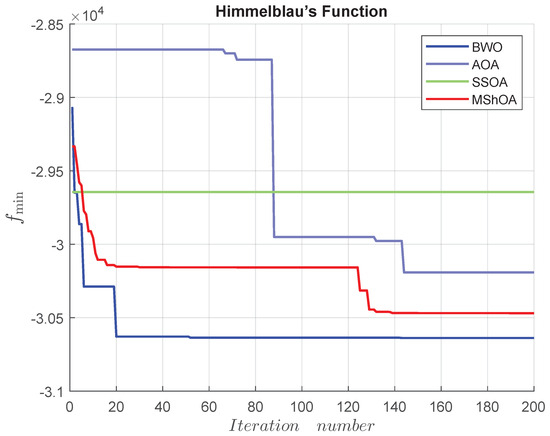
Figure 24. Convergence graph of Himmelblau’s function.

5.12. Optimal Power Flow

The optimal power flow (OPF) problem was initially considered an annex to the conventional economic dispatch (ED) problem because both problems were solved simultaneously [73]. The OPF has changed over time into a non-linear optimization problem that tries to find the operating conditions of an electrical system while considering the power balance equations and the constraints of the transmission network [74,75]. The mathematical formulation of the OPF is described in Equation (33); this equation is called the canonical form:

$$\begin{array}{cc}\mathrm{Minimize}\hfill & J(x,u),\hfill \\ \\ \mathrm{Subject}\mathrm{to}:\hfill & g(x,u)=0,\hfill \\ \hfill & h(x,u)\le 0\hfill \\ \\ \mathrm{Where}:\hfill & J(x,u)=\mathrm{the} \mathrm{oobjective} \mathrm{function},\hfill \\ \hfill & g(x,u)=\mathrm{the} \mathrm{set} \mathrm{of} \mathrm{equality} \mathrm{constraints},\hfill \\ \hfill & h(x,u)=\mathrm{the} \mathrm{inequality} \mathrm{constraints},\hfill \end{array}$$

(33)

In Equation (34), the set of control variables u is defined, which includes $P_G$ (active power generation at PV buses), $V_G$ (voltage magnitudes at PV buses), $Q_C$ (VAR compensators), and T (transformer tap settings). The parameter $NG$ is the number of generators, $NC$ is the number of VAR compensators, and $NT$ is the number of regulating transformers.

$$\begin{array}{c}\hfill u^T=\left[P_{G_2}\cdots P_{G_{NG}},V_{G_1}\cdots V_{G_{NG}},Q_{C_1}\cdots Q_{C_{NC}},T_1\cdots T_{NT}\right]\end{array}$$

(34)

In Equation (35), the set of state variables $x^T$ are

• $P_{G1}$—active output power (generation) of the reference node.
• $V_L$—voltage at the load node.
• $Q_G$—reactive power at the output (generation) of all generators.
• $S_l$—transmission line.

$$\begin{array}{c}\hfill x^T=\left[P_{G_1},V_{L_1}\cdots V_{L_{NL}},Q_{G_1}\cdots Q_{G_{NC}},S_{l_1}\cdots S_{l_{nl}}\right]\end{array}$$

(35)

where the parameter $NL$ is the number of load nodes and $nl$ is the number of transmission lines.

The constraints of the active power equality $\left(P\right)$ are defined in Equation (36), which indicates that the active power injected into node $\left(i\right)$ is equal to the sum of the active power demanded at node $\left(i\right)$ plus the active power losses in the transmission lines connected to the node:

$$\begin{array}{c}\hfill P_{Gi}-P_{Di}-V_i\sum _{j=1}^{NB}{V}_j\left[G_{ij}\cos \left({\theta }_{ij}\right)+B_{ij}\sin \left({\theta }_{ij}\right)\right]=0\end{array}$$

(36)

The constraints of the reactive power equality $\left(Q\right)$ are defined in Equation (37), which indicates that the reactive power injected into node $\left(i\right)$ is equal to the reactive power demanded at node $\left(i\right)$ plus the reactive power associated with the flows in the transmission lines connected to the node:

$$\begin{array}{c}\hfill Q_{Gi}-Q_{Di}-V_i\sum _{j=1}^{NB}{V}_j\left[G_{ij}\sin \left({\theta }_{ij}\right)+B_{ij}\cos \left({\theta }_{ij}\right)\right]=0\end{array}$$

(37)

The real and reactive power equality constraints are defined in Equations (36) and (37), respectively, where

• $P_G$—the active power generation.
• $Q_G$—the reactive power generation.
• $P_D$—the active load demand.
• $Q_D$—the reactive load demand.
• $NB$—the number of buses.
• $G_{ij}$—the conductance between buses i and j.
• $B_{ij}$—the susceptance between buses i and j.
• $Y_{ij}=G_{ij}+j{B}_{ij}$ (the admittance matrix).

The inequality constraints in an optimal power flow (OPF) problem [76] cover the operational limits of the system’s components. The generator constraints are represented by Equation (38), and these constraints are shown in Table 35:

$$\begin{array}{c}\hfill V_{G_i}^{min}\le V_{G_i}\le V_{G_i}^{max},i=1,\cdots ,NG\\ \hfill P_{G_i}^{min}\le P_{G_i}\le P_{G_i}^{max},i=1,\cdots ,NG\\ \hfill Q_{G_i}^{min}\le Q_{G_i}\le Q_{G_i}^{max},i=1,\cdots ,NG\end{array}$$

(38)

Table 35. Generator inequality constraints.

	Min	Max	Initial
$P_{G1}$	50	200	99.23
$P_{G2}$	20	80	80
$P_{G5}$	15	50	50
$P_{G8}$	10	35	20
$P_{G11}$	10	30	20
$P_{G13}$	12	40	20
$V_{G1}$	0.95	1.1	1.05
$V_{G2}$	0.95	1.1	1.04
$V_{G5}$	0.95	1.1	1.01
$V_{G8}$	0.95	1.1	1.01
$V_{G11}$	0.95	1.1	1.05
$V_{G13}$	0.95	1.1	1.05

The transformer constraints are described in Equation (39) and in Table 36:

$$\begin{array}{c}\hfill T_i^{min}\le T_i\le T_i^{max},i=1,\cdots ,NT\end{array}$$

(39)

Table 36. Transformer inequality constraints.

	Min	Max	Initial
$T_{11}$	0.9	1.1	1.078
$T_{12}$	0.9	1.1	1.069
$T_{15}$	0.9	1.1	1.032
$T_{36}$	0.9	1.1	1.068

The shunt VAR compensator constraints are defined by Equation (40) and in Table 37:

$$\begin{array}{c}\hfill Q_{Ci}^{min}\le Q_{GCi}\le Q_{Ci}^{max},i=1,\cdots ,NG\end{array}$$

(40)

Table 37. Shunt VAR compensator inequality constraints.

	Min	Max	Initial
$Q{C}_{10}$	0	5	0
$Q{C}_{12}$	0	5	0
$Q{C}_{15}$	0	5	0
$Q{C}_{17}$	0	5	0
$Q{C}_{20}$	0	5	0
$Q{C}_{21}$	0	5	0
$Q{C}_{23}$	0	5	0
$Q{C}_{24}$	0	5	0
$Q{C}_{29}$	0	5	0

Finally, the security constraints are represented in Equation (41):

$$\begin{array}{c}\hfill V_{L_i}^{min}\le V_{L_i}\le V_{L_i}^{max},i=1,\cdots ,NL\\ \hfill S_{l_i}\le S_{l_i}^{max},i=1,\cdots ,nl\end{array}$$

(41)

Following the previously described methodology in Section 5, the Mantis Shrimp Optimization Algorithm (MShOA), the Beluga Whale Optimization (BWO), the Arithmetic Optimization Algorithm (AOA), and the Synergistic Swarm Optimization Algorithm (SSOA) are applied to the optimal power flow problem for the IEEE-30 Bus test system; see Figure 25. Under these tests, three case studies were analyzed: the optimization of the total fuel cost for generation, the optimization of active power losses, and the optimization of reactive power losses.

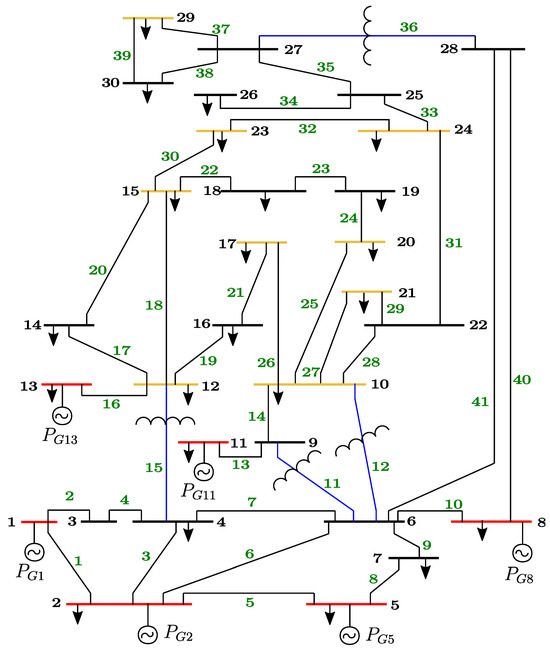
Figure 25. IEEE 30-bus system.

Case 1 included the total fuel cost of the six generating units connected at buses 1, 2, 5, 8, 11, and 13. The objective function was defined as follows:

$$\begin{array}{c}\hfill J=\sum _{i=1}^{NG}{f}_i(\$/h)\end{array}$$

(42)

where the quadratic function $f_i$ is described in [76].

The objective functions for Case 2 and Case 3, which involved optimizing the active power losses and optimizing the reactive power losses, respectively, are described in Equations (43) and (44):

$$\begin{array}{c}\hfill J=\sum _{i=1}^{NB}{P}_i=\sum _{i=1}^{NB}{P}_{Gi}-\sum _{i=1}^{NB}{P}_{Di}\end{array}$$

(43)

$$\begin{array}{c}\hfill J=\sum _{i=1}^{NB}{Q}_i=\sum _{i=1}^{NB}{Q}_{Gi}-\sum _{i=1}^{NB}{Q}_{Di}\end{array}$$

(44)

The convergence graphs analysis showed that MShOA outperformed the Beluga Whale Optimization (BWO), Arithmetic Optimization Algorithm (AOA), and Synergistic Swarm Optimization Algorithm (SSOA) in all three cases of this study, as illustrated in Figure 26, Figure 27 and Figure 28, respectively. The tests were conducted with a population size of 30 and 500 iterations. The minimum values obtained by each algorithm for each case are summarized in Table 38.

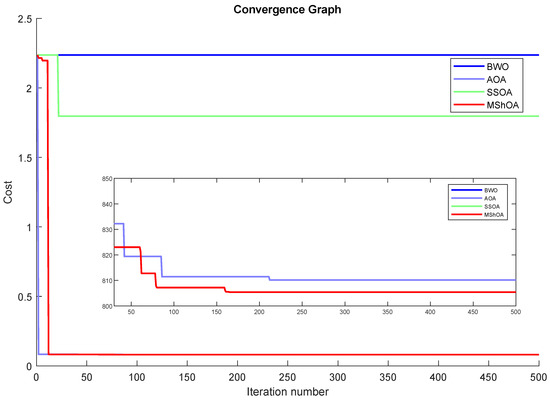
Figure 26. Case 1: minimization of fuel cost.

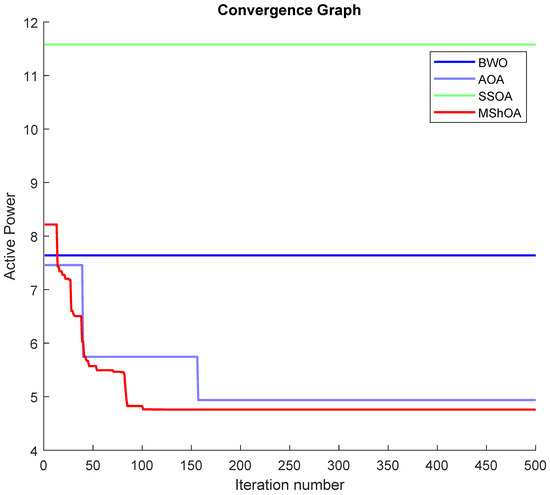
Figure 27. Case 2: minimization of active power transmission losses.

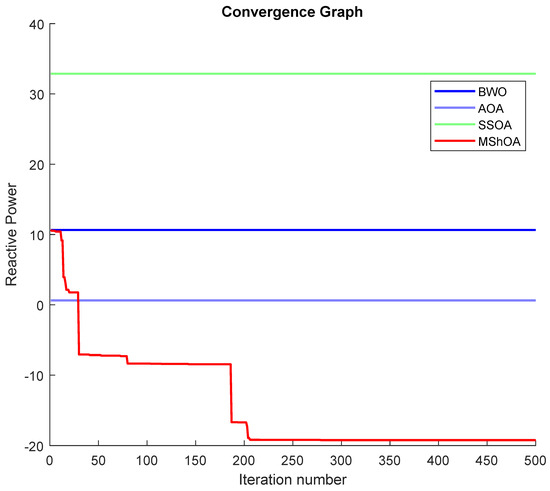
Figure 28. Case 3: minimization of reactive power transmission losses.

Table 38. Obtained results.

Minimization Studies	BWO	MShOA	SSOA	AOA
Fuel cost	$2.237\times {10}^4$	$8.054\times {10}^2$	$1.797\times {10}^4$	$8.102\times {10}^2$
Active power	$7.640\times {10}^0$	$4.758\times {10}^0$	$1.158\times {10}^1$	$4.936\times {10}^0$
Reactive power	$1.065\times {10}^1$	$-1.923\times {10}^1$	$3.288\times {10}^1$	$6.280\times {10}^{-1}$

6. Conclusions

This paper discusses a novel metaheuristic optimization technique inspired by the behavior of the mantis shrimp, called the Mantis Shrimp Optimization Algorithm (MShOA). The shrimp’s behavior includes three strategies: forage (food search); attack (the mantis shrimp strike); and burrow, defense, and shelter (hole defense and shelter). These strategies are triggered by the type of polarized light detected by the mantis shrimp.

The algorithm’s performance was evaluated on 20 testbench functions, on 10 real-world optimization problems taken from IEEE CEC2020, and on 3 study cases related to the optimal power flow problem: optimization of fuel cost in electric power generation, and optimization of active and reactive power losses. In addition, the algorithm’s performance was compared with fourteen algorithms selected from the scientific literature.

The statistical analysis results indicate that MShOA outperformed CFOA, ALO, DO, EMA, GWO, LCA, MAO, MPA, SSA, TSA, and WOA. In addition, it proved to be competitive with BWO, AOA, and SSOA.

Results and conclusions of this study:

• The mantis shrimp’s biological strategies modeled in this study included polarization principles in optics as new methods for optimization goals.
• MShOA has no parameters to configure in the modeling of strategies. The only parameters are those common to all bio-inspired algorithms, e.g., population size and number of iterations.
• The Wilcoxon rank and Friedman tests were performed to analyze the 10 unimodal and 10 multimodal functions. The Wilcoxon test results indicate that MShOA outperformed all the other algorithms in unimodal functions. In addition, it ranked first in the Friedman test. Furthermore, in the Wilcoxon test, MShOA outperformed the following algorithms: SSA, EMA, ALO, MAO, and CFOA in multimodal functions. Additionally, it ranked second in the Friedman statistical tests. These results demonstrate that MShOA has a remarkable balance between local and global searches.
• The set of 20 functions, unimodal and multimodal, was analyzed with Wilcoxon and Friedman statistical tests. The Wilcoxon test results indicate that MShOA outperformed the following optimization algorithms: CFOA, ALO, DO, EMA, GWO, LCA, MAO, MPA, SSA, TSA, and WOA. On the other hand, the Friedman test analysis shows that MShOA was ranked second.
• MShOA demonstrated outstanding results in 80% of the real-world IEEE CEC2020 engineering problems: process synthesis problem, process synthesis and design problem, process flow sheeting problem, welded beam design, planetary gear train design optimization problem, and tension/compression spring design.
• In the optimal power flow (OPF) problem study cases, MShOA obtained better solutions than BWO, AOA, and SSOA.
• MShOA was able to effectively solve real-world problems with unknown search spaces.

The proposed algorithm demonstrated competitive performances. However, it has some limitations that open avenues for future work. Currently, it is designed for single-objective optimization and has not yet been extended to handle multi-objective scenarios. Additionally, while it performed well on the tested optimal power flow (OPF) cases, its generalization to more complex or large-scale OPF models remains to be fully explored. Future work will address these limitations by extending the algorithm to multi-objective optimization and evaluating its applicability to broader and more diverse OPF problem instances.