Nonparametric Transformation Models for Double-Censored Data with Crossed Survival Curves: A Bayesian Approach
Abstract
1. Introduction
- Contribute a novel method for survival prediction under nonparametric transformation models with double-censored data, especially for the fixed censoring scheme.
- Incorporate categorical heteroscedasticity in nonparametric transformation models so as to model crossed survival curves.
- With categorical heteroscedasticity, evidence the significance of the effect of baseline log (RNA) levels in the randomized AIDs clinical trial.
2. Data, Model, and Assumptions
2.1. Data Structure
2.2. Nonparametric Transformation Models
3. Likelihood and Priors
3.1. Likelihood Function
3.2. Dirichlet Process Mixture Model
3.3. Pseudo-Quantile I-Splines Prior
3.3.1. Random Censoring Knot Selection
- Step 1: Choose empirical quantiles of exact time-to-events as interior knots, where each knot and , such that .
- Step 2: For , if , interpolate a new knot .
- Step 3: For , if , then interpolate another new knot .
- Step 4: Sort all the chosen and interpolated knots in ascending order resulting in the final selected interior knots.
3.3.2. Fixed Censoring Knot Selection
- Step 1 (pseudo-left-censored data generation):Generate pseudo observations from some distribution (e.g., Weibull, gamma) such that all .
- Step 2 (pseudo-right-censored data generation):Generate pseudo observations from the same distribution such that all .
- Step 3 (pseudo-quantile computation):Let . Compute and .
- Step 4 (quantile averaging):Compute . Choose N averaged empirical quantiles of the combined time-to-events as interior knots, where each knot and . Output this series as the finally selected interior knots.
4. Transformation Models with Crossed Survival Curves
ANOVA Dependent Dirichlet Process Prior
5. Posterior Inference
5.1. Posterior Prediction and Nonparametric Estimation
5.2. Posterior Projection and Parametric Estimation
5.3. Assumptions
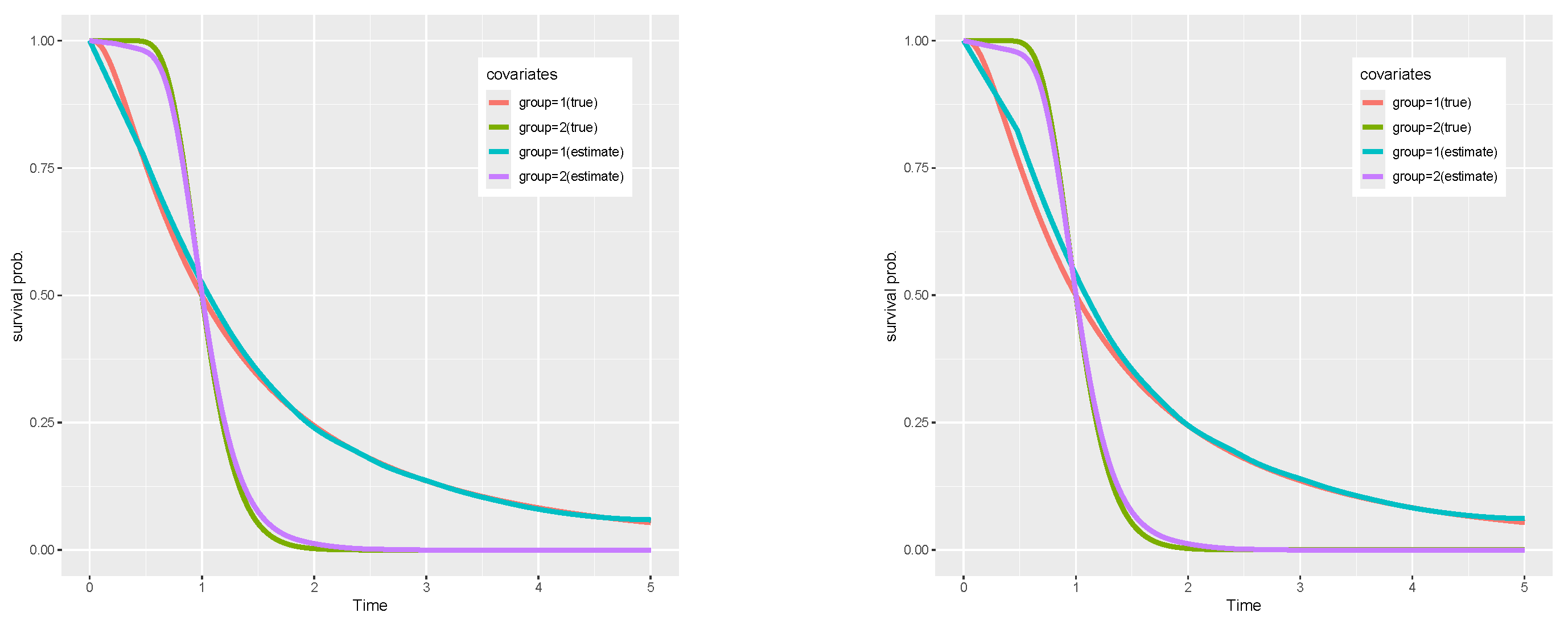
6. Simulations
- Case R-1: Non-PH/PO/AFT:
- Case R-2: PH model:
- Case R-3: PO model:
- Case R-4: AFT model:
- Case F-1: Non-PH/PO/AFT:
- Case F-2: PH model:
- Case F-3: PO model:
- Case F-4: AFT model:
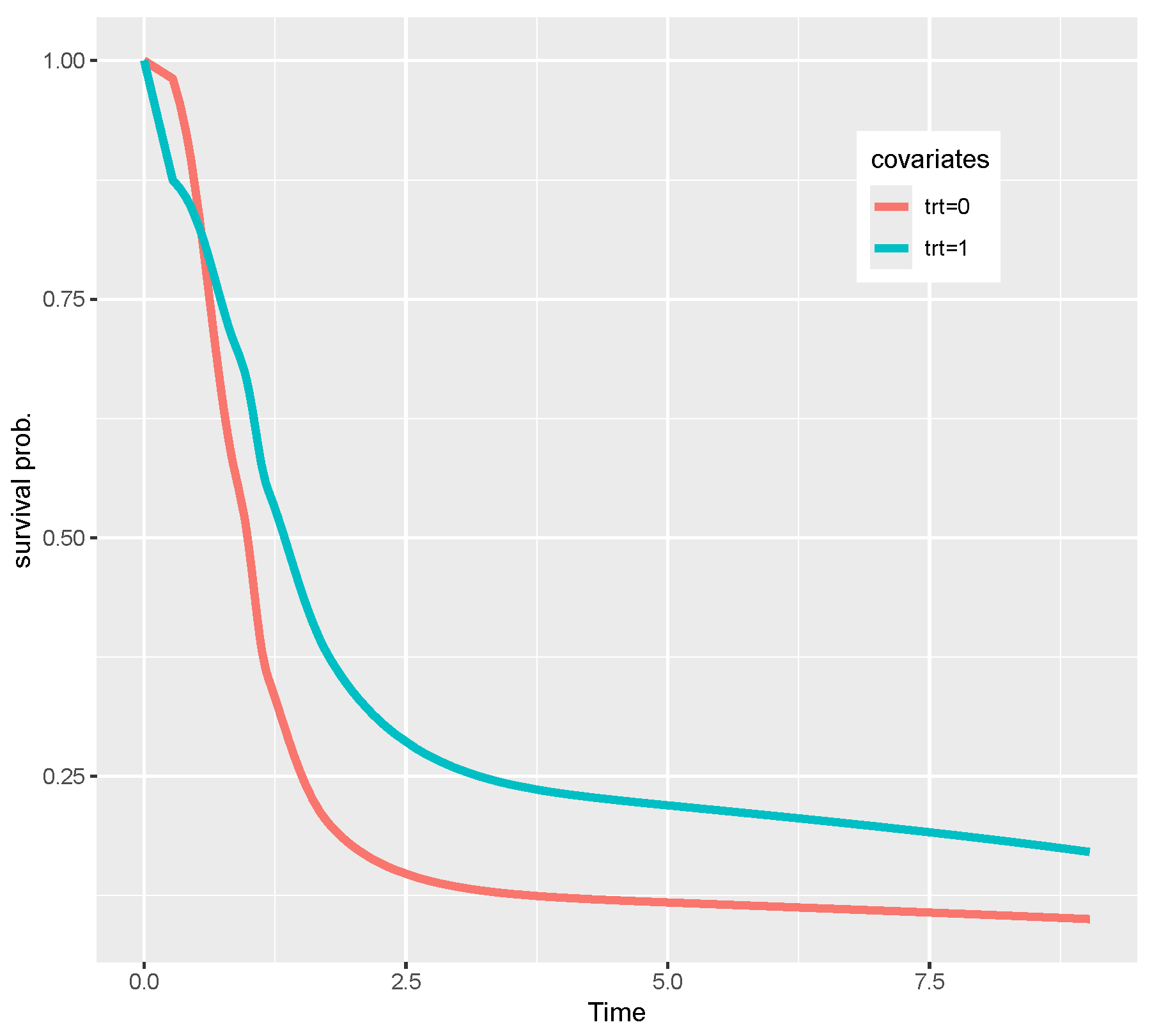
7. Real Data Analysis
8. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J. Asymptotic properties of nonparametric estimation based on partly interval-censored data. Stat. Sin. 1999, 9, 501–519. [Google Scholar]
- Gao, F.; Zeng, D.; Lin, D.Y. Semiparametric estimation of the accelerated failure time model with partly interval-censored data. Biometrics 2017, 73, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Gehan, E.A. A Generalized Two-Sample Wilcoxon Test for Doubly Censored Data. Biometrika 1965, 52, 650–653. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.J.; Peer, P.G. A study on effectiveness of screening mammograms. Int. J. Epidemiol. 2000, 29, 803–806. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.; Rocke, D.M. Multivariate survival analysis with doubly-censored data: Application to the assessment of Accutane treatment for fibrodysplasia ossificans progressiva. Stat. Med. 2002, 21, 2547–2562. [Google Scholar] [CrossRef]
- Cai, T.; Cheng, S. Semiparametric Regression Analysis for Doubly Censored Data. Biometrika 2004, 91, 277–290. [Google Scholar] [CrossRef]
- Sun, J. The Statistical Analysis of Interval-Censored Failure Time Data; Springer: New York, NY, USA, 2006. [Google Scholar]
- Turnbull, B.W. Nonparametric Estimation of a Survivorship Function with Doubly Censored Data. J. Am. Stat. Assoc. 1974, 69, 169–173. [Google Scholar] [CrossRef]
- Chang, M.N. Weak Convergence of a Self-Consistent Estimator of the Survival Function with Doubly Censored Data. Ann. Stat. 1990, 18, 391–404. [Google Scholar] [CrossRef]
- Gu, M.G.; Zhang, C.H. Asymptotic Properties of Self-Consistent Estimators Based on Doubly Censored Data. Ann. Stat. 1993, 21, 611–624. [Google Scholar] [CrossRef]
- Mykland, P.A.; Ren, J. Algorithms for Computing Self-Consistent and Maximum Likelihood Estimators with Doubly Censored Data. Ann. Stat. 1996, 24, 1740–1764. [Google Scholar] [CrossRef]
- Zhang, Y.; Jamshidian, M. On algorithms for the nonparametric maximum likelihood estimator of the failure function with censored data. J. Comput. Graph. Stat. 2004, 13, 123–140. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, B.; Jang, W. Asymptotic properties of the maximum likelihood estimator for the proportional hazards model with doubly censored data. J. Multivar. Anal. 2010, 101, 1339–1351. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, J.; Jang, W. An EM algorithm for the proportional hazards model with doubly censored data. Comput. Stat. Data Anal. 2013, 57, 41–51. [Google Scholar] [CrossRef]
- Cheng, S.; Wei, L.; Ying, Z. Analysis of transformation models with censored data. Biometrika 1995, 82, 835–845. [Google Scholar] [CrossRef]
- Chen, K.; Jin, Z.; Ying, Z. Semiparametric analysis of transformation models with censored data. Biometrika 2002, 89, 659–668. [Google Scholar] [CrossRef]
- Zeng, D.; Lin, D. Efficient estimation of semiparametric transformation models for counting processes. Biometrika 2006, 93, 627–640. [Google Scholar] [CrossRef]
- de Castro, M.; Chen, M.H.; Ibrahim, J.G.; Klein, J.P. Bayesian transformation models for multivariate survival data. Scand. J. Stat. 2014, 41, 187–199. [Google Scholar] [CrossRef]
- Li, S.; Hu, T.; Wang, P.; Sun, J. A Class of Semiparametric Transformation Models for Doubly Censored Failure Time Data. Scand. J. Stat. 2018, 45, 682–698. [Google Scholar] [CrossRef]
- Hothorn, T.; Kneib, T.; Bühlmann, P. Conditional transformation models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 3–27. [Google Scholar] [CrossRef]
- Hothorn, T.; Möst, L.; Bühlmann, P. Most likely transformations. Scand. J. Stat. 2018, 45, 110–134. [Google Scholar] [CrossRef]
- Zhou, H.; Hanson, T. A unified framework for fitting Bayesian semiparametric models to arbitrarily censored survival data, including spatially referenced data. J. Am. Stat. Assoc. 2018, 113, 571–581. [Google Scholar] [CrossRef]
- Kowal, D.R.; Wu, B. Monte Carlo inference for semiparametric Bayesian regression. J. Am. Stat. Assoc. 2024, 120, 1063–1076. [Google Scholar] [CrossRef] [PubMed]
- Zhong, C.; Yang, J.; Shen, J.; Liu, C.; Li, Z. On MCMC mixing under unidentified nonparametric models with an application to survival predictions under transformation models. arXiv 2024, arXiv:2411.01382. [Google Scholar] [CrossRef]
- Horowitz, J.L. Semiparametric estimation of a regression model with an unknown transformation of the dependent variable. Econometrica 1996, 64, 103–137. [Google Scholar] [CrossRef]
- Ye, J.; Duan, N. Nonparametric n−1/2-consistent estimation for the general transformation models. Ann. Stat. 1997, 25, 2682–2717. [Google Scholar] [CrossRef]
- Chen, S. Rank Estimation of Transformation Models. Econometrica 2002, 70, 1683–1697. [Google Scholar] [CrossRef]
- Mallick, B.K.; Walker, S. A Bayesian semiparametric transformation model incorporating frailties. J. Stat. Plan. Inference 2003, 112, 159–174. [Google Scholar] [CrossRef]
- Song, X.; Ma, S.; Huang, J.; Zhou, X.H. A semiparametric approach for the nonparametric transformation survival model with multiple covariates. Biostatistics 2007, 8, 197–211. [Google Scholar] [CrossRef]
- Cuzick, J. Rank regression. Ann. Stat. 1988, 16, 1369–1389. [Google Scholar] [CrossRef]
- Gørgens, T.; Horowitz, J.L. Semiparametric estimation of a censored regression model with an unknown transformation of the dependent variable. J. Econom. 1999, 90, 155–191. [Google Scholar] [CrossRef]
- Zeng, D.; Lin, D. Efficient estimation for the accelerated failure time model. J. Am. Stat. Assoc. 2007, 102, 1387–1396. [Google Scholar] [CrossRef]
- Ramsay, J.O. Monotone regression splines in action. Stat. Sci. 1988, 3, 425–441. [Google Scholar] [CrossRef]
- MacEachern, S.N. Dependent Nonparametric Processes. In Proceedings of the Section on Bayesian Statistical Science; American Statistical Association: Alexandria, VA, USA, 1999. [Google Scholar]
- De Iorio, M.; Müller, P.; Rosner, G.L.; MacEachern, S.N. An ANOVA model for dependent random measures. J. Am. Stat. Assoc. 2004, 99, 205–215. [Google Scholar] [CrossRef]
- Lo, A.Y. On a class of Bayesian nonparametric estimates: I. Density estimates. Ann. Stat. 1984, 12, 351–357. [Google Scholar] [CrossRef]
- Sethuraman, J. A constructive definition of Dirichlet priors. Stat. Sin. 1994, 4, 639–650. [Google Scholar]
- Kottas, A. Nonparametric Bayesian survival analysis using mixtures of Weibull distributions. J. Stat. Plan. Inference 2006, 136, 578–596. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ishwaran, H.; James, L.F. Approximate Dirichlet process computing in finite normal mixtures: Smoothing and prior information. J. Comput. Graph. Stat. 2002, 11, 508–532. [Google Scholar] [CrossRef]
- Zhong, C.; Ma, Z.; Shen, J.; Liu, C. Dependent Dirichlet Processes for Analysis of a Generalized Shared Frailty Model. In Computational Statistics and Applications; Løpez-Ruiz, R., Ed.; Chapter 5; IntechOpen: Rijeka, Croatia, 2021. [Google Scholar]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.A.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76, 1–32. [Google Scholar] [CrossRef]
- Absil, P.A.; Malick, J. Projection-like retractions on matrix manifolds. SIAM J. Optim. 2012, 22, 135–158. [Google Scholar] [CrossRef]
| Notation | Definition |
|---|---|
| True time-to-event data | |
| p-dimensional covariate vector | |
| q-dimensional Categorical covariate vector | |
| Left/right censoring data | |
| Observed time-to-event data | |
| Indicators for left-censored/uncensored/right-censored | |
| The nonnegative monotone transformation | |
| The vector of regression coefficients | |
| The multiplicative model error in transformation model | |
| I-spline basis | |
| N | The number of knots in I-splines functions |
| Maximum observed time | |
| Empirical quantile function for variable X |
| Proposed Method | spBayesSurv | Li2018 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Case R-1 | |||||||||
| Mean | 0.605 | 0.557 | 0.537 | 0.430 | 0.420 | 0.411 | 0.618 | 0.583 | 0.562 |
| Bias | 0.028 | −0.020 | −0.041 | −0.147 | −0.157 | −0.166 | −0.041 | −0.006 | 0.015 |
| PSD | 0.086 | 0.065 | 0.065 | 0.180 | 0.094 | 0.094 | 0.187 | 0.092 | 0.092 |
| RMSE | 0.098 | 0.072 | 0.079 | 0.233 | 0.189 | 0.195 | 0.181 | 0.090 | 0.091 |
| SDE | 0.095 | 0.075 | 0.069 | 0.181 | 0.105 | 0.103 | 0.177 | 0.090 | 0.091 |
| CP | 0.88 | 0.94 | 0.89 | 0.84 | 0.56 | 0.55 | 0.95 | 0.97 | 0.94 |
| Case R-2 | |||||||||
| Mean | 0.588 | 0.569 | 0.552 | 0.685 | 0.695 | 0.668 | 0.573 | 0.596 | 0.577 |
| Bias | 0.011 | −0.008 | −0.026 | 0.108 | 0.118 | 0.091 | 0.005 | −0.018 | 0.001 |
| PSD | 0.118 | 0.084 | 0.082 | 0.240 | 0.134 | 0.132 | 0.183 | 0.100 | 0.099 |
| RMSE | 0.101 | 0.081 | 0.099 | 0.268 | 0.197 | 0.164 | 0.155 | 0.112 | 0.104 |
| SDE | 0.101 | 0.081 | 0.099 | 0.246 | 0.159 | 0.138 | 0.155 | 0.111 | 0.105 |
| CP | 0.96 | 0.93 | 0.87 | 0.92 | 0.86 | 0.90 | 0.99 | 0.93 | 0.90 |
| Case R-3 | |||||||||
| Mean | 0.576 | 0.552 | 0.559 | 0.493 | 0.524 | 0.538 | 0.484 | 0.511 | 0.513 |
| Bias | −0.001 | −0.025 | −0.018 | −0.084 | −0.053 | −0.039 | 0.093 | 0.066 | 0.064 |
| PSD | 0.182 | 0.123 | 0.122 | 0.304 | 0.161 | 0.159 | 0.234 | 0.117 | 0.115 |
| RMSE | 0.158 | 0.118 | 0.115 | 0.296 | 0.164 | 0.175 | 0.240 | 0.118 | 0.129 |
| SDE | 0.159 | 0.116 | 0.114 | 0.285 | 0.156 | 0.172 | 0.222 | 0.099 | 0.113 |
| CP | 0.97 | 0.96 | 0.95 | 0.98 | 0.95 | 0.92 | 0.95 | 0.95 | 0.89 |
| Case R-4 | |||||||||
| Mean | 0.621 | 0.545 | 0.543 | 0.402 | 0.394 | 0.394 | 0.650 | 0.655 | 0.654 |
| Bias | 0.044 | −0.032 | −0.035 | −0.176 | −0.183 | −0.183 | −0.072 | −0.078 | −0.077 |
| PSD | 0.105 | 0.080 | 0.079 | 0.156 | 0.087 | 0.086 | 0.211 | 0.114 | 0.113 |
| RMSE | 0.112 | 0.088 | 0.081 | 0.235 | 0.203 | 0.202 | 0.206 | 0.139 | 0.130 |
| SDE | 0.104 | 0.082 | 0.073 | 0.156 | 0.088 | 0.087 | 0.193 | 0.115 | 0.106 |
| CP | 0.92 | 0.93 | 0.94 | 0.77 | 0.47 | 0.51 | 0.94 | 0.90 | 0.90 |
| Proposed Method | spBayesSurv | Li2018 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Case F-1 | |||||||||
| Mean | 0.596 | 0.560 | 0.555 | 0.378 | 0.408 | 0.413 | 0.621 | 0.585 | 0.582 |
| Bias | 0.018 | −0.017 | −0.022 | −0.199 | −0.168 | −0.164 | −0.044 | −0.007 | −0.005 |
| PSD | 0.112 | 0.079 | 0.079 | 0.300 | 0.154 | 0.156 | 0.217 | 0.101 | 0.100 |
| RMSE | 0.109 | 0.079 | 0.080 | 0.417 | 0.233 | 0.230 | 0.213 | 0.103 | 0.087 |
| SDE | 0.108 | 0.078 | 0.077 | 0.369 | 0.162 | 0.162 | 0.209 | 0.103 | 0.087 |
| CP | 0.96 | 0.97 | 0.95 | 0.80 | 0.75 | 0.79 | 0.96 | 0.97 | 0.98 |
| Case F-2 | |||||||||
| Mean | 0.583 | 0.559 | 0.560 | 0.601 | 0.602 | 0.597 | 0.583 | 0.569 | 0.570 |
| Bias | 0.006 | −0.018 | −0.018 | 0.024 | 0.024 | 0.019 | −0.005 | 0.008 | 0.007 |
| PSD | 0.127 | 0.091 | 0.089 | 0.234 | 0.133 | 0.132 | 0.176 | 0.098 | 0.095 |
| RMSE | 0.128 | 0.095 | 0.096 | 0.258 | 0.138 | 0.145 | 0.187 | 0.094 | 0.101 |
| SDE | 0.129 | 0.094 | 0.095 | 0.254 | 0.137 | 0.144 | 0.188 | 0.094 | 0.101 |
| CP | 0.90 | 0.93 | 0.94 | 0.92 | 0.92 | 0.93 | 0.95 | 0.95 | 0.94 |
| Case F-3 | |||||||||
| Mean | 0.589 | 0.525 | 0.544 | 0.414 | 0.438 | 0.442 | 0.533 | 0.527 | 0.534 |
| Bias | 0.012 | −0.053 | −0.033 | −0.163 | −0.139 | −0.135 | 0.044 | 0.051 | 0.043 |
| PSD | 0.216 | 0.150 | 0.146 | 0.312 | 0.165 | 0.164 | 0.247 | 0.120 | 0.118 |
| RMSE | 0.185 | 0.148 | 0.159 | 0.335 | 0.226 | 0.212 | 0.221 | 0.128 | 0.135 |
| SDE | 0.186 | 0.148 | 0.159 | 0.294 | 0.179 | 0.164 | 0.217 | 0.118 | 0.128 |
| CP | 0.93 | 0.93 | 0.95 | 0.95 | 0.82 | 0.88 | 0.95 | 0.92 | 0.92 |
| Case F-4 | |||||||||
| Mean | 0.633 | 0.544 | 0.529 | 0.295 | 0.288 | 0.290 | 0.662 | 0.618 | 0.612 |
| Bias | 0.055 | −0.034 | −0.048 | −0.282 | −0.290 | −0.287 | −0.084 | −0.041 | −0.034 |
| PSD | 0.108 | 0.084 | 0.084 | 0.123 | 0.069 | 0.070 | 0.222 | 0.111 | 0.111 |
| RMSE | 0.118 | 0.085 | 0.096 | 0.305 | 0.297 | 0.296 | 0.219 | 0.110 | 0.112 |
| SDE | 0.105 | 0.079 | 0.083 | 0.117 | 0.064 | 0.071 | 0.203 | 0.103 | 0.107 |
| CP | 0.89 | 0.91 | 0.92 | 0.41 | 0.01 | 0.04 | 0.95 | 0.95 | 0.96 |
| Case R-1 | Case R-2 | |||||
|---|---|---|---|---|---|---|
| Z | Proposed | spBayesSurv | Li2018 | Proposed | spBayesSurv | Li2018 |
| 0.085 | 0.601 | 0.440 | 0.227 | 0.214 | 0.246 | |
| 0.134 | 1.029 | 0.215 | 0.555 | 0.473 | 0.073 | |
| 0.112 | 0.899 | 0.278 | 0.582 | 0.472 | 0.055 | |
| Case R-3 | Case R-4 | |||||
| Z | Proposed | spBayesSurv | Li2018 | Proposed | spBayesSurv | Li2018 |
| 0.088 | 0.257 | 0.311 | 0.223 | 0.197 | 0.284 | |
| 0.130 | 0.178 | 0.173 | 0.295 | 0.158 | 0.116 | |
| 0.125 | 0.213 | 0.223 | 0.373 | 0.153 | 0.095 | |
| Case F-1 | Case F-2 | |||||
| Z | Proposed | spBayesSurv | Li2018 | Proposed | spBayesSurv | Li2018 |
| 0.231 | 0.529 | 0.375 | 0.302 | 0.244 | 0.255 | |
| 0.181 | 0.250 | 0.347 | 0.497 | 0.332 | 0.359 | |
| 0.142 | 0.336 | 0.332 | 0.555 | 0.333 | 0.267 | |
| Case F-3 | Case F-4 | |||||
| Z | Proposed | spBayesSurv | Li2018 | Proposed | spBayesSurv | Li2018 |
| 0.161 | 0.323 | 0.384 | 0.216 | 0.271 | 0.386 | |
| 0.271 | 0.247 | 0.324 | 0.235 | 0.261 | 0.486 | |
| 0.239 | 0.234 | 0.318 | 0.277 | 0.204 | 0.360 | |
| Random Censoring | Fixed Censoring | |||||
|---|---|---|---|---|---|---|
| Mean | 0.569 | 0.578 | 0.565 | 0.562 | 0.555 | 0.564 |
| Bias | −0.009 | 0.001 | −0.013 | −0.015 | −0.023 | −0.013 |
| PSD | 0.093 | 0.092 | 0.094 | 0.118 | 0.120 | 0.116 |
| RMSE | 0.066 | 0.059 | 0.065 | 0.0.066 | 0.069 | 0.070 |
| SDE | 0.095 | 0.091 | 0.096 | 0.119 | 0.122 | 0.114 |
| CP | 0.96 | 0.95 | 0.96 | 0.97 | 0.96 | 0.94 |
| Proposed Method (Model (1)) | Proposed Method (Model (7)) | |||
|---|---|---|---|---|
| trt | baseRNA | trt | baseRNA | |
| Est | 0.956 | 0.256 | \ | 0.565 |
| SD | 0.050 | 0.150 | \ | 0.159 |
| 95% CI | (0.826, 1.000) | (−0.009, 0.564) | \ | (0.317, 0.836) |
| spBayes PH | spBayes PO | |||
| trt | baseRNA | trt | baseRNA | |
| Est | 1.058 | 0.245 | 1.437 | 0.382 |
| SD | 0.258 | 0.194 | 0.330 | 0.264 |
| 95% CI | (0.571, 1.583) | (−0.138, 0.623) | (0.803, 2.097) | (−0.141, 0.893) |
| Li2018 PH r = 0 | Li2018 PO r = 1 | |||
| trt | baseRNA | trt | baseRNA | |
| Est | 0.982 | 0.067 | 1.291 | 0.145 |
| SD | 0.272 | 0.180 | 0.308 | 0.261 |
| 95% CI | (0.449, 1.516) | (−0.285, 0.419) | (0.688, 1.894) | (−0.365, 0.656) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Ni, R.; Chen, S.; Ma, Z.; Zhong, C. Nonparametric Transformation Models for Double-Censored Data with Crossed Survival Curves: A Bayesian Approach. Mathematics 2025, 13, 2461. https://doi.org/10.3390/math13152461
Xu P, Ni R, Chen S, Ma Z, Zhong C. Nonparametric Transformation Models for Double-Censored Data with Crossed Survival Curves: A Bayesian Approach. Mathematics. 2025; 13(15):2461. https://doi.org/10.3390/math13152461
Chicago/Turabian StyleXu, Ping, Ruichen Ni, Shouzheng Chen, Zhihua Ma, and Chong Zhong. 2025. "Nonparametric Transformation Models for Double-Censored Data with Crossed Survival Curves: A Bayesian Approach" Mathematics 13, no. 15: 2461. https://doi.org/10.3390/math13152461
APA StyleXu, P., Ni, R., Chen, S., Ma, Z., & Zhong, C. (2025). Nonparametric Transformation Models for Double-Censored Data with Crossed Survival Curves: A Bayesian Approach. Mathematics, 13(15), 2461. https://doi.org/10.3390/math13152461






