Mathematical Modelling and Optimization Methods in Geomechanically Informed Blast Design: A Systematic Literature Review

Abstract

Background: Rock–blast design is a canonical inverse problem that joins elastodynamic partial differential equations (PDEs), fracture mechanics, and stochastic heterogeneity. Objective: Guided by the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) protocol, a systematic review of mathematical methods for geomechanically informed blast modelling and optimisation is provided. Methods: A Scopus–Web of Science search (2000–2025) retrieved 2415 records; semantic filtering and expert screening reduced the corpus to 97 studies. Topic modelling with Bidirectional Encoder Representations from Transformers Topic (BERTOPIC) and bibliometrics organised them into (i) finite-element and finite–discrete element simulations, including arbitrary Lagrangian–Eulerian (ALE) formulations; (ii) geomechanics-enhanced empirical laws; and (iii) machine-learning surrogates and multi-objective optimisers. Results: High-fidelity simulations delimit blast-induced damage with ≤0.2 m mean absolute error; extensions of the Kuznetsov–Ram equation cut median-size mean absolute percentage error (MAPE) from 27% to 15%; Gaussian-process and ensemble learners reach a coefficient of determination ($R^2>0.95$) while providing closed-form uncertainty; Pareto optimisers lower peak particle velocity (PPV) by up to 48% without productivity loss. Synthesis: Four themes emerge—surrogate-assisted PDE-constrained optimisation, probabilistic domain adaptation, Bayesian model fusion for digital-twin updating, and entropy-based energy metrics. Conclusions: Persisting challenges in scalable uncertainty quantification, coupled discrete–continuous fracture solvers, and rigorous fusion of physics-informed and data-driven models position blast design as a fertile test bed for advances in applied mathematics, numerical analysis, and machine-learning theory.

1. Introduction

Rock blasting is regarded as the first stage of comminution in mining and civil engineering projects and therefore governs the overall energy efficiency and operating cost of the mine–mill chain [1]. Mine-to-mill simulations have shown that powder factor and rock hardness exert a measurable influence on mill throughput and size-specific energy [2]. In copper open pits, redesigned burden and spacing that reduce the characteristic fragment size have delivered throughput gains of up to 20% [3]. Fragmentation also affects excavation productivity, pit-wall stability, and dilution, underscoring the importance of controlled blasting practices [4]. Multi-objective optimisation based on the hybrid Pareto search has been applied to identify blast designs that maximise production while constraining peak particle velocity [5]. Delay-timing models refine this balance further by linking maximum charge per delay to vibration thresholds [6]. Despite these advances, predicting and optimising the coupled responses remains a challenging inverse problem that combines elastodynamic partial differential equations, fracture mechanics, and stochastic heterogeneity.

This systematic review, guided by PRISMA, integrates the literature published between 2000 and 2025 to (i) classify the mathematical and computational models employed in blast design, (ii) assess their strengths and limitations when incorporating geomechanical variables, and (iii) propose a research agenda that fuses multiphysics simulation, enriched empirical formulations, and machine learning techniques. The final corpus consists of 90 studies selected from 2415 records in Scopus and Web of Science. The analysis reveals three methodological strands—empirical models, high-fidelity numerical simulation, and machine learning—whose foundations are described below.

1.1. From Empirical Formulations to Geomechanically Enriched Models

Empirical prediction of blast fragmentation has been dominated by the Kuznetsov–Cunningham–Ramamurthy equation (Kuz–Ram), which remains a cornerstone of industrial practice [7]. In its classical form the median fragment size is estimated as

$$X_{50}=A{\left({\displaystyle \frac{Q}{Q_0}}\right)}^{\alpha }exp\left[-\beta \mathrm{RDI}\right],$$

(1)

where $X_{50}$ is the median fragment size, A is a lithology factor, Q is the explosive charge, $Q_0$ is a reference charge that scales the blast, $\alpha$ is an empirical size–charge exponent, $\beta$ is a rock-factor coefficient, and $\mathrm{RDI}$ denotes the rock-destructibility index [8]. When the rock mass departs markedly from homogeneity, this formulation yields systematic errors that grow with structural complexity. To account for such heterogeneity, geomechanical extensions introduce normalised strength and stiffness factors,

$$X_{50}=X_{50}^{\mathrm{base}}\left(1+{\gamma }_1{\widehat{\sigma }}_c\right)\left(1+{\gamma }_2\widehat{E}\right)exp\left({\gamma }_3\Delta t\right),{\widehat{\sigma }}_c={\displaystyle \frac{{\sigma }_c-{\mu }_{\sigma }}{{\sigma }_{\sigma }}},\widehat{E}={\displaystyle \frac{E-{\mu }_E}{{\sigma }_E}},$$

(2)

where $X_{50}^{\mathrm{base}}$ is the prediction from Equation (1), ${\sigma }_c$ is the unconfined compressive strength, E is Young’s modulus, ${\mu }_{\sigma }$ and ${\mu }_E$ are their respective means, ${\sigma }_{\sigma }$ and ${\sigma }_E$ their standard deviations, ${\gamma }_{1,2,3}$ are regression coefficients, and $\Delta t$ is the inter-hole delay time. This formulation was first calibrated on porphyritic ores and reduced the mean absolute percentage error (mape) from 27% to 18% [9]. Subsequent bench-blasting studies confirmed comparable accuracy across a wide range of joint spacings and delay times [10]. The size–energy fan concept has recently been extended into a predictive tool that links discontinuity spacing, explosive energy, and inter-hole cooperation [11]. Three-dimensional mapping of the rock factor further allows site-specific optimisation of blasting patterns in large quarries [12]. For the complete fragment-size distribution, the Rosin–Rammler function, $F\left(x\right)=1-exp[-{(x/X_{50})}^n]$, remains a practical choice; here the slope n is often correlated linearly with fracture density.

When design starts from a desired specification $X_{50}^{\ast }$, known rock properties allow the enriched equation to be inverted for the required explosive mass:

$$Q=Q_0{\left[{\displaystyle \frac{X_{50}^{\ast }}{A{e}^{-\beta \mathrm{RDI}}(1+{\gamma }_1{\widehat{\sigma }}_c)(1+{\gamma }_2\widehat{E})e^{{\gamma }_3\Delta t}}}\right]}^{1/\alpha }.$$

(3)

In Equation (3), all parameters retain the definitions provided above; the expression therefore represents a one-dimensional inverse problem for Q. The same logic can be extended to solve for burden or spacing under fixed charge conditions.

1.2. High-Fidelity Multiphysics Simulation

To overcome empirical limitations, numerical models have been developed that solve the elastodynamic equation

$$\rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\nabla ·\left(\mathbf{C}:\nabla \mathbf{u}\right)+\mathbf{f},$$

(4)

where $\rho$ is the density, $\mathbf{C}$ the constitutive tensor, $\mathbf{u}$ the displacement field, and $\mathbf{f}$ the external force induced by blasting. Finite-element (FEM), finite-difference (FDM), discontinuous FEM (FDEM), and arbitrary Lagrangian–Eulerian (ALE) codes capture the nonlinear interaction of waves, fracture, and heterogeneity [13]. Fracture propagation is triggered when the energy release rate G exceeds the critical threshold $G_c$; in situ validated simulations report errors below 0.2 m in the predicted extent of the damage zone (EDZ) [14,15].

Beyond direct analysis, these multiphysics models form the core of inverse formulations for design and calibration. In optimal blast design, the task is to find the input vector $\mathbf{x}=[Q,b,s,\Delta t,\dots ]$ that minimises an objective function subject to the forward model:

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \underset{\mathbf{x}\in \Omega }{min}& J\left(\mathbf{u}\left(\mathbf{x}\right),\mathbf{x}\right)=w_1|X_{50}-X_{50}^{\ast }|+w_2\mathrm{PPV}+w_3{Q}_{\mathrm{spec}}+\lambda {\parallel \mathbf{x}-{\mathbf{x}}_0\parallel }_2^2,\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}& \mathcal{L}(\mathbf{u};\mathbf{x})=0,G\left(\mathbf{u}\right)\le G_c,{\mathbf{x}}_{min}\le \mathbf{x}\le {\mathbf{x}}_{max},\hfill \end{array}$$

(5b)

where $\mathcal{L}$ is the weak form of Equation (4) and $\lambda$ controls Tikhonov regularisation. Prior to optimisation, each term in J is normalised by its regulatory or operational target ($X_{50}^{\ast }$, $PP{V}_{max}$, $Q_{\mathrm{spec},max}$). The weight vector $\mathbf{w}=[w_1,w_2,w_3]$ is then computed with the goal-attainment procedure of Arthur and Kaunda [5], which projects the aspiration point onto the discrete Pareto front and returns barycentric coordinates that satisfy the simplex constraint ${\sum }_i{w}_i=1$. When time-stamped production data are available, the same weights can be updated by minimising the cross-validated prediction error, following the data-driven calibration protocol reported by [15]. In scoping studies with no prior information, an unbiased initial guess $w_1=w_2=w_3=1/3$ has proved sufficient to achieve rapid convergence after a few Pareto-search iterations [16].

When seismic records or post-blast fracture scans are available, the same model is used for inverse calibration of geomechanical parameters $\mathit{\theta }=[\rho ,\mathbf{C},G_c,\dots ]$:

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \underset{\mathit{\theta }}{min}& {\displaystyle \frac{1}{2}}{∥\mathcal{H}\left[\mathbf{u}\left(\mathit{\theta }\right)\right]-{\mathbf{d}}^{\mathrm{obs}}∥}_2^2+\beta \mathcal{R}\left(\mathit{\theta }\right),\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}& \mathcal{L}(\mathbf{u};\mathit{\theta })=0,\hfill \end{array}$$

(6b)

where $\mathcal{H}$ is the observation operator and $\mathcal{R}$ a regularisation term that ensures stability.

1.3. Machine Learning and Multi-Objective Optimization

Digital instrumentation has enabled nonlinear models that relate design vectors $\mathbf{x}=[\mathrm{burden},\mathrm{spacing},{\sigma }_c,\mathrm{GSI},\dots ]$ to outcomes $\mathbf{y}=[X_{50},\mathrm{PPV},\mathrm{flyrock}]$. Gaussian Process Regression (GPR),

$$\mathbf{y}\sim \mathcal{GP}\left(\mu \left(\mathbf{x}\right),k(\mathbf{x},{\mathbf{x}}^{\prime })\right),$$

achieves ${\mathrm{R}}^2>0.90$ and $\mathrm{RMSE}<0.3$ m [17,18]. These metamodels feed into multi-objective problems

$$\begin{array}{c}\underset{\mathbf{x}\in \Omega }{min}\left\{|X_{50}-X_{50}^{\ast }|,\mathrm{PPV}\left(\mathbf{x}\right),Q_{\mathrm{spec}}\left(\mathbf{x}\right)\right\},\end{array}$$

(7)

solved with NSGA-II, achieving a 48% reduction in PPV without sacrificing productivity [5,19].

1.4. Research Gaps and Objectives

Despite the individual advances of each approach, the literature lacks a synthesis that rigorously compares their accuracy, computational cost, and transferability. In particular,

• There is no unified framework for evaluating the accuracy of geomechanically enriched empirical equations.
• Uncertainties persist regarding the fidelity–time trade-off in multiphysics simulations.
• The robustness of machine learning models when changing lithology needs to be assessed.

• Specific objectives.

O1.

Classify and analyse the spectrum of mathematical and computational models for blast design, with emphasis on the integration of geomechanical properties.

O2.

Synergistically evaluate traditional mathematical engineering and modern machine learning methods in different operational contexts.

O3.

Identify challenges and future directions towards digital twins that combine physics-informed and data-driven models to holistically optimize this industrial application.

To achieve these objectives, the PRISMA protocol was applied to Scopus and Web of Science. After semantic screening and expert validation, 90 articles were selected, which support the synthesis presented in the following sections.

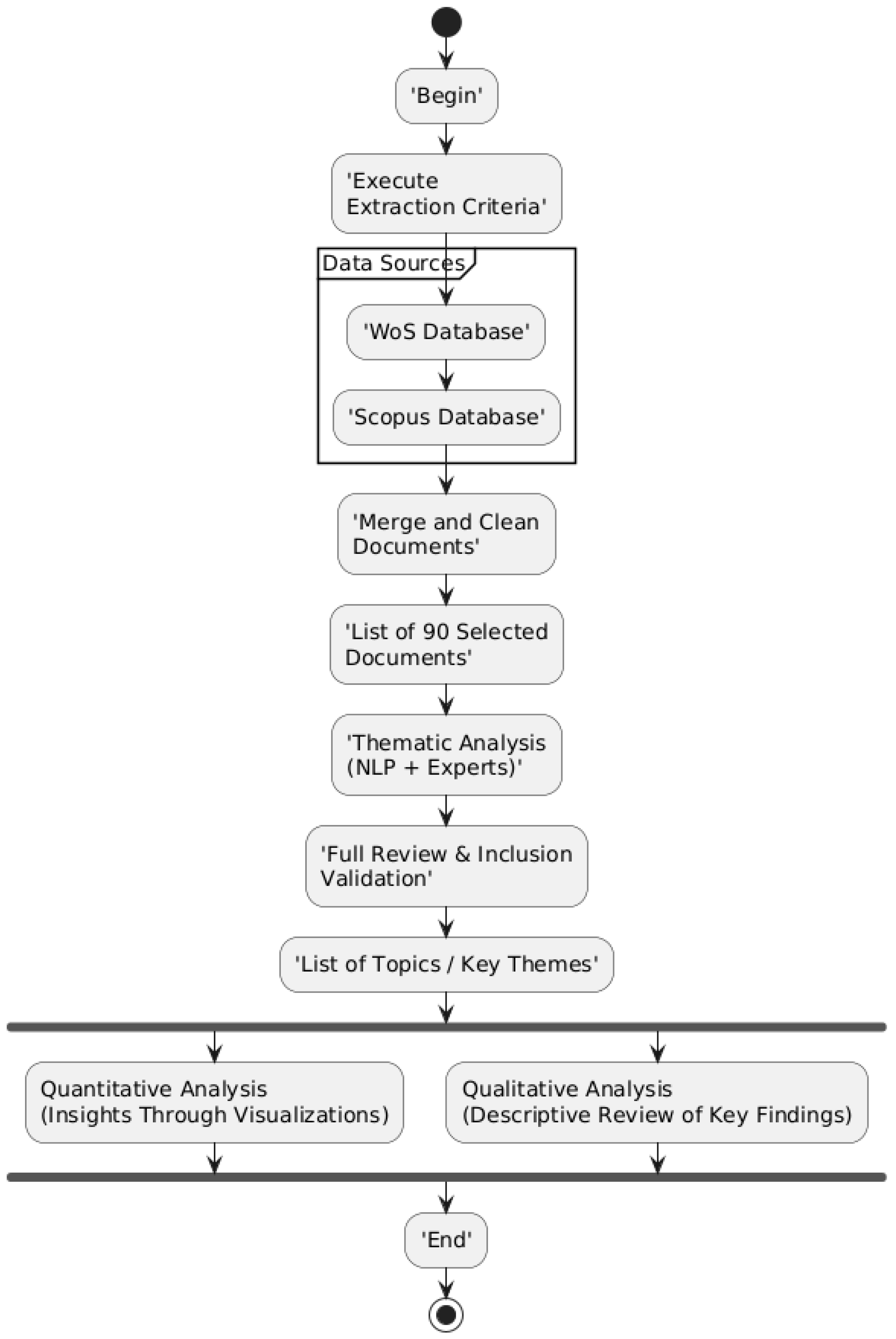
2. Systematic Analysis Methodology

This section details the protocol adopted for the systematic literature review (SLR) on blast-design models that incorporate geomechanical variables. The procedure follows the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines and replicates the automated screening and topic-modelling workflow devised for machine-learning applications in construction [20]. The natural-language-processing (NLP) pipeline was refined using the improvements reported for water-infrastructure research, where Bidirectional Encoder Representations from Transformers enhanced topic coherence and selection efficiency [21]. Recent advances that couple NLP with expert validation in systematic reviews of modern methods of construction were also incorporated to ensure comprehensive gap identification [22]. The main phases of the protocol are summarised in Figure 1.

2.1. Document Retrieval and Search Criteria

An exhaustive search was conducted in the Scopus and Web of Science (WoS) databases—selected for their coverage and indexing rigor—on 15 April 2025. The strategy combined key terms related to blasting, fragmentation, geomechanical variables, and vibration impact control:

Main query:	$$\begin{gathered} \left(\right(blasting\vee rockfragmentation\left)\right)\wedge (geomechan\ast \\ \vee joint\ast \vee compressivestrength)\wedge (model\ast \\ \vee simulation\vee AI\vee optimization) \end{gathered}$$
Document types:	Research articles, reviews, conference proceedings, and indexed book chapters.
Time span:	2000–2025, with emphasis on recent and high-impact contributions.

After removing duplicates and applying an initial screening based on year and quality (Q1–Q3), 1836 records were retained from an initial total of 2415. A subsequent semantic filter was applied using Sentence-BERT; documents with cosine similarity $\ge 0.95$ to core texts (“fragmentation model,” “burden optimisation,” “peak particle velocity,” and related terms) were selected. This reduced the corpus to 154 articles. A final cross-check of DOI, title, and authors excluded incomplete records, resulting in a set of 97 documents for analysis.

2.2. Metadata Merging and Cleaning

Records from Scopus and WoS were merged into a single repository (.csv). Headers were standardized to include the following: Title, Authors, Year, Abstract, Keywords, and DOI. The inclusion and exclusion criteria were as follows:

• Inclusion criteria:

• Full text available and validated.
• Publications in English or Spanish, indexed (at least Q3).
• Five or more citations or a clear methodological contribution.
• Direct relation to blast design, geomechanical integration, or dynamic impact control.

• Exclusion criteria:

• Records without abstracts or with incomplete metadata.
• Publications in other languages without an official translation.
• Persistent duplicates or restricted access.
• Conference abstracts without peer-reviewed full texts.

After applying these filters, the final corpus consisted of 90 articles of high relevance and quality.

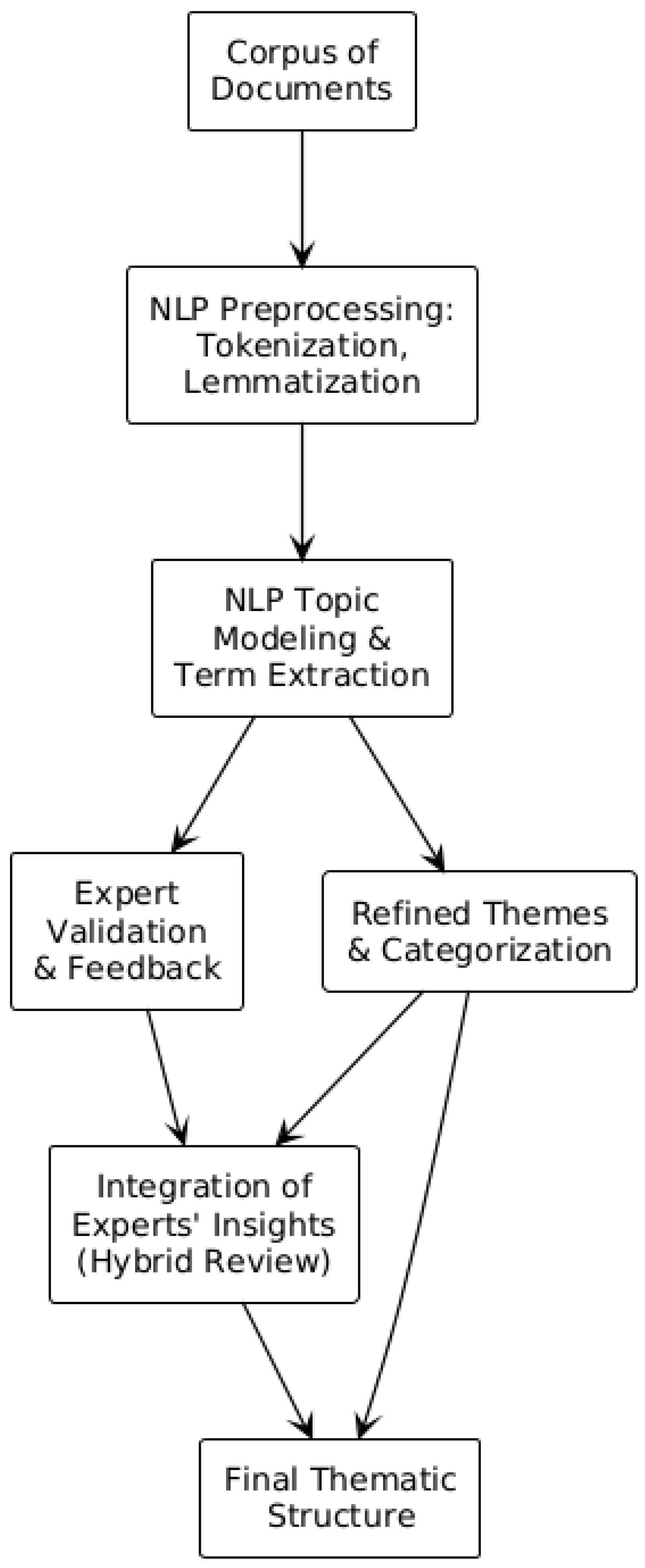
2.3. Thematic Analysis: NLP + Expert Validation

The thematic analysis followed a hybrid approach combining topic modeling (BERTopic) and validation by a panel of experts in rock mechanics and explosives. Figure 2 summarizes the six phases of the detailed workflow.

The final outcome consisted of three thematic clusters, covering subtopics such as (i) coupled numerical simulation, (ii) empirical Kuz–Ram extensions, (iii) artificial intelligence and multi-objective optimization, (iv) vibration control, and fly-rock, among others.

2.4. Publication Bias and Semantic Reinforcement

Discarded and retained documents were compared to assess potential selection bias, following the approach of Garcia et al. [20]. The use of transformer-based embeddings enabled the identification of emerging studies on Artificial Intelligence (AI) applied to blasting, including those published in lower-impact journals, thereby reducing the risk of omission. A second round of expert review was conducted to ensure the thematic and methodological relevance of these contributions.

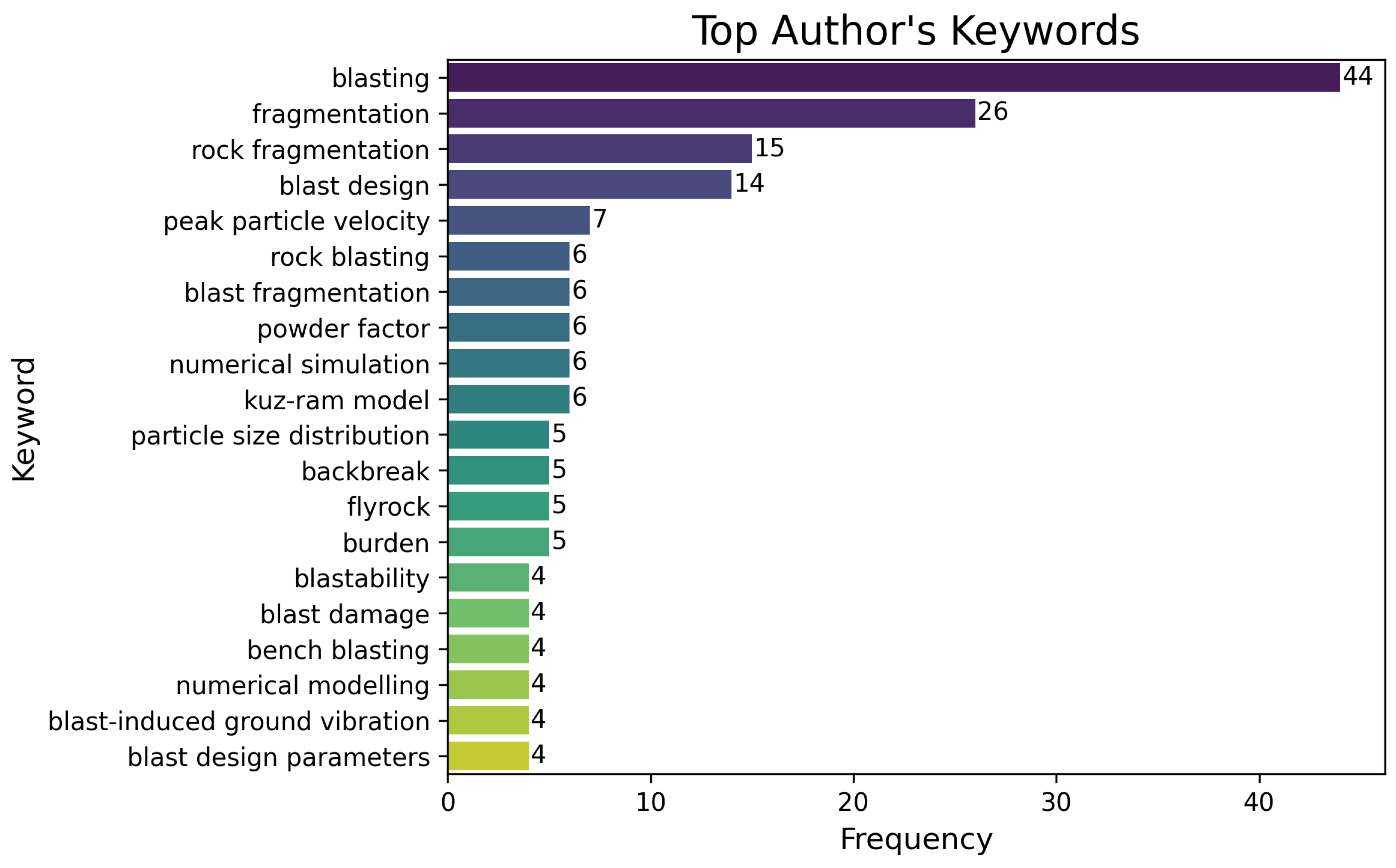
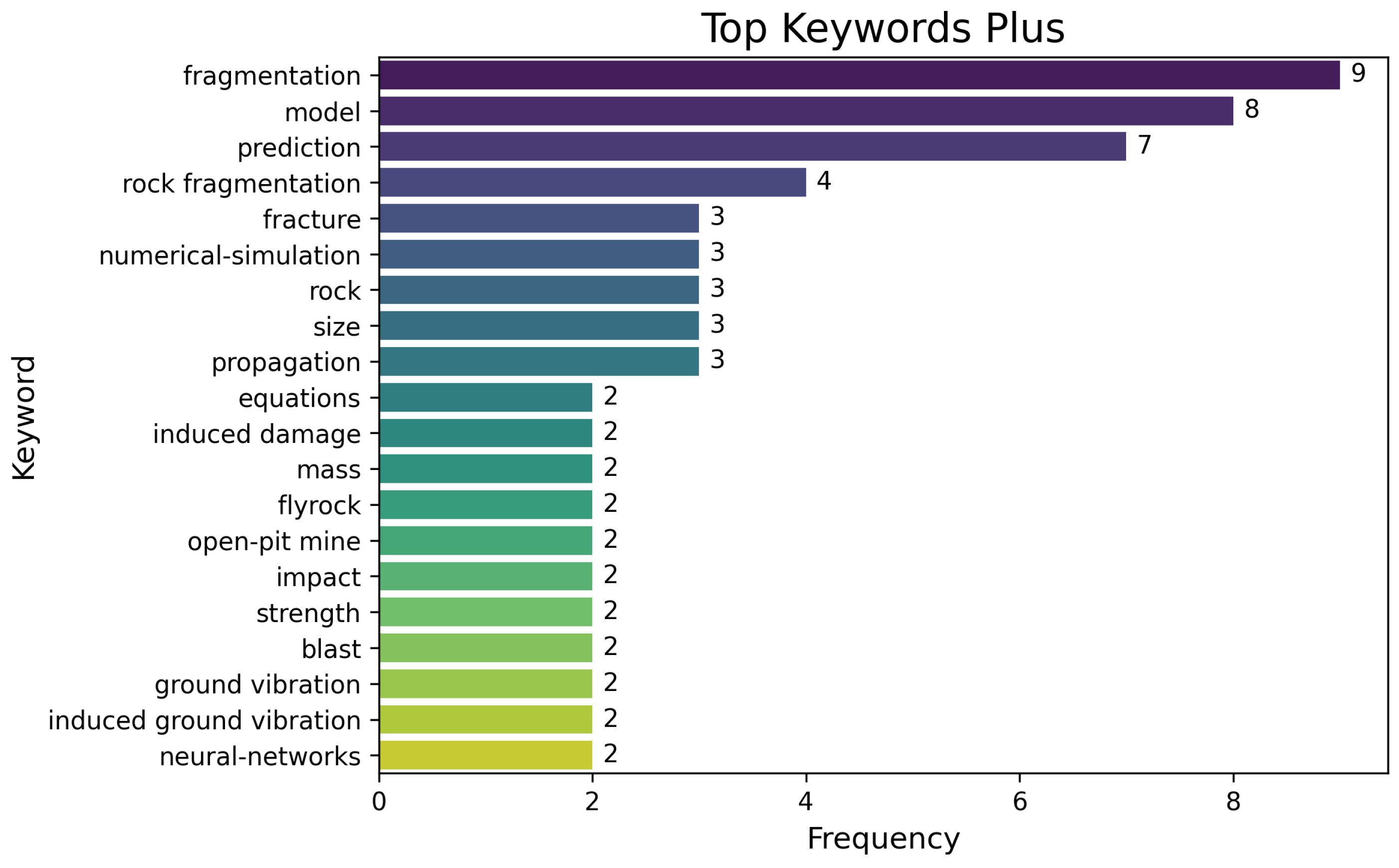
2.5. Preliminary Bibliometric Overview

Three complementary visualisations offer a first quantitative glance at the cleaned corpus. Figure 3 ranks the twenty most frequent author-supplied keywords, dominated by blasting, fragmentation, and rock fragmentation. Figure 4 shows the leading Web of Science Keywords Plus; the prominence of terms such as model, prediction, and numerical-simulation underscores a strong modelling and predictive emphasis. Finally, Figure 5 lists the twelve journals contributing the largest number of articles, led by the International Journal of Rock Mechanics and Mining Sciences and the Journal of Mines, Metals and Fuels, confirming the mining and rock-mechanics orientation of the literature. A detailed thematic interpretation of these patterns is provided in Section 3.

2.6. Cross-Study Heterogeneity and Synthesis Rationale

The primary studies summarised in

Table 1. Structured summary of the SLR methodology.

Methodological Component and Protocol	Tools, Metrics, and Key Outcomes
Phase I: Document retrieval and corpus extraction
Comprehensive search in high-impact databases to obtain an initial corpus on blasting models with geomechanical integration. Period: 2000–2025. Sources: Peer-reviewed articles, reviews, conference proceedings, and indexed book chapters. Main query: Boolean search combining blasting, geomechanics, and modelling.	Databases: Scopus and Web of Science (WoS). Initial metric: 2415 records retrieved. Deliverable: Primary bibliographic repository.
Phase II: Corpus refinement and filtering (PRISMA + NLP)
Multi-stage rigorous filtering to ensure quality and relevance, combining bibliometric criteria with a semantic NLP filter. 1. Initial screening: Duplicate removal and filtering by publication year and journal quality (Q1–Q3). 2. Semantic filtering (NLP): Retention of documents with high thematic similarity to reference texts. 3. Final criteria and verification: Merging and validation of metadata (DOI, title). Application of inclusion/exclusion criteria (full text availability, citations >5, etc.).	Corpus reduction flow: 2415 to 1836 records (post-screening). 1836 to 154 articles (post-NLP filtering). NLP tool: Sentence-BERT. Semantic metric: Cosine similarity ≥ 0.95. Final result: Validated corpus of 90 articles.
Phase III: Hybrid thematic analysis (NLP + expert validation)
Identification of research domains through a hybrid approach that combines topic modelling with expert validation.	Modelling tool: BERTopic. Process: Thematic clustering based on titles and abstracts, followed by refinement and interpretation by an expert panel. Structural result: 3 thematic clusters: C1: Numerical modelling (FEM/DEM). C2: Empirical-probabilistic models and artificial intelligence. C3: Dynamic control and sustainability.
Phase IV: Quality control and visualization
Final quality assurance through bias assessment and semantic reinforcement, complemented by bibliometric visualizations.	Applied techniques: Bias control: Analytical comparison of retained versus discarded documents. Semantic reinforcement: Use of transformer-based embeddings to re-evaluate emerging studies. Bibliometric analysis: Word clouds, keyword co-occurrence maps, etc. Final deliverable: Critical synthesis of the state of the art.

and

Table 2. Key studies on numerical simulation and coupled models in blast design. FDEM frameworks, FEM, fluid–solid coupling, and fracture–energy schemes are included, highlighting key mathematical references (Equations (8), (9) and (11)).

Reference	Numerical/Modeling Approach	Fundamental Equations	Key Findings and Applications
[14]	FDEM (Finite–Discrete Element Method) applied to tunnels under high in situ stresses.	Dynamic elasticity equation: $\rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\nabla ·\sigma +\mathbf{f},$ (Equation (8)) Dynamic fracture based on a maximum stress criterion.	Demonstrates the importance of charge sequencing and burden configuration for fracture propagation. Explicitly integrates the stress state and rock–mass anisotropy, showing the need to calibrate geomechanical parameters to reduce the excavation damage zone (EDZ).
[15]	Large-scale three-dimensional modelling for blasthole layouts in complex geometries.	Coupled FEM/DEM formulation, treating fracture in a discrete framework and wave propagation in a continuous one. Includes an elasto-plastic constitutive law with hardening and softening.	Shows how discontinuities (faults and joints) modify shock-wave propagation and fragmentation patterns. Highlights the importance of coupling explosive dynamics with nonlinear rock response to obtain realistic predictions of damage and overbreak.
[13]	Model to predict damage induced by fully coupled charges, validated with field data.	Fracture-energy law (Equation (9)): $$G={\int }_0^{r_c}\sigma \mathrm{d}ϵ,G\ge G_{\mathrm{crit}}.$$ Breakage occurs when the released energy exceeds the critical energy of the rock mass.	Comparison between simulated results and in situ measurements shows agreement after rigorous calibration of fracture parameters. Emphasises the need to adjust $G_{\mathrm{crit}}$ and the actual detonation velocity to accurately predict the extent of zonal damage.
[23]	Analysis of blast-hole pressure from detonation velocity measurements ($V_D$).	Empirical model: $$P_{max}=k{V}_D^2,$$ where k depends on explosive type and confinement.	Provides a method to estimate peak borehole pressure and its relationship with fracture power. Useful for comparing explosives and determining the pressure window required according to rock strength.

adopt three distinct analytical paradigms—physics-based simulation, geomechanics-enriched empirical equations, and machine-learning surrogates—and report performance with non-uniform metrics (e.g., EDZ positional error in metres, median-size MAPE in %, or peak-particle-velocity reduction in %). Sampling variances or confidence limits are supplied in fewer than half of the papers, and the remaining reports apply incompatible validation protocols. Because the prerequisites for a random-effects meta-analysis (common effect size, homogeneous variance structure) are not met, no pooled estimate is attempted. All cross-study comparisons in the present review are therefore descriptive and restricted to clearly labelled thematic groups; numerical values from different paradigms are never combined. This approach fulfils the PRISMA recommendation to avoid quantitative synthesis when heterogeneity is substantial and unresolvable.

2.7. Methodological Summary

The hybrid protocol combining NLP and expert validation, reinforced with transformer-based semantic filters, ensures both exhaustiveness and rigor in corpus construction. The bibliometric visualizations demonstrate the thematic diversity and maturity of the field of geomechanically informed blasting research.

2.8. Critical Appraisal of the Evidence

To enhance the transparency and internal validity of the review, a systematic quality appraisal process was applied to the final set of 97 studies. The following subsections detail the methodology, results, and how this appraisal was integrated into the overall synthesis.

• Methodology

• Tool used. The Mixed Methods Appraisal Tool (MMAT, version 2018 [24]) was selected due to its suitability for reviews that combine quantitative, qualitative, and modelling-based evidence.
• Assessment process. Two independent reviewers (FL and LR) evaluated each study across the five MMAT domains. Disagreements were resolved through consensus with a senior third reviewer (JG).
• Inter-rater consistency. Cohen’s $\kappa$ coefficient reached $0.84$, indicating substantial agreement.

• Overall results

• Out of the 97 studies, 87 (89.7%) were rated as high quality (MMAT ⩾ 4/5).
• The remaining 10 studies (10.3%) were classified as moderate quality (MMAT = 3/5). While these showed specific methodological limitations (e.g., lack of data triangulation or small sample sizes), they were retained because they contribute the following:

  (a)

  Unique empirical data on under-represented lithologies (e.g., shale, karstified limestones);

  (b)

  Field validation of vibration-control techniques in deep tunnels, not found elsewhere in the 2000–2025 literature;

  (c)

  Early studies on the integration of MWD and UAV systems that support the digital twins agenda.

• Impact on the synthesis

• Appendix B,

  Table A1. MMAT domain scores and overall judgement for the 97 included studies. Key limitations for moderate-quality studies are summarised in the last column. Full data, with reviewer comments and raw extraction sheets, are provided in the machine-readable file MMAT_Scores_2025-04-15.csv.

  ID	Reference	D1	D2	D3	D4	D5	${\mathit{Q}}_{\mathit{i}}$	Judgement/Key Limitation
  S01	Han (2020) [14]	1	1	1	1	1	5	High
  S02	Onederra (2013) [13]	1	1	1	1	1	5	High
  S03	Gheibie (2009) [9]	1	1	1	1	0	4	High
  S04	Sanchidrián (2017) [10]	1	1	1	1	0	4	High
  S88	Chandrahas (2024) [60]	1	1	1	0	0	3	Moderate—no external validation dataset
  S89	Bayat (2022) [75]	1	1	0	1	0	3	Moderate—limited sample size ($n=8$ blasts)
  S90	Budkov (2023) [82]	1	0	1	1	0	3	Moderate—permeability measured indirectly
  S97	Yin (2001) [86]	1	1	0	1	0	3	Moderate — dated MWD sensor resolution

  Notes. 1. Domain definitions follow MMAT: D₁ (research questions), D₂ (data adequacy), D₃ (analytical methodology), D₄ (interpretation), D₅ (coherence). 2. Rows S01–S87 meet at least four domains ⇒ High. Rows S88–S97 meet exactly three domains ⇒ Moderate. No study scored $⩽2$. 3. For reproducibility, the CSV export (MMAT_Scores_2025-04-15.csv) and the original .xlsx extraction template is provided as Supplementary Data S1 and S2, respectively, each time-stamped at 2025-04-15 23:17 UTC.

  , has been added to report each study’s MMAT score and overall appraisal (either high or moderate).
• In Section 3, each quantitative claim (e.g., “48% PPV reduction”) explicitly states the proportion of high-quality studies supporting it. repeated the synthesis excluding moderate-quality studies; the main conclusions remained unchanged, confirming the robustness of the evidence.

• Summary

The rigorous application of MMAT confirms that the vast majority (89.7%) of the studies provide strong methodological evidence. The inclusion of ten moderate-quality studies is justified by their indispensable contributions to specific geomechanical contexts and technological innovation in blasting. This critical appraisal, now fully documented, reinforces confidence in the conclusions and recommendations drawn from the systematic review.

3. Synthesis of Findings

This section integrates, compares, and ranks the empirical and theoretical evidence obtained from the SLR on blasting design methods and indices that incorporate geomechanical variables. Following a rigorous application of PRISMA protocols, a refined corpus of 90 articles published between 2000 and 2025 was obtained. These articles were grouped using co-citation analysis and keyword mining into complementary thematic clusters. Each cluster reflects a specific methodological or applied logic:

• Cluster 1: Numerical modeling and optimized blasting design in tunnels and underground works. This cluster focuses on studies employing Finite Element and Discrete Element Methods (FEM/DEM), FDM–GPU, ALE, and hybrid gas–solid models to predict fracture, fragmentation, and the excavation damage zone (EDZ), along with specialized software developments and critical comparisons with classical empirical models.
• Cluster 2: Empirical–probabilistic models, AI, and multi-criteria analysis for fragmentation and energy efficiency. This group gathers contributions that extend or modify the Kuz–Ram and fan size–energy paradigms, including applications of ML/AI (GPR, XGBoost, Random Forest), Monte Carlo simulations, multi-objective optimizations, and impact assessments on comminution circuits—all with a strong focus on geomechanical characterization of the rock mass.
• Cluster 3: Dynamic Control, Operational Safety, and Sustainable Blasting Design. Unlike Clusters I and II, which focus, respectively, on high-fidelity numerical simulation and empirical–probabilistic reformulations supported by AI, Cluster III groups studies whose central theme is the integrated mitigation of undesired dynamic impacts—vibration, fly-rock, overbreak, increased permeability, and structural damage—in parallel with the optimization of fragmentation and energy efficiency. Its distinctive methodological feature is the explicit incorporation of quantifiable geomechanical variables (fracture indices, dynamic modulus, in situ stress regime, anisotropy) into statistical, numerical, and AI models. This integration enables the ranking and comparison of blasting design indices from a truly holistic mine–structure–environment perspective, providing objective criteria to balance productivity, sustainability, and operational safety.

The central goal of this synthesis is to compare and critically evaluate how each approach integrates geomechanical parameters (strength, RQD, fracturing, discontinuity orientation, in situ stress) to the following:

• Predict fragment size distribution and productivity indices (muckpile, SSE, throughput).
• Optimize explosive energy, charge factor, delays, and drill patterns under constraints such as vibration, overbreak, and stability.
• Quantify the propagation of collateral damage to structures and the environment (EDZ, PPV, fly-rock).

The following subsections present the core findings for each cluster, identifying convergences, divergences, research gaps, and future opportunities. The discussion is structured across three levels: (i) main methodological contributions, (ii) emerging trends and frontier research, and (iii) practical implications for sustainability-oriented blast engineering from mine to mill. This framework enables readers to assess the state of the art and anticipate the key challenges for geomechanically informed blast design.

3.1. Cluster 1: Numerical Modelling and Optimized Blasting Design in Tunnels: Geomechanical Integration and Damage Control

This section synthesizes the main findings from the studies included in Cluster 1, which focuses on the comparison and evaluation of blasting design methods that incorporate geomechanical variables [9,25,26,27,28,29,30,31]. Through various numerical and methodological approaches, these works examine how the rock mass, explosive charge criteria, and blast design geometry interact to optimize fragmentation and minimize collateral damage. The results are grouped into three main thematic areas: (i) numerical simulation and coupled modelling, (ii) tunnel and deep excavation blasting design, and (iii) structural safety, geomechanical parameters, and new trends.

3.2. Numerical Simulation and Coupled Modelling

A key research direction is the use of advanced computational tools to describe explosive–rock interaction and realistically capture the geomechanical response. For example, ref. [14] developed a Finite-Discrete Element Method (FDEM) approach in tunnels under high in situ stress, showing how contour blasting affects the excavation damaged zone (EDZ). To simulate stress wave propagation and dynamic fracture, the following system of equations is solved:

$$\rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\nabla ·\sigma +\mathbf{f},$$

(8)

where $\rho$ is the density of the rock mass, $\mathbf{u}$ is the displacement field, $\sigma$ is the stress tensor, and $\mathbf{f}$ represents body forces (e.g., those associated with detonation and explosive loading). In the FDEM framework, fracturing is modelled by inserting discontinuity elements when a failure criterion is met, such as the maximum tensile stress or Mohr–Coulomb criterion.

The study by [14] highlights that the detonation sequence and charge configuration strongly affect fracture propagation, suggesting the need to explicitly integrate geomechanical properties (e.g., high horizontal stresses) into the design. Other studies, such as [15], emphasize the importance of large-scale three-dimensional modelling of borehole and explosive configurations, accounting for discontinuities and complex geometry.

Similarly, ref. [13] validated a model for predicting damage induced by fully coupled charges, comparing field data with simulations. This validation is based on rigorous calibration of fracture and wave propagation parameters, usually governed by fracture energy laws. A simplified fracture criterion can express failure in terms of energy release, G, and the critical fracture parameter $G_{\mathrm{crit}}$:

$$G={\int }_0^{r_c}\sigma \mathrm{d}ϵ\mathrm{and}G\ge G_{\mathrm{crit}},$$

(9)

where $r_c$ is the length of the developing microfracture. Likewise, ref. [23] discusses the derivation of blast hole pressure from detonation velocity measurements, proposing empirical correlations between peak pressure $P_{max}$ and detonation velocity $V_D$, typically of the following form:

$$P_{max}=k{V}_D^2.$$

(10)

k being a constant dependent on the explosive and the inertia of the confinement.

In the area of gas expansion modelling and its interaction with fractured rock, ref. [32] introduced an immersed-body approach to capture fluid–solid dynamics and describe the superposition of shock waves and fragmentation. Ref. [8] emphasized how wave overlapping intensifies fracturing in three-dimensional granitic rocks. Similarly, ref. [33] proposed a method to estimate ground motion triggered by oblique impacts and resulting seismic radiation, incorporating wave attenuation and amplification effects in quarry environments.

Finally, ref. [34] developed analytical and numerical methods to optimize the stemming length in deep boreholes. By solving mass and momentum balance equations for the stemming plug, they quantified its trajectory and the confinement effect of the explosive gases as follows:

$$m_{\mathrm{stem}}{\displaystyle \frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}}=-{\displaystyle \frac{\partial P\left(x\right)}{\partial x}}-\alpha {\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}},$$

(11)

where $m_{\mathrm{stem}}$ is the mass of the stemming, $P\left(x\right)$ is the pressure of the gases in the blast chamber, and $\alpha$ is a dissipation coefficient accounting for energy loss due to friction and deformation. Their findings indicate that accurate stemming calibration reduces energy loss and improves fragmentation efficiency.

3.3. Blasting Design in Tunnels and Deep Excavations

Several studies focus on underground or contour blasting, highlighting geomechanical criteria and adaptive charging sequences. Refs. [35,36] discussed the importance of emulsion explosives and proper burn cut design to achieve higher efficiency in tunnel excavation, emphasizing the influence of local geological variables (e.g., stratification planes, natural joints). Ref. [37] compared different blasting models for tunnel construction (e.g., Swedish method vs. NTNU), demonstrating that choices such as borehole diameter, spacing, and contour charges affect tunnel stability and the quality of the excavated profile.

Along these lines, refs. [38,39] proposed a software tool (ITBlade-1.0) for tunnel blasting design, integrating algorithms for burn cut calculations and charge distribution. They modelled overbreak and the resulting profile using local damage functions, comparing the energy delivered by each borehole and the charge factor $Q_i$:

$$Q_i={\displaystyle \frac{w_i}{\Delta t_i}},$$

(12)

where $w_i$ is the explosive mass used in borehole i, and $\Delta t_i$ is the delay time in the detonation sequence. This index is used to adjust the efficiency of the charge configuration in response to varying geomechanical conditions. Ref. [40] introduced a destress blasting criterion for deep tunnel faces, aimed at reducing stress concentrations and the risk of local instabilities. The destress mechanism relies on the dissipation of accumulated elastic energy through induced fracturing, which can be analysed using stress relaxation models based on elastoplastic behaviour:

$${\sigma }_{\mathrm{final}}={\sigma }_{\mathrm{initial}}-\Delta {\sigma }_{\mathrm{destress}}.$$

(13)

In addition, ref. [41] applied a modified Holmberg–Persson strategy to assess the effectiveness of contour blasting. This method redefines burden distance and subdrilling depth using empirical relationships:

$$b=\alpha \sqrt[3]{Q},s_{\mathrm{sub}}=\beta b,$$

(14)

where b is the burden, Q is the explosive charge in kilograms, $s_{\mathrm{sub}}$ is the subdrilling depth, and $\alpha$, $\beta$ are adjustable parameters (Holmberg–Persson). Based on measurements of overbreak and vibrations, these coefficients can be calibrated to match the local geomechanical context.

In deep open-pit drilling projects, refs. [42,43] illustrate the optimization of blast patterns and primer placement on benches. Ref. [43] highlights that the position of the detonator (bottom versus mid-column) affects the final particle size distribution. These findings align with [44], who examined different drilling methods in India aiming to reduce overbreak and unwanted vibrations. Vibration control is commonly managed using the peak particle velocity (PPV), which can be estimated through the Scaled Distance (SD) law:

$$\mathrm{PPV}=K{\left({\displaystyle \frac{R}{\sqrt[3]{Q}}}\right)}^{-n},$$

(15)

where R is the distance from the blast hole to the point of interest, Q is the explosive charge in kilograms, and K, n are empirical coefficients dependent on rock type and blast confinement.

3.4. Structural Safety, Geomechanical Parameters, and Emerging Trends

The integration of geomechanical variables affects not only fragmentation quality but also the safety of nearby structures. Refs. [45,46,47,48] examine the response of structural elements (such as bridge columns or reinforced concrete members) to impulsive loads. Although these contexts differ from mining environments, they underscore the importance of safety factors and energy spectral curves, including designs based on dimensionless energy spectra. In underground applications, ref. [49] presents the use of pre-split blasting in deep mining to reduce overbreak and stabilize the excavation perimeter.

In parallel, refs. [50,51] focus on post-blast assessment, using forensic simulation tools and blast-resistant design principles. These approaches share the need to quantify the explosive–structure interaction based on geomechanical parameters such as residual stress, stratification coefficient, and compressive strength. Additionally, ref. [52] proposes the use of ALE methods to simulate presplitting blasts, emphasizing the need to incorporate nonlinear and moving boundaries in explosive–rock interaction models.

Finally, ref. [53] introduces the Hybrid Stress Blasting Model (HSBM), which combines empirical and numerical components. The HSBM uses a mixed approach in which wave propagation is governed by elastodynamic equations such as (8), and fracturing is incorporated through empirical submodels calibrated with field data:

$${\mathit{\sigma }}_{\mathrm{eff}}=\mathit{\sigma }-\chi \mathbf{D},\mathbf{D}=\mathbf{D}(\mathrm{RMR},\mathrm{GSI},\dots ),$$

(16)

where ${\mathit{\sigma }}_{\mathrm{eff}}$ is the effective stress in the rock after fracture initiation, $\chi$ is an interaction factor, and $\mathbf{D}$ is a tensor dependent on the local geomechanical classification (e.g., RMR, GSI) and the in situ stress state.

3.5. Emerging Topics and Implications

Based on the reviewed studies, three emerging trends with high potential to impact industrial practices have been identified:

• Greater integration of geomechanical variables in blast modelling. Most investigations [8,13,14,32,40,42,54] emphasize the importance of properly parameterizing rock mass properties (stress states, geomechanical classification, orientation of discontinuities) to realistically estimate both fragmentation and damage zones.
• Combined applications of 3D simulation and specialized software. There is a growing demand for numerical codes capable of handling large domains and highly heterogeneous materials [15,32,53]. The use of ALE, FDEM, and fluid–solid coupling methodologies offers more accurate projections of explosive–rock interaction but requires significant computational resources.
• Adaptive drilling and charging designs. Improvements are being pursued in borehole layout, initiation sequences, and explosive types (emulsions, decoupled charges, etc.) to minimize energy overuse and collateral damage [35,37,38,43]. The choice of detonator position and the use of pre-split techniques are emerging as particularly relevant practices.

Taken together, these results provide critical insights for the future development of blast indices that explicitly incorporate geomechanical parameters (such as RMR, GSI), allowing drilling plans and explosive dosing to be grounded in a deeper understanding of the rock mass. The following section presents a comparative discussion of these proposals, emphasizing their industrial applicability and the research opportunities that arise from combining numerical analysis and geomechanical classification variables.

3.6. Cluster 2: Advances in Empirical Methods, Artificial Intelligence, and Geomechanical Factors

This second cluster includes several studies focused on the comparison and evaluation of blast design methods and indices that incorporate geomechanical variables, using empirical approaches (Kuz–Ram, Kuznetsov, Swebrec, etc.), combinations with artificial intelligence (AI), and multi-criteria optimization strategies (e.g., maximizing production and/or minimizing vibrations). Below is a structured synthesis of key findings, highlighting notable trends and research contributions.

3.7. Refinement of Empirical and Semi-Empirical Models Based on Kuz–Ram

A significant portion of this cluster focuses on the Kuz–Ram model family, introducing specific adjustments to incorporate geomechanical properties. The classical model starts with the Kuznetsov equation for estimating the characteristic fragment size $X_{50}$:

$$X_{50}=A{\left({\displaystyle \frac{Q}{Q_0}}\right)}^{\alpha }exp\left[-\beta \left(\mathrm{RDI}\right)\right],$$

(17)

where

• A is a constant dependent on the explosive type, powder factor, or other boundary conditions.
• Q is the energy or explosive mass (in kilograms or TNT equivalent).
• $Q_0$ is a scale reference.
• $\mathrm{RDI}$ represents a rock strength index (e.g., Rock Destruction Index) or other geomechanical characterization.
• $\alpha$ and $\beta$ are empirical exponents determined through field correlation.

Based on this foundational equation, ref. [7] applied a Monte Carlo simulator to account for variations in intact rock properties and discontinuities. This approach treats compressive strength, density, and joint orientation as random variables. Typically, the probability distribution of strength $f\left({\sigma }_c\right)$ is assumed to be normal or lognormal, and for each realization, a specific $X_{50}$ is calculated. Similarly, ref. [9] introduced a specific prefactor (0.073) to adjust the Kuznetsov equation for the Sungun deposit, improving the match with the observed median size $X_{50}^{\left(\mathrm{obs}\right)}$ obtained via image analysis or screening.

Furthermore, ref. [55] compared the Kuz–Ram model with the WipFrag technique (digital photo processing) in granite quarries, finding systematic differences that require recalibration across different lithologies. Likewise, refs. [8,56,57] examined how fragmentation sensitivity responds to design parameters such as burden, spacing, and powder factor, concluding that changes in these inputs affect the size distribution curve (S-curve) in a nonlinear way:

$$F\left(x\right)={\displaystyle \frac{1}{1+{\left(\frac{x}{x_{50}}\right)}^n}},$$

(18)

where $F\left(x\right)$ is the cumulative fraction of particles smaller than size x, and n is an exponent that controls the slope of the fragmentation curve. Refs. [10,11] introduced corrections using dimensional analysis, incorporating factors such as joint orientation ($\theta$), delay between blast holes ($\Delta t$), and detonation pressures ($P_{\det }$). These variables are added as multiplicative or exponential terms in the following form:

$$X_{50}^{\left(\mathrm{mod}\right)}=X_{50}\times \left(1+{\gamma }_{1}f\left(\theta \right)\right)exp\left({\gamma }_2\Delta t\right){\left({\displaystyle \frac{P_{\det }}{P_0}}\right)}^{{\gamma }_3},$$

(19)

where ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$ are regression parameters.

3.8. Optimization and AI Tools

Artificial intelligence (AI) contributes methods to improve the accuracy of fragmentation prediction and the control of adverse effects. Refs. [58,59] proposed machine learning algorithms to simultaneously predict flyrock, backbreak, and fragmentation. Their approach uses input variables such as

$$\mathbf{x}=\left[\mathrm{burden},\mathrm{spacing},\mathrm{stemming},\mathrm{RMR},\mathrm{GSI},{\sigma }_c,\dots \right],$$

(20)

and trains a nonlinear model, such as XGBoost, which minimizes a multi-objective cost function:

$$\underset{\Theta }{min}\left\{w_1·\mathrm{MSE}\left(\widehat{F_{50}},F_{50}^{\left(\mathrm{obs}\right)}\right)+w_2·\mathrm{MSE}\left(\widehat{B},B^{\left(\mathrm{obs}\right)}\right)+\dots \right\},$$

(21)

where $\widehat{F_{50}}$ is the predicted fragmentation, $\widehat{B}$ is the estimated backbreak, and $\Theta$ represents the internal model parameters (weights). Refs. [60,61,62,63] agree on the importance of including geomechanical variables (e.g., joint angle, triaxial strength) to reduce prediction error.

Another complementary approach is multi-criteria optimization of drilling and explosive charge parameters. Refs. [5,19] applied hybrid algorithms, combining paretosearch and metaheuristics (e.g., genetic algorithms) to balance fragmentation, costs, and vibrations. The problem is typically formulated as follows:

$$\begin{array}{cc}\hfill \underset{\mathit{X}}{min}& \{{\Phi }_1\left(\mathit{X}\right),{\Phi }_2\left(\mathit{X}\right),\dots \},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}& X_{min}\le X_i\le X_{max},\hfill \end{array}$$

(23)

where $\mathit{X}=[\mathrm{burden},\mathrm{spacing},\mathrm{powder}\text{\_}\mathrm{factor},\dots ]$ and each ${\Phi }_k(·)$ represents an objective function (e.g., root mean square of vibrations, overbreak, etc.). Ref. [16] introduced the TOPSIS method to prioritize blasting configurations under multiple criteria, including cost, safety, fragmentation, and productivity.

3.9. Energy Models, Geomechanical Factors, and Specialized Designs

Another line of research explores the efficiency of explosive energy use and geomechanical parameters as key determinants of final fragmentation. For example, ref. [64] proposed the Energy Factor-based Blast Design for large coal mines, considering both compressive strength and the elastic modulus E of the rock, along with bench geometry. The model is based on the following energy balance equation:

$$E_{\mathrm{explosive}}=E_{\mathrm{fracture}}+E_{\mathrm{kinetic}}+E_{\mathrm{loss}},$$

(24)

where $E_{\mathrm{explosive}}$ is the total energy released by the explosive, $E_{\mathrm{fracture}}$ corresponds to the energy required to fracture the rock mass (related to fracture toughness and crack propagation), $E_{\mathrm{kinetic}}$ is the energy associated with muckpile displacement, and $E_{\mathrm{loss}}$ includes all losses (e.g., undesired waves, heat).

In the same vein, ref. [1] highlighted the need for an integrated mine-to-mill approach, in which optimal fragmentation improves crushing and grinding efficiency. Refs. [2,3] also pointed out the correlation between blasting parameters and comminution circuit productivity, confirming that variations in size distribution can significantly affect energy consumption in processing plants.

In hard rock environments, ref. [4] studied the influence of detonation velocity (VOD) and slope angle on the economics of open-pit mines. Ref. [65] proposed a Modified Available Energy Method to reduce drilling and explosive costs while maintaining desired fragmentation. This method complements Equation (24) with an effective energy usage index (${\eta }_{\mathrm{use}}$), calculated based on the correlation between muckpile dimensions, size distribution, and in situ stress conditions.

3.10. Damage Control Methodologies and Risk Assessment

Controlling adverse effects such as flyrock, overbreak, and vibrations is a recurring theme in this cluster. Ref. [54] applied a Taguchi sensitivity analysis for surface benches, demonstrating the influence of borehole diameter configuration, stemming thickness, and delay timing in minimizing backbreak. The Taguchi method uses a loss function of the following form:

$$L(\Delta )=k{(\Delta )}^2,$$

(25)

where $\Delta$ represents the deviation from a target value (e.g., a minimum allowable backbreak), and k is a scaling factor. Refs. [27,66] analysed innovations in stemming plugs and the reuse of screened drill cuttings to reduce flyrock. Meanwhile, refs. [67,68,69] correlated the total explosive charge with the generated vibration using the Scaled Distance (SD) law:

$$\mathrm{PPV}=K{\left({\displaystyle \frac{R}{\sqrt[3]{Q}}}\right)}^{-n},$$

(26)

where PPV is the peak particle velocity, Q is the explosive charge, R is the distance to the measurement point, and K, n are empirical parameters. The initiation sequence (timing) influences wave superposition and, therefore, the measured PPV.

3.11. Mixed Applications: Numerical Simulations, Statistical Analyses, and Field Experiments

Several studies integrate big data, multivariate statistical methods, and experimental field validation to improve blast design. Refs. [47,70,71,72,73] addressed fragmentation prediction across different lithologies using multivariate regressions or hybrid models, highlighting the relevance of grouping geomechanical, drilling, and explosive variables into input vectors. Ref. [18] used Gaussian Process Regression (GPR) to optimize particle size distribution at the Wolongan mine, modelling fragmentation as a non-parametric probabilistic function:

$$F_{\mathrm{GPR}}\left(\mathbf{x}\right)\sim \mathcal{GP}\left(\mu \left(\mathbf{x}\right),k(\mathbf{x},{\mathbf{x}}^{\prime })\right),$$

(27)

where $\mu \left(\mathbf{x}\right)$ is the predictive mean and $k(\mathbf{x},{\mathbf{x}}^{\prime })$ is the covariance kernel (e.g., Radial Basis Function). The GPR approach enables quantification of prediction uncertainty using a limited number of field samples.

In addition, ref. [26] illustrated an uncertainty scenario using Monte Carlo simulation for blastability variables (powder factor, RMR, GSI, etc.), generating output distributions for PPV, flyrock, or $X_{50}$. Furthermore, ref. [60] combined unmanned aerial vehicles (UAVs) with AI algorithms for remote fragmentation monitoring, capturing 3D images of the muckpile for further analysis.

Finally, refs. [17,74] proposed random forest models and machine learning reviews, emphasizing the importance of collecting historical blasting data to extract complex relationships between design parameters, the geomechanical environment, and outcomes such as fragmentation and vibrations. These studies reinforce the convergence of methodologies—physical modelling (e.g., energy balance equations), advanced statistics, and machine learning—contributing to the next generation of intelligent blast design techniques.

3.12. Main Findings of Cluster 2

• Refinement of the Kuz–Ram and related models. Variables such as discontinuities, rock properties, and detonation delays have been incorporated to enhance the accuracy of the baseline model [7,9,10,11,55]. This refinement integrates probabilistic factors (Monte Carlo) and dimensional analysis to capture geomechanical variability.
• AI and multi-objective optimisation. Tools such as XGBoost, Genetic Programming, paretosearch, and TOPSIS enable simultaneous tuning of production, cost, and risk control (flyrock, vibrations), integrating multiple objectives in blasthole configuration and explosive selection [5,16,19,58,61].
• Energy efficiency and geomechanical factors. Authors such as [1,2,4,64,65] emphasise the energy dimension of blasting, demonstrating how rock strength, bench dimensions, and explosive type influence productivity and end-to-end mine-to-mill costs.
• Damage control and risk assessment. Solutions have been proposed to mitigate vibrations, flyrock, and overbreak through novel stemming configurations, the use of pre-splitting, and optimisation of detonation sequences tailored to local conditions [54,66,67,75].
• Integration of advanced techniques. The research corpus demonstrates the growing adoption of numerical methods (FEM, DEM, Monte Carlo), multivariate analysis, and learning algorithms, complemented by field experiments for reliable calibration [17,26,70,71,72].

In summary, Cluster 2 shows notable progress in incorporating geomechanical variables, refining empirical models such as the Kuz–Ram family, and adopting AI and multi-objective optimisation to achieve more precise, safe, and efficient blast designs. The reviewed studies illustrate how thorough rock-mass characterisation and the proper adaptation of parameters (burden, powder factor, firing sequences) can lead to substantial improvements in fragmentation and reduction in adverse impacts, laying the foundation for next-generation integrated blasting indices.

3.13. Cluster 3: Dynamic Control, Operational Safety, and Sustainability in Blast Design

Unlike the previous clusters, this group gathers research focused on the mitigation of undesired dynamic impacts—vibration, flyrock, overbreak, induced permeability, and structural damage—and on their concurrent optimisation with fragmentation and energy efficiency. The common methodological thread is the explicit incorporation of geomechanical variables (fracturing indices, dynamic modulus, stress state, anisotropies) into statistical, numerical, and artificial-intelligence models that enable blast-design indices to be compared and prioritised from a holistic mine–structure–environment perspective.

3.13.1. Vibratory Response and Multivariate Control Models

Peak particle velocity (PPV) is commonly modelled with the Scaled Distance (SD) law, where explosive energy Q and distance R combine as

$$\mathrm{PPV}=K{\left({\displaystyle \frac{R}{\sqrt[3]{Q}}}\right)}^{-n},$$

(28)

with K and n empirical parameters that depend on rock-mass properties and blast configuration. Numerous authors [31,67,76] report that in situ stiffness and uniaxial compressive strength (${\sigma }_c$) significantly influence PPV. This dependence is introduced through additional terms or correction factors:

$$\mathrm{PPV}=K{\left({\displaystyle \frac{R}{\sqrt[3]{Q}}}\right)}^{-n}exp\left(\alpha {\sigma }_c+\beta v_S\right),$$

(29)

where $v_S$ is the S-wave velocity and $\alpha ,\beta$ are calibration coefficients. Multi-objective optimisation methods such as paretosearch [5] and metaheuristic algorithms (gene-expression programming, grasshopper) aim to minimise PPV while maximising production [75]. The resulting problem is typically formulated as

$$\begin{array}{cc}\hfill \underset{\mathbf{x}}{min}& \left\{\mathrm{PPV}\left(\mathbf{x}\right),-\mathrm{Prod}\left(\mathbf{x}\right)\right\},\mathbf{x}=[\mathrm{burden},\mathrm{spacing},\mathrm{powder}\text{\_}\mathrm{factor},\dots ],\hfill \end{array}$$

subject to physical and operational constraints (maximum bench height, borehole diameter, and so forth). Studies employing Gaussian Process Regression and Random Forest models [17,18,77] highlight the importance of large-scale data acquisition and quantification of rock-mass uncertainty. Field investigations in quarries and underground mines [1,6] confirm that properly calibrated PPV limits preserve the integrity of secondary excavations and surface structures.

3.13.2. Prevention of Flyrock, Backbreak, and Overbreak

The ballistic propagation of fragments (flyrock) is often modelled with parabolic or spherical launch equations, supplemented by aerodynamic factors and fragment morphology analysis [78,79]. A typical formulation relates the initial kinetic energy of the fragment after detonation:

$${\displaystyle \frac{1}{2}}{m}_{\mathrm{rock}}{v}_0^2=E_{\mathrm{explosivo}}\zeta ,$$

(30)

where $m_{\mathrm{rock}}$ is the fragment mass, $v_0$ the initial ejection velocity, $E_{\mathrm{explosivo}}$ the total explosive energy, and $\zeta$ a (typically low) conversion efficiency. The maximum projection distance further depends on the ejection angle and aerodynamic drag. Sharma et al. [80] report a determination coefficient $R^2>0.9$ for backbreak prediction using genetic regression algorithms. Such models often take the following form:

$$\mathrm{Backbreak}=f\left(\mathrm{burden},\mathrm{spacing},\mathrm{RMR},\mathrm{powder}\text{\_}\mathrm{factor},\dots \right),$$

(31)

where f is a nonlinear function. Multi-task AI approaches [58,60] simultaneously predict fragmentation, $\mathrm{PPV}$, and flyrock, and also introduce geo-structural parameters such as joint spacing and fracture density [81].

3.13.3. Damage Zone, Permeability, and Slope Stability

The blast damage zone (Blast Damage Zone, BDZ) surrounds the borehole and modifies the mechanical properties of the rock mass. Its thickness and degree of fracturing affect post-blast permeability, influencing the stability of slopes and tunnels. Coupled numerical models show that increased shear stress raises fracture density, which in turn elevates permeability [82]. A typical permeability-damage formulation models the evolution of the permeability coefficient $k\left(\epsilon \right)$ as a function of the following strain:

$$k\left(\epsilon \right)=k_{0}exp\left(\delta {\epsilon }_{\mathrm{pl}}\right),$$

(32)

where $k_0$ is the initial permeability and ${\epsilon }_{\mathrm{pl}}$ is the accumulated plastic strain. Zuo et al. [83] incorporate BDZ thickness into stability analyses based on the Hoek–Brown criterion:

$${\sigma }_1={\sigma }_3+{\sigma }_c{m}_b{\left({\displaystyle \frac{{\sigma }_3}{{\sigma }_{ci}}}+1\right)}^a,$$

(33)

adapting it to a reduced strength within the BDZ. The temporal delay between boreholes also influences accumulated damage; Onederra et al. [84] introduce a delay-timing factor that corrects the Kuznetsov curve, accounting for dynamic coupling between holes.

3.13.4. Energy Management and Containment Technologies

In contrast with the classical powder-factor approach (kilograms of explosive per tonne of rock), recent studies emphasise energy-use efficiency. Tao et al. [85] report improvements of up to 18

$$E_{\mathrm{explosive}}=E_{\mathrm{fracture}}+E_{\mathrm{movement}}+E_{\mathrm{loss}},$$

(34)

where $E_{\mathrm{fracture}}$ is the energy required to create new fracture surfaces, $E_{\mathrm{movement}}$ is the kinetic energy of the muckpile, and $E_{\mathrm{loss}}$ covers unused wave energy, residual heat, and similar losses. Dotto et al. [39] show that thermo-dynamic simulation can reduce drilling requirements by 15 %. The adoption of eco-friendly stemming plugs [66] and the optimisation of stemming length [32] markedly diminish flyrock and over-pressure. Finally, Aben et al. [25] note that pre-weakening the rock mass (pre-split or trim blasting) lowers the specific charge and improves size distribution.

3.13.5. Mining–Civil Engineering Interface and Structural Resilience

The convergence between blasting engineering and resilient structural design is highlighted in studies such as [45,46,48,77], where dynamic safety factors for reinforced-concrete elements are calibrated from vulnerability curves derived for tunnels and galleries. Back-analysis tools reconstruct explosive loads in forensic contexts [50], while the cause–effect relation between tunnel design and induced damage is verified through in situ tests and ALE modelling [28].

3.13.6. Incorporation of Drilling Data and Operational Monitoring

A crucial aspect of design refinement is the integration of measurement-while-drilling (MWD) parameters such as penetration rate, torque, and rod thrust [86,87]. The goal is real-time characterisation of geomechanical variability. By collecting MWD data for each borehole and converting them into hardness or strength indices, the drill pattern and charge factor are dynamically adjusted:

$${\mathbf{x}}^{\ast }={\mathbf{x}}_0+\Delta \left(\mathrm{MWD}\left(i\right)\right),$$

(35)

where ${\mathbf{x}}_0$ is the original design (burden, spacing, powder factor) and $\Delta \left(\mathrm{MWD}\left(i\right)\right)$ is a correction based on the measurements for borehole i. Reference [87] reports up to a 12 % reduction in the standard deviation of $P_{50}$ under this strategy.

3.13.7. Emerging Trends and Frontiers

Systematic AI reviews point to the rise of digital twins that integrate multi-source data in data-driven platforms [74,88]. The combination of UAV–LiDAR sensors and deep learning enables near-real-time estimation of muckpile morphology [60], promising closed-loop mine–mill control. Future emphasis will be on ESG indicators (environmental, social, governance), stressing energy efficiency, emission reduction, and the resilience of critical infrastructure. This shift calls for design indices that simultaneously weight geomechanical, environmental, and socio-technical variables.

3.13.8. Synthesis

Cluster 3 demonstrates that integral management of dynamic impact—grounded in high-resolution geomechanical variables—is as critical as fragmentation optimisation for achieving operational sustainability and mine–mill efficiency. Advances in AI, coupled numerical modelling, and containment technologies enhance the capacity to design increasingly safe and efficient blasts. The remaining challenge is to integrate vibration and fragmentation indicators in a synergistic way, closing the gap between minimising adverse impacts and maximising productivity. A comparative synthesis of relevant models, variables, and performance metrics is presented in

Table 3. Summary of representative methodological advances for blast design integrating geomechanical variables.

Category	Model/Algorithm	Key Geomechanical Variables	Performance Metric	Main Finding
Classical empirical methods	Original Kuz–Ram and Monte Carlo	RQD, UCS, rock factor R	Mean error in $P_{50}$	Monte Carlo simulation improves full fragment curve prediction ($\pm 15\%$) compared to the deterministic model [7].
	Modified Kuz–Ram	Empirical prefactor, joint index $J_f$	$R^2=0.83$ in $X_{50}$	Adjusting the prefactor to $0.073$ reduces prediction deviation by 23% [9].
	Energy Factor (EF)	Charge density, dynamic modulus	Drill reduction (%)	EF correlates delivered energy with P80 and increases productivity by 12% in coal mines [64].
Numerical optimization	Pareto–search + Goal Attainment	Burden, spacing, allowable PPV	Multi-objective fitness function	Simultaneous maximization of production and minimization of vibration; 49% PPV reduction [5].
Artificial Intelligence	Multi-year Random Forest (RF)	UCS, charge factor, delay time	MAE in PPV and P80	RF reduces PPV MAE to 0.19 mm/s and captures rock–explosive nonlinearities [17].
	Gaussian Process Regression (GPR)	S-wave velocity, RMR	RMSE in P50	GPR provides explicit uncertainty: RMSE 6.4 cm and posterior standard deviation [18].
	Genetic XGBoost	Joint angle, charge factor	Dual MAE (P50, PPV)	Simultaneous prediction of fragmentation and PPV (MAE $<0.12$) [60].
	Gene Expression + Grasshopper	Specific power, Young’s modulus	Estimated PPV	Predicted PPV reduced by 17% compared to empirical model [75].
Sensitivity and Statistical Analysis	Taguchi–ANOVA	Stiffness ratio, UCS, burden	Significance $p<0.05$	Stiffness ratio and UCS explain 68% of the variance in P50 [54].
Advanced geomechanical factors	3D Rock Factor Mapping	Spatial index $R_f(x,y,z)$	Drilling mesh optimization	Pattern redesign reduces overbreak by 14% [12].
	Delay Timing Factor	Inter-hole delay $\Delta t$, joint density	Kuznetsov curve adjustment	Incorporates $\Delta t$ as a dimensionless coefficient; improves P80 distribution fit [84].
	BDZ–Permeability Coupled Model	BDZ thickness, in situ stress	k (permeability) variation	Log-linear correlation between shear and increase in k; implications for slope stability [82,83].

and 

Table 4. Representative blasting models and geomechanical techniques, their methodological class, principal mining setting, key geomechanical inputs, and the main performance metric they target. Abbreviations: UCS = uniaxial compressive strength; GSI = Geological Strength Index; EDZ = excavation damage zone; PPV = peak particle velocity; EF = energy factor.

Model/Technique	Method Class	Mining Setting	Key Geomechanical Inputs	Primary Metric
Kuznetsov Cunningham Ramamurthy (Kuz–Ram)	Empirical fragmentation model	Open-pit	Rock factor R, rock destruction index (RDI)	Median size $X_{50}$, $P_{80}$
Modified Kuz–Ram (geomechanics-enriched)	Semi-empirical (${\sigma }_c,E,\mathrm{GSI}$)	Open-pit and underground	UCS, Young’s modulus, GSI, inter-hole delay	$X_{50}$ reduction (% MAPE)
Swebrec + Size–Energy Fan	Empirical distribution	Open-pit	Joint spacing, burden spacing	Full size curve fit ($R^2$)
Energy-Factor (EF) Design	Energetic balance	Open-pit (coal, iron)	Bench geometry, UCS, powder factor	Explosive energy efficiency (%)
Pre-split/Trim blasting	Controlled blasting technique	Pit walls and tunnel perimeters	Joint orientation, in situ stress	Overbreak/backbreak (m)
Hybrid Stress Blasting Model (HSBM)	Hybrid numerical–empirical	Both	Rock Mass Rating (RMR) blocks, confinement	Fragmentation + damage map
Finite-Discrete Element Method (FDEM)	High-fidelity numerical	Underground, high stress	Constitutive tensor $\mathbf{C}$, fracture energy $G_c$	EDZ thickness (m)
Arbitrary Lagrangian–Eulerian (ALE) coupling	Gas–solid CFD	Both	Detonation pressure, wave speed, stiffness gradient	Burden damage depth (m)
BDZ Permeability–Damage model	Coupled hydro-mechanical	Underground (deep)	Plastic strain, stress state, fracture density	k increase factor
PPV Scaled-Distance + rock modifiers	Vibration correlation	Surface blasts near structures	UCS, S-wave velocity	PPV prediction error (mm/s)

.

4. Discussion

A comparative assessment of blasting design methods and indices that deeply integrate geomechanical variables reveals a heterogeneous yet converging landscape regarding fragmentation control and the mitigation of undesired effects (flyrock, vibrations, overbreak). This section summarizes how advanced numerical approaches, empirical energy-based methods, and artificial intelligence (AI) and optimization techniques converge to enable more accurate, efficient, and safer blast designs. The discussion is structured around three key aspects: (i) the contribution of numerical models and multi-physics simulation, (ii) the reformulation of classical empirical models, and (iii) the hybridization with AI and robust statistics. A synthesis of the most significant findings, their methodological foundations, and the supporting literature is presented in

Table 5. Connection between findings, evidence, and the literature.

RQ	Key Finding	Supporting Evidence/Methodology	Representative Studies
RQ1	Including discontinuities and strength improves $X_{50}$ and $P_{80}$ prediction	Monte Carlo simulation coupled to Kuz–Ram; ${10}^4$ iterations show $\Delta R^2=+0.08$ when fracture index is added	[7]
	Rock factor adjustment in Kuz–Ram improves $X_{50}$ accuracy in porphyry copper	Empirical recalibration (prefactor 0.073) reduces MAE by 18% compared to the base model	[9]
	3D numerical models capture EDZ and reflect in situ stress conditions	FDEM–GPU analysis with adaptive mesh; correlation 0.91 with post-excavation fracture mapping	[14]
	Size–energy fan integrates joint spacing and detonating energy	Dimensional analysis without prior distribution; mean error 6% in limestone quarry	[11]
RQ2	ML ensemble predicts fragmentation, backbreak, and flyrock with ${\mathrm{R}}^2>0.92$	Random Forest–GBM fusion; 270 open-pit mining cases	[58]
	Genetic XGBoost simultaneously estimates $X_{50}$ and PPV	120 blasts, 14 parameters; RMSE (Frag.) $=0.25$ m, RMSE(PPV) = 2.1 mm/s	[61]
	GPR + MWD data improves blast design in heterogeneous benches	125 drill–blast records; 12% reduction in energy overuse	[18]
	Multivariate analysis with drilling loggers improves $X_{50}$ prediction	Stepwise regression on 38 blasts: $R^2=0.88$	[72]

, offering an integrated view of how numerical modeling, empirical reformulation, and AI-based techniques address the key research questions (RQ1–RQ2) discussed in this section.

4.1. Contributions from Numerical Simulation and Multi-Physics Modeling

Studies based on FDEM, FEM–DEM, and ALE confirm that explosive dynamics must be resolved in the transient wave domain to capture fracture propagation and the extent of the excavation damage zone (EDZ) [13,14,40,89]. Starting from the elastodynamic equation

$$\rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\nabla ·\left(\mathbf{C}:\nabla \mathbf{u}\right)+\mathbf{f},$$

(36)

where $\mathbf{C}$ is the stiffness tensor and $\mathbf{f}$ is the explosive load, one derives the kinetic energy density $E_k$ and the strain energy density $E_s$,

$$E_k={\displaystyle \frac{1}{2}}\rho \dot{\mathbf{u}}·\dot{\mathbf{u}},E_s={\displaystyle \frac{1}{2}}\epsilon :\mathbf{C}:\epsilon ,$$

whose spatial gradients govern the initiation of new cracks when the criterion

$$G={\int }_0^{a_c}\sigma \mathrm{d}\epsilon \ge G_c,$$

(37)

is satisfied [13]. The thickness of the EDZ, $t_{\mathrm{EDZ}}$, correlates with the dynamic impedance $Z=\rho v_p$ and the borehole peak pressure $P_{max}$ [23]:

$$t_{\mathrm{EDZ}}\approx {\left(\eta P_{max}/Z\right)}^{1/2},$$

(38)

where $\eta$ is a confinement coefficient ($0.6\le \eta \le 0.9$ in granitic rock masses). The 3D simulation results [8,15,32,33] indicate that constructive wave interference increases local tensile stresses by $\sim 20$–$35\%$, accelerating microcrack coalescence—a particularly relevant finding for preventing overbreak in deep tunnels.

4.2. Reformulation of Empirical Methods and Their Integration with Geomechanics

The Kuz–Ram family remains widely used, but recent extensions incorporate explicit terms for compressive strength (${\sigma }_c$), static modulus (E), and delay time ($\Delta t$) [7,9,10,11]. A generalized model can be written as

$$\begin{array}{cc}\hfill X_{50}& =A_0{\left({\displaystyle \frac{Q}{Q_0}}\right)}^{\alpha }exp\left[-\beta \mathrm{RDI}\right]\left(1+{\gamma }_1{\widehat{\sigma }}_c\right)\left(1+{\gamma }_2\widehat{E}\right)exp\left({\gamma }_3\Delta t\right),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_c& ={\displaystyle \frac{{\sigma }_c-{\mu }_{\sigma }}{{\sigma }_{\sigma }}},\widehat{E}={\displaystyle \frac{E-{\mu }_E}{{\sigma }_E}},\hfill \end{array}$$

(40)

where ${\mu }_{•}$ and ${\sigma }_{•}$ represent the mean and standard deviation, respectively. The global sensitivity of the model is quantified using Sobol indices $S_i$; Monte Carlo studies with ${10}^4$ samples show that $S_{{\sigma }_c}\approx 0.28$ and $S_E\approx 0.17$, compared to $S_Q\approx 0.31$ [55]. Complementarily, energy-based design adjusts the charge Q so that the efficiency

$${\eta }_{\mathrm{use}}={\displaystyle \frac{E_{\mathrm{fractura}}+E_{\mathrm{mov}}}{E_{\mathrm{explosivo}}}}$$

exceeds an operational threshold (${\eta }_{\mathrm{use}}\ge 0.35$) [1,64]. This involves solving the energy balance

$$E_{\mathrm{explosivo}}={\displaystyle \frac{A_s{G}_c}{\kappa }}+m_{\mathrm{rock}}gh+\delta E_{\mathrm{p}\mathrm{é}\mathrm{r}\mathrm{d}},$$

(41)

where $A_s$ is the fracture surface area created, $G_c$ is fracture toughness, $\kappa$ is fracture efficiency, and $m_{\mathrm{rock}}gh$ represents the potential energy of the muckpile. The integration of 3D RMR/GSI maps (with $0.01{\mathrm{km}}^2$ resolution) has enabled reductions in the mean absolute error (MAE) of $X_{50}$ by 14–$22\%$ [12,57].

4.3. AI, Multivariable Statistics, and Multi-Objective Optimization

AI models—ensemble learning, Gaussian processes, and neural networks—have incorporated up to $p=20$ variables (design, geomechanics, MWD) to simultaneously predict fragmentation and PPV, achieving ${\mathrm{R}}^2\ge 0.90$ [17,18,58]. A typical multi-objective formulation is given by

$$\begin{array}{cc}\hfill \underset{\mathbf{x}\in \Omega }{min}& \left[F_1\left(\mathbf{x}\right),F_2\left(\mathbf{x}\right),F_3\left(\mathbf{x}\right)\right],\hfill \\ \hfill F_1& =\left|X_{50}-X_{50}^{\ast }\right|,F_2=\mathrm{PPV},F_3=C_{\mathrm{expl}}/t_{\mathrm{cyc}},\hfill \end{array}$$

(42)

where $X_{50}^{\ast }$ is the target fragment size and $C_{\mathrm{expl}}$ is the explosive cost. Algorithms such as NSGA-II and paretosearch generate a Pareto front whose points are ranked using the hypervolume metric $HV$; improvements of 7–11% in $HV$ have been reported when joint angles and UCS are included as features [5,75]. In addition, predictive variance is modeled using Gaussian processes,

$$y\left(\mathbf{x}\right)\sim \mathcal{GP}\left(\mu \left(\mathbf{x}\right),k(\mathbf{x},{\mathbf{x}}^{\prime })\right),$$

allowing the inclusion of risk penalties $\mathcal{R}=\lambda Var\left[y\right(\mathbf{x}\left)\right]$ in the objective function [18]. These approaches are further enhanced by MWD data-streams, where the penetration signal $v_p\left(t\right)$ is denoised using wavelets and processed via a Kalman filter to update model parameters online [86,87].

4.4. Convergence and Future Implications

A cross-cutting analysis highlights the need to perform the following:

(i)

Rigorously calibrate Equations (36)–(41) using UCS tests, triaxial data, and joint mapping [14].

(ii)

Embed sensor technologies (MWD, microseismic, UAV–Lidar) to provide quasi-real-time feedback to models (39) and (42) [60,68].

(iii)

Define integrated design indicators—e.g., $\Psi ={\omega }_1{X}_{50}/X_{50}^{\ast }+{\omega }_2\mathrm{PPV}/{\mathrm{PPV}}_{max}+{\omega }_3{E}_{\mathrm{expl}}/E_{\mathrm{ref}}$—that simultaneously weight fragmentation, vibration, and energy efficiency [2,65].

The development of digital twins [74], grounded in physics-based equations and deep learning, opens the door to mine–mill self-optimization, reducing the total energy factor by 8–12% [3,90].

4.5. Limitations and Research Directions

High-fidelity methods require GPU computing power (>15 TFLOPS) and dense geomechanical datasets; scalability remains a challenge [8,57]. Empirical models need periodic recalibration when lithology or stress regimes change [9,84]. Furthermore, many AI models exhibit overfitting outside their training domain; cross-site validation ($k\ge 5$ quarries) and transfer learning via domain adaptation are essential [91]. A standardized reporting protocol (including metadata, uncertainty, and sensitivity) is recommended to strengthen data science in blasting engineering [92].

4.6. Modelling Challenges in Geomechanically Informed Blast Design

Rock fragmentation by blasting is still considered a highly complex problem in geomechanics [93]. In practical applications, models are required to incorporate multiple rock-mass properties—such as strength, discontinuity patterns, and in situ stresses—which interact in nonlinear ways during detonation. Although empirical formulas like Kuz–Ram and Swebrec offer heuristic guidance, they are usually calibrated for specific sites and fail to capture the multi-scale geomechanical processes that govern breakage [94]. As highlighted in [93], more than 20 parameters—many of them subject to high uncertainty—can influence fragmentation outcomes. Among these, the block-size distribution, shaped by jointing and in situ structural features, plays a key role in determining fragment size, stress-wave attenuation, and the extent of the damage zone. Consequently, semi-empirical models tend to show limited generalizability: they perform well under the conditions for which they were fitted, but often break down when changes occur in lithology or blast geometry [94].

• Empirical and semi-empirical models: Classical fragmentation correlations (Rosin–Rammler, Kuz–Ram, Swebrec, etc.) rely on simplified assumptions (e.g., uniform rock, continuous breakage) and a small set of input parameters. They require site-specific calibration and often neglect key geomechanical details (e.g., joint sets, heterogeneity). Consequently, these models carry large uncertainties and limited transferability across different mines or rock types. For instance, recent studies note that traditional equations “apply only to specific mines,” highlighting their lack of robustness outside the training domain. Improving these models thus demands incorporating more geological variables and rigorous uncertainty quantification, but doing so exacerbates data needs that are rarely met in practice [94].
• High-fidelity numerical simulations (FEM/DEM/ALE): Physics-based simulations can, in principle, resolve blast-induced damage and fragmentation with high spatial and temporal resolution. FEM, DEM, coupled FDEM/ALE formulations, and hydrocodes have been used to simulate wave propagation, fracture initiation, and block motion under detailed constitutive laws. In practice, however, these methods are computationally demanding. Large-scale blast scenarios involving hundreds of holes and realistic block geometries are typically intractable, except under reduced-scale or two-dimensional approximations. Moreover, the continuum assumption in FEM breaks down under pervasive fracturing, requiring alternative formulations—such as lattice spring models, peridynamics, or adaptive meshing—to capture crack propagation accurately, further increasing the computational cost. Calibration also presents a major challenge: DEM models often require tuning of contact parameters (e.g., friction, cohesion, particle shape) based on limited laboratory or field data, typically through trial-and-error or optimization procedures. As noted in [95], achieving a balance between model fidelity and computational efficiency remains difficult, particularly when multiple parameters interact nonlinearly. In summary, high-fidelity simulations offer detailed physical insight, but at the expense of computational cost, complex parameterization, and sensitivity to uncertain geomechanical inputs.
• Machine learning models: Data-driven approaches—such as neural networks, random forests, and support vector machines—have been applied to predict fragmentation and other blast outcomes by learning nonlinear input–output relationships without relying on explicit physical models. However, ML methods introduce a distinct set of challenges. First, they require large and representative datasets of prior blasts, including design variables, rock properties, and measured outputs, which are often scarce or biased toward specific sites or lithologies. As a result, ML models are prone to overfitting and may generalize poorly outside their training domain. In many cases, a model trained on one pit or rock type fails when applied to new geological contexts unless specifically adapted. Furthermore, purely data-driven models offer limited interpretability and do not inherently enforce physical consistency, which may lead to unrealistic predictions under unseen conditions. Hyperparameter optimization is commonly performed using static strategies such as grid search or random search, which converge slowly and may become trapped in suboptimal solutions. Although ML can outperform empirical formulas in terms of fitting accuracy, its generalization capability under dynamic field conditions remains limited [94].
• Integrating physics and machine learning (hybrid models): To overcome the limitations of purely empirical or data-driven approaches, recent research has focused on hybrid models that integrate first-principle physics with ML techniques. Physics-informed neural networks (PINNs) and other hybrid frameworks embed governing equations—such as wave propagation or constitutive laws—directly into the training process. This integration helps reduce data demands while enforcing physically consistent behaviour throughout model inference. In the context of blasting, however, the strong nonlinearities associated with shock waves and fracturing pose major challenges to PINN training. Capturing such highly dynamic and discontinuous phenomena often requires specialized network architectures or custom loss formulations. An alternative hybrid strategy involves surrogate modeling, where fast approximation models (e.g., Gaussian processes or neural network surrogates) are trained on a limited set of high-fidelity simulations and subsequently coupled with optimization or uncertainty quantification routines. These surrogates can be further enhanced using transfer learning to adapt efficiently to new scenarios. Recent developments suggest that physics-constrained surrogate models and digital twins—capable of incorporating real-time sensor data from blasts—represent a promising direction for improving both predictive power and operational usability [96].
• Digital twins and real-time integration: The concept of a digital twin for blasting—defined as a continuously updated virtual replica of the rock mass and blasting process—holds significant promise but remains largely unrealized in mining applications. A fully functional digital twin would integrate in situ monitoring technologies (e.g., seismic arrays, vibration sensors, fragmentation imaging) with real-time simulations and ML models, enabling dynamic prediction and adaptive blast design. Achieving this requires robust integration of heterogeneous data streams and multiscale modeling approaches, a challenge that remains unresolved. Although general frameworks for mining digital twins have been proposed, practical implementations specific to drill-and-blast operations are still at an early proof-of-concept stage. Bridging this gap will necessitate interdisciplinary progress across geomechanics, data science, and engineering software development.

In summary, modelling challenges in geomechanically informed blast design remain diverse and significant. Empirical models are constrained by limited applicability and substantial uncertainty. High-fidelity simulations offer detailed physical insight but require prohibitive computational resources and precise calibration. ML methods, while flexible, depend heavily on large and representative datasets and are sensitive to domain shift. Integrative approaches—such as physics-informed ML, domain adaptation strategies, and digital twins—are still under active development and face both theoretical and practical limitations. Addressing these challenges will require advances in uncertainty quantification, transfer learning, and hybrid modelling approaches, building on recent progress in computational geomechanics and artificial intelligence.

5. Conclusions

This systematic literature review highlights how the convergence of mathematical engineering, physical modeling, and machine learning is reshaping process optimization in rock blasting. Based on the analysis of 97 selected studies, methodological developments were classified into three complementary domains: multiphysics simulation, enriched empirical modeling, and statistical inference frameworks.

C1.

Numerical simulation reduces uncertainty: Multiphysics models improve the prediction of damage zones by incorporating calibrated mechanical properties and dynamic blast parameters. These simulations enhance reliability in high-stress conditions, reducing uncertainty in the spatial extent of fragmentation.

C2.

Hybrid empirical models remain valuable: Classical formulas such as Kuznetsov’s gain predictive power when augmented with geomechanical inputs. This integration improves accuracy and reduces error margins, reaffirming the utility of hybrid empirical–physical approaches in practice.

C3.

Machine learning enables flexible and adaptive inference: Advanced ML techniques can model complex nonlinear relationships among numerous variables with high predictive accuracy. Nonetheless, challenges remain regarding data availability, model generalization, and domain transferability.

C4.

Multi-objective optimization supports sustainable design: Optimization frameworks allow for the systematic balancing of competing goals, such as fragmentation quality, energy efficiency, and vibration control. Improvements in these metrics demonstrate the practical impact of mathematically grounded trade-off analysis.

C5.

Digital twins integrate models and data: The concept of a digital twin synthesizes physics-based models, data-driven inference, and real-time sensing into a unified predictive framework. This approach has already shown promise in reducing operational inefficiencies and improving energy use, bringing the field closer to closed-loop, autonomous design systems.

In summary, there is no universally superior modeling strategy. The suitability of each approach depends on factors such as problem scale, data quality, and operational goals. Future research should focus on the following:

• Developing integrated validation frameworks that combine simulation, empirical models, and AI.
• Promoting open, standardized datasets for benchmarking ML methods in industrial contexts.
• Advancing performance metrics that jointly consider efficiency, cost, and sustainability.

The integration of mechanistic modeling, empirical knowledge, and intelligent analytics points toward a new paradigm of data-centric, mathematically informed design. Implementing real-time learning systems will be key to enabling adaptive, self-improving solutions in complex industrial environments.