Dynamic Snake Convolution Neural Network for Enhanced Image Super-Resolution
Abstract
1. Introduction
- (1)
- DSConv is embedded into the CNN architecture, leveraging its dynamic adjustment mechanism to capture intricate image detail features effectively.
- (2)
- An improved residual structure is utilized to facilitate efficient utilization of multi-level feature information within the network.
- (3)
- A parallel multi-scale convolution structure is integrated into the CNNs to enable the model to consolidate both local details and global structural information of the image.
2. Related Work
2.1. Residual Structures for Image Processing
2.2. Dynamic Convolution for Image Processing
2.3. Deep CNNs for Image Super-Resolution
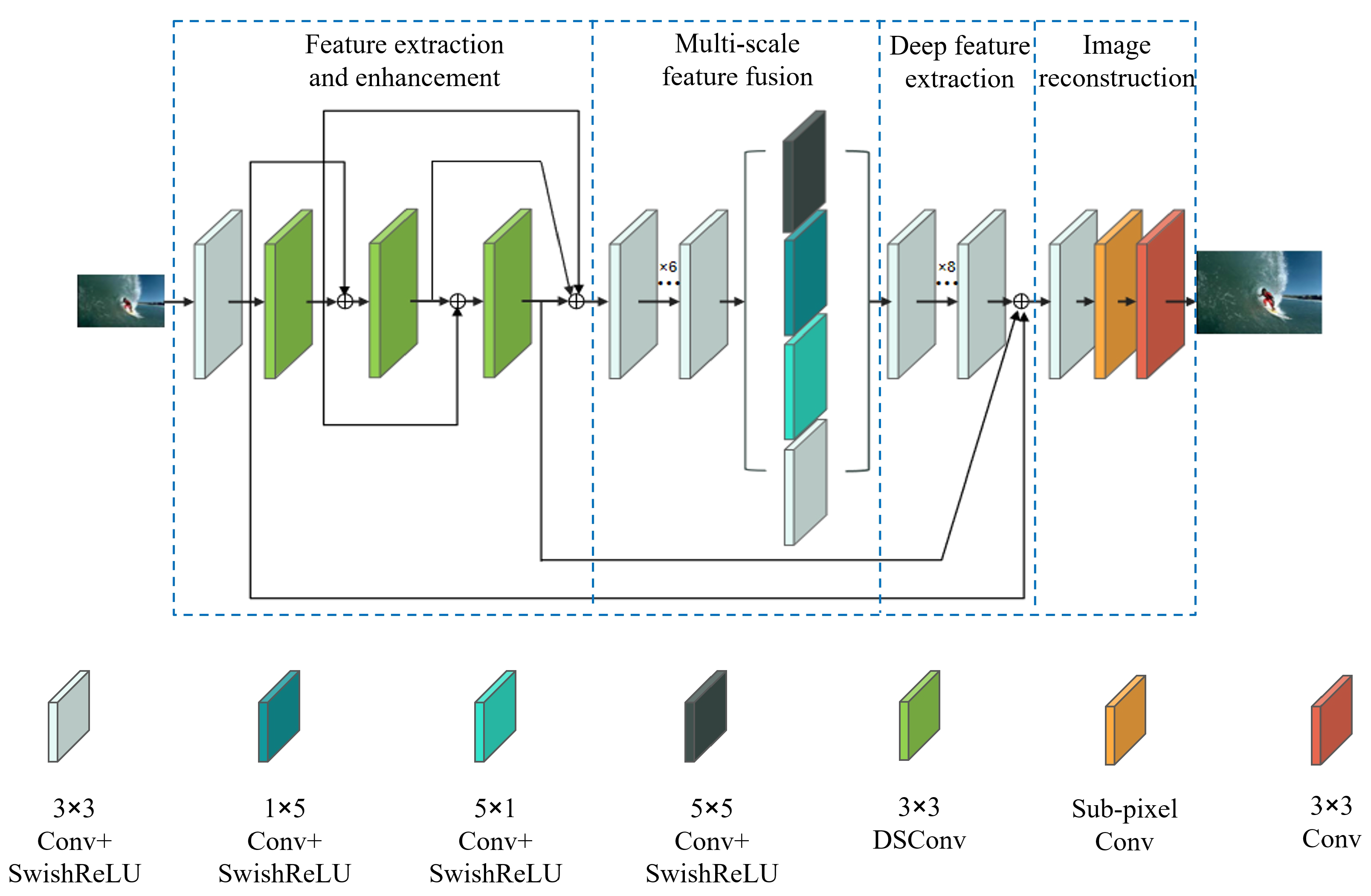
3. Proposed Method
3.1. Network Architecture
3.2. Loss Function
3.3. Improved Residual Structure
3.4. Feature Extraction and Enhancement Module
3.5. Multi-Scale Feature Fusion Module
4. Experimental Analysis and Results
4.1. Datasets
4.2. Experimental Settings
4.3. Ablation Study
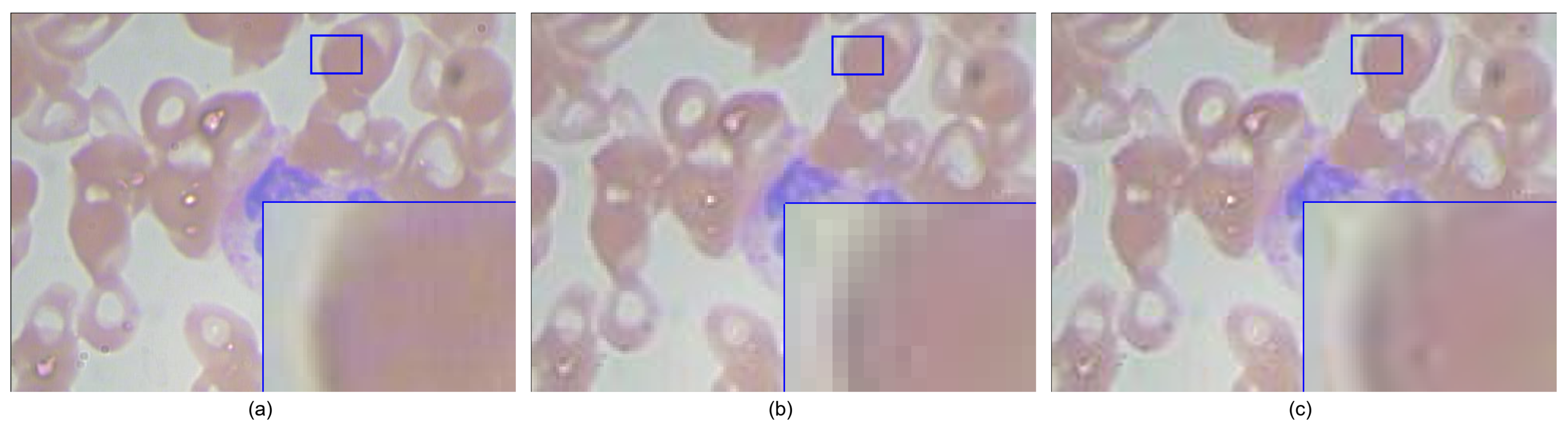
4.4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, C.; Zheng, M.; Lin, C.W.; Li, Z.; Zhang, D. Heterogeneous window transformer for image denoising. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 6621–6632. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Tian, C.; Zheng, M.; Li, B.; Zhang, Y.; Zhang, S.; Zhang, D. Perceptive self-supervised learning network for noisy image watermark removal. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 7069–7079. [Google Scholar] [CrossRef]
- Ma, L.; Li, N.; Zhu, P.; Tang, K.; Khan, A.; Wang, F.; Yu, G. A novel fuzzy neural network architecture search framework for defect recognition with uncertainties. IEEE Trans. Fuzzy Syst. 2024, 32, 3274–3285. [Google Scholar] [CrossRef]
- Li, N.; Xue, B.; Ma, L.; Zhang, M. Automatic Fuzzy Architecture Design for Defect Detection via Classifier-Assisted Multiobjective Optimization Approach. IEEE Trans. Evol. Comput. 2025. [Google Scholar] [CrossRef]
- Li, Y.; Sixou, B.; Peyrin, F. A review of the deep learning methods for medical images super resolution problems. IRBM 2021, 42, 120–133. [Google Scholar] [CrossRef]
- Wang, P.; Bayram, B.; Sertel, E. A comprehensive review on deep learning based remote sensing image super-resolution methods. Earth-Sci. Rev. 2022, 232, 104110. [Google Scholar] [CrossRef]
- Rasti, P.; Uiboupin, T.; Escalera, S.; Anbarjafari, G. Convolutional neural network super resolution for face recognition in surveillance monitoring. In Proceedings of the Articulated Motion and Deformable Objects: 9th International Conference, AMDO 2016, Palma de Mallorca, Spain, 13–15 July 2016; pp. 175–184. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar] [CrossRef]
- Li, Y.; Agustsson, E.; Gu, S.; Timofte, R.; Van, L. CARN: Convolutional Anchored Regression Network for Fast and Accurate Single Image Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, H.; Gu, J.; Zhang, Z. Attention in attention network for image super-resolution. arXiv 2021, arXiv:2104.09497. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Rahman, J.U.; Zulfiqar, R.; Khan, A. SwishReLU: A unified approach to activation functions for enhanced deep neural networks performance. arXiv 2024, arXiv:2407.08232. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016, Proceedings, Part IV 14; Springer: Cham, Switzerland, 2016; pp. 630–645. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 472–480. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Tian, C.; Zheng, M.; Jiao, T.; Zuo, W.; Zhang, Y.; Lin, C.W. A self-supervised CNN for image watermark removal. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 7566–7576. [Google Scholar] [CrossRef]
- Han, Y.; Huang, G.; Song, S.; Yang, L.; Wang, H.; Wang, Y. Dynamic neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7436–7456. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Yang, B.; Bender, G.; Le, Q.V.; Ngiam, J. Condconv: Conditionally parameterized convolutions for efficient inference. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Chen, Y.; Dai, X.; Liu, M.; Chen, D.; Yuan, L.; Liu, Z. Dynamic convolution: Attention over convolution kernels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11030–11039. [Google Scholar]
- He, T.; Shen, C.; Van Den Hengel, A. Dyco3d: Robust instance segmentation of 3d point clouds through dynamic convolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 354–363. [Google Scholar]
- Qi, Y.; He, Y.; Qi, X.; Zhang, Y.; Yang, G. Dynamic snake convolution based on topological geometric constraints for tubular structure segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 6070–6079. [Google Scholar]
- Tian, C.; Xu, Y.; Zuo, W.; Lin, C.W.; Zhang, D. Asymmetric CNN for image superresolution. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 52, 3718–3730. [Google Scholar] [CrossRef]
- Tian, C.; Zhang, X.; Zhang, Q.; Yang, M.; Ju, Z. Image super-resolution via dynamic network. CAAI Trans. Intell. Technol. 2024, 9, 837–849. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Tian, C.; Song, M.; Fan, X.; Zheng, X.; Zhang, B.; Zhang, D. A Tree-guided CNN for image super-resolution. IEEE Trans. Consum. Electron. 2025. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Ding, X.; Guo, Y.; Ding, G.; Han, J. ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. Ntire 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 114–125. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Carlson, R.E.; Fritsch, F.N. Monotone piecewise bicubic interpolation. SIAM J. Numer. Anal. 1985, 22, 386–400. [Google Scholar] [CrossRef]
- Dai, D.; Timofte, R.; Van Gool, L. Jointly Optimized Regressors for Image Super-resolution. Comput. Graph. Forum 2015, 34, 95–104. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, D.; Yang, J.; Han, W.; Huang, T. Deep Networks for Image Super-Resolution with Sparse Prior. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 370–378. [Google Scholar] [CrossRef]
- Timofte, R.; Desmet, V.; Vangool, L. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. In Computer Vision—ACCV 2014; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Schulter, S.; Leistner, C.; Bischof, H. Fast and accurate image upscaling with super-resolution forests. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3791–3799. [Google Scholar] [CrossRef]
- Mao, X.J.; Shen, C.; Yang, Y.B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Lu, Z.; Yu, Z.; Yali, P.; Shigang, L.; Xiaojun, W.; Gang, L.; Yuan, R. Fast Single Image Super-Resolution Via Dilated Residual Networks. IEEE Access 2019, 7, 109729–109738. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, K.; Chen, C.; Xu, L.; Lin, L. Structure-Preserving Image Super-Resolution via Contextualized Multitask Learning. IEEE Trans. Multimed. 2017, 19, 2804–2815. [Google Scholar] [CrossRef]
- Ren, H.; El-Khamy, M.; Lee, J. Image Super Resolution Based on Fusing Multiple Convolution Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1050–1057. [Google Scholar] [CrossRef]
- Zhang, K.; Gao, X.; Tao, D.; Li, X. Single Image Super-Resolution With Non-Local Means and Steering Kernel Regression. IEEE Trans. Image Process. 2012, 21, 4544–4556. [Google Scholar] [CrossRef]
- Bae, W.; Yoo, J.; Ye, J.C. Beyond Deep Residual Learning for Image Restoration: Persistent Homology-Guided Manifold Simplification. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1141–1149. [Google Scholar] [CrossRef]
- Xu, J.; Li, M.; Fan, J.; Zhao, X.; Chang, Z. Self-Learning Super-Resolution Using Convolutional Principal Component Analysis and Random Matching. IEEE Trans. Multimed. 2019, 21, 1108–1121. [Google Scholar] [CrossRef]
- Tian, C.; Zhuge, R.; Wu, Z.; Xu, Y.; Zuo, W.; Chen, C.; Lin, C.W. Lightweight image super-resolution with enhanced CNN. Knowl.-Based Syst. 2020, 205, 106235. [Google Scholar] [CrossRef]
- Chen, Y.; Pock, T. Trainable Nonlinear Reaction Diffusion: A Flexible Framework for Fast and Effective Image Restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1256–1272. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Khan, A.H.; Micheloni, C.; Martinel, N. IDENet: Implicit Degradation Estimation Network for Efficient Blind Super Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Seattle, WA, USA, 17–18 June 2024; pp. 6065–6075. [Google Scholar]
- Wen, W.; Guo, C.; Ren, W.; Wang, H.; Shao, X. Adaptive Blind Super-Resolution Network for Spatial-Specific and Spatial-Agnostic Degradations. IEEE Trans. Image Process. 2024, 33, 4404–4418. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Chen, B. New architecture of deep recursive convolution networks for super-resolution. Knowl.-Based Syst. 2019, 178, 98–110. [Google Scholar] [CrossRef]
- Huang, Y.; Li, S.; Wang, L.; Tan, T. Unfolding the alternating optimization for blind super resolution. Adv. Neural Inf. Process. Syst. 2020, 33, 5632–5643. [Google Scholar]
- Hui, Z.; Wang, X.; Gao, X. Fast and Accurate Single Image Super-Resolution via Information Distillation Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 723–731. [Google Scholar] [CrossRef]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A Persistent Memory Network for Image Restoration. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Zhou, P.; Guo, L. Multi-class geospatial object detection and geographic image classification based on collection of part detectors. ISPRS J. Photogramm. Remote Sens. 2014, 98, 119–132. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Cheng, G.; Zhou, P.; Han, J. Learning Rotation-Invariant Convolutional Neural Networks for Object Detection in VHR Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]





| Method | Kernel Adaptation | Training Stability | Primary Applications |
|---|---|---|---|
| DCN [27] | Point-wise offsets | Moderate | Object detection |
| CondConv [28] | Kernel weighting | High | Classification |
| DyConv [29] | Attention | High (w/annealing) | Keypoint detection |
| DSConv [31] | Iterative tracing | High | Curvilinear feature enhancement |
| Methods | Set5 (PSNR (dB)/SSIM) | Set14 (PSNR (dB)/SSIM) | B100 (PSNR (dB)/SSIM) |
|---|---|---|---|
| Baseline | 31.52/0.8854 | 27.96/0.7737 | 27.37/0.7284 |
| +DSConv | 31.63/0.8860 | 28.02/0.7742 | 27.38/0.7293 |
| +Enhanced Residual Structure | 31.65/0.8878 | 28.04/0.7758 | 27.40/0.7302 |
| +SwishReLU | 31.68/0.8886 | 28.05/0.7776 | 27.44/0.7319 |
| +Multi-Scale Enhancement | 31.70/0.8890 | 28.10/0.7777 | 27.46/0.7323 |
| Functions | Set5 (PSNR (dB)/SSIM) | Set14 (PSNR (dB)/SSIM) | B100 (PSNR (dB)/SSIM) |
|---|---|---|---|
| ReLU | 30.20/0.8560 | 27.11/0.7494 | 26.79/0.7089 |
| LeakyReLU | 30.25/0.8567 | 27.11/0.7501 | 26.82/0.7103 |
| BReLU-6 | 30.08/0.8568 | 27.07/0.7497 | 26.74/0.7095 |
| SwishReLU | 30.37/0.8604 | 27.21/0.7535 | 26.85/0.7121 |
| Datasets | Methods | ×2 | ×3 | ×4 |
|---|---|---|---|---|
| Set5 | Bicubic [43] | 33.66/0.9299 | 30.39/0.8682 | 28.42/0.8104 |
| JOR [44] | 36.58/0.9543 | 32.55/0.9067 | 30.19/0.8563 | |
| SRCNN [9] | 36.66/0.9542 | 32.75/0.9090 | 30.48/0.8628 | |
| SelfEx [42] | 36.49/0.9537 | 32.58/0.9093 | 30.31/0.8619 | |
| VDSR [13] | 37.53/0.9587 | 33.66/0.9213 | 31.35/0.8838 | |
| CSCN [45] | 36.93/0.9552 | 33.10/0.9144 | 30.86/0.8732 | |
| FSRCNN [10] | 37.00/0.9558 | 33.16/0.9140 | 30.71/0.8657 | |
| A+ [46] | 36.54/0.9544 | 32.58/0.9088 | 30.28/0.8603 | |
| RFL [47] | 36.54/0.9537 | 32.43/0.9057 | 30.14/0.8548 | |
| RED [48] | 37.56/0.9595 | 33.70/0.9222 | 31.33/0.8847 | |
| FDSR [49] | 37.40/0.9513 | 33.68/0.9096 | 31.28/0.8658 | |
| RCN [50] | 37.17/0.9583 | 33.45/0.9175 | 31.11/0.8736 | |
| DRCN [15] | 37.63/0.9588 | 33.82/0.9226 | 31.53/0.8854 | |
| CNF [51] | 37.66/0.9590 | 33.74/0.9226 | 31.55/0.8856 | |
| DnCNN [52] | 37.58/0.9590 | 33.75/0.9222 | 31.40/0.8845 | |
| LapSRN [18] | 37.52/0.9590 | - | 31.54/0.8850 | |
| WaveResNet [53] | 37.57/0.9586 | 33.86/0.9228 | 31.52/0.8864 | |
| CPCA [54] | 34.99/0.9469 | 31.09/0.8975 | 28.67/0.8434 | |
| LESRCNN [55] | 37.65/0.9586 | 33.93/0.9231 | 31.88/0.8903 | |
| TNRD [56] | 36.86/0.9556 | 33.18/0.9152 | 30.85/0.8732 | |
| ScSR [57] | 35.78/0.9485 | 31.34/0.8869 | 29.07/0.8263 | |
| IDENet [58] | 37.16/0.9521 | - | 31.57/0.8846 | |
| GLFDN [59] | 37.47/0.9545 | 33.86/0.9203 | 31.90/0.8869 | |
| DSRNet [33] | 37.61/0.9584 | 33.92/0.9227 | 31.71/0.8874 | |
| DSCNN (Ours) | 37.66/0.9589 | 33.94/0.9234 | 31.90/0.8909 |
| Datasets | Methods | |||
|---|---|---|---|---|
| Set14 | Bicubic [43] | 30.24/0.8688 | 27.55/0.7742 | 26.00/0.7027 |
| RFL [47] | 32.26/0.9040 | 29.05/0.8164 | 27.24/0.7451 | |
| SRCNN [9] | 32.42/0.9063 | 29.28/0.8209 | 27.49/0.7503 | |
| FDSR [49] | 33.00/0.9042 | 29.61/0.8179 | 27.86/0.7500 | |
| SelfEx [42] | 32.22/0.9034 | 29.16/0.8196 | 27.40/0.7518 | |
| VDSR [13] | 33.03/0.9124 | 29.77/0.8314 | 28.01/0.7674 | |
| DRRN [18] | 33.23/0.9136 | 29.96/0.8349 | 28.21/0.7720 | |
| CSCN [45] | 32.56/0.9074 | 29.41/0.8238 | 27.64/0.7578 | |
| FSRCNN [10] | 32.63/0.9088 | 29.43/0.8242 | 27.59/0.7535 | |
| A+ [46] | 32.28/0.9056 | 29.13/0.8188 | 27.32/0.7491 | |
| JOR [44] | 32.38/0.9063 | 29.19/0.8204 | 27.27/0.7479 | |
| RED [48] | 32.81/0.9135 | 29.50/0.8334 | 27.72/0.7698 | |
| RCN [50] | 32.77/0.9109 | 29.63/0.8269 | 27.79/0.7594 | |
| DRCN [15] | 33.04/0.9118 | 29.76/0.8311 | 28.02/0.7670 | |
| LapSRN [18] | 33.08/0.9130 | - | 28.19/0.7720 | |
| WaveResNet [53] | 33.09/0.9129 | 29.88/0.8331 | 28.11/0.7699 | |
| CPCA [54] | 31.04/0.8951 | 27.89/0.8038 | 26.10/0.7296 | |
| DnCNN [52] | 33.03/0.9128 | 29.81/0.8321 | 28.04/0.7672 | |
| NDRCN [60] | 33.20/0.9141 | 29.88/0.8333 | 28.10/0.7697 | |
| TNRD [56] | 32.51/0.9069 | 29.43/0.8232 | 27.66/0.7563 | |
| ScSR [57] | 31.64/0.8940 | 28.19/0.7977 | 26.40/0.7218 | |
| IDENet [58] | 32.84/0.9025 | - | 28.27/0.7678 | |
| DSCNN (Ours) | 33.28/0.9166 | 29.84/0.8386 | 28.17/0.7794 |
| Datasets | Methods | |||
|---|---|---|---|---|
| B100 | Bicubic [43] | 29.56/0.8431 | 27.21/0.7385 | 25.96/0.6675 |
| RFL [47] | 31.16/0.8840 | 28.22/0.7806 | 26.75/0.7054 | |
| SRCNN [11] | 31.36/0.8879 | 28.41/0.7863 | 26.90/0.7101 | |
| VDSR [13] | 31.90/0.8960 | 28.82/0.7976 | 27.29/0.7251 | |
| SelfEx [42] | 31.18/0.8855 | 28.29/0.7840 | 26.84/0.7106 | |
| DRRN [18] | 32.05/0.8973 | 28.95/0.8004 | 27.38/0.7284 | |
| FSRCNN [10] | 31.53/0.8920 | 28.53/0.7910 | 26.98/0.7150 | |
| TNRD [56] | 31.40/0.8878 | 28.85/0.7981 | 27.29/0.7253 | |
| CARN-M [16] | 31.92/0.8960 | 28.91/0.8000 | 27.44/0.7304 | |
| A+ [46] | 31.21/0.8863 | 28.29/0.7835 | 26.82/0.7087 | |
| JOR [44] | 31.22/0.8867 | 28.27/0.7837 | 26.79/0.7083 | |
| RED [48] | 31.96/0.8972 | 28.88/0.7993 | 27.35/0.7276 | |
| CSCN [45] | 31.40/0.8884 | 28.50/0.7885 | 27.03/0.7161 | |
| DRCN [15] | 31.85/0.8942 | 28.80/0.7963 | 27.23/0.7233 | |
| CNF [51] | 31.91/0.8962 | 28.82/0.7980 | 27.32/0.7253 | |
| LapSRN [18] | 31.80/0.8950 | - | 27.32/0.7280 | |
| NDRCN [60] | 32.00/0.8975 | 28.86/0.7991 | 27.30/0.7263 | |
| LESRCNN [55] | 31.95/0.8964 | 28.91/0.8005 | 27.45/0.7313 | |
| FDSR [49] | 31.87/0.8847 | 28.82/0.7797 | 27.31/0.7031 | |
| ScSR [57] | 30.77/0.8744 | 27.72/0.7647 | 26.61/0.6983 | |
| DnCNN [52] | 31.90/0.8961 | 28.85/0.7981 | 27.29/0.7253 | |
| DAN [61] | 31.76/0.8858 | 28.94/0.7919 | 27.51/0.7248 | |
| IDENet [58] | 31.65/0.8848 | - | 27.35/0.7235 | |
| DSRNet [33] | 31.96/0.8965 | 28.90/0.8003 | 27.43/0.7303 | |
| DSCNN (Ours) | 32.06/0.8983 | 28.94/0.8011 | 27.52/0.7342 |
| Datasets | Methods | |||
|---|---|---|---|---|
| Urban100 | Bicubic [43] | 26.88/0.8403 | 24.46/0.7349 | 23.14/0.6577 |
| SRCNN [9] | 29.50/0.8946 | 26.24/0.7989 | 24.52/0.7221 | |
| FDSR [49] | 30.91/0.9088 | 27.23/0.8190 | 25.27/0.7417 | |
| CARN-M [16] | 31.23/0.9193 | 27.55/0.8385 | 25.62/0.7694 | |
| JOR [44] | 29.25/0.8951 | 25.97/0.7972 | 24.29/0.7181 | |
| VDSR [13] | 30.76/0.9140 | 27.14/0.8279 | 25.18/0.7524 | |
| DRRN [18] | 31.23/0.9188 | 27.53/0.7378 | 25.44/0.7638 | |
| FSRCNN [10] | 29.88/0.9020 | 26.43/0.8080 | 24.62/0.7280 | |
| TNRD [56] | 29.70/0.8994 | 26.42/0.8076 | 24.61/0.7291 | |
| IDN [62] | 31.27/0.9196 | 27.42/0.8359 | 25.41/0.7632 | |
| WaveResNet [53] | 30.96/0.9169 | 27.28/0.8334 | 25.36/0.7614 | |
| RED [48] | 30.91/0.9159 | 27.31/0.8303 | 25.35/0.7587 | |
| DRCN [15] | 30.75/0.9133 | 27.15/0.8276 | 25.14/0.7510 | |
| A+ [46] | 29.20/0.8936 | 26.03/0.7973 | 24.32/0.7183 | |
| NDRCN [60] | 31.06/0.9175 | 27.23/0.8312 | 25.16/0.7546 | |
| MemNet [63] | 31.31/0.9195 | 27.56/0.8376 | 25.50/0.7630 | |
| DnCNN [52] | 30.74/0.9139 | 27.15/0.8276 | 25.20/0.7521 | |
| LESRCNN [55] | 31.45/0.9206 | 27.70/0.8415 | 25.77/0.7732 | |
| RFL [47] | 29.11/0.8904 | 25.86/0.7900 | 24.19/0.7096 | |
| ScSR [57] | 28.26/0.8828 | - | 24.02/0.7024 | |
| LapSRN [18] | 30.41/0.9100 | - | 25.21/0.7560 | |
| DAN [61] | 30.60/0.9060 | 27.65/0.8352 | 25.86/0.7721 | |
| SelfEx [42] | 29.54/0.8967 | 26.44/0.8088 | 24.79/0.7374 | |
| IDENet [58] | 30.22/0.9004 | - | 25.39/0.7585 | |
| DSRNet [33] | 31.41/0.9209 | 27.63/0.8402 | 25.65/0.7693 | |
| DSCNN (Ours) | 31.72/0.9244 | 27.69/0.8425 | 25.85/0.7787 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, W.; Wu, Z.; Zhu, Q.; Bi, T.; Li, B.; Tian, C. Dynamic Snake Convolution Neural Network for Enhanced Image Super-Resolution. Mathematics 2025, 13, 2457. https://doi.org/10.3390/math13152457
Xin W, Wu Z, Zhu Q, Bi T, Li B, Tian C. Dynamic Snake Convolution Neural Network for Enhanced Image Super-Resolution. Mathematics. 2025; 13(15):2457. https://doi.org/10.3390/math13152457
Chicago/Turabian StyleXin, Weiqiang, Ziang Wu, Qi Zhu, Tingting Bi, Bing Li, and Chunwei Tian. 2025. "Dynamic Snake Convolution Neural Network for Enhanced Image Super-Resolution" Mathematics 13, no. 15: 2457. https://doi.org/10.3390/math13152457
APA StyleXin, W., Wu, Z., Zhu, Q., Bi, T., Li, B., & Tian, C. (2025). Dynamic Snake Convolution Neural Network for Enhanced Image Super-Resolution. Mathematics, 13(15), 2457. https://doi.org/10.3390/math13152457






