Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme
Abstract
1. Introduction
2. Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme
2.1. Preliminaries of the Chinese Remainder Theorem
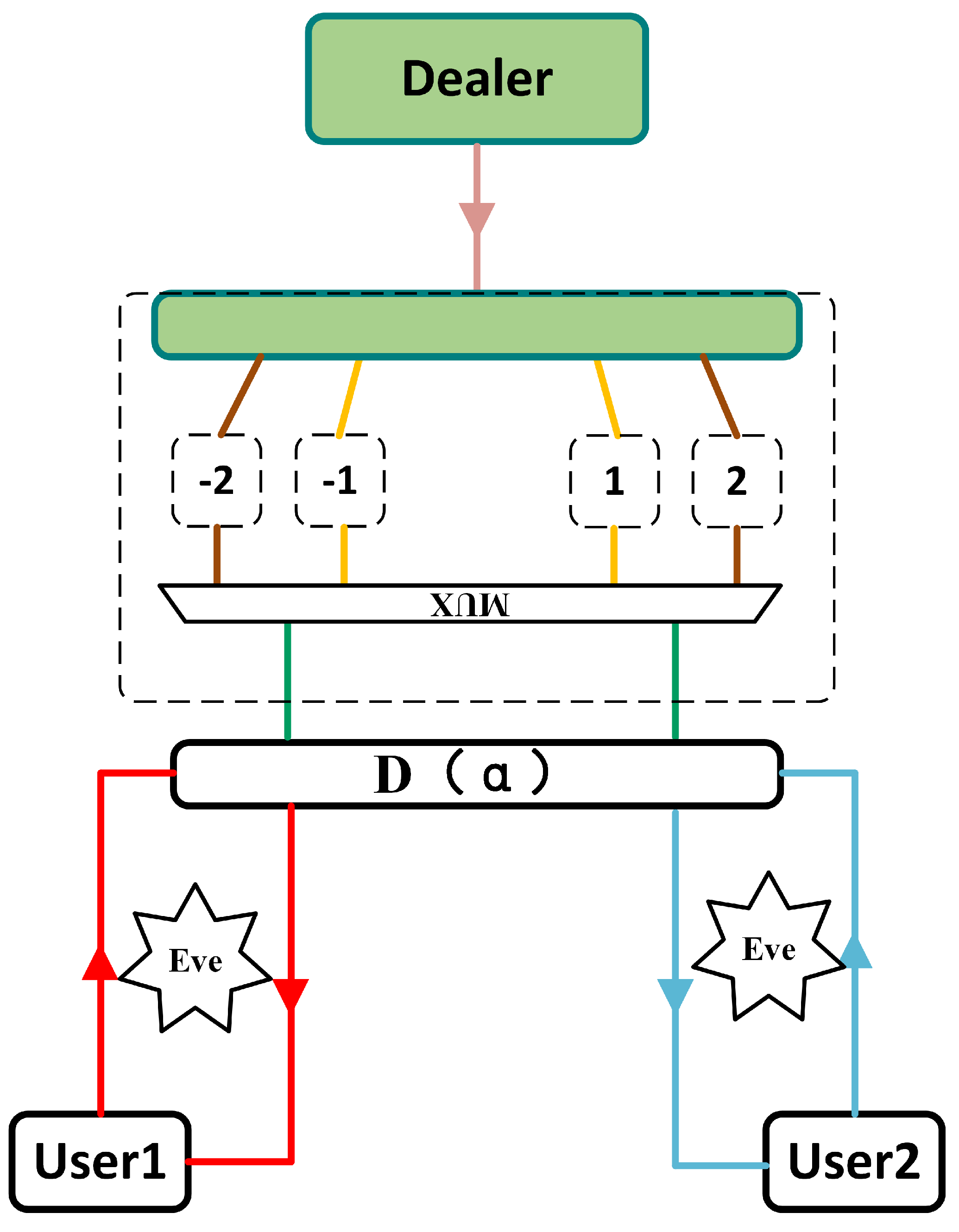
2.2. Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme
2.2.1. Initialization
2.2.2. Distribution
2.2.3. Reconstruction
3. Security Analysis
3.1. Mathematical and Structural Security Analysis
3.1.1. Mathematical Security Proof Based on the Chinese Remainder Theorem
- (1)
- Mathematical irreversibility: Knowing a single remainder (e.g., or ) cannot uniquely determine the original value X. For instance, if and , X could be 0, 2, 4, etc.; if and , X could be 0, 3, 6, etc. Thus, the information entropy of a single remainder is much lower than that of the complete secret, making it impossible to effectively recover the secret through exhaustive enumeration or reverse calculation.
- (2)
- Information entropy separation: As analyzed in the paper, the information entropy of each share (e.g., or ) is 1 bit and bits, respectively, while the entropy of the complete message X is bits. The information contained in a single share is insufficient to cover the entropy of the complete secret, preventing participants from inferring the global secret through local information
- (3)
- Time complexity: If an attacker attempts to guess other participants’ shares through a single remainder, they need to enumerate all possible combinations. Since the product of the moduli grows exponentially with the number of participants, the complexity of exhaustive search is too high to be feasible.
3.1.2. Structural Security Proof Based on Decentralization
3.2. Quantum Security
3.2.1. Quantum Security Analysis
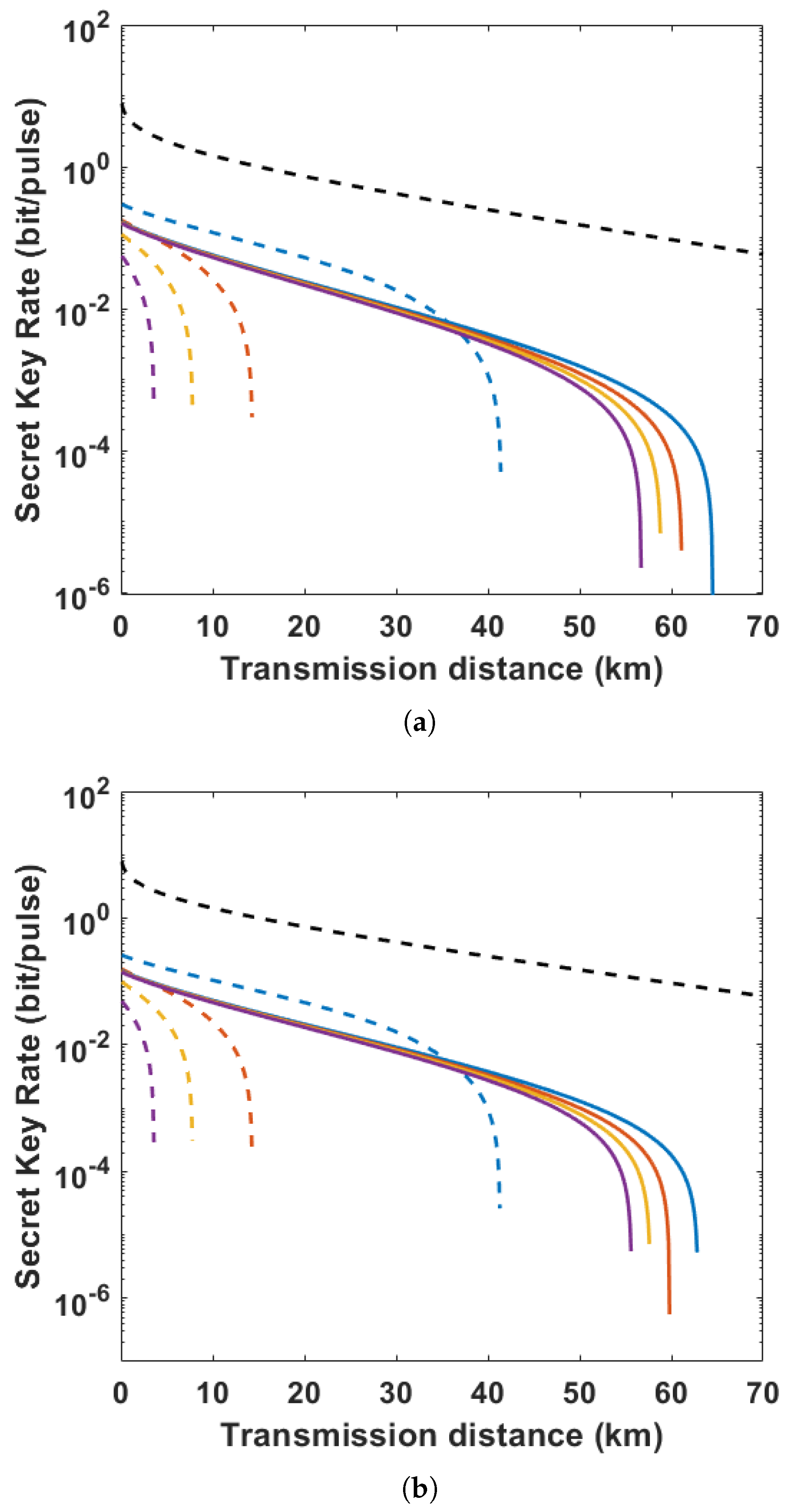
3.2.2. Numerical Simulation
- N is the total number of channels;
- is the effective length;
- is the channel spacing.
4. Performance Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| QSS | Quantum secret sharing |
| CV-QSS | Continuous-Variable Quantum Secret Sharing |
| OFC | Optical Frequency Comb |
| CRT | Chinese Remainder Theorem |
| WDM | Wavelength Division Multiplexing |
| TMSV | Two-Mode Squeezed Vacuum |
| PLL | Phase-Locked Loop |
| CV-QKD | Continuous-Variable Quantum Key Distribution |
| LDPC | Low-Density Parity-Check |
| HABS | Highly Asymmetric Beam Splitters |
| DQSS | Decentralized Quantum Secret Sharing |
| MLE | Maximum Likelihood Estimation |
| EC | Error Correction |
| AEP | Asymptotic Equipartition Property |
| SNR | Signal-to-Noise Ratio |
Appendix A
- M: Total signal states transmitted by Alice.
- m: Number of signal states (from a block M) for which Alice discloses the encoding k, with .
- p: Error correction (EC) success probability.
- : Finite-size key rate.
- : Total security error.
- : Asymptotic equipartition property term, defined as follows:where denotes the cardinality of the dealer’s outcome, which equals N in our scheme.
References
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef]
- Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162–168. [Google Scholar] [CrossRef]
- Zhang, Z.j.; Man, Z.x. Multiparty quantum secret sharing of classical messages based on entanglement swapping. Phys. Rev. A 2005, 72, 022303. [Google Scholar] [CrossRef]
- Kang, Y.; Guo, Y.; Zhong, H.; Chen, G.; Jing, X. Continuous Variable Quantum Secret Sharing with Fairness. Appl. Sci. 2019, 10, 189. [Google Scholar] [CrossRef]
- Schmid, C.; Trojek, P.; Bourennane, M.; Kurtsiefer, C.; Zukowski, M.; Weinfurter, H. Experimental Single Qubit Quantum Secret Sharing. Phys. Rev. Lett. 2005, 95, 230505. [Google Scholar] [CrossRef] [PubMed]
- Grice, W.P.; Qi, B. Quantum secret sharing using weak coherent states. Phys. Rev. A 2019, 100, 022339. [Google Scholar] [CrossRef]
- Peng, R.; Guo, Y.; Wang, Y.; Liao, Q. Decentralized continuous-variable quantum secret sharing. Quantum Inf. Process. 2023, 22, 368. [Google Scholar] [CrossRef]
- Liao, Q.; Liu, X.; Ou, B.; Fu, X. Continuous-Variable Quantum Secret Sharing Based on Multi-Ring Discrete Modulation. IEEE Trans. Commun. 2023, 71, 6051–6060. [Google Scholar] [CrossRef]
- Veselka, J.; Korotky, S. A multiwavelength source having precise channel spacing for WDM systems. IEEE Photonics Technol. Lett. 1998, 10, 958–960. [Google Scholar] [CrossRef]
- Millar, D.S.; Maher, R.; Lavery, D.; Koike-Akino, T.; Pajovic, M.; Alvarado, A.; Paskov, M.; Kojima, K.; Parsons, K.; Thomsen, B.C.; et al. Design of a 1 Tb/s Superchannel Coherent Receiver. J. Light. Technol. 2016, 34, 1453–1463. [Google Scholar] [CrossRef]
- Lorences-Riesgo, A.; Eriksson, T.A.; Fülöp, A.; Andrekson, P.A.; Karlsson, M. Frequency-Comb Regeneration for Self-Homodyne Superchannels. J. Light. Technol. 2016, 34, 1800–1806. [Google Scholar] [CrossRef]
- Lorences-Riesgo, A.; Mazur, M.; Eriksson, T.A.; Andrekson, P.A.; Karlsson, M. Self-homodyne 24 × 32-QAM superchannel receiver enabled by all-optical comb regeneration using brillouin amplification. Opt. Express 2016, 24, 29714–29723. [Google Scholar] [CrossRef] [PubMed]
- Mazur, M.; Lorences-Riesgo, A.; Schröder, J.; Andrekson, P.A.; Karlsson, M. High Spectral Efficiency PM-128QAM Comb-Based Superchannel Transmission Enabled by a Single Shared Optical Pilot Tone. J. Light. Technol. 2018, 36, 1318–1325. [Google Scholar] [CrossRef]
- Mazur, M.; Schröder, J.; Lorences-Riesgo, A.; Yoshida, T.; Andrekson, P.A. 11.5 bits/s/Hz PM-256QAM Comb-Based Superchannel Transmission by Combining Optical and Digital Pilots. 2018. Available online: https://api.semanticscholar.org/CorpusID:49190505 (accessed on 29 June 2025).
- Lundberg, L.; Mazur, M.; Lorences-Riesgo, A.; Karlsson, M.; Andrekson, P.A. Joint Carrier Recovery for DSP Complexity Reduction in Frequency Comb-Based Superchannel Transceivers. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Liu, C.; Pan, J.; Detwiler, T.; Stark, A.; Hsueh, Y.T.; Chang, G.K.; Ralph, S.E. Joint digital signal processing for superchannel coherent optical communication systems. Opt. Express 2013, 21, 8342–8356. [Google Scholar] [CrossRef]
- Souto, D.V.; Olsson, B.E.; Larsson, C.; Mello, D.A.A. Joint-Polarization and Joint-Subchannel Carrier Phase Estimation for 16-QAM Optical Systems. J. Light. Technol. 2012, 30, 3185–3191. [Google Scholar] [CrossRef]
- Lundberg, L.; Karlsson, M.; Lorences-Riesgo, A.; Mazur, M.; Torres-Company, V.; Schröder, J.; Andrekson, P.A. Frequency Comb-Based WDM Transmission Systems Enabling Joint Signal Processing. Appl. Sci. 2018, 8, 718. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, Y.; Huang, W.; Huang, D.; Guo, Y. Optical frequency comb-based multichannel parallel continuous-variable quantum key distribution. Opt. Express 2019, 27, 25314–25329. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Rueda, A.; Sedlmeir, F.; Kumari, M.; Leuchs, G.; Schwefel, H.G.L. Resonant electro-optic frequency comb. Nature 2019, 569, E11. [Google Scholar] [CrossRef]
- Spencer, D.T.; Drake, T.; Briles, T.C.; Stone, J.; Sinclair, L.C.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; Bluestone, A.; et al. An optical-frequency synthesizer using integrated photonics. Nature 2018, 557, 81–85. [Google Scholar] [CrossRef]
- Huang, J.; Chen, X.; Li, X.; Wang, J. Chip-based photonic graph states. AAPPS Bull. 2023, 33, 14. [Google Scholar] [CrossRef]
- Zeng, H.; Du, M.M.; Zhong, W.; Zhou, L.; Sheng, Y.B. High-capacity device-independent quantum secure direct communication based on hyper-encoding. Fundam. Res. 2024, 4, 851–857. [Google Scholar] [CrossRef]
- Shen, A.; Cao, X.Y.; Wang, Y.; Fu, Y.; Gu, J.; Liu, W.B.; Weng, C.X.; Yin, H.L.; Chen, Z.B. Experimental quantum secret sharing based on phase encoding of coherent states. Sci. China-Phys. Mech. Astron. 2023, 66, 260311. [Google Scholar] [CrossRef]
- Corcoran, B.; Mitchell, A.; Morandotti, R.; Oxenlowe, L.K.; Moss, D.J. Optical microcombs for ultrahigh-bandwidth communications. Nat. Photonics 2025, 19, 451–462. [Google Scholar] [CrossRef]
- Grosshans, F.; Grangier, P. Continuous Variable Quantum Cryptography Using Coherent States. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed]
- Fossier, S.; Diamanti, E.; Debuisschert, T.; Tualle-Brouri, R.; Grangier, P. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 114014. [Google Scholar] [CrossRef]
- Liu, X.; Chandrasekhar, S.; Winzer, P.J. Digital Signal Processing Techniques Enabling Multi-Tbs Superchannel Transmission: An overview of recent advances in DSP-enabled superchannels. IEEE Signal Process. Mag. 2014, 31, 16–24. [Google Scholar] [CrossRef]
- Temprana, E.; Myslivets, E.; Kuo, B.P.; Liu, L.; Ataie, V.; Alic, N.; Radic, S. Overcoming Kerr-induced capacity limit in optical fiber transmission. Science 2015, 348, 1445–1448. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Fiber-Optic Communication Systems, 4th ed.; John Wiley Sons: Hoboken, NJ, USA, 2010; ISBN 978-0-470-50511-3. Available online: https://www.wiley.com/en-us/Fiber+Optic+Communication+Systems%2C+4th+Edition-p-9780470505113 (accessed on 29 June 2025).
- Papanastasiou, P.; Pirandola, S. Continuous-variable quantum cryptography with discrete alphabets: Composable security under collective Gaussian attacks. Phys. Rev. Res. 2021, 3, 013047. [Google Scholar] [CrossRef]
- Ghorai, S.; Grangier, P.; Diamanti, E.; Leverrier, A. Asymptotic Security of Continuous-Variable Quantum Key Distribution with a Discrete Modulation. Phys. Rev. X 2019, 9, 021059. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, R.; Wang, Y.; Zhang, H.; Mao, Y.; Guo, Y. Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme. Mathematics 2025, 13, 2455. https://doi.org/10.3390/math13152455
Peng R, Wang Y, Zhang H, Mao Y, Guo Y. Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme. Mathematics. 2025; 13(15):2455. https://doi.org/10.3390/math13152455
Chicago/Turabian StylePeng, Runsheng, Yijun Wang, Hang Zhang, Yun Mao, and Ying Guo. 2025. "Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme" Mathematics 13, no. 15: 2455. https://doi.org/10.3390/math13152455
APA StylePeng, R., Wang, Y., Zhang, H., Mao, Y., & Guo, Y. (2025). Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme. Mathematics, 13(15), 2455. https://doi.org/10.3390/math13152455





