Design of Extended Dissipative Approach via Memory Sampled-Data Control for Stabilization and Its Application to Mixed Traffic System
Abstract
1. Introduction
- (1)
- According to the existing literature, the MSDC strategy is considered for the first time in the extended dissipative framework to examine the controllability and stabilization of an MTS with a single CAV and multiple heterogeneous HDVs.
- (2)
- We deal with the suggested integral terms by using the appropriate LKF and other inequality procedures, which results in the quadratically stable and extended dissipative condition.
- (3)
- The suggested MTS necessary condition, which makes the system more generic, was determined using the extended dissipative performance index framework, which includes , passivity, and dissipativity, which makes the system more general.
| Aspect | [1] | [2] | [3] | [7] | [8] | [9] | Our Paper |
|---|---|---|---|---|---|---|---|
| Sampled-data control | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✔ |
| Extended dissipative | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✔ |
| Traffic model | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
| LMI method | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✔ |
| Reference | Main Contribution | Relevance to Current Work |
|---|---|---|
| [23] | Studied robust stabilization for T-S fuzzy systems with time-varying delays and MSDC. | Our work applies these to an MTS, emphasizing comprehensive extended dissipativity. |
| [24] | Investigated nonfragile exponential synchronization of delayed complex dynamical networks with MSDC. | Our work focuses on extended dissipativity stabilization for an MTS, a distinct control objective and practical application domain. |
| [25] | Analyzed nonfragile consensus of multi-agent systems based on MSDC. | Our focus is extended dissipativity stabilization for specific MTS platoons and traffic flow optimization, a different problem. |
| [22] | Presented further results on stabilization of chaotic systems based on fuzzy MSDC. | Our paper applies MSDC (without fuzzy logic) to stabilize a practical MTS. |
| [26] | Conducted dissipativity analysis for T–S fuzzy systems under MSDC. | Our work extends this to extended dissipativity for an MTS, offering a comprehensive performance evaluation. |
| [27] | Explored finite-time stabilization of T–S fuzzy semi-Markov switching systems via coupling memory sampled-data control (CMSDC). | Our paper employs CMSDC for extended dissipativity and quadratic stability of an MTS, a different objective and application. |
2. Problem Formulation and Preliminaries
Design of Coupling Memory Sampled-Data Control (CMSDC)
- .
- .
3. Main Results
- If , the controller applies the delayed state with gain , assuming the signal was transmitted and received without issue.
- If , the controller instead uses the more recent state with gain , compensating for the loss of the delayed signal.
4. Numerical Example
- 1.
- Define System Parameters: Initialize the required system matrices including and with appropriate dimensions and the known parameters.
- 2.
- Define Control Gains: Introduce and for the controller gains and set up the unknown matrices , , , , , , , , , and .
- 3.
- Set Performance Matrices: Configure the weighting matrices for different performance indices (e.g., , passivity, and -Dissipativity).
- 4.
- Formulate LMI Constraints:
- Ensure positive definiteness of Lyapunov matrices.
- Incorporate stability conditions using system dynamics.
- Include delay-dependent terms for robustness.
- 5.
- Define Optimization Objective: Maximize the sampling period σ while maintaining feasibility.
- 6.
- Solve the LMI Problem: Use an LMI solver in MATLAB to check feasibility and determine optimal parameters.
- 7.
- Check Results: If a feasible solution exists, extract the maximum sampling period and controller gains; otherwise, Return to step 1 and adjust the sampling intervals and known parameters.
- ensures robustness against external disturbances (e.g., sudden braking or road slope), preventing amplification across the vehicle platoon.
- limits peak spacing or velocity deviations in response to energy-bounded driver inputs, thereby enhancing safety.
- Passivity guarantees energy-dissipative behavior, which helps avoid oscillations and improves stability in the presence of time delay and switching dynamics.
- -dissipativity provides a flexible framework to model and balance safety, comfort, and efficiency in mixed traffic environments.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Notation | Representation |
| Matrix A transposition/inverse | |
| Set of all real numbers | |
| -dimensional Euclidean space | |
| Matrix S is symmetric and positive-definite | |
| A column vector | |
| A block-diagonal matrix | |
| identity matrix | |
| ∗ | Symmetric terms in a matrix |
| Euclidean vector norm | |
| Zero matrix of size | |
| Space of square-integrable vector functions on | |
| Probability | |
| and | Maximum and minimum value |
| Supremum (least upper bound) |
References
- Wang, S.T.; Zhu, W.X.; Ma, X.L. Mixed traffic system with multiple vehicle types and autonomous vehicle platoon: Modeling, stability analysis and control strategy. Phys. A Stat. Mech. Its Appl. 2023, 632, 129293. [Google Scholar] [CrossRef]
- Jin, S.; Sun, D.H.; Zhao, M.; Li, Y.; Chen, J. Modeling and stability analysis of mixed traffic with conventional and connected automated vehicles from cyber physical perspective. Phys. A Stat. Mech. Its Appl. 2020, 551, 124217. [Google Scholar] [CrossRef]
- Qin, Y.; Luo, Q.; Wang, H. Stability analysis and connected vehicles management for mixed traffic flow with platoons of connected automated vehicles. Transp. Res. Part C Emerg. Technol. 2023, 157, 104370. [Google Scholar] [CrossRef]
- Abou Harfouch, Y.; Yuan, S.; Baldi, S. An adaptive switched control approach to heterogeneous platooning with intervehicle communication losses. IEEE Trans. Control Netw. Syst. 2017, 5, 1434–1444. [Google Scholar] [CrossRef]
- Hao, W.; Rong, D.; Zhang, Z.; Byon, Y.J.; Lv, N.; Chen, Y. Stability analysis and speed-coordinated control of mixed traffic flow in expressway merging area. J. Transp. Eng. Part A Syst. 2022, 148, 04022098. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E.; Spring, J.; Nowakowski, C.; Kawazoe, H.; Nakamura, M. Cooperative adaptive cruise control in real traffic situations. IEEE Trans. Intell. Transp. Syst. 2013, 15, 296–305. [Google Scholar] [CrossRef]
- Chang, X.; Li, H.; Rong, J.; Zhao, X.; Li, A.R. Analysis on traffic stability and capacity for mixed traffic flow with platoons of intelligent connected vehicles. Phys. A Stat. Mech. Its Appl. 2020, 557, 124829. [Google Scholar] [CrossRef]
- Yao, Z.; Hu, R.; Jiang, Y.; Xu, T. Stability and safety evaluation of mixed traffic flow with connected automated vehicles on expressways. J. Saf. Res. 2020, 75, 262–274. [Google Scholar] [CrossRef]
- Zheng, F.; Liu, C.; Liu, X.; Jabari, S.E.; Lu, L. Analyzing the impact of automated vehicles on uncertainty and stability of the mixed traffic flow. Transp. Res. Part C Emerg. Technol. 2020, 112, 203–219. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, K.; Zhang, Y.; Su, R. Traffic light scheduling for pedestrian-vehicle mixed-flow networks. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1468–1483. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, R. An optimization model and traffic light control scheme for heterogeneous traffic systems. Transp. Res. Part C Emerg. Technol. 2021, 124, 102911. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, W.X.; Xu, S. Filtering of Markovian jump delay systems based on a new performance index. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1250–1263. [Google Scholar] [CrossRef]
- Li, M.; Zhao, J.; Xia, J.; Zhuang, G.; Zhang, W. Extended dissipative analysis and synthesis for network control systems with an event-triggered scheme. Neurocomputing 2018, 312, 34–40. [Google Scholar] [CrossRef]
- Cai, X.; Wang, J.; Zhong, S.; Shi, K.; Tang, Y. Fuzzy quantized sampled-data control for extended dissipative analysis of T–S fuzzy system and its application to WPGSs. J. Frankl. Inst. 2021, 358, 1350–1375. [Google Scholar] [CrossRef]
- Cai, X.; Shi, K.; Sun, Y.; Cao, J.; Wen, S.; Qiao, C.; Tian, Z. Stability analysis of networked control systems under DoS attacks and security controller design with mini-batch machine learning supervision. IEEE Trans. Inf. Forensics Secur. 2023, 19, 3857–3865. [Google Scholar] [CrossRef]
- Cai, X.; Shi, K.; Sun, Y.; Cao, J.; Wen, S.; Tian, Z. Intelligent event-triggered control supervised by mini-batch machine learning and data compression mechanism for T-S fuzzy NCSs under DoS attacks. IEEE Trans. Fuzzy Syst. 2023, 32, 804–815. [Google Scholar] [CrossRef]
- Wu, Z.; Peng, H.; Li, F.; Huang, T.; Yang, C.; Gui, W. Extended dissipative analysis and taxiing control of fuzzy model based aircraft-on-ground systems via sliding mode approach. J. Frankl. Inst. 2022, 359, 4623–4641. [Google Scholar] [CrossRef]
- Gao, H.; Xia, J.; Zhuang, G.; Wang, Z.; Sun, Q. Nonfragile finite-time extended dissipative control for a class of uncertain switched neutral systems. Complexity 2017, 2017, 6581308. [Google Scholar] [CrossRef]
- Vadivel, R.; Njitacke, Z.T.; Shanmugam, L.; Gunasekaran, N. Dynamical analysis and reachable set estimation of TS fuzzy system with permanent magnet synchronous motor. Commun. Nonlinear Sci. Numer. Simul. 2023, 125, 107407. [Google Scholar] [CrossRef]
- Vadivel, R.; Wu, Y.; Chaisena, K.; Gunasekaran, N. New results on T–S fuzzy sampled-data stabilization for switched chaotic systems with its applications. Chaos Solitons Fractals 2022, 164, 112741. [Google Scholar] [CrossRef]
- Han, S.; Zhong, Q.; Cui, L.; Shi, K.; Cai, X.; Kwon, O.M. Extended dissipativity analysis for TS fuzzy systems based on reliable memory control and aperiodic sampled-data method. J. Frankl. Inst. 2022, 359, 2156–2175. [Google Scholar] [CrossRef]
- Liu, Y.; Park, J.H.; Guo, B.Z.; Shu, Y. Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans. Fuzzy Syst. 2017, 26, 1040–1045. [Google Scholar] [CrossRef]
- Ge, C.; Shi, Y.; Park, J.H.; Hua, C. Robust H∞ stabilization for T-S fuzzy systems with time-varying delays and memory sampled-data control. Appl. Math. Comput. 2019, 346, 500–512. [Google Scholar]
- Liu, Y.; Guo, B.Z.; Park, J.H.; Lee, S.M. Nonfragile exponential synchronization of delayed complex dynamical networks with memory sampled-data control. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 118–128. [Google Scholar] [CrossRef]
- Ge, C.; Park, J.H.; Hua, C.; Guan, X. Nonfragile consensus of multiagent systems based on memory sampled-data control. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 391–399. [Google Scholar] [CrossRef]
- Ge, C.; Park, J.H.; Hua, C.; Guan, X. Dissipativity analysis for T–S fuzzy system under memory sampled-data control. IEEE Trans. Cybern. 2019, 51, 961–969. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, D.; Qi, W.; Cao, J.; Shi, K. Finite-time stabilization of T–S fuzzy semi-Markov switching systems: A coupling memory sampled-data control approach. J. Frankl. Inst. 2020, 357, 11265–11280. [Google Scholar] [CrossRef]
- Wei, H.; Li, R.; Chen, C.; Tu, Z. Extended dissipative analysis for memristive neural networks with two additive time-varying delay components. Neurocomputing 2016, 216, 429–438. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Bahrami, S.; Kouvelas, A. Synthesis of output-feedback controllers for mixed traffic systems in presence of disturbances and uncertainties. IEEE Trans. Intell. Transp. Syst. 2022, 24, 6450–6462. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y.; Xu, Q.; Wang, J.; Li, K. Controllability analysis and optimal control of mixed traffic flow with human-driven and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7445–7459. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Fukui, M.; Kikuchi, M.; Hasebe, K.; Nakayama, A.; Nishinari, K.; Tadaki, S.i.; Yukawa, S. Traffic jams without bottlenecks—Experimental evidence for the physical mechanism of the formation of a jam. New J. Phys. 2008, 10, 033001. [Google Scholar] [CrossRef]

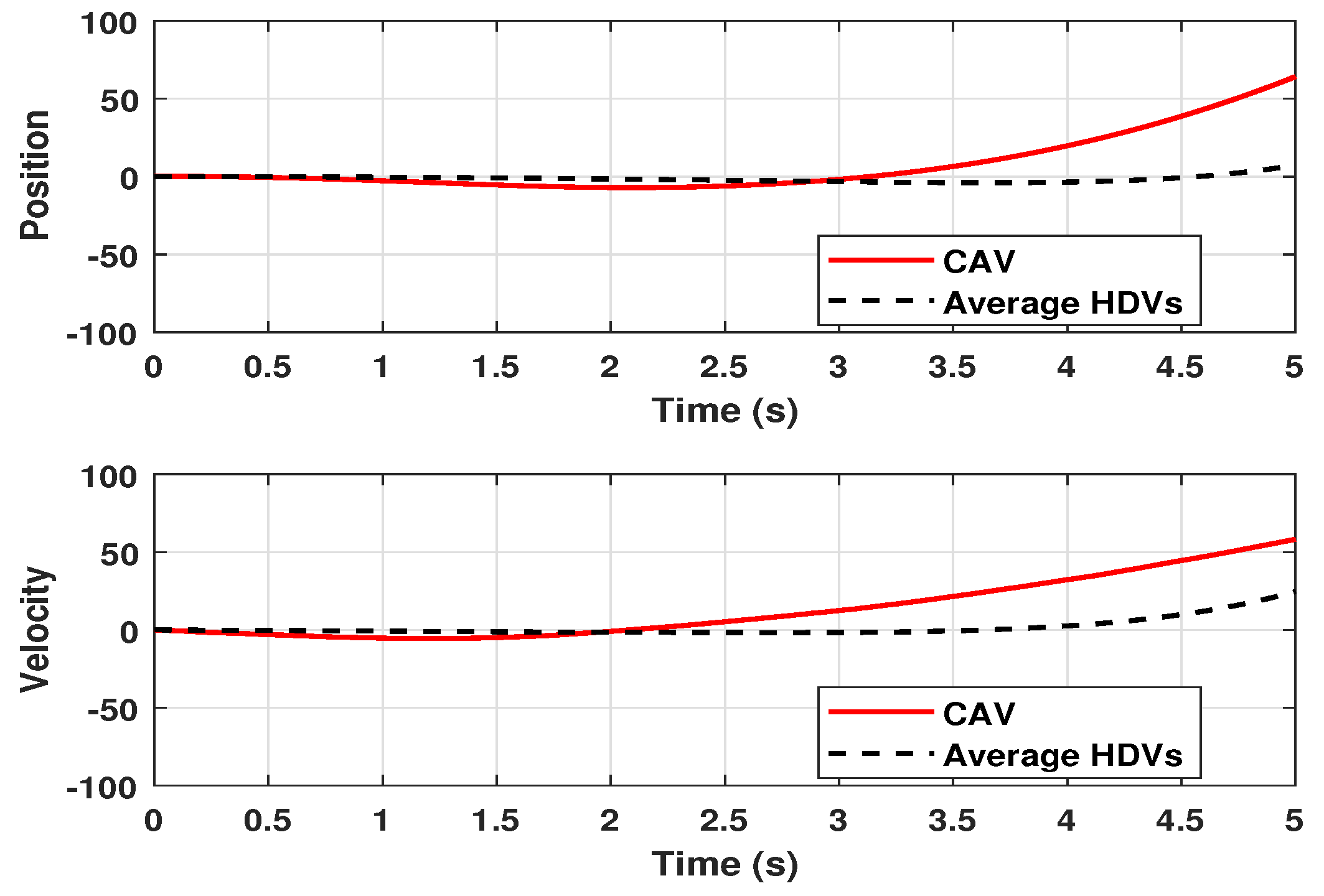
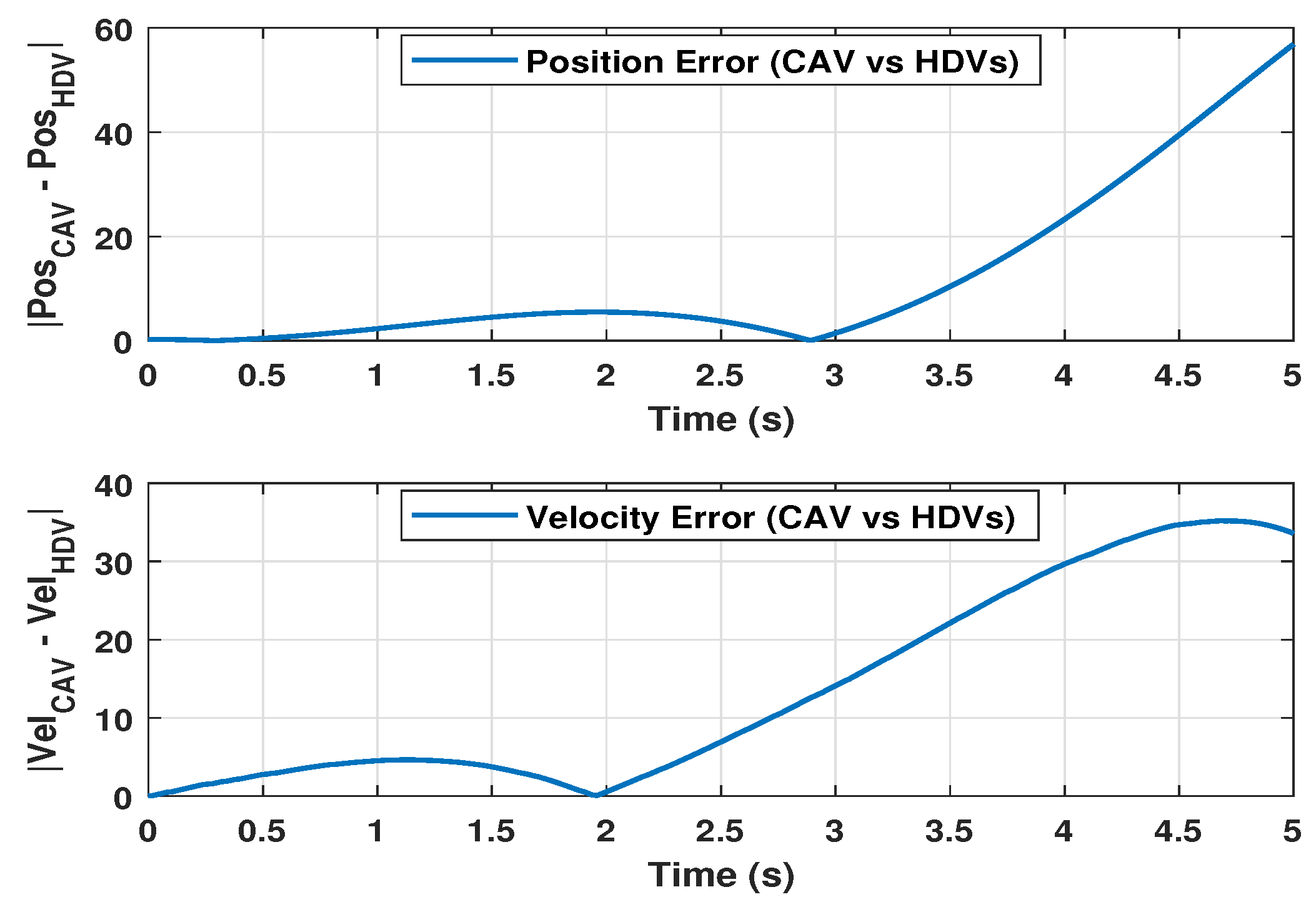

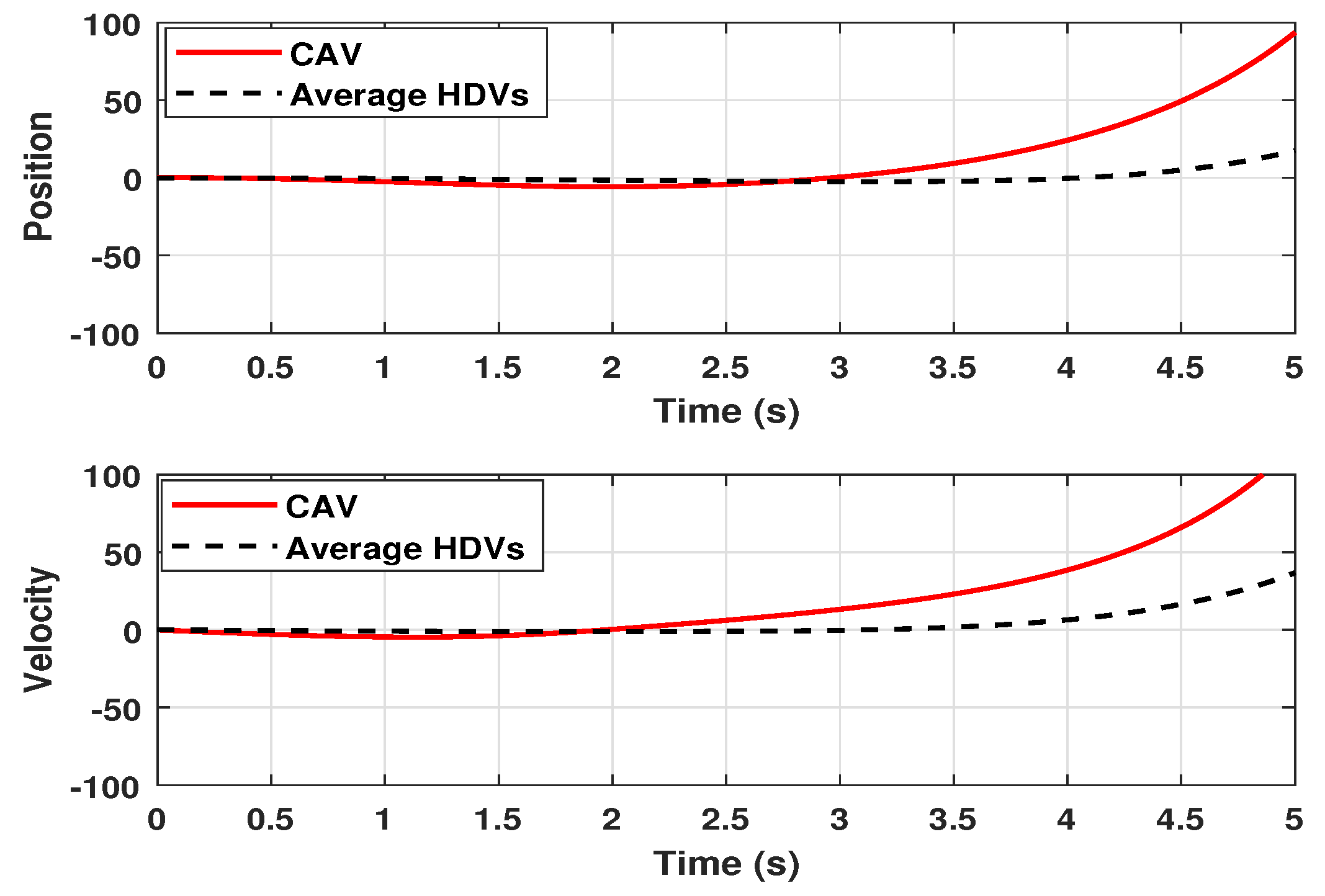
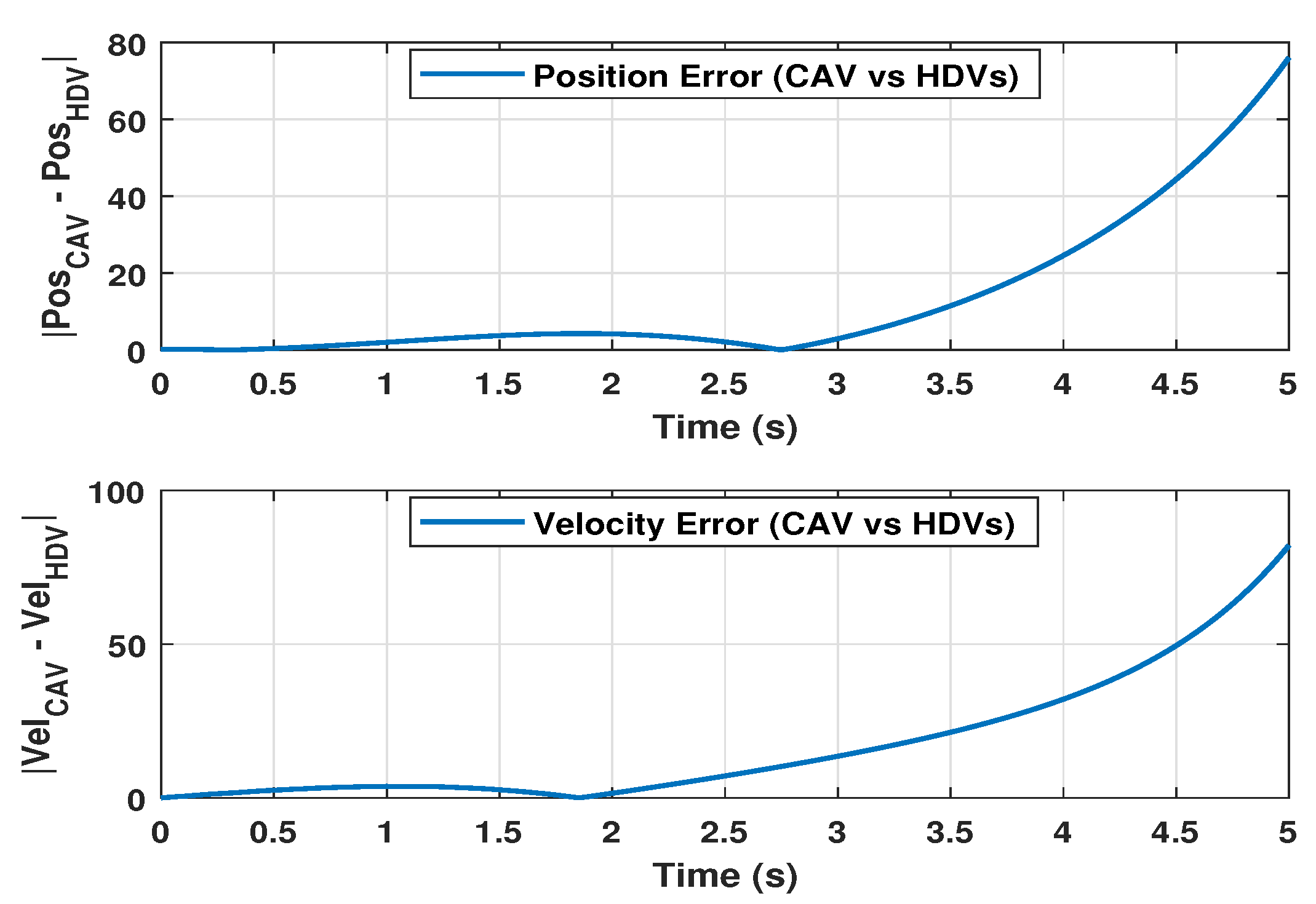

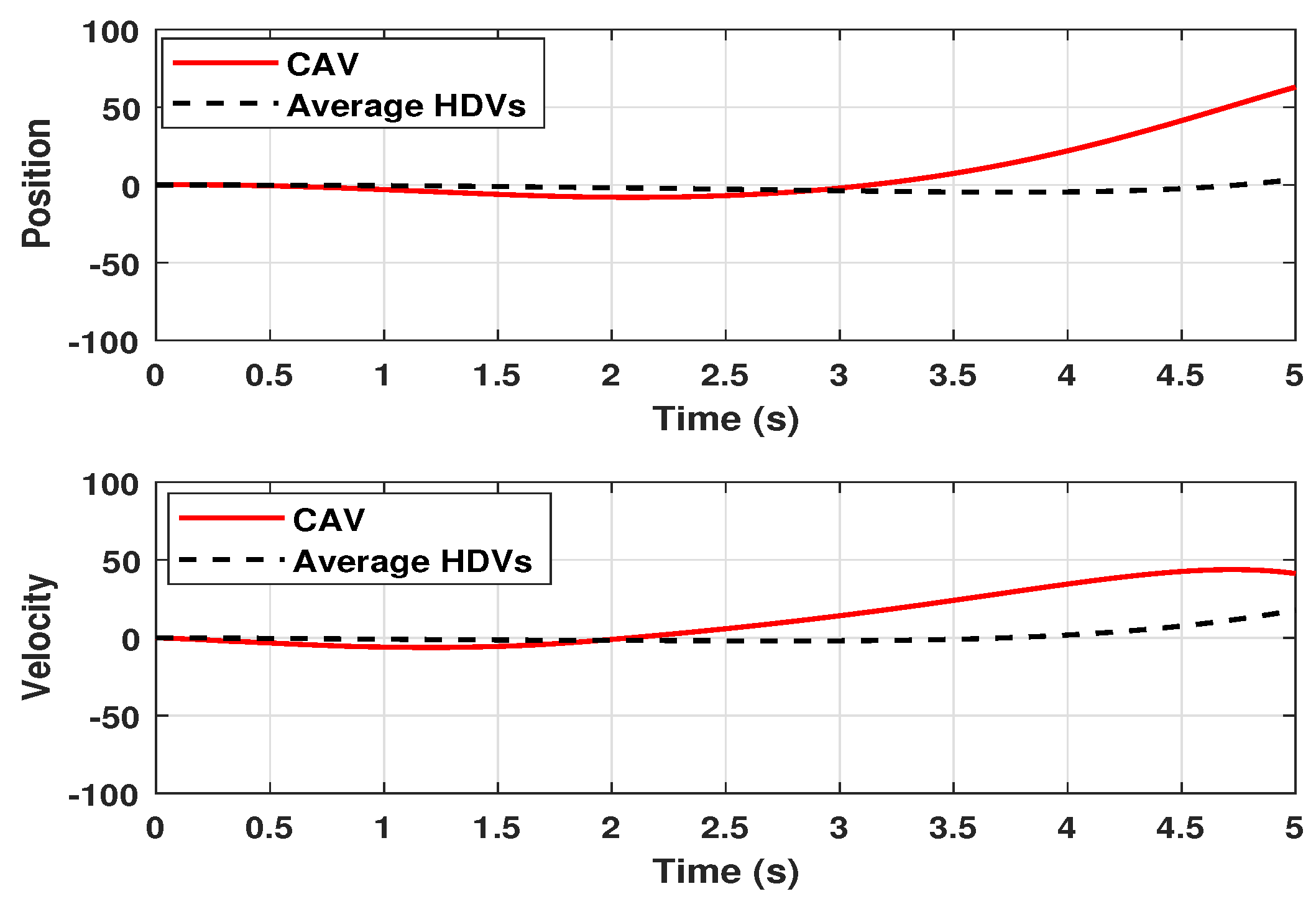


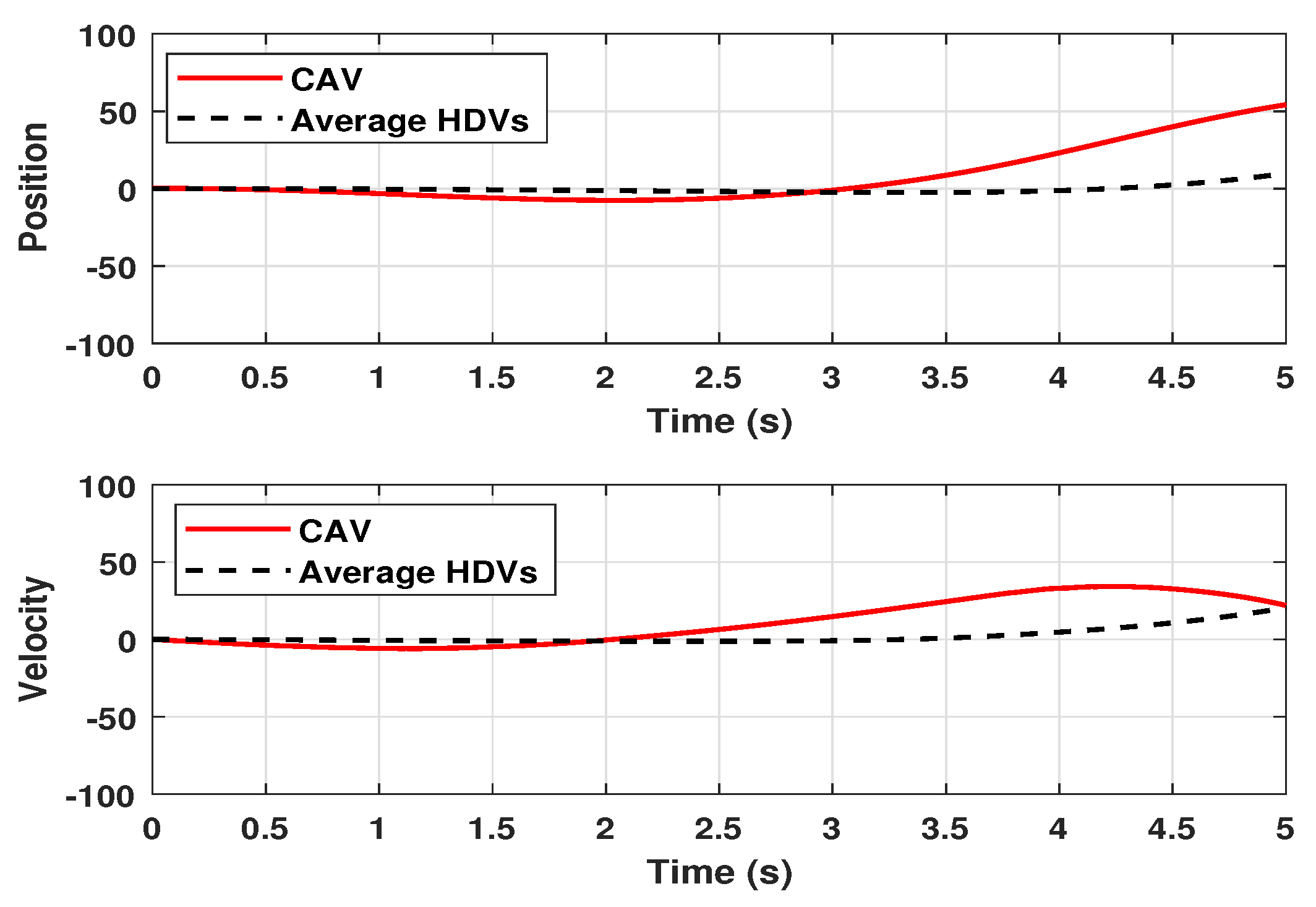

| 15 m/s | |
| 30 |
| Analysis | ||||
|---|---|---|---|---|
| case | 0 | 0 | ||
| case | 0 | 0 | I | |
| Passivity case | 0 | I | 0 | |
| -dissipativity case | I | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sukpol, W.; Rajarathinam, V.; Hammachukiattikul, P.; Pornphol, P. Design of Extended Dissipative Approach via Memory Sampled-Data Control for Stabilization and Its Application to Mixed Traffic System. Mathematics 2025, 13, 2449. https://doi.org/10.3390/math13152449
Sukpol W, Rajarathinam V, Hammachukiattikul P, Pornphol P. Design of Extended Dissipative Approach via Memory Sampled-Data Control for Stabilization and Its Application to Mixed Traffic System. Mathematics. 2025; 13(15):2449. https://doi.org/10.3390/math13152449
Chicago/Turabian StyleSukpol, Wimonnat, Vadivel Rajarathinam, Porpattama Hammachukiattikul, and Putsadee Pornphol. 2025. "Design of Extended Dissipative Approach via Memory Sampled-Data Control for Stabilization and Its Application to Mixed Traffic System" Mathematics 13, no. 15: 2449. https://doi.org/10.3390/math13152449
APA StyleSukpol, W., Rajarathinam, V., Hammachukiattikul, P., & Pornphol, P. (2025). Design of Extended Dissipative Approach via Memory Sampled-Data Control for Stabilization and Its Application to Mixed Traffic System. Mathematics, 13(15), 2449. https://doi.org/10.3390/math13152449






