Capturing Discontinuities with Precision: A Numerical Exploration of 3D Telegraph Interface Models via Multi-Resolution Technique
Abstract
1. Introduction
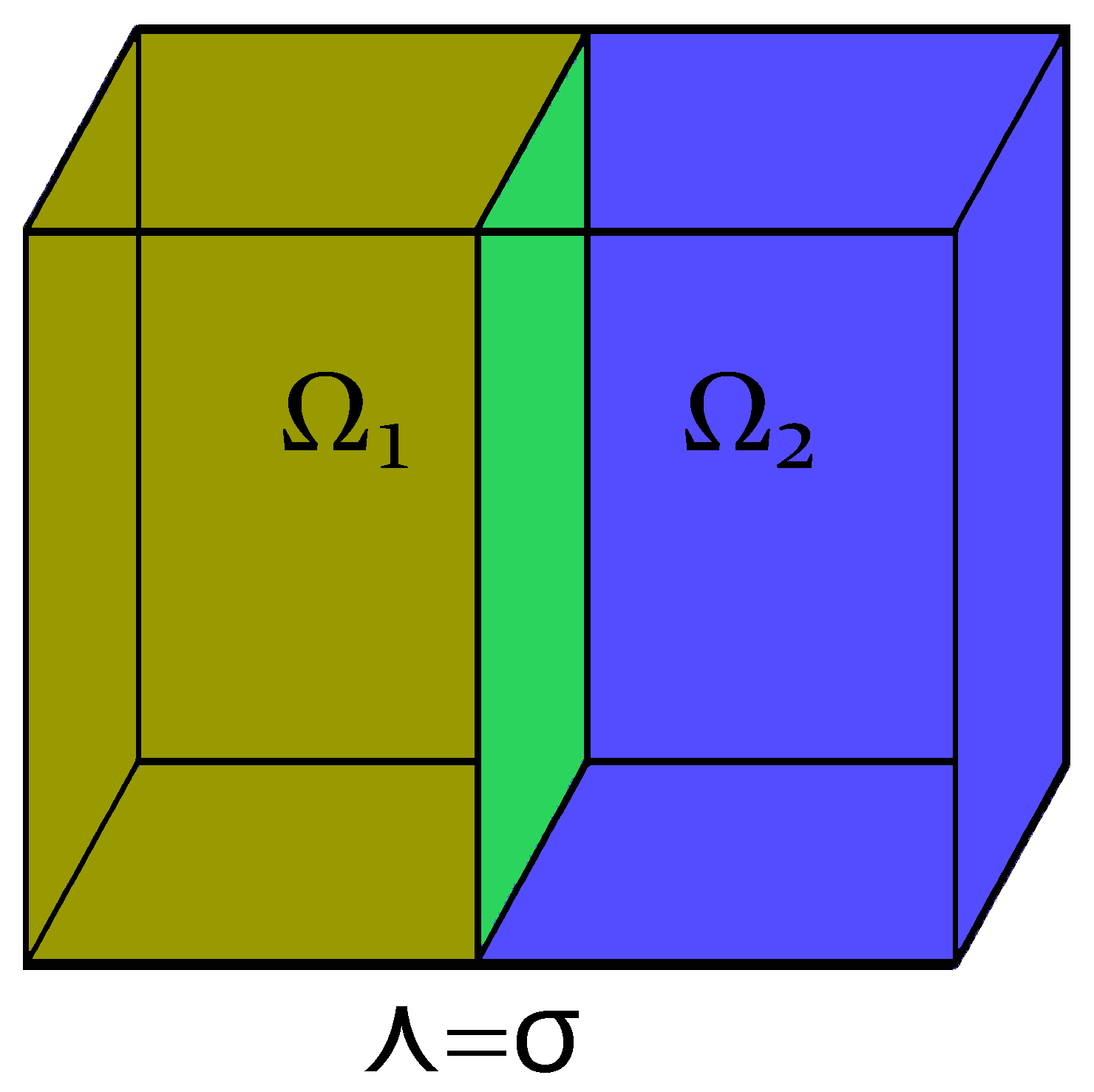
2. Governing Equations
2.1. Kronecker Tensor Product
2.2. Hadamard Product
3. Haar Wavelet Collocation Method
4. Temporal Approximations
5. Formulation of the Numerical Method
5.1. Linear Case
5.2. Nonlinear Case
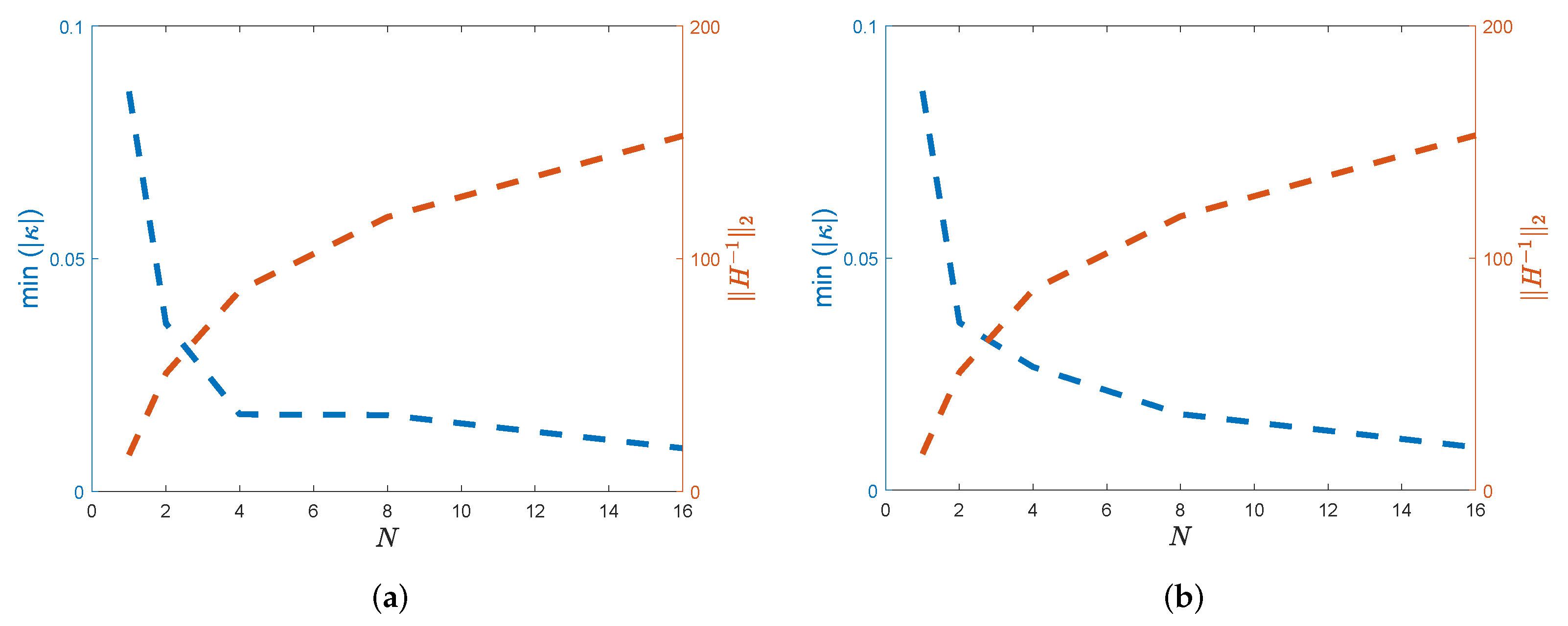
6. Convergence Criteria and Stability
6.1. Convergence of HWCM
6.2. Stability of HWCM
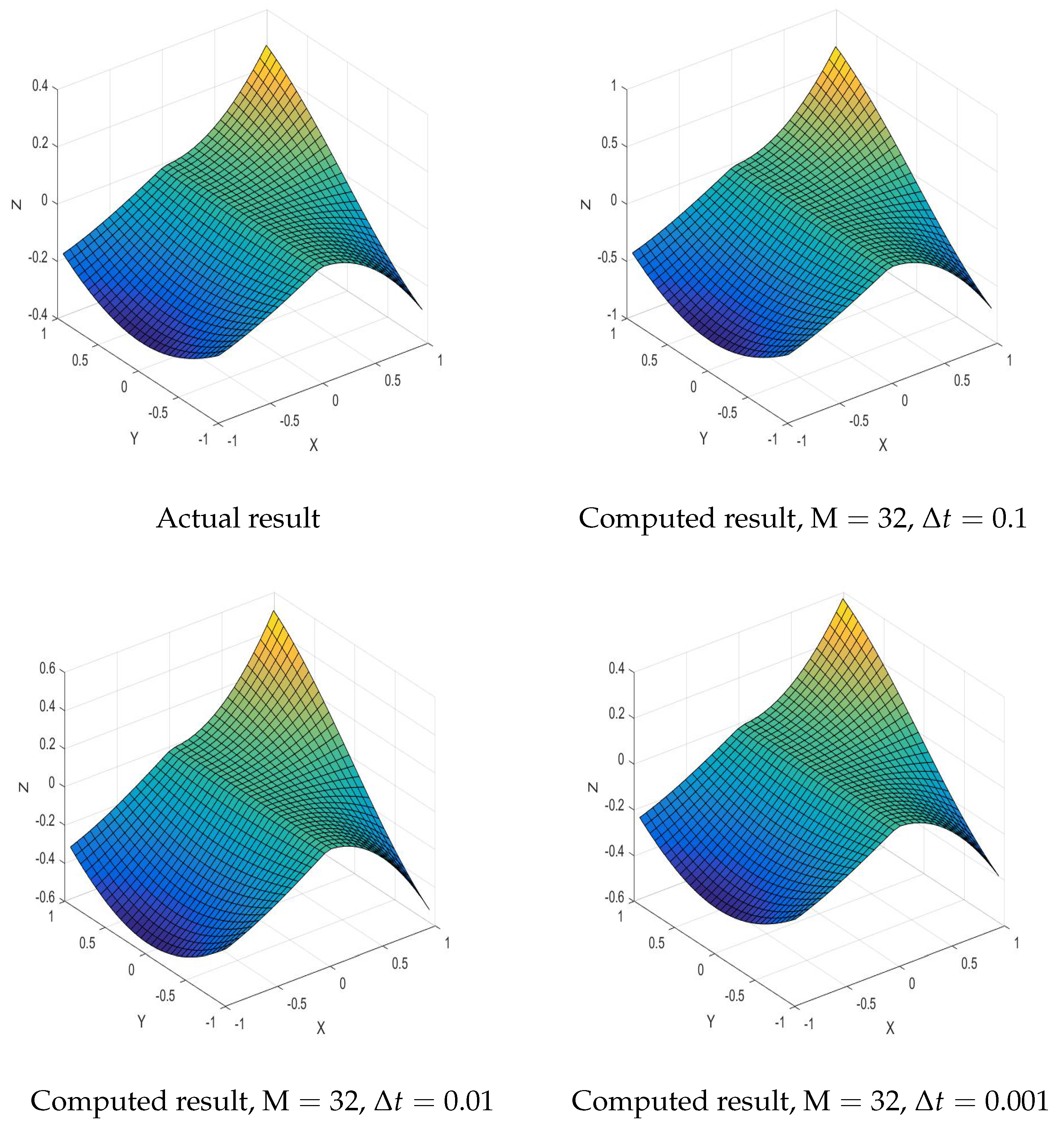
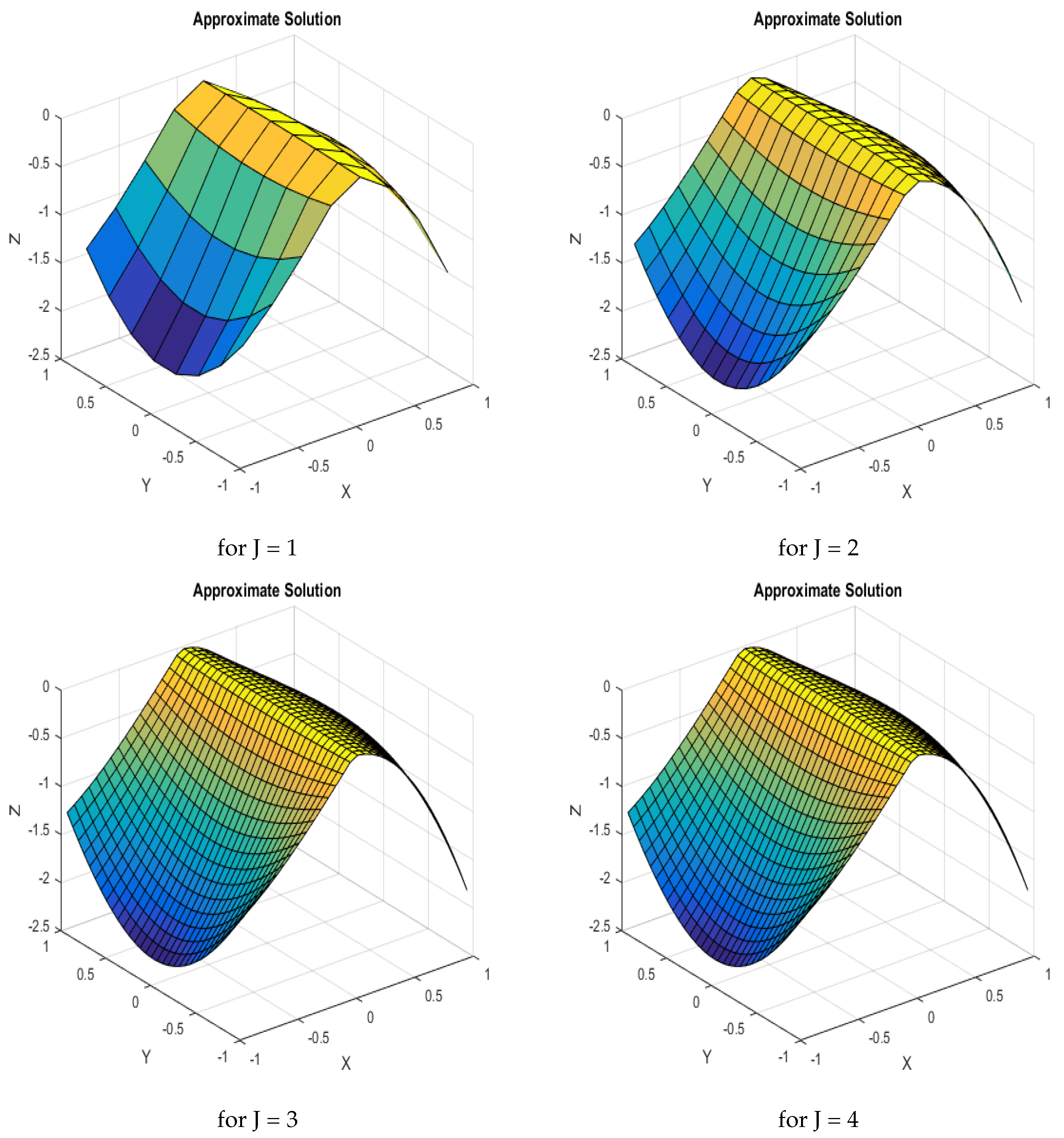
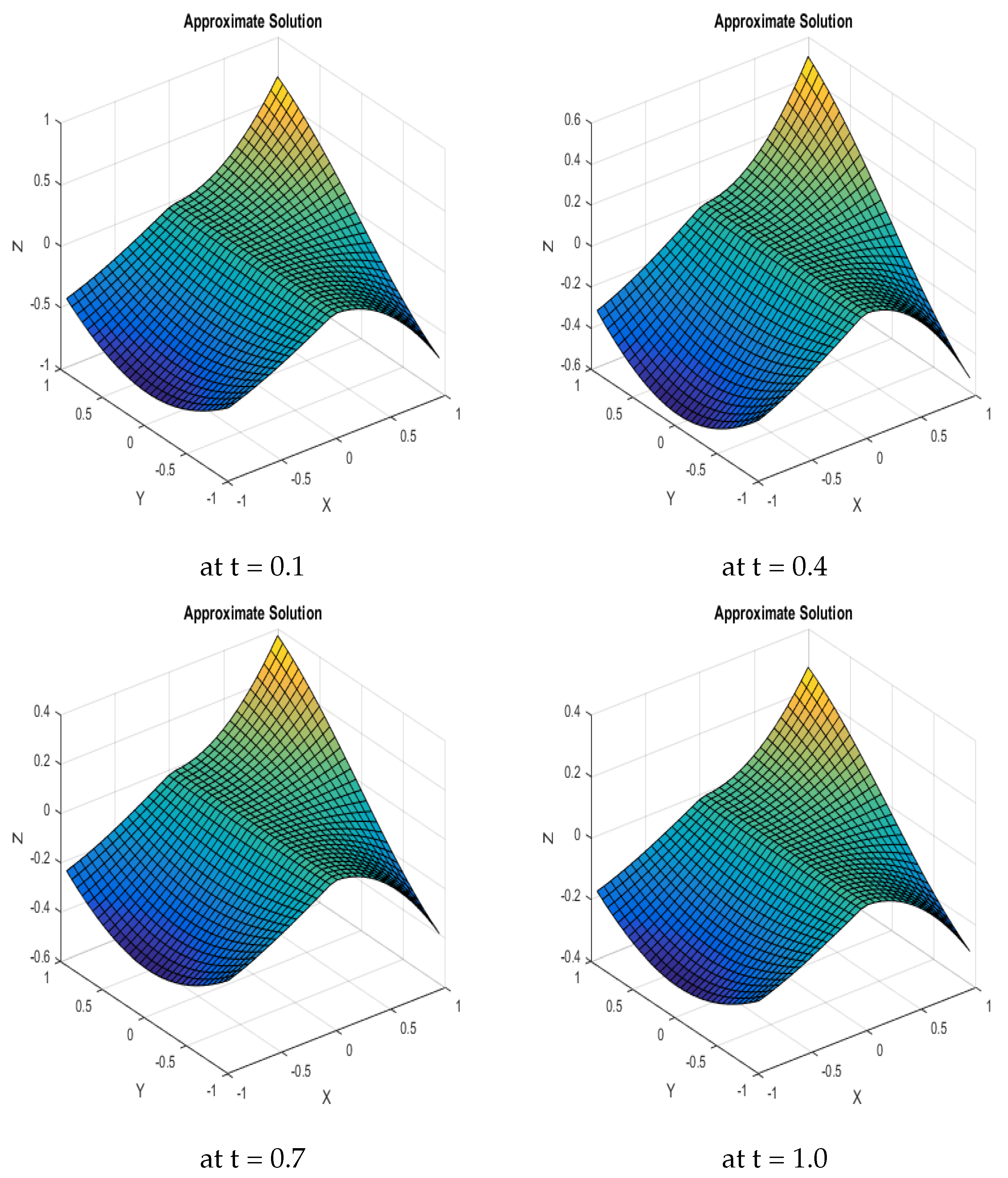
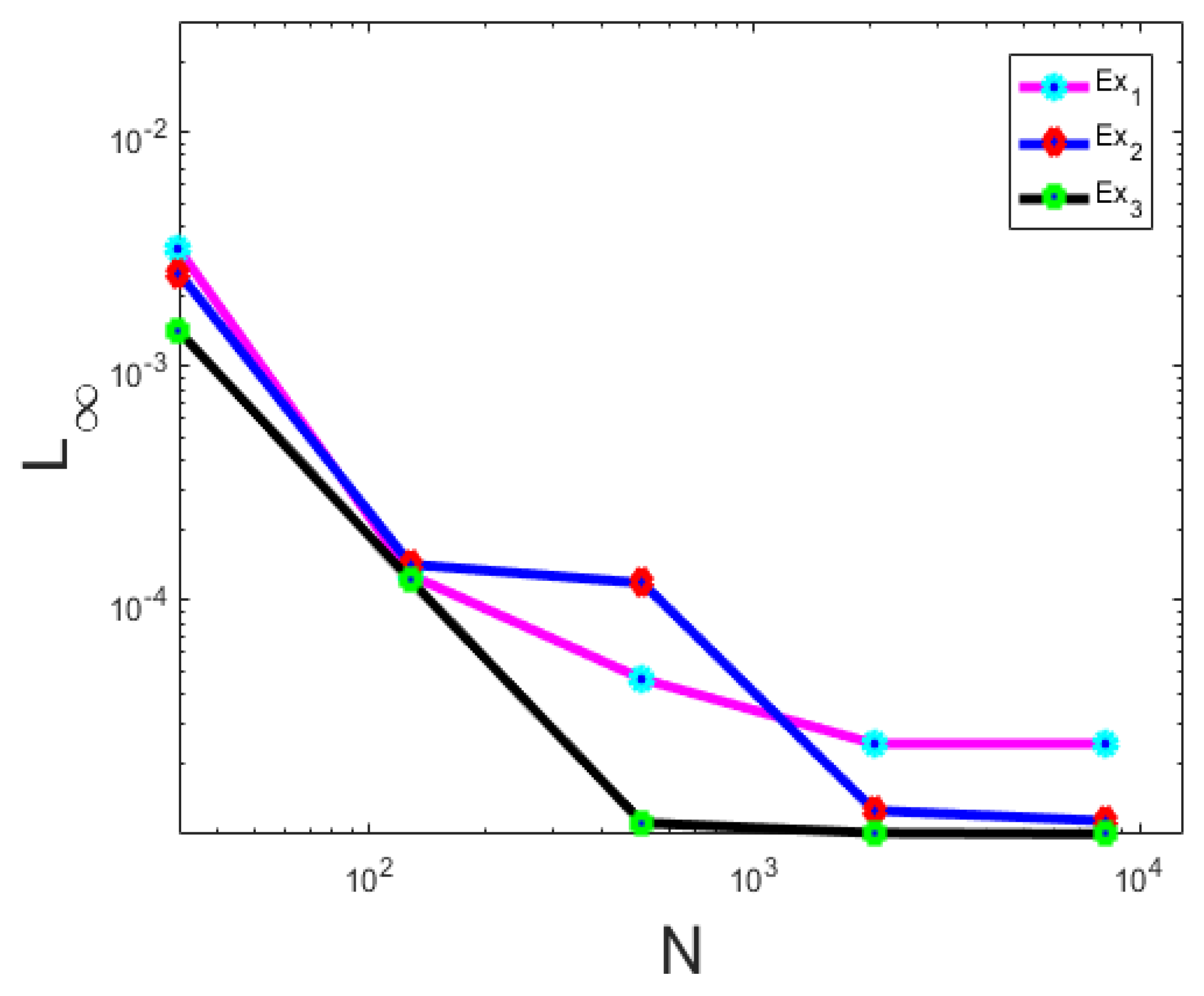
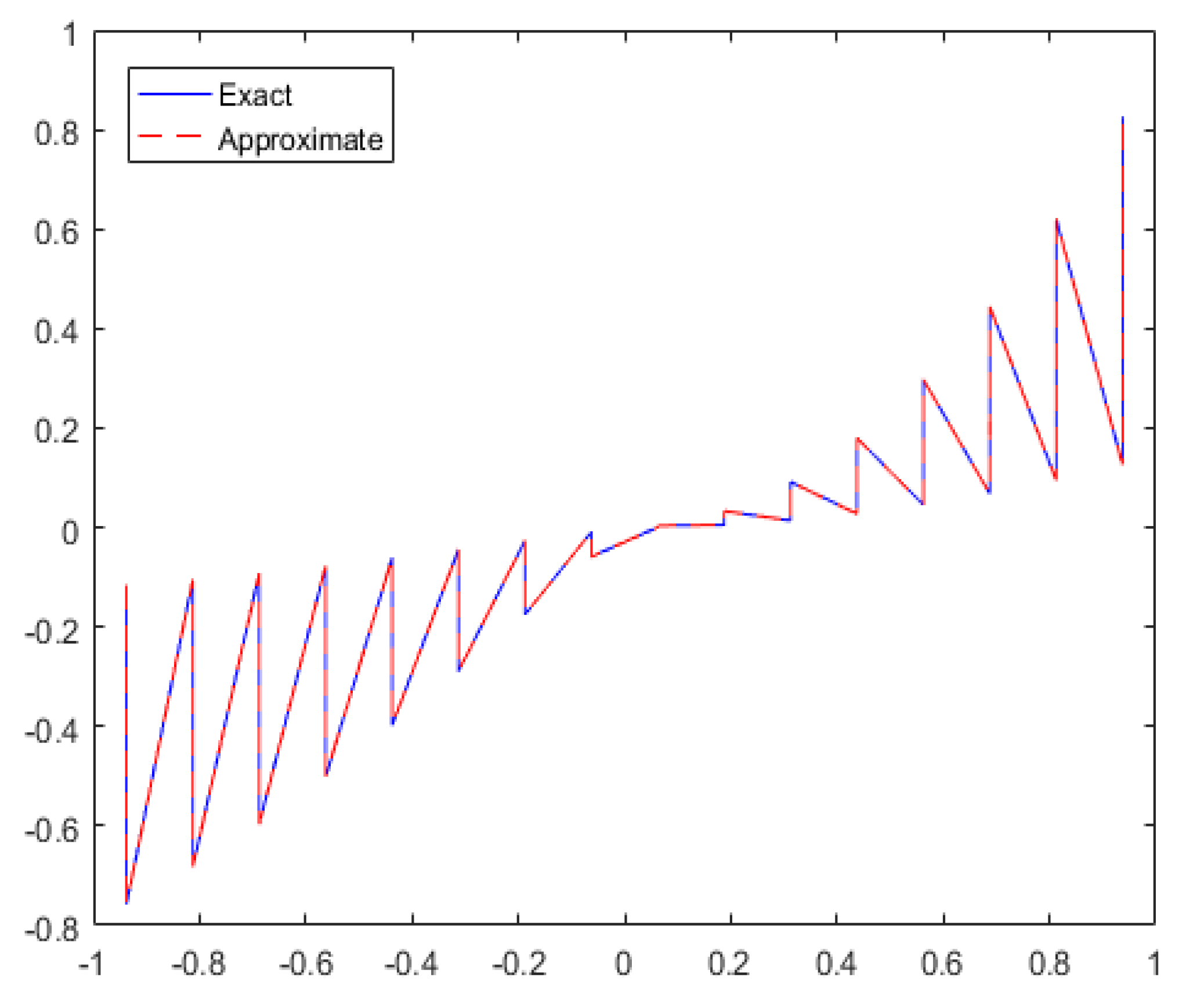
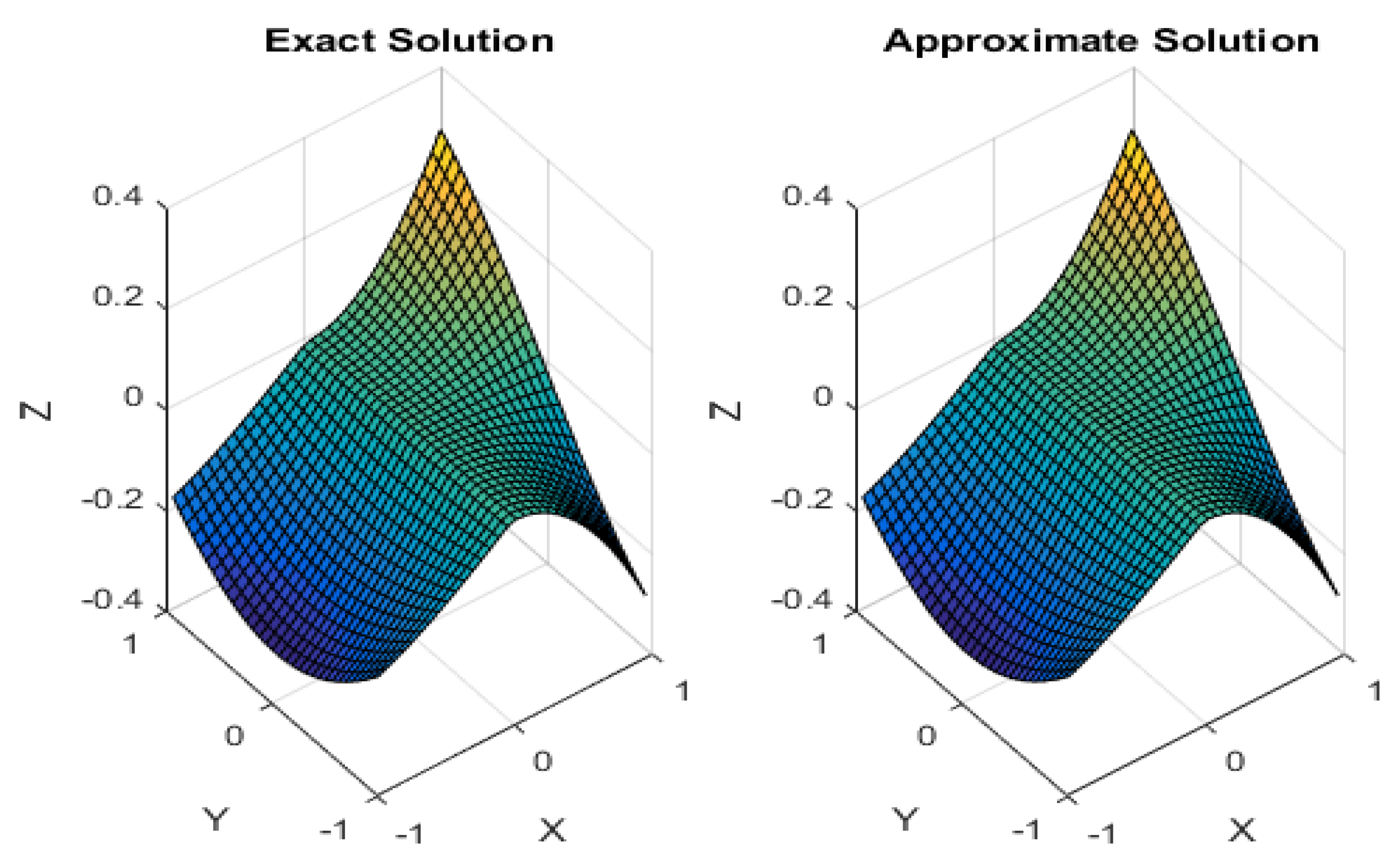
7. Numerical Validation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okubo, A. Application of the Telegraph Equation to Oceanic Diffusion; Chesapeake Bay Institute, The Johns Hopkins University: Baltimore, MD, USA, 1971. [Google Scholar]
- Asif, M.; Bilal, F.; Khan, I. Extension of Haar wavelet technique for numerical solution of three dimensional linear and nonlinear telegraph equations. Partial. Differ. Equ. Appl. Math. Model. 2023, 9, 100618. [Google Scholar] [CrossRef]
- Dhunde, R.R.; Waghmare, G.L. Double Laplace transform combined with iterative method for solving non-linear telegraph equation. J. Indian Math. Soc. 2016, 83, 221–230. [Google Scholar]
- Weston, V.H. Wave splitting of telegraph equation in and its application to inverse scattering. Inverse Probl. 1993, 9, 783–797. [Google Scholar] [CrossRef]
- Gao, F.; Chi, C. Unconditionally stable difference schemes for a one-space-dimensional linear hyperbolic equation. Appl. Math. Comput. 2007, 187, 1272–1276. [Google Scholar] [CrossRef]
- Ureña, F.; Gavete, L.; Benito, J.J.; García, A.; Vargas, A.M. Solving the telegraph equation in 2-D and 3-D using generalized finite difference method (GFDM). Eng. Anal. Bound. Elem. 2020, 112, 13–24. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X. Explicit High-Order Compact Difference Method for Solving Nonlinear Hyperbolic Equations. J. Comput. Phys. 2025, 400, 105678. [Google Scholar]
- Singh, I.; Kumari, U. Solving 2D and 3D Telegraph Equations with Elzaki Transform and Homotopy Perturbation Method. J. Mech. Contin. Math. Sci. 2024, 18–29. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Izadi, M.; Adel, W. Robust and Accurate Numerical Framework for Multi-Dimensional Fractional-Order Telegraph Equations Using Jacobi/Jacobi-Romanovski Spectral Technique. Bound. Value Probl. 2024, 2024, 131. [Google Scholar] [CrossRef]
- Xie, S.-S.; Yi, S.-C.; Kwon, T.I. Fourth-order compact difference and alternating direction implicit schemes for telegraph equations. Comput. Phys. Commun. 2012, 183, 552–569. [Google Scholar] [CrossRef]
- Karaa, S. Unconditionally stable ADI scheme of higher-order for linear hyperbolic equations. Int. J. Comput. Math. 2010, 87, 3030–3038. [Google Scholar] [CrossRef]
- Mohanty, R.K. An operator splitting technique for an unconditionally stable difference method for a linear three space dimensional hyperbolic equation with variable coefficients. Appl. Math. Comput. 2005, 162, 549–557. [Google Scholar] [CrossRef]
- Jiwari, R.; Pandit, S. A differential quadrature algorithm to solve the two dimensional linear hyperbolic telegraph equation with Dirichlet and Neumann boundary conditions. Appl. Maths. Comput. 2012, 218, 7279–7294. [Google Scholar] [CrossRef]
- Dehghan, M.; Salehi, R. A method based on meshless approach for the numerical solution of the two-space dimensional hyperbolic telegraph equation. Math. Methods Appl. Sci. 2012, 35, 1220–1233. [Google Scholar]
- Zhou, Y.C.; Zhao, S.; Feig, M.; Wei, G. High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. J. Comput. Phys. 2006, 213, 1–30. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Zhao, S. A matched interface and boundary method for solving multi-flow Navier Stokes equations with applications to geodynamics. J. Comput. Phys. 2012, 231, 223–242. [Google Scholar] [CrossRef]
- Xia, K.; Zhan, M.; Wei, G.W. MIB Galerkin method for elliptic interface problems. J. Comput. Appl. Math. 2014, 272, 195–220. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.; LeVeque, R.J. An immersed interface method for incompressible Navier-Stokes equations. SIAM J. Sci. Comput. 2003, 25, 832–856. [Google Scholar] [CrossRef]
- Liu, W.K.; Liu, Y.; Farrell, D.; Zhang, L. Immersed finite element method and its applications to biological systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 1722–1749. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.D.; Sideris, C.T. Convergence of the ghost fluid method for elliptic equations with interfaces. Maths. Comput. 2003, 72, 1731–1746. [Google Scholar] [CrossRef]
- LeVeque, R.J.; Li, Z. The Immersed Interface Method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 1994, 31, 1019–1044. [Google Scholar] [CrossRef]
- Imran, A.; Siraj, I.; Nadeem, H. Meshless and multi-resolution collocation techniques for steady state interface models. Int. J. Comput. Methods 2018, 15, 1750073. [Google Scholar]
- Imran, A.; Siraj, I. Nadeem H. Meshless and multi-resolution collocation techniques for parabolic interface models. Appl. Math. Comput. 2018, 335, 313–332. [Google Scholar]
- Matthew, A. On finite element method for linear hyperbolic interface problems. J. Niger. Math. Soc. 2018, 37, 41–55. [Google Scholar]
- Rana, G.; Asif, M.; Haider, N.; Bilal, R.; Ahsan, M.; Al-Mdallal, Q.; Jarad, F. A modified algorithm based on Haar wavelets for the numerical simulation of interface models. J. Funct. Spaces 2022, 2022, 1541486. [Google Scholar] [CrossRef]
- Asif, M.; Farooq, M.U.; Riaz, M.B.; Bilal, F.; Haider, N. Numerical assessment of hyperbolic type double interface problems via Haar wavelets. Partial. Differ. Equ. Appl. Math. 2024, 10, 100665. [Google Scholar] [CrossRef]
- Chen, Z.; Zou, Z. Finite element methods and their convergence for elliptic and parabolic interface problems. Numeri. Math. 1998, 79, 175–202. [Google Scholar] [CrossRef]
- Faheem, M.; Asif, M.; Haider, N.; Amin, R.; Mdallal, Q.A. Hybrid Haar wavelet and meshfree methods for hyperbolic double interface problems: Numerical implementations and comparative performance Analysis. Partial. Differ. Equ. Appl. Math. 2024, 11, 100773. [Google Scholar] [CrossRef]
- Masood, A.; Abdul, B.; Siraj, I. Local radial basis function collocation method for stokes equations with interface conditions. Eng. Anal. Bound. Elem. 2020, 119, 246–256. [Google Scholar]
- Masood, A.; Elisabeth, L. Local meshless methods for second order elliptic interface problems with sharp corners. J. Comput. Phys. 2020, 416, 109599. [Google Scholar] [CrossRef]
- Haider, N.; Aziz, I. Numerical solution of 2D and 3D elliptic-type interface models with regular interfaces. Eng. Comput. 2019, 35, 1081–1102. [Google Scholar] [CrossRef]
- Asif, M.; Faisal, B.; Mehnaz, S.; Rubi, B.; Haider, N. An efficient algorithm for the numerical solution of telegraph interface model with discontinuous coefficients via Haar wavelets. Alex Eng. J. 2023, 72, 275–285. [Google Scholar] [CrossRef]
- Asif, M.; Bilal, F.; Haider, N.; Jarad, F. Robust numerical techniques for modeling telegraph equations in multi-scale and heterogeneous environments. J. Appl. Math. Comput. 2025. [Google Scholar] [CrossRef]
- Aziz, I.; Asif, M. Haar wavelet collocation method for three-dimensional elliptic partial differential equations. Comput. Math. Appl. 2017, 73, 2023–2034. [Google Scholar] [CrossRef]
- Maleknejad, K.; Lotfi, T.; Mahdiani, K. Numerical solution of first kind Fredholm integral equations with wavelets-Galerkin method (WGM) and wavelets precondition. Appl. Math. Comput. 2007, 186, 794–800. [Google Scholar] [CrossRef]
- Dahmen, W.; Kurdila, A.; Oswald, P. Multiscale Wavelet Methods for Partial Differential Equations; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Wu, J. A wavelet operational method for solving fractional partial differential equations numerically. Appl. Math. Comput. 2009, 214, 31–40. [Google Scholar] [CrossRef]
- Imran, A.; Siraj, I.; Wajid, K. Quadrature rules for numerical integration based on Haar wavelets and hybrid functions. Comput. Math. Appl. 2011, 61, 2770–2781. [Google Scholar] [CrossRef]
- Asif, M.; Haider, N.; Qasem, A.; Imran, K. A Haar wavelet collocation approach for solving one and two-dimensional second-order linear and nonlinear hyperbolic telegraph equations. Numer. Methods Partial. Differ. Equ. 2020, 36, 1962–1981. [Google Scholar] [CrossRef]
- Siraj, I.; Aziz, I.; Fazal, H. A comparative study of numerical integration based on Haar wavelets and hybrid functions. Comput. Math. Appl. 2010, 59, 2026–2036. [Google Scholar] [CrossRef]
- Siraj, I.; Aziz, I.; Fayyaz, M. A new approach for numerical solution of integro-differential equations via Haar wavelets. Int. J. Comput. Math. 2013, 90, 1971–1989. [Google Scholar] [CrossRef]
- Jiwari, R.; Pandit, S.; Mittal, R.C. A differential quadrature algorithm for the numerical solution of the second-order one dimensional hyperbolic telegraph equation. Int. J. Nonlinear Sci. 2012, 13, 259–266. [Google Scholar]
- Jiwari, R.; Kumar, V.; Karan, R.; Alshomrani, A.S. Haar wavelet quasilinearization approach for MHD Falkner Skan flow over permeable wall via Lie group method. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 1332–1350. [Google Scholar] [CrossRef]
- Pandit, S.; Jiwari, R.; Bedi, K.; Koksal, M.E. Haar wavelets operational matrix based algorithm for computational modelling of hyperbolic type wave equations. Eng. Comput. 2017, 34, 793–814. [Google Scholar] [CrossRef]
- Lepik, U.; Hein, H. Haar Wavelets: With Applications; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Priyadarshi, G.; Kumar, R. Reconstruction of the parameter in parabolic partial differential equations using Haar wavelet method. Eng. Compu. 2020, 38, 2415–2433. [Google Scholar] [CrossRef]
- Hazarika, B.; Methi, G.; Aggarwal, R. Application of generalized Haar wavelet technique on simultaneous delay differential equations. J. Comput. Appl. Math. 2024, 449, 115977. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S. Introducing higher-order Haar wavelet method for solving three-dimensional partial differential equations. Int. J. Wavelets Multiresolution Inf. Process. 2024, 22, 2350040. [Google Scholar] [CrossRef]
- Lepik, U. Numerical solution of evolution equations by the Haar wavelet method. Appl. Math. Comput. 2007, 185, 695–704. [Google Scholar] [CrossRef]
- Chen, C. Haar wavelet method for solving lumped and distributed-parameter systems. IEE Proc.-Control Theory Appl. 1997, 144, 87–94. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; American Elsevier Publishing Company Inc.: New York, NY, USA, 1965. [Google Scholar]
- Ahsan, M.; Thanh, T.; Hussain, I. A multiresolution collocation method and its convergence for Burgers’ type equations. Math. Methods Appl. Sci. 2023, 46, 11702–11725. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]

| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | 0.3472 | |||||
| 2 | 5.1913 | |||||
| 3 | 30.1343 |
| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | 0.4996 | |||||
| 2 | 9.4118 | |||||
| 3 |
| Computational Order of Convergence | CPU Time (Seconds) | ||
|---|---|---|---|
| – | 0.0115 | ||
| 0.7932 | 0.1643 | ||
| 0.7001 | 0.2987 | ||
| 0.7711 | 0.3357 | ||
| 0.8547 | 0.6822 | ||
| 0.9749 | 0.8846 |
| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | 5.8319 | |||||
| 2 | 11.9520 | |||||
| 3 | 91.9531 |
| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | 7.9546 | |||||
| 2 | 53.9032 | |||||
| 3 |
| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | ||||||
| 2 | 58.3195 | |||||
| 3 |
| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | 3.5643 | |||||
| 2 | 49.0931 | |||||
| 3 |
| J | N | (M) | CPU Time Ratio (Seconds) | (M) | ||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 1 | 3.5710 | |||||
| 2 | 29.0913 | |||||
| 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ul Haq, K.S.; Asif, M.; Faheem, M.; Popa, I.-L. Capturing Discontinuities with Precision: A Numerical Exploration of 3D Telegraph Interface Models via Multi-Resolution Technique. Mathematics 2025, 13, 2391. https://doi.org/10.3390/math13152391
Ul Haq KS, Asif M, Faheem M, Popa I-L. Capturing Discontinuities with Precision: A Numerical Exploration of 3D Telegraph Interface Models via Multi-Resolution Technique. Mathematics. 2025; 13(15):2391. https://doi.org/10.3390/math13152391
Chicago/Turabian StyleUl Haq, Khawaja Shams, Muhammad Asif, Muhammad Faheem, and Ioan-Lucian Popa. 2025. "Capturing Discontinuities with Precision: A Numerical Exploration of 3D Telegraph Interface Models via Multi-Resolution Technique" Mathematics 13, no. 15: 2391. https://doi.org/10.3390/math13152391
APA StyleUl Haq, K. S., Asif, M., Faheem, M., & Popa, I.-L. (2025). Capturing Discontinuities with Precision: A Numerical Exploration of 3D Telegraph Interface Models via Multi-Resolution Technique. Mathematics, 13(15), 2391. https://doi.org/10.3390/math13152391








