Abstract
This work presents a solving method for problems of Ambrosetti-Prodi type involving p-Laplacian and p-pseudo-Laplacian operators by using adequate variational methods. A variant of the mountain pass theorem, together with a kind of Palais-Smale condition, is involved in order to obtain and characterize solutions for some mathematical physics issues. Applications of these results for solving some physical chemical problems evolved from the need to model real phenomena are displayed. Solutions for Dirichlet problems containing these two operators applied for modeling critical micellar concentration, as well as the volume fraction of liquid mixtures, have been drawn.
Keywords:
Ambrosetti-Prodi type problem; modeling real phenomena; mathematical physics problems; p-Laplacian; p-pseudo-Laplacian; variational methods; Dirichlet problem; Sobolev spaces; critical micellar concentration; volume fraction MSC:
35A01; 35A02; 35A15; 35J35; 35J40; 47J30
1. Introduction
Problems of the Ambrosetti-Prodi type represent an important class of models able to obtain and characterize solutions for many mathematical physics equations. This is a subject that is both highly debated and current, including a multitude of approaches, having many facets, a huge number of interpretations, and a lot of applications in real phenomena modeling.
The original Ambrosetti-Prodi problem [1] refers to the semilinear elliptic Dirichlet problem:
where Ω is a smooth bounded domain (open and connected) from RN, g in C0,α(), f: R → R a function of C2 class having the following properties:
(i) f (0) = 0,
(ii) f ″(t) > 0 ∀t and
In paper [1], it has been proven that there is a connected C1-manifold M in C0,α () that separates C0,α () into exactly two connected sets, O1 and O2, such that:
- If g ∈ O1, then (P) has no solution;
- If g ∈ M, then (P) has a unique solution;
- If g ∈ O2, then (P) has exactly two solutions.
Moreover, in [1], the solutions have been obtained in () by using the regularity imposed on f, g, and Ω.
Such an interesting structure of results has been widely exploited for a large palette of problems involving a rich and varied mathematical background and many important issues as proof instruments. To sustain this idea, we can firstly remind the demonstration proposed by Jabri in [2], who uses a variant of the mountain pass theorem (in the following MPT), together with a condition of the Palais-Smale type attributed to De Figueiredo and Solimini [3] given exactly for the above problem. In this manner, an extended research field is opened, as the following few examples can prove.
The classical main assumption from the central theorem of [1] evolved into another one where the positivity is not necessary, as is proven in [4]. In [5,6], the principal assumption refers to the derivative of the nonlinearity, which crosses the first eigenvalue when u tends to infinity, involving terms such as asymmetric crossing nonlinearity or jumping nonlinearities. When the free term g from (P) is a sum of two orthogonal terms, a different formulation of the result is obtained, as shown in [7]. The technique of upper and lower solutions has been capitalized in [8] in order to obtain an existence result generalizing the assumptions on the nonlinear term. The degree theory and the fixed-point index theory have been used by many authors to obtain multiplicity results of Ambrosetti-Prodi type, as [3,9,10,11] prove.
After these basic results, several works appeared that explore the set of solutions for problems with nonlinearities where the derivatives cross eigenvalues greater than the first one, like [12,13] prove, and which involve other boundary conditions, as issues concerning periodic boundary conditions or Neumann boundary conditions in [14,15,16,17,18,19] demonstrate.
In recent papers, this type of result is generalized and, involving an expansion of Laplace-Beltrami operator, construction of approximate solutions is performed by Khemiri et al. [20], or, considering the nonlinear Robin (p, q)-Laplace operator (i.e., the sum of a p-Laplace and a q-Laplace operator), which drives the parametric problems, optimal existence, multiplicity, and non-existence results have been developed by Papageorgiou et al. [21].
Optimal control, as a strategy to govern bifurcating solutions of nonlinear parametrized partial differential equations towards a wanted branch, allows for changing the solution profile and the stability of state solution branches. In this way, Pichi et al. [22] reconstructed each branch for optimal solution, characterizing the stability properties of the obtained controlled solutions, and they applied such results to several optimal control problems driven by bifurcating Navier-Stokes equations in a sudden-expansion channel. Bifurcation results are also the central point in the study of some nonlinear periodic differential equations when an Ambrosetti-Prodi frame is considered, like at Minhós et al. [23], where the arguments are based on Leray-Schauder’s topological degree, as at Mawhin [19] and, in [24,25], similar problems are treated using topological arguments. One of the most important reasons to choose such models and solving methods to draw many real phenomena is the possibility to find an appropriate numerical method to completely finish and visualize the solution, as is shown, for instance, in [20].
The p-Laplacian operator was involved in Ambrosetti-Prodi type problems in several works, as we can see in [26], where nonlinear perturbations of this type of operator depending on a real parameter, combined with homogeneous Dirichlet boundary conditions, and existence results for at least one and at least two solutions for certain intervals of parameter values are determined. Topological arguments together with the sub-supersolutions method and comparison principles for p-Laplacian have been used in [27] to obtain existence results for the Dirichlet problem with zero boundary conditions and jumping nonlinearities involving also the Leray-Schauder degree instrument.
But the subject of Ambrosetti-Prodi type problems remains actual as the work [28] involving the same instruments of comparison principles, degree theory, and topological methods, as also [29,30] prove.
In this paper, two problems of Ambrosetti-Prodi type for p-Laplacian and p-pseudo-Laplacian were approached, and the characterization of solutions has been obtained via a MPT variant and by using a certain type of Palais-Smale condition. These results have been involved in obtaining solutions for some mathematical physics problems evolved from the modeling of a new type of depollution method. The novelty of this work consists of the proof of the main theoretical results and, most importantly, the characterization of the solution of the real-world problem by involving this type of result.
2. Materials and Methods
Let us consider the semilinear elliptic Dirichlet problems:
where Ω is a smooth, bounded domain from RN, the conditions for the functions f and g will be established in the following. We search for weak solutions from (Ω) for the above two problems in the sense of . Concerning the two operators involved in the problems (1) and (2), they are the p-Laplacian and the p-pseudo-Laplacian, respectively, i.e.,
defined by
and
acting following the relation:
For all the details, properties, and other explanations related to these two important operators, one can consult the paper [31].
Weak solution. Let Ω be an open, bounded, nonempty set in RN, N > 1, f : Ω × R → R; the relation u = 0 on is considered in the sense of the trace (for the definition, one can see in [31], p. 17, Definition 2.8). from X = (Ω) is, by definition, a weak solution for (1) and (2) if = 0 on ∂Ω in the sense of the trace and
and
respectively.
For these two problems, we consider the Banach spaces ((Ω), ||·||1,p) and ((Ω), І·І1,p), where the norms introduced are ||u||1,p: = and ІuІ1,p: = , respectively, and = . For other details regarding these two important spaces, [31] can be consulted. Let be the first eigenvalue in of and , respectively, with homogeneous boundary condition. In the first case,
while in the second case, it is
(Rayleigh-Ritz quotient). Take into account the normalized eigenfunction (we use the same notation for both cases) corresponding to this eigenvalue. Assume (x) > 0 almost everywhere (a.e.) and its norm is considered equal to 1 (if necessary, by dividing by its norm) for both situations. If = {t: t ∈ R} ⊕ V (direct sum – algebraic meaning; such a vector subspace V exists as we can see, for instance, in [32]), one can consider the parametrized families of Dirichlet problems:
where f is locally Lipschitz and continuous on × R. Suppose that
Consider f to be a Carathéodory function. f : Ω × R → R is a Carathéodory function if: 10 f ( · , s) is Lebesgue measurable (L.m.) for any s in R; 20 f (x, · ) is continuous for any x in Ω\A, μ(A) = 0 (μ the Lebesgue measure). In this case, for any u from M (Ω), x → f (x, u(x)) is L.m. We impose the functional f to satisfy the growth condition:
where c ≥ 0, α ∈(Ω), with = 1 and 1 ≤ p ≤ if N ≥ 3 and 1 ≤ p ≤ +∞ if N = 2.
|f (x, s)| ≤ c|s|p−1 + α(x), ∀x ∈ Ω\A with μ(A) = 0 ∀s ∈ R,
We also consider that there exists a constant μ > p, such that,
where .
0 < μF(x, s) ≤ s f (x, s), ∀x ∈ Ω, ∀s ∈ R,
Definition 1.
Let X be a real normed space. A nonempty set
β of bounded parts of X, with the properties: = X; A
∈
β
⇒
−A
∈
β and λ A
∈
β (λ > 0); for every A, B in
β, there exists C in
β such that A
⊂ C and B
⊂ C, which is named bornology on X.
Let β be a bornology on X and f : X → locally finite in the point a (there is a neighbourhood of a on which f is finite). By definition, f is β-differentiable in a, if there exists φ in the dual X*, such that for every S in β, we have
(uniform limit on S for t → 0). φ is the β-derivative of f in a, and is denoted ∇β f (a). The notion “ f is β-differentiable on a subset of X” has the usual meaning.
Definition 2.
φ verifies the Palais-Smale condition on the level c, (PS)c, with respect to the bornology
β when, for any (un)n≥1 sequence of points in X, for which
this sequence has a convergent subsequence. c is a critical value for φ, that is, c = φ() and φ() = 0.
The first major instrument for the following development is a generalization from [33] of the MPT variant of Ambrosetti and Rabinowitz [34] given for the goal function of Fréchet C1-class, having the weaker condition v → ( ∙ )(v) upper semicontinuous for any v, the derivative being of Gâteaux type.
Mountain Pass Theorem.
Let X be a Banach space, φ: X → R continuous and Gâteaux differentiable with ( ∙ )(v) upper semicontinuous
∀v
∈ X. Suppose that for , from X and Ω, an open neighborhood of u0 such that ∈ X \ , we have
Let be
and
If φ verifies the (PS condition, then c is a critical value of φ and
c > max (φ(u0), φ(u1)). [33]
Remark 1.
The intuitive name “Mountain Pass” given to this theorem comes from a topographical situation that takes its source in the case X = R2 with the representation in the Euclidean space E3 of the elementary geometry. The conditions for , and φ show that the points : = (, φ()) and : = (, φ()) are lower than the mountain wall:
and are situated on both sides of it.The path
starts from and arrives at passing the mountain wall, since, as we have seen above,
But, the highest point of the path has the quota:
an attained supremum. So, taking into account the significance received by c, the “Mountain pass” intuitive denomination is seen to be well chosen.
{(x, y, φ(x, y)): (x, y) ∈ Fr Ω}
t → φ(g(t)), t ∈ [0, 1]
g([0, 1]) ∩ Fr Ω ≠ ∅.
Remark 2.
This theorem was obtained by Ambrosetti and Rabinowitz [34] under the assumption that φ is of Fréchet C1-class. The passage to “φ continuous with φ′w ( ∙ )(v) u.s.c., for any v ∈ X” was proposed by the author [33]. Obviously, the Gâteaux derivative in the above statement can be replaced by any β-derivative, β bornology on X ([35], Ch. I, 3.10).
To debate the problems (5) and (6), introduce the following two energy functionals, φ associated with (5) is φ: (Ω) → R, defined by
and for (6) is φ: (Ω) → R, defined by
representing the duality relation of and related to the two corresponding norms.
Definition 3.
Weak subsolutions and weak supersolutions of (5) and (6). Let Ω be an open bounded set of C 1 class in RN, N ≥ 3, f : Ω × R → R, respectively, a Carathéodory function and let ∈ (Ω). is a weak subsolution and a weak supersolution, respectively, of (5) or (6), if ≤ 0 on
∂Ω,
respectively, ≥ 0 on ∂Ω, and
or
3. Results
The results, which represent the aim of this work, are obtained by applying some auxiliary propositions based on MPT. To involve this theorem, two main properties should be proven: the mountain pass geometry and a condition of Palais-Smale type to be fulfilled.
Proposition 1.
Under the conditions (8) and (9), the functional φ satisfies the (PS)c condition for both cases.
Proof.
Firstly, fix t any in R. Take a sequence () of elements from (Ω) endowed with or І · І1,p, having the properties asked by Definition 2. (φ()) being convergent, it results bounded, hence, there exists C > 0 e.g. φ() ≤ C ∀n from a rank on. = 0 (Gâteaux weak derivative) means () bounded, hence there exists M > 0 e.g. ≤ M ∀n from a rank on. To complete the argumentation, one can apply the procedure followed in [36], p. 6, the unique difference consisting in writing of φ = Ψ − ψ1 − ψ2 instead of φ = Ψ − ψ, where Ψ(u) = |||| case of the first problem and Ψ(u) = ІuІ in case of the second problem, (u) = and (u) = , is a compact operator and (u) = . t being considered fixed, this last additional term does not change the situation presented there. The proving idea consists of showing that the considered sequence () from (Ω) is bounded and it has a Cauchy subsequence. Since both spaces ((Ω), ) and also ((Ω), І
· І1,p) are complete (see, for instance, in [31] for complete justification), any fundamental sequence is convergent. In the proof from [36], the weak (Gâteaux) derivative has been considered, which implies that the result is true by involving any β-derivative. □
Theorem 1.
Under the conditions (7)–(9), there exists a real number such that, for any t ≤ , the problems (5) and (6) have at least two solutions in (Ω), in the sense of (Ω).
Proof.
The proof follows the usual steps:
1. For any t ∈ R, the problems (5) and (6) admit a subsolution such that any supersolution of (5) and (6), respectively, satisfy:
and
2. There exists ∈ R such that, for any t ≤ , (5) and (6) have a classical supersolution .
3. Introduce K = {u ∈ (Ω): ≤ u ≤ }. K is a closed, convex subset of (Ω).
4. The functional φ restricted to K has a minimum in K that is a critical point of φ. The local minimum of φ in K is a local minimum of φ in (Ω).
5. Using MPT, a second solution for both problems exists.
Step 1. Regarding the existence of the subsolution , we can take into account the existence result from [26], correspondingly adapting Lemma 3.2 to the present conditions. One can remark that the above inequality between the normal derivatives of the sub- and supersolution is necessary to allow the application of a special kind of comparison principle, and in order to control the variation domain of the solution.
Step 2. To fulfil the requirement, we can adapt Proposition 3.1 from [27], together with its proof, to the conditions of the problems (5) and (6).
Step 3. Firstly, K is a nonempty set. To sustain this assertion, we can call Proposition 5.3 and Proposition 5.4 from [31] for problems (5) and (6), respectively. The proofs of these two results also assure the properties of this set K to be closed and convex.
Step 4. Proposition 5.2 from [31], combined with Theorem 5.1, and also Propositions 5.3 and 5.4 from the same cited work, establish the existence of the minimum in K, that is a critical point of φ, which is a local minimum of φ in (Ω).
Step 5. To apply MPT, the version displayed in Section 2 will be used, and, since the (PS)c condition for both problems has been proven in Proposition 3.1, only the MPT geometry should be shown to finish the demonstration. Regarding this last demand, we cite the proof of Theorem 1 from [36], which can be easily adapted to the conditions of the problems (5) and (6), respectively. □
Theorem 2.
Under the conditions (7), and with the linear growth condition:
where a, b > 0, then there exists t0 ∈ R such that, for any t ≤ t0, the problems (5) and (6) have at least two solutions in (Ω), in the sense of .
Remark 3.
The problems with linear growth conditions have solutions obtained and characterized in a manner similar to that of Theorem 1.
Remark 4.
Here, problems of Dirichlet type have been treated. It could be interesting to adapt the results to von Neumann or mixed problems, taking into consideration these types of problems in [9,22,24,37,38].
4. Discussion
4.1. The Real Problem
Recent evolutions in the field of nanomaterials and nanotechnologies created unprecedented perspectives for novel applications of emerging technologies in a wide range of domains of everyday life, including advanced materials, biotechnologies, renewable energies, nanomedicine, environmental protection, etc. The key element in the multi-functionality of nanomaterials resides in unexpectedly high energies existing in these micro- and nano-heterogeneous disperse systems. This is a principal reason why the transfer of know-how from laboratory to pilot and large scale is a challenging matter, since the processes usually encountered in classical industrial reactors are not valid in the case of nanofabrication. Indeed, the role of the reactor in nano-liquid–liquid dispersed systems is here played by micro- or nano-droplets, and the determinant parameters are related to surface phenomena as a result of special intermolecular forces at interface. In this context, innovative mathematical modeling methods have to be proposed and tested in order to properly simulate physical-chemical interactions and processes specific to nanofabrica-tion.
From previous research on different nanoparticles suspensions in thermotropic nematic media [39,40,41], a molecular reorientation has been noticed around the particle’s surface with a tendency of homeotropic alignment. Using electro-optical methods, the molecular orientation around the nanoparticles was experimentally studied. Thus, we determined the electrical Fredericks transition threshold for different nanoparticles concentrations at different temperatures to obtain more information about the anchoring angle between molecules and nanoparticles under the influence of an external electric field. A great advantage of this method is the optical anisotropy of the host, which allowed us to obtain information from the emergent intensity of a laser beam crossing through the sample. The proposed theoretical models were experimentally tested, and a good agreement between them was found. The mathematical modeling and computational simulations will be applied to the experimental data provided by the group belonging to the nano-fluid laboratory, which has sound expertise in the application of micro- and nanoemulsions to solve difficult problems related to the removal and reuse of organic and inorganic pollutants from waste or wastewater effluents. In this context, of major interest is selection of adequate conditions for microemulsion formation based on building phase diagrams in ternary systems: water/oil/surfactant. Diffusion of metal ions from the aqueous phase towards micelles from the organic phase is suggestively illustrated in Figure 1.
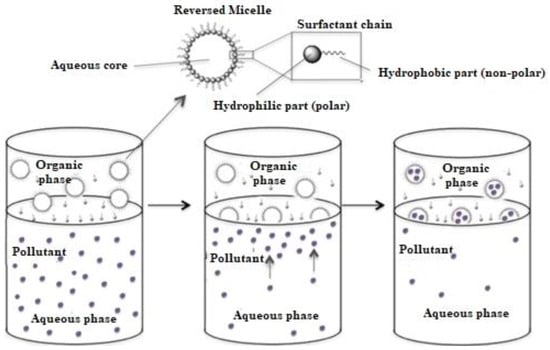
Figure 1.
Schematic representation of extraction process by micro-emulsification technique.
Under the action of surface tension forces, the particles of pollutants will migrate from the lower aqueous phase to the upper microemulsion phase and will be located inside the droplets of water surrounded by oil and protected by surfactant molecules.
One may stress that there is no mathematical model devoted to simulating physical–chemical phenomena encountered in these microemulsion processes, and not particularly those involved in the extraction and pre-concentration of heavy metals in order to be reused. This problem is of vital importance, since the transfer of experimental demonstrator data from laboratory to pilot and then to large scale, involving computer simulation of appropriate mathematical models, is not available at present. Indeed, this is a challenging problem to ensure the automatic control of the processes involving nanofabrication, and the conceptual mathematical model, laboratory protocol, and experimental demonstrator for microextraction of heavy metal pollutants are highly innovative. This unique character of molecular interactions nature in nano-heterogeneous systems induces an immense input of excess surface energy, which makes the possible unexpected resonance phenomena difficult to predict, such as active transport, forced diffusion, enhanced adsorption, photo-catalysis, etc. The physical-mathematical fundamentals in these nano-fluid systems might mimic biological phenomena at the cellular level, even though the dimensional order is lowered from micro to nano scale.
Interested in modeling the process described above and considering some models that use Poisson or Poisson-Boltzmann equation or other models for processes similar to ours found in [42,43,44,45,46], we developed the Ambrosetti-Prodi results presented above. Such a type of theoretical result can be powerful, taking into account the possibility of finding controlled solutions, to be continued in specific numerical methods to visualize the solution, as, for instance, is proven in [22]. Aiming the passage from laboratory to industrial scale, the mathematical model is of critical importance together with its computer simulation by usability of CFD (Computational Fluid Dynamics) program, for instance.
4.2. The Solution via Ambrosetti-Prodi Formulation
4.2.1. Concentration Modeling
When considering the colloidal solution depicted above in which we are interested in the Winsor II domain, the experimental behavior depends on various factors such as concentration, temperature, interfacial tension, electrostatic interactions/van der Waals, etc. The characterization of colloidal solutions involves some aspects described by equations of nonlinear diffusion (modeled with p-Laplacian), models with nonlinear chemical potentials, free energy with nonlinear functionals, structural bifurcations, and so on.
In the case when u represents the critical micellar concentration from the above-described dispersed systems, we obtain a problem of (5) form or, for a bit more complicated conditions, of type (6). In such cases, the p-Laplacian operator represents colloidal transport phenomena with aggregation/disaggregation. A result of Ambrosetti-Prodi type shows that, for certain values of the parameter t, two possible physical states of the colloidal system appear, two equilibrium configurations. These two states can correspond either to uniform concentrations and separate phases, or to different distributions of colloidal density (Winsor II), or to partial and complete aggregation. So, one obtains the physical meaning of this result: the colloidal system can reach two different equilibrium states for the same external conditions (for double solution), a unique, stable state for the unique solution case, and there is no equilibrium (phase collapse or instability may occur) associated with the “no solution” situation.
The existence of multiple solutions, particularly when bifurcations may occur, can complicate the interpretation and selection of physically meaningful solutions. For nonlinear models like those used for colloidal systems, such as phase separation, self-assembly, and Winsor phases, models involving the p-Laplacian (nonlinear reaction-diffusion equations) describing these systems, bifurcation points can yield uncertainty about which solutions are physically stable. When considering modeling micelle formation or phase distribution in Winsor II systems using a p-Laplacian model, an Ambrosetti-Prodi type result can specify when multiple equilibrium structures (droplets, layers, microemulsions) are mathematically admissible, provides the values of t for phase coexistence and/or metastable configuration appearance, and leads to numerical continuation and stability selection. In order to obtain the physical relevance, one can compute the energy associated with each solution; in this way, the physically realized solution minimizes the free energy function.
Relevant for applied research and engineering applications are the computational costs and nonlinear problems involving the p-Laplacian operator introduce substantial challenges due to their highly nonlinear character, degeneracy, or singularity, depending on the value of p. Cost mitigation strategies involve some numerical optimization methods, special discretization approaches, model reduction, and surrogate or hybrid modeling.
The implementation of advanced variational methods, such as those used in this paper, when treating nonlinear problems involving p-Laplacian or p-pseudo-Laplacian can be complicated from analytical and computational points of view. However, modeling possibilities obtained for the considered real phenomena well justify their usage.
This study will continue by determining concrete values for p and expressions for all the terms involved in relation to the described phenomena. This new work is justified by the possibilities opened by the proven results.
4.2.2. Volume Fraction Modeling
When u is the volume fraction (denoted also by ϕ) in colloidal solutions, in our case being Vwater/Voil, there exist models involving p-Laplacian in its description when the system is nonlinear and has anisotropic or nonhomogeneous diffusion; there exists aggregation or disaggregation depending on concentration or when the transport of colloidal particles is influenced by interactions depending on gradient.
The volume fraction appears in a general model with an equation of the form:
where u is the volume fraction of the colloidal phase (Winsor II), D is the diffusion coefficient dependent on concentration, and R is a reaction term. By applying the method of implicit time discretization, as shown in [47], one obtains the nonlinear equation of elliptic type. Then the work can be conducted by following the presented solving methods of one of the problems (5) and (6).
5. Conclusions
This paper develops a version of Ambrosetti-Prodi type result based on a certain variant of MPT and a special kind of (PS)c involving Dirichlet problems for p-Laplacian and p-pseudo-Laplacian operators.
The novelty of this work consists of obtaining two results, one of them related to a kind of Palais-Smale condition fulfilled by the functionals involved in the considered problems, which is used in the proof of the main theorem, this being the second proven result, its demonstration following the classical steps of a result of the Ambrosetti-Prodi type.
Possibilities to use this kind of result in modeling critical micellar concentration and volume fraction are presented. The special interest for these models is sustained by the need to have adequate mathematical models to draw solutions for an innovative depollution method (green and with zero waste) when one passes from laboratory scale to pilot scale. Our models refer to the extraction of pollutants in controlled colloids from Winsor II domain of phase diagrams in two liquid mixtures with surfactant.
The result obtained is considered to be important, taking into account the possibility of being involved, after the complete determination in relation to the laboratory data of the value of p of the main operator and the other functions of the equation, in modeling real phenomena and thus providing prospects for future research.
Funding
This research received no funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Ambrosetti, A.; Prodi, G. On the inversion of some differentiable mappings with singularities between Banach spaces. Ann. Mat. Pur. Appl. 1972, 93, 231–246. [Google Scholar] [CrossRef]
- Jabri, Y. The Mountain Pass Theorem. Variants, Generalizations and Some Applications; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- De Figueiredo, G.D.; Solimini, S. A variational approach to superlinear elliptic problems. Commun. Part. Diff. Eq. 1984, 9, 699–717. [Google Scholar] [CrossRef]
- Manes, A.; Micheletti, A.M. Un’estensione della teoria variazionale classica degli autovalori per operatori ellittici del secondo ordine. Boll. Un. Mat. Ital. 1973, 4, 285–301. [Google Scholar]
- Fučík, S. Remarks on a result by A. Ambrosetti and G. Prodi. Boll. Un. Mat. Ital. 1975, 4, 259–267. [Google Scholar]
- Fučík, S. Boundary value problems with jumping nonlinearities. Časopis Pěst. Mat. 1976, 101, 69–87. [Google Scholar] [CrossRef]
- Berger, M.S.; Podolak, E. On the solutions of a nonlinear Dirichlet problem. Indiana Univ. Math. J. 1974, 24, 837–846. [Google Scholar] [CrossRef]
- Kazdan, J.L.; Warner, F.W. Remarks on some quasilinear elliptic equations. Comm. Pure Appl. Math. 1975, 28, 567–597. [Google Scholar] [CrossRef]
- Amann, H.; Hess, P. A multiplicity result for a class of elliptic boundary value problems. Proc. R. Soc. Edinburgh Sect. A 1979, 84, 145–151. [Google Scholar] [CrossRef]
- Berestycki, H.; Lions, P.L. Sharp existence results for a class of semilinear elliptic problems. Bol. Soc. Brasil. Mat. 1981, 12, 9–19. [Google Scholar] [CrossRef][Green Version]
- Dancer, E.N. On the ranges of certain weakly nonlinear elliptic partial differential equations. J. Math. Pures Appl. 1978, 9, 351–366. [Google Scholar][Green Version]
- Lazer, A.C.; McKenna, P.J. On the number of solutions of a nonlinear Dirichlet problem. J. Math. Anal. Appl. 1981, 84, 282–294. [Google Scholar] [CrossRef]
- Solimini, S. Some remarks on the number of solutions of some nonlinear elliptic problems. Ann. Inst. Henri Poincaré Anal. Non Linéaire 1985, 2, 143–156. [Google Scholar] [CrossRef]
- Fabry, C.; Mawhin, J.; Nkashama, M.N. A multiplicity result for periodic solutions of forced nonlinear second order ordinary differential equations. Bull. Lond. Math. Soc. 1986, 18, 173–180. [Google Scholar] [CrossRef]
- Fonda, A.; Sfecci, A. On a singular periodic Ambrosetti-Prodi problem. Nonlinear Anal. 2017, 149, 146–155. [Google Scholar] [CrossRef]
- Mawhin, J. Ambrosetti-Prodi type results in nonlinear boundary value problems. Differential equations and mathematical physics (Birmingham, Ala., 1986). In Lecture Notes in Math; Springer: Berlin, Germany, 1987; Volume 1285, pp. 290–313. [Google Scholar]
- Ortega, R. Stability and index of periodic solutions of an equation of Duffing type. Boll. Un. Mat. Ital. B 1989, 7, 533–546. [Google Scholar]
- Ortega, R. Stability of a periodic problem of Ambrosetti-Prodi type. Differ. Integral Equ. 1990, 3, 275–284. [Google Scholar] [CrossRef]
- Mawhin, J. The periodic Ambrosetti-Prodi problem for nonlinear perturbations of the p-Laplacian. J. Eur. Math. Soc. (JEMS) 2006, 8, 375–388. [Google Scholar] [CrossRef]
- Khemiri, Z.; Mahmoudi, F.; Messaoudi, A. Concentration on submanifolds for an Ambrosetti-Prodi type problem. Calc. Var. 2017, 56, 19. [Google Scholar] [CrossRef]
- Papageorgiou, N.; Rădulescu, V.; Zhang, J. Ambrosetti-Prodi problems for the Robin (p, q)-Laplacian. Nonlinear Anal. Real World Appl. 2022, 67, 103640. [Google Scholar] [CrossRef]
- Pichi, F.; Strazzullo, M.; Ballarin, F.; Rozza, G. Driving bifurcating parametrized nonlinear PDEs by optimal control strategies: Application to Navier-Stokes equations with model order reduction. ESAIM M2AN 2022, 56, 1361–1400. [Google Scholar] [CrossRef]
- Minhós, F.; Oliveira, N. Bifurcation Results for Periodic Third-Order Ambrosetti-Prodi-Type Problems. Axioms 2022, 11, 387. [Google Scholar] [CrossRef]
- Repovš, D. Ambrosetti-Prodi problem with degenerate potential and Neumann boundary condition. Electron. J. Differ. Equ. 2018, 2018, 41. [Google Scholar]
- Sovrano, E. Ambrosetti-Prodi type result to a Neumann problem via a topological approach. Discrete Contin. Dyn. Syst. Ser. S 2018, 11, 345–355. [Google Scholar] [CrossRef]
- Koizumi, E.; Schmitt, K. Ambrosetti-Prodi-Type Problems for Quasilinear Elliptic Problems. Differ. Integral Equ. 2005, 18, 241–262. [Google Scholar] [CrossRef]
- Arcoya, D.; Ruiz, D. The Ambrosetti-Prodi Problem for the p-Laplace Operator. Commun. Partial Differ. Equ. 2006, 31, 849–865. [Google Scholar] [CrossRef]
- Alves, C.O.; de Lima, R.N.; Nóbrega, A.B. On an Ambrosetti-Prodi type problem in RN. J. Fixed Point Theory Appl. 2023, 25, 12. [Google Scholar] [CrossRef]
- de Lima, R.N.; Torres Ledesma, C.E.; Nóbrega, A.B. A fractional Ambrosetti-Prodi type problem in RN. J. Elliptic Parabol. Equ. 2023, 9, 355–387. [Google Scholar] [CrossRef]
- Minhós, F.; Oliveira, N. On periodic Ambrosetti-Prodi-type problems. AIMS Math. 2023, 8, 12986–12999. [Google Scholar] [CrossRef]
- Meghea, I. Solutions for Some Mathematical Physics Problems Issued from Modeling Real Phenomena: Part 1. Axioms 2023, 12, 532. [Google Scholar] [CrossRef]
- Meghea, C.; Meghea, I. Treatise on Differential Calculus and Integral Calculus for Mathematicians, Physicists, Chemists and Engineers in Ten Volumes; Philadelphia and Éditions des Archives Contemporaines; Old City Publishing: Paris, France, 2013; Volume 2. [Google Scholar]
- Meghea, I. Minimax theorem, Mountain Pass theorem and Saddle Point theorem in β-differentiability. Commun. Appl. Nonlin. Anal. 2003, 1, 55–66. [Google Scholar]
- Ambrosetti, A.; Rabinowitz, P.H. Dual variational methods in critical point theory and applications. J. Funct. Anal. 1973, 14, 349–381. [Google Scholar] [CrossRef]
- Meghea, I. Ekeland Variational Principles with Generalizations and Variants; Old City Publishing: Philadelphia, PA, USA; Éditions des Archives Contemporaines: Paris, France, 2009. [Google Scholar]
- Meghea, I. Application of a Variant of Mountain Pass Theorem in Modeling Real Phenomena. Mathematics 2022, 10, 3476. [Google Scholar] [CrossRef]
- Gasiński, L.; Papageorgiou, N.S. Positive Solutions for the Neumann p-Laplacian with Superdiffusive Reaction. Bull. Malays. Math. Sci. Soc. 2017, 40, 1711–1731. [Google Scholar] [CrossRef]
- Cabré, X.; Tan, J. Positive Solutions of Nonlinear Problems Involving the Square Root of the Laplacian. Adv. Math. 2010, 224, 2052–2093. [Google Scholar] [CrossRef]
- Cadar, D.; Olteanu, N.L.; Andrei, E.A.; Petcu, A.R.; Marin, A.C.; Meghea, A.; Mihaly, M. Synergism of thiocyanate ions and microinterfacial surface as driving forces for heavy multi-metals extraction. Arab. J. Chem. 2018, 11, 501–512. [Google Scholar] [CrossRef]
- Cadar, D.; Olteanu, N.L.; Rogozea, A.E.; Petcu, A.R.; Meghea, A.; Mihaly, M. Recovery of targeted hydrophilic compounds from simulated wastewaters using nonionic microemulsion systems. Proc. Saf. Environ. Prot. 2017, 109, 648–658. [Google Scholar] [CrossRef]
- Cadar, D.; Olteanu, N.L.; Andrei, E.A.; Meghea, A.; Petcu, A.R.; Mihaly, M. Fluid structures used for wastewaters treatment with complex load. Sep. Purif. Technol. 2018, 197, 1–7. [Google Scholar] [CrossRef]
- Miękisz, J.; Gomułkiewicz, J.; Miękisz, S. Mathematical models of ion transport through cell membrane channels. Math. Appl. 2014, 42, 39–62. [Google Scholar] [CrossRef]
- Oberman, G.J. Mathematical Modeling of the Drying of Sol Gel Microspheres. Doctoral Thesis, Queensland University of Technology, Brisbane, QLD, Australia, 2011. [Google Scholar]
- Cummings, J.T. Mathematical Modeling of Mixtures and Numerical Solution with Applications to Polymer Physics. Doctoral Dissertation, University of Tennessee, Knoxville, TN, USA, 2017. [Google Scholar]
- Flisyuk, O.; Martsulevich, N.; Meshalkin, V.; Garabadzhiu, A. Mathematical Modeling of Changes in the Dispersed Composition of Solid Phase Particles in Technological Apparatuses of Periodic and Continuous Action. Mathematics 2022, 10, 994. [Google Scholar] [CrossRef]
- Gubaidullin, D.; Gubaidullina, D.; Fedorov, Y. Mathematical Modeling of the Wave Dynamics of an Encapsulated Perfluorocarbon Droplet in a Viscoelastic Liquid. Mathematics 2023, 11, 1083. [Google Scholar] [CrossRef]
- Vázquez, J.L. Symmetrization and Mass Comparison for Degenerate Nonlinear Parabolic and related Elliptic Equations. Adv. Nonlinear Stud. 2005, 5, 87–131. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).