1. Introduction
In this article, a commutative ring with the identity shall be denoted by When an element , different from zero (0 ), exists such that , then the non-zero element is called a zero-divisor of R. is the collection of those zero-divisors in the ring R and .
The graph
has been defined, where
V denotes the set of vertices and
E denotes the set of edges of
G. When two distinct vertices of graph
G,
and
are adjacent to each other in graph
G, the notation
represents this. In a graph
G, the set of vertices adjacent to a vertex
c is called its neighborhood; this neighborhood is represented by the notation
.
refers to the complete graph with
m vertices and
refers to the complement of complete graph with
m vertices.
, the degree of vertex
c, represents the number of edges incident with
. If
, then
c is referred to as an isolated vertex. For every vertex
,
G is
k-regular if
. The distance
between two vertices
and
is the shortest path from
to
. Let
A be any square matrix and let
be its different eigenvalues with multiplicities
, respectively. The
of
A is then denoted by
(A), which is defined by
For a graph
G, the
matrix
is a
n-dimensional square matrix given by
The convex linear combinations of the adjacency matrix
of
G and the diagonal matrix of its vertices
were proposed by Nikiforov [
1]. This means that
for
where
is referred to as the generalized adjacency matrix or
matrix of
G. The vertex transmission in a graph is the sum of its distances to all other vertices in the graph
G. The transmission matrix
of
G is the diagonal matrix whose elements are the vertex transmissions and
is the distance matrix of graph
G defined as
Similarly, the generalized distance matrix
was presented by Cui, He, and Tian [
2] as the convex combination of
and
for
. If all the
eigenvalues of a graph
G are integers, then
G is said to be
integral.
Nikmehre et al. [
3] introduced the idea of a weakly zero-divisor graph of ring
R. The weakly zero-divisor graph of ring
R is represented by the symbol
. There are two distinct vertices,
and
, that are adjacent if and only if there exists
and
, satisfying the condition
. This undirected simple graph
has a vertex set as the set of non-zero zero-divisors of
R. Now, since the set of units of
are
, this implies that the set of non-zero zero-divisors of
are
. Hence, the order of
is
. The weakly zero-divisor graph’s spanning sub-graph is easily observed to be the zero-divisor graph of a ring.
In [
4], the authors derived new properties on the
matrix including inequalities that involve the largest vertex transmission and the spectral radii of the distance matrix, distance signless Laplacian matrix, and
matrix. They also give a result for the spectrum of
matrix when
G is the
H-join of regular graphs.
Motivated by the results of [
4], we have calculated the
spectrum of the weakly zero-divisor graph of
for various values of
n. More information about the spectra of graphs and additional information on various types of graphs based on a commutative ring can be found in [
5,
6,
7,
8,
9,
10,
11]. The definitions, lemma’s, and theorems that are utilized to support the main results are analyzed in
Section 2.
eigenvalues of
are looked into in
Section 4, for
, where
, and
are prime numbers with
, and
being positive integers. Also, we calculate the
spectrum of the weakly zero-divisor
, for
, where
’s and
’s are distinct primes, and show that
is
integral.
2. Preliminaries
Definition 1. Let be a graph of order m with vertex set , and let be disjoint graphs of order for The generalized join graph is formed by taking the graphs and, whenever vertices and are adjacent in G, joined each vertex of to every vertex of .
indicates the number of positive divisors of a positive integer . For to not divide , we write . The greatest common divisor of and is denoted by The number of positive integers smaller than or equal to that are relatively prime to is indicated by Euler’s phi function . If , where are positive integers and are distinct primes, then is in .
Lemma 1 ([
12])
. If is a prime decomposition of , then Let
be the proper divisors of
n. For
consider the following sets
Moreover, observe that for
,
. As a result, the vertex set of
has a partition formed by the sets
.
as a result. The following lemma provides information about the cardinality of each
.
Lemma 2 ([
13] Proposition 2.1)
. Let be a proper divisor of n. Then, for . Lemma 3 ([
14])
. Let n be represented as , where are distinct primes and and . Then, consider the set of proper divisors of n, denoted as . If , then the induced sub-graph of by is Corollary 1 ([
14])
. Let be the proper divisor of positive integer The following assertions are true:- (1)
For , the induced subgraph of , formed by the vertices in the set , takes one of two forms: either or .
- (2)
For and , a vertex within is connected to either all or none of the vertices in in the graph
The sub-graphs created within the structure of can be classified as either complete graphs or empty graphs, as shown by the previously noted Corollary 1. Let the distinct proper divisors of n be , then the vertex set of simple graph is and for all .
Lemma 4 ([
14])
. where are all the proper divisors of n. The following theorem provides the generalized join graph’s spectrum in terms of the spectrum of the adjacency matrix of regular graphs.
Theorem 1 ([
4])
. Let H be a connected graph of order Let If, for , is a -regular graph of order then the spectrum of the H-join graphs iswhereHere, and are the distance from vertex i to j for 3. Methodology
Research in graph theory continues to flourish because it provides a link between discrete structures and pure as well as applied mathematics. Using sophisticated mathematical tools, the study’s method builds upon well-established ideas in algebra and graph theory to produce new results. Our efforts rely on using the content of existing research to expand on established findings and investigate fresh aspects of weakly zero-divisor graphs.
The analysis in this paper heavily relies on the use of matrix theory and linear algebra. In particular, spectral graph theory provides a strong framework for studying the interaction between algebraic and graph-theoretical characteristics, a crucial tool for capturing the structural features of the weakly zero-divisor graph of the ring
The primary objective of this study is to analyze the
spectra of the weakly zero-divisor graph
for a general class of
n,
, where
’s and
’s are the distinct primes. To achieve this, we use the concept of new results on the
-matrix of connected graphs, which was introduced by Diaz et al. [
4].
4. Results
We will prove the main results of this paper in this section. For
, the induced subgraph
of
, formed by the vertices in the set
, is either
or
Recall that the adjacency spectrum of complete graph
and its complement graph
on
l vertices is given by
Lemma 5. Let n be the product of two different primes and . Then, the graph ’s spectrum is given byThe remaining two eigenvalues of the graph are the roots of the characteristic polynomial Proof. The proper divisors of
n are
and
and
. Also, by the definition of
Now, by Lemma 4, we have
. Therefore, by Lemma 2 and Corollary 1, we have
and
. Therefore, by Theorem 1, the
spectrum of the graph
is
and the root of characteristic polynomial
of the matrix provided below can be used to determine the remaining two eigenvalues
where
. □
Theorem 2. For distinct prime and , the spectrum of the iswhere and the cardinality of the vertex set V of is given The remaining six eigenvalues of the graph are the eigenvalues of matrix (3). Proof. Let
, where
, note that
is a complete graph on vertices
. Now, by Lemma 4, we have
Therefore, by Lemma 2 and Corollary 1, we have
and
.
The cardinality of the vertex set V of is given by Also, we have and It follows that and for Therefore, by Theorem 1, the spectrum of the graph is
where
The matrix’s characteristic polynomial can be used to determine the remaining six eigenvalues,
where
and
□
Theorem 3. Let where , is a prime, and is a positive integer. Then, the spectrum of the graph consists of eigenvalue with multiplicity , where The other remaining , eigenvalues of the graph are eigenvalues of matrix (4). Proof. For
, where
j is a positive integer and
is a prime, the proper divisors of
are
By Lemma 4, we have
It follows that
, where
is the cardinality of vertex set
V of
. Therefore, by Lemma 2 and Corollary 1, we get
and
for
Therefore, by Theorem 1, the
spectrum of the graph
consists of eigenvalue
with multiplicity
And the roots of matrix (
4)’s characteristic polynomial can be used to determine the remained
eigenvalues,
where
and
□
Theorem 4. Let where a prime, and is a positive integer. Then, the spectrum of the graph consists of eigenvalue with multiplicity . The other remaining eigenvalues of the graph are eigenvalues of matrix (5). Proof. Similarly, as above for Theorem 3, we can prove that the
spectrum of the graph
consists of eigenvalue
with multiplicities
,
where
is the cardinality of vertex set
V of
.
The other remaining
,
eigenvalues of the graph
are eigenvalues of matrix (
5), which is obtained from matrix (
1), where
and
. □
If in Theorem 3, the resulting outcome gives the spectrum of .
Corollary 2. The spectrum of for consists of eigenvalue with multiplicity . The remaining 5, eigenvalues of the graph are eigenvalues of matrix (6),where and Theorem 5. For distinct primes and , . The spectrum of the consists of eigenvaluesThe cardinality of the vertex set V of is given by and the roots of the characteristic polynomial of matrix (7) provide the remaining eigenvalues. Proof. Let
, where
, note that
is complete graph on vertices
. By Lemma 4, we have
Therefore, by Lemma 2 and Corollary 1, we get
Consequently, the cardinality
of the vertex set
V of
is given by
and also
and
And it follows that
and
Therefore, by Theorem 1, the
spectrum of the graph
is
The roots of matrix (
7)’s characteristic polynomial can be used to determine the remaining eigenvalues
where
and
□
When we choose in Theorem 5, the conclusion can be derived.
Corollary 3. For distinct primes and , the spectrum of the graph is given byThe cardinality of the vertex set V of is given by and the remaining four eigenvalues of the graph are the eigenvalues of matrix (8). Proof. Let , where , note that is complete graph on vertices By Lemma 4, we have = . Therefore, by Lemma 2 and Corollary 1, we have and .
The cardinality
of the vertex set
V of
is given by
and
. It follows that
and
Therefore, by Theorem 1, the
spectrum of the graph
is
The matrix’s characteristic polynomial of the matrix given in (
8) can be used to determine the remaining four eigenvalues,
where
and
□
Example 1. The spectrum of the weakly zero-divisor graph of isThe remaining four eigenvalues of the graph (Figure 1) are the roots of the characteristic polynomial of matrix (9). From Corollary 3, the
spectrum of the graph
is given by
And the roots of characteristic polynomial of the matrix (
9) provided below, are remaining four
eigenvalues of the graph
where
Theorem 6. Let , where ’s and ’s are the distinct primes. Then, the spectrum of the consists of eigenvaluesThe cardinality of the vertex set V of the graph is given by and the characteristic polynomial of matrix (10) provides the remaining eigenvalues. Also, if the eigenvalues of matrix (10) are integers, then the weakly zero divisor graph of for is integral. Proof. Suppose that
, where
’s and
’s are the distinct primes. Let
Then, by Lemma 3, the following conclusions can be drawn: for each
, we have
, and for
, we have
The cardinality
of the vertex set
V of the graph
is
Also note that for
, we have
for all
and
Therefore, by Theorem 1, the
spectrum of the graph
is
Note that all these eigenvalues are integers. And the roots of matrix (
10)’s characteristic polynomial can be used to determine the remaining eigenvalues
where
and
If the eigenvalues of matrix (
10) are integers, then the weakly zero divisor graph of
for
is
integral. □
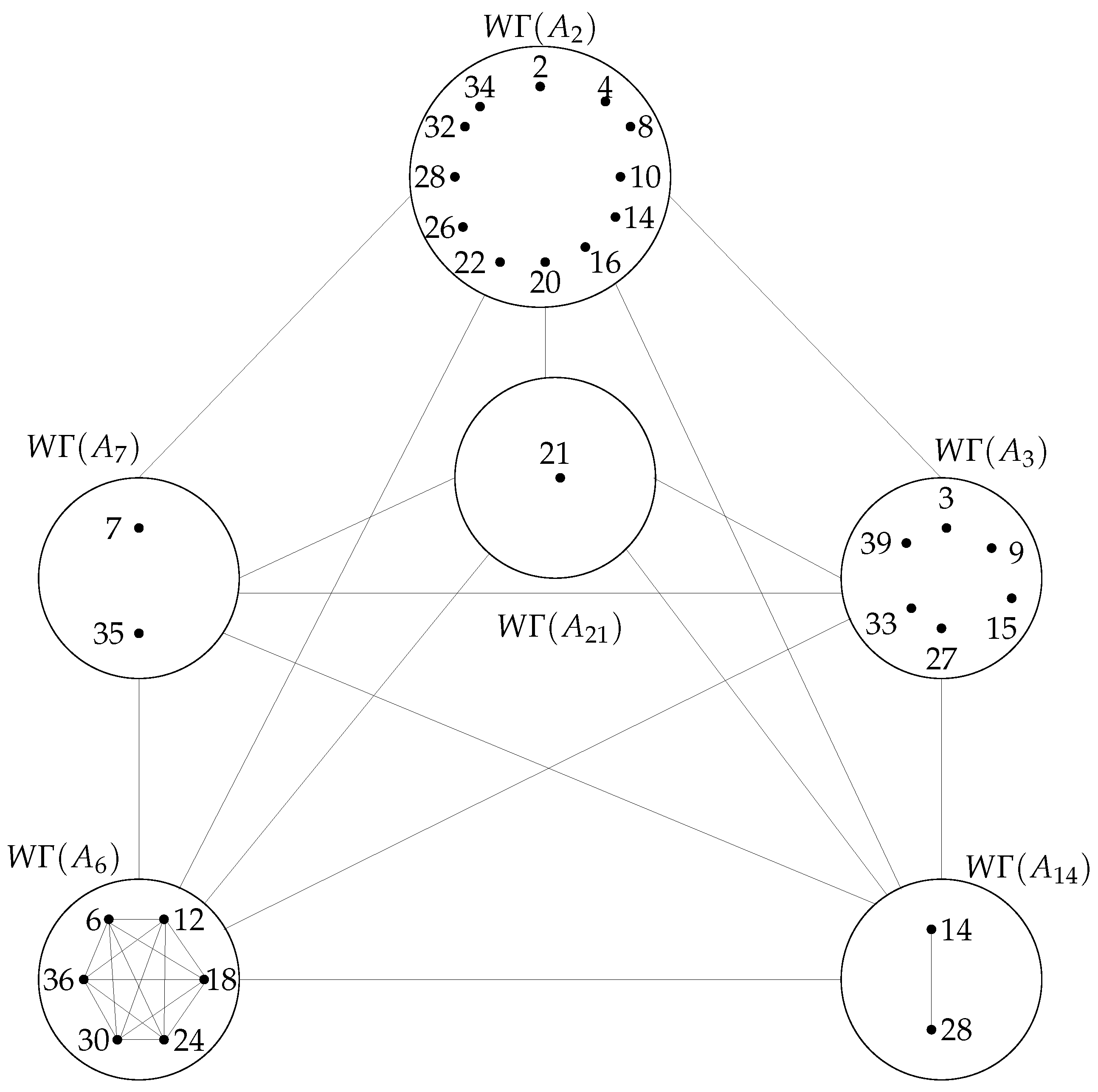
Example 2. The spectrum of the weakly zero-divisor graph of , shown in Figure 2, isThe six remaining eigenvalues of the graph are the eigenvalues of matrix (11). The proper divisors of 42 are 2, 3, 7, 6, 14, and
Note that
is a complete graph on vertices
, and 21. Now, by Lemma 4, we have
. Therefore, by Lemma 2 and Corollary 1, we have
and
. The cardinality
of the vertex set
V of
is 19. Now, according to the proper divisor sequence, we have
, and further, we have
, and
Consequently, the
spectrum of the graph
is given by Theorem 1.
And the matrix’s characteristic polynomial can be used to determine the remaining six eigenvalues
where
Figure 2.
Weakly zero-divisor graph .
Figure 2.
Weakly zero-divisor graph .
5. Conclusions and Further Work
In this study, we have explored the
spectrum of the weakly zero-divisor graph
for a general class of
n, where
and where
’s and
’s are the distinct primes. For this, we use the concept of new results on the
-matrix of connected graphs, which was introduced by Diaz et al. [
4]. We obtain the
eigenvalues for several arrangements by using thorough calculations and the basic algebraic properties of the weakly zero-divisor graph. This study shows how the algebraic structure of
and the spectral features of its associated graph interact, building on earlier findings regarding particular classes of
n.
The results show that the spectrum contains important information regarding the basic structure of weakly zero divisors. Specifically, the eigenvalue distributions and characteristic polynomials provide clarity on the modular arithmetic and divisors that underlie . The findings further support the significance of spectral graph theory in algebraic contexts by validating the existence of distinctive spectral patterns in specific classes of weakly zero-divisor graphs.
This study suggests various exciting paths for further exploration. One possible direction is to broaden the spectral analysis to encompass wider categories of finite commutative rings, with the goal of uncovering more profound connections between their algebraic characteristics and spectral parameters. An additional area worth exploring involves the investigation of further graph invariants, including the spectral radius, chromatic number, and connectivity, along with their relationships to the spectrum of weakly zero-divisor graphs. The spectra for higher powers of primes and rings with multiple prime factors could also be analyzed using sophisticated computer approaches, which could reveal complex patterns and features. Furthermore, it is necessary to conduct through research since the spectrum characteristics of weakly zero-divisor graphs may have useful implications in coding theory, cryptography, and error detection systems. It may be possible to identify significant similarities and differences between weakly zero-divisor graphs and other algebraically defined graphs, such as unit graphs or co-maximal graphs, by comparing their spectral properties.
Further one can calculate spectrum for co-zero divisor graphs, unit graphs, co-maximal graphs, and many more such graphs. This research not only deepens the theoretical insights into weakly zero-divisor graphs but also creates a strong basis for interdisciplinary studies that combine algebra, graph theory, and computational techniques.