Abstract
In this study, we outline a modified harmonic balance method for solving non-homogenous integrable dispersionless equations and obtaining the corresponding periodic solutions, a research field which shows limited investigation. This study is the first to solve this nonlinear problem, based on a recently developed harmonic balance method combined with Vieta’s substitution technique. A set of analytical formulas are generated from the modified harmonic balance method and used to compute the approximate periodic solutions of the dispersionless equations. The main advantage of this method is that the computation effort required in the solution procedure can be smaller. The results of the modified harmonic balance method show reasonable agreement with those obtained using the classic harmonic balance method. Our proposed solution method can decouple the nonlinear algebraic equations generated in the harmonic balance process. We also investigated the effects of various parameters on nonlinear periodic responses and harmonic convergence.
Keywords:
Vieta’s substitution; integrable-dispersionless equation; harmonic balance; periodic solution MSC:
65M99; 65P99; 37M05
1. Introduction
In recent decades, many studies have been conducted on the nonlinear differential equations used in various physics and wave propagation problems (e.g., [1,2,3,4,5]), of which the integrable dispersionless equations and corresponding solutions are particularly popular topics. Several authors showed that a coupled system is solvable using the inverse scattering method [1,2]. The corresponding generalized form was studied using the inverse scattering method, demonstrating some remarkable soliton properties. Popovic et al. [3] studied the framed curve families induced by real and complex coupled dispersionless-type equations with singular points. Special connections for framed base curves were used to generalize regular curves with linear independent conditions. Eren et al. [4] investigated an involute–evolute curve family induced by coupled dispersionless (CD) equations. Integrable generalized Heisenberg ferromagnet-type equations for the tangent, principal normal, and binormal unit vectors were presented. Hu et al. [5] analyzed coupled dispersionless-type equations and short pulse-type equations. The integrability of these equations was achieved by setting their Lax pairs geometrically. The corresponding multi-soliton solutions were obtained in the determinant form for the mSP and two-component SP equations. Yu and Zhang [6] studied the generalized coupled integrable dispersionless equations and developed two integrable discrete analogs: a semi-discrete system and a fully discrete one. They obtained the N-soliton solutions for the semi-discrete and fully discrete systems in the form of Casorati determinants. Xu et al. [7] presented a multi-component complex CID equation and confirmed its integrability using Lax pairs. They found the rich evolution properties of the one-soliton and two-soliton solutions. Lou and Yu [8] investigated an extension of the coupled integrable dispersionless equations which could represent a current-fed string within an external magnetic field. They presented the N-soliton solutions for a generalized system in the form of Casorati determinants. Kuetche et al. [9] used various independent variable transformations to investigate nonlinear coupled dispersionless evolution equations, obtaining an N-loop soliton solution. Victor et al. [10] explored the soliton structure of a coupled dispersionless system that involved a current-conducting string of infinite length within a magnetic field. Charalampidis et al. [11] developed trapped solitary-wave solutions of a coupled nonlinear Schrodinger system in 1 + 1 dimensions in the presence of an external, supersymmetric and complex PT-symmetric potential. Erbay et al. [12] developed numerical solitary-wave solutions for the Rosenau equation using two numerical algorithms based on the Petviashvili iteration method, with single or double power law nonlinearity. Liu et al. [13] and Leung et al. [14] adopted the Jacobi elliptic-function and residue harmonic balance methods to obtain periodic solutions for coupled integrable dispersionless equations. However, their transformed nonlinear equations did not contain non-homogenous terms, which we consider in this study. Lee [15] presented only one set of preliminary numerical results related to this problem, but their article contained no formulations.
On the other hand, some well-known approaches [16,17,18,19] have been developed for solving nonlinear differential equations and applied to various nonlinear oscillation problems. For example, Laghari et al. [18] presented a pragmatic approach which adopted the hybridization of nature-inspired optimization algorithms and Bernstein Polynomials. The advantage of the approach was that it could achieve the optimum numeric solution for the Nonlinear Optimal Control Problems of dynamical systems. The final results suggested that the proposed method could generate a better solution and surpass other methods mentioned in the literature. Baghani [19] used an iterative computational approach to solve nonlinear fractional optimal control problems. It was based on the left and right operational matrices of the second Chebyshev wavelets. The proposed method’s order of convergence was improved. Petromichelakis and Kougioumtzoglou [20] developed a computational algebraic geometry technique for determining the nonlinear normal modes of multi-degree-of-freedom nonlinear dynamic systems. Several numerical examples were used to demonstrate the effectiveness of the solution technique. The above approaches and corresponding solution forms were the most useful for solving particular nonlinear problems. Various harmonic balance methods have been developed in recent decades. Mittal et al. [21] studied the harmonic balance (HB) of the Giesekus model under large amplitude oscillatory shear deformation. The HB transformed the system of differential equations into a set of nonlinear algebraic equations in the Fourier coefficients. The results of the convergence studies showed that the difference between the HB and true solutions decayed exponentially with the number of harmonics. Numerical experiments found that the HB would be simultaneously about three orders of magnitude cheaper and several orders of magnitude more accurate than numerical integration. Li et al. [22] studied the nonlinear dynamic characteristics of spherical rubber isolators using experiments and simulations based on the harmonic balance method. The results were in line with the experimental results, showing the feasibility of using the nonlinear model to predict the vibration characteristics of thin-walled hallowed spherical rubber isolation systems. Kogelbauer and Breunung [23] investigated the validity of the harmonic balance method in a nonlinear, multi-degree-of-freedom mechanical system with time-periodic forcing and linear damping. They set some conditions to improve the approximate periodic solutions. The method showed the validity and accuracy of the harmonic balance method.
In this paper, we present the analytical periodic solutions for non-homogenous integrable dispersionless equations using a modified harmonic balance method [24,25], which was recently developed to solve nonlinear structural–acoustic and nonlinear vibration problems. The multi-level harmonic balance method is combined with Vieta’s substitution technique for solving non-homogenous integrable dispersionless equations and obtaining the corresponding periodic solution. The effects of various parameters on the nonlinear periodic responses and the harmonic convergences are investigated. This is the first work to solve the integrable dispersionless equations based on the above solution method. The multi-level harmonic balance method generated a set of uncoupled nonlinear algebraic equations which required much less computational time than the coupled nonlinear algebraic equations used in classic harmonic balance methods (e.g., [26]). Table 1 shows the numbers of nonlinear algebraic equations generated by the two methods, while Figure 1 shows that the computational effort required for solving uncoupled nonlinear equations is much lower. Note: the nonlinear equations were solved using MathCad 2001 installed on a computer with Intel i7-6700 and 16 GB RAM (Intel Corporation, Santa Clara, CA, USA).

Table 1.
Number of nonlinear algebraic equations generated in a cubic nonlinear differential equation.
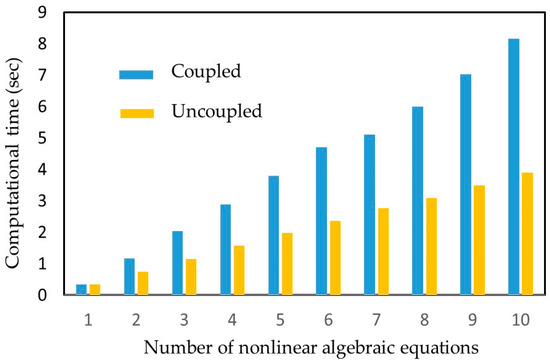
Figure 1.
Computational time versus number of nonlinear algebraic equations.
2. Background
In this section, we describe the logic of using the solution method for the nonlinear problem in this paper. In Section 2.1, the three original coupled dispersionless integrable equations are introduced. In Section 2.2, a wave transform is adopted to reduce the three original coupled dispersionless integrable equations into a second-order nonlinear ordinary differential equation. In Section 3.1 and Section 3.2, the harmonic balance method and Vieta’s substitution technique are introduced to solve the nonlinear ordinary differential equation.
2.1. Integrable Dispersionless Equations
Recently, coupled dispersionless integrable hierarchies and their generalizations have emerged in various fields of study, attracting great interest from many researchers. The second-order nonlinear ordinary differential equation mentioned above can be used to model a wide range of physical systems due to its ability to describe nonlinear periodic responses and chaotic responses. It is a fundamental model in nonlinear dynamics, with applications in mechanics, electrical circuits, and optics such as (1) a dynamic structure with a nonlinear stiffness term; (2) a circuit containing nonlinear inductors or capacitors; (3) a piezoelectric oscillator which exhibits a nonlinear relationship between applied stress and resulting strain; and (4) nonlinearly vibrating bridges under wind and traffic loads. Other than these four common examples, the specific structural–acoustic model shown in [24] can also be mathematically represented by this second-order nonlinear ordinary differential equation, which is additionally the outcome of the wave transform from the coupled dispersionless integrable equations. The homogeneous coupled integrable dispersionless equations (e.g., [13,14]) are given by
2.2. Wave Transform for Nonlinear Differential Equation
Consider the wave transform of to obtain the corresponding periodic solutions. After the transform, u is a function of .
Equations (4)–(6) are integrated into Equation (1), resulting in Equation (7).
where is the first derivative with respect to ξ, and k1 is the integration constant. Note that v, w, and uξ are periodic but u is not. After the integration of with respect to ξ, u is linearly proportional to ξ, and therefore it is non-periodic.
Equation (7) is integrated into Equations (2) and (3) to eliminate the variable u and to consider a periodic forcing term (or non-homogeneous term).
where and are constants; ; ; f = forcing function; and and are the second derivatives.
When setting w = v in Equation (8) and v = w in Equation (9), the two equations are identical (see Equation (10)). Therefore, it is implied that one of the solution forms can be obtained by setting v = w. Equation (10) is the well-known non-homogeneous Duffing equation
where y is a function of ; y = v or w. is the second derivative with respect to ξ.
3. Proposed Algorithm
3.1. Approximate Analytical Solution for Harmonic Excitation
In this subsection, the multi-level harmonic balance approach [24,25] is adopted as the solution method. Using Vieta’s substitution, outlined in the next subsection, the solutions can be found from a set of analytic formulas without using any nonlinear equation solver. Considering the harmonic excitation shown in Equation (10), the forcing function is set as cosine.
where P is the excitation magnitude, and ω = normalized excitation frequency.
The multi-level solution is expressed in the following form.
where L0, L1, L2, and Ln represent the corresponding solution levels, and y0, y1, y2, and yn are the zero-, 1st-, 2nd-, and nth-level approximations, given by
where a0,0, a1,0, a1,1, a2,0, a2,1, a2,2 an,0, an,1, and an,2 are the unknown coefficients found in the zero-, 1st-, 2nd-, and nth-level solution procedures. The first subscript of these coefficients represents the solution level, and the second subscript stands for the harmonic order. The general solution form is given by
Note that in this study, the derivations of the zero-, 1st-, and 2nd-level solutions and the corresponding analytical formulas are shown in detail.
In the zero-level approximation, the terms associated with L0 are collected to set up the following equation.
where is the function which contains the zero-level nonlinear terms; the first subscript represents “zero level”, and the second subscript represents “nonlinear”. (″) = d2/dξ2.
3.2. Vieta’s Substitution
Consider the zero-level harmonic balance of cos () to find the unknown coefficient, :
where is the zero-level harmonic balance function; the 1st subscript represents “zero level”, and the 2nd subscript represents “1st harmonics”. ; ; G0,3 = ¾; G0,1 = (−ω2 + α); G0,0 = P.
Consider Vieta’s substitution [25] and insert it into Equation (20).
where is a new variable; now and are functions of .
Then, Equation (20) can be further simplified.
Obviously, Equation (24) is a quadratic equation. Its solutions and can be found easily.
where ; ; .
The zero-level solution is given by
In the first-level approximation, Equations (12) and (14) are substituted into Equation (11), and then the linear terms associated with L1 are collected to set up the following equation.
where is the function which contains the 1st-level linear terms; the first subscript represents “1st level”, and the second subscript represents “linear”; (″) = d2/dξ2. and are the zero-level and first-level solutions, which are functions of ξ.
Equations (12) and (14) are substituted into Equation (11). Then, the following linear and nonlinear terms are collected to set up the following equation.
where is the function which contains the 1st-level nonlinear terms.
The 1st-level harmonic balances of cos () and cos (3) are then considered to find the unknown coefficients, a1,0 and a1,1:
where . is the 1st-level function for the harmonic balance of cos(τ); the first subscript represents “1st level”, and the second subscript represents “1st harmonics”.
For the 1st-level harmonic balance of cos(3),
where is the 1st-level function for the harmonic balance of cos(3τ); the second subscript represents “2nd harmonics”.
We insert Equation (32) into Equation (34).
where ; ; ; ; .
Again, consider Vieta’s substitutions
where is a new variable; now and are functions of .
Then, Equation (35) can be further simplified as follows:
Similarly to those of Equation (24), the quadratic solutions of Equation (39) and can be found easily.
where ; .
From Equation (32), . Hence, the 1st-level solution is given by
In the 2nd-level approximation, Equations (12) and (15) are substituted into Equation (11), and then, the linear terms associated with L2 are collected to set up the following equations:
where is the function which contains the 2nd-level linear terms. It should be noted that Φ2,l is used for the harmonic balance of cos(3τ), and does not contain the term 3y0 y12, in which the cos(3τ) component has been balanced in the 1st-level solution process.
Equations (12) and (15) are substituted into Equation (11). Then, the following linear and nonlinear terms are collected to set up the following equation.
where is the function which contains the 2nd-level nonlinear terms; is the second-level solution, which is a function of ξ.
The 2nd-level harmonic balances of cos(), cos(3), and cos(5) are then considered to find the unknown coefficients a2,0, a2,1, and a2,2.
where ; . is the 2nd-level function for the 2nd-level harmonic balance of ; the second subscript represents “1st harmonics”.
For the 2nd-level harmonic balance of cos(3),
where ; ; is the 2nd-level function for the harmonic balance of ; the second subscript represents “2nd harmonics”.
For the 2nd-level harmonic balance of cos(5),
where is the 2nd-level function for the harmonic balance of cos(5τ); the second subscript represents “3rd harmonics”.
By inserting Equations (48) and (51) into Equation (53), we obtain
where ; ; ; ; .
Again, consider Vieta’s substitutions,
where is a new variable; now and are functions of .
Then, Equation (54) can be rewritten as
Hence, the quadratic solutions of Equation (58) and can be found easily:
where ; β .
The 2nd-level unknowns a2,1, and a2,2 can be found from Equations (48) and (51), and the 2nd-level solution is given by
4. Results and Discussion
Table 2 and Table 3 show the convergence studies of the periodic response amplitudes at = 1.5 and 8 for various harmonic excitation magnitudes. The zero-, 1st-, and 2nd-level harmonic solutions were computed using the multi-level harmonic balance method combined with Vieta’s substitution technique. The 2nd-level solutions were normalized to 100. In cases of high excitation frequency (ω = 8), the maximum difference between the zero- and 2nd-level solutions was less than 3% for an excitation magnitude ranging from 1 to 10. In cases of low excitation frequency (ω = 1.5) and high excitation magnitude (p = 10), the maximum difference between the zero- and 2nd-level solutions was about 9%. In all cases, the maximum difference between the 1st- and 2nd-level solutions was less than 3%. It can be seen that for high excitation frequencies, the zero-level solutions are accurate enough; for low excitation frequencies, the 1st-level solutions are more acceptable and accurate. Figure 2 presents the comparisons between the frequency–amplitude curves obtained from the two proposed methods and the classic harmonic balance method (e.g., [26]). The results obtained from these methods are generally in good agreement. The main difference occurs in the low frequency range because the solution form of the proposed method is different from that in [26]. In the proposed method, there are two solution curves at the low frequency range. In the classical harmonic balance method, there is only one solution curve at the low frequency range, which branches out to become two around ω = 0.78.

Table 2.
Convergence study of y for various excitation magnitudes (= 1.5, α = 1, β = 2).

Table 3.
Convergence study of y for various excitation magnitudes (= 8, α = 1, β = 2).

Figure 2.
Comparisons between the frequency–amplitude curves obtained from the proposed method and the classical harmonic balance method (α =1, β = 2, p = 6) [26].
Figure 3 shows the amplitude of y plotted against the excitation frequency for various excitation magnitudes. The curves where p = 0 are referred to as back-bone curves or frequency–amplitude curves, from which the natural frequency of the nonlinear system can be found. There is an additional solution curve present along with the curves representing the three main solutions, which is due to the superharmonic phenomenon. In addition, a small abrupt change (about a 4.3% jump down) at a low frequency is found on each solution curve 1. In the low frequency range, the solution curves 2 and 3, which occur at the medium to high frequency ranges, do not exist. In the very high frequency range, the solution curves 1 and 2 are very close, while in the medium frequency range, each solution curve 2 approaches solution curve 3 and deviates from solution curve 1. At a particular medium frequency, each solution curve 2 meets with each solution curve 3. Our comparison between the solution curves of various excitation magnitudes shows that higher solution values are induced by higher excitation magnitudes in all cases, with the exception of some values on the additional solution curves. Figure 4 shows the amplitude of uξ plotted against the excitation frequency for various magnitudes. The main difference between the solution curves shown in Figure 3 and Figure 4 is that solution curves 1 and 2 in Figure 3 tend to be straight lines (i.e., linearly increasing), while those in Figure 4 tend to be concave lines. Figure 5 and Figure 6 show the 2D and 3D plots, respectively. In Figure 5, the multi-peak/trough waveform looks like a combination of several simple harmonic wave forms. In Figure 5, the magnitude of v is plotted against x and t. The 3D waveforms are projected in the 2D plot. Note that v and w are periodic; thus, uξ is also periodic. After the integration of with respect to ξ, u is linearly proportional to the parameter ξ, and therefore u is non-periodic and monotonically increases with ξ. Figure 7, Figure 8 and Figure 9 show the amplitude of y plotted against the excitation magnitude for various excitation frequencies. In Figure 7, in the cases of ω = 2 or 3, there are four solution curves corresponding to those in Figure 3. Each additional solution curve is almost horizontal. As previously mentioned, it is implied that they are inert to the excitation magnitude. Each solution curve 1 mildly increases with the excitation magnitude and meets the corresponding solution curve 2 at zero excitation magnitude. Each solution curve 2 and the corresponding solution curve 3 form a half ellipse. The difference between the cases of ω = 2 and 3 is that the solution curves of ω = 2 are lower and the half ellipse is smaller than in the case of ω = 3. In Figure 8, there are only two solution curves for ω = 0.95. It can be seen that, when the excitation frequency decreases from ω = 1.5 to 0.95, solution curves 2 and 3 disappear. It is implied that, at this frequency, only two real solutions can be obtained from the nonlinear algebraic equations generated from the proposed Vieta substitution technique and multi-level harmonic balance method. In addition, unlike ω = 1.5, the solution value of ω = 0.95 is zero when the excitation magnitude is also zero. Figure 9 shows the cases of ω = 0.75 and 0.95. There are two solution curves for these cases. At this frequency range, it can be seen that, unlike those shown in Figure 7, each additional solution curve mildly increases with the excitation magnitude; when compared with the others, each solution curve 1 is much more sensitive to the excitation magnitude. Recall the basic principles of “stiffness control at low frequency” and F ∝ D, where F is force and D is displacement; therefore, the higher the excitation magnitude, the higher the v magnitude. The solution curve 1 of ω = 0.95 is generally higher than that of ω = 0.75 In addition, there is a small abrupt change on each solution curve 1. The small abrupt change of ω = 0.95 occurs at a higher excitation magnitude.
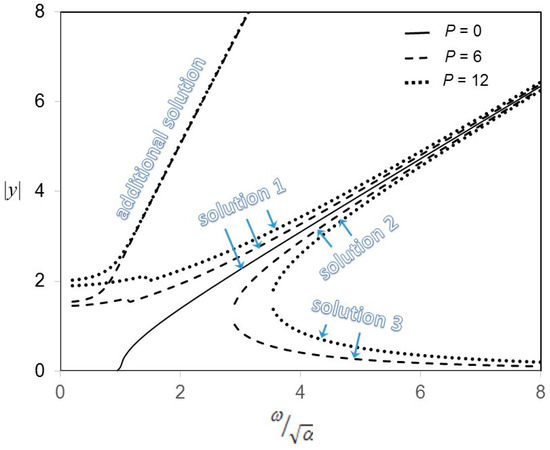
Figure 3.
Amplitude of y versus normalized excitation frequency for various excitation magnitudes (α = 1, β = 2).

Figure 4.
Amplitude of uξ versus normalized excitation frequency for various excitation magnitudes (α = 1, β = 2).
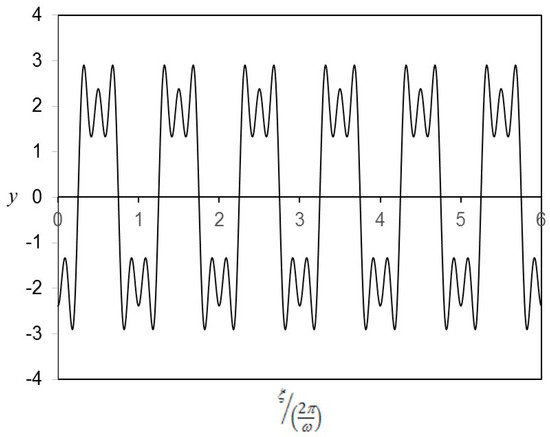
Figure 5.
y versus normalized ξ (α = 1, β = 2, ω = 0.5, p = 10).

Figure 6.
y plotted versus normalized x and t (α = 1, β = 2, ω = 0.5, p = 10).

Figure 7.
Amplitude of y versus excitation magnitude (α = 1, β = 2, ω = 2, and 3).

Figure 8.
Amplitude of y versus excitation magnitude (α = 1, β = 2, ω = 0.95, and 1.5).

Figure 9.
Amplitude of y versus excitation magnitude (α = 1, β = 2, ω = 0.75, and 0.95).
5. Conclusions
5.1. Verification
In this paper, we have presented a modified harmonic balance method for solving non-homogenous integrable dispersionless equations and obtained the corresponding periodic solutions. The results obtained showed reasonable agreement with those obtained from the classic harmonic balance method.
5.2. Key Finding
From this study, the key findings are as follows: (1) the three variables v, w, and uξ are periodic but u is not, because u is linearly proportional to the variable ξ, and therefore non-periodic; (2) the additional solution curves in the case of harmonic excitation are quite inert to the excitation magnitude; and (3) in the case of high excitation frequencies (ω = 8), the maximum difference between the zero- and 2nd-level solutions is less than 3%.
5.3. Methodological Advantage and Limitations
The main methodological advantage of this study is that, by using the analytical formulas, we were able to obtain solutions without using a nonlinear equation solver. This proposed solution method can decouple the nonlinear algebraic equations generated in the harmonic balance process. On the other hand, the main limitation of the proposed method is that in the decoupling process, the low-frequency nonlinear solutions obtained from the proposed method and from the classical harmonic balance method are somewhat different from each other.
5.4. Future Work
A future research goal is to develop new solution forms which can handle governing equations with other types of non-homogenous terms (e.g., damping terms linearly proportional to the first derivative).
Author Contributions
Data curation, M.I.K. and Y.-Y.L.; formal analysis, M.I.K. and Y.-Y.L.; investigation, M.I.K. and Y.-Y.L.; methodology, M.I.K., Y.-Y.L. and M.D.Z.; writing and editing, M.I.K., Y.-Y.L. and M.D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Konno, K.; Kakuhata, H. Interaction among growing, decaying and stationary solitons for coupled integrable dispersionless equations. J. Phys. Soc. 1995, 64, 2707–2709. [Google Scholar] [CrossRef]
- Kakuhata, H.; Konno, K. A generalization of coupled integrable, dispersionless system. J. Phys. Soc. 1996, 65, 340–341. [Google Scholar] [CrossRef]
- Popovic, N.; Eren, K.; Savic, A.; Ersoy, S. Framed curve families induced by real and complex coupled dispersionless-type equations. Mathematics 2023, 11, 3531. [Google Scholar] [CrossRef]
- Eren, K.; Yesmakhanova, K.; Ersoy, S.; Myrzakulov, R. Involute evolute curve family induced by the coupled dispersionless equations. Optik 2022, 270, 169915. [Google Scholar] [CrossRef]
- Hu, J.; Ji, J.L.; Yu, G.F. On the coupled dispersionless-type equations and the short pulse-type equations. J. Nonlinear Math. Phys. 2021, 28, 14–26. [Google Scholar] [CrossRef]
- Yu, G.F.; Zhang, Y.N. Integrable discretization and numerical simulations of the generalized coupled integrable dispersionless equations. J. Differ. Equ. Appl. 2019, 25, 408–429. [Google Scholar] [CrossRef]
- Xu, Z.W.; Yu, G.F.; Zhu, Z.N. Soliton dynamics to the multi-component complex coupled integrable dispersionless equation. Commun. Nonlinear Sci. Numer. Simul. 2016, 40, 28–43. [Google Scholar] [CrossRef]
- Lou, S.Y.; Yu, G.F. A generalization of the coupled integrable dispersionless equations. Math. Methods Appl. Sci. 2016, 39, 4025–4034. [Google Scholar] [CrossRef]
- Kuetche, V.K.; Bouetouand, T.B.; Kofane, T.C. On exact N-loop soliton solution to nonlinear coupled dispersionless evolution equations. Phys. Lett. A 2008, 372, 665–669. [Google Scholar] [CrossRef]
- Victor, K.K.; Betchewe, G.; Thomas, B.B.; Kofane, T.C. Miscellaneous rotating solitary waves to a coupled dispersionless system. Chin. Phys. Lett. 2009, 26, 090505. [Google Scholar] [CrossRef]
- Charalampidis, E.G.; Dawson, J.F.; Cooper, F.; Khare, A.; Saxena, A. Stability and response of trapped solitary wave solutions of coupled nonlinear Schrodinger equations in an external, PT- and supersymmetric potential. J. Phys. A Math. Theor. 2020, 53, 455702. [Google Scholar] [CrossRef]
- Erbay, H.A.; Erbay, S.; Erkip, A. Numerical computation of solitary wave solutions of the Rosenau equation. Wave Motion 2020, 98, 102618. [Google Scholar] [CrossRef]
- Liu, S.K.; Zhao, Q.; Liu, S.D. The periodic solutions for coupled integrable dispersionless equations. Chin. Phys. B 2011, 20, 040202. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Yang, H.X.; Guo, Z.J. Periodic wave solutions of coupled integrable dispersionless equations by residue harmonic balance. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4508–4514. [Google Scholar] [CrossRef]
- Lee, Y.Y. Modified residue harmonic balance solution for coupled integrable dispersionless equations with disturbance terms. J. Zhejiang Univ.—Sci. A 2019, 20, 300–304. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hasan, A.S.M.Z. Modified harmonic balance method for the solution of nonlinear jerk equations. Results Phys. 2018, 8, 893–897. [Google Scholar] [CrossRef]
- Andrianov, I.V.; Olevs’Kyy, V.I.; Awrejcewicz, J. Analytical perturbation method for calculation of shells based on 2d pade approximants. Int. J. Struct. Stab. Dyn. 2013, 13, 1340003. [Google Scholar] [CrossRef]
- Laghari, G.F.; Malik, S.A.; Khan, I.A.; Daraz, A.; Al Qahtani, S.A.; Ullah, H. Fitness Dependent Optimizer Based Computational Technique for Solving Optimal Control Problems of Nonlinear Dynamical Systems. IEEE Access 2023, 11, 38485–38501. [Google Scholar] [CrossRef]
- Baghani, O. SCW-iterative-computational method for solving a wide class of nonlinear fractional optimal control problems with Caputo derivatives. Math. Comput. Simul. 2022, 202, 540–558. [Google Scholar] [CrossRef]
- Petromichelakis, I.; Kougioumtzoglou, I.A. A computational algebraic geometry technique for determining nonlinear normal modes of structural systems. Int. J. Non-Linear Mech. 2021, 135, 103757. [Google Scholar] [CrossRef]
- Mittal, S.; Joshi, Y.M.; Shanbhag, S. The method of harmonic balance for the Giesekus model under oscillatory shear. J. Non-Newton. Fluid Mech. 2023, 321, 105092. [Google Scholar] [CrossRef]
- Li, H.; Yang, C.L.; Wang, S.X.; Su, P.; Zhu, Y.Q.; Zhang, X.Y.; Peng, Z.H.; Mu, Q.Q. Study on the nonlinear dynamic characteristics of spherical rubber isolators by experiments and simulations based on harmonic balance method. Int. J. Struct. Stab. Dyn. 2022, 22, 2250133. [Google Scholar] [CrossRef]
- Kogelbauer, F.; Breunung, T. When does the method of harmonic balance give a correct prediction for mechanical systems? Appl. Anal. 2021, 102, 425–443. [Google Scholar] [CrossRef]
- Lee, Y.Y. Nonlinear structure-extended cavity interaction simulation using a new version of harmonic balance method. PLoS ONE 2018, 13, e0199159. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.Y. Analytic formula for the vibration and sound radiation of a nonlinear duct. Shock. Vib. 2019, 2019, 9685142. [Google Scholar] [CrossRef]
- Lee, Y.Y. Structural-acoustic coupling effect on the nonlinear natural frequency of a rectangular box with one flexible plate. Appl. Acoust. 2002, 63, 1157–1175. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).