The Resistance Distance Is a Diffusion Distance on a Graph
Abstract
1. Introduction
2. Preliminaries
3. Results
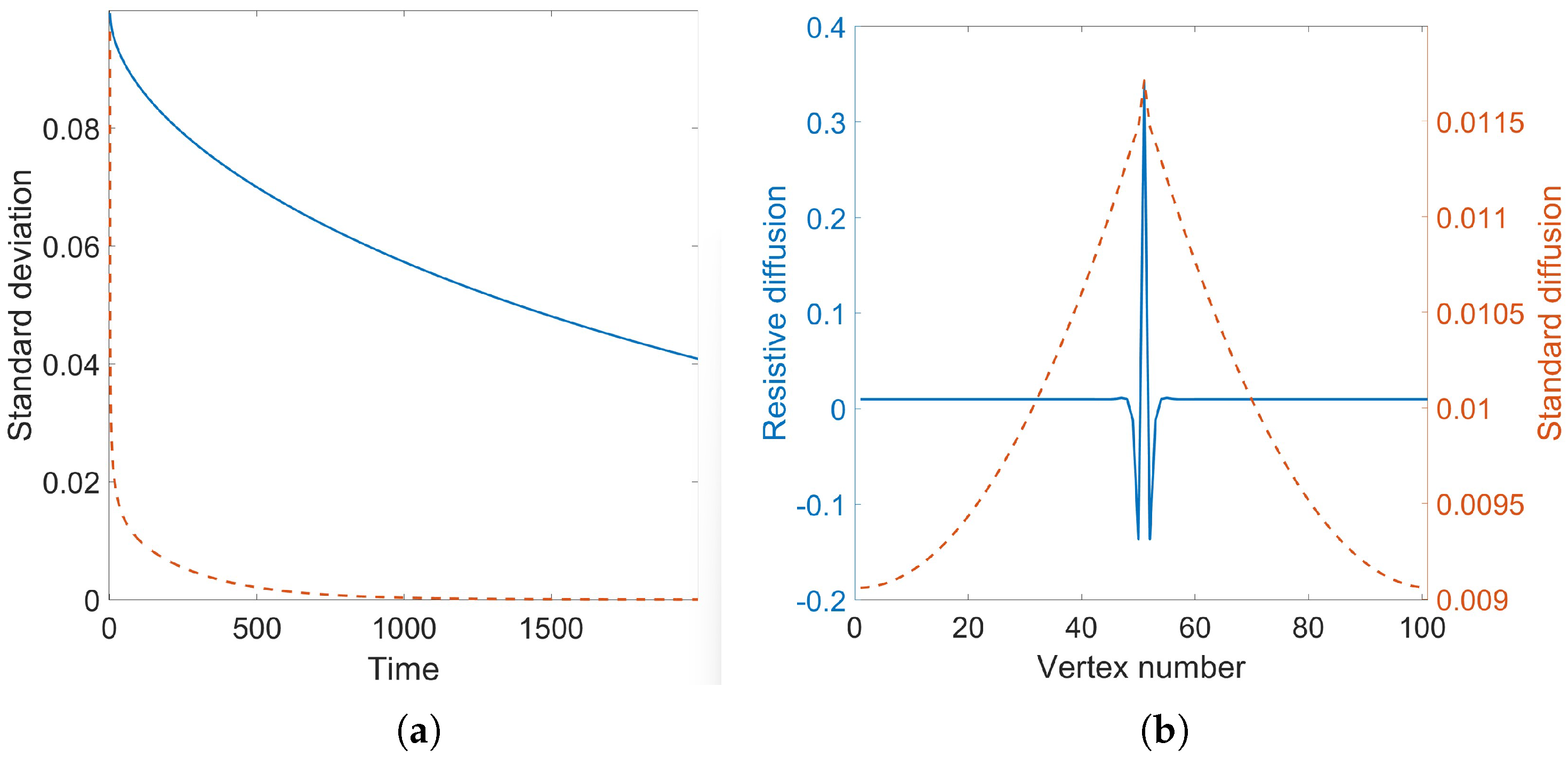
4. Resistance Distance as a Diffusion Distance
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kirchhoff, G. Ueber die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Vertheilung galvanischer Ströme geführt wird. Ann. Phys. 1847, 148, 497–508. [Google Scholar] [CrossRef]
- Kirchhoff, G. On the solution of the equations obtained from the investigation of the linear distribution of galvanic currents. IRE Trans. Circuit Theory 1958, 5, 4–7. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G. The Laplacian of a graph. In Algebraic Graph Theory; Springer: Berlin/Heidelberg, Germany, 2001; pp. 279–306. [Google Scholar]
- Merris, R. Laplacian matrices of graphs: A survey. Linear Algebra Appl. 1994, 197, 143–176. [Google Scholar] [CrossRef]
- Das, K.C. The Laplacian spectrum of a graph. Comput. Math. Appl. 2004, 48, 715–724. [Google Scholar] [CrossRef]
- Grone, R.; Merris, R.; Sunder, V.S. The Laplacian spectrum of a graph. SIAM J. Matrix Anal. Appl. 1990, 11, 218–238. [Google Scholar] [CrossRef]
- Mohar, B.; Alavi, Y.; Chartrand, G.; Oellermann, O. The Laplacian spectrum of graphs. Graph Theory Comb. Appl. 1991, 2, 871–898. [Google Scholar]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Pan, L.; Shao, H.; Mesbahi, M. Laplacian dynamics on signed networks. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 891–896. [Google Scholar]
- Ellens, W.; Spieksma, F.M.; Van Mieghem, P.; Jamakovic, A.; Kooij, R.E. Effective graph resistance. Linear Algebra Appl. 2011, 435, 2491–2506. [Google Scholar] [CrossRef]
- Klein, D.J.; Randić, M. Resistance distance. J. Math. Chem. 1993, 12, 81–95. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Gurvich, V.A. Metric and ultrametric spaces of resistances. Russ. Math. Surv. 1987, 42, 235–236. [Google Scholar] [CrossRef]
- Ghosh, A.; Boyd, S.; Saberi, A. Minimizing effective resistance of a graph. SIAM Rev. 2008, 50, 37–66. [Google Scholar] [CrossRef]
- Kagan, M.; Mata, B. A physics perspective on the resistance distance for graphs. Math. Comput. Sci. 2019, 13, 105–115. [Google Scholar] [CrossRef]
- Li, Z.; Xie, Z.; Li, J.; Pan, Y. Resistance distance-based graph invariants and spanning trees of graphs derived from the strong prism of a star. Appl. Math. Comput. 2020, 382, 125335. [Google Scholar] [CrossRef]
- Xiao, W.; Gutman, I. Resistance distance and Laplacian spectrum. Theor. Chem. Acc. 2003, 110, 284–289. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H. Some rules on resistance distance with applications. J. Phys. A Math. Theor. 2008, 41, 445203. [Google Scholar] [CrossRef]
- Chandra, A.K.; Raghavan, P.; Ruzzo, W.L.; Smolensky, R. The electrical resistance of a graph captures its commute and cover times. In Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 14–17 May 1989; ACM: New York, NY, USA, 1989; pp. 574–586. [Google Scholar]
- Doyle, P.G.; Snell, J.L. Random Walks and Electric Networks; American Mathematical Society: Providence, RI, USA, 1984; Volume 22. [Google Scholar]
- Nash-Williams, C.S.J.A. Random walk and electric currents in networks. Math. Proc. Camb. Philos. Soc. 1959, 55, 181–194. [Google Scholar] [CrossRef]
- Palacios, J.L. Resistance distance in graphs and random walks. Int. J. Quantum Chem. 2001, 81, 29–33. [Google Scholar] [CrossRef]
- Devriendt, K.; Ottolini, A.; Steinerberger, S. Graph curvature via resistance distance. Discrete Appl. Math. 2024, 348, 68–78. [Google Scholar] [CrossRef]
- Li, M.; Zhou, S.; Chen, G.; Lin, W.; Zhou, Q. Novel resistive distance descriptors on complex network. IEEE Access 2022, 10, 14548–14563. [Google Scholar] [CrossRef]
- Li, M.; Zhou, S.; Wang, D.; Chen, G. Identifying influential nodes based on resistance distance. J. Comput. Sci. 2023, 67, 101972. [Google Scholar] [CrossRef]
- Thulasiraman, K.; Yadav, M.; Naik, K. Network science meets circuit theory: Resistance distance, Kirchhoff index, and Foster’s theorems with generalizations and unification. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 66, 1090–1103. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Devriendt, K.; Cetinay, H. Pseudoinverse of the Laplacian and best spreader node in a network. Phys. Rev. E 2017, 96, 032311. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Bu, C. Detecting community structure in complex networks via resistance distance. Physica A 2019, 526, 120782. [Google Scholar] [CrossRef]
- Luxburg, U.; Radl, A.; Hein, M. Getting lost in space: Large sample analysis of the resistance distance. In Proceedings of the Advances in Neural Information Processing Systems 23: 24th Annual Conference on Neural Information Processing Systems 2010, Vancouver, BC, Canada, 6–9 December 2010; p. 23. [Google Scholar]
- Coifman, R.R.; Hirn, M.J. Diffusion maps for changing data. Appl. Comput. Harmon. Anal. 2014, 36, 79–107. [Google Scholar] [CrossRef]
- Coifman, R.R.; Kevrekidis, I.G.; Lafon, S.; Maggioni, M.; Nadler, B. Diffusion maps, reduction coordinates, and low dimensional representation of stochastic systems. Multiscale Model. Simul. 2008, 7, 842–864. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S. Diffusion maps. Appl. Comput. Harmon. Anal. 2006, 21, 5–30. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S.W. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proc. Natl. Acad. Sci. USA 2005, 102, 7426–7431. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Estrada, E. Communicability geometry captures traffic flows in cities. Nat. Hum. Behav. 2018, 2, 645–652. [Google Scholar] [CrossRef]
- Bartesaghi, P.; Clemente, G.P.; Grassi, R. Community structure in the world trade network based on communicability distances. J. Econ. Interact. Coord. 2020, 17, 405–441. [Google Scholar] [CrossRef]
- Estrada, E. The communicability distance in graphs. Linear Algebra Appl. 2012, 436, 4317–4328. [Google Scholar] [CrossRef]
- Estrada, E. Complex networks in the Euclidean space of communicability distances. Phys. Rev. E 2012, 85, 066122. [Google Scholar] [CrossRef]
- Lella, E.; Estrada, E. Communicability distance reveals hidden patterns of Alzheimer’s disease. Netw. Neurosci. 2020, 4, 1007–1029. [Google Scholar] [CrossRef] [PubMed]
- Alfakih, A.Y. Euclidean Distance Matrices and Their Applications in Rigidity Theory; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Balaji, R.R.B.; Bapat, R.B. On Euclidean distance matrices. Linear Algebra Appl. 2007, 424, 108–117. [Google Scholar] [CrossRef]
- Bapat, R.B. Graphs and Matrices; Springer: Berlin/Heidelberg, Germany, 2010; Volume 27. [Google Scholar]
- Gower, J.C. Properties of Euclidean and non-Euclidean distance matrices. Linear Algebra Appl. 1985, 67, 81–97. [Google Scholar] [CrossRef]
- Estrada, E. Conservative versus non-conservative diffusion toward a target in a networked environment. In Target Search Problems; Springer: Berlin/Heidelberg, Germany, 2024; pp. 511–540. [Google Scholar]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Lerman, K.; Ghosh, R. Network structure, topology, and dynamics in generalized models of synchronization. Phys. Rev. E 2012, 86, 026108. [Google Scholar] [CrossRef]
- JBarata, J.C.A.; Hussein, M.S. The Moore-Penrose pseudoinverse: A tutorial review of the theory. Braz. J. Phys. 2012, 42, 146–165. [Google Scholar] [CrossRef]
- Fontan, A.; Altafini, C. On the properties of Laplacian pseudoinverses. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5538–5543. [Google Scholar]
- Gutman, I.; Xiao, W. Generalized inverse of the Laplacian matrix and some applications. Bull. Acad. Serbe Sci. Arts Cl. Sci. Math. Nat. 2004, 15–23. [Google Scholar] [CrossRef]
- Saxena, A.; Tripathy, T.; Anguluri, R. Are the flows of complex-valued Laplacians and their pseudoinverses related? arXiv 2024, arXiv:2411.09254. [Google Scholar] [CrossRef]
- Van Mieghem, P. Graph Spectra for Complex Networks; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Devriendt, K. Effective resistance is more than distance: Laplacians, simplices and the Schur complement. Linear Algebra Appl. 2022, 639, 24–49. [Google Scholar] [CrossRef]
- Estrada, E. Is the pseudoinverse of the Laplacian a proper graph Laplacian? HAL Open Sci. 2025, preprint. [Google Scholar]
- Higham, N.J. Functions of Matrices: Theory and Computation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Marrero, J.A.; Ben Taher, R.; Rachidi, M. On explicit formulas for the principal matrix logarithm. Appl. Math. Comput. 2013, 220, 142–148. [Google Scholar] [CrossRef]
- De Abreu, N.M.M. Old and new results on algebraic connectivity of graphs. Linear Algebra Appl. 2007, 423, 53–73. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czech. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Andrade, E.; Dahl, G. Combinatorial Fiedler theory and graph partition. Linear Algebra Appl. 2024, 687, 229–251. [Google Scholar] [CrossRef]
- Song, H.; Wang, Q. Properties and applications of the eigenvector corresponding to the Laplacian spectral radius of a graph. Math. Probl. Eng. 2013, 2013, 524162. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrada, E. The Resistance Distance Is a Diffusion Distance on a Graph. Mathematics 2025, 13, 2380. https://doi.org/10.3390/math13152380
Estrada E. The Resistance Distance Is a Diffusion Distance on a Graph. Mathematics. 2025; 13(15):2380. https://doi.org/10.3390/math13152380
Chicago/Turabian StyleEstrada, Ernesto. 2025. "The Resistance Distance Is a Diffusion Distance on a Graph" Mathematics 13, no. 15: 2380. https://doi.org/10.3390/math13152380
APA StyleEstrada, E. (2025). The Resistance Distance Is a Diffusion Distance on a Graph. Mathematics, 13(15), 2380. https://doi.org/10.3390/math13152380





