Spectral Properties of the Harary Signless Laplacian and Harary Incidence Energy

Abstract

Let X be a partitioned matrix and let B its equitable quotient matrix. Consider a simple, undirected, connected graph G of order n. In this paper, we employ a technique based on quotient matrices derived from block-partitioned structures to establish new spectral results for the reciprocal distance signless Laplacian matrix. In particular, we identify a sequence of graphs whose eigenvalues are all integers. Furthermore, we introduce the concept of Harary incidence energy and extend known incidence energy results to the setting of the reciprocal distance signless Laplacian matrix. Finally, we characterize the Harary incidence energy of extremal graphs by examining vertex connectivity through the generalized graph join operation.

1. Introduction and Preliminaries

We begin by introducing the definition of an equitable quotient matrix and its associated spectral result, which will serve as a fundamental tool in the development of this work.

Definition 1

([1]). Let X be a complex matrix of order $n,$ described in the following block form

$$X=\left[\begin{array}{cccc}{X}_{1,1}& X_{1,2}& \dots & X_{1,r}\\ X_{2,1}& X_{2,2}& \dots & X_{2,r}\\ ⋮& ⋮& \ddots & ⋮\\ X_{r,1}& X_{r,2}& \dots & X_{r,r}\end{array}\right]$$

where the blocks $X_{i,j}$ are $n_i\times n_j$ matrices for any $1\le i,j\le r$ and $n=n_1+n_2+\cdots +n_r$. For $1\le i,j\le r$, let $b_{i,j}$ denote the average row sum of $X_{i,j}$, i.e., $b_{i,j}$ is the sum of all entries in $X_{i,j}$ divided by the number of rows. Then $B\left(X\right)=\left(b_{i,j}\right)$ is called the quotient matrix of X. If for each pair $i,j$, $X_{i,j}$ has a constant row sum, then $B\left(X\right)$ is called the equitable quotient matrix of X.

Theorem 1.

([2]). Let $B\left(X\right)$ be the equitable quotient matrix of X as defined in Definition 1. Then the spectrum of $B\left(X\right)$ is contained in the spectrum of X.

This work is motivated by the study of the spectral properties of matrices that are naturally associated with graphs. By employing quotient matrix techniques applied to block-partitioned matrices, we derive novel spectral results for the reciprocal distance signless Laplacian matrix and investigate its associated energy.

Throughout this paper, $G=(V,E)$ will denote a simple, undirected, connected graph with vertex set V and edge set E. The order of the graph is defined as the cardinality of its vertex set (denoted by $\left|V\right|$), while the size of the graph refers to the cardinality of its edge set (denoted by $\left|E\right|$). The matrix $A\left(G\right)$ denotes the adjacency matrix associated with the graph G of order n, whose eigenvalues are denoted by ${\lambda }_i\left(A\left(G\right)\right)$ for all $i=1,\dots ,n$.

The distance $d\left(v_i,v_j\right)=d_{i,j}$ between pairs of vertices $v_i$ and $v_j$ of G is defined as the length of the shortest path connecting $v_i$ and $v_j$. The neighbors of a vertex $v\in V$, denoted by $N\left(v\right)$, are all the vertices in V whose distance to v is equal to 1.

The Harary matrix of a graph G of order n, also known as the reciprocal distance matrix, is a matrix of order n that was independently introduced in [3,4], and is defined as

$$R{D}_{i,j}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{d\left(v_i,v_j\right)}}& \mathrm{if}i\ne j\\ 0& \mathrm{if}i=j.\end{array}\right.$$

Henceforward, we consider $i\ne j$ for $d\left(v_i,v_j\right)$.

The reciprocal distance degree of a vertex v, denoted by $RT\left(v\right)$, is given by

$$RT\left(v\right)=\sum _{\underset{u\ne v}{u\in V\left(G\right)}}{\displaystyle \frac{1}{d\left(u,v\right)}}.$$

We recall that a connected graph G is called a k-reciprocal distance degree regular graph if $R{T}_i=k$ for all $i\in \{1,2,\dots ,n\}$.

Let $RT\left(G\right)$ be the diagonal matrix $n\times n$ whose diagonal entries are denoted by $R{T}_{i,i}=R{T}_i=RT\left(v_i\right)$.

The Harary index of a graph G, denoted by $H\left(G\right)$, is defined in [3,4] as

$$H\left(G\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^n\sum _{j=1}^{n}R{D}_{i,j}={\displaystyle \frac{1}{2}}\sum _{\underset{u\ne v}{u,v\in V\left(G\right)}}{\displaystyle \frac{1}{d\left(u,v\right)}}.$$

Clearly,

$$H\left(G\right)={\displaystyle \frac{1}{2}}\sum _{v\in V\left(G\right)}RT\left(v\right).$$

In [5], the authors defined the reciprocal distance signless Laplacian matrix as

$$RQ\left(G\right)=RT\left(G\right)+RD\left(G\right).$$

Bounds for the spectral radius of the reciprocal distance signless Laplacian matrix were established in [6,7]. Furthermore, in [8], the authors provided bounds for the reciprocal distance signless Laplacian energy and characterized the graphs that attain some of these bounds. We mention some recent works on spectral radius and energy on matrices related to the distance and reciprocal distance are as follows: in [9] the authors show that the class of the complete bipartite graphs maximize the reciprocal distance Laplacian spectral radius among all the bipartite graphs with n vertices, and they show that the star graph is the unique graph having the maximum reciprocal distance Laplacian spectral radius in the class of trees with n vertices; in [10] bounds are obtained for the spectral radius and for the energy of the degree distance matrix and in [11] the authors obtain upper bounds for the reciprocal distance Laplacian spectral radius; moreover, they characterize the extremal graphs attaining this bound.

Furthermore, $RQ\left(G\right)$ is a real symmetric matrix, so we can write its eigenvalues in decreasing order

$${\lambda }_1\left(RQ\left(G\right)\right)\ge {\lambda }_2\left(RQ\left(G\right)\right)\ge \cdots \ge {\lambda }_{n-1}\left(RQ\left(G\right)\right)\ge {\lambda }_n\left(RQ\left(G\right)\right).$$

Since $RQ\left(G\right)$ is a non-negative matrix, its largest eigenvalue, ${\lambda }_1\left(RQ\left(G\right)\right)$ known as the Perron root, is denoted by $\rho \left(RQ\left(G\right)\right)$. Furthermore, as $RQ\left(G\right)$ is an irreducible matrix, so $\rho \left(RQ\left(G\right)\right)$ is a simple eigenvalue with a corresponding positive eigenvector.

Throughout this work, we adopt the following notations: ${\lambda }^{\left[t\right]}$ indicates that $\lambda$ is an eigenvalue with multiplicity t; ${\mathbf{e}}_i$ is the i-th canonical vector; ${\mathbf{1}}_n$ denotes the n-dimensional vector of ones; $I_n$ is the identity matrix of order n and $J_{r\times s}$ denotes the $r\times s$ matrix of ones. In particular, when $r=s$, we simply write $J_r=J_{r\times r}$.

Lemma 1

([7]). A connected graph G has only two distinct reciprocal distance signless Laplacian eigenvalues if and only if G is a complete graph. In particular, the $RQ\left(K_n\right)$-spectrum is $\{2(n-1),{(n-2)}^{[n-1]}\}$.

In [7], the authors established the following result.

Theorem 2.

([7]). Let G be a connected graph on n vertices and $m\ge n$ edges. Consider the connected graph $\tilde{G}$ obtained from G by the deletion of an edge. Let

$${\lambda }_1\left(RQ\left(G\right)\right),{\lambda }_2\left(RQ\left(G\right)\right),\dots ,{\lambda }_n\left(RQ\left(G\right)\right)$$

and

$${\lambda }_1\left(RQ\left(\tilde{G}\right)\right),{\lambda }_2\left(RQ\left(\tilde{G}\right)\right),\dots ,{\lambda }_n\left(RQ\left(\tilde{G}\right)\right)$$

be the reciprocal distance Laplacian spectra of G and $\tilde{G}$, respectively. Then, for all $i=1,\dots ,n$

$${\lambda }_i\left(RQ\left(\tilde{G}\right)\right)\le {\lambda }_i\left(RQ\left(G\right)\right).$$

An immediate consequence of Theorem 2 is presented in the following result.

Corollary 1.

Let G be a connected graph on n vertices. Then

$$\rho \left(RQ\right(G\left)\right)\le 2(n-1).$$

Theorem 3

([5]). Let G be a connected graph of order $n>2$. Then

$$\rho \left(RQ\left(G\right)\right)\ge {\displaystyle \frac{4H\left(G\right)}{n}}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

Theorem 4

([7]). Let G be a simple connected graph, such that, for $i=1,\dots ,n$, $R{T}_i$ is the reciprocal distance degree of vertex $v_i$. Then

$$\rho \left(RQ\left(G\right)\right)\ge 2\sqrt{{\displaystyle \frac{R{T}_1^2+R{T}_2^2+\cdots +R{T}_n^2}{n}}}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

2. Main Spectral Results

In this section, we present spectral results related to $RQ\left(G\right)$. Specifically, we characterize the spectrum of certain classes of graphs and investigate the spectral properties of the generalized join product of regular graphs. Using this construction, we explicitly determine the spectrum for specific graph families and, in particular, identify a sequence of graphs whose $RQ$-eigenvalues are all integers.

In graph theory, a pair of vertices u and v in G are called twins if they share the same neighborhood, with identical edge weights in the case of a weighted graph. Given u and v twin vertices, if $uv$ is an edge in G, they are called adjacent twins and if $uv$ is not an edge in G, they are called nonadjacent twins. The concept of twins has proven to be highly valuable in the study of graph spectra.

Theorem 5.

Let G be a connected graph of order n and U be a subset of $V\left(G\right)$ such that U is a set of nonadjacent twins, with $\left|U\right|=t>1$. Then $RT\left(v\right)=h$ is constant for each $v\in U$ and $\left(h-{\displaystyle \frac{1}{2}}\right)$ is an eigenvalue of $RQ\left(G\right)$ with multiplicity at least $t-1$.

Proof. 

Without loss of generality, we can label the vertices of U as $v_1,\dots ,v_t$. Then $d\left(v_i,v_k\right)=d\left(v_j,v_k\right)$ for all $v_i,v_j\in U$ and for all $v_k\in V\left(G\right)$, in particular, $d\left(v_i,v_j\right)=2$ for all $v_i,v_j\in U$. We note that $RT\left(v_i\right)=RT\left(v_j\right)$ for all $v_i,v_j\in U$. Let $h=RT\left(v_i\right)$ for all $v_i\in U$ and let $X_i={\mathbf{e}}_1-{\mathbf{e}}_{i+1}$ for $i=1,2,\dots ,t-1$. Then

$$RQ\left(G\right)X_i={\left[h-{\displaystyle \frac{1}{2}},0,\dots ,0,-h+{\displaystyle \frac{1}{2}},0,\dots ,0\right]}^T=\left(h-{\displaystyle \frac{1}{2}}\right)X_i.$$

Since $X_1,X_2,\dots ,X_{t-1}$ are linearly independent, $\left(h-{\displaystyle \frac{1}{2}}\right)$ is an eigenvalue of $RQ\left(G\right)$ with multiplicity at least $t-1$. □

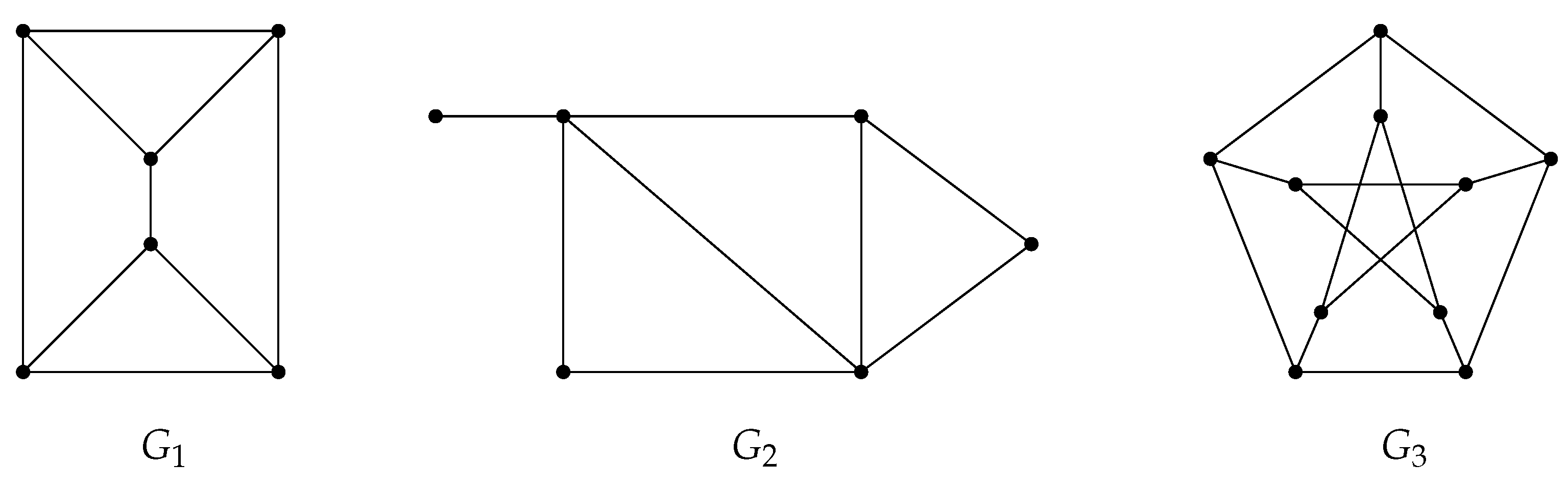
A double star graph, denoted as ${\mathcal{T}}_{a,b}$, is a graph formed by connecting the centers of the stars $S_{a+1}$ and $S_{b+1}$ with a single edge. We observe that all trees of diameter 3 are double star graphs (Figure 1).

Proposition 1.

Let ${\mathcal{T}}_{a,b}$ be a tree of diameter 3 and order $n=a+b+2\ge 4$. Then the $RQ$-eigenvalues are ${\left({\displaystyle \frac{3a+2b+3}{6}}\right)}^{[a-1]},{\left({\displaystyle \frac{2a+3b+3}{6}}\right)}^{[b-1]}$ together with the eigenvalues of the matrix

$$\left[\begin{array}{cccc}{\displaystyle \frac{6a+2b+3}{6}}& 1& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{b}{3}}\\ a& {\displaystyle \frac{2a+b+2}{2}}& 1& {\displaystyle \frac{b}{2}}\\ {\displaystyle \frac{a}{2}}& 1& {\displaystyle \frac{a+2b+2}{2}}& b\\ {\displaystyle \frac{a}{3}}& {\displaystyle \frac{1}{2}}& 1& {\displaystyle \frac{2a+6b+3}{6}}\end{array}\right].$$

Proof. 

Consider the following partition of the graph ${\mathcal{T}}_{a,b}$

$$\left\{V_1,\left\{u\right\},\left\{v\right\},V_2\right\}.$$

Clearly, $V_1$ and $V_2$ are independent sets to ${\mathcal{T}}_{a,b}$ such that for any $x,y\in V_1$, $N\left(x\right)=N\left(y\right)=u$ and for any $x,y\in V_2$, $N\left(x\right)=N\left(y\right)=v$.

We observe that for each vertex $v_i$ in $V_1$ we have that $R{T}_i={\displaystyle \frac{a-1}{2}}+1+{\displaystyle \frac{1}{2}}+{\displaystyle \frac{b}{3}}={\displaystyle \frac{3a+2b+6}{6}}$, analogously for each vertex $v_j$ in $V_2$, $R{T}_j={\displaystyle \frac{2a+3b+6}{6}}$. Then, using Theorem 5, we have that ${\displaystyle \frac{3a+2b+3}{6}}$ and ${\displaystyle \frac{2a+3b+3}{6}}$ are eigenvalues of $RQ\left({\mathcal{T}}_{a,b}\right)$ with multiplicities at least $a-1$ and $b-1$, respectively.

Let $R{T}_a={\displaystyle \frac{3a+2b+6}{6}}$ and $R{T}_b={\displaystyle \frac{2a+3b+6}{6}}$. Then $RQ\left({\mathcal{T}}_{a,b}\right)$ has the following block matrix form

$$RQ\left({\mathcal{T}}_{a,b}\right)=\left[\begin{array}{cccc}R{T}_{a}I+{\displaystyle \frac{1}{2}}[J_a-I_a]& \left[J_{a\times 1}\right]& {\displaystyle \frac{1}{2}}\left[J_{a\times 1}\right]& {\displaystyle \frac{1}{3}}\left[J_{a\times b}\right]\\ \left[J_{1\times a}\right]& {\displaystyle \frac{2a+b+2}{2}}& 1& {\displaystyle \frac{1}{2}}\left[J_{1\times b}\right]\\ {\displaystyle \frac{1}{2}}\left[J_{1\times a}\right]& 1& {\displaystyle \frac{a+2b+2}{2}}& \left[J_{1\times b}\right]\\ {\displaystyle \frac{1}{3}}\left[J_{b\times a}\right]& {\displaystyle \frac{1}{2}}\left[J_{b\times 1}\right]& \left[J_{b\times 1}\right]& R{T}_{b}I+{\displaystyle \frac{1}{2}}[J_b-I_b]\end{array}\right].$$

We observe that in the above equation, each block of the matrix $RQ\left({\mathcal{T}}_{a,b}\right)$ has a constant row sum. Then, if $B\left({\mathcal{T}}_{a,b}\right)$ denoted the equitable quotient matrix of $RQ\left({\mathcal{T}}_{a,b}\right)$, we have

$$B\left({\mathcal{T}}_{a,b}\right)=\left[\begin{array}{cccc}R{T}_a+{\displaystyle \frac{a-1}{2}}& 1& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{b}{3}}\\ a& R{T}_u& 1& {\displaystyle \frac{b}{2}}\\ {\displaystyle \frac{a}{2}}& 1& R{T}_v& b\\ {\displaystyle \frac{a}{3}}& {\displaystyle \frac{1}{2}}& 1& R{T}_b+{\displaystyle \frac{b-1}{2}}\end{array}\right].$$

Applying Theorem 1, the eigenvalues of $B\left({\mathcal{T}}_{a,b}\right)$ are eigenvalues of $RQ\left({\mathcal{T}}_{a,b}\right)$. Finally, replacing $R{T}_a={\displaystyle \frac{3a+2b+6}{6}}$, $R{T}_b={\displaystyle \frac{2a+3b+6}{6}}$, $R{T}_u={\displaystyle \frac{2a+b+2}{2}}$ and $R{T}_v={\displaystyle \frac{a+2b+2}{2}}$, the matrix given in Theorem is obtained. □

A bipartite graph is defined as a graph whose vertex set can be partitioned into two disjoint and independent subsets, denoted by $V_1$ and $V_2$, such that every edge joins a vertex of $V_1$ to a vertex of $V_2$. A notable example of a bipartite graph is the complete bipartite graph, in which each vertex in $V_1$ is adjacent to every vertex in $V_2$. A complete bipartite graph with $|V_1|=a$ and $|V_2|=b$ is denoted by $K_{a,b}$.

The following proposition establishes the eigenvalues of a complete bipartite graph with respect to the reciprocal distance signless Laplacian matrix.

Proposition 2.

Let $K_{a,b}$ be a complete bipartite graph on $n=a+b$ vertices. Then the spectrum of $RQ\left(K_{a,b}\right)$ is

$$\begin{array}{cc}\hfill \sigma \left(K_{a,b}\right)=& \left\{{\left({\displaystyle \frac{a+2b-2}{2}}\right)}^{\left[a-1\right]},{\left({\displaystyle \frac{2a+b-2}{2}}\right)}^{\left[b-1\right]},a+b-1+\sqrt{ab},a+b-1-\sqrt{ab}\right\}.\end{array}$$

Proof. 

Since $V_1$ and $V_2$ are independent sets to $K_{a,b}$ such that for any $x,y\in V_1$, $N\left(x\right)=N\left(y\right)=V_2$ and for any $x,y\in V_2$, $N\left(x\right)=N\left(y\right)=V_1$. Then for all $v_i\in V_1$ we obtain that $R{T}_i={\displaystyle \frac{a+2b-1}{2}}$ and for all vertices $v_j\in V_2$ we have that $R{T}_j={\displaystyle \frac{2a+b-1}{2}}$. Now, using Theorem 5, we have that ${\displaystyle \frac{a+2b-2}{2}}$ is an eigenvalue with multiplicity $a-1$ and ${\displaystyle \frac{2a+b-2}{2}}$ is an eigenvalue with multiplicity $b-1$.

Therefore, we have $n-2=a+b-2$ eigenvalues. We obtain the other two eigenvalues by applying the results of the quotient matrix given in Theorem 1. We will consider the following labeling of the vertices of $K_{a,b}$: we start by labeling the a vertices of the first independent set and end with the b vertices of the second independent set. Therefore, $RQ\left(K_{a,b}\right)$ has the following block form

$$\left[\begin{array}{cc}R{T}_a{I}_a+{\displaystyle \frac{1}{2}}\left(J_a-I_a\right)& J_{a\times b}\\ J_{b\times a}& R{T}_b{I}_b+{\displaystyle \frac{1}{2}}\left(J_b-I_b\right)\end{array}\right].$$

Notice that the four blocks have a constant row sum. Therefore, we can obtain from the equitable quotient matrix of $RQ\left(K_{a,b}\right)$

$$\left[\begin{array}{cc}a+b-1& b\\ a& a+b-1\end{array}\right].$$

Thus, the eigenvalues of this matrix are the remaining eigenvalues

$$a+b-1\pm \sqrt{ab}.$$

□

Corollary 2.

Let $S_n$ be the star graph on $n\ge 2$ vertices. Then the spectra of the reciprocal distance signless Laplacian matrix of $S_n$ is

$$\sigma \left(S_n\right)=\left\{n-1+\sqrt{n-1},{\left({\displaystyle \frac{n-1}{2}}\right)}^{\left[n-2\right]},n-1-\sqrt{n-1}\right\}.$$

Theorem 6.

Let G be a connected graph of order n and U be a subset of $V\left(G\right)$ such that U is a set of adjacent twins with $\left|U\right|=t>1$. Then $RT\left(v\right)=h^{\prime }$ is constant for each $v\in U$ and $\left(h^{\prime }-1\right)$ is an eigenvalue of $RQ\left(G\right)$ with multiplicity at least $t-1$.

Proof. 

Without loss of generality, we can label the vertices of U as $v_1,\dots ,v_t$. Then $d\left(v_i,v_k\right)=d\left(v_j,v_k\right)$ for all $v_i,v_j\in U$ and for all $v_k\in V\left(G\right)$, in particular, $d\left(v_i,v_j\right)=1$ for all $v_i,v_j\in U$. Thus $RT\left(v_i\right)=RT\left(v_j\right)$ for all $v_i,v_j\in U$. Let $h^{\prime }=RT\left(v_i\right)$ for all $v_i\in U$ and let $X_i={\mathbf{e}}_1-{\mathbf{e}}_{i+1}$ for $i=1,2,\dots ,t-1$. Then

$$RQ\left(G\right)X_i={\left[h^{\prime }-1,0,\dots ,0,-h^{\prime }+1,0,\dots ,0\right]}^T=\left(h^{\prime }-1\right)X_i.$$

Since $X_1,X_2,\dots ,X_{t-1}$ are linearly independent, $\left(h^{\prime }-1\right)$ is an eigenvalue of $RQ\left(G\right)$ with multiplicity at least $t-1$. □

A complete split graph, denoted by $C{S}_{a,n-a}$, is defined as a graph consisting of a clique on a vertices and an independent set on the remaining $n-a$ vertices, where each vertex in the clique is adjacent to every vertex in the independent set.

Proposition 3.

The eigenvalues of $RQ\left(C{S}_{a,n-a}\right)$ are

$${\left({\displaystyle \frac{n+a-2}{2}}\right)}^{\left[n-a-1\right]};{\left(n-2\right)}^{\left[a-1\right]};{\displaystyle \frac{2n+a-3\pm \sqrt{-3a^2+\left(4n-2\right)a+1}}{2}}.$$

Proof. 

Notice that the reciprocal degree distance of each vertex in the clique (of order a) is equal to $h^{\prime }=1\left(a-1\right)+1\left(n-a\right)=n-1$. Applying Theorem 6, we obtain that $n-2$ is $RQ$-eigenvalue of $C{S}_{a,n-a}$ with multiplicity at least $a-1$.

Analogously, for the independent set of order $n-a$ we have that $h={\displaystyle \frac{1}{2}}\left(n-a-1\right)+1\left(a\right)={\displaystyle \frac{\left(n+a-1\right)}{2}}.$ Applying the Theorem 5 we obtain that ${\displaystyle \frac{\left(n+a-1\right)}{2}}-{\displaystyle \frac{1}{2}}={\displaystyle \frac{\left(n+a-2\right)}{2}}$ is the $RQ$-eigenvalue of $C{S}_{a,n-a}$ with multiplicity at least $n-a-1$.

Thus, we have $n-2$ eigenvalues of $RQ\left(C{S}_{a,n-a}\right)$. We obtain the other two missing eigenvalues by applying the results of the quotient matrix given in Theorem 1. For this, we label the vertices of $C{S}_{a,n-a}$ in the following order: first the a vertices that form a clique, and then the $n-a$ independent vertices. Therefore, $RQ\left(C{S}_{a,n-a}\right)$ has the following block form

$$\begin{array}{ccc}\hfill RQ\left(C{S}_{a,n-a}\right)& =& \left[\begin{array}{cc}\left(n-1\right)I_a+J_a-I_a& J_{a\times \left(n-a\right)}\\ J_{\left(n-a\right)\times a}& {\displaystyle \frac{\left(n+a-1\right)}{2}}{I}_{n-a}+{\displaystyle \frac{1}{2}}\left(J_{n-a}-I_{n-a}\right)\end{array}\right]\hfill \\ & =& \left[\begin{array}{cc}\left(n-2\right)I_a+J_a& J_{a\times \left(n-a\right)}\\ J_{\left(n-a\right)\times a}& {\displaystyle \frac{\left(n+a-2\right)}{2}}{I}_{n-a}+{\displaystyle \frac{1}{2}}{J}_{n-a}\end{array}\right].\hfill \end{array}$$

We observe that the four blocks have a constant row sum. Therefore, the equitable quotient matrix of $RQ\left(C{S}_{a,n-a}\right)$ has the form

$$\left[\begin{array}{cc}n+a-2& n-a\\ a& n-1\end{array}\right].$$

Thus, the eigenvalues of this matrix

$${\displaystyle \frac{2n+a-3}{2}}\pm {\displaystyle \frac{\sqrt{-3a^2+\left(4n-2\right)a+1}}{2}}$$

are the remaining eigenvalues of $RQ\left(C{S}_{a,n-a}\right)$. □

Finally, in this section, we extend the spectral results for the reciprocal distance signless Laplacian matrix by employing the generalized join operation of graphs.

Let $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ be a two-vertex disjoint graph. The join of $G_1$ and $G_2$ is the graph $G=G_1\vee G_2$ such that $V\left(G\right)=V\left(G_1\right)\cup V\left(G_2\right)$ and $E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)\cup \{xy:x\in V\left(G_1\right),y\in V\left(G_2\right)\}$. This join operation can be generalized as follows [12]: Let $\mathcal{H}$ be a graph of order s. Let $V\left(\mathcal{H}\right)=\{v_1,\dots ,v_s\}$. Let $\{G_1,\dots ,G_s\}$ be a set of pairwise vertex-disjoint graphs. For $1\le i\le s$, the vertex $v_i\in V\left(\mathcal{H}\right)$ is assigned to the graph $G_i$. Let G be the graph obtained from the graphs $G_1,\dots ,G_s$ and the edges connecting each vertex of $G_i$ with all the vertices of $G_j$ if and only if $v_i,v_j\in E\left(\mathcal{H}\right)$. That is, G is the graph with the vertex set $V\left(G\right)={\bigcup }_{i=1}^{s}V\left(G_i\right)$ and the edge set

$$E\left(G\right)=\left(\bigcup _{i=1}^{s}E\left(G_i\right)\right)\bigcup \left(\bigcup _{v_i,v_j\in E\left(\mathcal{H}\right)}\{uv:u\in V\left(G_i\right),v\in V\left(G_j\right)\}\right).$$

This graph operation is denoted by

$$G=\underset{\mathcal{H}}{\bigvee }\{G_i:1\le i\le s\}.$$

The labeling of the vertices $1,\dots ,{\sum }_{i=1}^s{n}_i$ of G begins with the vertices of $G_1$, continuing with the vertices of $G_2,G_3,\dots ,G_{s-1}$ and finally with the vertices of $G_s$.

Let $\mathcal{H}$ be a connected graph of order $s,$ for $i=1,\dots ,s$, let $G_i$ be a ${\delta }_i$-degree regular connected graph of order $n_i$. Let $d_{i,j}^{\mathcal{H}}$ be the distance between $v_i,v_j\in V\left(\mathcal{H}\right)$. Here, with the above-mentioned labeling, the reciprocal distance signless Laplacian matrix of the $\mathcal{H}$-join $G={\displaystyle \underset{\mathcal{H}}{\bigvee }}\{G_i:1\le i\le s\}$ has the form

$$\begin{array}{ccc}\hfill RQ\left(G\right)& =& \left[\begin{array}{cccc}{Q}_1& {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{J}_{n_1\times n_2}& \dots & {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{J}_{n_1\times n_s}\\ {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{J}_{n_2\times n_1}& Q_2& & ⋮\\ ⋮& & \ddots & {\displaystyle \frac{1}{d_{s-1,s}^{\mathcal{H}}}}{J}_{n_{s-1}\times n_s}\\ {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{J}_{n_s\times n_1}& \dots & {\displaystyle \frac{1}{d_{s-1,s}^{\mathcal{H}}}}{J}_{n_s\times n_{s-1}}& Q_s\end{array}\right]\hfill \end{array}$$

(1)

where

$$Q_i=k_i{I}_{n_i}+{\displaystyle \frac{1}{2}}(J_{n_i}-I_{n_i}+A\left(G_i\right))$$

(2)

with

$$k_i={\displaystyle \frac{{\delta }_i+n_i-1}{2}}+\sum _{j\ne i}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}.$$

Notice that the matrices $Q_i$ defined in (2) are not necessarily the reciprocal distance signless Laplacian matrices $Q\left(G_i\right)$.

Thereby, using the results of the partitioned quotient matrix, we obtain the spectrum of the reciprocal distance signless Laplacian of the graph $G={\displaystyle \underset{\mathcal{H}}{\bigvee }}\{G_i:1\le i\le s\}$, where $\{G_1,\dots G_s\}$ is a family of regular graphs.

Lemma 2.

Let $Q_i$ be the diagonal blocks of the matrix defined in $\left(1\right)$ such that, for $i=1,\dots ,s$, $G_i$ is a ${\delta }_i$-regular connected graph of order $n_i$ with adjacency eigenvalues $\{{\delta }_i,{\lambda }_2,\dots ,{\lambda }_{n_i}\}$. Then the spectrum of $Q_i$ is

$$\sigma \left(Q_i\right)=\left\{{\delta }_i+n_i-1+\sum _{j\ne i}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}},k_i-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_2\left(A\left(G_i\right)\right),\dots ,k_i-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_{n_i}\left(A\left(G_i\right)\right)\right\},$$

with $k_i={\displaystyle \frac{{\delta }_i+n_i-1}{2}}+{\displaystyle \sum _{j\ne i}}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}$.

Proof. 

Since

$$Q_i=k_i{I}_{n_i}+{\displaystyle \frac{1}{2}}\left(J_{n_i}-I_{n_i}+A\left(G_i\right)\right)$$

is a non-negative matrix with constant row sum equal to $k_i+{\displaystyle \frac{n_i-1+{\delta }_i}{2}}$, where $k_i={\displaystyle \frac{{\delta }_i+n_i-1}{2}}+\sum _{j\ne i}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}$, then

$$Q_i{\mathbf{1}}_{n_i}=\left({\delta }_i+n_i-1+\sum _{j\ne i}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}\right){\mathbf{1}}_{n_i}.$$

Thus, the Perron eigenvalue of $Q_i$ is

$${\lambda }_1\left(Q_i\right)={\delta }_i+n_i-1+\sum _{j\ne i}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}.$$

Now, let $\{{\mathbf{1}}_{n_i},{\mathbf{u}}_{i,2},\dots ,{\mathbf{u}}_{i,n_i}\}$ be the orthogonal set of eigenvectors corresponding to the adjacency eigenvalues of the regular graph $G_i$, $\{{\delta }_i,{\lambda }_2,\dots ,{\lambda }_{n_i}\}$, respectively. We observe that, for $j=2,\dots ,n_i$, $J_{n_i}{\mathbf{u}}_{i,j}=0{\mathbf{u}}_{i,j}$ and $A\left(G_i\right){\mathbf{u}}_{i,j}={\lambda }_j{\mathbf{u}}_{i,j}$. Then

$$\begin{array}{ccc}\hfill Q_i{\mathbf{u}}_{i,j}& =& \left(k_i{I}_{n_i}+{\displaystyle \frac{1}{2}}(J_{n_i}-I_{n_i}+A\left(G_i\right))\right){\mathbf{u}}_{i,j}\hfill \\ & =& \left(k_i-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_j\right){\mathbf{u}}_{i,j}.\hfill \end{array}$$

Therefore, for $i=1,\dots ,s$ the spectrum of $Q_i$ is

$$\sigma \left(Q_i\right)=\left\{{\delta }_i+n_i-1+\sum _{j\ne i}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}},k_i-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_2\left(A\left(G_i\right)\right),\dots ,k_i-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_{n_i}\left(A\left(G_i\right)\right)\right\},$$

(3)

with $k_i={\displaystyle \frac{{\delta }_i+n_i-1}{2}}+{\displaystyle \sum _{j\ne i}}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}$. □

The following result is immediate.

Theorem 7.

Let $\mathcal{H}$ be a connected graph of order s and $G={\displaystyle \underset{\mathcal{H}}{\bigvee }}\{G_i:1\le i\le s\}$ where for each $i\in \{1,\dots ,s\}$, $G_i$ is a regular graph. Then, the spectrum of $RQ\left(G\right)$ is

$$\sigma \left(RQ\left(G\right)\right)=\bigcup _{i=1}^s\left(\sigma \left(Q_i\right)\setminus \left\{{\lambda }_1\left(Q_i\right)\right\}\right)\cup \sigma \left(F_s\right),$$

where ${\lambda }_1\left(Q_i\right)={\delta }_i+n_i-1+{\displaystyle \sum _{j\ne i}}{\displaystyle \frac{n_j}{d_{i,j}^{\mathcal{H}}}}$ and $F_s$ is the $s\times s$ matrix

$$F_s=\left[\begin{array}{cccccc}{\lambda }_1\left(Q_1\right)& {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{n}_2& {\displaystyle \frac{1}{d_{1,3}^{\mathcal{H}}}}{n}_3& \dots & {\displaystyle \frac{1}{d_{1,(s-1)}^{\mathcal{H}}}}{n}_{s-1}& {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{n}_s\\ {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{n}_1& {\lambda }_1\left(Q_2\right)& {\displaystyle \frac{1}{d_{2,3}^{\mathcal{H}}}}{n}_3& \dots & {\displaystyle \frac{1}{d_{2,(s-1)}^{\mathcal{H}}}}{n}_{s-1}& {\displaystyle \frac{1}{d_{2,s}^{\mathcal{H}}}}{n}_s\\ {\displaystyle \frac{1}{d_{1,3}^{\mathcal{H}}}}{n}_1& {\displaystyle \frac{1}{d_{2,3}^{\mathcal{H}}}}{n}_2& {\lambda }_1\left(Q_3\right)& \dots & {\displaystyle \frac{1}{d_{3,(s-1)}^{\mathcal{H}}}}{n}_{s-1}& {\displaystyle \frac{1}{d_{3,s}^{\mathcal{H}}}}{n}_s\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ {\displaystyle \frac{1}{d_{1,(s-1)}^{\mathcal{H}}}}{n}_1& {\displaystyle \frac{1}{d_{2,(s-1)}^{\mathcal{H}}}}{n}_2& {\displaystyle \frac{1}{d_{3,(s-1)}^{\mathcal{H}}}}{n}_3& \dots & {\lambda }_1\left(Q_{s-1}\right)& {\displaystyle \frac{1}{d_{(s-1),s}^{\mathcal{H}}}}{n}_s\\ {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{n}_1& {\displaystyle \frac{1}{d_{2,s}^{\mathcal{H}}}}{n}_2& {\displaystyle \frac{1}{d_{3,s}^{\mathcal{H}}}}{n}_3& \dots & {\displaystyle \frac{1}{d_{s-1,s}^{\mathcal{H}}}}{n}_{s-1}& {\lambda }_1\left(Q_s\right)\end{array}\right].$$

Proof. 

Let $G_i$ be a ${\delta }_i$-regular graph such that $\{{\mathbf{u}}_{i,1}={\mathbf{1}}_{n_i},{\mathbf{u}}_{i,2},\dots ,{\mathbf{u}}_{i,n_i}\}$ is a set of eigenvectors corresponding to the adjacency eigenvalues $\{{\delta }_i,{\lambda }_{i,2},\dots ,{\lambda }_{i,n_i}\}$. Then, using Lemma 2 we have that, for $j=2,\dots ,n_i$,

$$\begin{array}{ccc}\hfill RQ\left(G\right)\left[\begin{array}{c}0\\ ⋮\\ 0\\ {\mathbf{u}}_{i,j}\\ 0\\ ⋮\\ 0\end{array}\right]& =& \left[\begin{array}{cccc}{Q}_1& {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{J}_{n_1\times n_2}& \dots & {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{J}_{n_1\times n_s}\\ {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{J}_{n_2\times n_1}& Q_2& & ⋮\\ ⋮& & \ddots & {\displaystyle \frac{1}{d_{s-1,s}^{\mathcal{H}}}}{J}_{n_{s-1}\times n_s}\\ {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{J}_{n_s\times n_1}& \dots & {\displaystyle \frac{1}{d_{s-1,s}^{\mathcal{H}}}}{J}_{n_s\times n_{s-1}}& Q_s\end{array}\right]\left[\begin{array}{c}0\\ ⋮\\ 0\\ {\mathbf{u}}_{i,j}\\ 0\\ ⋮\\ 0\end{array}\right]\hfill \\ & =& \left(k_i-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_j\right)\left[\begin{array}{c}0\\ ⋮\\ 0\\ {\mathbf{u}}_{i,j}\\ 0\\ ⋮\\ 0\end{array}\right].\hfill \end{array}$$

Therefore, for $i=1,\dots ,s$ and for $j=2,\dots ,n_i$,

$$\left(\sigma \left(Q_i\right)\setminus \left\{{\lambda }_1\left(Q_i\right)\right\}\right)\subset \sigma \left(RQ\left(G\right)\right).$$

In the proof of Lemma 2, we mentioned that, for $i=1,\dots ,s$, the matrices $Q_i$ have constant row sum. Thus, it is easy to see that all blocks of the matrix $RQ\left(G\right)$, given in the Equation (1), have a constant row sum. Therefore, the remaining eigenvalues of $RQ\left(G\right)$ will be obtained from its quotient matrix, where the equitable quotient matrix of $RQ\left(G\right)$ is

$$F_s=\left[\begin{array}{cccccc}{\lambda }_1\left(Q_1\right)& {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{n}_2& {\displaystyle \frac{1}{d_{1,3}^{\mathcal{H}}}}{n}_3& \dots & {\displaystyle \frac{1}{d_{1,(s-1)}^{\mathcal{H}}}}{n}_{s-1}& {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{n}_s\\ {\displaystyle \frac{1}{d_{1,2}^{\mathcal{H}}}}{n}_1& {\lambda }_1\left(Q_2\right)& {\displaystyle \frac{1}{d_{2,3}^{\mathcal{H}}}}{n}_3& \dots & {\displaystyle \frac{1}{d_{2,(s-1)}^{\mathcal{H}}}}{n}_{s-1}& {\displaystyle \frac{1}{d_{2,s}^{\mathcal{H}}}}{n}_s\\ {\displaystyle \frac{1}{d_{1,3}^{\mathcal{H}}}}{n}_1& {\displaystyle \frac{1}{d_{2,3}^{\mathcal{H}}}}{n}_2& {\lambda }_1\left(Q_3\right)& \dots & {\displaystyle \frac{1}{d_{3,(s-1)}^{\mathcal{H}}}}{n}_{s-1}& {\displaystyle \frac{1}{d_{3,s}^{\mathcal{H}}}}{n}_s\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ {\displaystyle \frac{1}{d_{1,(s-1)}^{\mathcal{H}}}}{n}_1& {\displaystyle \frac{1}{d_{2,(s-1)}^{\mathcal{H}}}}{n}_2& {\displaystyle \frac{1}{d_{3,(s-1)}^{\mathcal{H}}}}{n}_3& \dots & {\lambda }_1\left(Q_{s-1}\right)& {\displaystyle \frac{1}{d_{(s-1),s}^{\mathcal{H}}}}{n}_s\\ {\displaystyle \frac{1}{d_{1,s}^{\mathcal{H}}}}{n}_1& {\displaystyle \frac{1}{d_{2,s}^{\mathcal{H}}}}{n}_2& {\displaystyle \frac{1}{d_{3,s}^{\mathcal{H}}}}{n}_3& \dots & {\displaystyle \frac{1}{d_{s-1,s}^{\mathcal{H}}}}{n}_{s-1}& {\lambda }_1\left(Q_s\right)\end{array}\right].$$

Then, applying Theorem 1, we obtain that

$$\sigma \left(F_s\right)\subset \sigma \left(RQ\left(G\right)\right).$$

□

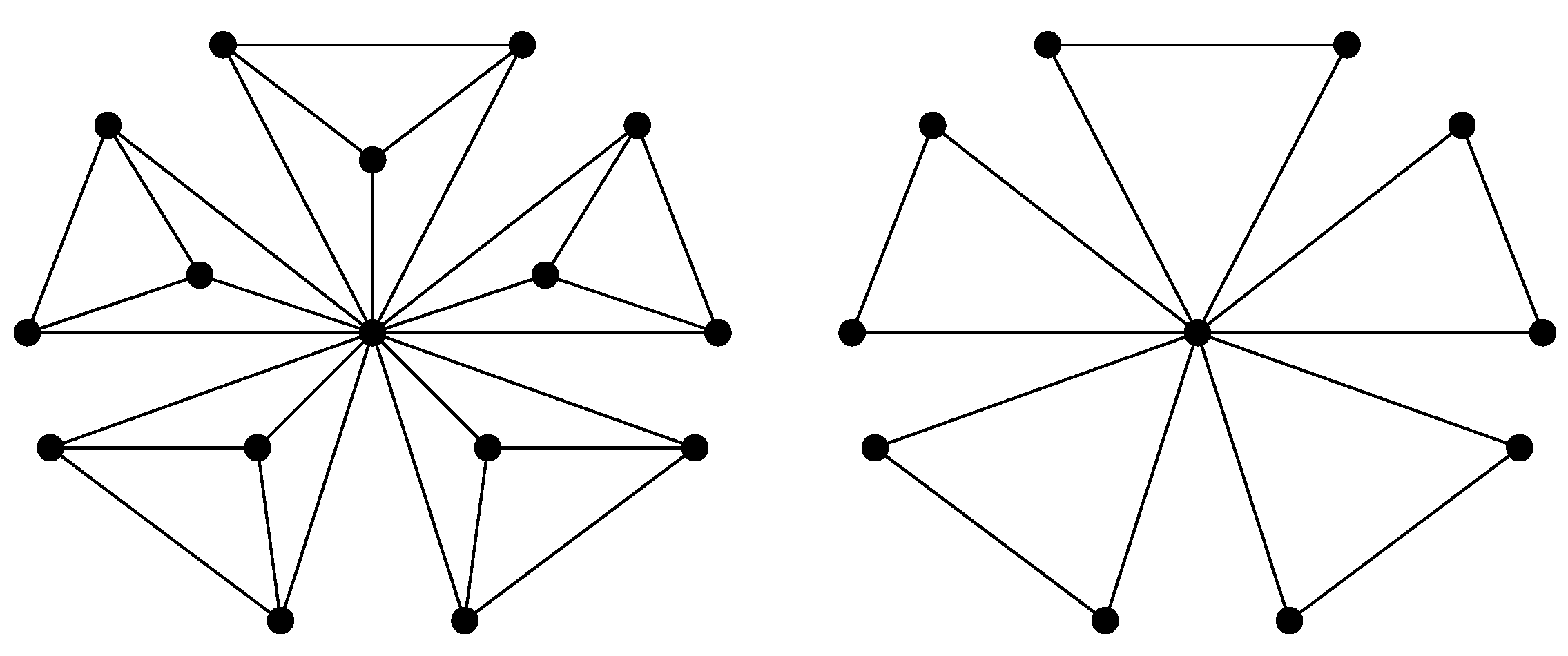
Example 1.

For $\mathcal{H}=P_5$, $G_1=C_5$, $G_2=P_2$, $G_3=K_4$, $G_4=C_4$ and $G_5=K_3$ the graph $G=\underset{P_5}{\bigvee }\{G_1,G_2,G_3,G_4,G_5\}$ is given in Figure 2.

Thus, the matrices given in Theorem 7 are

$$\begin{array}{cc}\hfill Q_1& =\left[\begin{array}{ccccc}{\displaystyle \frac{109}{12}}& 1& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1\\ 1& {\displaystyle \frac{109}{12}}& 1& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{1}{2}}& 1& {\displaystyle \frac{109}{12}}& 1& {\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1& {\displaystyle \frac{109}{12}}& 1\\ 1& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& 1& {\displaystyle \frac{109}{12}}\end{array}\right]Q_2=\left[\begin{array}{cc}13& 1\\ 1& 13\end{array}\right]\hfill \\ \hfill Q_3& =\left[\begin{array}{cccc}13& 1& 1& 1\\ 1& 13& 1& 1\\ 1& 1& 13& 1\\ 1& 1& 1& 13\end{array}\right]Q_4=\left[\begin{array}{cccc}{\displaystyle \frac{73}{6}}& 1& {\displaystyle \frac{1}{2}}& 1\\ 1& {\displaystyle \frac{73}{6}}& 1& {\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{1}{2}}& 1& {\displaystyle \frac{73}{6}}& 1\\ 1& {\displaystyle \frac{1}{2}}& 1& {\displaystyle \frac{73}{6}}\end{array}\right]\hfill \\ \hfill Q_5& =\left[\begin{array}{ccc}{\displaystyle \frac{107}{12}}& 1& 1\\ 1& {\displaystyle \frac{107}{12}}& 1\\ 1& 1& {\displaystyle \frac{107}{12}}\end{array}\right]F_5=\left[\begin{array}{ccccc}12.083& 2& 2& {\displaystyle \frac{4}{3}}& {\displaystyle \frac{3}{4}}\\ 5& 14& 4& 2& 1\\ {\displaystyle \frac{5}{2}}& 2& 16& 4& {\displaystyle \frac{3}{2}}\\ {\displaystyle \frac{5}{3}}& 1& 4& 14.667& 3\\ {\displaystyle \frac{5}{4}}& {\displaystyle \frac{2}{3}}& 2& 4& 10.917\end{array}\right]\hfill \end{array}$$

Using three decimal places, we have

$$\begin{array}{cc}\hfill \sigma \left(Q_1\right)& =\{12.083,8.{892}^{\left[2\right]},7.{774}^{\left[2\right]}\},\hfill \\ \hfill \sigma \left(Q_2\right)& =\{14,12\},\hfill \\ \hfill \sigma \left(Q_3\right)& =\{16,{12}^{\left[3\right]}\},\hfill \\ \hfill \sigma \left(Q_4\right)& =\{14.667,11.{667}^{\left[2\right]},10.667\},\hfill \\ \hfill \sigma \left(Q_5\right)& =\{10.917,7.{917}^{\left[2\right]}\}\hfill \end{array}$$

Therefore, applying Theorem 7, we conclude that

$$\begin{array}{c}\hfill \sigma \left(RQ\left(G\right)\right)=\{23.284,14.196,{12}^{\left[4\right]},11.714,11.{667}^{\left[2\right]},10.667,\\ \hfill 9.702,8.{892}^{\left[2\right]},8.771,7.{917}^{\left[2\right]},7.{774}^{\left[2\right]}\}.\end{array}$$

A wheel graph on $n\ge 4$ vertices, denoted by $W_n$, is a graph formed by connecting a single vertex to all vertices of a cycle of order $n-1$. It can be observed that $W_n=K_1\vee C_{n-1}$.

A generalized wheel graph on n vertices, denoted by $G{W}_{a,n-a}$, is a graph consisting of an independent set of order a and a cycle of the remaining $n-a$ vertices, such that each vertex in the cycle is adjacent to every vertex in the independent set. This graph can be expressed as the join product of two graphs or as a generalized join product:

$$G{W}_{a,n-a}=\overline{K_a}\bigvee C_{n-a}=\underset{S_{a+1}}{\bigvee }\{C_{n-a},K_1,K_1,\dots ,K_1\},$$

where for the expression on the right, the central vertex of $S_{a+1}$ is assigned to $C_{n-a}$ and each pending vertex of $S_{a+1}$ is assigned to $K_1$.

Since $\overline{K_a}$ is not a connected graph, and our definition of the join product is for connected graphs, ensuring that the distance between components is not indeterminate, we use the notation:

$$G{W}_{a,n-a}=\underset{S_{a+1}}{\bigvee }\{C_{n-a},K_1,K_1,\dots ,K_1\}.$$

Proposition 4.

Let $G{W}_{a,n-a}$ be a generalized wheel graph on n vertices. Then the eigenvalues of $RQ\left(G{W}_{a,n-a}\right)$ are ${\left({\displaystyle \frac{2n-a-2}{2}}\right)}^{[a-1]}$, $n\pm \sqrt{1+na-a^2}$ together with the eigenvalues of the form $\left({\displaystyle \frac{n+a}{2}}+cos\left({\displaystyle \frac{2\pi (n-a+1-j)}{n-a}}\right)\right)$ for $j=2,\dots ,n-a$.

Proof. 

The generalized join operation

$$G{W}_{a,n-a}=\underset{S_{a+1}}{\bigvee }\{C_{n-a},K_1,K_1,\dots ,K_1\},$$

we associate the cycle to the central vertex of the star and each vertex $K_1$ is associated with the pending vertices of the star. Considering the labeling in this same order, we have that the expressions given in (1) and (2), for the graph $G{W}_{a,n-a}$ are

$$\begin{array}{ccc}\hfill RQ\left(G{W}_{a,n-a}\right)& =& \left[\begin{array}{ccccc}{Q}_1& J_{n-a\times 1}& J_{n-a\times 1}& \dots & J_{n-a\times 1}\\ J_{1\times n-a}& Q_2& {\displaystyle \frac{1}{2}}& \dots & {\displaystyle \frac{1}{2}}\\ J_{1\times n-a}& {\displaystyle \frac{1}{2}}& Q_3& \ddots & ⋮\\ ⋮& ⋮& \ddots & \ddots & {\displaystyle \frac{1}{2}}\\ J_{1\times n-a}& {\displaystyle \frac{1}{2}}& \dots & {\displaystyle \frac{1}{2}}& Q_{a+1}\end{array}\right]\hfill \end{array}$$

where

$$Q_1={\displaystyle \frac{n+a+1}{2}}{I}_{n-a}+(J_{n-a}-I_{n-a}+A\left(C_{n-a}\right)),$$

and

$$Q_2=\cdots =Q_{a+1}={\left[{\displaystyle \frac{2n-a-1}{2}}\right]}_{1\times 1}.$$

Now, expression (3) for $Q_1$ becomes

$$\sigma \left(Q_1\right)=\left\{n+1,{\displaystyle \frac{n+a}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_{n-a}\left(A\left(C_{n-a}\right)\right),\dots ,{\displaystyle \frac{n+a}{2}}+{\displaystyle \frac{1}{2}}{\lambda }_2\left(A\left(C_{n-a}\right)\right)\right\},$$

Since the adjacency eigenvalues of the cycle of order p have the form $2cos\left({\displaystyle \frac{2\pi (p+1-j)}{p}}\right)$, then, from Theorem 7, for $j=2,\dots ,n-a$, we have that $\left({\displaystyle \frac{n+a}{2}}+cos\left({\displaystyle \frac{2\pi (n-a+1-j)}{n-a}}\right)\right)$ are eigenvalues of $RQ\left(G{W}_{a,n-a}\right)$.

Now, the matrix $F_s$ given in Theorem 7 has the form

$$F_{a+1}=\left[\begin{array}{cccccc}n+1& 1& 1& \dots & 1& 1\\ (n-a)& {\displaystyle \frac{2n-a-1}{2}}& {\displaystyle \frac{1}{2}}& \dots & {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\\ (n-a)& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{2n-a-1}{2}}& \dots & {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\\ ⋮& ⋮& & \ddots & & ⋮\\ (n-a)& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& \dots & {\displaystyle \frac{2n-a-1}{2}}& {\displaystyle \frac{1}{2}}\\ (n-a)& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}& \dots & {\displaystyle \frac{1}{2}}& {\displaystyle \frac{2n-a-1}{2}}\end{array}\right].$$

(4)

We recall that ${\mathbf{e}}_i$ denotes the i-th canonical vector. Then, for $i=3,\dots ,a+1$

$$F_{a+1}[{\mathbf{e}}_2-{\mathbf{e}}_i]={\displaystyle \frac{2n-a-2}{2}}\left[{\mathbf{e}}_2-{\mathbf{e}}_i\right].$$

Thus, ${\displaystyle \frac{2n-a-2}{2}}$ is an eigenvalue of $F_{a+1}$ with multiplicity $a-1$. From Theorem 7, we have that ${\displaystyle \frac{2n-a-2}{2}}$ is an eigenvalue of $RQ\left(G{W}_{a,n-a}\right)$ with multiplicity $a-1$.

We observe that the matrix $F_{a+1}$ given in (4) can be written in blocks as

$$F_{a+1}=\left[\begin{array}{cc}n+1& {\mathbf{1}}_a^T\\ (n-a){\mathbf{1}}_a& {\displaystyle \frac{2n-a-2}{2}}{I}_a+{\displaystyle \frac{1}{2}}{J}_a\end{array}\right],$$

where the four blocks have constant row sum. Thus, we can obtain the following equitable quotient matrix

$$\left[\begin{array}{cc}n+1& a\\ n-a& n-1\end{array}\right]$$

which has $n\pm \sqrt{1+na-a^2}$ as eigenvalues. From Theorems 1 and 7, we have that these eigenvalues are eigenvalues of $RQ\left(G{W}_{a,n-a}\right)$. □

Corollary 3.

Let $W_n$ be a wheel graph on n vertices. Then, the eigenvalues of $RQ\left(W_n\right)$ are 0, $2n$ together with the eigenvalues of the form $\left({\displaystyle \frac{n+1}{2}}+cos\left({\displaystyle \frac{2\pi (n-j)}{n-1}}\right)\right)$, for $j=2,\dots ,n-1$.

A friendship graph is a connected graph such that every pair of vertices has exactly one common neighbor. The triangle graph is the smallest order example of a friendship graph. The friendship graph of order $n=2p+1$ vertices, denoted by ${\mathcal{F}}_{2p+1}$, can be obtained from p copies of the cycle graph $C_3$ identifying a common vertex.

A windmill graph, denoted by $Wd(r+1,p)$, is a graph constructed for p copies of the complete graph $K_{r+1}$ identifying a common vertex. We observe that the friendship graph ${\mathcal{F}}_{2p+1}$ is isomorphic to $Wd(3,p)$. For examples of windmill graph and friendship graph, see Figure 3.

Proposition 5.

Let $Wd(r+1,p)$ be a windmill graph on $n=rp+1$ vertices. Then the spectrum of $RQ\left(Wd\right(r+1,p\left)\right)$ is

$$\left\{{{\displaystyle \frac{r(p+1)-2}{2}}}^{\left[p\right(r-1\left)\right]},{{\displaystyle \frac{r(p+2)-2}{2}}}^{[p-1]},{\displaystyle \frac{2rp+r-1\pm \sqrt{4rp+{(r-1)}^2}}{2}}\right\}.$$

Proof. 

Let $K_r$ be the complete graph of order r. We observe that

$$Wd(r+1,p)=\underset{S_{p+1}}{\bigvee }\{K_1,K_r,K_r,\dots ,K_r\},$$

where the central vertex of $S_{p+1}$ is assigned to $K_1$ and each pending vertex of $S_{p+1}$ is assigned to $K_r$. Considering the labeling in this same order, we have that

$$\begin{array}{ccc}\hfill RQ\left(Wd\right(r+1,p\left)\right)& =& \left[\begin{array}{ccccc}{Q}_1& {\mathbf{1}}_r^T& {\mathbf{1}}_r^T& \dots & {\mathbf{1}}_r^T\\ {\mathbf{1}}_r& Q_2& {\displaystyle \frac{1}{2}}{J}_r& \dots & {\displaystyle \frac{1}{2}}{J}_r\\ {\mathbf{1}}_r& {\displaystyle \frac{1}{2}}{J}_r& Q_3& \ddots & ⋮\\ ⋮& ⋮& \ddots & \ddots & {\displaystyle \frac{1}{2}}{J}_r\\ {\mathbf{1}}_r& {\displaystyle \frac{1}{2}}{J}_r& \dots & {\displaystyle \frac{1}{2}}{J}_r& Q_{p+1}\end{array}\right]\hfill \end{array}$$

where

$$Q_1={\left[rp\right]}_{1\times 1}$$

and

$$Q_2=\cdots =Q_{p+1}={\displaystyle \frac{r(p+1)}{2}}{I}_r+(J_r-I_r).$$

For $j=2,\dots ,p+1$, the spectrum of $Q_j$ is

$$\left\{{\displaystyle \frac{rp+3r-2}{2}},{{\displaystyle \frac{rp+r-2}{2}}}^{[r-1]}\right\}.$$

Thus, from Theorem 7 we have that ${\displaystyle \frac{r(p-1)-2}{2}}$ is an eigenvalue of $RQ\left(Wd\right(r+1,p\left)\right)$ with multiplicity $p(r-1)$, and the matrix $F_s$ can be written in blocks as

$$F_{p+1}=\left[\begin{array}{cc}rp& r{\mathbf{1}}_p^T\\ {\mathbf{1}}_p& {\displaystyle \frac{rp+3r-2}{2}}{I}_p+{\displaystyle \frac{r}{2}}(J_p-I_p)\end{array}\right].$$

We observe that, for $i=3,\dots ,p+1$

$$F_{p+1}[{\mathbf{e}}_2-{\mathbf{e}}_i]={\displaystyle \frac{rp+2r-2}{2}}\left[{\mathbf{e}}_2-{\mathbf{e}}_i\right].$$

Thus, ${\displaystyle \frac{r(p+2)-2}{2}}$ is an eigenvalue of $F_{p+1}$ with multiplicity $p-1$. From Theorem 7, we have that ${\displaystyle \frac{r(p+2)-2}{2}}$ is an eigenvalue of $RQ\left(Wd\right(r+1,p\left)\right)$ with multiplicity $p-1$.

Now, we observe that the four blocks of $F_{p+1}$ have a constant row sum, then we can obtain the following equitable quotient matrix

$$\left[\begin{array}{cc}rp& rp\\ 1& r(p+1)-1\end{array}\right]$$

which has ${\displaystyle \frac{2pr+r-1\pm \sqrt{4pr+{\left(r-1\right)}^2}}{2}}$ as eigenvalues. From Theorems 1 and 7, we have that these eigenvalues are eigenvalues of $RQ\left(Wd\right(r+1,p\left)\right)$. □

Since the friendship graph ${\mathcal{F}}_{2p+1}$ is isomorphic to $Wd(3,p)$, the following result is immediate.

Corollary 4.

Let ${\mathcal{F}}_{2p+1}$ be a friendship graph on the $n=2p+1$ vertices. Then the spectrum of $RQ\left({\mathcal{F}}_{2p+1}\right)$ is

$$\left\{p^{\left[p\right]},p+1^{[p-1]},{\displaystyle \frac{4p+1\pm \sqrt{8p+1}}{2}}\right\}.$$

We recall that a graph is an M-integral graph if the matrix M associated with the graph has only integer eigenvalues. From the above result, we can obtain the following Theorem.

Theorem 8.

Let G be a friendship graph of order n. The friendship graph is an $RQ$-integral graph when n belongs to the sequence ${\left\{3,7,13,21,31,43,\dots ,k^2+k+1,\dots \right\}}_{k\in \mathbb{N}}$.

Proof. 

Since $n=k^2+k+1$ if and only if $p={\displaystyle \frac{k(k+1)}{2}}$, then $\sqrt{8p+1}$ is an odd number. Therefore, all the eigenvalues given in Corollary 4 are integers. □

3. Bounds for Harary Incidence Energy

In this section, we derive results concerning the reciprocal distance signless Laplacian energy by employing a technique based on the quotient matrix of a block-partitioned matrix. Additionally, we extend the notion of incidence energy to the reciprocal distance signless Laplacian matrix by introducing the concept of Harary incidence energy, denoted by $HIE\left(G\right)$, and defined as follows:

$$HIE\left(G\right)=\sum _{i=1}^n\sqrt{{\lambda }_i\left(RQ\left(G\right)\right)}.$$

Finally, we characterize the Harary incidence energy of graphs with a given vertex connectivity using the generalized graph join operation.

The concept of graph energy originates in theoretical chemistry. In 1978, Ivan Gutman [13] introduced the energy of a graph in terms of the eigenvalues of its adjacency matrix, defined by

$$E\left(G\right)=\sum _{i=1}^n\left|{\lambda }_i\left(A\left(G\right)\right)\right|.$$

This invariant has been widely studied in mathematical chemistry as an approximation of the total $\pi$-electron energy of a molecule [14,15,16]. Over time, it has become evident that the relevance of this graph parameter extends well beyond chemistry. For example, it has been investigated in the context of extremal problems with respect to minimum and maximum energy within specific graph families [17,18,19], as well as in the derivation of upper and lower bounds for graph energy [20,21,22,23], and in the bounding the energy of the Harary matrix and its Laplacian variants [7,24].

Furthermore, in [25], the authors provide an overview of numerous works published in 2019 related to graph energy and summarize their key contributions. Notably, they emphasize applications of graph energy beyond the realm of mathematics. For example, in [26], the authors apply this concept to topics related to climate change. They construct a graph where the vertices represent concepts such as soil, climate, hydrogeomorphic features, and biotic features, connected by directed or undirected edges. In this context, the energy of the graph reflects the overall strength of positive and negative feedback loops of the system.

In 2009, Jooyandeh et al. [27] introduced the concept of incidence energy, defined as the sum of the singular values of the vertex–edge incidence matrix $I\left(G\right)$. This matrix, of size $n\times m$, has entries $(i,j)$ equal to 1 if vertex $v_i$ is incident to the edge $e_j$, and 0 otherwise.

The singular values of a matrix M are the non-negative square roots of the eigenvalues of $M{M}^T$. Since $M{M}^T$ and $M^{T}M$ share the same non-zero eigenvalues, the authors of [28,29] concluded that the incidence energy can be calculated as

$$IE\left(G\right)=\sum _{i=1}^n\sqrt{q_i\left(G\right)},$$

where $q_1\left(G\right)\ge q_2\left(G\right)\ge \cdots \ge q_n\left(G\right)$ are the signless Laplacian eigenvalues of G.

The vertex connectivity of a graph G, denoted by $\kappa \left(G\right)$, is the minimum number of vertices of G whose deletion disconnects G. It is conventional to define $\kappa \left(K_n\right)=n-1$.

Remark 1.

If $\tilde{G}$ is the connected graph obtained from G by deleting an edge, then from the definition of the reciprocal distance signless Laplacian matrix, we obtain $trace\left(RQ\left(\tilde{G}\right)\right)<trace\left(RQ\left(G\right)\right)$.

An immediate consequence of Theorem 2 is the following result.

Corollary 5.

If G and $\tilde{G}$ are connected graphs such that $\tilde{G}$ is obtained from G by the deletion of an edge, then

$$HIE\left(\tilde{G}\right)<HIE\left(G\right).$$

From Corollary 5 and Lemma 1, we obtain the following result.

Corollary 6.

Among all the connected graphs on the n vertices and on the $m\ge n$ edges, the complete graph $K_n$ has the largest Harary incidence energy. In particular

$$HIE\left(G\right)\le HIE\left(K_n\right)=\sqrt{2(n-1)}+(n-1)\sqrt{n-2}.$$

The equality holds if and only if G is the complete graph.

Theorem 9.

Let G be a graph on n vertices. Then

$$HIE\left(G\right)\le \sqrt{{\displaystyle \frac{4H\left(G\right)}{n}}}+\sqrt{{\displaystyle \frac{2H\left(G\right)(n-1)(n-2)}{n}}}.$$

The equality holds if and only if G is the complete graph.

Proof. 

Notice that $HIE\left(G\right)=\sqrt{\rho \left(RQ\right(G\left)\right)}+{\displaystyle \sum _{i=2}^n}\sqrt{{\lambda }_i\left(RQ\left(G\right)\right)}$. Using the Cauchy–Schwartz inequality, we obtain

$$\begin{array}{c}\hfill {\left(HIE\left(G\right)-\sqrt{\rho \left(RQ\right(G\left)\right)}\right)}^2\le (n-1){\displaystyle \sum _{i=2}^n}{\lambda }_i\left(RQ\left(G\right)\right)\end{array}$$

with equality if and only if ${\lambda }_2\left(RQ\left(G\right)\right)=\dots ={\lambda }_n\left(RQ\left(G\right)\right)$.

Thus

$$\begin{array}{c}\hfill HIE\left(G\right)\le \sqrt{\rho \left(RQ\right(G\left)\right)}+\sqrt{(n-1)\left(2H\right(G)-\rho (RQ\left(G\right)\left)\right)}.\end{array}$$

Let $q\left(x\right)$ be the real function such that

$$q\left(x\right)=\sqrt{x}+\sqrt{(n-1)\left(2H\right(G)-x)}.$$

(5)

We observe that $q\left(x\right)$ is a strictly decreasing function in the interval $\left({\displaystyle \frac{2H}{n}},2H\right)$ and a strictly increasing function in the interval $\left(0,{\displaystyle \frac{2H}{n}}\right)$.

From Theorem 3, we have ${\displaystyle \frac{4H}{n}}\le \rho \left(RQ\left(G\right)\right)$ with equality if and only if G is a reciprocal distance degree regular graph. Since

$${\displaystyle \frac{2H\left(G\right)}{n}}<{\displaystyle \frac{4H\left(G\right)}{n}}\le \rho \left(RQ\left(G\right)\right)<2H\left(G\right),$$

we obtain

$$HIE\left(G\right)\le \sqrt{{\displaystyle \frac{4H\left(G\right)}{n}}}+\sqrt{{\displaystyle \frac{2H\left(G\right)(n-1)(n-2)}{n}}}.$$

Furthermore, the above equalities hold if and only if ${\lambda }_2\left(RQ\left(G\right)\right)=\dots ={\lambda }_n\left(RQ\left(G\right)\right)$ and $\rho \left(RQ\left(G\right)\right)={\displaystyle \frac{4H\left(G\right)}{n}}$. Therefore, we have two cases:

(i)

If $\rho \left(RQ\left(G\right)\right)={\displaystyle \frac{4H\left(G\right)}{n}}={\lambda }_2\left(RQ\left(G\right)\right)=\dots ={\lambda }_n\left(RQ\left(G\right)\right)$ then $n=1$. Thus, $G=K_1$.

(ii)

If $\rho \left(RQ\left(G\right)\right)={\displaystyle \frac{4H\left(G\right)}{n}}\ne {\lambda }_2\left(RQ\left(G\right)\right)=\dots ={\lambda }_n\left(RQ\left(G\right)\right)$ then G has only two distinct reciprocal distance signless Laplacian eigenvalues. From Lemma 1, we conclude that G is the complete graph of order n.

Conversely, if G is a complete graph, then the equality is immediate. □

Theorem 10.

Let G be a graph on n vertices. Then

$$HIE\left(G\right)\le \sqrt[4]{{\displaystyle \frac{4{\displaystyle \sum _{i=1}^n}R{T}_i^2}{n}}}+\sqrt{(n-1)\left[2H\left(G\right)-\sqrt{{\displaystyle \frac{4{\displaystyle \sum _{i=1}^n}R{T}_i^2}{n}}}\right]}.$$

The equality holds if and only if G is the complete graph.

Proof. 

By Theorem 4 we obtain $\sqrt{{\displaystyle \frac{4{\displaystyle \sum _{i=1}^n}R{T}_i^2}{n}}}\le \rho \left(RQ\left(G\right)\right)$ with equality if and only if G is a reciprocal distance degree regular graph. Note that, by (5), $q\left(x\right)=\sqrt{x}+\sqrt{(n-1)\left(2H\right(G)-x)}$ is a strictly decreasing function in the interval $\left({\displaystyle \frac{2H}{n}},2H\right)$. Since

$${\displaystyle \frac{2H\left(G\right)}{n}}<\sqrt{{\displaystyle \frac{4{\displaystyle \sum _{i=1}^n}R{T}_i^2}{n}}}\le \rho \left(RQ\left(G\right)\right)<2H\left(G\right),$$

the result is similar to the proof of Theorem 9. □

Lemma 3

([30]). Let m and n be natural numbers such that $m\ge n>2$. Let $a_1,a_2,\dots ,a_m$ be positive real numbers. Then

$${\displaystyle \frac{2}{n}}{\left(\sum _{i=1}^m{a}_i\right)}^2>\sum _{i=1}^m{a}_i^2.$$

Theorem 11.

Let G be a graph of order $n>2$. Then

$$HIE\left(G\right)>\sqrt{nH\left(G\right)}.$$

Proof. 

Applying Lemma 3 to the definition of $HIE\left(G\right)$ we obtain

$${\left(HIE\left(G\right)\right)}^2>{\displaystyle \frac{n}{2}}\sum _{i=1}^n{\lambda }_i\left(RQ\left(G\right)\right)=nH\left(G\right).$$

Therefore,

$$HIE\left(G\right)>\sqrt{nH\left(G\right)}.$$

□

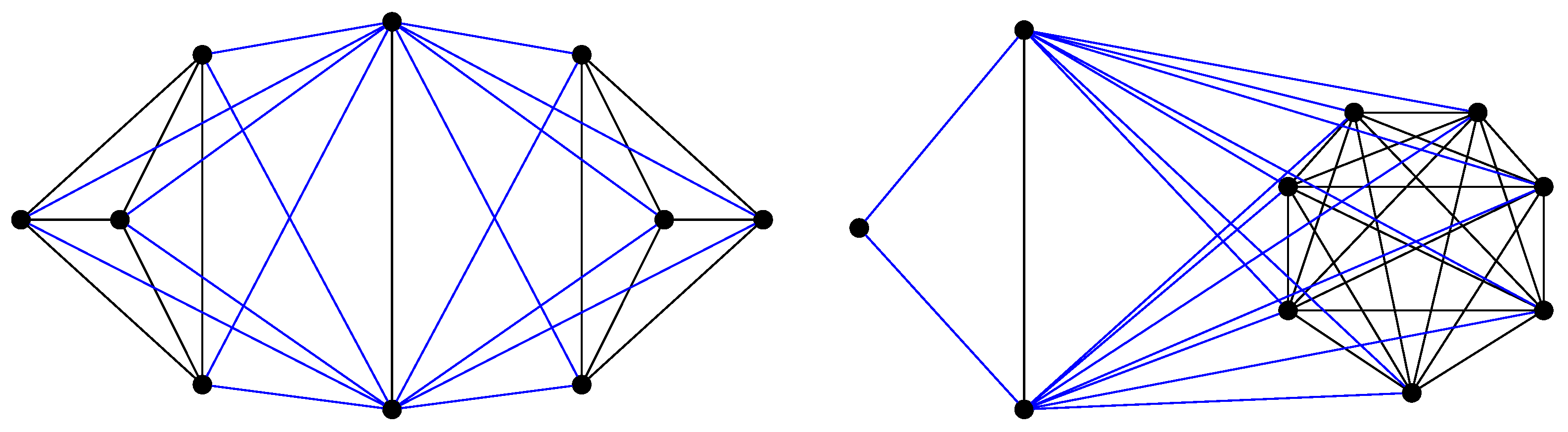
Example 2.

We consider the graphs $G_1$ and $G_2$ as depicted in Figure 4. Let $G_3$ be the Petersen graph, and $G_4$, $G_5$ and $G_6$ be the star $S_7$, the path $P_7$ and the cycle $C_7$ on seven vertices, respectively.

Using four decimal places, we show upper and lower bounds for the Harary incidence energy.

Upper bound	$G_1$	$G_2$	$G_3$	$S_7$	$P_7$	$C_7$
$HIE\left(G\right)$	$11.7324$	$11.3706$	$24.1968$	$13.4513$	$12.1621$	$13.1207$
Theorem 9	$11.7727$	$11.4410$	$24.2487$	$13.5345$	$12.3002$	$13.1961$
Theorem 10	$11.7727$	$11.4304$	$24.2487$	$13.5148$	$12.2921$	$13.1961$

Lower bound	$G_1$	$G_2$	$G_3$	$S_7$	$P_7$	$C_7$
$HIE\left(G\right)$	$11.7324$	$11.3706$	$24.1968$	$13.4513$	$12.1621$	$13.1207$
Theorem 11	$8.4853$	$8.2462$	$17.3205$	$9.7211$	$8.8346$	$9.4781$

Finally, in this section, we extend the upper bounds for the Harary incidence energy to all connected graphs of a given order, expressed in terms of vertex connectivity. Furthermore, we characterize the graphs for which these bounds are attained.

Let $\mathcal{V}(n,k)$ be the family of connected graphs G of order n such that $\kappa \left(G\right)\le k$.

For $i=1,2,3$, let $G_i$ be a ${\delta }_i$-regular graph of order $n_i$. Then $G=G_1\vee (G_2\cup G_3)$ is a graph of order $n=n_1+n_2+n_3$. Observe that

$$G_1\vee (G_2\cup G_3)\equiv \underset{P_3}{\bigvee }\{G_2,G_1,G_3\}$$

and

$$G_1\vee (G_2\cup G_3)\in \mathcal{V}(n,n_1).$$

Labeling the vertices of $G=G_1\vee (G_2\cup G_3)$ starting with the vertices of $G_1$, continuing with the vertices of $G_2$ and finishing with the vertices of $G_3$, and using the results obtained in the previous subsection, the reciprocal distance signless Laplacian matrix $RQ\left(G\right)$ is

$$RQ\left(G\right)=\left[\begin{array}{ccc}{Q}_1& J_{n_1\times n_2}& J_{n_1\times n_3}\\ J_{n_2\times n_1}& Q_2& {\displaystyle \frac{1}{2}}{J}_{n_2\times n_3}\\ J_{n_3\times n_1}& {\displaystyle \frac{1}{2}}{J}_{n_3\times n_2}& Q_3\end{array}\right]$$

where for $i=1,2,3$,

$$Q_i=k_i{I}_{n_i}+{\displaystyle \frac{1}{2}}(J_{n_i}-I_{n_i}+A\left(G_i\right))$$

(6)

and

$$\begin{array}{ccc}\hfill k_1& =& {\displaystyle \frac{1}{2}}(n_1-1)+{\displaystyle \frac{1}{2}}{\delta }_1+n_2+n_3\hfill \\ \hfill k_2& =& {\displaystyle \frac{1}{2}}(n_2-1)+{\displaystyle \frac{1}{2}}{\delta }_2+n_1+{\displaystyle \frac{1}{2}}{n}_3\hfill \\ \hfill k_3& =& {\displaystyle \frac{1}{2}}(n_3-1)+{\displaystyle \frac{1}{2}}{\delta }_3+n_1+{\displaystyle \frac{1}{2}}{n}_2.\hfill \end{array}$$

Clearly, the largest eigenvalues of $Q_1$, $Q_2$ and $Q_3$, given as in (6), are

$$\begin{array}{ccc}\hfill {\lambda }_1\left(Q_1\right)& =& (n_1-1)+{\delta }_1+n_2+n_3\hfill \\ \hfill {\lambda }_1\left(Q_2\right)& =& (n_2-1)+{\delta }_2+n_1+{\displaystyle \frac{1}{2}}{n}_3\hfill \\ \hfill {\lambda }_1\left(Q_3\right)& =& (n_3-1)+{\delta }_3+n_1+{\displaystyle \frac{1}{2}}{n}_2\hfill \end{array}$$

(7)

with eigenvectors ${\mathbf{e}}_{n_1}$, ${\mathbf{e}}_{n_2}$ and ${\mathbf{e}}_{n_3}$, respectively.

Utilizing these observations, we obtain the following result as a direct application of Theorem 7.

Proposition 6.

If $G=G_1\vee (G_2\cup G_3)$ and, for $i=1,2,3$, $G_i$ is a ${\delta }_i$-regular graph then

$$\sigma \left(RQ\left(G\right)\right)=\left(\sigma \left(Q_1\right)\cup \sigma \left(Q_2\right)\cup \sigma \left(Q_3\right)-\{{\lambda }_1\left(Q_1\right),{\lambda }_1\left(Q_2\right),{\lambda }_1\left(Q_3\right)\}\right)\cup \sigma \left(F_3\right)$$

where $Q_1,Q_2,Q_3$ are as in (6), ${\lambda }_1\left(Q_1\right),{\lambda }_1\left(Q_2\right),{\lambda }_1\left(Q_3\right)$ are as in (7) and

$$F_3=\left[\begin{array}{ccc}{\lambda }_1\left(Q_1\right)& n_2& n_3\\ n_1& {\lambda }_1\left(Q_2\right)& {\displaystyle \frac{1}{2}}{n}_3\\ n_1& {\displaystyle \frac{1}{2}}{n}_2& {\lambda }_1\left(Q_3\right)\end{array}\right]$$

(8)

Now, let n and k be positive integers, with $k\le n-1$ and consider the graph

$$G\left(j\right)=K_k\vee (K_j\cup K_{n-k-j})$$

where without loss of generality, we assume $1\le j\le \lfloor {\displaystyle \frac{n-k}{2}}\rfloor$. The following result is obtained by applying Proposition 6 to $RQ\left(G\right(j\left)\right)$.

Proposition 7.

Let $G\left(j\right)=K_k\vee (K_j\cup K_{n-k-j})$ such that $1\le j\le \lfloor {\displaystyle \frac{n-k}{2}}\rfloor$. Then

$$\begin{array}{ccc}\hfill \sigma \left(RQ\right(G\left(j\right))& =& \left\{f_1\left(j\right),f_2,f_3\left(j\right),{(n-2)}^{[k-1]},{\left({\displaystyle \frac{n+k+j-4}{2}}\right)}^{[j-1]},\right.\hfill \\ & & \left.{\left({\displaystyle \frac{2n-j-4}{2}}\right)}^{[n-k-j-1]}\right\},\hfill \end{array}$$

where $f_{1,3}\left(j\right)={\displaystyle \frac{5n+k-8\pm \sqrt{{(k-3n)}^2-32j(n-k-j)}}{4}}$ and $f_2=n-2$. In particular,

$$\begin{array}{ccc}\hfill HIE(K_k\vee (K_1\cup K_{n-k-1}))& =& k\sqrt{n-2}+(n-k-2)\sqrt{n-{\displaystyle \frac{5}{2}}}\hfill \\ & & +\sqrt{{\displaystyle \frac{5n+k-8+\sqrt{{(k-3n)}^2-32(n-k-1)}}{4}}}\hfill \\ & & +\sqrt{{\displaystyle \frac{5n+k-8-\sqrt{{(k-3n)}^2-32(n-k-1)}}{4}}}.\hfill \end{array}$$

Proof. 

We observe that for the graph $G\left(j\right)=K_k\vee (K_j\cup K_{n-k-j})$, the matrices $Q_1$, $Q_2$ and $Q_3$ in (6) are

$$\begin{array}{ccc}\hfill Q_1& =& (n-1)I_k+A\left(K_k\right)\hfill \\ \hfill Q_2& =& \left({\displaystyle \frac{n+k+j-2}{2}}\right)I_j+A\left(K_j\right)\hfill \\ \hfill Q_3& =& \left({\displaystyle \frac{2n-j-2}{2}}\right)I_{n-k-j}+A\left(K_{n-k-j}\right)\hfill \end{array}$$

respectively, and the matrix $F_3\left(G\left(j\right)\right)$ in (8) becomes

$$F_3=\left[\begin{array}{ccc}n+k-2& j& n-kj\\ k& {\displaystyle \frac{n+k+3j-4}{2}}& {\displaystyle \frac{n-k-j}{2}}\\ k& {\displaystyle \frac{j}{2}}& 2n-k-{\displaystyle \frac{3j}{2}}-2\end{array}\right].$$

Then

$$\begin{array}{ccc}\hfill \sigma \left(Q_1\right)& =& \{n+k-2,{(n-2)}^{[k-1]}\},\hfill \\ \hfill \sigma \left(Q_2\right)& =& \left\{{\displaystyle \frac{n+k+3j-4}{2}},{\left({\displaystyle \frac{n+k+j-4}{2}}\right)}^{[j-1]}\right\},\hfill \\ \hfill \sigma \left(Q_3\right)& =& \left\{{\displaystyle \frac{4n-2k-3j-4}{2}},{{\displaystyle \frac{2n-j-4}{2}}}^{[n-k-j-1]}\right\}\hfill \end{array}$$

and the spectrum of $F_3\left(G\left(j\right)\right)$ is

$$\sigma \left(F_3\left(G\left(j\right)\right)\right)=\{f_1\left(j\right),f_2,f_3\left(j\right)\},$$

where $f_{1,3}\left(j\right)={\displaystyle \frac{5n+k-8\pm \sqrt{{(k-3n)}^2-32j(n-k-j)}}{4}}$ and $f_2=n-2$. Since

$$HIE\left(G\right)=\sum _{i=1}^n\sqrt{{\lambda }_i\left(RQ\left(G\right)\right)}.$$

The result is obtained. □

Let

$$\mathcal{W}(n,k)=\{G\in \mathcal{V}(n,k):|E\left(G\right)|\ge n\}$$

and let

$$\begin{array}{ccc}\hfill \beta (n,k)& =& k\sqrt{n-2}+(n-k-2)\sqrt{n-{\displaystyle \frac{5}{2}}}\hfill \\ & & +\sqrt{{\displaystyle \frac{5n+k-8+\sqrt{{(k-3n)}^2-32(n-k-1)}}{4}}}\hfill \\ & & +\sqrt{{\displaystyle \frac{5n+k-8-\sqrt{{(k-3n)}^2-32(n-k-1)}}{4}}}.\hfill \end{array}$$

If $K_0$ denotes the empty graph, i.e., the graph without edges, then we have the following results.

Lemma 4.

Let $G\left(j\right)=K_k\vee (K_j\cup K_{n-k-j})$ for $1\le j\le \lfloor {\displaystyle \frac{n-k}{2}}\rfloor$. Then

$$HIE\left(G\left(⌊{\displaystyle \frac{n-k}{2}}⌋\right)\right)\le HIE\left(G\left(j\right)\right)\le HIE\left(G\left(1\right)\right).$$

Proof. 

From Proposition 7 we have

$$\begin{array}{ccc}\hfill HIE\left(G\right(j\left)\right)& =& k\sqrt{n-2}+(j-1)\sqrt{{\displaystyle \frac{n+k+j-4}{2}}}\hfill \\ & +& (n-k-j-1)\sqrt{{\displaystyle \frac{2n-j-4}{2}}}\hfill \\ & +& \sqrt{{\displaystyle \frac{5n+k-8+\sqrt{{(k-3n)}^2-32j(n-k-j)}}{4}}}\hfill \\ & +& \sqrt{{\displaystyle \frac{5n+k-8-\sqrt{{(k-3n)}^2-32j(n-k-j)}}{4}}}.\hfill \end{array}$$

We define the function

$$\begin{array}{ccc}\hfill f\left(x\right)& =& (x-1)\sqrt{{\displaystyle \frac{n+k+x-4}{2}}}+(n-k-x-1)\sqrt{{\displaystyle \frac{2n-x-4}{2}}}\hfill \\ & +& \sqrt{{\displaystyle \frac{5n+k-8+\sqrt{{(k-3n)}^2-32x(n-k-x)}}{4}}}\hfill \\ & +& \sqrt{{\displaystyle \frac{5n+k-8-\sqrt{{(k-3n)}^2-32x(n-k-x)}}{4}}}.\hfill \end{array}$$

We observe that $f\left(x\right)=f(n-k-x)$ for $x\in [0,n-k]$ and f is a strictly decreasing function in the interval $\left[1,{\displaystyle \frac{n-k}{2}}\right]$. Thus, the result is obtained. □

Theorem 12.

If $G\in \mathcal{W}(n,k)$, then

$$HIE\left(G\right)\le \beta (n,k),fork=1,\dots ,n-1.$$

(9)

Furthermore, the equality case in (9) holds if and only if $G=K_k\vee (K_1\cup K_{n-k-1}).$

Proof. 

Let $G\in \mathcal{W}(n,k)$. We first consider $k=n-1$. From Corollary 6, $HIE\left(G\right)\le HIE\left(K_n\right)$ with equality if and only if $G=K_n$. Moreover,

$$\beta (n,n-1)=\sqrt{2(n-1)}+(n-1)\sqrt{n-2}=HIE\left(K_n\right).$$

Then the result is true for $k=n-1$. Consider $1\le k\le n-2$ and let $G\in \mathcal{W}(n,k)$ then $HIE\left(G\right)$ is a maximum.

Let $S\subseteq V\left(G\right)$ such that $G\setminus S$ is a disconnected graph and $\left|S\right|=\kappa \left(G\right)$. We denote by $C_1,C_2,\dots ,C_r$ the r connected components of $G\setminus S$. Clearly $r\ge 2$. Suppose that $r>2$, then we can construct a new graph $G\cup \left\{e\right\}$ where e is an edge connecting a vertex in $C_1$ with a vertex in $C_2$. We can see that $G\cup \left\{e\right\}\in \mathcal{W}(n,k)$. By Corollary 5, we have

$$HIE\left(G\right)<HIE(G\cup \{e\left\}\right),$$

it is a contradiction, because G is the graph with maximum $HIE$. Therefore $r=2$, that is $G\setminus S=C_1\cup C_2$.

By definition $\left|S\right|\le k$. Now, we claim that $\left|S\right|=k$.

Suppose $\left|S\right|<k$. Since $G\setminus S=C_1\cup C_2$, we may construct a graph $H=G\cup \left\{e\right\}$ where e is an edge joining a vertex $u\in V\left(C_1\right)$ with a vertex $v\in V\left(C_2\right)$. We see that $H\setminus S$ is a connected graph and the deletion of the vertex u disconnected it, then $H\in \mathcal{W}(n,k)$. By Corollary 5, $HIE\left(G\right)<HIE\left(H\right)$, with is also a contradiction. Hence $G\setminus S=C_1\cup C_2$ and $\left|S\right|=k$. Let $|C_1|=j$. Then $|C_2|=n-k-j$. By repeated application of Corollary 5 we can conclude that

$$G=K_k\vee (K_j\cup K_{n-k-j})=G\left(j\right)$$

for some $1\le j\le \lfloor {\displaystyle \frac{n-k}{2}}\rfloor$. We have proved $HIE\left(G\right)\le HIE\left(G\right(j\left)\right)$ for all $G\in \mathcal{W}(n,k)$. From Lemma 4 we have that $HIE\left(G\right(j\left)\right)\le HIE\left(G\right(1\left)\right)$. Since $HIE\left(G\right(1\left)\right)=\beta (n,k)$, for $k=1,\dots n-1$, the equalities hold if and only if $G=K_k\vee (K_1\cup K_{n-k-1})$. □

Example 3.

For $n=10$ and $k=2$, the graphs with minimum and maximum Harary incidence energy are $G_1=K_2\bigvee (K_4\cup K_4)$ and $G_2=K_2\bigvee (K_1\cup K_7)$, respectively (Figure 5). In fact, using four decimal places, we have

$$HIE\left(K_2\vee (K_4\cup K_4)\right)=26.8650\mathrm{and}HIE\left(K_2\vee (K_1\cup K_7)\right)=28.4562.$$