Abstract
Reconfigurable Intelligent Surface (RIS) has emerged as a promising enabling technology for wireless communications, which significantly enhances system performance through real-time manipulation of electromagnetic wave reflection characteristics. In RIS-assisted communication systems, existing deep learning-based channel state information (CSI) feedback methods often suffer from excessive parameter requirements and high computational complexity. To address this challenge, this paper proposes LwCSI-Net, a lightweight autoencoder network specifically designed for RIS-assisted multiple-input single-output (MISO) systems, aiming to achieve efficient and low-complexity CSI feedback. The core contribution of this work lies in an innovative lightweight feedback architecture that deeply integrates multi-layer convolutional neural networks (CNNs) with attention mechanisms. Specifically, the network employs 1D convolutional operations with unidirectional kernel sliding, which effectively reduces trainable parameters while maintaining robust feature-extraction capabilities. Furthermore, by incorporating an efficient channel attention (ECA) mechanism, the model dynamically allocates weights to different feature channels, thereby enhancing the capture of critical features. This approach not only improves network representational efficiency but also reduces redundant computations, leading to optimized computational complexity. Additionally, the proposed cross-channel residual block (CRBlock) establishes inter-channel information-exchange paths, strengthening feature fusion and ensuring outstanding stability and robustness under high compression ratio (CR) conditions. Our experimental results show that for CRs of 16, 32, and 64, LwCSI-Net significantly improves CSI reconstruction performance while maintaining fewer parameters and lower computational complexity, achieving an average complexity reduction of 35.63% compared to state-of-the-art (SOTA) CSI feedback autoencoder architectures.
Keywords:
CSI feedback; reconfigurable intelligent surface; deep learning; ECA mechanism; lightweight convolutional neural network MSC:
94A05
1. Introduction
A Reconfigurable Intelligent Surface (RIS) is composed of a large number of low-cost passive reflecting elements and can dynamically reshape the wireless propagation environment by real-time control of electromagnetic wave amplitude, phase, or polarization [1]. By intelligently reflecting or transmitting incident signals, an RIS can enhance the received signal strength of the target users in multiple-input single-output (MISO) communication systems while suppressing multi-user interference and eavesdropping risks [2]. Compared to traditional relays or large-scale antenna arrays, RIS technology offers significant advantages, such as low power consumption, easy deployment, and high flexibility, thereby improving spectral efficiency and physical layer security [3]. As one of the key technologies for building intelligent wireless propagation environments, RIS is gradually becoming a critical enabler of 6G communication networks [4,5].
In RIS-assisted MISO systems, there are two primary operating modes: frequency-division duplex (FDD) [6] and time-division duplex (TDD) [7]. This paper focuses on the FDD mode, which is characterized by the use of different frequency bands for uplink and downlink transmissions, resulting in the loss of channel reciprocity that is typically present in TDD systems. In the FDD mode, acquiring channel state information (CSI) relies on a dedicated feedback mechanism, where the user equipments (UEs) must transmit the measured CSI back to the base station (BS) via a feedback link. The efficiency and the accuracy of this CSI feedback process directly impact the overall system performance. Therefore, designing a CSI feedback mechanism that is both efficient and accurate has become a critical research challenge in RIS-assisted MISO communication systems.
To address this challenge, researchers have proposed various methods for CSI compression and reconstruction. Among these, the traditional approaches primarily include codebook-based methods [8] and compressive sensing (CS) techniques [9]. However, both methods typically suffer from high computational complexity and a strong reliance on channel sparsity, making it difficult to meet the dual requirements of feedback efficiency and reconstruction accuracy in modern communication systems. Given the limitations of traditional techniques, deep learning has recently achieved remarkable success in fields such as computer vision and natural language processing [10]. Its powerful non-linear modeling capabilities and automatic feature-extraction mechanisms offer a new paradigm for CSI compression and feedback, and they have gradually established it as a prominent research direction in this domain.
CsiNet [11] was the first to introduce deep learning into the CSI feedback framework, employing an autoencoder to achieve effective compression and reconstruction of CSI. Subsequently, CLNet [12] incorporated a complex-valued input module that processes both the real and imaginary parts of the CSI, preserving its physical meaning while improving feedback accuracy. ENet [13] further exploited the sparsity of CSI in the angle-delay domain by independently compressing the real and imaginary components, thereby reducing redundancy. To capture temporal correlations, CsiNet–LSTM [14] and ConvlstmCsiNet [15] leveraged recurrent neural networks (RNNs), enhancing the modeling of time-varying channels. In variable-rate scenarios, SM-CsiNet+ and PM-CsiNet+ [16] proposed adaptive compression frameworks, addressing the CSI feedback rate flexibility problem for the first time. Additionally, the jigsaw puzzle training strategy (JPTS) [17] improved reconstruction performance by maximizing the mutual information between the original and reconstructed CSI. In the context of RIS-assisted systems, ref. [18] proposed a super-resolution neural network that captures spatial correlations among adjacent subcarriers and reflecting elements within the channel matrix, thereby enhancing estimation accuracy. CRNet [19], based on the CsiNet architecture, introduced a multi-resolution compression and reconstruction network to further reduce CSI redundancy. Ref. [20] proposed a deep learning model, CCA-Net, which employs criss-cross attention to fuse the spatiotemporal and complex features of CSI, improving reconstruction performance in FDD-based large-scale MIMO systems. Inspired by the success of the Transformer architecture in natural language processing, Quan-Transformer [21] was the first to apply it to the CSI feedback task in RIS-assisted systems, leveraging its strong feature-extraction capabilities to efficiently compress and represent the BS–RIS–UE cascaded channel. To address the signaling overhead introduced by quantized phase feedback in IRS systems, ref. [22] proposed two deep learning-based compression models, GAPSCN and S GAPSCN, which significantly reduce the feedback burden while maintaining high reconstruction accuracy. JDCNet [23] jointly optimized channel estimation and CSI feedback, effectively mitigating error accumulation caused by separate optimization. Regarding phase feedback compression, ref. [24] removed batch normalization layers and introduced denoising modules to address gradient vanishing and distribution mismatch issues during training, enabling efficient compression and reconstruction of quantized phase shifts (QPSs) under bandwidth constraints. ACNet [25] exploited temporal correlations between adjacent time slots to enhance CSI recovery performance. RIS–CsiNet [26] proposed a dual-timescale CSI feedback framework that jointly considers long- and short-term channel variations. Furthermore, RIS–CoCsiNet [27] explored the shared and unique components of user-side CSI, introducing a combination neural network and decoder at the base station to improve reconstruction quality in RIS-assisted communication systems. Its effectiveness was validated on two distinct channel datasets.
To reduce this complexity, it is essential to explore lightweight network design approaches, a topic that has not been thoroughly explored in the existing literature. Therefore, building upon our previously proposed lightweight CSI feedback network, LwCSI-Net [28], this study investigated the effectiveness of a lightweight strategy using CSI samples generated from channel models. Our experimental results demonstrate that the proposed method achieved superior reconstruction performance compared to other deep learning models [11,12,19,20] at compression ratios (CRs) of 16, 32, and 64, while significantly reducing computational complexity. Specifically, the average complexity was reduced by 35.63% from the original 28.58% [28]. The main contributions of this paper are summarized as follows:
- We propose a deep learning-based CSI feedback structure, called LwCSI-Net, designed to optimize the CSI feedback process in RIS-assisted communication systems. This method effectively enhances the accuracy and efficiency of CSI feedback.
- The LwCSI-Net model combines a one-dimensional convolutional network, an efficient channel attention (ECA) mechanism, and a CRBlock module. Through multi-level information fusion and processing during feature extraction, compression, and decompression, the model’s expressive power is further enhanced, maintaining high performance while ensuring lightweight design.
- Our numerical results show that the proposed LwCSI-Net network successfully reduces model complexity under high compression ratios while demonstrating excellent CSI reconstruction performance. The model also exhibits significant advantages in rapid learning, low error, and superior normalized mean square error (NMSE), particularly in complex environments, where it shows strong adaptability and robustness.
Notations
Scalars, vectors, and matrices are denoted by lowercase italic letters, bold lowercase letters, and bold uppercase letters, respectively. The input feature tensor is denoted by , with dimensions height × width. The channel from the base station to the RIS is represented by a complex matrix , and the channel from the RIS to the user is denoted by a column vector . The phase shift vector of the RIS is denoted by . The cascaded channel for the i-th user is denoted by . Discrete Fourier Transform matrices and are used for channel sparsification, with the frequency domain channel denoted as and the reconstructed channel by the decoder as . Common operators include the Frobenius norm , conjugate transpose , Kronecker product ⊗, diagonal matrix construction , and main diagonal extraction . Additionally, and denote the number of multipath components from the base station to the RIS and from the RIS to the user, respectively. and represent the number of RIS elements in the horizontal and vertical directions. The parameters of the encoder and decoder are denoted by and , respectively.
2. System Model
As illustrated in Figure 1, we investigated an FDD multi-user RIS-assisted multiple-input single-output (MISO) communication system. The system comprises a BS equipped with M antennas and U single-antenna UE nodes. In the considered downlink scenario, it is assumed that the direct links between the BS and the UEs are obstructed, such that an RIS mounted on a building surface is utilized to create non-line-of-sight (NLOS) wireless links for the blocked UEs. The RIS integrates N passive reflecting elements, enabling dynamic reconfiguration of electromagnetic waves through real-time adjustment of reflection coefficients. This configuration mechanism effectively reshapes the wireless propagation environment to enhance signal reception quality.
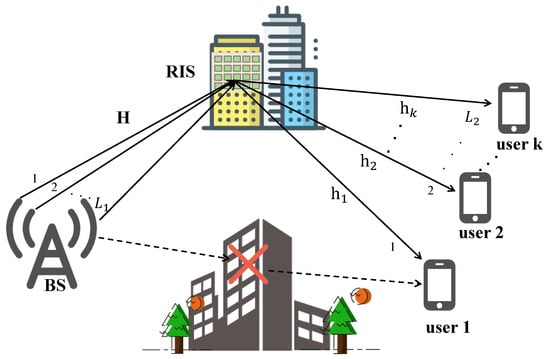
Figure 1.
Architecture of FDD multi-user MISO system with RIS assistance.
2.1. Signal Model
It is assumed that the CSI can be perfectly estimated at the UEs. The signal received by the i-th UE can be written as
where denotes the CSI vector between the RIS and the i-th UE, is the CSI matrix from the BS to the RIS, denotes the diagonal phase rotation matrix of the RIS reflection elements, with , and denoting the range of values of the constant amplitude coefficients and the phase coefficients of the reflective elements, respectively, is the precoded transmitted signal vector, and denotes the additive Gaussian white noise. Using the property of diagonal matrix, (1) can be reformulated as
where denotes the equivalent cascaded channel matrix for the i-th UE.
2.2. Channel Model
To model the channel effects of the RIS-assisted MISO systems, we adopt the channel modeling method proposed by [29]. Specifically, the channel matrix between the RIS and the BS is modeled as
The channel vector between the RIS and the UE is modeled as
based on the BS–RIS channel matrix defined in (3) and the RIS–UE channel vector in (4), combined with the cascaded channel definition , and we derive the explicit expression for the cascaded channel matrix at the i-th UE:
where is defined as the composite path gain, which characterizes the joint propagation effect of the l-th BS–RIS path and the -th RIS–UE path. Here, denotes the number of paths between the BS and RIS, and denotes the number of paths between the RIS and UE, where and . The vectors and represent the gains of the l-th path in the BS–RIS and RIS–UE links, respectively. Specifically, the superscripts BR and RU denote the device channels along the propagation paths from the BS to the RIS, and from the RIS to the UEs, respectively. The steering vector represents the antenna array response for the l-th path, and the superscript AOD denotes the angle of departure, which is the direction from which the signal is transmitted by the base station antenna array.
The detailed expressions for these three steering vectors are
where ⊗ denotes the Kronecker product, , , , represents the elements in the horizontal direction of the RIS, and represents the elements in the vertical direction. Considering the typical high placement of the RIS and the limited number of RIS–UE channel paths due to minimal scatterers, the RIS–UE CSI matrix exhibits sparsity in the angle domain. This sparse matrix can be derived using the Discrete Fourier Transform (DFT) [30] as follows:
where and are the and DFT matrices, respectively.
2.3. CSI Feedback Process
The lightweight CSI feedback architecture studied in this paper is shown in Figure 2. First, the UE obtains the transmitted channel matrix through the downlink and applies the DFT (9) to convert it into the frequency domain, resulting in the preprocessed . Then, the LwCSI-Net encoder is responsible for compressing the input channel state information, , which can be represented as
where represents the function of the LwCSI-Net encoder, denotes its parameters, and s is the compressed feature vector with length S; the corresponding compression ratio is defined as
where is the number of subcarriers in the system. The compressed feature vector output by the encoder is passed to the decoder located at the BS. The design of the LwCSI-Net decoder at the BS can be expressed as
where represents the function of the LwCSI-Net decoder at the BS, refers to the parameters of the decoder, and the goal of the decoder is to restore the CSI of the channel passed from the encoder.
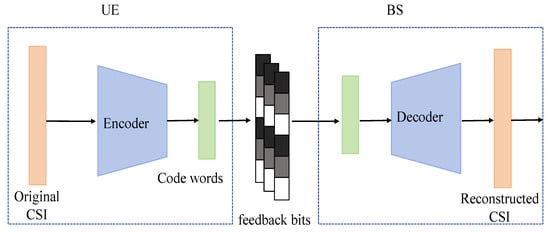
Figure 2.
Basic process of CSI feedback.
Finally, the channel state information is restored and reconstructed using an activation function for BS use. Therefore, the entire feedback process can be represented as
The goal of LwCSI-Net is to minimize the error between the original channel matrix and the reconstructed channel matrix . Specifically, this is achieved by optimizing the parameter sets of the encoder and decoder to find the optimal parameter combination, thereby minimizing this error:
By minimizing the squared Frobenius norm through this formula, the parameters and of the encoder and decoder are optimized, thereby achieving the best approximation of the channel matrix. The training procedure for solving the optimization problem in Equation (14) is detailed in Algorithm A1.
3. Proposed Lightweight CSI Feedback Network
For this section, we developed a deep learning-powered CSI feedback network using autoencoders, introducing an innovative, efficient CSI feedback network Figure 3 with a streamlined lightweight architecture for RIS-assisted communication. The specific network architecture and its design features will be introduced in the following subsections.
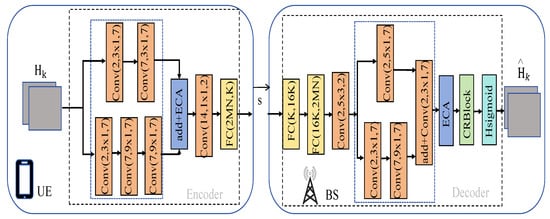
Figure 3.
Network architecture design of LwCSI-Net.
3.1. The Design of LwCSI-Net
The encoder at the user side is designed with two parallel convolutional paths to extract multi-level features. The first path consists of three convolution layers: Conv(2, 3 × 1, 7), Conv(7, 9 × 1, 7), and Conv(7, 9 × 1, 7). The second path consists of two convolution layers: Conv(2, 3 × 1, 7) and Conv(7, 3 × 1, 7). The outputs from both paths are fused using an addition operation to integrate information from the different convolutional pathways.
Next, the fused features pass through an ECA mechanism module (Figure 4b), which adaptively adjusts the channel weights based on local information, thereby enhancing important features. Finally, the output undergoes a convolutional layer for further processing and is then compressed by a fully connected (FC) layer with a compression ratio of K, resulting in the compressed vector s as the output. The length of the compressed vector s is denoted as S, where S = 2 × M × N.
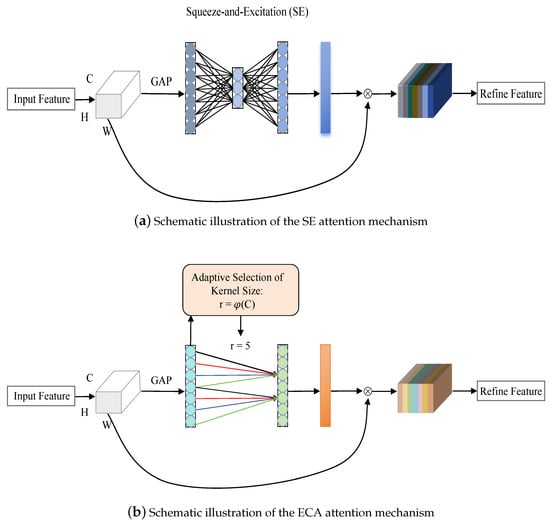
Figure 4.
Schematic illustrations of (a) SE and (b) ECA attention mechanisms.
The decoder at the BS receives the compressed signal s from the encoder. It first restores the compressed vector s, which has been reduced by a factor of K, using an FC layer. Subsequently, a series of convolutional operations are applied to recover the detailed information of the signal, including filters of various sizes, such as Conv(2, , 1) and Conv(2, , 7). Next, an ECA mechanism module (Figure 4b) is introduced, which adaptively adjusts the channel weights based on local information, thereby further enhancing key features. To enhance the feature-modeling capability of the network, this paper introduces the CRBlock module within the encoder, as illustrated in Figure 5. CRBlock adopts a dual-branch, multi-scale convolutional architecture designed to capture feature representations across varying receptive fields. The detailed update process of the CRBlock module is given by Equations (15)–(19):
where represents the convolutional operations of the first branch. The input feature tensor is first processed by a convolutional layer to extract local features. This is followed by a LeakyReLU activation function with a negative slope of 0.3 to introduce non-linearity. Then, a convolutional layer is applied to capture features with a larger receptive field. This branch is designed to integrate both local and wider contextual information, thereby enhancing feature diversity.
where denotes the output of the second branch, which applies a single convolutional layer directly to the input . This operation is intended to capture features within a medium receptive field, complementing the first branch and enabling a balanced perception of both local and mid-to-long range features.
where the features extracted from the two branches, (15) and (16), are concatenated along the channel dimension to form a new feature tensor . This operation fuses information from different receptive fields to enrich the feature representation.
where a convolution is applied to the concatenated tensor for feature fusion and channel compression. This allows the network to integrate information from both branches while controlling the parameter size.
where, in this step, a residual connection is formed by adding the fused feature (18) to the input residual tensor , followed by a LeakyReLU activation. This design helps mitigate the vanishing gradient problem commonly encountered in deep networks, thereby improving training stability and accelerating convergence. By incorporating residual connections, the CRBlock effectively alleviates the gradient vanishing issue commonly observed in deep networks, thereby improving training stability and accelerating convergence. Additionally, its multi-scale convolutional structure facilitates the recovery of fine-grained details and contextual semantics in the channel information, ultimately contributing to improved reconstruction quality. Finally, after this series of carefully designed processing steps, the signal is mapped onto the reconstructed signal through the Hsigmoid activation function
where is the linear output of the decoder, and the ReLU6 function limits the input value within the range of , aiming to approximate every detail of the original signal as accurately as possible.
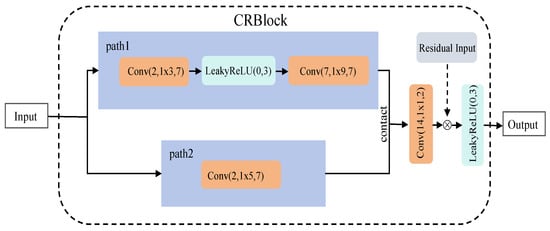
Figure 5.
A detailed design of the CRBlock module within the LwCSI-Net architecture.
3.2. Channel Attention
Attention mechanisms have been widely validated as significantly improving model performance in fields such as computer vision (CV) and natural language processing (NLP). Compared to more complex approaches like the self-attention mechanism in Transformers and spatial attention mechanisms in image processing, we initially adopted the more computationally efficient squeeze-and-excitation (SE) module, whose structure is shown in Figure 4a. The SE module extracts global channel-wise information through global average pooling (GAP), and it dynamically re-weights the importance of each channel, based on adaptive learning. This is followed by a lightweight fully connected layer to recalibrate the channel features. While maintaining low computational overhead, the SE module effectively enhances model performance.
However, the SE module still suffers from relatively large parameter counts and computational cost. To address this, we further explored alternative attention mechanisms and found that the ECA module significantly reduces the number of parameters by approximately 92% compared to the SE module. The detailed structure of ECA is illustrated in Figure 4b.
As shown in Figure 4b, the ECA mechanism first applies GAP to the input features, compressing spatial information into a channel-wise descriptor. It then models the inter-channel dependencies, using a 1D convolution with an adaptively determined kernel size, enabling efficient channel attention computation. The kernel size is defined by the following dynamic function:
where C denotes the number of input channels, is a scaling factor that controls the growth rate of the kernel size, and b is a bias term used to set the baseline. The notation indicates rounding to the nearest odd integer. This dynamic kernel design effectively captures crucial channel interactions while avoiding the need for manual tuning.
The computed channel weights are then passed through an Hsigmoid activation (20) and multiplied with the original features in a channel-wise manner, enabling adaptive feature refinement. This process is highly efficient and introduces negligible additional parameter overhead.
Compared to the SE module, the ECA mechanism offers significant advantages. By employing parameter-free one-dimensional convolution, ECA reduces the computational complexity from in SE to , resulting in approximately 92%-fewer parameters. Moreover, ECA avoids dimensionality reduction along the channel axis, thereby preserving complete channel information. This not only enhances feature representation but also effectively mitigates information loss.
4. Simulation Experiment and Result Analysis
In this section, we present the experimental design and compare the performance of the proposed LwCSI-Net network with the existing DL-based CSI feedback methods.
4.1. Experimental Design
The dataset generated using the Saleh–Valenzuela channel model considers a single-cell scenario, with the BS located at (0, 0), the user equipment at (300, 0), and the RIS positioned at (150, 100) between the BS and the user equipment. The RIS reflection surface is a 16 × 16 matrix, set M = N = 32, = = 4, = 4, and = 8. The entire dataset consists of independent channel instances, which are randomly divided into training, validation, and test datasets, with sizes of , , and , respectively. During training, we set the number of epochs to 1000, the batch size to 256, and the learning rate to to optimize the model’s performance.
Our experiments were carried out on an NVIDIA GeForce RTX 3090 GPU. The Xavier initialization strategy was used with the Adam optimizer to accelerate convergence. The base objective function used was the mean squared error (MSE), and normalization was applied to compute the normalized mean squared error (NMSE), which served as the primary metric for evaluating prediction accuracy.
Here, T represents the total number of samples used in the training process, while represents the Frobenius norm, defined as the square root of the sum of the squares of all elements in the matrix.
where the numerator represents MSE, while the denominator represents the average expected energy of the channel matrix.
4.2. Analysis of Results
LwCSI-Net is designed to realize a compact network architecture and minimal complexity. To demonstrate its advantages, this paper compares LwCSI-Net with four state-of-the-art methods, evaluating reconstruction accuracy, parameter quantity, and floating point calculations (FLOPs) on experimental data with CR values of 4, 16, 32, and 64.
As shown in Figure 6, with the increase in training epochs, the MSE of the LwCSI-Net architecture exhibited a clear downward trend, indicating that the network continuously optimized and adjusted its parameters to improve performance. This result demonstrates that LwCSI-Net not only reaches convergence quickly in the initial phases but also sustains low error values throughout the training process, highlighting its superior learning ability and higher stability in channel estimation and feedback tasks.
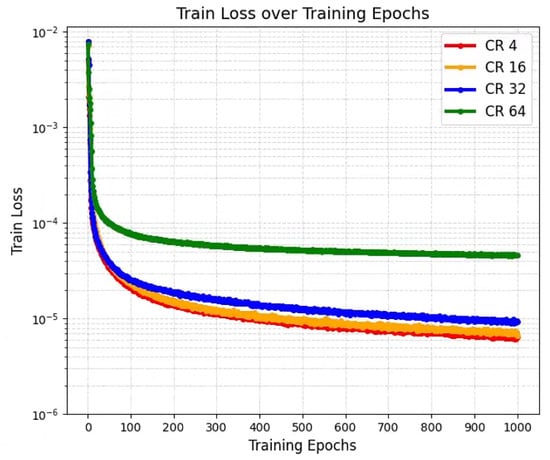
Figure 6.
Comparison of loss functions under different CRs.
As shown in Table 1, LwCSI-Net consistently demonstrated significantly lower FLOPs compared to the four mainstream models—namely, CsiNet, CRNet, CLNet, and CCA-Net-L—across all four CR settings. Moreover, this advantage became increasingly evident as the compression ratio increased. Specifically, at the extremely high compression ratio of CR = 64, the FLOPs of LwCSI-Net were more than 50% lower than those of the other three models, clearly highlighting its remarkable efficiency in maintaining low computational complexity.

Table 1.
Comparison the FLOPs of other models at different compression ratios.
As shown in Table 2, when the CRs were 16, 32, and 64, the number of parameters in LwCSI-Net was significantly lower than that of the other four models, fully demonstrating its design advantage in terms of model lightweighting. Furthermore, by combining the results from Table 1 and Table 2, it is evident that LwCSI-Net exhibits notable advantages over other feedback networks, in regard both to FLOPs and parameter count. These strengths not only reduce the model’s storage and computational costs but also enhance its practicality and deployment efficiency, making it especially suitable for resource-constrained communication scenarios.

Table 2.
Comparison of the number of parameters of other models under different compression ratios.
Table 3 shows the ablation experiment results of different modules, covering the NMSE performance of models A, B, C, D, E, and F under compression rates of 4, 16, 32, and 64. Specifically, Model A served as the baseline network composed solely of convolutional neural networks, Model B introduced the SE attention mechanism on this basis, Model C integrated the CRBlock module on Model A, Model D introduced a more efficient ECA module on the basis of Model A, Model E further integrated the SE attention mechanism on the basis of Model C, and Model F integrated the ECA module on Model C. From the experimental results, it can be seen that the model introducing the attention mechanism and CRBlock module outperformed the baseline model in all compression rate settings, verifying its effectiveness in feature extraction and compression modeling. Further comparison shows that Model F slightly outperformed Model E, with an average improvement of approximately 3.67% in NMSE performance, indicating that the ECA module possesses stronger representational capacity than the SE module in modeling inter-channel dependencies. In summary, the experimental results fully demonstrate the key role of the attention mechanism and CRBlock module in improving feature-representation capabilities and overall model performance. To provide a more intuitive demonstration of how each module affects the performance of LwCSI-Net, Figure 7 offers a clearer illustration.

Table 3.
Ablation study of different modules.
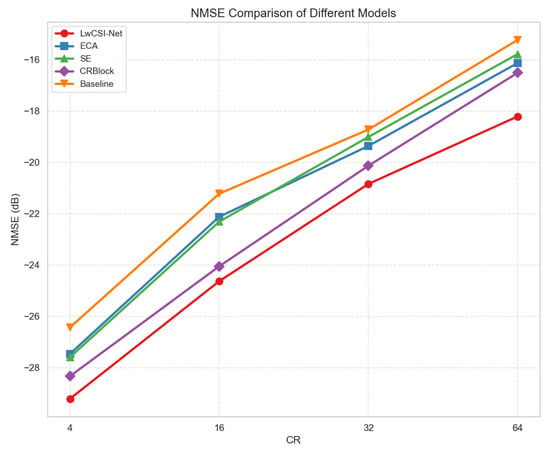
Figure 7.
The impact of different module integrations on the NMSE performance of network architectures.
In Figure 7, Baseline refers to the network’s basic version without any additional modules, ECA indicates the version with an attention mechanism added to the basic model, SE represents the version with an attention module added, and CRBlock refers to the version with the CRBlock module integrated into the basic model. LwCSI-Net, on the other hand, is the model that includes both the ECA and CRBlock modules. As shown in Figure 7, compared to the versions with only the CRBlock or attention modules, the baseline version performed relatively worse. LwCSI-Net achieved the lowest NMSE across all four CRs. It is clear from the figure that the LwCSI-Net network architecture delivered the best overall performance.
Figure 8 illustrates a comparison between the original CSI channel matrix and the reconstruction results under different compression ratios. Specifically, Figure 8a presents the original CSI channel matrix, where the amplitude distribution across different delay taps is intuitively visualized using a color gradient, clearly revealing the correlation between signal delay and amplitude. Figure 8b and Figure 8c show the reconstruction results with CRs of 4 and 64, respectively. Comparative analysis shows that when the CR was 4, the reconstructed matrix effectively preserved the characteristics of the original channel, with a high level of consistency in amplitude distribution. In contrast, when the CR was 64, although some fine-grained features were lost during reconstruction, the overall reconstruction accuracy could still exceed 95%.
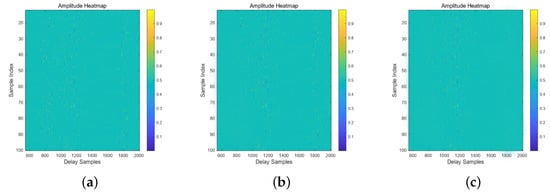
Figure 8.
Comparison of original CSI channel matrix data and reconstructed results at different compression ratios: (a) original CSI channel matrix; (b) reconstructed CSI matrix at CR of 4; (c) reconstructed CSI matrix at CR of 64.
As shown in Figure 9, the NMSE values of all the network architectures decreased as the compression ratio increased. Among all the models, LwCSI-Net consistently achieved the lowest NMSE across all compression ratios, demonstrating the best reconstruction performance, followed by CCA-Net-L, CLNet, CRNet, and CsiNet. Notably, under high compression ratios, LwCSI-Net exhibited a significant advantage over the other models, with an average NMSE reduction exceeding 50%, indicating its ability to maintain excellent reconstruction quality in highly compressed scenarios. Although the performance improvement of LwCSI-Net at low compression ratios was relatively modest, it still achieved an NMSE as low as −29.21, reflecting good reconstruction accuracy. Combined with the results in Figure 8, LwCSI-Net not only ensured reconstruction precision under high compression but also significantly reduced model complexity, achieving a favorable balance between performance and efficiency and outperforming the existing methods overall.
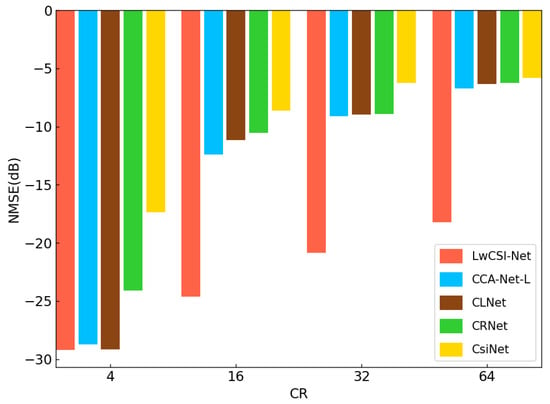
Figure 9.
NMSE values of different models at different compression ratios.
4.3. Analysis of Method Limitations
Although LwCSI-Net demonstrated strong reconstruction performance and computational efficiency across various compression ratios, particularly in high-compression scenarios, it still has several limitations. First, at a CR of 4, the performance improvement of LwCSI-Net over the other methods was limited, indicating that its advantages are more pronounced in high-compression environments. Second, while the model significantly reduced the number of parameters and floating point operations, some loss of fine-grained details remained at a CR of 64, which may have affected the accurate recovery of CSI. Furthermore, as the number of RIS reflection elements increases, the channel dimension grows accordingly, leading to a significant increase in training and inference complexity. This results in computational resource and time bottlenecks, limiting the model’s applicability in large-scale RIS systems. Although increasing the number of training epochs could improve the model’s fitting ability, it may also cause overfitting, thereby affecting the model’s generalization performance in practical scenarios. Finally, the proposed method was primarily evaluated on simulated datasets, and its generalization capability under real wireless channel conditions requires further investigation. These issues will be important directions for our future research.
5. Conclusions
This paper presents a novel lightweight autoencoder-based deep learning framework, LwCSI-Net, aimed at enabling efficient CSI feedback in RIS-assisted FDD communication systems. The proposed model integrates 1D-CNN, ECA Attention, and CRBlock, effectively simplifying the traditional autoencoder architecture while maintaining superior CSI reconstruction performance. Our simulation results demonstrate that under high compression ratios LwCSI-Net significantly outperforms the state-of-the-art methods, in terms of NMSE. Compared to our previous conference version, the average model complexity has been further reduced from 28.58% to 35.63%, reflecting substantial improvements in computational efficiency and model compactness. The ECA module enhances the model’s sensitivity to channel features, while the CRBlock improves feature representation and reconstruction quality, collectively strengthening robustness and generalization in dynamic RIS environments.
Moreover, LwCSI-Net features a compact architecture and low computational overhead, making it highly suitable for deployment on resource-constrained terminals and edge devices. Its energy-efficient design also aligns well with the development goals of 6G green communications. Beyond conventional mobile communication scenarios, LwCSI-Net demonstrates strong scalability and holds great potential in emerging applications such as edge intelligence and multi-agent cooperative networks.
Looking ahead, we aim to further enhance the model’s functionality and adaptability to address its current limitations. For instance, we plan to integrate multi-task learning frameworks to jointly optimize CSI feedback, channel estimation, and beamforming tasks. Additionally, the incorporation of meta-learning and online learning mechanisms is expected to improve the model’s adaptability and robustness in time-varying channel conditions. We intend to refine the model’s performance under low compression ratios to ensure consistent accuracy, and we also intend to evaluate its practical viability through more complex channel models and standardized datasets, thereby establishing a simulation platform that closely approximates real-world deployment conditions.
Author Contributions
Conceptualization, A.D. and W.X.; methodology, A.D. and Y.X.; validation, Y.X.; formal analysis, A.D. and J.Y.; writing—original draft preparation, Y.X.; writing—review and editing, A.D. and S.L.; visualization, Y.X. and S.L.; supervision, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Pilot Project for Integrated Innovation of Science, Education, and Industry of Qilu University of Technology (Shandong Academy of Sciences) under Grant 2024ZDZX08, the Shandong Provincial Natural Science Foundation under Grant ZR2023MF040, the National Natural Science Foundation of China (NSFC) under Grant 62272256, the Major Program of Shandong Provincial Natural Science Foundation for the Fundamental Research under Grant ZR2022ZD03, the Innovation Capability Enhancement Program for Small- and Medium-sized Technological Enterprises of Shandong Province under Grants 2022TSGC2180, and the Innovation Team Cultivating Program of Jinan under Grant 202228093.
Data Availability Statement
The data used in the manuscript can be generated according to the channel models mentioned in the paper.
Acknowledgments
Part of this research has been submitted to the WASA 2025 conference and has received an acceptance notification. The corresponding conference paper has now been officially published.
Conflicts of Interest
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. Optimization Procedure for Equation (14)
| Algorithm A1 Optimization Procedure for Equation (14) |
|
References
- Basharat, S.; Hassan, S.A.; Pervaiz, H.; Mahmood, A.; Ding, Z.; Gidlund, M. Reconfigurable intelligent surfaces: Potentials, applications, and challenges for 6G wireless networks. IEEE Wirel. Commun. 2021, 28, 184–191. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, W.; Xing, C.; Zhao, N.; Al-Dhahir, N.; Karagiannidis, G.K.; Yang, X. Intelligent integrated sensing and communication: A survey. Sci. China Inf. Sci. 2025, 68, 131301. [Google Scholar] [CrossRef]
- Shen, D.; Dai, L. Channel feedback for reconfigurable intelligent surface assisted wireless communications. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Virtual, 7–11 December 2020; pp. 1–5. [Google Scholar]
- Di Renzo, M.; Zappone, A.; Debbah, M.; Alouini, M.S.; Yuen, C.; De Rosny, J.; Tretyakov, S. Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Pan, C.; Zhou, G.; Zhi, K.; Hong, S.; Wu, T.; Pan, Y.; Ren, H.; Renzo, M.D.; Lee Swindlehurst, A.; Zhang, R.; et al. An Overview of Signal Processing Techniques for RIS/IRS-Aided Wireless Systems. IEEE J. Sel. Top. Signal Process. 2022, 16, 883–917. [Google Scholar] [CrossRef]
- Liang, H.W.; Chung, W.H.; Kuo, S.Y. FDD-RT: A simple CSI acquisition technique via channel reciprocity for FDD massive MIMO downlink. IEEE Syst. J. 2016, 12, 714–724. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G. No Downlink Pilots Are Needed in TDD Massive MIMO. IEEE Trans. Wirel. Commun. 2017, 16, 2921–2935. [Google Scholar] [CrossRef]
- An, J.; Xu, C.; Wu, Q.; Ng, D.W.K.; Di Renzo, M.; Yuen, C.; Hanzo, L. Codebook-based solutions for reconfigurable intelligent surfaces and their open challenges. IEEE Wirel. Commun. 2022, 31, 134–141. [Google Scholar] [CrossRef]
- Shin, B.S.; Oh, J.H.; You, Y.H.; Hwang, D.D.; Song, H.K. Limited channel feedback scheme for reconfigurable intelligent surface assisted MU-MIMO wireless communication systems. IEEE Access 2022, 10, 50288–50297. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.K.; Jin, S.; Li, G.Y. Overview of deep learning-based CSI feedback in massive MIMO systems. IEEE Trans. Commun. 2022, 70, 8017–8045. [Google Scholar] [CrossRef]
- Wen, C.K.; Shih, W.T.; Jin, S. Deep learning for massive MIMO CSI feedback. IEEE Wirel. Commun. Lett. 2018, 7, 748–751. [Google Scholar] [CrossRef]
- Ji, S.; Li, M. CLNet: Complex input lightweight neural network designed for massive MIMO CSI feedback. IEEE Wirel. Commun. Lett. 2021, 10, 2318–2322. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, W.; Liang, L.; Wang, N.; Li, G.Y.; You, X. A lightweight deep network for efficient CSI feedback in massive MIMO systems. IEEE Wirel. Commun. Lett. 2021, 10, 1840–1844. [Google Scholar] [CrossRef]
- Wang, T.; Wen, C.K.; Jin, S.; Li, G.Y. Deep learning-based CSI feedback approach for time-varying massive MIMO channels. IEEE Wirel. Commun. Lett. 2018, 8, 416–419. [Google Scholar] [CrossRef]
- Li, X.; Wu, H. Spatio-Temporal Representation With Deep Neural Recurrent Network in MIMO CSI Feedback. IEEE Wirel. Commun. Lett. 2020, 9, 653–657. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.K.; Jin, S.; Li, G.Y. Convolutional Neural Network-Based Multiple-Rate Compressive Sensing for Massive MIMO CSI Feedback: Design, Simulation, and Analysis. IEEE Trans. Wirel. Commun. 2020, 19, 2827–2840. [Google Scholar] [CrossRef]
- Ji, S.; Li, M. Enhancing Deep Learning Performance of Massive MIMO CSI Feedback. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 4949–4954. [Google Scholar]
- Wang, Y.; Lu, H.; Sun, H. Channel estimation in IRS-enhanced mmWave system with super-resolution network. IEEE Commun. Lett. 2021, 25, 2599–2603. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, J.; Song, J. Multi-resolution CSI feedback with deep learning in massive MIMO system. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Wang, B.; Teng, Y.; Lau, V.; Han, Z. Cca-net: A lightweight network using criss-cross attention for csi feedback. IEEE Commun. Lett. 2023, 27, 1879–1883. [Google Scholar] [CrossRef]
- Xie, W.; Zou, J.; Xiao, J.; Li, M.; Peng, X. Quan-transformer based channel feedback for RIS-aided wireless communication systems. IEEE Commun. Lett. 2022, 26, 2631–2635. [Google Scholar] [CrossRef]
- Yu, X.; Li, D. Phase shift compression for control signaling reduction in IRS-aided wireless systems: Global attention and lightweight design. IEEE Trans. Wirel. Commun. 2024, 23, 8528–8541. [Google Scholar] [CrossRef]
- Feng, H.; Xu, Y.; Zhao, Y. Deep Learning-Based Joint Channel Estimation and CSI Feedback for RIS-Assisted Communications. IEEE Commun. Lett. 2024, 28, 1860–1864. [Google Scholar] [CrossRef]
- Yu, X.; Li, D.; Xu, Y.; Liang, Y.C. Convolutional autoencoder-based phase shift feedback compression for intelligent reflecting surface-assisted wireless systems. IEEE Commun. Lett. 2021, 26, 89–93. [Google Scholar] [CrossRef]
- Peng, Z.; Li, Z.; Liu, R.; Pan, C.; Yuan, F.; Wang, J. Deep Learning-Based CSI Feedback for RIS-Aided Massive MIMO Systems With Time Correlation. IEEE Wirel. Commun. Lett. 2024, 13, 2060–2064. [Google Scholar] [CrossRef]
- Guo, J.; Chen, W.; Wen, C.K.; Jin, S. Deep learning-based two-timescale CSI feedback for beamforming design in RIS-assisted communications. IEEE Trans. Veh. Technol. 2022, 72, 5452–5457. [Google Scholar] [CrossRef]
- Guo, J.; Yang, X.; Wen, C.K.; Jin, S.; Li, G.Y. Deep Learning-Based CSI Feedback for RIS-Assisted Multi-User Systems. IEEE Trans. Commun. 2025, 73, 4974–4989. [Google Scholar] [CrossRef]
- Xue, Y.; Dong, A.; Li, S.; Yu, J.; Jia, J. Lightweight Attention-Based CNN Architecture for CSI Feedback of RIS-Assisted MISO Systems. In Proceedings of the International Conference on Wireless Artificial Intelligent Computing Systems and Applications, Tokyo, Japan, 24–26 June 2025; Springer: Berlin/Heidelberg, Germany, 2025; pp. 340–350. [Google Scholar]
- Zhi, K.; Pan, C.; Ren, H.; Wang, K.; Elkashlan, M.; Di Renzo, M.; Schober, R.; Poor, H.V.; Wang, J.; Hanzo, L. Two-timescale design for reconfigurable intelligent surface-aided massive MIMO systems with imperfect CSI. IEEE Trans. Inf. Theory 2022, 69, 3001–3033. [Google Scholar] [CrossRef]
- Shen, D.; Dai, L. Dimension reduced channel feedback for reconfigurable intelligent surface aided wireless communications. IEEE Trans. Commun. 2021, 69, 7748–7760. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).