Abstract
To address the challenges of image inpainting in scenarios with extensive or irregular missing regions—particularly detail oversmoothing, structural ambiguity, and textural incoherence—this paper proposes an Image Structure-Guided (ISG) framework that hierarchically integrates structural priors with semantic-aware texture synthesis. The proposed methodology advances a two-stage restoration paradigm: (1) Structural Prior Extraction, where adaptive edge detection algorithms identify residual contours in corrupted regions, and a transformer-enhanced network reconstructs globally consistent structural maps through contextual feature propagation; (2) Structure-Constrained Texture Synthesis, wherein a multi-scale generator with hybrid dilated convolutions and channel attention mechanisms iteratively refines high-fidelity textures under explicit structural guidance. The framework introduces three innovations: (1) a hierarchical feature fusion architecture that synergizes multi-scale receptive fields with spatial-channel attention to preserve long-range dependencies and local details simultaneously; (2) spectral-normalized Markovian discriminator with gradient-penalty regularization, enabling adversarial training stability while enforcing patch-level structural consistency; and (3) dual-branch loss formulation combining perceptual similarity metrics with edge-aware constraints to align synthesized content with both semantic coherence and geometric fidelity. Our experiments on the two benchmark datasets (Places2 and CelebA) have demonstrated that our framework achieves more unified textures and structures, bringing the restored images closer to their original semantic content.
Keywords:
image inpainting; structural prior guidance; generative adversarial networks; multi-scale attention; spectral normalization; deep learning MSC:
68T07
1. Introduction
Image inpainting is one of fundamental tasks in computer vision that aims to restore missing or corrupted regions in an image while ensuring that the restored content blends naturally with the original structure and texture. This capability has a wide range of applications, including photo restoration, object removal, medical imaging, and video editing. However, achieving high-quality inpainting results remains challenging, particularly when dealing with large missing regions or complex semantic structures. Early inpainting methods primarily relied on diffusion-based and texture synthesis techniques. The Blind Spot Compensation by Backward Propagation (BSCB) model [1], inspired by partial differential equations (PDEs), used a diffusion process to propagate edge information into missing regions. Similarly, exemplar-based texture synthesis, introduced by Criminisi et al. [2], filled missing areas by sampling similar patches from the undamaged portions of an image. While effective for small holes, these methods have struggled with complex scenes and large-area missing regions.
With the advancement of deep learning, the neural network-based models have been applied to inpainting by learning high-level feature representations. Pathak et al. [3] pioneered the use of Generative Adversarial Networks (GANs) for inpainting via their Context Encoder (CE) model, which introduced adversarial training to predict missing content. However, the CE model mainly focuses on the missing areas, failing to leverage information from unmasked regions, which led to texture inconsistencies. To address the issue, Lizuka et al. [4] introduced a dual-discriminator model to improve local and global consistency. This dual discriminator strategy aims to improve the consistency of the repaired images in terms of local details and overall structure. Yang et al. [5] achieved promising results by incorporating texture synthesis concepts into a fine-grained repair network. In the classic U-net architecture, Laube et al. [6] proposed an improvement strategy to more effectively handle image inpainting tasks by introducing skip connections, which effectively transmit pixel information from the undamaged parts of the image to the damaged areas, thereby assisting in the image inpainting process.
In recent years, image inpainting techniques have expanded into multimodal and 3D scenarios. Wender et al. [7] applied frequency-domain inpainting principles to Neural Radiance Fields (NeRFs), proposing a NeRF-based object removal framework that achieves seamless erasure of target objects in 3D scenes through implicit representation editing. Shamsolmoali et al. [8] developed the TransInpaint network, which introduces a context-adaptive mechanism to exploit cross-region semantic correlations via Transformer-based long-range modeling, thereby enhancing the robustness of content inference under large-area missing conditions. Chen et al. [9] recently proposed a large-mask multivariate inpainting framework that integrates discrete latent code representations with bidirectional Transformer prediction. Through a three-stage “encode-predict-decode” pipeline, this approach deeply fuses image prior knowledge with generative inpainting, maintaining visual plausibility even under extreme mask ratios.
However, existing deep learning-based inpainting algorithms still face several unresolved issues. When confronted with significant pixel loss, networks may struggle to effectively restore global semantic information, resulting in inconsistencies in the content of the repaired images. Furthermore, when dealing with non-rectangular damage, the generated predictions may lack reasonable representation of the image’s structural content, leading to some distortion and blurriness. Additionally, without effectively utilizing certain extra information from the undamaged parts of the image, it is challenging to leverage this structural information to assist and guide the final repair.
To address these issues, this paper proposes a structure-guided image inpainting algorithm model. The network follows a repair strategy of “structure-first, details-later.” The first stage focuses on restoring the edge structure of the damaged image, outputting a black-and-white edge map containing the basic structural information of the image to be repaired, which belongs to the coarse repair process. In the second stage, the complete structure map predicted in the first stage is used as guidance to repair the texture details and color information of the missing regions. While maintaining the overall structural integrity of the image, this stage further enhances the visual quality of the image. Guided by structural information, the texture inpainting network can strengthen the generation of the image’s contours, making the final inpainting result more realistic and refined. Both stages of the network use GAN. The specific approach and innovations are summarized as follows:
- To better utilize the structural features, which are key characteristics of images, we employ Holistically Nested Edge Detection (HED) [10] to extract edge structures in the image inpainting task. By utilizing the extracted structural information to assist in network training, this approach can more effectively constrain the network learning process, alleviate blurriness in the images, and improve repair quality.
- During the structural inpainting stage, the gated convolution is used to replace traditional convolution in the iterative training process, allowing the generator to effectively learn the relationship between the structural information of known regions and the masked areas. By combining multi-scale discriminator architecture and reconstructing loss functions, the spectral normalization is introduced into the discriminator network to stabilize training.
- In the texture inpainting stage, this paper incorporates an attention mechanism to capture more accurately the effective features of the regions that require repair and combines global and local dual discriminator structures to produce more realistic and accurate inpainting results.
2. Relation Work
Recent advances in image inpainting can be broadly categorized into three types: (1) Convolutional Neural Network (CNN)-based, (2) Transformer-based, and (3) Generative model-based, such as GANs and diffusion models. Each of these approaches offers unique strengths and limitations in addressing the challenges of structural coherence, texture synthesis, and large-hole restoration.
2.1. Convolutional Neural Network (CNN)-Based Methods
CNNs, with their powerful feature extraction capabilities, have become foundational in image inpainting. Early work focused on encoder–decoder architectures to learn contextual information for generating missing regions. Hui Zheng et al. (2020) proposed a Dense Multi-scale Fusion Network (DMFN) [11] for fine-grained image inpainting, incorporating a self-guided regression loss and geometric alignment constraints. This method leverages dense combinations of dilated convolutions to achieve high receptive fields and employs a discriminator with local and global branches to ensure content consistency, substantially improving inpainted image quality. Traditional convolution-based methods often fill missing regions with substitute values, leading to color discrepancies and blurring. To address this, Liu et al. (2018) introduced partial convolution for irregular mask inpainting [12], proposing a mechanism to automatically update layer-wise masks by setting weights to zero in missing regions, thereby avoiding erroneous filling. However, partial convolution still faces challenges such as strong mask dependency and insufficient long-range dependency modeling. Suvorov et al. [13] proposed the LaMa framework, which employs Fast Fourier Convolution (FFC) to accelerate million-pixel image processing by leveraging the frequency-domain global receptive field properties, resulting in a threefold increase in inference speed compared to conventional methods. This is to further harmonize global structures and local details. To address limitations in frequency-domain methods, Chu et al. [14] improved LaMa’s FFC module by proposing Unbiased Fast Fourier Convolution (UFFC), which suppresses high-frequency noise interference through frequency-domain feature normalization, significantly enhancing the quality of complex texture generation. Deep Neural Networks and Attention Mechanism for Image Inpainting (DNNAM) [15] was introduced by Chen et al. in 2024. It interposes spatial-attention and channel-attention modules between the encoder and decoder to dynamically recalibrate feature weights. Compared to pure Transformer-based approaches, DNNAM maintains high inpainting quality while offering faster training and inference speeds, making it well suited for real-time applications.
2.2. Transformer-Based Methods
Transformer models, with their superior long-range dependency modeling capabilities, have introduced novel paradigms for image inpainting. Zhou et al. proposed TransFill [16], which encodes images via Transformers to capture long-range dependencies and guides inpainting with these features, yielding more consistent and natural results than CNN-based approaches. Hassani et al. introduced NAT [17], which reduces computational complexity through local neighborhood attention mechanisms while preserving global modeling capabilities, enabling efficient high-resolution image inpainting. Li et al. [18] first introduced the global self-attention mechanism into inpainting tasks through their Mask-Aware Transformer (MAT). By dynamically aggregating long-range contextual information via mask-aware attention weights, this approach achieved a significant improvement of 2.7 dB in PSNR metrics on the Places2 dataset to address the efficiency bottleneck in high-resolution image inpainting. In the direction of dynamic mask optimization, Ko et al. [19] proposed a Continuous Mask Tuner (CMT) that adjusts mask coverage through layer-wise self-attention, progressively guiding the model to inpaint missing regions from coarse to fine. This method resolves boundary artifacts caused by traditional fixed masks. Image Completion Transformer (ICT) [20] is a Transformer-based image completion framework designed to produce high-fidelity and multimodal inpainting results through holistic context modeling. By pioneering the application of the Transformer’s self-attention mechanism to image completion, ICT captures the global geometric and semantic relationships within an image, enabling the precise reconstruction of intricate structures in missing regions. In 2021, Kaiming He et al. proposed Masked Autoencoders Are Scalable Vision Learners (MAE) [21]. The core idea of MAE is to randomly mask out portions of an image and then train an autoencoder to reconstruct the occluded regions. In 2021, Zhao et al. proposed co-modulation GAN (CoModGAN) [22]. CoModGAN introduces a co-modulation mechanism that jointly applies conditional style vectors—extracted from the masked input—and stochastic style vectors—sampled from random noise—in a single affine transformation to modulate the weights of each convolutional layer in the generator. Inpainting Transformer (ITrans) [23] was proposed by Miao et al. in 2024. It employs a convolutional encoder–decoder architecture for feature extraction and image synthesis, into which global and local Transformer modules are inserted to flexibly capture contextual information at multiple scales.
2.3. Generative Model-Based Methods
Diffusion models, probability-based generative approaches that iteratively denoise data to synthesize images, have demonstrated exceptional performance in inpainting, particularly for large missing regions and complex scenes. Lugmayr et al. proposed RePaint [24], utilizing a Denoising Diffusion Probabilistic Model (DDPM) to generate inpainted regions by iteratively adding and removing noise. RePaint does not require task-specific training but relies on DDPM’s reverse denoising process, guided by known image regions, to produce contextually coherent results. Shortly thereafter, Litu et al. provided theoretical insights into RePaint [25], mathematically analyzing key mechanisms such as convergence and contextual consistency during denoising. Liu et al. introduced Tractable Steering [26], a method to guide diffusion models by aligning intermediate variables with known image regions at each denoising step, ensuring high consistency between generated and contextual content. Corneanu et al. (2024) proposed LatentPaint [27], which combines latent space optimization with diffusion models for efficient inference without costly training, achieving realistic inpainting results directly in the latent space. Fan et al. [28] designed a second-order generative model, SCMFF, which generates structural constraints via an edge restoration network to drive the image inpainting network in fusing multi-scale features. This effectively mitigates semantic conflicts and enhances the naturalness of inpainted regions. Jain et al. [29] focused on the synergistic generation of structure and texture. By adopting a coarse-to-fine strategy based on StyleGAN [30], they first generated low-resolution structural skeletons and then fused multi-level texture features through encoder skip connections, achieving semantically consistent high-frequency detail reconstruction. A Plug-and-Play Image Inpainting Model with Decomposed Dual-Branch Diffusion (BrushNet) [31], presented by Ju et al. in 2024, leverages a decomposed dual-branch architecture to markedly enhance both the semantic coherence and visual quality of inpainting results.
3. Method
3.1. Network Architecture
The structure of the image inpainting network consists of two main parts: the structure restoration network and the texture restoration network, both of which are based on GAN. The structure restoration network is responsible for processing high-frequency information in the image, namely the edge structure, which is crucial for ensuring the accuracy and rationality of the overall repaired image structure. The texture restoration network, on the other hand, handles the texture and details, which are important for the final image’s texture and realism. The overall network structure is shown in Figure 1. The generators of both networks are designed based on an encoder–decoder structure tailored for their respective tasks at each stage. The discriminator in the structure restoration network adopts a multi-scale discriminator, while the texture restoration network uses a dual-discriminator setup comprising a global and a local discriminator.
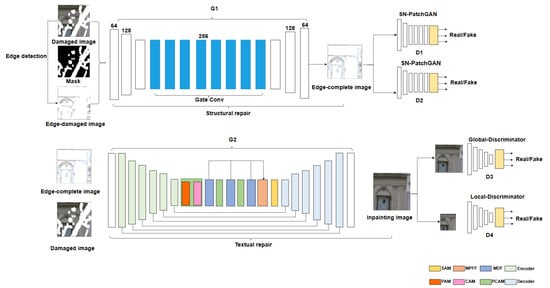
Figure 1.
Our network configuration—a hierarchical adversarial network with two specialized generators. Structural restoration: encoder–decoder with multi-scale residual blocks, supervised by a multi-scale discriminator for edge coherence. Texture restoration: attention-augmented skip-connections in the generator, constrained by dual discriminators.
Our model completes the restoration in three stages: 1. Edge Detection Stage: The HED (Holistically nested Edge Detection) edge detection algorithm is used to extract the edge structure of the damaged input image. First, the damaged image is preprocessed by converting the RGB input image into a grayscale image , resulting in a single-channel image. Then, the HED algorithm extracts the edge structure of the damaged image, resulting in an incomplete edge map . 2. Structure Restoration Stage: As shown in Equation (1), the incomplete edge map , mask image M, and grayscale image are used as the input for the structure restoration network. The mask image indicates the shape of the missing region, where pixel values of missing areas are 1, and other areas are 0. The structure restoration network adopts the GAN framework, consisting of a generator and a discriminator. The discriminator is composed of two spectral-normalized Markovian discriminators that operate at different scales. The generator and discriminator engage in adversarial training, eventually leading the generator to produce a complete edge structure map.
As shown in Equation (2), the generator and discriminator undergo adversarial training until a Nash equilibrium is reached, and the generator is capable of producing a semantically consistent complete edge structure map .
3. Texture Restoration Stage: As shown in Equation (3), is the complete edge structure map obtained by combining the predicted structure in the output from the second stage and the unbroken parts of the incomplete structure from the first stage. As shown in Equation (4), the overall input for this stage’s network is a concatenation of the damaged image and the complete edge structure map along the channel dimension, denoted as .
3.2. Network Structure in the Test Phase
During the testing phase, since only the trained image restoration model is needed for testing, only the generator path corresponding to the training phase is used to generate images. The testing process for the model restoration proceeds as follows: 1. Edge Detection: The damaged image is input into the edge detection network to extract edge information. 2. Structure Restoration: The detected edge results and the damaged image are input into the structure restoration network’s generator G1 (Figure 1), which generates a complete edge structure for the image. 3. Texture Restoration: The complete edge image and the damaged image are then input into the texture restoration network’s generator G2 (Figure 1), producing the final restored image.
3.3. Structural Repair Network
The generator network’s first layer is a normalization layer, followed by two sequences of downsampling layers. The middle part of the network contains a gated convolution sequence with residual connections for feature extraction, consisting of eight gated convolutions. The downsampling modules use 4 × 4 convolutional kernels to maintain the feature dimensions while minimizing information loss, thus reducing the computational complexity. Gated convolutions improve the management of feature information flow by integrating gating mechanisms, allowing the network to adaptively filter and update important features during backpropagation. This enhances the model’s ability to recognize and extract high-frequency structural features, while reducing the impact of less relevant features.
The gated convolution layers promote advanced spatial feature interaction, which is essential for capturing complex spatial dependencies. The 12th and 13th layers are upsampling layers that gradually restore the image to its original resolution. The structure of the generator in the structure restoration network is depicted in Figure 2.
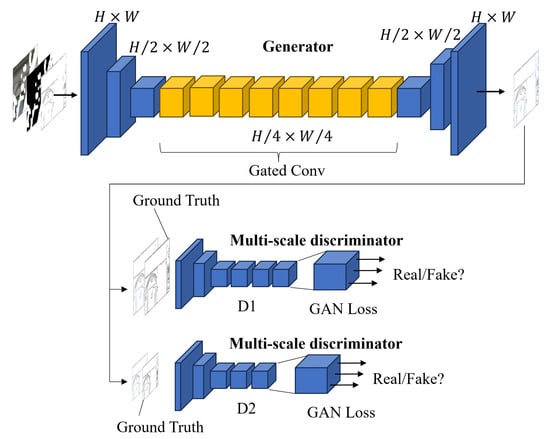
Figure 2.
Structure Repair Network Generator. The edge repair phase consists of eight gated convolutional blocks that are sampled and then discriminated by a multiscale discriminator.
The discriminator network consists of two spectral-normalized Markov discriminators working at different scales. These discriminators engage in adversarial training with the generator. The small-scale discriminator focuses on the global structure’s coherence, while the large-scale discriminator guides the generator to produce detailed textures. Spectral normalization is introduced to improve the detail quality of the predicted image structure and stabilize the training process. Combined with the hinge loss function, this improves the accuracy of edge structure restoration.
3.4. Texture Repair Network
The structure of the texture restoration network’s generator is shown in Figure 3. After obtaining the complete edge structure information from the structure restoration network, the image containing the complete edge structure and the damaged image are fed into the second-stage network. The texture restoration network primarily employs a multi-scale feature fusion approach for deep feature extraction. Through the combination of different convolution kernels, the network extracts and fuses multi-scale and deep-level image features.
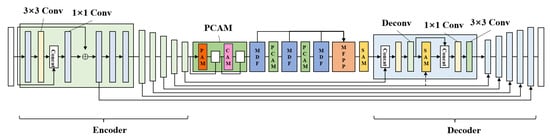
Figure 3.
Structure of texture repair network generator.
The generator consists of convolutional downsampling blocks, a partial convolutional attention module (PCAM), a multiscale pyramid feature fusion module (MPFF), a self-attention mechanism block, and convolutional upsampling blocks. The downsampling module is made up of convolution layers, normalization layers, and ReLU activation function layers. By stacking multiple convolution layers, the network progressively abstracts and extracts higher-level image features, as illustrated in Figure 4. The input of the convolutional downsampling module is skip-connected with the output of the 3 × 3 convolution, fusing feature maps at different scales. The input of the first convolutional downsampling block is skip-connected with the output of the 1 × 1 convolution of the second block, while the 3 × 3 convolution outputs of the second to sixth downsampling blocks are skip-connected with the 1 × 1 convolution outputs of the previous block. By utilizing multiple 1 × 1 convolution layers, non-linear activation functions are introduced into each convolution layer, enhancing the model’s expressive power and non-linear mapping capabilities.
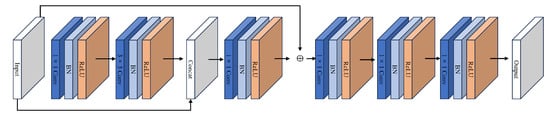
Figure 4.
Structure of texture repair network downsampling module.
The convolutional upsampling module consists of transposed convolution layers, a self-attention mechanism module, normalization layers, and ReLU activation layers, as shown in Figure 5. It is composed of 1 × 1 convolutions, transposed convolutions, self-attention feature modules, and 3 × 3 convolutions. The network contains six sets of convolutional upsampling modules, corresponding to the convolutional downsampling modules. The input of each upsampling module is a combination of the output from the previous upsampling module and the output of the corresponding 3 × 3 convolution layer from the downsampling module. By skip-connecting the downsampling and upsampling layers, the shallow information lost during feature extraction is restored in the decoding stage, enabling the network to retain more original details.
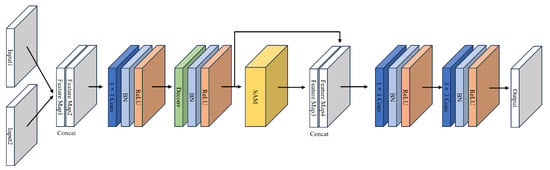
Figure 5.
Structure of the sampling module on the texture repair network.
The multi-scale pyramid feature fusion (MPFF) is composed of dilated convolutions with different dilation rates. Dilated convolutions can exponentially increase the receptive field without changing the size of the convolution kernel, allowing the model to capture more extensive contextual information. The attention mechanism block includes self-attention, channel attention, and pixel attention blocks to capture relationships between internal image features. Additionally, skip connections between the encoder and decoder facilitate direct information transmission, enabling the network to effectively fuse multi-scale features while ensuring that both fine-grained and coarse-grained information captured during encoding and decoding is fully utilized. This improves the quality of image restoration, both in detail recovery and overall structural reconstruction.
The structure of the texture restoration network’s discriminator is illustrated in Figure 6. The global discriminator evaluates the entire image, calculating the global difference between the generated image and the ground truth, while the local discriminator assesses differences between specific regions of the ground truth and the generated image. Both global and local discriminators [4] extract high-level semantic features from input images through downsampling operations, computing the corresponding global and local losses. To focus on the repaired areas, pixels in the unbroken regions of both the ground truth and the repaired image are set to zero, leaving only the repaired areas for the local discriminator to process. This approach allows the local discriminator to adapt to training on irregular missing regions.
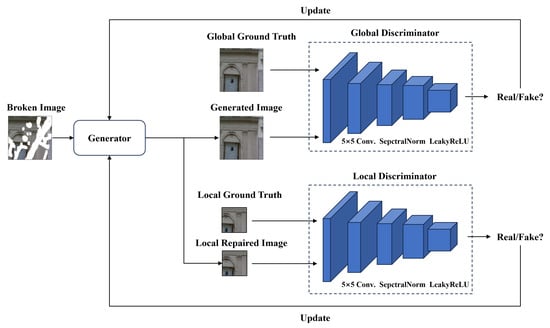
Figure 6.
Discriminative structure of texture repair network.
The global and local discriminators use convolutional layers to extract image features, with the same structure but different inputs. All convolutional layers use 5 × 5 kernels to capture broader image features in a single operation. Smaller convolution kernels might cause the discriminator’s loss to quickly approach zero, indicating insufficient training or that the generator is too easily deceiving the discriminator. The 5 × 5 kernel helps maintain stability in training. Spectral normalization and LeakyReLU activation are applied after each convolutional layer to further enhance model performance.
The Channel Attention Module (CAM) [32] enables models to autonomously focus on feature channels relevant to missing regions while suppressing less informative ones. By dynamically weighting channel-wise features, The Context Aggregation Module (CAM) effectively reduces redundant computations and enhances generalization capabilities through its adaptive mechanism designed for diverse corrupted inputs. Specifically, CAM analyzes the characteristics of different corrupted images and selectively processes relevant information, avoiding unnecessary calculations for redundant or uninformative regions. This selective processing not only optimizes computational efficiency but also enables the model to learn more robust features that are applicable across various types of image corruption. As a result, the model equipped with CAM can better generalize to unseen corrupted inputs, demonstrating improved performance on different datasets and real-world scenarios compared to models without such an adaptive mechanism. Multi-scale discriminators [33] improve the balance between high-frequency detail preservation and low-frequency structural generation in GAN. Compared to single-scale discriminators, multi-scale architectures extract diverse features across resolutions, capturing both global layouts and local textures. This approach enlarges the effective receptive field, strengthens inter-region correlations, and provides multi-level gradient signals to guide the generator toward photorealistic outputs.
3.5. Loss Function
3.5.1. Structure Restoration Network Loss Function
The structure restoration network primarily focuses on restoring the damaged edges of an image, producing a black-and-white structural edge map containing the fundamental structural information of the image to be repaired. The network emphasizes the structural information of the damaged image. The pre-processing of the input for the structure restoration network is as follows. Let the input real image sample be x, the edge map extracted by the edge detection algorithm be , and the grayscale image be . The processed grayscale image is defined as , where M is a binary mask image, and the damaged edge map is . The network’s input consists of the grayscale image , the edge map , and the binary mask M. The process of the structure restoration network is represented by Equation (5):
where represents the processing of the generator network, and denotes the predicted complete edge map. The discriminator network inputs are and the edge map extracted by the edge detection algorithm is denoted as . The combined loss of the structure restoration network includes loss, feature matching loss, and the hinge loss of the generative network, as defined by Equation (6):
where represents the pixel-level reconstruction loss, represents the spectral normalization Markov discriminator loss, and is the feature matching loss. and are weights to balance these losses. The generator is shown in Equation (7). The spectral normalization Markov discriminator is defined in Equation (8).
is the Markov discriminator, and the generator’s predicted structure is denoted as , with z representing the damaged input image. The loss measures the pixel-level error between the ground truth and predicted values, as shown in Equation (9):
The encoding process in the structure restoration network is represented by . Similar to perceptual loss, feature matching loss compares intermediate activation maps of the discriminator network to constrain the training process. Unlike perceptual loss, feature matching loss only compares specific layers’ activation maps in the discriminator network. The feature matching loss is defined in Equation (10):
where denotes the number of elements in the I activation layer, is the real complete edge structure map, and is the predicted edge map generated by the generator. represents the activation map in the I selected layer of the discriminator network.
3.5.2. Texture Restoration Network Loss Function
The loss function of the texture restoration network comprises pixel reconstruction loss, perceptual loss, style loss, and adversarial loss. The pixel reconstruction loss helps the network learn to reduce the pixel-level differences between the generated image and the original image, directly optimizing the details and clarity of the image. Perceptual loss ensures that the generated image visually resembles the real image, while style loss helps the network capture and replicate the style characteristics of the original image, enhancing consistency in structural restoration. Let the real image sample be x, and the sampling process of the encoder be represented as . M is a binary image mask. The pixel reconstruction loss computes the distance between the generated image and the ground truth, as defined by Equation (11):
To avoid blurring in the restoration results caused by relying solely on pixel reconstruction loss, perceptual loss is introduced, as proposed by Johnson et al. [34]. Unlike pixel reconstruction loss, perceptual loss compares consistency between different levels of feature representations, ensuring similarity in multi-scale features between low-resolution and high-resolution images, as defined by Equation (12):
where is the activation map of the I layer of the pre-trained VGG19 network [34], and represents the number of elements in the activation map of the I layer. denotes the noisy input image, and represents the denoised output image. Since the texture restoration stage involves pixel filling in the damaged area, style loss is introduced to ensure consistency between the style of the generated pixels and the unbroken region, helping to merge the style of the original image into the generated area. Style loss measures the distance between the Gram matrices of deep features from the real and generated images at the I layer, as defined by Equation (13):
where is the Gram matrix constructed from the activation map of the i-th layer. denotes the noisy input image, and represents the denoised output image. The final style loss for the texture restoration network consists of global and local discriminator style losses, as expressed in Equation (14):
where and are hyperparameters balancing the different losses, with a ratio of 3:2. The adversarial loss focuses on the high-frequency details of the image and is computed using a cross-entropy loss function, as shown in Equation (15):
By combining the above loss functions, the total loss L is obtained, as expressed in Equation (16):
where , , , and are adjustment parameters. These loss functions accelerate the network’s training process, improving the quality of the restored image during training. During testing, the network parameters are fixed, and loss functions are not computed.
4. Experiments
4.1. Environment
For a fair comparison, we use publicly available models tested on the same masks. In the experiments, we used Ubuntu 20.04.1, with a hardware setup consisting of two Intel E5-2680V3 CPUs, two NVIDIA TITAN V GPUs with 12 GB VRAM each, and 128 GB of RAM. The framework chosen for implementation was PyTorch (version 1.8.0), and the Adam optimizer was used to optimize the networks. All images, including the mask images, were resized to 256 × 256 before being fed into the network for training. A BatchSize of 8 was used per GPU.
The learning rate was initially set to , and to prevent overfitting or oscillations as the model approached an optimal solution, it was reduced to . The Adam optimizer was configured with the first moment () set to 0.5 and the second moment () to space stability during training. The structure and texture repair networks were trained using specific loss functions and parameters. For the structure repair network, the weighted parameters were set to = 1, = 1, and = 10, while for the texture repair network, the parameters were = 1, = 0.1, = 250, and = 0.2. These values were fine-tuned using a combination of experimental methods and binary search to find the most optimal settings for network training.
4.2. Datasets
The experiments in this study used two benchmark datasets, CelebA [35] and Places2 [36], to verify the effectiveness of the proposed model for image inpainting. Places2: This dataset is notable for its large sample size and rich diversity, covering a wide range of indoor and outdoor scenes. It provides a challenging environment for testing image inpainting across various context types. CelebA focuses on face images, featuring a large number of samples with diverse face orientations and types. This dataset is ideal for evaluating the model’s performance in face image restoration, a task that requires preserving fine facial details and structure.
For both datasets, 100,000 images were selected, with 90,000 images used for training the structure and texture repair networks, and 10,000 images reserved for testing. To simulate missing areas in the images, the study employed an irregular mask dataset from a previous study, which was designed to represent unpredictable damage or occlusions. During training, various transformations were applied to the masks, such as random rotations, horizontal flips, and vertical flips, to increase the model’s robustness to different orientations and perspectives, enhancing its ability to generalize to unseen scenarios. This strategy also effectively augmented the training data, improving the model’s capacity to handle various types of distortions.
4.3. Training Process
The training process for the proposed model is divided into two main parts: pre-training and joint training.
4.3.1. Pre-Training Phase
Structure Repair Network: Initially, the structure repair network is pre-trained. During each training iteration, m samples are randomly selected from the dataset. Edge Structure Extraction: These samples undergo preprocessing, where an edge detection algorithm is applied to extract the edge structures. The images are then converted to grayscale. Irregular Masking: The extracted edge structures and grayscale images are subjected to irregular masking to simulate the degradation process. This results in m damaged edge structure images and grayscale images.
Edge Structure Prediction: These preprocessed samples are fed into the structure repair network to predict complete edge structures. The generated edge structures are then validated using the discriminator network, which is trained using feature matching loss, adversarial loss, and L1 reconstruction loss. Training Cycle: After every k rounds of training for the discriminator, the structure generation network is trained to update the generator parameters.
4.3.2. Texture Repair Network Training
The texture repair network follows a similar training approach, first training the discriminator before training the generator. The m complete edge structure images (from the structure repair network) and the masked original images are input into the texture repair network’s generator, producing m repaired images. These generated images and the corresponding ground truth images are sent to the discriminator, where multiple loss functions—pixel reconstruction loss, perceptual loss, style loss, and adversarial loss—are used to update the discriminator parameters. After k rounds of training for the discriminator, the structure repair network’s completed images are fed back into the texture repair network’s generator to update its parameters.
4.3.3. Joint Training
During joint training, the processes for both networks run concurrently; the structure generator and texture generator work together to generate images that the texture discriminator cannot classify as real or fake. The texture discriminator attempts to distinguish between real data samples and generated samples. This alternating training helps each generator focus on its specific repair task, improving the overall performance of the model. This structured approach allows for effective training and collaboration between the networks, ensuring that both structural integrity and textural details are adequately restored in the images. The overall flow chart for training is shown in Figure 7.
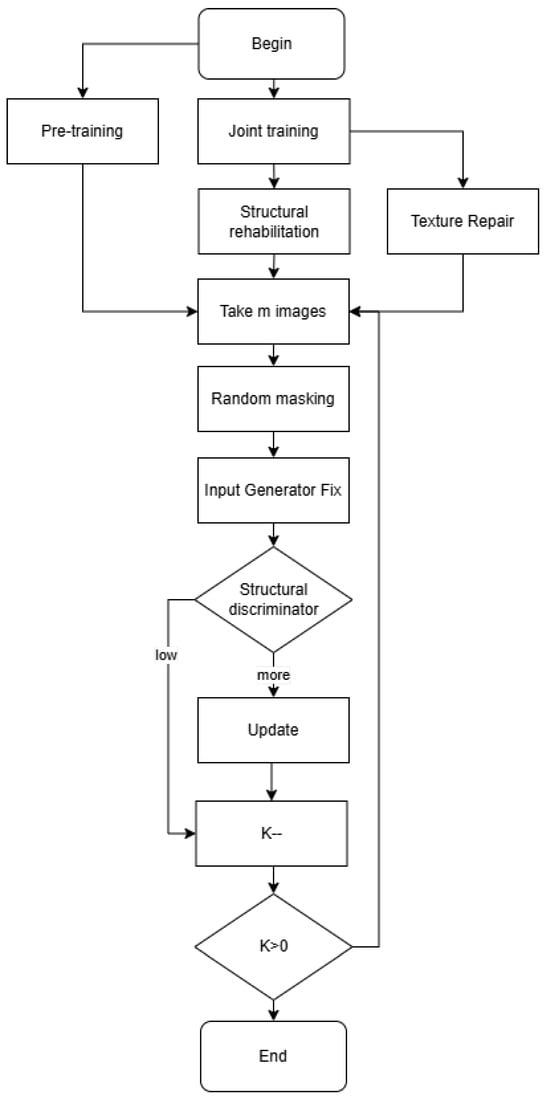
Figure 7.
Overall flow chart for training, illustrating the process of taking m images for training and discriminating them afterwards, training for k rounds.
4.4. Analysis of Experimental Results
To assess the efficacy of the proposed repair model, this section conducts a comparison with several cutting-edge models renowned for their remarkable inpainting outcomes. All these models adhere to a two-stage GAN framework for image inpainting. The models chosen for comparison are as follows: (1) Mask-Aware Transformer for Large Hole Image Inpainting (MAT) [18]: This approach introduces a Transformer-based architecture integrated with dynamic mask-aware attention to tackle large-hole image inpainting. By decoupling masked features and noise generation into dual branches, MAT effectively merges global structural consistency with local texture refinement, thereby achieving high-fidelity results on high-resolution images. (2) Contextual Attention-based Image Inpainting (CA) [37]: This model employs a content-aware attention mechanism, which focuses on relevant regions of the image during the inpainting process. This mechanism ensures that the generated content remains coherent with the contextual information of surrounding pixels. (3) Transformer with Partial Convolutions for Image Inpainting (TransInpaint) [8]: This hybrid methodology combines the global context modeling capability of Transformers with the spatial adaptability of partial convolutions. TransInpaint leverages self-attention to capture long-range dependencies and utilizes partial convolutions to concentrate on valid pixels around irregular holes, thereby enhancing both structural integrity and texture details. It demonstrates robustness in handling complex masks and achieves competitive performance on benchmarks such as Paris Street View. (4) EdgeConnect: Structure Guided Image Inpainting using EdgeConnect Prediction (EC) [38]: This technique integrates edge prediction with texture synthesis, utilizing pre-existing edge information to guide the inpainting process and enhance the structural integrity of the restored regions.
4.4.1. Quantitative Analysis
For quantifying the data, PSNR and SSIM [39] metrics were employed to evaluate the peak signal-to-noise ratio and structural similarity index of the repair results across different models, focusing on varying datasets and corresponding missing areas. The experimental results are presented in tables summarizing these comparisons.
As shown in Table 1, the performance metrics of this algorithm significantly outperform those of the other comparison algorithms. The gated convolution sequence embedded within the structural repair network effectively filters out low-correlation pixels, enhancing the network’s ability to associate high-correlation image content with damaged areas. This improves the consistency between the undamaged regions and the generated areas, allowing the model to more accurately extract and restore the structural features of the image. With the aid of structural information, the final output of the texture repair network exhibits better structural consistency, confirming that the two-stage network model possesses excellent repair performance.

Table 1.
Image inpainting performance comparison on Places2 dataset. ↑ stands for higher data values for better performance. ↓ stands for lower data values for better performance.
As shown in Table 2, the performance of the network model on the CelebA dataset surpasses that on the Places2 dataset. This is mainly because the images in the CelebA dataset, consisting of facial images, typically have clearer contours and more distinct features. As a result, the model can more easily identify and leverage these features during image restoration, leading to improved precision and quality in repairs. On the other hand, the Places2 dataset comprises a variety of different scenes, which are generally more complex and diverse than the images in CelebA. The Places2 images contain more intricate details, textures, and often more noise and distortion. Thus, repairing these images requires the model to use more sophisticated and efficient algorithms, which can reduce the overall restoration accuracy and quality.

Table 2.
Image inpainting performance comparison on CelebA dataset. ↑ stands for higher data values for better performance. ↓ stands for lower data values for better performance.
As shown in Table 3, on the Image-net dataset, our method outperforms other comparative methods across multiple metrics. In terms of PSNR, our method achieves 27.6, which is higher than ICT, LaMa, MAT, TransInpaint, and EdgeConnect. For SSIM, ours surpasses LaMa, TransInpaint, and EdgeConnect, and is competitive with ICT and MAT. Regarding LPIPS, ours is better than ICT, LaMa, MAT, TransInpaint, and EdgeConnect. For FID, our 7.6 outperforms all others like ICT, LaMa, MAT, TransInpaint, and EdgeConnect. This shows that our method has excellent performance in image restoration on the Image-net dataset, with advantages in both objective quality metrics and perceptual similarity, effectively restoring image details and structural information.

Table 3.
Comparison of methods based on performance metrics on Image-net dataset. ↑ stands for higher data values for better performance. ↓ stands for lower data values for better performance.
From the overall results, it is evident that the proposed model shows improvements across various metrics on both datasets. This suggests that the generative adversarial network (GAN) training in the model is more stable, and the quality of the generated repair images is significantly better. These results validate the effectiveness of the proposed algorithm in image restoration tasks.
4.4.2. Qualitative Analysis
Figure 8 shows the restoration results of the proposed model compared to other algorithms on the Places2 dataset. As observed in the figure, the CA algorithm struggles with color consistency, leading to blurring in finer details. Specifically, at the edges of missing regions, there is an unnatural transition between colors and a visible disconnect between the restored area and the original image. Additionally, for scene images, CA results in distorted and unnatural structures, especially in reconstructing textures and semantic information of objects like buildings. It also performs poorly when the missing regions are large, demonstrating limited effectiveness beyond smaller gaps. In contrast, both the EC (EdgeConnect) and the proposed model excel in recovering complex structural information, particularly in maintaining edge consistency around damaged areas. However, EC falls short in terms of image clarity, as seen in the first row of results, where it fails to clearly reconstruct the pink stripes on a door and inaccurately restores the red color of the door. There is a significant improvement in the effect of the MAT method. However, there are still some cases of uneven color. Both EC and the proposed model, however, demonstrate superior color consistency and seamless blending at the edges of the damaged regions. From a subjective visual perspective, the proposed model shows impressive restoration performance on the Places2 dataset, particularly when dealing with irregular masks. This highlights its effectiveness in restoring both texture and structural details in complex scenes.

Figure 8.
Sample of repair results on the Places2 dataset. CA restoration has obvious noise of artifacts. Compared with EC, our restoration has a more natural connection between the vessel and the environment, with good structural coherence. And compared with MAT, our restoration has a more realistic wall texture and lighting effect of the hut.
Figure 9 presents a comparison of restoration results between the proposed model and the CA, MAT, and EC on the CelebA dataset. The results indicate that the proposed model excels in restoring facial details accurately, preserving semantic integrity, and avoiding pixel blurring. Specifically, it demonstrates superior performance in reconstructing complex facial structures, ensuring that the restored images look more natural and consistent. In contrast, the CA model fails to adequately restore the semantic information of facial images, leading to significant blurring. This is particularly evident in the first and third rows of the comparison, where the eyes in the restored images show clear inconsistencies, resulting in visually unrealistic outcomes. The MAT model also suffers from some blurring, such as the eyes and mouth. This distortion prevents the model from generating a realistic appearance. While the EC model achieves relatively good restoration results, it still struggles with some blurring, especially in finer details like facial textures. Compared to the proposed model, EC falls short in producing detailed and precise textures. Overall, the results show that the proposed model outperforms the other models on the CelebA dataset when handling irregular masks, yielding visually superior restoration results. The restored regions blend more seamlessly with the surrounding intact areas, creating a more natural and coherent appearance.

Figure 9.
Sample of repair results on the CelebA dataset. Compared with the EC method, ours restores a more natural transition of light and shadow on the faces of the restored characters, and there is no hard difference between light and dark. Compared to MAT, ours restores fine textures such as hair strands with no blurring or clutter.
Figure 10 shows the comparison of the restoration effects of our model and other models on the Image-net dataset. Experiments indicate that our method outperforms other methods in terms of the accuracy of image restoration, the degree of detail restoration, and the overall visual effect. In the three images, before restoration, the stingray in the first image, the rooster in the second image, and the cutlery in the third image are obscured by irregular white areas, making it difficult to distinguish the details. The EC method has restored them, but there are obvious shortcomings, such as poor restoration of the stingray pattern, rooster feathers, and cutlery pattern. The MAT method has improved somewhat, but it still cannot restore the real appearance completely, such as the texture of the skin of the stingray, the luster of the rooster feathers, and the color details of the cutlery are not sufficiently fine. The details of the skin texture of the stingray, the shine of the rooster’s feathers and the color of the tableware are not fine enough. In contrast, our method not only accurately restores the clear outlines, delicate textures and vivid colors of the subject, but also perfectly renders its real texture, and the restored image is almost the same as the original one.
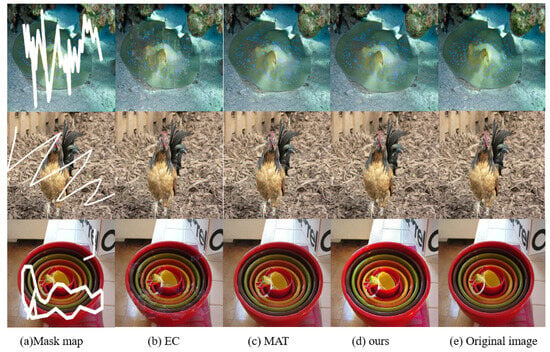
Figure 10.
Sample of repair results on Image-net dataset. EC and MAT methods failed to fully restore clarity and texture, while our method accurately recovers sharp outlines, vivid details, and natural textures, matching the original images closely.
4.5. Ablation Experiments
To evaluate the impact of various components on the model’s repair performance and understand their functions, an ablation study was conducted. This study re-trained the model on the Places2 dataset under the same hardware conditions after removing different modules from the overall network. The modified models were compared against the full model using the same test images, with quantitative comparisons performed using four objective metrics: PSNR, SSIM, LPIPS, and FID.
4.5.1. Impact of Edge Structure Guidance on Model Performance
To examine how using edge structure maps as priors affects the final image restoration, the structural restoration network was removed in this experiment. Instead, images with missing areas were directly fed into the texture restoration network. The results were compared with those from the complete model, both subjectively and through objective metrics.
As shown in Figure 11, without the guidance of auxiliary structural information, the restored images exhibit significant structural deficiencies. The model struggles to correctly identify texture boundaries, leading to a loss of semantic structure and poor visual appearance. Clear restoration artifacts are visible, with evident discontinuities between the restored areas and intact regions. When structural information is incorporated, the texture restoration network can better discern image boundaries. When the edge structure map has reasonable semantics, the restored image likewise reflects a coherent semantic structure. This demonstrates the importance of edge structure guidance for achieving higher-quality image restoration.

Figure 11.
Ablation experiment results. Full model is more accurate in the details, such as the texture of the house doors and windows; the color and shadow are more natural, and the overall visual effect is close to the original image, which has significant advantages over the unstructured bootstrap module.
As seen in Figure 12, the inclusion of gated convolution significantly enhances the restoration results. The gated convolution operation filters out low-correlation features, allowing the gate selection unit and feature extraction unit to update the filter parameters based on the changes in features after each convolution operation. The learned gating signals help determine which information should be retained or suppressed, effectively reducing the propagation of irrelevant information. Through this mechanism, when training the generative adversarial network iteratively, the model can effectively learn the relationship between the known regions’ structural information and the damaged portions. This helps suppress the influence of less correlated pixel regions on the structural prediction, thereby improving the rationality and accuracy of the generated image’s edge structure. This approach strengthens the coherence between the restored areas and the intact regions, leading to more seamless and realistic repair outcomes.

Figure 12.
Graph of ablation experiment results. Compared with the ungated convolutional sequence, the Full model outlines the image with more complete and clearer lines, which is an obvious advantage in detail rendering, and can better reproduce the structural features of the image.
From the comparison of various metrics in Table 3, it is evident that structural information has a significant impact on the final restoration performance of the model. Edge structure contour information provides a representation of the basic shapes and spatial relationships of objects within an image. This structural outline acts as crucial guidance for the texture restoration network, allowing it to better align with the overall structure of the image.
During the texture detail restoration process, the network can use structural information to generate textures that are more consistent with the surrounding environment, thus maintaining the overall coherence and continuity of the image. After incorporating structural priors, the generated images show significant improvement in the SSIM. By leveraging the edge structure contour information, the texture restoration network can more accurately determine which areas require texture filling and what characteristics the filled texture should have. This helps guide the network in generating more realistic and naturally coherent texture details, ultimately improving the overall quality of the restoration.
4.5.2. Impact of the Attentional Characteristics Module on Model Performance
To verify the impact of using attention feature modules on the final image restoration task, experiments were conducted by removing different attention modules from the texture detail restoration model while keeping other conditions constant. The system architecture is constructed based on the Multiscale Pyramid Feature Fusion Module (MPFF) and the Multiscale Dilated Fusion (MDF) as foundational components. Specifically, the model was retrained without the channel and partial Convolutional Attention Module (PCAM module) and without the self-attention feature module (SAM module). These modified models were compared with the full model under the same hardware conditions, and the results of the comparison experiments are presented in Table 4 and Table 5.

Table 4.
Comparison of evaluation indicators. ↑ stands for higher data values for better performance. ↓ stands for lower data values for better performance.

Table 5.
Comparison of evaluation indicators. ↑ stands for higher data values for better performance. ↓ stands for lower data values for better performance.
Based on the experimental results, it can be concluded that the attention mechanism modules significantly improve the image restoration network’s performance. The attention modules help the model focus on relevant information, leveraging the self-similarity within the image. This enhancement allows the model to effectively restore damaged regions with higher quality. By introducing the channel attention module, the network can better learn and understand the content of the image, improving its ability to represent features. Each channel in the image represents different color and texture details. The channel attention module captures dependencies between channels and assigns weights based on their importance, which helps the network capture detailed information and contextual relationships across the image. The self-attention mechanism allows the model to focus on both the damaged regions and the surrounding context. This helps the model accurately capture important features for repairing the missing areas. The self-attention mechanism leverages the self-similarity in the image, guiding the network to focus on small but similar features across different locations and scales. This leads to more precise and realistic texture detail in the final restoration result. In summary, both the channel attention and self-attention modules contribute to the model’s ability to capture detailed textures and context, resulting in a significant improvement in the quality of the restored images.
4.5.3. Impact of Various Layers in the VGG-Based Perceptual Loss on Model Performance
As shown in Table 6, in the exploration of model performance influenced by VGG-based perceptual loss, different layer combinations exhibit distinct impacts on key evaluation metrics. For the combination of conv1_2 + conv2_2, the model achieves a PSNR value of 28.5 and an SSIM value of 0.89. These values indicate a certain level of performance in terms of reconstructing image quality, where PSNR measures the ratio between the maximum possible power of a signal and the power of corrupting noise, and SSIM evaluates the structural similarity between the generated and original images. When examining the combination of conv3_3 + conv4_3, a more favorable performance is observed. The PSNR reaches 30.1, and the SSIM is 0.93. This substantial improvement suggests that these middle-level layers play a crucial role in capturing more discriminative and structurally relevant features for the perceptual loss. The higher PSNR implies a reduction in noise-like artifacts, and the increased SSIM reflects a closer match in structural information with the ground truth. For the single layer conv5_3, the PSNR is 29.2 and the SSIM is 0.90. Although the performance is slightly lower than that of conv3_3 + conv4_3, it still demonstrates a relatively good ability to preserve image structure and reduce distortion. This indicates that deeper layers like conv5_3 also contribute significantly to the perceptual quality, but perhaps in a different manner compared to the combined middle-level layers.

Table 6.
Performance metrics for different layer combinations. ↑ stands for higher data values for better performance.
5. Discussions and Future Work
Our proposed model, despite its remarkable achievements, faces certain limitations. Model performance limitation: The model performance decreases significantly when dealing with large hole areas and complex texture structures. For large-area holes, it is difficult for the current model to accurately predict the structure and details of the missing regions, leading to deficiencies in structural coherence and semantic consistency of the restored images. In complex texture scenes, the model is unable to accurately capture the subtle changes and complex patterns of the texture, and the restoration results often show blurred, distorted, or repetitive textures, which cannot achieve the ideal visual effect. Computational resource limitation: The computational complexity of the model increases dramatically when dealing with images containing large holes or complex textures. Due to the need to deal with more unknown information and complex features, the training and reasoning time of the model grows significantly, and the demand for computational resources is higher, which limits the application of the model in scenes with high real-time requirements or limited resources.
We plan to design a layered attention module, with the bottom layer focusing on cross-modal matching of local texture details and the top layer used for global semantically guided structural alignment, to solve the semantic conflict problem in cross-scale texture mixing scenarios. We also plan to extend the current 2D image restoration model to 3D scene understanding, and study how to deal with hole restoration and texture filling in 3D space to provide more powerful technical support for virtual reality, augmented reality, 3D modeling and other fields. Explore multimodal restoration: We plan to carry out research on multimodal image restoration, combining RGB images, depth maps, semantic maps and other modal information to provide richer contextual clues for the model, and further improve the restoration effect of the model in complex scenes, so that it can generate more realistic and accurate restoration results.
6. Conclusions
This study presents a comprehensive framework for image inpainting that systematically integrates structural priors and advanced deep learning architectures to address critical challenges in visual restoration tasks. We implement a hierarchical discriminator architecture incorporating spectral normalization and adversarial hinge loss optimization. This configuration enables progressive refinement of edge reconstruction accuracy across spatial frequencies while maintaining training stability. The generator network integrates a hybrid attention mechanism with pyramidal feature fusion, enabling simultaneous processing of local texture patterns and global contextual coherence. This multi-scale fusion strategy is further enhanced through skip-connected dilation convolutions that expand the network’s receptive field without sacrificing detail resolution. The experimental results substantiate three key advancements: (1) effective mitigation of boundary artifacts through physics-informed structural constraints; (2) enhanced texture synthesis via attention-based multi-scale feature correlation; (3) improved generalization capabilities across diverse inpainting scenarios. This work provides both theoretical insights into structural prior utilization and practical solutions for complex image restoration challenges, particularly in medical imaging and heritage conservation applications where geometric accuracy is paramount.
Author Contributions
Conceptualization, L.Z., T.Z. and H.Y.; Software, C.W.; Writing—original draft, T.Z.; Writing—review & editing, F.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “the Open Research Fund of Anhui Province Key Laboratory of Machine Vision Detection and Perception”, “the Basic Science Center Program of the National Natural Science Foundation of China (62388101)” and “the Shaanxi Province Natural Science Basic Research Program (2024JC-YBMS-560)”.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image inpainting. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 417–424. [Google Scholar]
- Criminisi, A.; Pérez, P.; Toyama, K. Region filling and object removal by exemplar-based inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef] [PubMed]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Alexei, A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. Acm Trans. Graph. (ToG) 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Yang, C.; Lu, X.; Lin, Z.; Shechtman, E.; Wang, O.; Li, H. High-resolution image inpainting using multi-scale neural patch synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6721–6729. [Google Scholar]
- Laube, P.; Grunwald, M.; Franz, M.O. Image inpainting for high-resolution textures using CNN texture synthesis. arXiv 2017, arXiv:1712.03111. [Google Scholar]
- Weder, S.; Garcia-Hernando, G.; Monszpart, A.; Pollefeys, M.; Brostow, G.J.; Firman, M.; Vicente, S. Removing objects from neural radiance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 16528–16538. [Google Scholar]
- Shamsolmoali, P.; Zareapoor, M.; Granger, E. Transinpaint: Transformer based image inpainting with context adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 849–858. [Google Scholar]
- Chen, H.; Zhao, Y. Don’t look into the dark: Latent codes for pluralistic image inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 7591–7600. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-Nested Edge Detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Hui, Z.; Li, J.; Wang, X.; Gao, X. Image fine-grained inpainting. arXiv 2020, arXiv:2002.02609. [Google Scholar] [CrossRef]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 85–100. [Google Scholar]
- Suvorov, R.; Logacheva, E.; Mashikhin, A.; Remizova, A.; Ashukha, A.; Silvestrov, A.; Kong, N.; Goka, H.; Park, K.; Lempitsky, V. Resolution-robust large mask inpainting with fourier convolutions. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2149–2159. [Google Scholar]
- Chu, T.; Chen, J.; Sun, J.; Lian, S.; Wang, A.; Zuo, Z.; Zhao, L.; Xing, W.; Lu, D. Rethinking fast fourier convolution in image inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 23195–23205. [Google Scholar]
- Chen, Y.; Xia, R.; Yang, K.; Zou, K. DNNAM: Image Inpainting Algorithm via Deep Neural Networks and Attention Mechanism. J. Appl. Soft Comput. 2024, 154, 111392. [Google Scholar] [CrossRef]
- Zhou, Y.; Barnes, C.; Shechtman, E.; Amirghodsi, S. Transfill: Reference-guided image inpainting by merging multiple color and spatial transformations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 2266–2276. [Google Scholar]
- Hassani, A.; Walton, S.; Li, J.; Li, S.; Shi, H. Neighborhood attention transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 6185–6194. [Google Scholar]
- Li, W.; Lin, Z.; Zhou, K.; Qi, L.; Wang, Y.; Jia, J. Mat: Mask-aware transformer for large hole image inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10758–10768. [Google Scholar]
- Ko, K.; Kim, C.S. Continuously masked transformer for image inpainting. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 13169–13178. [Google Scholar]
- Wan, Z.; Zhang, J.; Chen, D. High-Fidelity Pluralistic Image Completion with Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 4692–4701. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16000–16009. [Google Scholar]
- Zhao, S.; Cui, J.; Sheng, Y.; Dong, Y.; Liang, X.; Chang, E.; Xu, Y. Large Scale Image Completion via Co-Modulated Generative Adversarial Networks. arXiv 2021, arXiv:2103.10428. [Google Scholar] [CrossRef]
- Miao, W.; Wang, L.; Lu, H.; Huang, K.; Shi, X.; Liu, B. ITrans: Generative Image Inpainting with Transformers. J. Multimed. Syst. 2024, 30, 21. [Google Scholar] [CrossRef]
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Gool, L.V. Repaint: Inpainting using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11461–11471. [Google Scholar]
- Rout, L.; Parulekar, A.; Caramanis, C.; Shakkottai, S. A theoretical justification for image inpainting using denoising diffusion probabilistic models. arXiv 2023, arXiv:2302.01217. [Google Scholar] [CrossRef]
- Liu, A.; Niepert, M.; Van den Broeck, G. Image inpainting via tractable steering of diffusion models. arXiv 2023, arXiv:2401.03349. [Google Scholar] [CrossRef]
- Corneanu, C.; Gadde, R.; Martinez, A.M. Latentpaint: Image inpainting in latent space with diffusion models. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 4334–4343. [Google Scholar]
- Fan, Y.; Shi, Y.; Zhang, N.; Chu, Y. Image inpainting based on structural constraint and multi-scale feature fusion. IEEE Access 2023, 11, 16567–16587. [Google Scholar] [CrossRef]
- Jain, J.; Zhou, Y.; Yu, N.; Shi, H. Keys to better image inpainting: Structure and texture go hand in hand. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 208–217. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4401–4410. [Google Scholar]
- Ju, X.; Liu, X.; Wang, X.; Bian, Y.; Shan, Y.; Xu, Q. BrushNet: A Plug-and-Play Image Inpainting Model with Decomposed Dual-Branch Diffusion. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 150–168. [Google Scholar]
- Qiu, J.; Gao, Y. Position and channel attention for image inpainting by semantic structure. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 1290–1295. [Google Scholar]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-resolution image synthesis and semantic manipulation with conditional gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8798–8807. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Computer Vision–ECCV 2016; Springer: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep learning face attributes in the wild. In Proceedings of the IEEE International Conference on Computer Vision, Boston, MA, USA, 7–12 June 2015; pp. 3730–3738. [Google Scholar]
- Zhou, B.; Lapedriza, A.; Khosla, A.; Oliva, A.; Torralba, A. Places: A 10 million image database for scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1452–1464. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5505–5514. [Google Scholar]
- Nazeri, K.; Ng, E.; Joseph, T.; Qureshi, F. Ebrahimi, M Edgeconnect: Generative image inpainting with adversarial edge learning. arXiv 2019, arXiv:1901.00212. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6626–6637. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).