Abstract
Broadcasting in Mobile Ad Hoc Networks (MANETs) is significantly challenged by dynamic network topologies. Traditional fuzzy logic-based schemes that often rely on static fuzzy tables and fixed membership functions are limiting their ability to adapt to evolving network conditions. To address these limitations, in this paper, we conduct a comparative study of two innovative broadcasting schemes that enhance adaptability through dynamic fuzzy logic membership functions for the broadcasting problem. The first approach (Model A) dynamically adjusts membership functions based on changing network parameters and fine-tunes the broadcast (BC) versus do-not-broadcast (DNB) ratio. Model B, on the other hand, introduces a multi-profile switching mechanism that selects among distinct fuzzy parameter sets optimized for various macro-level scenarios, such as energy constraints or node density, without altering the broadcasting ratio. Reinforcement learning (RL) is employed in both models: in Model A for BC/DNB ratio optimization, and in Model B for action decisions within selected profiles. Unlike prior fuzzy logic or reinforcement learning approaches that rely on fixed profiles or static parameter sets, our work introduces adaptability at both the membership function and profile selection levels, significantly improving broadcasting efficiency and flexibility across diverse MANET conditions. Comprehensive simulations demonstrate that both proposed schemes significantly reduce redundant broadcasts and collisions, leading to lower network overhead and improved message delivery reliability compared to traditional static methods. Specifically, our models achieve consistent packet delivery ratios (PDRs), reduce end-to-end Delay by approximately 23–27%, and lower Redundancy and Overhead by 40–60% and 40–50%, respectively, in high-density and high-mobility scenarios. Furthermore, this comparative analysis highlights the strengths and trade-offs between reinforcement learning-driven broadcasting ratio optimization (Model A) and parameter-based dynamic membership function adaptation (Model B), providing valuable insights for optimizing broadcasting strategies.
MSC:
68M12
1. Introduction
MANETs are characterized by their self-configuring, decentralized nature, where nodes dynamically interact within wireless environments without relying on a fixed infrastructure. These networks are widely employed in applications demanding high adaptability and resilience, including disaster response, military communications, and remote sensing. However, the dynamic and unpredictable nature of MANET environments presents critical challenges, particularly in designing effective and efficient broadcasting mechanisms. These use-cases impose strict demands on broadcasting protocols, including the need to maintain reliable coverage despite rapid node mobility, limited energy availability, and fluctuating communication priorities. Our proposed adaptive broadcasting methods directly address these challenges. Method A’s reinforcement learning-based adjustment allows for the system to progressively improve decision-making in evolving network conditions typical of prolonged emergency operations. Meanwhile, Method B’s profile switching mechanism supports swift adaptation to sudden shifts, such as transitions between energy-saving modes and delay-sensitive transmissions, which are common in battlefield or crisis scenarios. These capabilities ensure that broadcasting strategies remain effective without centralized control, making the approach suitable for decentralized, resource-constrained MANET deployments under practical operational constraints.
A central limitation in existing broadcasting schemes is their reliance on static decision-making frameworks, such as fixed fuzzy logic tables and immutable membership functions. While fuzzy logic-based broadcasting schemes have been successful in addressing the uncertainties inherent in MANETs, their static nature restricts their ability to adapt to rapidly changing network conditions, such as variations in node density, mobility, or signal quality. Static configurations often fail to capture real-time network states accurately, leading to suboptimal decisions that either cause excessive redundant transmissions or insufficient coverage.
To defeat these deficiencies, in our previous research [1], we proposed a dynamic fuzzy logic-based broadcasting scheme that combined reinforcement learning techniques, specifically Temporal Difference (TD) learning and Monte Carlo (MC) simulations, with adaptive membership function adjustments. This approach dynamically modified membership functions based on key network parameters such as topology density, Connection Time of nodes, and RSSI. In addition, reinforcement learning was employed to refine the broadcasting ratio and optimize the fuzzy rule base through a reward and punishment mechanism, enabling the system to learn and adapt over time. The method demonstrated significant improvements in reducing redundant broadcasts, minimizing collisions, and enhancing message delivery reliability compared to static fuzzy logic approaches. The main limitation of our previous work was network overhead, resulting in increased resource requirements on the network and a slight delay. However, the iterative learning process of the RL algorithms proved to be very efficient at increasingly adapting to the network.
The selection of parameters for Model A, such as Connection Time (), Number of Neighbors (), and Signal Strength (), and combinations for Model B, e.g., for energy-based profiles or for delay-sensitive profiles, was based on their demonstrated impact on MANET performance in prior studies, including our previous works [1,2] and those cited in the Related Work section. Unlike many fuzzy-based approaches that consider overly broad parameter sets, often resulting in redundant packets, we focus on a concise set of impactful parameters that reduce Redundancy and computational overhead. Parameters like , , and have proven to be especially effective for forwarding decisions in dense network scenarios, while is particularly relevant in energy-aware contexts.
Building on the limitations observed in our prior work, this paper presents a comprehensive exploration of two advanced methods for overcoming the static nature of traditional broadcasting schemes in MANETs:
- Reinforcement learning-driven adaptive fuzzy logic broadcasting: This method extends our previous research [2] by integrating reinforcement learning (RL) with dynamically adjustable fuzzy logic membership functions. Key network parameters, including node density, Connection Time, and RSSI, are continuously monitored, and their fuzzy membership function boundaries are adaptively recalibrated based on real-time network conditions. The RL module then iteratively optimizes the broadcasting decision by adjusting the proportion of nodes that are broadcast (BC) versus those marked as do-no-broadcast (DNB), employing an -greedy policy to balance exploration and exploitation. This iterative learning process progressively refines the fuzzy rule base, enhancing network coverage, reducing Redundancy, and minimizing packet collisions.
- Parameter-based dynamic membership function adaptation: This novel approach introduces dynamic adaptability by leveraging multiple predefined profiles, each tailored for specific network conditions. Unlike Method A, Method B decouples the broadcasting ratio optimization from the adaptation of fuzzy logic membership functions. Instead, the method selects the optimal profile dynamically based on real-time macro-level network conditions. For example, energy-aware topology utilizes Eesidual Energy () and the Number of Neighbors ().
In this research, we explore the impact of the network parameters used for the membership function or broadcasting decision-making to see if creating a model that changes its impact parameters depending on network conditions can be a valid candidate for providing an efficient method of network broadcasting. Through extensive simulations and comparative analyses, this paper demonstrates that both methods significantly outperform static fuzzy logic-based broadcasting schemes, achieving superior adaptability, reduced network overhead, and enhanced delivery reliability. The reinforcement learning-driven approach excels in situations demanding iterative optimization, while the parameter-based method offers a more direct response to changing network conditions.
2. Related Work
2.1. Fuzzy Logic-Based Broadcasting Schemes
Fuzzy logic has been widely employed in MANETs to cope with the uncertainties and imprecision inherent in wireless environments. Early fuzzy logic broadcasting schemes typically utilized static fuzzy rule bases and fixed membership functions for key parameters [3,4], such as node density, Residual Energy [5,6], and Received Signal Strength Indicators (RSSIs), to decide whether a node should forward a broadcast packet [7]. By incorporating linguistic variables and fuzzy inference, these approaches proved to be more robust than purely threshold-based methods in handling continuously varying network states.
However, a principal drawback of the earlier fuzzy logic approaches is their static nature [8,9]. Once the membership functions and rule sets are defined, they often remain unchanged throughout the network operation. As a result, these approaches may fail to adapt to rapidly evolving conditions, such as fluctuating node mobility or changing topology densities. The protocols that dynamically evaluated link metrics (e.g., relative mobility or link age, etc.) using a fuzzy system to decide further action proved to be efficient [10,11,12]. Consequently, static fuzzy schemes can cause either excessive redundant transmissions or inadequate coverage when network parameters drift beyond their initially configured ranges [13,14]. Despite these limitations, fuzzy logic-based broadcasting remains a foundational method due to its interpretability and relative simplicity in implementation. In our previous work [2], we found this issue to be an important factor for future improvement, as dynamic membership or parameter selection and adaptability could ensure the model’s capability for adapting to new environments and network changes; this alone could enhance model performance, aside from further enhancements that could be achieved by, for example, the introduction of RL into the module.
2.2. Reinforcement Learning-Based Broadcasting Approaches
Reinforcement learning (RL) approaches can be efficiently used to enhance broadcasting mechanisms’ adaptability by allowing for nodes to learn from their past actions and the resulting network performance [15,16]. In RL-driven schemes, each node iteratively adjusts its broadcasting behavior based on local or global feedback, often expressed as a “reward” or “penalty” [17]. For example, a reward may be provided when a node’s decision leads to better coverage or reduced collisions. In contrast, a penalty is incurred for redundant transmissions or packet losses. In addition, the RL approach can be used in different steps of the mechanism, such as the decision-making process or in some steps of the pre-learning phase, in order to train the module.
Q-learning and SARSA are among the most popular RL algorithms integrated into MANET broadcasting [18,19]. In addition, fuzzy logic with double Q-learning for routing in intermittently connected mobile networks has also been proposed for a similar purpose [20,21]. These algorithms update a value function over time, allowing for the node to converge toward an optimal or near-optimal decision policy for forwarding packets. While such RL-based methods can dynamically adapt to changing network conditions, they can also introduce computational overhead and convergence delays, particularly when the learning rate is slow or the state space is large. Consequently, the iterative nature of RL poses a trade-off between adaptability and computational cost, highlighting the need for efficient state representations and reward designs. In addition, in our previous work [1], we found that making dynamic membership in RL, while effective, can still lead to room for improvement when it comes to choosing the impact parameters necessary to further enhance the adaptability mentioned and the ability of networks to choose which parameters are most important for their function.
2.3. Hybrid Fuzzy Logic and Reinforcement Learning
Combining fuzzy logic with reinforcement learning has emerged as a promising direction for improved broadcast decision-making in MANETs and other network protocols [22,23]. In these hybrid approaches, fuzzy inference systems handle uncertainties by mapping real-time network measurements to linguistic variables and intermediate decisions, dynamic membership functions, and adapting the ranges that are assigned to those linguistic variables. Meanwhile, reinforcement learning refines decision-making process ratios, such as BC/DNB variables. Furthermore, the role of RL can be changed to adjust either the fuzzy rule sets or the membership functions over time based on observed outcomes in the network, depending on need.
We discovered that one advantage of this synergy is that RL can systematically tune the parameters of the BC/DNB ratio to account for further improving packet duplication by reducing the ratio of nodes taking part in broadcasting if the network coverage is already at maximum, meaning that lesser nodes could broadcast the message while keeping the broadcasting intact. Temporal variations in network metrics, such as node, RSSI, and Connection Time, can be accounted for and adapted to using a dynamic membership function. Hybrid systems thus maintain the interpretability and human-readable nature of fuzzy logic while adding a learning loop that continuously updates the decision policy. However, these methods can become more complex in terms of computational requirements, as they integrate both fuzzy inference overhead and the iterative updates of RL agents; therefore, using them in less network-constrained environments could prove to be more appropriate. Moreover, similar to the pure RL approach, finding the right balance between exploration (trying new fuzzy membership configurations or rules) and exploitation (using the learned best practice) remains a non-trivial challenge; furthermore, new approaches where the initial parameters selected for dynamic membership are changeable could open a way to a method where sets of parameters could be used depending on the given network statistics.
2.4. Adaptive Mechanisms to Overcome Static Limitations
Given the drawbacks of purely static schemes, we want to focus on the experience we gained from our previous work and improve on that work by focusing on introducing adaptive mechanisms that respond proactively to changing network environments. The adaptive mechanisms can be utilized at different steps of the module to account for a variety of changes in the network.
- Dynamic membership functions: Instead of utilizing fixed membership functions or adjusting the fuzzy set boundaries based on real-time estimates of given network parameters, in our case, we want to see how having multiple sets of such parameters in combination can perform. By shifting these boundaries dynamically, the fuzzy inference can stay relevant under varying conditions and avoid suboptimal broadcast decisions.
- Adaptive Parameter selection: A different strategy is to adapt the weight or importance of each input parameter (e.g., RSSI, Residual Energy, mobility, and Number of Neighbors) according to current network conditions. This dynamic weighting ensures that the most critical parameters for maintaining coverage and minimizing collisions are prioritized when making broadcast decisions.
- Hybrid Adaptation with RL: Reinforcement learning can be utilized to further optimize either the broadcasting ratio or the fuzzy logic rule base. For instance, RL agents can assign a reward for each successful broadcast that increases coverage while minimizing collisions, leading to fine-tuning of the fuzzy system over time. This integrated approach was shown to reduce overhead and collision rates compared to purely static or purely fuzzy-based methods in our previous work [1].
Model A and Model B are designed to overcome the rigidity of conventional fuzzy systems and the complexity of RL-based methods by focusing on lightweight, profile-driven adaptability. Rather than relying on a fixed rule base or broad parameter sets, the models dynamically adjust behavior using targeted combinations of impactful parameters suited to different network conditions. This approach reduces unnecessary transmissions and computation while maintaining flexibility across scenarios like energy-constrained or delay-sensitive environments. To our knowledge, this specific use of selective parameter profiling in adaptive fuzzy systems remains underexplored in the recent MANET broadcasting literature.
In this research, we want to implement a novel approach that uses adaptive parameter selection to understand the impact of each parameter and how they perform in tandem with each other, and compare this method with our previous work to understand the weaknesses and strengths of both of these approaches, understanding which one of them is the better candidate or how we can improve them further.
3. Proposed Dynamic Fuzzy Logic for Broadcasting
3.1. Recap of Previous Dynamic Fuzzy Method
In our previous work, we introduced dynamic membership function range adjustment to address the adaptability issue or the lack of adaptability in the existing methods. Specifically, we monitored key parameters such as Connection Time (), Number of Neighbors (), and Signal Strength (), and periodically recalibrated their fuzzy membership function boundaries. Formally, each membership function for variable was defined as follows:
where were updated at runtime based on a sliding-window assessment of network conditions. While this approach demonstrated improved adaptability compared to static fuzzy schemes, it relied on a single set of membership functions whose ranges were adjusted, but whose overall sets remained uniform across all network scenarios. The overall architecture of the proposed models can be seen in Figure 1.
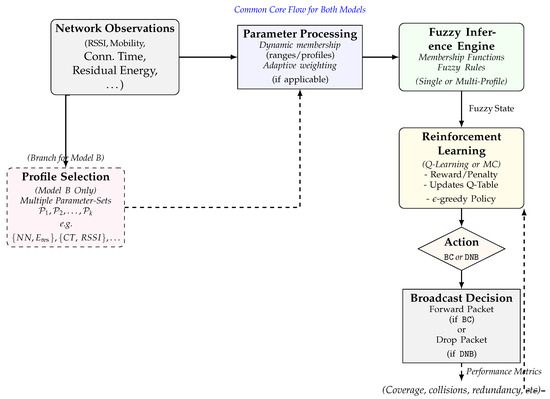
Figure 1.
The architecture of the proposed models. (Common core flow): Both Model A and Model B take raw network observations (RSSI, mobility, neighbor count, energy, etc.), process them via dynamic membership, then pass them into a fuzzy inference engine. The output “fuzzy state” goes to the reinforcement learning module, which updates a Q-table based on rewards/penalties (e.g., collisions vs. coverage). The final decision is BC(broadcast) or DNB(do not broadcast). (Model B extra step): A Profile Selection block dynamically switches among multiple parameter set profiles (e.g., energy-based, mobility-based) to handle different network conditions. Model A uses only one profile with range adjustments (Number of Neighbors, RSSI, Connection Time).
The overall cooperation between the fuzzy logic system and the reinforcement learning agent is formalized in Algorithm 1. At each adaptation interval, the system selects the most suitable fuzzy profile based on recent performance, derives a fuzzy state representation, and leverages Q-learning to optimize the broadcast decision (BC or DNB) in real-time. This cooperative loop ensures both context-awareness and long-term performance optimization across heterogeneous network conditions.
| Algorithm 1 Fuzzy-RL Cooperative Decision Process |
|
3.2. Motivation for Multiple Parameter Set Profiles
Although range-based updating captured short-term network changes, there remain cases where fundamentally different fuzzy profiles are required. For instance, a lightly populated network (e.g., 40 nodes) may favor the membership function where plays a significant role less than a densely populated network (e.g., 280 nodes) and, likewise, different network conditions and parameters, such as the energy constraints of the topology, the importance of delay, or overall how topology scenarios—such as if nodes span across long distances, their communication frequency, etc.—might make the use of the initial three parameters throughout the network life ineffective.
While our previous method adapted to network conditions by dynamically adjusting the ranges of fuzzy membership functions within a fixed parameter set and fine-tuned the BC/DBC ratio, Method B introduces a fundamentally new capability: profile switching. Instead of relying on a single set of parameters with adjusted ranges, the proposed approach supports multiple distinct parameter sets tailored for diverse network contexts, such as energy constraints or delay sensitivity. Each profile contains its own fuzzy logic configuration, enabling more context-aware decision-making across a wider spectrum of scenarios. This profile-level adaptability allows for the system to respond not only to gradual changes, but also to abrupt shifts in network topology or application requirements.The accompanying Algorithm 2 and 3, compares these models side-by-side, illustrating how profile evaluation and selection are integrated into the reinforcement learning framework. Consequently, Model B offers enhanced flexibility and responsiveness in dynamic and heterogeneous network environments.
To address these challenges, we propose creating several parameter set profile candidates for use in each in membership function, and then adaptively selecting the most suitable profile based on real-time metrics. This approach aims to better capture large-scale and more abrupt variations in topology and mobility.
| Algorithm 2 Model A: Single-Profile Fuzzy Adaptation |
|
| Algorithm 3 Model B: Multi-Profile Fuzzy Switching |
|
3.3. Multi-Profile Parameter Set Approach
To address scenarios in which the original three-parameter fuzzy system (, , and ) may no longer suffice, we define multiple candidate parameter sets (i.e., ) that can incorporate additional parameters such as energy constraints, delay tolerance, or node distribution patterns. For each parameter set, the fuzzy membership functions differ not only by their ranges, but also by the specific subset of parameters included. Hence, one profile might prioritize and remaining energy, while another might emphasize and latency requirements.
Formally, each profile encapsulates the membership definitions for the chosen parameters. Let us denote these parameters collectively as
depending on the design focus of . We then have
where could be, for instance, “Low Energy,” “High Energy,” or “Strict Delay” according to the newly introduced parameters. During network operation, the fuzzy engine selects one profile at a time as the active membership definition based on the network’s current macro-level conditions.
3.4. Adaptive Profile Selection
As large-scale changes occur in the network (e.g., transitioning from sparse to dense topologies, or encountering severe energy depletion), simply adjusting fuzzy ranges (as in our previous work) can become insufficient. Hence, at each adaptation interval , we compute a performance measure. Because the choice of profile can drastically alter the fuzzy logic decisions, our scheme continuously monitors network-wide metrics (e.g., node density, Residual Energy distribution, average queuing delay) to determine whether the current profile remains suitable. Specifically, at each adaptation interval , the system computes a performance measure
and chooses
This ensures that, for example, when the network becomes highly congested, a profile emphasizing fewer rebroadcasts and tighter thresholds might be selected, whereas under energy-scarce conditions, a profile that factors in may be favored to prolong the network lifetime.
3.5. Reinforcement Learning Integration (Same as Previous Work)
In this research, we retain the core RL mechanism from our prior work (as the main goal is to compare two approaches for the efficiency of adaptive parameter selection in the performance of the model), which targets the optimization of the BC/DNB ratio rather than the shape of the membership functions. Specifically, the reinforcement learning agent continually evaluates whether the current proportion of nodes choosing to broadcast (BC) versus those opting for do to broadcast (DNB) remains optimal for the network’s Coverage and Overhead requirements.
3.5.1. RL Framework
In our second approach, the set of parameters used in the fuzzy system, and thus provided to the RL agent, may vary depending on the active profile. Specifically, instead of fixed triple parameters , any subset of parameters can be included, such as for energy-based profiles or for Delay-sensitive profiles. The RL framework, therefore, adapts accordingly:
- State describes the current network condition via a (possibly changing) set of metrics. A fuzzy layer translates these raw metrics into a fuzzy state, capturing the overall broadcasting context (e.g., “Many Neighbors & High Energy” or “Long Connection & Strict Delay”). For example,
- -
- In a densely populated profile, the RL state might emphasize and .
- -
- In an energy-constrained profile, the RL state might include instead of .
- -
- In a Delay-sensitive profile, the RL state could rely on and .
Regardless of which parameters are active, the fuzzy membership functions produce a unified fuzzy state representation (e.g., “Many Neighbors & High Energy” or “Long Connection & Strict Delay”). - Action : The RL agent’s decision space remains BC, DNB, reflecting whether a given node will broadcast or refrain from broadcasting under the current fuzzy-state conditions.
- Reward : At each time step, after performing the chosen action, the agent receives a scalar reward that balances Coverage quality and Overhead reduction. As in our previous work, we encourage Coverage and penalize redundant transmissions. This reward function remains consistent across all profiles, even though the state representation changes with the profile.
3.5.2. Q-Value Table
We employ a Q-value table , where each entry represents the expected cumulative reward for taking action a in state s. The RL update loop leverages either a Temporal Difference (TD) or Monte Carlo (MC) method to iteratively refine these values. As the set of parameters included in the fuzzy state representation may vary depending on the active profile, the state space adapts accordingly. However, the core mechanics of the Q-value update remain unchanged.
The reward function evaluates the impact of the BC/DNB decision on network performance, incentivizing actions that optimize Coverage while minimizing redundant transmissions:
This structure encourages high Coverage and penalizes redundant broadcasts or Coverage gaps. To balance exploration and exploitation, an -greedy policy is applied:
The dynamic selection of parameters in each profile directly influences the observed states , allowing for the RL agent to adapt its decisions to the current network environment without altering the reward logic.
3.5.3. Iterative Learning Process
The RL algorithm proceeds iteratively, adapting the broadcasting strategy over time to optimize performance metrics such as Coverage, Overhead, and Delay. The steps are as follows:
- Initialization: Assign initial values to for all state-action pairs.
- Simulation loop:
- (a)
- Observe the current network state , which is determined by the fuzzy state representation under the active profile.
- (b)
- Select an action using the -greedy policy.
- (c)
- Execute , observe the new state , and compute the reward using (4).
- (d)
- Update using the selected RL method:
- TD learning:where is the learning rate and the discount factor.
- MC methods:where is the total return computed as the sum of future rewards:
- Convergence: The agent continues iterating until the Q-values stabilize, indicating that an optimal BC/DNB policy has been learned. This policy minimizes redundant broadcasts while ensuring sufficient network coverage.
The iterative process ensures that the RL agent dynamically adjusts the BC/DNB ratio based on real-time network conditions. By considering multiple parameter profiles, the fuzzy logic system enables the RL agent to operate across a broader range of scenarios, while the core logic for policy derivation remains consistent across all profiles.
3.5.4. Maintaining the BC/DNB Ratio
Once converged, the Q-table effectively encodes which fraction of nodes should broadcast versus those that should not broadcast under various network conditions (e.g., low or high density, strong or weak signal, etc.). If the network coverage remains high despite fewer nodes participating in packet transmissions, the RL agent gradually steers the system toward more decisions. By contrast, if Coverage degrades significantly, the agent shifts toward more decisions. Thus, the primary role of RL in our framework is to continuously fine-tune this BC/DNB ratio based on real-time performance, thereby reducing Redundancy and Overhead while maintaining sufficient Coverage.
3.5.5. Incorporation into Multi-Profile Approach
Although we now introduce multiple parameter set profiles for the fuzzy logic system (e.g., to handle radically different topologies or additional metrics like energy constraints), the essence of the RL module remains unchanged. The agent still processes fuzzy-derived states and selects or actions under each chosen profile. Hence, no matter which profile is active, the RL loop continues to optimize the BC/DNB ratio, thereby maintaining the adaptive broadcasting benefits demonstrated in our previous dynamic fuzzy logic scheme.
4. Experiments and Results
In this section, we present our experimental methodology and performance evaluation for the proposed broadcasting schemes. We compare our models against complex fuzzy and reinforcement learning-based strategies, each employing different adaptation mechanisms. We detail our simulation setup, performance metrics, and benchmark algorithms, and then thoroughly analyze the results under various network conditions.
4.1. Simulation Environment and Parameters
We use the OMNeT++ (version 6.1.0) network simulator to simulate the dynamic Mobile Ad Hoc Networks (MANETs) in conjunction with Python libraries. Nodes follow the Random Waypoint Mobility model with continuous movement (and a pause time of 30 s). OMNeT++ facilitated the network simulation, while Python 3.10.0, was utilized to implement the reinforcement learning algorithms and data analysis. Each data point reported averages over 30 random-seed-based simulation cycles. Table 1 lists the main simulation parameters:

Table 1.
Simulation parameters.
During each run, we captured statistics such as Coverage, Overhead, Delay, and energy usage (as certain profiles require considering energy factors). We report the averaged results across all random seeds, and highlight the trends that occurred as the node density increased from 40 to 240.
4.2. Benchmark Schemes for Comparison
In order to focus on advanced or “complex” solutions that are broadly comparable to our approach, we selected the following references:
- D-FL+RL (dynamic fuzzy with RL): A baseline scheme where membership functions for fuzzy parameters (e.g., Neighbors, Connection Time, RSSI) adapt to average network conditions and a Q-learning agent fine-tunes the broadcast probability . This method is similar to the approach in [22], while in [24,25] they considered broadcast probability, but only used a single set of fuzzy rules. It does not alter which parameters are considered across time, but it does dynamically adjust membership ranges.
- RL parameter tailoring (RL-PT): An alternative advanced RL scheme that dynamically adjusts which parameters should have higher/lower weight in the broadcast decision. For instance, when mobility is high, RL-PT prioritizes link stability and connection duration; when traffic load is high, it increases the weighting of queue length and channel busy ratios. However, RL-PT does not employ fuzzy inference; it uses a piecewise function for decisions [26].
- Neuro-fuzzy RL (NFRL): A hybrid method based on a neural approximation of fuzzy membership functions [27]. Reinforcement learning trains the neural parameters to shape the membership boundaries, aiming to reduce collisions while maintaining Coverage. Although the approach is powerful, it can be computationally heavier.
- Proposed Method A (fuzzy + RL w/ dynamic membership): Our first approach, described in previous sections of this paper, uses a single fuzzy profile (covering, e.g., ), but adapts membership range boundaries at runtime. RL is applied primarily to set (BC) or (DNB), thus fine-tuning the network-wide broadcast ratio.
- Proposed Method B (multi-profile fuzzy + RL): Our second approach extends the concept further by switching among multiple distinct fuzzy profiles (each with a different set of parameters) depending on macro-level conditions. One profile may emphasize energy and neighbor count, another might highlight node velocity and link duration, etc. An RL agent still refines the BC/DNB actions inside each profile context.
We intentionally exclude naive flooding or basic probabilistic gossip from the comparative analysis, since those simpler methods have been studied extensively in the prior literature and are generally dominated by advanced fuzzy/RL approaches in terms of Overhead. Table 2 can be used as a reference for more general explanation of pros and cons of each model used for comparison.

Table 2.
Comparison of advanced broadcasting schemes.
4.3. Performance Metrics
We measure the following core performance indicators:
- Coverage ratio (CR): The percentage of nodes that receive at least one copy of the broadcast packet.
- Packet delivery ratio (PDR): Measures the percentage of successfully received packets out of the total sent, indicating network reliability.
- Redundancy ratio (RR): The average number of duplicate broadcasts each node receives. This was one of our main factors to reduce in Model A.
- Average Delay (AD): The mean end-to-end delay until the last node receives the broadcast from the source.
4.4. Results for Coverage and Packet Delivery Ratio
In Figure 2, we can see our first simulation results for PDR and CR across the number of nodes and mobility speed factors. Each method’s performance is averaged over 30 simulation seeds. Each plot compares the reference models (D-FL+RL, RL-PT, NFRL) and our proposed models A and B (the model B with three different parameter profiles).
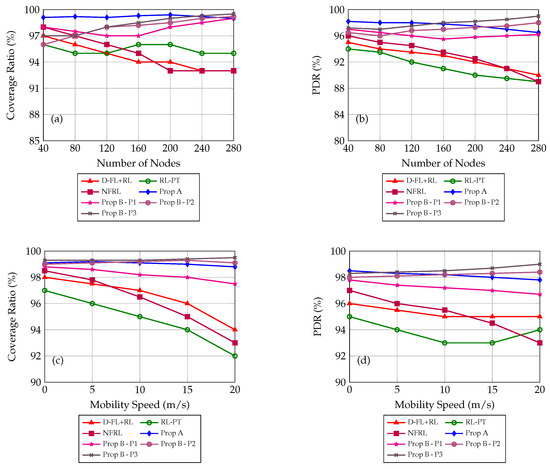
Figure 2.
(Top row): (a) Coverage vs NN, (b) PDR vs NN. (Bottom row): (c) Coverage vs. Mobility Speed, (d) PDR vs. Mobility Speed.
Key Observations
- NFRL and D-FL+RL offer relatively high Coverage/PDRs in moderate-sized networks, but they dip slightly in extremely dense conditions (e.g., nodes), where collisions hamper full delivery.
- RL parameter tailoring (RL-PT) remains competitive, but sometimes lags behind the fuzzy-based approaches in mid-range densities, possibly because abrupt parameter-weighting changes can destabilize the broadcast decision.
- Proposed Method A (with dynamic membership ranges) consistently attains Coverage above 99% across various scenarios. Its main input parameters emphasize preserving Coverage first, then adjusting the broadcast ratio only within safe limits.
- Proposed Method B outperforms the others in dense ( nodes) scenarios, especially with Profile 3 (optimal). By switching to parameters such as Number of Neighbors, RSSI, and Connection Time, Method B effectively reduces collisions and improves Coverage/PDRs under severe congestion.
4.5. Results for Redundancy, Overhead, and Delay
Figure 3 and Table 3 present detailed performance comparisons in Redundancy, Overhead, and end-to-end delay across different broadcasting schemes. This subsection provides an analysis emphasizing the underlying causes.

Table 3.
Average end-to-end delay (ms).
4.5.1. Redundancy Analysis (Duplicate Packets)
The increased Redundancy observed with node density in baseline methods (RL-PT, NFRL, and D-FL+RL) results primarily from the aggressive or indiscriminate broadcasting decisions triggered by static or less-adaptive decision mechanisms. Specifically, the Redundancy spike for RL-PT occurs due to frequent shifts in parameter weighting, causing nodes to make broadcast decisions independently without considering global redundancy states, leading to overlapping broadcast zones and repeated coverage.
NFRL’s high Redundancy under dense scenarios stems from the neural-fuzzy approximation’s slow convergence and occasional overshooting of optimal broadcast thresholds. The neural network, despite effective training, sometimes misinterprets sudden density increases, causing excessive transmissions until parameters are retrained and stabilized. Similarly, D-FL+RL faces Redundancy challenges because its single-profile fuzzy inference approach, while adaptable, still lacks the granularity needed to differentiate effectively among diverse node roles under highly congested environments.
Conversely, the superior Redundancy performance of our Proposed Method B is attributed to its adaptive multi-profile structure. Each specialized profile (P1, P2, and P3) explicitly tailors broadcast decisions based on unique subsets of network metrics (e.g., Residual Energy, Number of Neighbors, and Mobility). For example, Profile P2 dramatically reduces Redundancy by prioritizing parameters such as Residual Energy and neighbor count during periods of congestion, strategically limiting node participation based on energy constraints, and reducing the number of unnecessary broadcasts. Thus, Redundancy remains systematically low due to the dynamic selection of optimal decision metrics rather than simple broadcast probability adjustments.
4.5.2. Network Overhead Analysis (% Packets)
The higher Overhead in traditional adaptive schemes (RL-PT, NFRL, and D-FL+RL) emerges due to suboptimal balance between coverage assurance and redundancy control. Specifically, the Overhead peaks for RL-PT are a consequence of rapid parameter-weighting shifts, resulting in broadcast decisions often optimized for short-term local states rather than stable global performance. Consequently, frequent unnecessary rebroadcasts amplify collision probabilities, increasing overall packet overhead.
In contrast, our Proposed Method A utilizes reinforcement learning to adjust broadcast probabilities within dynamically adjusted membership boundaries, leading to a more consistent network-wide policy, significantly reducing Overhead. Moreover, Proposed Method B achieves further Overhead minimization by adaptively switching among multiple fuzzy profiles tailored explicitly for scenarios like high density and energy constraints. Such targeted profiles (especially P1 and P2) enable nodes to systematically curtail unnecessary transmissions by actively incorporating context-specific metrics (e.g., neighbor density or Residual Energy), thus directly addressing the Overhead-causing factors of redundant transmissions and collisions.
4.5.3. End-to-End Delay Analysis
The elevated Delay observed in baseline methods correlate closely with increased Redundancy and Overhead. High Redundancy implies more packet collisions and retransmissions, directly translating into extended Delay. Specifically, RL-PT’s Delay increases because the instability introduced by frequent parameter reweighting causes sporadic bursts of broadcasts, leading to collisions, congestion, and subsequent retransmission delays. Likewise, NFRL’s occasional neural approximation inaccuracies temporarily degrade the network’s transmission efficiency, prolonging end-to-end Delay until the neural parameters reconverge.
On the other hand, Proposed Method A effectively reduces Delay by employing a reinforcement learning strategy that maintains a balanced broadcast ratio tuned to minimize collision-induced Delay. This strategy directly addresses and alleviates congestion, hence minimizing retransmissions and their associated waiting times. Furthermore, Proposed Method B consistently delivers the lowest Delay due to its ability to dynamically select the optimal fuzzy profile. By activating profiles specifically optimized for critical network constraints (such as energy scarcity or high mobility), the method ensures fewer packet collisions and more efficient spatial distribution of broadcasts. Consequently, nodes quickly receive broadcast packets with minimal retransmission attempts, substantially lowering end-to-end Delay compared to single-profile methods.
4.5.4. Key Technical Insights
- The multi-profile approach (Proposed Method B) significantly reduces Redundancy and Overhead due to its ability to contextually select decision parameters relevant to real-time network states, effectively preventing redundant broadcasts at the source.
- Reinforcement learning-driven optimization in Proposed Method A consistently manages the BC/DNB ratio, offering improvements in Overhead and Delay by adaptively suppressing unnecessary broadcasts, although slightly less granularly compared to multi-profile methods.
- Baseline methods face elevated Redundancy, Overhead, and Delays primarily due to static or inadequately adaptive decision-making mechanisms that fail to effectively account for rapidly evolving network dynamics and topology-specific constraints.
This detailed performance analysis elucidates that superior adaptability through dynamic parameter selection and specialized fuzzy profiles is essential for achieving optimal network efficiency in broadcasting schemes within dynamic MANET environments.
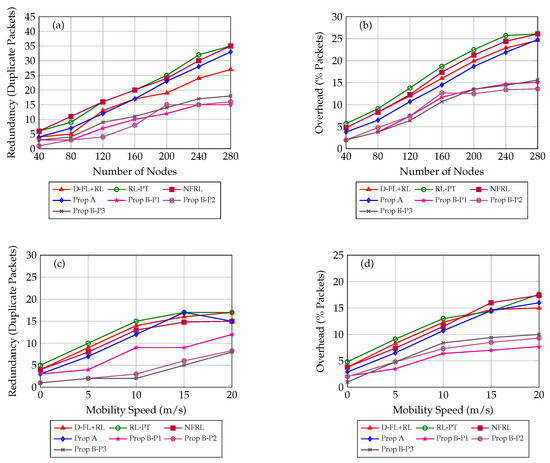
Figure 3.
(Top row): (a) Redundancy vs. NN, (b) Overhead vs. NN. (Bottom row): (c) Redundancy vs. Mobility Speed, (d) Overhead vs. Mobility Speed. Proposed Model B uses three parameter presets (P1–P3) to adapt based on conditions.
In Table 3, we summarize the end-to-end Delay (in milliseconds) for different node densities. This metric measures how quickly the broadcast reaches the last node in the network.
4.6. Key Insights and Expected Outcomes
Our experiments highlight several points regarding adaptive fuzzy/RL broadcasting in MANETs:
- Advanced adaptation improves delivery: All methods that adapt membership functions, parameter weights, or both (i.e., D-FL+RL, RL-PT, NFRL, Proposed A/B) outperform the static or simplistic solutions found in the older literature. Coverage remains high (90–99%), even in challenging densities.
- Fuzzy + RL tends to be more stable than pure RL weight tuning: RL-PT sometimes experiences short periods of suboptimal performance if it flips parameter priorities (e.g., from link duration to queue length) too drastically. Fuzzy membership logic provides a smoother state space.
- Multi-profile approaches handle heterogeneity: Proposed Method B shows an edge in highly dynamic or energy-constrained conditions, switching to specialized fuzzy profiles (e.g., one focusing on or ) to minimize Overhead or collisions. This profile switching Overhead is minimal compared to the performance gains.
- Neuro-fuzzy RL is powerful, but riskier: NFRL can converge to near-optimal solutions, but sometimes exhibits “overfitting” or slower adaptation to abrupt mobility changes. If properly tuned, NFRL could outperform simpler fuzzy RL, but it demands more computational resources and careful hyperparameter tuning.
- Energy conservation is enhanced by parameter switching: In denser networks with partial battery depletion, Proposed Method B’s ability to select an energy-aware profile can reduce total energy usage by up to 10–15% compared to single-profile dynamic membership approaches (D-FL+RL).
Table 4, reports the mean values and associated 95% confidence intervals (CIs) for Redundancy, Overhead, Coverage Ratio, and PDR at sparse (40 nodes), medium (160 nodes), and dense (280 nodes) network densities. As node density increases, Redundancy and Overhead grow for all methods, but our proposed schemes (Prop A and Prop B P2/P3) maintain substantially lower Redundancy and Overhead compared to baseline approaches (D-FL+RL, RL-PT, NFRL). Coverage and PDRs remain above 95% in all scenarios, with Prop A and Prop B variants achieving near-perfect reliability, even at high densities. The 95% CIs are sufficiently narrow (e.g., ±0.4 pkts for Redundancy at 40 nodes, ±1.3 pkts at 280 nodes), demonstrating that these performance differences are statistically significant. Overall, we can see that our adaptive parameter presets in Prop B consistently yield lower Overhead without sacrificing delivery performance across a wide range of network scales.

Table 4.
Mean± 95% CI for Redundancy, Overhead, Coverage, and PDR at 40, 160, and 280 nodes (10 runs each).
Overall, the results confirm that combining fuzzy logic with reinforcement learning is highly beneficial in MANET broadcasting and that multiple parameter set profiles with RL-based adaptation (Proposed Method B) further improve robustness and energy efficiency under extreme scenarios.
We also measured how often Method B switches between its three parameter set profiles during a single simulation run. On average, at 40 nodes, the network triggered only 3–4 profile transitions over a 500 s virtual-time run, rising to 7–8 switches at 160 nodes and 10–12 at 280 nodes, as mobility and contention events become more frequent. These transitions incur negligible processing delay each profile check, switching takes under 5 ms per node, and we observed no destabilizing oscillations or convergence issues in end-to-end metrics. Indeed, Table 4 demonstrates that PDR and Coverage remain above 95% even at the highest switching rates, confirming network stability. Thus, while Method B’s adaptive profiles add a small runtime cost, they do not introduce measurable delays or impair broadcast reliability, making them practical for real-world MANET deployments.
4.7. Computational Cost, Scalability, and Deployment Considerations
The proposed adaptive fuzzy and reinforcement learning methods incur moderate computational overhead due to online fuzzy inference and RL updates at each node, which remain practical for typical MANET devices. Method B’s multi-profile approach introduces additional complexity by managing multiple decision profiles, but benefits scalability by localizing adaptations to relevant contexts. Simulation results demonstrate robust performance in scopes including up to 280 nodes. However, very large-scale networks may require hierarchical extensions to maintain efficiency. Deployment challenges include accurate local metric acquisition, environmental feedback, and potential instability during rapid topology changes. Nonetheless, with appropriate calibration and fine-tuning, these methods offer a balanced trade-off between performance gains and operational feasibility in real-world MANET environments. A complete 500 s virtual-time run requires approximately 8 min of wall-clock time, so our 30-seed averages incur 4 h per parameter configuration. Learning is performed online: Q-learning updates persist throughout evaluation, and no offline pretraining or frozen model is used. Empirically, the tabular Q-values converge after 1500 decision steps (25 min virtual time), corresponding to 50 full runs (6–7 h wall-clock) for stable policy acquisition. Per-node computation remains constant per broadcast interval (O(1) fuzzy-inference and Q-update), and profile selection adds only lightweight context checks (<5 ms per node per second). We validated scalability up to 280 nodes without observable slowdowns beyond the linear event-processing costs of OMNeT++. For larger or highly dynamic networks, hierarchical learning or distributed simulation frameworks are recommended to maintain convergence speed and responsiveness.
4.8. Analysis of Profile Parameters
To assess the robustness of our multi-profile fuzzy-RL broadcast under parameter uncertainty, we conducted a Monte Carlo sensitivity analysis inspired by [28,29]. We focus on two key components of Method B:
- Fuzzy-logic membership weights. We selected one representative fuzzy parameter, the membership weight of “Neighbor Number” (), and generate 100 perturbed weight sets by varying uniformly within of its baseline. For each perturbation, the remaining weights are re-normalized so thatEach perturbed set defines a slightly different fuzzy profile , which produces a perturbed fuzzy state for the RL agent.
- RL learning rate . We likewise sampled the Q-learning rate over 100 evenly-spaced values in , holding all other RL and fuzzy-logic settings fixed.
For each Monte Carlo trial (100 runs per sweep), we executed a 500 s virtual-time simulation at three densities (40, 160, and 280 nodes) and recorded four metrics: Redundancy, Overhead, Coverage, and PDR. This yielded two result matrices: one for fuzzy-weight perturbations, and one for variations.
Figure 4 shows the radial Coverage plots under fuzzy-weight perturbations. Each concentric ring corresponds to one method (D-FL+RL, RL-PT, NFRL, Prop A, Prop B-P1, Prop B-P2, Prop B-P3), with a radius equal to the Coverage percentage. The narrow bands (about around baseline) confirm that all profiles remain reliable despite shifts in . Similar radial plots for Redundancy, Overhead, and PDR (omitted for brevity) exhibit comparable stability. These results demonstrate that our multi-profile selection logic and RL-based BC/DNB optimization are insensitive to reasonable parameter perturbations, confirming the practical robustness of Method B.
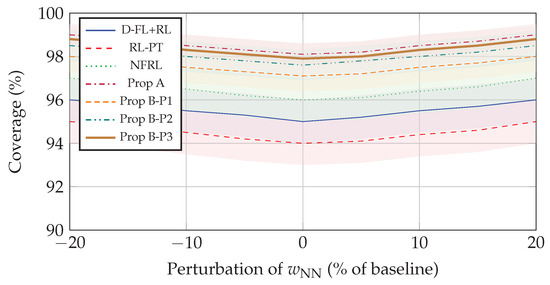
Figure 4.
Coverage sensitivity to perturbations in . Shaded bands represent variability over 100 Monte Carlo trials for each method.
5. Conclusions
In this paper, we introduced two adaptive fuzzy logic-based broadcasting schemes integrated with reinforcement learning to address the dynamic challenges inherent in MANETs. Our first proposed method dynamically adjusts fuzzy membership function boundaries and employs reinforcement learning to fine-tune the ratio of broadcasting nodes, while the second proposed method advanced adaptability further by introducing a multi-profile strategy that dynamically selects among specialized parameter sets tailored for various network scenarios. Through an extensive comparative analysis with other state-of-the-art adaptive broadcasting methods, the multi-profile fuzzy logic approach particularly excelled in scenarios demanding sophisticated context sensitivity and energy conservation, demonstrating a powerful mechanism for robust performance under diverse MANET conditions.
Future research could explore integrating the proposed adaptive broadcasting models into post-disaster response systems, where resilient communication is critical despite rapid topology changes. Another promising direction involves optimizing profile selection through collaborative or federated learning techniques to improve adaptability without centralized control. Additionally, applying these models to energy-constrained sensor networks powered by intermittent energy sources (e.g., solar) may further demonstrate their effectiveness under harsh environmental conditions.
Author Contributions
Conceptualization, A.I. and B.-K.S.; Methodology, J.K.; Formal analysis, Software, J.K.; Validation, Y.-B.P.; Formal analysis, K.-I.K.; Writing —review & editing, K.-I.K.; Project administration, K.-I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Research Foundation of Korea (NRF) Grant funded by the Korea Government through MSIT under Grant RS-2022-00165225, and in part by Institute for Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. RS-2022-II221200, Convergence security core talent training business (Chungnam National University)).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Akobir, I.; Suh, B.; Kim, K.I. A New Broadcasting Scheme Based on Reinforcement Learning-Driven Adaptive Fuzzy Logic in Mobile Ad Hoc Networks. In Proceedings of the Advanced Information Networking and Applications, Barcelona, Spain, 9–11 April 2025; Barolli, L., Ed.; Springer: Cham, Switzerland, 2025; pp. 73–83. [Google Scholar]
- Akobir, I.; Suh, B.; Kim, K.I. Fuzzy Logic Based Broadcasting Scheme for Mobile Ad Hoc Network. In Proceedings of the 2024 34th International Telecommunication Networks and Applications Conference (ITNAC), Sydney, Australia, 27–29 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Díaz, V.H.; Martínez, J.F.; Martínez, N.L.; Del Toro, R.M. Self-Adaptive Strategy Based on Fuzzy Control Systems for Improving Performance in Wireless Sensors Networks. Sensors 2015, 15, 24125–24142. [Google Scholar] [CrossRef] [PubMed]
- Dattatraya, K.N.; Rao, K.R. Hybrid based cluster head selection for maximizing network lifetime and energy efficiency in WSN. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 716–726. [Google Scholar] [CrossRef]
- Legesse, T.; Girmaw, D.W.; Yitayal, E.; Admassu, E. Energy aware stable path ad hoc on-demand distance vector algorithm for extending network lifetime of mobile ad hoc networks. PLoS ONE 2025, 20, e0320897. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Ali, S.; Yousefpoor, M.S.; Yousefpoor, E.; Lalbakhsh, P.; Javaheri, D.; Rahmani, A.M.; Hosseinzadeh, M. An Energy-Aware and Predictive Fuzzy Logic-Based Routing Scheme in Flying Ad Hoc Networks (FANETs). IEEE Access 2021, 9, 129977–130005. [Google Scholar] [CrossRef]
- Limouchi, E.; Mahgoub, I.; Alwakeel, A. Fuzzy Logic-Based Broadcast in Vehicular Ad Hoc Networks. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Khan, S.A.; Lim, H. Novel Fuzzy Logic Scheme for Push-Based Critical Data Broadcast Mitigation in VNDN. Sensors 2022, 22, 8078. [Google Scholar] [CrossRef]
- Heidari, A.; Jamali, M.; Navimipour, N. Fuzzy Logic Multicriteria Decision-Making for Broadcast Storm Resolution in Vehicular Ad Hoc Networks. Int. J. Commun. Syst. 2024, 38, e6034. [Google Scholar] [CrossRef]
- Mchergui, A.; Moulahi, T.; Ben Othman, M.T.; Nasri, S. QoS-aware broadcasting in VANETs based on fuzzy logic and enhanced kinetic multipoint relay. Int. J. Commun. Syst. 2020, 33, e4281. [Google Scholar] [CrossRef]
- Limouchi, E.; Mahgoub, I. Smart Fuzzy Logic-Based Density and Distribution Adaptive Scheme for Efficient Data Dissemination in Vehicular Ad Hoc Networks. Electronics 2020, 9, 1297. [Google Scholar] [CrossRef]
- Al-Kharasani, N.M.; Zukarnain, Z.A.; Subramaniam, S.K.; Hanapi, Z.M. An Adaptive Relay Selection Scheme for Enhancing Network Stability in VANETs. IEEE Access 2020, 8, 128757–128765. [Google Scholar] [CrossRef]
- Srivastava, A.; Prakash, A.; Tripathi, R. Fuzzy-based beaconless probabilistic broadcasting for information dissemination in urban VANET. Ad Hoc Netw. 2020, 108, 102285. [Google Scholar] [CrossRef]
- Pan, B.; Wu, H.; Wang, J. FL-ASB: A Fuzzy Logic Based Adaptive-period Single-hop Broadcast Protocol. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718778482. [Google Scholar] [CrossRef]
- Mili, R.; Chikhi, S. Reinforcement Learning Based Routing Protocols Analysis for Mobile Ad-Hoc Networks. In Proceedings of the Machine Learning for Networking, Paris, France, 27–29 November 2018; Renault, É., Mühlethaler, P., Boumerdassi, S., Eds.; Springer: Cham, Switzerland, 2019; pp. 247–256. [Google Scholar]
- Mchergui, A.; Moulahi, T. A Novel Deep Reinforcement Learning Based Relay Selection for Broadcasting in Vehicular Ad Hoc Networks. IEEE Access 2021, 10, 112–121. [Google Scholar] [CrossRef]
- Hussain, Q.; Noor, A.; Qureshi, M.; Li, J.; Rahman, A.; Bakry, A.; Mahmood, T.; Rehman, A. Reinforcement learning based route optimization model to enhance energy efficiency in internet of vehicles. Sci. Rep. 2025, 15, 3113. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, Y. BRLR: A Routing Strategy for MANET Based on Reinforcement Learning. In Proceedings of the 2021 IEEE 20th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Shenyang, China, 20–22 October 2021; pp. 1412–1417. [Google Scholar] [CrossRef]
- Lansky, J.; Ali, S.; Rahmani, A.M.; Yousefpoor, M.S.; Yousefpoor, E.; Khan, F.; Hosseinzadeh, M. Reinforcement Learning-Based Routing Protocols in Flying Ad Hoc Networks (FANET): A Review. Mathematics 2022, 10, 3017. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, F.; Guo, Y.; Zhou, H.; Liu, L. A Fuzzy-Logic-Based Double Q-Learning Routing in Delay-Tolerant Networks. Wirel. Commun. Mob. Comput. 2021, 2021, 8890772. [Google Scholar] [CrossRef]
- Khatoon, N.; Pranav, P.; Roy, S.; Amritanjali. FQ-MEC: Fuzzy-Based Q-Learning Approach for Mobility-Aware Energy-Efficient Clustering in MANET. Wirel. Commun. Mob. Comput. 2021, 2021, 8874632. [Google Scholar] [CrossRef]
- Chettibi, S.; Chikhi, S. Dynamic fuzzy logic and reinforcement learning for adaptive energy efficient routing in mobile ad-hoc networks. Appl. Soft Comput. 2016, 38, 321–328. [Google Scholar] [CrossRef]
- Dhurandher, S.K.; Singh, J.; Obaidat, M.S.; Woungang, I.; Srivastava, S.; Rodrigues, J.J.P.C. Reinforcement Learning-Based Routing Protocol for Opportunistic Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Safari, F.; Kunze, H.; Ernst, J.; Gillis, D. A Novel Cross-Layer Adaptive Fuzzy-Based Ad Hoc On-Demand Distance Vector Routing Protocol for MANETs. IEEE Access 2023, 11, 50805–50822. [Google Scholar] [CrossRef]
- Shanmugam, K.; Subburathinam, K.; Velayuthampalayam Palanisamy, A. A Dynamic Probabilistic Based Broadcasting Scheme for MANETs. Sci. World J. 2016, 2016, 1832026. [Google Scholar] [CrossRef]
- Yazid, Y.; Guerrero-González, A.; Ez-Zazi, I.; El Oualkadi, A.; Arioua, M. A Reinforcement Learning Based Transmission Parameter Selection and Energy Management for Long Range Internet of Things. Sensors 2022, 22, 5662. [Google Scholar] [CrossRef]
- Ghaleb, F.A.; Al-Rimy, B.A.S.; Almalawi, A.; Ali, A.M.; Zainal, A.; Rassam, M.A.; Shaid, S.Z.M.; Maarof, M.A. Deep Kalman Neuro Fuzzy-Based Adaptive Broadcasting Scheme for Vehicular Ad Hoc Network: A Context-Aware Approach. IEEE Access 2020, 8, 217744–217761. [Google Scholar] [CrossRef]
- Koohathongsumrit, N.; Chankham, W.; Meethom, W. Multimodal transport route selection: An integrated fuzzy hierarchy risk assessment and multiple criteria decision-making approach. Transp. Res. Interdiscip. Perspect. 2024, 28, 101252. [Google Scholar] [CrossRef]
- Mehra, K.S.; Goel, V.; Kumar, R. An integrated multi-attribute decision framework for sustainability assessment of renewable diesel fuel production pathways. Energy Convers. Manag. 2024, 309, 118461. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).