Abstract
Large language models (LLMs), built upon Transformer architectures, have demonstrated remarkable performance in a wide range of natural language processing tasks. However, their practical deployment—especially in long-context scenarios—is often hindered by the computational and memory costs associated with managing the key–value (KV) cache during inference. Optimizing this process is therefore crucial for improving LLM efficiency and scalability. In this study, we propose a novel entropy-guided KV caching strategy that leverages the distribution characteristics of attention scores within each Transformer layer. Specifically, we compute the entropy of attention weights for each head and use the average entropy of all heads within a layer to assess the layer’s contextual importance. Higher-entropy layers—those exhibiting broader attention dispersion—are allocated larger KV cache budgets, while lower-entropy (sink-like) layers are assigned smaller budgets. Instead of selecting different key–value tokens per head, our method selects a common set of important tokens per layer, based on aggregated attention scores, and caches them uniformly across all heads within the same layer. This design preserves the structural integrity of multi-head attention while enabling efficient token selection during the prefilling phase. The experimental results demonstrate that our approach improves cache utilization and inference speed without compromising generation quality. For example, on the Qwen3 4B model, our method reduces memory usage by 4.18% while preserving ROUGE score, and on Mistral 0.1v 7B, it reduces decoding time by 46.6%, highlighting entropy-guided layer analysis as a principled mechanism for scalable long-context language modeling.
Keywords:
LLM; KV cache; transformer; LLM inference optimization; attention entropy; memory-efficient caching MSC:
68T50
1. Introduction
LLMs, such as those based on the Transformer architecture [1], have become essential tools in natural language processing (NLP), powering applications ranging from dialogue systems to scientific content generation. As these models scale in size and input sequence length, the computational cost of inference becomes a major bottleneck, especially in real-time or resource-constrained environments. In particular, efficient inference is crucial for enabling responsive and accessible LLM-based services.
To address these challenges, various optimization strategies have been proposed to accelerate inference without degrading output quality. One widely adopted technique is key–value (KV) caching, which stores past hidden states (keys and values) during autoregressive generation to avoid redundant computation in self-attention modules [2]. During each decoding step t, instead of recomputing all previous hidden representations {}, the model accesses precomputed key and value from cache to compute attention. This effectively reduces the per-step cost of attention from recomputing per step to simply referencing and multiplying existing vectors.
However, traditional KV caching approaches typically store all tokens for all layers and all heads, regardless of their contextual relevance. Since these caches grow linearly with the number of tokens and layers, the total memory footprint becomes quadratic over long sequences [3], i.e., , where L is the number of layers and T the number of past tokens. This uniform storage leads to memory inefficiency and redundancy, as many cached key–value pairs receive little to no attention during actual generation.
Prior studies [4,5,6,7,8,9,10,11,12] have attempted to improve cache efficiency by introducing dynamic or sparse caching mechanisms, yet many rely on per-head token selection strategies that are difficult to reconcile with the multi-head attention structure of Transformers. Specifically, storing different token subsets per head can disrupt the structural coherence required for multi-head concatenation and residual integration.
To overcome these limitations, we propose a novel KV cache allocation strategy based on layer-wise attention entropy analysis. Specifically, we compute the entropy of attention scores for each head and use their average to determine the contextual importance of each layer. Layers exhibiting broader attention dispersion (i.e., higher entropy) are allocated larger KV cache budgets, while layers with more sink-like attention patterns receive smaller budgets. Rather than selecting distinct tokens for each head, we identify a shared set of important tokens for each layer using aggregated attention scores during the prefilling phase. This design preserves the integrity of multi-head attention while enabling efficient and semantically meaningful cache utilization. Our method thus provides a principled and scalable approach for memory-efficient inference in long-context LLMs.
2. Related Work
In Transformer-based LLMs, the key–value (KV) cache is a crucial component for efficient autoregressive decoding. By storing hidden states from previous tokens, models can avoid redundant computation in self-attention layers. However, the vanilla KV caching strategy, which stores KV pairs for all tokens across all layers and heads, results in significant memory consumption and computational redundancy. This becomes particularly problematic in scenarios requiring real-time inference or deployment on resource-constrained environments such as mobile or edge devices, where memory efficiency is critical.
To address these limitations, several recent studies have explored selective KV caching strategies. H2O (Heavy-Hitter Oracle) [13] introduces a dynamic caching mechanism that retains only the top-k tokens with the highest attention scores along with the most recent tokens at each decoding step. This approach preserves critical context while reducing unnecessary memory overhead. StreamingLLM [14] takes a complementary approach by identifying frequently attended “sink tokens” such as [BOS] or punctuation marks, and caches only those tokens along with the most recent ones. This results in a fixed-size cache that preserves essential dependencies without growing linearly with input length.
Recent work has extended these ideas with more structured or adaptive methods. Buzz [15] proposes a beehive-structured sparse KV cache that partitions the token sequence into segments and identifies heavy-hitter tokens within each segment. This localized approach improves contextual relevance while maintaining a sparse and efficient cache. NACL [16] introduces a runtime-adaptive eviction strategy that monitors token utility during inference. Rather than relying on static heuristics, NACL dynamically removes tokens with low contextual impact based on live attention patterns, making it applicable across tasks without retraining.
Scissorhands [17] builds on the persistence-of-importance hypothesis, which assumes that truly important tokens maintain their relevance over multiple decoding steps. It selectively retains such tokens while pruning short-lived ones, reducing cache size while preserving long-range dependencies. Keyformer [18] takes a more discriminative approach by learning to select key tokens for retention, based on their contribution to downstream attention flows. It applies token selection at each layer independently, enabling fine-grained control of cache size with minimal loss in performance.
SepLLM [19] introduces a compression strategy that replaces contiguous segments of tokens with learned separator tokens. These tokens serve as proxies that summarize the semantic content of entire spans, allowing the model to retain important information while dramatically reducing memory usage. This method trades some granularity for extreme efficiency and shows strong results in long-context scenarios.
While all of these methods aim to reduce the computational and memory overhead of KV caching, they vary in how they identify and retain important context. Our approach differs by allocating cache budgets dynamically per head based on the entropy of attention distributions. This enables more fine-grained, head-aware caching that adjusts to the internal dynamics of the model at each decoding step, offering an adaptive and principled alternative to fixed strategies.
3. Entropy-Guided Layer Budget Allocation
In Transformer-based language models, self-attention operates through multiple attention heads in each layer, enabling the model to capture diverse contextual dependencies. While these heads attend to different positions in the input sequence, their attention distributions often exhibit varying degrees of focus—some concentrating heavily on a few tokens (sink-like), while others distribute attention more broadly. To exploit this variability, we propose a dynamic key–value (KV) cache allocation strategy that leverages the attention entropy across heads to assign cache budgets in a layer-wise manner.
Specifically, we compute the entropy of the attention distribution for each head and average the values within each layer to estimate the contextual importance of that layer. Based on this entropy-derived importance score, we allocate larger cache budgets to layers [20] with broader (i.e., higher entropy) attention patterns, and smaller budgets to layers with low-entropy, sink-like heads.
To maintain structural and semantic coherence, we select a shared set of top-k tokens per layer using aggregated attention scores and apply this uniformly across all heads within the same layer. This ensures that multi-head attention remains aligned while allowing memory-efficient caching. The selected tokens are determined during the prefill phase, enabling efficient and context-sensitive KV caching during subsequent autoregressive decoding. This process is illustrated in Figure 1, which compares our entropy-guided caching strategy with static and sink-based approaches during both the prefill and decoding phases.
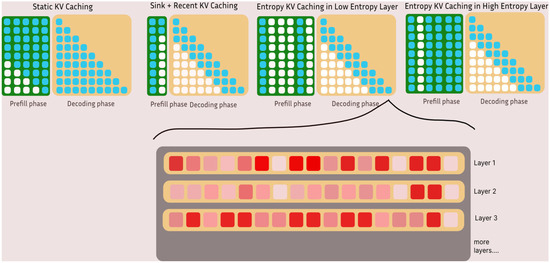
Figure 1.
Comparison of three KV caching strategies during prefill and decoding phases. From left to right: (i) static caching stores all keys/values regardless of context importance; (ii) sink + recent caching reduces memory usage but risks losing critical long-range context; and (iii) our proposed entropy-guided caching retains top- tokens selected during prefill and supplements them with sink and recent tokens during decoding. The number of top- and recent tokens is dynamically determined per layer based on the average entropy of its attention heads.
Importantly, this selection process is grounded in an information-theoretic rationale. The entropy of an attention distribution quantifies the uncertainty or diversity in how attention is spread across tokens. A high entropy indicates that the head integrates information from a broad range of context, whereas a low entropy reflects concentrated focus on a few tokens. By averaging each heads entropies [21,22,23,24,25,26,27] at each layer, we obtain a layer-level estimate of its contextual integration capacity. This enables us to assign larger cache budgets to information-rich layers, which are more likely to contribute semantically meaningful content during generation. The resulting cache retains only high-utility positions, supporting both inference efficiency and generation quality.
3.1. Measuring Attention Entropy per Head
At decoding step t, let the attention distribution of layer , head be denoted as , where T is the number of previous tokens. This distribution is derived via the standard softmax of scaled dot-product attention:
We define the Shannon entropy of this distribution as:
A lower entropy indicates that the attention mass is highly concentrated on a few key positions—i.e., a sink behavior—while a higher entropy implies a broader and more diverse focus across tokens. This entropy serves as a proxy for the contextual richness that each head demands. To obtain the contextual importance of each layer, we aggregate the entropy values of all its heads. Layers with higher average entropy are interpreted as more contextually demanding and are therefore assigned larger cache budgets.
3.2. Determining Layer Importance via Average Attention Entropy
We compute the entropy for all attention heads within each Transformer layer and average them to define a layer-wise importance score
Layers with higher average entropy are interpreted as more contextually important, as they tend to attend over a broader range of tokens. Based on this importance score, we allocate a larger KV cache budget to layers with higher entropy. Unlike earlier approaches that consider head-level allocation, our method assigns cache budgets at the layer level and selects a common set of informative tokens per layer, which are then shared across all heads. This design ensures architectural consistency in multi-head attention while enabling entropy-aware memory optimization.
3.3. Cache Budget Allocation and Token Selection
During the prefill phase, we compute the attention weights for all tokens in the input sequence and estimate the entropy of each head’s attention distribution within each layer. The layer-wise importance score is then computed by averaging head entropies, and a total cache budget is distributed proportionally across layers based on their relative entropy:
where denotes the number of tokens to cache for layer , and is the average entropy of that layer as defined in Section 3.2.
For each layer, we compute the attention score for each token position by aggregating attention weights across all heads in prefill phase:
Here, denotes the attention weight from token position i to token t, computed by head h in layer l. represents the total number of tokens in the input sequence used during the prefill stage. We then select the tokens with the highest scores and store their corresponding key–value pairs in the cache. These tokens reflect globally important context information identified prior to decoding.
During the decoding phase, the final KV cache used for attention in each layer consists of:
- The top- tokens selected from the prefill phase in each layer;
- A fixed number of recent tokens;
- A single sink token (typically the first token in the sequence).
The layer-specific cache budget is split evenly between global and local contexts:
This hybrid token selection approach ensures that the cache captures both long-range semantic dependencies and short-term contextual continuity, while maintaining efficiency through entropy-aware allocation.
To enhance reproducibility and clarity, we summarize the entropy-guided KV caching algorithm in Algorithm 1. The procedure consists of three main steps: (1) computing head-wise attention entropy per layer, (2) assigning a layer-wise KV budget between predefined min/max, and (3) selecting tokens via a top-k attention score and recent-token fallback.
| Algorithm 1: Entropy-Guided KV Caching (Pseudocode) |
| for each layer L: entropy_L = mean([entropy(head_i) for head_i in layer L]) budget_L = scale(entropy_L, min=8, max=128) top_k_tokens = select_top_k_tokens(attn_score_L, k=budget_L//2) recent_tokens = select_recent_tokens(k=budget_L//2) cache_L = top_k_tokens + recent_tokens |
Table 1 summarizes the per-layer computational complexity of the three KV caching strategies considered in this work. All methods operate under a fixed token budget k, limiting the number of retained past tokens. Static caching uniformly preserves the most recent k tokens without any selection overhead. Sink caching filters recent tokens based on sink-like attention patterns, introducing minimal selection cost. In contrast, our entropy-guided strategy dynamically allocates layer-wise budgets using attention entropy and performs top-k selection based on aggregated attention scores, resulting in additional sorting overhead (O(T log T)). Despite this cost, the method remains efficient due to the constrained attention window (O(H × k × d)) and provides greater adaptability across layers.

Table 1.
Complexity analysis of KV caching methods.
3.4. Empirical Observations and Prefill–Decode Consistency
Empirical analysis revealed that many heads in intermediate layers exhibited very low entropy, frequently attending to a small, fixed set of tokens. These heads display a sink-like behavior, and caching only the dominant tokens is sufficient.
Furthermore, we observed a strong correlation between the cumulative attention scores in the prefill stage and token usage during decoding, indicating that our entropy-guided selection in the prefill phase closely reflects actual attention patterns during generation. This validates the reliability of entropy as a signal for proactive and selective caching, leading to both efficiency and quality retention. Figure 2 illustrates this consistency between prefill and decode phases.
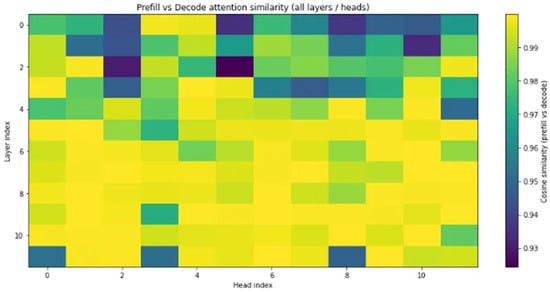
Figure 2.
Visualization of the cosine similarity between attention score distributions in the prefill and decode phases, across all layers and heads of the model. Each cell represents the similarity between the attention weights computed at prefill time and those observed during actual autoregressive decoding, for a specific head in a specific layer. Higher similarity values (closer to 1.0, shown in yellow) indicate that the attention patterns established during prefill remain stable throughout decoding, while lower values (darker regions) suggest deviation or instability. The overall high similarity across most heads and layers demonstrates that prefill-phase attention entropy serves as a reliable predictor of attention behavior during inference. This finding empirically supports the core assumption of our caching strategy—that the tokens identified as important based on prefill attention can be safely reused during decoding without significant semantic loss.
4. Experiment
In this experiment, we evaluated the effectiveness of the proposed entropy-guided KV caching strategy, which allocates cache budgets based on a combination of sink token selection, top-k attention scoring, and recent token retention. This method was compared against two baseline strategies: static caching, which stores all past tokens uniformly across layers and heads, and recent-only caching, which retains only a fixed number of the most recent tokens without regard to attention distribution.
The comparison was conducted using three instruction-tuned language models: LLaMA 3.2 3B [28] Instructed, Mistral 0.1v 7B Instructed [29], and Qwen3 4B [30]. For each model and caching method, we evaluatde generation quality using ROUGE scores, while measuring inference efficiency in terms of end-to-end generation latency and peak GPU memory consumption. All experiments were conducted on a single NVIDIA V100 GPU. We used the Transformers library version 4.51.3, and set the do_sample parameter to False to ensure deterministic generation and eliminate uncertainty in performance evaluation.
Specifically, we recorded the total wall-clock time required to generate a complete output sequence, rather than measuring throughput in tokens per second. This provides a more realistic estimate of user-perceived latency during inference.
We considered three representative caching strategies in our evaluation. The static caching method retains nearly all past tokens across layers and heads, effectively approximating a full key–value cache. The sink caching method resembles the StreamLLM [13] approach, storing only recent tokens with sink-like attention characteristics to reduce memory usage aggressively. Our proposed method, in contrast, adaptively allocates cache based on attention entropy. To determine which tokens to cache, we adopted a layer-wise selection strategy guided by attention entropy. The entropy of each attention head was computed, and their average was taken to estimate the contextual importance of each layer. According to this importance score, a key–value cache budget was assigned per layer, ranging between a predefined minimum and maximum (e.g., from 8 to 128 tokens). Within each layer, half of the allocated budget was reserved for top-k tokens, which were selected based on aggregated attention scores across all heads. This procedure ensures that token selection is performed independently for each layer, in accordance with its attention entropy characteristics.
This setup enables a comprehensive analysis of how entropy-based token selection contributes to efficient long-context inference across models of different sizes. We evaluated the models on three long-document summarization datasets from the LongBench benchmark: GovReport [31], MultiNews [31], and PubMed [32]. GovReport consists of U.S. government reports and requires summarizing formal, technical documents with structured content. MultiNews is a multi-document summarization dataset that aggregates information from multiple news articles into a coherent summary. PubMed includes biomedical research abstracts and full-length articles, demanding precise summarization of domain-specific scientific text. These datasets present diverse challenges in terms of content structure, language domain, and input length, making them well-suited for evaluating the effectiveness of entropy-guided caching in long-context scenarios.
To ensure consistency and reduce variability, we randomly sampled 10 examples from each dataset for evaluation. GovReport contains approximately 19K examples with an average input length of ~5600 tokens. MultiNews includes around 56K examples with a mean input length of ~2100 tokens, while PubMed comprises about 133K biomedical abstracts and long-form articles, averaging ~2900 tokens per input. This sampling strategy allows us to assess the generalizability of our method across documents of varying lengths and domains without incurring excessive computational overhead.
Table 2 describes the ROUGE score, memory consumption, and decoding latency of three KV caching strategies—static, sink, and the proposed entropy-guided method—across three instruction-tuned models (LLaMA 3.2 3B, Mistral 0.1v 7B, and Qwen3 4B) and three summarization datasets (GovReport, MultiNews, and PubMed), with output length fixed to 512 tokens. The results show that entropy caching consistently achieves a favorable trade-off: it maintains ROUGE scores comparable to or exceeding static caching while significantly outperforming the sink method. For example, on GovReport, it achieves the highest ROUGE for both LLaMA and Mistral with lower memory usage. On MultiNews and PubMed, it outperforms or matches both baselines while using fewer resources. Figure 3 illustrates the performance of Mistral 0.1v 7B on the GovReport dataset across the three KV caching strategies. The entropy-guided method achieves the highest ROUGE-1 score (0.301), significantly outperforming both static (0.245) and sink (0.231) caching, indicating superior summarization quality. In terms of memory usage, entropy caching consumes slightly more GPU memory (17,227 MB) than static (17,002 MB) and sink (16,812 MB), but this overhead is modest given the substantial gain in output quality. Although the decoding time of entropy caching (26.5 s) is marginally higher than static (25.3 s) and sink (24.1 s), the increase is minor and justified by the quality improvement. Overall, Figure 3 confirms that entropy-guided caching provides a favorable trade-off for long-context summarization: maintaining superior ROUGE scores with minimal additional resource cost.

Table 2.
Comparison of ROUGE-1 score, memory usage, and decoding time across three KV caching strategies (Static, Sink, Entropy) at fixed input length (512 tokens).
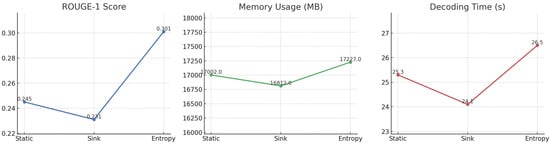
Figure 3.
Visualization of results from Table 1 Mistral 0.1v 7B Govreport dataset: ROUGE-1 score, memory usage, and decoding time for static, sink, and entropy-guided KV caching strategies with fixed output length (512 tokens).
Table 3 describes the effect of increasing decoding length (1024 and 2048 tokens) on memory usage and inference time for each caching method across the three models. As decoding length increases, entropy-guided caching scales more efficiently than static caching, offering significant reductions in both memory footprint and latency. For instance, in LLaMA 3.2 3B at 1024 tokens, entropy-guided caching reduces decoding time from 49.7 s (static) to 31.5 s (entropy-guided). Although the sink strategy is slightly faster, it introduces greater instability and quality degradation. Entropy caching offers a more stable and balanced alternative, preserving quality while delivering comparable efficiency. Additionally, the one-time overhead introduced during the prefill phase (for entropy estimation and token scoring) is minimal, accounting for only 3.5% of total decoding time at 1024 tokens and dropping to 1.8% at 2048 tokens. Among the evaluated models, Qwen3 4B exhibited the most notable improvements under the entropy-guided caching strategy. Therefore, Figure 4 focuses on this model to illustrate the comparative performance across caching methods in terms of memory usage and decoding latency. Figure 4 illustrates the memory usage and decoding latency of the Qwen3 4B model under three KV caching strategies—static, sink, and entropy-guided caching. Among the methods, entropy-guided caching exhibits competitive performance in terms of both speed and memory efficiency. It achieves a decoding time of 38.8 s, which is substantially lower than that of static caching (70.5 s) and also notably lower than sink caching (49.4 s). In terms of memory usage, entropy-guided caching consumes 15,481 MB, which is slightly lower than sink caching (15,500 MB) and significantly less than static caching (16,076 MB). These results suggest that entropy-guided caching offers a balanced trade-off between inference efficiency and resource usage, especially in long-context scenarios.

Table 3.
Comparison of memory usage and decoding time across KV caching strategies under varying decoding lengths (1024 and 2048 tokens).
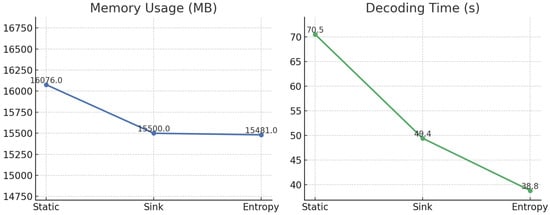
Figure 4.
Visualization of results from Table 2 Qwen3 4B: memory usage and decoding time for each caching strategy (static, sink, entropy) across different decoding lengths (1024 and 2048 tokens).
5. Conclusions
The experimental results demonstrate that entropy-guided KV caching achieves both reduced memory usage and faster decoding speed without sacrificing generation quality. These improvements are particularly pronounced under long decoding lengths (e.g., 2048 tokens), where static caching becomes inefficient and recent-only caching often fails to retain semantically important context. By leveraging the entropy of attention distributions to allocate cache budgets per layer, our method dynamically prioritizes tokens that are contextually significant, allowing for more effective utilization of limited memory resources.
Compared to prior approaches—such as fixed-length recent token caching or sink token heuristics—our method provides a more principled and data-driven alternative. It adapts the cache contents based on model behavior observed during the prefill phase, rather than relying on static positions or predefined window sizes. This not only enhances performance but also offers interpretability by highlighting which tokens are most salient to the model’s decision-making process.
Nonetheless, the current approach has several limitations. First, the selection of top-k tokens is based solely on cumulative attention scores from the prefill phase. While this helps avoid redundancy, it may overlook important tokens that emerge during later decoding steps. Second, assigning shared top-k tokens across all heads in a layer may obscure fine-grained head-specific patterns. Third, the fixed 50:50 budget split between top-k tokens and the sink + recent pool is not adaptable to tasks or layers with skewed demands for global versus local context, which may lead to suboptimal cache usage. Furthermore, the assumption that mean entropy across heads reliably reflects layer importance may not hold for short inputs or domain-shifted data, leading to noisy or inefficient budget allocation. Finally, computing per-head entropy and cumulative attention scores incurs a one-time overhead of which, while acceptable for moderate sequence lengths, may become a bottleneck in very large models or extremely long documents.
Future research could explore hybrid cache-allocation schemes that combine entropy-based top-k selection with lightweight mechanisms to track attention drift during decoding. An adaptive cache scheduler may dynamically adjust the budget ratio between top-k and recent/sink tokens per layer or per task—potentially using a reinforcement learning controller that monitors latency and memory usage in real time. Additionally, compressing cached key–value pairs through techniques such as 8-bit quantization or low-rank projection [33,34,35,36,37,38,39] could enable more tokens to be stored without increasing the memory footprint.
Another promising direction is the integration of alternative attention mechanisms such as linear or kernelized attention, which could further reduce inference costs by lowering the quadratic complexity of standard attention—particularly when paired with entropy-guided token filtering. Moreover, the effectiveness of head-wise attention scores in the autoregressive decoding phase remains an open question; while useful during prefill, their utility for guiding dynamic cache updates warrants further investigation.
Finally, current top-k selection strategies do not explicitly address semantic redundancy, potentially leading to inefficient cache usage. Incorporating redundancy-aware or diversity-promoting selection criteria could improve token utility. The reliance on entropy as a proxy for importance may also be problematic in cases where attention sharpness fails to align with semantic informativeness. Incorporating complementary signals—such as token gradients, prediction confidence, or information gain—may lead to more robust and adaptive cache allocation strategies.
Author Contributions
Conceptualization, H.K. and Y.J.; methodology, H.K.; software, H.K.; validation, H.K.; formal analysis, H.K.; investigation, H.K.; resources, H.K.; data curation, H.K.; writing—original draft preparation, H.K.; writing—review and editing, Y.J.; visualization, H.K.; supervision, Y.J.; project administration, Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institute for Information and Communications Technology Promotion (IITP) under grant No. IITP-2025-RS-2022-00156394. It was also supported by the RISE Program of Kumoh National Institute of Technology.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
During the preparation of this manuscript, the authors used OpenAI GPT-4o (May 2024 version) for proofreading suggestions. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| LLM | Large language model |
| KV | Key–value |
| BOS | Beginning of sequence |
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Available online: https://arxiv.org/abs/1706.03762 (accessed on 2 June 2025).
- Dao, T.; Fu, D.; Ermon, S.; Ré, A.; Ré, C. FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness. In Proceedings of the Advances in Neural Information Processing Systems 35 (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; Available online: https://arxiv.org/abs/2205.14135 (accessed on 2 June 2025).
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The Long-Document Transformer. arXiv 2020, arXiv:2004.05150. Available online: https://arxiv.org/abs/2004.05150 (accessed on 2 June 2025).
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 30 April 2020; Available online: https://arxiv.org/abs/2001.04451 (accessed on 2 June 2025).
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient Transformers: A Survey. arXiv 2020, arXiv:2009.06732. Available online: https://arxiv.org/abs/2009.06732 (accessed on 2 June 2025).
- Choromanski, K.; Likhosherstov, V.; Dohan, D.; Song, X.; Gane, A.; Sarlos, T.; Hawkins, P.; Davis, J.; Mohiuddin, A.; Kaiser, L.; et al. Rethinking Attention with Performers. In Proceedings of the International Conference on Learning Representations (ICLR), Vienna, Austria, 4 May 2021; Available online: https://arxiv.org/abs/2009.14794 (accessed on 2 June 2025).
- Zhang, B.; Titov, I.; Sennrich, R. Sparse Attention with Linear Unit. In Proceedings of the ACL, Online, 7–11 November 2021. [Google Scholar]
- Michel, P.; Levy, O.; Neubig, G. Are Sixteen Heads Really Better Than One? In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; Available online: https://arxiv.org/abs/1905.10650 (accessed on 2 June 2025).
- Jain, S.; Wallace, B.C. Attention Is Not Explanation. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; Available online: https://arxiv.org/abs/1902.10186 (accessed on 2 June 2025).
- Wiegreffe, S.; Pinter, Y. Attention is not not Explanation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP), Vancouver, BC, Canada, 8–14 December 2019; Available online: https://arxiv.org/abs/1908.04626 (accessed on 2 June 2025).
- Takase, S.; Okazaki, N. Sparse Attention with Linear Units. In Proceedings of the Association for Computational Linguistics (ACL), Online, 5–10 July 2020; Available online: https://arxiv.org/abs/2104.07012 (accessed on 2 June 2025).
- Clark, K.; Khandelwal, U.; Levy, O.; Manning, C.D. What Does BERT Look at? An Analysis of BERT’s Attention. In Proceedings of the BlackboxNLP Workshop at ACL, Florence, Italy, 1 August 2019; Available online: https://arxiv.org/abs/1906.04341 (accessed on 2 June 2025).
- Zhang, Z.; Sheng, Y.; Zhou, T.; Chen, T.; Zheng, L.; Cai, R.; Song, Z.; Tian, Y.; Ré, C.; Barrett, C.; et al. HO: Heavy-Hitter Oracle for Efficient Generative Inference of Large Language Models. In Proceedings of the 37th Conference on Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 10–16 December 2023; Available online: https://arxiv.org/abs/2306.14048 (accessed on 2 June 2025).
- Xiao, G.; Tian, Y.; Chen, B.; Han, S.; Lewis, M. Efficient Streaming Language Models with Attention Sinks. In Proceedings of the ICLR, Vienna, Austria, 7–11 May 2024; Available online: https://arxiv.org/pdf/2309.17453 (accessed on 2 June 2025).
- Zhao, J.; Fang, Z.; Li, S.; Yang, S.; He, S. BUZZ: Beehive-structured sparse KV cache with segmented heavy hitters for efficient LLM inference. arXiv 2024, arXiv:2410.23079. Available online: https://arxiv.org/abs/2410.23079 (accessed on 2 June 2025).
- Chen, Y.; Wang, G.; Shang, J.; Cui, S.; Zhang, Z.; Liu, T.; Wang, S.; Yu, D.; Wu, H. NACL: A general and effective KV cache eviction framework for LLMs at inference time. arXiv 2024, arXiv:2408.03675. Available online: https://arxiv.org/abs/2408.03675 (accessed on 2 June 2025).
- Liu, Z.; Desai, A.; Liao, F.; Wang, W.; Xie, V.; Xu, Z.; Kyrillidis, A.; Shrivastava, A. Scissorhands: Exploiting the persistence ofimportance hypothesis for LLM KV cache compression at testtime. In Proceedings of the Advances in Neural Information Processing Systems 36: Annual Conference on Neural Information Processing Systems 2023, NeurIPS 2023, New Orleans, LA, USA, 10–16 December 2023; Available online: https://arxiv.org/abs/2305.17118 (accessed on 2 June 2025).
- Adnan, M.; Arunkumar, A.; Jain, G.; Nair, P.J.; Soloveychik, I.; Kamath, P. Keyformer: KV cache reduction through key tokens selection for efficient generative inference. In Proceedings of the Seventh Annual Conference on Machine Learning and Systems, MLSys 2024, Santa Clara, CA, USA, 13–16 May 2024; Available online: https://arxiv.org/abs/2403.09054 (accessed on 2 June 2025).
- Chen, G.; Shi, H.; Li, J.; Gao, Y.; Ren, X.; Chen, Y.; Jiang, X.; Li, Z.; Liu, W.; Huang, C. Sepllm: Accelerate large language modelsby compressing one segment into one separator. arXiv 2024, arXiv:2412.12094. Available online: https://arxiv.org/abs/2412.12094 (accessed on 2 June 2025).
- Sun, Y.; Dong, L.; Huang, S.; Ma, S.; Xia, Y.; Xue, J.; Wang, J.; Wei, F. Retentive Network: A Successor to Transformer for Large Language Models. arXiv 2023, arXiv:2307.08621. Available online: https://arxiv.org/pdf/2307.08621 (accessed on 2 June 2025).
- Fu, Y.; Cai, Z.; Asi, A.; Xiong, W.; Dong, Y.; Xiao, W. Not all heads matter: A head-level KV cache compression method with integrated retrieval and reasoning. arXiv 2024, arXiv:2410.19258. Available online: https://arxiv.org/abs/2410.19258 (accessed on 2 June 2025).
- Xiao, G.; Tang, J.; Zuo, J.; Guo, J.; Yang, S.; Tang, H.; Fu, Y.; Han, S. Duoattention: Efficient long-context LLM inference with retrieval and streaming heads. arXiv 2024, arXiv:2410.10819. Available online: https://openreview.net/forum?id=cFu7ze7xUm (accessed on 3 June 2025).
- Cai, Z.; Zhang, Y.; Gao, B.; Liu, Y.; Liu, T.; Lu, K.; Xiong, W.; Dong, Y.; Chang, B.; Hu, J.; et al. PyramidKV: Dynamic KV cache compression based on pyramidal information funneling. arXiv 2024, arXiv:2406.02069. Available online: https://arxiv.org/abs/2406.02069 (accessed on 2 June 2025).
- Yang, D.; Han, X.; Gao, Y.; Hu, Y.; Zhang, S.; Zhao, H. PyramidInfer: Pyramid KV cache compression for high-throughput LLM inference. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (ACL), Bangkok, Thailand, 11–16 August 2024; pp. 3258–3270. Available online: https://arxiv.org/abs/2405.12532 (accessed on 2 June 2025).
- Zhou, X.; Wang, W.; Zeng, M.; Guo, J.; Liu, X.; Shen, L.; Zhang, M.; Ding, L. DynamicKV: Task-aware adaptive KV cache compression for long context LLMs. In Proceedings of the Thirteenth International Conference on Learning Representations (ICLR), Vienna, Austria, 7–11 May 2024; Available online: https://openreview.net/forum?id=uHkfU4TaPh (accessed on 3 June 2025).
- Wang, A.; Chen, H.; Tan, J.; Zhang, K.; Cai, X.; Lin, Z.; Han, J.; Ding, G. PrefixKV: Adaptive prefix KV cache is what vision instruction-following models need for efficient generation. arXiv 2024, arXiv:2412.03409. Available online: https://arxiv.org/abs/2412.03409 (accessed on 2 June 2025).
- Zhang, X.; Du, C.; Du, C.; Pang, T.; Gao, W.; Lin, M. SimLayerKV: A Simple Framework for Layer-Level KV Cache Reduction. 2024. Available online: https://openreview.net/forum?id=UjSmUlUU6y (accessed on 3 June 2025).
- Grattafiori, A.; Dubey, A.; Jauhri, A.; Pandey, A.; Kadian, A.; Al-Dahle, A.; Letman, A.; Mathur, A.; Schelten, A.; Vaughan, A. LLaMA 3: Open Foundation and Instruction Models. arXiv 2024, arXiv:2404.14219. Available online: https://arxiv.org/abs/2407.21783 (accessed on 2 June 2025).
- OpenChat Team. Mistral 7B: Open-Weight Language Models for Everyone. arXiv 2023, arXiv:2310.06825. Available online: https://arxiv.org/abs/2310.06825 (accessed on 2 June 2025).
- Qwen Team, Alibaba DAMO Academy. Qwen: A Scalable and High-Performance Language Model Family. arXiv 2023, arXiv:2309.16609. Available online: https://arxiv.org/abs/2505.09388 (accessed on 2 June 2025).
- Ding, Y.; Qin, Y.; Jiang, Z.; Wu, Q.; Lin, Z.; Wang, Y.; Xu, K.; Shen, Y.; Chen, W.; Xie, X. LongBench: A Bilingual, Multitask Benchmark for Long Context Understanding. arXiv 2023, arXiv:2308.14508. Available online: https://arxiv.org/abs/2308.14508 (accessed on 2 June 2025).
- Cohan, A.; Dernoncourt, F.; Kim, D.S.; Bui, T.; Kim, S.; Chang, W.; Goharian, N. A Discourse-Aware Attention Model for Abstractive Summarization of Long Documents. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT), New Orleans, LA, USA, 1–6 June 2018; pp. 615–621. Available online: https://arxiv.org/abs/1710.06071 (accessed on 2 June 2025).
- Hooper, C.; Kim, S.; Mohammadzadeh, H.; Mahoney, M.W.; Shao, Y.S.; Keutzer, K.; Gholami, A. KVQuant: Towards 10 Million Context Length LLM Inference with KV Cache Quantization. arXiv 2024, arXiv:2401.18079. Available online: https://arxiv.org/abs/2401.18079 (accessed on 2 June 2025).
- Liu, R.; Bai, H.; Lin, H.; Li, Y.; Gao, H.; Xu, Z.; Hou, L.; Yao, J.; Yuan, C. IntactKV: Improving Large Language Model Quantization by Keeping Pivot Tokens Intact. arXiv 2024, arXiv:2403.01241. [Google Scholar]
- Duanmu, H.; Yuan, Z.; Li, X.; Duan, J.; Zhang, X.; Lin, D. SKVQ: Sliding-window Key and Value Cache Quantization for Large Language Models. arXiv 2024, arXiv:2405.06219. Available online: https://arxiv.org/abs/2403.01241 (accessed on 2 June 2025).
- Liu, Z.; Yuan, J.; Jin, H.; Zhong, S.; Xu, Z.; Braverman, V.; Chen, B.; Hu, X. KIVI: A Tuning-Free Asymmetric 2-bit Quantization for KV Cache. arXiv 2024, arXiv:2402.02750. Available online: https://arxiv.org/abs/2402.02750 (accessed on 2 June 2025).
- Yue, Y.; Yuan, Z.; Duanmu, H.; Zhou, S.; Wu, J.; Nie, L. WKVQuant: Quantizing Weight and Key/Value Cache for Large Language Models Gains More. arXiv 2024, arXiv:2402.12065. Available online: https://arxiv.org/abs/2402.12065 (accessed on 2 June 2025).
- Kang, H.; Zhang, Q.; Kundu, S.; Jeong, G.; Liu, Z.; Krishna, T.; Zhao, T. GEAR: An Efficient KV Cache Compression Recipe for Near-Lossless Generative Inference of LLM. arXiv 2024, arXiv:2403.05527. Available online: https://arxiv.org/abs/2403.05527 (accessed on 2 June 2025).
- Yang, J.Y.; Kim, B.; Bae, J.; Kwon, B.; Park, G.; Yang, E.; Kwon, S.J.; Lee, D. No Token Left Behind: Reliable KV Cache Compression via Importance-Aware Mixed Precision Quantization. arXiv 2024, arXiv:2402.18096. Available online: https://arxiv.org/abs/2402.18096 (accessed on 2 June 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).