Numerical Comparisons of Heuristic Stress Topology Optimization Methods

Abstract

Mitigating excessive stress, a primary cause of structural failure, deformation, and premature fatigue, is critical in engineering design. Evolutionary (BESO) and proportional topology optimization (PTO) are standard heuristic approaches, yet their relative computational efficiency and accuracy for stress problems are not well understood. Addressing this gap, this paper conducts the first comprehensive comparisons of BESO and PTO for the stress minimization problem, also investigating the impact of the p-norm. Optimization results reveal PTO’s significant advantage in computational speed. BESO sometimes produces designs with lower maximum stresses, though with higher structural compliance.

1. Introduction

Excessive stress will lead to early fracture, deformation, and fatigue damage, reducing the service life and security of the machinery. The traditional stiffness design is usually unable to meet the structural strength requirements, because there are significant differences between strength design and stiffness design [1]. Stress optimization is a complex research topic due to its computational singularity. Furthermore, how to improve the computational efficiency and accuracy of stress optimization methods is a difficult and important research topic [2,3].

The topology optimization technique possesses the characteristics of high design efficiency and large design freedom and is widely used in the conceptual design stage of engineering structures [4,5,6]. Some scholars have carried out relevant studies on stress-related topological optimization [7,8,9,10]. Duysinx and Bendsøe [8] first considered the continuum topology optimization under segmented stress constraints. The micro-continuous structure was proposed to interpolate the stiffness and allowable stress, and it was combined with the relaxation method to solve the singular phenomenon. Cheng and Guo [7] put forward an ε-relaxation method to eliminate the singular phenomenon. Le et al. [11] used density filters to control micro-structural size and used the density-based method with penalization to drive stress elements to generate 0–1 solutions. Allaire and Jouve [12] adopted the integration of global stress as the level set objective function. Van Miegroet and Duysinx [13] combined the extended finite element and level set methods to study the shape optimization problem, aiming to minimize the maximum stress. Xia et al. [14] first applied the bi-directional evolutionary structural optimization (BESO) method to stress optimization, which has some advantages. For example, optimization results usually possess clear boundaries, fundamentally avoiding the singular phenomena, which is attributed to the solid-void nature of BESO. Yaping Lai et al. [15] utilized BESO and multi-material BESO methods to propose a novel and unique pedestrian bridge design by applying topology optimization algorithms in the conceptual design and detailed structural design of bridges. In the work of Hélio Luiz Simonetti et al. [16], a qualitative comparison of the BESO and Smooth ESO (SESO) methods was conducted, revealing that both methods can effectively generate optimal topologies for three-dimensional structural systems when considering the effects of minimizing flexibility and structural self-weight. Biyikli and To [17] proposed a simple and efficient proportional topology optimization (PTO) method, which eliminates some numerical difficulties that emerged from analytical derivations and sensitivity calculations.

As classical heuristic algorithms, both the BESO and PTO methods have the merits of conceptual simplicity and calculational efficiency. However, their optimization efficiency and accuracy in the commonly concerned stress problem have always been a hot topic for many researchers. This paper first and in detail compares the optimization efficiency and accuracy of heuristic methods in stress optimization, through 3D bridge examples. Moreover, the influence of p-norm on the stress designs is also examined. This study is committed to providing good advice for designers to obtain more stable and reliable engineering structures.

2. Optimization Formulation and Sensitivity Analysis

The mathematical formulation to minimize the structural global stress, when subjected to material usage, is described as follows:

$$\left\{\begin{array}{ll}\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}:& {\sigma }_p \mathrm{i}\mathrm{n} \mathrm{B}\mathrm{E}\mathrm{S}\mathrm{O},{\sigma }_{vM} \mathrm{i}\mathrm{n} \mathrm{P}\mathrm{T}\mathrm{O}\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o}:& \mathbf{K}\mathbf{U}=\mathbf{F}\\ & V_1\left(x\right)={\sum }_{i=1}^{num}{x}_i{v}_i\le V_{\mathrm{req}}\\ & V_2\left(x\right)={\sum }_{i=1}^{num}{\rho }_i{v}_i\le V_{\mathrm{req}}\\ & x_i=0 or 1,i=1,2,\dots ,num,\mathrm{i}\mathrm{n} \mathrm{B}\mathrm{E}\mathrm{S}\mathrm{O}\\ & 0 \le {\rho }_{min}\le {\rho }_i\le 1,i=1,2,\dots ,num,\mathrm{i}\mathrm{n} \mathrm{P}\mathrm{T}\mathrm{O}\end{array}\right.$$

(1)

where ${\sigma }_p$ and ${\sigma }_{vM}$ are the p-norm stress in BESO, and the von Mises stress in PTO. K, U, and F are the stiffness matrix, displacement, and external force imposed on the structure, respectively. V₁(x) is the material volume constraint in the BESO method, and V₂(x) is the material volume constraint in the PTO method during the optimization. x_i is the design variable in BESO, v_i is the elemental volume, V_req is the required material usage, and num is the total number of elements. ${\rho }_i$ is the density variable in PTO and ${\rho }_{min}$ is the minimal density value to prevent the calculational singularity.

Design variables in BESO are binary, while the PTO design variable is continuous. The objective function defined in Equation (1) is to minimize the maximum stress, which is nondifferentiable. Hence, it cannot be directly used with sensitivity methods. Instead, BESO uses the p-norm to measure von Mises stress during the optimization, whereas PTO does not require a sensitivity analysis. Therefore, the parameter p is not needed to evaluate structural stress. The p-norm stress can be calculated as

$${\sigma }_p={\left({\sum }_{i=1}^{num}{\sigma }_{vm,i}^p\right)}^{{\displaystyle \frac{1}{p}}}$$

(2)

where ${\sigma }_{vm,i}$ is the von Mises stress of the elemental center, and p is the stress exponent. When p is equal to 1, the averaged stress can be obtained. Furthermore, if the p-value approaches infinity, the stress value can be maximized. In brief, the larger the p-value, the more accurate the calculation of the maximum von Mises stress. However, excessive p will lead to optimization problems, and the optimization program will experience severe oscillations. Hence, the p-value must be appropriately selected to ensure the smooth optimization. At the same time, the maximum von Mises stress can be well approximated. For more information about the selection of p, please check [8]. The von Mises stress is computed as

$${\sigma }_{vM}={\left({\mathsf{\sigma }}^T\mathbf{V}\mathsf{\sigma }\right)}^{1/2}$$

(3)

$\mathsf{\sigma }$ signifies the stress in Voigt notation, and V means the stress coefficient matrix. In the 2D case, the von Mises stress can be calculated as

$${\sigma }_{vM}=\sqrt{{\sigma }_x^2+{\sigma }_y^2-{\sigma }_x{\sigma }_y+3{\sigma }_{xy}^2}$$

(4)

${\sigma }_x$ and ${\sigma }_y$ are normal stresses along the horizontal and vertical directions, respectively. ${\sigma }_{xy}$ is the coupling stress along two directions.

To approximately obtain 0/1 solutions, the elemental stiffness in PTO can be written as

$$E\left(\rho \right)=E_{min}+{\rho }^p{E}_0$$

(5)

E_min is a small stiffness value (10⁻³ used in this study) related to void elements, so as to avoid the calculational singularity; E₀ is the solid stiffness matrix. p is the penalty factor, and p = 3 is used in this study.

Both the sensitivity analysis and filtering are needed in BESO. To successfully perform evolutionary optimization, the sensitivity information of the global stress with respect to the design variables needs to be primarily provided. According to the p-norm stress defined in Equation (2), the derivative of ${\sigma }_p$ related to the design variable is written as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_p}{\mathsf{\partial }{x}_j}}={\sigma }_p^{1-p}\left({\sum }_{i=1}^{num}{\sigma }_{vm,i}^{p-1}{\displaystyle \frac{\mathsf{\partial }{\sigma }_{vm,i}}{\mathsf{\partial }{x}_j}}\right),j=1,2,\dots ,num.$$

(6)

According to Equation (3), the derivative of elemental stress related to the stress vector is

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_{vm}}{\mathsf{\partial }\mathsf{\sigma }}}={\displaystyle \frac{1}{2}}{\left({\mathsf{\sigma }}^T\mathbf{V}\mathsf{\sigma }\right)}^{-1/2}2{\mathsf{\sigma }}^T\mathbf{V}={\sigma }_{vm}^{-1}{\mathsf{\sigma }}^T\mathbf{V}$$

(7)

so the derivative of the von Mises stress with respect to the design variable can be obtained as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_{vm,i}}{\mathsf{\partial }{x}_j}}={\sigma }_{vm,i}^{-1}{\mathsf{\sigma }}_i^T\mathbf{V}{\displaystyle \frac{\mathsf{\partial }{\sigma }_i}{\mathsf{\partial }{x}_j}}$$

(8)

where the effective stress vector can be expressed as ${\sigma }_i={\mathit{D}}_0{\mathit{B}}_i{\mathit{u}}_i$, we can find that the stiffness matrix D₀ and elemental strain–displacement matrix B are independent of design variables. The above derivative can be further written as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_{vm,i}}{\mathsf{\partial }{x}_j}}={\sigma }_{vm,i}^{-1}{\mathsf{\sigma }}_i^T\mathbf{V}{\mathbf{D}}_0{\mathbf{B}}_i{\mathbf{L}}_i{\displaystyle \frac{\mathsf{\partial }\mathbf{U}}{\mathsf{\partial }{x}_j}}$$

(9)

where L_i is the nodal displacements related to the i-th element, which satisfies ${\mathit{u}}_i={\mathit{L}}_i\mathbf{U}$. Differentiating both sides of the balance equation KU = F, we can obtain

$${\displaystyle \frac{\mathsf{\partial }\mathbf{K}}{\mathsf{\partial }{x}_j}}\mathbf{U}+\mathbf{K}{\displaystyle \frac{\mathsf{\partial }\mathbf{U}}{\mathsf{\partial }{x}_j}}=0$$

(10)

Substitute the above formula into Equation (9), and it can be rewritten as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_{vm,i}}{\mathsf{\partial }{x}_j}}=-{\sigma }_{vm,i}^{-1}{\mathit{\sigma }}_i^T\mathit{V}{\mathit{D}}_0{\mathit{B}}_i{\mathit{L}}_i{\mathit{K}}^{-1}{\displaystyle \frac{\mathsf{\partial }\mathit{K}}{\mathsf{\partial }{x}_j}}\mathit{U}$$

(11)

Substitute Equation (11) into Equation (6), the derivative of the p-norm stress with respect to the design variable should be expressed as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_p}{\mathsf{\partial }{x}_j}}=-{\sigma }_p^{1-p}\left({\sum }_{i=1}^{num}{\sigma }_{vm,i}^{p-2}{\mathsf{\sigma }}_i^T\mathbf{V}{\mathbf{D}}_0{\mathbf{B}}_i{\mathbf{L}}_i\right){\mathbf{K}}^{-1}{\displaystyle \frac{\mathsf{\partial }\mathbf{K}}{\mathsf{\partial }{x}_j}}\mathbf{U}$$

(12)

Using the solution of the following adjoint problem:

$$\mathbf{K}\mathsf{\lambda }={\sum }_{i=1}^{num}{\sigma }_{vm,i}^{p-2}{\left({\mathbf{D}}_0{\mathbf{B}}_i{\mathbf{L}}_i\right)}^T\mathbf{V}{\sigma }_i$$

(13)

The right side of the above formulation is assembled according to body forces, so Equation (12) can be further written as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_p}{\mathsf{\partial }{x}_j}}=-{\sigma }_p^{1-p}{\mathsf{\lambda }}^T{\displaystyle \frac{\mathsf{\partial }\mathbf{K}}{\mathsf{\partial }{x}_j}}\mathbf{U}$$

(14)

the derivative of the stiffness matrix with respect to the design variable should be expressed as

$${\displaystyle \frac{\mathsf{\partial }\mathbf{K}}{\mathsf{\partial }{x}_j}}={\sum }_{i=1}^{num}{\mathbf{L}}_i^T{\displaystyle \frac{{\mathbf{k}}_j}{\mathsf{\partial }{x}_j}}{\mathbf{L}}_i={\mathbf{L}}_j^T{\mathbf{k}}_j^{\left(0\right)}{\mathbf{L}}_j$$

(15)

both ${\mathit{k}}_j$ and ${\mathit{k}}_j^{\left(0\right)}$ are elemental stiffness matrices, related to element j and the solid element, respectively. They can be respectively written as

$${\mathbf{k}}_j=x_j\int {\mathbf{B}}_j^T{\mathbf{D}}_0{\mathbf{B}}_{j}d{\mathsf{\Omega }}_j\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\mathrm{and}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\mathbf{k}}_j^{\left(0\right)}=\int {\mathbf{B}}_j^T{\mathbf{D}}_0{\mathbf{B}}_{j}d{\mathsf{\Omega }}_j$$

(16)

in which ${\mathsf{\Omega }}_j$ is the j-th elemental domain. Substitute Equation (15) into Equation (14), and the sensitivity information of the p-norm stress with respect to the design variable should be finally expressed as

$${\displaystyle \frac{\mathsf{\partial }{\sigma }_p}{\mathsf{\partial }{x}_j}}=-{\sigma }_p^{1-p}{\mathsf{\lambda }}_j^T{\mathbf{k}}_j^{\left(0\right)}{\mathbf{u}}_j$$

(17)

${\mathit{\lambda }}_j$ is the adjoint nodal vector with respect to element j.

3. Numerical Example

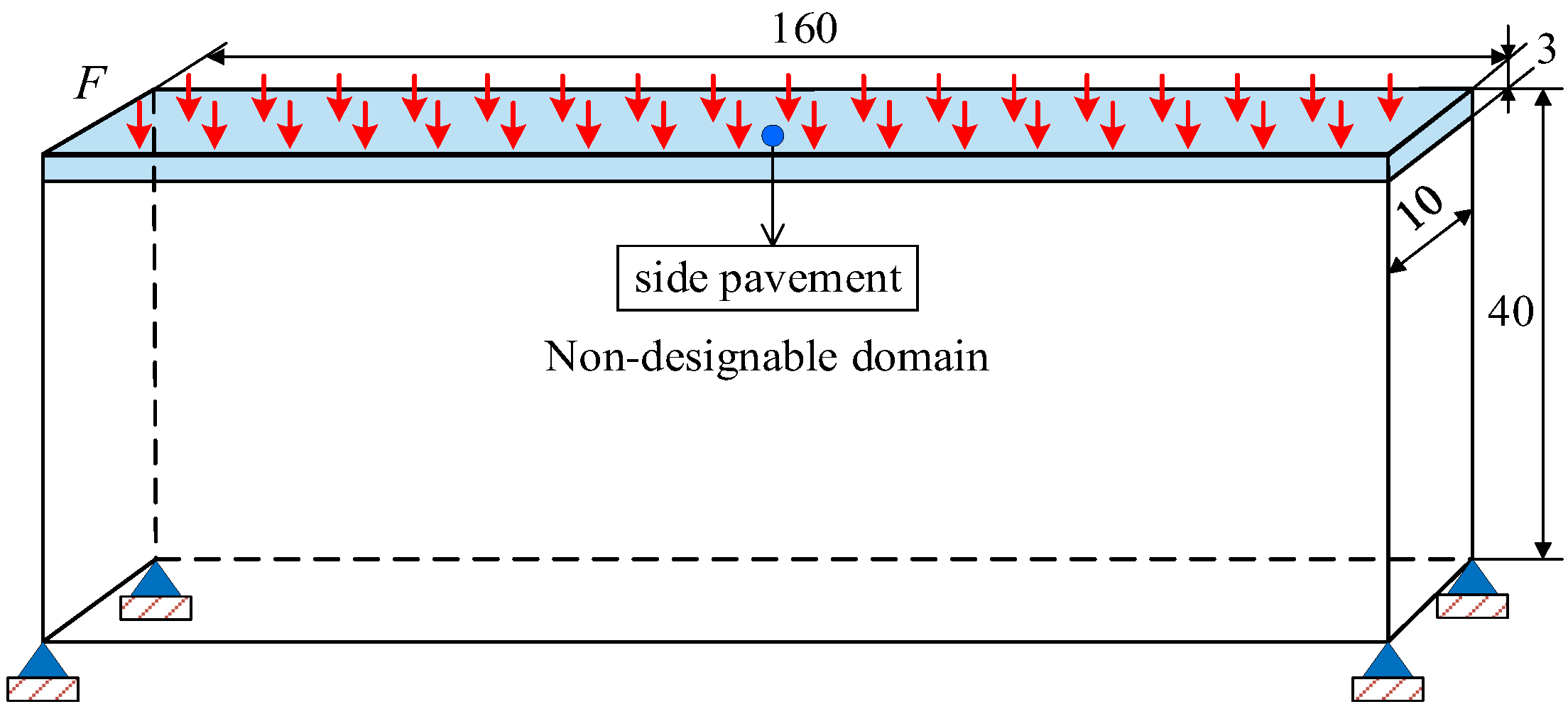
In this section, the computational accuracy and efficiency of PTO and BESO methods are compared through a 3D bridge structure, which is shown in Figure 1. The sizes of the design domain and non-designable domain are 160 × 10 × 37 and 160 × 10 × 3 elements, respectively. The non-designable domain refers to the side pavement. The four vertices at the bottom of the structure are fixed. According to European standards, the load for a pedestrian bridge is 5 kN/m². Since this design simplifies the model and employs a dimensionless design, a uniform force F = 0.01 N is applied to each unit on the bridge deck. The material used for optimization is an isotropic material. The material usage is taken as 0.3, and the filter radii are set to 2. To discuss the influence of p-norm on the 3D structural design, p takes three cases, such as 2, 3, and 4, in the BESO method. Figure 2 depicts the evolutionary topologies under four cases.

Table 1. Numerical results under the PTO and BESO methods.

Case	Method	The Maximum Stress (MPa)	Iteration Number	Total Optimization Time (s)	Compliance Values (N·mm)
Case 1	PTO	6.763	100	2975.5793	817.7253
Case 2	BESO_p = 2	6.792	100	5845.4522	797.5808
Case 3	BESO_p = 3	6.399	100	5538.1949	853.4656
Case 4	BESO_p = 4	6.336	100	5309.2488	1003.5918

lists all the numerical results, and Figure 3 depicts the iteration curves under the PTO and BESO methods.

As depicted in Figure 2, in all cases, the bridge structure converges to a clear and reasonable topological result. In Case 1, both the lateral supports and the longitudinal supports branch into four rods. In Case 2, neither the lateral supports nor the longitudinal supports branch; both are solid, continuous structures. In Case 3, the left and right supports are solid continuous structures, while the upper part of the longitudinal support is a continuous structure, and the lower part branches into four members. In Case 4, the left and right supports are solid continuous structures, while the longitudinal support branches into four members and is locally reinforced on both sides. Intuitively speaking, the final topology obtained by the PTO method is smoother than that obtained by the BESO method. Under four operating conditions, the maximum stress in the structure occurs at the same location, namely the fixed corner, indicated by the red circle. This also demonstrates the accuracy and effectiveness of the two heuristic algorithms in calculating structural stress.

As listed in Table 1, PTO has tremendous advantages over BESO methods in terms of total optimization and each iteration, which illustrates that PTO has obvious merit in terms of calculational efficiency. As the p-norm increases in BESO, the structural stress decreases, but the structural compliance gradually increases. For Case 2 with p = 2, the maximum stress in the PTO method is smaller than that in BESO, explaining that the PTO method has advantages in terms of trace amounts in the maximum stress, but the structural compliance in BESO is smaller than that in PTO. For Cases 3 and 4, the maximum stresses in BESO are smaller than those in PTO, but the structural compliances in PTO are smaller than those in BESO. The above analysis indicates that BESO has advantages in the maximum stress calculation, while sacrificing structural compliance.

As depicted in Figure 3, the four cases stably converge with the final designs. PTO optimizes from a uniform density of 0.3, and the stress value first decreases and then stabilizes at a certain value. The BESO method starts with full designs, and the iteration curves are more stable than those in PTO. Case 2 gradually increases to a certain value of 6.792, and Cases 3 and 4 are stable enough during the optimization, due to the increase in p-norm.

4. Conclusions

This paper first investigates the calculational efficiency and accuracy of heuristic algorithms in solving the stress minimization problem. The methods considered are BESO and PTO methods; both of them are density-based optimization methods. BESO is sensitive, while PTO is insensitive. A numerical example explains that PTO has unparalleled advantages over BESO in calculation efficiency. For a 3D bridge structure with p = 2, the final stress values in PTO are smaller than those obtained in BESO. In BESO, the stress value gradually decreases with the increase in p, and the compliance obtained by p = 3 and p = 4 is greater than that obtained by PTO. This situation explains that the calculational accuracy in stress and compliance calculation is problem-dependent. Hence, if the engineering requirement in calculational accuracy is not high, we can fully use the PTO method to solve the stress-related optimization problem, due to its unparalleled efficiency.