Roman Domination of Cartesian Bundles of Cycles over Cycles

Abstract

A Roman dominating function f of a graph $G=(V,E)$ assigns labels from the set $\{0,1,2\}$ to vertices such that every vertex labeled 0 has a neighbor labeled 2. The weight of an RDF f is defined as $w\left(f\right)={\sum }_{v\in V}f\left(v\right)$, and the Roman domination number, ${\gamma }_R\left(G\right)$, is the minimum weight among all RDFs of G. This paper studies the domination and Roman domination numbers in Cartesian bundles of cycles. Furthermore, the constructed optimal patterns improve known bounds and suggest even better bounds might be achieved by combining patterns, especially for bundles involving shifts of order $4k$ and $5k$.

1. Introduction

Domination in graphs is a foundational area in graph theory, involving the selection of certain vertices to control the rest of the graph. Among the many extensions of this idea, Roman domination stands out due to its historical interpretation and mathematical novelty. It is inspired by a strategic problem: how to deploy limited forces across a network of locations to ensure that every unguarded site is within immediate reach of reinforcements.

Formally, a Roman dominating function (RDF) assigns a label 0, 1, or 2 to each vertex under the condition that any vertex labeled 0 must be adjacent to at least one vertex labeled 2. In this context, a vertex with label 2 represents a location sufficiently fortified to defend itself and an adjacent unguarded neighbor. The goal is to minimize the total weight, the sum of the assigned values, across the graph. The concept of Roman domination in graphs was first popularized by Stewart [1] through a historical analogy involving the defense of the Roman Empire. This idea was later formalized and thoroughly analyzed by Cockayne et al. [2], who introduced the Roman domination number and studied its properties for various graph classes. In [3], Kämmerling and Volkmann introduced the concept of Roman k-domination, which generalizes the classical Roman domination by requiring that each vertex assigned 0 must be adjacent to at least k vertices assigned 2. For a more detailed overview of different variants of Roman domination, the reader is referred to [4,5].

Graph bundles are a generalization of both graph products and covering graphs [6,7]. Interestingly, some well-known interconnection networks, such as twisted hypercubes [8,9] and multiplicative circulant graphs [10], can be interpreted as specific types of Cartesian graph bundles. One of the advantages of such structures is that they can achieve smaller diameters compared to traditional graph products [11,12], making them attractive for use in early supercomputer architectures [13].

Several classical graph invariants have been studied in graph bundles, including the domination number [14] and the chromatic number [15], highlighting their theoretical richness and potential for practical applications.

Some recent research has focused on various domination parameters in graph products, graph bundles, and related constructions. Ganesamurthy et al. [16] determined exact values and tight upper bounds for the connected power domination number ${\gamma }_P\left(G\right)$ of Cartesian products. Anderson and Kuenzel [17] established the lower bound which holds for trees whose domination and power domination numbers coincide. In a further refinement of the well-known Clark–Suen bound, Tout [18] proved a lower bound of the triple Cartesian product of graphs.

Domination in bundles has also received attention. Brezovnik et al. [19] studied 2-rainbow domination in Cartesian graph bundles over cycles and established bounds up to an additive constant, which is similar to the situation in products of cycles. In a related work, Hu and Sohn [20] provided exact values for total and paired domination numbers in $C_m$-bundles over $C_n$, which are structurally related to toroidal meshes.

Several domination variants have recently been investigated in various product settings. Klavžar et al. [21] analyzed orientable domination in Cartesian, lexicographic, and corona products. Cabrera Martinez et al. [22] examined Roman domination in direct and rooted products, and in [23], Cabrera Martinez provided exact formulas for the total Roman domination in rooted products. A comprehensive survey on double Roman domination [24] addresses Cartesian, strong, and direct products and outlines several open problems.

Recently, Vaidya and Pandit [25] proposed a framework for global equitable domination in Cartesian products such as $P_n\square P_2$, $C_n\square P_2$, and $C_n\square K_m$, providing valuable benchmarks for studying domination variants.

In this paper, we contribute to this line of research by investigating Roman domination in Cartesian products and graph bundles, aiming to bridge the gap between classical product results and more complex bundled structures. The following result generalizes previous findings on the Roman domination number of Cartesian product of cycles [26].

Our main result is summarized in the following theorems.

Theorem 1.

Let $C_n{\square }^{\phi }{C}_m$ be the Cartesian graph bundle of two cycles, where φ is an automorphism of the fiber $C_m$. Then, the Roman domination number of $C_n{\square }^{\phi }{C}_m$ is

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)=\left\{\begin{array}{cc}{\displaystyle ⌈\frac{3n}{2}⌉,}\hfill & m=3,\hfill \\ 2n,\hfill & m=4\mathit{or}(m=5\mathit{and}\phi ={\sigma }_{\ell }\mathit{is}a\mathit{cyclic}\mathit{shift}\mathit{and}2n\equiv \ell mod5),\hfill \\ 2n+1,\hfill & m=5\mathit{and}\phi \mathit{is}a\mathit{reflection},\hfill \\ 2n+2,\hfill & m=5,\phi ={\sigma }_{\ell }\mathit{is}a\mathit{cyclic}\mathit{shift}\mathit{and}2n\not\equiv \ell mod5.\hfill \end{array}\right.$$

Theorem 2.

Let $C_n{\square }^{\phi }{C}_m$ be a Cartesian graphs bundle with fiber $C_m$ over base $C_n$.

Then, the Roman domination number of $C_n{\square }^{\phi }{C}_m$ satisfies the following upper bounds:

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\le \left\{\begin{array}{cc}⌈{\displaystyle \frac{3n}{2}}⌉k,\hfill & m=3k,\hfill \\ 2nk,\hfill & m=4k,\hfill \\ 2(n+1)k,\hfill & m=5k.\hfill \end{array}\right.$$

2. Preliminaries

Formally, Roman domination in graphs was introduced by Cockayne et al. [2] as follows. Given a graph $G=(V,E)$, a function $f:V\to \{0,1,2\}$ induces a partition of V into three sets: $V_0=\{v\in V\mid f\left(v\right)=0\}$, $V_1=\{v\in V\mid f\left(v\right)=1\}$, and $V_2=\{v\in V\mid f\left(v\right)=2\}$. We have $n=n_0+n_1+n_2$, where $|V_i|=n_i$ for $i=0,1,2$. Since there exists a one-to-one correspondence between such functions and ordered partitions $(V_0,V_1,V_2)$ of V, we will write $f=(V_0,V_1,V_2)$.

A function $f=(V_0,V_1,V_2)$ is called a Roman dominating function (an RDF) if every vertex in $V_0$ is adjacent to at least one vertex in $V_2$. The weight of an RDF f is defined as

$$w\left(f\right)=\sum _{v\in V}f\left(v\right)=n_1+2n_2.$$

(1)

The Roman domination number, ${\gamma }_R\left(G\right)$, is the minimum weight over all possible RDF-s of G. If a function $f=(V_0,V_1,V_2)$ is an RDF and has weight $w\left(f\right)={\gamma }_R\left(G\right)$, we call it a ${\gamma }_R$-function.

It is well known that $\gamma \left(G\right)\le {\gamma }_R\left(G\right)\le 2\gamma \left(G\right)$, where $\gamma \left(G\right)$ denotes the domination number of G [2]. The only graphs satisfying ${\gamma }_R\left(G\right)=\gamma \left(G\right)$ are edgeless graphs. A graph is referred to as a Roman graph if ${\gamma }_R\left(G\right)=2\gamma \left(G\right)$. It was shown that this equality holds if and only if G admits a ${\gamma }_R\left(G\right)$-function in which no vertex is assigned value 1, i.e., $f\left(v\right)\in \{0,2\}$ for all $v\in V\left(G\right)$ [2].

Two graphs G and H are said to be isomorphic if there exists a bijective mapping $\phi :V\left(G\right)\to V\left(H\right)$ that preserves adjacency as well as non-adjacency. That is, $\phi$ is an isomorphism if for every pair of vertices $i,j\in V\left(G\right)$, it holds that $ij\in E\left(G\right)$ if and only if $\phi \left(i\right)\phi \left(j\right)\in E\left(H\right)$. When such an isomorphism maps a graph onto itself, it is called an automorphism. The identity automorphism on a graph G is denoted by ${\mathrm{id}}_G$ or simply $\mathrm{id}$ when the context is clear. The cycle graph $C_n$ on n vertices is defined by the vertex set $V\left(C_n\right)=\{0,1,\dots ,n-1\}$, where two vertices i and j are adjacent if and only if $i\equiv j\pm 1modn$. If G and H are isomorphic, we write shortly $G\simeq H$.

Cartesian graph bundles extend the concept of Cartesian graph products by introducing additional structure.

Let B and G be graphs, and let $\mathrm{Aut}\left(G\right)$ denote the automorphism group of G. We associate an automorphism of G to each pair of adjacent vertices $u,v\in V\left(B\right)$ through a mapping

$$\phi :A\left(B\right)\to \mathrm{Aut}\left(G\right),$$

where $A\left(B\right)$ stands for the set of all arcs in graph B. For simplicity, we denote $\phi (u,v)={\phi }_{u,v}$ with the assumption that ${\phi }_{v,u}={\phi }_{u,v}^{-1}$ for all $u,v\in V\left(B\right)$.

We now define a graph X with a vertex set given by the Cartesian product $V\left(X\right)=V\left(B\right)\times V\left(G\right)$. Adjacency in X is determined as follows: vertices $(b_1,g_1)$ and $(b_2,g_2)$ are adjacent if and only if one of the following holds:

• $b_1=b_2$ and $g_1{g}_2\in E\left(G\right)$, or
• $b_1{b}_2\in E\left(B\right)$ and $g_2={\phi }_{b_1,b_2}\left(g_1\right)$.

The resulting graph X is referred to as a Cartesian graph bundle, where B serves as the base and G as the fiber, and we denote this by $X=B{\square }^{\phi }G$.

It is a classical result that Cartesian products of graphs admit a unique factorization (modulo isomorphism and permutation of factors) [27], whereas a single graph can have multiple non-equivalent representations as graph bundles [28]. When all mappings ${\phi }_{u,v}$ are identities, the bundle reduces to the standard Cartesian product:

$$X=B{\square }^{\phi }G=B\square G.$$

Additionally, if the base graph is a tree, then the bundle can always be represented as a Cartesian product regardless of the automorphism assignment:

$$T{\square }^{\phi }G\cong T\square G$$

for any graph G, tree T, and mapping $\phi$ [6,7].

For our purposes, it is also important to observe that any Cartesian graph bundle constructed over a cycle can be relabeled so that all automorphisms, except possibly one, are identities [15].

As established in [15], graph bundles exhibit a locally product-like structure. Specifically, any pair of adjacent fibers induces a subgraph isomorphic to the Cartesian product of the fiber and the complete graph $K_2$. This localized product structure inherently determines an isomorphism between the neighbouring fibers—interpretable as an automorphism acting on the fiber itself. Therefore, when the fiber is a cycle, the possible nontrivial automorphisms are limited to cyclic rotations (shifts) and reflections, corresponding to the symmetries of the cycle. Fixing $V\left(C_n\right)=\{0,1,2,\dots ,n-1\}$, we denote ${\phi }_{n-1,0}=\alpha$, ${\phi }_{i-1,i}=id$ for $i=1,2,\dots ,n-1$, and write $C_n{\square }^{\phi }G=C_n{\square }^{\alpha }G.$ Additional illustrations of Cartesian graph bundles are provided in [29].

In [2], the authors determined the exact Roman domination number for several graph families. For example, for paths and cycles of order n, the value is

$${\gamma }_R\left(P_n\right)={\gamma }_R\left(C_n\right)=⌈{\displaystyle \frac{2n}{3}}⌉.$$

Moreover, for the $2\times n$ grid graph, which is the Cartesian product $P_2\square P_n$, it was shown that

$${\gamma }_R(P_2\square P_n)=n+1.$$

For Cartesian products involving cycles, such as $C_m\square C_n$, only partial results and bounds are known, and determining the exact Roman domination number remains an open problem in general. For small m values, exact values of ${\gamma }_R(C_n\square C_m)$ are provided in [26]:

• Roman domination number for the Cartesian product of $C_n$ and $C_3$:

  $${\gamma }_R(C_n\square C_3)=⌈{\displaystyle \frac{3n}{2}}⌉.$$

  (2)
• Roman domination number for the Cartesian product of $C_n$ and $C_4$:

  $${\gamma }_R(C_n\square C_4)=2n.$$

  (3)
• Roman domination number for the Cartesian product of $C_n$ and $C_5$:

  $${\gamma }_R(C_n\square C_5)=\left\{\begin{array}{cc}2n,\hfill & \mathrm{if}n\in \{5k\mid k\in \mathbb{N}\},\hfill \\ 2n+2,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

  (4)
• Roman domination number for the Cartesian product of $C_n$ and $C_6$:

  $${\gamma }_R(C_n\square C_6)=\left\{\begin{array}{cc}⌊{\displaystyle \frac{8n}{3}}⌋,\hfill & \mathrm{if}n\in \{6k\mid k\in \mathbb{N}\},\hfill \\ ⌊{\displaystyle \frac{8n}{3}}⌋+1,\hfill & \mathrm{if}n\in \{6k+5,18k+3,18k+8,18k+13\mid k\in {\mathbb{N}}_0\},\hfill \\ ⌊{\displaystyle \frac{8n}{3}}⌋+2,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

  (5)

In [26], closed expressions that hold for arbitrary n were obtained using the algebraic method [30], and then constructions of the corresponding ${\gamma }_R$-functions are given. Obviously, for a given instance, there are often many ${\gamma }_R$-functions. When n is large, it is known that the ${\gamma }_R$-function can be naturally constructed by repeating certain patterns. Below, we provide some examples, not necessarily the same as in [26], that will also be used later when considering the graph bundles.

2.1. Case $m=3$

By definition, the vertex set of $C_n\square C_m$ is the Cartesian product of vertex sets of factors. So, let us consider functions defined as follows. Assume n is even and recall the labeling of $V\left(C_n\right)=\{0,1,2,\dots ,n-1\}$. For even indices i, choose the second index $j\left(i\right)\in \{0,1,2\}$ such that $j\left(i\right)\ne j(i\pm 2)$ and set $f(i,j)=2$. This is clearly possible. Then, for odd indices i, choose j that is different from both $j(i-1)$ and $j(i+1)$. (All other vertices are assigned 0). Clearly, this defines a ${\gamma }_R$-function f with $w\left(f\right)=⌈{\displaystyle \frac{3n}{2}}⌉={\displaystyle \frac{3n}{2}}$.

$$\left[\begin{array}{cccccc}2& 0& 1& 0& 1& \dots \\ 1& 0& 0& 2& 0& \dots \\ 0& 2& 0& 0& 0& \dots \\ & 0& 1& 2& 3& \dots \end{array}\right].$$

(6)

For odd n values, we can use the construction above (see Pattern (6)) for $n+1$ and ignore the last column. The restriction of f to $V\left(C_n\right)\times V\left(C_3\right)$ is a ${\gamma }_R$-function f having weight $⌈{\displaystyle \frac{3n}{2}}⌉$.

2.2. Case $m=4$

In this case, the pattern is

$$\left[\begin{array}{cccc}3& 0& 0& \dots \\ 2& 0& 2& \dots \\ 1& 0& 0& \dots \\ 0& 2& 0& \dots \\ & 0& 1& \dots \end{array}\right].$$

(7)

Note that once chosen $j\left(i\right)$ for some i, i.e., the position for assigning a 2 in the i-th column, only one vertex on the i-th fiber remains undominated, so we have to assign either a 2 to one of its neighbors or 1 to both neighbors. Clearly, in the first case, the two consecutive columns are dominated by vertices assigned to them. This immediately implies that for even n values, we have ${\gamma }_R$-functions of weight $2n$.

For odd n values, we proceed as follows. Set for $i\in \{0,1,\dots n-2\}$

$$f(i,j)=\left\{\begin{array}{cc}2\hfill & \mathrm{if}i\mathrm{even}\mathrm{and}j=0,\hfill \\ 2\hfill & \mathrm{if}i\mathrm{odd}\mathrm{and}j=2,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(8)

In addition, define $f(n-1,1)=1$ and $f(n-1,3)=1$ (and $f(n-1,0)=0,$ $f(n-1,2)=0$). This gives a ${\gamma }_R$-function f of weight $2n$; see the part of assignment with column $n-1$ emphasized (bold) below:

$$\left[\begin{array}{ccccccc}3& 0& 0& \mathbf{1}& 0& 0& \dots \\ 2& 0& 2& 0& 0& 2& \dots \\ 1& 0& 0& \mathbf{1}& 0& 0& \dots \\ 0& 2& 0& 0& 2& 0& \dots \\ & 0& 1& 2& 3& 4& \dots \end{array}\right].$$

(9)

2.3. Case $m=5$

The pattern

$$\left[\begin{array}{cccccccccccc}4& 0& 0& 2& 0& 0& \dots & 0& 0& 2& 0& 0\\ 3& 0& 0& 0& 0& 2& \dots & 0& 0& 0& 0& 2\\ 2& 0& 2& 0& 0& 0& \dots & 0& 2& 0& 0& 0\\ 1& 0& 0& 0& 2& 0& \dots & 0& 0& 0& 2& 0\\ 0& 2& 0& 0& 0& 0& \dots & 2& 0& 0& 0& 0\\ & 0& 1& 2& \dots & & & & & \dots & n-2& n-1\end{array}\right].$$

(10)

gives a ${\gamma }_R$-function of weight $2n$ for $n=5k$. For $n\ne 5k$, we know that some columns have to be dominated by additional legions, according to the results of [26].

For a later reference, note that the positions of the vertices with $f(i,j)=2$ are given by the rule $j\equiv 2imod5$, $i=0,1,\dots ,n-1$. In the table (matrix), the row 0 is the lowest, and row $n-1$ is the highest row.

Remark 1.

Note that the pattern is essentially unique. Namely, all ${\gamma }_R$-functions are given by $f(i,j(i\left)\right)=2$ exactly when $j\left(i\right)=a\pm 2i$ for $a=0,1,2,3,4$.

3. Graph Bundles

3.1. Bundles of Cycles over Cycles

The automorphism group of a cycle graph $C_m$ consists of cyclic shifts and reflections, which preserve the adjacency structure of the graph. These automorphisms are described as follows:

• A cyclic shift (or rotation) ${\sigma }_{\ell }$, for $0\le \ell <m$, is defined by

  $${\sigma }_{\ell }\left(i\right)\equiv i+\ell modm,$$

  for all $i\in \{0,1,\dots ,m-1\}$. The case $\ell =0$ corresponds to the identity automorphism.
• A reflection without fixed points ${\rho }_0$ is defined by

  $${\rho }_0\left(i\right)=m-i-1,$$

  and exists only when m is even.
• A reflection with exactly one fixed point ${\rho }_1$ is given by

  $${\rho }_1\left(i\right)=m-i-1.$$
  It always applies when m is odd. In this case, the unique fixed point is $i={\displaystyle \frac{m-1}{2}}$.
• A reflection with two fixed points ${\rho }_2$ is defined as

  $${\rho }_2\left(0\right)=0,{\rho }_2\left(i\right)=m-i\mathrm{for}i=1,\dots ,m-1.$$
  This occurs when m is even, and the fixed points are precisely $i=0$ and $i={\displaystyle \frac{m}{2}}$.

Fixing a value of m, we define the set of vertices ${\mathcal{C}}^{\left(i\right)}=\{(i,1),(i,2),\dots ,(i,m)\}$ for each $i\in \left[n\right]$ and refer to it as the i-th column of the graph $C_n{\square }^{\phi }{C}_m$.

3.2. Upper Bounds for Graph Bundles

In this subsection, we discuss the upper bounds for the bundles $C_n{\square }^{\phi }{C}_3$, $C_n{\square }^{\phi }{C}_4$, and $C_n{\square }^{\phi }{C}_5$.

Proposition 1.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_3$ where φ is any isomorphism. Then

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_3\right)\le ⌈{\displaystyle \frac{3n}{2}}⌉.$$

(11)

Proof. 

Recall that the vertex sets of the bundle $C_n{\square }^{\phi }{C}_3$ and the product $C_n\square C_3$ are both $V\left(C_n\right)\times V\left(C_m\right)$. The only possible difference are the edges between fiber $n-1$ and fiber 0. Consider Pattern (6) for the Cartesian product and recall the construction of the ${\gamma }_R$-function f. Observe that the same construction provides an RDF f for $C_n{\square }^{\phi }{C}_3$, with, possibly, different choices of indices $j\left(i\right)$ for $i=n-1$ and $n-2$. □

To provide more insight, we now present several possible RDFs, each corresponding to different examples. For each case, we specify the structure of the function under a particular choice of the mapping $\phi$ in the product $C_n{\square }^{\phi }{C}_m$.

We begin with the first case, where ${\phi }_{n-1,0}={\sigma }_{\ell }$ is a cyclic shift in the last row of $C_n{\square }^{\phi }{C}_m$, and assume that ${\phi }_{i,i+1}=\mathrm{id}$ for all other i.

The construction is based on periodic patterns along the $C_m$ direction, using blocks of consecutive rows. The case where all transition functions are trivial (including the last one) was already proved in [26], since $⌈{\displaystyle \frac{3n}{2}}⌉$ is the exact bound for the Roman domination number of $C_n\square C_m$.

First, consider the example when $n=100$ and $n\equiv 0mod4$. With some corrections on the last columns, Patterns (12) and (13) give the desired RDF-s for $C_n{\square }^{\phi }{C}_m$.

$$\left[\begin{array}{ccccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}0\\ \mathbf{1}\\ 0\end{array}& \begin{array}{c}\mathbf{2}\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ \mathbf{1}\end{array}& \begin{array}{c}\mathbf{2|1}\\ \mathbf{1|0}\\ \mathbf{0|2}\end{array}& \begin{array}{lllll}0& 0& 2& 0& \dots \\ 2& 0& 0& 0& \dots \\ 0& 1& 0& 1& \dots \end{array}\hfill \\ \dots & 92& 93& 94& 95& 96& 97& 98& 99& {\phi }_{n-1,0}& \begin{array}{lllll}0& 1& 2& 3& \dots \end{array}\hfill \end{array}\right]$$

(12)

$$\left[\begin{array}{ccccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\end{array}& \begin{array}{c}0\\ 0\\ \mathbf{1}\end{array}& \begin{array}{c}\mathbf{2|0}\\ \mathbf{1|2}\\ \mathbf{0|1}\end{array}& \begin{array}{lllll}2& 0& 0& 0& \dots \\ 0& 1& 0& 1& \dots \\ 0& 0& 2& 0& \dots \end{array}\hfill \\ \dots & 92& 93& 94& 95& 96& 97& 98& 99& {\phi }_{n-1,0}& \begin{array}{lllll}0& 1& 2& 3& \dots \end{array}\hfill \end{array}\right]$$

(13)

The cases $n\equiv 2mod4$ are illustrated on the examples $n=98$.

$$\left[\begin{array}{ccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}\mathbf{1}\\ 0\\ 0\end{array}& \begin{array}{c}\mathbf{2|1}\\ \mathbf{1|0}\\ \mathbf{0|2}\end{array}& \begin{array}{lllll}0& 0& 2& 0& \dots \\ 2& 0& 0& 0& \dots \\ 0& 1& 0& 1& \dots \end{array}\hfill \\ \dots & 92& 93& 94& 95& 96& 97& {\phi }_{n-1,0}& \begin{array}{lllll}0& 1& 2& 3& \dots \end{array}\hfill \end{array}\right]$$

(14)

$$\left[\begin{array}{ccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 2\end{array}& \begin{array}{c}0\\ \mathbf{1}\\ 0\end{array}& \begin{array}{c}\mathbf{2|0}\\ \mathbf{1|2}\\ \mathbf{0|1}\end{array}& \begin{array}{lllll}2& 0& 0& 0& \dots \\ 0& 1& 0& 1& \dots \\ 0& 0& 2& 0& \dots \end{array}\hfill \\ \dots & 92& 93& 94& 95& 96& 97& {\phi }_{n-1,0}& \begin{array}{lllll}0& 1& 2& 3& \dots \end{array}\hfill \end{array}\right]$$

(15)

The remaining cases are $n\equiv 1,3mod4$. Observe that the RDFs for $n=97$ and $n=99$ are obtained by just removing the last column in solutions for $n=98$ and $n=100$.

Now, assume $\phi$ is a reflection and assume wlog fixes the vertex corresponding to row 1. For $n=100$, in the example of case $n\equiv 0mod4$, we have

$$\left[\begin{array}{ccccccccccc}\dots & 0& 1& 0& \mathbf{1}& \mathbf{2}|\mathbf{0}& 2& 0& 0& 0& \dots \\ \dots & 0& 0& 2& 0& \mathbf{1}|\mathbf{1}& 0& 0& 2& 0& \dots \\ \dots & 2& 0& 0& 0& \mathbf{0}|\mathbf{2}& 0& 1& 0& 1& \dots \\ \dots & 96& 97& 98& 99& {\phi }_{n-1,0}& 0& 1& 2& 3& \dots \end{array}\right]$$

(16)

Similarly, we need to fix only the last column in case $n=98$

$$\left[\begin{array}{ccccccccccccc}\dots & 0& 1& 0& 1& 0& 0& \mathbf{2}|\mathbf{0}& 2& 0& 0& 0& \dots \\ \dots & 0& 0& 2& 0& 0& \mathbf{1}& \mathbf{1}|\mathbf{1}& 0& 0& 2& 0& \dots \\ \dots & 2& 0& 0& 0& 2& 0& \mathbf{0}|\mathbf{2}& 0& 1& 0& 1& \dots \\ \dots & 92& 93& 94& 95& 96& 97& {\phi }_{n-1,0}& 0& 1& 2& 3& \dots \end{array}\right]$$

(17)

As for shifts, the remaining cases $n=97$ and $n=99$ are handled by removing the last column in solutions for $n=98$ and $n=100$.

Proposition 2.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_4$ where φ is any isomorphism. Then

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_4\right)\le 2n.$$

(18)

Proof. 

As in the proof of Proposition 1, start with a ${\gamma }_R$-function f for $C_n\square C_4$. Observe that for $n\ge 2$, the same function based on Pattern (7) is also a ${\gamma }_R$ function for $P_n\square C_4$ and therefore trivially also for $C_n{\square }^{\phi }{C}_4$. □

Remark 2.

Note that an alternative proof can be obtained by applying Proposition 2 from [14], which states that $\gamma \left(C_n{\square }^{\phi }{C}_4\right)=n$, together with the fact that the Roman domination number is bounded above by $2\gamma$.

The case $m=5$ needs a more detailed analysis. We first consider the cases where the nontrivial isomorphism is a shift.

Proposition 3.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a shift ${\sigma }_{\ell }$. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)\le \left\{\begin{array}{cc}2n,\hfill & \mathrm{if}2n+\ell \equiv 0mod5\hfill \\ 2n+2,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

(19)

Proof. 

Let us begin with Pattern (10) on $P_n{\square }^{\phi }{C}_5$. Note that in the general case, one of the vertices in the $(n-1)$-th copy of the fiber needs to be dominated from fiber 0, and, similarly, one of the vertices in the 0th copy of the fiber needs to be dominated from fiber $n-1$. If this is not the case, we can assign 1 to each of the two vertices to obtain an RDF of total weight $w\left(f\right)=2n+2$, as needed. In some cases, we can do better. Assume that $\ell \equiv 2nmod5$. If $n=5k$, then $\ell =0$, and we obtain the same pattern as in the case of products. In all the other cases, we provide RDFs of weight $w\left(f\right)=2n$ below.

• $n=5k+1,\ell =-2\equiv 3mod5$.

  $$\left[\begin{array}{ccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 2\end{array}& \begin{array}{c}0\\ 0\\ 2\\ 0\\ 0\end{array}& \begin{array}{c}2\\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 2\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 2\end{array}& \begin{array}{c}\mathbf{4|2}\\ \mathbf{3|1}\\ \mathbf{2|0}\\ \mathbf{1|4}\\ \mathbf{0|3}\end{array}& \begin{array}{llllll}0& 2& 0& 0& 0& \dots \\ 0& 0& 0& 2& 0& \dots \\ 2& 0& 0& 0& 0& \dots \\ 0& 0& 2& 0& 0& \dots \\ 0& 0& 0& 0& 2& \dots \end{array}\hfill \\ \dots & & & & 5k-2& 5k-1& 5k& {\phi }_{n-1,0}& \begin{array}{llllll}0& 1& 2& 3& 4& \dots \end{array}\hfill \end{array}\right]$$

  (20)
• $n=5k+2,\ell =-4\equiv 1mod5$.

  $$\left[\begin{array}{ccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 2\\ 0\\ 0\end{array}& \begin{array}{c}2\\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 2\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 2\end{array}& \begin{array}{c}0\\ 0\\ 2\\ 0\\ 0\end{array}& \begin{array}{c}\mathbf{4|0}\\ \mathbf{3|4}\\ \mathbf{2|3}\\ \mathbf{1|2}\\ \mathbf{0|1}\end{array}& \begin{array}{llllll}2& 0& 0& 0& 0& \dots \\ 0& 0& 2& 0& 0& \dots \\ 0& 0& 0& 0& 2& \dots \\ 0& 2& 0& 0& 0& \dots \\ 0& 0& 0& 2& 0& \dots \end{array}\hfill \\ \dots & & & & 5k-1& 5k& 5k+1& {\phi }_{n-1,0}& \begin{array}{llllll}0& 1& 2& 3& 4& \dots \end{array}\hfill \end{array}\right]$$

  (21)
• $n=5k+3,\ell =-6\equiv 4mod5$.

  $$\left[\begin{array}{cccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \\ \dots \\ \dots \end{array}& \begin{array}{c}0\\ 0\\ 2\\ 0\\ 0\end{array}& \begin{array}{c}2\\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 2\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 2\end{array}& \begin{array}{c}0\\ 0\\ 2\\ 0\\ 0\end{array}& \begin{array}{c}2\\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}\mathbf{4|3}\\ \mathbf{3|2}\\ \mathbf{2|1}\\ \mathbf{1|0}\\ \mathbf{0|4}\end{array}& \begin{array}{llllll}0& 0& 0& 0& 2& \dots \\ 0& 2& 0& 0& 0& \dots \\ 0& 0& 0& 2& 0& \dots \\ 2& 0& 0& 0& 0& \dots \\ 0& 0& 2& 0& 0& \dots \end{array}\hfill \\ \dots & & & & & 5k& 5k+1& 5k+2& {\phi }_{n-1,0}& \begin{array}{llllll}0& 1& 2& 3& 4& \dots \end{array}\hfill \end{array}\right]$$

  (22)
• $n=5k+4,\ell =-8\equiv 2mod5$.

  $$\left[\begin{array}{cccccccccc}\begin{array}{c}\dots \\ \dots \\ \dots \\ \dots \\ \dots \end{array}& \begin{array}{c}2\\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 2\\ 0\end{array}& \begin{array}{c}0\\ 2\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 0\\ 2\end{array}& \begin{array}{c}0\\ 0\\ 2\\ 0\\ 0\end{array}& \begin{array}{c}2\\ 0\\ 0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 0\\ 2\\ 0\end{array}& \begin{array}{c}\mathbf{4|1}\\ \mathbf{3|0}\\ \mathbf{2|4}\\ \mathbf{1|3}\\ \mathbf{0|2}\end{array}& \begin{array}{llllll}0& 0& 0& 2& 0& \dots \\ 2& 0& 0& 0& 0& \dots \\ 0& 0& 2& 0& 0& \dots \\ 0& 0& 0& 0& 2& \dots \\ 0& 2& 0& 0& 0& \dots \end{array}\hfill \\ \dots & & & & & 5k+1& 5k+2& 5k+3& {\phi }_{n-1,0}& \begin{array}{llllll}0& 1& 2& 3& 4& \dots \end{array}\hfill \end{array}\right]$$

  (23)

□

Remark 3.

Note that this result has already been partially proven by Lemma 3 from [14], which establishes an upper bound for the cases of $\ell \equiv 2nmod5$.

Next, we show that the upper bound for the case of graph bundles $C_n{\square }^{\phi }{C}_5$, where $\phi$ is a reflection, appears to be smaller.

Proposition 4.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a reflection. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)\le 2n+1.$$

(24)

Proof. 

First, observe that for a given n, all graph bundles $C_n{\square }^{\phi }{C}_5$ where $\phi$ is a reflection are isomorphic. We will construct an RDF of weight $2n+1$ for several small n. By inductive argument, the constructions generalize to all n. Assume that the reflection fixes row 2 in all cases.

To obtain an RDF of the desired weight, we use a translated pattern (not the one defined with $j\left(i\right)=2i$ as we did before).

In the tables below, most of the fibers appear twice to illustrate clearly the reflected pattern. The update of the pattern is emphasized as a bold 1, appearing either in column 0 or in column $n-1$.

$n=3$.

$$\left[\begin{array}{cccccccc}\dots & 0& 0& \mathbf{0}|\mathbf{4}& 2& 0& 0& \dots \\ \dots & 2& 0& \mathbf{1}|\mathbf{3}& 0& 0& 2& \dots \\ \dots & 0& 0& \mathbf{2}|\mathbf{2}& 0& 0& 0& \dots \\ \dots & 0& 2& \mathbf{3}|\mathbf{1}& 0& 2& 0& \dots \\ \dots & 0& 0& \mathbf{4}|\mathbf{0}& \mathbf{1}& 0& 0& \dots \\ \dots & 1& 2& {\phi }_{n-1,0}& 0& 1& 2& \dots \end{array}\right]$$

$n=4$.

$$\left[\begin{array}{cccccccccc}\dots & 2& 0& 0& \mathbf{0}|\mathbf{4}& 0& 0& 0& 2& \dots \\ \dots & 0& 0& 0& \mathbf{1}|\mathbf{3}& 2& 0& 0& 0& \dots \\ \dots & 0& 2& 0& \mathbf{2}|\mathbf{2}& 0& 0& 2& 0& \dots \\ \dots & 0& 0& 0& \mathbf{3}|\mathbf{1}& \mathbf{1}& 0& 0& 0& \dots \\ \dots & 0& 0& 2& \mathbf{4}|\mathbf{0}& 0& 2& 0& 0& \dots \\ \dots & 1& 2& 3& {\phi }_{n-1,0}& 0& 1& 2& 3& \dots \end{array}\right]$$

$n=5$.

$$\left[\begin{array}{cccccccccc}\dots & 2& 0& \mathbf{0}|\mathbf{4}& 2& 0& 0& 0& 0& \dots \\ \dots & 0& 0& \mathbf{1}|\mathbf{3}& 0& 0& 2& 0& 0& \dots \\ \dots & 0& 2& \mathbf{2}|\mathbf{2}& 0& 0& 0& 0& 2& \dots \\ \dots & 0& 0& \mathbf{3}|\mathbf{1}& 0& 2& 0& 0& 0& \dots \\ \dots & 0& \mathbf{1}& \mathbf{4}|\mathbf{0}& 0& 0& 0& 2& 0& \dots \\ \dots & 3& 4& {\phi }_{n-1,0}& 0& 1& 2& 3& 4& \dots \end{array}\right]$$

$n=6$.

$$\left[\begin{array}{cccccccccccccc}\dots & 2& 0& 0& 0& \mathbf{1}& \mathbf{0}|\mathbf{4}& 0& 0& 0& 2& 0& 0& \dots \\ \dots & 0& 0& 0& 2& 0& \mathbf{1}|\mathbf{3}& 2& 0& 0& 0& 0& 2& \dots \\ \dots & 0& 2& 0& 0& 0& \mathbf{2}|\mathbf{2}& 0& 0& 2& 0& 0& 0& \dots \\ \dots & 0& 0& 0& 0& 2& \mathbf{3}|\mathbf{1}& 0& 0& 0& 0& 2& 0& \dots \\ \dots & 0& 0& 2& 0& 0& \mathbf{4}|\mathbf{0}& 0& 2& 0& 0& 0& 0& \dots \\ \dots & 1& 2& 3& 4& 5& {\phi }_{n-1,0}& 0& 1& 2& 3& 4& 5& \dots \end{array}\right]$$

$n=7$. (Observe that an RDF for $n=2$ is obtained by just deleting columns 2 to 6.)

$$\left[\begin{array}{cccccccccccc}\dots & 2& 0& \mathbf{0}|\mathbf{4}& 0& 0& 2& 0& 0& 0& 0& \dots \\ \dots & 0& 0& \mathbf{1}|\mathbf{3}& \mathbf{1}& 0& 0& 0& 2& 0& 0& \dots \\ \dots & 0& 2& \mathbf{2}|\mathbf{2}& 0& 2& 0& 0& 0& 0& 2& \dots \\ \dots & 0& 0& \mathbf{3}|\mathbf{1}& 0& 0& 0& 2& 0& 0& 0& \dots \\ \dots & 0& 0& \mathbf{4}|\mathbf{0}& 2& 0& 0& 0& 0& 2& 0& \dots \\ \dots & 5& 6& {\phi }_{n-1,0}& 0& 1& 2& 3& 4& 5& 6& \dots \end{array}\right]$$

Finally, observe that we can obtain an RDF for $n+5$ by inserting 5 columns of the pattern; hence, by induction, we have the constructions for all $n\ge 2$. □

3.3. Graph Bundles $C_n{\square }^{\phi }{C}_3$, $C_n{\square }^{\phi }{C}_4$, and $C_n{\square }^{\phi }{C}_5$

Exact values for Roman domination are proven here for the cases $m=3,4$ and 5. More precisely, for fixed m values, we define $LBB\left(n\right)$, a lower bound for $C_n{\square }^{\phi }{C}_m$ (the minimum over all $\phi$), and $LBP\left(n\right)$, a lower bound for the product $C_n\square C_m$.

Clearly, $LBB\left(n\right)\le LBP\left(n\right)$ as the product is a special case: a trivial bundle.

On the other hand, we have $LBP\left(n\right)\le LBB\left(n\right)$ for some but not all m. In particular, we show here that $LBP\left(n\right)=LBB\left(n\right)$ for $m=3$ and 4 and later provide examples showing that for $m=5$, we have $LBB\left(n\right)<LBP\left(n\right)$ for some n. In words, for some n, the Roman domination number of the product is smaller or equal to the Roman domination number of bundles, while in some cases, there are graph bundles with smaller Roman domination numbers than the Roman domination number of the product.

Theorem 3.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_3$ where φ is any isomorphism. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_3\right)=⌈{\displaystyle \frac{3n}{2}}⌉.$$

(25)

Proof. 

By Proposition 1, the upper bound has already been established. It remains to prove the corresponding lower bound. Recall that for all $n\ge 2$, ${\gamma }_R(C_n\square C_3)=⌈{\displaystyle \frac{3n}{2}}⌉$. Assume that there is a $n_0$ such that ${\gamma }_R\left(C_{n_0}{\square }^{\phi }{C}_3\right)<⌈{\displaystyle \frac{3n_0}{2}}⌉.$ Then, we claim that there is a n such that ${\gamma }_R(C_n\square C_3)<⌈{\displaystyle \frac{3n}{2}}⌉$, which is in contradiction to (2).

First, let $n_0$ be odd, and let $\phi$ be a reflection. As $n_0$ is odd, ${\gamma }_R\left(C_{n_0}{\square }^{\phi }{C}_3\right)<⌈{\displaystyle \frac{3n_0}{2}}⌉$ means

$${\gamma }_R\left(C_{n_0}{\square }^{\phi }{C}_3\right)\le {\displaystyle \frac{3(n_0-1)}{2}}+1<⌈{\displaystyle \frac{3n_0}{2}}⌉={\displaystyle \frac{3(n_0-1)}{2}}+2.$$

Let us construct a graph bundle H over $C_{2n_0}$ and fiber $C_3$ as follows. Set ${\phi }_{n_0-1,n_0}={\phi }_{2n_0-1,0}=\phi$, and let all other isomorphism be identities. It is clear that H is isomorphic to the Cartesian product, $H\simeq C_{2n_0}\square C_3$. Clearly, repeating twice the RDF for $C_{n_0}{\square }^{\phi }{C}_3$ yields an RDF for H with

$$w\left(f\right)=2⌈{\displaystyle \frac{3n}{2}}⌉=2({\displaystyle \frac{3(n-1)}{2}}+1)<{\displaystyle \frac{3n}{2}}.$$

Thus, for $n=2n_0$, we have a contradiction.

If $\phi$ is a shift, then we construct H, a bundle over $C_n=C_{3n_0}$ from three copies to obtain contradiction, as in the previous case.

The case when n is odd can be treated analogously. As the proof proceeds in the same manner, we omit the details and leave it to the reader.

Thus, we can conclude that there is no graph bundle with ${\gamma }_R\left(C_n{\square }^{\phi }{C}_3\right)<⌈{\displaystyle \frac{3n}{2}}⌉$, hence the lower bound. □

Theorem 4.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_4$ where φ is any isomorphism. Then

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_4\right)=2n.$$

(26)

Proof. 

By Proposition 2, the upper bound has been proved, so it remains to establish the lower one to complete the argument. Recall that for all $n\ge 2$, ${\gamma }_R(C_n\square C_4)=2n$. Assume that there is a $n_0$ such that ${\gamma }_R\left(C_{n_0}{\square }^{\phi }{C}_4\right)<2n_0.$ Then, by a construction analogous to one in the proof of Theorem 3 (using either two copies of the bundle for reflection, or four for a shift), we obtain a n such that ${\gamma }_R(C_n\square C_4)<2n$, which is in contradiction to (3). As the proof is analogous to the previous case ($C_3$), we omit the details. □

Proposition 5.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_m$ where φ is any isomorphism. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\ge {\displaystyle \frac{2}{5}}mn.$$

(27)

Proof. 

Note that a vertex v with $f\left(v\right)=2$ covers the demand of itself and its four neighbors, while a vertex v with $f\left(v\right)=1$ only covers the demand of itself. Hence, in the optimal case, all the demands are covered by vertices with $f\left(v\right)=2$, so we need at least $\left|V\right(G\left)\right|$ of them implying the weight of f is (at least) $w\left(f\right)={\displaystyle \frac{2}{5}}mn$. □

For $m=5$, Proposition 5 directly implies the lower bound $2n$.

Corollary 1.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_m$ where φ is any isomorphism. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)\ge 2n.$$

(28)

In special cases, we can prove better lower bounds. Below, we provide an alternative proof that provides a lower bound that improves the one of Corollary 1 in some cases. We start with a technical lemma that will be used to give a better bound lower bound for bundles with reflections and a better lower bound for certain bundles with shifts.

Lemma 1.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is any isomorphism. Then, for any ${\gamma }_R$-function f, the weight of f on each fiber (cycle $C_m$) is at least 2.

Proof. 

Assume f is a ${\gamma }_R$-function of $C_n{\square }^{\phi }{C}_5$. Denote $f_i=f\left(C_5^{\left(i\right)}\right)={\sum }_{j=0}^{4}f(i,j)$. We want to show that $f_i\ge 2$ for all i. Assume $f_i<2$ for some i. If $f_i=0$, then all vertices of the fiber $C_5^i$ need to be dominated from a neighboring fiber, or, equivalently, at least one of its neighbors must have weight 2. Hence, the weights $f_{i-1}+f_{i+1}\ge 10$. Similarly, if $f_i=1$, then $f_{i-1}+f_{i+1}\ge 8$.

It follows from Corollary 1 that the average weight of a fiber is too large for f to be a ${\gamma }_R$-function. Hence, we must have $f_i\ge 2$ for all fibers. We omit the details. □

Note that the immediate consequence of Lemma 1 is the fact that three consecutive fibers of weight 2 must follow Pattern (10). Furthermore, it provides a necessary and sufficient condition for a bundle to attain a lower bound $2n$.

Lemma 2.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$. If ${\gamma }_R\left(G\right)=2n$, then φ must be a shift ${\sigma }_{\ell }$ and $n\equiv \ell mod5$.

Proof. 

Assume ${\gamma }_R\left(G\right)=2n$, and since by Lemma 1 each fiber has weight at least 2, it implies that each fiber has a weight of exactly 2. This, in turn, implies that a ${\gamma }_R$-function f must follow Pattern (10). The domination of fibers $i=1,2,\dots ,n-2$ is obvious because in the pattern, each fiber has two vertices dominated from the neighboring fibers. This may not be true for the fibers 0 and $n-1$. More precisely, the fiber $n-1$ needs the vertex $(n-1,2(n-1)+2mod5)$ to be covered by fiber 0, and similarly, the fiber 0 needs the vertex $(0,3)$ to be covered by fiber $n-1$. Hence, if we define $\tilde{f}$ with $\tilde{f}(0,3)=1$, $\tilde{f}(n-1,2nmod5)=1$, and $\tilde{f}=f$ on all other vertices, we assure that, by construction, $\tilde{f}$ is an RDF of weight at most $2n+2$.

Now, we analyze in which cases we can do better. Recall that by Pattern (10), we have $f(0,0)=2$ and $f(n-1,2(n-1)mod5)=2$. The neighbor of vertex (0, 3) in fiber $n-1$ must have a weight of 2, and the neighbor of $(0,0)$ in fiber $n-1$ is dominated by fiber 0. On the other hand, we also know that according to the pattern, the vertex $(n-1,2(n-1)+2mod5)=(n-1,2nmod5)$ needs to be dominated from fiber 0. Thus, the two conditions more formally read:

$$\phi \left(2\right(n-1)mod5)\equiv 3mod5,$$

(29)

and

$$\phi (2nmod5)\equiv 0mod5.$$

(30)

We now consider shifts and reflections separately.

(defined as ${\sigma }_{\ell }\left(i\right)\equiv i+\ell mod5$). The two conditions now read:

$$2(n-1)+\ell \equiv 3mod5,$$

(31)

and

$$2n+\ell \equiv 0mod5.$$

(32)

Obviously, the two congruences are equivalent. Write $n=5k+i$; hence, the condition (32) reads

$$10k+2i+\ell \equiv 0mod5,$$

(33)

which means that conditions (31) and (32) are fulfilled exactly when $\ell \equiv -2(nmod5)$. Consequently, if $\phi$ is a shift, then ${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)=2n$, if $\ell \equiv 2nmod5$.

Now, consider the case when $n\not\equiv \ell mod5$. Note that we cannot dominate both $(0,3)$ and $(n-1,2nmod5)$ with one additional legion, implying ${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\ge 2n+2$.

The two conditions now read:

$$\rho \left(2\right(n-1)mod5)\equiv 3mod5,$$

(34)

and

$$\rho (2nmod5)\equiv 0mod5.$$

(35)

Clearly, conditions (34) and (35) can not hold simultaneously; hence, if $\phi$ is a reflection, ${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)>2n$. □

From Lemma 2 and from the fact that for any graph, the domination number is upper bounded by the Roman domination number, we infer that the lower bound for the domination number of any bundle with cyclic shift (except for the case when $\ell \not\equiv 2nmod5$) is greater than n. Additionally, Proposition 3 from [14] shows that the domination number in those cases is at most $n+1$. Consequently, we have the following result.

Proposition 6.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a cyclic shift and where $\ell \not\equiv 2nmod5$. Then,

$$\gamma \left(C_n{\square }^{\phi }{C}_5\right)=2n+1.$$

(36)

From the proof of the last lemma, we also read the following two implications, giving more precise lower bounds for specific isomorphisms.

Proposition 7.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a reflection. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)\ge 2n+1.$$

(37)

Proposition 8.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a shift ${\sigma }_{\ell }$. Then, if $2n+\ell \not\equiv 0mod5$,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)\ge 2n+2.$$

(38)

Propositions 4 and 7 together give the exact value for the Roman domination of graph bundles with reflection.

Theorem 5.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a reflection. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)=2n+1.$$

(39)

In the following, we will determine the exact value in the specific cases where the fiber of a bundle is $C_5$.

Theorem 6.

Let G be a Cartesian graph bundle $C_n{\square }^{\phi }{C}_5$ where φ is a cyclic shift. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_5\right)=\left\{\begin{array}{cc}2n,\hfill & \mathrm{if}2n+\ell \equiv 0mod5\hfill \\ 2n+2,\hfill & \mathit{otherwise}.\hfill \end{array}\right..$$

(40)

Proof. 

By Proposition 3, the upper bound is proved. From Lemma 2, Corollary 1, and Proposition 8, the lower bound is attained. Therefore, the theorem is proved. □

3.4. More Upper Bounds for Roman Domination of Bundles

In this section, we will generalize our bundle constructions to include fibers that are integer multiples of 3, 4, and 5, leading to upper bounds for the associated bundles. Let us start by obtaining the upper bound for ${\gamma }_R\left(C_n{\square }^{\phi }{C}_{5k}\right)$. Consequently, the resulting bounds will also apply to the Roman domination number of the corresponding Cartesian products.

Theorem 7.

Let $m\ge 5$ and $n\ge 6$. Let ${\phi }_{n-1,0}={\sigma }_{\ell }$ be any automorphism in the last row of $C_n{\square }^{\phi }{C}_m$ and assume that ${\phi }_{i,i+1}=\mathrm{id}$ for all other i. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\le \left\{\begin{array}{cc}⌈{\displaystyle \frac{3n}{2}}⌉k,\hfill & m=3k,\hfill \\ 2nk,\hfill & m=4k,\hfill \\ 2(n+1)k,\hfill & m=5k.\hfill \end{array}\right.$$

Proof. 

The construction is based on the afore-derived periodic patterns along the $C_m$ direction, using blocks of consecutive rows. In the case where all transition functions are trivial (including the last one), this gives an upper bound for the Roman domination number of $C_n\square C_m$. The construction in this case consists of joined patterns from [26]. We demonstrate this with an example for $m=8$ and $n\equiv 1mod4$.

$$\left[\begin{array}{cccccccc}\dots & 0& 0& 0& |& 0& 0& \dots \\ \dots & 0& 2& 0& |& 0& 2& \dots \\ \dots & 0& 0& 0& |& 0& 0& \dots \\ \dots & 2& 0& 2& |& 2& 0& \dots \\ \dots & 0& 0& 0& |& 0& 0& \dots \\ \dots & 0& 2& 0& |& 0& 2& \dots \\ \dots & 0& 0& 0& |& 0& 0& \dots \\ \dots & 2& 0& 2& |& 2& 0& \dots \\ \dots & & n-2& n-1& |& 0& 1& \dots \end{array}\right]$$

(41)

In the next, suppose that all transition functions are trivial except one:

$${\phi }_{i,i+1}=\mathrm{id}\mathrm{for}\mathrm{all}i\ne n-1,\mathrm{and}{\phi }_{n-1,0}={\sigma }_{\ell }.$$

If we successively apply patterns for $m=3,4,5$, we obtain patterns for each $m=3k,4k,5k$. More precisely, in the case $m=3$, let us consider functions defined as follows. Assume n is even and recall the labeling of $V\left(C_n\right)=\{0,1,2,\dots ,n-1\}$. For even indices i, choose the second index $j\left(i\right)\in \{0,1,2\}$ such that $j\left(i\right)\ne j(i\pm 2)$ and set $f(i,j(i\left)\right)=2$, $f(i,j(i)+3)=2$, … $f(i,j(i)+3(k-1\left)\right)=2$. This is clearly possible. Then, for odd indices i, choose j that is different from both $j(i-1)$ and $j(i+1)$. Set $f(i,j(i\left)\right)=f(i,j(i)+3)=f(i,j(i)+3(k-1\left)\right)=1$. (All other vertices are assigned 0.) Clearly, this defines a ${\gamma }_R$-function f with $w\left(f\right)=k⌈{\displaystyle \frac{3n}{2}}⌉={\displaystyle \frac{3kn}{2}}$.

$$\left[\begin{array}{c}\begin{array}{cccccc}\dots & 0& 1& 0& 1& \dots \\ \dots & 0& 0& 2& 0& \dots \\ \dots & 2& 0& 0& 0& \dots \end{array}\\ \dots \\ \begin{array}{cccccc}\dots & 0& 1& 0& 1& \dots \\ \dots & 0& 0& 2& 0& \dots \\ \dots & 2& 0& 0& 0& \dots \end{array}\end{array}\right].$$

(42)

For odd n, we use the construction above for $n+1$ and ignore the last column. The restriction of f to $V\left(C_n\right)\times V\left(C_{3k}\right)$ is a ${\gamma }_R$-function f having weight $k⌈{\displaystyle \frac{3n}{2}}⌉$.

In the same manner, we prove the theorem for $m=4k$. Due to the better readability, we provide an example of an RDF for reflections with two fixed points, when $m=8$ and $n=4i+1$. It follows that the weight of the corresponding function is precisely $4n$.

$$\left[\begin{array}{cccccccc}\dots & 0& 0& 0& \mathbf{7}|\mathbf{5}& 0& 0& \dots \\ \dots & 0& 2& 0& \mathbf{6}|\mathbf{6}& 0& 2& \dots \\ \dots & 0& 0& 0& \mathbf{5}|\mathbf{7}& 0& 0& \dots \\ \dots & 2& 0& 2& \mathbf{4}|\mathbf{0}& 2& 0& \dots \\ \dots & 0& 0& 0& \mathbf{3}|\mathbf{1}& 0& 0& \dots \\ \dots & 0& 2& 0& \mathbf{2}|\mathbf{2}& 0& 2& \dots \\ \dots & 0& 0& 0& \mathbf{1}|\mathbf{3}& 0& 0& \dots \\ \dots & 2& 0& 2& \mathbf{0}|\mathbf{4}& 2& 0& \dots \\ \dots & & n-2& n-1& {\phi }_{n-1,0}& 0& 1& \dots \end{array}\right]$$

(43)

Similarly, when $m=5k$, the constructions consist of joined patterns from RDFs obtained by Propositions 3 and 4. Below is an example of the pattern for the case of a cyclic shift where $m=10$ and $n=5i+2$, and $\ell =2$. Note that the weight of the corresponding function equals $4n+4$.

(44)

Lastly, we provide an example of the pattern for the case where $m=10$ and $n=5i+2$, and $\ell =1$. Observe that the weight of the corresponding function is $4n$.

(45)

□

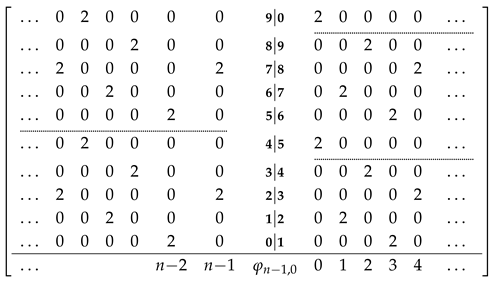
The general lower bound given in Proposition 5 implies the following lower bounds for special cases $m=3k$, $m=4k$, and $m=5k$.

Lemma 3.

Let $m\ge 3$ and $n\ge 6$. Let ${\phi }_{n-1,0}={\sigma }_{\ell }$ be any automorphism in the last row of $C_n{\square }^{\phi }{C}_m$ and assume that ${\phi }_{i,i+1}=\mathrm{id}$ for all other i. Then,

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\ge \left\{\begin{array}{cc}{\displaystyle \frac{6}{5}}nk,\hfill & m=3k,\hfill \\ {\displaystyle \frac{8}{5}}nk,\hfill & m=4k,\hfill \\ 2nk,\hfill & m=5k.\hfill \end{array}\right.$$

Note that the lower bounds for $m=3$ and $m=4$ given in Theorems 3 and 4 are stronger; however, it does not seem possible to extend them, for example lower bound for $m=4$ to $m=8$ as $2\times 2n=4n$. To the contrary, we believe that the bounds from Lemma 3 are asymptotically best possible in the sense that the gap to exact values vanishes with growing k. Summarizing the upper bounds of Theorem 7 and Lemma 3, we can write the next theorem.

Theorem 8.

Let $m\ge 5$ and $n\ge 6$. Let ${\phi }_{n-1,0}={\sigma }_{\ell }$ be any automorphism in the last row of $C_n{\square }^{\phi }{C}_m$ and assume that ${\phi }_{i,i+1}=\mathrm{id}$ for all other i. Then,

• ${\displaystyle \frac{6}{5}}nk\le {\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\le ⌈{\displaystyle \frac{3n}{2}}⌉k$ for m = 3k;
• ${\displaystyle \frac{8}{5}}nk\le {\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\le 2nk$ for m = 4k;
• $2nk\le {\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)\le 2(n+1)k$ for m = 5k;

At least for the case when $m=5k$, we strongly believe that the lower bound is tight, and conjecture that for $2n+\ell \equiv 0mod5$, we have

$${\gamma }_R\left(C_n{\square }^{\phi }{C}_m\right)={\displaystyle \frac{2}{5}}mn=2nk.$$

(46)

4. Conclusions

In this paper, we studied the domination and Roman domination numbers of Cartesian bundles of cycles. By explicitly constructing optimal dominating and Roman dominating patterns, we obtained exact values for the Roman domination numbers in several cases. Additionally, we resolved the open case from [14] concerning the domination number of cyclic shifts, where one of the cycles is of length 5. By combining some of the introduced patterns, we could potentially provide improved bounds for bundles with shifts of order $4k$ and $5k$.

Moreover, we observed that bundles such as $C_n\square C_m$ for $m=4$ and $m=5$, specifically when $\ell \equiv 2nmod5$, are Roman graphs.

An interesting direction for further research would be extending these methodologies to study double Roman domination numbers in graph bundles. This extension could reveal additional structural insights and deeper combinatorial properties.

Another open problem for future work is to explore the domination and Roman domination properties of bundles containing cycles of lengths $6k$, $7k$, and beyond, which remain largely uninvestigated.