Abstract
We propose an efficient Nyström-based unitary subspace method for low-complexity two-dimensional (2D) direction-of-arrival (DOA) estimation in uniform rectangular array (URA) signal processing systems. The conventional high-resolution DOA estimation methods often suffer from excessive computational complexity, particularly when dealing with large-scale antenna arrays. The proposed method addresses this challenge by combining the Nyström approximation with a unitary transformation to reduce the computational burden while maintaining estimation accuracy. The signal subspace is approximated using a partitioned covariance matrix, and a real-valued transformation is applied to further simplify the eigenvalue decomposition (EVD) process. Furthermore, the linear prediction coefficients are estimated via a weighted least squares (WLS) approach, enabling robust extraction of the angular parameters. The 2D DOA estimates are then derived from these coefficients through a closed-form solution, eliminating the need for exhaustive spectral searches. Numerical simulations demonstrate that the proposed method achieves comparable estimation performance to state-of-the-art techniques while significantly reducing computational complexity. For a fixed array size of , the proposed method demonstrates significant computational efficiency, requiring less than of the running time compared to conventional ESPRIT, and only of the time required by ML methods, while maintaining similar performance. This makes it particularly suitable for real-time applications where computational efficiency is critical. The novelty lies in the integration of Nyström approximation and unitary subspace techniques, which jointly enable efficient and accurate 2D DOA estimation without sacrificing robustness against noise. The method is applicable to a wide range of array processing scenarios, including radar, sonar, and wireless communications.
MSC:
94A12; 93E10; 65T50
1. Introduction
Direction of arrival (DOA) estimation techniques are commonly used to determine the angle or direction of a signal. This technique is applicable in various fields such as radar, sonar, and mobile communications [1,2,3,4]. The localization of signals in space using signal processing techniques involves employing a two-dimensional (2D) DOA estimation of a uniform rectangular array (URA). A URA is an antenna array that comprises multiple rows and columns of sensor elements. URA-based DOA estimation methods are useful when the signal arrives from a 2D plane, which may include signals from multiple angles or directions that require localization and identification. The use of a URA enables the separation and individual processing of signals from different directions, resulting in accurate localization information.
Over the past several decades, various approaches have been developed to address the DOA estimation problem. Among these techniques, subspace-based methods, including multiple signal classification (MUSIC) and estimation of signal parameters via rotational invariance technique (ESPRIT), along with their enhanced versions such as root-MUSIC and Unitary-ESPRIT, are the most prominent super-resolution methods [5,6]. The 2D MUSIC algorithm estimates 2D DOA by utilizing the noise subspace of a received dataset’s covariance matrix from a URA [7], but its computation is intensive due to the required 2D search for the spectrum. To address this issue, researchers have proposed efficient methods like search-free 2D ESPRIT [8] and the matrix pencil approach [9,10], which require extra pairing processes in some cases. Most of these methods focus on multi-snapshot cases for 2D DOA estimation. However, real-world scenarios may limit the available snapshots due to physical constraints like fast time-variant channel scenarios in mobile communication or sonar signal processing. Researchers have explored using compressed sensing to estimate parameters with small sample sizes [11,12]. Single-snapshot DOA estimation is crucial in applications like automotive radar systems, where only one snapshot is available to estimate multiple spatial sources. Therefore, several DOA estimation algorithms have been proposed for single snapshot cases [13,14,15]. It is important that any direction-finding algorithm used in real-world scenarios be computationally efficient and rely on only a limited number of array snapshots. Many computationally efficient methods have been proposed to solve DOA estimation, such as real-valued eigenvalue decomposition (EVD) or singular value decomposition (SVD)-based methods [16,17]. The problem of DOA estimation is addressed in [16] with real-valued computations by considering the real part of the array output covariance matrix and the imaginary part of the array output covariance matrix separately, which coincides with the intersection of the original noise subspace and its conjugate subspace. A real-valued root-MUSIC algorithm that reduces the computation is proposed in [17]; it exploits the EVD/SVD of a real-valued covariance matrix to extract a real-valued noise subspace, which reduces the complexity by a factor of about four compared to root-MUSIC. The problem of 2D DOA estimation for URA signals is linked to the compressive sensing trilinear model in [18], in which the proposed algorithm not only requires no spectral peak searching but also has better angle estimation performance than the estimation of the ESPRIT algorithm with low computational complexity. An efficient 2D DOA estimation algorithm based on OMP for URA is proposed in [19]. The main idea of it is to reduce the number of atoms in the complete dictionary of the OMP algorithm to reduce the amount of computation required. A low complexity 2D DOA estimation and self-calibration for URA with gain-phase error is developed in [20], the URA is modeled as the Kronecker product of two uniform linear arrays (ULAs) to decouple the 2D DOA estimation. Then, several well-calibrated auxiliary array elements are added in the two ULAs, based on which the rotation invariant factor of the URA destroyed by the gain-phase error is reconstructed by solving constrained optimization problems. The problem of 2D DOA estimation for coherent sources using an EMVS array with URA geometry is addressed in [21], where three novel PARAFAC approaches are proposed to eliminate the rank deficiency of the source matrix via data rearrangement. Unlike existing smoothing-based algorithms, this approach does not reduce the number of available measurements. Recently, deep neural network (DNN) studies on DOA estimations have attracted more and more attention, providing an alternative method for dealing with the DOA problem and successfully showing its potential application. However, the computational complexity may be higher compared with classical methods [22].
This paper introduces a novel approach for the fast 2D DOA estimation of URA signals in the single snapshot case. The approach is based on the Nyström approximation [23,24]. To simplify the denoising process, the Nyström method is initially applied to the received data, providing an approximation of the signal’s subspace. Subsequently, to further reduce the complexity, the 2D DOA is estimated using the obtained subspaces and a unitary subspace-based method, where the covariance matrix is computed from a real-valued computation. The main contributions of this manuscript are the following: (1) Utilize the Nyström method to obtain the signal subspace for estimating the 2D DOA, avoiding computing the EVD or SVD of the signal. (2) Utilize the unitary subspace-based algorithm, which makes use of the principal singular vectors and an iterative process to estimate the 2D DOA of the URA signals, avoiding the complex-valued decomposition of computation, which reduces the computational complexity.
The paper is structured as follows: Section 2 introduces the array signal model. Section 3 describes the application of the Nyström approximation method and the unitary subspace-based method for obtaining 2D DOA estimation. Section 4 presents the results of computer simulations conducted to evaluate the performance of the proposed method and compare it with existing algorithms. Finally, Section 5 concludes the paper.
Notation
In this paper, the boldface lowercase letters denote vectors and boldface uppercase letters denote matrices. Superscripts such as , , , , and represent transpose, complex conjugate, Hermitian transpose, pseudo inverse, and matrix inverse, respectively. denotes the expectation operator and is the diagonal matrix operator. The denotes an estimate of a. is the identity matrix, and denotes the set of complex numbers.
2. Signal Model
A URA comprising omnidirectional antennas arranged in an configuration with interelement spacing d is under consideration [18,19]. The URA is being subjected to P far-field narrowband signal sources arriving from the directions , with , where p ranges from 1 to P. The first sensor is set as the reference sensor. The received signal of the sensor located at is defined as a single snapshot.
The received signal comprises the wavefront of the pth signal, with a wavelength of , and white Gaussian noise assumed to have a noise power of . The objective of the 2D DOA estimation problem is to estimate the DOA, represented by , from the received signals. As this paper considers the single-tone case, is assumed known in the signal model; then, the signal becomes
We assume and for simplicity.
3. Algorithm Development
3.1. The Nyström Approximation
To analyze the signal, we initially transform the signal represented in (1) to a matrix format.
the matrices are derived from the components of both the signal and the noise, and , , and
In traditional approaches, the covariance matrix is usually calculated by utilizing numerous snapshots subsequent to receiving the signal . Nevertheless, in the scenario of single snapshot signals, there are insufficient snapshots to eliminate noise from the signal by computing the covariance matrix. As an alternative, we can decompose the signal matrix as
where s is the wavefront, and
where denotes the transpose operator, and are the same as that in (2). We see that the elements in and have linear factor (LP) relations. Here, LP is a scalar multiplier that scales a variable or signal linearly. In traditional ideas, we can perform the EVD or SVD on to obtain the subspace with high complexity; therefore, we apply the Nyström approximation to obtain the signal subspace.
In the Nyström method, we first divide the signal matrix into two parts [24]
where and are parts of
where K is a parameter defined by users, and . We have the covariance matrices of and
where is the covariance matrix of , is the covariance matrix of and .
When noise is present, the covariance matrices cannot be computed with (10) and (11); hence, we use an approximation approach to estimate the covariance matrices [18,19].
Before proceeding with the covariance matrices, it is typically required for the matrix to have a full rank. To accomplish this, we set the value of K to be greater than but less than the minimum of M and N, i.e., . Our simulations have demonstrated that the value of K does not necessarily need to increase with an increase in the number of array sensors, M. Instead, a specific value of K is adequate for precise DOA estimation while simultaneously reducing computational complexity.
We can perform EVD or SVD on and to obtain the subspace [25]
the eigenvector matrix and the corresponding eigenvalue matrix are obtained, where contains the eigenvalues in descending order. Additionally, we define . By utilizing (14), we can establish the relationship among , , and .
We use and to obtain another matrix
with the use of (15), (16) is written as
To orthogonalize , we use and to construct
and
we perform EVD on , then
The eigenvalue matrix is obtained with , and is derived from the corresponding eigenvector matrix , where represents the ith eigenvector. Since the signal number is known, we use the first column vectors of matrix to construct the signal subspace, i.e., [24]. Furthermore, as satisfies the Equation (21), where
Then, we obtain the subspace of the signal. We summarize the process to obtain the signal subspace in Table 1.

Table 1.
Nyström approximation.
3.2. The Unitary Estimation of DOA
Upon acquiring the signal subspace through eigenvalue decomposition of the covariance matrix, various subspace-based algorithms can be implemented for 2D DOA estimation. While conventional methods like MUSIC theoretically achieve superior resolution by exploiting orthogonality between signal and noise subspaces, their computational complexity grows exponentially with the search grid density—which is particularly challenging for 2D angle estimation requiring joint azimuth–elevation searches. This issue becomes more pronounced in multi-tone scenarios where additional parameter pairing procedures are mandatory. However, in our single-tone signal case, this parameter matching complexity is inherently avoided, allowing direct subspace utilization. To address the computational burden while preserving the accuracy of the estimation, we adopt a subspace method based on unit transformation [26]. This approach transforms the complex-valued array manifold into a real-valued domain through unitary matrix operations. First, we introduce the unitary transform process.
It is a well-known fact that the covariance matrix is a matrix with complex values, as well as . To simplify computational complexity, we can transform it into a real-valued covariance using a unitary transform [27]. For simplicity, we use other than or in the following process. First, we define
where * is the conjugate operator, means the real part of the matrix, is an exchange matrix with ones in its antidiagonal and 0 otherwise. is defined as [27]:
where is an zero vector. The SVD of the real-valued covariance matrix is,
where and are the signal and noise subspaces of the real value, respectively. To obtain the estimate of DOA, we can use subspace methods such as root-MUSIC [28] or Unitary ESPRIT [27]. Since in the Nyström approximation, Section 3.1 is now obtained from real-valued and , and we use to denote the real-valued . Then, the EVD of the real-valued is
Since we are considering a single-tone signal, the first column of the signal subspace , denoted as , contains the information of the signal. In traditional methods, the signal subspace can be directly used to estimate the DOA, such as the MUSIC method, which needs a great time consumption due to the grid search of the spectrum peak. To reduce the computation complexity, we use a real-valued method to estimate the DOA. In order to estimate the DOA from the real-valued eigenvector matrix, we first define two selection matrices.
By utilizing the property of shift invariance and assuming that the noise disturbance is significantly smaller compared to the signal power, we can deduce
Then
We use the real and image part of , denoted as and . Then, we have
We follow the LP property to have
and , and . To estimate the LP factor, we use the WLS approach, which is
and is the weighting matrix defined as [29]
and . Then, the LP factor is estimated as
And we substitute into (33), where is the error of the real one and the estimate of
At the beginning of the iteration, we use
For the LP factor , we define it as
Then,
Since , we get
After we get the estimate of , we can also perform the same process to estimate by performing the real-valued SVD on . Then,
where , , and are calculated from the same process as . Since we are considering single-tone signals, no parameter pairing method is needed here.
Then, the estimations of the 2D DOA are computed from and as
and
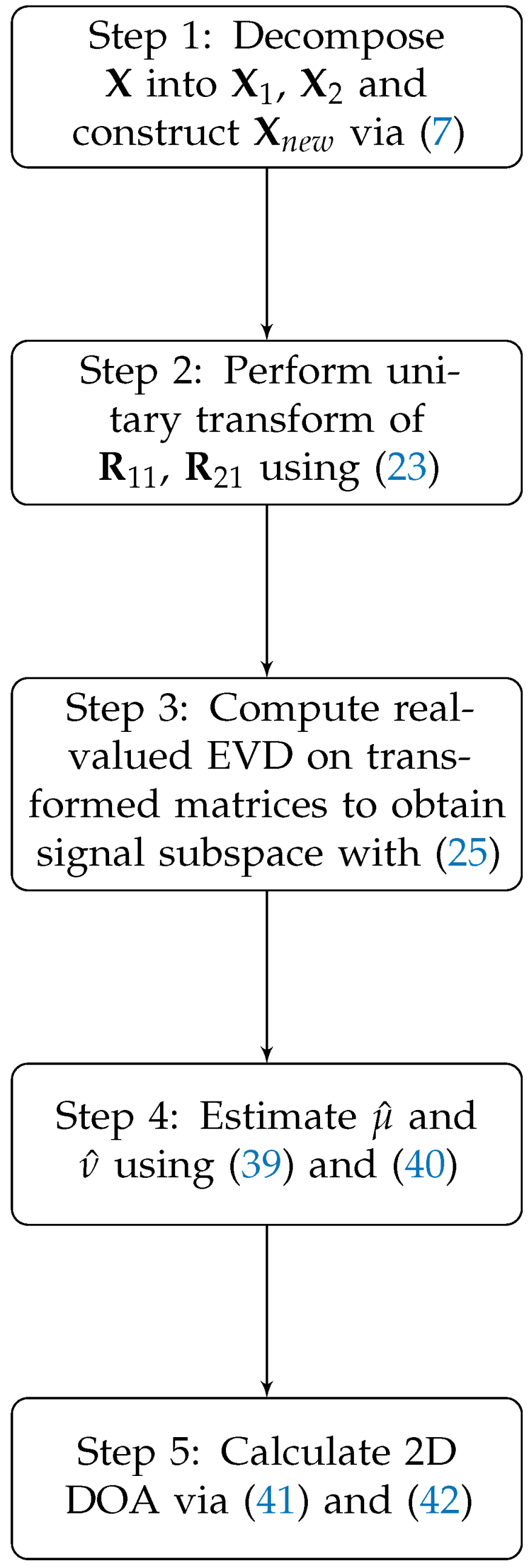
Since all of the parameters are estimated from a real-valued process, the complexity is significantly reduced compared with a complex-valued process. The estimation process is summarized in Figure 1.
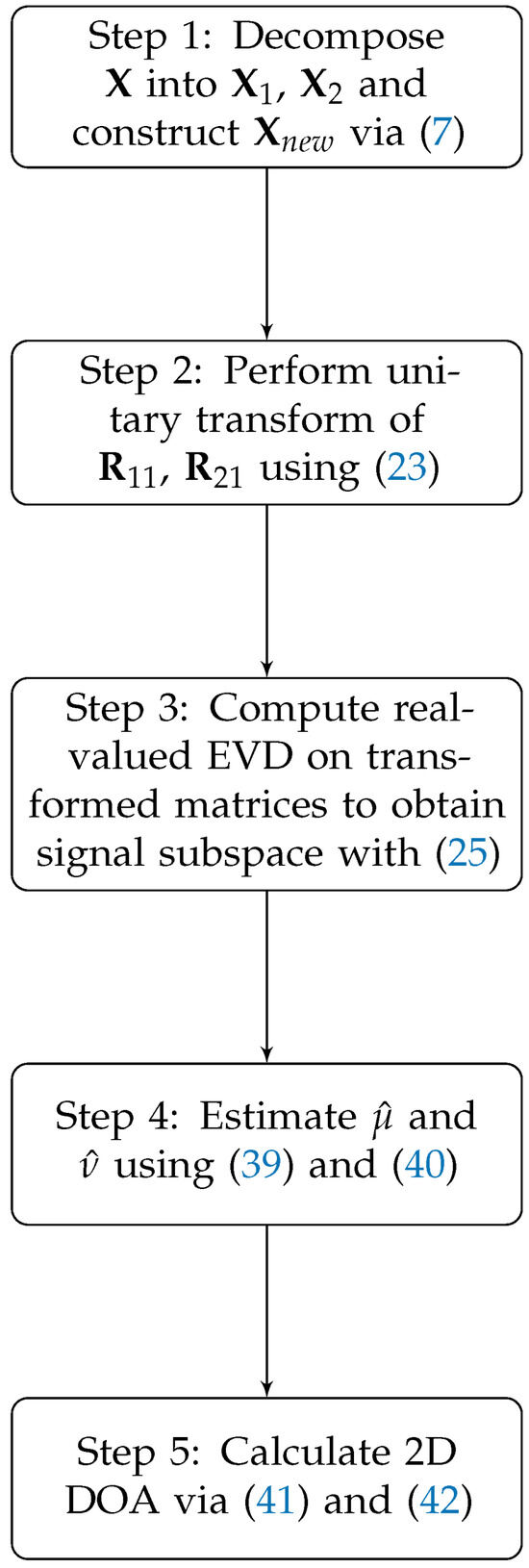
Figure 1.
Flowchart of the proposed algorithm.
3.3. Computational Complexity Analysis
The computational complexity in our analysis is primarily evaluated in terms of matrix multiplication operations, which serve as the standard metric in computational mathematics. Our detailed analysis reveals that the principal computational burden of the proposed method stems from two key operations: (1) the Nyström approximation for obtaining the equivalent signal subspace, and (2) the unitary estimation process of DOA. To compute and , we require and flops, respectively. Meanwhile, we use the Nyström approximation that just needs flops to construct the signal subspace. Then, the total flops of the Nyström approximation is . The process of unitary estimation of DOA needs if we do not use the Nyström approximation [26]; it becomes when we use the subspaces obtained from the Nyström approximation. As established in [30], real-valued matrix operations require only approximately one-fourth (1/4) of the computational resources compared to their complex-valued counterparts. While the ESPRIT method needs [31] and ML needs multiplications [32], respectively. The simulation results are shown in the last simulation of Section 4.
4. Simulation Results
In this section, we validate the effectiveness of the proposed approach through computer simulations. We compare its performance with the ESPRIT method [31] and the ML method [32]. To assess performance, we utilized the RMSE, which is calculated by comparing the estimated DOA with the actual DOA. The SNR is defined as SNR = (dB), where represents the signal power and represents the noise power.
We set the 2D DOA of the URA as and . The RMSE is computed as
We perform computer simulations using Monte Carlo trials, as we have found that increasing the number of trials does not contribute significantly to improving the results.
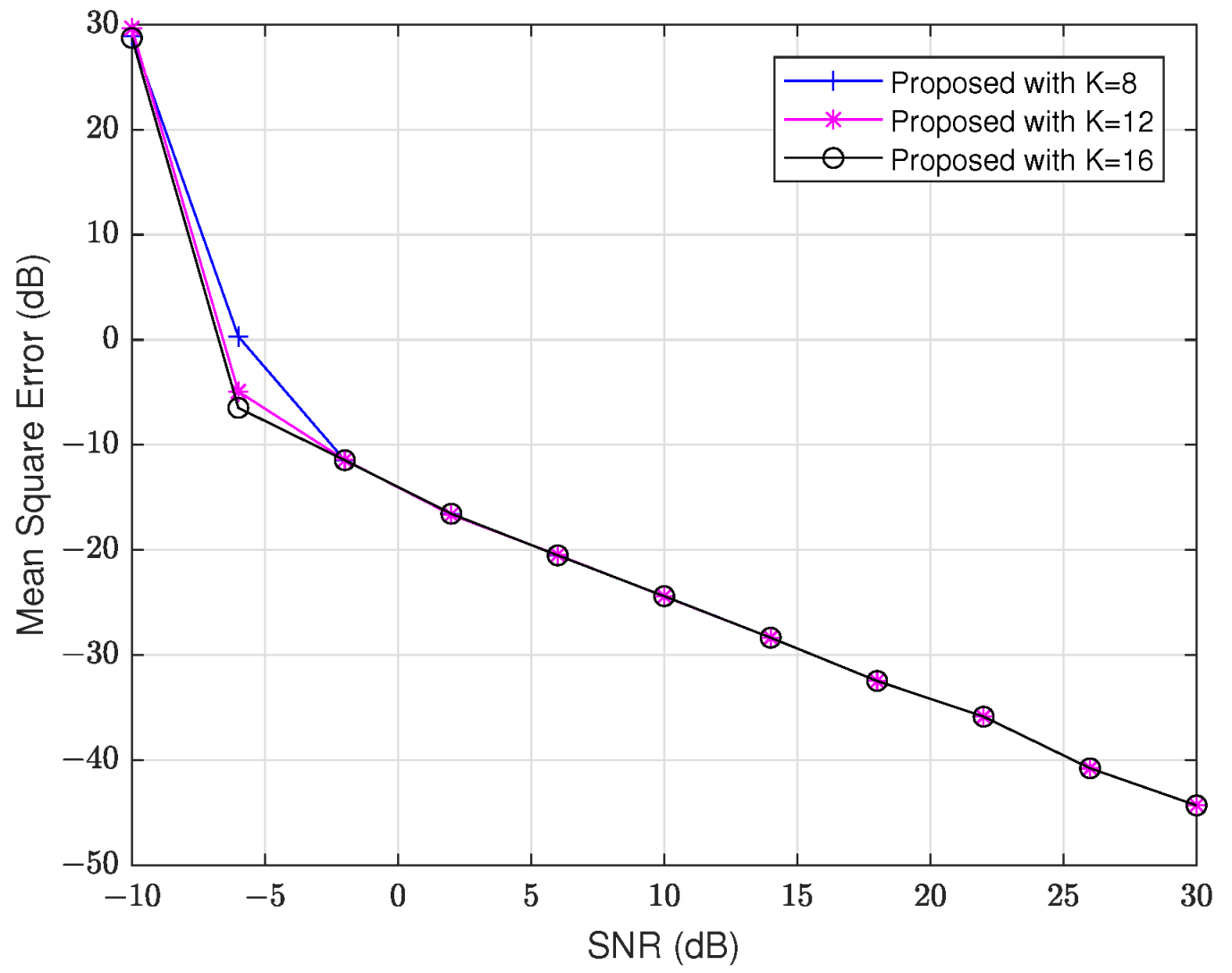
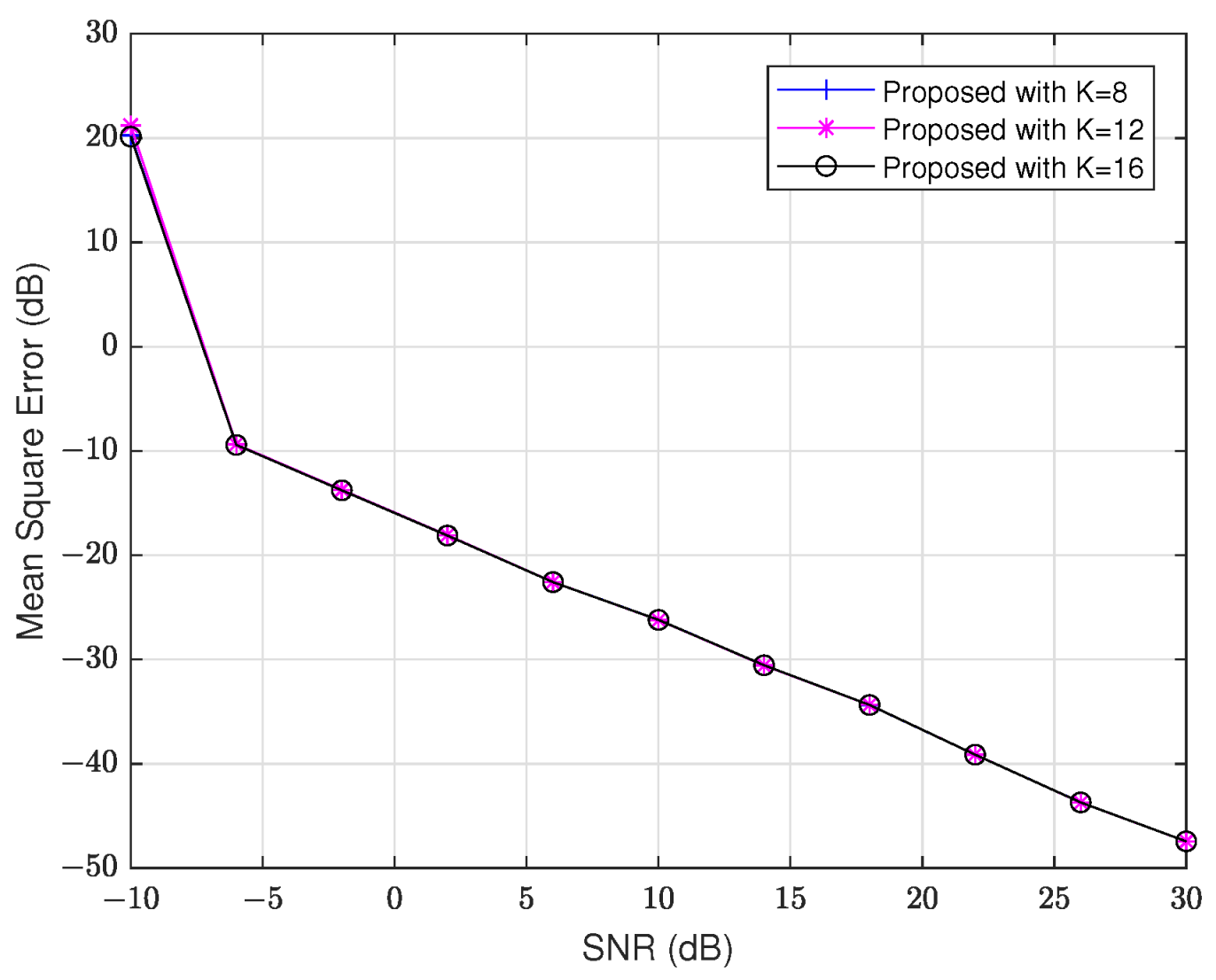
We start by comparing the MSE versus SNR of the Nyström approximation method for different values of K. SNR ranges from −10 dB to 30 dB, and the array size is . In this method, we need to define the parameter K, so we use , , and in the simulation to evaluate the performance of our approach under different K values. The results are illustrated in Figure 2 and Figure 3. From these figures, we observe that the MSE of the proposed algorithm remains consistent for different K values when SNR is larger than dB. This suggests that the performance does not significantly change with increasing K in higher SNR scenarios. Therefore, in the following simulations, we choose to use . Unless otherwise stated, the remaining parameters remain unchanged in the remaining experiments.
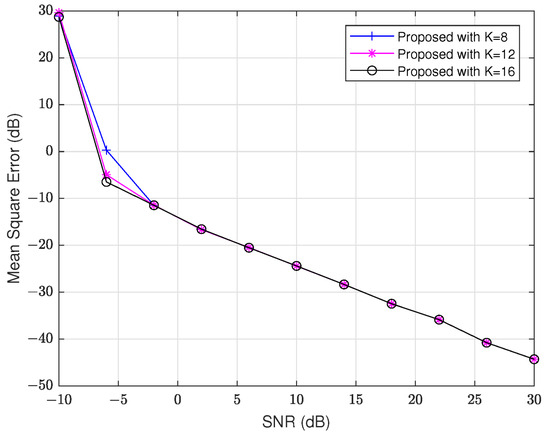
Figure 2.
MSE of versus SNR with different K.
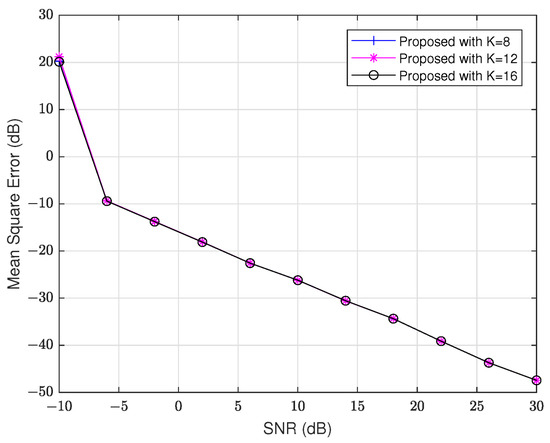
Figure 3.
MSE of versus SNR with different K.
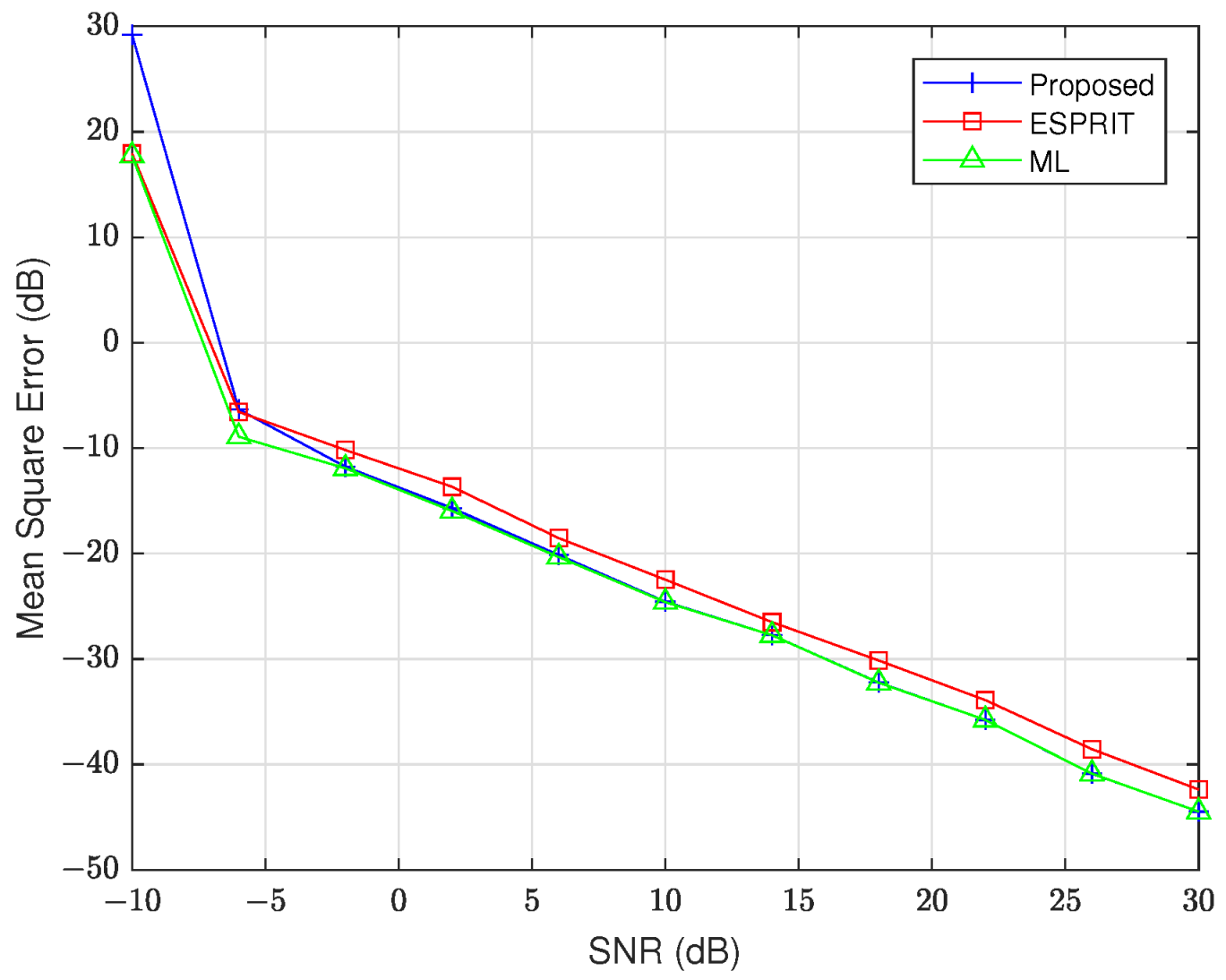
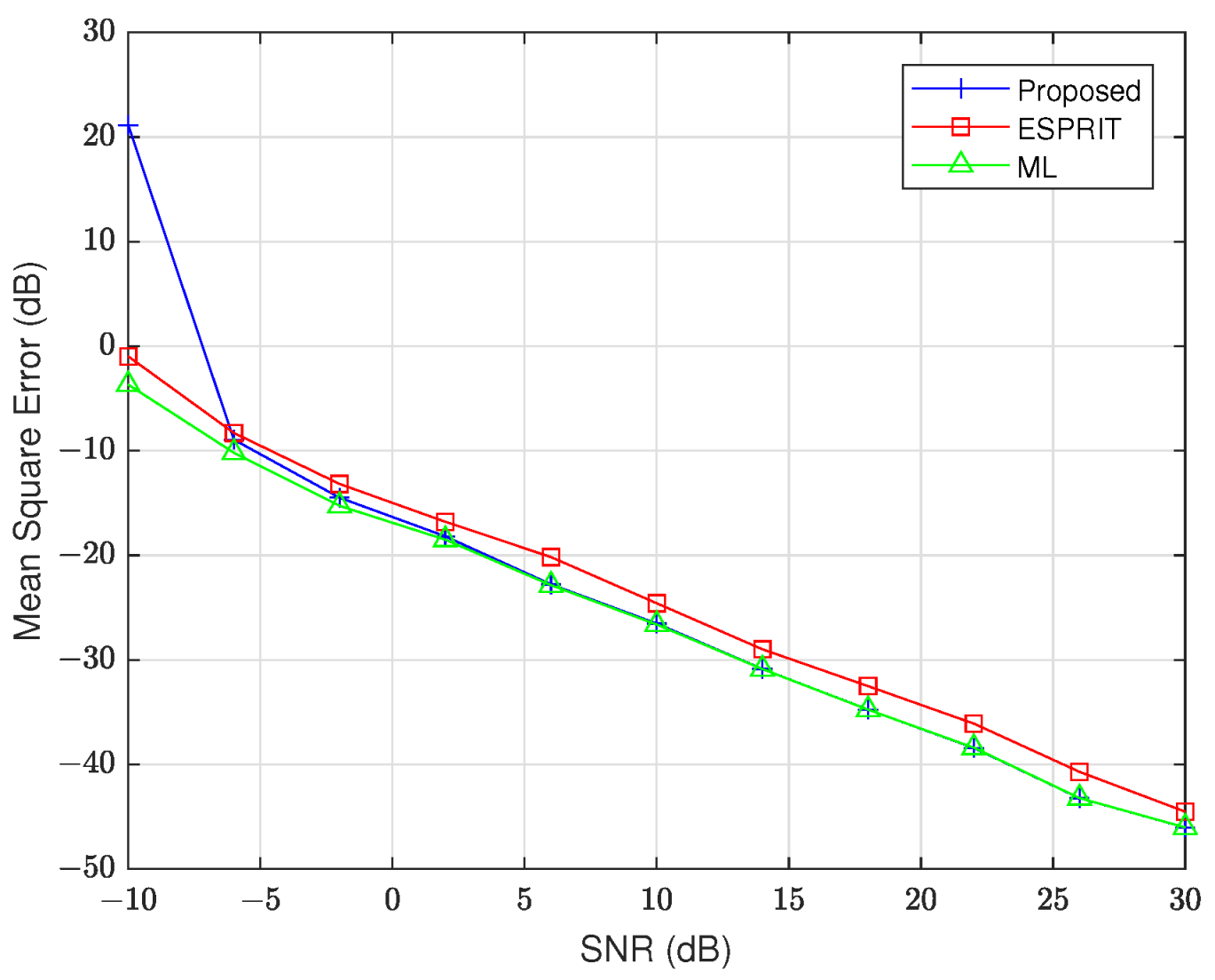
To further evaluate the performance of our proposed method, we compare it with the ESPRIT and ML techniques, using in the Nyström approximation. The remaining data settings remain the same as in the first simulation. The results of this comparison are presented in Figure 4 and Figure 5. From these figures, we see that all three evaluated methods—our proposed algorithm, ML, and ESPRIT—demonstrate statistically indistinguishable estimation accuracy when SNR exceeds the −5 dB threshold. These findings indicate that the proposed algorithm has equivalent accuracy compared to the benchmark ML, where precision matters most.
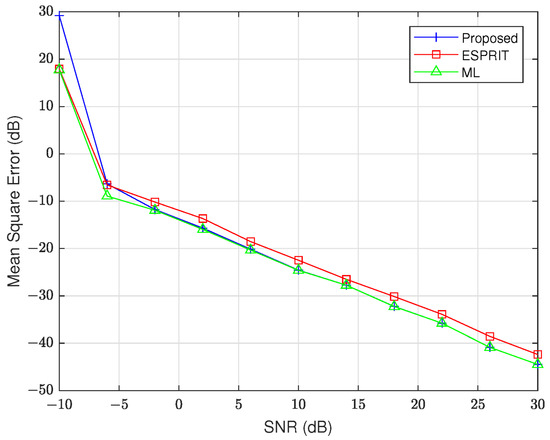
Figure 4.
MSE of versus SNR.
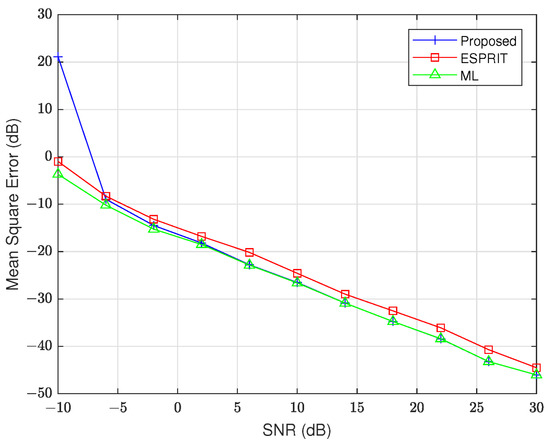
Figure 5.
MSE of versus SNR.
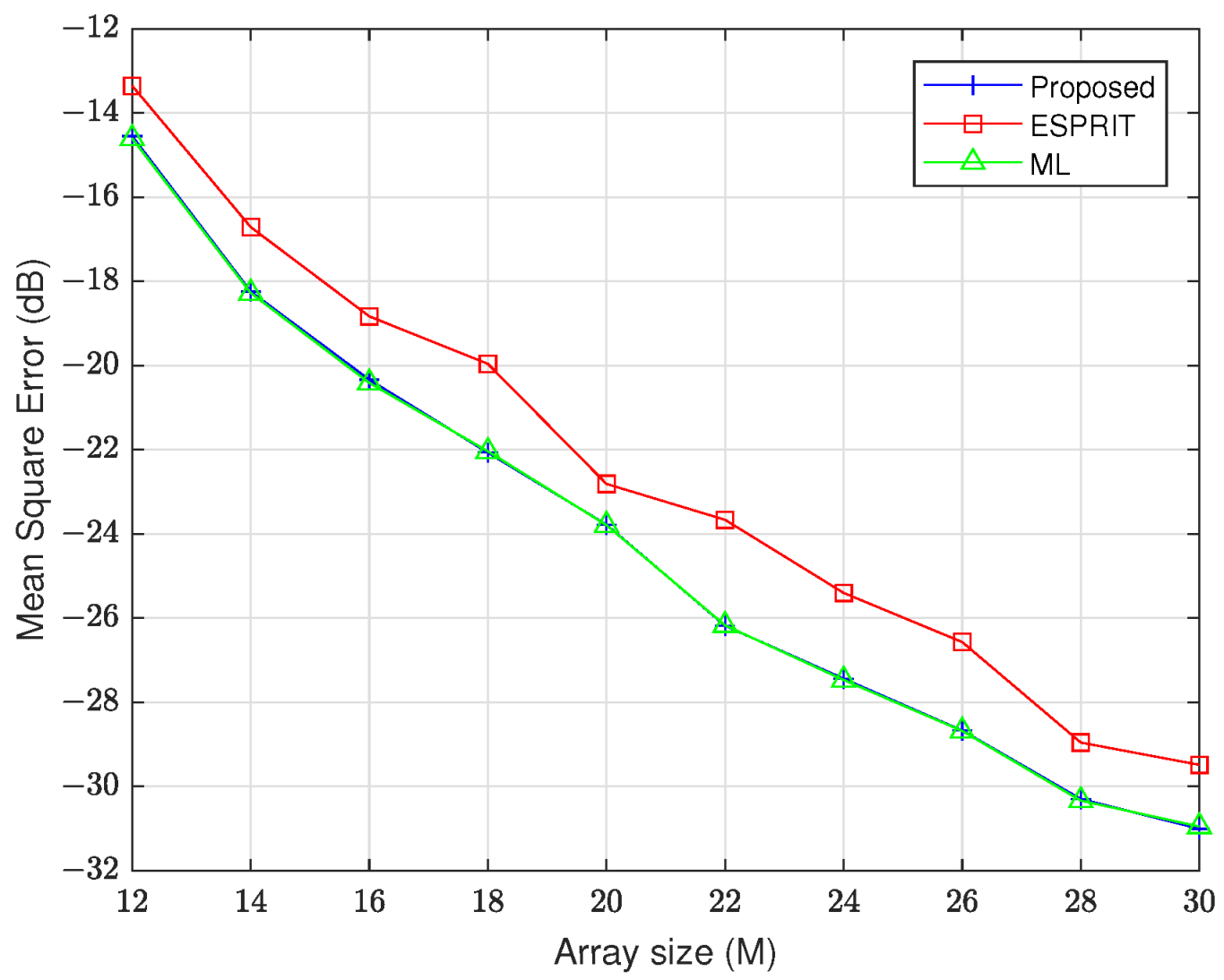
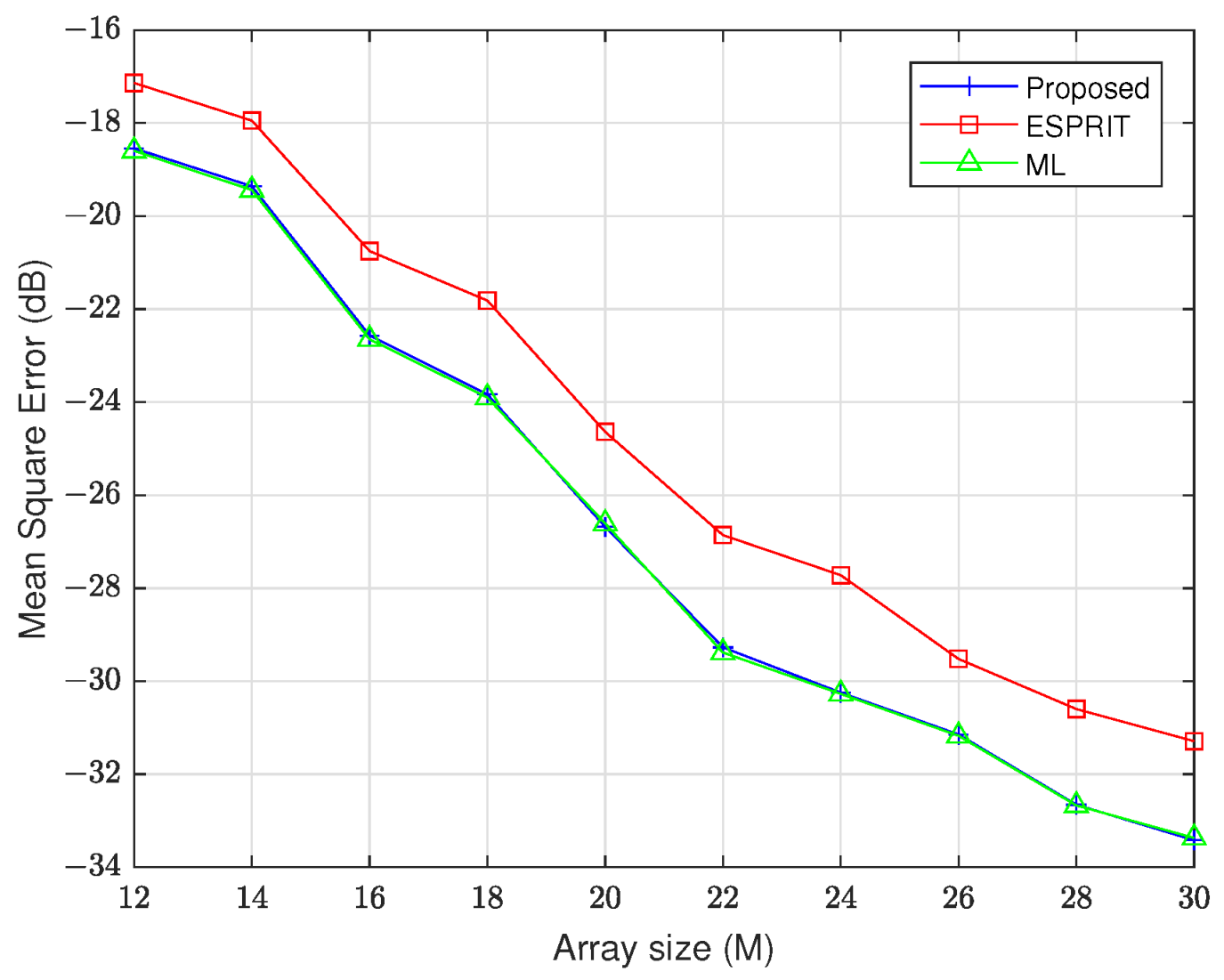
In the following experiment, we conducted a comprehensive MSE analysis to systematically assess estimation accuracy under varying array configurations, spanning array numbers from 12 to 30. The results are shown in Figure 6 and Figure 7. These figures demonstrate that the proposed method achieves superior estimation accuracy compared to ESPRIT while maintaining statistically equivalent performance to the ML benchmark. We find that the array numbers increase, and the performance of all methods improves.
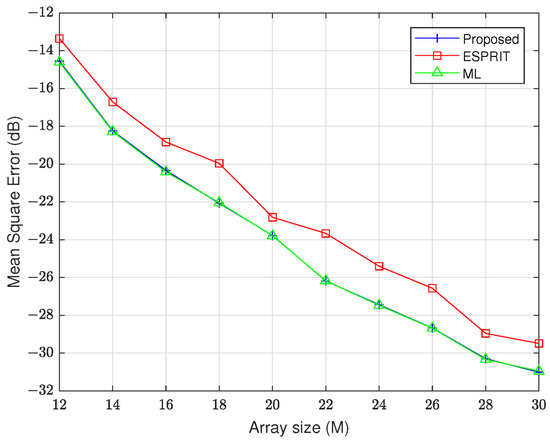
Figure 6.
MSE of versus array number.
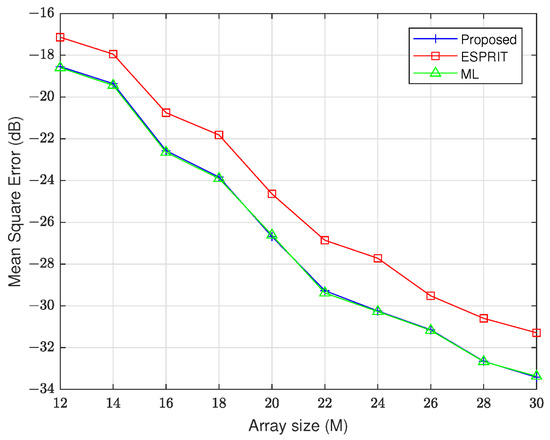
Figure 7.
MSE of versus array number (M = N).
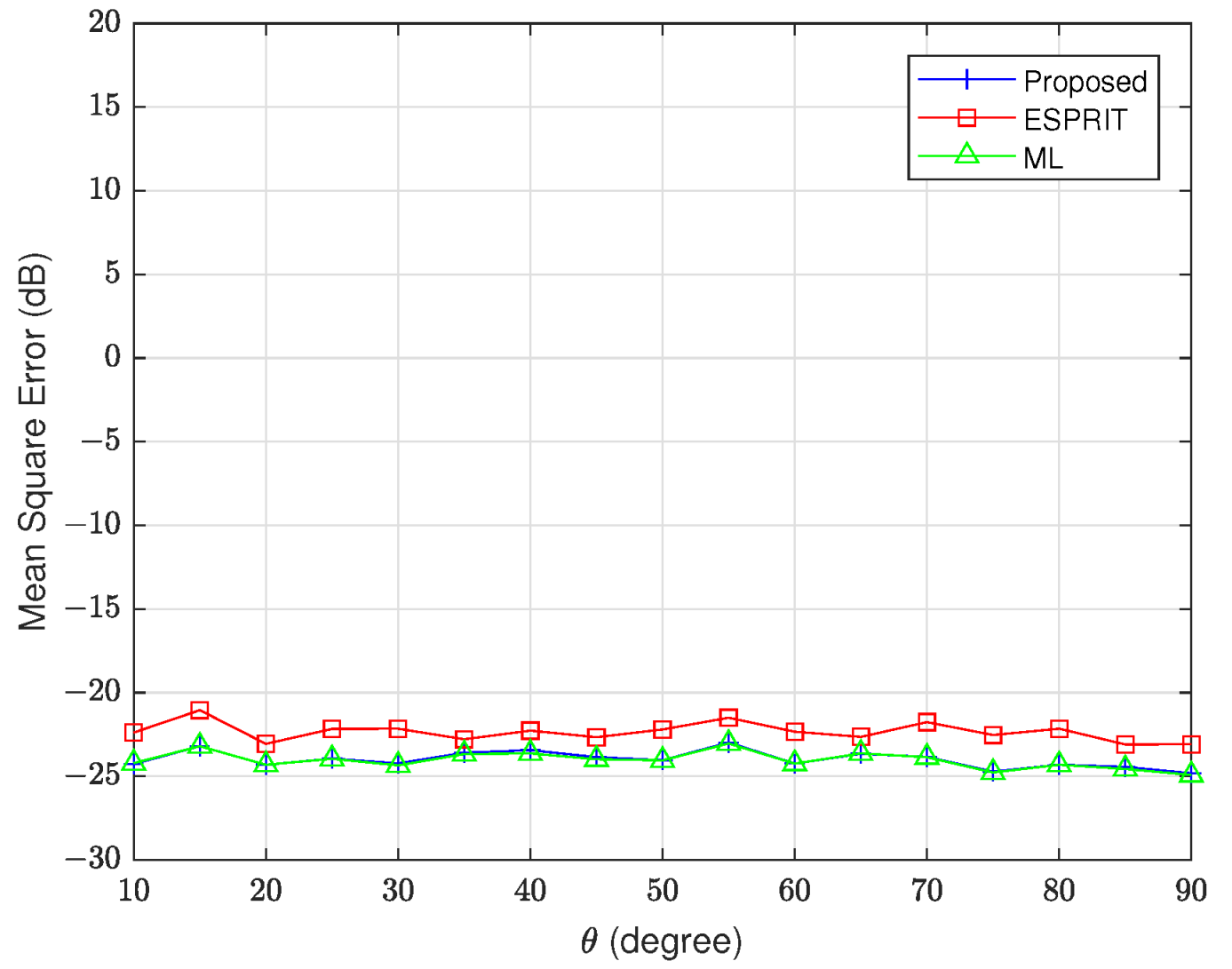
To rigorously evaluate the angular discrimination capability of our proposed algorithm, we conducted a targeted resolution test under controlled conditions. The fourth experiment is designed to assess the method’s precision in distinguishing closely spaced sources while maintaining azimuthal accuracy with fixed elevation angle and azimuth angles varying from to , while the other data settings remain the same as in the previous simulation. As demonstrated in Figure 8, the proposed method achieves angular resolution performance statistically equivalent to the ML benchmark while outperforming ESPRIT across the tested azimuth range, which again verifies the accuracy of the proposed method.
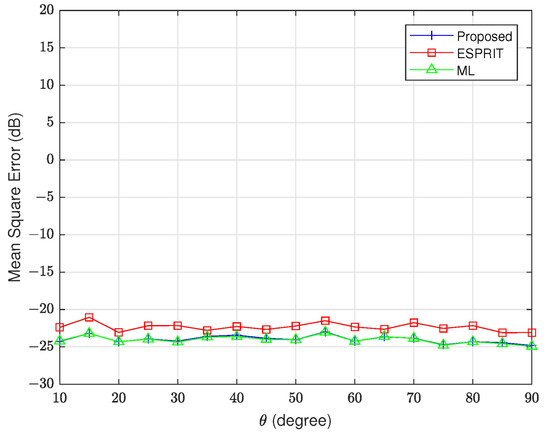
Figure 8.
Angle resolution with fixed and changing .
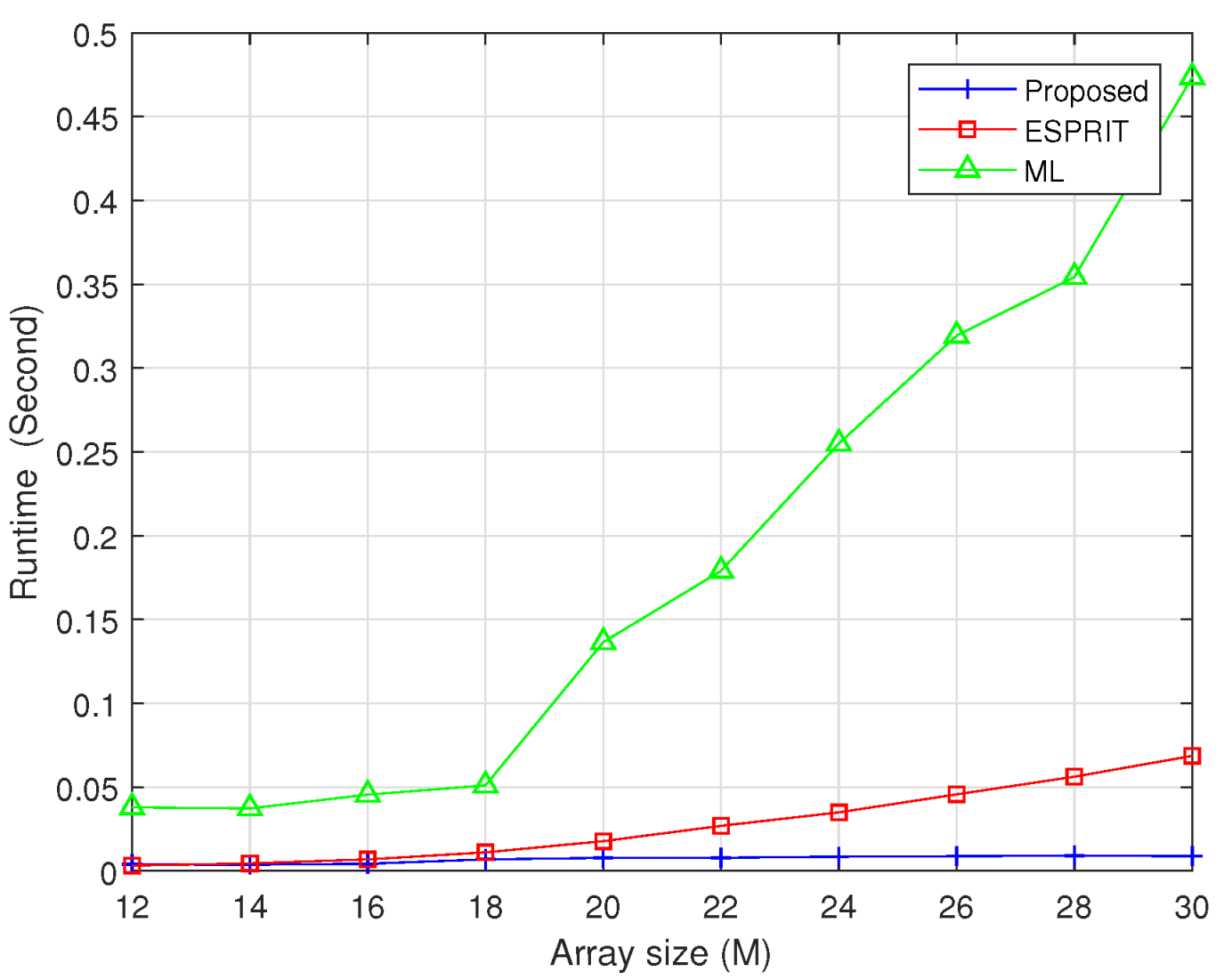
The fundamental computational advantage of our proposed method lies in its exclusive use of real-valued operations for signal subspace derivation. Traditional subspace-based algorithms rely extensively on complex-number arithmetic throughout their processing chains—from covariance matrix construction to eigenvalue decomposition and spectral search. Each complex multiplication requires four real multiplications and two real additions, while complex matrix decompositions demand substantially higher floating-point operations than their real-valued equivalents. By systematically transforming the entire computational workflow into the real domain through unitary matrix operations, our approach bypasses this inherent inefficiency. To quantitatively validate these theoretical advantages, we designed a comprehensive runtime benchmark comparing our method against two techniques: ESPRIT, ML. Experiments were conducted on a standardized computing platform with fixed hardware specifications to ensure fair comparison. The average CPU runtime is measured across 500 independent trials under identical signal conditions. This metric serves as a direct proxy for computational complexity, reflecting the aggregate costs of matrix construction, decomposition, and parameter estimation. Figure 9 shows that the proposed algorithm exhibits exceptional stability in computational load when the array number increases from 12 to 30. As seen from the figure, the running time of the ML method increases quickly, with the array number becoming larger, while the ESPRIT method grows slowly. Our proposed method maintains near-constant execution time. To give a further detailed view, we also give the running time under different array sizes in Table 2, which again, unequivocally confirms the lowest computational complexity of our approach among the methods of comparison.
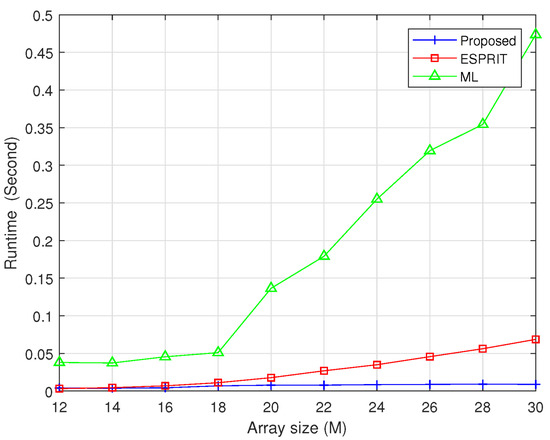
Figure 9.
Running time comparison versus array number (M = N).

Table 2.
Comparison of Running Time (Second).
5. Conclusions
In conclusion, a novel and efficient technique has been proposed for estimating the 2D DOA of signals from a URA. The proposed method combines the Nyström method for obtaining the signal subspace and a unitary subspace-based algorithm for estimating the 2D DOA. By utilizing the Nyström method, we are able to acquire the signal subspace efficiently. The obtained subspace is then utilized in the unitary subspace-based algorithm, which makes use of the principal singular vectors and an iterative process to estimate the 2D DOA of the URA signals. Since the covariance matrix is computed with real-valued decomposition, the complexity of DOA estimation is significantly reduced. Simulation results have been presented to demonstrate the effectiveness and performance of the proposed method. These results validate the capability of the proposed technique in accurately estimating the 2D DOA of signals from a URA while achieving improved computational efficiency. The integration of the Nyström approximation with unitary subspace techniques represents a novel approach to balancing accuracy and complexity in 2D DOA estimation. With a fixed array size of M = N = 20, the proposed method demonstrates significant computational efficiency, requiring less than of the running time compared to conventional ESPRIT and only of the time required by ML methods, while maintaining similar performance. The method’s efficiency stems from both algorithmic innovations and careful exploitation of array geometry properties. Future work could explore adaptive parameter selection and robustness enhancements while maintaining the core computational benefits demonstrated in this study and multi-tone signal cases. The proposed technique offers a computationally efficient high-resolution angle estimation solution, particularly suitable for resource-constrained systems, such as modern radar and 5G beamforming applications, where both accuracy and real-time processing are paramount.
Author Contributions
Conceptualization, F.L.; Methodology, L.Y., K.W. and F.L.; Software, L.Y. and K.W.; Validation, L.Y.; Formal analysis, L.Y. and K.W.; Investigation, F.L.; Resources, F.L.; Data curation, K.W.; Writing—original draft, L.Y.; Writing—review & editing, L.Y., K.W. and F.L.; Supervision, F.L.; Project administration, F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hubei Province (Grant No. 2022CFC061).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Z.; Wang, W.; Huang, Y.; Liu, S. Decoupled 2-D direction of arrival estimation in L-shaped array. IEEE Commun. Lett. 2017, 21, 1989–1992. [Google Scholar] [CrossRef]
- Jian, L.; Wang, X.; Shi, J.; Lan, X. Robust sparse bayesian learning scheme for DOA estimation with non-circular sources. Mathematics 2022, 10, 923. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, X.; Ding, L.; Jin, X.; Zhang, Q. DOA-estimation method based on improved spatial-smoothing technique. Mathematics 2024, 12, 45. [Google Scholar] [CrossRef]
- Cui, J.; Pan, W.; Wang, H. Direction of arrival estimation method based on eigenvalues and eigenvectors for coherent signals in impulsive noise. Mathematics 2024, 12, 832. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Wax, M.; Shan, T.-J.; Kailath, T. Spatio-temporal spectral analysis by eigenstructure methods. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 817–827. [Google Scholar] [CrossRef]
- Zoltowski, M.; Haardt, M.; Mathews, C. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary esprit. IEEE Trans. Signal Process. 1996, 44, 316–328. [Google Scholar] [CrossRef]
- Fernandez del Rio, J.; Catedra-Perez, M. The matrix pencil method for two-dimensional direction of arrival estimation employing an l-shaped array. IEEE Trans. Antennas Propag. 1997, 45, 1693–1694. [Google Scholar] [CrossRef]
- Yilmazer, N.; Sarkar, T.K. 2-D unitary matrix pencil method for efficient direction of arrival estimation. Digit. Signal Process. 2006, 16, 767–781. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Yan, S.; Hou, C. Single snapshot DOA estimation by compressive sampling. Appl. Acoust. 2013, 74, 926–930. [Google Scholar] [CrossRef]
- Wang, X.H.; Mao, X.P.; Zhang, N.T. Single-snapshot DOA estimation based on compressed sensing in pcr systems. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 528–531. [Google Scholar]
- Radich, B.; Buckley, K. Single-snapshot DOA estimation and source number detection. IEEE Signal Process. Lett. 1997, 4, 109–111. [Google Scholar] [CrossRef]
- Jagannath, R. Detection and estimation of multiple DoA targets with single snapshot measurements. In Proceedings of the 2019 National Conference on Communications (NCC), Bangalore, India, 20–23 February 2019; pp. 1–6. [Google Scholar]
- Chang, A.C.; Shen, C.C. Orthogonal projection DOA estimation with a single snapshot. IEICE Trans. Commun. 2013, E96-B, 1215–1217. [Google Scholar] [CrossRef]
- Yan, F.-G.; Jin, M.; Liu, S.; Qiao, X.-L. Real-valued MUSIC for efficient direction estimation with arbitrary array geometries. IEEE Trans. Signal Process. 2014, 62, 1548–1560. [Google Scholar] [CrossRef]
- Yan, F.-G.; Shuai, L.; Wang, J.; Shi, J.; Jin, M. Real-valued root-MUSIC for DOA estimation with reduced-dimension EVD/SVD computation. Signal Process. 2018, 152, 1–12. [Google Scholar] [CrossRef]
- Yu, H.; Qiu, X.; Zhang, X.; Wang, C.; Yang, G. Two-dimensional direction of arrival (DOA) estimation for rectangular array via compressive sensing trilinear model. Int. J. Antennas Propag. 2015, 2015, 297572. [Google Scholar] [CrossRef]
- Wang, C.; Hu, J.; Zhang, Q.; Yuan, X. An efficient 2D DOA estimation algorithm based on OMP for rectangular array. Electronics 2023, 12, 1634. [Google Scholar] [CrossRef]
- Guo, Y.; Hu, X.; Feng, W.; Gong, J. Low-complexity 2D DOA estimation and self-calibration for uniform rectangle array with gain-phase error. Remote Sens. 2022, 14, 3064. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, F.; Shi, J.; He, J.; Truong, T.-K. 2D-DOA estimation for coherent signals via a polarized uniform rectangular array. IEEE Signal Process. Lett. 2023, 30, 893–897. [Google Scholar] [CrossRef]
- Liu, W. Super resolution DOA estimation based on deep neural network. Sci. Rep. 2020, 10, 19859. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Wang, F.; Zhang, C. Large-scale eigenvector approximation via Hilbert space embedding Nyström. Pattern Recognit. 2014, 48, 1904–1912. [Google Scholar] [CrossRef]
- Dakulagi, V. A new approach to achieve a trade-off between direction-of-arrival estimation performance and computational complexity. IEEE Commun. Lett. 2021, 25, 1183–1186. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, S.; Peng, G.; Yang, W. Improved eigenstructure-based 2D DOA estimation approaches based on Nyström approximation. China Commun. 2019, 16, 139–147. [Google Scholar]
- Qian, C.; Huang, L.; So, H.C.; Sidiropoulos, N.D.; Xie, J. Unitary PUMA algorithm for estimating the frequency of a complex sinusoid. IEEE Trans. Signal Process. 2015, 63, 5358–5368. [Google Scholar] [CrossRef]
- Haardt, M.; Nossek, J.A. Unitary ESPRIT: How to obtain increased estimation accuracy with a reduced computational burden. IEEE Trans. Signal Process. 1995, 43, 1232–1242. [Google Scholar] [CrossRef]
- Pesavento, M.; Gershman, A.B.; Haardt, M. Unitary root-MUSIC with a real-valued eigendecomposition: A theoretical and experimental performance study. IEEE Trans. Signal Process. 2000, 48, 1306–1314. [Google Scholar] [CrossRef] [PubMed]
- So, H.C.; Chan, F.K.W.; Lau, W.H.; Chan, C.F. An efficient approach for two-dimensional parameter estimation of a single-tone. IEEE Trans. Signal Process. 2010, 58, 1999–2009. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y. Low complexity root-music algorithm for angle estimation in monostatic mimo radar. Syst. Eng. Electron. 2017, 39, 2434–2440. [Google Scholar]
- Kuroda, T.; Kikuma, N.; Inagaki, N. DOA estimation and pairing method in 2D-ESPRIT using triangular antenna array. Electron. Commun. Japan Part I Commun. 2003, 86, 59–68. [Google Scholar] [CrossRef]
- Chan, A.Y.J.; Litva, J. MUSIC and maximum likelihood techniques on two-dimensional DOA estimation with uniform circular array. IEE Proc.-Radar Sonar Navig. 1995, 142, 105–114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).