A Hybrid GAS-ATT-LSTM Architecture for Predicting Non-Stationary Financial Time Series
Abstract
1. Introduction
1.1. Context
1.2. State of the Art
2. Materials and Methods
2.1. Data Acquisition
2.2. GAS Model
2.3. Volatility
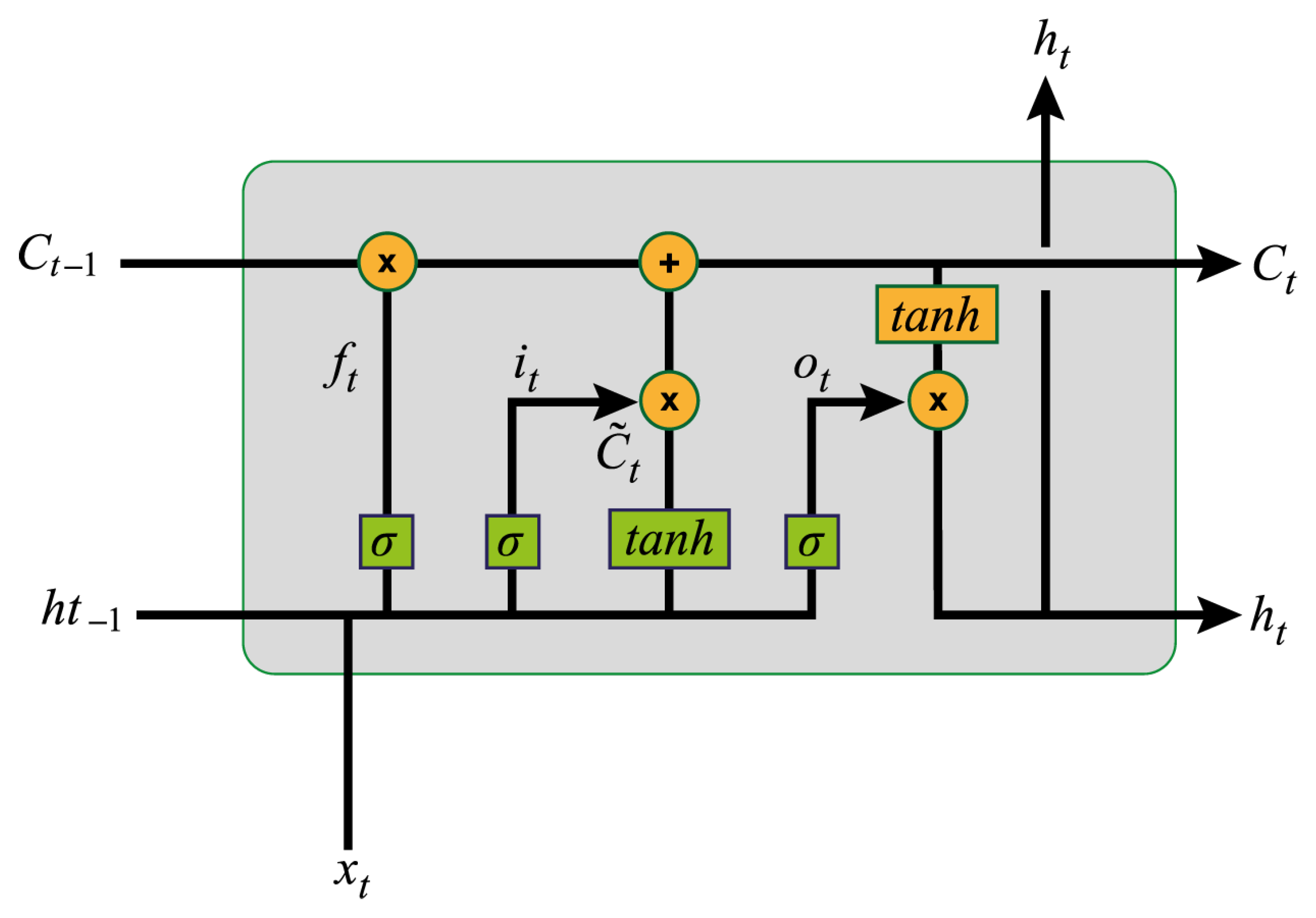
2.4. Long Short-Term Memory (LSTM)
2.5. Attention Mechanism (ATT)
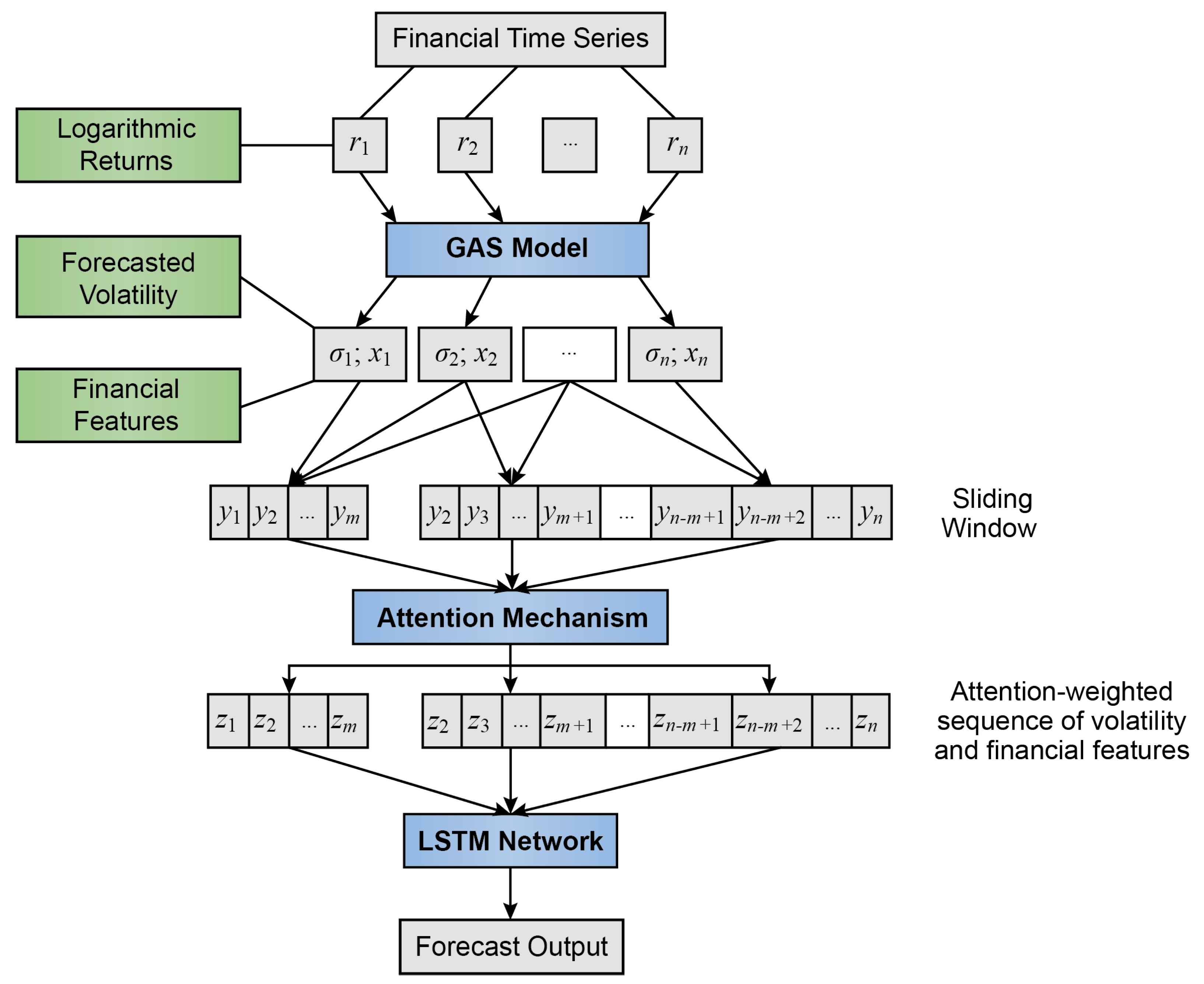
2.6. Hybrid GAS-ATT-LSTM Model
2.7. Data Processing
2.8. Data Partitioning
2.9. Experimental Setting
2.10. Evaluation Metrics
3. Results and Discussion
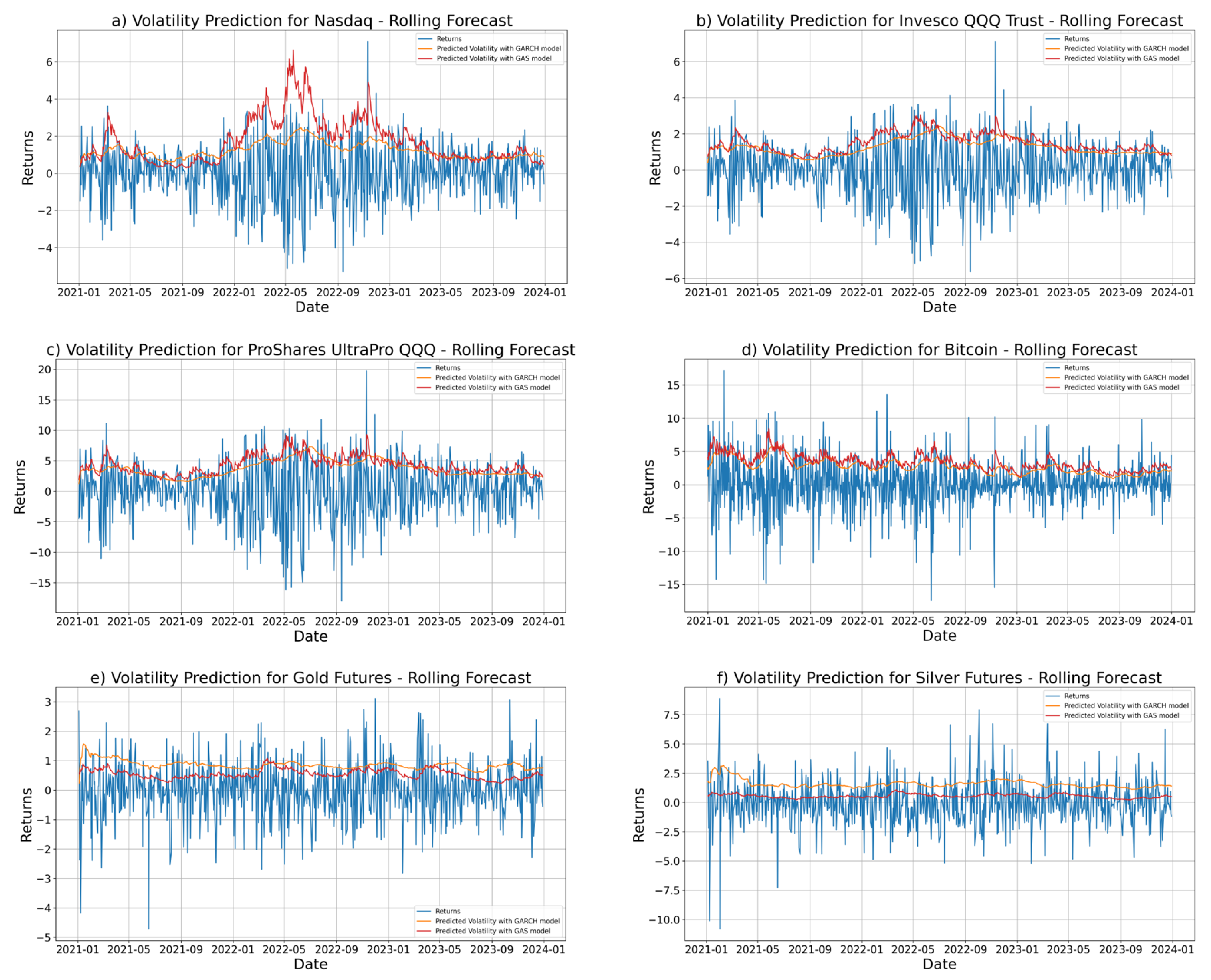
3.1. Volatility Analysis
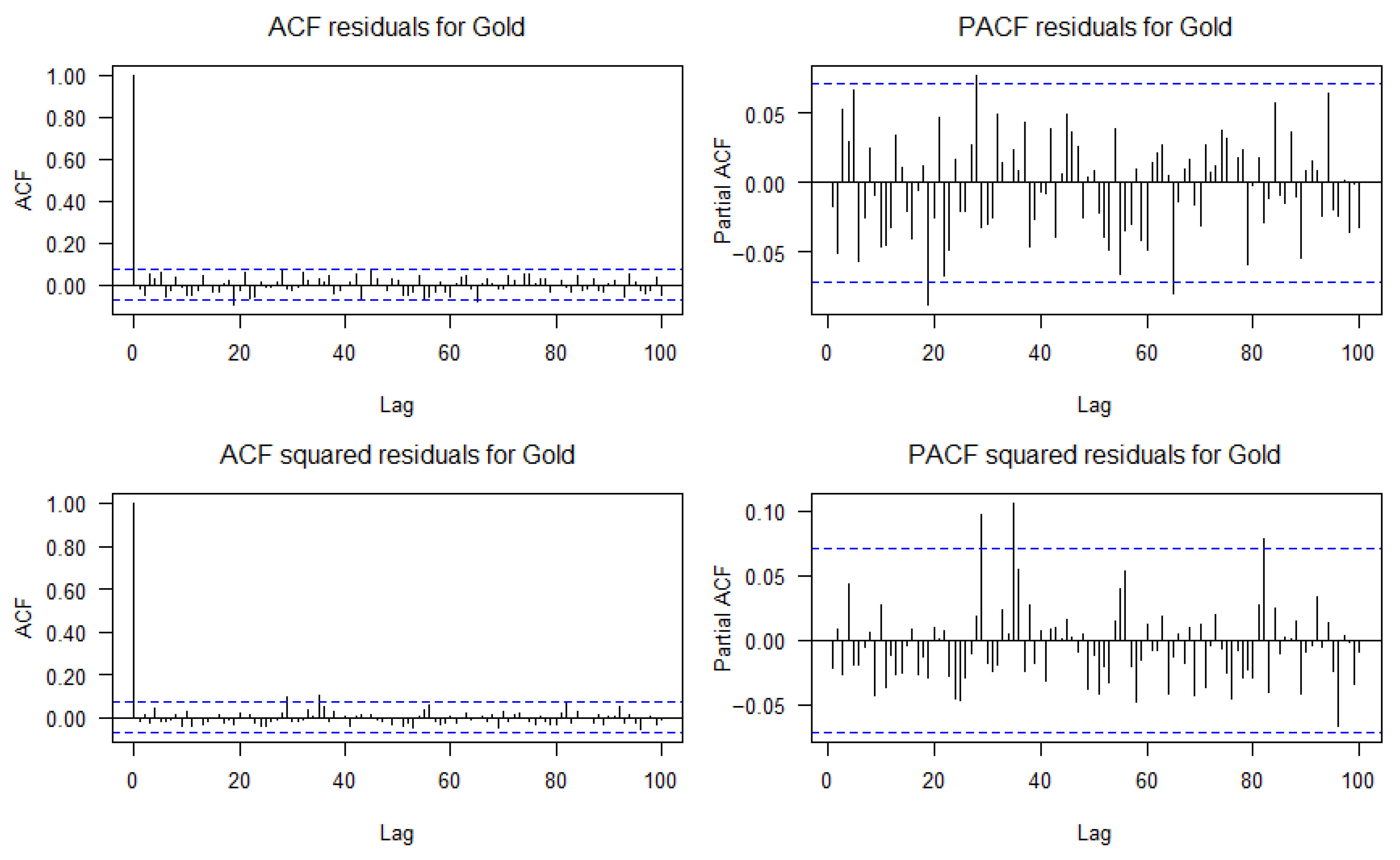
- Ljung–Box test, used to detect the presence of autocorrelation in the residuals and to evaluate whether the model correctly captures the time structure of the series.
- ARCH-LM test, applied to the squared residuals to identify potential ARCH effects, i.e., the presence of conditional heteroskedasticity not explained by the model.
3.2. Results with a 3-Day Sliding Window
3.3. Results with a 5-Day Sliding Window
3.4. Results with a 7-Day Sliding Window
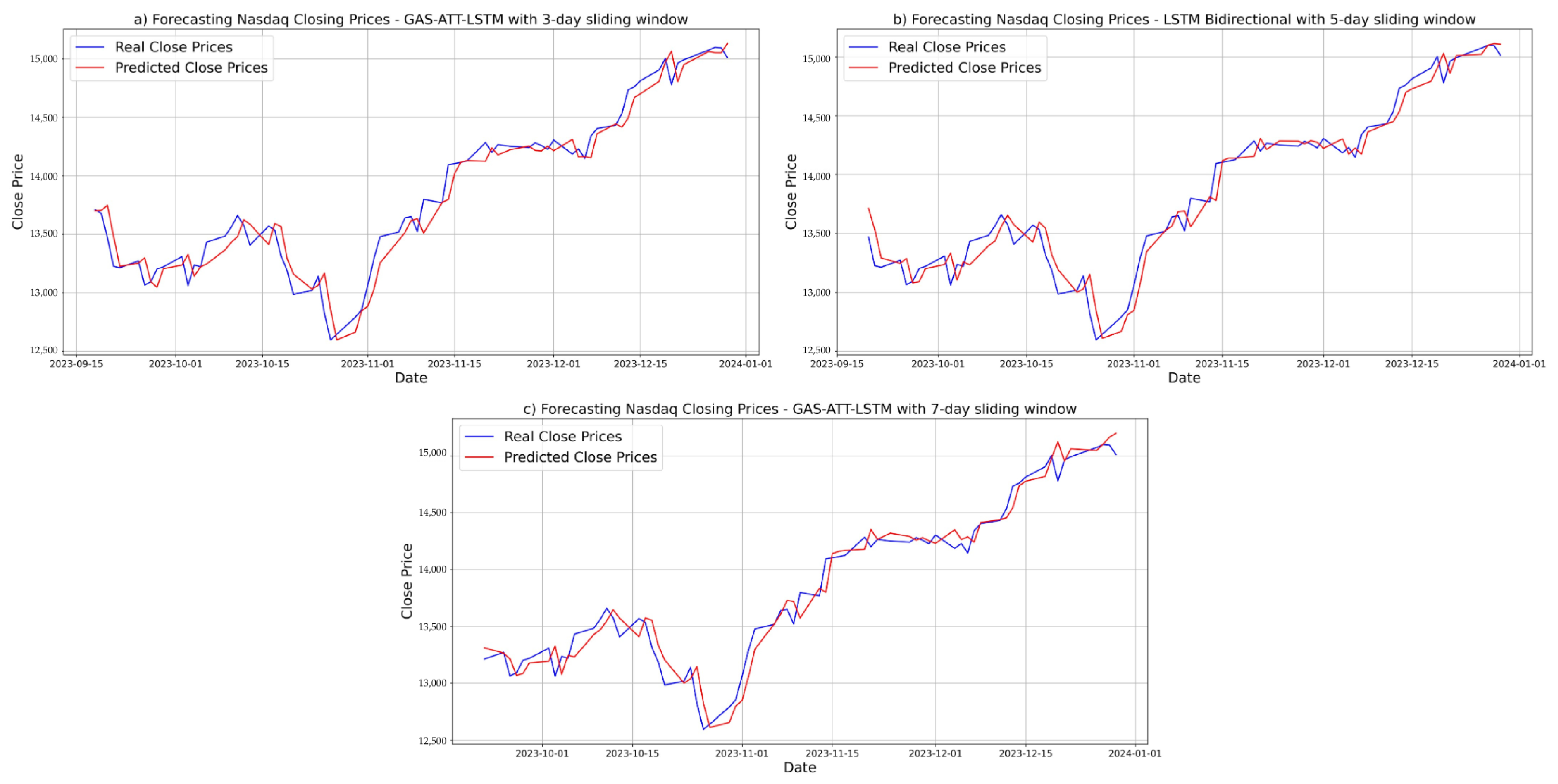
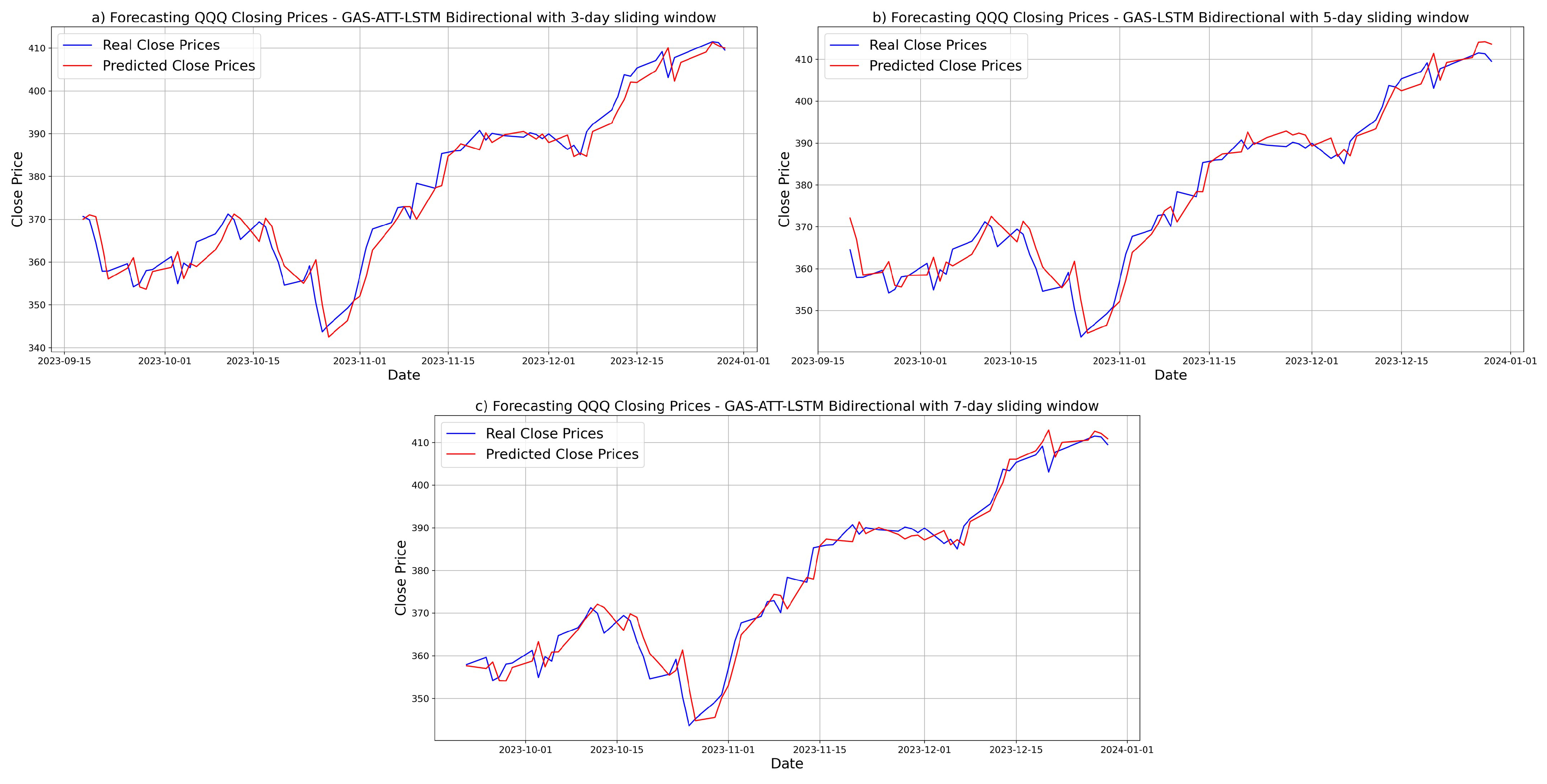
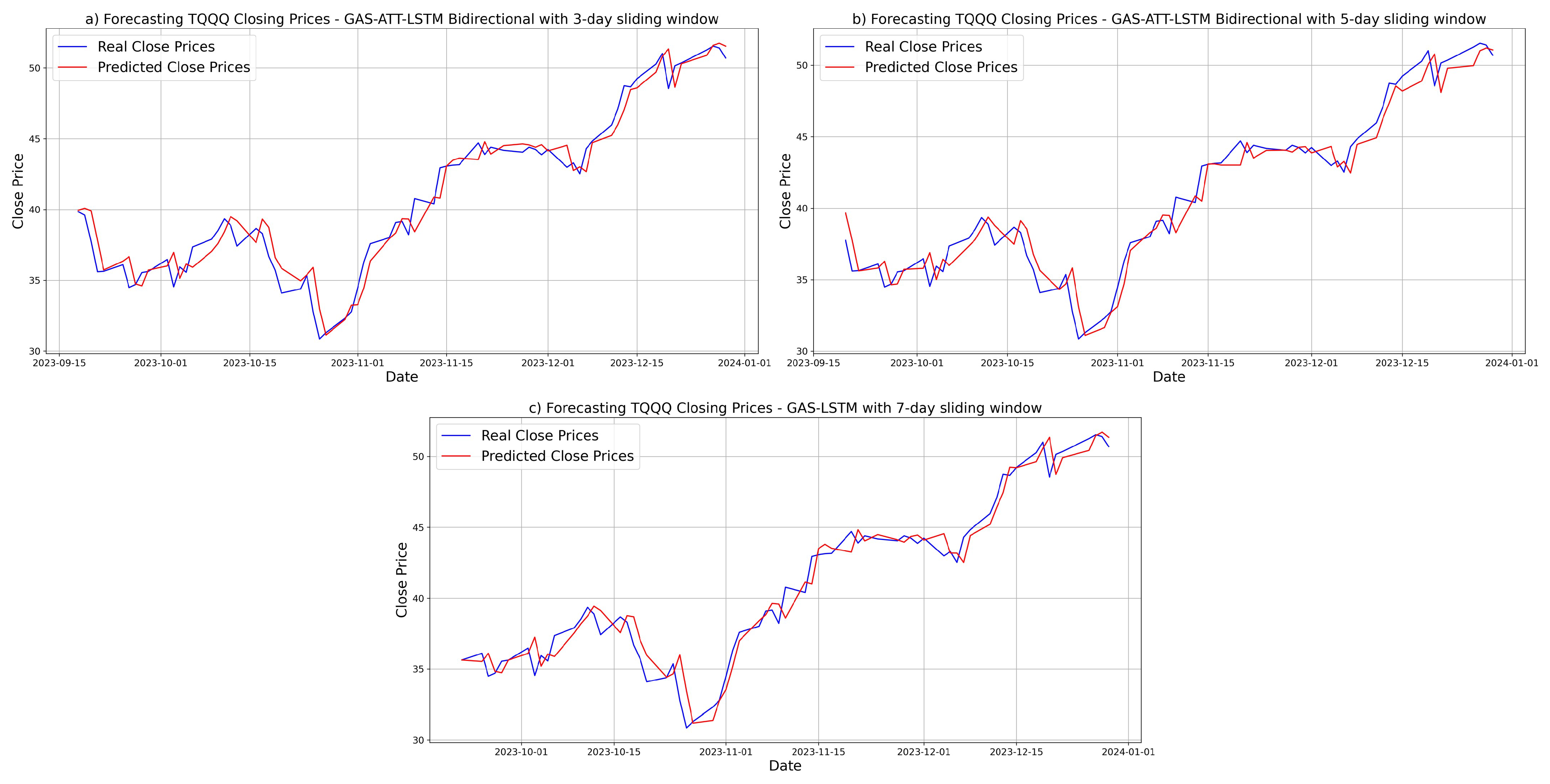
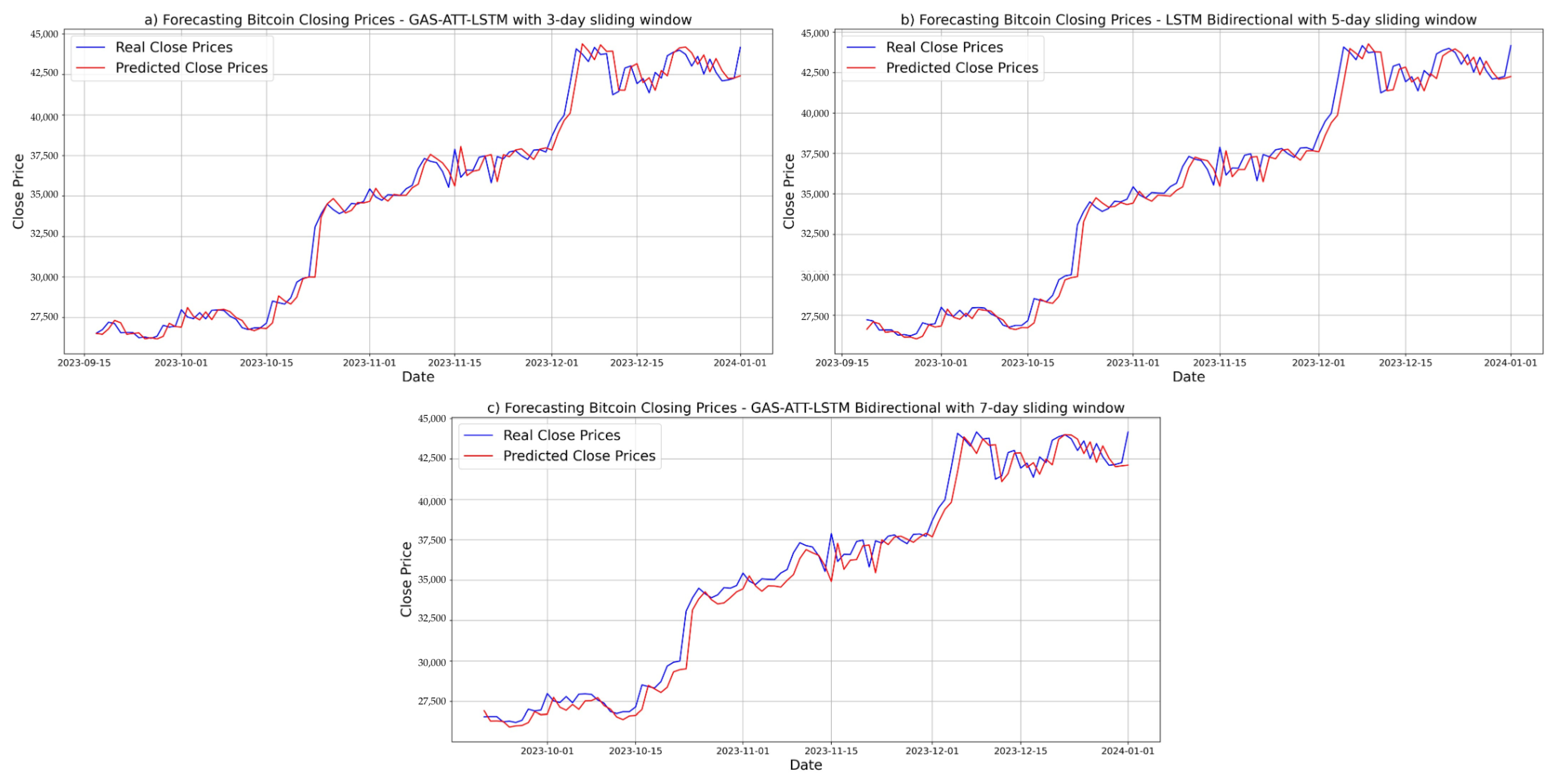
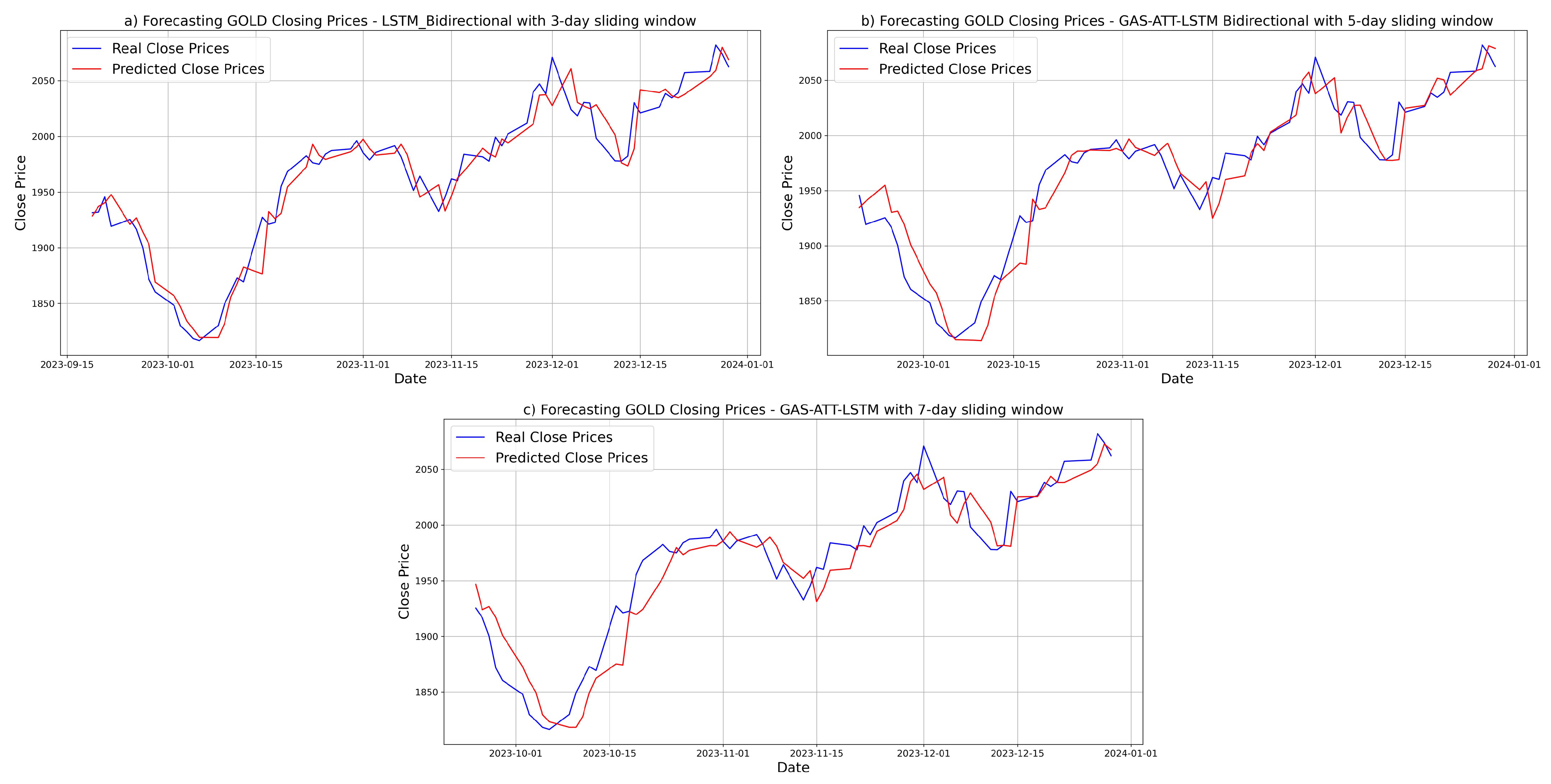
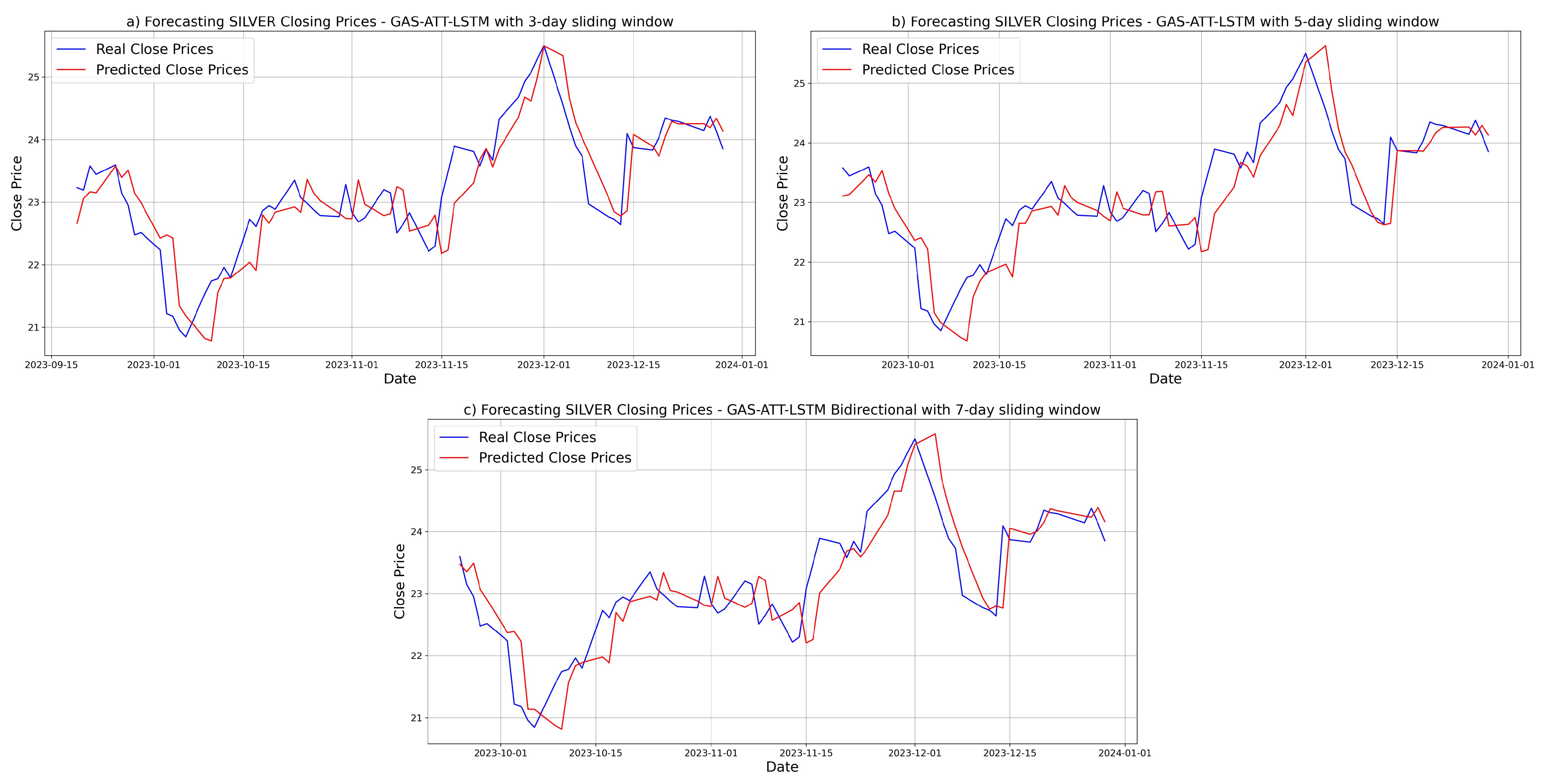
3.5. Forecasting Results and Visual Analysis
3.5.1. Prediction Results for Nasdaq
3.5.2. Prediction Results for QQQ
3.5.3. Prediction Results for TQQQ
3.5.4. Prediction Results for Bitcoin
3.5.5. Prediction Results for GOLD
3.5.6. Prediction Results for SILVER
3.6. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GAS | Generalized Autoregressive Score |
| LSTM | Long Short-Term Memory |
| ATT | Attention Mechanism |
| GARCH | Generalized Autoregressive Conditional Heteroscedasticity |
| QQQ | Invesco QQQ Trust |
| TQQQ | ProShares UltraPro QQQ |
| GOLD | Gold futures prices |
| SILVER | Silver futures prices |
| ACF | Autocorrelation Function |
| PACF | Partial Autocorrelation Function |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
Appendix A. ACF and PACF of Residuals and Squared Residuals for the Six Financial Assets
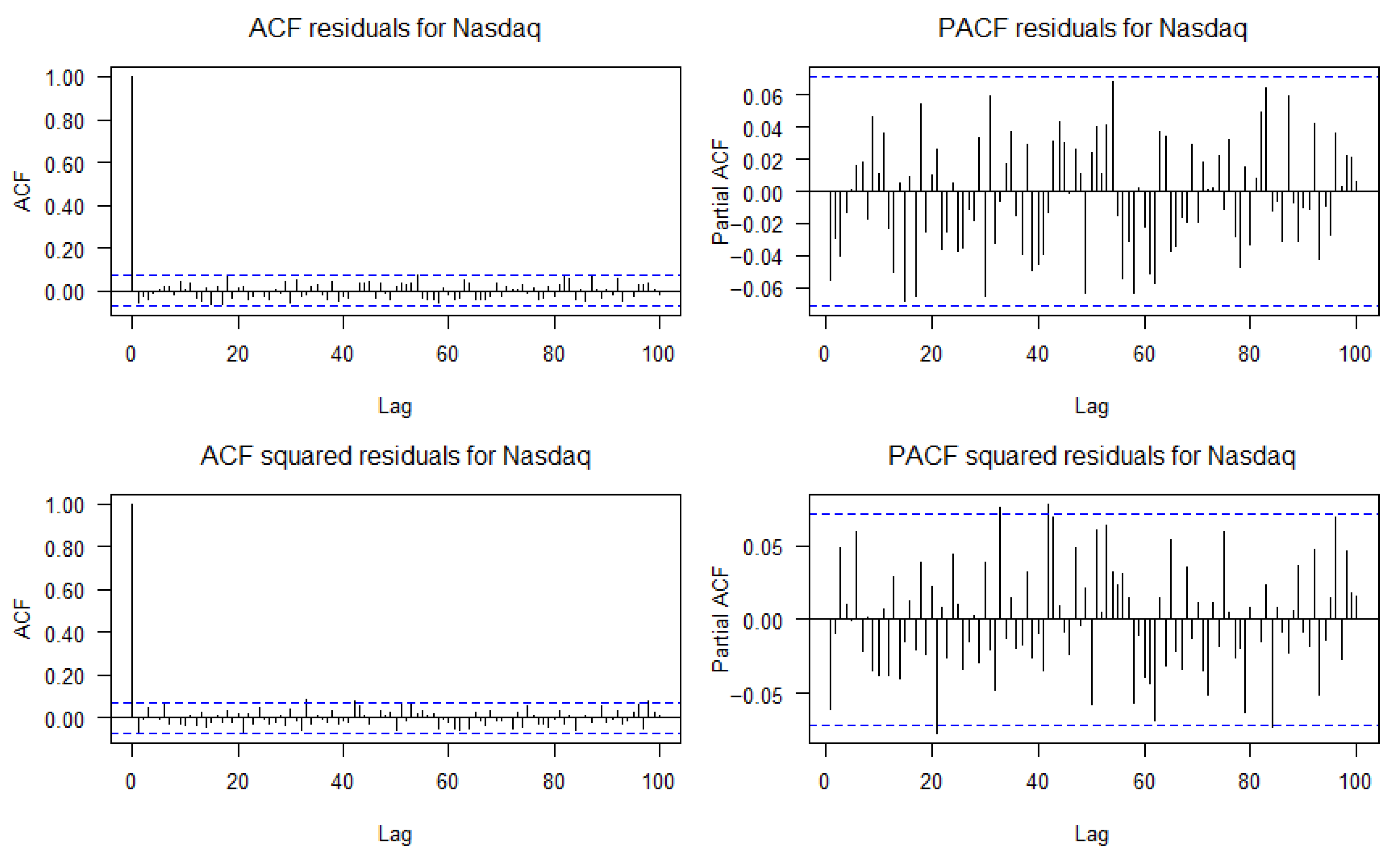
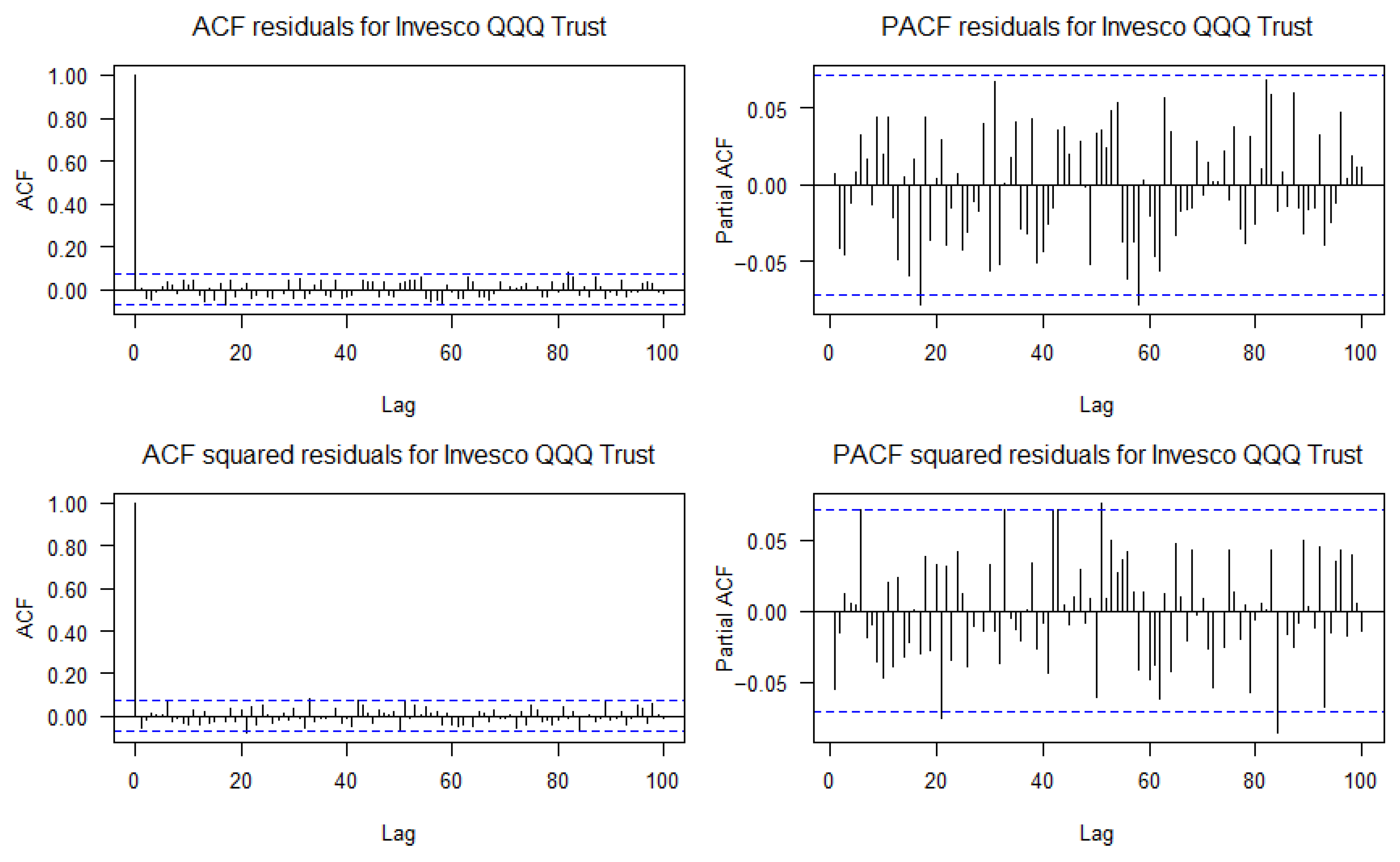
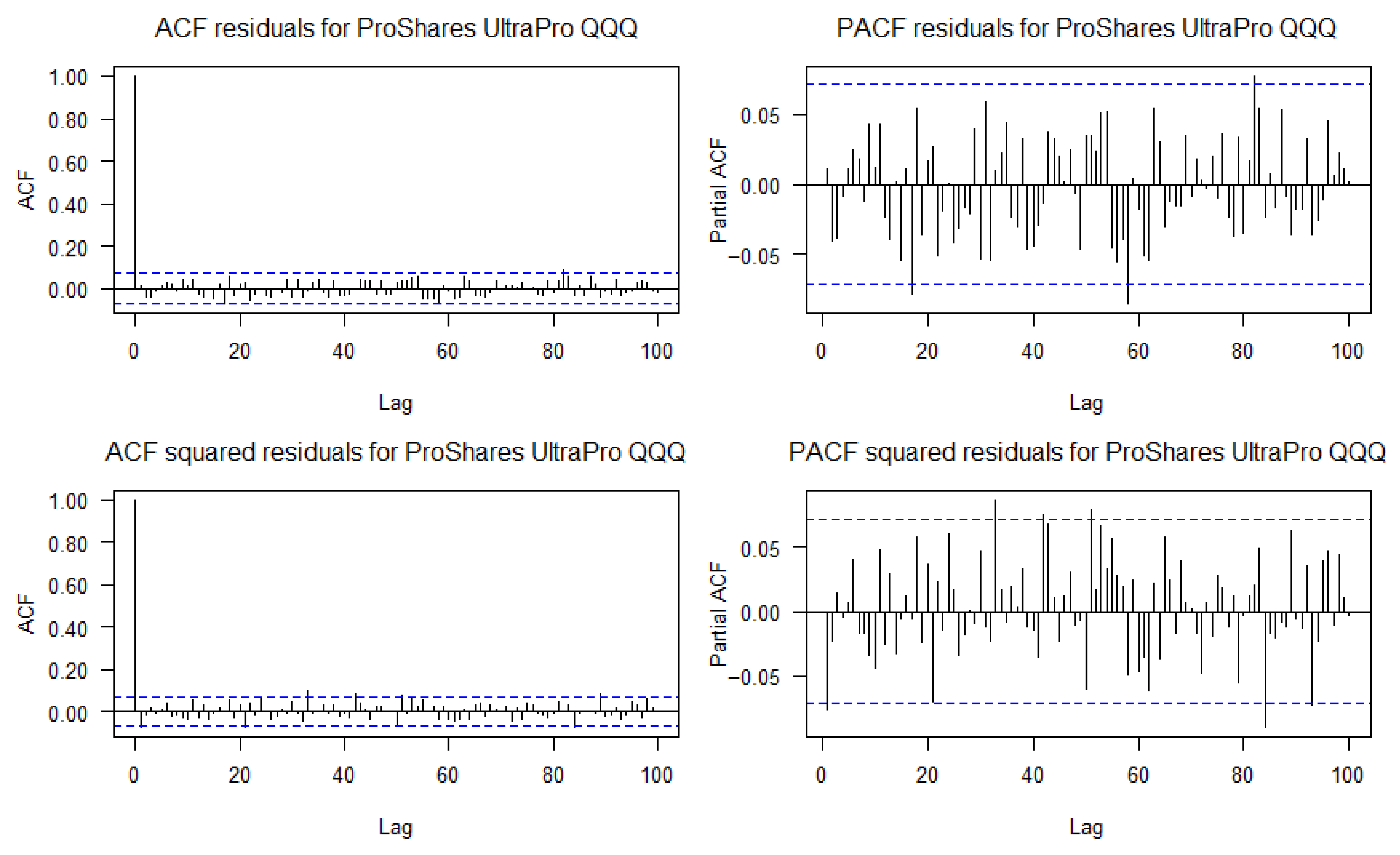
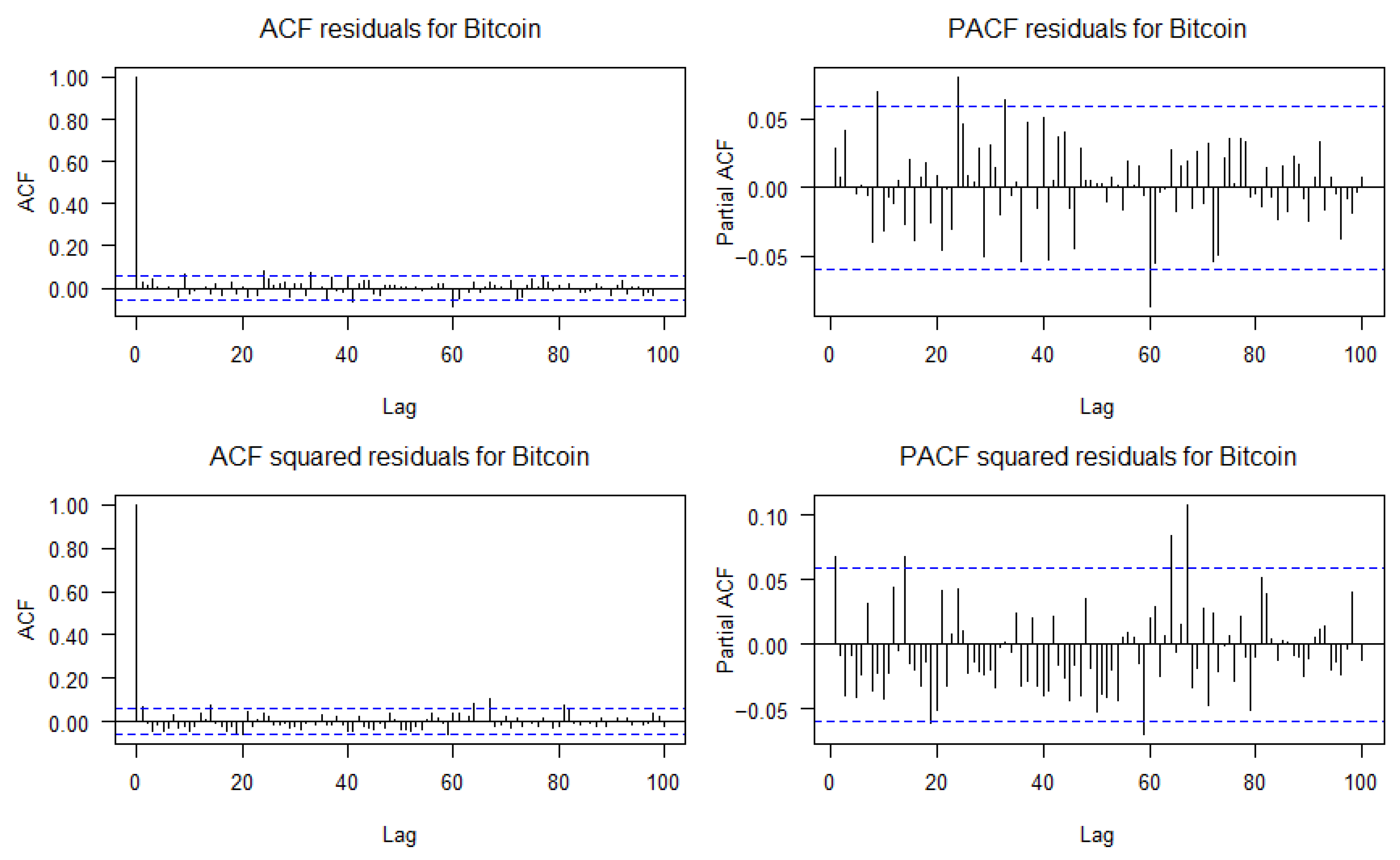

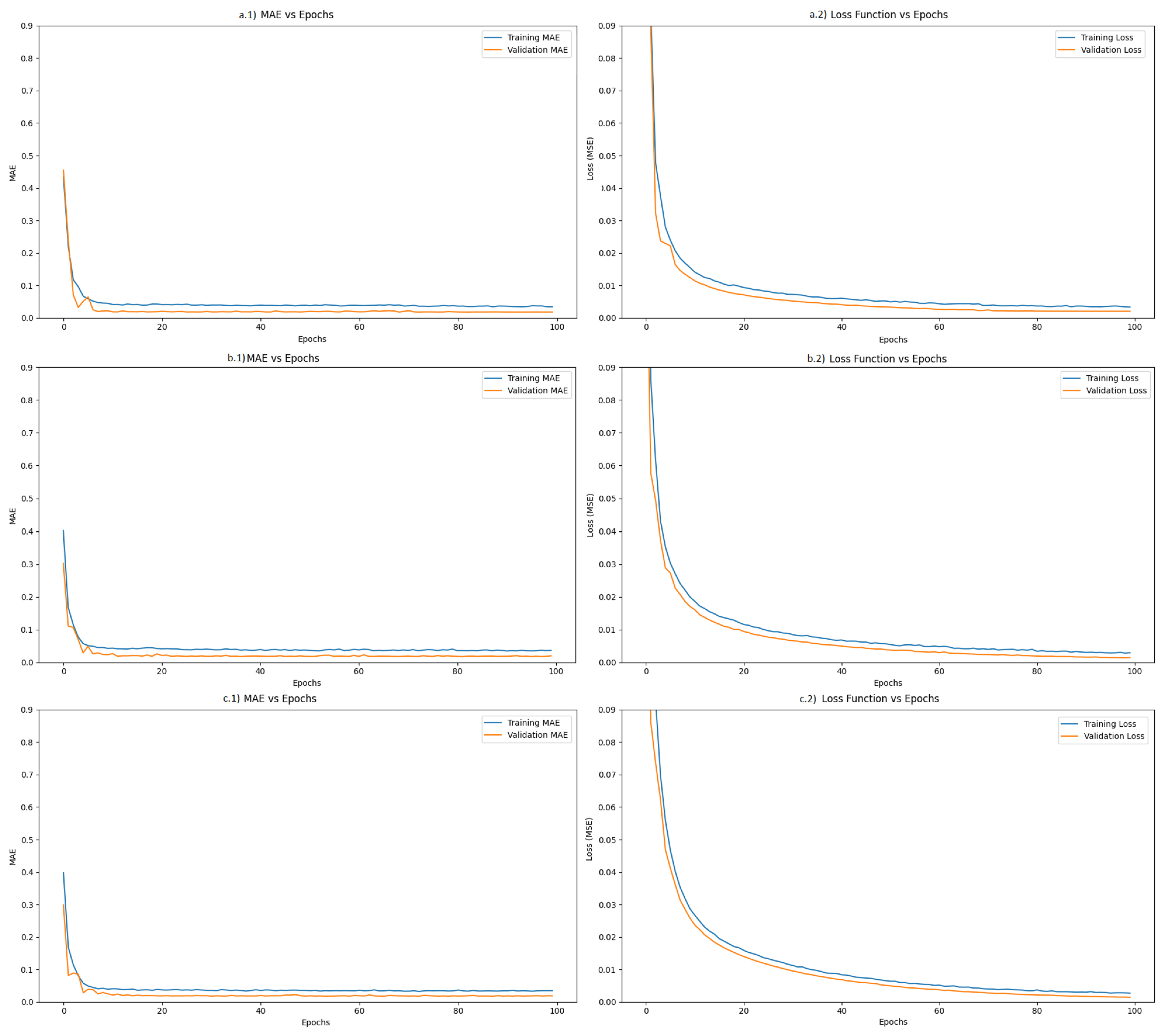
Appendix B. Learning Curves
References
- Zhang, G.P.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Cheng, C.; Sa-Ngasoongsong, A.; Beyca, O.; Le, T.; Yang, H.; Kong, Z.; Bukkapatnam, S.T.S. Time series forecasting for nonlinear and non-stationary processes: A review and comparative study. IIE Trans. 2015, 47, 1053–1071. [Google Scholar] [CrossRef]
- Gao, Z.; Kuruoğlu, E.E. Attention based hybrid parametric and neural network models for non-stationary time series prediction. Expert Syst. 2024, 41, e13419. [Google Scholar] [CrossRef]
- Di-Giorgi, G.; Salas, R.; Avaria, R.; Ubal, C.; Rosas, H.; Torres, R. Volatility forecasting using deep recurrent neural networks as GARCH models. Comput Stat. 2025, 40, 3229–3255. [Google Scholar] [CrossRef]
- Zhao, P.; Zhu, H.; Ng, W.S.H.; Lee, D.L. From GARCH to Neural Network for Volatility Forecast. arXiv 2024, arXiv:2402.06642. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Hsieh, D.A. Nonlinear Dynamics in Financial Markets: Evidence and Implications. Financ. Anal. J. 1995, 51, 55–62. [Google Scholar] [CrossRef]
- Makatjane, K.D.; Xaba, D.L.; Moroke, N.D. Application of Generalized Autoregressive Score Model to Stock Returns. Int. J. Econ. Manag. Eng. 2017, 11. [Google Scholar]
- Creal, D.; Koopman, S.J.; Lucas, A. Generalized autoregressive score models with applications. J. Appl. Econ. 2013, 28, 777–795. [Google Scholar] [CrossRef]
- Harvey, A.C. Dynamic Models for Volatility and Heavy Tails: With Applications to Financial and Economic Time Series; Cambridge University Press: Cambridge, UK, 2013; pp. 8–16. [Google Scholar] [CrossRef]
- Cox, D.R. Statistical analysis of time-series: Some recent developments. Scand. J. Stat. 1981, 8, 110–111. [Google Scholar]
- Benjamin, M.A.; Rigby, R.A.; Stasinopoulos, D.M. Generalized autoregressive moving average models. J. Am. Stat. Assoc. 2003, 98, 214–223. [Google Scholar] [CrossRef]
- Shephard, N. Generalized Linear Autoregressions; Economics Papers; Economics Group, Nuffield College, University of Oxford: Oxford, UK, 1995. [Google Scholar]
- Cipollini, F.; Engle, R.; Gallo, G. Vector Multiplicative Error Models: Representation and Inference. In Econometrics Working Papers Archive; Università degli Studi di Firenze, Dipartimento di Statistica, Informatica, Applicazioni “G. Parenti”: Firenze, Italy, 2006; p. 55. [Google Scholar]
- Deshpande, V. Implementation of Long Short-Term Memory (LSTM) Networks for Stock Price Prediction. RJCSE 2023, 4, 60–72. [Google Scholar] [CrossRef]
- Gupta, P.; Malik, S.; Apoorb, K.; Sameer, S.; Vardhan, V.; Ragam, P. Stock Market Analysis Using Long Short-Term Model. EAI Endorsed Trans. Scalable Inf. Syst. 2023, 11. [Google Scholar] [CrossRef]
- Maknickienė, N.; Maknickas, A. Application of Neural Network for Forecasting of Exchange Rates and Forex Trading. In Proceedings of the 7th International Scientific Conference “Business and Management 2012, Vilnius, Lithuania, 10–11 May 2012. [Google Scholar] [CrossRef]
- Kim, H.Y.; Won, C.H. Forecasting the volatility of stock price index: A hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst. Appl. 2018, 103, 25–37. [Google Scholar] [CrossRef]
- Gao, Z.; He, Y.; Kuruoglu, E.E. A Hybrid Model Integrating LSTM and Garch for Bitcoin Price Prediction. In Proceedings of the IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), Gold Coast, Australia, 25–28 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Kakade, K.A.; Mishra, A.K.; Ghate, K.; Gupta, S. Forecasting Commodity Market Returns Volatility: A Hybrid Ensemble Learning GARCH-LSTM Based Approach. SSRN Electron. J. 2022, 29, 103–117. [Google Scholar] [CrossRef]
- Verma, S. Forecasting volatility of crude oil futures using a GARCH–RNN hybrid approach. Intell. Sys. Acc. Fin. Mgmt. 2021, 28, 130–142. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Kale, D.C.; Elkan, C.; Wetzel, R. Learning to Diagnose with LSTM Recurrent Neural Networks. arXiv 2015, arXiv:1511.03677. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2015, arXiv:1409.0473. [Google Scholar]
- Itti, L.; Koch, C. Computational modelling of visual attention. Nat. Rev. Neurosci. 2001, 2, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Lin, W.; Wang, J.Z. A Dual-Attention-Based Stock Price Trend Prediction Model with Dual Features. IEEE Access 2019, 7, 148047–148058. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, X.; Zhiyuli, A.; Zhang, S.; Xu, R.; Wu, B. AT-LSTM: An Attention-Based LSTM Model for Financial Time Series Prediction. IOP Conf. Ser. Mater. Sci. Eng. 2019, 569, 052037. [Google Scholar] [CrossRef]
- Dai, Z.; Li, J.; Cao, Y.; Zhang, Y. SALSTM: Segmented Self-Attention LSTM for Long-Term Forecasting. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Zhang, L. LSTMGA-QPSBG: An LSTM and Greedy Algorithm-Based Quantitative Portfolio Strategy for Bitcoin and Gold. In Proceedings of the 2nd International Conference Bigdata Blockchain and Economy Management (ICBBEM) 2023, EAI, Hangzhou, China, 19–21 May 2023. [Google Scholar] [CrossRef]
- Ardia, D.; Boudt, K.; Catania, L. Generalized autoregressive score models in R: The GAS package. J. Stat. Softw. 2019, 88, 1–28. [Google Scholar] [CrossRef]
- Ahmed, M.T.; Naher, N. Modelling & Forecasting Volatility of Daily Stock Returns Using GARCH Models: Evidence from Dhaka Stock Exchange. J. Econ. Bus. 2021, 4, 74–89. [Google Scholar] [CrossRef]
- Ogunniran, M.O.; Tijani, K.R.; Benson, R.I.; Kareem, K.O.; Moshood, L.O.; Olayiwola, M.O. Methodological insights regarding the impact of COVID-19 dataset on stock market performance in African countries: A computational analysis. J. Amasya Univ. Inst. Sci. Technol. 2024, 5, 1–16. [Google Scholar] [CrossRef]
- Samuel, R.T.A.; Chimedza, C.; Sigauke, C. Framework for Simulation Study Involving Volatility Estimation: The GAS Approach. Preprints 2023, 2023061735. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ubal, C.; Di-Giorgi, G.; Contreras-Reyes, J.E.; Salas, R. Predicting the Long-Term Dependencies in Time Series Using Recurrent Artificial Neural Networks. Mach. Learn. Knowl. Extr. 2023, 5, 1340–1358. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. arXiv 2014, arXiv:1409.3215. [Google Scholar] [CrossRef]

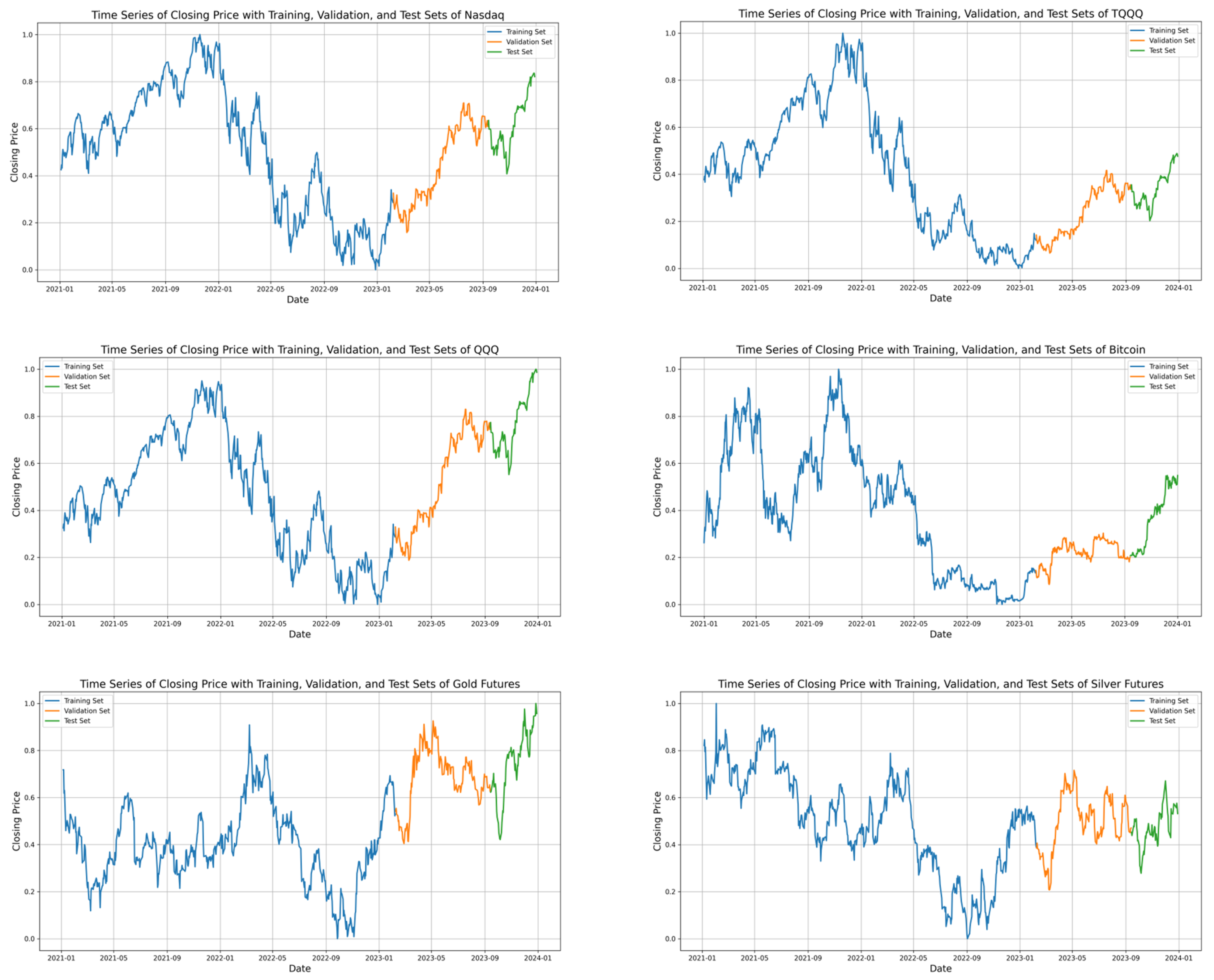
| Dataset | Start Date | End Date | Training | Validation | Test |
|---|---|---|---|---|---|
| Nasdaq | 4 January 2021 | 29 December 2023 | 527 | 150 | 76 |
| QQQ | 4 January 2021 | 29 December 2023 | 527 | 150 | 76 |
| TQQQ | 4 January 2021 | 29 December 2023 | 527 | 150 | 76 |
| Bitcoin | 1 January 2021 | 1 January 2024 | 767 | 219 | 110 |
| GOLD | 4 January 2021 | 29 December 2023 | 527 | 150 | 76 |
| SILVER | 4 January 2021 | 29 December 2023 | 527 | 150 | 76 |
| Dataset | Estimation from | Estimation to |
|---|---|---|
| Nasdaq | 1 January 1971 | 1 January 2021 |
| QQQ | 3 October 1999 | 1 January 2021 |
| TQQQ | 2 November 2010 | 1 January 2021 |
| Bitcoin | 17 September 2014 | 1 January 2021 |
| GOLD | 30 August 2000 | 1 January 2021 |
| SILVER | 30 August 2000 | 1 January 2021 |
| Dataset | Ljung–Box p-Value | ARCH-LM p-Value | Conclusion ( Not Rejected) |
|---|---|---|---|
| Nasdaq | 0.5417 | 0.4434 | ✓ |
| QQQ | 0.5827 | 0.5445 | ✓ |
| TQQQ | 0.5645 | 0.3887 | ✓ |
| Bitcoin | 0.5249 | 0.1343 | ✓ |
| GOLD | 0.1710 | 0.9955 | ✓ |
| SILVER | 0.1710 | 0.9955 | ✓ |
| Dataset | Model | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| Nasdaq | LSTM Bidirectional | 122.44 | 149.01 | 0.89 |
| GARCH-LSTM Bidirectional | 136.93 | 163.95 | 0.99 | |
| ATT-LSTM | 125.77 | 156.01 | 0.91 | |
| GAS-LSTM | 114.00 | 144.22 | 0.83 | |
| GAS-LSTM Bidirectional | 115.47 | 146.73 | 0.84 | |
| GAS-ATT-LSTM | 109.58 | 142.82 | 0.80 | |
| GAS-ATT-LSTM Bidirectional | 135.45 | 165.48 | 0.98 | |
| QQQ | LSTM Bidirectional | 3.10 | 14.86 | 0.83 |
| GARCH-LSTM Bidirectional | 3.17 | 15.71 | 0.85 | |
| ATT-LSTM | 3.00 | 15.14 | 0.81 | |
| GAS-LSTM | 3.14 | 15.49 | 0.84 | |
| GAS-LSTM Bidirectional | 3.01 | 15.09 | 0.81 | |
| GAS-ATT-LSTM | 3.06 | 15.22 | 0.82 | |
| GAS-ATT-LSTM Bidirectional | 2.98 | 14.29 | 0.80 | |
| TQQQ | LSTM Bidirectional | 0.91 | 1.17 | 2.32 |
| GARCH-LSTM Bidirectional | 1.01 | 1.27 | 2.54 | |
| ATT-LSTM | 0.93 | 1.20 | 2.37 | |
| GAS-LSTM | 0.91 | 1.20 | 2.34 | |
| GAS-LSTM Bidirectional | 1.04 | 1.30 | 2.63 | |
| GAS-ATT-LSTM | 0.91 | 1.21 | 2.34 | |
| GAS-ATT-LSTM Bidirectional | 0.89 | 1.17 | 2.28 | |
| Bitcoin | LSTM Bidirectional | 585.83 | 848.04 | 1.62 |
| GARCH-LSTM Bidirectional | 558.30 | 819.87 | 1.54 | |
| ATT-LSTM | 648.90 | 919.12 | 1.80 | |
| GAS-LSTM | 618.75 | 882.84 | 1.71 | |
| GAS-LSTM Bidirectional | 603.95 | 860.50 | 1.69 | |
| GAS-ATT-LSTM | 545.70 | 802.22 | 1.51 | |
| GAS-ATT-LSTM Bidirectional | 650.63 | 926.86 | 1.79 | |
| GOLD | LSTM Bidirectional | 12.73 | 16.45 | 0.65 |
| GARCH-LSTM Bidirectional | 15.36 | 19.59 | 0.78 | |
| ATT-LSTM | 12.98 | 16.68 | 0.66 | |
| GAS-LSTM | 12.95 | 16.71 | 0.66 | |
| GAS-LSTM Bidirectional | 13.55 | 17.53 | 0.69 | |
| GAS-ATT-LSTM | 13.96 | 18.19 | 0.71 | |
| GAS-ATT-LSTM Bidirectional | 13.09 | 16.96 | 0.66 | |
| SILVER | LSTM Bidirectional | 0.321 | 0.414 | 1.390 |
| GARCH-LSTM Bidirectional | 0.313 | 0.410 | 1.354 | |
| ATT-LSTM | 0.316 | 0.412 | 1.368 | |
| GAS-LSTM | 0.312 | 0.410 | 1.348 | |
| GAS-LSTM Bidirectional | 0.317 | 0.411 | 1.369 | |
| GAS-ATT-LSTM | 0.310 | 0.406 | 1.338 | |
| GAS-ATT-LSTM Bidirectional | 0.313 | 0.405 | 1.350 |
| Dataset | Model | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| Nasdaq | LSTM Bidirectional | 108.38 | 137.69 | 0.80 |
| GARCH-LSTM Bidirectional | 163.49 | 188.05 | 1.17 | |
| ATT-LSTM | 175.18 | 197.73 | 1.26 | |
| GAS-LSTM | 116.21 | 144.14 | 0.85 | |
| GAS-LSTM Bidirectional | 122.28 | 149.94 | 0.89 | |
| GAS-ATT-LSTM | 112.27 | 144.62 | 0.82 | |
| GAS-ATT-LSTM Bidirectional | 174.94 | 199.55 | 1.25 | |
| QQQ | LSTM Bidirectional | 3.29 | 16.68 | 0.88 |
| GARCH-LSTM Bidirectional | 3.45 | 18.12 | 0.92 | |
| ATT-LSTM | 3.55 | 18.07 | 0.95 | |
| GAS-LSTM | 3.51 | 17.69 | 0.94 | |
| GAS-LSTM Bidirectional | 3.17 | 16.34 | 0.85 | |
| GAS-ATT-LSTM | 3.53 | 18.08 | 0.94 | |
| GAS-ATT-LSTM Bidirectional | 3.89 | 21.02 | 1.04 | |
| TQQQ | LSTM Bidirectional | 1.13 | 1.36 | 2.81 |
| GARCH-LSTM Bidirectional | 1.14 | 1.37 | 2.83 | |
| ATT-LSTM | 1.05 | 1.26 | 2.60 | |
| GAS-LSTM | 1.05 | 1.26 | 2.63 | |
| GAS-LSTM Bidirectional | 0.94 | 1.22 | 2.41 | |
| GAS-ATT-LSTM | 1.08 | 1.31 | 2.68 | |
| GAS-ATT-LSTM Bidirectional | 0.93 | 1.18 | 2.34 | |
| Bitcoin | LSTM Bidirectional | 575.71 | 841.10 | 1.59 |
| GARCH-LSTM Bidirectional | 620.82 | 873.19 | 1.73 | |
| ATT-LSTM | 607.26 | 874.47 | 1.66 | |
| GAS-LSTM | 667.51 | 940.06 | 1.81 | |
| GAS-LSTM Bidirectional | 1008.96 | 1287.32 | 2.74 | |
| GAS-ATT-LSTM | 653.17 | 894.27 | 1.84 | |
| GAS-ATT-LSTM Bidirectional | 678.12 | 940.55 | 1.88 | |
| GOLD | LSTM Bidirectional | 12.61 | 16.87 | 0.64 |
| GARCH-LSTM Bidirectional | 13.23 | 17.46 | 0.67 | |
| ATT-LSTM | 12.76 | 16.93 | 0.65 | |
| GAS-LSTM | 13.63 | 17.40 | 0.69 | |
| GAS-LSTM Bidirectional | 12.41 | 16.55 | 0.63 | |
| GAS-ATT-LSTM | 12.35 | 16.46 | 0.63 | |
| GAS-ATT-LSTM Bidirectional | 12.44 | 16.45 | 0.63 | |
| SILVER | LSTM Bidirectional | 0.317 | 0.423 | 1.362 |
| GARCH-LSTM Bidirectional | 0.318 | 0.433 | 1.376 | |
| ATT-LSTM | 0.306 | 0.427 | 1.319 | |
| GAS-LSTM | 0.307 | 0.422 | 1.327 | |
| GAS-LSTM Bidirectional | 0.310 | 0.427 | 1.335 | |
| GAS-ATT-LSTM | 0.305 | 0.428 | 1.311 | |
| GAS-ATT-LSTM Bidirectional | 0.316 | 0.435 | 1.355 |
| Dataset | Model | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| Nasdaq | LSTM Bidirectional | 108.93 | 138.35 | 0.80 |
| GARCH-LSTM Bidirectional | 125.92 | 150.21 | 0.91 | |
| ATT-LSTM | 106.67 | 135.96 | 0.78 | |
| GAS-LSTM | 124.48 | 148.49 | 0.91 | |
| GAS-LSTM Bidirectional | 111.36 | 137.55 | 0.81 | |
| GAS-ATT-LSTM | 104.10 | 134.71 | 0.76 | |
| GAS-ATT-LSTM Bidirectional | 149.32 | 171.81 | 1.08 | |
| QQQ | LSTM Bidirectional | 3.00 | 13.92 | 0.80 |
| GARCH-LSTM Bidirectional | 3.24 | 15.42 | 0.86 | |
| ATT-LSTM | 2.86 | 13.75 | 0.77 | |
| GAS-LSTM | 2.96 | 14.56 | 0.79 | |
| GAS-LSTM Bidirectional | 3.64 | 17.98 | 0.97 | |
| GAS-ATT-LSTM | 4.05 | 21.08 | 1.08 | |
| GAS-ATT-LSTM Bidirectional | 2.68 | 13.03 | 0.72 | |
| TQQQ | LSTM Bidirectional | 0.98 | 1.20 | 2.47 |
| GARCH-LSTM Bidirectional | 1.02 | 1.24 | 2.57 | |
| ATT-LSTM | 1.02 | 1.29 | 2.55 | |
| GAS-LSTM | 0.84 | 1.12 | 2.15 | |
| GAS-LSTM Bidirectional | 0.88 | 1.15 | 2.26 | |
| GAS-ATT-LSTM | 1.30 | 1.49 | 3.22 | |
| GAS-ATT-LSTM Bidirectional | 1.05 | 1.31 | 2.60 | |
| Bitcoin | LSTM Bidirectional | 631.93 | 885.57 | 1.72 |
| GARCH-LSTM Bidirectional | 635.32 | 882.55 | 1.79 | |
| ATT-LSTM | 722.13 | 993.65 | 1.96 | |
| GAS-LSTM | 627.68 | 863.26 | 1.74 | |
| GAS-LSTM Bidirectional | 606.07 | 861.48 | 1.68 | |
| GAS-ATT-LSTM | 655.51 | 914.13 | 1.83 | |
| GAS-ATT-LSTM Bidirectional | 602.90 | 857.42 | 1.66 | |
| GOLD | LSTM Bidirectional | 14.24 | 18.10 | 0.72 |
| GARCH-LSTM Bidirectional | 13.47 | 17.46 | 0.68 | |
| ATT-LSTM | 14.01 | 17.92 | 0.71 | |
| GAS-LSTM | 14.63 | 18.97 | 0.74 | |
| GAS-LSTM Bidirectional | 13.34 | 17.47 | 0.68 | |
| GAS-ATT-LSTM | 13.01 | 17.18 | 0.66 | |
| GAS-ATT-LSTM Bidirectional | 14.32 | 18.47 | 0.72 | |
| SILVER | LSTM Bidirectional | 0.312 | 0.418 | 1.343 |
| GARCH-LSTM Bidirectional | 0.316 | 0.419 | 1.365 | |
| ATT-LSTM | 0.299 | 0.409 | 1.291 | |
| GAS-LSTM | 0.318 | 0.422 | 1.373 | |
| GAS-LSTM Bidirectional | 0.306 | 0.415 | 1.316 | |
| GAS-ATT-LSTM | 0.298 | 0.419 | 1.281 | |
| GAS-ATT-LSTM Bidirectional | 0.296 | 0.406 | 1.273 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astudillo, K.; Flores, M.; Soliz, M.; Ferreira, G.; Varela-Aldás, J. A Hybrid GAS-ATT-LSTM Architecture for Predicting Non-Stationary Financial Time Series. Mathematics 2025, 13, 2300. https://doi.org/10.3390/math13142300
Astudillo K, Flores M, Soliz M, Ferreira G, Varela-Aldás J. A Hybrid GAS-ATT-LSTM Architecture for Predicting Non-Stationary Financial Time Series. Mathematics. 2025; 13(14):2300. https://doi.org/10.3390/math13142300
Chicago/Turabian StyleAstudillo, Kevin, Miguel Flores, Mateo Soliz, Guillermo Ferreira, and José Varela-Aldás. 2025. "A Hybrid GAS-ATT-LSTM Architecture for Predicting Non-Stationary Financial Time Series" Mathematics 13, no. 14: 2300. https://doi.org/10.3390/math13142300
APA StyleAstudillo, K., Flores, M., Soliz, M., Ferreira, G., & Varela-Aldás, J. (2025). A Hybrid GAS-ATT-LSTM Architecture for Predicting Non-Stationary Financial Time Series. Mathematics, 13(14), 2300. https://doi.org/10.3390/math13142300










