The Geometric Characterizations of the Ramanujan-Type Entire Function

Abstract

In the present paper, we present certain geometric properties, such as starlikeness, convexity of order $\eta (0\le \eta <1)$, and close-to-convexity, in an open unit disk of the normalized form of Ramanujan-type entire functions. As a consequence, a specific range of parameters is derived such that this function belongs to Hardy spaces ${\mathcal{H}}^{\infty }$ and ${\mathcal{H}}^r.$ Finally, as an application, we present the monotonicity property of the Ramanujan-type entire function using the method of subordination factor sequences.

1. Introduction and Preliminaries

Special functions play a central role in many branches of mathematics and physics due to their appearance in the solutions of differential equations, integral transforms, and mathematical physics. They are also fundamental tools in engineering, quantum mechanics, and number theory. For example, the Rogers–Ramanujan identities are widely used in various fields of science and engineering, including statistical mechanics and combinatorics. We refer the reader to [1,2,3,4]. As a generalization of some Rogers–Ramanujan type identities, Ramanujan introduced the following function, which is now commonly referred to as the Ramanujan entire function (or the q-Airy function) [5]:

$$A_q\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k{q}^{k^2}}{{(q;q)}_k}}{z}^k,\left(z\in \mathbb{C},q\in (0,1)\right),$$

(1)

where ${(a;q)}_k$ is the q-shifted factorials defined as follows:

$${(a;q)}_0=1\mathrm{and}{(a,q)}_k=\prod _{j=0}^{k-1}(1-a{q}^j),(k\ge 1).$$

(2)

In [6], the authors considered a generalization of the Ramanujan entire function defined in the following form:

$$A_q^{\left(\alpha \right)}(a;z)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(a;q)}_k{q}^{\alpha k^2}}{{(q;q)}_k}}{z}^k,\left(a,z\in \mathbb{C},\alpha >0,q\in (0,1)\right).$$

(3)

It is worth mentioning that, in this particular case, we have

$$\begin{array}{cc}\hfill A_q^{\left(1\right)}(0;z)& =A_q(-z).\hfill \end{array}$$

(4)

For additional properties of the Ramanujan-type entire function defined by (3), we refer the interested reader to recent papers [6,7,8], as well as the references cited therein.

Geometric function theory is an important branch of complex analysis that studies analytic and univalent functions through their geometric properties, such as univalence, starlikeness, convexity, and close-to-convexity. It plays a crucial role in understanding conformal mappings and the structure of analytic functions defined on the unit disk, with deep connections to special functions. Nowadays, the geometric behavior of special functions has been widely studied by many authors, notably for its applications to univalent functions and to the theory of special functions. In this direction, the interested reader can refer to some recent papers [9,10,11,12,13,14,15,16,17,18,19,20,21] and the references therein.

Our aim in the present paper is to study some geometric properties of the following normalized form of the Ramanujan-type entire function defined by

$$\begin{array}{cc}\hfill {\mathbf{A}}_q^{\left(\alpha \right)}(a;z)& =z{A}_q^{\left(\alpha \right)}(a;z)\hfill \\ \hfill & =\sum _{k=0}^{\infty }{\displaystyle \frac{{(a;q)}_k{q}^{\alpha k^2}}{{(q;q)}_k}}{z}^{k+1},\left(a,z\in \mathbb{C},\alpha >0,q\in (0,1)\right).\hfill \end{array}$$

(5)

Now, we recall some notions and basic definitions related to geometric function theory. Let $\mathcal{H}$ denote the class of all analytic functions in the unit disk:

$$\mathcal{D}=\left\{z\in \mathbb{C}:\left|z\right|<1\right\}.$$

Let $\mathcal{A}$ be a class of analytic function $f\in \mathcal{H}$ satisfying $f\left(0\right)=f^{\prime }\left(0\right)-1=0$ such that

$$f\left(z\right)=z+\sum _{k=1}^{\infty }{a}_k{z}^{k+1},\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

(6)

A function $f:E\subseteq \mathbb{C}⟶\mathbb{C}$ is said to be univalent in a domain E if it never takes the same value twice: that is, if $f\left(z_1\right)=f\left(z_2\right)$ for $z_1,z_2\in E$ implies that $z_1=z_2.$

A function $f\in \mathcal{A}$ is known as a starlike function (with respect to the origin) in $\mathcal{D}$ if f is univalent in $\mathcal{D}$ and the domain $f\left(\mathcal{D}\right)$ is starlike with respect to the origin in $\mathbb{C}.$ Let us denote the class of starlike functions in $\mathcal{D}$ by ${\mathcal{S}}^{\ast }.$ Moreover, the analytical description of the starlike functions can be stated as follows [22]:

$$\Re \left({\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>0\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

Moreover, we recall the class of starlike functions of order $\eta (0\le \eta <1)$ denoted by ${\mathcal{S}}^{\ast }\left(\eta \right)$, which is defined as follows [23]:

$$\Re \left({\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right)>\eta \mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

An analytic function $f\left(z\right)$ in $\mathcal{A}$ is said to be convex in $\mathcal{D}$ if $f\left(z\right)$ is a univalent function in $\mathcal{D}$ with $f\left(\mathcal{D}\right)$ as a convex domain in $\mathbb{C}.$ We denote the class of convex functions by $\mathcal{C},$ which can also be described as follows [22]:

$$f\in \mathcal{C}⟺\Re \left(1+{\displaystyle \frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}}\right)>0,\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

In addition, if

$$\Re \left(1+{\displaystyle \frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}}\right)>\eta ,\mathrm{for}\mathrm{all}z\in \mathcal{D},$$

where $\eta \in [0,1)$, then f is called convex of order $\eta .$ We denote the class of convex functions of order $\eta$ by $\mathcal{C}\left(\eta \right).$ We remark that for all $\eta \in [0,1)$, we have

$${\mathcal{S}}^{\ast }\left(\eta \right)\subseteq {\mathcal{S}}^{\ast }\left(0\right)={\mathcal{S}}^{\ast },\mathcal{C}\left(\eta \right)\subseteq \mathcal{C}\left(0\right)=\mathcal{C}.$$

An analytic function $f:\mathcal{D}⟶\mathbb{C}$ is said to be close-to-convex with respect to a convex function $\phi :\mathcal{D}⟶\mathbb{C}$ if

$$\Re \left({\displaystyle \frac{f^{\prime }\left(z\right)}{{\phi }^{\prime }\left(z\right)}}\right)>0,\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

Additionally, for a given $\eta (0\le \eta <1)$, we introduce the following class of analytic functions described in [22] by the following:

$$\begin{array}{cc}\hfill \mathcal{P}\left(\eta \right)& =\left\{p\in \mathcal{H}\left(\mathcal{D}\right),p\left(0\right)=1;\Re \left(p\right(z\left)\right)>\eta \right\}.\hfill \end{array}$$

Assume that $f\left(z\right)$ and $g\left(z\right)$ are analytic in $\mathcal{D}.$ Then, $f\left(z\right)$ is subordinate to $g\left(z\right)$ in $\mathcal{D},$ denoted by $f\left(z\right)\prec g\left(z\right)$ (or $f\prec g$), if there exists a Schwartz function $w\left(z\right),$ which is analytic in $\mathcal{D}$, that satisfies the conditions $w\left(0\right)=0$ and $\left|w\right(z\left)\right|<1$ for any $z\in \mathcal{D}$ such that

$$f\left(z\right)=g\left(w\right(z\left)\right),\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

Let ${\mathcal{H}}^{\infty }$ denote the space of all bounded analytic functions in $\mathcal{D}$. For any $\kappa \in (0,\infty ]$ and any function $f\in \mathcal{H}$ and $r\in [0,1)$, we set

$${\mathcal{M}}_{\kappa }(r;f)=\left\{\begin{array}{cc}{\left({\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }{\left|f\left(r{e}^{i\theta }\right)\right|}^{\kappa }\right)}^{{\displaystyle \frac{1}{\kappa }}},\hfill & \mathrm{if}0<\kappa <\infty ,\hfill \\ & \hfill \\ \underset{\left|z\right|\le r}{max}\left|f\left(z\right)\right|,\hfill & \mathrm{if}\kappa =\infty .\hfill \end{array}\right.$$

It is well-known that $f\in \mathcal{D}$ belongs to Hardy space ${\mathcal{H}}^{\kappa },$ where $0<\kappa \le \infty$, if the set $\left\{{\mathcal{M}}_{\kappa }(r;f)|r\in [0,1)\right\}$ is bounded. Moreover, we note that for $0<\nu \le \mu \le \infty$, we have

$${\mathcal{H}}^{\infty }\subset {\mathcal{H}}^{\mu }\subset {\mathcal{H}}^{\nu }.$$

The convolution $f\ast g$ or Hadamard product [22] of two power series

$$f\left(z\right)=z+\sum _{k=1}^{\infty }{a}_k{z}^{k+1},$$

and

$$g\left(z\right)=z+\sum _{k=1}^{\infty }{b}_k{z}^{k+1},$$

is defined as the following power series:

$$f\ast g\left(z\right)=z+\sum _{k=1}^{\infty }{a}_k{b}_j{z}^{k+1}.$$

Here, and in what follows, we use ${\mathrm{\Gamma }}_q\left(x\right)$ to denote the q-gamma function, which is defined for a positive real number x and $0<q<1$ by

$${\mathrm{\Gamma }}_q\left(x\right)={(1-q)}^{1-x}\prod _{j=0}^{\infty }{\displaystyle \frac{1-q^{j+1}}{1-q^{j+x}}}.$$

(7)

The q-digamma function ${\psi }_q\left(x\right)$ is an important function related to the q-gamma function, which is defined by

$${\psi }_q\left(x\right)={\displaystyle \frac{{\mathrm{\Gamma }}_q^{\prime }\left(x\right)}{{\mathrm{\Gamma }}_q\left(x\right)}}.$$

From (7), for $0<q<1$ and for each real variable $x>0,$ we get

$$\begin{array}{cc}\hfill {\psi }_q\left(x\right)& =-log(1-q)+log\left(q\right)\sum _{j=0}^{\infty }{\displaystyle \frac{q^{j+x}}{1-q^{j+x}}}\hfill \\ \hfill & =-log(1-q)+log\left(q\right)\sum _{j=1}^{\infty }{\displaystyle \frac{q^{jx}}{1-q^j}}.\hfill \end{array}$$

(8)

2. Some Useful Lemmas

In order to prove our main results, the following preliminary lemmas will be helpful.

Lemma 1

([24]). Let us assume that the analytic function $f\left(z\right)$ takes the following form:

$$f\left(z\right)=z+\sum _{k=2}^{\infty }{a}_k{z}^k,(z\in \mathcal{D}).$$

If

$$0\le \cdots \le (k+1)a_{k+1}\le k{a}_k\le \cdots \le 1,$$

or if

$$1\le \cdots \le k{a}_k\le (k+1)a_{k+1}\le \cdots \le 2,$$

then function $f\left(z\right)$ is close-to-convex with respect to $-log(1-z).$

Lemma 2

([24]). If $f:\mathbb{D}⟶\mathbb{C}$ is a close-to-convex function, then it is univalent in $\mathcal{D}.$

Lemma 3

([24]). Suppose that the analytic function $f\left(z\right)$ possesses the following form:

$$f\left(z\right)=z+\sum _{k=1}^{\infty }{b}_{2k+1}{z}^{2k+1},(z\in \mathcal{D}).$$

If

$$0\le \cdots \le (2k+1)b_{2k+1}\le \cdots \le 3b_3\le 1,$$

or if

$$1\le 3b_3\le \cdots \le (2k+1)b_{2k+1}\le \cdots \le 2,$$

then the function $f\left(z\right)$ is close-to-convex with respect to ${\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1+z}{1-z}}\right),$ and it is univalent in $\mathcal{D}.$

Lemma 4.

Let $a>0$ and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q),$ then the function $f_{q,a}$ defined on $(0,\infty )$ by

$$f_{q,a}\left(x\right)=q^{ax}{\mathrm{\Gamma }}_q(x+a),$$

(9)

is decreasing on $(0,\infty ).$

Proof. 

With some computation, we get

$$\begin{array}{cc}\hfill f_{q,a}^{\prime }\left(x\right)& =f_{q,a}\left(x\right)\left[alog\left(q\right)+{\psi }_q(x+a)\right]\hfill \\ & =:f_{q,a}\left(x\right)·{\tilde{f}}_{q,a}\left(x\right).\hfill \end{array}$$

(10)

From (8) it follows that

$${\tilde{f}}_{q,a}^{\prime }\left(x\right)={\psi }_q(x+a)>0,$$

for all $min(a,x)>0$ and $q\in (0,1).$ Therefore, the function $x\mapsto {\tilde{f}}_{q,a}\left(x\right)$ is increasing on $(0,\infty )$ and satisfies

$$\underset{x⟼\infty }{lim}{\tilde{f}}_{q,a}\left(x\right)=alog\left(q\right)-log(1-q)\le 0.$$

This, in turn, implies that $f_{q,a}^{\prime }\left(x\right)\le 0,$, and consequently, the function $x\mapsto f_{q,a}\left(x\right)$ is decreasing on $(0,\infty )$ under the given assumptions. □

Lemma 5

([25]). If a function is $f\in \mathcal{C}\left(\eta \right)(0\le \eta <1)$ and is not of the following form:

$$\left\{\begin{array}{cc}{n}_1+{\displaystyle \frac{n_{2}z}{{(1-z{e}^{i\omega })}^{1-2\nu }}},\hfill & \nu \ne {\displaystyle \frac{1}{2}},\hfill \\ & \\ n_1+n_{2}log(1-z{e}^{i\omega }),\hfill & \nu ={\displaystyle \frac{1}{2}},\hfill \end{array}\right.$$

for $n_1,n_2\in \mathbb{C},$ and for $\omega \in \mathbb{R},$ then each of the following statements holds true:

(i).

If $\nu \ge {\displaystyle \frac{1}{2}}$, then $f\in {\mathcal{H}}^{\infty }.$

(ii).

If $\nu \in [0,{\displaystyle \frac{1}{2}})$, then there exists $\delta =\delta \left(f\right)>0$ such that $f\in {\mathcal{H}}^{\delta +{\displaystyle \frac{1}{1-2\nu }}}.$

Lemma 6.

Let ${\left(f_n\right)}_{n\ge 0}$ be a non-negative sequence such that $f_0=1,f_n-f_{n+1}\ge 0$, and $f_n-2f_{n+1}+f_{n+2}\ge 0$ for all $n\in \left\{0,1,2,\cdots \right\}$; then, the inequality

$$\Re \left(1+\sum _{k=1}^{\infty }{f}_n{z}^n\right)>{\displaystyle \frac{1}{2}},$$

holds for all $z\in \mathcal{D}.$

Lemma 7

([26]). The following assertions are equivalent:

1.

The infinite sequence ${\left(b_k\right)}_{k\ge 1}$ of complex numbers is a subordination factor sequence.

2.

The following inequality

$$\Re \left({\displaystyle \frac{1}{2}}+\sum _{k=1}^{\infty }{b}_k{z}^k\right)>0,$$

holds for all $z\in \mathcal{D}.$

3. Close-to-Convexity of the Ramanujan-Type Entire Function

Our aim in this section is to discuss some sufficient conditions concerning the parameters of the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$, which guarantee the close-to-convexity with respect to the functions

$$-log(1-z)\mathrm{and}{\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1+z}{1-z}}\right).$$

Our first main result in this section is the following theorem.

Theorem 1.

Let $\alpha >0,a\in [0,1]$ and $q\in (0,1/e).$ If $\alpha \ge max(1-a,a+3/5),$ then the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$, defined by (5), is close-to-convex with respect to the function $-log(1-z),$ and consequently, it is univalent in $\mathcal{D}.$

Proof. 

We use Lemma 1 to prove that the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ defined by (5) is close-to-convex with respect to the function $log(1-z).$ For convenience, let us write

$$U_k=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathit{k}=0\hfill \\ {\displaystyle \frac{k{(q^a;q)}_k{q}^{\alpha k^2}}{{(q;q)}_k}},\hfill & \mathrm{if}\mathit{k}\ge 1\hfill \end{array}\right.$$

(11)

From (2) and (11), it follows that

$$\begin{array}{cc}\hfill U_0-U_1& ={\displaystyle \frac{1-q-q^{\alpha }+q^{a+\alpha }}{1-q}}\hfill \\ \hfill & =:{\displaystyle \frac{\mathrm{\Xi }(a,\alpha ;q)}{1-q}}.\hfill \end{array}$$

(12)

Moreover, we have

$$\begin{array}{cc}\hfill \mathrm{\Xi }(a,\alpha ;q)& =q^{a+\alpha }\left[1+{\left({\displaystyle \frac{1}{q}}\right)}^{a+\alpha }-{\left({\displaystyle \frac{1}{q}}\right)}^a-{\left({\displaystyle \frac{1}{q}}\right)}^{a+\alpha -1}\right]\hfill \\ \hfill & =q^{a+\alpha }\sum _{j=1}^{\infty }{\displaystyle \frac{\left[{(a+\alpha )}^j-{(a+\alpha -1)}^j-a^j\right]{log}^j(1/q)}{j!}}.\hfill \end{array}$$

(13)

By using the fact that

$${(x+y)}^n\ge x^n+y^n,(n\ge 1,min(x,y)>0),$$

we obtain

$${\left(a+\alpha \right)}^j={\left([a+\alpha -1]+1\right)}^j\ge {\left(a+\alpha -1\right)}^j+1,(\forall j\ge 1).$$

(14)

Having in mind the above inequality and (13), we obtain

$$\mathrm{\Xi }(a,\alpha ;q)\ge q^{a+\alpha }\sum _{j=1}^{\infty }{\displaystyle \frac{(1-a^j){log}^j(1/q)}{j!}},$$

(15)

and the last expression is non-negative for all $a\in [0,1]$ and $q\in (0,1).$ With this observation and with the help of (12), we conclude that $U_0\ge U_1.$ Now, we prove that $U_k\ge U_{k+1}$ for all $k\ge 1.$ Let $k\ge 1$ be fixed. By definitions (11) and (2), we have

$$\begin{array}{cc}\hfill U_k-U_{k+1}& =U_k\left[1-\left({\displaystyle \frac{k+1}{k}}\right)·{\displaystyle \frac{q^{\alpha (2k+1)}(1-q^{a+k})}{1-q^{k+1}}}\right]\hfill \\ \hfill & \ge U_k\left[1-{\displaystyle \frac{2q^{\alpha (2k+1)}(1-q^{a+k})}{1-q^{k+1}}}\right]\hfill \\ \hfill & ={\displaystyle \frac{U_k·{\mathrm{\Omega }}_k(a,\alpha ;q)}{1-q^{k+1}}},\hfill \end{array}$$

(16)

where

$$\begin{array}{cc}\hfill {\mathrm{\Omega }}_k(a,\alpha ;q)& =1-q^{k+1}-2q^{\alpha (2k+1)}+2q^{\alpha (2k+1)+a+k}\hfill \\ \hfill & =q^{\alpha (2k+1)+a+k}\left[{\left({\displaystyle \frac{1}{q}}\right)}^{\alpha (2k+1)+a+k}-{\left({\displaystyle \frac{1}{q}}\right)}^{\alpha (2k+1)+a-1}-2{\left({\displaystyle \frac{1}{q}}\right)}^{a+k}+2\right]\hfill \\ \hfill & =q^{\alpha (2k+1)+a+k}\hfill \\ \hfill & \times \sum _{j=1}^{\infty }{\displaystyle \frac{[{\left(\alpha (2k+1)+a+k\right)}^j-{\left(\alpha (2k+1)+a-1\right)}^j-2\left({a+k)}^j\right]{log}^j(1/q)}{j!}}.\hfill \end{array}$$

Therefore, we obtain

$${\displaystyle \frac{{\mathrm{\Omega }}_k(a,\alpha ;q)}{q^{\alpha (2k+1)+a+k}}}=[(1-a)-(a+k)]log(1/q)+{\rm Y}(a,\alpha ;q),$$

(17)

where

$$\begin{array}{cc}\hfill {\rm Y}(a,\alpha ;q)& =\sum _{j=2}^{\infty }{\displaystyle \frac{[{\left(\alpha (2k+1)+a+k\right)}^j-{\left(\alpha (2k+1)+a-1\right)}^j-2\left({a+k)}^j\right]{log}^j(1/q)}{j!}}\hfill \\ \hfill & =:\sum _{j=2}^{\infty }{\displaystyle \frac{{\mathbf{a}}_j(a,\alpha ,k){log}^j(1/q)}{j!}}.\hfill \end{array}$$

(18)

From the following inequality

$${(a+b)}^n\ge a^n+b^n+na{b}^{n-1},(n\ge 2,min(a,b)>0),$$

(19)

we obtain

$$\begin{array}{cc}\hfill {\left(\alpha (2k+1)+a+k\right)}^j& ={\left[\left(\alpha (2k+1)\right)+\left(a+k\right)\right]}^j\hfill \\ \hfill & \ge {\left(\alpha (2k+1)\right)}^j+{\left(a+k\right)}^j+j\alpha (2k+1){\left(a+k\right)}^{j-1}.\hfill \end{array}$$

Hence, from the above inequality, for $j\ge 2$, we obtain

$$\begin{array}{cc}\hfill {\mathbf{a}}_j(a,\alpha ,k)& \ge {\left(\alpha (2k+1)\right)}^j-{\left(\alpha (2k+1)+a-1\right)}^j+{(a+k)}^{j-1}\left[k(2j\alpha -1)+j\alpha -a\right]\hfill \\ \hfill & \ge (5\alpha -1-a){(a+k)}^{j-1}.\hfill \end{array}$$

(20)

So, by combining (20) and (18), we get

$$\begin{array}{cc}\hfill {\rm Y}(a,\alpha ;k)& \ge (5\alpha -1-a)\sum _{j=2}^{\infty }{\displaystyle \frac{{(a+k)}^{j-1}{log}^j(1/q)}{j!}}\hfill \\ \hfill & ={\displaystyle \frac{(5\alpha -1-a)(a+k){log}^2(1/q)}{2}}+(5\alpha -1-a)\sum _{j=3}^{\infty }{\displaystyle \frac{{(a+k)}^{j-1}{log}^j(1/q)}{j!}}\hfill \\ \hfill & >{\displaystyle \frac{(5\alpha -1-a)(a+k){log}^2(1/q)}{2}}\hfill \end{array}$$

Moreover, since $q\le {\displaystyle \frac{1}{e}}$ and in view of the above inequality, we infer

$${\rm Y}(a,\alpha ;k)>{\displaystyle \frac{(5\alpha -1-a)(a+k)log(1/q)}{2}}.$$

(21)

By virtue of (17) and (21), we establish that

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathrm{\Omega }}_k(a,\alpha ;q)}{q^{\alpha (2k+1)+a+k}}}& >{\displaystyle \frac{2(1-a)+(5\alpha -a-3)(a+k)log(1/q)}{2}}\hfill \\ \hfill & \ge 0,\hfill \end{array}$$

(22)

under the given conditions. Hence, owing to (16) and (22), we deduce that the sequence ${\left\{U_k\right\}}_{k\ge 1}$ is decreasing. Consequently, we have shown that $U_k-U_{k+1}\ge 0$ for all $k\ge 0.$ So, by applying Lemma 1, we establish that the function $z\mapsto {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is close-to-convex with respect to the function $log(1-z)$, and it is univalent in $\mathcal{D}$ by the means of Lemma 2. The proof of Theorem 1 is thus completed. □

Theorem 2.

Let $\alpha >0,a\in [0,1/3]$ and $q\in (0,1/e).$ If $\alpha \ge max(1-a,a+3/5),$ then the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$, defined by (5), is close-to-convex with respect to the function ${\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1+z}{1-z}}\right),$ and consequently, it is univalent in $\mathcal{D}.$

Proof. 

By the definition (5), we get

$$\begin{array}{cc}\hfill {\mathbf{B}}_q^{\left(\alpha \right)}(q^a;z)& :={\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z^2)}{z}}\hfill \\ \hfill & =z+\sum _{k=1}^{\infty }{V}_{2k+1}{z}^{2k+1},(z\in \mathcal{D}),\hfill \end{array}$$

where $V_1=1$ and $V_{2k+1}={\displaystyle \frac{{(q^a;q)}_k{q}^{\alpha k^2}}{{(q;q)}_k}}$ for all $k\ge 1.$ Hence, owing to (2) and (14), we establish that

$$\begin{array}{cc}\hfill {(q;q)}_1·(V_1-3V_3)& =1-q-3q^{\alpha }+3q^{\alpha +a}\hfill \\ \hfill & =q^{\alpha +a}\left[{\left({\displaystyle \frac{1}{q}}\right)}^{a+\alpha }-{\left({\displaystyle \frac{1}{q}}\right)}^{a+\alpha -1}-3{\left({\displaystyle \frac{1}{q}}\right)}^a+3\right]\hfill \\ \hfill & =q^{\alpha +a}\sum _{j=1}^{\infty }{\displaystyle \frac{\left[{(a+\alpha )}^j-{(a+\alpha -1)}^j-3a^j\right]{log}^j(1/q)}{j!}}\hfill \\ \hfill & \ge q^{\alpha +a}\sum _{j=1}^{\infty }{\displaystyle \frac{(1-3a^j){log}^j(1/q)}{j!}},\hfill \end{array}$$

and the last expression is non-negative by our assumptions. This implies that $1\ge 3V_3.$ Now, we want to prove that ${\left\{(2k+1)V_{2k+1}\right\}}_{k\ge 1}$ is a decreasing sequence. Moreover, it is important to note that

$$\begin{array}{c}\hfill (2k+1)V_{2k+1}=\left({\displaystyle \frac{2k+1}{k}}\right)·U_k,(\forall k\ge 1),\end{array}$$

where the sequence ${\left\{U_k\right\}}_{k\ge 1}$ is defined by (11). Then, by the above relation, we conclude that the sequence ${\left\{(2k+1)V_{2k+1}\right\}}_{k\ge 1}$ is decreasing as the product of two positive and decreasing sequences. Finally, according to Lemma 3, we conclude that the desired result follows. □

4. Further Geometric Properties of the Ramanujan-Type Entire Function

This section investigates essential geometric properties, including the starlikeness and convexity of order $\eta (0\le \eta <1)$ of the normalized form of the Ramanujan-type entire function defined by (5). In addition, we determine the conditions for this function’s inclusion in Hardy spaces and bounded analytic functions. Moreover, we derive some sufficient conditions for which the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)/z$ belongs to the class $\mathcal{P}\left(\eta \right).$

Our first main result in this section is as follows.

Theorem 3.

Let $a>0,\alpha \ge a+1$, and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q)$, and there exists a real constant η such that

$$0\le \eta \le 1-{\displaystyle \frac{q^{a+1}(1-q^a){(1+q)}^2}{1-q-q^{a+1}(1-q^a)(1+q)}}.$$

(23)

Also, assume that the following inequality

$$q^{a+1}(1-q^a)<{\displaystyle \frac{1-q}{1+q}},$$

(24)

holds true; then, ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)\in {\mathcal{S}}^{\ast }\left(\eta \right).$

Proof. 

In order to prove the required result, it suffices to show that

$$\Re \left({\displaystyle \frac{z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)}{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)}}\right)>\eta ,\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

For this objective in view, it suffices to prove that

$$\left|{\displaystyle \frac{z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)}{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)}}-1\right|<1-\eta ,\mathrm{for}\mathrm{all}z\in \mathcal{D}.$$

(25)

By virtue of the relation

$${\displaystyle \frac{{\mathrm{\Gamma }}_q(a+k)}{{\mathrm{\Gamma }}_q\left(a\right)}}={\displaystyle \frac{{(q^a;q)}_k}{{(1-q)}^k}},$$

(26)

and (5), we infer

$${\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)=\sum _{k=0}^{\infty }{\displaystyle \frac{{(1-q)}^k{\mathrm{\Gamma }}_q(a+k)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}{z}^{k+1}.$$

(27)

Differentiating both sides of the above equation, we get

$$\begin{array}{cc}\hfill \left|{\left({\mathbf{A}}_q^{\left(\alpha \right)}\right)}^{\prime }(q^a,z)-{\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)}{z}}\right|& <\sum _{k=1}^{\infty }{\displaystyle \frac{k{(1-q)}^k{\mathrm{\Gamma }}_q(a+k)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}\hfill \\ \hfill & =\sum _{k=1}^{\infty }{\displaystyle \frac{k{(1-q)}^k\left[q^{ak}{\mathrm{\Gamma }}_q(a+k)\right]q^{k(\alpha k-a)}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}\hfill \\ \hfill & =\sum _{k=1}^{\infty }{\displaystyle \frac{k{(1-q)}^k{f}_{q,a}\left(k\right)q^{k(\alpha k-a)}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}},\hfill \end{array}$$

(28)

where $f_{q,a}\left(x\right)$ is defined by (9). It is worth mentioning that the function $x\mapsto f_{q,a}\left(x\right)$ is decreasing on $(0,\infty )$. This observation together with (28) and the following estimation

$${\displaystyle \frac{1}{{(q;q)}_k}}\le {\displaystyle \frac{1+q}{{(1-q^2)}^k}},k\in \mathbb{N},$$

(29)

yields the following:

$$\begin{array}{cc}\hfill \left|{\left({\mathbf{A}}_q^{\left(\alpha \right)}\right)}^{\prime }(q^a,z)-{\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)}{z}}\right|& <{\displaystyle \frac{q^a(1-q^a)}{1-q}}\sum _{k=1}^{\infty }{\displaystyle \frac{k{q}^{k(\alpha k-a)}}{{(1+q)}^{k-1}}}.\hfill \end{array}$$

(30)

Since $\alpha \ge a+1,$ for $q\in (0,1)$, we get

$$q^{k(\alpha k-a)}\le q^k,(k\ge 1).$$

(31)

Having in mind the above inequality and (30), we obtain

$$\begin{array}{c}\hfill \left|{\left({\mathbf{A}}_q^{\left(\alpha \right)}\right)}^{\prime }(q^a,z)-{\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)}{z}}\right|<{\displaystyle \frac{q^{a+1}(1-q^a){(1+q)}^2}{1-q}},(\forall z\in \mathcal{D}).\end{array}$$

(32)

On the other hand, from (27), (29), and (31), it follows that

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)}{z}}\right|& =\left|1+\sum _{k=1}^{\infty }{\displaystyle \frac{{(1-q)}^k{\mathrm{\Gamma }}_q(a+k)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}{z}^{k+1}\right|\hfill \\ \hfill & \ge 1-\left|\sum _{k=1}^{\infty }{\displaystyle \frac{{(1-q)}^k{\mathrm{\Gamma }}_q(a+k)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}{z}^{k+1}\right|\hfill \\ \hfill & >1-\sum _{k=1}^{\infty }{\displaystyle \frac{{(1-q)}^k{\mathrm{\Gamma }}_q(a+k)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}\hfill \\ \hfill & \ge 1-{\displaystyle \frac{q^a(1-q^a)}{1-q}}\sum _{k=1}^{\infty }{\displaystyle \frac{q^{k(\alpha k-a)}}{{(1+q)}^{k-1}}}\hfill \\ \hfill & \ge 1-{\displaystyle \frac{q^{a+1}(1-q^a)}{(1-q)}}\sum _{k=1}^{\infty }{\displaystyle \frac{q^{k-1}}{{(1+q)}^{k-1}}}\hfill \\ \hfill & ={\displaystyle \frac{1-q-q^{a+1}(1-q^a)(1+q)}{1-q}},\hfill \end{array}$$

(33)

and the last expression is positive from the condition (24). By using the fact that

$$\left|z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)]/{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)-1\right|=\left|{\left({\mathbf{A}}_q^{\left(\alpha \right)}\right)}^{\prime }(q^a,z)-{\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)}{z}}\right|\left|{\displaystyle \frac{z}{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a,z)}}\right|,$$

for $z\in \mathcal{D}$ and owing to (32) and (33), we establish that

$$\left|{\displaystyle \frac{z{\mathbf{A}}_q^{\left(\alpha \right)}{]}^{\prime }(q^a;z)}{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)}}-1\right|<{\displaystyle \frac{q^{a-1}(1-q^a){(1+q)}^2}{1-q-q^{a-1}(1-q^a)(1+q)}},(\forall z\in \mathcal{D}).$$

Hence, by combining the above inequality and (23), we obtain the asserted inequality (25). Thus, the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)\in {\mathcal{S}}^{\ast }\left(\eta \right)$ is obtained. The proof of Theorem 3 is thus completed. □

By setting $\eta =0$ in Theorem 3, we obtain the following result.

Corollary 1.

Let $a>0,\alpha \ge a+1$, and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q)$. Also, suppose that

$$q^a(1-q^a)\le {\displaystyle \frac{1-q}{q(1+q)(1+2q)}}.$$

Then, the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is starlike on $\mathcal{D}.$

Taking $a=1$ in the above corollary, we have the following result.

Corollary 2.

Let $q\in (0,{\displaystyle \frac{1}{2}}]$; then, the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q;z)$ is starlike in $\mathcal{D}.$

Example 1.

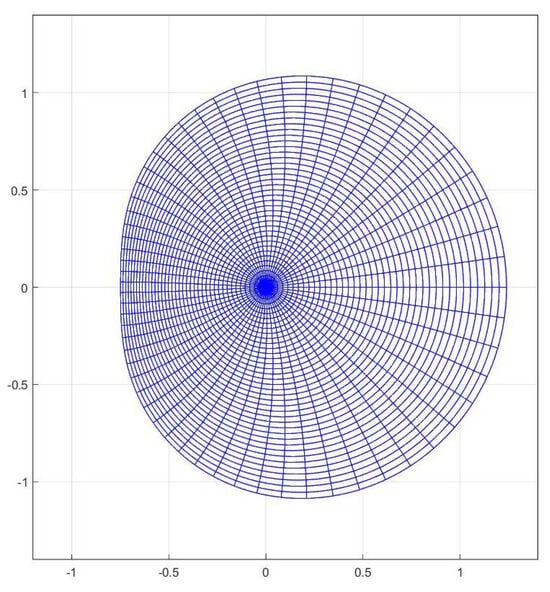
The function ${\mathbf{A}}_{{\displaystyle \frac{1}{3}}}^{\left(2\right)}({\displaystyle \frac{1}{3}};z)$ is starlike in $\mathcal{D}.$ See also Figure 1.

Figure 1. Image of the open unit disk under the function ${\mathbf{A}}_{{\displaystyle \frac{1}{2}}}^{\left(2\right)}({\displaystyle \frac{1}{2}};z)$.

Theorem 4.

Let $a>0,\alpha \ge a+1$, and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q)$, and there exists a real constant η such that

$$0\le \eta <1-{\displaystyle \frac{2q^{a+1}(1-q^a){(1+q)}^3}{1-q-q^{a+1}(1-q^a){(1+q)}^2}}.$$

(34)

If the following inequality

$$q^a(1-q^a)<{\displaystyle \frac{1-q}{q{(1+q)}^2}},$$

(35)

is valid, then the following

$${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)\in \mathcal{C}\left(\eta \right),$$

holds true for all $z\in \mathcal{D}.$

Proof. 

To show that

$$\Re \left(1+{\displaystyle \frac{z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{″}(q^a;z)}{{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)}}\right)>\eta ,(z\in \mathcal{D}),$$

it is sufficient to show that

$$\left|{\displaystyle \frac{z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{″}(q^a;z)}{{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)}}\right|<1-\eta ,(z\in \mathcal{D}),$$

(36)

From (27), (29), (31), and Lemma 4, it follows that, for $z\in \mathcal{D}$, we have

$$\begin{array}{cc}\hfill \left|z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{″}(q^a;z)\right|& <{\displaystyle \frac{q^{a+1}(1-q^a)}{1-q}}\sum _{k=1}^{\infty }{\displaystyle \frac{k(k+1)q^{k-1}}{{(1+q)}^{k-1}}}\hfill \\ \hfill & ={\displaystyle \frac{2q^{a+1}(1-q^a){(1+q)}^3}{1-q}}.\hfill \end{array}$$

(37)

Again, by using (27), (29), (31), and (4), we establish that

$$\begin{array}{cc}\hfill \left|{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)\right|& >1-\sum _{k=1}^{\infty }{\displaystyle \frac{k{(1-q)}^k{\mathrm{\Gamma }}_q(k+a)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}\hfill \\ \hfill & =1-\sum _{k=1}^{\infty }{\displaystyle \frac{k{(1-q)}^k{f}_{q,a}\left(k\right)q^{k(\alpha k-a)}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}\hfill \\ \hfill & \ge 1-{\displaystyle \frac{q^a(1-q^a)}{1-q}}\sum _{k=1}^{\infty }{\displaystyle \frac{k{(1-q)}^k{q}^k}{{(q;q)}_k}}\hfill \\ \hfill & \ge 1-{\displaystyle \frac{q^{a+1}(1-q^a)}{1-q}}\sum _{k=1}^{\infty }{\displaystyle \frac{k{q}^{k-1}}{{(1+q)}^{k-1}}}\hfill \\ \hfill & =1-{\displaystyle \frac{q^{a+1}(1-q^a){(1+q)}^2}{1-q}}>0.\hfill \end{array}$$

(38)

Having in mind (37) and (38), for $z\in \mathcal{D}$, we obtain

$$\left|{\displaystyle \frac{z{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{″}(q^a;z)}{{\left[{\mathbf{A}}_q^{\left(\alpha \right)}\right]}^{\prime }(q^a;z)}}\right|<{\displaystyle \frac{2q^{a+1}(1-q^a){(1+q)}^3}{1-q-q^{a+1}(1-q^a){(1+q)}^2}}.$$

Finally, by combining the above inequality with (34), we obtain (36). Hence, the theorem follows. □

Corollary 3.

Under the assumptions of Theorem 5, the following assertions hold:

(a).

If $\nu \in [0,{\displaystyle \frac{1}{2}})$, then ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)\in {\mathcal{H}}^{{\displaystyle \frac{1}{1-2\nu }}}.$

(b).

If $\nu \ge {\displaystyle \frac{1}{2}}$, then ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)\in {\mathcal{H}}^{\infty }.$

Proof. 

By using the definition of the Gaussian hypergeometric function that reads as follows ([27], Equations (15) and (21)):

$${}_2\mathit{F}_1\left[\begin{array}{c}a,b\\ c\end{array}|z\right]=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(a\right)}_k{\left(b\right)}_k}{{\left(c\right)}_k}}{\displaystyle \frac{z^k}{k!}},$$

where ${\left(\lambda \right)}_n$ is the Pochhammer symbol defined by

$${\left(\lambda \right)}_0=1\mathrm{and}{\left(\lambda \right)}_n=\lambda (\lambda +1)\cdots (\lambda +n-1),(n\ge 1),$$

we establish that

$$\begin{array}{cc}\hfill n_1+{\displaystyle \frac{n_{2}z}{{(1-z{e}^{i\omega })}^{1-2\nu }}}& =n_1+n_{2}z·{}_2\mathit{F}_1\left[\begin{array}{c}1,1-2\nu \\ 1\end{array}|z{e}^{i\omega }\right],\hfill \\ \hfill & =n_1+n_2\sum _{k=0}^{\infty }{\displaystyle \frac{{(1-2\nu )}_k}{k!}}{e}^{ik\omega }{z}^{k+1},\left(\nu \ne {\displaystyle \frac{1}{2}}\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill n_1+n_{2}log(1-z{e}^{i\omega })& =n_1+n_{2}z·{}_2\mathit{F}_1\left[\begin{array}{c}1,1\nu \\ 2\end{array}|z{e}^{i\omega }\right]\hfill \\ \hfill & =n_1-n_2\sum _{k=0}^{\infty }{\displaystyle \frac{e^{ik\omega }}{k+1}}{z}^{k+1},\left(\nu \ne {\displaystyle \frac{1}{2}}\right),\hfill \end{array}$$

for $n_1,n_2\in \mathbb{C}$ and for the real $\omega .$ Hence, since $\omega$ is real, the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ defined by (27) cannot be of the form $n_1+n_{2}z·{(1-z{e}^{i\omega })}^{2\nu -1}$ for $\nu \ne {\displaystyle \frac{1}{2}}$ or of the form $n_1+n_{2}log(1-z{e}^{i\omega })$ for $\nu ={\displaystyle \frac{1}{2}}.$ In addition, from Theorem 5, the function $z\mapsto {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is convex of order $\eta$ in $\mathbb{D}$ under the given conditions. Finally, by the means of Lemma 5, the desired result can be obtained straightforwardly. □

Taking $\nu =0$ in Theorem 5, we obtain the following sufficient condition for the convexity of the normalized Ramanujan entire function defined by (27).

Corollary 4.

Let $a>0,\alpha \ge a+1$, and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q).$ If the following inequality

$$q^a(1-q^a)<{\displaystyle \frac{1-q}{q{(1+q)}^2(2q+3)}},$$

(39)

is valid, then the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is convex in $\mathcal{D}.$

Corollary 5.

For $a\ge 2$ and $q\in (0,q_1)$, where $q_1\approx 0.3754\cdots$ is the root on $(0,1)$ of the equation $(x^2+x)(2x+3)-1=0$, the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q;z)$ is convex in $\mathcal{D}.$

Example 2.

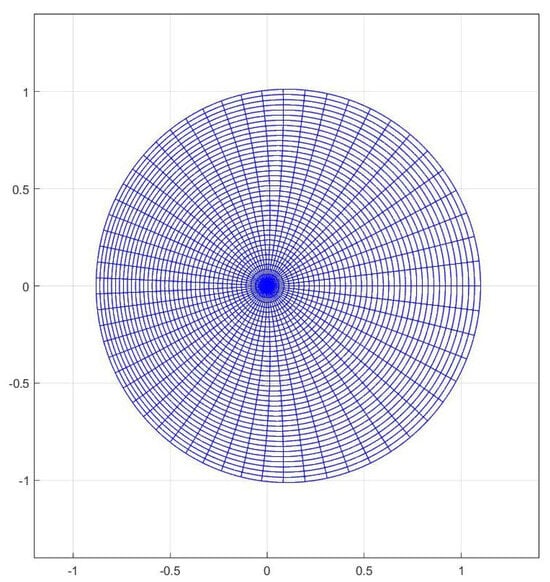
The function $z\mapsto {\mathbf{A}}_{{\displaystyle \frac{1}{3}}}^{\left(2\right)}({\displaystyle \frac{1}{3}};z)$ is convex in $\mathcal{D}.$ See also Figure 2.

Figure 2. Image of the open unit disk under the function ${\mathbf{A}}_{{\displaystyle \frac{1}{3}}}^{\left(2\right)}({\displaystyle \frac{1}{3}};z)$.

Theorem 5.

Let $a>0,\alpha \ge a+1$ and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q)$, and there exists a real constant η such that

$$0\le \eta \le 1-{\displaystyle \frac{q^{a+1}(1-q^a)(1+q)}{1-q}}.$$

(40)

Then, the following

$${\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)}{z}}\in \mathcal{P}\left(\eta \right),$$

holds for all $z\in \mathcal{D}.$

Proof. 

Let us define the function $\mathrm{\Delta }:\mathbb{D}⟶\mathbb{C}$ by

$${\mathrm{\Delta }}_q\left(z\right)={\displaystyle \frac{1}{1-\eta }}\left[{\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)}{z}}-\eta \right],$$

From (27) and (29), it follows that

$$\begin{array}{cc}\hfill \left|{\mathrm{\Delta }}_q\left(z\right)-1\right|& =\left|{\displaystyle \frac{1}{1-\eta }}\left\{1+\sum _{k=1}^{\infty }{\displaystyle \frac{{(1-q)}^k{\mathrm{\Gamma }}_q(k+a)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}{z}^k-\eta \right\}-1\right|\hfill \\ \hfill & <{\displaystyle \frac{1}{1-\eta }}\sum _{k=1}^{\infty }{\displaystyle \frac{{(1-q)}^k{\mathrm{\Gamma }}_q(k+a)q^{\alpha k^2}}{{\mathrm{\Gamma }}_q\left(a\right){(q;q)}_k}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{1-\eta }}\sum _{k=1}^{\infty }{\displaystyle \frac{{\mathrm{\Gamma }}_q(k+a)q^{\alpha k^2}}{{(1+q)}^{k-1}{\mathrm{\Gamma }}_q\left(a\right)}}\hfill \\ \hfill & ={\displaystyle \frac{1}{1-\eta }}\sum _{k=1}^{\infty }{\displaystyle \frac{f_{q,a}\left(k\right)q^{k(\alpha k-a)}}{{(1+q)}^{k-1}{\mathrm{\Gamma }}_q\left(a\right)}},\hfill \end{array}$$

(41)

where $f_{q,a}$ is defined by (9). By using Lemma 4 and (31), we obtain for all $z\in \mathcal{D}$ that

$$\begin{array}{cc}\hfill \left|{\mathrm{\Delta }}_q\left(z\right)-1\right|& <{\displaystyle \frac{q^a(1-q^a)}{(1-\eta )(1-q)}}\sum _{k=1}^{\infty }{\displaystyle \frac{q^k}{{(1+q)}^{k-1}}}\hfill \\ \hfill & ={\displaystyle \frac{q^{a+1}(1-q^a)(1+q)}{(1-\eta )(1-q)}}\hfill \\ \hfill & \le 1,\hfill \end{array}$$

(42)

under the given condition (40). This completes the proof of this theorem. □

Taking the value $\eta =1$ in Theorem 5, we obtain the following corollary.

Corollary 6.

Let $a>0,\alpha \ge a+1$, and $q\in (0,1)$ such that $alog\left(q\right)\le log(1-q).$ In addition, if the following

$$q^a(1-q^a)\le {\displaystyle \frac{1-q}{q(1+q)}},$$

holds, then

$$\Re \left({\displaystyle \frac{{\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)}{z}}\right)>0,(\forall z\in \mathcal{D}).$$

5. An Application: A Monotonicity Property of the Ramanujan-Type Entire Function

The goal of the present section is to present the monotonicity property of the normalized Ramanujan-type entire function using the method of subordination factor sequences.

Proposition 1.

For $\beta >\alpha >0$ and $0<q<1$ such that $10(\alpha -\beta )log\left(q\right)>3+\sqrt{129}$, the following holds:

$$\Re \left(1+\sum _{k=1}^{\infty }{q}^{(\beta -\alpha )k^2}{z}^k\right)>{\displaystyle \frac{1}{2}},(\forall z\in \mathcal{D}).$$

(43)

Proof. 

We use Lemma 6 to prove inequality (43). Let $\beta >\alpha >0.$ For convenience, let us write

$$v_k=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}k=0\hfill \\ q^{(\beta -\alpha )k^2},\hfill & \mathrm{if}k\ge 1\hfill \end{array}\right.$$

(44)

It is easily seen that the sequence ${\left\{v_k\right\}}_{k\ge 0}$ is decreasing under the given conditions. Moreover, we have

$$\begin{array}{cc}\hfill q^{4\alpha }(v_0-2v_1+v_2)& =q^{4\alpha }-2q^{\beta +3\alpha }+q^{4\beta }\hfill \\ \hfill & =q^{4\beta }\left(1+{\left({\displaystyle \frac{1}{q}}\right)}^{4(\beta -\alpha )}-2{\left({\displaystyle \frac{1}{q}}\right)}^{3(\beta -\alpha )}\right)\hfill \\ \hfill & =q^{4\beta }\sum _{j=1}^{\infty }{\displaystyle \frac{(4^j-2·3^j){\left[(\beta -\alpha )log(1/q)\right]}^j}{j!}}\hfill \\ \hfill & =q^{4\beta }(\sum _{j=1}^3{\displaystyle \frac{(4^j-2·3^j){\left[(\beta -\alpha )log(1/q)\right]}^j}{j!}}\hfill \\ & +\sum _{j=4}^{\infty }{\displaystyle \frac{(4^j-2·3^j){\left[(\beta -\alpha )log(1/q)\right]}^j}{j!}})\hfill \\ \hfill & \ge q^{4\beta }\sum _{j=1}^3{\displaystyle \frac{(4^j-2·3^j){\left[(\beta -\alpha )log(1/q)\right]}^j}{j!}}\hfill \\ & =:q^{4\beta }(\beta -\alpha )log(1/q)·\mathrm{P}\left((\beta -\alpha )log(1/q)\right),\hfill \end{array}$$

(45)

and the last expression is non-negative, since $\mathrm{P}\left(x\right):={\displaystyle \frac{5}{3}}{x}^2-x-2\ge 0$ for all $x\ge {\displaystyle \frac{3+\sqrt{129}}{10}}.$ Now, we consider the function $g_q:[1,\infty )⟶\mathbb{R}$ defined by

$$g_q\left(x\right)=q^{(\beta -\alpha )x^2},\left(x>0;q\in (0,1)\right).$$

A straightforward calculation would yield

$${\displaystyle \frac{g_q^{″}\left(x\right)}{g_q\left(x\right)}}=2(\beta -\alpha )log\left(q\right)h_q\left(x\right),$$

(46)

where $h_q\left(x\right)=1+2(\beta -\alpha )log\left(q\right)x^2.$ We note that the function $x\mapsto h_q\left(x\right)$ is decreasing on $[1,\infty )$ for all $q\in (0,1)$ and $\beta >\alpha >0.$ Moreover, we have

$$\begin{array}{cc}\hfill h_q\left(1\right)& =1+2(\beta -\alpha )log\left(q\right)\hfill \\ \hfill & \le 1-{\displaystyle \frac{3+\sqrt{129}}{5}}<0,\hfill \end{array}$$

which in turn implies that $h_q\left(x\right)<0$ for all $x\ge 1.$ From this observation and (46), we deduce that the function $x\mapsto g_q\left(x\right)$ is convex on $[1,\infty ).$ Then, for all $x_1,x_2\ge 1$ and $\kappa \in [0,1]$, we get

$$g_q(\kappa x_1+(1-\kappa )x_2)\le \kappa g_q\left(x_1\right)+(1-\kappa )g_q\left(x_2\right).$$

Choosing $x_1=k,x_2=k+2(k\ge 1)$ and $\lambda ={\displaystyle \frac{1}{2}},$ the above inequality reduces to the following

$$2g_q(k+1)\le g_q\left(k\right)+g_q(k+2),$$

Observe that the above inequality is equivalent to $v_k-2v_{k+1}+v_{k+2}\ge 0$ for all $k\ge 1.$ By this observation and (45), we deduce that ${\left\{v_k\right\}}_{k\ge 0}$ is a convex sequence. In conclusion, ${\left\{v_k\right\}}_{k\ge 0}$ is a non-negative convex decreasing sequence. Finally, Lemma 6 helps us establish the desired result. □

Theorem 6.

Let $a>0,q\in (0,1)$ such that $alog\left(q\right)\le log(1-q)$ and (39) holds. If $\beta >\alpha \ge a+1$ such that $10(\alpha -\beta )log\left(q\right)>3+\sqrt{129}$, then the following inclusion holds:

$${\mathbf{A}}_q^{\left(\beta \right)}(q^a;\mathcal{D})\subset {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;\mathcal{D}),$$

(47)

where ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is defined by (5).

Proof. 

Owing to Lemma 7 and Proposition 1, we conclude that the sequence ${\left\{q^{(\beta -\alpha )k^2}\right\}}_{k\ge 1}$ is a subordination factor. Hence, we conclude that the following subordination

$${\mathbf{A}}_q^{\left(\beta \right)}(q^a;z)={\mathbf{C}}_q(\alpha ,\beta ;z)\ast {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)\prec {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z),$$

holds true for all $z\in \mathbb{D}$, where

$${\mathbf{C}}_q(\alpha ,\beta ;z)=\sum _{k=0}^{\infty }{q}^{(\beta -\alpha )k^2}{z}^{k+1}.$$

However, by means of Corollary 4, the function $z\mapsto {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is convex in $\mathcal{D}$. In addition, we have ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;0)={\mathbf{A}}_q^{\left(\beta \right)}(q^a;0).$ Then, the subordination ${\mathbf{A}}_q^{\left(\beta \right)}(q^a;z)\prec {\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)$ is equivalent to the inclusion (47). □

Remark 1.

For recent papers on monotonicity properties regarding some analytic functions, such as Bessel, generalized Bessel, q-Bessel, Struve, and Lommel functions, we refer the interested reader to ing [28,29,30,31].

6. Conclusions

In our present paper, we presented several geometric properties of the Ramanujan-type entire function, such as starlikeness, convexity, and close-to-convexity, inside the unit disk $\mathcal{D}.$ In addition, a specific range of parameters is derived so that this function is included in Hardy spaces and bounded analytic functions. We also determined and derived some conditions for which the function ${\mathbf{A}}_q^{\left(\alpha \right)}(q^a;z)/z$ belongs to the class $\mathcal{P}\left(\eta \right).$ As an application, we established the monotonicity property of the normalized form of the Ramanujan-type entire function.