Chirped Soliton Perturbation and Benjamin–Feir Instability of Chen–Lee–Liu Equation with Full Nonlinearity
Abstract
1. Introduction
2. Description of Method
3. Governing Model and Mathematical Analysis
4. Chirped Soliton Solutions
4.1. Ansatz with Hyperbolic Tangent Function
4.2. Ansatz with Hyperbolic Secant Function
4.3. Auxiliary Equation Method
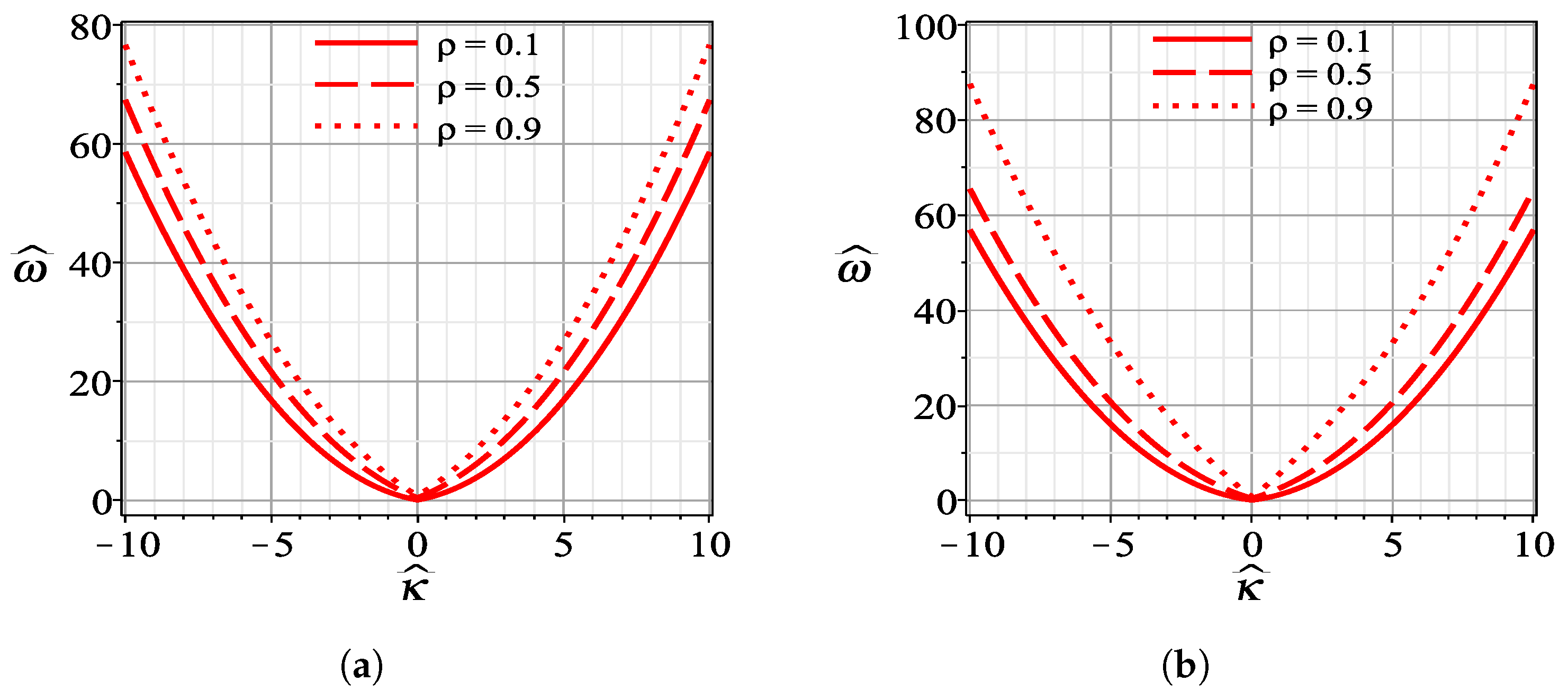
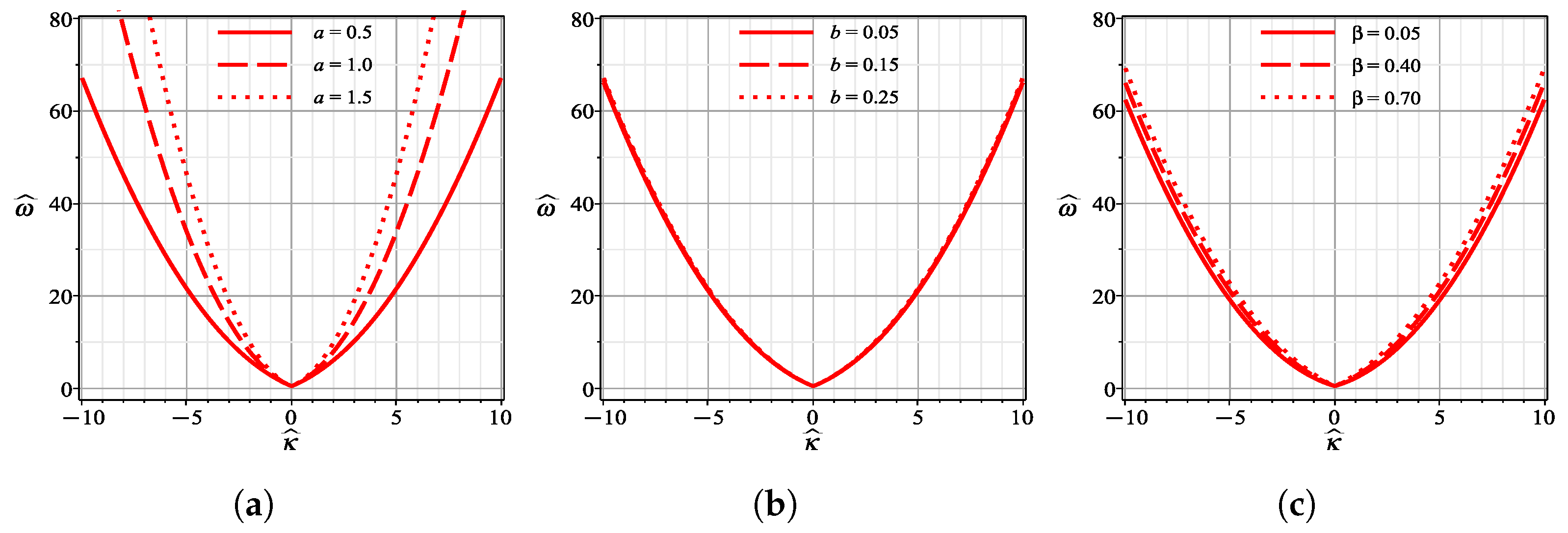
5. Modulation Instability Analysis
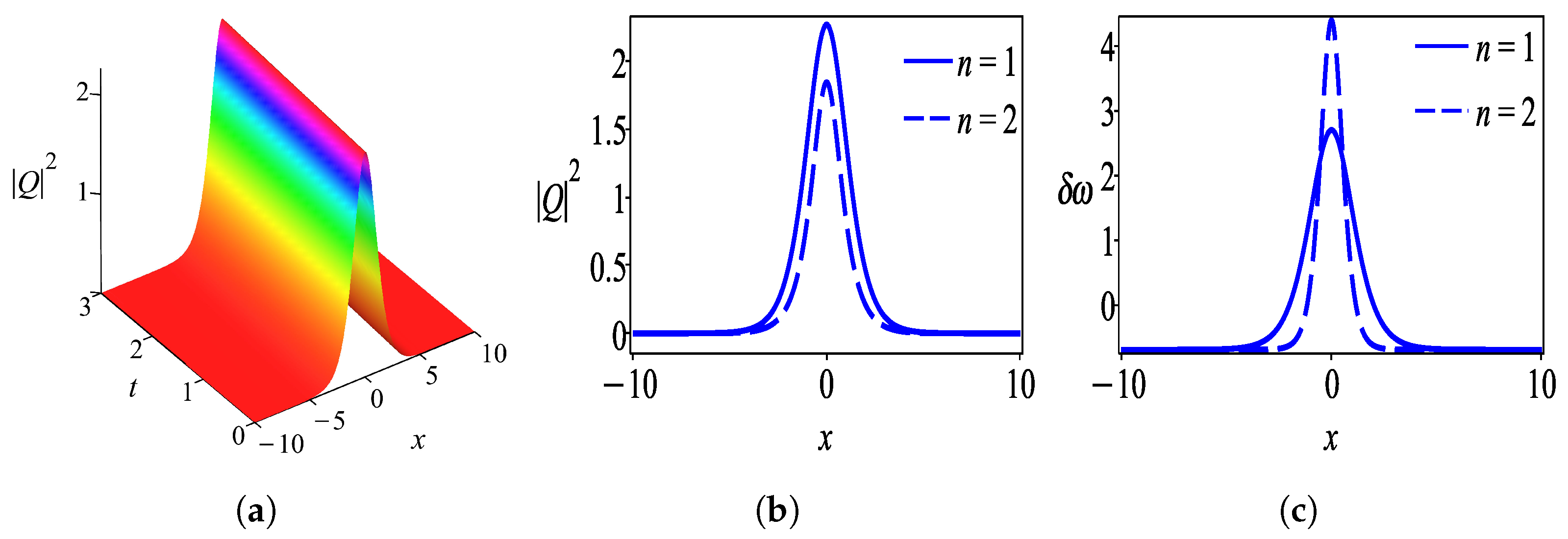
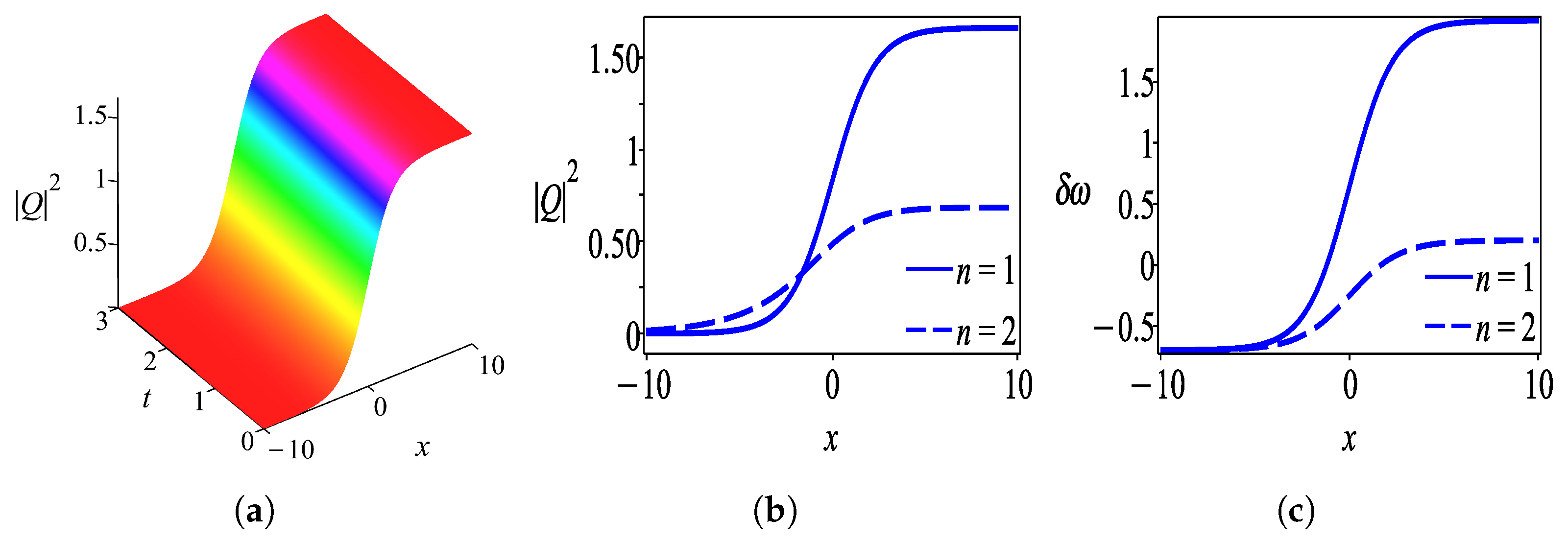
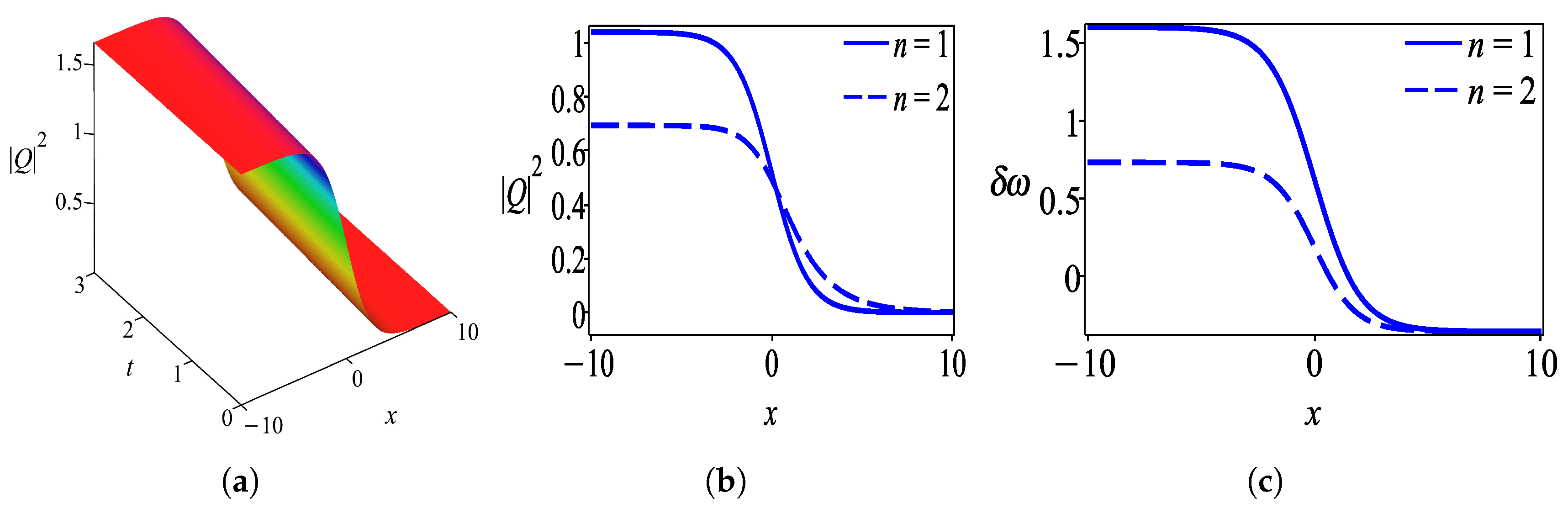
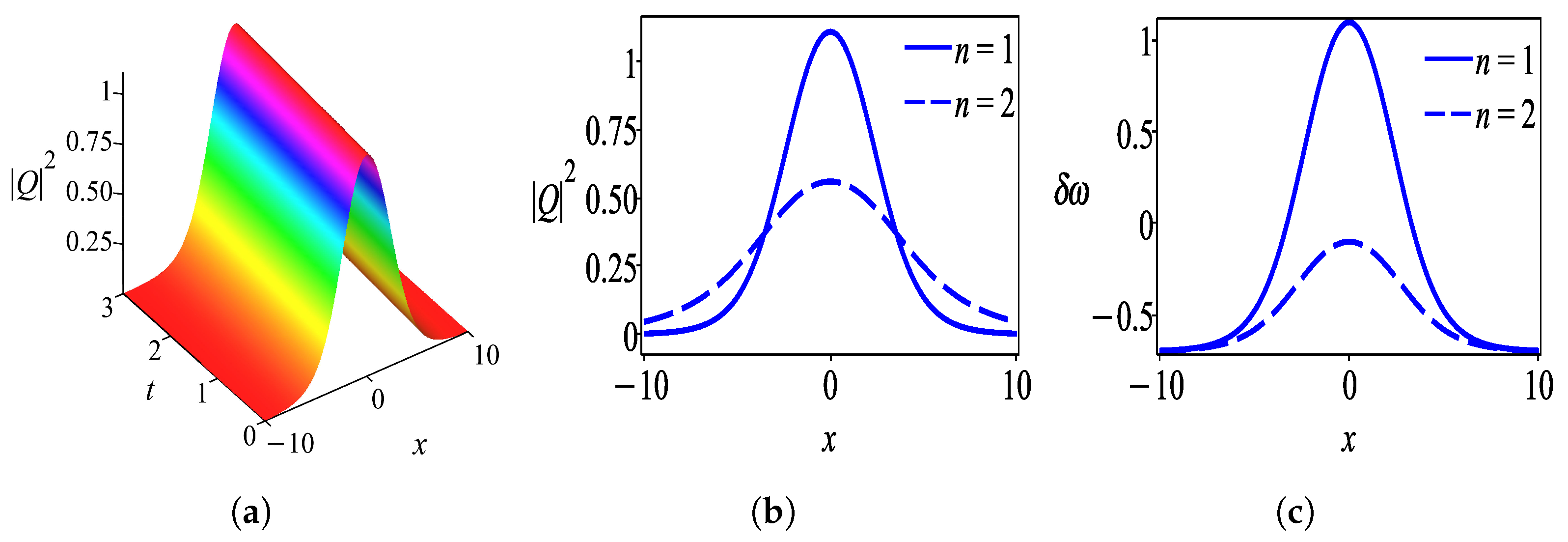
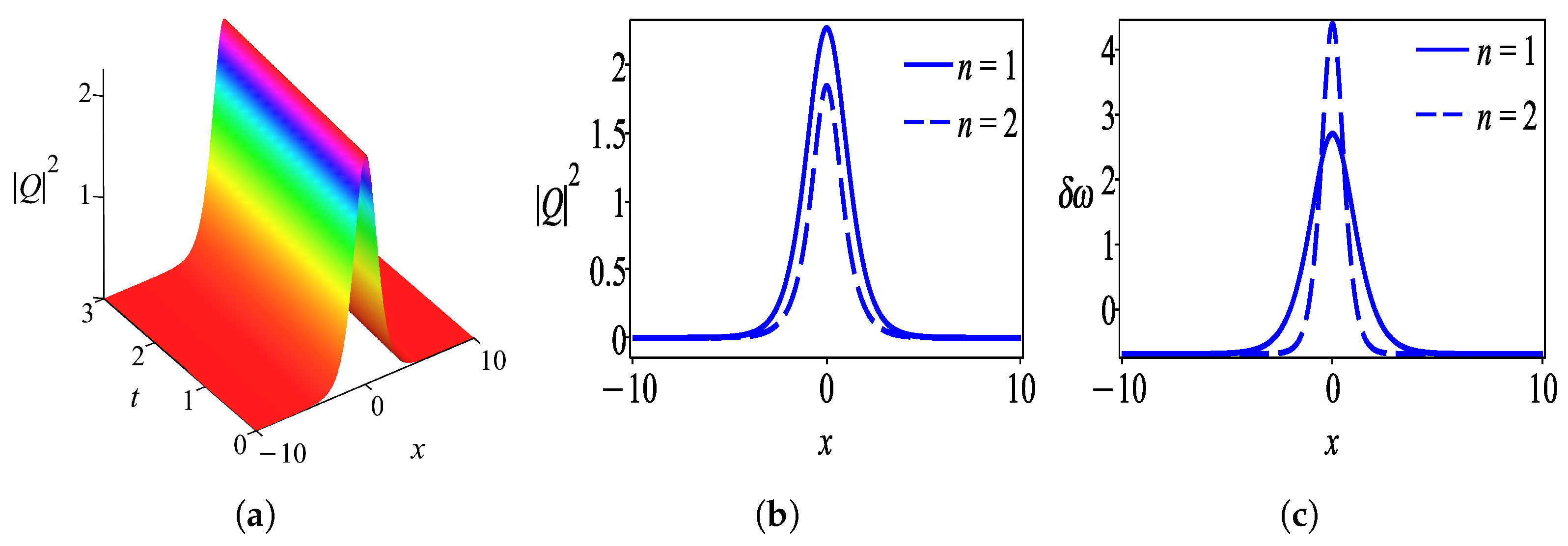
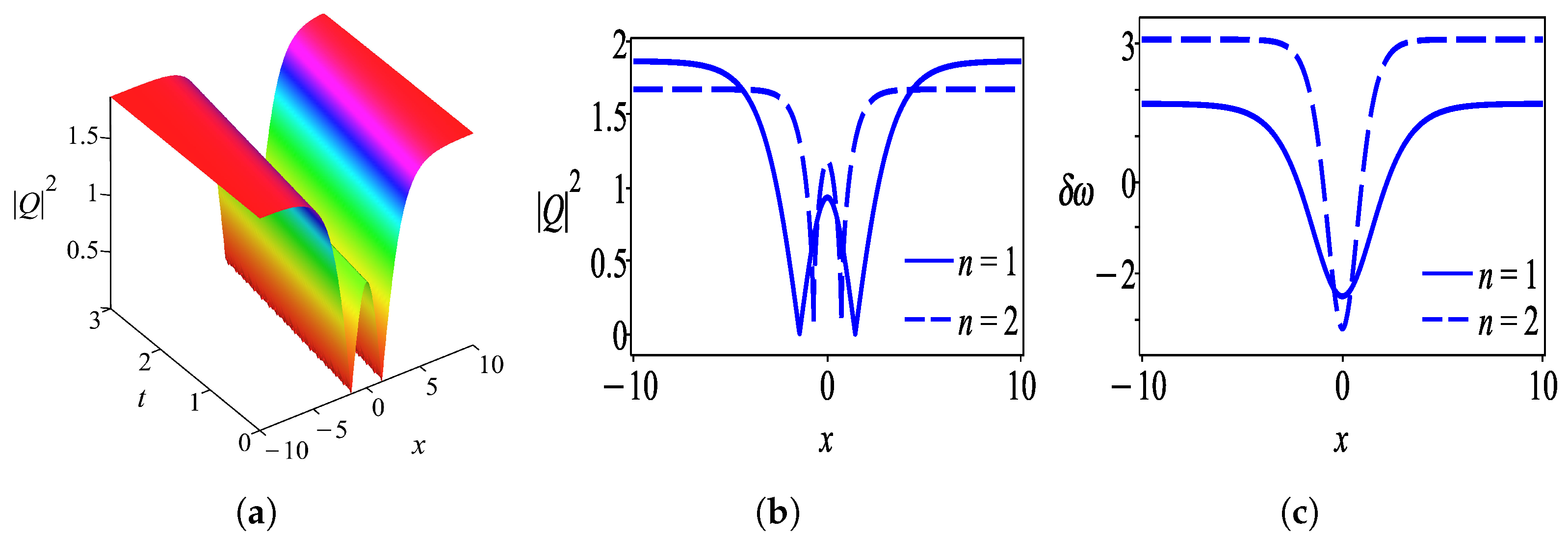
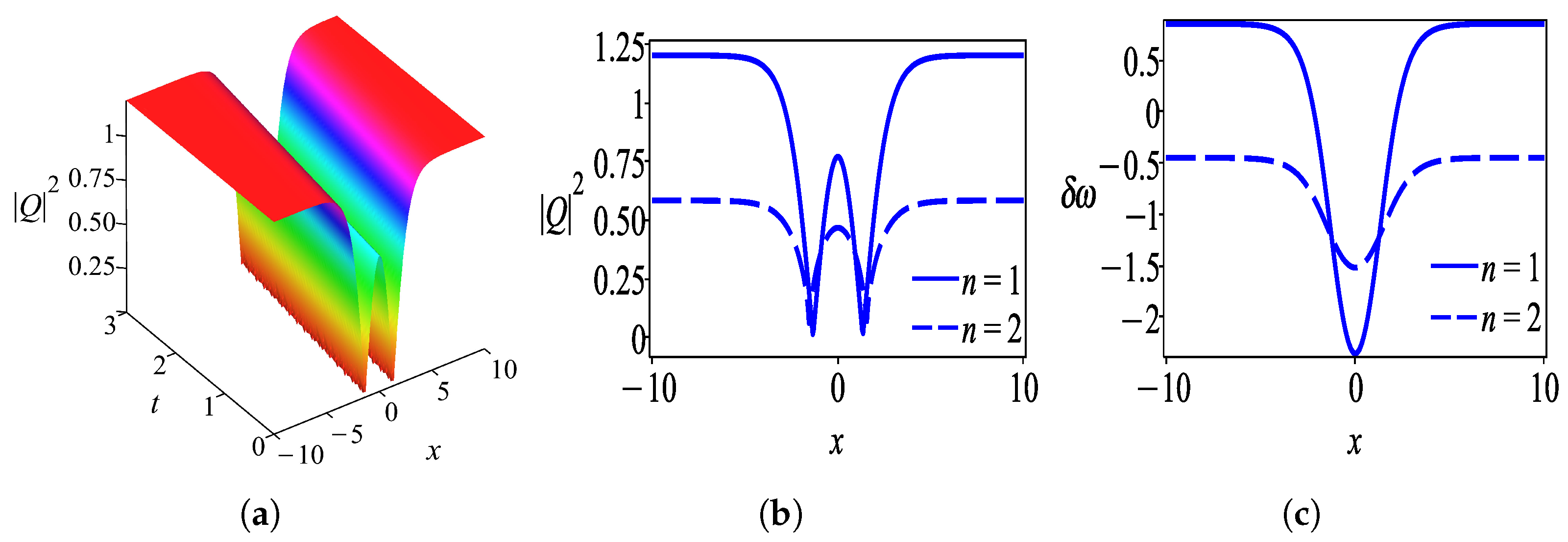
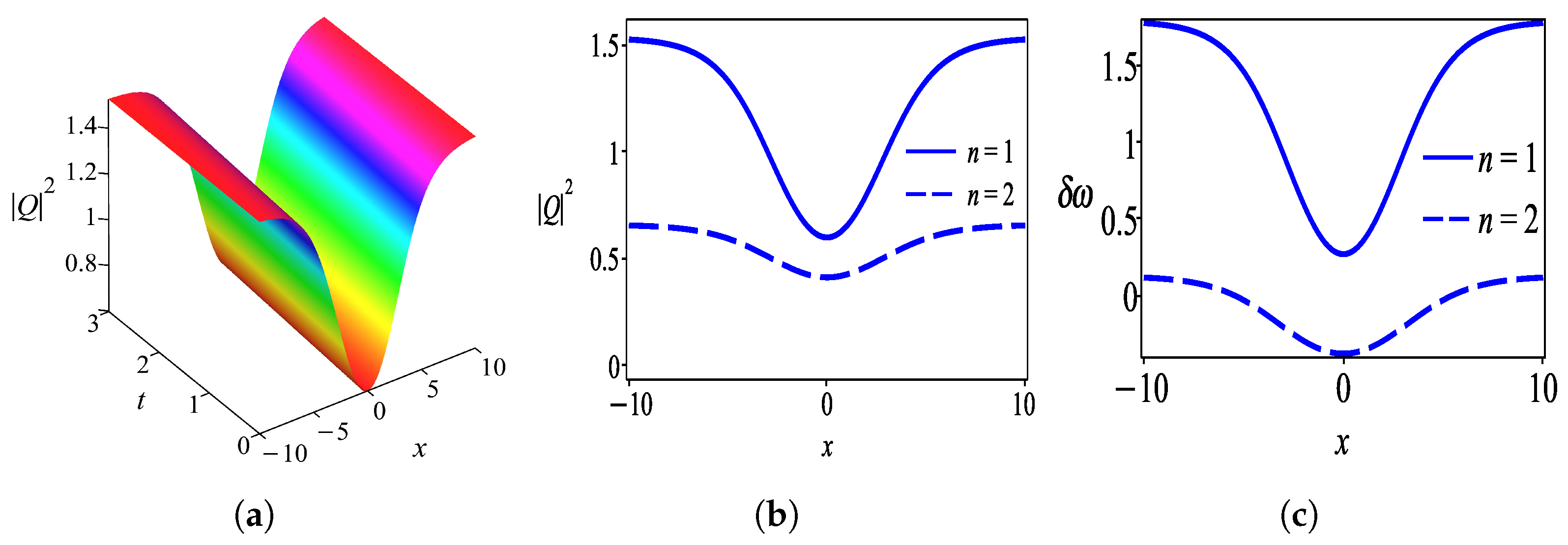
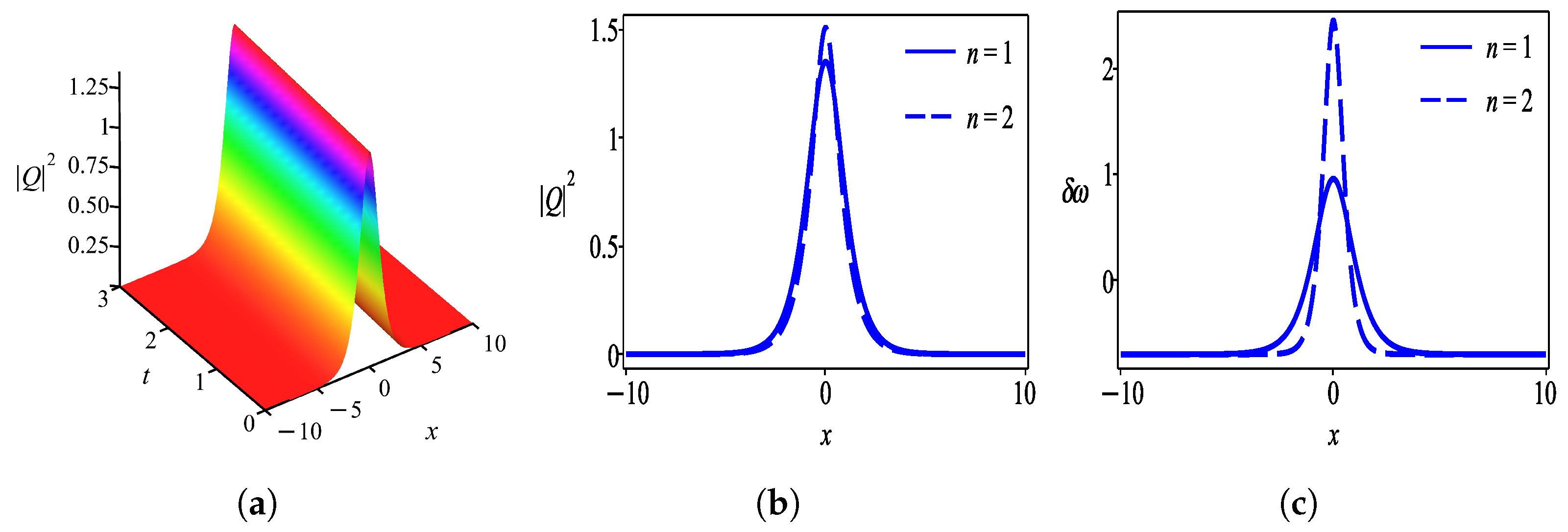
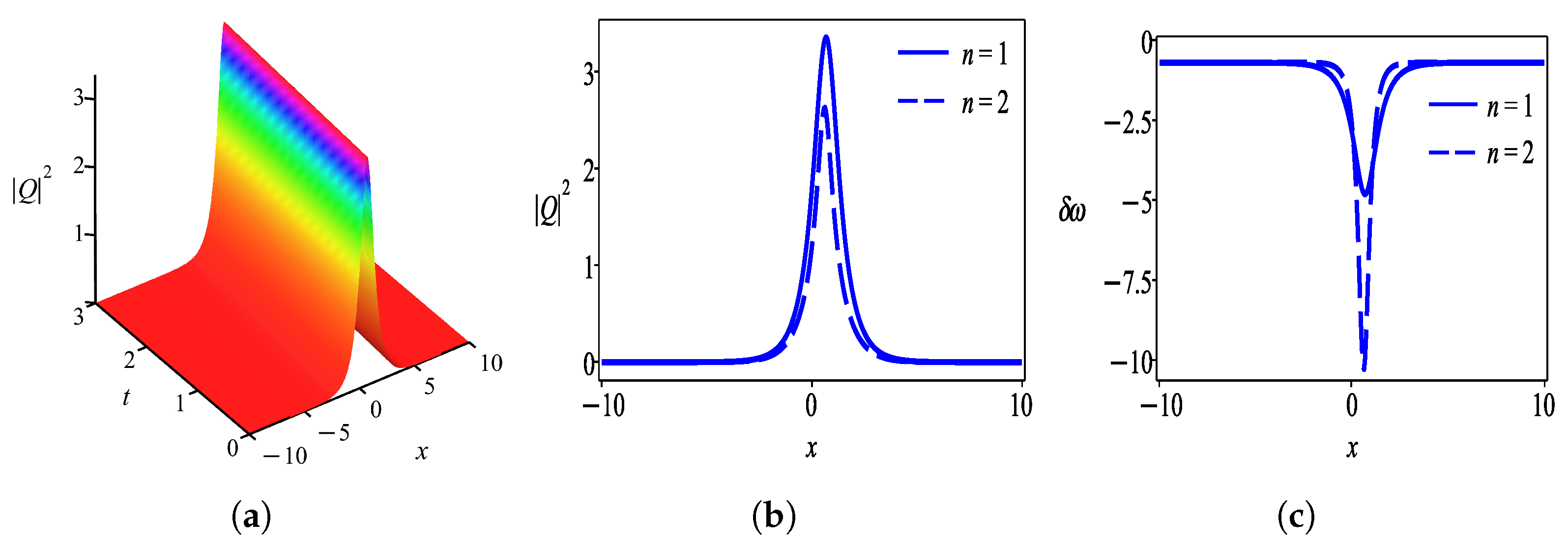
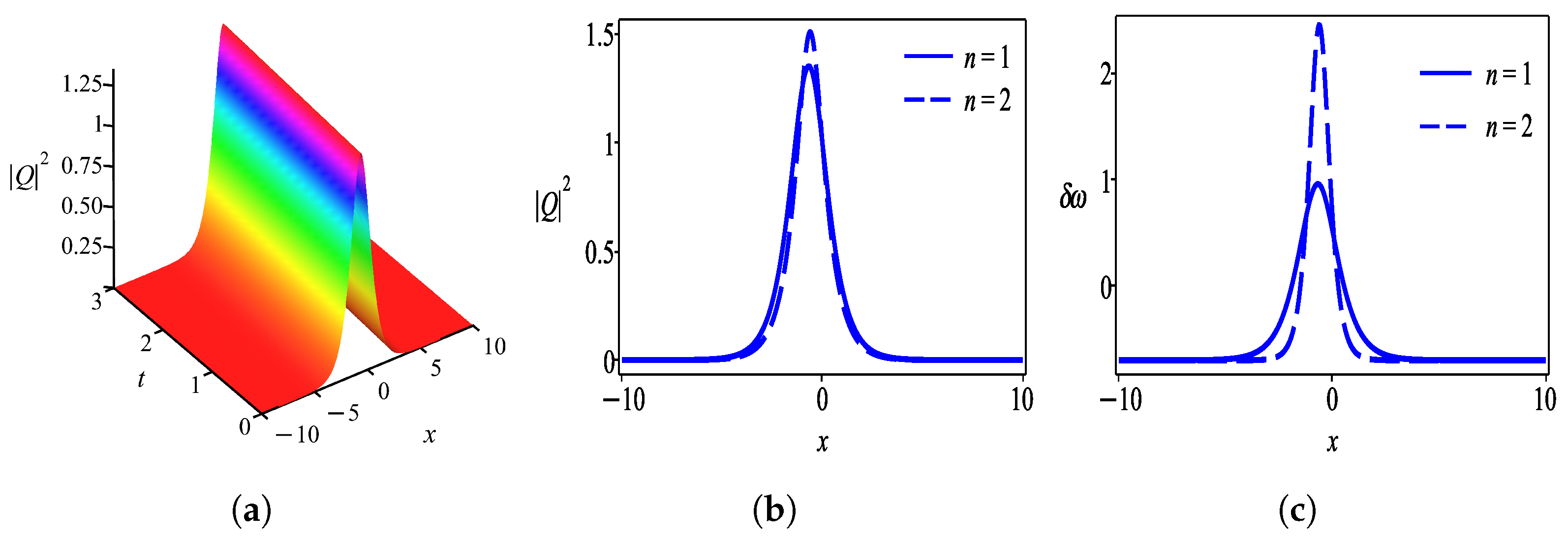
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Malomed, B.A. Two-dimensional solitons in nonlocal media: A brief review. Symmetry 2022, 14, 1565. [Google Scholar] [CrossRef]
- Zhao, H.; Malomed, B.A.; Smalyukh, I.I. Topological solitonic macromolecules. Nat. Commun. 2023, 14, 4581. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, A.; Kodama, Y. Solitons in Optical Communications; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Agrawal, G.P. Nonlinear fiber optics. In Nonlinear Science at the Dawn of the 21st Century; Springer: Berlin, Germany, 2000; pp. 195–211. [Google Scholar]
- Kivshar, Y.S.; Luther-Davies, B. Dark optical solitons: Physics and applications. Phys. Rep. 1998, 298, 81–197. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Kundu, A.; Lakshmanan, M. Coupled nonlinear Schrödinger equations with cubic-quintic nonlinearity: Integrability and soliton interaction in non-Kerr media. Phys. Rev. E 1999, 60, 3314. [Google Scholar] [CrossRef]
- Hong, W.P. Optical solitary wave solutions for the higher order nonlinear Schrödinger equation with cubic-quintic non-Kerr terms. Opt. Commun. 2001, 194, 217–223. [Google Scholar] [CrossRef]
- Al-Ghafri, K.; Krishnan, E.; Biswas, A. Optical solitons for the cubic–quintic nonlinear Schrödinger equation. AIP Conf. Proc. 2018, 2046, 020002. [Google Scholar]
- Kudryashov, N.A.; Safonova, D.V.; Biswas, A. Painlevé analysis and a solution to the traveling wave reduction of the Radhakrishnan—Kundu—Lakshmanan equation. Regul. Chaotic Dyn. 2019, 24, 607–614. [Google Scholar] [CrossRef]
- Kudryashov, N.A. The Radhakrishnan–Kundu–Lakshmanan equation with arbitrary refractive index and its exact solutions. Optik 2021, 238, 166738. [Google Scholar] [CrossRef]
- Alshehri, A.M.; Alshehri, H.M.; Alshreef, A.N.; Kara, A.H.; Biswas, A.; Yıldırım, Y. Conservation laws for dispersive optical solitons with Radhakrishnan–Kundu–Lakshmanan model having quadrupled power-law of self-phase modulation. Optik 2022, 267, 169715. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. On the analytical optical soliton solutions of perturbed Radhakrishnan–Kundu–Lakshmanan model with Kerr law nonlinearity. Opt. Quantum Electron. 2022, 54, 371. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J. Optical solitons to the Radhakrishnan–Kundu–Lakshmanan equation by two effective approaches. Eur. Phys. J. Plus 2022, 137, 1–10. [Google Scholar] [CrossRef]
- Malomed, B.A. New findings for the old problem: Exact solutions for domain walls in coupled real Ginzburg-Landau equations. Phys. Lett. A 2022, 422, 127802. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S. Soliton behaviours for the conformable space–time fractional complex Ginzburg–Landau equation in optical fibers. Symmetry 2020, 12, 219. [Google Scholar] [CrossRef]
- Aslan, E.C.; Tchier, F.; Inc, M. On optical solitons of the Schrödinger-Hirota equation with power law nonlinearity in optical fibers. Superlattices Microstruct. 2017, 105, 48–55. [Google Scholar] [CrossRef]
- Biswas, A.; Hubert, M.B.; Justin, M.; Betchewe, G.; Doka, S.Y.; Crepin, K.T.; Ekici, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Chirped dispersive bright and singular optical solitons with Schrödinger–Hirota equation. Optik 2018, 168, 192–195. [Google Scholar] [CrossRef]
- Tang, L. Dynamical behavior and traveling wave solutions in optical fibers with Schrödinger–Hirota equation. Optik 2021, 245, 167750. [Google Scholar] [CrossRef]
- Kumar, S.; Hamid, I.; Abdou, M. Dynamic frameworks of optical soliton solutions and soliton-like formations to Schrödinger–Hirota equation with parabolic law non-linearity using a highly efficient approach. Opt. Quantum Electron. 2023, 55, 1261. [Google Scholar] [CrossRef]
- Ivanov, S.K. Riemann problem for the light pulses in optical fibers for the generalized Chen-Lee-Liu equation. Phys. Rev. A 2020, 101, 053827. [Google Scholar] [CrossRef]
- Bilal, M.; Hu, W.; Ren, J. Different wave structures to the Chen–Lee–Liu equation of monomode fibers and its modulation instability analysis. Eur. Phys. J. Plus 2021, 136, 385. [Google Scholar] [CrossRef]
- Mohamed, M.S.; Akinyemi, L.; Najati, S.; Elagan, S. Abundant solitary wave solutions of the Chen–Lee–Liu equation via a novel analytical technique. Opt. Quantum Electron. 2022, 54, 141. [Google Scholar] [CrossRef]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. Optical soliton solutions to Chen Lee Liu model by the modified extended tanh expansion scheme. Optik 2021, 245, 167643. [Google Scholar] [CrossRef]
- El-Shiekh, R.M.; Gaballah, M. Novel optical waves for the perturbed nonlinear Chen-Lee-Liu equation with variable coefficients using two different similarity techniques. Alex. Eng. J. 2024, 86, 548–555. [Google Scholar] [CrossRef]
- Chen, H.; Lee, Y.; Liu, C. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Phys. Scr. 1979, 20, 490. [Google Scholar] [CrossRef]
- Triki, H.; Babatin, M.; Biswas, A. Chirped bright solitons for Chen–Lee–Liu equation in optical fibers and PCF. Optik 2017, 149, 300–303. [Google Scholar] [CrossRef]
- Triki, H.; Zhou, Q.; Moshokoa, S.P.; Ullah, M.Z.; Biswas, A.; Belic, M. Chirped w-shaped optical solitons of Chen–Lee–Liu equation. Optik 2018, 155, 208–212. [Google Scholar] [CrossRef]
- Triki, H.; Hamaizi, Y.; Zhou, Q.; Biswas, A.; Ullah, M.Z.; Moshokoa, S.P.; Belic, M. Chirped singular solitons for Chen-Lee-Liu equation in optical fibers and PCF. Optik 2018, 157, 156–160. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Biswas, A.; Zhou, Q.; Alfiras, M.; Moshokoa, S.P.; Belic, M. Chirped singular and combo optical solitons for Chen–Lee–Liu equation with three forms of integration architecture. Optik 2019, 178, 172–177. [Google Scholar] [CrossRef]
- Mohammed, A.; Bakodah, H.; Banaja, M.; Alshaery, A.; Zhou, Q.; Biswas, A.; Moshokoa, S.P.; Belic, M.R. Bright optical solitons of Chen-Lee-Liu equation with improved Adomian decomposition method. Optik 2019, 181, 964–970. [Google Scholar] [CrossRef]
- Bansal, A.; Biswas, A.; Zhou, Q.; Arshed, S.; Alzahrani, A.K.; Belic, M.R. Optical solitons with Chen–Lee–Liu equation by Lie symmetry. Phys. Lett. A 2020, 384, 126202. [Google Scholar] [CrossRef]
- Chow, K.; Ng, T.W. Periodic solutions of a derivative nonlinear Schrödinger equation: Elliptic integrals of the third kind. J. Comput. Appl. Math. 2011, 235, 3825–3830. [Google Scholar] [CrossRef]
- Chow, K.W.; Yip, L.P.; Grimshaw, R. Novel solitary pulses for a variable-coefficient derivative nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 2007, 76, 074004. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A. W-shaped optical solitons of Chen–Lee–Liu equation by Laplace–Adomian decomposition method. Opt. Quantum Electron. 2018, 50, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Chabchoub, A.; He, J. Higher-order rogue wave dynamics for a derivative nonlinear Schrödinger equation. Rom. J. Phys. 2017, 62, 31. [Google Scholar]
- Yang, Y.; Wang, X.; Yan, Z. Optical temporal rogue waves in the generalized inhomogeneous nonlinear Schrödinger equation with varying higher-order even and odd terms. Nonlinear Dyn. 2015, 81, 833–842. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Qiu, D.; Zhang, Y.; Porsezian, K.; He, J. Rogue wave solutions of a higher-order Chen–Lee–Liu equation. Phys. Scr. 2015, 90, 055207. [Google Scholar] [CrossRef]
- Liu, P.; Chen, Y.; Chai, X. Soliton and rogue wave excitations in the Chen–Lee–Liu derivative nonlinear Schrödinger equation with two complex P T-symmetric potentials. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 013120. [Google Scholar] [CrossRef]
- Peng, W.Q.; Pu, J.C.; Chen, Y. PINN deep learning method for the Chen–Lee–Liu equation: Rogue wave on the periodic background. Commun. Nonlinear Sci. Numer. Simul. 2022, 105, 106067. [Google Scholar] [CrossRef]
- Biswas, A. Chirp-free bright optical soliton perturbation with Chen–Lee–Liu equation by traveling wave hypothesis and semi-inverse variational principle. Optik 2018, 172, 772–776. [Google Scholar] [CrossRef]
- Kudryashov, N.A. General solution of the traveling wave reduction for the perturbed Chen-Lee-Liu equation. Optik 2019, 186, 339–349. [Google Scholar] [CrossRef]
- Houwe, A.; Abbagari, S.; Almohsen, B.; Betchewe, G.; Inc, M.; Doka, S.Y. Chirped solitary waves of the perturbed Chen–Lee–Liu equation and modulation instability in optical monomode fibres. Opt. Quantum Electron. 2021, 53, 286. [Google Scholar] [CrossRef]
- Tarla, S.; Ali, K.K.; Yilmazer, R.; Osman, M. On dynamical behavior for optical solitons sustained by the perturbed Chen–Lee–Liu model. Commun. Theor. Phys. 2022, 74, 075005. [Google Scholar] [CrossRef]
- Esen, H.; Ozdemir, N.; Secer, A.; Bayram, M. On solitary wave solutions for the perturbed Chen–Lee–Liu equation via an analytical approach. Optik 2021, 245, 167641. [Google Scholar] [CrossRef]
- Akinyemi, L.; Ullah, N.; Akbar, Y.; Hashemi, M.S.; Akbulut, A.; Rezazadeh, H. Explicit solutions to nonlinear Chen–Lee–Liu equation. Mod. Phys. Lett. B 2021, 35, 2150438. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Sankar, M.; Krishnan, E.V.; Khan, S.; Biswas, A. Chirped gap solitons in fiber Bragg gratings with polynomial law of nonlinear refractive index. J. Eur. Opt. Soc.-Rapid Publ. 2023, 19, 30. [Google Scholar] [CrossRef]
- Aydemir, T. New exact optical soliton solutions of the derivative nonlinear Schrödinger equation family. Opt. Quantum Electron. 2024, 56, 1018. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of the Chen–Lee–Liu equation with arbitrary refractive index. Optik 2021, 247, 167935. [Google Scholar] [CrossRef]
- Zhang, W. Exact chirped solutions of perturbed Chen-Lee-Liu equation with refractive index. Heliyon 2023, 9, e20409. [Google Scholar] [CrossRef]
- Li, Z. Qualitative analysis and explicit solutions of perturbed Chen–Lee–Liu equation with refractive index. Results Phys. 2024, 60, 107626. [Google Scholar] [CrossRef]
- Alphonse, H.; Jamilu, S.; Zakia, H.; Doka, S. Solitary pulses of the conformable derivative nonlinear differential equation governing wave propagation in low-pass electrical transmission line. Phys. Scr. 2020, 95, 045203. [Google Scholar]
- El-Ganaini, S.; Kumar, H. A variety of new traveling and localized solitary wave solutions of a nonlinear model describing the nonlinear low-pass electrical transmission lines. Chaos Solitons Fractals 2020, 140, 110218. [Google Scholar] [CrossRef]
- Sabi’u, J.; Tala-Tebue, E.; Rezazadeh, H.; Arshed, S.; Bekir, A. Optical solitons for the decoupled nonlinear Schrödinger equation using Jacobi elliptic approach. Commun. Theor. Phys. 2021, 73, 075003. [Google Scholar] [CrossRef]
- Nuruzzaman, M.; Kumar, D.; Paul, G.C. Fractional low-pass electrical transmission line model: Dynamic behaviors of exact solutions with the impact of fractionality and free parameters. Results Phys. 2021, 27, 104457. [Google Scholar] [CrossRef]
- Al-Ghafri, K.; Krishnan, E.; Biswas, A. W-shaped and other solitons in optical nanofibers. Results Phys. 2021, 23, 103973. [Google Scholar] [CrossRef]
- Yomba, E. The extended Fan’s sub-equation method and its application to KdV–MKdV, BKK and variant Boussinesq equations. Phys. Lett. A 2005, 336, 463–476. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ghafri, K.S.; Biswas, A. Chirped Soliton Perturbation and Benjamin–Feir Instability of Chen–Lee–Liu Equation with Full Nonlinearity. Mathematics 2025, 13, 2261. https://doi.org/10.3390/math13142261
Al-Ghafri KS, Biswas A. Chirped Soliton Perturbation and Benjamin–Feir Instability of Chen–Lee–Liu Equation with Full Nonlinearity. Mathematics. 2025; 13(14):2261. https://doi.org/10.3390/math13142261
Chicago/Turabian StyleAl-Ghafri, Khalil S., and Anjan Biswas. 2025. "Chirped Soliton Perturbation and Benjamin–Feir Instability of Chen–Lee–Liu Equation with Full Nonlinearity" Mathematics 13, no. 14: 2261. https://doi.org/10.3390/math13142261
APA StyleAl-Ghafri, K. S., & Biswas, A. (2025). Chirped Soliton Perturbation and Benjamin–Feir Instability of Chen–Lee–Liu Equation with Full Nonlinearity. Mathematics, 13(14), 2261. https://doi.org/10.3390/math13142261






