Abstract
The objective of the present study is to detect chirped optical solitons of the perturbed Chen–Lee–Liu equation with full nonlinearity. By virtue of the traveling wave hypothesis, the discussed model is reduced to a simple form known as an elliptic equation. The latter equation, which is a second-order ordinary differential equation, is handled by the undetermined coefficient method of two forms expressed in terms of the hyperbolic secant and tangent functions. Additionally, the auxiliary equation method is applied to derive several miscellaneous solutions. Various types of chirped solitons are revealed such as W-shaped, bright, dark, gray, kink and anti-kink waves. Taking into consideration the existence conditions, the dynamical behaviors of optical solitons and their corresponding chirp are illustrated. The modulation instability of the perturbed CLL equation is examined by means of the linear stability analysis. It is found that all solutions are stable against small perturbations. These entirely new results, compared to previous works, can be employed to understand pulse propagation in optical fiber mediums and dynamic characteristics of waves in plasma.
Keywords:
chirped solitons; perturbed Chen–Lee–Liu equation; undetermined coefficient method; auxiliary equation scheme; modulation instability MSC:
78A60
1. Introduction
Solitons have become an attractive type of solution for nonlinear partial differential equations because of their potential role in revealing different complex aspects of nonlinear physical phenomena. Optical fibers are one of the prominent fields in science and engineering that highly benefits from the significant physical properties of solitons [1,2]. In the field of optical fibers, solitons are known as optical solitons and have been found to have excellent capacity to propagate long distances without attenuation and changing their shapes [3,4,5]. Hence, optical pulses are considered as eminent carriers of information signals in optical telecommunication systems. Due to the high intensity of propagating pulses, the self-steepening effect takes place in the medium and causes a reduction in the group velocity of the pulses [6]. The presence of self-steepening is crucial to ensure the formations of optical pulses with ultrashort width (<100 fs) in optical fiber communication systems, and thus, higher-order effects are inevitable [7,8]. To study the dynamical features of optical solitons dominated by the self-steepening influence, one can deal with the model of nonlinear Schrödinger equation and its family of equations like the Radhakrishnan–Kundu–Lakshmanan equation [9,10,11,12,13], Ginzburg–Landau equation [14,15], Schrödinger–Hirota equation [16,17,18,19], Chen–Lee–Liu equation [20,21,22,23,24] and others. Moreover, chirped solitons are closer to a realistic situation. One encounters noisy sound along fiber optic cables during such pulse propagations, which is accounted for with chirped solitons. Such sound can be heard in computer data storage rooms where all the complicated wiring of the entire firm’s software system is stored and maintained.
As stated above, the Chen–Lee–Liu (CLL) equation is one of the important models that can be discussed to investigate soliton transmission through optical fibers and nonlinear wave propagation in plasmas. This model was created by Chen et al. in 1979 [25]. The CLL equation is one of three forms of the derivative nonlinear Schrödinger equation (DNLSE) and it is known as the DNLSE-II equation. The other two forms are the Gerdjikov–Ivanov equation and the Kaup–Newell equation, which are denoted by the DNLSE-I and DNLSE-III equations. The model of the CLL equation is given by
where is a complex-valued function representing the soliton profile. The term with parameter a stands for group velocity dispersion, while the term with b refers to the effect of the self-steepening phenomena. It is known that the standard CLL equation belongs to the family of integrable equations that can be solved by applying the inverse scattering transform. Equation (1) characterizes an optical pulse propagating in a monomode fiber. Thus, in the past, many authors [26,27,28,29,30,31,32,33,34] have attempted to derive solitonic-type solutions. Additionally, various structures of rogue wave solutions to Equation (1) have been reported by some scholars [35,36,37,38,39].
The CLL equation has been developed in distinct forms so as to be implemented in different physical media such as birefringent fibers, fiber Bragg gratings and others. The perturbed CLL equation is one of these extended forms which has a vital role in describing sub-picosecond soliton transmission through optical fibers. The dimensionless form of the perturbed CLL equation is [40]
This equation is a generalization of the standard CLL Equation (1) which can be recovered when the Hamiltonian perturbation terms are neglected, i.e., . Equation (2) has been intensively studied by a lot of scholars to detect optical soliton solutions [41,42,43,44,45]. Miscellaneous forms of soliton solutions are procured such as bright, dark and singular optical solitons. Further to this, different periodic wave structures in terms of trigonometric and Jacobi elliptic functions are obtained.
Our intention in this work is to investigate the chirped optical solitons of the perturbed CLLE with full nonlinearity, which is a generalized form to Equation (2). The details of this article are described in the following sections. Section 2 elucidates the strategy of the undetermined coefficient method, which has two functional forms [46]. In Section 3, the discussed model is analyzed and reduced to an elliptic-type equation by using the traveling wave theory. Section 4 displays the derivation of wave solutions by the auxiliary equation scheme and the undetermined coefficient method with two functional structures of the hyperbolic secant and tangent functions. In Section 5, the technique of linear stability analysis is employed to diagnose the modulation instability of the discussed model. The interpretations of obtained results are presented in Section 6. Finally, our conclusion is summarized in Section 7.
2. Description of Method
Herein, we present the process of applying the undetermined coefficient method as follows. Consider a nonlinear partial differential equation (NLPDE) in the form
where is an unknown function and P is a polynomial in u and its various partial derivatives. Based on the traveling wave transformation given by
the NLPDE (3) reduces to a nonlinear ordinary differential equation (NLODE) of the form
where prime denotes the derivative with respect to . We assume that Equation (5) has a solution in the form of a finite series as
where is expressed in two different functional structures. The first expression of has a hyperbolic tangent function, introduced as
while the second form has a hyperbolic secant function addressed as
where and are constants to be identified. The parameter m is a positive integer which can be identified by balancing the highest-order derivative term with the nonlinear term in Equation (5). The purpose of expressing the function in terms of the hyperbolic tangent function is that its derivatives are expressed in the form of the hyperbolic secant function. On the other hand, it provides us with targeted soliton solutions.
To achieve the goal of implementing this method, we substitute (6) along with (7) into Equation (5) to arrive at a polynomial in with different powers. Collecting all coefficients with the same powers of and equating them to zero leads to a set of algebraic equations for and . Finally, solving this set of equations simultaneously, various exact solutions of Equation (3) can be derived through inserting the obtained values of and into (6) together with (7). Similarly, performing the same process using (8) instead of (7), this gives us a system of algebraic equations that yields distinct values for and which are plugged into (6) alongside (8) to create several cases of solutions to Equation (3).
3. Governing Model and Mathematical Analysis
The perturbed CLLE with full nonlinearity is described by [47]
One can see that Equation (9) is a generalization of the perturbed CLL Equation (2) when . The unknown function represents the soliton profile which depends on the spatial variable x and the temporal coordinate t. In Equation (9), the first term stands for the evolution term, the second term denotes the chromatic dispersion (CD) and the third term accounts for the nonlinear dispersion (ND). The terms with the coefficients and define, respectively, the inter-modal dispersion (IM), the self-steepening (SS) phenomena and the nonlinear dispersion terms.
The model (9) is discussed by Kudryashov [48] using the traveling wave hypothesis to investigate various exact solutions. In particular, periodic and solitary waves are detected with the effect of full nonlinearity. In addition, the exact chirped solutions of Equation (9) are investigated in [49] using the trial equation method and complete discrimination system for polynomials. Different forms of solutions are obtained such as rational solutions, solitary wave solutions, triangular function solutions and doubly periodic elliptic function solutions. Further to this, the qualitative analysis and explicit solutions of Equation (9) are studied in [50]. By means of bifurcation analysis, several explicit solutions including Jacobian function solutions and hyperbolic function solutions are created.
To handle Equation (9) analytically, let us consider the traveling wave transformation
where represents the traveling coordinate of a soliton wave while and are real functions identifying the amplitude component of the soliton and the nonlinear phase shift, respectively. The parameters and are real constants denoting the wave number and the soliton velocity.
Substituting (10) into Equation (9) leads to its decomposition into real and imaginary components. The equation of the real part is given by
while the equation of the imaginary part has the form
where and the prime is the derivative with respect to . Equation (12) can be integrated, after multiplying by q, to arrive at
where the integration constant is set to zero. As is known, the general formula for a chirp is introduced as
Hence, from Equation (13), the chirping expression can be created as
Upon substituting Equation (13) into Equation (11), one can come to an equation with the form
Multiplying by and integrating with respect to , this gives rise to
where the integration constant is taken to be zero. In order to extract an analytic closed-form solution for the proposed model, the complicated structure of Equation (17) has to be reformulated in a simple form. Thus, multiplying Equation (17) by reduces it to the form
where the constants are defined as
Let us introduce the variable transformation of the form
which converts Equation (18) into
For convenience, Equation (21) is converted to a second-order differential equation by differentiating it once to induce
This type of equation is found to appear in many physical and natural applications. It has been found by many authors to reveal distinct forms of solutions via implementing several mathematical tools such as the Sinh–Gordon method [51], new modified sub-ODE method [52], Jacobi elliptic method [53], -expansion method [54], and soliton ansatz [55]. The various solutions to the elliptic Equation (22) combined with the relations (10) and (20) give rise to the general form of exact solutions for Equation (9) as
where the nonlinear phase shift represented by the function can be acquired through integrating Equation (13) as
where is a constant phase. Our aim now is to deal with Equation (22) by using the undetermined coefficient method so as to extract the soliton-type solutions for the model (9).
4. Chirped Soliton Solutions
The chirped soliton solutions of the perturbed CLLE are retrieved here by means of the auxiliary equation scheme and the undetermined coefficient method [46], which is proposed in two forms with the hyperbolic secant and tangent functions as follows.
4.1. Ansatz with Hyperbolic Tangent Function
We assume that Equation (22) has a solution expressed as
where and are constants to be identified. Making use of ansatz (25), Equation (22) generates a polynomial in with different powers. Equating all coefficients of all powers of to zero, this yields a system of algebraic equations that identifies the values of constants and . Solving this system leads to the following cases of solutions.
Case 1.
under the constraint conditions
Using the outcome (26) with (23), one can reach an exact solution in the form of a chirped dark soliton for Equation (9) as
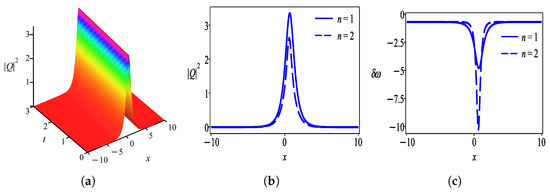
where and . (Figure 1).
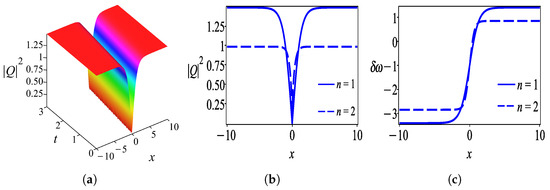
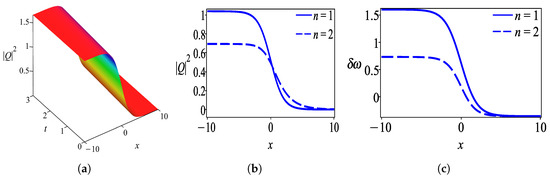
Figure 1.
Intensity profile of dark soliton given by solution (28) with parameter values . (a) 3D-plot of dark soliton, (b) 2D-plot of dark soliton, and (c) chirping profile.
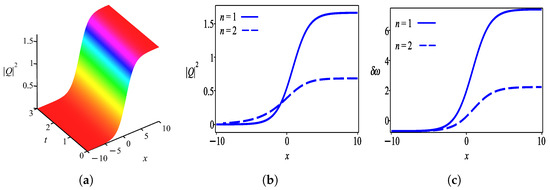
Case 2.
under the constraint conditions
Applying these findings to (23), an exact solution in the form of a chirped bright soliton for Equation (9) is obtained as
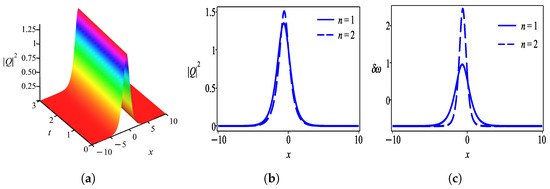
where and . (Figure 2).
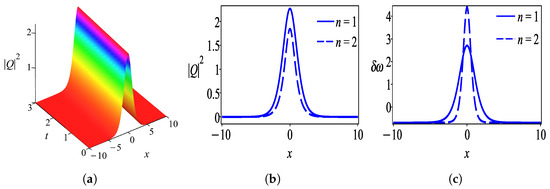
Figure 2.
Intensity profile of bright soliton given by solution (31) with parameter values . (a) 3D-plot of bright soliton, (b) 2D-plot of bright soliton, and (c) chirping profile.
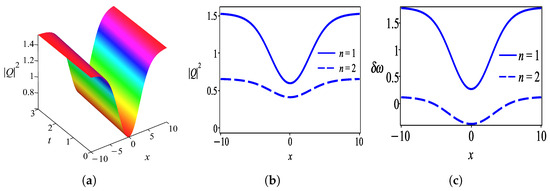
Case 3.
under the constraint conditions
Making use of (32) with (23), an exact solution in the form of a chirped soliton for Equation (9) is secured as
where and . (Figure 3).
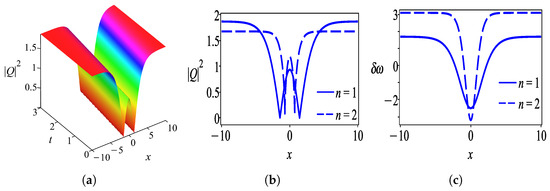
Case 4.
under the constraint conditions
Utilizing the result (35) with (23), an exact solution in the form of a chirped kink-type soliton for Equation (9) is acquired as
where and . (Figure 4).
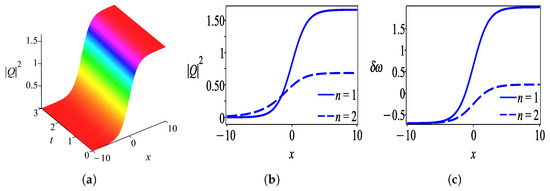
4.2. Ansatz with Hyperbolic Secant Function
We suppose that Equation (22) has an exact soliton solution presented as
where and are constants to be determined. Substituting (41) into Equation (22) yields a polynomial in of various powers. Equating each coefficient in this polynomial to zero induces a set of algebraic equations. Solving them simultaneously gives rise to the following cases of solutions.
Case 1.
under the constraint conditions
By virtue of (42) with (23), one can arrive at an exact solution in the form of a chirped bright soliton for Equation (9) as
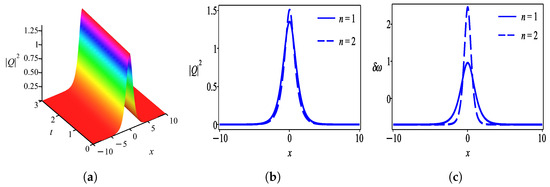
where and . (Figure 6).
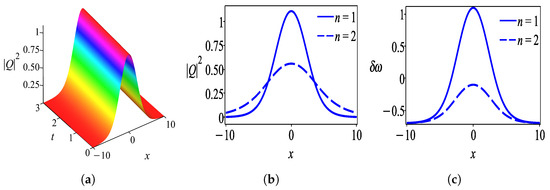
Case 2.
under the constraint conditions
Based on these findings, an exact solution in the form of a chirped bright soliton for Equation (9) is derived as
where and . (Figure 7).
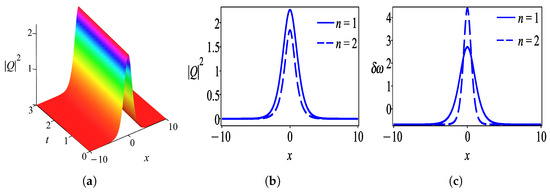
Case 3.
under the constraint conditions
As a consequence of using (48) in company with (23), an exact solution in the form of a chirped soliton structure for Equation (9) is deduced as
where and . (Figure 8).
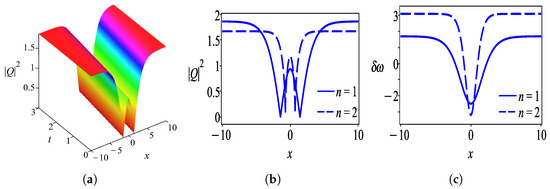
Case 4.
under the constraint conditions
Exploiting these findings along with (23) leads to retrieving an exact solution in the form of a chirped soliton wave for Equation (9) as
where and . (Figure 9).
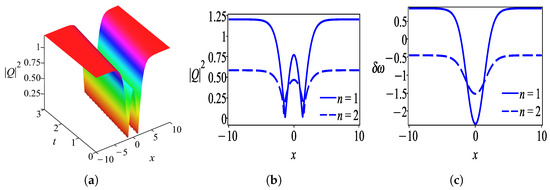
4.3. Auxiliary Equation Method
Our purpose here is to apply the auxiliary equation method to obtain the solution of Equation (21). We consider the transformation of the form
which converts Equation (21) to
where is the derivative of W with respect to , is a constant to be determined, and the constants are given by
It is found that Equation (58) admits several hyperbolic function solutions [56]. As a result, a variety of optical soliton solutions for Equation (9) are retrieved below.
Family 2. The singular optical soliton is obtained as
which similarly demands
and , .
Family 3. The bright optical soliton in another form is acquired as
which implies
and , , . (Figure 12).
Family 4. One can retrieve the soliton structure presented as
which similarly requests
and , , . (Figure 13).
Family 5. The new structure of the optical soliton is given as
which necessitates , , where
and are arbitrary constants. (Figure 14).
5. Modulation Instability Analysis
The linear stability analysis technique is utilized here to diagnose the modulation instability of the perturbed CLLE (9). To use this strategy, assume that Equation (9) has the perturbed steady-state solution given by
where is the normalized optical power while is a small perturbation and . The perturbation is examined by utilizing linear stability analysis. Substituting Equation (70) into Equation (9) and collecting the linearized terms, the following equation is obtained:
where * denotes the conjugate of the complex function . Considering that the solution of Equation (71) has the form
where and are the normalized wave number and frequency of perturbation, respectively. Substituting ansatz (72) into Equation (71), we find a couple of equations in and by splitting the coefficients of and presented as
The coupled equations (73) can be formulated in matrix form for the coefficients of and . The existence of a non-trivial solution to this matrix implies that the determinant must be zero. Hence, it brings about the dispersion relation of the form
One can reach the solution to the dispersion relation (74) for given by
This relation between the frequency and wave number reveals the situation of the steady-state stability which is dependent upon the existence of a complex solution for . Obviously, it can be noted that is always . Accordingly, this implies that is real for all values of and therefore, the steady state is stable against small perturbations. The dependence of perturbation frequency on the normalized wave number is described in Figure 15.
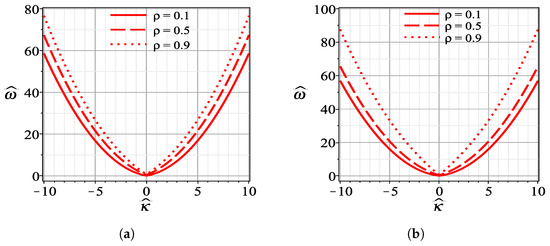
Figure 15.
The dispersion relation between frequency and wave number given in (75) with parameter values . (a) and (b) .
6. Results and Discussion
As it has been seen above, the algorithm employed to investigate the chirped optical solitons appears to be very efficient in extracting distinct forms of solutions. Each expression of the two forms of undetermined coefficient schemes generated five different solitonic solutions. The obtained solutions are illustrated graphically to shed light on their dynamic behaviors. It is found that these solutions describe miscellaneous structures of chirped solitons such as W-shaped, bright, dark, gray, singular, kink and anti-kink waves. The optical solitons are depicted in 2D and 3D plots along with their corresponding chirp by selecting suitable parameter values when and .
Firstly, we discuss the behaviors of solutions obtained by the undetermined coefficient approach in the form of a hyperbolic tangent function. Figure 1 shows the intensity profile of the dark optical soliton for solution (28) which is plotted with parameter values . Figure 2 characterizes the bright soliton wave for solution (31) with parameter values . Further to this, we observed that solution (34) has the profile of a W-shaped wave as demonstrated in Figure 3 with thesame parameter values as in Figure 2 except . One can see that Figure 4 exhibits a kink wave profile for solution (37) while Figure 5 describes an anti-kink wave profile for solution (40), where both graphs are plotted with the same parameter values as in Figure 2 except . The behaviors of solutions retrieved by the undetermined coefficient approach that is expressed in the form of the hyperbolic secant function are elucidated as follows. Figure 6 displays the intensity profile of the bright optical soliton for solution (44) with the same parameter values as in Figure 4 except . Similarly, Figure 7 presents the structure of a bright soliton wave for solution (47) with the same parameter values as in Figure 2. Moreover, the graphs in Figure 8 and Figure 9 depict the profile of a W-shaped wave for solutions (50) and (53), respectively, with the same parameter values as in Figure 3. The behavior of solution (56) represents a gray soliton structure as delineated in Figure 10 with the same parameter values as in Figure 4. One can observe that solutions (60), (64), and (66) obtained by the auxiliary equation technique represent a bright soliton wave as shown in Figure 11, Figure 12 and Figure 13. Finally, the illustration of solution (68) describes a kink wave profile as presented in Figure 14.
The influence of physical parameters such as chromatic dispersion (CD), nonlinear dispersion (ND) and self-steepening (SS) on the evolution of optical solitons is reported. In particular, the domination of these parameters has been examined on the amplitude variation of the dark soliton wave given by solution (28). It can be seen in Figure 16a that the uniform increase in CD results in an approximately regular rise in the soliton amplitude. In comparison to CD, the large values of ND and SS cause the amplitude to soar up rapidly as exhibited in Figure 16b,c.
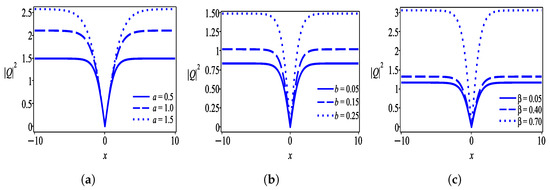
Similarly, the effects of CD, ND and SS on the dispersion relation are detected as shown in Figure 17. One can see from Figure 17a that CD causes remarkable variation in perturbation frequency, , while ND has a negligible influence on as presented in Figure 17b. The impact of SS on is more or less moderate as plotted in Figure 17c.
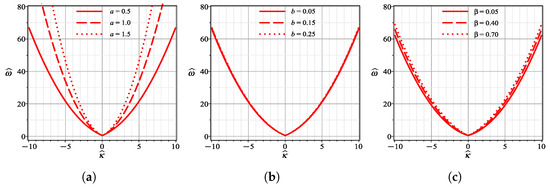
Figure 17.
Effects of CD (a), ND (b) and SS (c) on the dispersion relation (75) with parameter values .
Comparing the results shown here with those obtained in previous studies, Kudryashov [41] discussed the optical soliton solutions of the perturbed CLL equation by exploiting the Weierstrass and Jacobi elliptic functions. Several solitary waves are extracted including bright, dark and singular solutions as well as periodic wave solutions. Furthermore, Zhang [49] dealt with Equation (9) using the trial equation method and a complete discrimination system to acquire exact chirped solutions. The obtained solutions are Jacobi elliptic functions, singular periodic functions and singular solitons. Additionally, Li [50] applied bifurcation analysis to Equation (9) so as to perform qualitative analysis and study explicit solutions. The constructed explicit solutions consist of Jacobi function solutions and hyperbolic function solutions. Some soliton solutions are created such as bright and kink waves. All of the soliton wave solutions obtained in those previous studies are entirely different from the ones procured in this work.
7. Conclusions
The current work studied the chirped optical solitons of the perturbed Chen–Lee–Liu equation with full nonlinearity. Having two forms in terms of hyperbolic secant and tangent functions, the method of undetermined coefficients is exploited to generate the solutions. Each form of the implemented scheme results in five different soliton solutions. Further to this, utilizing the auxiliary equation technique provided five distinct solutions as well. The structures of the derived chirped solitons include W-shaped, bright, dark, gray, singular, kink and anti-kink waves. The validity conditions for the existence of these solitons are given. The intensity profiles of the retrieved solitons together with their associated chirping are illustrated. The repercussions of chromatic dispersion, nonlinear dispersion and self-steepening on the evolution of soliton amplitude are inspected. A high amount of them is found to dramatically enhance the amplitude of dark solitons. In addition to this, the modulation instability of the perturbed CLL model is examined with the aid of linear stability analysis. It has been noticed that chromatic dispersion and self-steepening exert a significant effect on the dispersion relation compared to the nonlinearity impact, which has a negligible effect in varying the perturbation frequency. Based on the obtained solutions, it can be concluded that the undetermined coefficient approach is a powerful technique to derive several forms of optical soliton solutions. Additionally, the extracted results can be exploited for applications related to optical fiber systems as well as plasma physics.
Author Contributions
Conceptualization, K.S.A.-G.; methodology, K.S.A.-G. and A.B.; formal analysis, K.S.A.-G. and A.B.; writing—original draft preparation, K.S.A.-G.; writing—review and editing, K.S.A.-G. and A.B.; supervision, K.S.A.-G. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
K. S. Al-Ghafri gratefully acknowledges support provided by University of Technology and Applied Sciences, Ibri, Oman, through the Internal Research Funding Program, grant number IRG-IBRI-25-47.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Malomed, B.A. Two-dimensional solitons in nonlocal media: A brief review. Symmetry 2022, 14, 1565. [Google Scholar] [CrossRef]
- Zhao, H.; Malomed, B.A.; Smalyukh, I.I. Topological solitonic macromolecules. Nat. Commun. 2023, 14, 4581. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, A.; Kodama, Y. Solitons in Optical Communications; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Agrawal, G.P. Nonlinear fiber optics. In Nonlinear Science at the Dawn of the 21st Century; Springer: Berlin, Germany, 2000; pp. 195–211. [Google Scholar]
- Kivshar, Y.S.; Luther-Davies, B. Dark optical solitons: Physics and applications. Phys. Rep. 1998, 298, 81–197. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Kundu, A.; Lakshmanan, M. Coupled nonlinear Schrödinger equations with cubic-quintic nonlinearity: Integrability and soliton interaction in non-Kerr media. Phys. Rev. E 1999, 60, 3314. [Google Scholar] [CrossRef]
- Hong, W.P. Optical solitary wave solutions for the higher order nonlinear Schrödinger equation with cubic-quintic non-Kerr terms. Opt. Commun. 2001, 194, 217–223. [Google Scholar] [CrossRef]
- Al-Ghafri, K.; Krishnan, E.; Biswas, A. Optical solitons for the cubic–quintic nonlinear Schrödinger equation. AIP Conf. Proc. 2018, 2046, 020002. [Google Scholar]
- Kudryashov, N.A.; Safonova, D.V.; Biswas, A. Painlevé analysis and a solution to the traveling wave reduction of the Radhakrishnan—Kundu—Lakshmanan equation. Regul. Chaotic Dyn. 2019, 24, 607–614. [Google Scholar] [CrossRef]
- Kudryashov, N.A. The Radhakrishnan–Kundu–Lakshmanan equation with arbitrary refractive index and its exact solutions. Optik 2021, 238, 166738. [Google Scholar] [CrossRef]
- Alshehri, A.M.; Alshehri, H.M.; Alshreef, A.N.; Kara, A.H.; Biswas, A.; Yıldırım, Y. Conservation laws for dispersive optical solitons with Radhakrishnan–Kundu–Lakshmanan model having quadrupled power-law of self-phase modulation. Optik 2022, 267, 169715. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. On the analytical optical soliton solutions of perturbed Radhakrishnan–Kundu–Lakshmanan model with Kerr law nonlinearity. Opt. Quantum Electron. 2022, 54, 371. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J. Optical solitons to the Radhakrishnan–Kundu–Lakshmanan equation by two effective approaches. Eur. Phys. J. Plus 2022, 137, 1–10. [Google Scholar] [CrossRef]
- Malomed, B.A. New findings for the old problem: Exact solutions for domain walls in coupled real Ginzburg-Landau equations. Phys. Lett. A 2022, 422, 127802. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S. Soliton behaviours for the conformable space–time fractional complex Ginzburg–Landau equation in optical fibers. Symmetry 2020, 12, 219. [Google Scholar] [CrossRef]
- Aslan, E.C.; Tchier, F.; Inc, M. On optical solitons of the Schrödinger-Hirota equation with power law nonlinearity in optical fibers. Superlattices Microstruct. 2017, 105, 48–55. [Google Scholar] [CrossRef]
- Biswas, A.; Hubert, M.B.; Justin, M.; Betchewe, G.; Doka, S.Y.; Crepin, K.T.; Ekici, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Chirped dispersive bright and singular optical solitons with Schrödinger–Hirota equation. Optik 2018, 168, 192–195. [Google Scholar] [CrossRef]
- Tang, L. Dynamical behavior and traveling wave solutions in optical fibers with Schrödinger–Hirota equation. Optik 2021, 245, 167750. [Google Scholar] [CrossRef]
- Kumar, S.; Hamid, I.; Abdou, M. Dynamic frameworks of optical soliton solutions and soliton-like formations to Schrödinger–Hirota equation with parabolic law non-linearity using a highly efficient approach. Opt. Quantum Electron. 2023, 55, 1261. [Google Scholar] [CrossRef]
- Ivanov, S.K. Riemann problem for the light pulses in optical fibers for the generalized Chen-Lee-Liu equation. Phys. Rev. A 2020, 101, 053827. [Google Scholar] [CrossRef]
- Bilal, M.; Hu, W.; Ren, J. Different wave structures to the Chen–Lee–Liu equation of monomode fibers and its modulation instability analysis. Eur. Phys. J. Plus 2021, 136, 385. [Google Scholar] [CrossRef]
- Mohamed, M.S.; Akinyemi, L.; Najati, S.; Elagan, S. Abundant solitary wave solutions of the Chen–Lee–Liu equation via a novel analytical technique. Opt. Quantum Electron. 2022, 54, 141. [Google Scholar] [CrossRef]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Yusuf, A.; Sulaiman, T.A. Optical soliton solutions to Chen Lee Liu model by the modified extended tanh expansion scheme. Optik 2021, 245, 167643. [Google Scholar] [CrossRef]
- El-Shiekh, R.M.; Gaballah, M. Novel optical waves for the perturbed nonlinear Chen-Lee-Liu equation with variable coefficients using two different similarity techniques. Alex. Eng. J. 2024, 86, 548–555. [Google Scholar] [CrossRef]
- Chen, H.; Lee, Y.; Liu, C. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Phys. Scr. 1979, 20, 490. [Google Scholar] [CrossRef]
- Triki, H.; Babatin, M.; Biswas, A. Chirped bright solitons for Chen–Lee–Liu equation in optical fibers and PCF. Optik 2017, 149, 300–303. [Google Scholar] [CrossRef]
- Triki, H.; Zhou, Q.; Moshokoa, S.P.; Ullah, M.Z.; Biswas, A.; Belic, M. Chirped w-shaped optical solitons of Chen–Lee–Liu equation. Optik 2018, 155, 208–212. [Google Scholar] [CrossRef]
- Triki, H.; Hamaizi, Y.; Zhou, Q.; Biswas, A.; Ullah, M.Z.; Moshokoa, S.P.; Belic, M. Chirped singular solitons for Chen-Lee-Liu equation in optical fibers and PCF. Optik 2018, 157, 156–160. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Biswas, A.; Zhou, Q.; Alfiras, M.; Moshokoa, S.P.; Belic, M. Chirped singular and combo optical solitons for Chen–Lee–Liu equation with three forms of integration architecture. Optik 2019, 178, 172–177. [Google Scholar] [CrossRef]
- Mohammed, A.; Bakodah, H.; Banaja, M.; Alshaery, A.; Zhou, Q.; Biswas, A.; Moshokoa, S.P.; Belic, M.R. Bright optical solitons of Chen-Lee-Liu equation with improved Adomian decomposition method. Optik 2019, 181, 964–970. [Google Scholar] [CrossRef]
- Bansal, A.; Biswas, A.; Zhou, Q.; Arshed, S.; Alzahrani, A.K.; Belic, M.R. Optical solitons with Chen–Lee–Liu equation by Lie symmetry. Phys. Lett. A 2020, 384, 126202. [Google Scholar] [CrossRef]
- Chow, K.; Ng, T.W. Periodic solutions of a derivative nonlinear Schrödinger equation: Elliptic integrals of the third kind. J. Comput. Appl. Math. 2011, 235, 3825–3830. [Google Scholar] [CrossRef]
- Chow, K.W.; Yip, L.P.; Grimshaw, R. Novel solitary pulses for a variable-coefficient derivative nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 2007, 76, 074004. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Biswas, A. W-shaped optical solitons of Chen–Lee–Liu equation by Laplace–Adomian decomposition method. Opt. Quantum Electron. 2018, 50, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, L.; Chabchoub, A.; He, J. Higher-order rogue wave dynamics for a derivative nonlinear Schrödinger equation. Rom. J. Phys. 2017, 62, 31. [Google Scholar]
- Yang, Y.; Wang, X.; Yan, Z. Optical temporal rogue waves in the generalized inhomogeneous nonlinear Schrödinger equation with varying higher-order even and odd terms. Nonlinear Dyn. 2015, 81, 833–842. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Qiu, D.; Zhang, Y.; Porsezian, K.; He, J. Rogue wave solutions of a higher-order Chen–Lee–Liu equation. Phys. Scr. 2015, 90, 055207. [Google Scholar] [CrossRef]
- Liu, P.; Chen, Y.; Chai, X. Soliton and rogue wave excitations in the Chen–Lee–Liu derivative nonlinear Schrödinger equation with two complex P T-symmetric potentials. Chaos Interdiscip. J. Nonlinear Sci. 2025, 35, 013120. [Google Scholar] [CrossRef]
- Peng, W.Q.; Pu, J.C.; Chen, Y. PINN deep learning method for the Chen–Lee–Liu equation: Rogue wave on the periodic background. Commun. Nonlinear Sci. Numer. Simul. 2022, 105, 106067. [Google Scholar] [CrossRef]
- Biswas, A. Chirp-free bright optical soliton perturbation with Chen–Lee–Liu equation by traveling wave hypothesis and semi-inverse variational principle. Optik 2018, 172, 772–776. [Google Scholar] [CrossRef]
- Kudryashov, N.A. General solution of the traveling wave reduction for the perturbed Chen-Lee-Liu equation. Optik 2019, 186, 339–349. [Google Scholar] [CrossRef]
- Houwe, A.; Abbagari, S.; Almohsen, B.; Betchewe, G.; Inc, M.; Doka, S.Y. Chirped solitary waves of the perturbed Chen–Lee–Liu equation and modulation instability in optical monomode fibres. Opt. Quantum Electron. 2021, 53, 286. [Google Scholar] [CrossRef]
- Tarla, S.; Ali, K.K.; Yilmazer, R.; Osman, M. On dynamical behavior for optical solitons sustained by the perturbed Chen–Lee–Liu model. Commun. Theor. Phys. 2022, 74, 075005. [Google Scholar] [CrossRef]
- Esen, H.; Ozdemir, N.; Secer, A.; Bayram, M. On solitary wave solutions for the perturbed Chen–Lee–Liu equation via an analytical approach. Optik 2021, 245, 167641. [Google Scholar] [CrossRef]
- Akinyemi, L.; Ullah, N.; Akbar, Y.; Hashemi, M.S.; Akbulut, A.; Rezazadeh, H. Explicit solutions to nonlinear Chen–Lee–Liu equation. Mod. Phys. Lett. B 2021, 35, 2150438. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Sankar, M.; Krishnan, E.V.; Khan, S.; Biswas, A. Chirped gap solitons in fiber Bragg gratings with polynomial law of nonlinear refractive index. J. Eur. Opt. Soc.-Rapid Publ. 2023, 19, 30. [Google Scholar] [CrossRef]
- Aydemir, T. New exact optical soliton solutions of the derivative nonlinear Schrödinger equation family. Opt. Quantum Electron. 2024, 56, 1018. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of the Chen–Lee–Liu equation with arbitrary refractive index. Optik 2021, 247, 167935. [Google Scholar] [CrossRef]
- Zhang, W. Exact chirped solutions of perturbed Chen-Lee-Liu equation with refractive index. Heliyon 2023, 9, e20409. [Google Scholar] [CrossRef]
- Li, Z. Qualitative analysis and explicit solutions of perturbed Chen–Lee–Liu equation with refractive index. Results Phys. 2024, 60, 107626. [Google Scholar] [CrossRef]
- Alphonse, H.; Jamilu, S.; Zakia, H.; Doka, S. Solitary pulses of the conformable derivative nonlinear differential equation governing wave propagation in low-pass electrical transmission line. Phys. Scr. 2020, 95, 045203. [Google Scholar]
- El-Ganaini, S.; Kumar, H. A variety of new traveling and localized solitary wave solutions of a nonlinear model describing the nonlinear low-pass electrical transmission lines. Chaos Solitons Fractals 2020, 140, 110218. [Google Scholar] [CrossRef]
- Sabi’u, J.; Tala-Tebue, E.; Rezazadeh, H.; Arshed, S.; Bekir, A. Optical solitons for the decoupled nonlinear Schrödinger equation using Jacobi elliptic approach. Commun. Theor. Phys. 2021, 73, 075003. [Google Scholar] [CrossRef]
- Nuruzzaman, M.; Kumar, D.; Paul, G.C. Fractional low-pass electrical transmission line model: Dynamic behaviors of exact solutions with the impact of fractionality and free parameters. Results Phys. 2021, 27, 104457. [Google Scholar] [CrossRef]
- Al-Ghafri, K.; Krishnan, E.; Biswas, A. W-shaped and other solitons in optical nanofibers. Results Phys. 2021, 23, 103973. [Google Scholar] [CrossRef]
- Yomba, E. The extended Fan’s sub-equation method and its application to KdV–MKdV, BKK and variant Boussinesq equations. Phys. Lett. A 2005, 336, 463–476. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).