Abstract
This paper presents a distributed optimization algorithm for time-varying objective functions utilizing a prescribed-time convergent multi-agent system within undirected communication networks. Departing from conventional time-invariant optimization paradigms with static optimal solutions, our approach specifically addresses the challenge of tracking dynamic optimal trajectories in evolving environments. A novel continuous-time distributed optimization algorithm is developed based on prescribed-time consensus, guaranteeing the consensus attainment among agents within a user-defined timeframe while asymptotically converging to the time-dependent optimal solution. The proposed methodology enables explicit predetermination of convergence duration, representing a significant advancement over existing asymptotic convergence methods. Moreover, two simulation examples on the rendezvous problem and multi-robots control are presented to validate the theoretical results, exhibiting precise time-controlled convergence characteristics and effective tracking performance for time-varying optimization targets.
Keywords:
distributed optimization; prescribed-time consensus; time-varying function; multiagent system MSC:
93D50
1. Introduction
Distributed optimization is widely encountered in various areas, such as optimal control [1], Nash equilibrium [2] and smart grids [3]. To deal with these optimization problems, a variety of distributed optimization methods grounded on multi-agent systems have been designed. For example, the classical optimization methods include the alternating direction multiplier method [4], push-sum method [5], Lagrangian multiplier method [6], and so on. In addition, there are distributed optimization methods based on control theory [7,8,9]. Note that the aforementioned works are concentrated on distributed optimization problems with time-independent cost functions and searching for some constant optimal solutions, i.e., the cost functions and optimal solutions are independent of time.
Generally, time-varying optimization problems appear in a large amount of practical applications because the local performance functions or the constraints of engineering technology might evolve over time, such as in time-varying environment allocation [10], network traffic management [11], and optimal matching and formation of multi-robot systems [12]. In such cases, for time-varying distributed optimization, it is required to track an optimal trajectory instead of some fixed points, which is more challenge in comparison with time-invariant optimization problems. Recently, time-varying distributed optimization has attracted many researchers’ increasing attention. For example, ref. [13] proposes a prediction-correction method to deal with a matter of unconstrained optimization subject to time-varying objective functions. With the addition of a term of Newton correction, ref. [14] extends the prediction-correction method [13] into a continuous-time multi-agent system for addressing time-varying distributed optimization problems with inequality constraints. Furthermore, ref. [15] proposes an interior-point method on account of a log-barrier penalty function for general time-varying constraints with an exponential convergent rate to optimal solutions.
To cope with time-varying optimization problems with time-dependent quadratic cost functions, ref. [16] develops a distributed gradient searching approach to track optimal trajectories. To solve a bounded constraint, ref. [17] presents a distributed projected-gradient algorithm, which is convergent to a neighborhood of optimal solutions asymptotically. Furthermore, in order to track and follow the exact time-varying optimal solutions, ref. [18] proposes a distributed protocol based on sliding control. In practical applications, there are expectations that the convergence can be arrived within a finite time for some requirements. For example, a group of robots are required to achieve an expected formation, and preserve signal connectivity in finite time or fixed time in the meantime, minimizing the cost/energy functions [19,20,21,22,23]. However, the aforementioned distributed optimization methods are only capable of reaching agreement over infinite time. In particular, ref. [20] investigated a finite-time consensus tracking control problem in uncertain nonlinear multi-agent systems, showing that the all signals remain semi-global practical finite-time stable, and the tracking errors converge to a neighborhood of the origin in finite time. However, the time for reaching consensus is not given explicitly. Ref. [19] develops a distributed law to achieve a finite-time consensus, where the consensus time heavily counts on agents’ original states. To overcome these drawbacks, on the basis of fixed-time stability [24], fixed-time convergent algorithms are presented in [23,25] for time-dependent distributed optimization. In these algorithms, the time for achieving fixed-time consensus is independent of initial conditions.
However, the upper bound of settling time functions for both distributed fixed-time and finite-time algorithms is dominated by the controller parameters, communication networks, and number of agents. For these limitations, some topics on prescribed-time consensus for nonlinear systems have been developed recently. The notion of prescribed-time stability can be found in [26,27,28,29], where the dynamic system can reach at the state agreement in a preset time. For example, ref. [26] proposes a consensus-based algorithm to enable all agents to reach the Nash equilibrium within a prescribed time. Inspired by these observations, a prescribed-time convergent algorithm is designed for distributed optimization with time-varying cost functions in this paper.
The main contributions of this paper are summarized as follows. First, the time-varying distributed optimization approach proposed herein generalizes prior works [4,6,7,30,31,32] on time-invariant distributed optimization. Moreover, the time-varying objective functions in [10] can be regarded as a special case of this framework. Second, the proposed algorithm allows arbitrary initial conditions and relaxes bound constraints on the optimal state, in contrast to the distributed optimization algorithms in [17,22,33]. Specifically, ref. [33] requires initial states to be bounded, while [17,22] necessitate bounded derivatives of optimal solutions. Third, the presented algorithm achieves prescribed-time consensus with a preset settling time, in contrast to the infinite-time consensus approaches in [13,14,15,16,17,18,33]; the finite-time consensus methods in [19,22,34] with the settling time function depending on original conditions; and the fixed-time consensus methods in [23,35] with the settling time governed by control parameters, number of agents, and communication network.
2. Preliminaries
2.1. Notations
Let and be the real number set and nonnegative real number set. Let , be the column vectors, where all elements in the vectors are 1 and 0, respectively. represents the identity matrix. The superscripts and stand for the transpose and Euclidean norm, respectively. For , we denote and , in which the symbol of is the abbreviation for the signum function. The symbol of represents the second smallest eigenvalue of the matrix L. Let be the Kronecker product of matrices and .
2.2. Graph Theory
Consider a multi-agent system that contains N agents. The graph is modeled to describe the interaction among agents, where is the set of vertexes, with is the set of edges, and is the adjacent matrix. In , its entry when , otherwise . Let node neighbors be . The edge indicates that the information can be transmitted between node and node . In addition, a path is defined when there is an edge sequence between node and node in the manner of , . An undirected graph is deemed connected if there exists a path between any pairs of vertexes. Let be the incidence matrix, and it is represented as when the node i is the beginning of an edge , and when the node i is the ending of an edge , otherwise . is the Laplacian matrix associated with graph , where its elements are represented as , and with . It is noted that there are , , and for an undirected graph.
2.3. Problem Formulation
Consider a dynamic equation
where is the state of system (1), is the initial time, and is a nonlinear function. If at some points g is discontinuous, then the solution to (1) is described as the Filippov solution [36].
Lemma 1
([27]). Define as a domain that contains equilibrium points of system (1). Suppose and to be continuous and positive definite functions on . For a real-valued continuously differentiable function , if there exist a constant and a time interval such that
- (i)
- (ii)
- ,
- (iii)
- , ,
then an equilibrium point is prescribed-time stable, where τ is a time interval, , and T is set in advance.
Lemma 2
([27]). For , if , there is
For there is
Lemma 3
([37]). For if , the following inequality holds:
Lemma 4
([38]). When is a convex and continuously differentiable function with respect to , will be minimized at if and only if the gradient .
3. Main Results
Here, a multi-agent system consisting of n agents is considered based on an undirected communication graph. Assume that the agents in the multi-agent system meet the dynamics defined below:
where is the state of the ith agent, and is the control input.
Assumption 1.
The graph associated with the communication topology of the multi-agent system is connected and undirected.
Remark 1.
Unlike static optimization problems with some fixed points, time-varying ones result in time-dependent optimal solutions, increasing the challenge of algorithm design. To the best of our knowledge, there are limited works on time-varying distributed optimization problems with prescribed-time convergence. These novel results have been attained under strict assumptions. Interesting future research directions include relevant extensions by the relaxation of Assumption 1 on undirected graphs to directed topologies.
Definition 1.
The multi-agent system (3) is said to achieve prescribed-time consensus if and only if
and for with any initial conditions, where the value of T is set offline in advance.
For a multi-agent system, every agent i is assigned a local state , , and privately owns a local objective function , with . Note that the local state and cost function are only known to agent i itself. A distributed protocol is designed to guarantee that all agents collaboratively trace the optimal trajectory for the following time-varying convex optimization:
Assumption 2.
The time-varying cost function is at least twice continuously differentiable with respect to x and t. In addition, for any x and t, the Hessian matrix is invertible.
It is worth noting that the time-varying optimization problem (4) can be regarded as an equivalence of the consensus problem in multi-agent systems, where all agents arrive at a consensus and at the same time minimize the whole total objective function, i.e.,
where , and . For simplicity, we remove the time dependence associated with the variables when appropriate.
To deal with problem (5), the distributed protocol is proposed for the ith agent as below:
where , ,
, , and . The terms and are the first derivative and the Hessian matrix of the cost function with respect to , respectively. Moreover, is the partial derivative of the gradient with respect to . In the distributed protocol (6), the purpose of is to reach a prescribed-time consensus, while the terms of and aim at tracing the evolution in line with the local cost function and urging the state toward the time-dependent optimal solutions.
Assumption 3.
There exists a constant such that for , where is defined in (6).
Furthermore, system (3) combined with the distributed protocol (6) is capable of being compactly notated as in the form below:
where , and with if the node i is an endpoint that an edge leaves, and if the node i is an endpoint that an edge enters, otherwise .
Theorem 1.
Proof.
Define , , and
Then, there is
It is easy to see that if .
Furthermore, substituting (8) into (7), we can obtain
where
The fact that is used follows. Choose a candidate Lyapunov function , where The time derivative of along (9) is described as
According to Formulas (9) and (10), for , one can obtain
Lemmas 2 and 3 are utilized to obtain the first and the second inequalities, respectively, and the last inequality holds due to .
Furthermore, on one hand, we have
On the other hand, one can obtain
Combining this with the Formulas (11)–(13), for , Formula (10) is able to be rewritten as the following representation:
in which , and .
According to the definition of , Formula (14) can be rewritten as
Let ; one obtains
If , then (15) can be transformed as . It can be obtained that , where and . Then, the time derivative of is able to be translated into . Therefore, it can be observed that there is and when . As a result of it can be noted that for and for . Based on Lemma 1, system (3) is prescribed-time stable, and for .
Theorem 2.
Proof.
Based on Theorem 1, the multi-agent system (3) with the distributed law (6) achieves a consensus in prescribed time, i.e., for .
Define . According to the above analysis, one can obtain for . Construct a Lyapunov function
where is positive definite with respect to . Then, according to Assumptions 1 and 3, for , the time derivative of can be described as follows:
Therefore, there is for . This indicates that will be asymptotic convergent to zero, i.e., . Based on Lemma 4, the time-varying cost function will be minimized as . □
4. Examples and Simulations
4.1. Prescribed-Time Rendezvous
The rendezvous problem can be modeled as a consensus problem [39], and it is depicted as the following strongly convex optimization:
For the shortest distance rendezvous problem in two-dimensional space, we set . A communication network with 10 agents and circular connectivity is used for (16). Let . The parameter is set as , and the control gain .
The simulation results are displayed in Figure 1 with the prescribed time s and Figure 2 with the prescribed time s. In Figure 1a and Figure 2a, it is shown that the states based on algorithm (6) can reach consensus within the respective prescribed times, where the convergent time can be preset by the designer and is independent of any initial conditions. The errors between the state and optimal solution are displayed in Figure 1b and Figure 2b, which show that the errors eventually converge to zero. It should be noted that the times at which the errors converge are almost close to the prescribed times.
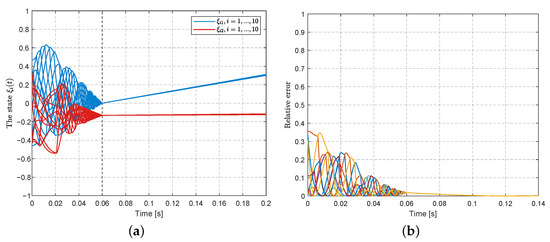
Figure 1.
Prescribed-time rendezvous with s: (a) the trajectory of state ; (b) the evolution of relative errors .
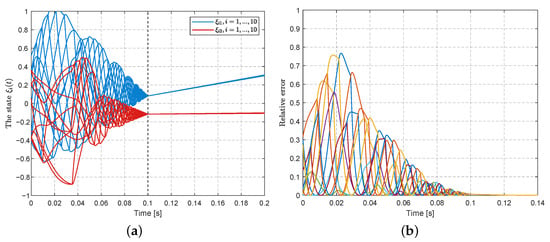
Figure 2.
Prescribed-time rendezvous with s: (a) the trajectory of state ; (b) the evolution of relative errors .
4.2. Multi-Robots Control
In this subsection, the target for a multi-agent system with n agents is to cope with the multi-robot control problem. In the system, an amount of smart agents are required to trace a moving point and sustain a certain formation. The example is inspired by a formation control problem in [33,40], where a distributed controller based on multi-agent systems is desired to address the following modeled optimization problem:
where is a scaling factor, and and are the location position and reference point of agent i, respectively.
We set and . The expected formation of the multi-robots team is reformulated as , which moves a rotating rectangle. The parameters in (6) are selected as and for .
The communication topological graph associated with the introduced multi-agent system is illustrated in Figure 3. The relative errors with the prescribed time s are described in Figure 4. It can be seen that the errors between the optimums and states converge to zero as the time approaches s, which is almost equal to the preset time. To make a rectangle formation, let , , , . Figure 5 illustrates the transient positions of four robots at several sampling times: each corresponding to a specific time , s, s, s, s, and s. The agents are represented by different colored circles: Agent 1 in red, Agent 2 in green, Agent 3 in blue, and Agent 4 in magenta. Additionally, there are two special points marked: the target point in black and the optimal point in cyan. It can be seen that the robots are moving towards an optimal point over time and can constitute the rectangle formation moving around the target point.
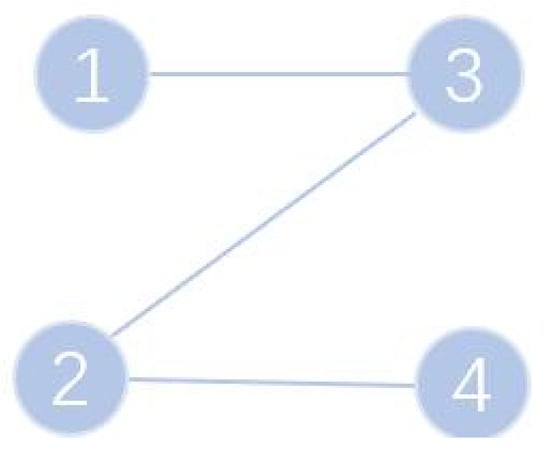
Figure 3.
Communication topology with four agents.
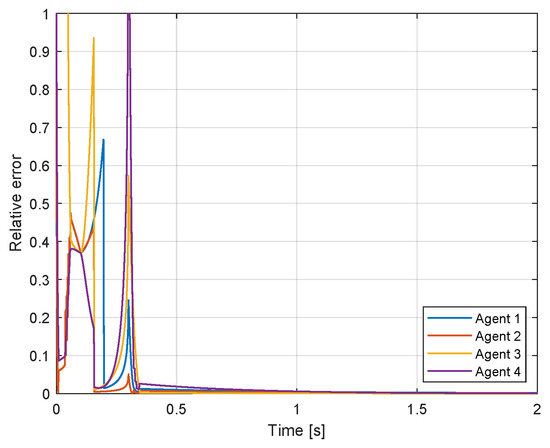
Figure 4.
The evolution of relative errors.
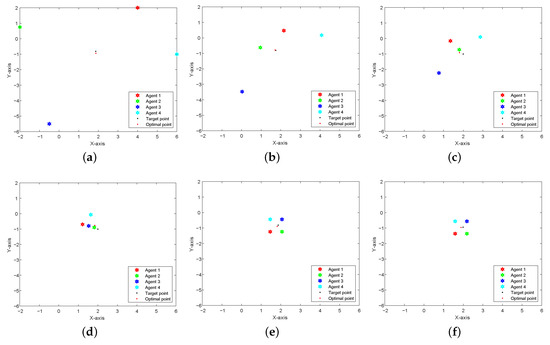
Figure 5.
The trajectories of four agents’ positions at: (a) ; (b) s; (c) s; (d) s; (e) s; (f) s.
5. Conclusions
This paper investigates a type of time-varying optimization problem on the basis of multi-agent systems with continuous single-integrator dynamics in a distributed manner. Based on the predefined-time consensus controller, a new distributed law is presented to guarantee that all agents reach a consensus in a preset time while minimizing the sum of time-dependent local cost functions. Unlike the existent distributed consensus algorithms for time-varying optimization on account of multi-agent systems, the time for reaching consensus herein can be prescribed in advance. On the basis of Lyapunov stability theory and convex optimization theory, the prescribed-time convergence and asymptotic optimality of the presented approach are proven. Lastly, the effectiveness of the designed algorithm is examined through two simulations.
Author Contributions
Conceptualization, Y.Z.; methodology, Y.Z.; validation, Y.Z., S.L., and J.Z.; investigation, Y.Z. and S.L.; writing—original draft, Y.Z.; writing—review and editing, Y.Z., S.L., and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Specialized Foundation of Zhejiang University of Science and Technology, under Grant 2025QN067, and the Young Scientists Fund of the Natural Science Foundation of Zhejiang Province, under Grant LQN25F030017.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Ren, W.; Sorensen, N. Distributed coordination architecture for multi-robot formation control. Robot. Auton. Syst. 2008, 56, 324–333. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Xue, Y.; Qin, S. Event-Triggered Adaptive Nash Equilibrium Seeking Algorithm Over Unbalanced Digraph. IEEE Trans. Autom. Control 2025, 1–8. [Google Scholar] [CrossRef]
- Liu, N.; Zhao, S.; Qin, S. A power reformulation continuous-time algorithm for nonconvex distributed constrained optimization over multi-agent systems. Neurocomputing 2021, 449, 258–269. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, J.; Gao, W.; Wang, Y.; Wei, M. Differentially private distributed online optimization via push-sum one-point bandit dual averaging. Neurocomputing 2024, 572, 127184. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Wang, M. Distributed optimization with hybrid linear constraints for multi-agent networks. Int. J. Robust Nonlinear Control 2022, 32, 2069–2083. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q. A review of distributed optimization: Problems, models and algorithms. Neurocomputing 2022, 483, 446–459. [Google Scholar] [CrossRef]
- An, L.; Yang, G.H. Distributed Optimal Coordination for Heterogeneous Linear Multiagent Systems. IEEE Trans. Autom. Control 2022, 67, 6850–6857. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Huang, N. Finite-time/fixed-time distributed optimization for nonlinear multi-agent systems with time-varying cost function. Neurocomputing 2024, 583, 127589. [Google Scholar] [CrossRef]
- Wang, B.; Fei, Q.; Wu, Q. Distributed Time-Varying Resource Allocation Optimization Based on Finite-Time Consensus Approach. IEEE Control Syst. Lett. 2021, 5, 599–604. [Google Scholar] [CrossRef]
- Su, W. Traffic Engineering and Time-Varying Convex Optimization. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, 2009. [Google Scholar]
- Liu, Q.; Wang, M. A projection-based algorithm for optimal formation and optimal matching of multi-robot system. Nonlinear Dyn. 2021, 5, 599–604. [Google Scholar] [CrossRef]
- Simonetto, A.; Koppel, A.; Mokhtari, A.; Leus, G.; Ribeiro, A. Prediction-correction methods for time-varying convex optimization. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 666–670. [Google Scholar]
- Rahili, S.; Ren, W. Distributed Continuous-Time Convex Optimization With Time-Varying Cost Functions. IEEE Trans. Autom. Control 2017, 62, 1590–1605. [Google Scholar] [CrossRef]
- Fazlyab, M.; Paternain, S.; Preciado, V.M.; Ribeiro, A. Prediction-Correction Interior-Point Method for Time-Varying Convex Optimization. IEEE Trans. Autom. Control 2018, 63, 1973–1986. [Google Scholar] [CrossRef]
- Ye, M.; Hu, G. Distributed optimization for systems with time-varying quadratic objective functions. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 3285–3290. [Google Scholar]
- Huang, B.; Zou, Y.; Meng, Z. Distributed continuous-time constrained convex optimization with general time-varying cost functions. Int. J. Robust Nonlinear Control 2021, 31, 2222–2236. [Google Scholar] [CrossRef]
- Sun, S.; Ren, W. Distributed Continuous-Time Optimization with Time-Varying Objective Functions and Inequality Constraints. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju Island, Republic of Korea, 4–18 December 2020; pp. 5622–5627. [Google Scholar]
- Ning, B.; Han, Q.L.; Zuo, Z. Distributed Optimization of Multiagent Systems with Preserved Network Connectivity. IEEE Trans. Cybern. 2019, 49, 3980–3990. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Huang, Y.; Wei, L. Adaptive Fuzzy Command Filtered Finite-Time Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Unknown Input Saturation and Unknown Control Directions. Mathematics 2022, 10, 4656. [Google Scholar] [CrossRef]
- Wang, D.; Gao, Z.; Wang, D. Distributed finite-time optimization algorithms with a modified Newton–Raphson method. Neurocomputing 2023, 536, 73–79. [Google Scholar] [CrossRef]
- Sun, C.; Feng, Z.; Hu, G. Time-Varying Optimization-Based Approach for Distributed Formation of Uncertain Euler–Lagrange Systems. IEEE Trans. Cybern. 2022, 52, 5984–5998. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Zuo, Z. Distributed Optimization for Multiagent Systems: An Edge-Based Fixed-Time Consensus Approach. IEEE Trans. Cybern. 2019, 49, 122–132. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Fang, X.; Wen, G. Distributed optimal coordination of multi-agent systems with coupled objective functions: A fixed-time estimation-based approach. Automatica 2025, 175, 112213. [Google Scholar] [CrossRef]
- Xu, B.; Li, Y.X. Prescribed-time fully distributed Nash equilibrium seeking of nonlinear multi-agent systems over unbalanced digraphs. Automatica 2024, 169, 111847. [Google Scholar] [CrossRef]
- Pal, A.K.; Kamal, S.; Yu, X.; Nagar, S.K.; Xiong, X. Free-Will Arbitrary Time Consensus for Multiagent Systems. IEEE Trans. Cybern. 2022, 52, 4636–4646. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Liu, Q.; Wang, J. A Specified-Time Convergent Multiagent System for Distributed Optimization With a Time-Varying Objective Function. IEEE Trans. Autom. Control 2024, 69, 1257–1264. [Google Scholar] [CrossRef]
- Chang, S.; Wang, Y.; Zuo, Z.; Yang, H.; Luo, X. Robust prescribed-time containment control for high-order uncertain multi-agent systems with extended state observer. Neurocomputing 2023, 559, 126782. [Google Scholar] [CrossRef]
- Nedic, A.; Ozdaglar, A.; Parrilo, P.A. Constrained consensus and optimization in multi-agent networks. IEEE Trans. Autom. Control 2010, 55, 922–938. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Liu, Q. Consensus of Heterogeneous Nonlinear Multiagent Systems with Duplex Control Laws. IEEE Trans. Autom. Control 2019, 64, 5140–5147. [Google Scholar] [CrossRef]
- Lin, P.; Ren, W.; Wang, H.; Al-Saggaf, U.M. Multiagent Rendezvous With Shortest Distance to Convex Regions with Empty Intersection: Algorithms and Experiments. IEEE Trans. Cybern. 2019, 49, 1026–1034. [Google Scholar] [CrossRef]
- Simonetto, A.; Leus, G. Distributed asynchronous time-varying constrained optimization. In Proceedings of the 2014 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 2142–2146. [Google Scholar]
- Sun, C.; Feng, Z.; Hu, G. Distributed Time-Varying Formation and Optimization with Inequality Constraints of a Multi-Robot System. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 629–634. [Google Scholar]
- Feng, Z.; Hu, G. A Distributed Constrained Optimization Approach for Spatiotemporal Connectivity-Preserving Rendezvous of Multi-Robot Systems. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 987–992. [Google Scholar]
- Filippov, A. Differential Equations with Discontinuous Righthand Sides; Kluwer Academic: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Hardy, G.; Littlewood, J.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Bazaraa, M.; Sherali, H.; Shetty, C. Nonlinear Programming; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Pilloni, A.; Pisano, A.; Franceschelli, M.; Usai, E. A discontinuous algorithm for distributed convex optimization. In Proceedings of the 2016 14th International Workshop on Variable Structure Systems (VSS), Nanjing, China, 1–4 June 2016; pp. 22–27. [Google Scholar]
- Borrelli, F.; Keviczky, T. Distributed LQR Design for Identical Dynamically Decoupled Systems. IEEE Trans. Autom. Control 2008, 53, 1901–1912. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).