Dynamical Analysis and Optimization of Combined Vibration Isolator with Time Delay
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions and Paper Organization
- We propose a combined vibration isolation system that combines a grounded dynamic vibration absorber with a quasi-zero stiffness isolator, augmented by a time-delay feedback control scheme to improve dynamic performance.
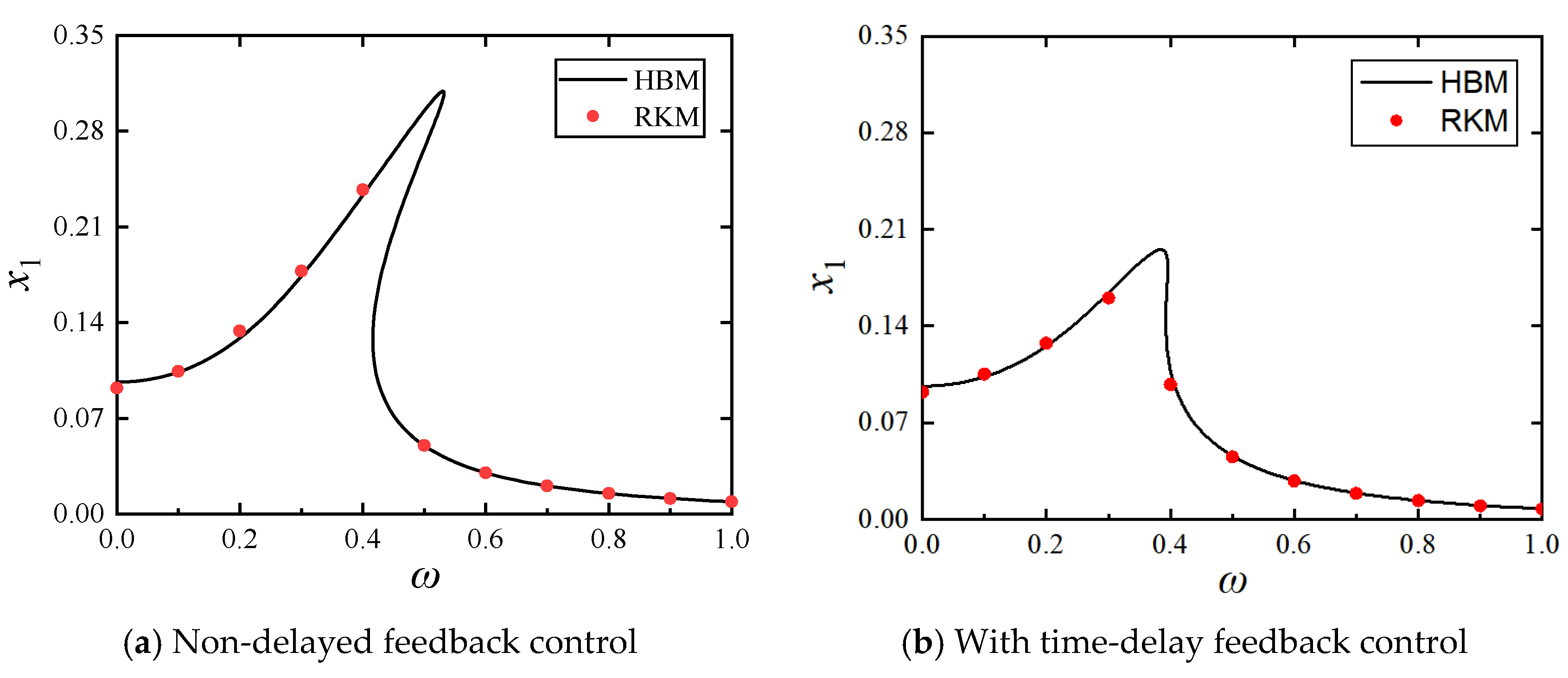
- The harmonic balance method was employed to obtain the system’s dynamic response under harmonic excitation, yielding both amplitude frequency response curves and force transmissibility curves.
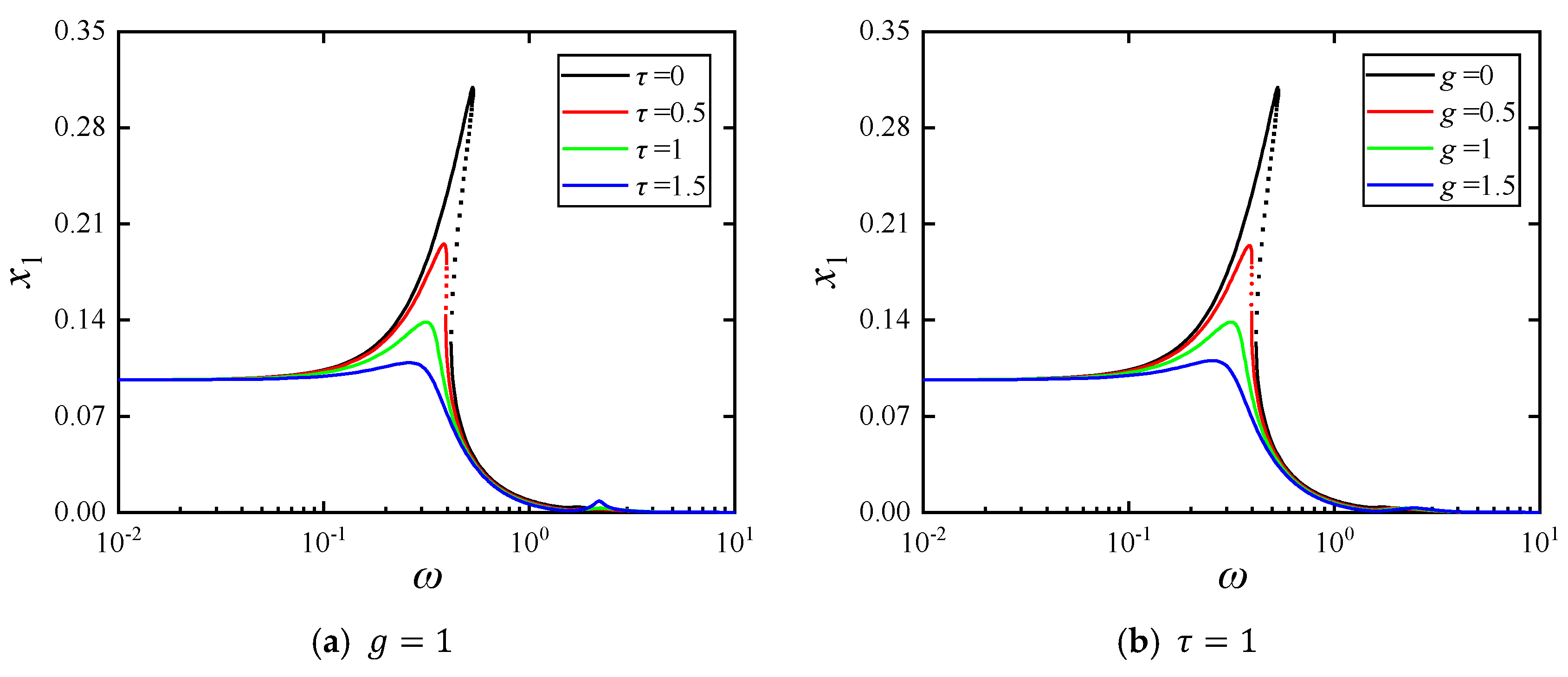
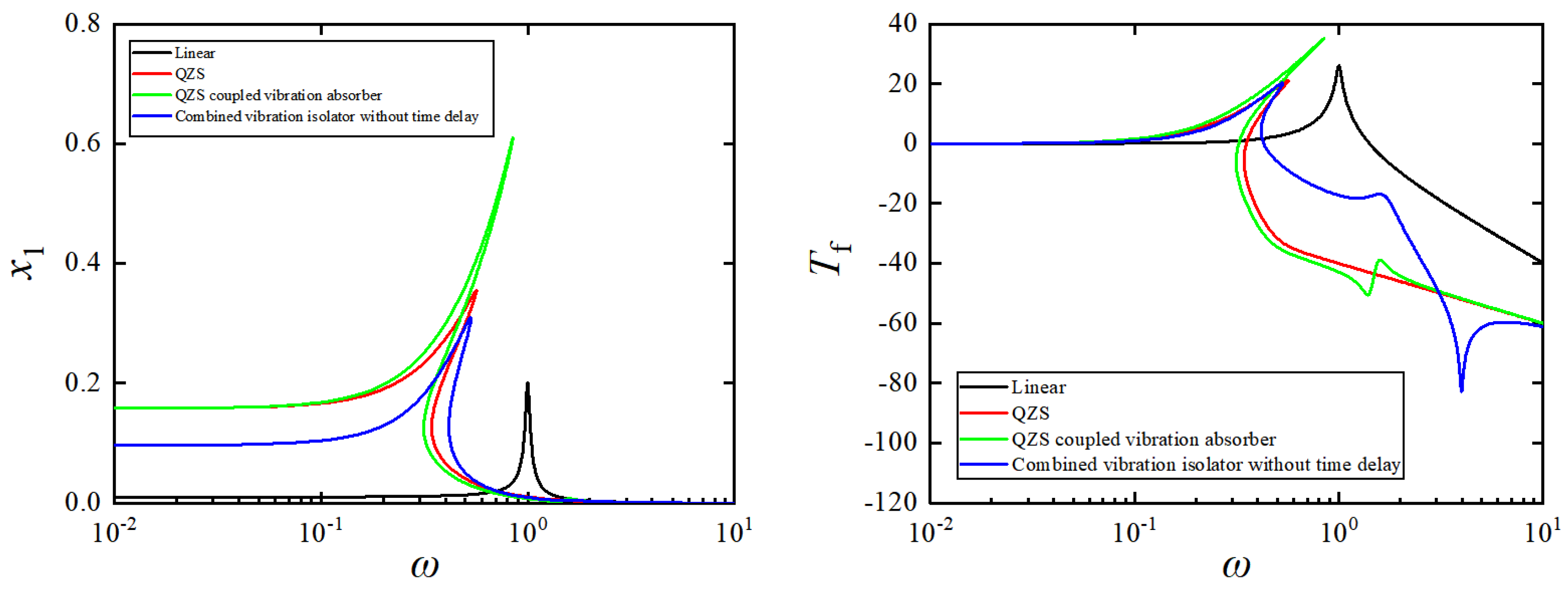
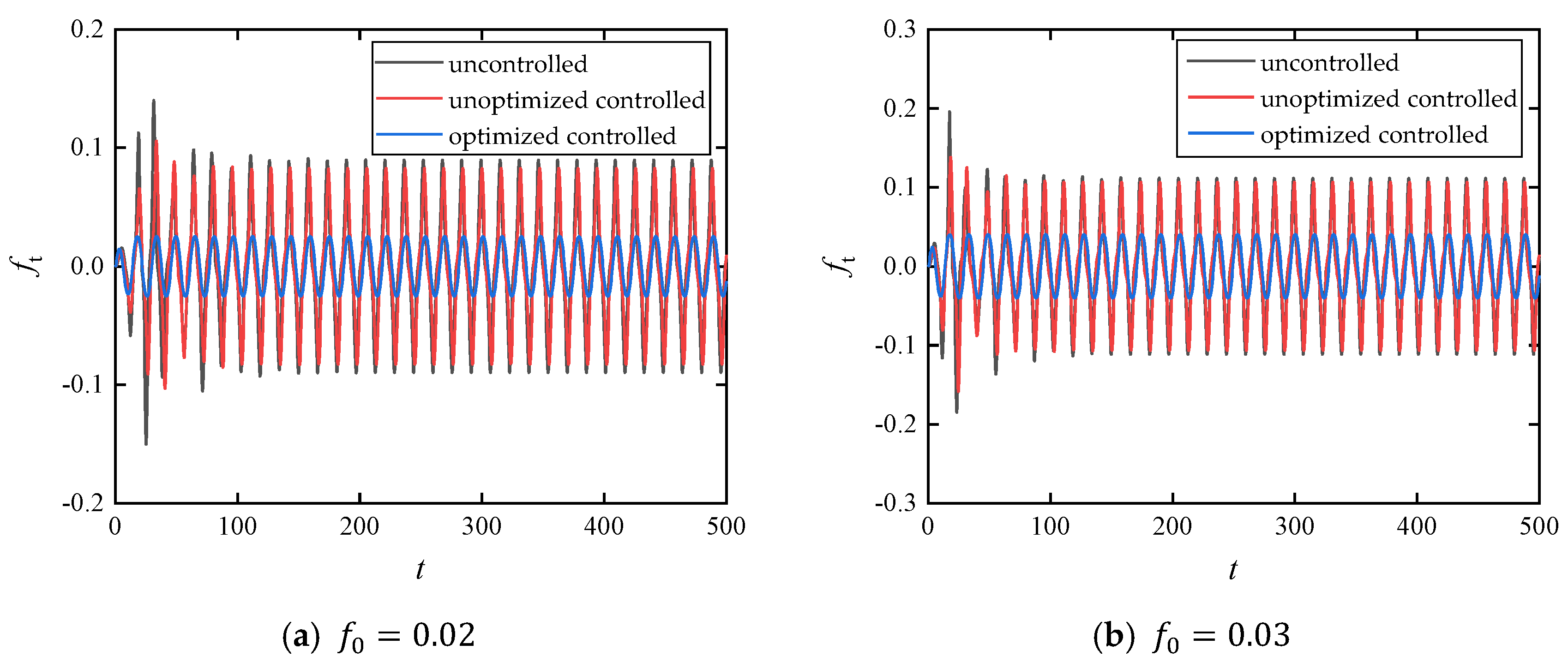
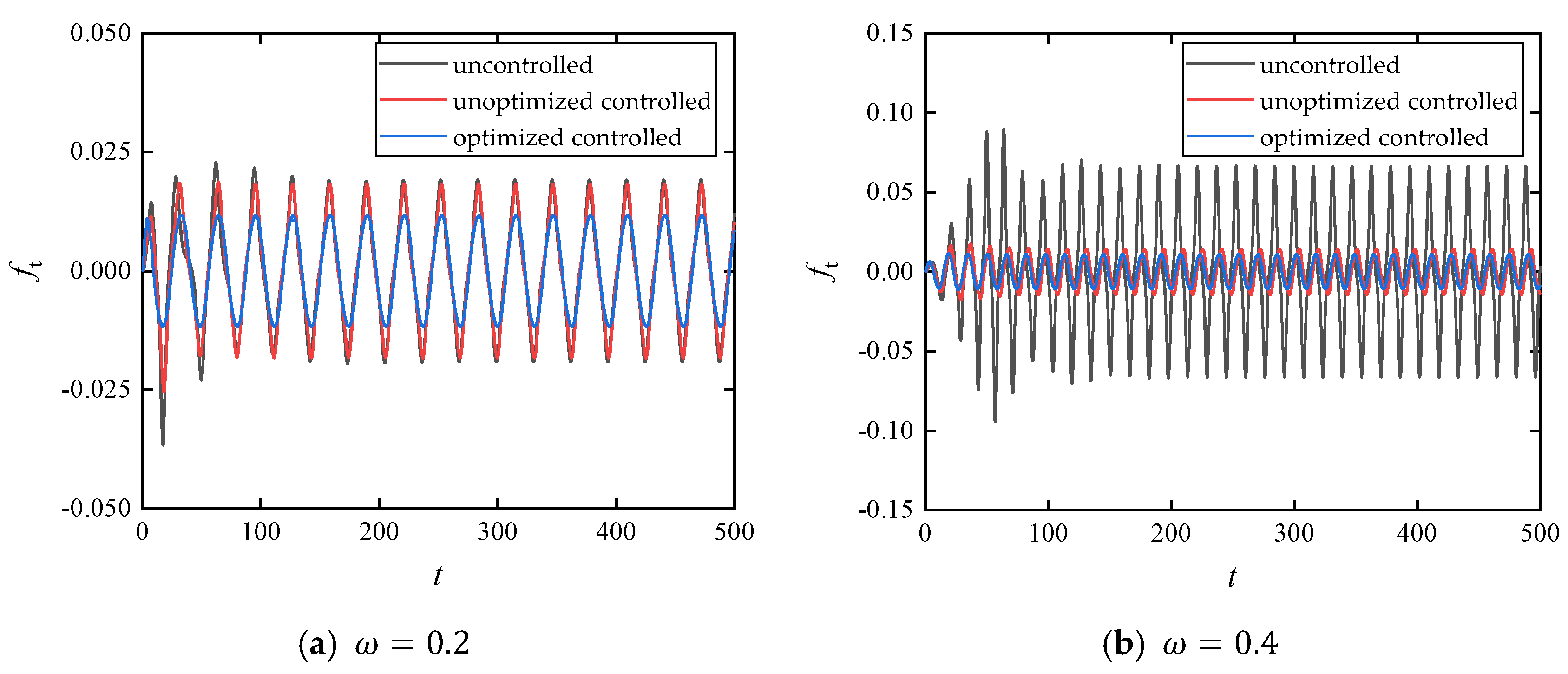
- We observed that the introduction of time-delay feedback control significantly suppresses the primary resonance peak in the amplitude–frequency response curve, while the unstable jump phenomenon gradually vanishes. In comparison with the uncontrolled configuration and the non-optimized delay control system, the optimized delay parameters demonstrate superior performance in reducing force transmissibility and enhancing vibration isolation.
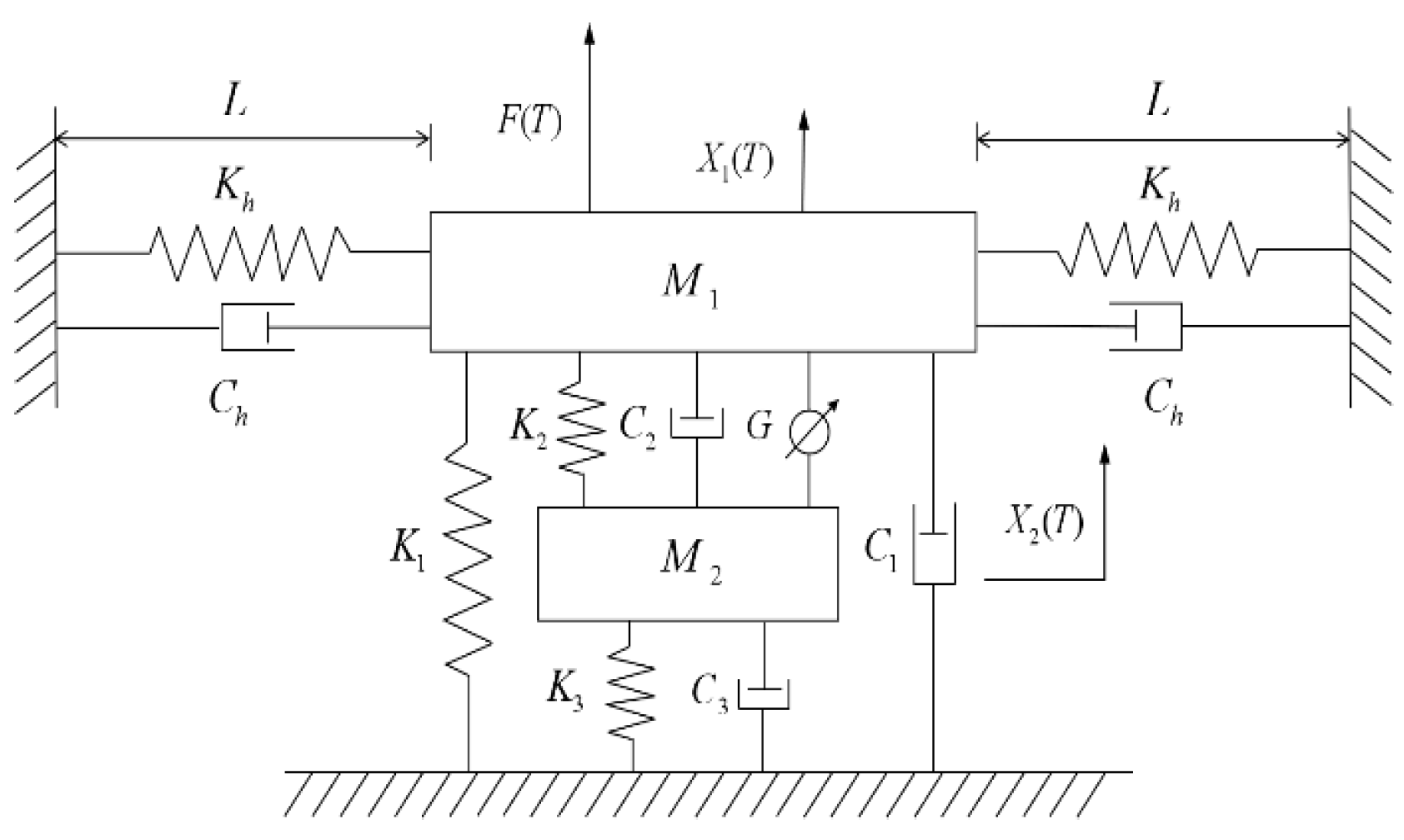
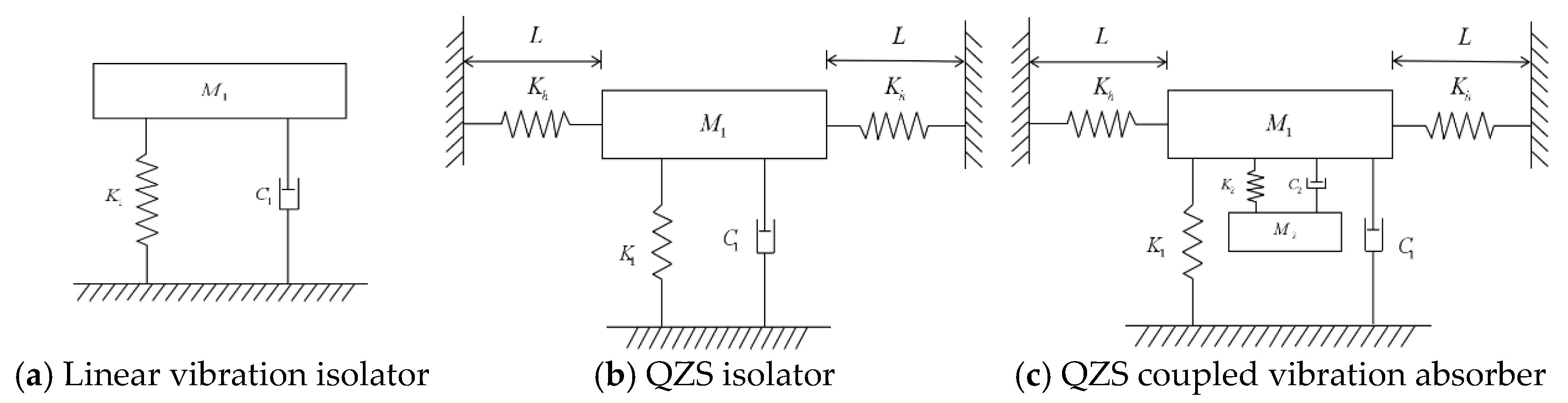
2. Mechanical Model
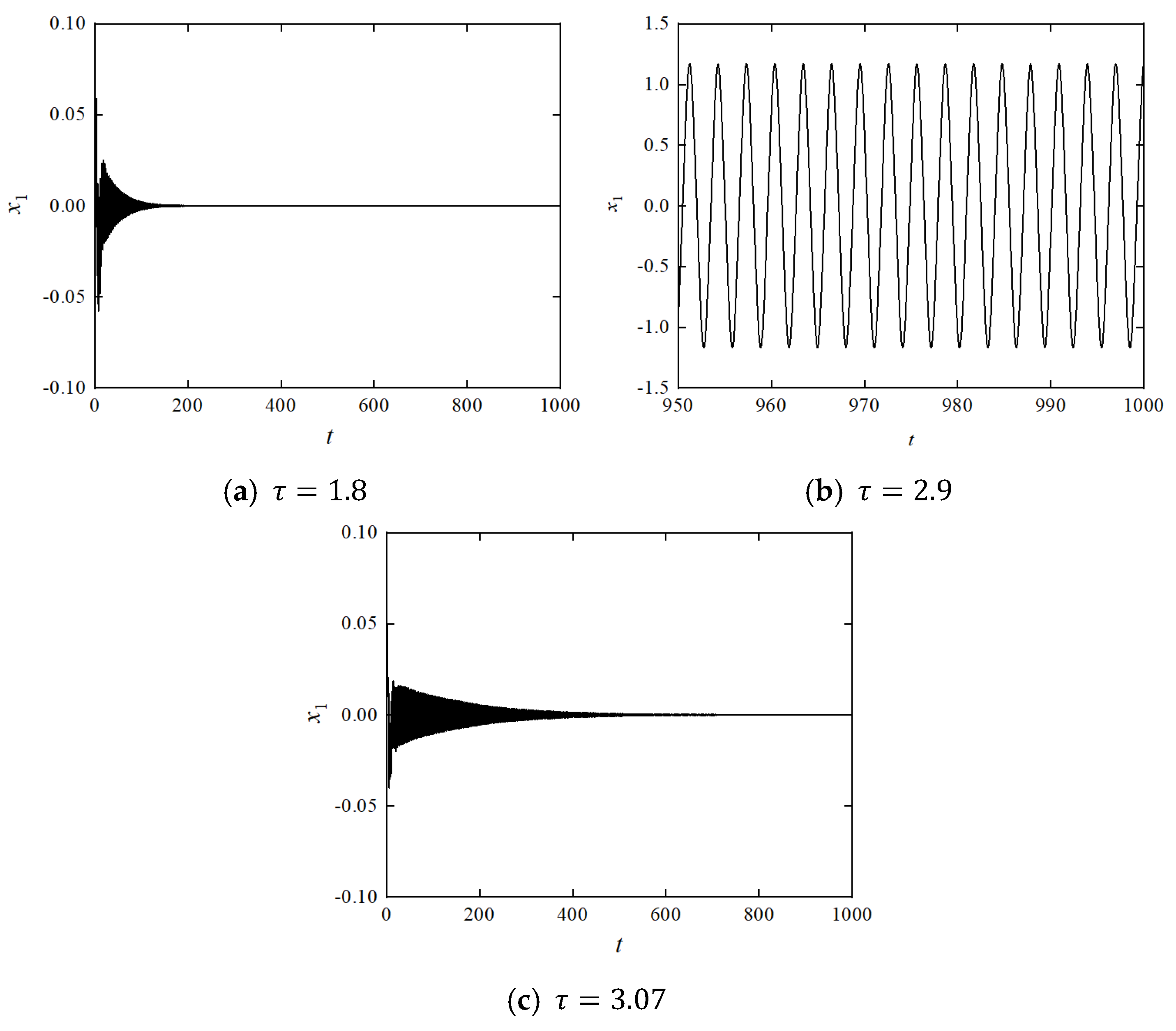
3. Stability Analysis
3.1. System Linearization
3.2. Stability Assessment
4. Dynamic Analysis of Systems
4.1. Harmonic Balance Method
- ;;
- ; ;
- ;;
- ;;;;
- ;;;;
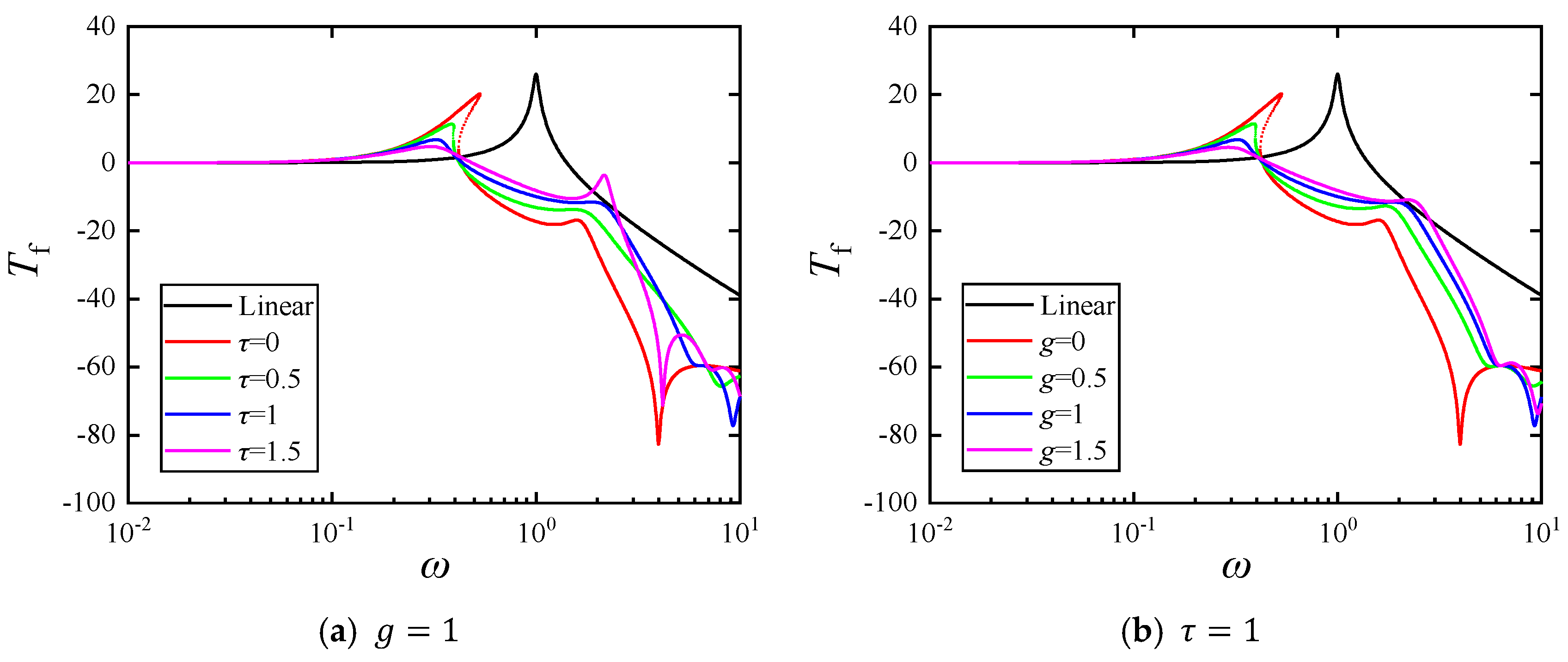
4.2. Force Transmissibility
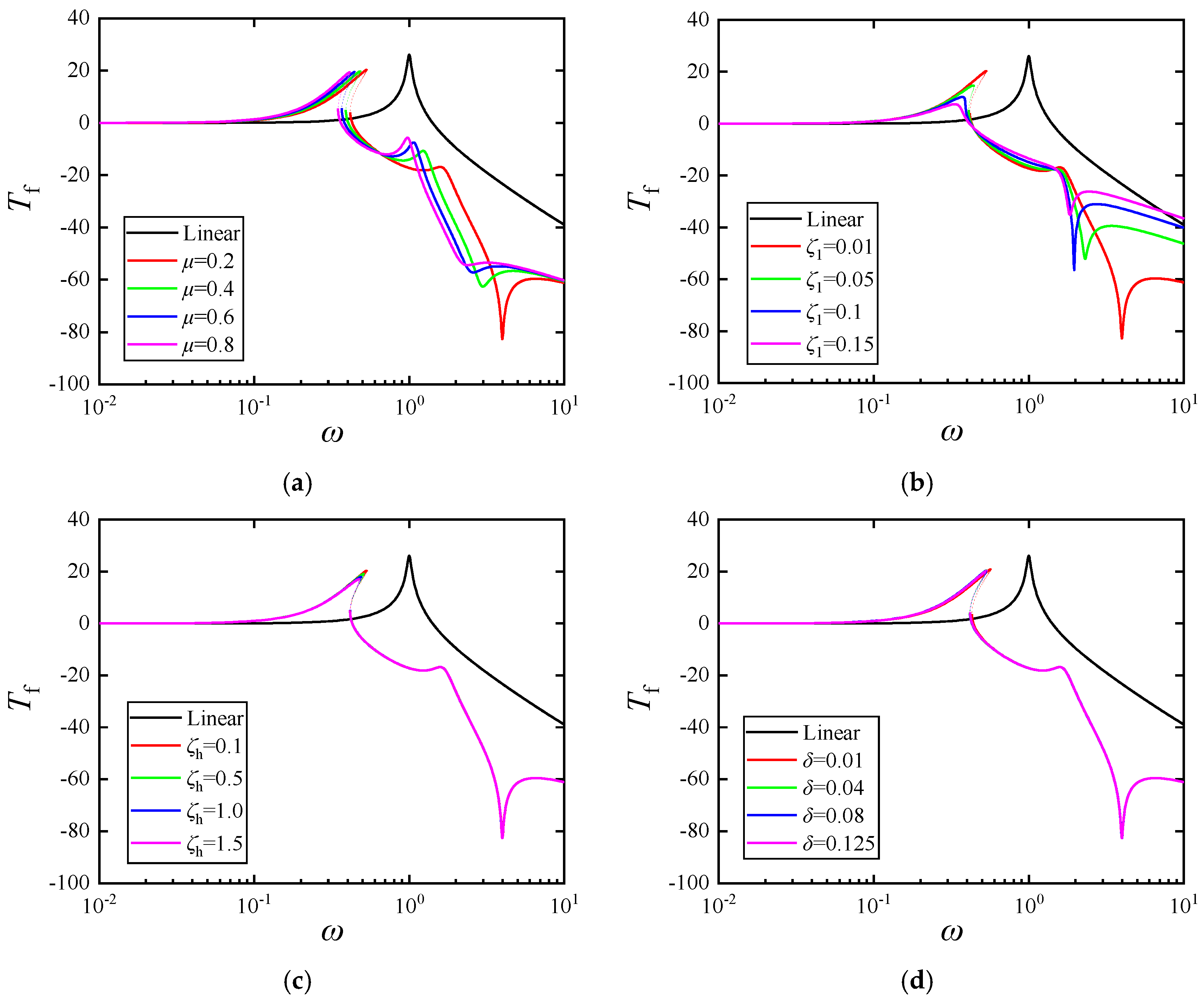
4.3. Influence of Primary System Parameters on Vibration Isolation Performance
4.4. Comparison of Isolation Models
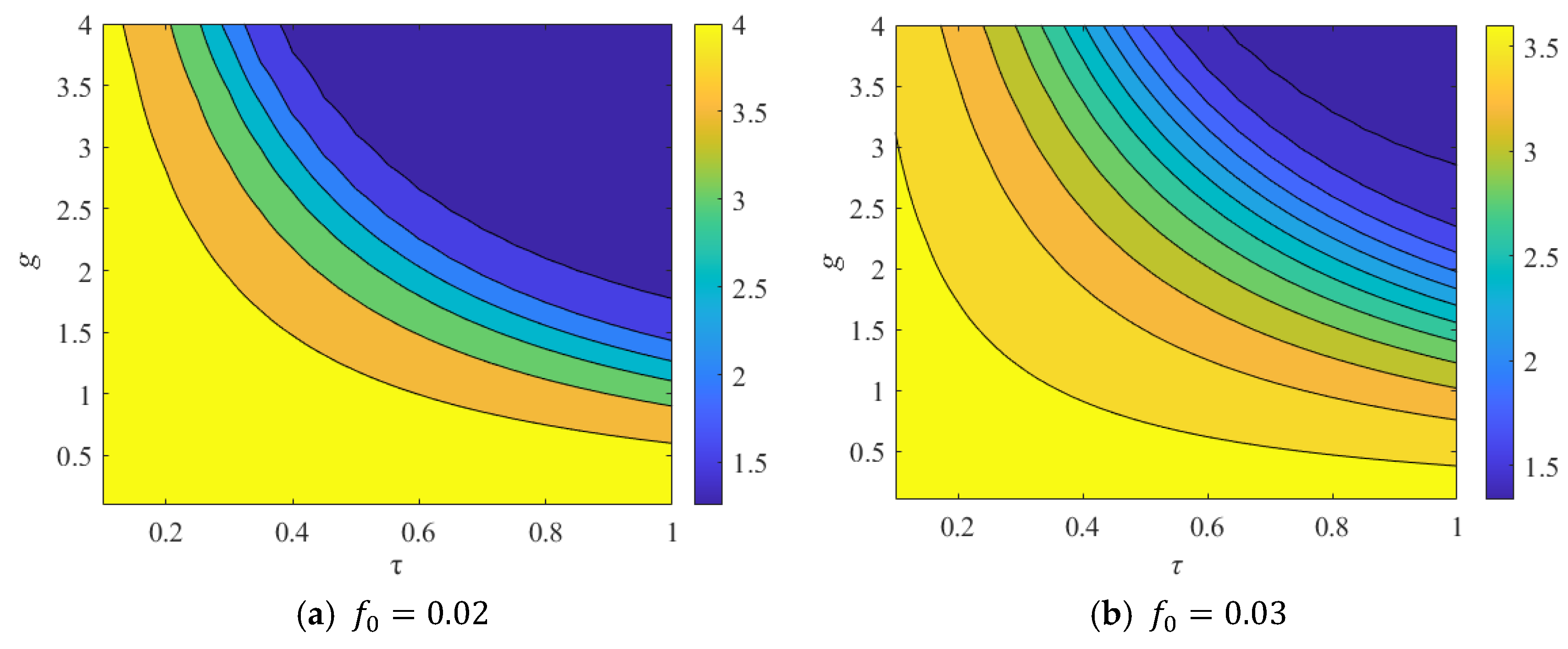
5. Parameter Optimization
6. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Basta, E.; Ghommem, M.; Emam, S. Flutter control and mitigation of limit cycle oscillations in aircraft wings using distributed vibration absorbers. Nonlinear Dyn. 2021, 106, 1975–2003. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C.; Qian, F.; Dhupia, J.S.; Wu, M. A variable parameter ambient vibration control method based on quasi-zero stiffness in robotic drilling systems. Machines 2021, 9, 67. [Google Scholar] [CrossRef]
- Sun, Y.; Gong, D.; Zhou, J.; Sun, W.J.; Xia, Z.H. Low frequency vibration control of railway vehicles based on a high static low dynamic stiffness dynamic vibration absorber. Sci. China Technol. Sci. 2019, 62, 60–69. [Google Scholar] [CrossRef]
- Saeed, A.S.; Nasar, R.A.; Al-Shudeifat, M.A. A review on nonlinear energy sinks: Designs analysis and applications of impact and rotary types. Nonlinear Dyn. 2023, 111, 1–37. [Google Scholar] [CrossRef]
- Ding, H.; Chen, L.Q. Designs, analysis and applications of nonlinear energy sinks. Nonlinear Dyn. 2020, 100, 3061–3107. [Google Scholar] [CrossRef]
- Chen, D.; Wang, N.; Chen, Z.; Yu, Y. Parametrically excited vibrations in a nonlinear damped triple-well oscillator with resonant frequency. Vib. Eng. Technol. 2022, 10, 781–788. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V., Jr. Force and Displacement Transmissibility of a Nonlinear Isolator with High-Static-Low-Dynamic-Stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. Increase of quasi-zero stiffness region using two pairs of oblique springs. Mech. Syst. Signal Process. 2020, 144, 106975. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Gatti, G. A nonlinear quasi-zero stiffness vibration isolator with quintic restoring force characteristic: A fundamental analytical insight. J. Vib. Control 2024, 30, 4185–4198. [Google Scholar] [CrossRef]
- Zou, W.; Cheng, C.; Ma, R.; Hu, Y.; Wang, W. Performance analysis of a quasi-zero stiffness vibration isolation system with scissor-like structures. Arch. Appl. Mech. 2021, 91, 117–133. [Google Scholar] [CrossRef]
- Wang, Z.; He, C.; Xu, Y.; Li, D.; Liang, Z.; Ding, W.; Kou, L. Static and Dynamic Analysis of 6-DOF Quasi-Zero-Stiffness Vibration Isolation Platform Based on Leaf Spring Structure. Mathematics 2022, 10, 1342. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, S.; Li, Z.; Hu, Z.; Li, Z. Semi-Active Suspension Control Strategy Based on Negative Stiffness Characteristics. Mathematics 2024, 12, 3346. [Google Scholar] [CrossRef]
- Ren, M.Z. A variant design of the dynamic vibration absorber. J. Sound Vib. 2001, 245, 762–770. [Google Scholar] [CrossRef]
- Liu, K.F.; Liu, J. The damped dynamic vibration absorbers: Revisited and new result. J. Sound Vib. 2005, 284, 1181–1189. [Google Scholar] [CrossRef]
- Shen, Y.J.; Sui, P.; Wang, X. Performance analysis and optimization of bimodal nonlinear energy sink. Nonlinear Dyn. 2023, 111, 16813–16830. [Google Scholar] [CrossRef]
- Long, X.; Zheng, P.; Ren, S. Active delayed control of turning and milling dynamics. J. Comput. Nonlinear Dyn. 2017, 12, 051022. [Google Scholar] [CrossRef]
- Udwadia, F.; VonBremen, H.; Phohomsiri, P. Time-delayed control design for active control of structures: Principles and applications. Struct. Control Health Monit. 2007, 14, 27–61. [Google Scholar] [CrossRef]
- Mao, X.; Ding, W. Nonlinear dynamics and optimization of a vibration reduction system with time delay. Commun. Nonlinear Sci. Numer. Simul. 2023, 122, 107220. [Google Scholar] [CrossRef]
- Vyhlídal, T.; Michiels, W.; Neusser, Z.; Bušek, J.; Šika, Z. Analysis and optimized design of an actively controlled two-dimensional delayed resonator. J. Mech. Syst. Signal Process. 2022, 178, 109195. [Google Scholar] [CrossRef]
- Gao, Q.; Liu, Y.; Cai, J.; Wu, H.; Long, Z. Complete stability analysis and optimization of the extended delayed resonator with virtual batural frequency adjustment. J. Dyn. Sys. Meas. Control 2023, 145, 011002. [Google Scholar] [CrossRef]
- Sun, X.T.; Xu, J. Vibration control of nonlinear Absorber–Isolator-Combined structure with time-delayed coupling. Int. J. Non-Linear Mech. 2016, 83, 48–58. [Google Scholar] [CrossRef]
- Ji, G.; Li, S.; Feng, G.; Li, Z.; Shen, X. Time-delay compensation control and stability analysis of vehicle semi-active suspension systems. Mech. Syst. Signal Process. 2025, 228, 112414. [Google Scholar] [CrossRef]
- Cai, J.; Gao, Q.; Zhang, X. Proportional-retarded control of a quasi-zero-stiffness vibration isolator. J. Sound Vib. 2024, 578, 118309. [Google Scholar] [CrossRef]
- Liao, X.; Liu, F.; Chen, L.; Lee, H.P.; Ma, X. On the optimal cubic feedback gain and time delay of quasi-zero stiffness vibration isolators: Analytical and numerical study. J. Vib. Eng. Technol. 2024, 12, 5007–5020. [Google Scholar] [CrossRef]
- Xing, Y.Z.; Yang, D.X. A combined vibration isolation system capable of isolating large amplitude excitation. Nonlinear Dyn. 2024, 112, 2523–2544. [Google Scholar] [CrossRef]
- Wang, F.; Xu, J. Parameter design for a vibration absorber with time-delayed feedback control. J. Acta Mech. Sin. 2019, 35, 624–640. [Google Scholar] [CrossRef]




| Parameters | Symbol | Units | Value |
|---|---|---|---|
| Primary system mass | kg | 1 | |
| absorber mass | kg | 0.2 | |
| vertical stiffness | 2400 | ||
| 960 | |||
| 240 | |||
| horizontal stiffness | 300 | ||
| horizontal damping | 70 | ||
| 7 | |||
| vertical damping | 20 | ||
| 40 | |||
| spring compression length | m | 0.067 | |
| spring natural length | m | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, X. Dynamical Analysis and Optimization of Combined Vibration Isolator with Time Delay. Mathematics 2025, 13, 2188. https://doi.org/10.3390/math13132188
Wang Y, Li X. Dynamical Analysis and Optimization of Combined Vibration Isolator with Time Delay. Mathematics. 2025; 13(13):2188. https://doi.org/10.3390/math13132188
Chicago/Turabian StyleWang, Yaowei, and Xiangyu Li. 2025. "Dynamical Analysis and Optimization of Combined Vibration Isolator with Time Delay" Mathematics 13, no. 13: 2188. https://doi.org/10.3390/math13132188
APA StyleWang, Y., & Li, X. (2025). Dynamical Analysis and Optimization of Combined Vibration Isolator with Time Delay. Mathematics, 13(13), 2188. https://doi.org/10.3390/math13132188






