The Role of Misclassification and Carbon Tax Policies in Determining Payment Time and Replenishment Strategies for Imperfect Product Shipments
Abstract
1. Introduction
- (1)
- Advance payment—buyers pay in full before receiving the goods or services.
- (2)
- Cash payment—buyers pay upon receiving the goods or services.
- (3)
- Credit payment—buyers are granted a delay payment period by the seller.
2. Notation and Assumptions
| Notation: | |
| Purchasing cost per item in dollars. | |
| Selling price per item of a good product in dollars, where | |
| Scrap price per item in dollars, i.e., selling price of a defective product, where . | |
| Payment time in unit time (a decision variable). | |
| Proportion of defective-quality items produced, where . | |
| Probability of classifying a good item as defective, i.e., probability of type I error. | |
| Probability of classifying a defective item as good, i.e., probability of type II error. | |
| Inspecting rate per unit time. | |
| Inspecting cost per item in dollars. | |
| Ordering cost per order in dollars. | |
| Penalty cost per item in dollars, i.e., cost of accepting a defective item. | |
| Price discount per item per unit time in dollars when an advance payment is adopted. | |
| Holding cost per item per unit time in dollars. | |
| Interest rate per unit time. | |
| CO2 emissions generated during the procurement of a single unit of a product. | |
| CO2 emissions generated during the inspection of a single unit of a product. | |
| CO2 emissions associated with keeping a single unit of inventory per unit of time. | |
| CO2 emissions generated during the ordering process. | |
| Unit carbon tax. | |
| Demand rate per unit time, where and . | |
| Rate of default risk, where , , , and . | |
| Order quantity for each cycle. | |
| Length of replenishment cycle in unit time (a decision variable). | |
| Total profit per unit time in dollars, where . | |
- Assumptions:
- (1)
- Shortages are not allowed.
- (2)
- As stated in Jaggi et al. [39], it is observed that the credit period offered by the retailer to customers has a positive impact on demand. Hence, the longer the credit period is, the greater the demand. Conversely, the earlier the advance payment is, the less demand. As a result, the demand rate is a function of the payment time . Specifically, , where and .There are three types of payment time. (i) is an advance payment, (ii) is a cash payment on delivery, and (iii) is a credit payment. The seller offers a price discount per unit time for attracting more buyers when the advance payment is adopted. Specifically, the selling price per item of a good product is if the payment time is less than zero and the advance payment is used.
- (3)
- Inspection should be conducted on all items to classify them as either good or defective. It is assumed that the quantity of good products is at least equal to the demand during the inspection period to avoid shortages. Specifically, .
- (4)
- Due to defects in some products, to ensure that the order quantity is sufficient, it is assumed that the quantity of good products is at least equal to the adjusted demand, which is equal to the actual demand plus the number of good products classified as defective. For the sake of simplicity, we only consider that the quantity of good products equals the adjusted demand. Specifically, .
- (5)
- Good items are sold at unit price in the general market. Each defective product is sold as scrap at a unit price of .
- (6)
- Due to type I error, some good products are classified as defective and sold at unit price , resulting in loss of revenue. This loss of revenue is the cost of rejecting these good products.
- (7)
- Due to type II error, some products sold to meet demand may be defective. The defective products will be returned to the seller later and will be destroyed. The seller pays compensation to the buyer. The penalty cost is the cost of accepting these defective products.
- (8)
- As stated in Li et al. [45], it is evident that a 30-year mortgage has a higher default risk than a 15-year mortgage. Likewise, the longer the credit period is, the higher the percentage that the buyer will not be able to pay off the debt obligation. In short, the longer the credit period is, the higher the default risk. As a result, the rate of default risk is a function of payment time. The default risk does not exist when an advance payment is adopted. Hence, it exists when . The longer the credit period is, the greater the risk of default. The default risk is zero when a cash payment is adopted, i.e., and . The default risk is 100% when a credit payment is adopted and payment time tends to infinity, i.e., and .
- (9)
- The carbon tax policy serves as a primary strategy for mitigating carbon emissions. This policy framework focuses solely on the taxation of total carbon emissions, with no consideration given to other factors or mechanisms, such as trading or allowances. The seller’s carbon emissions predominantly stem from a range of operational activities, including tasks like ordering, purchasing, inspecting, and storage.
- (10)
- The ending inventory is zero.
3. Proposed Models
- (a)
- The ordering cost ;
- (b)
- The purchasing cost ;
- (c)
- The inspecting cost ;
- (d)
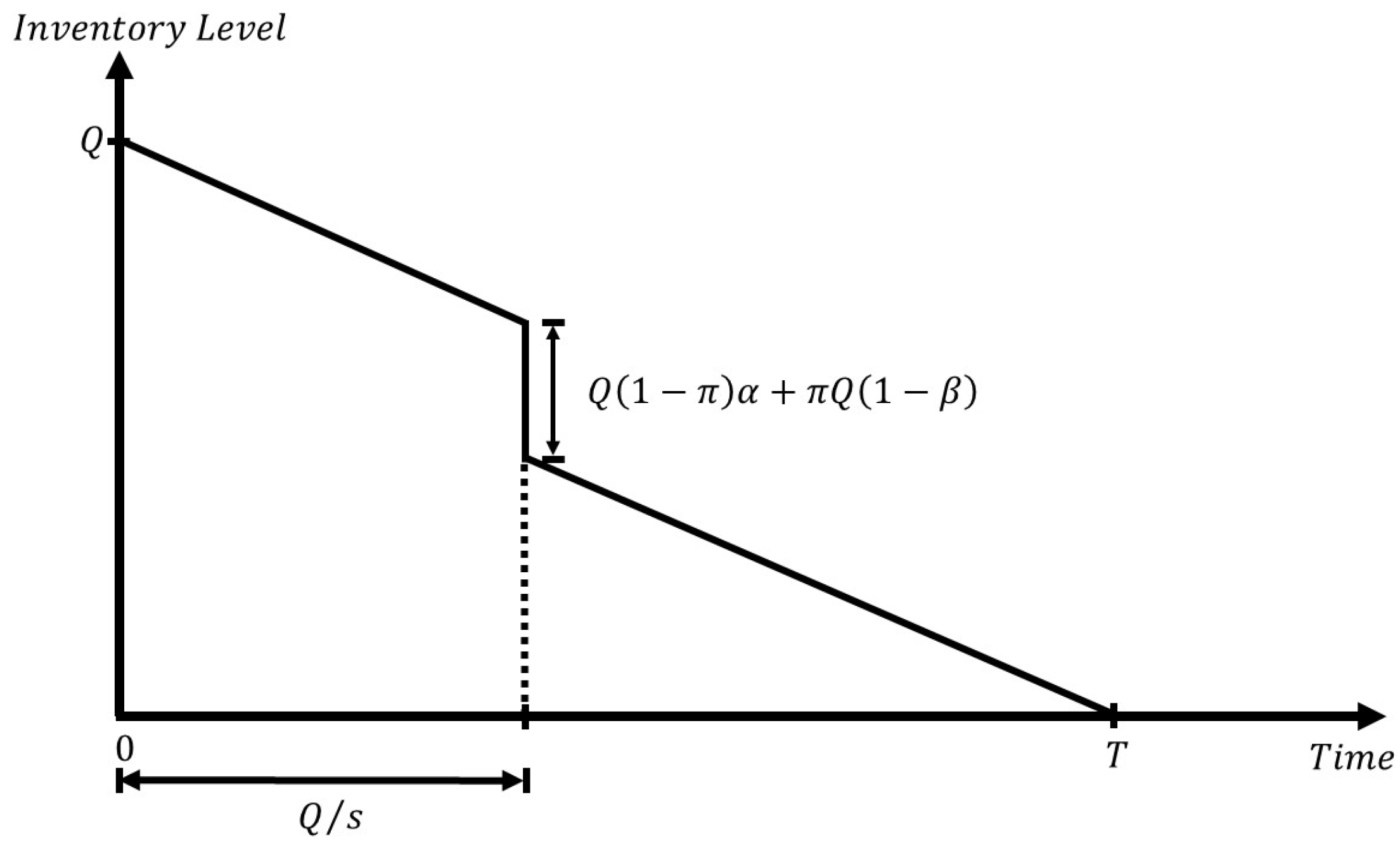
- The holding cost = (see Figure 1);
- (e)
- The loss of revenue = ;
- (f)
- The penalty cost = ;
- (g)
- The carbon tax. The seller’s amount of CO2 emissions includes those from the buying, holding, inspecting, and ordering processes. Therefore, the carbon tax is equal to the unit carbon tax multiplied by the seller’s amount of CO2 emissions. Thus, the carbon tax amount is
- (h)
- The sales revenue;
- (i)
- The interest earned (lost).
- Case 1: (cash payment or advance payment)
- (h)
- The sales revenue = ;
- (i)
- The interest earned =
- (h)
- The sales revenue = ;
- (i)
- The interest lost = .
4. Theoretical Results
| Algorithm 1: Determine the Optimal Solution | |
| Step 0: Input the values of parameters. | |
| Step 1: Calculate and . | |
| Step 1.1 Step 1.2 Step 1.3 | Using Equations (12) and (13), obtain and . If , then substitute and into Equations (9)–(11) and calculate the determinant of the Hessian matrix . If , then substitute and into Equation (6) and calculate . Otherwise, . . |
| Step 2: Calculate . | |
| Step 2.1 Step 2.2 Step 2.3 | Using Equations (20) and (21), obtain and . If , then substitute and into Equations (17)–(19) and calculate the determinant of the Hessian matrix . If , then substitute and into Equation (14) and determine . Otherwise, . If . |
| Step 3: Set , and then the optimal solution is obtained. | |
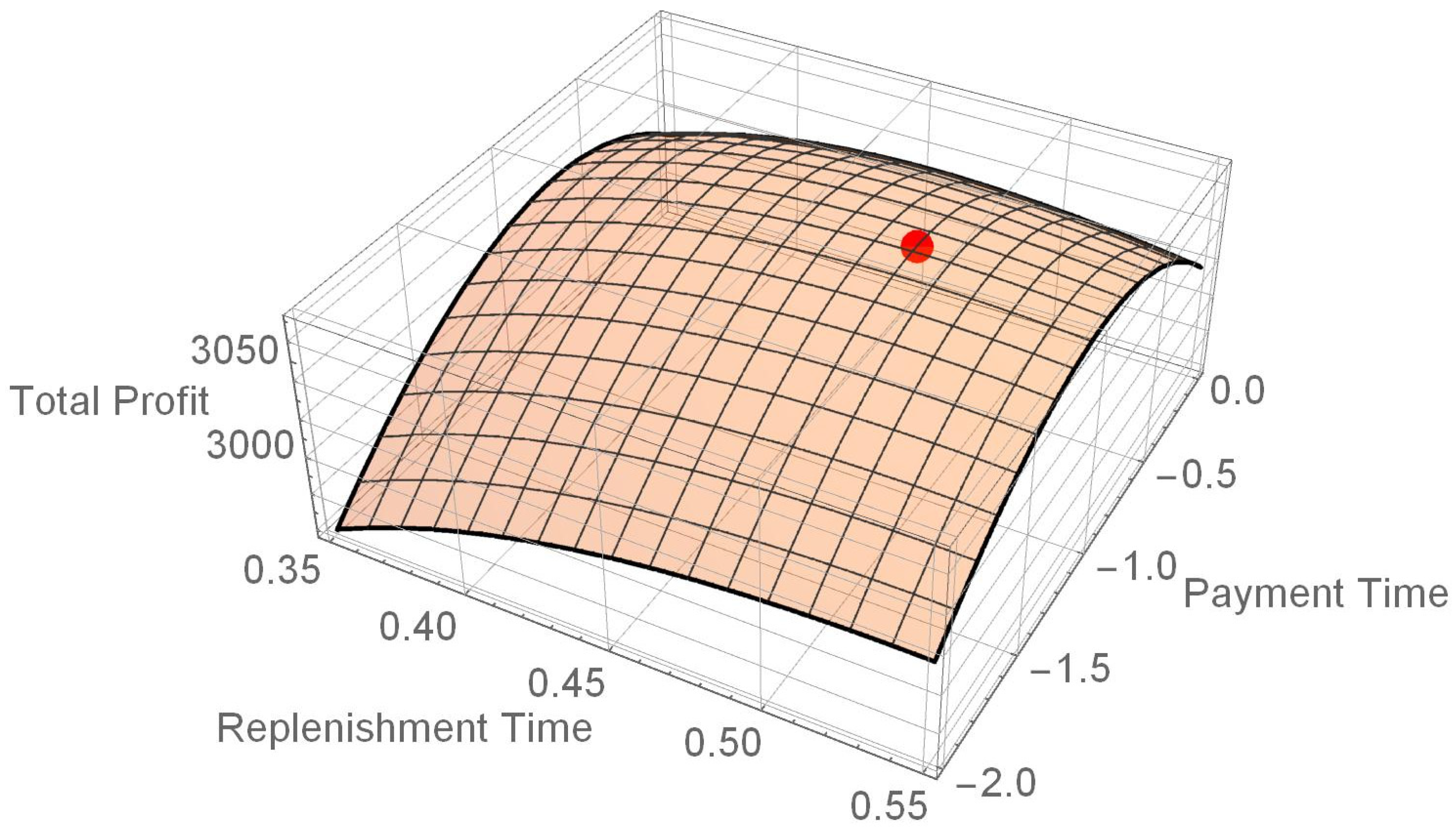
5. Numerical Examples
| Step | Hessian Matrix | ||
| 1 | |||
| 2 |
- (1)
- When the slope of payment time is , the optimal payment time ; hence, advance payment is adopted.
- (2)
- When the slope of payment time is , the optimal payment time ; hence, cash payment is adopted.
- (3)
- When the slope of payment time is , the optimal payment time ; hence, credit payment is adopted.
- (4)
- The larger the slope is, the larger the optimal order quantity and the optimal carbon tax amount are, but the shorter the optimal replenishment time is.
- (5)
- The value of optimal total annual profit is smallest when cash payment is adopted.
6. Sensitivity Analysis
- (1)
- As the coefficient of default risk increases, the optimal replenishment time also increases, whereas the optimal payment time , the optimal order quantity , the optimal carbon tax amount , and the optimal total annual profit all decrease. The impacts of the interest rate , the proportion of defective-quality items produced , the probability of type I error , the probability of type II error , the unit purchasing cost , the unit inspecting cost , and the unit penalty cost on the optimal solutions are identical to those of the coefficient of default risk on the optimal solutions . The analysis reveals that as parameters , , , , , , and increase, the decision-maker should extend the replenishment cycle, shorten the credit payment period, and reduce the order quantity. Consequently, both the optimal carbon tax amount and the total annual profit decrease.
- (2)
- A higher value of the coefficient of payment time leads to higher values of the optimal payment time , the optimal order quantity , the optimal carbon tax amount , and the optimal total annual profit but lower optimal replenishment time . The demand rate coefficient , the unit selling price of a good product p, and the unit scrap price w have the same impact on the optimal solutions as the coefficient of payment time . These results indicate that as parameters , b, p, and w increase, the decision-maker should shorten the replenishment cycle, extend the credit payment period, and increase the order quantity. Meanwhile, both the optimal carbon tax amount and the total annual profit increase.
- (3)
- When the holding cost (or the carbon emissions produced from holding ) increases, the optimal payment time , the optimal replenishment time , the optimal order quantity , the optimal carbon tax amount , and the optimal total annual profit all decrease. The analysis reveals that as parameters and increase, the decision-maker should shorten the replenishment cycle and the credit payment period and reduce the order quantity. At the same time, both the optimal carbon tax amount and the total annual profit decrease.
- (4)
- An increase in the unit carbon tax results in an increase in optimal replenishment time and optimal carbon tax amount but a decrease in the optimal payment time , the optimal order quantity , and the optimal total annual profit . The way (the carbon emission produced from the process of buying a unit product) and (the carbon emission produced from the process of inspecting a unit product) affect the optimal solutions is the same as how the unit carbon tax affects them. These results show that as parameters , , and increase, the decision-maker should extend the replenishment cycle, shorten the credit payment period, and decrease the order quantity. Meanwhile, the optimal carbon tax amount increases, but the total annual profit decreases.
- (5)
- The greater the value of (the carbon emission generated during the order process), the higher the values of the optimal replenishment time , the optimal order quantity , and the optimal carbon tax amount but the lower the values of the optimal payment time and the optimal total annual profit . The analysis indicates that as parameter increases, the decision-maker should extend the replenishment cycle, shorten the credit payment period, and increase the order quantity. At the same time, the optimal carbon tax amount increases, but the total annual profit decreases.
- (6)
- As the ordering cost grows, the optimal replenishment time and the optimal order quantity rise correspondingly, while the optimal payment time , the optimal carbon tax amount , and the optimal total annual profit decline. These results indicate that as parameter increases, the decision-maker should extend the replenishment cycle, shorten the credit payment period, and increase the order quantity. At the same time, both the optimal carbon tax amount and the total annual profit decrease.
- (7)
- When the inspecting rate increases, the optimal payment time , the optimal replenishment time , the optimal order quantity , the optimal carbon tax amount , and the optimal total annual profit all increase. The analysis shows that as parameter increases, the decision-maker should extend the replenishment cycle and the credit payment period and increase the order quantity. Meanwhile, both the optimal carbon tax amount and the total annual profit increase.
7. Management Implications
- (1)
- The empirical evidence demonstrated that increases in misclassification probability, default risk coefficient, interest rate, proportion of defective items, unit purchasing cost, unit inspection cost, and unit penalty cost necessitated strategic adjustments wherein decision-makers should extend replenishment intervals, curtail credit payment periods, and reduce order quantities. Consequently, these adjustments precipitated a decline in both optimal carbon tax amounts and total annual profitability.
- (2)
- The analytical findings substantiated those elevations in payment time coefficient, demand rate coefficient, unit selling price of quality-conforming products, and unit scrap value and induced decision-makers to implement operational modifications including shortened replenishment cycles, extended credit periods, and increased order quantities. Concurrently, these strategic adaptations facilitated increases in both optimal carbon tax amounts and aggregate annual profit metrics.
- (3)
- The comprehensive analysis elucidated that incremental increases in holding costs or carbon emissions associated with inventory storage compelled decision-makers to adopt operational strategies characterized by shortened replenishment cycles, reduced credit payment periods, and diminished order quantities. These strategic recalibrations subsequently engendered decreases in both optimal carbon taxation levels and total annual profit margins.
- (4)
- The empirical investigation revealed that as unit carbon tax values and carbon emissions were attributable to procurement and inspection, decision-makers exhibited a propensity to extend replenishment cycles, contract credit periods, and decrease order quantities. These operational adjustments culminated in elevated optimal carbon tax amounts while simultaneously precipitating reductions in total annual profitability.
- (5)
- The research outcomes indicated that heightened carbon emissions per ordering event induced decision-makers to implement strategic modifications including extended replenishment cycles, increased order quantities, and reduced credit payment periods. Concomitantly, these adjustments resulted in elevated optimal carbon tax amounts while adversely affecting total annual profit metrics.
- (6)
- The empirical results demonstrated that increases in ordering costs necessitated strategic adaptations wherein decision-makers extended replenishment cycles, augmented order quantities, and reduced credit payment durations. Simultaneously, these operational modifications precipitated decreases in both optimal carbon tax amounts and total annual profitability.
- (7)
- The empirical investigation indicated that a higher inspection rate led the decision-maker to extend both the replenishment cycle and the credit payment period, while also increasing the order quantity. Concurrently, the optimal carbon tax and the total annual profit also exhibited an upward trend.
- (8)
- The empirical evidence suggested that incremental increases in price discount structures induced decision-makers to extend advance payment periods and augment order quantities while concurrently reducing replenishment cycle durations. These strategic adaptations resulted in elevated optimal carbon tax amounts, whereas total annual profitability experienced a concomitant decline.
8. Conclusions
- (1)
- When the probability of misclassification (type I or type II error) or the default risk coefficient rises, the optimal replenishment time increases, and the optimal credit payment time decreases, leading to a reduction in the optimal order quantity, carbon tax amount, and total profit. The interest rate, proportion of defective items, unit purchasing cost, unit inspection cost, and unit penalty cost exhibit similar effects on these optimal solutions. The findings suggest that when the probability of misclassification, default risk coefficient, interest rate, proportion of defective items, unit purchasing cost, unit inspection cost, and unit penalty cost increase, the decision-maker should extend the replenishment time, shorten the credit payment time, and reduce the order quantity. Consequently, both the optimal carbon tax amount and the total annual profit decline.
- (2)
- An increase in the coefficient of payment time results in a shorter optimal replenishment time; a longer optimal credit payment period; and an increase in the optimal order quantity, carbon tax amount, and total profit. These effects are also observed with changes in the demand rate coefficient, unit selling price of a good product, and unit scrap price. These findings indicate that increases in the payment time coefficient, demand rate coefficient, unit selling price of good-quality products, and unit scrap value lead the decision-maker to shorten the replenishment cycle, extend the credit period, and increase the order quantity. Concurrently, both the optimal carbon tax amount and total annual profit rise.
- (3)
- Higher holding costs or greater carbon emissions associated with inventory storage reduce the optimal replenishment time and credit payment time, subsequently lowering the optimal order quantity, carbon tax amount, and overall profit. The analysis reveals that increases in holding costs or carbon emissions related to inventory storage prompt the decision-maker to shorten the replenishment cycle and credit payment period, as well as reduce the order quantity. Consequently, both the optimal carbon tax amount and the total annual profit decline.
- (4)
- As the unit carbon tax rises, the optimal replenishment cycle extends, and the carbon tax amount increases, but the credit payment period shortens, ultimately lowering the optimal order quantity and total profit. These patterns also hold for carbon emissions associated with purchasing and inspecting a unit product. The results show that as the unit carbon tax and the carbon emissions from purchasing and inspecting each product rise, the decision-maker tends to lengthen the replenishment cycle, shorten the credit period, and decrease the order quantity. This leads to an increase in the optimal carbon tax amount and a reduction in total annual profit.
- (5)
- A higher level of carbon emissions per order leads to longer optimal replenishment time, larger order quantity, and higher carbon tax amount but results in a shorter optimal credit payment time and reduced total profit. The results suggest that an increase in carbon emissions per order causes the decision-maker to lengthen the replenishment cycle, raise the order quantity, and reduce the credit payment period. Simultaneously, the optimal carbon tax amount rises, while the total annual profit decreases.
- (6)
- When the ordering cost increases, both the optimal replenishment time and order quantity expand, whereas the optimal credit payment time, the optimal carbon tax amount, and total profit all decrease. The results show that an increase in ordering costs causes the decision-maker to lengthen the replenishment cycle, increase the order quantity, and reduce the credit payment period. Meanwhile, both the optimal carbon tax amount and total annual profit decrease.
- (7)
- A higher inspection rate contributes to increases in the optimal credit payment time, replenishment time, order quantity, carbon tax amount, and total profit. The results suggest that an increase in the inspection rate causes the decision-maker to lengthen the replenishment cycle and credit payment period, as well as raise the order quantity. At the same time, both the optimal carbon tax and total annual profit rise.
- (8)
- A larger price discount results in a higher optimal order quantity and carbon tax amount while shortening the optimal advance payment time and replenishment time. This also leads to a reduction in the total optimal profit. The results suggest that as price discounts increase, the decision-maker tends to extend the advance payment period and increase the order quantity, while shortening the replenishment cycle. Simultaneously, the optimal carbon tax amount rises, whereas the total annual profit declines.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paknejad, M.J.; Nasri, F.; Affisco, J.F. Defective units in a continuous review (s,Q) system. Int. J. Prod. Res. 1995, 33, 2767–2777. [Google Scholar] [CrossRef]
- Salameh, M.K.; Jaber, M.Y. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, D.S.; Park, M.S. Economic production quantity model with imperfect-quality items, two-way imperfect inspection and sales return. Int. J. Prod. Econ. 2009, 121, 255–265. [Google Scholar] [CrossRef]
- Wang, C.H.; Dohi, T.; Tsai, W.C. Coordinated procurement/inspection and production model under inspection errors. Comput. Ind. Eng. 2010, 59, 473–478. [Google Scholar] [CrossRef]
- Rezaei, J. Economic order quantity and sampling inspection plans for imperfect items. Comput. Ind. Eng. 2016, 96, 1–7. [Google Scholar] [CrossRef]
- Das, B.C.; Das, B.; Mondal, S.K. An integrated production-inventory model with defective item dependent stochastic credit period. Comput. Ind. Eng. 2017, 110, 255–263. [Google Scholar] [CrossRef]
- Manna, A.K.; Dey, J.K.; Mondal, S.K. Imperfect production inventory model with production rate dependent defective rate and advertisement dependent demand. Comput. Ind. Eng. 2017, 104, 9–22. [Google Scholar] [CrossRef]
- Sarkar, S.; Giri, B.C. Stochastic supply chain model with imperfect production and controllable defective rate. Int. J. Syst. Sci. Oper. Logist. 2018, 5, 133–146. [Google Scholar] [CrossRef]
- Hauck, Z.; Rabta, B.; Reiner, G. Joint quality and pricing decisions in lot sizing models with defective items. Int. J. Prod. Res. 2021, 241, 108255. [Google Scholar] [CrossRef]
- Karakatsoulis, G.; Skouri, K. Optimal reorder level and lot size decisions for an inventory system with defective items. Appl. Math. Model. 2021, 92, 651–668. [Google Scholar] [CrossRef]
- Hauck, Z.; Rabta, B.; Reiner, G. Coordinating quality decisions in a two-stage supply chain under buyer dominance. Int. J. Prod. Res. 2023, 264, 108998. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M.; Moualek, I. An economic order quantity model for an imperfect production process with entropy cost. Int. J. Prod. Econ. 2009, 118, 26–33. [Google Scholar] [CrossRef]
- Mondal, B.; Bhunia, A.K.; Maiti, M. Inventory models for defective items incorporation marketing decisions with variable production cost. Appl. Math. Model. 2009, 33, 2845–2852. [Google Scholar] [CrossRef]
- Lin, T.Y. An economic order quantity with imperfect quality and quantity discounts. Appl. Math. Model. 2010, 34, 3158–3165. [Google Scholar] [CrossRef]
- Sana, S.S. A production inventory model in an imperfect production process. Eur. J. Oper. Res. 2010, 200, 451–464. [Google Scholar] [CrossRef]
- Sarker, B.; Sana, S.S.; Chaudhuri, K.S. Optimal reliability, production lot size and safety stock in an imperfect production system. Int. J. Math. Oper. Res. 2010, 2, 467–490. [Google Scholar] [CrossRef]
- Khan, M.; Jaber, M.Y.; Bonney, M. An economic order quantity (EOQ) for items with imperfect quality and inspection errors. Int. J. Prod. Econ. 2011, 133, 113–118. [Google Scholar] [CrossRef]
- Sarker, B.; Moon, I. An EPQ model with inflation in an imperfect production system. Appl. Math. Comput. 2011, 217, 6159–6167. [Google Scholar] [CrossRef]
- Sarkar, B.; Saren, S. Product inspection policy for an imperfect production system with inspection errors and warranty cost. Eur. J. Oper. Res. 2016, 248, 263–271. [Google Scholar] [CrossRef]
- Yu, H.F.; Hsu, W.K. An integrated inventory model with immediate return for defective items under unequal-sized shipments. J. Ind. Prod. Eng. 2016, 34, 70–77. [Google Scholar] [CrossRef]
- Pal, S.; Mahapatra, G.S. A manufacturing-oriented supply chain model for imperfect quality with inspection errors, stochastic demand under rework and shortages. Comput. Ind. Eng. 2017, 106, 229–314. [Google Scholar] [CrossRef]
- Hauck, Z.; Rabta, B.; Reiner, G. Analysis of screening decisions in inventory models with imperfect quality items. Int. J. Prod. Res. 2020, 118, 26–33. [Google Scholar] [CrossRef]
- Beranek, M.; Buscher, U. Optimal price and quality decisions of a supply chain game considering imperfect quality items and market segmentation. Appl. Math. Model. 2021, 91, 1227–1244. [Google Scholar] [CrossRef]
- Dye, C.Y.; Yang, C.T. Sustainable trade credit and replenishment decisions with credit-linked demand under carbon emission constraints. Eur. J. Oper. Res. 2015, 244, 187–200. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M.; Astanti, R.D. Three-echelon supply chain model considering carbon emission and item deterioration. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 368–383. [Google Scholar] [CrossRef]
- Jain, R.; Mittal, M.; Mangla, S.K.; Baraiya, R. Optimizing Supply Chain Strategies for Deteriorating Items and Imperfect Manufacturing under Carbon Emission Regulations. Comput. Ind. Eng. 2023, 182, 109350. [Google Scholar] [CrossRef]
- Chang, C.T.; Tseng, Y.T. The impacts of payment schemes and carbon emission policies on replenishment and pricing decisions for perishable products in a supply chain. Mathematics 2024, 12, 1033. [Google Scholar] [CrossRef]
- Sabzevar, N.; Enns, S.T.; Bergerson, J.; Kettunen, J. Modeling competitive firms’ performance under price-sensitive demand and cap-and-trade emissions constraints. Int. J. Prod. Econ. 2017, 184, 193–209. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Z.; Chen, S.C.; Cárdenas-barrón, L.E.; Skouri, K. Optimal replenishment decisions for perishable products under cash, advance, and credit payments considering carbon tax regulations. Int. J. Prod. Econ. 2020, 223, 107514. [Google Scholar] [CrossRef]
- An, S.; Li, B.; Song, D.; Chen, X. Green credit financing versus trade credit financing in a supply chain with carbon emission limits. Eur. J. Oper. Res. 2021, 292, 125–142. [Google Scholar] [CrossRef]
- Lu, C.J.; Gu, M.; Lee, T.S.; Yang, C.T. Impact of carbon emission policy combinations on the optimal production-inventory decisions for deteriorating items. Expert Syst. Appl. 2022, 201, 117234. [Google Scholar] [CrossRef]
- Fu, K.; Li, Y.; Mao, H.; Miao, Z. Firms’ production and green technology strategies: The role of emission asymmetry and carbon taxes. Eur. J. Oper. Res. 2023, 305, 1100–1112. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Z.; Tiwari, S.; Yang, L. Pricing and replenishment strategy for a perishable product under variable payment schemes and cap-and-trade regulation. Transp. Res. Part E 2023, 174, 103129. [Google Scholar] [CrossRef]
- He, P.; Sun, Y. The impact of retailer’s carbon tax on the price and carbon reduction decisions in supply chain. Comput. Ind. Eng. 2024, 190, 110034. [Google Scholar] [CrossRef]
- Goyal, S.K. Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1985, 36, 335–338. [Google Scholar] [CrossRef]
- Zhang, A.X. Optimal advance payment scheme involving fixed per-payment costs. Omega 1996, 24, 577–582. [Google Scholar] [CrossRef]
- Teng, J.T. On economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 2002, 53, 915–918. [Google Scholar] [CrossRef]
- Chang, C.T.; Ouyang, L.Y.; Teng, J.T. An EOQ model for deteriorating items under supplier credits linked to ordering quantity. Appl. Math. Model. 2003, 27, 983–996. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Goyal, S.K.; Goel, S.K. Retailer’s optimal replenishment decisions with credit-linked demand under permissible delay in payments. Eur. J. Oper. Res. 2008, 190, 130–135. [Google Scholar] [CrossRef]
- Thangam, A.; Uthayakumar, R. Two-echelon trade credit financing for perishable items in a supply chain when demand depends on both selling price and credit period. Comput. Ind. Eng. 2009, 57, 773–786. [Google Scholar] [CrossRef]
- Maiti, A.K.; Maiti, M.K.; Maiti, M. Inventory model with stochastic lead-time and price dependent demand incorporating advance payment. Appl. Math. Model. 2009, 33, 2433–2443. [Google Scholar] [CrossRef]
- Ouyang, L.Y.; Chang, C.T. Optimal production lot with imperfect production process under permissible delay in payments and complete backlogging. Int. J. Prod. Econ. 2013, 144, 610–617. [Google Scholar] [CrossRef]
- Liao, J.J.; Huang, K.N.; Ting, P.S. Optimal strategy of deteriorating items with capacity constraints under two-levels of trade credit policy. Appl. Math. Comput. 2014, 233, 647–658. [Google Scholar] [CrossRef]
- Chang, C.T.; Soong, P.Y.; Cheng, M.C. The influences of defective items and trade credits on replenishment decision. Int. J. Inf. Manag. Sci. 2017, 28, 113–132. [Google Scholar]
- Li, R.; Skouri, K.; Teng, J.T.; Yang, W.G. Seller’s optimal replenishment policy and payment term among advance, cash, and credit payments. Int. J. Prod. Econ. 2018, 197, 35–42. [Google Scholar] [CrossRef]
- Majumder, P.; Bera, U.K.; Maiti, M. An EPQ model of deteriorating substitute items under trade credit policy. Int. J. Oper. Res. 2019, 34, 162–212. [Google Scholar] [CrossRef]
- Panda, G.C.; Khan, M.A.; Shaikh, A.A. A credit policy approach in a two-warehouse inventory model for deteriorating items with price- and stock-dependent demand under partial backlogging. J. Ind. Eng. Int. 2019, 15, 147–170. [Google Scholar] [CrossRef]
- Bi, G.; Wang, P.; Wang, D.; Yin, Y. Optimal credit period and ordering policy with credit-dependent demand under two-level trade credit. Int. J. Prod. Econ. 2021, 242, 108311. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Z.; Tiwari, S.; Tao, Z. Retailer’s optimal strategy for a perishable product with increasing demand under various payment schemes. Ann. Oper. Res. 2022, 315, 899–929. [Google Scholar] [CrossRef]
- Chang, C.T.; Cheng, M.C.; Ouyang, L.Y. Deteriorating inventory model with advance-cash-credit payment schemes and partial backlogging. Soft Comput. 2025, 29, 2279–2295. [Google Scholar] [CrossRef]
- Teng, J.T.; Krommyda, I.P.; Skouri, K.; Lou, K.R. A comprehensive extension of optimal ordering policy for stock-dependent demand under progressive payment scheme. Eur. J. Oper. Res. 2011, 215, 97–104. [Google Scholar] [CrossRef]
- Chern, M.S.; Pan, Q.; Teng, J.T.; Chan, Y.L.; Chen, S.C. Stackelberg solution in a vendor-buyer supply chain model with permissible delay in payments. Int. J. Prod. Econ. 2013, 144, 397–404. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Pentico, D.W.; Jabalameli, M.S.; Aryanezhad, M. An economic order quantity model with multiple partial prepayments and partial backordering. Math. Comput. Model. 2013, 57, 311–323. [Google Scholar] [CrossRef]
- Yang, H.L.; Chang, C.T. A two-warehouse partial backlogging inventory model for deteriorating items with permissible delay in payment under inflation. Appl. Math. Model. 2013, 37, 2717–2726. [Google Scholar] [CrossRef]
- Taleizadeh, A.A. An economic order quantity model for deteriorating item in a purchasing system with multiple prepayments. Appl. Math. Model. 2014, 38, 5357–5366. [Google Scholar] [CrossRef]
- Wang, W.C.; Teng, J.T.; Lou, K.R. Seller’s optimal credit period and cycle time in a supply chain for deteriorating items with maximum lifetime. Eur. J. Oper. Res. 2014, 232, 315–321. [Google Scholar] [CrossRef]
- Wu, J.; Ouyang, L.Y.; Cárdenas-barrón, L.E.; Goyal, S.K. Optimal credit period and lot size for deteriorating items with expiration dates under two-level trade credit financing. Eur. J. Oper. Res. 2014, 237, 898–908. [Google Scholar] [CrossRef]
- Chen, S.C.; Teng, J.T. Inventory and credit decisions for time-varying deteriorating items with up-stream and down-stream trade credit financing by discounted cash-flow analysis. Eur. J. Oper. Res. 2015, 243, 566–575. [Google Scholar] [CrossRef]
- Teng, J.T.; Cárdenas-barrón, L.E.; Chang, H.J.; Wu, J.; Hu, Y. Inventory lot-size policies for deteriorating items with expiration dates and advance payments. Appl. Math. Model. 2016, 40, 8605–8616. [Google Scholar] [CrossRef]
- Li, R.; Chan, Y.L.; Chang, C.T.; Cárdenas-barrón, L.E. Pricing and lot-sizing policies for perishable products with advance-cash-credit payments by a discounted cash-flow analysis. Int. J. Prod. Econ. 2017, 193, 578–589. [Google Scholar] [CrossRef]
- Chang, C.T.; Ouyang, L.Y.; Teng, J.T.; Lai, K.K.; Cárdenas-Barrón, L.E. Manufacturer’s pricing and lot-sizing decisions for perishable goods under various payment terms by a discounted cash flow analysis. Int. J. Prod. Econ. 2019, 218, 83–95. [Google Scholar] [CrossRef]
- Li, R.; Liu, Y.; Teng, J.T.; Tsao, Y.C. Optimal pricing, lot-sizing and backordering decisions when a seller demands for an advance-cash-credit payment scheme. Eur. J. Oper. Res. 2019, 278, 283–295. [Google Scholar] [CrossRef]
- Zou, X.; Tian, B. Retailer’s optimal ordering and payment strategy under two-level and flexible two-part trade credit policy. Comput. Ind. Eng. 2020, 142, 106317. [Google Scholar] [CrossRef]
- Li, R.; Teng, J.T.; Chang, C.T. Lot-sizing and pricing decisions for perishable products under three-echelon supply chains when demand depends on price and stock-age. Ann. Oper. Res. 2021, 307, 303–328. [Google Scholar] [CrossRef]
- Lin, F.; Wang, W.C.; Teng, J.T.; Cárdenas-barrón, L.E. Pricing and lot-sizing decision for fresh goods when demand depends on unit price, displaying stocks and product age under generalized payments. Eur. J. Oper. Res. 2022, 296, 940–952. [Google Scholar]
- Tsao, Y.C.; Pantisoontorn, A.; Vu, T.L.; Chen, T.H. Optimal production and predictive maintenance decisions for deteriorated products under advance-cash-credit payments. Int. J. Prod. Econ. 2024, 269, 109132. [Google Scholar] [CrossRef]
- Teng, J.T.; Lou, K.R. Seller’s optimal credit period and replenishment time in a supply chain with up-stream and down-stream trade credits. J. Glob. Optim. 2012, 53, 417–430. [Google Scholar] [CrossRef]


| References | Demand Function | Payment Type | Inspection Error | Carbon Policy |
|---|---|---|---|---|
| Chang et al. [61] | Price | ACC | No | No |
| Chang and Tseng [27] | Price and stock age | ACC | No | Cap-and-trade and carbon tax |
| Chang et al. [50] | Constant | ACC | No | No |
| Chen and Teng [58] | Credit | Credit | No | No |
| Chern et al. [52] | Credit | Credit | No | No |
| Jain et al. [26] | Constant | No | No | Cap-and-trade, carbon tax and carbon offset |
| Jaggi et al. [39] | Credit | Credit | No | No |
| Khan et al. [17] | Constant | No | Yes | No |
| Li et al. [45] | Payment time | ACC | No | No |
| Li et al. [64] | Price and stock age | ACC | No | No |
| Li et al. [62] | Price | ACC | No | No |
| Pal and Mahapatra [21] | Stochastic | No | Yes | No |
| Rezaei [5] | Constant | No | Yes | No |
| Sabzevar et al. [28] | Price | No | No | Cap-and-trade |
| Shi et al. [29] | Constant | ACC | No | Carbon tax |
| Tsao et al. [66] | Constant | ACC | No | No |
| Wang et al. [4] | Constant | No | Yes | No |
| Wang et al. [56] | Credit | Credit | No | No |
| Wu et al. [57] | Constant | ACC | No | No |
| Yoo et al. [3] | Constant | No | Yes | No |
| This paper | Payment time | ACC | Yes | Carbon tax |
| Hessian Matrix | ||||||
|---|---|---|---|---|---|---|
| Decision | ||||||
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Trend | ↘ | ↗ | ↘ | ↘ | ↘ | |
| Trend | ↗ | ↘ | ↗ | ↗ | ↗ | |
| Trend | ↘ | ↘ | ↘ | ↘ | ↘ | |
| Trend | ↘ | ↗ | ↘ | ↗ | ↘ | |
| Trend | ↘ | ↗ | ↗ | ↗ | ↘ | |
| Trend | ↘ | ↗ | ↗ | ↘ | ↘ | |
| Trend | ↗ | ↗ | ↗ | ↗ | ↗ | |
| Decision | ||||||
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Trend | ↗ | ↘ | ↗ | ↗ | ↘ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-T.; Tseng, Y.-T. The Role of Misclassification and Carbon Tax Policies in Determining Payment Time and Replenishment Strategies for Imperfect Product Shipments. Mathematics 2025, 13, 1820. https://doi.org/10.3390/math13111820
Chang C-T, Tseng Y-T. The Role of Misclassification and Carbon Tax Policies in Determining Payment Time and Replenishment Strategies for Imperfect Product Shipments. Mathematics. 2025; 13(11):1820. https://doi.org/10.3390/math13111820
Chicago/Turabian StyleChang, Chun-Tao, and Yao-Ting Tseng. 2025. "The Role of Misclassification and Carbon Tax Policies in Determining Payment Time and Replenishment Strategies for Imperfect Product Shipments" Mathematics 13, no. 11: 1820. https://doi.org/10.3390/math13111820
APA StyleChang, C.-T., & Tseng, Y.-T. (2025). The Role of Misclassification and Carbon Tax Policies in Determining Payment Time and Replenishment Strategies for Imperfect Product Shipments. Mathematics, 13(11), 1820. https://doi.org/10.3390/math13111820






