A Simulated Annealing Approach for the Homogeneous Capacitated Vehicle Routing Problem

Abstract

This study addresses the Capacitated Vehicle Routing Problem (CVRP) known to be NP-hard. In this problem, a set of customers with varying demands is considered. To solve the problem, routes were generated for several vehicles with identical capacity, which were responsible for delivering products to a set of geographically dispersed customers. The purpose of the problem is to minimize the total cost of all routes. This problem was solved by applying the metaheuristic Simulated Annealing (SA) and incorporating four different neighborhoods to improve the initial solution generated randomly. In the SA, a set of cooling factors is used. The best solution obtained by SA is refined by the use of Hill Climbing using a double neighborhood. The algorithm was tested with instances from the literature in order to measure its effectiveness in solution quality and execution time. We tested the approach with 106 instances from the literature and obtained the optimum in 93 instances. The average time in most instances was less than five minutes. Delivery companies can benefit from this approach. They only need to identify the depot, the clients, and the distance between locations, and this approach can be used with relative ease.

1. Introduction

Every day, companies around the world face challenges related to optimizing their resources. These include companies that offer product transportation services or are fully dedicated to delivering goods. In recent years, the demand for home delivery has increased considerably for many reasons. For example, during the COVID-19 pandemic, consumer demand for home delivery services increased.

Shipping and logistics companies have become a highly sought-after service, and with this, the need for efficient route planning for their deliveries has increased. Poor route management can represent a significant and constant loss of resources and, in turn, generate problems that indirectly lead to significant revenue losses. One of the most common problems in logistics decision-making is finding ways to reduce transportation costs and improve customer service by identifying the best routes for a vehicle to follow to minimize travel time or distance. This problem is known as the Capacitated Vehicle Routing Problem (CVRP).

The vehicle routing problem arose as a generalization of the traveling salesman problem (TSP). This problem consists of a salesman who must visit a finite number of places (places where his clients are located). He must visit each location only once and return to the starting point. The solution to this problem consists of building the route that minimizes the distance that the agent has to travel. Stated another way, it consists of finding the shortest route that visits each city from a given list only once and returns to the city of origin. The CVRP arose from the problem known as multi-agent traveler (M-TSP). The M-TSP shares a similar approach, but it differs in that it does not involve customer demand or vehicle capacity. Instead, the M-TSP considers a set of M traveling agents where each customer must be visited exactly once by a single agent. Each salesman starts at the same place, called a depot, and must return to it when he finishes visiting his clients.

The Capacitated Vehicle Routing Problem (CVRP) arises in a company that must deliver a certain product among its customers and wants to find the route (or set of routes) with the lowest cost, which starts from a warehouse, visits each customer and returns to the same starting point. Each route is covered with a vehicle with a fixed capacity, and the demand of each customer is variable. The CVRP can be seen as an m-TSP, with the additional characteristics that each customer is associated with a demand and each vehicle has a capacity.

In the field of logistics, or even more specifically in the field of transportation, the problem of vehicle routing is one of the most important issues for many companies, due to the great loss of resources that can be caused by the lack of an adequate methodology for planning distribution routes. The vehicle routing problem answers the question “What is the optimal set of routes for a fleet of vehicles to satisfy the demands of a given set of customers?”; that is, the problem requires the delivery of a certain product, stored in a single location, to geographically dispersed customers who have a certain demand. The VRP involves the service of a delivery company, a depot and a given set of vehicles, which move on a given road network, to deliver products to a set of customers. Thus the problem determines a set of routes (one route for each given vehicle that starts and ends at the depot) such that all customer demands are satisfied and the transportation cost is minimized.

The VRP variant addressed in this paper is known as the “Capacitated Vehicle Routing Problem” (CVRP). In this variant, there is only one depot and each customer has a known demand that cannot be divided. Each vehicle has a fixed capacity and all vehicle capacities are identical. Likewise, each customer has coordinates that help us determine their location and also the distance between each customer and depot.

A literature review on the problem and the various solution methods previously employed is presented in Section 2. The mathematical model of the CVRP is described in Section 3. In Section 4 the description of the solution method—the Simulated Annealing metaheuristic—is presented along with the obtained results. In Section 5 and Section 6, a brief conclusion is given.

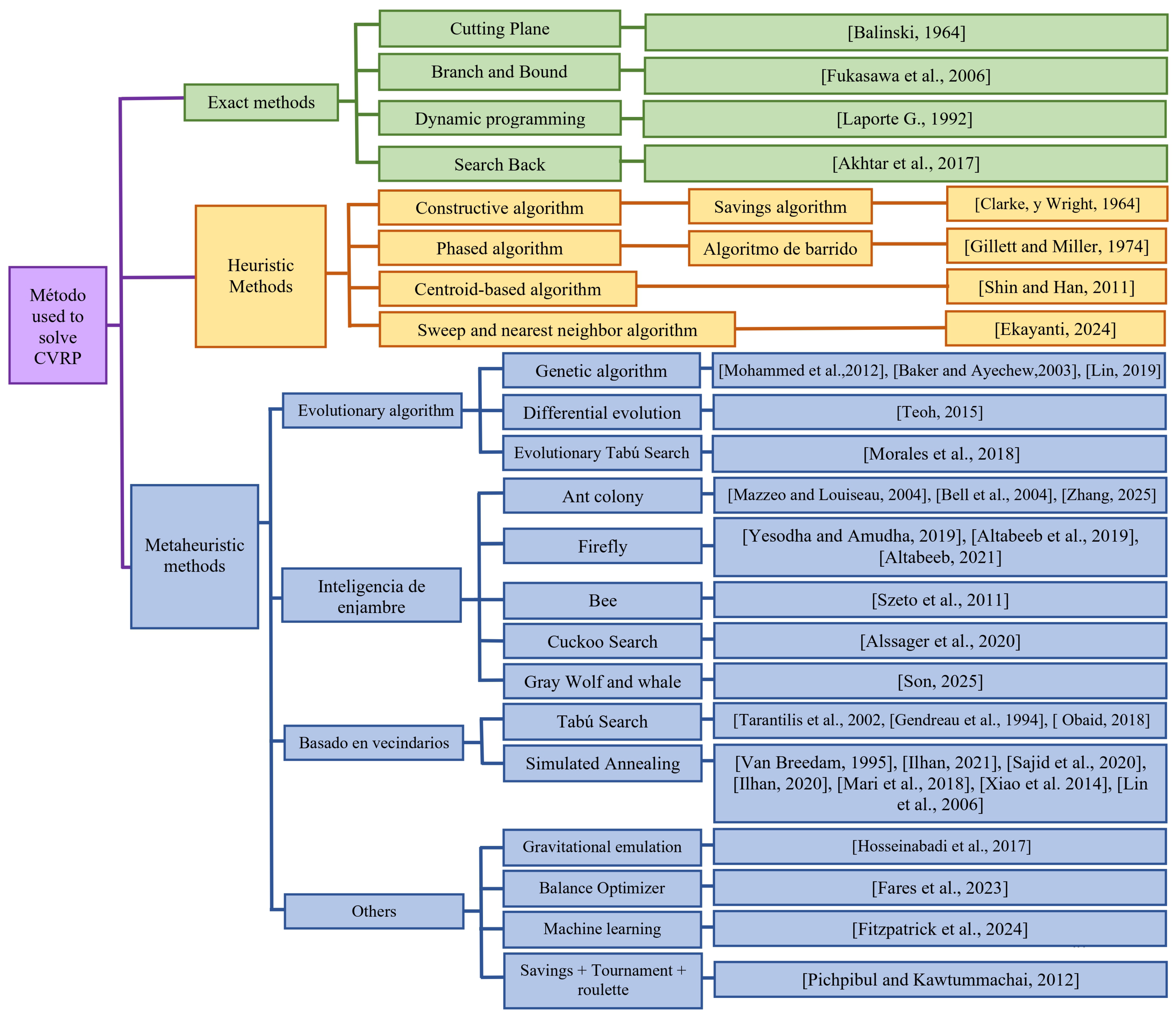
2. Literature Review

The origin of CVRP dates back to 1959, when George Dantzig and John Ramser [1] introduced the first definition of the problem. They described a real application of gasoline delivery to service stations and proposed the first mathematical model. In this article, they define the problem as “the determination of the optimal route for a fleet of vehicles departing from one or more depots (warehouses) to meet the demand of several geographically dispersed customers”.

Five years later, in 1964, Clarke & Wright [2] developed the first algorithm that was effective in solving CVRP, known as the savings algorithm. A diagram was developed to illustrate some of the work conducted on the vehicle routing problem (VRP) (see Figure 1).

2.1. Exact Methods

In the study by Balinski and Quandt [3], an integer formulation of the problem is solved. They used the algorithm known as cutting plane.

In [4], Fukasawa et al. present a bifurcation and cut algorithm that combines two approaches: one associated with traditional route relaxation and the other defined by limit, grade and capacity restrictions. They present a branch-cut-price algorithm that combines two approaches: intersection of two polytopes, one associated with a traditional Lagrange relaxation and the other defined by bounds, degrees and capacity constraints.

In [5] six representative examples are provided: two direct tree search methods based on different relaxations, a dynamic programming formulation and three integer linear programming algorithms. In the work of [6] is presented a backtracking algorithm on a CVRP problem to optimize waste collection routes to reduce economic costs and environmental impacts.

2.2. Heuristic Methods

Gillett and Miller [7] developed an algorithm called the “Sweep algorithm” to solve vehicle dispatch problems, and it consists of two parts: a forward step and a backward step that forms the routes in reverse order. Ref. [8] presents a heuristic algorithm based on centroids. The proposed algorithm consists of three phases: group construction, group adjustment and route establishment.

In [9] a combination of the Sweep and Nearest Neighbor algorithms was applied to address CVRP. The Sweep algorithm was used to group collection points according to their polar angle with respect to the depot. Within each group, the Nearest Neighbor algorithm was implemented to optimize the visit sequence, minimizing the total travel distance by sequentially selecting the next closest point. The Haversian distance was used to calculate the distances between points; the Euclidean method was not used.

2.3. Metaheuristic Methods

Concerning the methods used for the CVRP, a number of approaches can be enumerated as examples.

With regard to genetic algorithms, the work of Mohammed et al. [10] performs a chromosomal representation: the gene is encoded as numbers that are assigned to the chromosome. The number represents the sequence of stops (locations) at which goods are delivered. This coding is used to sort problems in which some crosses and mutations are corrected to maintain chromosome consistency.

Baker and Ayechew [11] performed a study on the application of a genetic algorithm to the basic problem of vehicle routing, for which the following is described: given n clients and m vehicles, the chromosome for an individual solution is shaped as a string of length n. The solution of a traveling salesman problem is required for each vehicle in order to make the transition from an implicit solution to an explicit one, allowing a value to be associated with each member of the population.

The metaheuristic proposed in [14] integrates a two-stage solution process: first, a set of feasible CVRP routes is obtained using a tabu search algorithm (Tabu-Search—TS), and second, a genetic algorithm (GA) is integrated to improve the feasibility of each route. The result of this is an evolutionary tabu search metaheuristic (Evolutive Tabu-Search—E-TS).

In [12], a hybrid order-aware genetic algorithm is proposed for the capacity vehicle routing problem in the Internet of Things. The method features a problem-specific initialization strategy and crossover operator. The former combines sweeping with randomization to address the trade-off between diversity and convergence, while the latter integrates neighborhood search heuristics to simultaneously find the best-fit offspring and check constraints.

Teoh et al. [13] developed an improved differential evolution with integrated local search (DELS) algorithm. The DELS approach generates a final solution using classical algorithmic operators of mutation, crossover, and selection.

There are many works using swarm intelligence algorithms to tackle this problem. For example, regarding the Ant Colony Optimization (ACO) algorithm, an ACO algorithm was developed in [15] for the CVRP, inspired by an analogy with the behavior of a real-life ant colony when it searches for food, and the authors proposed a metaheuristic technique: ants are procedures that construct solutions to an optimization problem. Another author [16] also worked with Ant Colony Optimization, where they were inspired by the mechanism by which ants communicate: through a chemical called pheromone.

In [17], ACO is hybridized with the k-means algorithm to help ACO to avoid local optimization. They used a path saving factor to improve the quality of the solutions and dynamically adjust the pheromone volatilization coefficient.

Another swarm algorithm is the firefly algorithm. The firefly technique used in [18] attempts to improve the quality of an initial solution by using a Clarke–Wright saving algorithm and a local search technique, and its performance is compared with the standard firefly algorithm and enhanced firefly. In [19] a CVRP-FA algorithm is proposed, which is the result of a hybridization of a firefly algorithm with two local search procedures. The objective function is to minimize the total distance of all routes in the corresponding firefly. Ref. [20] proposes a hybrid cooperative firefly algorithm (CVRP-CHFA) with multiple firefly algorithm (FA) populations. Each FA is hybridized with two types of local search (i.e., improved 2-opt as local search and 2-h-opt as mutation operator) and genetic operators. The proposed FAs periodically communicate to exchange some solutions (fireflies).

In [21] the implementation of an artificial bee colony algorithm is proposed and an improved version of this heuristic is also proposed. The algorithm belongs to a class of swarm intelligence algorithms that are inspired by the intelligent behavior of honey bees to find nectar sources around their hives. In the proposed algorithm, bees are divided into three types: worker bees, bystanders, and scouts.

In [22] a cuckoo search algorithm was implemented, the Cuco search (CS or cuckoo search) is a popular metaheuristic based on the reproductive strategy of the bird species: Cuco. Breeding parasitism is an interesting feature of the cuckoo bird, in which a cuckoo female lays her eggs in another bird’s nest observed and lets the host bird incubate and breed the cuckoo chicks.

In [23] a hybrid gray wolf and whale optimization algorithm (hGWOAM) is presented for CVRP. In addition to integrating the enhanced whale optimization algorithm (EWOA) and the gray wolf optimizer (GWO), the combination with tournament selection, adversarial learning, and mutation techniques is added.

The tabu search proposed by Glover [36] has been used to solve the CVRP, too. For example, ref. [24] describes a list-based threshold acceptance algorithm (LBTA); ref. [25] presents a tabu search heuristic for the problem of generating vehicle routes with capacity and route length restrictions.

In [26] the structure of their proposed model is planned with the objective that the program does not require a substantial database to store the data; for this reason, a tabu search is used, which speeds up the use of the program execution to acquire the solution.

Regarding the Simulated Annealing (SA) approach, in [27] the use of improvement methods based on Simulated Annealing is reported; the improvement methods considered aim at the relocation and/or exchange of stops or chains of stops between different routes, starting from a feasible initial solution. In the study of [28] a simulated cross-operator annealing algorithm called ISA-CO was proposed. In [37] hybrid Genetic and Simulated Annealing is proposed.

Other approaches based in SA include the population-based method [38], temperature reheating [29], hybrid SA with Variable Neighbourhood Search [30] and SA with local search [31]. Our approach is the only one that uses different alphas to the temperature reheating method.

Several other metaheuristic approaches have been used to solve the CVRP. Some examples include the following:

In [32] a local search algorithm of gravitational emulation was presented. This is based on the law of gravity and a group interactions. The proposed algorithm uses two of the four basic parameters of speed and gravitational force in physics, based on the concepts of random search and search agents, focusing in the fact that they are a collection of masses interacting with each other according to Newtonian gravity and the laws of motion.

An approach based on the balance optimizer (EO) algorithm was presented in [33]. The performance of the EO was then compared to that of an artificial bee colony algorithm, a particle swarm optimization algorithm, and a whale optimization algorithm.

In [34] a heuristic is proposed to solve the vehicle routing problem (CVRP) that integrates a machine learning heuristic with linear programming techniques. At the beginning, the problem instance is dynamically divided into smaller subproblems and a machine heuristic is applied to the smaller subproblems. This allows the machine learning heuristic to always operate on smaller problems similar in size to those for which it has been trained. Machine learning heuristics generate many solutions for each subproblem which are then combined using a fixed partition approach.

In [35] an algorithm is proposed based on the Clarke and Wright (CW) saving algorithm; the result was to hybridize the CW with tournament and roulette selections to obtain a new algorithm, ICW, which is based on calculating the savings when combining two clients in the same route. In the sequential version, a route is expanded until no more can be merged, and in the parallel version several routes can be built in parallel.

CVRP is a problem in which much literature is still published to address route design while the total distance is minimized and the capacity constraint is not broken.

3. Mathematical Model

The basic vehicle routing problem can be named as VRP or CVRP. The problem consists mainly in obtaining a set of routes using the smallest number of vehicles and minimizing the distance traveled. The routes must all start in a single depot and return to it, after having satisfied the deterministic (previously known) and indivisible demands of a set of customers (or clients). The clients are geographically dispersed and have different demands. The vehicle capacity is the maximum allowed demand that each vehicle can transport. This is the constraint that gives name to the problem.

A “route” is considered an ordered road or route previously generated for a journey; in this case, for the purpose of delivery of products to customers, each of the routes is assigned to a different vehicle and the number of customers for each route is determined by the capacity of the vehicles.

The general components that are established for the study of a routing problem are customers, vehicles, storage, restrictions and targets. There are three restrictions on CVRP:

• Visit each client (node) only once.
• Start the tour and return to the starting point (depot).
• Do not exceed vehicle capacity.

The CVRP model determines a number of routes with minimum total cost; this cost is the result of the sum of the distances obtained between arcs belonging to all routes.

The following indices, parameters and variables are used for the model of CVRP of [39]:

• Indices
  The model indices are as follows:
  • i = starting node $i(1,2,.....,n)$;
  • j = arrival node $j(1,2,....,n)$;
  • n = total nodes;
  • k = vehicle $k(1,2,....,K)$.
• Parameters
  The parameters of the problem are as follows:
  • $C_{ij}$ = transport cost from node i to node j;
  • $d_j$ = demand at node j;
  • M = capacity of resource k;
  • n = number of customers.
• Variables
  The variables defined are as follows:
  • $x_{ij}^k$ = 1 if the vehicle k is assigned to traverse the arc from node i to node j or zero otherwise.
  • $y_{ij}$ = 1 if the path is from i to j or zero otherwise.
  • K = number of vehicles to be used.

So, the model is [40]

Minimize

$$\sum _{(i,j){\in }_A}{C}_{ij}{Y}_{ij}$$

(1)

subject to

$$\sum _{i\le k\le K}{x}_{ij}^k=Y_{ij};\forall i,j$$

(2)

$$\sum _{i\le j\le n}{y}_{ij}=1;\forall i$$

(3)

$$\sum _{i\le j\le n}{y}_{ij}=1;\forall j$$

(4)

$$\sum _{i\le j\le n}{y}_{0j}=k;$$

(5)

$$\sum _{i\le j\le n}{y}_{i0}=k;$$

(6)

$$\sum _{i\le j\le n}\sum _{1\le j\le n}{d}_i{x}_{ij}^k\le M;\forall k$$

(7)

$$\sum _{i\in Q}\sum _{j\in Q}{y}_{ij}\le \left|Q\right|-1$$

(8)

$$\forall subsetQof(1,2,\dots n)k\le K$$

(9)

$$y_{ij}\in \{0,1\};\forall (i,j)\in A$$

(10)

$$x_{ij}^k\in \{0,1\};\forall (i,j)\in A,\forall k$$

(11)

Set A is defined as $A=\{(i,j)y_{i,j}=1\}$ (to each pair of arcs $(i,j)$ such that $y=1$).

Thus the equations of the model are described as follows:

Equation (1) is the objective function of the CVRP model; it minimizes the distance traveled. Equation (2) is responsible for making explicit the relationship between variables x and y. If a vehicle uses the route from i to j (some $x_{i,j}^k=1$), then $y_{i,j}$ will be one. Vehicle k is used on the arc $(i,j)$. In Equations (3) and (4) the variable $y_{i,j}$ indicates the activation of the arc (it indicates that the route has been completed). Both constraints ensure that every customer is an intermediate node on some route (that no customers are forgotten). Equations (5) and (6) indicate that k is the number of vehicles used in the solution and that all those leaving the depot or warehouse must return to it; this means that all routes must be traveled. It is ensured in Equation (7) that the capacity of any vehicle is not exceeded for any value of k. In (8) it is ensured that the solution does not contain cycles by using Q representing the set of nodes 1, 2, … n. In other words, it tells us that the number of paths must be the existing paths. The inequation (9) limits the number of vehicles to be used in the solution. Equations (10) and (11) indicate that both the variables $x_{ij}^k$ and $y_{ij}$ are binary (they can only take the value 0 or 1). An example of a solution can be seen in Figure 2. The capacity of the vehicle in this example is 15. Route 1 includes nodes 1, 8, 9, and 0. The sum of the weight in this route is 13. Route 2 contains nodes 1, 2, 3, and 4. The sum of the weight in this route is 15, which is the maximum allowed.

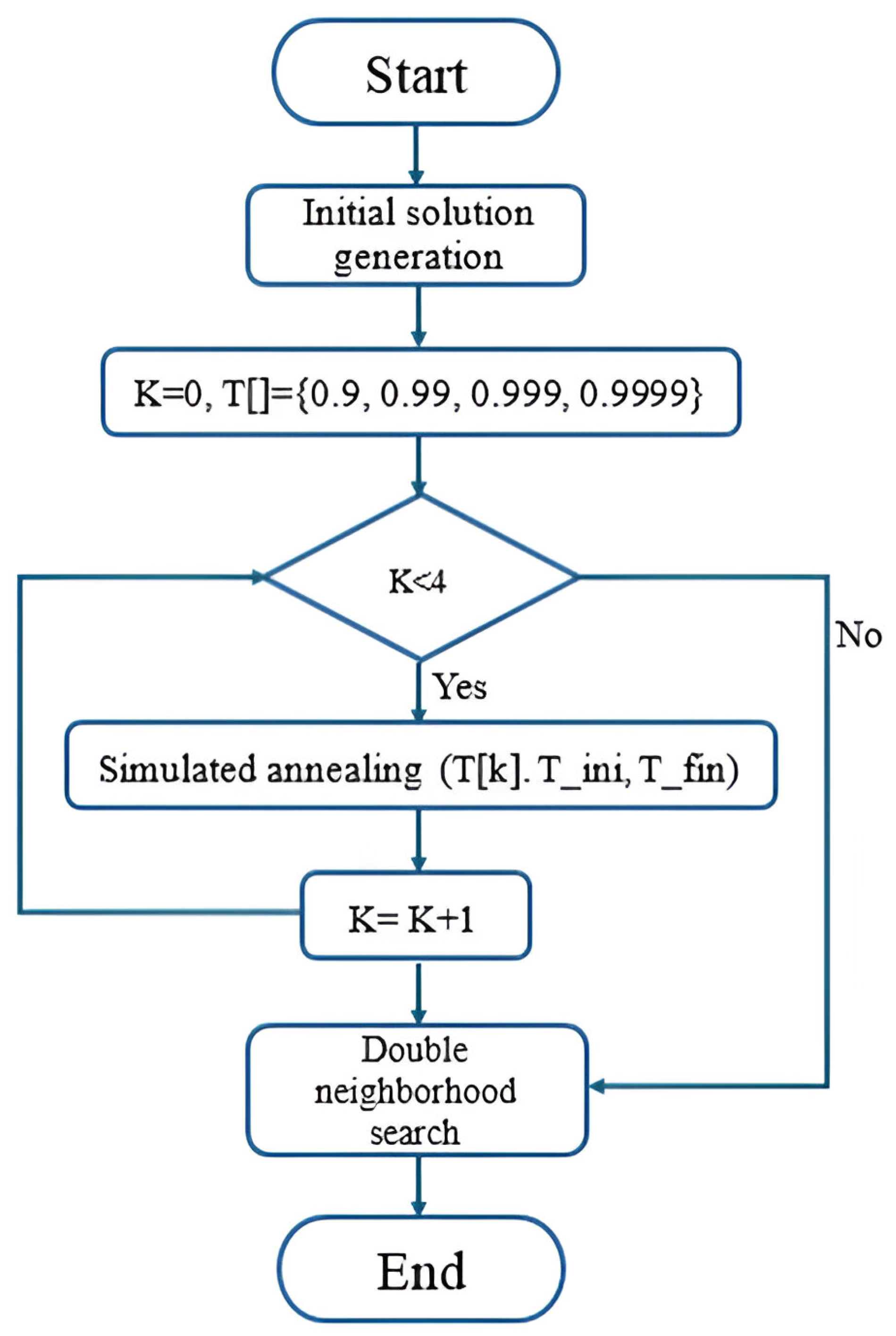
4. Methodology

To tackle the CVRP problem, a procedure was first designed to obtain a feasible initial solution. The solution was then improved using the Simulated Annealing (SA) algorithm. Finally, the solution was further improved using a Hill Climbing algorithm with a double neighborhood. The framing research question of this research is as follows: with an implementation of SA with re-heat, increasing parameter alpha and using a local search with a double neighbourhood to improve the solution, is it possible to obtain results of “good” quality? This question is addressed in this section and the next. The general algorithm (Algorithm 1) is shown in Figure 3.

Algorithm 1 Pseudocode of the main function

$A=0.9,0.99,0.999,0.9999$ $S=Feasible\_Solution\left(\right)$ $T_{ini}=Z\left(S\right);$ $T_{fin}=0.00001$ for  $i=0;i<NUM\_TEMPERATURAS;i++$  do     $alpha=A\left[i\right];$     $S_{best}=SA(T_{ini},T_{fin},alpha,S)$     $Return S_{best};$ end for

4.1. Initial Solution

The function that generates the initial solution works as follows: For an empty route $R_1$, customers randomly selected are assigned to the route. When a customer is selected, the vehicle’s capacity is always checked to ensure it is not exceeded. When it is no longer possible to assign other customer, another empty route is generated. This process is repeated until no more customers remain to be assigned. It should be noted that the initial solution does not consider the distance between customers, only their demand. As an example of an initial solution, the “E-n16-k3” instance from Christofides and Eilon E [41] was used. This solution would be visually appreciated as depicted in Figure 4.

4.2. Simulated Annealing

The metaheuristic technique of Simulated Annealing (SA) is an analogy that simulates the physical cooling process of solid annealing. SA is a neighborhood search algorithm for combinatorial optimization problems based on the Boltzmann distribution; this means that, to escape from local optima, the algorithm allows certain movements that worsen the objective function [42]. The Simulated Annealing (SA) algorithm was selected due to its capacity to escape local optima, provided that the temperature is sufficiently high. Another interesting feature is the guarantee of finding a global optimum (at least when certain theoretical conditions are met).

Implementation of neighbourhoods: A “neighbourhood” refers to the set of neighbouring solutions generated by perturbations or modifications in each iteration based on an initial solution. In each iteration of the algorithm, a client exchange is performed, and the cost of the new solution is calculated. A comparison of these values allows for an assessment of whether the modification improved or worsened the quality. The four neighbourhoods (corresponding to four different types of movements) applied in the algorithm in this work are the following:

• Same-route swapping ($N_1$): The first perturbation mechanism employed is the swapping of two customers on the same route. To achieve this, two customers are randomly selected and swap places. With this change in order, the cost of the solution will also change, as it will alter the total distance of that route and, consequently, the cost of the entire solution. This swapping does not alter the total route capacity, as both customer demands were previously considered.
• Interchanging Different Routes ($N_2$): The second neighbourhood used is similar to the previous one, except that the routes are different. That is, two clients or nodes are interchanged, but they belong to different routes. Two clients are randomly selected (this time belonging to different routes), and before performing the interchange, the feasibility of the interchange is verified. This interchange requires verifying the capacities of both vehicles to avoid exceeding the maximum capacity M of any vehicle.
• Relocate ($N_3$): For the third neighborhood, only one node is randomly selected from any route and inserted in the same route in another position. The client can be inserted in any order on the route: it is inserted randomly in any position.
• Reinsertion ($N_4$): For the fourth neighborhood, one client $c_1$ is randomly selected from any route $R_1$, and inserted in another route $R_2$. Upon insertion of $c_1$ into $R_2$, it was verified that the sum of demand of $R_2$ did not exceed the maximum capacity M. The node is removed from the route to which it was previously assigned and reinserted into another. Again, the client can be inserted randomly in any position of the receiving route $R_2$.

Some examples of neighborhoods are shown in Figure 5.

To obtain a new solution $S^{\prime }$, an operation is performed in the following manner. Given an existing solution S, the set F of feasible neighbors is calculated using the four neighborhoods. A random solution $S^{\prime }$ from the set F is then chosen and evaluated. The solution $S^{\prime }$ is accepted if its cost is less than or equal to the cost of S. In cases where the cost is greater, a random number r is generated in the range [0,1]. The difference $\delta =cost\left(S^{\prime }\right)-cost\left(S\right)$ is then computed, and if the condition $r<e^{-\delta /\tau }$ is satisfied, the solution $S^{\prime }$ is accepted. The condition of termination is when $\tau$ reaches the temperature $T_{fin}$; this means that the system is “frozen” and it is not possible to escape from the local optimum to continue the search (see Algorithm 2).

Algorithm 2 Pseudocode of SA

$Z_{min}\leftarrow z\leftarrow cost\left(S\right);\tau \leftarrow T_0;S_{best}\leftarrow S;$ while  $\tau \le T_f$  do     $cont\leftarrow 0;$     while $cont\le MAXITER$ do         $S^{\prime }\leftarrow perturb\left(S\right);$         $\delta \leftarrow cost\left(S^{\prime }\right)-cost\left(S\right);$         if $Uni(0,1)<e^{-\delta /\tau }or\delta <0$ then            $S\leftarrow S^{\prime };$         end if         if $cost\left(S\right)<cost\left(S_{best}\right)$ then            $zmin\leftarrow cost\left(S\right);S_{best}\leftarrow S;$         end if         $cont\leftarrow cont+1;$     end while     $\tau \leftarrow a\tau ;$ end while

Note: $T_{ini}$ is updated according to the acceptance percentage. If the acceptance percentage of a temperature $\tau$ is less than 95%, $T_0$ will take the value of $\tau :T_0=\tau$.

4.3. Double-Neighborhood Search

After running the Simulated Annealing, a double-neighborhood search is performed. This is achieved by taking the best solution found so far by the Simulated Annealing, and applying two neighbourhoods to it, using one neighbourhood after another to increase the solution’s diversification. The process with a given solution S applies all the possible neighbourhoods $N_1,N_1$. Thus, we can explore all possible solutions found by applying neighbourhood $N_1$ twice. Afterwards, if an improvement in S is not found, the algorithm searches in the neighbourhood $N_1,N_2$; again, all the possible neighbours are explored. The process continues until a better solution $S^{\prime }$ is found or all possible combinations of neighbourhoods are explored and no improvement is found.

The search for a better solution using double neighborhoods is illustrated in Figure 6. The solutions are explored until the second level of the tree. When a better solution is found it will be the new root and the search is reset. The process continues until any improvement is found.

4.4. Parameters of SA

The values tested for $MAXITER$ were 500, 1000, 1500 and 2000 iterations. Based on the results obtained, the value chosen for the internal cycle was 1000 iterations. $T_{ini}$ was set equal to the value of function objective of the initial solution. $T_{fin}$ was set equal to $1\times {10}^{-5}$. The SA performed multiple re-heating steps, and in each one, $alpha$ takes a different value, begins with $0.9$ and ends with $0.9999$.

5. Results

Our algorithm was executed on a computer with the following features: Windows 10, Intel i64470 processor, 3.4 GHZ, 16 GB, and Visual Studio 2012 under C++ language.

The results obtained in this work are presented below in column 3 of each table, respectively, with the processing time in column 4. In addition, they are compared with some results from the corresponding literature: KMACO [17], CHFA [20], Dyn-BCP [4], DELS [13], ICW [35], and OHGA [12] and, for the Taillard benchmark, GELS [32], OCGA [43], AGES [44], and JCell2o1i [45]. These algorithms were chosen because they extensively used the benchmark proposed in the literature, regardless of the approach used, where other approaches only used a subset smaller than the instances available in the literature. In all tables, the best-known solution appears in the column title as “BKS”. When a solution is optimal, it is marked in bold and with an asterisk (*). Our approach, Simulated Annealing with Hill Climbing and Double Neighbourhoods, is in the column titled “SAHDN”.

The instances used to test our proposal have different origins. The 27 instances of type “A”, 23 instances of type “B” and 24 instances of type “P” were proposed by Augerat et al. in [46]. The 13 instances of type “E” and 5 instances of type “M” were proposed by Christofides and Eilon E. in [41]. Fisher proposed three instances of type “F” in [47]. Finally, Rochat and Taillard proposed 13 instances in [48].

In

Table 1. Group A results table. The results of our proposed method, SA with Hill Climbing and Double Neighbourhoods (SAHDN), are in the third column. The optimum are marked in bold and an asterisk.

Instance	BKS	KMACO	CHFA	Dyn-BCP	DELS	ICW	OHGA	SAHDN	Time	Avg
A-n32-k5	784 *	784 *	784 *	-	784 *	784 *	784 *	784 *	56.11	784 *
A-n33-k5	661 *	661 *	661 *	-	661 *	661 *	661 *	661 *	53.64	661 *
A-n33-k6	742 *	742 *	742 *	-	742 *	742 *	742 *	742 *	57.14	742 *
A-n34-k5	778 *	778 *	778 *	-	778 *	778 *	778 *	778 *	55.56	778 *
A-n36-k5	799 *	799 *	799 *	-	799 *	799 *	799 *	799 *	56.33	799 *
A-n37-k5	669 *	669 *	669 *	669 *	669 *	669 *	669 *	669 *	60.21	669 *
A-n37-k6	949 *	949 *	949 *	949 *	949 *	949 *	949 *	949 *	58.83	949 *
A-n38-k5	730 *	730 *	730 *	730 *	730 *	730 *	730 *	730 *	58.83	730 *
A-n39-k5	822 *	822 *	822 *	822 *	822 *	822 *	822 *	822 *	57.77	822.01
A-n39-k6	831 *	831 *	831 *	831 *	831 *	831 *	833	831 *	64.41	832.42
A-n44-k6	937 *	937 *	937 *	937 *	937 *	937 *	937 *	937 *	63.69	937 *
A-n45-k6	944 *	944 *	944 *	944 *	944 *	944 *	953	944 *	61.27	954.42
A-n45-k7	1146 *	1146 *	1146 *	1146 *	1146 *	1146 *	1146 *	1146 *	70.88	1146.05
A-n46-k7	914 *	914 *	914 *	914 *	914 *	914 *	914 *	914 *	73.79	914 *
A-n48-k7	1073 *	1073 *	1073 *	1073 *	1073 *	1073 *	1073 *	1073 *	73.99	1073.22
A-n53-k7	1010 *	1010 *	1010 *	1010 *	1010 *	1010 *	1017	1010 *	79.55	1014.63
A-n54-k7	1167 *	1169	1167 *	1167 *	1167 *	1167 *	1167 *	1167 *	82.66	1167.71
A-n55-k9	1073 *	1074	1073 *	1073 *	1073 *	1073 *	1074	1073 *	86.31	1073.17
A-n60-k9	1354 *	1374	1354 *	1354 *	1354 *	1354 *	1355	1354 *	95.68	1357.8
A-n61-k9	1034 *	1035	1035	1034 *	1035	1034 *	1035	1034 *	83.52	1035.49
A-n62-k8	1288 *	1297	1294	1288 *	1288 *	1298	1308	1288 *	94.8	1297.9
A-n63-k9	1616 *	1631	1616 *	1616 *	1624	1616 *	1630	1616 *	89.24	1626.98
A-n63-k10	1314 *	1327	1315	1314 *	1316	1314 *	1329	1314 *	97.54	1318.87
A-n64-k9	1401 *	1427	1411	1401 *	1416	1415	1416	1401 *	105.22	1414.16
A-n65-k9	1174 *	1177	1177	1174 *	1181	1174 *	1184	1174 *	88.66	1179.6
A-n69-k9	1159 *	1159 *	1159 *	1159 *	1165	1159 *	1170	1159 *	111.64	1166.78
A-n80-k10	1763 *	1768	1763 *	1763 *	1779	1772	1790	1763 *	118.17	1778.59

, using type “A” as an example, our algorithm was able to obtain the optimum for the 27 instances. The average time is between one and two minutes by running type “A” in all instances.

In

Table 2. Results with instances of type B. In the results marked with (a), OHGA gives better results but with a different value of k. A value that was either the same or better was able to be obtained using the same value of k that was used in OHGA. The optimum are marked in bold and an asterisk.

Instance	BKS	KMACO	CHFA	Dyn-BCP	DELS	ICW	OHGA	SAHDN	Time	Avg
B-n31-k5	672 *	672 *	672 *	-	672 *	672 *	672 *	672 *	55.23	672 *
B-n34-k5	788 *	788 *	788 *	-	788 *	788 *	788 *	788 *	64.25	788 *
B-n35-k5	955 *	955 *	955 *	-	955 *	955 *	955 *	955 *	67.5	955 *
B-n38-k6	805 *	805 *	805 *	805 *	805 *	805 *	805 *	805 *	69.46	805.05
B-n39-k5	549 *	549 *	549 *	549 *	549 *	549 *	549 *	549 *	73.73	549 *
B-n41-k6	829 *	829 *	829 *	829 *	829 *	829 *	829 *	829 *	70.33	829.26
B-n43-k6	742 *	742 *	742 *	742 *	742 *	742 *	742 *	742 *	74.85	742.02
B-n44-k7	909 *	909 *	909 *	909 *	909 *	909 *	909 *	909 *	80.14	909.02
B-n45-k5	751 *	751 *	751 *	751 *	751 *	751 *	751 *	751 *	75.87	751.06
B-n45-k6	678 *	678 *	678 *	678 *	678 *	678 *	680	678 *	67.52	681.91
B-n50-k7	741 *	741 *	741 *	741 *	741 *	741 *	741 *	741 *	84.94	741 *
B-n50-k8	1312 *	1317	1312 *	1312 *	1313	1312 *	1315	1312 *	82.8	1312.84
B-n51-k7	1032 *	1034	1032 *	1032 *	1033	-	(a)	1032 *	82.8	1312.84
B-n52-k7	747 *	747 *	747 *	747 *	747 *	751	747 *	747 *	90.04	747.06
B-n56-k7	707 *	710	707 *	707 *	707 *	707 *	711	707 *	104.99	707.68
B-n57-k7	1153 *	1165	-	1153 *	1166	-	(a)	1153 *	94.02	1202.56
B-n57-k9	1598 *	1608	1603	1598 *	1599	1598 *	1603	1598 *	101.61	1602.12
B-n63-k10	1496 *	1530	1496 *	1496 *	1504	-	1531	1496 *	109.48	1516.11
B-n64-k9	861 *	866	861 *	861 *	861 *	861 *	867	861 *	94.68	862.98
B-n66-k9	1316 *	1323	1316 *	1316 *	1322	1320	1324	1316 *	104.7	1321.54
B-n67-k10	1032 *	1036	1033	1032 *	1032 *	1032 *	1042	1032 *	105.49	1038.35
B-n68-k9	1272 *	1277	1273	1272 *	1281	1281	1290	1273	113.07	1286.63
B-n78-k10	1221 *	1228	1221 *	1221 *	1230	1238	1245	1221 *	119.66	1236.93

, for these instances of type “B”, we were able to obtain the optimum in 22 of 23 instances. In instance B-n51-k7, OHGA obtains 1017 but increases the number of routes by one, thus using k = “8”. A solution of 1016 with k = “8” was obtained. This result is not displayed in the table, as it is considered a different instance from the original proposed. In B-n51-k7, the optimum reported in the literature was obtained by using the original value of k. For instance B-n57-k7, a solution of 1140 was reported by OHFA, once again with the number of routes increased by one. The same value was obtained by using the same k from OHFA. This result is also not displayed in the table because it can be considered another instance. The average time of our algorithm is between 55 and 120 s by running type “B” in all instances.

In

Table 3. The Simulated Annealing with Hill Climbing and Double Neighbourhoods (SAHDN) tested in Group E of instances. The optimum are marked in bold and an asterisk.

Instance	BK	CHFA	Dyn-BCP	DELS	ICW	OHGA	SAHDN	Time
E-n13-k4	247 *	-	247 *	247 *	-	-	247 *	22.11
E-n22-k4	375 *	375 *	375 *	375 *	375 *	375 *	375 *	35.41
E-n23-k3	569 *	569 *	569 *	569 *	569 *	569 *	569 *	44
E-n30-k3	534 *	534 *	534 *	534 *	534 *	503	534 *	56.91
E-n31-k7	379 *	-	379 *	390	-	-	379 *	43.01
E-n33-k4	835 *	835 *	835 *	835 *	835 *	835 *	835 *	59.92
E-n51-k5	521 *	521 *	521 *	521 *	521 *	521 *	521 *	70.12
E-n76-k7	682 *	682 *	682 *	689	686	692	682 *	118.54
E-n76-k8	735 *	736	735 *	738	742	740	735 *	99.29
E-n76-k10	830 *	-	830 *	843	839	843	830 *	92.1
E-n76-k14	1021 *	-	1021 *	1042	1027	1038	1021 *	91.83
E-n101-k8	815 *	-	815 *	822	821	822	815 *	217.66
E-n101-k14	1067 *	1071	1067 *	1086	1084	1095	1069	166.09

, for instances of type “E” our algorithm managed to obtain the optimal value for 12 of the 13 instances. The average execution time ranges from 22 s to 4 min. On instance E-n30-k3, OHGA obtained 503, but increased the number of routes by one, using k = “3”. The same result was also obtained with one fewer route; however, it is considered a different instance from the original proposal. The optimal value reported in the literature was also obtained using the original value of k.

In

Table 4. Results of SAHDN in Group F compared against other methods. The optimum are marked in bold and an asterisk.

Instance	BK	CHFA	Dyn-BCP	ICW	OHGA	SAHDN	Time
F-n45-k4	724 *	-	724 *	724 *	724 *	724 *	77.38
F-n72-k4	237 *	237 *	237 *	237 *	237 *	237 *	114.02
F-n135-k7	1162 *	1163	1162 *	1162 *	-	1162 *	938.58

, for instances of type “F,” our algorithm was able to obtain the optimal value for all three instances. The average execution time ranges from a minute and a half to 16 min for this group of instances.

In

Table 5. Results of our approach for the instances of type M. The optimum are marked in bold and an asterisk.

Instance	BK	CHFA	Dyn-BCP	SAHDN	Time
M-n101-k10	820 *	829	820 *	820 *	262.62
M-n121-k7	1034 *	1034 *	1034 *	1034 *	262.77
M-n151-k12	1015 *	1021	-	1030	702.39
M-n200-k16	1274 *	-	-	1355	346.85
M-n200-k17	1275 *	1289	-	1311	2076.29

, for instances of type “M,” our algorithm was able to obtain the optimal value for two of the five instances. The average execution time ranges from 6 to 34.5 min for this group of instances.

In

Table 6. SAHDN when compared against another approach. The optimum are marked in bold and an asterisk.

Instance	BK	KMACO	CHFA	Dyn-BCP	DELS	ICW	OHGA	SAHDN	Time
P-n16-k8	450 *	450 *	450 *	450 *	450 *	450 *	450 *	450 *	24.14
P-n19-k2	212 *	212 *	212 *	212 *	212 *	212 *	212 *	212 *	28.56
P-n20-k2	216 *	216 *	216 *	216 *	216 *	216 *	216 *	216 *	29.46
P-n21-k2	211 *	211 *	211 *	211 *	211 *	211 *	211 *	211 *	32.96
P-n22-k2	216 *	216 *	216 *	216 *	216 *	216 *	216 *	216 *	34.06
P-n22-k8	603 *	603 *	603 *	603 *	603 *	603 *	603 *	603 *	41.41
P-n23-k8	529 *	529 *	529 *	529 *	533	529 *	529 *	529 *	27.61
P-n40-k5	458 *	458 *	458 *	458 *	458 *	458 *	458 *	458 *	57.6
P-n45-k5	510 *	510 *	510 *	510 *	510 *	510 *	510 *	510 *	62.91
P-n50-k7	554 *	556	554 *	554 *	554 *	554 *	556	554 *	65.67
P-n50-k8	631 *	643	631 *	631 *	641	631 *	630	632	55.88
P-n50-k10	696 *	701	696 *	696 *	696 *	696 *	700	696 *	64.69
P-n51-k10	741 *	744	741 *	741 *	742	741 *	741 *	741 *	62.87
P-n55-k7	568 *	574	568 *	568 *	568 *	568 *	568 *	568 *	74.81
P-n55-k10	694 *	702	694 *	694 *	694 *	697	698	694 *	73.21
P-n55-k15	989 *	-	-	989 *	989 *	-	989 *	989 *	67.37
P-n60-k10	744 *	757	744 *	744 *	744 *	744 *	749	744 *	76.83
P-n60-k15	968 *	984	968 *	968 *	968 *	968 *	985	968 *	83.05
P-n65-k10	792 *	792 *	792 *	792 *	792 *	792 *	797	792 *	91
P-n70-k10	827 *	842	827 *	827 *	827 *	827 *	841	827 *	89.86
P-n76-k4	593 *	598	593 *	593 *	593 *	597	600	593 *	108.37
P-n76-k5	627 *	632	627 *	627 *	629	627 *	630	627 *	110.82
P-n101-k4	681 *	692	681 *	681 *	685	681 *	696	681 *	309.8

, for instances of type “P”, our algorithm obtained the optimal value for 22 of the 23 instances. The average execution time ranges from 1.5 to 5.5 min for this group of instances. On instance P-n55-k15, our algorithm obtains 959, but increases the number of routes by one, using k = “14”. This result is considered a different instance from the original proposal.

For the “Taillard” instances in

Table 7. Table of results for the Taillard group. The results for our proposal, SA with Hill Climbing and Double Neighborhoods (SAHDN), are shown in the third column. The optimum are marked in bold and an asterisk.

Instance	BK	GELS	OCGA	AGES	JCell2o1i	SAHDN	Time
tai75a	1618.36 *	1618.36 *	1618.36 *	1618.36 *	1618.36 *	1618.36 *	160.67
tai75b	1344.62 *	1344.62 *	1344.63	1344.64	1344.62 *	1344.62 *	157.99
tai75c	1291.01 *	1291.01 *	1291.01 *	1291.01 *	1291.01 *	1291.01 *	163.29
tai75d	1365.42 *	1365.42 *	1365.42 *	1365.42 *	1365.42 *	1365.42 *	179.73
tai100a	2041.34 *	2041.34 *	2050.64	2041.34 *	2047.90	2050.12	258.46
tai100b	1939.9 *	1947.07	1939.9 *	1939.9 *	1940.36	1940.5	264.19
tai100c	1406.2 *	1406.2 *	1408.40	1406.2 *	1411.66	1413.95	266.61
tai100d	1580.46 *	1581.25	1581.22	1581.25	1584.20	1580.46 *	271.08
tai150a	3055.23 *	3069.14	3055.23 *	3055.23 *	3056.41	3072.14	805.39
tai150b	2727.03 *	-	2755.09	2727.67	2732.75	2743.38	811.57
tai150c	2358.66 *	-	-	-	2364.08	2370.26	1112.79
tai150d	2645.39 *	2659.02	2660.33	2645.40	2654.69	2674.85	1072.59

, the optimal solution was obtained in 5 of the 12 instances where the algorithm was tested. Although some optima were able to be obtained, the algorithm’s performance was not particularly strong. The average run time for our algorithm is between 2 and a half and 18 min across all “Taillard” instances.

Overall, the algorithm was tested on a total of 106 instances, yielding 93 optimal results, or 87.73%. Regarding processing time, the results ranged from 22 to about 2100 s, depending on the size of the instance. The algorithm works well in small and medium instances, for two reasons: Firstly, an alpha near to 1 is used, so the exploration of SA is quite good in these instances. The second reason is that the double neighbourhood helps in escaping local optima, increasing the movements explored. This approach is scalable to other variants of CVRP. However, the drawback of this algorithm will be the same in all the variants: the size. We test the algorithm in instance tai385 with 385 nodes, and the average time is above 20,000 s with solutions of low quality.

Simulated Annealing has a theoretical guarantee of finding the global optimum when the temperature descends very slowly. The alpha used in this work, being near to one, helps to obtain good solutions in the instances of CVRP problems. The double neighborhood helps in escaping the local optima and enhances the search of the algorithm. Both of these characteristics strengthen the search. If SAHDN is compared against the SA published in [28,29,37,38], SAHDN outperforms in quality of results. Only in the set of instances of type “A” does SAHDN find the optimum in all sets, while the other approaches only achieve this in a subset of them.

Logistics and distribution firms can implement this approach with the following steps. The first step is to feed the algorithm with the necessary data. This includes all customer order information, such as delivery addresses, the distance between localities and cargo weight or volume. It also requires detailed data on the vehicle fleet, including capacity. Another step is to customize the approach to the specific business context. This involves defining the objective function—what the firm wants to minimize or maximize. For example, a company might prioritize minimizing fuel consumption, reducing total travel time, or maximizing the number of completed deliveries. The algorithm’s constraints, like vehicle capacity, must also be coded in to ensure the generated routes are feasible and practical. Finally, once the data and constraints are set, the algorithm runs to find an optimal set of routes. The output is a series of optimized routes for each vehicle, which are then dispatched to drivers.

6. Conclusions and Future Work

A proposal based on Simulated Annealing was presented to solve the CVRP, which consists of finding an initial feasible random solution, which is then improved by the implementation of the heuristic method. Four different neighborhood types were implemented to extend the algorithm search during initial solution perturbations. The best solution obtained was improved by a double neighborhood search. For the evaluation, the algorithm solved a total of 106 instances with different numbers of clients (different sizes), obtaining the optimal result in 93 of them, which corresponds to 87.73% of the total. The proposed approach showed robustness and competitiveness with other approaches when it was tested in many instances in the literature. It is possible to use this algorithm to solve real problems in delivery companies with fewer than two hundred deliveries. A possible approach involves using K-means to group the clients in sets of adequate size and then solve them. As future work, it is proposed to use this approach in a different variant of the problem, such as Vehicle Routing Problem with Time Windows, or electrical vehicle routing with recharging stations. A hybridization of Simulated Annealing with a genetic algorithm can be considered to develop a memetic algorithm. Another methaheuristic based on neighbourhoods instead of SA can be employed, like tabu search or Iterated Local Search. Finally, paralleling can be used to speed up and improve the search.