Abstract
Composite integral formulas offer greater accuracy by dividing the interval into smaller subintervals, which better capture the local behavior of function. In the finite volume method for solving differential equations, composite formulas are mostly used on control volumes to achieve high-accuracy solutions. In this work, error estimates of the composite Simpson’s formula for differentiable convex functions are established. These error estimates can be applied to general subdivisions of the integration interval, provided the integrand satisfies a first-order differentiability condition. To this end, a novel and general integral identity for differentiable functions is established by considering general subdivisions of the integration interval. The new integral identity is proved in a manner that allows it to be transformed into different identities for different subdivisions of the integration interval. Then, under the convexity assumption on the integrand, sharp error bounds for the composite Simpson’s formula are proved. Moreover, the well-known Hölder’s inequality is applied to obtain sharper error bounds for differentiable convex functions, which represents a significant finding of this study. Finally, to support the theoretical part of this work, some numerical examples are tested and demonstrate the efficiency of the new bounds for different partitions of the integration interval.
MSC:
26D10; 26A51; 26D15
1. Introduction
The composite Simpson’s formula is a fundamental numerical integration technique that enhances the accuracy of the standard Simpson’s rule by partitioning the integration interval into smaller subintervals and applying Simpson’s rule to each one. This approach significantly improves precision, particularly for smooth and well-behaved functions, making it a preferred choice in practical applications. Compared to other numerical integration methods such as the trapezoidal rule or the midpoint rule, the composite Simpson’s formula typically provides higher accuracy for the same number of function evaluations. However, other methods may be preferred depending on the function’s properties or computational constraints, for example, when the integrand has discontinuities or exhibits low smoothness. The composite form of the Simpson’s formula is in ([1], p. 206):
where and n is even.
A crucial aspect of its effectiveness is the error bound, which provides an estimate of the approximation error. The existing absolute error bound for the composite Simpson’s formula is
This bound indicates that the error decreases rapidly as n increases, demonstrating the efficiency of the method. The higher-order derivative term in the bound reflects the dependence of accuracy on the smoothness of the function, ensuring reliable numerical integration under appropriate conditions.
In recent years, several works have been conducted to relax the conditions on integrands by the composite Formula (1). For example, the authors used the first differentiability conditions on the convex functions and derived the error bounds of the Simpson’s formula [2,3]. Following this work, the inequality theory for convex functions has garnered attention from researchers worldwide, who have established error bounds for various quadrature formulas applied to convex functions. For example, error bounds of Simpson’s formula for convex functions and various generalized convex functions were developed in [4,5,6,7,8,9]. However, these works are only valid for the standard Simpson’s formula, which takes the following form ( in (1)):
Thus, the existing error bounds are fixed because Formula (2) represents a particular case of the general form (1). Error bounds for differentiable convex functions in other quadrature formulas can be found in [10,11,12,13]. Recent researches have extensively explored error bounds for quadrature formulas in fractional calculus, particularly focused on Simpson’s rule and other numerical integration methods. For instance, studies have investigated Simpson-like integral inequalities for twice-differentiable -convex functions using -fractional integrals [14], as well as Simpson-type integral inequalities involving generalized -convexity in the local fractional differentiable sense [15]. Further works have established fractional Newton-type inequalities for various function classes [16] and multi-parameterized integral inequalities for multiplicative Riemann–Liouville fractional integrals [17]. Beyond Simpson’s rule, research has been extended to Newton-type inequalities under multiplicative Katugampola fractional integrals [18], symmetrical Hermite–Hadamard-type inequalities derived from multiplicative fractional integrals [19], and fractional Euler–Maclaurin-type inequalities for diverse function classes [20]. Additional contributions include corrected Euler–Maclaurin-type inequalities for twice differentiable functions [21] and fractional Newton-type inequalities for the Caputo fractional operator [22]. These studies collectively advance the theoretical framework for error analysis in fractional numerical integration.
Very recently, the study of error bounds for quadrature formulas in quantum calculus has attracted significant attention. For instance, error bounds of Simpson’s formula for convex functions in the quantum setting have been established via newly defined quantum integrals [23], as well as through extensions for quantum differentiable convex functions [24,25,26]. Beyond Simpson’s rule, research has expanded to include Milne-type inequalities for convex functions with computational analysis in quantum calculus [27], Hermite–Hadamard-type inequalities for strongly -convex functions [28], and quantum Ostrowski inequalities for q-differentiable convex functions [29]. Additionally, Ostrowski-type integral inequalities for functions of two variables in the quantum framework have been investigated [30]. These contributions collectively advance the understanding of numerical integration errors in quantum calculus.
To support the generalized analysis framework used in this study, we refer to recent work that extends classical approximation methods such as Simpson-type inequalities to more general settings [31]. However, all prior works have focused on standard forms of quadrature formulas, and their error bounds are not valid for composite forms of quadrature formulas. To obtain better accuracy of error bounds, composite formulas are important because by increasing the number of partitions, one can attain high-accuracy results and error bounds.
In this study, sharp error bounds for the composite Simpson’s formula applied to differentiable convex functions are established, contributing to the refinement of numerical integration techniques. To achieve this, a novel integral identity, which is valid for a general partition of the integration interval, is first derived, providing a foundational result for error estimation. The power mean inequality and the Hölder’s inequality are then utilized to generalize these bounds, offering a more comprehensive framework for evaluating the accuracy of composite quadrature formulas. The obtained estimates not only improve upon existing results but also provide deeper insights into the behavior of numerical integration errors for convex functions. To demonstrate the efficiency of the derived error bounds, numerical experiments are conducted on a variety of test functions. The results consistently show that as the number of subintervals n increases, the error bounds progressively decrease. This behavior aligns with theoretical expectations, confirming that the refined bounds accurately capture the error reduction inherent in the composite Simpson’s formula. The convergence of the error bounds with increasing n further validates the sharpness and effectiveness of the proposed estimates, reinforcing their practical significance in numerical integration for differentiable convex functions. Moreover, numerical examples are tested to demonstrate the utility of new results for different values of n.
The rest of the paper is organized as follows. Section 2 gives several error inequalities related to the composite Simpson’s formula and some existing inequalities in the literature, which are special cases of new results. In Section 3, the theoretical work is tested by numerous examples. Finally, concluding remarks and future directions are given in Section 4.
2. Main Results
This section is devoted to the main results of this work. A general and novel integral identity is established, which plays a pivotal role in proving the error bound of the composite Simpson’s formula and is valid for any subdivision of the integral interval. Subsequently, some new error bounds of the composite Simpson’s formula are derived for differentiable convex functions. Unlike existing bounds, these error bounds are not limited to particular subdivisions of the integral interval but hold for arbitrary subdivision. This section not only presents new results but also demonstrates that many existing results are the particular cases of the proposed framework. It is important to note that the existing bounds for convex functions tend to lose accuracy when applied over long intervals due to fixed-point assumptions. In contrast, the new results presented in this work offer improved accuracy across a broader range of functions and interval lengths, as they do not impose restrictive conditions on the choice of evaluation points within the integration domain.
For the sake of simplicity and better understanding, we denote the space of Lebesgue-integrable functions over the interval as The space of convex functions on with a continuous n-derivative is represented as while denotes the space of all functions on whose n-derivatives are continuous.
Here, we start with the following novel identity, which is the backbone of the new error bounds. In fact, the left part of the following equality (3) presents the error for the composite Simpson’s formula. In the coming results, for an even n, , and
Lemma 1.
Let be a differentiable function over . If , then we have the following equality:
Proof.
Now, from integration by parts and change of variables in integration, it follows that
To deal with , we expand it as
Thanks to integration by parts, we have
Thus, by using the calculated values in (5), we have
which completes the proof. □
Following the derivation of foundational results for error estimation, we turn to error bounds for once-differentiable convex functions. A key advantage of the new error estimates is that they apply to functions , whereas existing bounds for composite Simpson’s formulas in classical calculus typically require . Thus, the new results impose weaker conditions on the integrand compared to older ones.
Here, we give the following error estimates under the conditions of Lemma 1. For the sake of brevity, we consider
Theorem 1.
Let be a convex function, then the following inequality holds:
Proof.
Operate the absolute on both sides of equality (3) in Lemma 1, and using the convexity property on , we have
Now using the fact that , we have
This ends the proof. □
Remark 1.
By setting in Theorem 1, then we obtain the following well-known Simpson’s inequality:
which has been proved in [2,3], and references are cited in them for different classes of functions.
Now, we give another sharp error bound for the composite Simpson’s formula with the help of the well-known power mean integral inequality. We use the convexity property for parallel with the power mean inequality and obtain the following new bound under the assumptions of Lemma 1.
Theorem 2.
Let be a convex function, then the following inequality holds:
Proof.
Operate the absolute on both sides of equality (3) in Lemma 1 and using the power mean integral inequality, we have
From the convexity property for , we have
which completes the proof. □
One can easily observe that inequality (7) is the more general form of inequality (6). Inequality (6) can be attained for in inequality (7). However, inequality (7) covers the bounds for different values of and by the variation of q, one can attain more efficient bounds.
Here, we give another sharp error bound for the Formula (1). We use the well–known Hölder’s inequality along with convexity of and the Lemma 1. Under the assumptions of Lemma 1, we have the following theorem.
Theorem 3.
Let be a convex function, then the following inequality holds:
where
Proof.
From Lemma 1, the well-known Hölder’s inequality and convexity of , it follows
which completes the proof. □
3. Numerical Tests
This section emphasizes the efficiency/validity of the new error bounds for the composite Simpson’s formula. It is observed that the new error bounds are significantly sharper than the existing ones. For the sake of simplicity, we represent the order of convergence of Simpson’s formula with in all numerical tables. The error is calculated from the left-hand sides of the new theorems, and for the order of convergence, we use the following formula:
where means the previous error and means the current error.
Let us start with the first example.
Example 1.

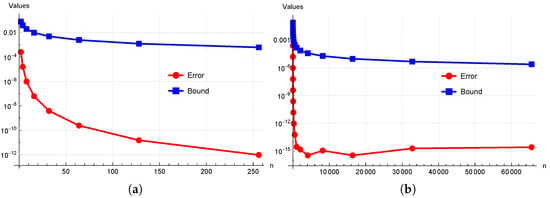
Let be a function defined as . The derivative of the function is , which is continuous and convex over . The performance and efficiency of the newly proposed error bounds in Theorem 1 for the composite Simpson’s formula is clearly demonstrated in Table 1. The data indicate a significant reduction in the error bound with increasing value of partitions n. Notably, as n becomes sufficiently large, the error bound of the composite Simpson’s formula approaches to zero, which is clear from Figure 1. In Figure 1, the blue line represents the error bound, and the red line represents the error of Simpson’s formula. Furthermore, the table highlights that Simpson’s formula attains its order of convergence, which is the 4.

Table 1.
Efficiency of error bounds for composite Simpson’s formula.

Figure 1.
The role of partition n in inequality (6). (a) . (b) .
Here, we give another example to show more authenticity of the new results.
Example 2.

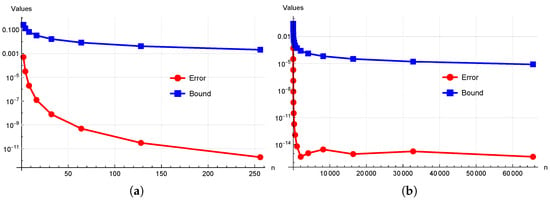
Let be a function defined as . The derivative of the function is , which is continuous and convex over . The performance and efficiency of the newly proposed error bounds in Theorem 1 for the composite Simpson’s formulas is clearly demonstrated in Table 2. The data indicate a significant reduction in the error bounds with increasing value of partitions n. Notably, as n becomes sufficiently large, the error bound of the composite Simpson’s formula approaches zero, which is clear from Figure 2. In Figure 2, the blue line represents the error bound, and the red line represents the error of Simpson’s formula. Furthermore, the table highlights that Simpson’s formula attains its order of convergence, which is 4.

Table 2.
Efficiency of error bounds for composite Simpson’s formula.

Figure 2.
The role of partition n in inequality (6). (a) . (b) .
Now, we give an example to test the error bounds established in inequality (8) with the help of the well-known Hölder’s inequality. For this, we consider the same Examples 1 and 2 for the sake of the bounds comparison. It is important and interesting to mention here that the error bounds obtained in (8) are much better than those for (6).
Example 3.

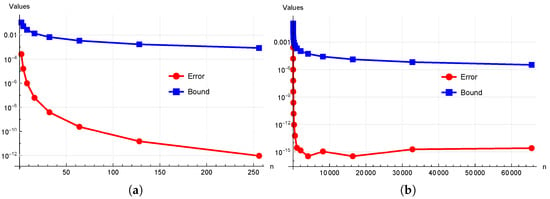
We consider Example 1 here with the same interval and other particulars. However, we use Theorem 3 to show the error bounds. From Table 3, one can observe the efficiency of the error bounds established in (8). Figure 3 is also evidence for the sharp error bounds established in Theorem 3, which is because of the use of Hölder’s inequality. Moreover, we can obtain the behavior of the bounds for different values of p and q with

Table 3.
Efficiency of error bounds for composite Simpson’s formula with .

Figure 3.
The role of partition n in inequality (8). (a) . (b) .
Example 4.

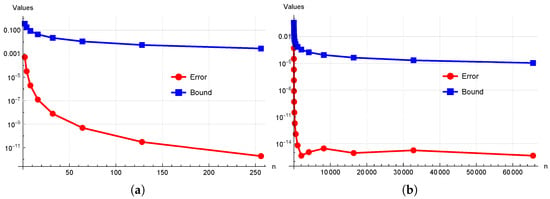
We consider Example 2 here with the same interval and other particulars. However, we use Theorem 3 to show the error bounds. From Table 4, one can observe the efficiency of the error bounds established in (8). Figure 4 is also evidence for the sharp error bounds established in Theorem 3, which is because of the use of Hölder’s inequality.

Table 4.
Efficiency of error bounds for composite Simpson’s formula with .

Figure 4.
The role of partition n in inequality (8). (a) . (b) .
4. Conclusions
In this work, sharp error bounds for the composite Simpson’s formula applied to convex functions have been established. A key component of this study was the derivation of a novel integral identity, valid for a general partition of the integration interval, which served as the foundation for obtaining precise error estimates. By utilizing the power mean inequality, more general and refined bounds were formulated, offering deeper insights into the behavior of numerical integration errors for convex functions. To evaluate the performance of the derived error bounds, numerical experiments were conducted. The results in the figures show that the error bounds decrease as the number of subintervals n increases, indicating improved accuracy with finer partitions. However, the precise asymptotic behavior remains a topic for further investigation. This confirms the accuracy and reliability of the proposed estimates, making them highly relevant for applications in numerical analysis.
For future research, several directions can be explored. First, the established framework can be extended to other quadrature formulas, such as the Newton–Cotes rules of higher order, to further enhance the accuracy of numerical integration schemes. Second, the error bounds could be analyzed in the context of fractional calculus to investigate their behavior in non-integer order integration settings. Additionally, the impact of different convexity classes, such as s-convex or harmonically convex functions, on the derived bounds can be studied to generalize the results. Lastly, exploring the integration of these improved error estimates with adaptive quadrature methods could lead to more efficient numerical schemes for solving complex integral equations.
Author Contributions
Investigation, W.L., Y.W., I.B.S. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets generated and analyzed during this study are available from the corresponding author upon reasonable request.
Acknowledgments
We would like to express my gratitude to School of Mathematics, Hohai University, China for providing the necessary resources and facilities that facilitated this research.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Cengage Learning: Boston, MA, USA, 2010. [Google Scholar]
- Alomari, M.; Darus, M.; Dragomir, S.S. New inequalities of Simpson’s type for s-convex functions with applications. Res. Rep. Collect. 2009, 12, 1–19. [Google Scholar]
- Sarikaya, M.Z.; Set, E.; Özdemir, M.E. On new inequalities of Simpson’s type for s-convex functions. Comput. Math. Appl. 2010, 60, 2191–2199. [Google Scholar] [CrossRef]
- Alomari, M.; Hussain, S. Two inequalities of Simpson type for quasi-convex functions and applications. Appl. Math. E-Notes 2011, 11, 110–117. [Google Scholar]
- Chun, L.; Qi, F. Inequalities of Simpson type for functions whose third derivatives are extended s-convex functions and applications to means. J. Comput. Anal. Appl. 2015, 19, 555–569. [Google Scholar]
- Qaisar, S.; He, C.; Hussain, S. A generalizations of Simpson’s type inequality for differentiable functions using (α,m)-convex functions and applications. J. Inequalities Appl. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Tunc, M.; Yildiz, C.; Ekinci, A. On some inequalities of Simpson’s type via h-convex functions. Hacet. J. Math. Stat. 2013, 42, 309–317. [Google Scholar]
- Sarikaya, M.Z.; Aktan, N. On the generalization of some integral inequalities and their applications. Math. Comput. Model. 2011, 54, 2175–2182. [Google Scholar] [CrossRef]
- Kashuri, A.; Mohammed, P.O.; Abdeljawad, T.; Hamasalh, F.; Chu, Y. New Simpson type integral inequalities for s-convex functions and their applications. Math. Probl. Eng. 2020, 2020, 8871988. [Google Scholar] [CrossRef]
- Cakmak, M. The differentiable h-convex functions involving the Bullen inequality. Acta Univ. Apulensis 2021, 65, 29–36. [Google Scholar]
- Sarikaya, M.Z. On the some generalization of inequalities associated with Bullen, Simpson, midpoint and trapezoid type. Acta Univ. Apulensis Math. Inform. 2023, 73, 33–52. [Google Scholar]
- Vivas–Cortez, M.; Javed, M.Z.; Awan, M.U.; Noor, M.A.; Dragomir, S.S. Bullen-Mercer type inequalities with applications in numerical analysis. Alex. Eng. J. 2024, 96, 15–33. [Google Scholar] [CrossRef]
- Du, T.; Yuan, X. On the parameterized fractal integral inequalities and related applications. Chaos Solitons Fractals 2023, 170, 113375. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, L.E.I.; Du, T. Simpson-like inequalities for twice differentiable (s,P)-convex mappings involving with AB-fractional integrals and their applications. Fractals 2023, 31, 2350024. [Google Scholar] [CrossRef]
- Zhou, Y.; Du, T. The Simpson-type integral inequalities involving twice local fractional differentiable generalized (s,P)-convexity and their applications. Fractals 2023, 31, 2350038. [Google Scholar] [CrossRef]
- Hezenci, F.; Budak, H. Fractional Newton-type integral inequalities by means of various function classes. Math. Methods Appl. Sci. 2025, 48, 1198–1215. [Google Scholar] [CrossRef]
- Du, T.; Long, Y. The multi-parameterized integral inequalities for multiplicative Riemann–Liouville fractional integrals. J. Math. Anal. Appl. 2025, 541, 128692. [Google Scholar] [CrossRef]
- Ai, D.; Du, T. A study on Newton-type inequalities bounds for twice* differentiable functions under multiplicative Katugampola fractional integrals. Fractals 2025, 2550032. [Google Scholar] [CrossRef]
- Peng, Y.; Özcan, S.; Du, T. Symmetrical Hermite-Hadamard type inequalities stemming from multiplicative fractional integrals. Chaos Solitons Fractals 2024, 183, 114960. [Google Scholar] [CrossRef]
- Hezenci, F.; Budak, H. Fractional Euler-Maclaurin-type inequalities for various function classes. Comput. Appl. Math. 2024, 43, 261. [Google Scholar] [CrossRef]
- Hezenci, F. Fractional inequalities of corrected Euler–Maclaurin-type for twice-differentiable functions. Comput. Appl. Math. 2023, 42, 92. [Google Scholar] [CrossRef]
- Mahajan, Y.; Nagar, H. Fractional Newton-type integral inequalities for the Caputo fractional operator. Math. Methods Appl. Sci. 2025, 48, 5244–5254. [Google Scholar] [CrossRef]
- Budak, H.; Erden, S.; Ali, M.A. Simpson and Newton type inequalities for convex functions via newly defined quantum integrals. Math. Methods Appl. Sci. 2021, 44, 378–390. [Google Scholar] [CrossRef]
- Tunc, M.; Göv, E.; Balgecti, S. Simpson type quantum integral inequalities for convex functions. Miskolc Math. Notes 2018, 19, 649–664. [Google Scholar] [CrossRef]
- Ali, M.A.; Budak, H.; Zhang, Z. A new extension of quantum Simpson’s and quantum Newton’s type inequalities for quantum differentiable convex functions. Math. Methods Appl. Sci. 2022, 45, 1845–1863. [Google Scholar] [CrossRef]
- Ali, M.A.; Budak, H.; Zhang, Z.; Yildirim, H. Some new Simpson’s type inequalities for coordinated convex functions in quantum calculus. Math. Methods Appl. Sci. 2021, 44, 4515–4540. [Google Scholar] [CrossRef]
- Mateen, A.; Zhang, Z.; Ali, M.A. Some Milne’s rule type inequalities for convex functions with their computational analysis on quantum calculus. Filomat 2024, 38, 3329–3345. [Google Scholar] [CrossRef]
- Mishra, S.K.; Sharma, R.; Bisht, J. Hermite–Hadamard-type inequalities for strongly (α,m)-convex functions via quantum calculus. J. Appl. Math. Comput. 2024, 70, 4971–4994. [Google Scholar] [CrossRef]
- Noor, M.A.; Awan, M.U.; Noor, K.I. Quantum Ostrowski inequalities for q-differentiable convex functions. J. Math. Inequal. 2016, 10, 1013–1018. [Google Scholar] [CrossRef]
- Budak, H.; Ali, M.A.; Tunc, T. Quantum Ostrowski-type integral inequalities for functions of two variables. Math. Methods Appl. Sci. 2021, 44, 5857–5872. [Google Scholar] [CrossRef]
- Stojiljković, V. Simpson type Tensorial Inequalities for Continuous functions of Selfadjoint operators in Hilbert Spaces. Palest. J. Math. 2024, 13, 41–50. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).