Mixed-Order Fuzzy Time Series Forecast
Abstract
1. Introduction
2. FTS and Mixed-Order FLR Models
2.1. Review of Fuzzy Time Series
2.2. Mixed-Order FLRs
- (i)
- If has a nonempty prediction, has the same prediction, but not vice versa;
- (ii)
- has more empty predictions than because of Equation (13);
- (iii)
- is simpler than because of the lower FLR orders.
3. The Proposed FTS Forecast
3.1. FTS Forecast Based on an mth Mixed-Order FLR
| Algorithm 1: Generation of the mth mixed-order FLRs |
 |
| Algorithm 2: The FLR selection |
 |
- Case I.
- If the one-step fuzzy forecast is a single fuzzy set, like , the defuzzified value of fuzzy set is defined aswhere represents the observations corresponding to the next state , which has a fuzzy logical relationship: , is the total number of observations whose next state is . Hence, the solution to Equation (19) is .
- Case II.
- If the one-step fuzzy forecast is an empty set, like , the defuzzified value is calculated by the master voting scheme [20]:where is the center value of the observations in fuzzy set , . Since there is no nonempty FLR as the basis in this case, the left-hand side of the empty FLR is the only useful information in the prediction. The weighted average of the centers is employed, and the greatest weight m is given to the center of because is the most recent fuzzy set for the prediction.
- Case III.
- If the one-step fuzzy forecast is multiple fuzzy sets, like , the defuzzified value is the average of the forecasting fuzzy set.
3.2. Choice of the Mixed-Order m
| Algorithm 3: Selection of mixed-order m |
 |
4. Experimental Results
4.1. Performance Evaluation on Time Series Data with Varying Characteristics
4.2. The Effectiveness of the Mixed-Order FLRs
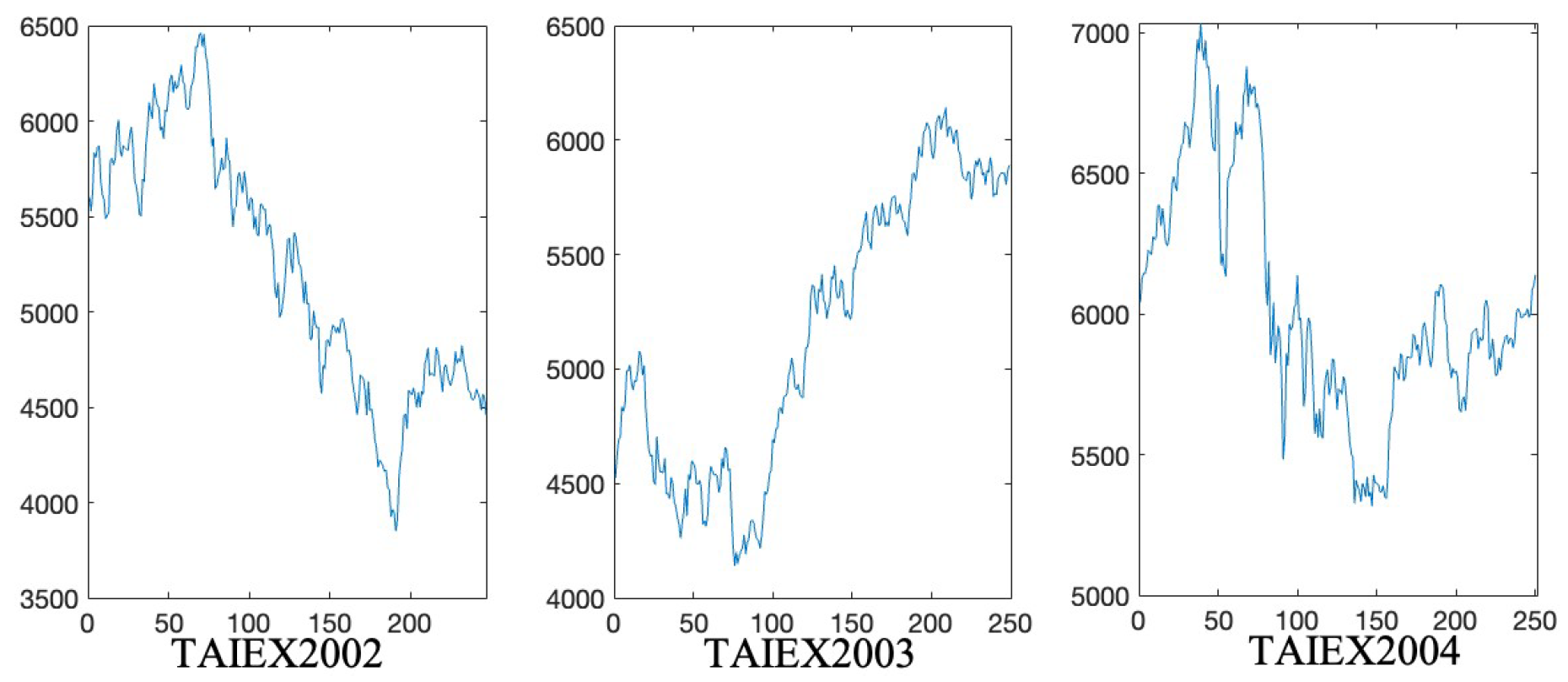
4.3. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs of Theorems
- (i)
- Suppose . Note that is the probability that is complete. It follows thatwhere is the combination number.
- (ii)
- Suppose . Then, , since . Even if all m-order FLRs are different, there still exist empty m-order FLRs. Hence, is incomplete, and . Similarly, all for .
- (i)
- If and with , then . Thus, is the corresponding sub-FLR.
- (ii)
- If for every , then . Thus, is the corresponding sub-FLR.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series-part I. Fuzzy Sets Syst. 1993, 54, 1–9. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its model. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series-part II. Fuzzy Sets Syst. 1994, 62, 1–8. [Google Scholar] [CrossRef]
- Wu, H.; Long, H.; Jiang, J. Handling forecasting problems based on fuzzy time series model and model error learning. Appl. Soft Comput. 2019, 78, 109–118. [Google Scholar] [CrossRef]
- Yolcu, O.C.; Yolcu, U. A novel intuitionistic fuzzy time series prediction model with cascaded structure for financial time series. Expert Syst. Appl. 2023, 215, 119336. [Google Scholar] [CrossRef]
- Dixit, A.; Jain, S. Intuitionistic fuzzy time series forecasting method for non-stationary time series data with suitable number of clusters and different window size for fuzzy rule generation. Inf. Sci. 2023, 623, 132–145. [Google Scholar] [CrossRef]
- Wang, B.; Liu, X.; Chi, M.; Li, Y. Bayesian network based probabilistic weighted high-order fuzzy time series forecasting. Expert Syst. Appl. 2024, 237, 121430. [Google Scholar] [CrossRef]
- Shi, X.; Wang, J.; Zhang, B. A fuzzy time series forecasting model with both accuracy and interpretability is used to forecast wind power. Appl. Energy 2024, 353, 122015. [Google Scholar] [CrossRef]
- Wu, B.; Wang, L. Two-stage decomposition and temporal fusion transformers for interpretable wind speed forecasting. Energy 2024, 288, 129728. [Google Scholar] [CrossRef]
- Didugu, G.; Gandhudi, M.; Alphonse, P.J.A.; Gangadharan, G.R. VWFTS-PSO: A novel method for time series forecasting using variational weighted fuzzy time series and particle swarm optimization. Int. J. Gen. Syst. 2025, 54, 540–559. [Google Scholar] [CrossRef]
- Bose, M.; Mali, K. Designing fuzzy time series forecasting models: A survey. Int. J. Approx. Reason. 2019, 111, 78–99. [Google Scholar] [CrossRef]
- Panigrahi, S.; Behera, H.S. Fuzzy time series forecasting: A survey. In Computational Intelligence in Data Mining: Proceedings of the International Conference on ICCIDM; Springer: Berlin/Heidelberg, Germany, 2020; pp. 641–651. [Google Scholar] [CrossRef]
- Orang, O.; de Lima e Silva, P.C.; Guimarães, F.G. Time series forecasting using fuzzy cognitive maps: A survey. Artif. Intell. Rev. 2023, 56, 7733–7794. [Google Scholar] [CrossRef]
- Huarng, K. Heuristic models of fuzzy time series for forecasting. Fuzzy Sets Syst. 2001, 123, 369–386. [Google Scholar] [CrossRef]
- Huarng, K. Effective length of intervals to improve forecasting in fuzzy time-series. Fuzzy Sets Syst. 2001, 123, 387–394. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.H.; Basaran, M.A.; Yolcu, U.; Uslu, V.R. A new approach based on the optimization of the length of intervals in fuzzy time series. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2011, 22, 15–19. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.H.; Yolcu, U.; Uslu, V.R.; Basaran, M.A. Finding an optimal interval length in high order fuzzy time series. Expert Syst. Appl. 2010, 37, 5052–5055. [Google Scholar] [CrossRef]
- Chen, S.M.; Chung, N.Y. Forecasting enrollments using high-order fuzzy time series and genetic algorithms. Int. J. Intell. Syst. 2006, 21, 485–501. [Google Scholar] [CrossRef]
- Kuo, I.H.; Horng, S.J.; Kao, T.W.; Lin, T.L.; Lee, C.L.; Pan, Y. An improved method for forecasting enrollments based on fuzzy time series and particle swarm optimization. Expert Syst. Appl. 2009, 36, 6108–6117. [Google Scholar] [CrossRef]
- Chen, M.Y. A high-order fuzzy time series forecasting model for internet stock trading. Future Gener. Comput. Syst. 2014, 37, 461–467. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Pedrycz, W.; Shao, Y. Determination of temporal information granules to improve forecasting in fuzzy time series. Expert Syst. Appl. 2014, 41, 3134–3142. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X. Fuzzy forecasting based on automatic clustering and axiomatic fuzzy set classification. Inf. Sci. 2015, 294, 78–94. [Google Scholar] [CrossRef]
- Wu, H.; Long, H.; Wang, Y.; Wang, Y. Stock index forecasting: A new fuzzy time series forecasting method. J. Forecast. 2021, 40, 653–666. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Panigrahi, S.; Behera, H.S. A study on leading machine learning techniques for high order fuzzy time series forecasting. Eng. Appl. Artif. Intell. 2020, 87, 103245. [Google Scholar] [CrossRef]
- Pattanayak, R.M.; Behera, H.S.; Panigrahi, S. A novel high order hesitant fuzzy time series forecasting by using mean aggregated membership value with support vector machine. Inf. Sci. 2023, 626, 494–523. [Google Scholar] [CrossRef]
- Li, S.T.; Cheng, Y.C.; Lin, S.Y. A FCM based deterministic forecasting model for fuzzy time series. Comput. Math. Appl. 2008, 56, 3052–3063. [Google Scholar] [CrossRef]
- Kuo, I.H.; Horng, S.J.; Chen, Y.H.; Run, R.S.; Kao, T.W.; Chen, R.J.; Lai, J.L.; Lin, T.L. Forecasting TAIEX based on fuzzy time series and particle swarm optimization. Expert Syst. Appl. 2010, 37, 1494–1502. [Google Scholar] [CrossRef]
- Ye, F.; Zhang, L.; Zhang, D.; Fujita, H.; Gong, Z. A novel forecasting method based on multi-order fuzzy time series and technical analysis. Inf. Sci. 2016, 367–368, 41–47. [Google Scholar] [CrossRef]
- Huarng, K.; Yu, T.H.K.; Hsu, Y.W. A multivariate heuristic model for fuzzy time-series forecasting. IEEE Trans. Syst. Man Cybern.-Part B Cybern. 2007, 37, 836–846. [Google Scholar] [CrossRef]
- Chen, S.M. Forecasting enrollments based on fuzzy time series. Fuzzy Sets Syst. 1996, 81, 311–319. [Google Scholar] [CrossRef]
- Yu, T.H.K.; Huarng, K.H. A bivariate fuzzy time series model to forecast the TAIEX. Expert Syst. Appl. 2008, 34, 2945–2952. [Google Scholar] [CrossRef]
- Chen, S.M.; Chang, Y.C. Multi-variable fuzzy forecasting based on fuzzy clustering and fuzzy interpolation techniques. Inf. Sci. 2010, 180, 4772–4783. [Google Scholar] [CrossRef]
- Sullivan, J.; Woodall, W.H. A comparison of fuzzy forecasting and Markov modeling. Fuzzy Sets Syst. 1994, 64, 279–293. [Google Scholar] [CrossRef]
- Chen, S.M.; Chen, C.D. TAIEX forecasting based on fuzzy time series and fuzzy variation groups. IEEE Trans. Fuzzy Syst. 2010, 19, 1–12. [Google Scholar] [CrossRef]
- Bas, E.; Egrioglu, E.; Kolemen, E. A novel intuitionistic fuzzy time series method based on bootstrapped combined pi-sigma artificial neural network. Eng. Appl. Artif. Intell. 2022, 114, 105030. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Pérez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Jiang, J. Multivariate functional-coefficient regression models for nonlinear vector time series data. Biometrika 2014, 101, 689–702. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, S.; Jiang, S.; Ding, L.; Lin, H.; Wang, W. Fast cross-validation for kernel-based algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1083–1096. [Google Scholar] [CrossRef]
- Shrestha, B.P.; Duckstein, L.; Stakhiv, E.Z. Fuzzy rule-based modeling of reservoir operation. J. Water Resour. Plan. Manag. 1996, 122, 262–269. [Google Scholar] [CrossRef]
- Ozkan, I.; Turksen, I.B. Upper and lower values for the level of fuzziness in FCM. In Fuzzy Logic: A Spectrum of Theoretical & Practical Issues; Springer: Berlin/Heidelberg, Germany, 2007; pp. 99–112. [Google Scholar] [CrossRef]
- Cheng, S.H.; Chen, S.M.; Jian, W.S. Fuzzy time series forecasting based on fuzzy logical relationships and similarity measures. Inf. Sci. 2016, 327, 272–287. [Google Scholar] [CrossRef]
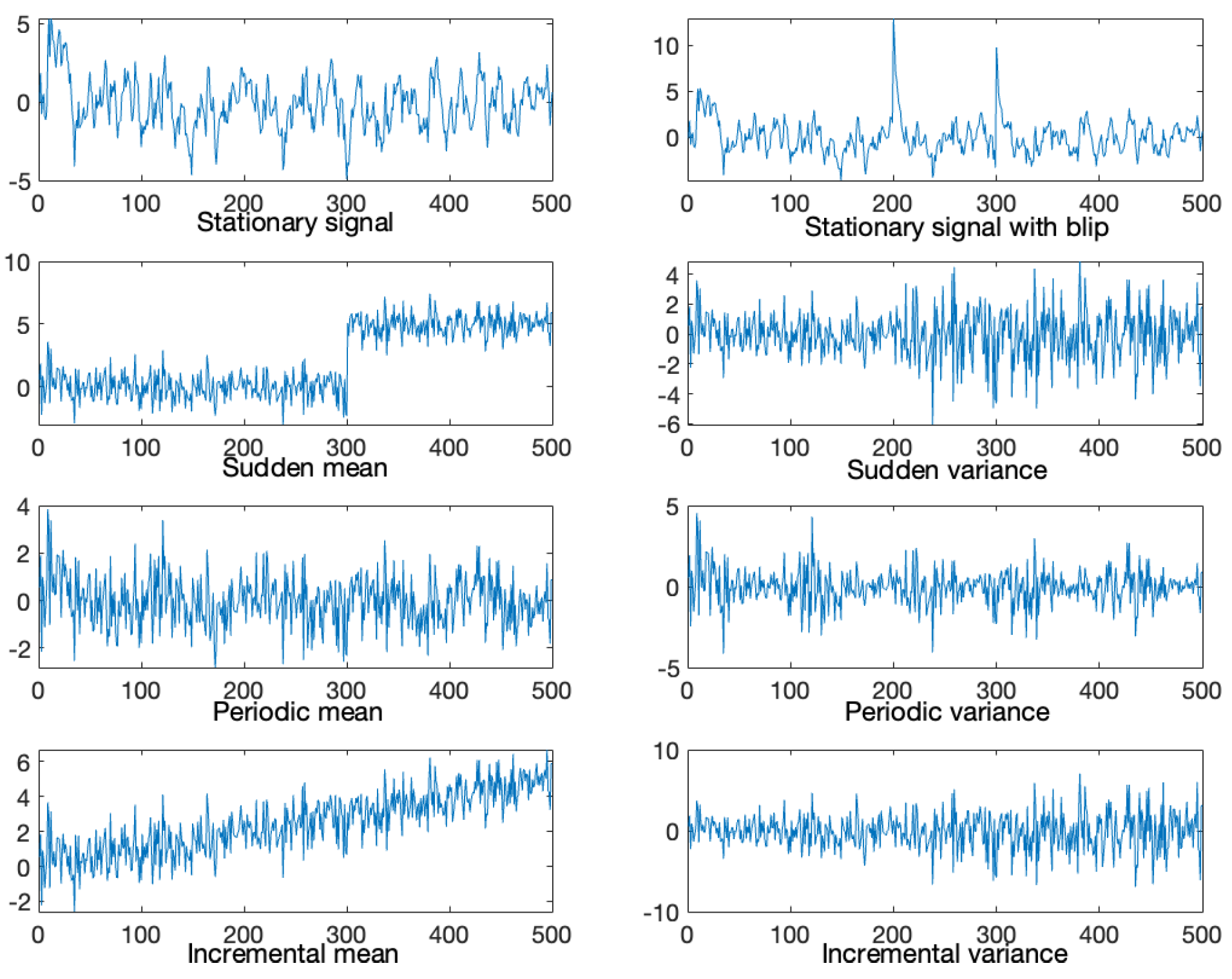

| Model | Mixed-Order | 1-Order | 2-Order | 3-Order | 4-Order | 5-Order |
|---|---|---|---|---|---|---|
| stationary | 0.8235 | 0.8955 | 1.1270 | 1.0258 | 0.9462 | 0.9435 |
| with blip | 0.8211 | 0.8986 | 1.0879 | 1.0346 | 0.9465 | 0.9461 |
| sud mean | 0.9954 | 3.8836 | 2.8186 | 2.6188 | 2.6030 | 2.5867 |
| sud var | 1.6564 | 1.6575 | 1.9790 | 1.8039 | 1.7923 | 1.7938 |
| per mean | 0.8923 | 1.0137 | 1.1211 | 1.0262 | 0.9150 | 0.9150 |
| per var | 0.6403 | 0.6506 | 0.8664 | 0.6956 | 0.6769 | 0.6771 |
| inc mean | 0.9941 | 2.6994 | 2.7321 | 2.6395 | 2.5189 | 2.4948 |
| inc var | 2.8946 | 2.8045 | 3.0898 | 3.0272 | 3.0090 | 3.0166 |
| Model | Mixed-Order | 1-Order | 2-Order | 3-Order | 4-Order | 5-Order |
|---|---|---|---|---|---|---|
| RMSE | 0.1030 | 0.1789 | 0.1102 | 0.1215 | 0.1351 | 0.1393 |
| No. | Methods | 2002 | 2003 | 2004 | Average RMSE |
|---|---|---|---|---|---|
| 1 | Huarng et al.’s method (Use NASDAQ) [31] | 95.15 | 65.51 | 73.57 | 78.08 |
| 2 | Huarng et al.’s method (Use Dow Jones) [31] | 93.73 | 72.95 | 73.49 | 80.06 |
| 3 | Huarng et al.’s method (Use M1b) [31] | 97.10 | 75.23 | 82.01 | 84.78 |
| 4 | Huarng et al.’s method (Use NASDAQ & Dow Jones) [31] | 93.48 | 65.51 | 73.49 | 77.49 |
| 5 | Huarng et al.’s method (Use NASDAQ & M1b) [31] | 97.15 | 70.76 | 73.48 | 80.46 |
| 6 | Huarng et al.’s method (Use NASDAQ & Dow Jones & M1b) [31] | 95.73 | 70.76 | 72.35 | 79.61 |
| 7 | The mixed-order method (with equal intervals and single variable) | 80.68 | 55.67 | 76.54 | 70.96 |
| 8 | AR (1) model [35] | 97.09 | 91.67 | 79.94 | 89.57 |
| 9 | AR (2) model [35] | 89.80 | 66.58 | 60.33 | 72.24 |
| 10 | Chen’s fuzzy time series model [32] | 101.00 | 74.00 | 84.00 | 86.33 |
| 11 | Univariate conventional regression model [33] | 116.00 | 329.00 | 146.00 | 197.00 |
| 12 | Univariate neural network-based fuzzy time series model [33] | 84.00 | 56.00 | 116.00 | 85.33 |
| 13 | The mixed-order method (univariate) | 74.04 | 60.57 | 61.40 | 65.34 |
| 14 | Bivariate conventional regression model [33] | 77.00 | 54.00 | 85.00 | 72.00 |
| 15 | Bivariate neural network-based fuzzy time series model [33] | 85.00 | 58.00 | 67.00 | 70.00 |
| 16 | Bivariate neural network-based fuzzy time series model use subsitutes [33] | 80.00 | 58.00 | 67.00 | 68.33 |
| 17 | Chen & Chang’s method (Use NASDAQ) [34] | 73.06 | 66.36 | 60.48 | 66.63 |
| 18 | Chen & Chang’s method (Use Dow Jones) [34] | 79.81 | 64.08 | 82.32 | 75.40 |
| 19 | Chen & Chang’s method (Use M1b) [34] | 96.06 | 90.27 | 100.10 | 95.48 |
| 20 | Chen & Chang’s method (Use NASDAQ & Dow Jones) [34] | 72.33 | 60.29 | 68.07 | 66.90 |
| 21 | Chen & Chang’s method (Use NASDAQ & M1b) [34] | 76.48 | 53.51 | 69.29 | 66.43 |
| 22 | Chen & Chen’s method (Use Dow Jones) [36] | 74.65 | 66.02 | 58.89 | 66.52 |
| 23 | Chen & Chen’s method (Use NASDAQ) [36] | 71.01 | 65.14 | 61.94 | 66.03 |
| 24 | Chen & Chen’s method (Use M1b) [36] | 85.85 | 63.10 | 67.29 | 72.08 |
| 25 | Chen & Chen’s method (Use M1b & Dow Jones) [36] | 77.96 | 60.32 | 65.86 | 68.05 |
| 26 | Chen & Chen’s method (Use M1b & NASDAQ) [36] | 74.05 | 67.83 | 65.09 | 68.99 |
| 27 | Chen & Chen’s method (Use NASDAQ & Dow Jones & M1b) [36] | 77.38 | 60.65 | 65.09 | 67.71 |
| 28 | LSTM-FTS method | 89.00 | 92.00 | 70.00 | 84.00 |
| 29 | NN-FTS method | 80.00 | 58.00 | 67.00 | 68.00 |
| 30 | The mixed-order method (use opening price) | 73.14 | 57.93 | 56.38 | 62.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Long, H.; Jiang, J. Mixed-Order Fuzzy Time Series Forecast. Mathematics 2025, 13, 1705. https://doi.org/10.3390/math13111705
Wu H, Long H, Jiang J. Mixed-Order Fuzzy Time Series Forecast. Mathematics. 2025; 13(11):1705. https://doi.org/10.3390/math13111705
Chicago/Turabian StyleWu, Hao, Haiming Long, and Jiancheng Jiang. 2025. "Mixed-Order Fuzzy Time Series Forecast" Mathematics 13, no. 11: 1705. https://doi.org/10.3390/math13111705
APA StyleWu, H., Long, H., & Jiang, J. (2025). Mixed-Order Fuzzy Time Series Forecast. Mathematics, 13(11), 1705. https://doi.org/10.3390/math13111705







