Abstract
Group anomaly detection is a subfield of pattern recognition that aims at detecting anomalous groups rather than individual anomalous points. However, existing approaches mainly target the unusual aggregate of points in high-density regions. In this way, unusual group behavior with a number of points located in low-density regions is not fully detected. In this paper, we propose a systematic approach based on extreme value theory (EVT), a field of statistics adept at modeling the tails of a distribution where data are sparse, and one-class support measure machines (OCSMMs) to quantify anomalous group behavior comprehensively. First, by applying EVT to a point process model, we construct an analytical model describing the likelihood of an aggregate within a group with respect to low-density regions, aimed at capturing anomalous group behavior in such regions. This model is then combined with a calibrated OCSMM, which provides probabilistic outputs to characterize anomalous group behavior in high-density regions, enabling improved assessment of overall anomalous group behavior. Extensive experiments on simulated and real-world data demonstrate that our method outperforms existing group anomaly detectors across diverse scenarios, showing its effectiveness in quantifying and interpreting various types of anomalous group behavior.
Keywords:
group anomaly detection; extreme value theory; point processes; one-class support measure machine; uninorm MSC:
60G70
1. Introduction
Anomaly detection is a critical task in data analysis that differs substantially from traditional classification. While classification typically involves the modeling of two or more classes with labeled data and comparable sample sizes, anomaly detection focuses on distinguishing between “normal” and “anomalous” samples, often characterized by an imbalanced class distribution, where anomalous samples are rare. A key assumption in anomaly detection is that the training data comprise only normal samples (throughout this paper, the term “normal” consistently signifies what is usual and regular. When discussing distributions, we employ the term “Gaussian distribution” instead of “normal distribution”) [1]. Let be a multivariate random variable representing d feature components with distribution function . Traditional approaches to anomaly detection focus on a point model () in the feature space of that captures distribution characteristics of normal point samples (which typically reside in high-density regions) to identify anomalies deviating from this model (so-called pointwise anomaly detection).
Group anomaly detection extends pointwise anomaly detection to scenarios where a sample is not an individual point () but a group of points () representing a sample of the group variable (, where share a common distribution function ()). Group anomalies can arise in diverse contexts, such as irregular sequences of measured heartbeats [2]. When applied to the detection of wind turbine failures, group anomalies are observed as shifts of signal sequences [3]. Group anomalies also appear in the usage patterns of urban bicycle rental systems [4]. Although pointwise anomaly detectors could theoretically be applied in group scenarios if a representative feature set for the group variable were extractable [5], these methods face the following significant challenges in practical applications: (i) Constructing a representative feature set that adequately encapsulates diverse group-level characteristics is often difficult, especially when the number of training groups is limited and the variable () comprising the group is high-dimensional. (ii) Achieving interpretability of the group-level feature set in terms of the spatial configuration of points in the original feature space of remains nontrivial. As a result, specialized methods for group anomaly detection have been developed, which bypass group feature extraction and allow for direct analysis within the original feature space of .
This paper presents a statistical approach for group anomaly detection, aiming to construct a framework to analytically quantify various types of anomalous group behavior. Given normal groups in the training set, the points across all normal groups collectively define a common, potentially complex distribution with a density of . Thresholding the density () partitions the feature space of into high-density and low-density regions, thereby enabling all possible anomalous group behavior to be systematically classified into two types: (i) point-based anomalous group behavior, where a group exhibits unusual collective behavior among its points labeled as belonging to low-density regions, and (ii) distribution-based anomalous group behavior, referring to a group whose distribution pattern of points labeled as belonging to high-density regions differs from that in any normal group in the training set. Such categorization is in line with existing work but is statistically underpinned through the density function expressed as [6,7,8,9,10]. Figure 1 provides a visual illustration of the two types of group anomalies. The blue points in the two-dimensional input space represent points from all normal groups and collectively characterize the underlying point distribution, where densely clustered areas correspond to high-density regions and sparse areas indicate low-density regions. Figure 1a shows groups with point-based anomalous group behavior, where each group with red borders in the test set contains an unusual aggregate of points located in low-density regions. Figure 1b illustrates groups with distribution-based anomalous group behavior. Although the purple points are situated in high-density regions, the groups with purple borders exhibit distribution patterns that substantially differ from any of the patterns observed among the normal training groups. Groups exhibiting both types of behavior are considered anomalous on both fronts.
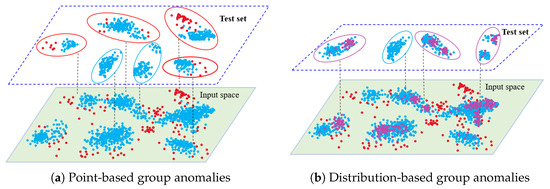
Figure 1.
Illustration of two types of anomalous group behavior. The blue points represent all individual points from the normal groups in the training set. The red points represent low-density region points, whereas the purple points are high-density region points. The boundaries of individual normal groups are not explicitly shown.
Existing models for group anomaly detection face two critical limitations, which motivate the development of our novel statistical approach. First, while a wide range of popular models excel at detecting distribution-based anomalous group behavior, they exhibit a significant weakness in identifying point-based anomalous group behavior. For example, models like the One-Class Support Measure Machine (OCSMM) [7], Support Measure Data Description (SMDD) [11], and the neural network model proposed by Chalapathy et al. [8] primarily assess how the distribution pattern of points (labeled as belonging to high-density regions) in a test group deviates from that of normal training groups while largely neglecting the crucial aggregation behavior of points in low-density regions within this test group. In domains like health monitoring, both types of group anomalies are crucial, and the failure to effectively detect point-based anomalous group behavior can lead to spurious alarms. Although models like the Mixture of Gaussian Mixture Model (MGMM) [6] and the Flexible Genre Model (FGM) [12] attempt to address both types of group anomalies, they often exhibit higher sensitivity towards distribution-based anomalous group behavior. This imbalance in sensitivity is further illustrated in Section 2 and Section 5.
The second limitation lies in modeling point-based anomalous group behavior, where the strategy of most models that combine (pointwise) anomaly scores is flawed. The main reason is that low-density region points need to be considered as a whole to capture their aggregate behavior; otherwise, the multiple hypothesis-testing problem will manifest. The point-based group anomaly detection problem can be stated as follows:
H0.
is a group of points drawn from the distribution of ;
H1.
is an anomalous group with respect to the distribution of .
Clearly, it is a multiple hypothesis-testing problem where more than one hypothesis is being tested—more specifically, one hypothesis for each individual point being anomalous or not. For a group size of , this simplifies to classic (pointwise) anomaly detection, where the likelihood () can be directly used as an anomaly score [13]. However, for , the risk of wrongly classifying a group () as anomalous considerably increases. Indeed, while the type-I error for can be controlled at a significance level of , the likelihood of making at least one type-I error among all n hypotheses corresponds to . As a result, the decisions made by these models become unreliable.
This work aims to develop an effective method to address the aforementioned limitations and accurately evaluate the anomalousness of a group. We integrate a likelihood model based on Extreme Value Theory (EVT) with a calibrated OCSMM within a unified framework. Each component is designed to specifically target a distinct form of anomalous group behavior, with the likelihood model being employed to characterize the low-density regions and avoid the multiple hypothesis-testing problem, whereas the calibrated OCSMM is intended to capture deviations in the distributional structure of high-density regions across groups. Leveraging the complementary information captured by each component, these two components are subsequently combined through a constructed uninorm to generate an overall anomaly score. Specifically, the contributions of this paper are described as follows:
- We offer a novel framework where EVT is applied to a Point Process Model (PPM) in order to fully capture the spatial configuration that is hidden in the data points situated in low-density regions.
- An analytical result is proven to approximate the distribution of the PPM. Based on this result, a point-based anomaly score is defined to evaluate the anomalous extent of a group with respect to low-density regions, effectively addressing the multiple hypothesis-testing problem.
- We extend the existing OCSMM framework to yield probabilistic outputs, thereby enabling the construction of a distribution-based anomaly score that exclusively assesses the anomalous extent of a group with respect to high-density regions. OCSMM is chosen for this purpose because it effectively captures the distributional characteristics of normal groups in high-density regions, without redundantly incorporating information from low-density regions, thereby avoiding overlap with the previously constructed point-based anomaly score.
- A uninorm is constructed to effectively combine the above two scores, each focusing on the anomalous extent of one of the group’s two complementary aspects. The resulting overall anomaly score provides a comprehensive measure of the group’s anomalousness.
The remainder of this paper is structured as follows. In Section 2, existing approaches for group anomaly detection are reviewed and analyzed. Section 3 provides the necessary knowledge of EVT and PPM, which is crucial for constructing our model. Subsequently, Section 4 introduces our novel method for group anomaly detection. In Section 5, the method is evaluated on both synthetic and real-world datasets. Section 6 concludes this paper.
2. Related Work
As our study is concerned with group anomaly detection, we focus our literature review on this area rather than (pointwise) anomaly detection methods. Following classic pointwise anomaly detection, early developments in group anomaly detection methods combined the individual predicted scores generated by pointwise anomaly detectors into a single score for a statistical decision [14]. For instance, in the image analysis research of Hazel [15], a pointwise detector was used to identify anomalous pixels that were subsequently gathered into anomalous groups. Das et al. [16] classified groups according to a high fraction of individual anomalous points within a group. Belhadi et al. [17] combined different data mining techniques to identify groups of sequence outliers. Mohod and Janeja [18] adapted density-based clustering methods to discover spatially anomalous groups (windows) of arbitrary shape. Das et al. [19] also introduced a group anomaly detection framework based on scan statistics to detect clusters with increased counts of spatial data. More recently, Pehlivanian and Neill [20] extended scan statistics to detect contiguous group anomalies in ordered data. However, scan statistics are based on the number of instances within a region but discard their relative location in space. Moreover, these methods are ineffective in addressing the multiple hypothesis-testing problem.
With the advancement of statistical techniques, there is a growing interest in detecting unusual group behavior, especially in high-density regions. Some representative models have been proposed. Muandet and Schölkopf [7] introduced OCSMM, which extends the One-Class Support Vector Machine (OCSVM) [21] to groups. By adapting the kernel in OCSVM for the mapping of points into feature space to the kernel mean embedding mapping of groups into feature space, OCSMM extracts distribution information from normal groups and separates them from the origin. SMDD [11] also utilizes the kernel mean embedding technique, but it is based on the idea of constructing a minimum enclosing ball [22]. Ting et al. [23] proposed the isolation distribution kernel to quantify distribution similarities within groups. Fisch et al. [24] introduced a statistical approach for detecting both collective and point anomalies with a linear computational cost. Other approaches, such as those proposed by Yu et al. [25], Song et al. [9], and Chalapathy et al. [8], are tailored for specific application areas. However, these models consistently fail to handle scenarios where both point-based and distribution-based anomalous group behavior occur within the same group. Some efforts have been made to detect both types of anomalous group behavior, such as MGMM [6] and FGM [12], which are strongly related to the topic model of Latent Dirichlet Allocation (LDA) [26]. Topic models are often used in natural language processing to classify a collection of documents, each of which is typically concerned with multiple topics and where each topic is represented by a cluster of multiple words. MGMM considers each group as a mixture of Gaussian-distributed topics, while FGM defines flexible structures called “genres” to model topic distributions. Scores are then defined to measure point-based and distribution-based anomalous group behavior and combined using a weight function. However, these models tend to focus primarily on the distribution of points in high-density regions, as the topic generation process is less affected by points in low-density regions, particularly when these points are sparse. As a result, they exhibit significant bias in detecting point-based anomalous group behavior.
In recent years, to develop a suitable model for point-based anomalous group behavior, researchers have explored considering low-density region points as an integral component. Luca et al. [2,27,28] investigated the use of EVT to extract features characterizing the aggregate of points in low-density regions (also termed extreme risk regions) of . This involves summarizing aggregation information from extreme points in terms of the mean, maximum excess of , or the number of extremes with respect to some threshold. While these models address the multivariate hypothesis-testing problem by employing such features to characterize aggregated extreme behavior, questions remain about how to identify a comprehensive feature set that effectively captures this behavior.
3. Background Knowledge
In this section, the necessary concepts of EVT and the related PPM are introduced, which play an essential role in the remainder of the paper. For more details about the proofs of the presented theorems, we refer to [29]. The key notations and abbreviations used throughout this paper are summarized in Table 1.

Table 1.
Summary of notations and abbreviations.
3.1. Extreme Value Theory
EVT is a statistical discipline with the objective of modeling the stochastic behavior of a univariate process at unusually large (or small) levels. It has already been proven useful in many applications, such as reliability analysis, structural health monitoring, meteorology, and financial risk assessment [30,31,32].
The central result in EVT is the Fisher–Tippett theorem concerning the limiting distribution of
where are i.i.d. univariate random variables with a common distribution function ().
Theorem 1 (Fisher-Tippet-Gnedenko).
If there exist sequences of normalizing constants and such that the following convergence in distribution holds:
then the non-degenerate limiting distribution () is a member of the so-called Generalized Extreme Value (GEV) family of distributions:
If , then the domain of the distribution is restricted to the set expressed as .
If the shape parameter () is negative, zero, or positive, then the corresponding distributions () belongs to the Weibull, Gumbel, or Fréchet family, respectively. Thus, the shape parameter () thus determines the behavior in the tails of the distribution ().
The GEV family provides a model for block maxima, i.e., maxima of a sequence ). However, for relatively large n values, few block maxima are available from the data, which can lead to unreliable estimates of [30]. To overcome this problem, the peaks-over-threshold method can be used, which avoids the need for blocking. This method infers a model from all observations that exceed some high threshold.
Theorem 2 (Pickands-Balkema-De Haan).
For a given sufficiently close to 0, the sequence of thresholds expressed as is considered, where and denote the normalizing constants as defined in (1). If (1) holds for some member () of the GEV family, then the distribution of the exceedances (), conditional on , satisfies the following limiting property:
where is the scale parameter for exceedances relative to the threshold (). The distribution expressed as
denotes the family of Generalized Pareto Distributions (GPDs) with in the case of and in the case of .
These two classical models represent the cornerstone of Extreme Value Theory. When the prior distribution of Z is unknown, the three parameters, i.e., the shape parameter () and the normalizing constants ( and ), need to be estimated for practical applications. For a range of commonly encountered distributions, such as the gamma, exponential, Gaussian, and beta distributions, Embrechts et al. [29] presented direct sample estimation formulas for the , , and parameters. In cases where populations have the extreme value distribution of the Gumbel case (), the scale parameter () and the normalizing constants ( and ) can be estimated as follows [29]:
where the latter is the mean excess function.
3.2. Point Process Model
A (spatial) PPM in Euclidean space can be viewed as a random variable () defined over all possible point patterns in some subspace () of (), where a realized point pattern is given by [33] A PPM integrates stochastic information about the number of points and their individual locations in the feature space. It can be shown that the stochastic properties of a PPM are fully characterized by so-called counting measures with respect to the corresponding subsets [34], which are obtained by mapping a pattern () to the number of points that fall in a subset (A) of :
where for and for . An important concept associated with a counting measure is its expectation ( ). Clearly, a realization () can be fully reconstructed by considering the counting measures corresponding to all possible subsets (A) of .
The PPM can be used to elegantly characterize the extremes in a way that unifies the models presented in Theorems 1 and 2 [30].
Theorem 3 (Point Process Characterization).
When the limiting distribution (3) of the block maxima of the univariate random variable (Z) holds, the PPM of patterns consisting of exceedances of the block with respect to the threshold (), i.e.,
converges to a Poisson point process as . The corresponding counting measure () converges in distribution to a Poisson distribution:
where is the expectation of the counting measure.
For the Gumbel case, where , it can be shown that .
4. A Statistical Framework for Modeling Group Behavior
This section introduces the Extreme Value Support Measure Machine (EVSMM), a novel statistical method for comprehensively quantifying how anomalous a group is compared to normal training groups. The foundation of EVSMM involves characterizing the group-level normal behavior of normal training groups within the d-dimensional point feature space (). We quantitatively analyze group behavior by modeling the statistical characteristics of two complementary parts within the group: the low-density region and the high-density region. The EVSMM operates through a two-step process. First, two scores are constructed to quantify how unusual the parts of a group situated in the low-density and high-density regions are. Second, an effective way to combine these two scores is proposed by using a constructed uninorm aggregation function, whose roots trace back to the fusion of certainty factors in highly successful early-day expert systems. The following sections detail the rationale and necessity behind the construction steps of EVSMM.
4.1. Two Key Scores
We start with the construction of two scores to quantify the anomaly extent of a group’s low-density and high-density regions.
4.1.1. PPM of Exceedances
In this section, we propose a PPM framework that models the spatial configuration of exceedances with respect to a decision boundary in its full generality. We then derive an asymptotic distribution, valid as , which is used as an approximation to model the aggregate of exceedances.
Let be a d-dimensional random variable, with no distributional assumptions imposed on . Consider a training set of normal groups (), where each group () has a varying size (), with . The objective is to comprehensively quantify the unusual behavior of a group with respect to low-density regions, which entails characterizing the aggregate behavior of exceedances, as determined by a certain number of exceedances, and their various locations within low-density regions. The aggregate of exceedances within group is given by
for large values of . The low-density regions are defined by the decision boundary (, where is the threshold in the peak over threshold model introduced in Theorem 2).
As previously described, this study begins by analyzing the distribution of points across all training groups, which describes the probability space of d-dimensional variable . As our framework is not restricted to a particular density estimator, any suitable method could be adopted to estimate the probability density function (). To illustrate this flexibility, We mention several representative alternatives, such as parametric models like Gaussian Mixture Models (GMMs), non-parametric approaches like Projection Pursuit Density Estimation (PPDE), and random projection-based techniques for high-dimensional data. In our experiments, we adopt Kernel Density Estimation (KDE), a widely used non-parametric method that does not require prior assumptions about the data distribution. We explicitly clarify that KDE is used solely as an example and is not necessarily the optimal choice for all scenarios. Next, the transformation of is applied, mapping the multivariate random variable () to the univariate random variable (Y). Consequently, within each group (), sample is transformed into sample within as follows:
Therefore, the exceedances of , whether they are extremely large (the right tail) or small (the left tail) values in the case of a univariate X or occupy diverse locations within low-density regions in the case of a multivariate , correspond solely to the left tail of Y. As Y is the probability density, it is bounded below by zero, which guarantees the existence of an extreme value distribution in its left tail. Moreover, Clifton et al. [35] proved that the distribution of minima () can be approximated by a Weibull distribution. A Weibull distribution, with a lower bound at zero, describes the behavior of small values of densities near zero [30]. To correct the skewness in the distribution of Y near zero, a logarithmic transformation () is applied:
mapping the short tail of the Weibull distribution near zero to the right tail of a Gumbel distribution for maxima:
where denotes a cumulative distribution within the Gumbel family. In this way, the multivariate, complex, low-density regions () are transformed into regions on the real line. The significance of transforming to Z not only lies in mapping low-density regions from a high-dimensional space to the right tail in a one-dimensional space but also in making it possible to exploit the well-established theoretical results for the Gumbel case () in EVT. Within a group () of n observations of Z, we study those points that exceed the threshold () and consider them as an aggregate:
where denotes the number of exceedances in w.r.t. . In what follows, we derive an analytical result to determine the asymptotic distribution of such aggregate of exceedances as . Note that, although i.i.d. random variables are considered, the results can be applied to time series data by considering the residuals after fitting a time series model.
To tackle the above problem in its full generality, is viewed as a realized non-empty point pattern of a PPM. First, the probabilistic model of individual exceedances is derived using the limiting property (3) in Theorem 2 for (i.e., the Gumbel case). As a result, for large n, the likelihood of an exceedance can be approximated by:
where and and are defined in (5). Second, the aggregating behavior of these exceedances is analyzed. The aggregate of exceedances with respect to low-density regions is fully characterized by the counting measure introduced in Section 3.2. From Section 3.1, it follows that
where and . These approximations motivate the definition of a probability measure, referred to as the PPM of exceedances, with the following likelihood:
where k denotes the observed size of and . In the theorem below, we prove that the distribution of the likelihoods () is asymptotically given by a random variable () of mixed type. Random variables of mixed type are neither discrete nor continuous but are a mixture of both [36]. The discrete component results from the likelihoods () that describe cases when there are no exceedances in . This corresponds to a discontinuity in the CDF that can be described using the Heaviside step function:
Theorem 4.
Consider a random variable (Z) that satisfies the following limiting property:
where , with , is determined by a sequence of thresholds in which
The random variables () of likelihoods (), as defined in (9), converge in distribution to a random variable () with the CDF:
where denotes the CDF of an Erlang distribution with shape parameter k and scale 1 and . In particular, it holds that
Proof.
First, we determine the distribution of given the number of exceedances (). We have
According to (11), the rescaled exceedances () converge in distribution to an exponential random variable with a scale of as . Therefore, according to the continuous mapping theorem (stating that convergence is preserved by a continuous transformation [29]), the sum of k such independent exceedances converges to the distribution of a sum of k exponential random variables with a scale of . Thus, the limiting distribution of , conditioned on , is given by an Erlang distribution with shape parameter k and rate parameter 1.
The cumulative distribution function of can be found using the law of total probability:
The latter part is the limiting CDF of , which we denote as . Transforming back to the original distribution by means of , one obtains the desired result for :
□
As a brief summary, we propose the likelihood measure () to evaluate group samples. The likelihood measure of a group is constructed based on the pattern of its exceedances—taking into account both the individual locations of low-density regions and their aggregate behavior. The derived analytical form () describes the distribution of this likelihood measure and plays a central role in quantifying the group’s probabilistic anomaly extent. Notably, similar to the Central Limit Theorem, a key advantage of EVT—the foundation of our framework—is that, while the asymptotic theory requires large n values, in practice, the method often performs well even for moderate values of n. To validate the analytical expression in (13), we conducted a simulation experiment. For this purpose, we generated 2000 groups from a one-dimensional standard Gaussian distribution (), with each group size sampled from a Poisson distribution with a mean of 50. In practice, such group size selection entails a trade-off between bias and variance, as a small group size leads to an estimation bias, whereas a large group size results in an increased estimation variance. Next, the likelihood () is calculated for each group with respect to an aggregate of exceedances, and the CDF of the likelihood is examined. The empirical CDF of is then compared with the asymptotic CDF given by (13). As shown in Figure 2, the empirical CDF approximates the analytical CDF quite well.
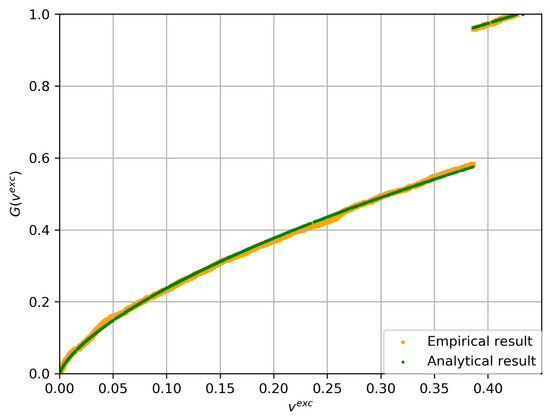
Figure 2.
Comparison between the empirical distribution (yellow curve) and the analytical expression (green curve) of the likelihood (). The empirical CDF, based on 2000 simulated groups, closely matches the asymptotic CDF derived in Theorem 4. This result supports the practical validity of the analytical formulation.
Based on the above analytical result, the first score is constructed using the expression of CDF in (13), which assesses the anomaly extent of a group () with respect to low-density regions. Addressing the multiple-hypothesis problem is critical, because as the number of points forming a group increases, the exceedances are expected to become more extreme, and their number is expected to grow. The proposed likelihood concept encompasses both the probability of each individual exceedance location and the probability of the size of the aggregate of exceedances within a group. Through the likelihood concept, all exceedances within a group are treated as a unified whole. Accordingly, the first score, termed the point-based group anomaly score, is defined as follows:
where denotes the likelihood, as defined in (9), of the aggregate of exceedances () with respect to the threshold (). A high anomaly score () indicates that there is a small probability of observing a group with a lower likelihood of the aggregate of exceedances than in any other group. We summarize the practical implementation of the model in Algorithm 1.
4.1.2. A Calibrated OCSMM Model
In this section, we construct the distribution-based group anomaly score by calibrating the OCSMM to quantify the anomaly extent of the group with respect to high-density regions. Basically, the OCSMM extends OCSVM by classifying groups () instead of individual points () [37]. The core concept behind OCSMM involves applying the kernel trick to map the mean embeddings of training groups into a feature space, where they are separated from the origin by a hyperplane. For more details about OCSMM, we refer to Appendix A.
| Algorithm 1 PPM of exceedances: point-based group anomaly score. |
|
There are several key reasons for selecting OCSMM. First, it is specifically designed to capture the distribution characteristics within each normal group and demonstrates robustness to outliers in low-density regions, providing a stable and reliable representation of distribution information for the training group set with respect to high-density regions. This capability complements the model proposed in the previous section, which focuses on low-density regions. Second, OCSMM leverages the kernel trick, enabling efficient modeling of the decision boundaries for complex group structures. By using the mean kernel embeddings, OCSMM computes inner products in high-dimensional spaces without requiring explicit group feature transformations. Third, OCSMM is firmly grounded in statistical learning theory, kernel mean embedding theory, and optimization theory. Its formulation as a convex optimization problem, with clearly defined constraints, ensures that a unique global optimum can be reliably determined.
Although OCSMM provides a flexible and mathematically robust framework, its output is inherently binary, producing classifications without any probability estimates. While the decision function generates continuous scores, classification is determined solely by the sign of the output. These scores indicate relative distances from the decision boundary, but they do not provide a direct probabilistic interpretation.
As far as we are aware, there has been no prior research specifically focused on the probabilistic calibration of OCSMM. A critical challenge in this process is generating anomalous group samples, a necessary step for calibration due to the inherent scarcity of anomalous samples in both classical anomaly detection and group anomaly detection tasks. The following section details our calibration procedure, including the choice of the calibration method and the steps for generating anomalous groups.
We argue that, among various calibration methods, sigmoid fitting is particularly suitable for calibrating OCSMM. Unlike binning methods and isotonic regression, which often introduce discontinuities and risk overfitting, sigmoid fitting is specifically designed for binary classification problems and performs robustly on imbalanced data. In addition, sigmoid fitting offers flexibility and computational efficiency, which makes it advantageous for handling large datasets. Furthermore, sigmoid fitting assumes a monotonic relationship between decision scores and class probabilities, an assumption that aligns well with the behavior of OCSMM’s decision scores. Based on these considerations, sigmoid fitting was chosen as the calibration method.
The decision function of the OCSMM model trained on the training group set is denoted as . Let represent the calibrated score of a group () based on the output of . Then, sigmoid fitting is performed as follows:
where g and q are parameters estimated by solving the following regularized, unconstrained optimization problem:
where and
for . The numbers of samples labeled as 1 () and () are denoted by and , respectively. For calibration related to a pointwise classifier (e.g., SVM or OCSVM), Platt used the Levenberg–Marquardt (LM) algorithm to solve (18) [38]. Later, this was improved by Lin et al. [39], who demonstrated that (18) is a convex optimization problem and presented a more robust algorithm with proven theoretical convergence to solve it.
To calibrate the group classifier OCSMM, it is essential to generate anomalous groups rather than individual anomalous points. Inspired by previous work on anomalous points [40,41,42], we adapted these ideas for groups. To generate anomalous points, the central assumption is that, spatially, all such points lie outside high-density regions. Building upon this assumption, previous studies have focused on constructing anomalous points for an optimal calibration, where a threshold on the density () is determined to classify a point as anomalous or not. However, anomalous groups cannot be generated by the same approach as anomalous points, as they exhibit more complex structural behavior. Unlike anomalous points, anomalous groups may not only deviate spatially from high-density regions but can also significantly overlap with normal groups. These simulated groups are specifically constructed to introduce mild deviations from normal patterns near the decision boundary, serving as informative references for the calibration of the OCSMM score. Based on the above analysis, we propose the following algorithm for the generation of anomalous groups.
Algorithm 2 starts by generating the group centers. A key difference between Algorithm 2 and the pointwise calibration methods discussed earlier is that the threshold, a hyperparameter used to define the boundary of high-density regions, is removed. This modification allows group centers to be located in both high-density and low-density regions. The next step focuses on ensuring that anomalous groups exhibit as much diversity in their distribution characteristics as possible. To achieve this, the covariance matrix is generated randomly under constraints derived from the covariance matrices of the normal groups in the training set. Then, a new anomalous group for the calibration is generated by sampling from a multivariate Gaussian distribution, using the group center as the location and the generated covariance matrix as the scale.
| Algorithm 2 Generation of a set of anomalous groups () for the calibration. |
|
Algorithm 2 avoids generating extreme groups that would be too easily detected and eliminates the need for the intricate threshold determination step required in methods of generating anomalous points. This design provides a pragmatic approach to addressing the scarcity of labeled group anomalies and aims to improve probabilistic interpretability rather than explicitly simulating specific unknown anomalous behavior. After obtaining the anomalous groups, the sigmoid calibration technique is applied. We then define a distribution-based anomaly score as the calibrated OCSMM score () to quantify how anomalous the high-density region of a group is. The overall steps for obtaining the distribution-based anomaly score () using calibrated OCSMM are summarized in Algorithm 3.
| Algorithm 3 The calibrated OCSMM: distribution-based group anomaly score. |
|
4.2. Extreme Value Support Measure Machine
In previous sections, we introduced two group anomaly scores to evaluate two complementary parts of the group: a point-based anomaly score for a group’s low-density region, denoted as , and a distribution-based anomaly score for a group’s high-density region, denoted as . Specifically, assesses the anomalousness of the aggregate entity of exceedances within the low-density regions. In contrast, evaluates whether the distributional characteristics of points, considered as an aggregate within the high-density regions, deviate significantly from those observed in the training groups. The next step is to develop an integrated framework that effectively leverages both probabilistic scores to capture the overall level of anomalousness.
For this purpose, we take inspiration from the way certainty factors are combined, encountered in the early days of expert systems such as PROSPECTOR [43] and MYCIN [44] capable of reasoning under uncertainty. Functions such as Van Melle’s combining function [45], typically of type , are well thought-out functions designed for that purpose. Only in the 1990s [45], after linearly rescaling to functions of type was it realized that they were examples of a broader class of aggregation functions on the unit interval called uninorms. Uninorms operate on the unit interval of , providing a systematic way to combine probabilistic scores. In our case, the two probabilistic scores, each within the range of , align particularly well with uninorms, which are binary operations capable of meeting these engineering demands.
We now argue that uninorms with a neutral element (e), which acts as a hyperparameter, are ideally suited for our purpose. In engineering applications with multiple measures assessing different aspects of a system, it is essential that when more than one measure exceeds a given threshold (triggering alarms for specific aspects), the overall measure should reflect a more severe status of the system. For instance, in health monitoring, when a patient exhibits multiple anomalous health indicators, we tend to consider the overall health condition to be worse. Constructing a single measure that exceeds any anomalous health indicator when assessed on the same scale provides more informative insights into the patient’s condition. In such cases, traditional weighting methods, such as weighted averaging and t-conorms (e.g., maximum), either dilute dominant signals or fail to model mutual reinforcement. Uninorms offer a principled mechanism to capture both synergistic and antagonistic effects, which is critical in group anomaly scenarios involving dual sources of evidence.
A uninorm is a symmetric, associative, increasing binary operation on with a neutral element (). The case of corresponds to the well-known t-norms (including the minimum operation), and the case corresponds to the well-known t-conorms (including the maximum operation). Due to its associativity, any uninorm (U) is either conjunctive (i.e., ) or disjunctive (i.e., ). The structure of a uninorm with a neutral element (e) is expressed as follows [46]: on , it behaves as a rescaled t-norm, taking values below the minimum; on , it behaves as a rescaled t-conorm, taking values above the maximum; an on the remaining parts of the unit square (i.e., ), it behaves as a compensatory (also called averaging) operator, taking values between the minimum and the maximum. Given a t-norm and a t-conorm, one can always build a uninorm by considering the minimum or maximum (one of the two extremes) as a compensatory operator.
In our case, suppose that exactly one of the anomaly scores takes a value higher than e; then, one would consider this an indication of the group being anomalous, irrespective of the other score and, thus, consider it as the overall anomaly score. Hence, to construct a uninorm, we consider the maximum as compensatory operator a viable choice. However, if both anomaly scores exceed e, then they could be seen as reinforcing one another and act synergistically, yielding an overall score exceeding the maximum of the individual scores. Similarly, if both anomaly scores take a value lower than e, then they should act antagonistically, yielding an overall score lower than their minimum. The symmetry of the uninorm expresses that both anomaly scores play the same role.
The most famous uninorm exhibiting the desired synergistic and antagonistic behavior is the operator with neutral element :
with either or . This operation is nothing else but a rescaled version of the function used for combining certainty factors in the PROSPECTOR rule-based system. Without going into detail, we note that all members of the important class of representable uninorms are isomorphic to this iconic operator, illustrating its central role.
Recalling our argumentation above that, on , the selected uninorm should preferably act as the maximum, we can modify the operator (keeping the underlying t-norm and t-conorm), resulting in the uninorm () used in our final aggregation method. It is given by
The detailed derivation of the uninorm () based on operator is provided in Appendix A. As a result, the combination of the two anomaly scores is completed. We present the full procedure of the proposed model EVSMM in Algorithm 4.
| Algorithm 4 Extreme value support measure machine (EVSMM). |
|
5. Experiments
In this section, we present extensive experiments to demonstrate the effectiveness of the proposed EVSMM in detecting unusual group behavior. The performance of the EVSMM is compared with five other group anomaly detectors: the discriminant SMDD model (https://github.com/jorjasso/SMDD-group-anomaly-detection, accessed on 28 May 2025) [11], the OCSMM (https://github.com/kdgutier/ocsmm, accessed on 28 May 2025) [7] and its calibrated output based on a sigmoid transformation (Cali-OCSMM), the generative MGMM model (https://www.cs.cmu.edu/%7Elxiong/gad/gad.html, accessed on 28 May 2025) [6], and an extreme value model (EVM) based on Extreme Value Theory [2].
5.1. Experiments on Synthetic Data
We performed an experiment using synthetic data with a set-up comparable to the one used in [6,7,8,9,11]. Following these references, the normal groups are simulated from two Gaussian mixture distributions in the plane that each consists of four components. The mixing proportions for the Gaussian mixtures are expressed as and . To generate a normal group, probabilities are assigned to determine which Gaussian mixing proportion is applied. The selected Gaussian mixing proportion is then used to generate the group. The components of both mixtures are centered at , , , and and share the covariance matrix (, where is the identity matrix).
Three types of anomalous groups are considered: (i) point-based anomalous groups, (ii) distribution-based anomalous groups, and (iii) groups that are anomalous as a mixture of unusual low-density and high-density regions. The threshold for identifying low-density regions is determined based on a mean residual plot. To generate groups with varying extents of point-based anomalous behavior, the number of low-density regions is randomly chosen according to a Poisson distribution with a mean of , truncated at zero to ensure the presence of at least one anomalous point. For a more detailed investigation of the impact of , additional experiments were conducted with varying values (as presented later). These experiments reveal that as increases, other group anomaly detectors, such as MGMM, begin to achieve performance comparable to that of our model. This phenomenon occurs because an increase in the number of exceedances gradually transforms point-based anomalous group behavior into distribution-based anomalous group behavior. Groups exhibiting various distribution-based anomalous behaviors are simulated through a Gaussian mixture distribution with the same centers as the normal groups but different mixing proportions. The proportions , as used in [7], are complemented by including three additional configurations: , , and . A mixed anomalous group contains both an aggregate of points in low-density regions and an aggregate of points randomly simulated from unusual mixing proportions in high-density regions.
To evaluate our method with varying extents of distribution-based and point-based anomalous behavior, nine distinct cases were designed to ensure a diverse representation of anomalous group configurations in the test set. The corresponding experiments consider varying fractions of the three types of anomalous groups, defined as , , , , , , , , and (the first component representing point-based anomalous groups, the second representing distribution-based groups, and the third representing a mixture thereof). In each of the experiments, we injected 60 anomalous groups into the test set according to the corresponding proportions.
We used 1000 normal groups for training. The training involves a 10-fold cross-validation: in each run, the dataset is randomly partitioned into ten parts, of which seven are used for training, two for hyperparameter optimization in a validation step, and one for testing. In the proposed EVSMM approach, two hyperparameters are subject to tuning: in the Cali-OCSMM model, controlling the kernel width, and e, the threshold in the uninorm that determines the aggregation behavior when combining anomaly scores designed to evaluate complementary aspects of the group. These hyperparameters are optimized using a grid search strategy guided by nested cross-validation, where and . The group size is simulated using a Poisson distribution with a mean of . Model performance is analyzed based on the ROC curve and the AUC metric. The detailed results are presented in Figure 3, Figure 4 and Figure 5 and Appendix A.
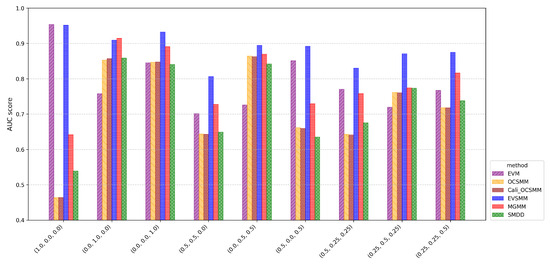
Figure 3.
Average AUC scores (10-fold cross-validation) for nine synthetic cases. EVSMM consistently achieves strong performance across all cases, while EVM excels in detecting point-based group anomalies. In contrast, OCSMM, MGMM, and SMDD are more effective for distribution-based group anomalies, as reflected in cases with higher proportions of such groups.
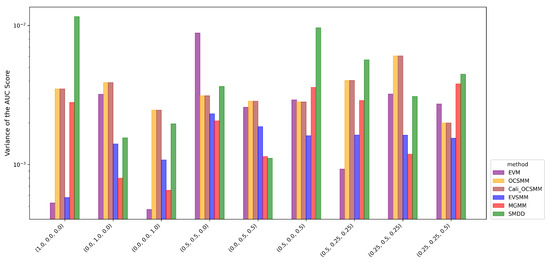
Figure 4.
Variance of AUC scores (logarithmic scale) based on 10-fold cross-validation for nine synthetic cases. EVSMM exhibits stable performance with low variance across most cases. MGMM shows lower variance than EVSMM in cases with few point-based group anomalies.
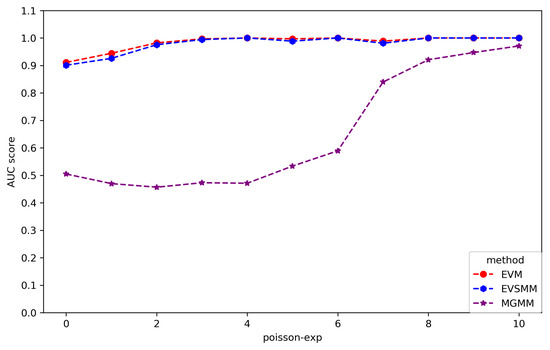
Figure 5.
Average AUC score (10-fold cross-validation) for the synthetic data where the mean number () of anomalous points in each group is varied between 0 and 10. EVSMM and EVM maintain stable performance across the entire range, and MGMM shows clear performance improvement as increases, reflecting its sensitivity to the number of exceedances when quantifying point-based group anomalies.
To ensure robust performance, and e were jointly tuned via grid search, using AUC as the selection criterion within a nested 10-fold cross-validation framework. Across all folds and experimental cases, the optimal value consistently converged to . As a result, only the values of e are reported in Table 2, which summarizes the fold-wise optimal e for each synthetic anomaly case. The final row reports the optimal value of e for each case based on its frequency across folds.

Table 2.
Values of hyperparameter e across 10-fold cross-validation for synthetic data cases.
In contrast to the other approaches, from the results shown in Figure 3, it follows that EVSMM achieves consistently competitive performance across all cases. MGMM is also relatively effective compared to other models, achieving AUC scores exceeding in eight out of nine cases. However, it is observed that MGMM is less performant in evaluating point-based anomalous groups that have a limited number of exceedances. Although MGMM is designed to detect group anomalies of different types, its ability to detect point-based anomalous group behavior requires a sufficient number of exceedances, as examined further through experiments with varying values. Based on the results in the cases of and , it is clear that the EVM is particularly suited to effectively detect point-based group anomalies. Although half of the groups in the case of exhibit varying extents of distribution-based anomalous group behavior, EVM stands out for its ability to quantify point-based anomalous group behavior across all groups. However, when compared with the outcomes from the case of , it becomes evident that EVM is unable to address the distribution-based anomalous group behavior present in half of the groups in the case of . SMDD, MGMM, and OCSMM are particularly suited for groups with an unusual aggregate of points in high-density regions, as shown in the cases of and , where every group exhibits a varying extent of distribution-based anomalous behavior, resulting in higher AUC values for the these models. Also in the cases of and , with a high proportion of distribution-based group anomalies, three models show their detection capabilities. In Appendix A, we show comprehensive ROC curves for all nine cases, allowing for comparison of the performances of various approaches.
Figure 4 shows the variance of the AUC scores on a logarithmic scale. Overall, EVSMM shows a satisfactory stability of AUC scores. In cases with a relatively low proportion of point-based group anomalies, MGMM has a lower variance than EVSMM. OCSMM and Cali-OCSMM have the same variance in all cases, confirming that the sigmoid calibration is effective. Appendix A shows an alternative graphical representation using box plots to compare the AUC scores among various methods for each case.
Furthermore, we conducted an experiment focused exclusively on point-based group anomalies, specifically by varying the number of points located in low-density regions within groups. In our previous experiments, we assumed that the number of points in low-density regions is governed by a Poisson distribution with an expectation parameter of . Here, we vary this parameter from 0 to 10 and look at the effect on the performance of MGMM, EVM, and EVSMM, all of which possess the ability to evaluate point-based anomalous group behavior. Figure 5 reveals that as the number of points in low-density regions increases, the performance of MGMM becomes comparable with that of EVM and EVSMM. However, when the number is lower, MGMM fails to quantify point-based anomalous behavior. This can be attributed to the gradual transition of point-based anomalous group behavior into distribution-based anomalous group behavior as the number of exceedances increases. As indicated the previous results, although the overall performance of MGMM is not as strong as that of EVSMM, MGMM exhibits greater sensitivity to this transition compared to other models that excel in detecting distribution-based group anomalies.
5.2. Experiments on the Sloan Digital Sky Survey Data
In this section, we evaluate the EVSMM on the Sloan Digital Sky Survey (SDSS) dataset. This dataset includes information on millions of celestial objects, such as stars, galaxies, and various other astronomical phenomena. It provides detailed measurements of the positions, brightness, and spectra of these objects. Our focus is on studying a subset of galaxies that consists of a large volume of 4000-dimensional spectra of about galaxies. We adopt the 1000-dimensional feature vectors derived from the original 4000-dimensional spectra, as provided in the publicly available benchmark dataset used in prior studies [6,7,9,11]. We then apply principal component analysis (PCA) to further reduce the data to four dimensions. The resulting four principal components retain approximately of the total variance. Specifically, PC1, PC2, PC3, and PC4 account for , , , and of the total variance, respectively. This reduced representation is subsequently used as input for density estimation. Specifically, KDE is performed on the resulting four-dimensional features, thereby mitigating the impact of high dimensionality on the estimation process.
Xiong et al. [6] were the first to utilize the SDSS dataset for group anomaly detection. They identified 505 spatial groups of galaxies using a constructed neighborhood graph, where each connected component in the graph represents a group. Then, they conducted group anomaly detection on these 505 groups without prior knowledge of any group anomaly labels. The results gained positive recognition from astronomers. Furthermore, in order to ensure a statistically meaningful comparison among various methods, artificial anomaly injections were employed to address the absence of labels, a method that was commonly adopted in subsequent research [6,7,9,11,47].
Building on the injection method used in previous studies, we increased the complexity of the injected anomalous groups to avoid configurations that are trivial to distinguish. Point-based, distribution-based, and mixed anomalous groups are constructed by randomly selecting existing points from the training group set. Specifically, point-based group anomalies are generated by aggregating galaxies located in low-density regions, with aggregate sizes following a Poisson distribution with , whereas distribution-based group anomalies are constructed by randomly selecting galaxies from high-density regions, with the constraint that the selected galaxies are not all drawn from the same group. We consider six cases, where, in each case, a total of 50 anomalous groups are injected with proportions of point-based, distribution-based, and mixed anomalous groups set to , , , , and , respectively.
During a nested 10-fold cross-validation procedure, the optimal value of was consistently selected as 1.4 across all folds. The corresponding values of e selected in each fold are reported in Table 3. This table shows the fold-wise tuning results for each SDSS anomaly case, and the final row presents the most frequently selected value across folds.

Table 3.
Values of hyperparameter e across 10-fold cross-validation for SDSS data cases.
As shown in Figure 6, EVSMM demonstrates consistently high AUC scores across all cases, outperforming achieving performance comparable to that of other methods. In Figure 7, which shows the variance of the AUC scores on a logarithmic scale, we observe that EVSMM stands out for both high AUC scores and low variance, showcasing its ability to effectively and reliably handle various types of group anomalies. While MGMM achieves high AUC scores in many cases, its performance is less stable in configurations dominated by point-based group anomalies, as reflected in its higher variance. EVM and Cali-OCSMM perform well at detecting distribution-based group anomalies but exhibit less stability compared to EVSMM. On this real-world dataset, we observe that SMDD exhibits notable variability in its AUC score variances across different data configurations. This may suggest that, compared to other methods, the stability of SMDD is more affected by the dataset properties, resulting in marked discrepancies in variance values.
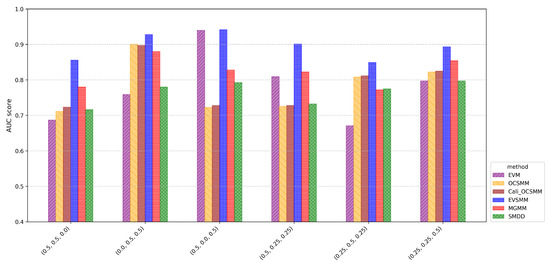
Figure 6.
Average of the AUC scores (10-fold cross-validation) for the SDSS data across different anomaly configurations. EVSMM consistently achieves high AUC values and outperforms other methods across all cases. MGMM shows uneven performance depending on the anomaly configuration.
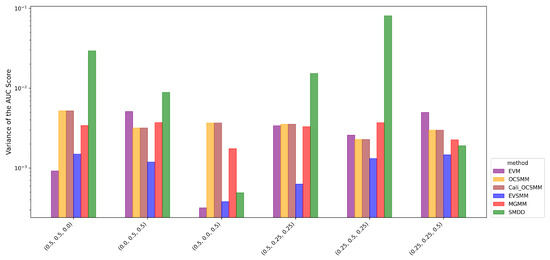
Figure 7.
Variance of the AUC scores (shown on a logarithmic scale) (10-fold cross-validation) for the SDSS data. EVSMM consistently exhibits a low variance, indicating strong stability across all cases. SMDD shows fluctuating variances, particularly under configurations involving point-based or mixed group anomalies.
The performances of OCSMM and Cali-OCSMM are very similar, indicating that the calibration method for the OCSMM is effective for the SDSS data. In Appendix A, we show the ROC curves and box plots of the AUC scores for each case. These results highlight the effectiveness and robustness of EVSMM, particularly in scenarios with mixed anomaly types with varying extents of anomalous behavior. While MGMM shows strong potential, its sensitivity to specific configurations (e.g., , ) warrants further investigation to enhance its stability and performance.
6. Conclusions and Future Work
In this work, we have proposed an efficient method for comprehensively detecting group anomalies, termed EVSMM. The method integrates a PPM based on EVT and a calibrated OCSMM, which evaluate complementary aspects of the target group, with the scores subsequently being integrated using a constructed uninorm. Indeed, through the PPM, we formally construct the likelihood for an aggregate of low-density regions within a group and, more importantly, derive the analytical distribution of the likelihood. The calibrated OCSMM quantifies the aggregate of points within high-density regions, addressing the limitation of its raw output, which provides only classification without probability estimates. Through this calibration, a novel approach is introduced for generating diverse anomalous groups, which offers a reference for future research on the calibration and validation of group models. A uninorm is constructed to combine two anomaly scores with the ability to locally synergize, antagonize, and weigh these scores relative to the threshold e.
Extensive experiments show that existing group anomaly detection approaches, such as OCSMM, MGMM, and SMDD, are mainly focused on the detection of distribution-based group anomalies but lack the ability to comprehensively quantify diverse group anomalies. Alternative approaches that are built upon methods centered around the detection of individual anomalous points tend to inaccurately model point-based anomalous group behavior and face challenges managing the multiple-hypothesis problem. The proposed EVSMM effectively quantifies various anomalous group behaviors and, unlike existing methods, provides a probability-based anomaly score that enhances interpretability and utility in practical applications.
Future work opens several promising and exciting directions. One direction lies in extending our model beyond anomaly detection to risk prediction tasks in climate-related applications. For example, EVSMM can be applied to evaluate heat waves, which are defined as consecutive periods of high temperatures. Each period can be treated as a group, with its severity assessed based on the joint characteristics of duration and intensity. In addition to retrospective evaluation, the model can be used for risk assessment of future extreme events. Another relevant direction is the assessment of persistent extreme rainfall, where clusters of intense precipitation across consecutive time intervals can be modeled as groups using high-resolution precipitation data. The model can further support prediction by estimating the likelihood of future events under varying environmental conditions. These applications demonstrate how group-level modeling can be leveraged not only for anomaly detection but also for probabilistic risk assessment in climate science. Another focus will be a deeper investigation into the performance of our model in group anomaly detection tasks. This involves two aspects. On the one hand, we should keep exploring the model’s ability to detect varying extents of anomalous behavior, extending research beyond evaluating the test-set accuracy. Specifically, our plan is to study the relationship between the entropy of groups and the anomaly scores to gain further insights into its capabilities. On the other hand, we intend to explore more meaningful real-world group anomaly detection tasks to assess the practical utility and robustness of our approach. One particular aspect that can be studied is the robustness of the method against noisy data. Since the likelihood of a group is evaluated based on the entire aggregate of exceedances, we expect that, to some extent, noisy observations—such as random low-density points scattered in otherwise normal groups—do not affect the distribution of the likelihood substantially unless their number exceeds a statistically meaningful level. However, further investigation could provide deeper insight into the precise effect of noisy data on the detection of the different types of group anomalies examined in this work. These directions are expected to provide a clearer understanding of the model’s strengths and uncover novel applications.
Author Contributions
Conceptualization, S.L. and L.A.; methodology, S.L., B.D.B. and L.A.; formal analysis, S.L., B.D.B. and L.A.; writing—original draft preparation, L.A.; writing—review and editing, S.L. and B.D.B.; supervision, S.L. and B.D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Flemish Government under the “Onderzoeksprogramma Artificiële Intelligentie (AI) Vlaanderen” programme, the BOF Research Fund (No. BOFCHN2021000401) of Ghent University, and the China Scholarship Council (No. 202106280033).
Data Availability Statement
We provide the ZIP file EVSMM_project_python contains the project description, datasets, the Python code, (developed using Python 3.10.13) output results, and information on the running time.
Acknowledgments
Lixuan An would like to extend her heartfelt gratitude to her colleagues Nusret Ipek, Lisheng Jiang, Yuan Gao, Taotao Cao, Max Savery, Baoying Shan, Yafei Cheng, Yuntian Wang, Maxime Van Haeverbeke, Baoying Zhu, Feiqiang Liu, and Haoxiang Zhao, for their invaluable support and discussion during her study abroad.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This section includes examples of uninorms and the derivation of uninorm based on operator , as well as additional concepts of OCSVM and OCSMM and detailed descriptions of experiments.
Appendix A.1
This subsection first presents several examples of uninorms. Subsequently, the derivation of uniform constructed based on is provided.
Appendix A.1.1. Examples of Uninorms
Uninorms are examples of a broader class of aggregation functions on the unit interval. The study of aggregation functions is one of the most important subfields of fuzzy set theory [48,49]. Most common aggregation functions are increasing n-ary operations on a real interval that also satisfy some boundary conditions. Of particular importance are associative binary aggregation functions on the real unit interval, as they can be extended unambiguously to a higher number of arguments. Additionally, such associative operations are assumed to be symmetric and have a neutral element. This leads to the concept of a uninorm [50], a symmetric, associative, increasing binary operation on with a neutral element (). The case of corresponds to the well-known t-norms (including the minimum operation), and the case of corresponds to the well-known t-conorms (including the maximum operation). Due to its associativity, any uninorm (U) is either conjunctive (i.e., ) or disjunctive (i.e., ). The structure of a uninorm with a neutral element (e) is expressed as follows [46]: on , it behaves as a rescaled t-norm, taking values below the minimum; on , it behaves as a rescaled t-conorm, taking values above the maximum; and on the remaining parts of the unit square (i.e., ), it behaves as a compensatory (also called averaging) operator, taking values between the minimum and the maximum. Given a t-norm and a t-conorm, one can always build a uninorm by considering minimum or maximum (one of the two extremes) as a compensatory operator.
Some basic examples of uninorms with neutral element () are the following:
- (i)
- The function expressed as , defined asThe semantics are described as follows: considering e as a threshold of satisfaction, the evaluation in the case of two evaluations meeting the threshold results in the highest score or the lowest score otherwise.
- (ii)
- The function expressed as , defined asThe semantics are described as follows: considering e as a threshold of satisfaction, the evaluation in the case of two evaluations not meeting the threshold results in the lowest score or the highest score otherwise.
Appendix A.1.2. Derivation of Uninorm Uano Based on U3Π
The most famous uninorm with the desired synergistic and antagonistic behavior is operator with neutral element :
with either or .
Proposition A1.
Consider a uninorm (U) with a neutral element (). The operations () defined by [51]
are a t-norm and a t-conorm, respectively.
According to Proposition A1, we obtain the following t-norm and t-conorm induced by :
Proposition A2.
Consider a t-norm (T), a t-conorm (S), and . The operation () defined by [51]
is a uninorm with a neutral element (e).
According to Proposition A2, the uninorm () induced by and is expressed as follows:
Appendix A.2. OCSVM and OCSMM
The goal of an OCSVM is to map the data into a feature space where they can be separated from the origin by some hyperplane. In order to find this hyperplane, an optimization problem is formulated, aiming to maximize the margin between the hyperplane and the origin. In particular, consider a training set of N instances () that can be considered as i.i.d. realizations of a random variable (). To estimate the support of (i.e., the region in space where the bulk of the data reside), Schölkopf et al. [21] proposed the following optimization problem:
where is a feature map projecting each into a high-dimensional space. The slack variables () allow points to be at the wrong side of the hyperplane, although this is discouraged by the penalizing factor () in the cost function. The offset () represents the distance from the origin to the hyperplane in the transformed feature space and is adjusted during optimization to maximize the margin while ensuring that the majority of the data lies on or beyond the hyperplane.
The solution of the constrained optimization problem (A5) results in a decision function () that can be used to classify a data point as being anomalous or not. In particular, a new data point () is classified as normal only when . Through maximization of a Lagrangian function subject to the so-called Karush–Kuhn–Tucker conditions, the decision function can be computed in terms of a kernel function that operates on pairs of instances:
where m is the number of support vectors () and represents the Lagrange multipliers associated with the support vectors. The kernel function is defined as follows:
allowing the computation of inner products in the high-dimensional feature space () without explicitly performing the mapping. This property, known as the kernel trick, significantly reduces computational complexity and enables the model to handle non-linear patterns in the input space effectively. A commonly used kernel is the Gaussian kernel, which has already been successfully applied to many practical problems.
The OCSMM is an extension of the OCSVM for the classification of a group () of i.i.d. realizations of a random variable () instead of the classification of individual points only [37]. We denote a probability distribution that represents a group associated with random variable as . The OCSMM is applied to a space of probability distributions, aiming to separate the probability distributions representing normal groups from the probability distributions representing anomalous groups. To do so, probability distributions are represented as expectation functions in a reproducing kernel Hilbert space ) [52,53]. Formally, we denote a data space (e.g., ) as and let be the set of all probability distributions () on . Consider a distribution () on . Then, all l i.i.d. realizations of are denoted as , and suppose i.i.d. samples are available from each distribution (). The kernel meaning embedding () is defined with respect to a kernel, i.e., , as follows:
and we denote as . Intuitively, the mean embedding provides a feature representation of the probability distributions in . One can show that the scalar product on is given by
The optimization problem of OCSMM can be formulated in as follows:
where the slack variables () describe margin errors. The hyperparameter is a penalty parameter controlling the proportion of anomalous groups. When is small, the number of anomalous groups is small compared to the number of normal groups. A large value implies that there is a considerable number of anomalous groups. In the anomaly detection task, anomalous behavior is always rare, such that should be set to a small value.
Similarly to OCSVM, the optimization problem in (A8) can be solved using the method of Lagrange multipliers, leading to a kernel representation of the decision function given by
where the kernel (K) applied to two distributions ( and ) is given by
For two groups of points ( and ) coming from distributions and , respectively, the empirical form of K can be obtained as follows:
Appendix A.3. Detailed Description of Experiments
In this section, we present ROC curves to compare the performances of the various methods applied to the synthetic data and the SDSS data. Furthermore, we show box plots of the AUC scores obtained in the different runs of the 10-fold cross-validation.
The Receiver Operating Characteristic (ROC) plot is a widely used tool to evaluate the performance of a classifiers. It shows the True-Positive Rate (TPR) as a function of the False-Positive Rate (FPR) for various classification thresholds. This provides a visual representation of the trade-offs between TPR (also known as sensitivity) and specificity. An ROC curve is a graphical evaluation tool that avoids the choice of a classification threshold, which generally depends on the specific needs of an application. Based on the ROC curve, one can calculate the Area Under the Curve (AUC) which is a performance metric of the classifier algorithm. The AUC score is equal to the probability that a randomly selected positive example is ranked higher by the classifier than a randomly selected negative example. A good classifier has an AUC close to 1.0, while a random classifier has an AUC near 0.5. The AUC score indicates the classifier’s ability to distinguish between positive and negative classes, where higher scores indicate better performance.
The ROC plots shown in Figure A1 and Figure A3 display the performance of our method compared to other methods for group anomaly detection on the synthetic data and the SDSS data. The ROC curves of our method, represented in blue, consistently demonstrate superior detection performance across all cases, as evidenced by their higher true-positive rates (TPRs) and lower false-positive rates (FPRs) compared to competing methods. The optimal thresholds of the models are determined by selecting the largest TPR while minimizing the FPR.
Figure A2 and Figure A4 show box plots of the AUC scores for the synthetic data and the SDSS data in the different runs of the 10-fold cross-validation experiments. The results underscore the reliable performance of our method, EVSMM, as reflected by its consistently high AUC scores and narrow variability across all cases. Furthermore, the box plots reveal that EVSMM exhibits lower variance in AUC scores compared to other methods, such as MGMM, which also performs quite well in overall AUC scores, as shown previously in Figure A1 and Figure A3. This demonstrates not only EVSMM’s effectiveness in detecting anomalies but also its robustness and reliability compared to other methods.
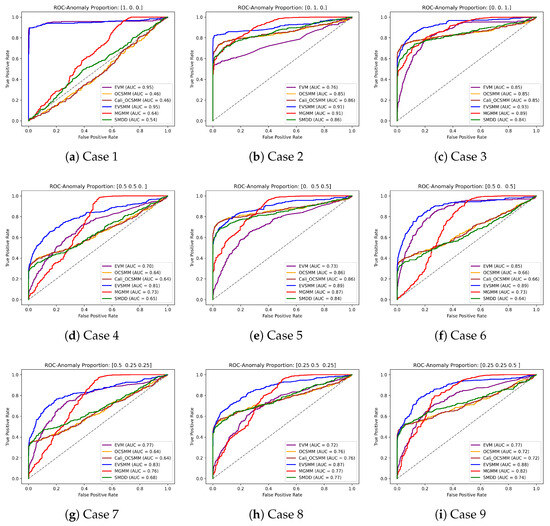
Figure A1.
The ROC curves of the experiments on synthetic data.
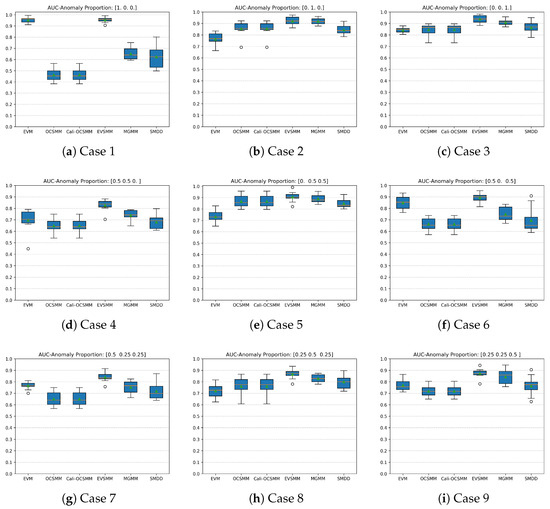
Figure A2.
Box plots of the AUC scores across different runs of the experiments on synthetic data.
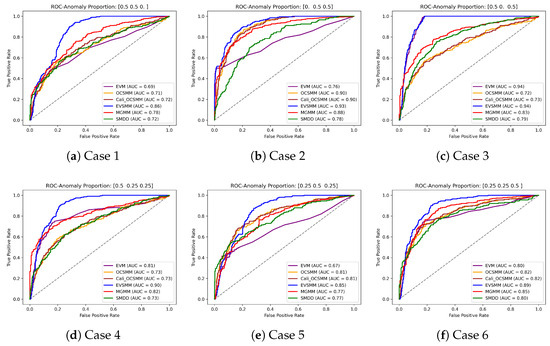
Figure A3.
ROC curves of the experiments on the SDSS data.
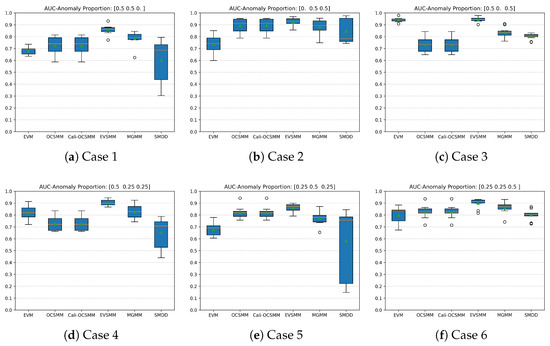
Figure A4.
Box plots of the AUC scores across different runs of the experiments on the SDSS data.
References
- Lee, W.; McCormick, T.H.; Neil, J.; Sodja, C.; Cui, Y. Anomaly detection in large-scale networks with latent space models. Technometrics 2022, 64, 241–252. [Google Scholar] [CrossRef]
- Luca, S.; Pimentel, M.A.; Watkinson, P.J.; Clifton, D. Point process models for novelty detection on spatial point patterns and their extremes. Comput. Stat. Data Anal. 2018, 125, 86–103. [Google Scholar] [CrossRef]
- Jin, H.; Yin, G.; Yuan, B.; Jiang, F. Bayesian Hierarchical Model for Change Point Detection in Multivariate Sequences. Technometrics 2022, 64, 177–186. [Google Scholar] [CrossRef]
- Lohrer, A.; Binder, J.J.; Kröger, P. Group anomaly detection for spatio-temporal collective behaviour scenarios in smart cities. In Proceedings of the 15th ACM SIGSPATIAL International Workshop on Computational Transportation Science, Seattle, WA, USA, 1 November 2022; pp. 1–4. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Xiong, L.; Póczos, B.; Schneider, J.; Connolly, A.; VanderPlas, J. Hierarchical probabilistic models for group anomaly detection. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 789–797. [Google Scholar]
- Muandet, K.; Schölkopf, B. One-class support measure machines for group anomaly detection. In Proceedings of the 29th Conference on Uncertainty in Artificial Intelligence, Bellevue, WA, USA, 11–15 August 2013; pp. 449–458. [Google Scholar]
- Chalapathy, R.; Toth, E.; Chawla, S. Group anomaly detection using deep generative models. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Dublin, Ireland, 10–14 September 2018; pp. 173–189. [Google Scholar]
- Song, W.; Dong, W.; Kang, L. Group anomaly detection based on Bayesian framework with genetic algorithm. Inf. Sci. 2020, 533, 138–149. [Google Scholar] [CrossRef]
- Kasieczka, G.; Nachman, B.; Shih, D. New Methods and Datasets for Group Anomaly Detection From Fundamental Physics. In Proceedings of the 27th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Event, Singapore, 14–18 August 2021; pp. 1–11. [Google Scholar]
- Guevara, J.; Canu, S.; Hirata, R. Support measure data description for group anomaly detection. In Proceedings of the ODDx3 Workshop on Outlier Definition, Detection, and Description at the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015. [Google Scholar]
- Xiong, L.; Póczos, B.; Schneider, J. Group anomaly detection using flexible genre models. In Proceedings of the Advances in Neural Information Processing Systems, Vienna, Austria, 20–23 September 2011; pp. 1071–1079. [Google Scholar]
- Tarassenko, L.; Hayton, P.; Cerneaz, N.; Brady, M. Novelty detection for the identification of masses in mammograms. In Proceedings of the 4th International Conference on Artificial Neural Networks, Cambridge, UK, 26–28 June 1995; pp. 442–447. [Google Scholar]
- Dietterich, T.G. Machine learning for sequential data: A review. In Proceedings of the Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition and Structural and Syntactic Pattern Recognition, Windsor, ON, Canada, 6–9 August 2002; pp. 15–30. [Google Scholar]
- Hazel, G.G. Multivariate Gaussian MRF for multispectral scene segmentation and anomaly detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1199–1211. [Google Scholar] [CrossRef]
- Das, K.; Schneider, J.; Neill, D.B. Anomaly pattern detection in categorical datasets. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 169–176. [Google Scholar]
- Belhadi, A.; Djenouri, Y.; Srivastava, G.; Cano, A.; Lin, J.C.W. Hybrid group anomaly detection for sequence data: Application to trajectory data analytics. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9346–9357. [Google Scholar] [CrossRef]
- Mohod, P.; Janeja, V.P. Density-Based Spatial Anomalous Window Discovery. Int. J. Data Warehous. Min. 2022, 18, 1–23. [Google Scholar] [CrossRef]
- Das, K.; Schneider, J.; Neill, D.B. Detecting Anomalous Groups in Categorical Datasets; Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Pehlivanian, C.A.; Neill, D.B. Efficient optimization of partition scan statistics via the consecutive partitions property. J. Comput. Graph. Stat. 2023, 32, 712–729. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Tax, D.M.; Duin, R.P. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Ting, K.; Xu, B.; Washio, T.; Zhou, Z. Isolation distributional kernel: A new tool for point and group anomaly detection. IEEE Trans. Knowl. Data Eng. 2023, 35, 2697–2710. [Google Scholar] [CrossRef]
- Fisch, A.T.; Eckley, I.A.; Fearnhead, P. A linear time method for the detection of collective and point anomalies. Stat. Anal. Data Mining ASA Data Sci. J. 2022, 15, 494–508. [Google Scholar] [CrossRef]
- Yu, R.; He, X.; Liu, Y. Glad: Group anomaly detection in social media analysis. ACM Trans. Knowl. Discov. Data 2015, 10, 1–22. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Luca, S.; Karsmakers, P.; Vanrumste, B. Anomaly detection using the Poisson process limit for extremes. In Proceedings of the 2014 IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014; pp. 370–379. [Google Scholar]
- Luca, S.; Clifton, D.A.; Vanrumste, B. One-class classification of point patterns of extremes. J. Mach. Learn. Res. 2016, 17, 1–21. [Google Scholar]
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events: For Insurance and Finance; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Aguirre-Salado, A.I.; Venancio-Guzmán, S.; Aguirre-Salado, C.A.; Santiago-Santos, A. A novel tree ensemble model to approximate the generalized extreme value distribution parameters of the pm2.5 maxima in the mexico city metropolitan area. Mathematics 2022, 10, 2056. [Google Scholar] [CrossRef]
- Anggraeni, W.; Supian, S.; Sukono.; Halim, N.B.A. Earthquake catastrophe bond pricing using extreme value theory: A mini-review approach. Mathematics 2022, 10, 4196. [Google Scholar] [CrossRef]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Daley, D.J.; Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Clifton, D.A.; Hugueny, S.; Tarassenko, L. Novelty detection with multivariate extreme value statistics. J. Signal Process. Syst. 2011, 65, 371–389. [Google Scholar] [CrossRef]
- Soong, T.T. Fundamentals of Probability and Statistics for Engineers; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Lin, H.T.; Lin, C.J.; Weng, R.C. A note on Platt’s probabilistic outputs for support vector machines. Mach. Learn. 2007, 68, 267–276. [Google Scholar] [CrossRef]
- Clifton, L.; Clifton, D.A.; Zhang, Y.; Watkinson, P.; Tarassenko, L.; Yin, H. Probabilistic novelty detection with support vector machines. IEEE Trans. Reliab. 2014, 63, 455–467. [Google Scholar] [CrossRef]
- Tax, D.M.; Duin, R.P. Uniform object generation for optimizing one-class classifiers. J. Mach. Learn. Res. 2001, 2, 155–173. [Google Scholar]
- Markou, M.; Singh, S. A neural network-based novelty detector for image sequence analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1664–1677. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Nilsson, N.J. Subjective Bayesian methods for rule-based inference systems. In Proceedings of the 1976 National Computer Conference and Exposition, New York, NY, USA, 7–10 June 1976; pp. 1075–1082. [Google Scholar]
- Buchanan, B.; Shortliffe, E. Rule-Based Expert Systems: The MYCIN Experiments of the Stanford Heuristic Programming Project; Stanford University: Stanford, CA, USA, 1984. [Google Scholar]
- De Baets, B.; Fodor, J. Van Melle’s combining function in MYCIN is a representable uninorm: An alternative proof. Fuzzy Sets Syst. 1999, 104, 133–136. [Google Scholar] [CrossRef]
- Fodor, J.C.; Yager, R.R.; Rybalov, A. Structure of uninorms. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1997, 5, 411–427. [Google Scholar] [CrossRef]
- Póczos, B.; Xiong, L.; Schneider, J. Nonparametric divergence estimation with applications to machine learning on distributions. In Proceedings of the 27th Conference on Uncertainty in Artificial Intelligence, Barcelona, Spain, 14–17 July 2011; pp. 599–608. [Google Scholar]
- Grabisch, M. Aggregation Functions; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Yager, R.R.; Rybalov, A. Uninorm aggregation operators. Fuzzy Sets Syst. 1996, 80, 111–120. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Springer Science & Business Media: New York, NY, USA, 2013; Volume 8. [Google Scholar]
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Smola, A.; Gretton, A.; Song, L.; Schölkopf, B. A Hilbert space embedding for distributions. In Proceedings of the International Conference on Algorithmic Learning Theory, Sendai, Japan, 1–4 October 2007; pp. 13–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).