On the Spectral Radius of the Maximum Degree Matrix of Graphs

Abstract

Let G be a graph with n vertices, and let $d_G\left(u\right)$ denote the degree of vertex u in $G.$ The maximum degree matrix ${\mathcal{M}}_G$ of G is the square matrix of order n whose $(u,v)$-entry is equal to $max{d}_G\left(u\right),d_G\left(v\right)$ if vertices u and v are adjacent in G, and zero otherwise. Let $B_{p,q,r}$ be the graph obtained from the complete graph $K_p$ by removing an edge $uv$, and identifying vertices u and v with the end vertices $u\prime$ and $v\prime$ of the paths $P_q$ and $P_r$, respectively. Let $\mathbb{G}n,d$ denote the set of simple, connected graphs with n vertices and diameter d. A graph in $\mathbb{G}n,d$ that attains the largest spectral radius of the maximum degree matrix is called a maximizing graph. In this paper, we first characterize the spectrum of the maximum degree matrix for graphs of the form $B_{n-i+2,i,d-i}$, where $1\le i\le \lfloor \frac{d}{2}\rfloor$. Furthermore, for $d\ge 2,$ we prove that the maximizing graph in $\mathbb{G}n,d$ is $Bn-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil .$ Finally, if $d\ge 4$ is an even integer, then the spectral radius of the maximum degree matrix in $B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$ can be computed as the largest eigenvalue of a symmetric tridiagonal matrix of order ${\displaystyle \frac{d}{2}}+1$.

1. Introduction

Let G be a simple undirected graph of order n with vertex set $V\left(G\right)=v_1,v_2,\dots ,v_n$ and edge set $E\left(G\right)$. The cardinality of a set S is denoted by $♯S$. For $u\in V\left(G\right),$ let $N_G\left(u\right)$ and $d_G\left(u\right)$ denote the set of neighbors of vertex u and $♯N_G\left(u\right)$, respectively. The degree of the vertex u is $d_G\left(u\right)$.

The multiset of the eigenvalues of a symmetric square matrix M is called the spectrum of M and is denoted by $Sp\left(M\right)$.

If $C=\left(c_{ij}\right)$ is an $n\times n$ complex matrix and $M=\left(m_{ij}\right)$ is an $n\times n$ non-negative matrix such that $\left|C\right|\le M$ ($\left|c_{ij}\right|\le m_{ij}$ for all $i,j$), then M is said to dominate C. For more properties of matrix, see [1,2].

The distance between the vertices $v_i$ and $v_j$ in a connected graph G is denoted by $d_G(v_i,v_j)$, and the diameter of G is defined as

$$diam\left(G\right)=max{d}_G(v_i,v_j):i,j=1,\dots ,n.$$

The maximum degree matrix $\mathcal{M}G=\left(mij\right)$ of G, as defined in [3], is the square matrix of order n whose $(i,j)$-entry is equal to $max{d}_G\left(v_i\right),d_G\left(v_j\right)$ if the vertices $v_i$ and $v_j$ are adjacent, and 0 otherwise.

Let $\varphi \left(G\right)$ be the characteristic polynomial of ${\mathcal{M}}_G$, that is,

$$\begin{array}{ccc}\hfill \varphi \left(G\right)& =& det(\mu I-{\mathcal{M}}_G)\hfill \\ & =& |\mu I-{\mathcal{M}}_G|\hfill \\ & =& {\mu }^n+c_1{\mu }^{n-1}+c_2{\mu }^{n-2}+\dots +c_n.\hfill \end{array}$$

In [3], Adiga et al. established the coefficients $c_i$ of ${\mu }^{n-i}$ for $i=0,1,2,3$ in $\varphi \left(G\right)$.

The eigenvalues of ${\mathcal{M}}_G$ are called the maximum degree eigenvalues of G. To develop our results, we denote the spectral radius of ${\mathcal{M}}_G$ by ${\mu }_1\left(G\right)$.

We use the summation symbol to add numbers, as is commonly done, and also to sum or subtract edges in a graph.

In a graph G without isolated vertices, the maximum degree matrix ${\mathcal{M}}_G$ is a non-negative irreducible matrix. By the Perron–Frobenius Theorem, there exists an eigenvector of ${\mathcal{M}}_G$ associated with the spectral radius ${\mu }_1\left(G\right)$ with strictly positive entries. We denote this eigenvector as $\mathbf{x}\left(G\right)$ or simply $\mathbf{x}$, and it is called the principal eigenvector of ${\mathcal{M}}_G$. Any other eigenvector associated with ${\mu }_1\left(G\right)$ is a scalar multiple of $\mathbf{x}$. For more properties of graphs, see [4,5]

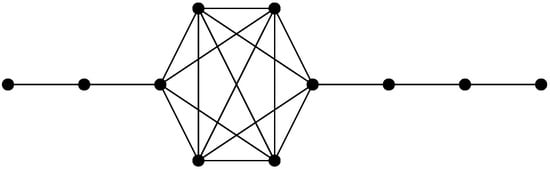
Let $B_{p,q,r}$ be the graph obtained from a complete graph $K_p$ by deleting an edge $uv$ and identifying the vertices u and v with the end vertices $u\prime$ and $v\prime$ of the paths $P_q$ and $P_r$, respectively; see Figure 1. Observe that $B_{p,q,r}$ is a graph on $p+q+r-2$ vertices and $diam\left(B_{p,q,r}\right)=q+r$.

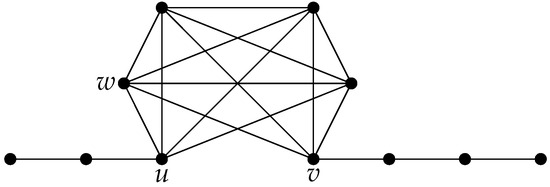
Figure 1. The graph $B_{6,3,4}$ has 11 vertices and $diam\left(B_{6,3,4}\right)=7$.

In [6], the authors show that the graph $B_{n-d+2,\lfloor d/2\rfloor ,\lceil d/2\rceil }$ maximizes the spectral radius among graphs with n vertices and diameter $d\ge 2$. In [7], the authors prove that for the given positive integers n and $d\ge 2$, among all connected graphs of order n and diameter d, the maximal signless Laplacian spectral radius is attained uniquely by the graph $B_{n-d+2,\lfloor d/2\rfloor ,\lceil d/2\rceil }$. In [8], several extremal results are presented concerning the spectral radius of the matrix $A_{\alpha }=\alpha D+(1-\alpha )A$, where $0\le \alpha \le 1$, which generalizes the two previous results. Here, A and D denote the adjacency and degree diagonal matrices of the graph, respectively.

The goal of this paper is to show that among all graphs of order n and diameter $d\ge 2$, the graph that uniquely attains the largest spectral radius of the maximum degree matrix is $B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$. Furthermore, we characterize the maximum degree eigenvalues of $B_{n-i+2,i,d-i}$ for $1\le i\le \lfloor \frac{d}{2}\rfloor$. Finally, if $d\ge 4$ is an even integer, the spectral radius of the maximum degree matrix of $B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$ can be computed as the largest eigenvalue of a symmetric tridiagonal matrix of order ${\displaystyle \frac{d}{2}}+1$.

2. Preliminaries

In this section, we present some results pertaining to the spectral radius of the maximum degree matrix of a connected graph G.

Lemma 1.

Let G be a connected graph and consider $u,v$ two vertices in $V\left(G\right)$. Let

$$\{v_1,\dots ,v_s\}\subseteq N_G\left(v\right)\setminus (N_G\left(u\right)\cup \left\{u\right\})$$

and

$$G_u=G-\sum _{i=1}^{s}v{v}_i+\sum _{i=1}^{s}u{v}_i,$$

for $s\ge 1$. Suppose that $d_{G_u}\left(u\right)\ge d_G\left(v\right)$. Let

$$\mathbf{x}\left(G\right)={\left[\begin{array}{ccccc}{x}_1& x_2& \dots & \dots & x_n\end{array}\right]}^T$$

be the principal eigenvector of ${\mathcal{M}}_G.$ If $x_u\ge x_v$, then

$${\mu }_1\left(G_u\right)>{\mu }_1\left(G\right).$$

Proof. 

By hypothesis, $x_u\ge x_v$. Then,

$$\begin{array}{ccc}\hfill {\mu }_1\left(G_u\right)-{\mu }_1\left(G\right)& \ge & {\mathbf{x}}^T{\mathcal{M}}_{G_u}\mathbf{x}-{\mathbf{x}}^T{\mathcal{M}}_G\mathbf{x}\hfill \\ & =& 2\sum _{i=1}^s\left(max\{d_{G_u}\left(u\right),d_G\left(v_i\right)\}{x}_u-max\{d_G\left(v\right),d_G\left(v_i\right)\}{x}_v\right)x_i\hfill \\ & \ge & 0.\hfill \end{array}$$

Suppose that ${\mu }_1\left(G_u\right)={\mu }_1\left(G\right)$. Then, by the above inequality, we get

$${\mathbf{x}}^T{\mathcal{M}}_{G_u}\mathbf{x}={\mu }_1\left(G_u\right).$$

Since ${\mathcal{M}}_{G_u}$ is a real symmetric matrix, we have

$${\mathcal{M}}_{G_u}\mathbf{x}={\mu }_1\left(G_u\right)\mathbf{x}.$$

Thus

$$\begin{array}{ccc}\hfill {\mu }_1\left(G_u\right)x_u& =& \sum _{w\in N_{G_u}\left(u\right)}max\{d_{G_u}\left(u\right),d_{G_u}\left(w\right)\}{x}_w\hfill \\ & =& \sum _{w\in N_G\left(u\right)}max\{d_{G_u}\left(u\right),d_{G_u}\left(w\right)\}{x}_w+\sum _{i=1}^{s}max\{d_{G_u}\left(v\right),d_{G_u}\left(v_i\right)\}{x}_i\hfill \\ & \ge & \sum _{w\in N_G\left(u\right)}max\{d_G\left(u\right),d_G\left(w\right)\}{x}_w+\sum _{i=1}^{s}max\{d_{G_u}\left(v\right),d_{G_u}\left(v_i\right)\}{x}_i\hfill \\ & =& {\mu }_1\left(G\right)x_u+\sum _{i=1}^{s}max\{d_{G_u}\left(v\right),d_{G_u}\left(v_i\right)\}{x}_i.\hfill \end{array}$$

Hence, ${\mu }_1\left(G_u\right)>{\mu }_1\left(G\right)$ as

$$\sum _{i=1}^{s}max\{d_{G_u}\left(v\right),d_{G_u}\left(v_i\right)\}{x}_i>0.$$

The proof is complete. □

Corollary 1.

Let G be a connected graph and consider $u,v$ two vertices in $V\left(G\right)$. Let

$$\{v_1,\dots ,v_s\}\subseteq N_G\left(v\right)\setminus (N_G\left(u\right)\cup \left\{u\right\}),$$

$$\{u_1,\dots ,u_t\}\subseteq N_G\left(u\right)\setminus (N_G\left(v\right)\cup \left\{v\right\}),$$

$$G_u=G-\sum _{i=1}^{s}v{v}_i+\sum _{i=1}^{s}u{v}_i,$$

and

$$G_v=G-\sum _{i=1}^{t}u{u}_i+\sum _{i=1}^{t}v{u}_i,$$

for $s,t\ge 1$. Suppose $d_{G_u}\left(u\right)\ge d_G\left(v\right)$ and $d_{G_v}\left(v\right)\ge d_G\left(u\right)$. Then, ${\mu }_1\left(G_u\right)>{\mu }_1\left(G\right)$ or ${\mu }_1\left(G_v\right)>{\mu }_1\left(G\right)$.

Proof. 

Let

$$\mathbf{x}\left(G\right)={\left[\begin{array}{ccccc}{x}_1& x_2& \dots & \dots & x_n\end{array}\right]}^T$$

(1)

the principal eigenvector of G then $x_u\le x_v$ or $x_v\le x_u.$ By Lemma 1, the result follows. □

By [9] [Theorem 2.1], we recall that if M is a non-negative irreducible matrix that dominates a complex matrix C, then the spectral radius of M is greater than the spectral radius of C. The following result is an immediate consequence of this remarkable theorem.

Lemma 2.

Let G and H be a connected graph and a proper subgraph of G, respectively. Then

$${\mu }_1\left(H\right)<{\mu }_1\left(G\right).$$

Let M be a square matrix. Let $\left|\begin{array}{c}M\end{array}\right|$ and $\tilde{M}$ denote the determinant of M and the submatrix obtained from M by deleting its last row and column, respectively. We recall the following result.

Lemma 3

([10]). For $i,j=1,2,\dots ,m,$ let $X_i$ be a matrix of the order $k_i\times k_i$, ${\theta }_{i,j}$ be an arbitrary scalar and $Y_{i,j}={\left(y_{i_{{\mathbf{i}}_1},j_{{\mathbf{j}}_1}}\right)}_{1\le {\mathbf{i}}_1\le k_i,1\le {\mathbf{j}}_1\le k_j}$ be the matrix of the order $k_i\times k_j$ with $y_{i_{k_i},j_{k_j}}=1$ and zero otherwise. Then,

$$\left|\begin{array}{ccccc}{X}_1& {\theta }_{1,2}{Y}_{1,2}& \dots & {\theta }_{1,m-1}{Y}_{1,m-1}& {\theta }_{1,m}{Y}_{1,m}\\ {\theta }_{2,1}{Y}_{1,2}^T& X_2& \dots & \dots & {\theta }_{2,m}{Y}_{2,m}\\ {\theta }_{3,1}{Y}_{1,3}^T& {\theta }_{3,2}{Y}_{2,3}^T& \ddots & \dots & ⋮\\ ⋮& ⋮& ⋮& X_{m-1}& {\theta }_{m-1,m}{Y}_{m-1,m}\\ {\theta }_{m,1}{Y}_{1,m}^T& {\theta }_{m,2}{Y}_{2,m}^T& \dots & {\theta }_{m,m-1}{Y}_{m-1,m}^T& X_m\end{array}\right|$$

$$=\left|\begin{array}{ccccc}\left|\begin{array}{c}{X}_1\end{array}\right|& {\theta }_{1,2}\left|\begin{array}{c}\widetilde{X_2}\end{array}\right|& \dots & {\theta }_{1,m-1}\left|\begin{array}{c}\widetilde{X_{m-1}}\end{array}\right|& {\theta }_{1,m}\left|\begin{array}{c}\widetilde{X_m}\end{array}\right|\\ {\theta }_{2,1}\left|\begin{array}{c}\widetilde{X_1}\end{array}\right|& \left|\begin{array}{c}{X}_2\end{array}\right|& \dots & \dots & {\theta }_{2,m}\left|\begin{array}{c}\widetilde{X_m}\end{array}\right|\\ {\theta }_{3,1}\left|\begin{array}{c}\widetilde{X_1}\end{array}\right|& {\theta }_{3,2}\left|\begin{array}{c}\widetilde{X_2}\end{array}\right|& \ddots & \dots & ⋮\\ ⋮& ⋮& ⋮& \left|\begin{array}{c}{X}_{m-1}\end{array}\right|& {\theta }_{m-1,m}\left|\begin{array}{c}\widetilde{X_m}\end{array}\right|\\ {\theta }_{m,1}\left|\begin{array}{c}\widetilde{X_1}\end{array}\right|& {\theta }_{m,2}\left|\begin{array}{c}\widetilde{X_2}\end{array}\right|& \dots & {\theta }_{m,m-1}\left|\begin{array}{c}\widetilde{X_{m-1}}\end{array}\right|& \left|\begin{array}{c}{X}_m\end{array}\right|\end{array}\right|.$$

3. Results

In this section, we begin by recalling the following definition.

Definition 1

([11]). Let G be a connected graph. A path P in G with end vertices u and v is called a diametral path of G if P has $diam\left(G\right)+1$ vertices and $d_G(u,v)=diam\left(G\right)$.

Let $n\ge d+2$ with $d\ge 3$. For $1\le i\le d-1$, the graph $B_{n-d+2,i,d-i}$ with n vertices is isomorphic to the graph obtained from the complete graph $K_{n-(d+1)}$ and a path P with $d+1$ vertices, $v_1,v_2,\dots ,v_{d+1}$, by adding edges to connect each vertex of the complete graph $K_{n-(d+1)}$ with the vertices $v_i,v_{i+1},v_{i+2}$ (Figure 2).

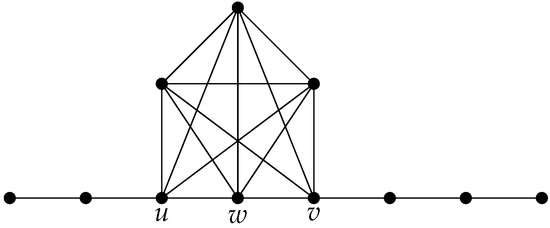
Figure 2. Graph isomorphic to the graph in Figure 1.

For each connected graph G, we label the vertices of G such that the first $diam\left(G\right)+1$ vertices, $v_1,\dots ,v_{diam\left(G\right)+1},$ are the vertices of a diametral path in G. Let

$$X^G=v_1,\dots ,v_{diam\left(G\right)+1}.$$

Lemma 4.

Let G be a connected graph. Let $v\notin X^G$. If $v_p,v_t\in N_G\left(v\right)\cap X^G$, then

$$\left|t-p\right|\le 2.$$

Proof. 

Let $v_p,v_t\in N_G\left(v\right)\cap X^G$ with $p<t$ (if $t<p$, we proceed analogously). We claim that $t-p\le 2$. Suppose $t-p>2$. Then, there are at least two vertices $v_q,v_r\in X^G$ with $p<q<r<t$.

Thus, the set of vertices

$$\left(X^G\setminus v_{p+1},\dots ,v_{t-1}\right)\cup v$$

can be used to build a new path of length less than $diam\left(G\right)$ connecting $v_1$ to $v_{diam\left(G\right)+1}$, which is a contradiction. Therefore, the result follows. □

In the following result, we denote the complement of $X^G$ by ${\left(X^G\right)}^c.$ Note that $G\cong P_n$ if and only if $n=diam\left(G\right)+1$.

Lemma 5.

Let G be a connected graph on the vertices n. Let $n>diam\left(G\right)+1$. Then, there exists a graph $H_0^G$ with n vertices and a diameter less than or equal to $diam\left(G\right)$ such that G is a subgraph of $H_0^G$ which verifies the following conditions:

1. 

The vertices in ${\left(X^G\right)}^c$ are the vertices of the complete graph;

$$K_{n-\left(diam\right(G)+1)},$$

2. 

Each vertex in ${\left(X^G\right)}^c$ is adjacent to exactly three consecutive vertices in $X^G,$;

3. 

${\mu }_1\left(G\right)\le {\mu }_1\left(H_0^G\right).$

Proof. 

Let G be a connected graph on n vertices. Clearly, we can see that in the process of adding edges between the vertices in ${\left(X^G\right)}^c,$ the diameter of the new graph is less than or equal to $diam\left(G\right)$. We construct the graph $H_0^G$ as follows:

1.

Starting with G, we construct a graph $H_0^{G*}$ by adding edges, if necessary between the vertices in ${\left(X^G\right)}^c$, until these form the complete graph $K_{n-\left(diam\right(G)+1)}$.

2.

As per Lemma 4, each vertex in ${\left(X^G\right)}^c$ is adjacent to at most three consecutive vertices $X^G$. Finally, we construct the graph $H_0^G$, adding edges in $H_0^{G*}$ such that each vertex in ${\left(X^G\right)}^c$ is adjacent exactly to three consecutive vertices in $X^G$.

3.

It follows from Lemma 2.

The proof is complete. □

Remark 1.

Note that if G is a path on n vertices, then

$$G\cong H_0^G.$$

Let $H_0^G$ be a connected graph as in Lemma 5. Note that the vertices of ${\left(X^G\right)}^c$ in $H_0^G$ are the vertices of the complete graph $K_{n-\left(diam\right(G)+1)}$. Considering $H_0^G$, we will say that the two vertices u and v in ${\left(X^G\right)}^c$ are related if and only if $N_{H_0^G}\left(u\right)\cap X^G=N_{H_0^G}\left(v\right)\cap X^G$. Note that the above is an equivalence relation. Let $R_1,\dots ,R_s$ be the cliques in $H_0^G$ determined by the equivalence classes of the above relation.

The cliques $R_1,\dots ,R_s$ have the following properties:

1.

All the vertices in $R_i$ are connected to the same three consecutive vertices in $X^G$, for $i=1,\dots ,s$.

2.

Each vertex in $R_i$ is adjacent to all the vertices in $R_j$ for $i\ne j$.

Considering the construction of $H_0^G$ starting from the graph G, we can assume, without a loss of generality, the following:

If $a<b$,

$$N_{H_0^G}\left(w\right)\cap X^G=\{v_i,v_{i+1},v_{i+2}\}\mathrm{for} \mathsf{each} w\in V(R_a)$$

and

$$N_{H_0^G}\left(w^{*}\right)\cap X^G=\{v_j,v_{j+1},v_{j+2}\}\mathrm{for} \mathsf{each} w^{*}\in V\left(R_b\right)$$

then $1\le i<j\le diam\left(G\right)-1$.

Thereby, by the construction of the graph $H_0^G$, the following result is an immediate consequence of Lemma 5.

Theorem 1.

Let $G\in {\mathbb{G}}_{n,d}$ with $d\ge 2$. Let $H_0^G$ be as in Lemma 5 with $s=1$. Then,

$${\mu }_1\left(G\right)\le {\mu }_1\left(B_{n-d+2,i,d-i}\right)$$

for some $1\le i\le \lfloor \frac{d}{2}\rfloor$.

Corollary 2.

Let $G\in {\mathbb{G}}_{n,d}$ and $d=2$. Then,

$${\mu }_1\left(G\right)\le {\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }).$$

Lemma 6

([12]). Let N be a non-negative irreducible symmetric matrix with the spectral radius $\rho \left(N\right)$. If there exists a positive vector $Y>0$ and a positive real β such that $NY<\beta Y$, then $\rho \left(N\right)<\beta$.

Definition 2

([13]). An internal path in a graph G is a path with a sequence of distinct vertices $v_0,\dots ,v_{k+1}$, $k\ge 0$, where $v_{i-1}$ is adjacent to $v_i$, $1\le i\le k+1$, $d_G\left(v_0\right)\ge 3$, $d_G\left(v_{k+1}\right)\ge 3$, and $d_G\left(v_i\right)=2,$ for all $1\le i\le k$.

Remark 2.

If the number of cliques $s>1$, we reduce $H_0^G$ to a $B_{p,q,r}$ having the spectral radius of the maximum degree matrix larger than ${\mu }_1\left(H_0^G\right)$. This would be achieved by induction on s. In this process, the following result plays an important role in this work.

Lemma 7.

Let G be a connected graph with n vertices and $uv$ some edge on an internal path with $k+2$ vertices of $G,$ respectively. We subdivide the edge $uv$ by a vertex $w\notin V\left(G\right)$ such that the edges $uw$, $wv$ are added to G. We denote this new graph as $G_{uv}$. Then,

$${\mu }_1\left(G_{uv}\right)<{\mu }_1\left(G\right).$$

Proof. 

Let $\mathbf{x}$ be the principal eigenvector of ${\mathcal{M}}_G$ and $x_i$ be the corresponding component of $v_i$. Clearly, $x_i>0$. By replacing the labels if necessary we may assume that $x_0\le x_{k+1}$.

Let

$$t=\underset{0\le j\le k+1}{min}\{j:x_j\le x_{\ell }:\forall \ell ,0\le \ell \le k+1\}.$$

So, $t<k+1.$ Without a loss of generality, we may assume that $u=v_t$, $v=v_{t+1}$.

If $t\ne 0$, take $\mathbf{y}$ to be the vector obtained from $\mathbf{x}$ by inserting an additional component $x_w$ equal to $x_t$ between the positions t and $t+1$.

For the vertex u, we have

$$\begin{array}{ccc}\hfill {\mu }_1\left(G\right)x_t& =& d_G\left(v_{t-1}\right)x_{t-1}+d_G\left(v_{t+1}\right)x_{t+1}\hfill \\ & \ge & d_G\left(v_{t-1}\right)x_{t-1}+2x_t.\hfill \end{array}$$

For the vertex w, we have

$$\begin{array}{ccc}\hfill {\mu }_1\left(G\right)x_w={\mu }_1\left(G\right)x_t& =& d_G\left(v_{t-1}\right)x_{t-1}+d_G\left(v_{t+1}\right)x_{t+1}\hfill \\ & >& d_G\left(v_{t+1}\right)x_{t+1}+2x_t.\hfill \end{array}$$

Then, ${\mathcal{M}}_{G_{uv}}\mathbf{y}<{\mu }_1\left(G\right)\mathbf{y}$. By Lemma 6, we have ${\mu }_1\left(G_{uv}\right)<{\mu }_1\left(G\right)$.

Consequently, we will suppose that $t=0$. Let S be the set of neighbors of $v_0$ other than $v_1$, and let $s={\displaystyle \sum _{v_j\in S}}{x}_j$.

If ${\displaystyle \sum _{v_j\in S}}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j\ge d_G\left(v_0\right)x_0$, then we construct $\mathbf{y}$ as above with $x_w=x_0$.

For the vertex u, we have

$$\begin{array}{ccc}\hfill {\mu }_1\left(G\right)x_0& =& \sum _{v_j\in S}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j+max\{d_G\left(v_0\right),d_G\left(v_1\right)\}{x}_1\hfill \\ & \ge & \sum _{v_j\in S}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j+d_G\left(v_0\right)x_0.\hfill \end{array}$$

(2)

For the vertex w, we have

$$\begin{array}{ccc}\hfill {\mu }_1\left(G\right)x_w& =& {\mu }_1\left(G\right)x_0\hfill \\ & =& \sum _{v_j\in S}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j+max\{d_G\left(v_0\right),d_G\left(v_1\right)\}{x}_1\hfill \\ & \ge & d_G\left(v_0\right)x_0+d_G\left(v_1\right)x_1.\hfill \end{array}$$

(3)

If $k\ge 1$, then $d_G\left(v_1\right)=2$, so the strict inequality in (3) is true. Then, ${\mathcal{M}}_{G_{uv}}\mathbf{y}<{\mu }_1\left(G\right)\mathbf{y}$. By Lemma 6, we have ${\mu }_1\left(G_{uv}\right)<{\mu }_1\left(G\right)$.

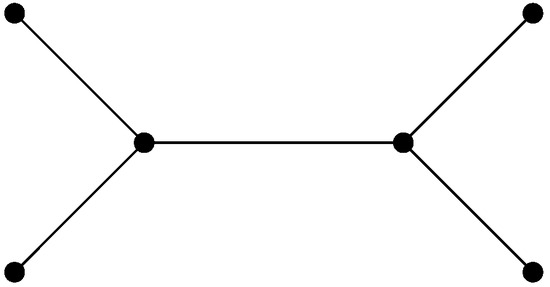
Let $k=0$, and suppose the equalities (2) and (3) are true. Then, $d_G\left(v_0\right)=d_G\left(v_1\right)$ and ${\mu }_1\left(G\right)=2d_G\left(v_0\right)$. Since $d_G\left(v_0\right)=d_G\left(v_1\right)$ and the graph $W_6$ depicted in Figure 3 is a proper subgraph of G, then ${\mu }_1\left(G\right)>d_G\left(v_0\right){\lambda }_1\left(W_6\right)>2d_G\left(v_0\right)$ where ${\lambda }_1\left(W_6\right)$ is the spectral radius of $W_6$, which is a contradiction. Then, ${\mathcal{M}}_{G_{uv}}\mathbf{y}<{\mu }_1\left(G\right)\mathbf{y}$. By Lemma 6, we have ${\mu }_1\left(G_{uv}\right)<{\mu }_1\left(G\right)$.

Figure 3. The graph $W_6$.

Finally, suppose that ${\displaystyle \sum _{v_j\in S}}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j<d_G\left(v_0\right)x_0$. In this case, we construct $\mathbf{y}$ from $\mathbf{x}$ by replacing $x_0$ with s and inserting $x_w$ equal to $x_0$.

Now,

$$\sum _{v_j\in S}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j+d_G\left(v_0\right)x_0<2d_G\left(v_0\right)x_0.$$

Furthermore,

$${\mu }_1\left(G\right)s=\sum _{v_j\in S}{\mu }_1\left(G\right)x_j\ge \sum _{v_j\in S}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_0\ge (♯S)d_G\left(v_0\right)x_0.$$

For the vertex w, we have

$$\begin{array}{ccc}\hfill {\mu }_1\left(G\right)x_w={\mu }_1\left(G\right)x_0& =& \sum _{v_j\in S}max\{d_G\left(v_0\right),d_G\left(v_j\right)\}{x}_j+max\{d_G\left(v_0\right),d_G\left(v_1\right)\}{x}_1\hfill \\ & \ge & \sum _{v_j\in S}{d}_G\left(v_0\right)x_j+d_G\left(v_1\right)x_1.\hfill \end{array}$$

Therefore, it follows that ${\mathcal{M}}_{G_{uv}}\mathbf{y}<{\mu }_1\left(G\right)\mathbf{y}$. By Lemma 6, we have

$${\mu }_1\left(G_{uv}\right)<{\mu }_1\left(G\right).$$

The proof is complete. □

Definition 3

([14]). The contraction of an edge $uv$ in a graph G is the identification of the vertices u and v into a single vertex w such that the edges incident to w are precisely the distinct edges (excluding $uv$) that were incident to either u or v in G.

Theorem 2.

Let $G\in {\mathbb{G}}_{n,d}$ with $d\ge 3$. Let $H_0^G$ be as in Lemma 5 and let $s=2$. Then,

$${\mu }_1\left(G\right)\le {\mu }_1\left(B_{n-d+2,i,d-i}\right)$$

for some $1\le i\le \lfloor \frac{d}{2}\rfloor$.

Proof. 

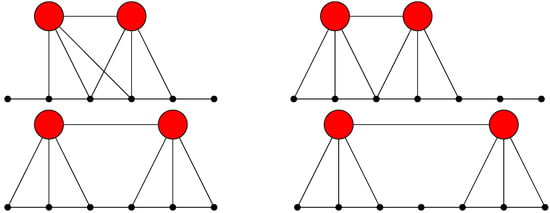
Let G be a connected graph with n vertices and $diam\left(G\right)=d$. Let $H_0^G$ be as in Lemma 5 and $s=2$. Considering the construction of graph $H_0^G$, we can assume without a loss of generality that

$$N_{H_0^G}\left(w\right)\cap X^G=\{v_i,v_{i+1},v_{i+2}\}\mathsf{f}\mathsf{o}\mathsf{r} \mathsf{e}\mathsf{a}\mathsf{c}\mathsf{h} w\in V(R_1)$$

and

$$N_{H_0^G}\left(w^{*}\right)\cap X^G=\{v_j,v_{j+1},v_{j+2}\}\mathsf{f}\mathsf{o}\mathsf{r} \mathsf{e}\mathsf{a}\mathsf{c}\mathsf{h} w^{*}\in V\left(R_2\right)$$

for some $1\le i<j\le d-1$. Keeping the previous notation in mind, four situations can occur in the graph $H_0^G$: $\left(A\right)$$j=i+1$, $\left(B\right)$$j=i+2$, $\left(C\right)$$j=i+3$, and $\left(D\right)$$j>i+3$ (Figure 4).

Figure 4. These graphs illustrate to $H_0^G$ in the case $\left(A\right)$, $\left(B\right)$, $\left(C\right)$ and $\left(D\right)$.

Case$\left(\mathbf{A}\right)$:

Let

$$H_u=H_0^G-\sum _{w^{*}\in V\left(R_2\right)}v{w}^{*}+\sum _{w^{*}\in V\left(R_2\right)}u{w}^{*}$$

(4)

and

$$H_v=H_0^G-\sum _{w\in V\left(R_1\right)}uw+\sum _{w\in V\left(R_1\right)}vw,$$

(5)

where $u=v_i$ and $v=v_{i+3}$.

Clearly, $d_{H_u}\left(u\right)\ge d_{H_0^G}\left(v\right)$ and $d_{H_v}\left(v\right)\ge d_{H_0^G}\left(u\right)$. By application of Corollary 1, we obtain

$${\mu }_1\left(H_1^G\right)>{\mu }_1\left(H_0^G\right)$$

where $H_1^G=H_u$ or $H_1^G=H_v$.

Since in $H_1^G$, all vertices in ${\left(X^G\right)}^c$ are adjacent to the same three consecutive vertices in $X^G$, by Theorem 1, we obtain the result.

For Case $\left(\mathbf{B}\right)$, we have $1\le i\le d-3$.

Let $H_u$ and $H_v$ be as in (4) and (5), respectively, where $u=v_{i+1}$ and $v=v_{i+3}$. Clearly, $d_{H_u}\left(u\right)>d_{H_0^G}\left(v\right)$ and $d_{H_v}\left(v\right)>d_{H_0^G}\left(u\right)$.

By application from Corollary 1, we get

$${\mu }_1\left(H_1^G\right)>{\mu }_1\left(H_0^G\right)$$

where $H_1^G=H_u$ or $H_1^G=H_v$.

Suppose ${\mu }_1\left(H_u\right)>{\mu }_1\left(H_0^G\right)$. If $d_{H_u}\left(v_{i+4}\right)\ge 3$, by Lemma 7, we have ${\mu }_1\left(H_2^G\right)>{\mu }_1\left(H_u\right)$ where $H_2^G$ is the graph obtained of $H_u$ by the contraction of the edge $v_{i+3}{v}_{i+4}$ to a new vertex $\beta$. Let $H_3^G$ be the graph obtained of $H_2^G$ by attaching a new pendant vertex to the vertex $\beta$. By Lemma 2, ${\mu }_1\left(H_3^G\right)>{\mu }_1\left(H_2^G\right)$.

Suppose $d_{H_u}\left(v_{i+4}\right)=2$. Let $H_2^G$ be the graph obtained of $H_1^G$ by attaching a new pendant vertex to the vertex $v_{i+4}$. By Lemma 2, ${\mu }_1\left(H_2^G\right)>{\mu }_1\left(H_1^G\right)$. By Lemma 7, we get ${\mu }_1\left(H_3^G\right)>{\mu }_1\left(H_2^G\right)$ where $H_3^G$ is the graph obtained of $H_2^G$ by the contraction of the edge $v_{i+3}{v}_{i+4}$ to a new vertex $\beta$. The cliques $R_1$ and $R_2$ in $H_3^G$ are as in $\left(A\right)$. By applying $\left(A\right)$ to $H_3^G$, the result follows.

If ${\mu }_1\left(H_v\right)>{\mu }_1\left(H_0^G\right)$, then the way to reason is analogously.

Case$\left(\mathbf{C}\right)$:

Let $H_u$ and $H_v$ be as in (4) and (5), respectively, where $u=v_{i+2}$ and $v=v_{i+3}$. Clearly, $d_{H_u}\left(u\right)>d_{H_0^G}\left(v\right)$ and $d_{H_v}\left(v\right)>d_{H_0^G}\left(u\right)$. By application of Corollary 1, we get

$${\mu }_1\left(H_1^G\right)>{\mu }_1\left(H_0^G\right)$$

where $H_1^G=H_u$ or $H_1^G=H_v$.

Suppose ${\mu }_1\left(H_u\right)>{\mu }_1\left(H_0^G\right)$. By Lemma 7, we have ${\mu }_1\left(H_2^G\right)>{\mu }_1\left(H_u\right)$, where $H_2^G$ is the graph obtained of $H_u$ by the contraction of the edge $v_{i+2}{v}_{i+3}$ to a new vertex $\omega$. By Lemma 2, we obtain ${\mu }_1\left(H_3^G\right)>{\mu }_1\left(H_2^G\right)$, where $H_3^G$ is the graph obtained of $H_2^G$ by attaching a new vertex to one of the pending vertices. The cliques $R_1$ and $R_2$ in $H_3^G$ are as in $\left(B\right)$. By applying $\left(B\right)$ to $H_3^G$, the result follows.

If ${\mu }_1\left(H_v\right)>{\mu }_1\left(H_0^G\right)$, then the way to reason is analogously.

Case$\left(\mathbf{D}\right)$: $j=i+l$ with $l\ge 4$.

By Lemma 7, we have ${\mu }_1\left(H_1^G\right)>{\mu }_1\left(H_0^G\right)$, where $H_1^G$ is the graph obtained of $H_0^G$ after contracting $l-3$ edges on the internal path $v_{i+2}\dots v_{i+l}$. By Lemma 2, we get ${\mu }_1\left(H_2^G\right)>{\mu }_1\left(H_1^G\right)$, where $H_2^G$ is the graph obtained of $H_1^G$ by attaching a path on $l-3$ vertices to one of the pending vertices. The cliques $R_1$ and $R_2$ in $H_2^G$ are as in $\left(C\right)$. By applying $\left(C\right)$ to $H_2^G$, the result follows. □

As an immediate consequence of Theorems 1 and 2, we obtain the following result.

Corollary 3.

Let $G\in {\mathbb{G}}_{n,d}$ and $d=3$. Then,

$${\mu }_1\left(G\right)\le {\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }).$$

Theorem 3.

Let $G\in {\mathbb{G}}_{n,d}$. Let $H_0^G$ be as in Lemma 5. Let $s\ge 2$. Then,

$${\mu }_1\left(G\right)\le {\mu }_1\left(B_{n-d+2,i,d-i}\right)$$

for some $1\le i\le \lfloor \frac{d}{2}\rfloor$.

Proof. 

Applying induction on s. The case $s=2$ is given in Theorem 2. Let $s>2$. Suppose that the result holds for $s-1$.

First, suppose that there exist two cliques $R_i$ and $R_{i+1}$ satisfying condition (A) in Theorem 2. In this case, $R_i$ and $R_{i+1}$ are reduced to a single clique such that their vertices are connected to the same three consecutive vertices in $X^G$. By the induction hypothesis, the result follows.

Now, suppose that there is no pair of cliques satisfying condition (A) as in Theorem 2. Then, we consider the two cliques $R_1$ and $R_2$ and apply the techniques used in cases (B), (C), or (D) of Theorem 2 to reduce them to a single clique whose vertices are connected to the same three consecutive vertices in $X^G$. Again, by the induction hypothesis, the result follows. □

4. The Largest Spectral Radius of the Maximum Degree Matrix Among All Graphs with a Given Order and Diameter

In this section, we characterize the maximum degree eigenvalues of $B_{n-d+2,i,d-i}$ for $1\le i\le \lfloor \frac{d}{2}\rfloor$. In particular, we prove that $-(n-d+1)$ is always an eigenvalue of $B_{n-d+2,i,d-i}$ with multiplicity $n-d-1$, and that the remaining eigenvalues are precisely the eigenvalues of a non-negative symmetric tridiagonal matrix of order $d+1$.

4.1. Maximum Degree Eigenvalues of $B_{n-d+2,i,d-i}$ with $1\le i\le \lfloor \frac{d}{2}\rfloor$

We recall that given two disjoint graphs $G_1$ and $G_2$, the join of $G_1$ and $G_2$ is the graph $G=G_1\vee G_2$, such that $V\left(G\right)=V\left(G_1\right)\cup V\left(G_2\right)$ and

$$E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)\cup xy:x\in V\left(G_1\right),y\in V\left(G_2\right).$$

This operation can be generalized as follows [14,15]. Let H be a graph with k vertices, and let $V\left(H\right)=1,\dots ,k$. Let $G_1,G_2,\dots ,G_k$ be a family of pairwise disjoint graphs. For each j, the vertex $j\in V\left(H\right)$ is assigned to the graph $G_j$. Let G be the graph obtained from the graphs $G_1,G_2,\dots ,G_k$ and the edges connecting every vertex of $G_i$ to all vertices of $G_j$ for each edge $ij\in E\left(H\right)$. That is,

$$V\left(G\right)=\bigcup _{i=1}^{k}V\left(G_i\right),$$

$$E\left(G\right)=\left(\bigcup _{i=1}^{k}E\left(G_i\right)\right)\cup \left(\bigcup _{ij\in E\left(H\right)}uv:u\in V\left(G_i\right),v\in V\left(G_j\right)\right).$$

This graph is called the H-join of the graphs $G_1,\dots ,G_k$ and is denoted by

$$G=\underset{H}{\bigvee }{G}_j:1\le j\le k.$$

If $n_i$ is the order of $G_i$ for $i=1,2,\dots ,k$, then the H-join of $G_1,\dots ,G_k$ is a graph of order $n_1+n_2+\dots +n_k$.

Examples of this operation on graphs can be seen in the graphs $B_{n-d+2,i,d-i}$. In fact, $B_{n-d+2,1,d-1}$ is the $P_{d+1}$-join of the regular graphs $G_1=P_1$, $G_2=K_{n-d}$, $G_3=\dots =G_{d+1}=P_1$. For $i=2,\dots ,\lfloor \frac{d}{2}\rfloor$, and the graph $B_{n-d+2,i,d-i}$ is the $P_{d+1}$-join of the graphs $G_1=\dots =G_i=P_1$, $G_{i+1}=K_{n-d}$, $G_{i+2}=\dots =G_{d+1}=P_1$.

Example 1.

The graph $B_{6,3,4}$ as a $P_8$-join is the graph in Figure 5:

Figure 5. Graph $B_{6,3,4}$.

In [14], the spectrum of the adjacency matrix of the H-join of regular graphs is obtained. The version of this result for the maximum degree matrix is given below, and its proof is analogous.

Theorem 4.

If $G\cong {\displaystyle \underset{H}{\bigvee }}\{G_j:1\le j\le k\}$ and $G_j$ is a graph $r_j$-regular for $j=1,2,\dots ,k$, then

$$Sp\left({\mathcal{M}}_G\right)=\bigcup _{G_j\ne P_1}\{(s_i+r_i){\lambda }_i\left(G_j\right):j\ne 1\}\cup Sp\left(M_k\right)$$

where

$$M_k=\left[\begin{array}{cccc}{r}_1(s_1+r_1)& {\delta }_{12}\sqrt{n_1{n}_2}& \dots & {\delta }_{1k}\sqrt{n_1{n}_k}\\ {\delta }_{12}\sqrt{n_1{n}_2}& r_2(s_2+r_2)& \ddots & ⋮\\ ⋮& \ddots & \ddots & {\delta }_{(k-1)k}\sqrt{n_{k-1}{n}_k}\\ {\delta }_{1k}\sqrt{n_1{n}_k}& \dots & {\delta }_{(k-1)k}\sqrt{n_{k-1}{n}_k}& r_k(s_k+r_k)\end{array}\right],$$

$${\delta }_{i,j}=\left\{\begin{array}{cc}max\{s_i+r_i,s_j+r_j\}\hfill & \mathrm{if}ij\in E\left(H\right)\hfill \\ 0\hfill & otherwise,\hfill \end{array}\right.$$

${\lambda }_i\left(G_j\right)$ is the i-th eigenvalue of the adjacency matrix of $G_j$ and

$$s_j=\sum _{ij\in E\left(H\right)}{n}_i,$$

for $j=1,2,\dots ,k$.

Remark 3.

Now, we denote by I the identity matrix, J the matrix with ones on the skew diagonal, and F the matrix whose entries are all zeros except for the entry in the last row and first column, which is equal to $n-d+1$. The order of each of these matrices is clear from the context in which they are used.

Definition 4

([16]). Let $\alpha >0$. Let

$$R\left(\alpha \right)=(1+\alpha )\left[\begin{array}{ccc}0& \sqrt{\alpha }& 0\\ \sqrt{\alpha }& \alpha -1& \sqrt{\alpha }\\ 0& \sqrt{\alpha }& 0\end{array}\right] and S\left(\alpha \right)=(1+\alpha )\left[\begin{array}{cc}0& \sqrt{\alpha }\\ \sqrt{\alpha }& \alpha -1\end{array}\right].$$

Let $r\left(\mu \right)=\varphi \left(R\right(\alpha \left)\right)$ and $s\left(\mu \right)=\varphi \left(S\right(\alpha \left)\right).$

The application of Theorem 4 to each graph $B_{n-d+2,i,d-i}$ allows us to characterize its maximum degree eigenvalues. We begin by introducing the matrix $D_1=\left[0\right]$, and for $s\ge 2$, the symmetric tridiagonal matrix of order $s\times s$

$$D_s=\left[\begin{array}{ccccc}0& 2& & & \\ 2& 0& 2& & \\ & 2& \ddots & \ddots & \\ & & \ddots & 0& 2\\ & & & 2& 0\end{array}\right].$$

Clearly, $D_s={\mathcal{M}}_{P_s}$. From the recursion formula for symmetric tridiagonal matrices [16], we have

$$\varphi \left(D_s\right)=\mu \varphi \left(D_{s-1}\right)-4\varphi \left(D_{s-2}\right)$$

(6)

where $\varphi \left(D_1\right)=\mu$, $\varphi \left(D_0\right)=1$ and $\varphi \left(D_{-1}\right)=0$.

Theorem 5.

Let $\alpha =n-d$. The maximum degree eigenvalues of

$B_{n-d+2,i,d-i}$ are $-(\alpha +1)$ with multiplicity $\alpha -1$ and the eigenvalues of the symmetric tridiagonal matrix of order $(d+1)\times (d+1)$

$$T_i=\left[\begin{array}{cc}{X}_i& F\\ F^T& D_{d-i-1}\end{array}\right]$$

where

$$X_1=R\left(\alpha \right),$$

and

$$X_i=\left[\begin{array}{cc}{D}_{i-1}& F\\ F^T& R\left(\alpha \right)\end{array}\right]$$

when $2\le i\le \lfloor \frac{d}{2}\rfloor$.

Corollary 4.

The largest eigenvalue of $T_i$ is the spectral radius of the maximum degree matrix of $B_{n-d+2,i,d-i}$. The eigenvalues of $T_i$ are simple.

Proof. 

From Theorem 5, the maximum degree eigenvalues of $B_{n-d+2,i,d-i}$ are $-(\alpha +1)$ and the eigenvalues of $T_i$. Let ${\mu }_1\left(T_i\right)$ be the largest eigenvalue of $T_i$. Since the largest eigenvalue of a Hermitian matrix is greater than or equal to any diagonal entry, it follows that ${\mu }_1\left(T_i\right)\ge {\alpha }^2-1>-(\alpha +1)$. Then ${\mu }_1\left(T_i\right)$ is the spectral radius of the maximum degree matrix of $B_{n-d+2,i,d-i}$. Since $T_i$ is a symmetric tridiagonal matrix with nonzero co-diagonal entries, its eigenvalues are simple. □

4.2. Determination of the Maximizing Graph in ${\mathbb{G}}_{n,d}$

In this subsection, we determine the graph with the largest spectral radius of the maximum degree matrix among all connected graphs with a given diameter.

Lemma 8.

Let $s\ge 1$ and $t\ge 1$. Let T be the symmetric tridiagonal matrix of order $s+t$ given by

$$T=\left[\begin{array}{cc}{A}_s& F\\ F^T& J{C}_{t}J\end{array}\right]$$

where

$$A_s=\left[\begin{array}{cccc}{a}_1& b_1& & \\ b_1& a_2& \ddots & \\ & \ddots & \ddots & b_{s-1}\\ & & b_{s-1}& a_s\end{array}\right]$$

and

$$C_t=\left[\begin{array}{cccc}{c}_1& d_1& & \\ d_1& c_2& \ddots & \\ & \ddots & \ddots & d_{t-1}\\ & & d_{t-1}& c_t\end{array}\right].$$

Then

$$\begin{array}{c}\hfill \varphi \left(T\right)=\varphi \left(A_s\right)\varphi \left(C_t\right)-{(n-d+1)}^2\varphi \left(A_{s-1}\right)\varphi \left(C_{t-1}\right),\end{array}$$

and particularly, $\varphi \left(A_0\right)=\varphi \left(C_0\right)=1$.

Proof. 

Considering that $J^2=I$, we have

$$\left[\begin{array}{cc}I& \\ & J\end{array}\right]\left[\begin{array}{cc}{A}_s& F\\ F^T& J{C}_{t}J\end{array}\right]\left[\begin{array}{cc}I& \\ & J\end{array}\right]=\left[\begin{array}{cc}{A}_s& FJ\\ J{F}^T& C_t\end{array}\right]=U.$$

Then, $\varphi \left(T\right)=\varphi \left(U\right)$. Note that $FJ$ is a matrix whose entries are zero except the entry in the last row and the last column which is equal to $n-d+1$. Finally, by Lemma 3, the result follows. □

Lemma 9.

Let $s\ge 1$ and $t\ge 1$. Then,

$$\varphi \left(D_s\right)\varphi \left(D_t\right)-\varphi \left(D_{s-1}\right)\varphi \left(D_{t+1}\right)=4\left(\varphi \left(D_{s-1}\right)\varphi \left(D_{t-1}\right)-\varphi \left(D_{s-2}\right)\varphi \left(D_t\right)\right).$$

Proof. 

Applying a similar argument as in Lemma 8 to $D_{s+t}$ with $A_s=D_s$ and $C_t=D_t$, we have

$$\begin{array}{ccc}\hfill \varphi \left(D_{s+t}\right)& =& \varphi \left(D_s\right)\varphi \left(D_t\right)-4\varphi \left(D_{s-1}\right)\varphi \left(D_{t-1}\right).\hfill \end{array}$$

(7)

Suppose that $s\ge 2$. Analogously, if $A_{s-1}=D_{s-1}$ and $C_{t+1}=D_{t+1}$, we have

$$\varphi \left(D_{s+t}\right)=\varphi \left(D_{s-1}\right)\varphi \left(D_{t+1}\right)-4\varphi \left(D_{s-2}\right)\varphi \left(D_t\right).$$

(8)

For $s=1$, Equation (8) is immediate by (6) and $\varphi \left(D_{-1}\right)=0$. Considering (7) and (8), the result follows. □

By repeatedly applying Lemma 9, we obtain the following result.

Corollary 5.

For $t\ge s\ge 1$,

$$\varphi \left(D_s\right)\varphi \left(D_t\right)-\varphi \left(D_{s-1}\right)\varphi \left(D_{t+1}\right)=4^{s-1}\left[\mu \varphi \left(D_{t-s+1}\right)-\varphi \left(D_{t-s+2}\right)\right].$$

Remark 4.

We will now discuss the difference between the characteristic polynomials of $T_i$ and $T_{i+1}$. From Lemma 8,

$$\begin{array}{ccc}\hfill \varphi \left(T_1\right)& =& r\left(\mu \right)\varphi \left(D_{d-2}\right)-{(\alpha +1)}^{2}s\left(\mu \right)\varphi \left(D_{d-3}\right)\hfill \end{array}$$

(9)

where $\alpha =n-d$ with $d\ge 4$.

Replacing this in (9) and using $\varphi \left(D_0\right)=1$ and $\varphi \left(D_{-1}\right)=0$, we have

$$\begin{array}{ccc}\hfill \varphi \left(T_1\right)& =& r\left(\mu \right)\varphi \left(D_0\right)\varphi \left(D_{d-2}\right)-{(1+\alpha )}^{2}s\left(\mu \right)\varphi \left(D_{-1}\right)\varphi \left(D_{d-2}\right)\hfill \\ & -& {(1+\alpha )}^{2}s\left(\mu \right)\varphi \left(D_0\right)\varphi \left(D_{d-3}\right)\hfill \\ & +& {(1+\alpha )}^4(\mu -{\alpha }^2+1)\varphi \left(D_{-1}\right)\varphi \left(D_{d-3}\right).\hfill \end{array}$$

Let $2\le i\le \lfloor \frac{d}{2}\rfloor$. By Lemma 8,

$$\begin{array}{ccc}\hfill \varphi \left(T_i\right)& =& \varphi \left(X_i\right)\varphi \left(D_{d-i-1}\right)-{(\alpha +1)}^2\varphi \left(\widetilde{X_i}\right)\varphi \left(D_{d-i-2}\right)\hfill \end{array}$$

(10)

where $X_i=\left[\begin{array}{cc}{D}_{i-1}& F\\ F^T& R\left(\alpha \right)\end{array}\right]$, $\widetilde{X_i}=\left[\begin{array}{cc}{D}_{i-1}& F\\ F^T& S\left(\alpha \right)\end{array}\right]$, $\alpha =n-d$ with $d\ge 4$. By applying Lemma 8 to $X_i$ and $\widetilde{X_i}$, we have

$$\varphi \left(X_i\right)=r\left(\mu \right)\varphi \left(D_{i-1}\right)-{(1+\alpha )}^{2}s\left(\mu \right)\varphi \left(D_{i-2}\right)$$

and

$$\varphi \left(\widetilde{X_i}\right)=s\left(\mu \right)\varphi \left(D_{i-1}\right)-{(1+\alpha )}^2(\mu -{\alpha }^2+1)\varphi \left(D_{i-2}\right).$$

By replacing these identities in (10), we have

$$\begin{array}{ccc}\hfill \varphi \left(T_i\right)& =& r\left(\mu \right)\varphi \left(D_{i-1}\right)\varphi \left(D_{d-i-1}\right)-{(1+\alpha )}^{2}s\left(\mu \right)\varphi \left(D_{i-2}\right)\varphi \left(D_{d-i-1}\right)\hfill \\ & -& {(1+\alpha )}^{2}s\left(\mu \right)\varphi \left(D_{i-1}\right)\varphi \left(D_{d-i-2}\right)\hfill \\ & +& {(1+\alpha )}^4(\mu -{\alpha }^2+1)\varphi \left(D_{i-2}\right)\varphi \left(D_{d-i-2}\right).\hfill \end{array}$$

Consequently, for $1\le i\le \lfloor \frac{d}{2}\rfloor -1$, we have

$$\begin{array}{ccc}\hfill \varphi \left(T_{i+1}\right)-\varphi \left(T_i\right)& =& r\left(\mu \right)[\varphi \left(D_i\right)\varphi \left(D_{d-i-2}\right)-\varphi \left(D_{i-1}\right)\varphi \left(D_{d-i-1}\right)]\hfill \\ & -& {(1+\alpha )}^{2}s\left(\mu \right)[\varphi \left(D_i\right)\varphi \left(D_{d-i-3}\right)-\varphi \left(D_{i-1}\right)\varphi \left(D_{d-i-2}\right)]\hfill \\ & -& {(1+\alpha )}^{2}s\left(\mu \right)[\varphi \left(D_{i-1}\right)\varphi \left(D_{d-i-2}\right)-\varphi \left(D_{i-2}\right)\varphi \left(D_{d-i-1}\right)]\hfill \\ & +& {(1+\alpha )}^4(\mu -{\alpha }^2+1)[\varphi \left(D_{i-1}\right)\varphi \left(D_{d-i-3}\right)-\varphi \left(D_{i-2}\right)\varphi \left(D_{d-i-2}\right)].\hfill \end{array}$$

By applying Corollary 5 on the four polynomial differences of the last identity, we have

$$\begin{array}{ccc}\hfill \varphi \left(T_{i+1}\right)-\varphi \left(T_i\right)& =& 4^{i-2}(4r\left(\mu \right)\left[\mu \varphi \left(D_{d-2i-1}\right)-\varphi \left(D_{d-2i}\right)\right]\hfill \\ & -& 4{(1+\alpha )}^{2}s\left(\mu \right)\left[\mu \varphi \left(D_{d-2i-2}\right)-\varphi \left(D_{d-2i-1}\right)\right]\hfill \\ & -& {(1+\alpha )}^{2}s\left(\mu \right)\left[\mu \varphi \left(D_{d-2i}\right)-\varphi \left(D_{d-2i+1}\right)\right]\hfill \\ & +& {(1+\alpha )}^4(\mu -{\alpha }^2+1)\left[\mu \varphi \left(D_{d-2i-1}\right)-\varphi \left(D_{d-2i}\right)\right]).\hfill \end{array}$$

From the recursion formula for symmetric tridiagonal matrices [16], we have

$$\varphi \left(T_{i+1}\right)-\varphi \left(T_i\right)=4^{i-1}\left(4r\left(\mu \right)-{(1+\alpha )}^2\mu s\left(\mu \right)+{(1+\alpha )}^4(\mu -{\alpha }^2+1)\right)\varphi \left(D_{d-2i-2}\right).$$

Considering that

$$r\left(\mu \right)=\mu (s\left(\mu \right)-\alpha {(\alpha +1)}^2)and s\left(\mu \right)={\mu }^2-({\alpha }^2-1)\mu -\alpha {(\alpha +1)}^2.$$

Through simple algebraic calculations, we have

$$4r\left(\mu \right)-{(1+\alpha )}^2\mu s\left(\mu \right)+{(1+\alpha )}^4(\mu -{\alpha }^2+1)=-(\alpha -1)[\mu p\left(\mu \right)+{(1+\alpha )}^5]$$

where

$$p\left(\mu \right)=(\alpha +3){\mu }^2-(\alpha +3)({\alpha }^2-1)\mu -{(\alpha +1)}^2({\alpha }^2+4\alpha -1).$$

Therefore,

$$\varphi \left(T_{i+1}\right)-\varphi \left(T_i\right)=-4^{i-1}(\alpha -1)[\mu p\left(\mu \right)+{(1+\alpha )}^5]\varphi \left(D_{d-2i-2}\right).$$

(11)

Since $B_{n-d+2,i,d-i}$ and $B_{n-d+2,d-i,i}$ are isomorphic graphs, for $1\le i\le \lfloor \frac{d}{2}\rfloor$, we prove the following result.

Theorem 6.

Let $\alpha =n-d$ with $d\ge 4$. Then,

$${\mu }_1\left(B_{\alpha +2,i,d-i}\right)={\mu }_1\left(B_{\alpha +2,d-i,i}\right)<{\mu }_1\left(B_{\alpha +2,i+1,d-i-1}\right)={\mu }_1\left(B_{\alpha +2,d-i-1,i+1}\right)$$

for $1\le i\le \lfloor \frac{d}{2}\rfloor -1.$

Proof. 

Let $1\le i\le \lfloor \frac{d}{2}\rfloor -1$. We know, by Corollary 4, that the spectral radius of the maximum degree matrix of $B_{\alpha +2,i,d-i}$ is the largest eigenvalue of the matrix $T_i$ of the order $(d+1)\times (d+1)$. Let

$${\alpha }_1={\mu }_1\left(B_{\alpha +2,i,d-i}\right)>{\alpha }_2>\dots >{\alpha }_d>{\alpha }_{d+1}$$

and

$${\beta }_1={\mu }_1\left(B_{\alpha +2,i+1,d-i-1}\right)>{\beta }_2>\dots >{\beta }_d>{\beta }_{d+1}$$

the eigenvalues of the matrices $T_i$ and $T_{i+1}$, respectively. Then

$$\varphi \left(T_i\right)=(\mu -{\alpha }_1)(\mu -{\alpha }_2)\dots (\mu -{\alpha }_{d+1})$$

and

$$\varphi \left(T_{i+1}\right)=(\mu -{\beta }_1)(\mu -{\beta }_2)\dots (\mu -{\beta }_{d+1}).$$

By (11), we have

$$\varphi \left(T_{i+1}\right)-\varphi \left(T_i\right)=-4^{i-1}(\alpha -1)[\mu p\left(\mu \right)+{(1+\alpha )}^5]\varphi \left(D_{d-2i-2}\right).$$

Thereby,

$$\begin{array}{ccc}\hfill \prod _{j=1}^{d+1}(\mu -{\beta }_j)-\prod _{j=1}^{d+1}(\mu -{\alpha }_j)& =& -4^{i-1}(\alpha -1)[\mu p\left(\mu \right)+{(1+\alpha )}^5]\varphi \left(D_{d-2i-2}\right).\hfill \end{array}$$

Considering $\mu ={\alpha }_1$, we get

$$\begin{array}{ccc}\hfill \prod _{j=1}^{d+1}({\alpha }_1-{\beta }_j)& =& -4^{i-1}(\alpha -1)[{\alpha }_{1}p\left({\alpha }_1\right)+{(1+\alpha )}^5]\varphi \left(D_{d-2i-2}\right).\hfill \end{array}$$

(12)

We claim that ${\beta }_1>{\alpha }_1$. Suppose that ${\beta }_1\le {\alpha }_1$. Then, ${\alpha }_1\ge {\beta }_j$ for $j=1,2,3,\dots ,d+1$. Then, the left side of (12) is non-negative. Clearly,

$${\mu }_1\left(B_{\alpha +2,i+1,d-i-1}\right)>(\alpha +1){\displaystyle \frac{\alpha -1+\sqrt{{\alpha }^2+6\alpha +1}}{2}},$$

which implies $p\left({\alpha }_1\right)>0$. Furthermore, $\alpha >1$ and $\varphi \left(D_{d-2i-2}\right)\left({\alpha }_1\right)>0$, then the right side of (12) is negative, which is a contradiction. Therefore, ${\beta }_1>{\alpha }_1$. □

Theorem 7.

Let $G\in {\mathbb{G}}_{n,d}$ with $d\ge 2$. Then,

$${\mu }_1\left(G\right)\le {\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }),$$

the equality is given if and only if $G\cong B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$.

Proof. 

If $d=2,3,$ the result is verified by Corollaries 2 and 3. Now, let $d\ge 4$. Suppose $n>d+1$. The result is verified by Theorems 1, 3 and 6. Now, suppose $n=d+1$. By Remark 1, $G\cong P_n\cong B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$. The proof is complete. □

Theorem 8.

Let $n\ge d+1\ge 3$. Then,

$${\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })>{\mu }_1(B_{n-d+1,\lfloor \frac{d+1}{2}\rfloor ,\lceil \frac{d+1}{2}\rceil }).$$

Proof. 

Let $v_1,v_2,\dots ,v_{d+2}$ be the vertices in a diameter path of

$$B_{n-d+1,\lfloor \frac{d+1}{2}\rfloor ,\lceil \frac{d+1}{2}\rceil }.$$

We obtain a new graph $G_1$, and add two edges that connect the vertex $v_{d+2}$ with the two vertices $v_{d-1},v_d$. By Lemma 2,

$${\mu }_1\left(G_1\right)>{\mu }_1(B_{n-d+1,\lfloor \frac{d+1}{2}\rfloor ,\lceil \frac{d+1}{2}\rceil }).$$

(13)

It is easy to see that $G_1$ has diameter d. If $n=d+2$, by Theorem 6, we have ${\mu }_1\left(G_1\right)\le {\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })$, the result is verified. Suppose $n>d+2$. Let $X^{G_1}=\{v_1,\dots ,v_{d+1}\}$. We obtain a graph $G_2$ and add edges that connect the vertex $v_{d+2}$ with all the vertices of $V\left(G_1\right)-(X^{G_1}\cup \left\{v_{d+2}\right\})$.

By Lemma 2,

$${\mu }_1\left(G_2\right)>{\mu }_1\left(G_1\right).$$

(14)

Considering the construction of graph $G_2$, we have

$$N_{G_2}\left(v_{d+2}\right)\cap X^{G_1}=\{v_{d-1},v_d,v_{d+1}\}$$

and

$$N_{G_2}\left(w\right)\cap X^{G_1}=\{v_{\lfloor \frac{d+1}{2}\rfloor },v_{\lfloor \frac{d+1}{2}\rfloor +1},v_{\lfloor \frac{d+1}{2}\rfloor +2}\}$$

for each $w\in V\left(G_1\right)-(X^{G_1}\cup \left\{v_{d+2}\right\})$. Keeping the previous notation in mind, four situations can occur in the graph $G_2$ as mentioned below:

(A)

$d=\lfloor \frac{d+1}{2}\rfloor +2$

(B)

$d=\lfloor \frac{d+1}{2}\rfloor +3$

(C)

$d=\lfloor \frac{d+1}{2}\rfloor +4$

(D)

$d>\lfloor \frac{d+1}{2}\rfloor +4$.

Using the same techniques in the proof of Theorem 2, cases (A), (B), (C) and (D), with $j=d-1$ and $i=\lfloor \frac{d+1}{2}\rfloor$, we can conclude that

$${\mu }_1\left(B_{n-d+2,k,d-k}\right)>{\mu }_1\left(G_2\right)$$

(15)

for some $1\le k\le \lfloor \frac{d}{2}\rfloor$.

From (13), (14), (15) and Theorem 6, the proof is complete. □

Theorem 9.

Let G be a connected graph on n vertices and let $diam\left(G\right)\ge d$. If $d=1$, then ${\mu }_1\left(G\right)={\mu }_1\left(K_n\right)$. If $d\ge 2$, then

$${\mu }_1\left(G\right)\le {\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }).$$

The equality holds if and only if $G\cong B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$.

Proof. 

If $d=1$, then $G\cong K_n$. Let $d\ge 2$. Let $\widehat{G}$ be the graph with the largest spectral radius of the maximum degree matrix among all the graphs on n vertices and diameter greater than or equal to d. Suppose $diam(\widehat{G})>d$.

By Theorem 7,

$$\widehat{G}\cong B_{n-diam\left(\widehat{G}\right)+2,\lfloor \frac{diam\left(\widehat{G}\right)}{2}\rfloor ,\lceil \frac{diam\left(\widehat{G}\right)}{2}\rceil }.$$

Let $diam(\widehat{G})=k+1$. By Theorem 8, we have

$${\mu }_1(B_{n-k+2,\lfloor \frac{k}{2}\rfloor ,\lceil \frac{k}{2}\rceil })>{\mu }_1(B_{n-k+1,\lfloor \frac{k+1}{2}\rfloor ,\lceil \frac{k+1}{2}\rceil }),$$

which is a contradiction. Then, $diam(\widehat{G})=d$. Due to Theorem 7, the proof is complete. □

5. Computing the Largest Spectral Radius of the Maximum Degree Matrix of Graphs with a Given Order and Diameter

Among various graph matrices, the maximum degree matrix has emerged as a recent tool to capture interactions between vertex degrees and adjacency. Given a graph G, this matrix encodes, for each edge, the maximum degree between the incident vertices, and zero otherwise.

In this context, an important extremal problem arises: identifying connected graphs, among all those with a fixed number of vertices n and diameter $d,$ that maximize the spectral radius of their maximum degree matrix. This problem not only deepens our understanding of the spectral behavior of such matrices but also connects with classical extremal graph theory and structural optimization.

This section focuses on the analytical computation of the largest possible spectral radius of the maximum degree matrix among all graphs with fixed order and diameter, using known characterizations and structural properties of special graph classes.

From Theorem 5, ${\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })$ can be computed as the largest eigenvalue of the symmetric tridiagonal matrix $T_{\lfloor \frac{d}{2}\rfloor }$.

Theorem 10.

If $d=3$, then ${\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })$ can be computed as the largest eigenvalue of the symmetric tridiagonal matrix $T_1$ of order 4 with diagonal entries

$$\{0,n^2-6n+8,0,0\}$$

and co-diagonal entries

$$\{(n-2)\sqrt{n-3},(n-2)\sqrt{n-3},n-2\}.$$

If $d\ge 4$, then ${\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })$ can be computed as the largest eigenvalue of the symmetric tridiagonal matrix $T_{\lfloor \frac{d}{2}\rfloor }$ with diagonal entries

$$\underset{\lfloor \frac{d}{2}\rfloor }{\underbrace{0,\dots ,0}},{(n-d)}^2-1,\underset{\lceil \frac{d}{2}\rceil }{\underbrace{0,\dots ,0}}$$

and co-diagonal entries

$$\underset{\lfloor \frac{d}{2}\rfloor -2}{\underbrace{2,\dots ,2}},n-d+1,(n-d+1)\sqrt{n-d},(n-d+1)\sqrt{n-d},n-d+1,\underset{\lceil \frac{d}{2}\rceil -2}{\underbrace{2,\dots ,2}}.$$

In [17], the authors show that the signless Laplacian spectral radius of $B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil }$ can be computed as the largest eigenvalue of a symmetric tridiagonal matrix of the order ${\displaystyle \frac{d}{2}}+1$ whenever d is an even integer. The corresponding version of this result for the maximum degree matrix is given below.

Theorem 11.

If $d\ge 4$ is an even integer, then ${\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })$ can be computed as the largest eigenvalue of a symmetric tridiagonal matrix of the order ${\displaystyle \frac{d}{2}}+1$ with the diagonal

$$\underset{\lfloor \frac{d}{2}\rfloor }{\underbrace{0,\dots ,0}},{(n-d)}^2-1$$

and co-diagonal entries

$$\underset{\lfloor \frac{d}{2}\rfloor -2}{\underbrace{2,\dots ,2}},n-d+1,(n-d+1)\sqrt{2(n-d)}.$$

Proof. 

Let d be an even integer. From Theorem 10, ${\mu }_1(B_{n-d+2,\lfloor \frac{d}{2}\rfloor ,\lceil \frac{d}{2}\rceil })$ can be computed as the largest eigenvalue of

$$T_{\lfloor \frac{d}{2}\rfloor }=\left[\begin{array}{ccc}U& \mathbf{b}& \mathbf{0}\\ {\mathbf{b}}^T& {(n-d)}^2-1& {\mathbf{b}}^{T}J\\ \mathbf{0}& J\mathbf{b}& JUJ\end{array}\right]$$

of order $d+1$, where

$$U=\left[\begin{array}{ccccc}0& 2& & & \\ 2& 0& \ddots & & \\ & \ddots & \ddots & 2& \\ & & & 0& n-d+1\\ & & & n-d+1& 0\end{array}\right]$$

${\mathbf{b}}^T=\left[\begin{array}{ccccc}0& \dots & \dots & 0& (n-d+1)\sqrt{n-d}\end{array}\right]$.

Consider the orthogonal matrix

$$L={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{ccc}I& \mathbf{0}& J\\ {\mathbf{0}}^T& \sqrt{2}& {\mathbf{0}}^T\\ -J& \mathbf{0}& I\end{array}\right].$$

Simple algebraic calculations show that

$$L{T}_{\lfloor \frac{d}{2}\rfloor }{L}^T=\left[\begin{array}{ccc}U& \sqrt{2}\mathbf{b}& \mathbf{0}\\ \sqrt{2}{\mathbf{b}}^T& {(n-d)}^2-1& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& JUJ\end{array}\right].$$

Then, the eigenvalues of $T_{\lfloor \frac{d}{2}\rfloor }$ are the eigenvalues of $\left[\begin{array}{cc}U& \sqrt{2}\mathbf{b}\\ \sqrt{2}\mathbf{b}& {(n-d)}^2-1\end{array}\right]$ and the eigenvalues of U. Since that the eigenvalues of U strictly interlace the eigenvalues of $\left[\begin{array}{cc}U& \sqrt{2}\mathbf{b}\\ \sqrt{2}\mathbf{b}& {(n-d)}^2-1\end{array}\right]$. □

6. Conclusions

Finally, this study provides a fundamental analysis of the maximum degree matrix and its spectral radius, highlighting its structural relevance to extreme graph theory. Some questions arising from this work are future research that will explore additional spectral invariants derived from the maximum degree matrix, incorporating combinatorial parameters such as graph coloring and a deeper investigation of its eigenvalues.