Brauer Analysis of Thompson’s Group F and Its Application to the Solutions of Some Yang–Baxter Equations
Abstract
1. Introduction
Contributions
2. Preliminaries
2.1. Background
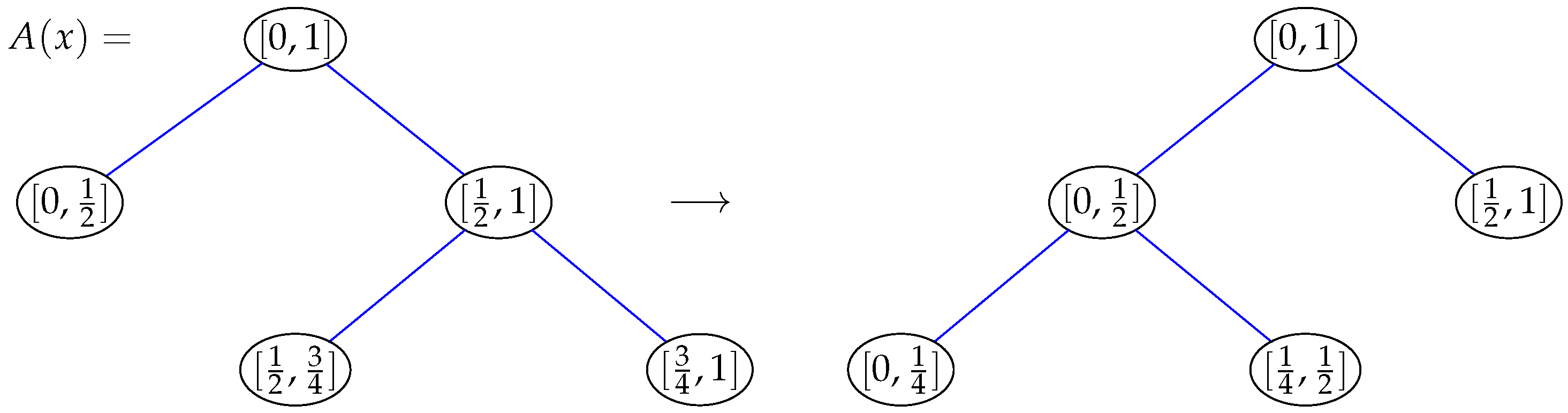
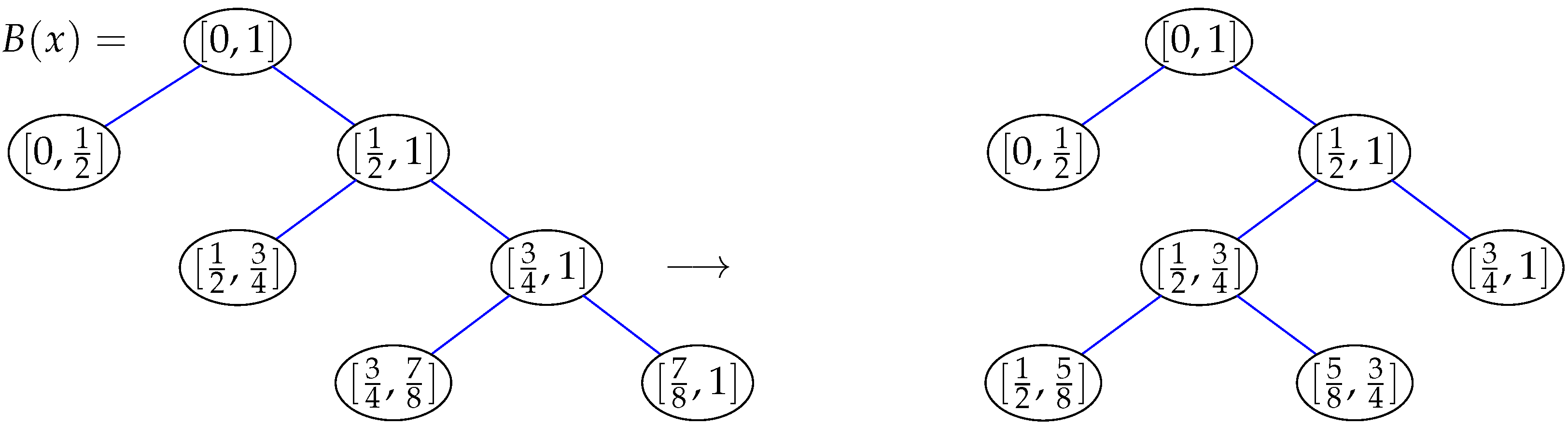
2.2. Thompson’s Group F
- F is torsion-free, contains free semi-group on two generators, and contains no nonabelian free group.
- Every subgroup of F is finite rank free abelian or contains an infinite rank free abelian subgroup.
- Every proper quotient of F is abelian.
- is simple and .
2.3. Tree Operations
- is defined in such a way that if v is a tree root and w is a vertex in another tree, link the trees containing v and w by adding the edge , making w the parent of v.
- divides a given rooted tree into two new trees by deleting the edge from a vertex v (which is not a tree root) to its parent.
- turns a tree containing a vertex v inside out by making v the root of the tree.
2.4. Yang–Baxter Equation and Its Solutions
- is an abelian group;
- is a group.
- 1.
- .
- 2.
- .
- 3.
- The map defined by is a non-degenerate involutive set-theoretical solution of the YBE.
2.5. Multisets and Brauer Configuration Algebras
- Each letter has associated a linear ordered set or successor sequence , where , is the collection of all multisets containing m and , with , and , , if .
- If is the size of the multiset , then , .
- There exists a map ) such that , where is said to be the valency of m. If and (), then (). In particular, the successor sequence associated with m is , if .
- , if and are special cycles at vertices and contained in the same polygon . These are relations of type .
- , where is a special cycle at vertex and f is its first arrow. In particular, if is an arrow defined by with , then is a relation of this type provided that in such a case, is a special cycle at . These relations are said to be of type .
- , where and are arrows in defined by successor sequences and with , and . These relations are said to be of type .
- Any Brauer configuration algebra induced by a Brauer configuration is multiserial, and there exists a bijective correspondence between the set of indecomposable projective -modules and the set of multisets or polygons .
- The number of summands in the heart of an indecomposable projective -module equals the number of nontruncated vertices in the corresponding polygon. Where, () denotes the Jacobson radical (socle) of the indecomposable projective -module P.
- We note that any graph gives rise to a Brauer configuration of type M, where and . Cañadas et al. [25] proved that the covering graph induced by a Brauer configuration defined by a graph is isomorphic to if and only if is a disjoint union of copies of connected hair graphs of type , where is an n-point cycle and .
- , .
- .
- .
- , , .
- , , for the remaining vertices or letters.
- The Brauer configuration algebra induced by the Brauer configuration is indecomposable as an algebra, .
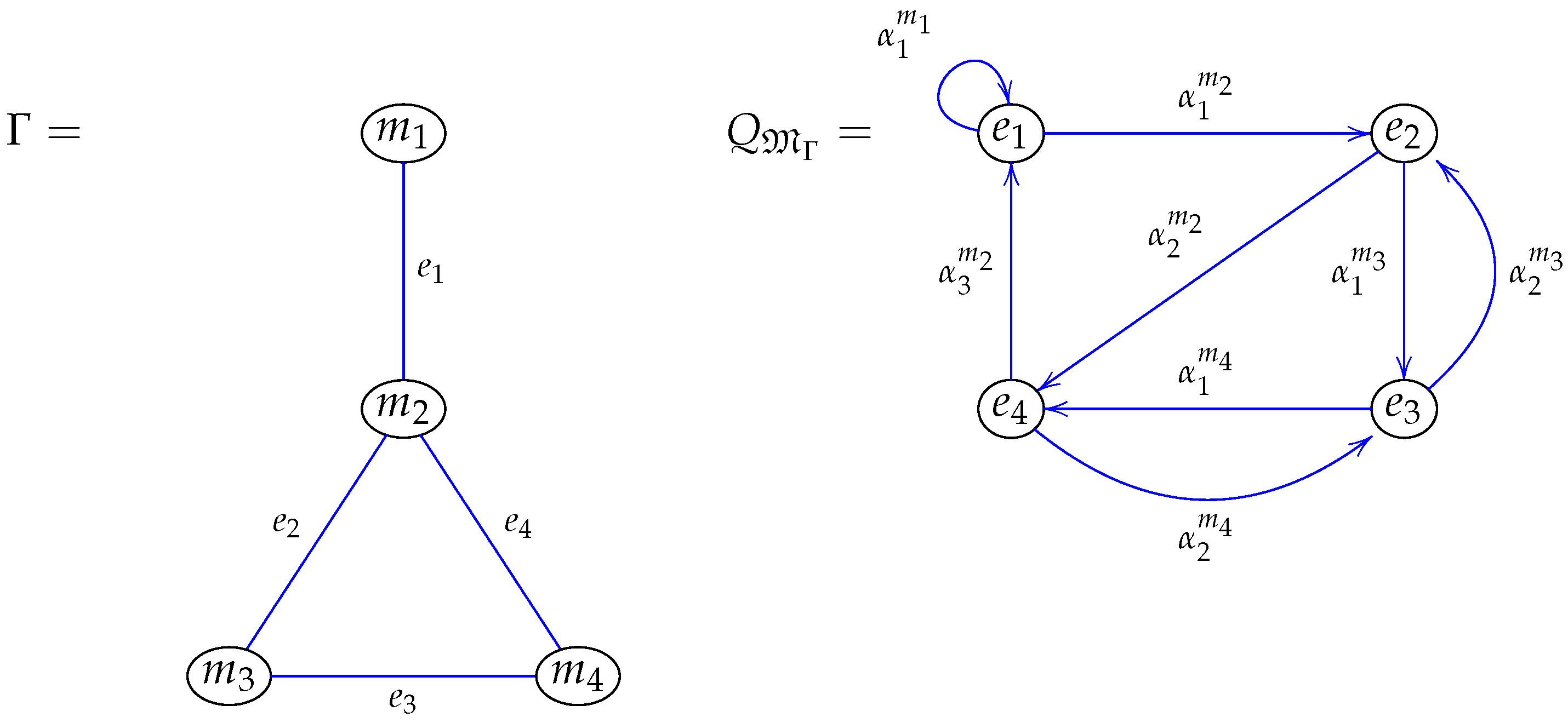
- Figure 4 shows Brauer quivers and . The following are examples of relations contained in the admissible ideal . Relations in are defined in the same fashion.
- 1.
- , , for all possible values of p and q.
- 2.
- , .
- 3.
- .
- 4.
- .
- 5.
- .
- 6.
- .
- 7.
- ; ; .
- For fixed, it holds that .
- and are isomorphic as algebras.
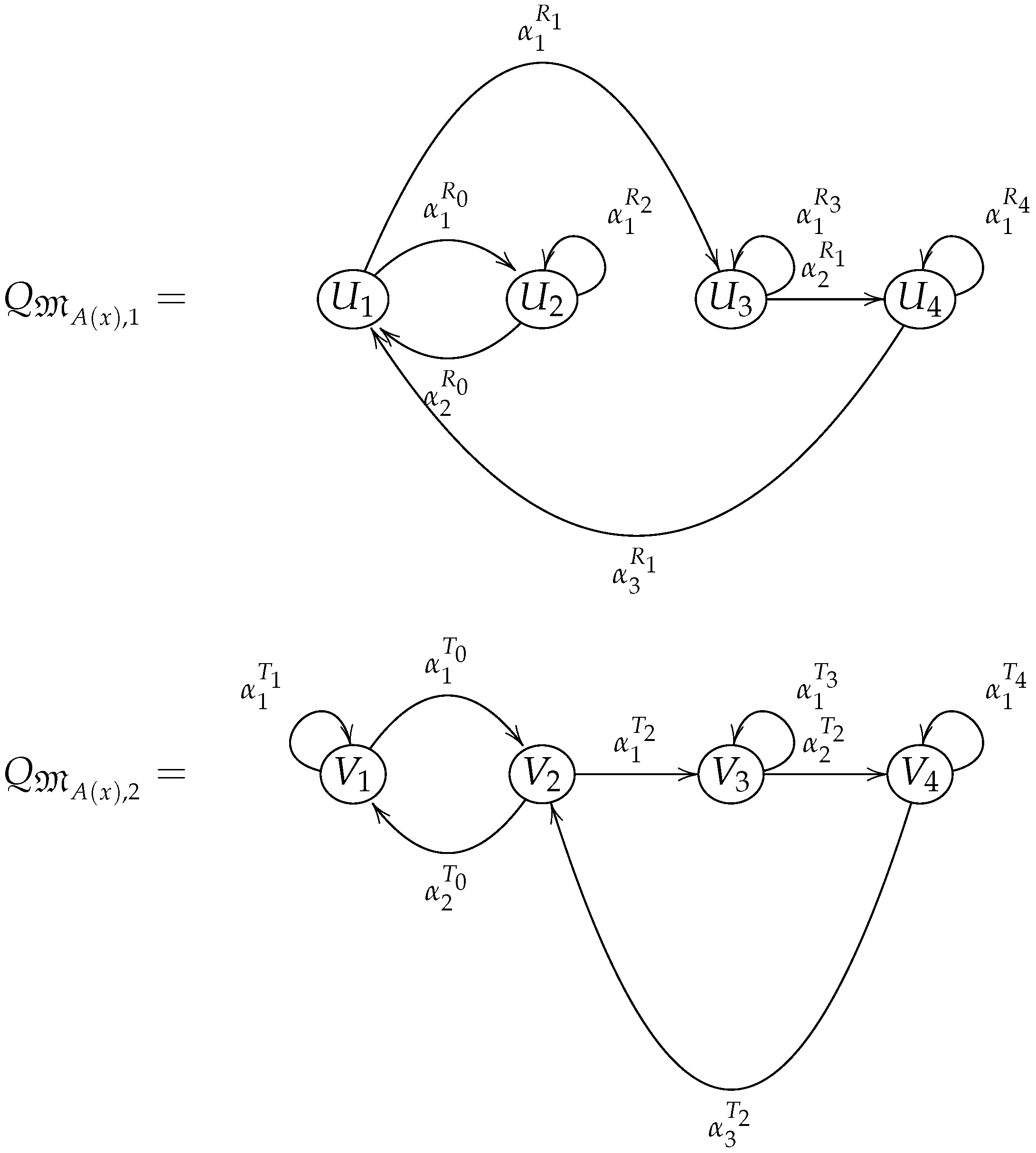
- is the Brauer configuration algebra induced by the generator of Thompson’s group F. Thus, .
- For fixed, it holds that . Note that there are three vertices with valency one and four polygons (see Formula (18)).
2.6. Entropy of a Graph
- .
- .
- The degree of the vertices gives their valency values, i.e., , and , for .
- The multiplicity values of the elements of M (vertices of the Brauer configuration ) are , , , and .
- Circular orderings associated with vertices , areThese circular orderings define the orientation . The symbol in a circular ordering means that occurs q times at the polygon (edge) .
- The Brauer quiver induced by the Brauer configuration is such that the set of vertices and there exists an arrow if and only if there exists a relation in the circular ordering associated with the vertex (see Figure 5).
- The Brauer configuration algebra is the bound quiver algebra induced by the Brauer configuration , the following are examples of relations contained in the admissible ideal .
- 1.
- , , , .
- 2.
- , , , .
- 3.
- if , for all values of r and s.
- The Brauer configuration algebra is indecomposable as an algebra and reduced, provided that the Brauer quiver is connected and , for any .
- Since Γ is a hair graph of type , then the covering graph is isomorphic to Γ, whose entropies , , and (the entropy of the Brauer configuration ) are as follows:
- 1.
- .
- 2.
- .
- 3.
- , provided that . In [25], Cañadas et al. proved that if Γ is a Dynkin or Euclidean diagram, then allows for giving approximations of .
- The dimensions of the Brauer configuration algebra and its corresponding center are given by the following identities:
3. Main Results
3.1. Brauer Analysis of Thompson’s Group F
- 1.
- is indecomposable as an algebra.
- 2.
- .
- 3.
- .
- 4.
- .
- 5.
- .
- 6.
- .
- is indecomposable as an algebra provided that the binary tree , which induces , is connected.
- Note that the number of edges of the binary tree is . Furthermore, , , and . Then, .
- .
- .
- Note that, , then .
- , then . We are done.
3.2. Solutions of the Yang–Baxter Equation Arising from Covering Graphs
- If , , , and , then=.On the other hand,.
- If , , with h, i, and f arbitraries, then=.On the other hand,.
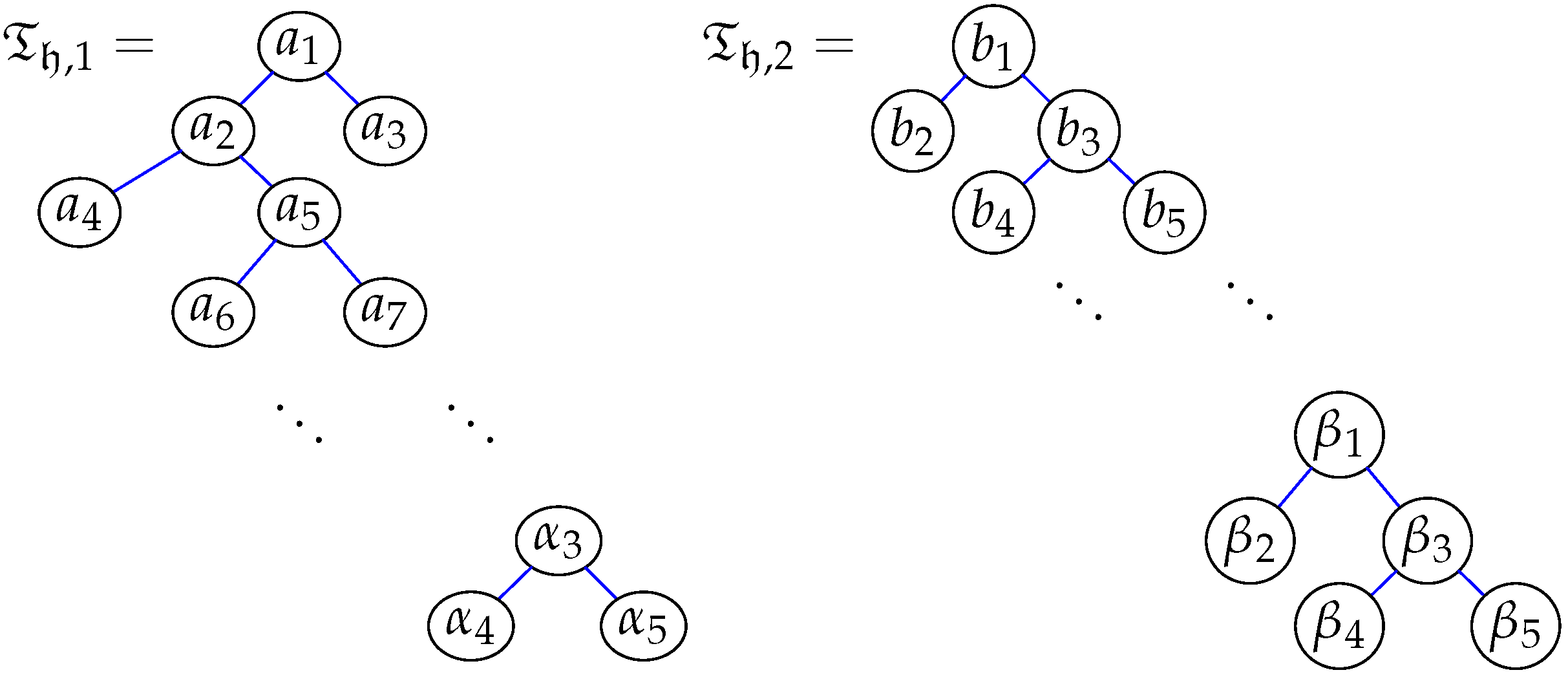
3.3. Brauer Analysis of Thompson’s Group F via Christoffel Words
- 1.
- , .
- 2.
- .
- 3.
- .
- 1.
- is indecomposable as an algebra.
- 2.
- .
- 3.
- .
- 4.
- The covering graph is a 4-point linear path.
- If denotes the polygon defined by the word , , then , hence the Brauer quiver induced by the Brauer configuration is connected. Therefore, the algebra is indecomposable as an algebra.
- We note that, if , and are rational numbers whose Christoffel words are , and , respectively. Then, , , , and . Therefore, , , , . Furthermore, , , , . Where, , denotes the number of occurrences of the number h in the polygon . Thus, and , then .
- Note that, for any , and , and the number of loops in the Brauer quiver induced by the Brauer configuration is . Then, .
- , where is the chain induced by the expansions of .
4. Conclusions
- Applying Brauer analysis to generators of Thompson’s group T and V is an open problem. Such an analysis can include giving values of the super edge-magic total strength of covering graphs, as Deepthi defined in [45].
- Another task for the future consists of giving new solutions of the Yang–Baxter equation arising from the Brauer configuration algebras induced by generators of Thompson’s group T and V.
- Applying Brauer analysis to quantum circuits is a task to be addressed in the future, assuming quantum gates as elements of the ground set M and quantum circuits as elements of a collection of multisets denoted in this paper.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Binary tree defined by Thompson’s group generator | |
| Christoffel path | |
| Covering graph of a Brauer quiver | |
| Dimension of a Brauer configuration algebra | |
| Dimension of the center of a Brauer configuration algebra | |
| Entropy of a graph | |
| Entropy of a Brauer configuration induced by a graph | |
| Hair graph | |
| Brauer configuration algebra | |
| Rotation graph whose set of vertices are n-vertex binary trees | |
| M | Set of vertices of a Brauer configuration |
| Collection of polygons of a Brauer configuration | |
| Brauer configuration | |
| Multiplicity function of a Brauer configuration | |
| Orientation of a Brauer configuration | |
| valency of a vertex x | |
| YBE | Yang–Baxter equation |
| Center of a Brauer configuration algebra |
References
- Brin, M.; Squier, C. Groups of piecewise linear homeomorphisms of the real line. Inventiones. Math. 1985, 79, 485–498. [Google Scholar] [CrossRef]
- Higman, G. Finitely Presented Infinite Simple Groups; Notes on Pure Mathematics; Dept. of Pure Mathematics, Dept. of Mathematics, I.A.S., Australian National University: Canberra, Australia, 1974; Volume 8, Available online: https://api.semanticscholar.org/CorpusID:116374349 (accessed on 12 August 2024).
- Brown, K.S. Finiteness properties of groups. J. Pure Appl. Algebra 1987, 44, 45–75. [Google Scholar] [CrossRef]
- McKenzie, R.; Thompson, R.J. An Elementary Construction of Unsolvable Word Problems in Group Theory; Boone, W.W., Cannonito, F.B., Lyndon, R.C., Eds.; Word Problems: North-Holland, The Netherlands, 1973; pp. 35–55. Available online: https://api.semanticscholar.org/CorpusID:118246987 (accessed on 15 August 2024).
- Freyd, P.; Heller, A. Splitting homotopy idempotents. J. Pure Appl. Algebra 1993, 89, 93–106. [Google Scholar] [CrossRef]
- Ohshika, K.; Papadopoulos, A.; Penner, R.C.; Wienhard, A. New trends in Teichmüller theory and mapping class groups. Oberwolfach Rep. 2018, 15, 2475–2534. [Google Scholar] [CrossRef]
- Sleator, D.D.; Tarjan, R.E. A data structure for dynamic trees. J. Comput. Syst. Sci. 1983, 26, 362–391. [Google Scholar] [CrossRef]
- Sleator, D.D.; Tarjan, R.E.; Thurston, W.P. Rotation distance, triangulations, and hyperbolic geometry. J. Am. Math. Soc. 1988, 1, 122–135. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Bravo, G. Dyck path categories and its relationships with cluster algebras. J. Algebra Its Appl. 2022, 23, 2430001. [Google Scholar] [CrossRef]
- Green, E.L.; Schroll, S. Brauer configuration algebras: A generalization of Brauer graph algebras. Bull. Sci. Math. 2017, 121, 539–572. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Gutierrez, I.; Mendez, O.M. Brauer Analysis of Some Cayley and Nilpotent Graphs and Its Application in Quantum Entanglement Theory. Symmetry 2024, 16, 570. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Angarita, M.A.O. Brauer configuration algebras for multimedia based cryptography and security applications. Multimed. Tools. Appl. 2021, 80, 23485–23510. [Google Scholar] [CrossRef]
- Yang, C.N. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 1967, 19, 1312–1315. [Google Scholar] [CrossRef]
- Lieb, E.H.; Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 1963, 130, 1605–1616. [Google Scholar] [CrossRef]
- Baxter, R.J. Partition function for the eight-vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Lieb, E.H. Exact analysis of an interacting Bose gas. II. The excitation spectrum. Phys. Rev. 1963, 130, 1616–1624. [Google Scholar] [CrossRef]
- Caudrelier, V.; Crampé, N. Exact results for the one-dimensional many-body problem with contact interaction: Including a tunable impurity. Rev. Math. Phys. 2007, 19, 349–370. [Google Scholar] [CrossRef]
- Aharonov, D.; Jones, V.; Landau, Z. A Polynomial Quantum Algorithm for Approximating the Jones Polynomial. Algorithmica 2009, 55, 395–421. [Google Scholar] [CrossRef]
- Pachos, J.K. The Jones polynomial algorithm. In Introduction to Topological Quantum Computation; Cambridge University Press: Cambridge, UK, 2012; pp. 157–176. [Google Scholar] [CrossRef]
- Dehornoy, P. The group of parenthesized braids. Adv. Math. 2006, 205, 354–409. Available online: https://www.sciencedirect.com/science/article/pii/S0001870805002045 (accessed on 25 July 2024). [CrossRef]
- Jones, F.R.V. Some unitary representations of Thompson’s groups F and T. J. Comb. Algebra 2017, 1, 1–44. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Ballester-Bolinches, A.; Gaviria, I.D.M. Solutions of the Yang-Baxter equation arising from Brauer configuration algebras. Computation 2022, 11, 2. [Google Scholar] [CrossRef]
- Rump, W. Modules over braces. Algebra Discret. Math. 2006, 2, 127–137. Available online: https://admjournal.luguniv.edu.ua/index.php/adm/article/view/892 (accessed on 15 July 2024).
- Cedó, F.; Jespers, E.; Oniński, J. Braces and the Yang-Baxter equation. Commun. Math. Phys. 2014, 327, 101–116. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Espinosa, P.F.F.; Nieto, J.G.R.; Mendez, O.M.; Arteaga-Bastidas, R.H. Extended Brauer Analysis of Some Dynkin and Euclidean Diagrams. ERA 2024, 32, 5752–5782. [Google Scholar] [CrossRef]
- Schroll, S. Brauer Graph Algebras. In Homological Methods, Representation Theory, and Cluster Algebras; Assem, I., Trepode, S., Eds.; CRM Short Courses; Springer: Cham, Switzerland, 2018; pp. 177–223. [Google Scholar] [CrossRef]
- Espinosa, P.F.F. Categorification of Some Integer Sequences and Its Applications. Ph.D. Thesis, National University of Colombia, Bogotá, Colombia, 2021. Available online: https://repositorio.unal.edu.co/handle/unal/79501 (accessed on 1 July 2024).
- Belk, J.M. Thompson’s Group F. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2004. Available online: https://pi.math.cornell.edu/~belk/Thesis.pdf (accessed on 1 July 2024).
- Burillo, J. Introduction to Thompson’s Group F. UPC Universitat Politècnica de Catalunya. Available online: https://api.semanticscholar.org/CorpusID:250274227 (accessed on 5 July 2024).
- Cannon, J.W.; Floyd, W.J.; Parry, W.R. Introductory notes on Richard Thompson’s groups. L’Enseignement Mathématique 1996, 42, 215–256. Available online: https://www.imo.universite-paris-saclay.fr/~emmanuel.breuillard/Cannon.pdf (accessed on 18 August 2024).
- Nichita, F.F. Introduction to the Yang-Baxter equation with open problems. Axioms 2012, 1, 33–37. [Google Scholar] [CrossRef]
- Drinfeld, V.G. On Unsolved Problems in Quantum Group Theory; Lecture Notes Math.; Springer: Berlin, Germany, 1992; Volume 1510, pp. 1–8. [Google Scholar] [CrossRef]
- Ballester-Bolinches, A.; Esteban-Romero, R.; Fuster-Corral, N.; Meng, H. The structure group and the permutation group of a set-theoretical solution of the quantum Yang-Baxter equation. Mediterr. J. Math. 2021, 18, 1347–1364. [Google Scholar] [CrossRef]
- Etingof, P.; Soloviev, A.; Guralnick, R. Indecomposable set-theoretical solutions to the quantum Yang-Baxter equation on a set with a prime number of elements. J. Algebra 2001, 242, 709–719. [Google Scholar] [CrossRef]
- Nichita, F.F. Yang-Baxter equations, computational methods and applications. Axioms 2015, 4, 423–435. [Google Scholar] [CrossRef]
- Etingof, P.; Schedler, T.; Soloviev, A. Set-theoretical solutions to the quantum Yang-Baxter equation. Duke Math. J. 1999, 100, 169–209. [Google Scholar] [CrossRef]
- Gateva-Ivanova, T.; Van den Bergh, M. Semigroups of I-type. J. Algebra 1998, 206, 97–112. [Google Scholar] [CrossRef]
- Guarnieri, L.; Vendramin, L. Skew braces and the Yang-Baxter equation. Math. Comput. 2017, 85, 2519–2534. Available online: https://www.jstor.org/stable/90010152 (accessed on 3 March 2024). [CrossRef]
- Andrews, G.E. The Theory of Partitions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Sierra, A. The dimension of the center of a Brauer configuration algebra. J. Algebra 2018, 510, 289–318. [Google Scholar] [CrossRef]
- Rashevsky, N. Life, information theory, and topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Trucco, E. A note on the information content of graphs. Bull. Math. Biol. 1956, 18, 129–135. [Google Scholar] [CrossRef]
- Frosini, A.; Tarsissi, L. The characterization of the minimal paths in the Christoffel tree according to a second-order balancedness. Developments in Language Theory-DLT2020; Tampa, USA. 2020, pp. 1–14. Available online: https://hal.science/hal-02495529v1 (accessed on 20 August 2024).
- Sloane, N.J.A. The On-Line Encyclopedia of Integer Sequences. Available online: https://oeis.org/A009350 (accessed on 19 August 2024).
- Deepthi, N.S. Super Edge-magic Total Strength of Some Unicyclic Graphs. Ars Comb. 2024, 159, 73–85. [Google Scholar] [CrossRef]

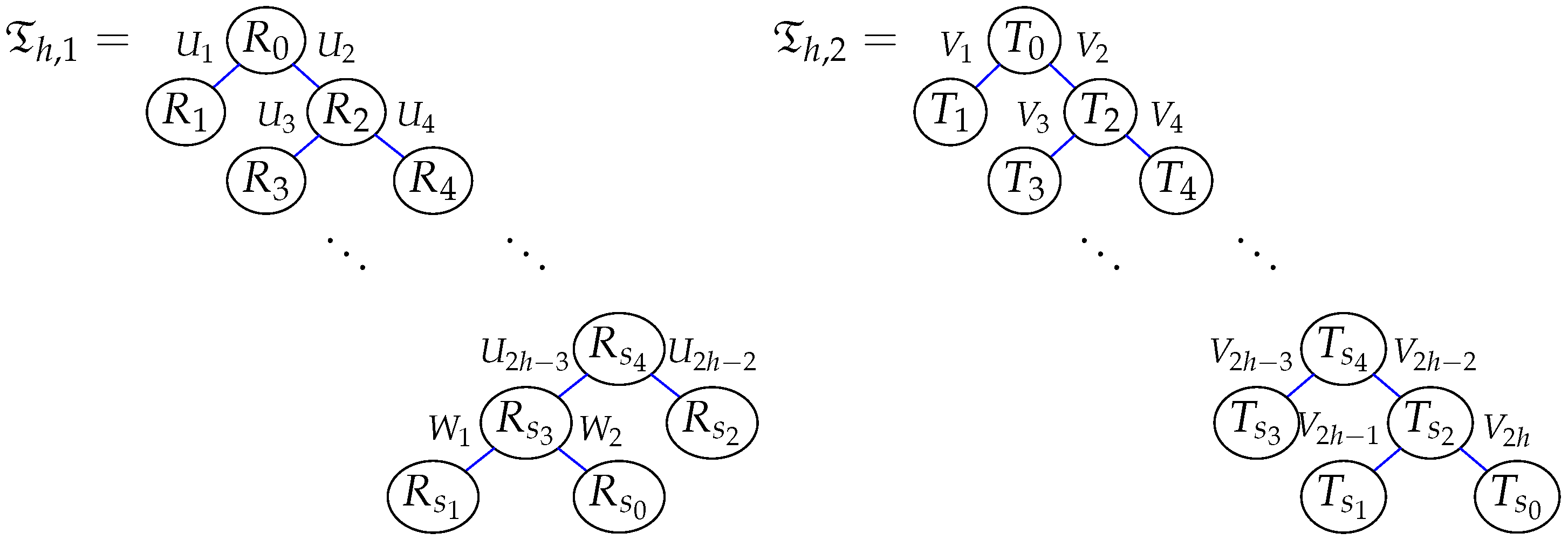

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cañadas, A.M.; Rodríguez-Nieto, J.G.; Salazar-Díaz, O.P.; Velásquez, R.; Giraldo, H. Brauer Analysis of Thompson’s Group F and Its Application to the Solutions of Some Yang–Baxter Equations. Mathematics 2025, 13, 1127. https://doi.org/10.3390/math13071127
Cañadas AM, Rodríguez-Nieto JG, Salazar-Díaz OP, Velásquez R, Giraldo H. Brauer Analysis of Thompson’s Group F and Its Application to the Solutions of Some Yang–Baxter Equations. Mathematics. 2025; 13(7):1127. https://doi.org/10.3390/math13071127
Chicago/Turabian StyleCañadas, Agustín Moreno, José Gregorio Rodríguez-Nieto, Olga Patricia Salazar-Díaz, Raúl Velásquez, and Hernán Giraldo. 2025. "Brauer Analysis of Thompson’s Group F and Its Application to the Solutions of Some Yang–Baxter Equations" Mathematics 13, no. 7: 1127. https://doi.org/10.3390/math13071127
APA StyleCañadas, A. M., Rodríguez-Nieto, J. G., Salazar-Díaz, O. P., Velásquez, R., & Giraldo, H. (2025). Brauer Analysis of Thompson’s Group F and Its Application to the Solutions of Some Yang–Baxter Equations. Mathematics, 13(7), 1127. https://doi.org/10.3390/math13071127








