Abstract
This paper addresses the problem of optimal -filtering for a class of continuous-time linear McKean–Vlasov stochastic differential equations under sampled measurements. The main tool used to solve the filtering problem is a forward jump matrix linear differential equation with a Riccati-type jumping operator. More specifically, the stabilizing solution of such a jump Riccati-type equation plays a key role.
Keywords:
H2-filtering; stochastic systems; sampled measurements; McKean–Vlasov equations; jump Riccati equations MSC:
93B53; 93C27; 93C57; 93E11; 60H10
1. Introduction
Estimating a remote signal from the measurements of another observed signal is a classical problem in the systems theory with numerous applications in different real life problems. Such a problem is usually named in the literature a signal filtering problem or signal estimation/observation problem. The problem of filtering is fundamental in control theory. Since the pioneering works of Kalman and Bucy derived in the 1960s (see [,]), a huge amount of contributions has been made in this field stimulated by successful implementation in many applications including aerospace, signal processing, geophysics, etc.
On the other hand, control of McKean–Vlasov stochastic differential equations (SDEs) has attracted significant attention in the last decade. This is partly due to the fact that such SDEs can effectively characterize dynamical systems of large populations subject to a mean-field interaction. McKean–Vlasov SDEs appeared initially in the works of [,]. There are already several important contributions related to this type of stochastic systems from the control perspective [,,,,,]. More recently, LQ control problems as well as LQ games for such systems have been investigated by [,,,,,]. To the best of the authors’ knowledge, it seems that the filtering problem for McKean–Vlasov SDEs has been addressed in the literature very marginally when compared to the control counterpart. Very recently, we addressed in [] a filtering problem for a class of linear periodic McKean–Vlasov SDEs where the metric used as an optimality measure of the proposed estimation scheme belongs to the -type norm setting. In [], the proposed filter is fed at its input with continuous-time measurements in order to generate the optimal state estimation. Note, however, that in modern control systems like digital control as well as networked control, the assumption of measurement continuity is no longer valid and one has to deal with a sampled-data setting. For deterministic systems and constant sampled-data rate, stability as well as optimal control problems have been successfully solved in the literature thanks to a discrete-time equivalent representation of the original system where such a representation is obtained without any kind of approximation. In the stochastic framework, the discrete-time equivalent representation cannot be obtained. This explains why sampled-data control for stochastic systems did not receive the attention it deserves until the last few years [,,,,,].
In the present paper, we will consider the problem of -optimal filtering for a class of linear McKean–Vlasov SDEs under sampled measurements. Such a problem is addressed under an impulsive SDE setting. The class of admissible filters consists of deterministic impulsive linear systems with arbitrary dimension of the state space. We show that the dimension of the optimal filter is equal to two times the dimension of the system under consideration. The corresponding feedback gain of the optimal filter is constructed based on the stabilizing solution of an adequately defined system of forward jump matrix linear differential equation with a Riccati-type jumping operator. The result obtained in this article can be viewed as an extension of the author’s results from [] to the sampled-data case.
This paper is organized as follows: Section 2 gives the mathematical model of the considered class of systems and describes the filtering problem. Section 3 gives several preliminary results related to the stability of McKean–Vlasov SDEs that will be used in Section 4 in order to obtain the formulae for the computation of the performance value. The main results are given in Section 5. Some numerical experiments are included in Section 6.
2. Problem Formulation
2.1. Notations
Let be a given probability space. In this work, , is an -dimensional standard Wiener process defined on . For precise definitions and useful properties of the stochastic processes, we refer for example to [,].
For each , is the -algebra generated by the random vectors , . For , the -algebra . We assume that for each , the -algebra is augmented with all subsets with . For each , denotes the conditional expectation with respect to the -algebra , while denotes the mathematical expectation. Let , be a sequence of -dimensional independent random vectors. stands for the smallest -algebra generated by the random vectors , , , , where is given. The superscript ⊤ denotes the transposition of a vector or a matrix. If , we denote the set of random vectors which are -measurable and .
2.2. Model Description
We consider the dynamical system having the state space representation described by the following mean-field linear stochastic differential equations (MF-SLDE):
where are the state parameters of the dynamical system , while is the remote signal which must be estimated. In (2), are the measurements at the instance time , , being the sampling period. In (1) and (2), , , , are stochastic processes which satisfy the following assumption:
Hypothesis 1
(). (i) is a -dimensional standard Wiener process, i.e., , , , for all , being the identity matrix of size ;
- (ii)
- is a -dimensional standard Wiener process with zeros mean and , for all , being a known matrix;
- (iii)
- is a sequence of -dimensional independent random vectors with zero mean and , for all ;
- (iv)
- is a sequence of -dimensional independent random vectors with zero mean and , for all , is a known matrix of appropriate dimension;
- (v)
- , , , are independent stochastic processes.
The differential equations of the form (1a) are known in the literature as mean-field stochastic linear differential equations (MF-SLDE) (see [,,,,,]).
2.3. The Filtering Problem
Our aim is to design a dynamic linear system (named filter) which, fed with the measured values , , generates at its output a signal which must be the best estimate of the output signal of the dynamical system . Since a filter is activated by a discrete-time signal and it must provide at its output a continuous-time signal , we consider that the most appropriate state-space representation of such a filter is of the following form:
where are the state parameters of the filter . In our approach, the dimension of the state space of the filters is not prefixed. In (3), , ,, are arbitrary matrices subject only to the constraint that the corresponding jump linear differential equation (JLDE)
is exponentially stable (ES) (see []).
We denote the set of all filters having the state-space representation of the form (3) with arbitrary dimension , with the property that the corresponding JLDE (4) is ES. The elements of are called admissible filters. In order to measure the quality of the estimation achieved by an admissible filter , we introduce the following performance criterion:
The problem we want to address in this work requires us to find an admissible filter satisfying the following optimality condition:
In Section 4, we shall compute the value of the function (5) achieved by an admissible filter . We shall see that the value of the right-hand side of (5) does not depend on the initial time and nor the initial states of the dynamical system and of the filter. In Section 5, we shall provide a set of conditions which allow us to construct the optimal filter .
Before doing so, we first discuss in Section 3 some aspects related to the mean-square stability of a system obtained when a filter (3) verifying (4) is coupled to an MF-SLDE (1a).
3. Several Preliminary Issues
3.1. Mean-Square Stability of a MF-SLDE
Let be a solution of the MF-SLDE (1). We set
. Bearing in mind the properties of the stochastic integrals of Itô-type, we obtain that is the solution of the following initial value problem (IVP):
In this case, the measured output (2) becomes
where
From (7), it follows that
.
If is a solution of the IVP (8a)–(8b), we set . Employing (11), we obtain that with
By direct calculation based on Itô’s formula, we obtain via (8a)–(8b) and (12) that is the solution of the following IVP on the space :
where is described by
Equipped with the inner product
becomes a Hilbert space. Moreover, is an ordered Hilbert space with respect to the ordering relation ≽ induced by the convex cone . Here, means that is a positive semi-definite matrix.
The adjoint operator with respect to the inner product (15) of defined in (14) is with
Based on the operator , we may consider the following IVP on the Hilbert space :
The IVP (13) is a particular case of (17) when , . According to Theorem 2.6.1 from [], we may infer that the linear differential Equation (17a) defined a positive evolution on the ordered Hilbert space . This means that if is a solution of the IVP (17), then , whenever .
Definition 1.
We say that the zero solution of the MF-SLDE (1a) is
- (i)
- exponentially stable in the mean-square sense (ESMS) if its solutions are satisfying, , where , are constants not depending upon t, , ,
- (ii)
- MF-strong exponentially stable (MF-SES) if the linear differential equation (17a) is exponentially stable, which means that the solutions of the IVP (17) are satisfying, , , being constants not depending upon t, , , .
Here and in the sequel, denotes the euclidian norm of a symmetric matrix.
Proposition 1.
Under the assumption , the zero solution of the MF-SLDE (1a) is ESMS if it is MF-SES.
Proof.
Let us assume that the zero solution of the MF-SLDE (1a) is MF-SES. Bearing in mind that the IVP (13) is a special case of (17), we obtain via (12) that
for all , . Taking into account that , , we obtain from (20) that , . This allows us to conclude that the solution is satisfying (18) because from (7), we have . Thus, the proof is complete. □
The next developments from this paper are performed under the following assumption:
Hypothesis 2
(). The zero solution of the MF-SLDE (1a) is MF-SES.
Following step by step the proof of Proposition 3.2 from [], we obtain a set of conditions equivalent to the assumption .
Proposition 2.
Under the assumption (i), the following are equivalent:
- (i)
- holds;
- (ii)
- the zero solution of the SLDEis ESMS and is a Hurwitz matrix;
- (iii)
- the eigenvalues of the linear operator defined in (14) are located in the half-plane .
3.2. Resulting Jump Linear Stochastic System
Plugging (9) in (3), we obtain the following resulting (closed-loop) jump linear system (JLSS):
where , and
Let and , be arbitrary. Let be the solution of the resulting JLSS (21) corresponding to the initial par . Starting from (21c), we may write successively
for all , where we denote
According to (23), we may rewrite the performance criterion (5) in the following equivalent form:
Employing Itô’s formula on each interval , and , respectively, we obtain the following:
Proposition 3.
Under the assumption , the function defined by (24) is the solution of the following IVP:
where
for all , being the integer with the property that .
Let be the linear subspace of symmetric matrices of sine having the structure
where , are arbitrary symmetric matrices of size and is an arbitrary matrix from , while , are arbitrary matrices from . One checks that is a closed linear subspace. Hence, it is a Hilbert space with respect to the restriction of the inner product (15).
Remark 1.
Based on (10), (11), and (27), one can show that if is the solution of the jump matrix linear differential Equations (26a) and (26b) with the initial condition, lies in for any whenever . Particularly, the solution of the IVP (26) is in for all .
Further, we denote the linear subspace of formed by the matrices
where , , are arbitrary matrices from .
Remark 2.
From (29), one sees that is an isomorphism between the subspaces and .
Let be the linear operator defined by
for all .
Remark 3.
By direct calculation involving (10a), (10b), (29), and (30), we obtain the equality
for all , , being related by via (29).
From (31), we may infer that the spectrum of defined by (30) coincides with the spectrum of the operator introduced in (14).
The next result will play an important role in the computation of the limit from the right-hand side of (25).
Theorem 1.
Under the assumptions , , for each admissible filter , the zero solution of the corresponding jump matrix linear differential equation (JMLDE)
is exponentially stable with respect to the invariant subspace . This means that
for all , , , being constants which are not depending upon t, , and being a norm on .
Proof.
See Appendix A. □
Corollary 1.
Under the assumptions , , for each admissible filter , the eigenvalues of the linear operator are located in the disk .
Proof.
Based on the one-to-one correspondence between the set of the solutions of the JMLDE (32) and the set of the solutions of the discrete-time linear equation on
one shows that under the considered assumptions, the zero solution of (34) is ES, which leads to the desired conclusion. □
4. Computation of the Performance Value Achieved by an Admissible Filter
In this section, we show how one computes the value of the functional (5) which measures the performance achieved by an admissible filter .
Proposition 4.
Under the assumptions , , for each admissible filter , the corresponding non-homogeneous forward jump matrix linear differential equation (FJMLDE)
has a unique bounded solution . This solution has the following properties:
- (i)
- is a continuously differentiable function on each interval , left-continuous in , ;
- (ii)
- , ;
- (iii)
- is a periodic function of period h.
Proof.
Let us consider the linear affine equation on the Hilbert space
where
Bearing in mind that is an eigenvalue of the linear operator if and only if it is an eigenvalue of the linear operator , we obtain via Corollary 1 that, under the considered assumptions, the eigenvalues of the operator are located in the disk . Based on (iii) and (iv) from Theorem 2.6 in [] we may conclude that Equation (36) has a unique solution . Moreover, because from (37), it follows that .
We set
if . From (38), we deduce that . With this equality, (38) becomes
for all , . From (36) and (39), written for k replaced by , we obtain
Hence, the function defined by (38) satisfies (35b). Also, from (38), one sees that is differentiable on each interval and it satisfies (35a).
Since and is a positive operator for all , we may conclude via (38) that , . Finally, (38) allows us to deduce by direct calculations that for all . Thus, we have shown that is a bounded solution of the FJMLDE (35). □
The next result provides a formula for the computation of the value of the performance achieved by an admissible filter.
Theorem 2.
Under the assumptions , , the value of the performance criterion (5) achieved by an admissible filter is given by
being the unique bounded solution of the corresponding non-homogeneous FJMLDE (26a)–(26b).
Proof.
Let be arbitrary but fixed. According to Proposition 4, the corresponding non-homogeneous FJMLDE (26a)–(26b) has a unique solution which is bounded on . Using the equivalent version of (5) given in (25) we obtain that
Since is a solution of (32), we may infer via (33) that , for all . Hence, we obtain
, for all .
Substituting the above equality in (41), we obtain that
Since is a bounded function, we may obtain that
for all . For the last equality from (43) we took into account that is a periodic function of period h. Finally, from (42) and (43), we obtain that (40) holds. Thus, the proof is complete. □
Let , be the partition of the matrix such that and . Employing (22), (27), we obtain the following partition of the FJMLDE (26a)–(26b) written for its bounded on solution:
where
being introduced in (10e).
From (44), it follows that is continuously differentiable and solves the linear ordinary differential equation on the Hilbert space
being the linear operator defined by (30).
Proposition 5.
Under the assumptions , , the ordinary differential Equation (48) has a unique bounded solution . Moreover, is a constant function that solves the algebraic equation
and has the structure
where is the unique solution of the linear algebraic equation
Proof.
First, let us remark that Proposition, 2 together with Remark 3, allows us to deduce that under the assumption , the eigenvalues of the linear operator are located in the semi-plane . Invoking Theorem 2.3.7 (ii)–(iii) from [], we may conclude that under these conditions, the ordinary differential Equation (48) has a unique bounded solution and, additionally, that solution is a constant one. Taking as the partition of the matrix such that , we obtain via (10a), (10b), (10f) that , and is a solution of Equation (51).
From Proposition 2 (ii), we may conclude that (51) has a unique solution; this means that . Hence, the proof is complete. □
5. State Space Representation of the Optimal Filter
5.1. Forward Jump Matrix Linear Differential Equation with Riccati-Type Jumping Operator
We consider the following FJMLDE on the Hilbert space :
where
with , are defined in (10a)–(10b), while , are defined in (47). In (53), is the unique solution of Equation (49). Employing Proposition 5, we obtain that under the assumption , we have
Since the right-hand side of (52b) looks like a Riccati-type operator arising in connection with a discrete-time linear quadratic (LQ) control problem, we shall call Equation (52) an FJMLDE with Riccati-type jumping operator.
Definition 2.
A solution of the FJMLDE (52) is a stabilizing solution if the following hold:
- (a)
- , are invertible matrices;
- (b)
- the zero solution of the closed-loop JLDE onis ES, where
By direct calculation, the FJMLDE (52) written for instead of may be rewritten as
Remark 4.
(a) From (57), we may infer that under the assumptions , , the bounded and stabilizing solution of the FJMLDE (52) satisfies , .
- (b)
- From Proposition 2 (ii), we deduce that under the assumptions , , the eigenvalues of the matrices and are located in the half plane . Hence, is a Hurwitz matrix.
- (c)
- Substracting (52) (written for replaced by ) from (48), we obtain that is a bounded solution of the following FJMLDE:where .Since and is a Hurwitz matrix, we can show that (58) has a unique bounded solution and, additionally, this solution is positive semi-definite. So, under the assumptions , , the bounded and stabilizing solution of the FJMLDE (52), if any, satisfies
- (d)
- Let be the partition of the matrix , such that . Employing (50) and (59), we may conclude that, necessarily, , for all . Hence, under the assumptions , , the bounded and stabilizing solution of the FJMLDE with Riccati-type jumping operator (52), if any, has the structurewhere solves the FJMLDE with Riccati-type jumping operator of dimension n
Adapting Definition 2 to the case of the FJMLDE (61), we say that is a stabilizing solution of the FJMLDE with Riccati-type jumping operator (61) if , are invertible matrices and the zero solution of the closed-loop jump linear differential equation on
is ES, where
The next result establishes a relationship between the stabilizing solution of the FJMLDE with Riccati-type jumping operator (61) and the stabilizing solution of the FJMLDE with Riccati-type jumping operator (52).
Lemma 1.
Assume that the assumptions , hold. Under these conditions, if is the bounded and stabilizing solution of the FJMLDE (61), then constructed as in (60) is the bounded and stabilizing solution of the FJMLDE (52). In this case, (56) becomes
being defined in (63).
Proof.
Employing (10a), (47), one shows that the zero solution of (55) is ES where is computed as in (64). The details are omitted. □
The result stated in the above Lemma leads us to pay special attention to the problem of existence of the bounded and stabilizing solution of the FJMLDE (61) in order to obtain informations about the existence of the bounded and stabilizing solution of the FJMLDE (52).
From (61a), we obtain
Substituting (61b) in (65), we obtain that the sequence of the values of the globally defined solution of the FJMLDE (61) solves the forward discrete-time Riccati equation (FDTRE)
where
Since (66) is a time-invariant discrete-time Riccati equation, its bounded and stabilizing solution, if any, is a constant sequence and satisfies the discrete-time algebraic Riccati equation (DTARE)
We recall that is a stabilizing solution of the DTARE (68) if the eigenvalues of the matrix lie in the disk , where
We set
From (68) and (70) (written for ), one obtains that
for all .
Letting , in (70), we obtain via (71) that
Further, differentiating (70) on the interval , we obtain that
From (72) and (73) one sees that defined in (70) is a solution of the FJMLDE (61). Furthermore, is just the unique bounded and stabilizing solution of (61). Summarizing the previous developments, we can state the following:
Proposition 6.
Under the assumptions , , if the DTARE (68) has a stabilizing solution which satisfies the condition , then the FJMLDE (61) has a bounded and stabilizing solution which is a periodic function of period h and satisfies the condition , .
Remark 5.
From (63) and (71), we may infer that the stabilizing gain (63) does not depend upon k and it can be computed as
being the unique stabilizing solution of the DTARE (68). In this case, (64) becomes
5.2. Optimal Filter
Theorem 3.
Assume the following:
- (a)
- the assumptions , hold;
- (b)
- the DTARE (68) has a stabilizing solution which satisfies the condition
Let be associated to the stabilizing solution via (74) and be defined as in (75). We consider the filter with being the dimension of its state-space and with a state-space representation described as follows:
where . Under the considered assumptions, the filter lies in and minimizes the cost (5), of which the minimal value is given by
where is defined in (70).
Proof.
See Appendix B. □
6. Numerical Experiments
From Theorem 3, it appears that in order to construct the optimal -filter, one has to compute the stabilizing solution of the DTARE (68) which verifies the sign condition (76). The coefficients of DTARE (68) depend on the unique solution of the non-homogeneous Lyapunov-type algebraic Equation (51). Hence, in order to synthesize the optimal filter, one has first to solve Equations (51) and (68), respectively. In order to solve (51), we use the same method as the one described in []. Equation (68) being a standard DTARE, we use existing numerical solvers in MATLAB 2020b ©. More specifically, we use the function idare.
For the numerical application, we generate the following system matrices:
For the above parameters, the assumption is satisfied. The unique solution of the Lyapunov-type algebraic Equation (51) as well as the unique stabilizing solution of the DTARE (68) are given by
respectively. The associated optimal filter gain is given by
Figure 1 shows the evolution of the estimation error for one realization of the stochastic processes.
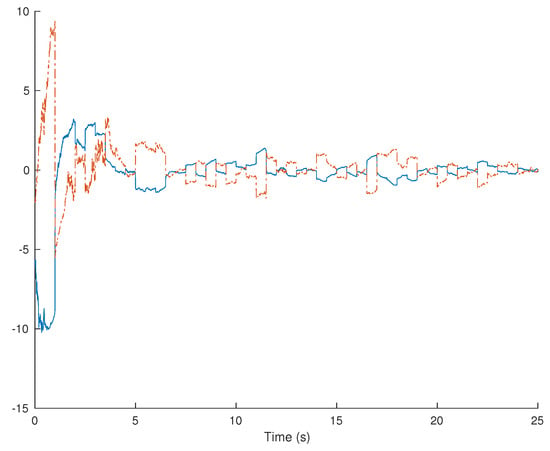
Figure 1.
Estimation error: .
We have also performed Monte-Carlo simulations (corresponding to different realizations of the stochastic processes). We have considered 1000 realizations. The corresponding results are summarized in Figure 2.
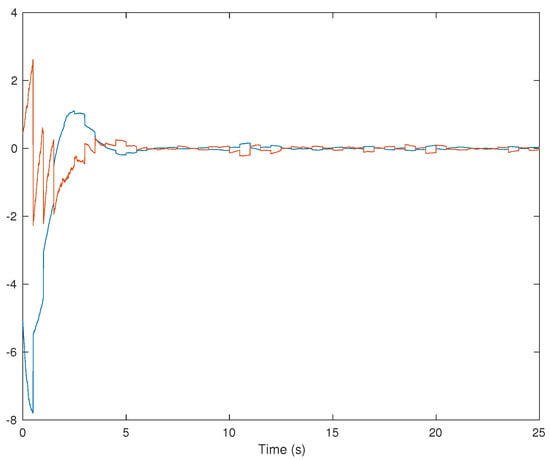
Figure 2.
Monte-Carlo simulation.
7. Conclusions
In this work, we dealt with the problem of the optimal estimation of a remote signal generated by a dynamical system modeled by a McKean–Vlasov type system of linear stochastic differential equations subject to additive white noise perturbations. We assumed that only measurements (of another signal generated by the dynamical system under consideration) at some discrete-time instances are available in order to activate the dynamical filter which has to provide the best estimation of the remote signal.
Since in the considered filtering/estimation problem, an admissible filter is fed to its input by a discrete-time signal and has to provide to its output a continuous-time signal, we assumed that the more appropriate class of admissible filters are those having the state-space representation in the form of a jump linear system, as in (3).
In our approach, the dimension of the state-space of an admissible filter (often named the order of the filter) is not prefixed. In Theorem 3, we have shown that among all admissible filters of arbitrary order , the best estimation of the remote signal generated by the given dynamical system is achieved by a filter having the order equal to twice the dimension of the state-space of the dynamical system under consideration. We have provided explicit formulae of the optimal filter. To this end, we have used the stabilizing solution of an adequately defined forward jump matrix linear differential equation (FJMLDE) with a Riccati-type jumping operator. We have shown how we can reduce the computation of such a solution to the computation of the stabilizing solution of a discrete-time algebraic Riccati equation (DTARE) for which there exist efficient numerical procedures. It is worth mentioning that the state-space representation of the optimal filter is computed offline, which facilitates its implementation. It remains a challenge for future research directions to compare the performances of the optimal filter of the form (77) with the performances of a filter whose gain matrices are computed online. Another research direction would be to consider the case when the time between two consecutive measurement samples is not constant but modeled by a stochastic process.
Author Contributions
Conceptualization, V.D.; methodology, V.D.; software, S.A.; validation, V.D. and S.A.; writing—original draft preparation, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proof of Theorem 1
Let be the solution of the JMLDE (32) corresponding to the initial pair . According to Remark 1, we know that for all . Based on (28), we have the partition
where , and . Employing (22), (27), (30), we obtain the following partition of the JMLDE (32):
where is the integer with the property that .
From (A1), we deduce that is a solution of the linear ordinary differential equation
Bearing in mind , Proposition 2 (iii), and Remark 3 we may infer that
for all , where , do not depend upon t, , . From (10a), we obtain via Proposition 2 (ii) that is a Hurwitz matrix if the assumption holds. Hence, the eigenvalues of the matrix are located in the disk . On the other hand, the exponential stability of the zero solution of the JLDE (4) is equivalent to the fact that the eigenvalues of the matrix are also in the disk . So, the eigenvalues of the operator are in the disk . From (A2), we deduce that the sequence solves the following discrete-time linear equation:
where . By considering (A4), we may infer that , , , . This allows us to deduce via (A2b) that
for all . Since , , , we may conclude via (A5) that
where , do not depend upon t, , , . Further, from (A3), we deduce that solves the following DTLE on the space :
with
Invoking again (A4) together with (A6), we obtain
Hence,
for all , with , do not depend upon , , , . Since if , , we may conclude via (A7) that
where , do not depend upon t, , , , . Taking into account that , we may conclude via (A4), (A6), and (A8) that (33) holds. Hence, the proof is completed.
Appendix B. Proof of Theorem 3
The fact that the filter lies in is obvious because in this case, the corresponding JLDE (4) coincides with (55) and it is ES. Further, we show that the filter (77) achieves the minimal value of the cost (4).
First, let us remark that under the assumption (b) from the statement, we obtain via Proposition 6 that the FJMLDE with Riccati-type jumping operator (61) has a bounded and stabilizing solution . Further, Lemma 1 guarantees the existence of the bounded and stabilizing solution of the FJMLDE (52). The corresponding stabilizing matrix gain is given by (75).
Let be an arbitrary but fixed admissible filter. The value of the performance (5) achieved by the filter is given by (40). Let be the partition of the unique bounded solution , of the corresponding non-homogeneous FJMLDE of type (26a)–(26b) with , .
We define , . By direct calculations, involving (44)–(46), (52) and taking into account (50), (53), (54), we obtain that is a bounded solution of the following non-homogeneous FJMLDE:
where
From (75) and (A10), we deduce via (28) that . Hence, is an invariant subspace of the FJMLDE (A9). Invoking Theorem 1, we may infer that under the assumptions , , the zero solution of the corresponding JMLDE of the form (32) is ES with respect to the invariant subspace . Employing Proposition 3 and Theorem 3 from [], we deduce that there exists a function satisfying
and being the adjoint operators of the linear operators defined via (27). Bearing in mind the formulae of the adjoint operators of type (27), we obtain from (A11) that also solves
where , and for all . Based on Proposition 4.2 from [], we may conclude that the zero solution of the following JLDE on the space
is ES. Applying Proposition 3.2 from [], we may conclude that the exponential stability of the zero solution of (A13) guarantees that the non-homogeneous FJMLDE (A9)–(A10) has a unique bounded solution and, additionally, this solution satisfies
Further, we rewrite (40) in the form
According to (A14) we may infer that
for any admissible filter . Now, we show that in the special case of the filter described by (77), the inequality (A16) becomes equality. Let us remark that in the special case of the filter , we have
where is the 11-block of
By direct calculation, involving (22), (52), (77), (A9), (A14), we obtain that is a bounded solution of the following non-homogeneous FJMLDE:
where is the stabilizing gain matrix defined by (75). Invoking again Proposition 3.2 from [], we deduce that the FJMLDE (A18) has a unique bounded on solution. So, , . Substituting this in (A17), we obtain that in the special case of the filter described by (77), we have . Hence, in the case of the filter described by (77), the equality (A15) becomes
From (A16) and (A19), we deduce that
This shows that the filter achieves the minimal value of the cost function (5), which means that its output provides the best estimation of the signal . Finally, employing (60), we deduce that (A19) coincides with (78). Thus, the proof ends.
References
- Kalman, R. A new approach to linear filtering and prediction problems. ASME Trans. Part D J. Basic Eng. 1960, 82, 34–45. [Google Scholar] [CrossRef]
- Kalman, R.; Bucy, R.S. New results in linear filtering and prediction theory. ASME Trans. Part D J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Kac, M. Foundations of kinetic theory. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1956; Volume III, pp. 171–197. [Google Scholar]
- McKean, H.P. Propagation of chaos for a class of non-linear parabolic equations. Lect. Ser. Differ. Equ. 1967, 7, 41–57. [Google Scholar]
- Ahmed, N.U.; Ding, X. Controlled McKean–Vlasov equations. Commun. Appl. Anal. 2001, 5, 183–206. [Google Scholar]
- Ahmed, N.U. Nonlinear diffusion governed by McKean–Vlasov equation on Hilbert space and optimal control. SIAM J. Control Optim. 2007, 46, 356–378. [Google Scholar] [CrossRef]
- Andersson, D.; Djehiche, B. A maximum principle for SDEs of mean-field type. Appl. Math. Optim. 2011, 63, 341–356. [Google Scholar] [CrossRef]
- Buckdahn, R.; Djehiche, B.; Li, J. A general maximum principle for SDEs of mean-field type. Appl. Math. Optim. 2011, 64, 197–216. [Google Scholar] [CrossRef]
- Meyer-Brandis, T.; Oksendal, B.; Zhou, X.Y. A mean-field stochastic maximum principle via Malliavin calculus. Stochastics 2012, 84, 643–666. [Google Scholar] [CrossRef]
- Park, J.Y.; Balasubramaniam, P.; Kang, Y.H. Controllability of McKean–Vlasov stochastic integrodifferential evolution equation in Hilbert spaces. Numer. Funct. Anal. Optim. 2008, 29, 1328–1346. [Google Scholar] [CrossRef]
- Moon, J. Linear-quadratic mean field stochastic zero-sum differential games. Automatica 2020, 120, 109067. [Google Scholar] [CrossRef]
- Huang, J.; Li, X.; Yong, J. A linear-quadratic optimal control problem for mean-field stochastic differential equations in infinite horizon. Math. Control Relat. Fields 2015, 5, 97–139. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Wu, Z. Mean-Field Stochastic Linear-Quadratic Optimal Control Problems: Open-Loop Solvabilities. ESAIM Control Optim. Calc. Var. 2017, 23, 1099–1127. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Wu, Z. Mean-Field Linear-Quadratic Stochastic Differential Games. J. Differ. Equ. 2021, 120, 109067. [Google Scholar] [CrossRef]
- Tian, R.; Yu, Z.; Zhang, R. A closed-loop saddle point for zero-sum linear-quadratic stochastic differential games with mean-field type. Syst. Control Lett. 2020, 136, 104624. [Google Scholar] [CrossRef]
- Yong, J. Linear-Quadratic Optimal Control Problems for Mean-Field Stochastic Differential Equations. SIAM J. Control Optim. 2013, 51, 2809–2838. [Google Scholar] [CrossRef]
- Dragan, V.; Aberkane, S. Optimal Estimation of a Signal Generated Using a Dynamical System Modeled with McKean–Vlasov Stochastic Differential Equations. Entropy 2024, 26, 483. [Google Scholar] [CrossRef]
- Briat, C. Stability analysis and stabilization of stochastic linear impulsive, switched and sampled-data systems under dwell-time constraints. Automatica 2016, 74, 279–287. [Google Scholar] [CrossRef]
- Dragan, V.; Aberkane, S.; Popa, I.L. Optimal H2 filtering for periodic linear stochastic systems with multiplicative white noise perturbations and sampled measurements. J. Frankl. Inst. 2015, 352, 5985–6010. [Google Scholar] [CrossRef]
- Gabriel, G.W.; Geromel, J.C. Performance evaluation of sampled-data control of Markov jump linear systems. Automatica 2017, 84, 212–215. [Google Scholar] [CrossRef]
- Gabriel, G.W.; Conçalves, T.R.; Geromel, J.C. Optimal and Robust Sampled-Data Control of Markov Jump Linear Systems: A Differential LMI Approach. IEEE Trans. Autom. Control 2018, 63, 3054–3060. [Google Scholar] [CrossRef]
- Geromel, J.C.; Gabriel, G.W. Optimal H2 state feedback sampled-data control design of Markov Jump Linear Systems. Automatica 2015, 54, 182–188. [Google Scholar] [CrossRef]
- Geromel, J.C. Differential Linear Matrix Inequalities. In Sampled-Data Systems Filtering and Control; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Oksendal, B.K. Stochastic Differential Equations: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Friedman, A. Stochastic Differential Equations and Applications; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Ichikawa, A.; Katayama, H. Linear Time-Varying Systems and Sampled-data Systems. In Lecture Notes in Control and Information Sciences; Springer: London, UK, 2001. [Google Scholar]
- Dragan, V.; Morozan, T.; Stoica, A.M. Mathematical Methods in Robust Control of Linear Stochastic Systems, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Dragan, V.; Morozan, T.; Stoica, A.M. Mathematical Methods in Robust Control of Discrete-Time Linear Stochastic Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Dragan, V.; Aberkane, S. H2 optimal filtering for continuous-time periodic linear stochastic systems with state-dependent noise. Syst. Control Lett. 2014, 66, 35–42. [Google Scholar] [CrossRef]
- Dragan, V.; Aberkane, S.; Popa, I.L.; Morozan, T. On the stability and mean square stabilization of a class of a linear stochastic systems controlled by impulses. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2023, 15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).