Abstract
Blockchain technology, serving as the backbone for decentralized systems, facilitates secure and transparent transactional data storage across a distributed network of nodes. Blockchain platforms rely on distributed ledgers to enable secure peer-to-peer transactions without central oversight. As these systems grow in complexity, analyzing their topological structure and vulnerabilities requires robust mathematical frameworks. This paper explores applications of graph theory for modeling blockchain networks to evaluate decentralization, security, privacy, scalability and NFT Mapping. We use graph metrics like degree distribution and betweenness centrality to quantify node connectivity, identify network bottlenecks, trace asset flows and detect communities. Attack vectors are assessed by simulating adversarial scenarios within graph models of blockchain systems. Overall, translating blockchain ecosystems into graph representations allows comprehensive analytical insights to guide the development of efficient, resilient decentralized infrastructures.
MSC:
05C68; 68R10; 68U01
1. Introduction
Blockchain technology has emerged as a disruptive innovation for decentralized record-keeping and transaction processing in digital networks. Some key features offered by public blockchain networks include distributed consensus, persistency of recorded data, anonymity of users, and tolerance to malicious attacks [1]. These properties distinguish blockchains from traditional centralized databases and financial systems. However, as blockchain platforms scale up with wider adoption, analysis of their underlying complex network architecture becomes crucial. Issues like network congestion, privacy leaks, malicious attacks, and centralization trends need to be monitored and addressed [2]. This requires studying topological structures and interactions between network components. Graph theory provides an appropriate mathematical framework to model and analyze the connectivity and relationships within complex systems including communication, social, biological, and infrastructure networks [3,4].
Graph theory facilitates a profound understanding of a network’s foundational properties, which cannot be achieved without referring to network science. Network science plays a pivotal role in understanding the dynamic and structural properties of networks and provides valuable insights into the applications of blockchain.
This work focuses on establishing mathematical theorems that enable a more granular theoretical representation of blockchain networks. It demonstrates the applications of graph theory and network analysis techniques to evaluate the critical facets of blockchain platforms, including decentralization trends, security threats, scalability issues, simulation modeling and asset mapping. Rigorous mathematical analysis provides data-driven insights to guide the development of efficient, resilient decentralized digital ledgers and techniques to analyze blockchain systems and address challenges in their design and operation. An extensive application of network science is beyond the scope of this work.
Table 1 presents a holistic summary of graph theory’s contribution and proofs that can provide insight and improvement to blockchain technology.

Table 1.
Holistic summary of the contribution.
Graph theory has been widely recognized for its diverse applications across various fields. Gangrade et al. [5] discuss the applications of graph coloring in different practical scenarios, highlighting the versatility of graph theory. Similarly, Majeed and Rauf [6] emphasize the extensive use of graphs in computer science and social networks, showcasing the relevance of graph theory in modern technological domains. Raza et al. [7] delve into the significance of domination in graph theory and its wide applicability in different fields. Moreover, Ahmad et al. [8] showcase the interdisciplinary nature of algebraic graph theory, indicating its potential for future applications. Holmes et al. [9] explore the application of graph theory in plasma chemical reaction engineering, demonstrating how graph visualization and algorithms can aid in analyzing reaction networks. El-Mesady and Bazighifan [10] discuss the applications of mutually orthogonal graph squares in various communication and design domains, showcasing the practical implications of graph theory concepts.
Graph theory was also explored to solve many real-world problems with multi-dynamic and rapidly evolving characteristics. It provides an apt abstraction for modeling the topological structure and interactions within blockchain networks. Some of the recent applications demonstrated by researchers include advanced treatment for epilepsy based on Epileptogenic Zone localization [11], network vulnerability analysis by finding the secure dominating set [12], Alzheimer’s Disease investigation [13], and techniques to place PMU in an electrical power network [14]. But the list is not comprehensive, Table 2’s references collectively highlight the broad spectrum of applications of graph theory in a wide range of the computer science field.

Table 2.
Graph theory application in Computer Science (CS) and Information Technology (IT).
Graph theory has been applied in various ways in the field of blockchain. Qu et al. [35] use hypergraphs to create a blockchain model that reduces storage consumption and enhances security. Tsoulias et al. [36] incorporate graph models in blockchain functionality, allowing for data analysis and visualization of changes in blockchain data. Abay et al. [37] find that topological features computed from the blockchain graph using persistent homology are useful in predicting Bitcoin price dynamics. Shen et al. [38] use graph neural networks for DApp fingerprinting, where a graph structure called Traffic Interaction Graph (TIG) is used to represent encrypted DApp flows, leading to accurate classification. Liu et al. [39] use big graph analytics and learning techniques to infer the identity of nodes in blockchain transaction graphs.
The past literature conveys how graph theory applications highlight the fundamental role of graphs in modeling real-world problems and optimizing various systems across different disciplines. The interdisciplinary nature of graph theory allows for innovative solutions and insights into complex problems, making it a valuable tool in modern research and practical applications. Most of the existing work has used graph theory in specific applications, and complete graph theory applications for blockchain are under-explored. Blockchain, being relatively recent in its evolution, has a wide scope for cross-domain and interdisciplinary adoption. This work serves as a quick exploration of employing graph theory to real-world problems and data focused on blockchain, providing theoretical grounds and direction for future research.
2. Background
In graph theory, networks are represented as graphs with vertices (nodes) connected by edges (links) [40]. When the incidence relation is not necessarily symmetrical, we have arcs and keep the edge for symmetrical relations. An edge connecting a vertex to itself is called a loop. Except specified otherwise, we consider loopless graphs with at most one edge/arc between two vertices. Vertices may represent individual actors while edges capture relationships between them [3]. Network analysis using graph models helps discover crucial properties like connectivity trends, influential nodes, community structures and vulnerability to attacks. Blockchain platforms can be naturally modeled as transaction graphs, with vertices as users or system components like miners and smart contracts, while transaction links or messaging channels may be shown as graph edges [4]. Such network graphs keep evolving dynamically as new blocks are added to the chain. The graph mappings uncover hidden patterns, clusters, bottlenecks and weaknesses that are not evident otherwise. These findings have implications for improving system efficiency, security and privacy. Next, we briefly introduce blockchain technology and overview some applications of graph theory for general network analysis.
3. Blockchain Technology Overview
A blockchain is essentially an expanding record of data stored in containers called blocks, with cryptographic validation to ensure tamper-resistance and transparency [1,41]. Each block contains a timestamp and a link to the previous block, thus chaining them together in proper sequence from the genesis block. Transactions are recorded in blocks after validation by miners over P2P overlay networks based on consensus protocols like proof-of-work and proof-of-stake. All participating nodes maintain the latest replicated copies of the distributed ledger. Key advantages of blockchain infrastructure include persistence [42], provenance tracking of assets [43], and disintermediation from centralized control [44]. Blockchains also enable smart contracts which are automated executable programs stored on-chain.
4. Relevant Concepts from Graph Theory
We briefly recap some common graph metrics and analytical methods that would be relevant for blockchain networks [3]:
- 1.
- Degree centrality identifies highly connected nodes that interact with many others in the network [45].
- 2.
- Betweenness centrality identifies nodes that bridge different communities, enabling the flow of information [46].
- 3.
- Closeness centrality measures how fast information from one vertex can reach others via minimum links [47,48].
- 4.
- Clustering analyzes whether a network partitions into densely interconnected communities with sparse connections among them [49,50].
- 5.
- Bridges, cut vertices, and articulation points are crucial connectors whose removal can fragment graphs [51,52].
- 6.
- Shortest paths, network diameter, and average path lengths indicate how easily nodes can reach each other [53,54].
- 7.
- Resilience evaluates a network’s vulnerability to random failures or targeted attacks on nodes or edges [55].
These graph properties are mirrored in blockchain platforms through influential miners, network partitions caused by regional regulations, bottleneck links that affect transaction speeds, and systemic risks from the failure of critical mining pools. Applying graph theory can, therefore, offer actionable insights to enhance the system’s design, efficiency, and security [36].
5. Graph Theory Application in Blockchain Systems
In this section, we review some specific applications of graph theory for blockchain network analysis along five major dimensions—decentralization, security and privacy, scalability, simulations and manipulation [56].
Analyzing decentralization, metrics derived from the connectivity patterns and community structure within blockchain graphs determine whether decision-making power and asset ownership concentrate among a few dominant players. Skewed degree distributions or highly interconnected hubs highlight centralization risks [57].
Evaluating security: simulating attack mechanisms like Sybils and Denial-of-Service within graph models of blockchain systems allows evaluating consensus resilience even before deployment. Graph metrics also uncover network vulnerabilities [58].
Preserving privacy: Advanced graph analysis can compromise anonymity by uncovering patterns in transaction histories to uniquely identify entities within the network. Clustering and classification techniques quantify re-identification risks [59].
Managing scalability: Graph algorithms localized performance bottlenecks, enabling targeted optimizations to improve transaction throughput like sharding and structured peer networking. Comparisons between baseline and stressed system graphs determine breaking points [60].
NFT manipulation mapping: Utilizing graph theory to analyze the patterns and transactions of NFTs on blockchain networks sheds light on wash trading activities, where individuals artificially inflate the value of NFTs through self-directed trades [61]. By examining the graph’s edges and nodes representing transactions and participants, respectively, we can identify cyclical trading patterns that indicate possible manipulation [62]. This analysis not only enhances the transparency and integrity of the NFT market but also assists in the development of regulatory and monitoring tools to combat fraudulent activities [63].
The subsequent sections elaborate on these applications, and provide mathematical proofs and network simulations to demonstrate the problem-solving efficacy of graph theoretic approaches within the blockchain domain.
5.1. Analyzing Network Decentralization
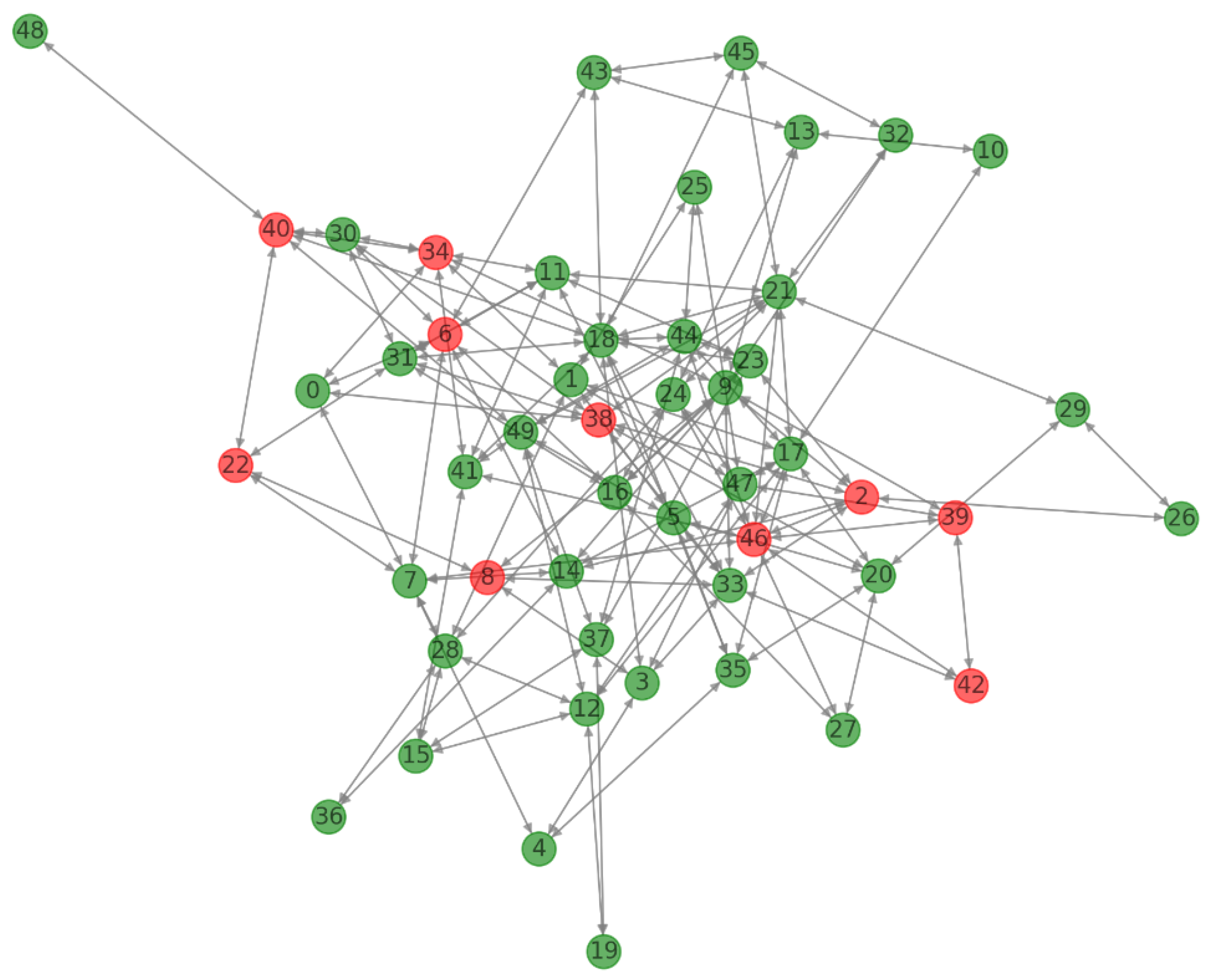
An oft-cited benefit of public blockchains is the decentralization of control from single authorities in favor of distributed governance [64]. However, recent studies indicate growing oligopolies in mining pools and increasing centralization risks from protocols favoring stronger validators [65]. Graph analysis provides effective techniques to track such trends over time. The nodes and edges would correspond to actual network participants and their interactions, which could be analyzed for decentralization aspects such as centralization risks, power distribution, or collaboration dynamics.
5.1.1. Mining Pool Power
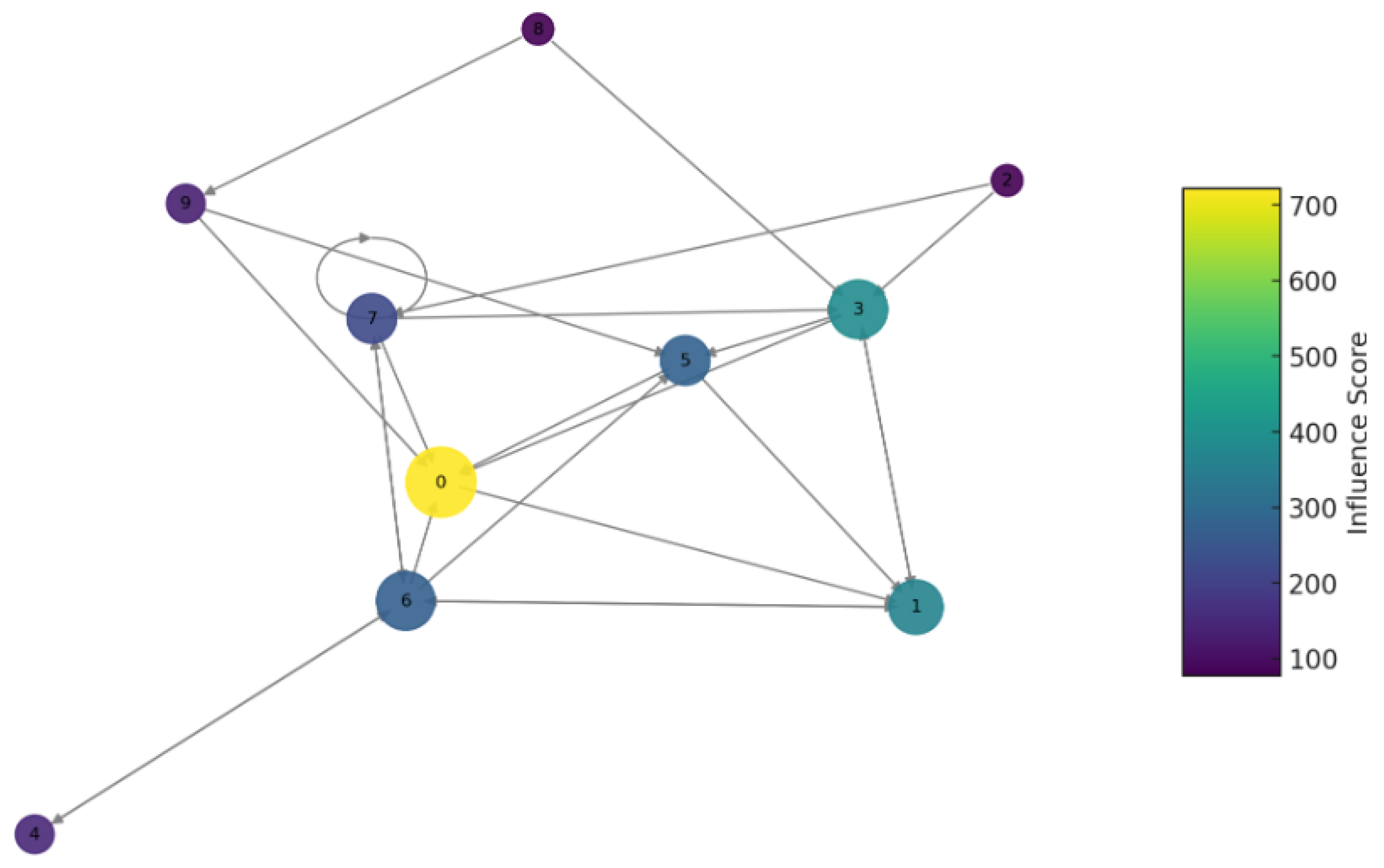
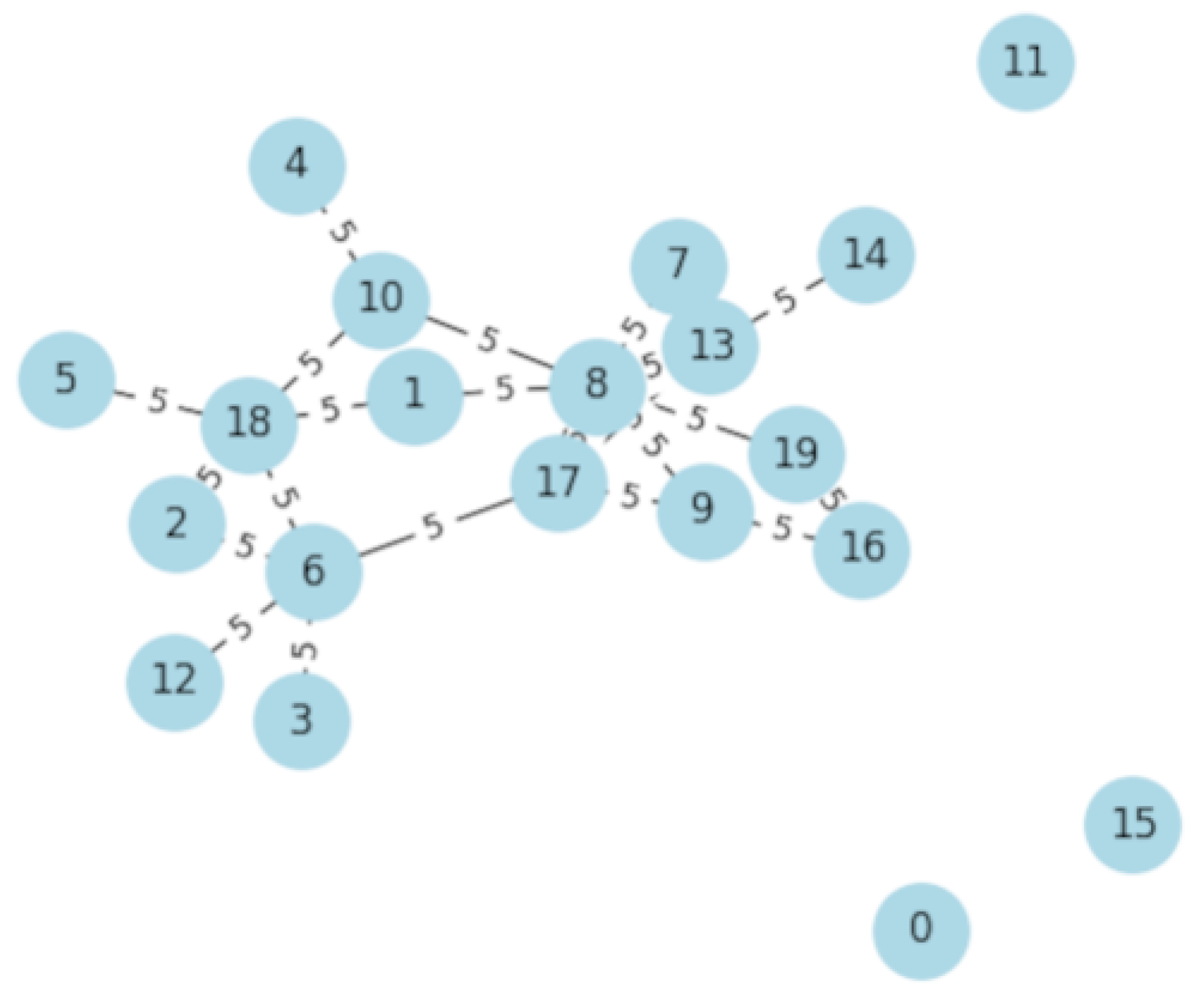
The mining landscape can be modeled as a dynamic graph with dominant pools occupying highly connected hub nodes as shown in Figure 1. Monitoring degree distribution skewness, betweenness centrality and the emergence of a few super-connected hubs can quantitatively track centralization among miners [66].

Figure 1.
Mining Pool Power.
Assumption 1.
- Graph Model: The blockchain network is modeled as a dynamic graph , where V represents the set of mining pools, and E represents the connections between them.
- Degree of a Node: The degree of a node in G represents the number of connections a mining pool has with other pools.
- Wealth and Power Correlation: The mining power of a pool is directly proportional to its degree in the graph.
- Network Growth: New nodes (mining pools) prefer to connect to existing nodes with higher degrees (a preferential attachment model, akin to the Barabási–Albert model).
Application Statement 1.
- In a blockchain network modeled as a graph following the above assumptions, the network naturally evolves towards a state of increased centralization of mining power.
Proof.
- (a)
- Initial State Analysis:Let be the initial state of the graph, where is relatively large and the degree distribution is uniform or near-uniform.
- (b)
- Preferential Attachment:Define the attachment probability for a new node connecting to an existing node v.New nodes prefer to attach to existing nodes v with higher . each new node is connected to k other ones, each one of those connections is chosen according to the probabilities
- (c)
- Degree Distribution Evolution:Over time, the degree distribution for becomes skewed, favoring nodes with initially higher degrees.The skewness can be represented by the increase in variance over time: for . The variance could increase but still tend to a limit. It seems like the usual argument for the skewness of such a network is that the degree distribution follows a power law. It is indeed the case in the Barabási–Albert model
- (d)
- Correlation of Degree and Mining Power:Let mining power of a node v be proportional to its degree: .Thus, is also increasingly skewed as becomes skewed.
- (e)
- Centralization:Centralization can be quantified by a metric , where increases as the skewness in increases.Formally, for , indicating increased centralization over time.
- (f)
- Implications for Network Security and Decentralization:Security risk and decentralization level can be formally defined.Increased implies increased and decreased .
□
Figure 1 graph is semi-randomly generated to illustrate the concept. In a real-world scenario, the nodes and edges would correspond to actual network participants and their interactions, which could be analyzed for decentralization aspects such as centralization risks, power distribution, or collaboration dynamics. Nodes represent entities within the network like mining pools, stakeholders, and developers. Edges signify the relationships or interactions between these entities. Node Color indicates the mining power of each node, which, for simplicity is assumed to be directly proportional to its degree. The color scale, from light to dark, illustrates the range of mining power across the network, with darker nodes possessing higher mining power. Node Size, corresponds to the degree of each node, with larger nodes having more connections. The size variation visually emphasizes the nodes that are more central to the network’s structure, highlighting the preferential attachment growth model’s impact.
The visualization of Figure 1 offers a nuanced view of the network, underlining the relationship between a node’s degree (and thereby its mining power) and its centrality within the network. Such a representation aids in understanding the centralization of mining power within blockchain networks, providing insights into how certain nodes (or mining pools) can dominate based on their connectivity and influence.
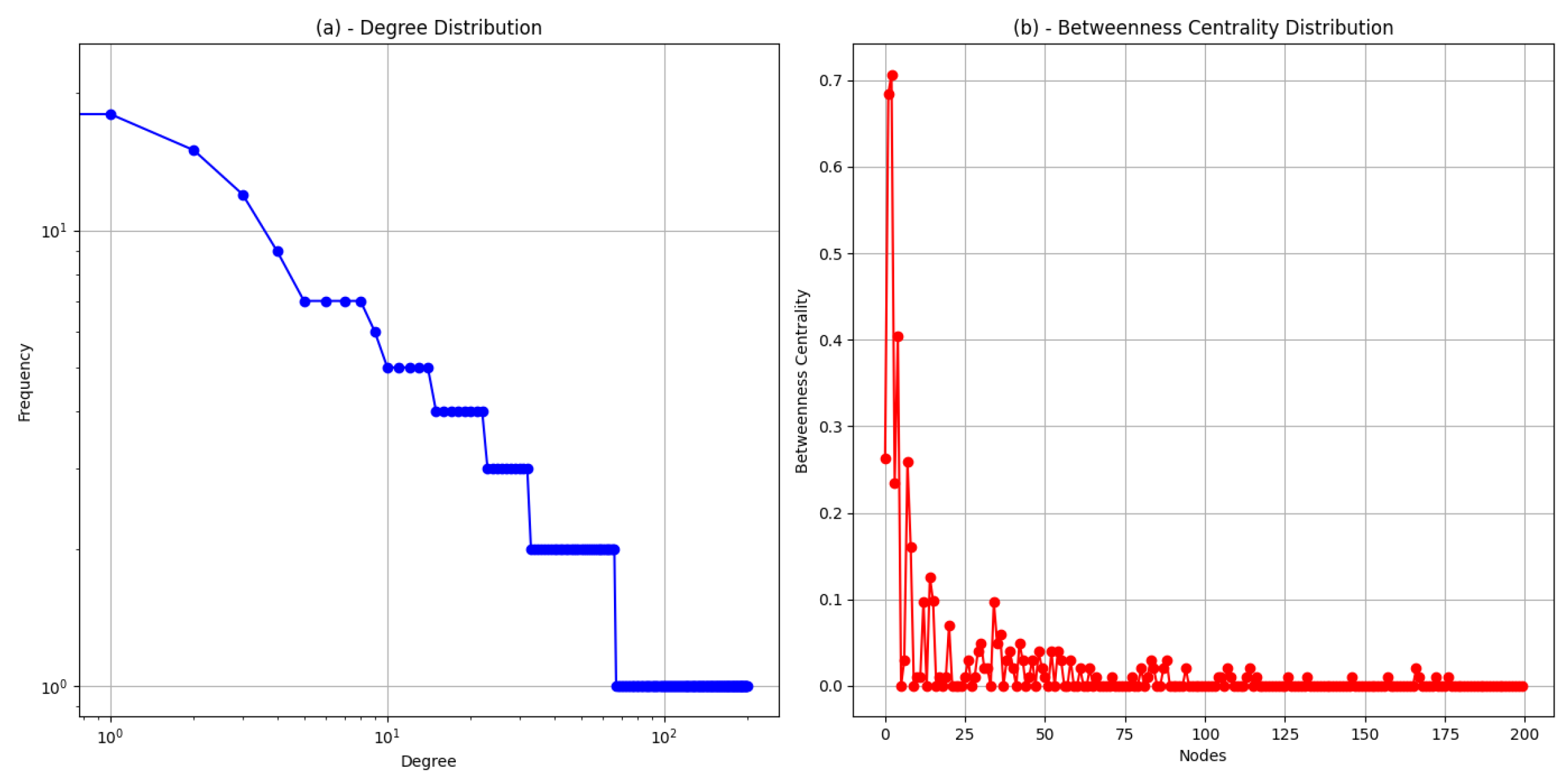
Figure 2 visualizations illustrate the theoretical evolution of a blockchain network towards centralization, based on the assumptions and theorem statement provided. Degree Distribution Figure 2a: The degree distribution follows a power law, characteristic of networks that evolve according to preferential attachment. This indicates that a few nodes (mining pools) become highly connected over time, representing the centralization of mining power. The log-log plot shows that a few nodes have a high degree while the majority have a low degree, which aligns with the concept of centralization as fewer entities control a larger portion of the network’s power. Betweenness Centrality Distribution Figure 2b: The betweenness centrality values across nodes show variation, indicating that some nodes play a more critical role in the network as intermediaries in transactions or information flow. Nodes with higher betweenness centrality are pivotal in connecting various parts of the network, further highlighting the potential central points of control or influence within the network.
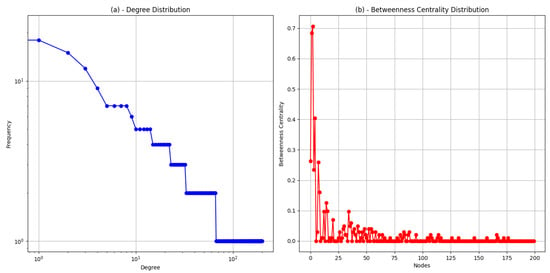
Figure 2.
Distribution and Betweenness.
This proof outlines the theoretical evolution of a blockchain network’s mining power distribution towards centralization under specific graph-theoretic and network growth assumptions. It demonstrates how the dynamics of network growth and connectivity can influence the distribution of mining power in blockchain networks.
5.1.2. Stake Pool Power
For proof-of-stake consensus, the graph analysis of delegate nodes and their stake ratios determine the relative influences of validator pools and the likelihood of collusion. Figure 3 graph illustrates the concept of staking delegations in a proof-of-stake blockchain network [67]. In an actual blockchain network, these edges would represent real staking delegations from one pool to another, and their analysis could reveal patterns of stake distribution, possible centralization of power, and the overall structure of the stake delegation network. Nodes represent stake pools. Directed edges (arrows) represent staking delegations between pools.
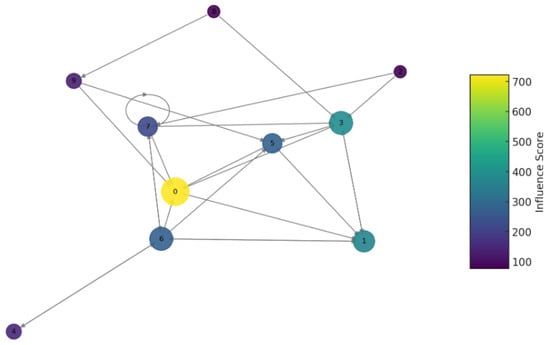
Figure 3.
Stake Pool.
Assumption 2.
- Graph Model: The blockchain network is modeled as a (weighted) directed graph , where each node represents a stake pool and each arc represents staking delegation from pool u to pool v.
- Stake Representation: The weight of each node corresponds to the total stake delegated to the pool v.
- Influence by Stake: The influence or power of a stake pool is directly proportional to its total stake.
- Network Dynamics: New stakeholders tend to delegate their stake to pools with higher existing stakes, modeling a preferential attachment similar to the Barabási–Albert model.
Application Statement 2.
- In a blockchain network modeled as a directed graph following the above assumptions, the network evolves towards a state where a small number of stake pools accumulate a disproportionately large amount of total stake, indicating a trend towards centralization of stake power.
Proof.
- (a)
- Initial State Analysis:Let represent the initial state of the graph, with denoting the stake for each pool , where is relatively uniform across .
- (b)
- Preferential Attachment Dynamics:Define , the probability of a new stakeholder delegating their stake to pool v. New stakeholders are more likely to delegate to pools with higher , following preferential attachment.
- (c)
- Evolution of Stake Distribution:As time progresses, this dynamic leads to an evolved graph at time t, where the distribution of for becomes increasingly skewed. This skewness is represented by an increasing variance: for .
- (d)
- Centralization of Stake Power:Quantify centralization at time t with , which increases with the skewness of . Formally, for , indicating a trend towards increased centralization of stake power.
□
In Figure 3, the Node Color represents the influence score of each stake pool, with the color scale indicating the level of influence based on both the stake and the pool’s position within the network’s structure. Lighter colors denote higher influence scores. Node Size, corresponds to the total stake of each pool, allowing for a direct visual comparison between a pool’s stake and its overall influence within the network. Color Bar (Influence Score), aids in interpreting the influence scores, with the gradient showing the range of influence scores across the network from low to high.
This proof demonstrates that under the given assumptions and network dynamics, a blockchain network’s stake distribution evolves towards increased centralization, with a few stake pools gaining a majority of the total stake. This centralization of stake power can have implications on the network’s security and governance, potentially contradicting the decentralized ethos of blockchain technology.
5.1.3. Wealth Concentration
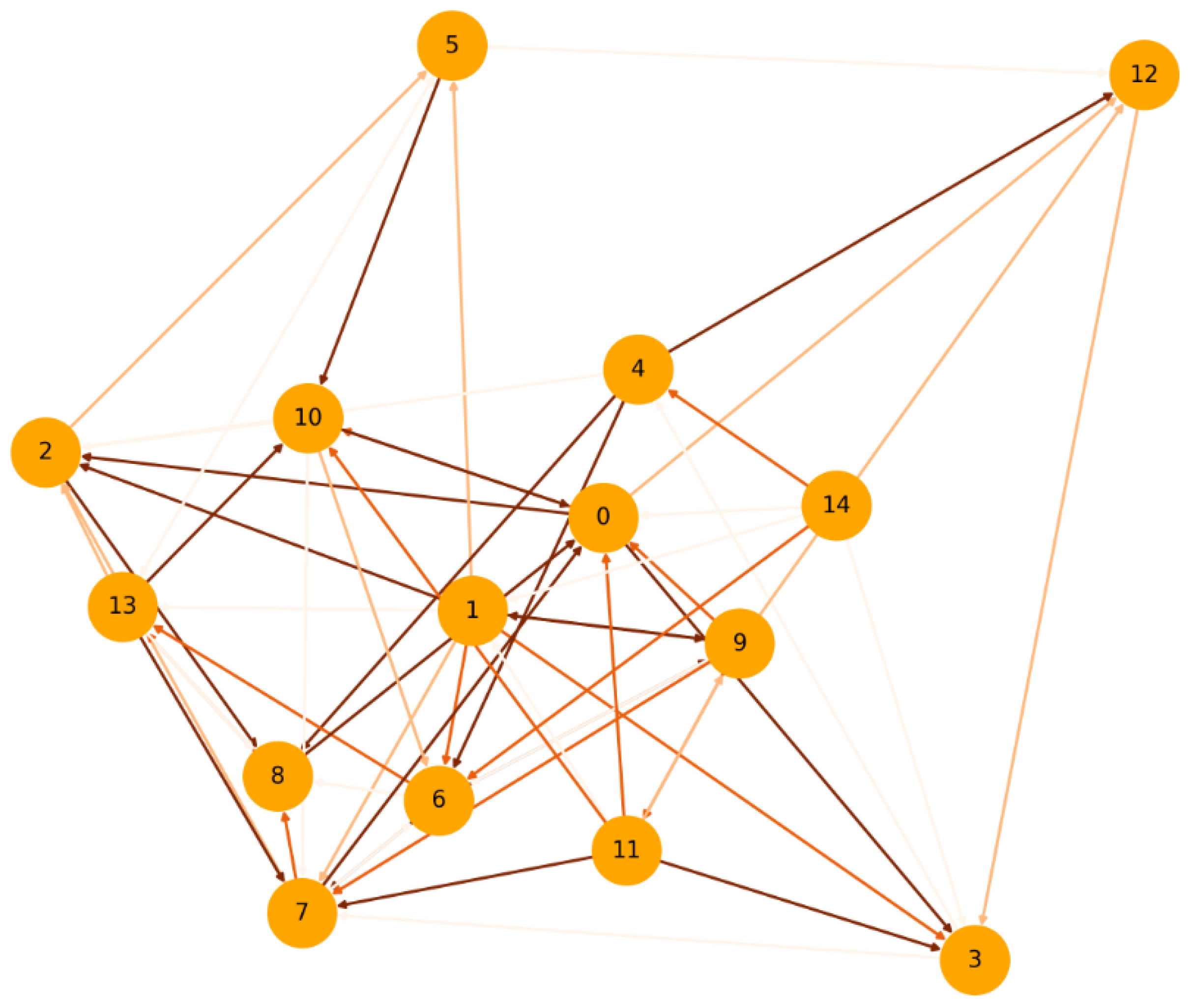
The degree and strength distribution of transaction graphs can identify the concentration of token ownership and flow among addresses over time [68]. Figure 4 is a representation of the Wealth concentration constructed from actual transaction data and the analysis would focus on identifying nodes (addresses) with a high number and value of incoming and outgoing transactions, indicating the concentration of wealth. Nodes represent individual addresses or wallets in a blockchain network. Directed edges (arrows) signify transactions between these addresses. The width and color intensity of the edges reflect the transaction value (with thicker, darker edges indicating higher values).
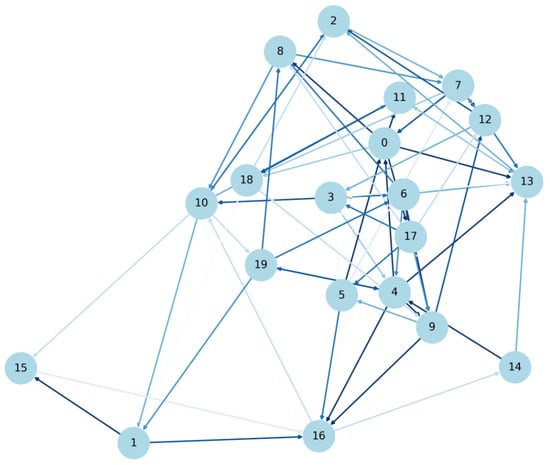
Figure 4.
Wealth Concentration.
Assumption 3.
- Graph Model: The blockchain transaction network is modeled as a weighted directed graph , where:
- −
- V represents addresses (wallets) in the network.
- −
- E represents transactions between addresses.
- −
- W is a set of weights on the edges, where each weight represents the value of the transaction from address u to address v.
- Degree of a Node: The degree of a node (address) in G represents the number of transactions involving that address. The degree is the number of wallet transactions.
- Strength of a Node: The strength of a node is defined as the sum of the weights (transaction values) of the edges connected to the node. This represents the total value of transactions for that address.
- Wealth and Transaction Correlation: An address’s wealth is assumed to correlate with both its degree and strength in the graph.
Application Statement 3.
- In a blockchain transaction network modeled as a weighted directed graph, a skewed degree and strength distribution indicates a concentration of token ownership and transactional flow among a limited number of addresses, suggesting wealth concentration.
Proof.
- (a)
- Degree and Strength Analysis:Analyze the degree distribution and the strength distribution in graph G. A uniform distribution implies decentralized token flow, while a skewed distribution indicates concentration.
- (b)
- Skewness of Distributions:Apply skewness metrics to D and S. High skewness values in D and S indicate that a few addresses have much higher degrees and strengths, respectively.
- (c)
- Wealth Concentration Inference:Given the correlation between an address’s wealth and its degree/strength, the skewness in D and S can be interpreted as indicators of wealth concentration. A few addresses (high-degree, high-strength nodes) dominate the total token flow, indicating wealth concentration.
- (d)
- Temporal Evolution:By examining the evolution of D and S over time, trends in wealth concentration can be identified. Increasing skewness over time suggests increasing wealth concentration.
□
This proof demonstrates that by analyzing the degree and strength distributions in a transaction graph of a blockchain network, it is possible to identify trends of wealth concentration. High skewness in these distributions over time indicates an increasing concentration of wealth among fewer addresses, which can have significant implications for the network’s decentralization and security.
5.1.4. Developer Concentration
Analyzing collaboration graphs and code contribution statistics for blockchain platforms can detect excessive dependencies on a few core developers [69] as depicted in Figure 5. The node in the graph represents developers, lighter shade links for less contribution and darker shades for higher contribution.
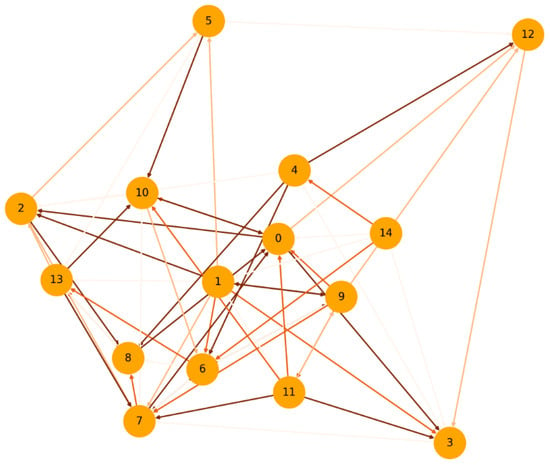
Figure 5.
Developer Concentration.
Assumption 4.
- Graph Model: The collaboration network is modeled as a directed graph , where:
- −
- V represents the set of developers.
- −
- E represents collaborative relationships (e.g., working on the same project or module).
- −
- W is a set of weights on the edges, where each weight quantifies the level of collaboration or contribution from developer u to developer v.
- Degree of a Node: The in-degree and out-degree of a node v represent the number of contributions received by and made by developer v, respectively.
- Strength of a Node: The strength of a node is defined as the sum of the weights of the outgoing edges connected to v, reflecting the total impact of a developer’s contributions.
- Core Developer Identification: A core developer is identified by high out-degree, high strength, or a combination of both, indicating significant influence or dependency in the network.
Application Statement 4.
- In a blockchain platform’s collaboration network modeled as a weighted directed graph, a skewed distribution of degrees and strengths among developers indicates excessive dependencies on a few core developers.
Proof.
- (a)
- Degree and Strength Analysis:Define the in-degree and out-degree of a node (developer) v in graph G as and , respectively. These represent the number of contributions received by and made by developer v. The strength of a node is the sum of the weights of the edges connected to v, quantifying the impact of a developer’s contributions: .
- (b)
- Skewness of Distributions:Analyze the skewness of the degree distributions and , and the strength distribution . High skewness indicates a small number of developers (nodes) with significantly higher degrees or strengths.
- (c)
- Dependency Inference:A core developer can be identified by high values of , , and . If the skewness in , , or S is high, it indicates a network structure with excessive dependency on a few developers.
- (d)
- Network Health and Robustness:A network’s robustness and sustainability can be at risk if it is overly dependent on a few core developers. The temporal evolution of , , and S can be examined to understand how these dependencies change over time.
□
This proof demonstrates that graph theory can be effectively used to analyze developer collaboration networks in blockchain platforms. By examining the degree and strength distributions, one can identify if there are excessive dependencies on a few core developers, which can be critical for understanding the network’s health and sustainability.
Thus, graph metrics enable the ongoing quantification of decentralization levels across various facets. Network visualizations also easily highlight the growth of hubs, clusters and disparities.
5.2. Evaluating Security and Privacy
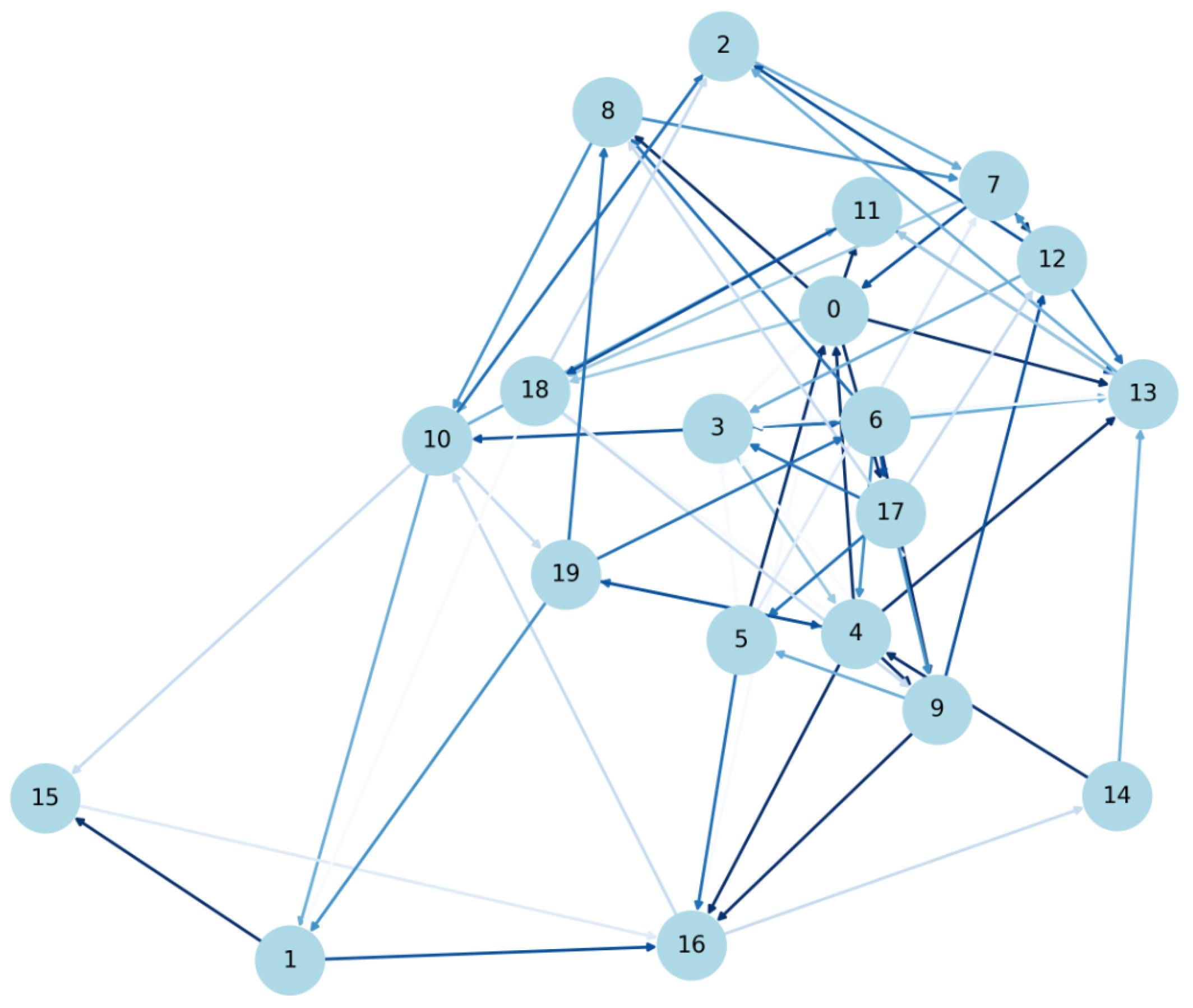
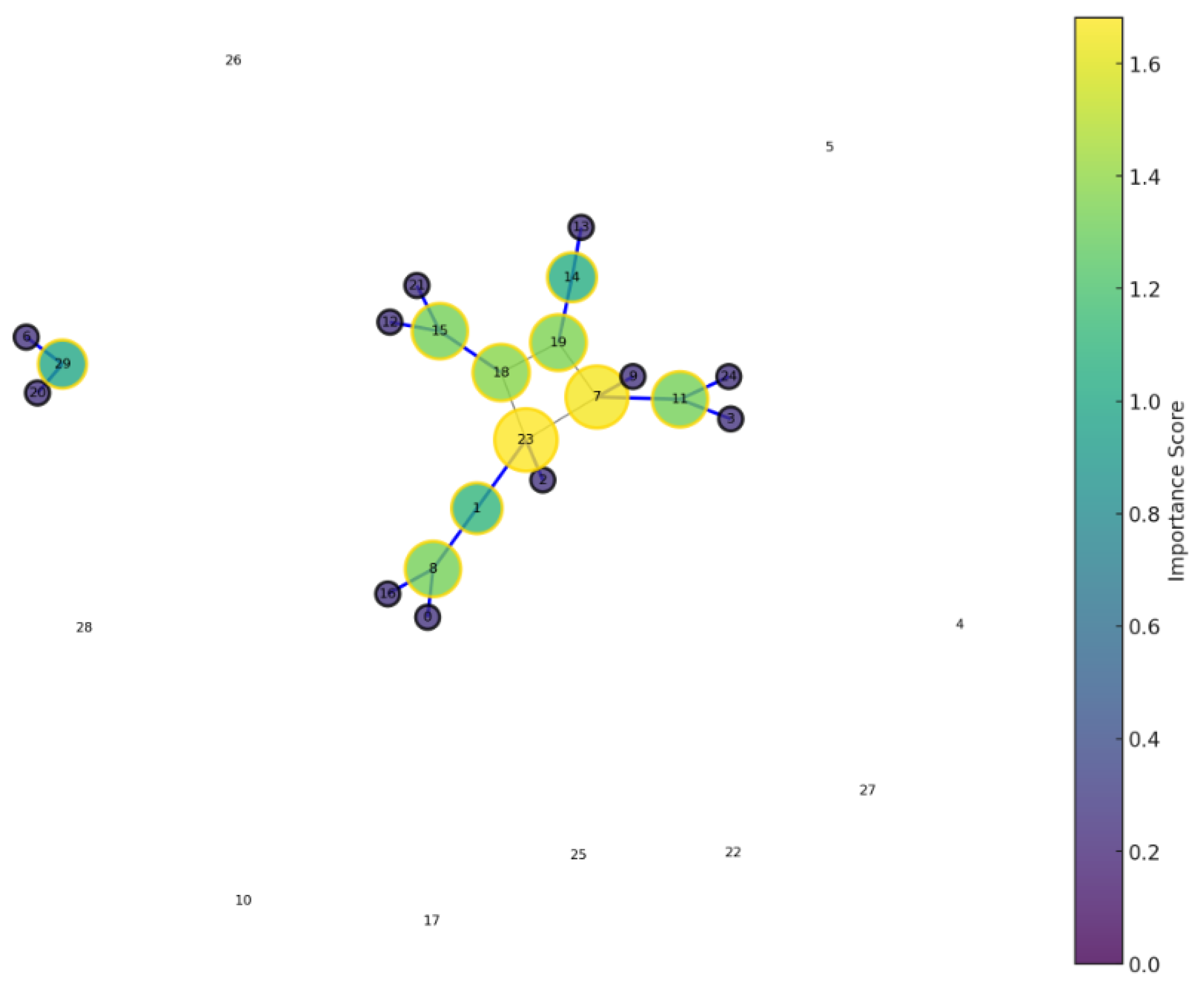
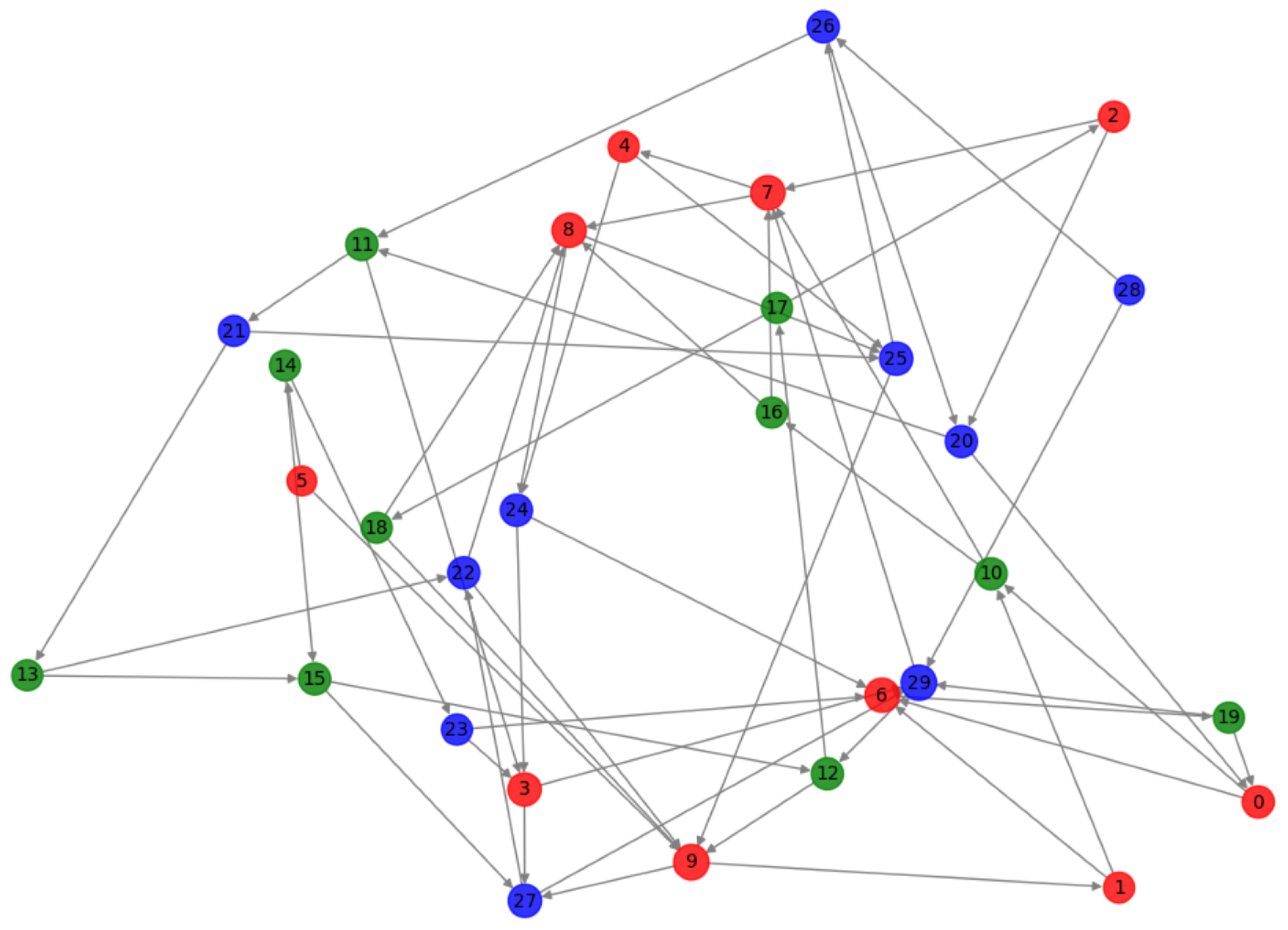
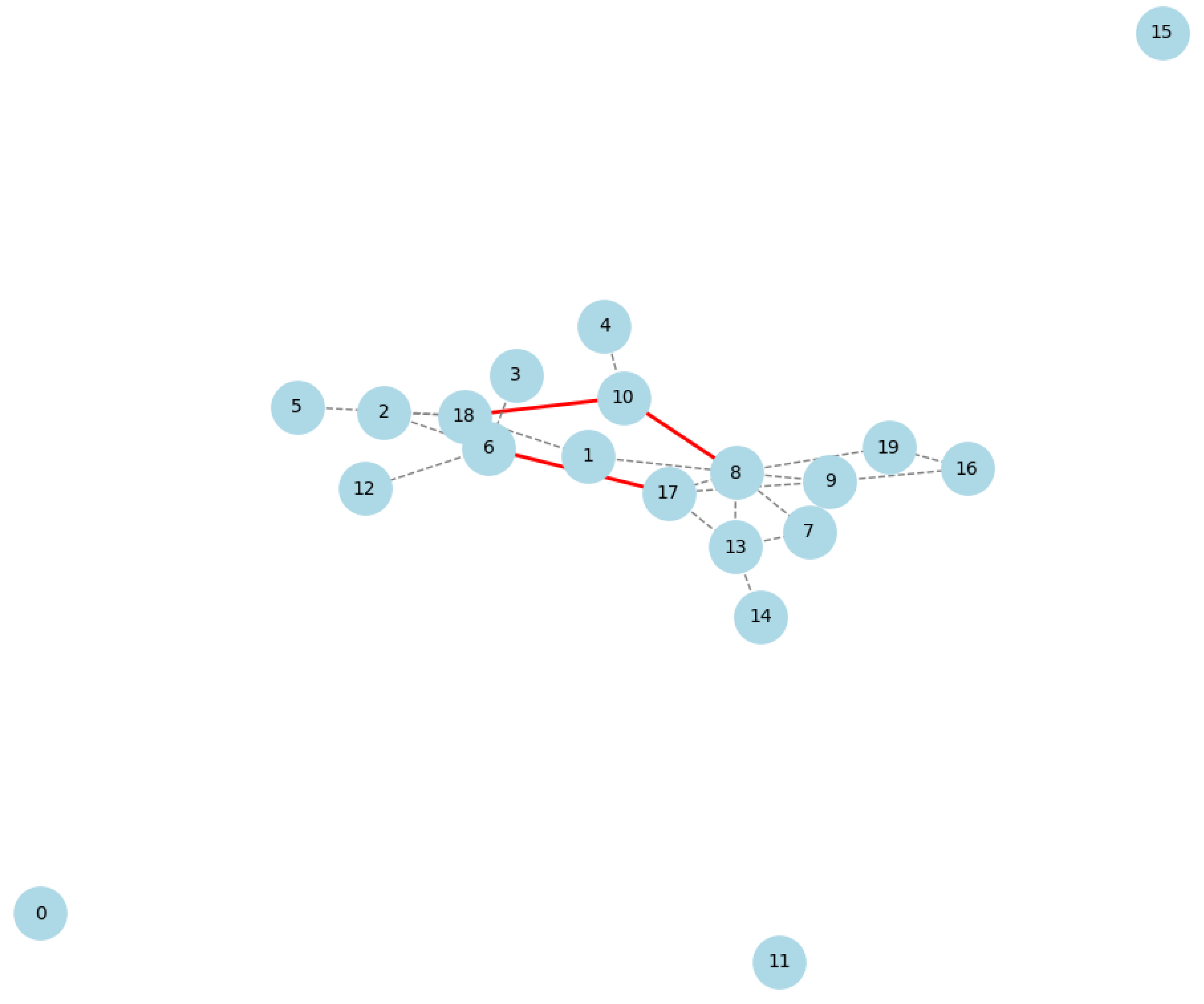
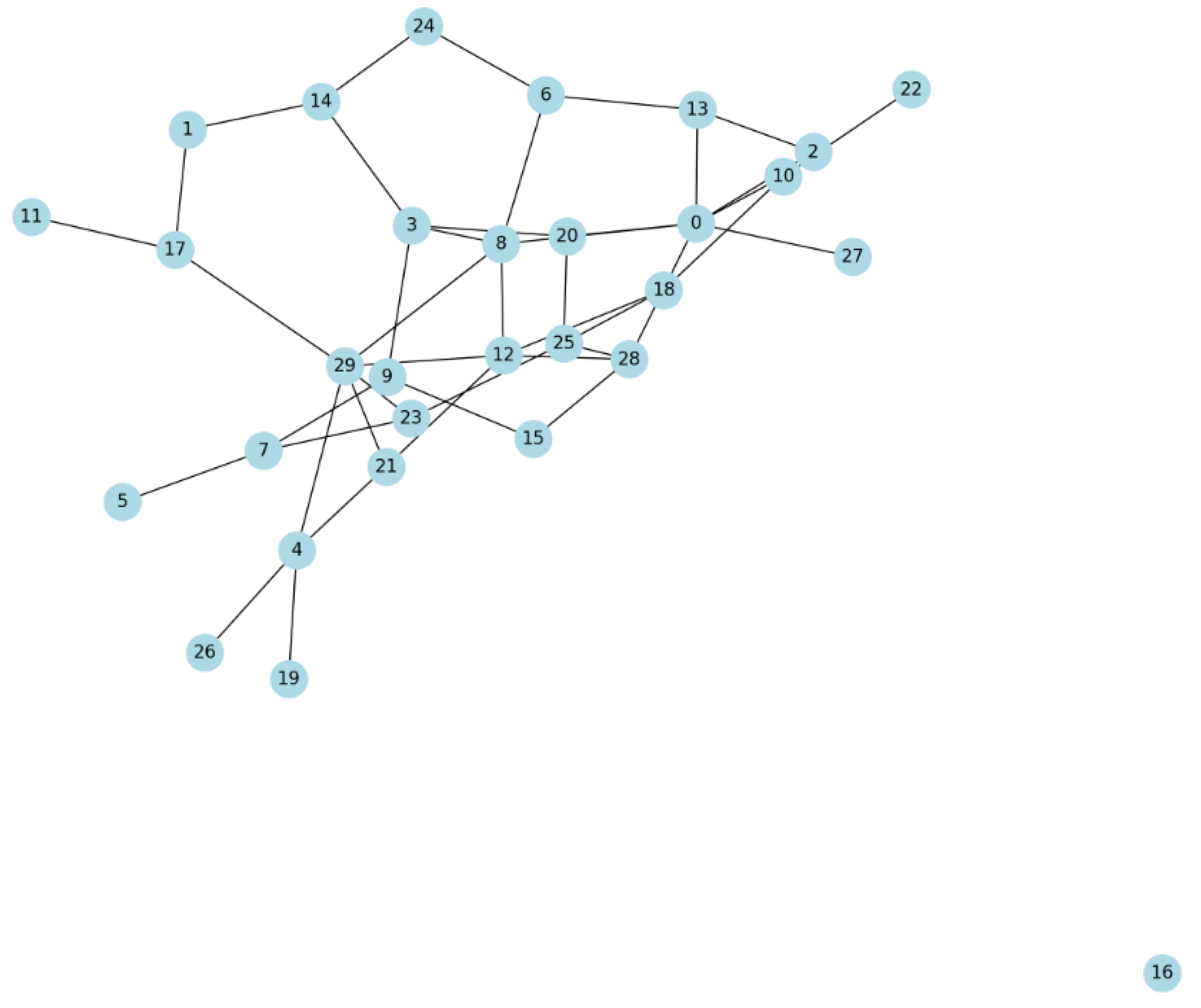
Public blockchains aim to provide security and privacy for user transactions. However, incidents of thefts and data leaks frequently occur [70]. Figure 6 graph helps evaluate such vulnerabilities and how critical nodes, articulation points, and bridges can be identified in a network. In a real-world scenario, these elements could represent vulnerable points in a blockchain network, where targeted attacks could significantly disrupt the network’s topology and functionality.
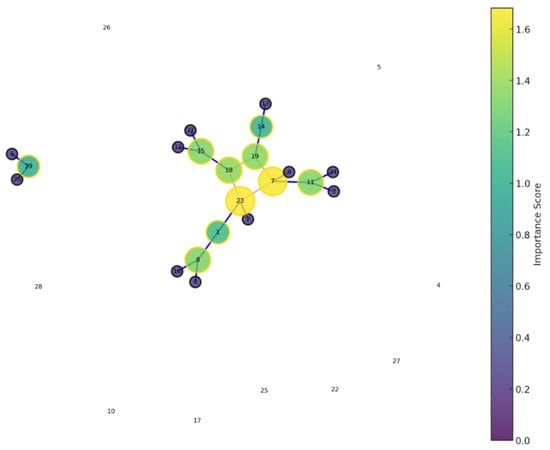
Figure 6.
Topological Attack.
5.2.1. Topological Attacks
Critical nodes whose failure fragments networks widely are attractive attack vectors. Graph metrics like betweenness centrality, bridges and articulation points detect such components [71].
Assumption 5.
- Graph Model: The blockchain network is modeled as an undirected, connected graph , where:
- −
- V represents the set of nodes (miners, validator pools).
- −
- E represents connections between the nodes.
- Critical Nodes: Nodes whose removal fragments the network topology into multiple disconnected components.
- Articulation Points: Nodes whose removal increases the number of connected components in the graph.
- Bridges: Edges whose removal disconnects the graph.
Application Statement 5.
- Nodes with high betweenness centrality are critical articulation points or bridges in a blockchain network. Targeted removal of such nodes presents an effective topological attack vector to fragment the network.
Proof.
- (a)
- Betweenness Centrality: The betweenness centrality of a node is defined as:Where is the total number of shortest paths from s to t, and is the number of those paths passing through node v.
- (b)
- Critical Node Identification:Nodes with higher values participate in more shortest paths in the network. The removal of such nodes leads to disconnecting components previously connected via them.
- (c)
- Network Robustness:Analyzing the distribution of betweenness centrality scores over time provides insight into the emergence of critical nodes and quantifies network resilience against topological attacks.
□
Figure 6 combines betweenness centrality, articulation point status, and degree, offering a comprehensive measure of a node’s role in the network. Node Size and Color, reflect the importance score, larger and more intensely colored nodes indicating higher importance. Node Border Color, Articulation points are highlighted with a gold border, distinguishing them as nodes whose removal would significantly impact network connectivity. Edges with gray representing standard connections and blue highlighting bridges are crucial links whose removal would fragment the network.
This proves that betweenness centrality can effectively identify critical components in blockchain networks that serve as attractive targets for malicious attacks aimed at fragmenting the network topology.
5.2.2. Threat Modelling
Blockchain technology is renowned for its security features; however, lots of studies prove that the security mechanism of blockchain exposes its vulnerability especially when the blockchain suffers attacks [72]. Ideal systems do not exist and so blockchain has a number of problems, requiring attention on the security vulnerabilities [73]. Based on [74] we narrowed down threat to (1) Domain Name System (DNS) Attacks, (2) Phishing Attacks, (3) Border Gateway Protocol (BGP), (4) Eclipse Attacks, (5) Distributed Denial of Service Attacks (DDoS), and (6) 51% attack categories under the network context [72,75]. In the section, we have employed the Erdős–Rényi model, a common model for generating random graphs, which is used to simulate the network topology [76] for simulating the threat model [77].
DNS Attacks. In the realm of blockchain technology, DNS attacks pose a serious threat to the integrity of network communication. The Domain Name System (DNS) acts in translating domain names to IP addresses. However, if compromised, it can lead to the isolation of network participants. Graph theory provides an analytical framework to model and study the repercussions of such attacks. Here, we present a graph theory-based mathematical proof of how DNS attacks can isolate users and miners from the genuine network.
Assumption 6.
- Let us consider the following assumptions within our graph model:
- A directed graph : A directed graph where V is the set of nodes representing users, miners, and DNS servers, and E represents the communication links between these nodes.
- Node Function : Each node is assigned a role indicating whether it is a user/miner (U) or a DNS server (D).
- DNS Integrity : Each DNS server node d has a status indicating whether it is legitimate (L) or compromised/malicious (M).
Application Statement 6.
- For a blockchain network represented by graph G with assumptions as stated, DNS attacks can isolate a subset of nodes , such that U consists solely of users and miners from the genuine network by manipulating the resolutions provided by DNS servers.
Proof.
- (a)
- Attack Initiation: An attacker manipulates a subset of DNS server nodes such that their status for all is changed from L to M.
- (b)
- Resolution Compromise: As users and miners initiate DNS queries, these requests are intercepted by . Thus, the set of edges from U now points to , and their integrity status for all changes from V to I.
- (c)
- Network Isolation: The DNS resolutions from redirect U to endpoints outside the genuine blockchain network resulting in an isolation set .
- (d)
- Isolation Quantification: The isolation metric is defined as the ratio of the number of isolated user/miner nodes to the total number of user/miner nodes, i.e., . If , it implies that the DNS attack was successful in isolating at least a portion of the network’s participants.
□
In the Figure 7 Nodes labeled “User_x” nodes represent individual users within the network.The nodes labeled “DNS_Legit” represent legitimate DNS servers. The nodes labeled “DNS_Malicious” represent DNS servers that have been compromised or are malicious. Edges represent communication links or DNS queries made from users to DNS servers. Black edges represent legitimate DNS queries directed towards legitimate DNS servers. Red edges signify DNS queries that have been redirected to the malicious DNS servers due to the DNS attack. Green nodes indicate non-compromised, functioning DNS servers. Blue nodes represent unaffected users or users who are not the current target of the attack. Red nodes indicate DNS servers that have been compromised and are under the control of an attacker. From the graph Figure 7, we can infer that the network is under a DNS attack, where certain DNS queries from users are being intercepted and redirected to malicious DNS servers. This redirection can lead to a range of malicious activities, such as phishing, spreading malware, or data interception. The graph visually demonstrates the extent of the DNS attack, showing which users are potentially affected by the compromised DNS servers.
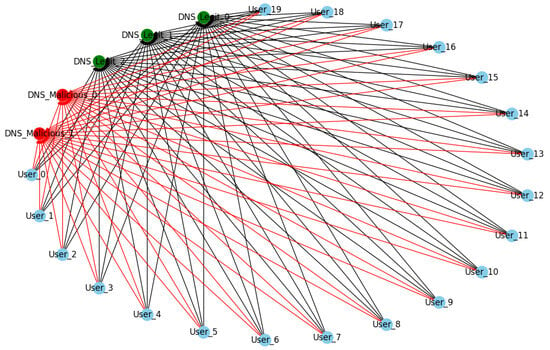
Figure 7.
DNS attack.
DNS attacks have the potential to disrupt the normal functionality of a blockchain network by isolating users and miners from the real network. This graph theory-based proof highlights the critical need for secure DNS protocols and the implementation of robust, decentralized resolution mechanisms within blockchain infrastructures to safeguard against such vulnerabilities. The integrity and reliability of blockchain communications rely on the ability to resist such isolation attacks, reinforcing the network’s foundational premise of decentralized security.
Phishing attacks. Graph theory offers a systematic way to model and analyze the dynamics of phishing attacks in a network, especially in the context of blockchain where key compromise can lead to significant security breaches. This is a graph theory-based mathematical model to understand phishing for key compromise.
Assumption 7.
- Let us construct a graph to model the blockchain network where:
- −
- V: Set of nodes, representing users of the blockchain network.
- −
- E: Set of edges representing trust relationships or communication channels between users.
- Each node v has an associated trust level , representing the user’s vulnerability to phishing attacks, with a higher trust level indicating greater susceptibility.
Application Statement 7.
- A phishing attack within a blockchain network graph G can result in private key theft if the attacker can successfully deceive a subset of nodes , where nodes in have a high trust level .
Proof.
- (a)
- Targeting High Trust Nodes: The attacker identifies nodes with high trust levels by analyzing the graph for nodes with the most edges, indicating a high interaction with other nodes, and therefore, higher visibility for phishing attacks.
- (b)
- Trust Exploitation: Through phishing techniques, the attacker attempts to compromise nodes in by exploiting their trust levels. Let be the threshold above which the nodes are highly susceptible. Then, .
- (c)
- Key Compromise: The attacker crafts deceptive messages that are sent across edges to nodes in . If a node is deceived, its private key is considered compromised, transitioning its status to .
- (d)
- Asset Theft: Using the compromised private keys, the attacker gains access to the nodes’ assets and can perform unauthorized transactions, leading to theft.
□
The critical importance of user awareness and secure communication within blockchain networks. The trust levels within a network, as modeled by graph G, are directly correlated to the vulnerability of users to such attacks.
Network Representation. Let be a directed graph where V represents the set of nodes (participants) in the network, and E represents the set of directed edges (communications or transactions) between these nodes.
Node Attributes. Each node has several attributes:
- Key Status : Indicates whether the private key of the node is compromised (C) or secure (S).
- Phishing Susceptibility : A probabilistic measure of the node’s vulnerability to phishing attacks, ranging from 0 (immune) to 1 (highly susceptible).
Edge Dynamics. Edges in E represent potential channels through which phishing attacks can be propagated or information can be exchanged, such as email communications, social media interactions, or blockchain transactions.
Attack Dynamics. A phishing attack targets a subset of nodes where the attacker attempts to compromise the private keys of these nodes through deceptive communication. The success of phishing on each node depends on , the phishing susceptibility of the node.
Compromise Propagation. Once a node’s key is compromised (), the attacker can utilize this node to further propagate the attack within the network, increasing the reach of the phishing campaign.
Representation of the Attack’s Impact
- Initial Compromise Set : The set of nodes initially targeted and successfully compromised by the phishing attack.
- Propagation Function F: A function that models how the attack propagates through the network from the initial set of compromised nodes.
- Total Compromised Set : The set of nodes that are eventually compromised as a result of both the initial attack and subsequent propagation. is derived by applying F to and the network G.
- Network Vulnerability Index (NVI): A metric to quantify the overall impact of the phishing attack on the network. It is given by:
Figure 8 represents a model of a blockchain network under the threat of phishing attacks. Nodes represent network participants, color-coded based on their key status: nodes in red have compromised keys (C), while nodes in green have secure keys (S). Edges represent potential communication channels through which phishing attacks can be propagated or through which information is exchanged among participants. The network includes both initially targeted nodes for phishing attacks (selected based on a higher susceptibility to phishing) and nodes that may potentially be compromised through network propagation. This graph-theory-based simulation illustrates the dynamics of phishing attacks within a network, highlighting the importance of understanding both the structural vulnerabilities and behavioral aspects that make nodes susceptible to phishing. By analyzing such models, network administrators and blockchain protocol designers can develop strategies to detect and mitigate the risk of key compromise through phishing attacks, thereby enhancing the overall security and resilience of the network.
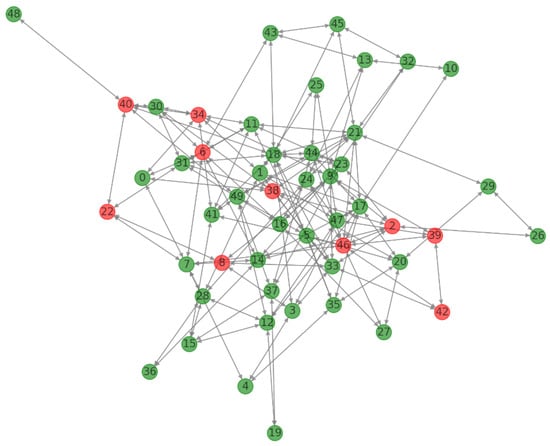
Figure 8.
Phishing Attacks.
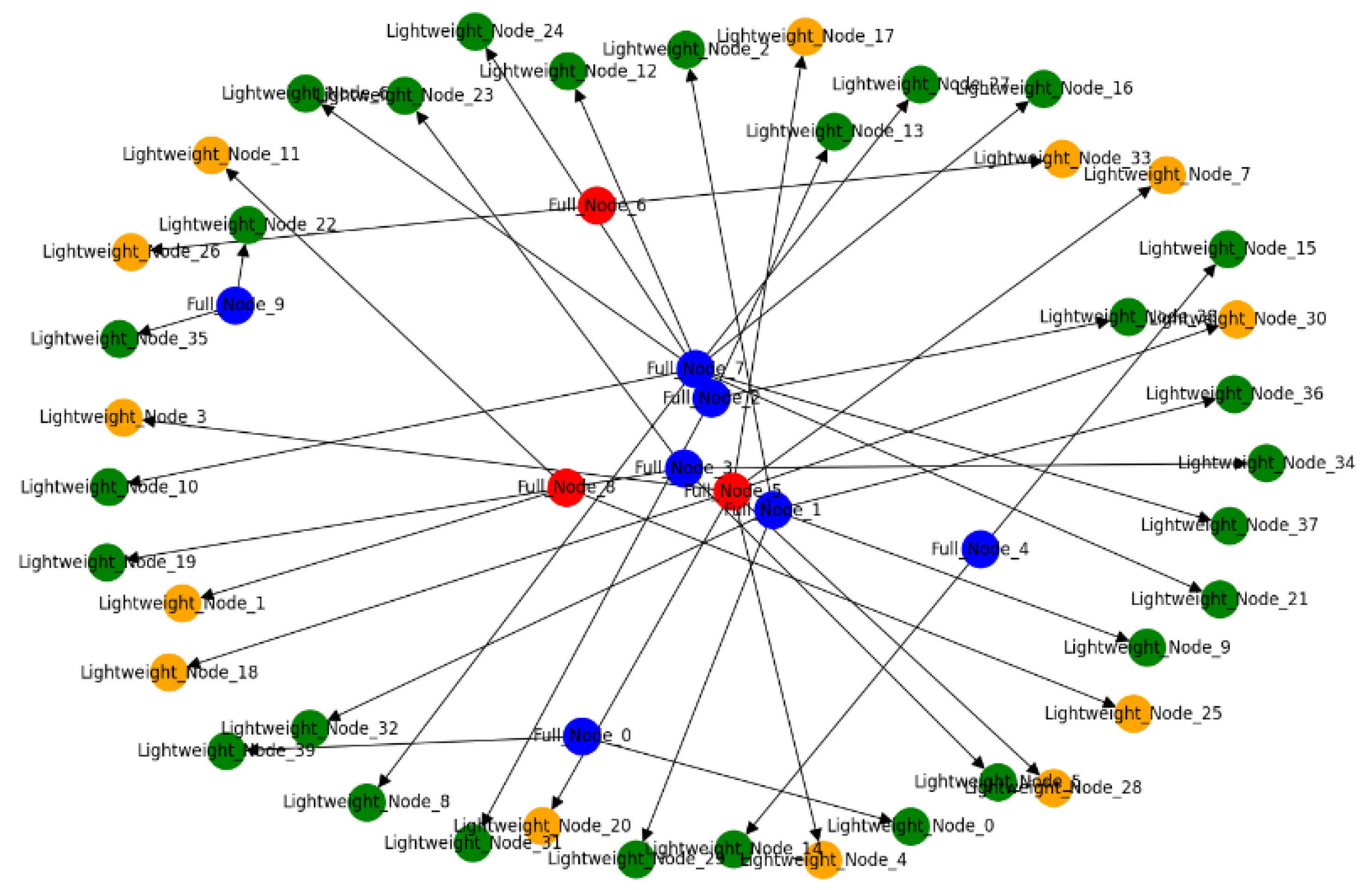
BGP hijacking affects the routing on the Internet by maliciously rerouting traffic through an attacker-controlled system. In blockchain networks, full nodes play a critical role in maintaining the network’s integrity. If these are compromised, the reliability of the lightweight nodes that depend on them can also be compromised, leading to spatial partitioning within the network.
Assumption 8.
- We assume a graph , where:
- −
- V: Set of nodes, partitioned into full nodes and lightweight nodes , such that and .
- −
- E: Set of directed edges representing communication links, with representing links between full nodes and representing links from full nodes to lightweight nodes.
- Node Status : Indicates whether a node is secure (S) or compromised (C).
- Routing Path : Ordered list of nodes a message traverses from u to v.
Application Statement 8.
- In a blockchain network subject to BGP hijacks, if an attacker compromises a subset of full nodes , it can induce a spatial partitioning where the associated lightweight nodes , which rely on compromised full nodes, are also controlled by the attacker.
Proof.
- (a)
- BGP Hijacking Initiation: Attacker gains control of one or more full nodes by diverting their incoming and outgoing routing paths. For all , changes from S to C.
- (b)
- Routing Path Alteration: The routing paths for and are altered to pass through , if not already. For all , if , then is in .
- (c)
- Spatial Partitioning Effect: The network experiences spatial partitioning where only receives blockchain data from . The integrity of the data received by is compromised, and the attacker can control the blockchain view of .
- (d)
- Control over Lightweight Nodes: The attacker manipulates blockchain data flowing to , effectively controlling these nodes.
□
Figure 9 graph represents a simulated blockchain network and illustrates the impact of BGP hijacking on network participants. The graph contains two types of nodes, full nodes and lightweight nodes, each playing a different role in the blockchain network. Full nodes, labeled as “Full_Node_x”, are responsible for maintaining a complete copy of the blockchain ledger and validating transactions. Lightweight nodes, labeled as “Lightweight_Node_x”, rely on full nodes for transaction validation and network information. The color of the nodes indicates their security status. Green nodes are secure and operating as intended. Red nodes have been compromised through BGP hijacking, indicating that an attacker controls them. The attacker can manipulate the data that flow through these nodes, potentially leading to incorrect transaction validations or false information being fed to the rest of the network. The orange nodes in the graph represent a state that is between the secure represented in green and compromised in red statuses. Edges connecting the nodes represent communication paths. In the context of a BGP hijack, these paths may be altered to route through compromised nodes, which is a critical aspect of the attack as it can lead to network partitioning and isolation of certain nodes from the rest of the network.
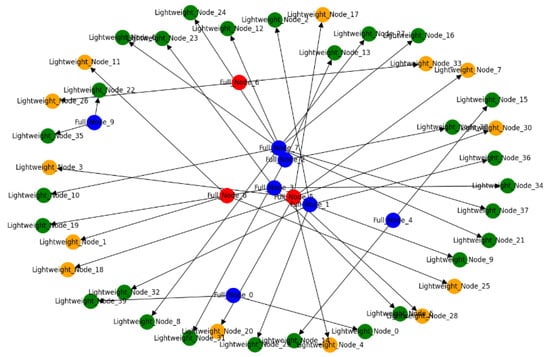
Figure 9.
BGP hijacking.
The graph organizes nodes in layers, with full nodes being more centrally located, representing their pivotal role in the network’s operation. The lightweight nodes are positioned around the periphery, demonstrating their reliance on the full nodes for information.
The compromised full nodes (central red nodes) effectively create a false sub-network that can mislead the connected lightweight nodes. This spatial partitioning demonstrates the potential of a BGP hijack to disrupt blockchain network operations by isolating and controlling segments of the network. The simulation aims to visualize how BGP hijacks can lead to significant vulnerabilities within blockchain infrastructures, particularly for those nodes that do not hold a full copy of the blockchain and depend on others for accurate information. In the context of BGP hijacking and blockchain, an orange node indicates a full node that is under attack but not fully compromised, or it could signify a node whose status is uncertain or in the process of being verified.
BGP hijacking can lead to a spatial partitioning of a blockchain network by compromising the integrity of full nodes and, by extension, controlling associated lightweight nodes. The model highlights the critical importance of securing full nodes against such routing attacks, as they are pivotal in ensuring the correct operation of lightweight nodes within the blockchain infrastructure. This proof highlights the need for robust, secure routing protocols and practices within blockchain networks to prevent such disruptive spatial partitioning.
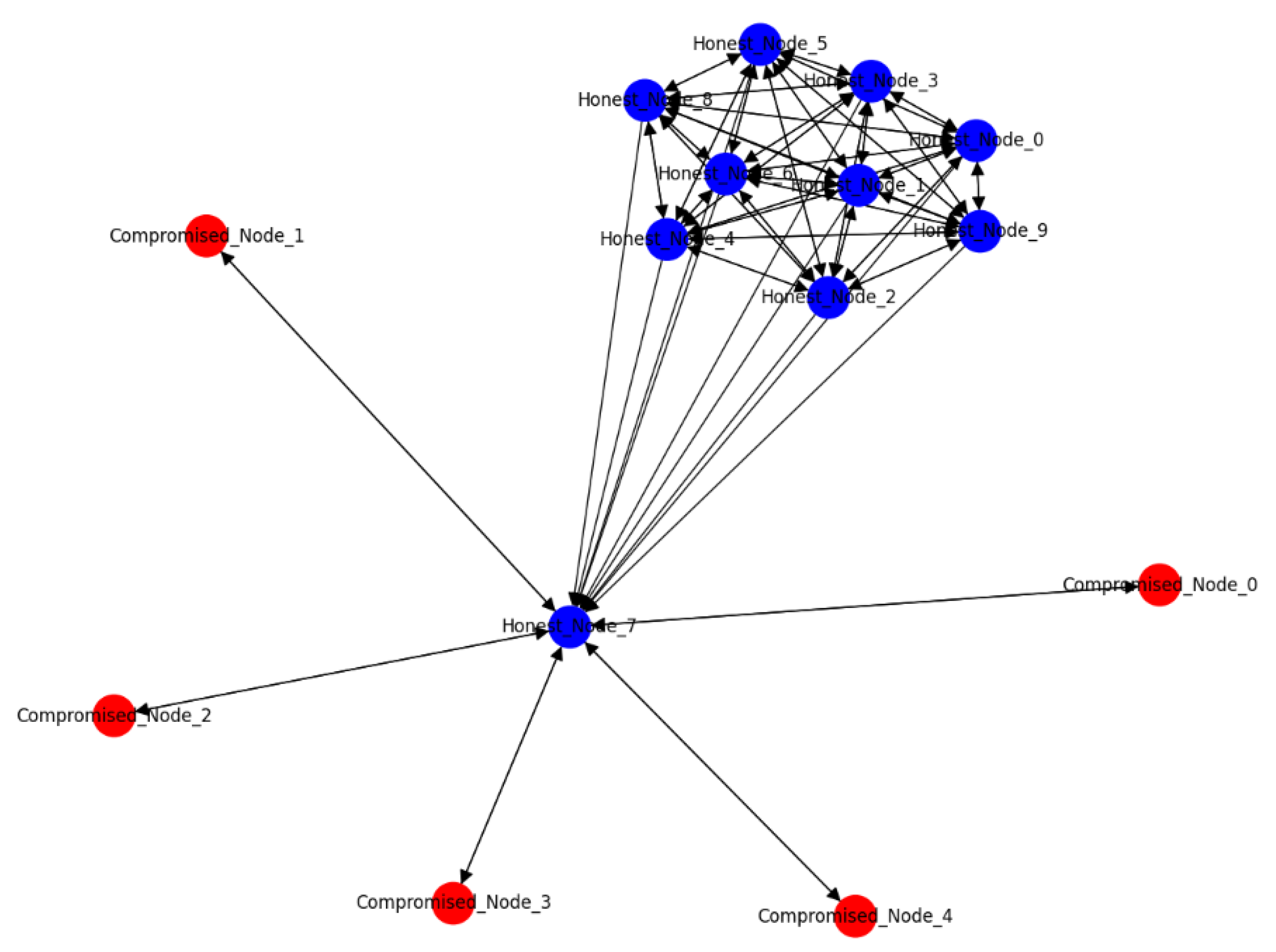
Eclipse attack is characterized by the isolation of honest nodes in a blockchain network. The adversary strategically places compromised nodes to intercept or eclipse the victim’s connections, controlling their view of the network and potentially leading to double-spending or other fraudulent activities.
Assumption 9.
- Let us consider a graph where:
- −
- V: Set of nodes, representing the blockchain participants.
- −
- E: Set of directed edges representing network connections between nodes.
We further categorize the nodes as:- −
- : Set of honest nodes.
- −
- : Set of compromised nodes controlled by the attacker.
Application Statement 9.
- For a blockchain network represented by graph G, an attacker can successfully conduct an Eclipse attack on a subset of honest nodes by ensuring all connections to and from are with nodes in , thus controlling the flow of information to the isolated nodes.
Proof.
- (a)
- Isolation of Honest Nodes: The attacker infiltrates the network, adding or compromising nodes to become part of . The attacker then uses these nodes to form all direct connections with the target honest node .
- (b)
- Manipulation of Network Traffic: For each edge where and , the attacker redirects e such that , effectively controlling the communication channels.
- (c)
- Impact of Isolation: The information received by any is now fully controlled by , leading to a scenario where h is eclipsed from the genuine blockchain network. This prevents h from receiving valid transactions and blocks, effectively isolating it from the true state of the blockchain.
□
Figure 10 is a representation of a network that includes both honest and compromised nodes, illustrating a scenario of eclipse attack within a blockchain network. Blue nodes are labeled “Honest_Node_x” and represent the honest participants in the network, normal or secure status, meaning these nodes are functioning correctly and have not been compromised. Red nodes are labeled “Compromised_Node_x” and indicate nodes that have been compromised or are under the control of an attacker. Edges, the lines between the nodes represent connections or potential pathways for communication or data flow between the nodes.
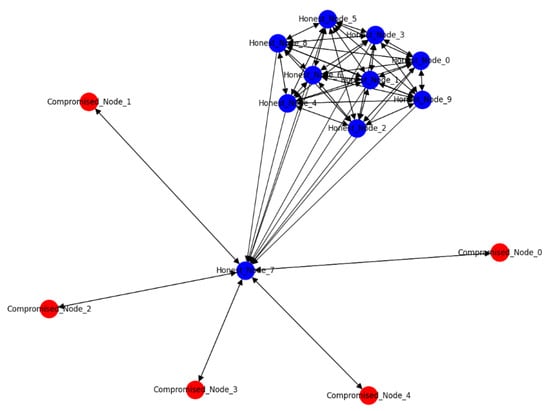
Figure 10.
Eclipse attack.
The graph could be used to understand the impact of the compromised nodes on the network, particularly how the honest nodes are influenced or isolated due to these compromised nodes. In an eclipse attack, the compromised nodes may be strategically positioned to control the communication of the honest nodes, effectively isolating them from the rest of the network. The goal of such an attack could be to feed false information or prevent honest nodes from accessing the true state of the blockchain.
The model demonstrates that through an Eclipse attack, the adversary can control the information available to certain nodes in the blockchain network, which can have severe implications, such as facilitating double spending or denying service. The graph’s theoretical approach to this proof provides a clear depiction of the attack’s potential and highlights the importance of establishing secure and diverse peer-to-peer connections within blockchain networks to mitigate such risks.
DDOS Attack on blockchain networks aims to overload the network by flooding nodes with a large number of requests or malformed transactions. When executed in tandem with a 51% attack, the malicious actor may also have enough control over the network to prevent legitimate transactions from being confirmed, effectively causing a denial of service.
Assumption 10.
- We model the blockchain network as a graph where:
- −
- V: Set of nodes in the blockchain network, where each node v represents a participant (e.g., user, miner, full node).
- −
- E: Set of edges representing connections or potential transaction paths between nodes.
- Each node v has a capacity representing the maximum number of transactions it can process per time unit. A DDoS attack is modeled by increasing the demand on the node’s resources to exceed .
Application Statement 10.
- For a blockchain network represented by graph G, a successful DDoS attack is achieved by creating a demand on nodes such that for a significant subset , leading to service failure for those nodes.
Proof.
- (a)
- Attack Initialization: The attacker distributes a set of malicious nodes or botnets within the network that initiate the attack.
- (b)
- Overwhelming Network Resources: Each malicious node generates a number of transactions directed at nodes in V, such that .
- (c)
- Exploiting Network Control: If combined with a 51% attack, the attacker can prioritize malicious transactions or invalidate legitimate ones, increasing the network’s congestion. The attacker can create intentional forks by generating blocks at a rate that overwhelms the network’s ability to reach consensus, further contributing to the denial of service.
- (d)
- Service Failure: A significant number of nodes are unable to process legitimate transactions, leading to service failure as defined by the inability of the network to perform its intended operations.
□
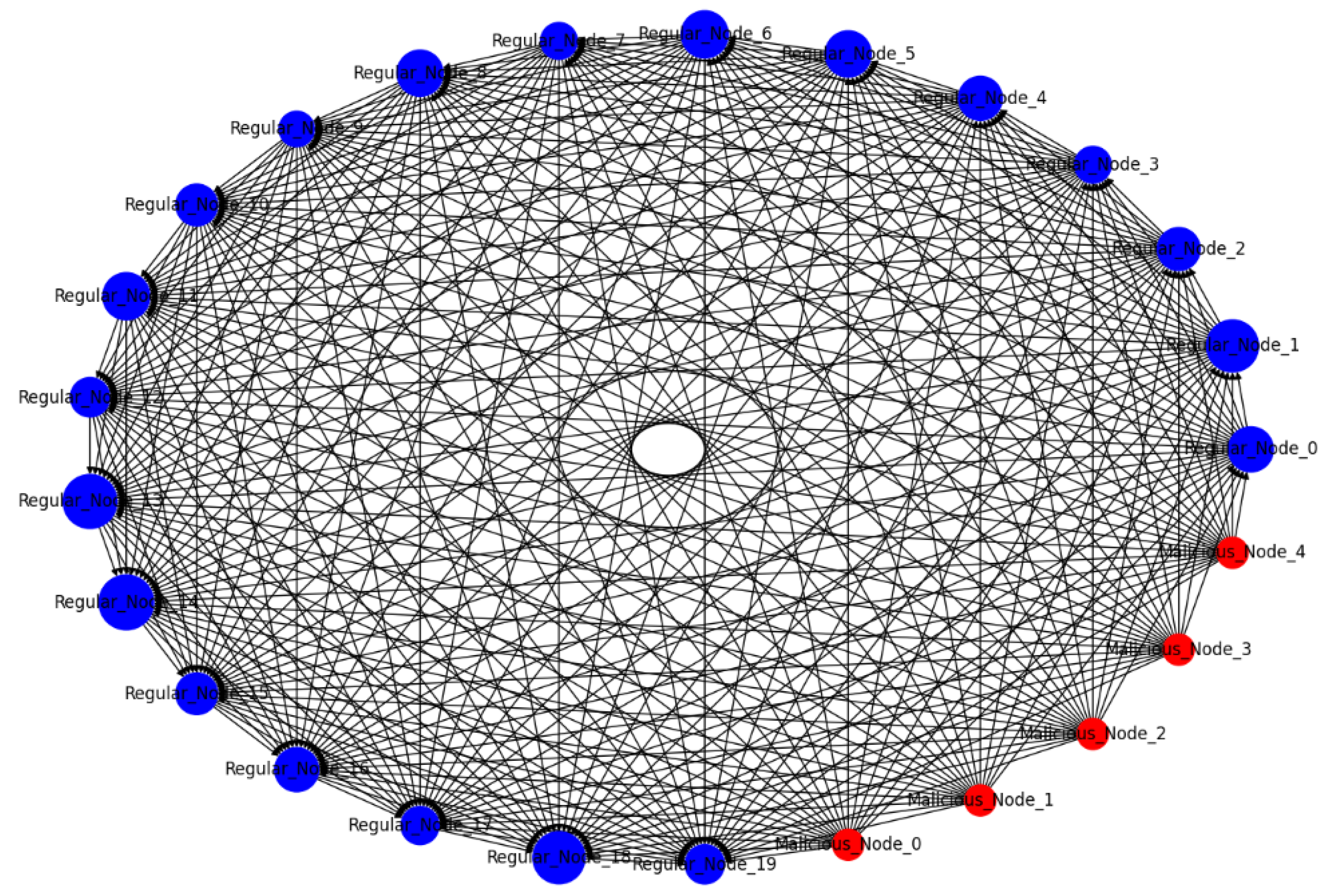
Figure 11 depicts a highly interconnected network of nodes in a blockchain system. Nodes labeled “Regular_Node_x” are honest participants in the blockchain network. Nodes labeled “Malicious_Node_x” probably represent attackers or compromised nodes that may be part of a coordinated attack. Edges’ dense interconnections shown by the multitude of lines between nodes imply a network where each node is in communication with many others, which is typical for peer-to-peer networks in blockchain systems. The blue color of the “Regular_Node_x” suggests they are standard, uncorrupted nodes. The red color of the “Malicious_Node_x” nodes implies danger or corruption, indicative of nodes that may be initiating malicious activities like a DDoS attack. The dense web of connections signifies that the network has a high level of redundancy and connectivity, which is usually a strength for resilience and distributed consensus. However, the presence of malicious nodes within this web can be a significant threat. The malicious can flood the network with superfluous requests, transactions, or blocks, attempting to overwhelm the system’s computational resources, thereby slowing down or even halting legitimate network operations.
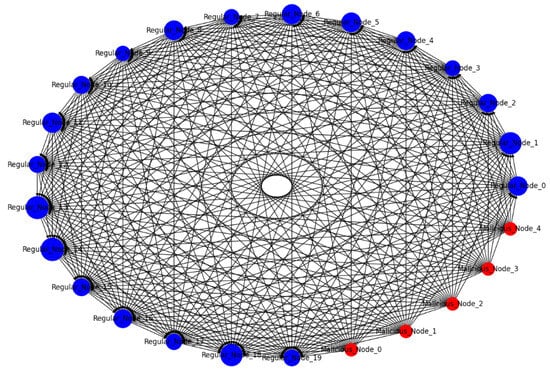
Figure 11.
DDoS attack.
The model concludes that a DDoS attack, particularly when coupled with a 51% attack or intentional forks, can cripple a blockchain network’s functionality. This highlights the importance of implementing robust transaction validation mechanisms, anti-spam measures, and network capacity planning to mitigate the impact of DDoS and related attacks on blockchain systems. The resilience of blockchain networks against such attacks is crucial for maintaining service continuity and trust in the system.
51% attack in the context of blockchain technology occurs when a single entity gains control of the majority of the network’s hash rate, enabling it to unilaterally alter the blockchain’s state. This mathematical model, underpinned by graph theory, seeks to encapsulate the dynamics of such an attack.
Assumption 11.
- Consider a blockchain network represented as a weighted directed graph where:
- −
- V: Set of nodes, where each node v represents a miner in the network.
- −
- E: Set of directed edges representing hash rate contributions from one node to another (in the case of pool mining).
- −
- : Weight of edge e, representing the hash rate directed from one node to another.
Application Statement 11.
- In a blockchain network graph G, an entity controlling a set of nodes , such that the sum of outbound hash rate weights from surpasses 50% of the total network’s hash rate, can perform a 51% attack.
Proof.
- (a)
- Let be the total network hash rate, computed as the sum of weights of all outbound edges in G:
- (b)
- An attacker controls a subset of nodes . Let be the hash rate controlled by the attacker, calculated as:
- (c)
- For the attacker to perform a 51% attack, must be greater than half of :
□
This would enable the attacker to:
- Prevent transaction confirmations: By choosing not to include them in the blocks they mine.
- Halt payments: By ignoring blocks containing certain transactions, preventing them from being confirmed.
- Double-spend coins: by creating a private fork of the blockchain and then releasing it to replace the previously agreed-upon blocks.
The control of the majority hash rate allows the attacker to have the longest chain, which is considered the valid chain by honest nodes, thus enabling them to manipulate the blockchain.
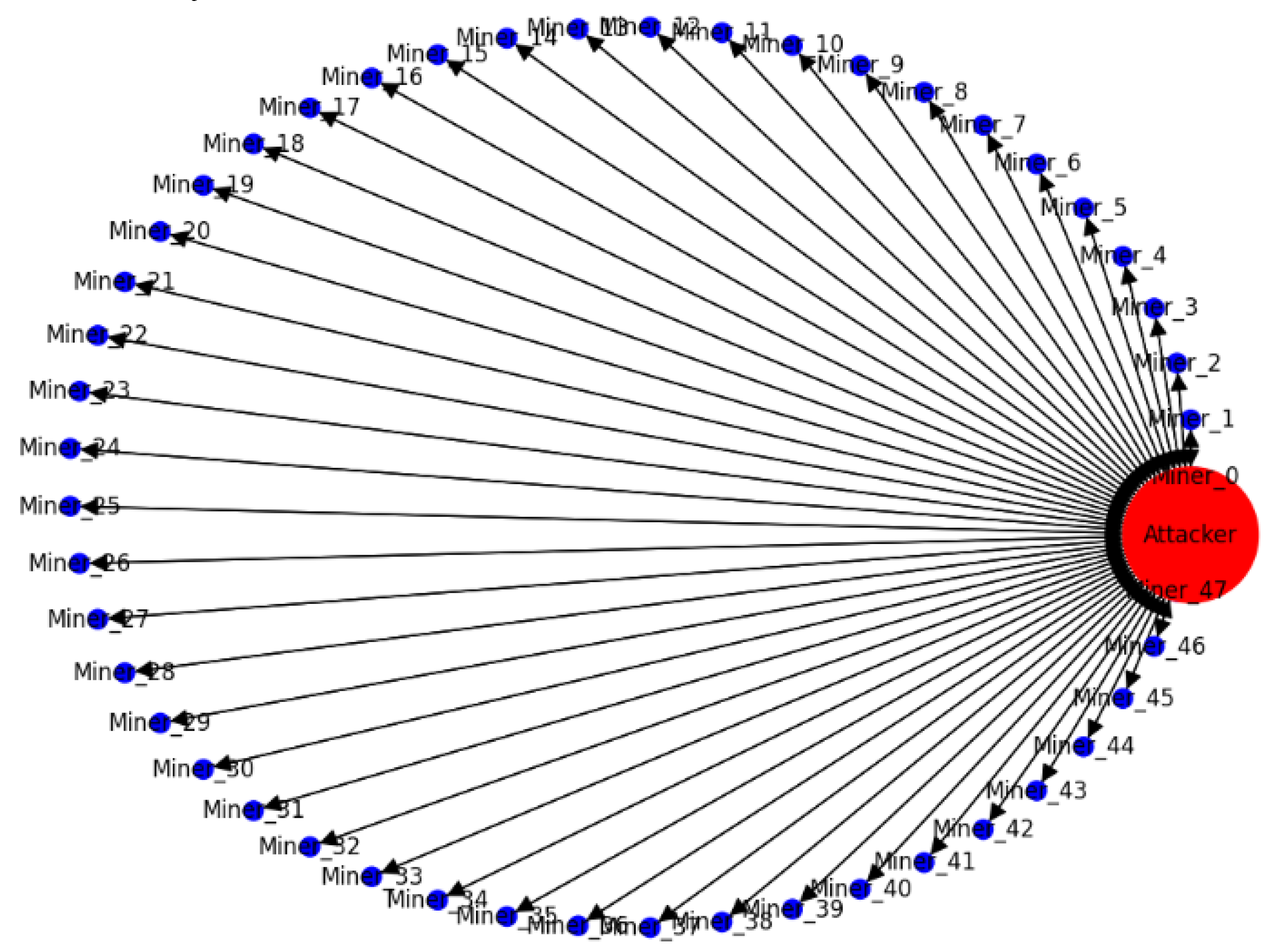
Figure 12 illustrates a 51% attack scenario on a blockchain network, which is characterized by a single entity—the attacker—having a majority control over the network’s mining power.
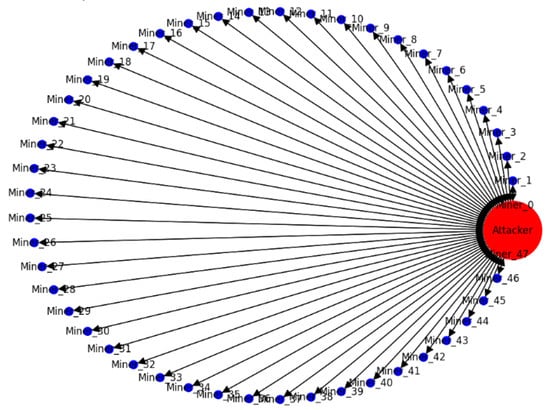
Figure 12.
51% attack.
Nodes, labeled as “Miner_x” represent individual mining participants in the blockchain network. The node labeled as “Attacker” represents the entity that has gained control over a significant portion of the network’s mining power. Edges from the “Attacker” node to the “Miner” nodes indicate the direction of control or influence. It implies that the attacker has a direct or indirect influence over the individual miners, possibly because they are part of a mining pool controlled by the attacker or are malicious nodes themselves. The “Miner” nodes are colored blue, which could represent normal miners in the network. The “Attacker” node is colored red, a common color to signify danger or a warning, in this case representing the malicious entity conducting the attack. The “Attacker” node is significantly larger than the “Miner” nodes, representing its larger hash rate relative to the individual miners. The graph theory-based model conclusively demonstrates that if an entity can accumulate more than half of the hash rate in a blockchain network, it possesses the capability to undermine the network’s integrity. This proof highlights the intrinsic security risks within proof-of-work blockchain systems and highlights the necessity for distributed and balanced hash rate distribution to safeguard against 51% attacks.
Through the lens of graph theory, we have explored a variety of attack vectors: phishing attacks that lead to private key theft, 51% attacks that compromise the integrity of the blockchain, DDoS attacks that overwhelm network resources, and DNS and BGP hijacks that reroute traffic to compromise data integrity and availability. Threat modeling is an indispensable part of designing and maintaining secure blockchain networks. It not only aids in identifying and understanding potential threats but also in developing comprehensive strategies to mitigate such risks and ensure the continuity, integrity, and trustworthiness of blockchain systems.
5.2.3. Deanonymization
Malicious actors often try linking user identities across blockchain transactions to compromise privacy. Clustering and classification algorithms on user graphs generate fingerprint profiles that quantify re-identification risks [78]. Figure 13 demonstrates how advanced analysis techniques, including clustering and classification, apply to network structure to uncover hidden patterns and compromise user privacy. By simulating clusters and highlighting transaction activity levels, it provides a visual context for understanding the deanonymization risks in blockchain networks.
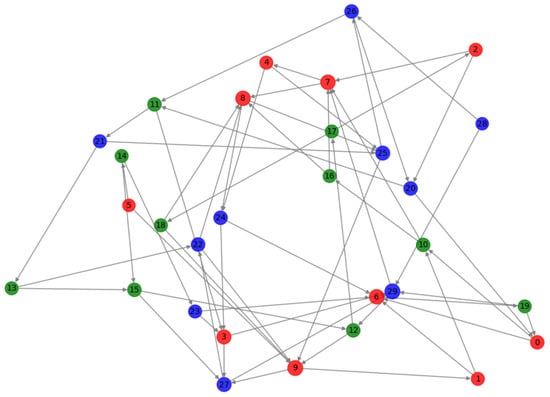
Figure 13.
Deanonymization.
Nodes represent individual wallets in the blockchain network. Directed edges (arrows) signify transactions between these wallets. The transaction activity level of each wallet can help identify highly active wallets relevant to the analysis for deanonymization. Node Color simulates clustering results, with nodes color-coded to represent hypothetical clusters identified in a deanonymization effort. These clusters could indicate wallets with common spending patterns or other characteristics that algorithms have grouped together, potentially revealing user identities.
Assumption 12.
- The blockchain transaction network is a graph with wallets as nodes and transactions as edges .
- User identities are anonymized behind wallet addresses.
- Transactions have attributes like timestamps, and coin values transferred.
Application Statement 12.
- Clustering algorithms applied on user transaction subgraphs can reveal common spending patterns that fingerprint user identities in blockchain networks.
Proof.
- (a)
- Construct transaction subgraphs induced by each user k’s wallets .
- (b)
- Apply graph clustering methods (e.g., K-means) on based on transaction attributes and temporal patterns to separate coin mixes.
- (c)
- Use resulting clusters as features to train classifier model identifying user k.
- (d)
- Apply to full transaction graph G to predict the presence of user k’s payments.
□
Thus by extracting distinctive transaction features and styles from known user subgraphs, deanonymization classifier models can be constructed to compromise wider blockchain privacy. Graph clustering enables the creation of fingerprint profiles that quantify re-identification risks for blockchain users.
5.2.4. Tracking Ransom Payments
Ransomware groups use mixes of coin transactions across accounts to mask extorted payments. But network analysis reveals identifiable payment flows by correlating transaction times, values and links between groups of addresses [79].
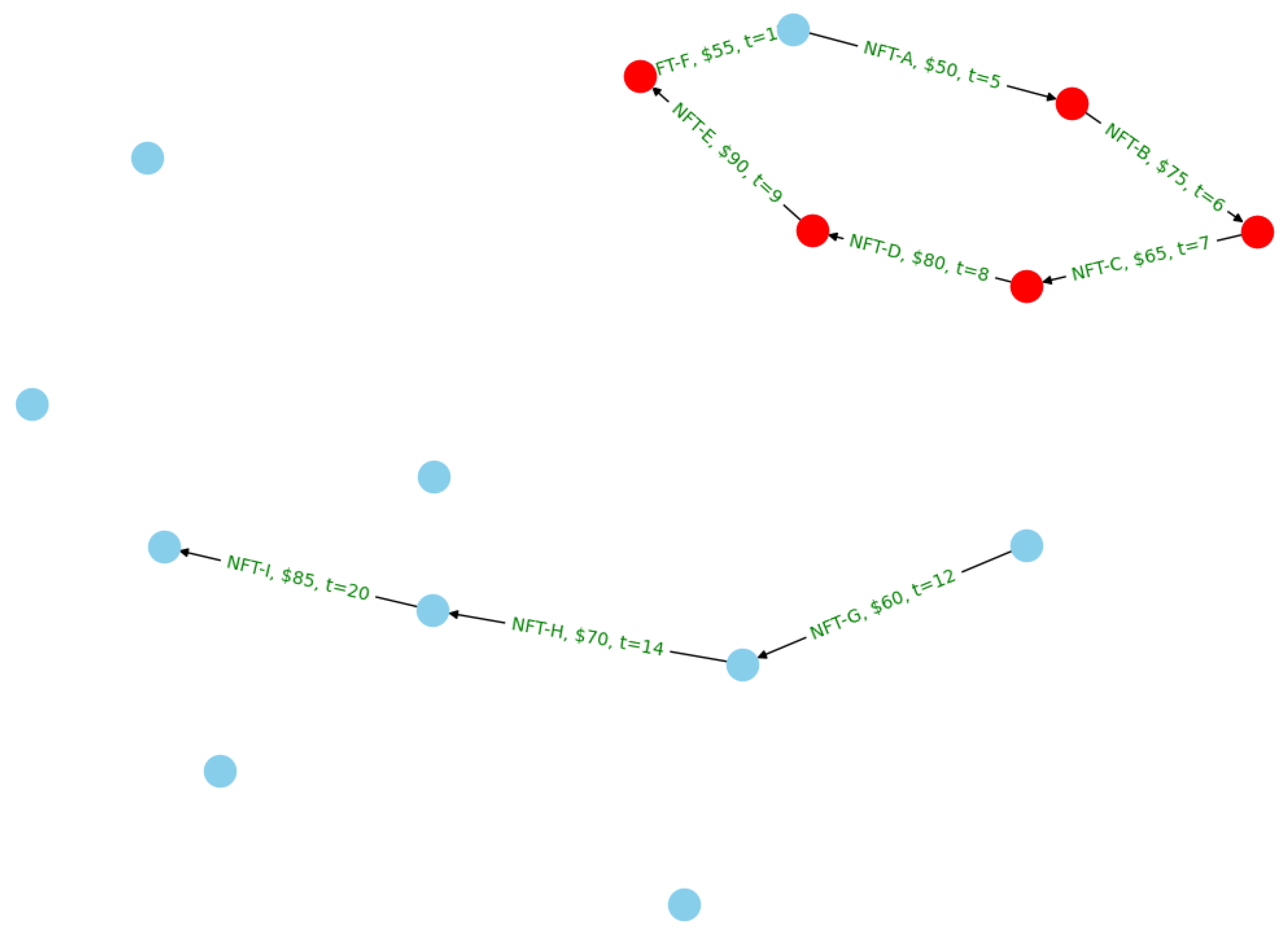
Figure 14 is a simplified representation, aimed at demonstrating the underlying structure of ransomware payment flows in a blockchain transaction network. The actual process of unmixing coin transactions and tracking ransom payments involves a more complex and nuanced analysis of transaction attributes and connectivity patterns. The visualization serves to illustrate how ransomware groups move extorted payments through various wallet addresses. The complexity and inter-connectedness of these transactions can be seen, showcasing the challenge in tracking and analyzing these flows. Nodes represent wallet addresses within the blockchain network. Directed edges (arrows) signify ransom-related transactions between these wallets.
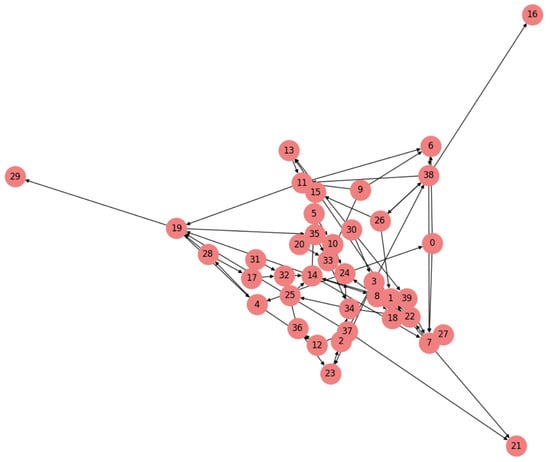
Figure 14.
Tracking Ransom Payments.
Assumption 13.
- The blockchain transaction network is a temporal graph with wallet addresses as nodes , transactions as edges , and timestamps on edges.
- Ransomware groups mix coins across multiple wallets to hide payment trails.
Application Statement 13.
- Correlating transaction timing, value flow patterns and connectivity trails between groups of addresses on temporal transaction graphs can reveal identifiable ransomware payment flows.
Proof.
- (a)
- Apply the Modularity Optimization algorithm for community detection on transaction graph G to cluster related wallets A into campaigns.
- (b)
- Construct subgraphs induced by each ransomware wallet group .
- (c)
- Apply network flow modeling and tracking on based on transaction amounts, timings and unmixing of trails between clusters to trace laundered payments.
□
This allows tracing obfuscated ransom transfers on blockchain networks via combined analysis of graphs, flows and temporal patterns. Multi-faceted network analysis techniques facilitate tracking ransomware payments on blockchain platforms despite coin mixing attempts.
Thus, graph techniques enable enhanced the modeling, prediction and containment of security threats by uncovering hidden relationships and activity patterns.
5.3. Managing Scalability
Performance limitations like network congestion and transaction delays prevent blockchains from scaling for mass adoption. Graph theory provides analytical approaches as well as solutions to address scalability issues [80]. The scope of this section is limited to theoretical representation.
5.3.1. Bench Marking Delays
The shortest path lengths and the diameter in baseline transaction graphs represent best-case timings. Growth trends in these metrics during peak loads or attacks quantify the extent of performance impacts [81]. Figure 15, ensuring a connected graph focusing on the largest connected component necessary to compute these metrics and benchmark delays effectively. Nodes represent entities in the blockchain network. Edges represent transactions between these entities, with weights indicating transaction delays.
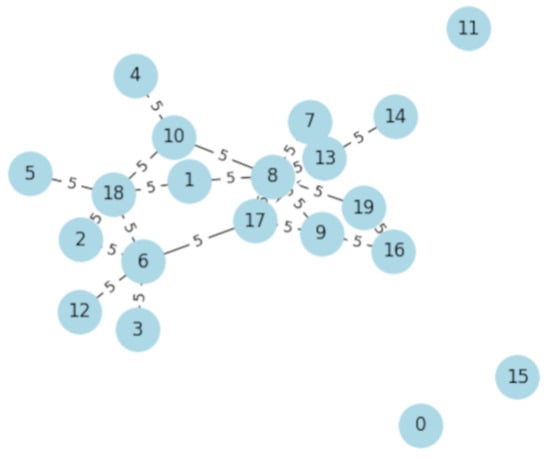
Figure 15.
Benchmarking Delays.
Assumption 14.
- The blockchain network is modeled as a transaction graph with average edge weight representing delays.
- Shortest path lengths characterize best-case timings.
Application Statement 14.
- Tracking growth trends in shortest path lengths and diameter of the baseline transaction graph during network attacks or congestion quantifies lower bounds on performance degradation.
Proof.
- (a)
- Measure average shortest path , diameter D and average degree on G.
- (b)
- Under attacks/congestion, adjust G by increasing edge weights to .
- (c)
- Re-compute shortest paths and diameter on updated G.
- (d)
- Benchmark slowdown as (Also compare and ).
□
This quantifies the extent of performance impacts under adverse events. Analyzing structural graph metrics on baseline vs stressed blockchain networks provides lower bound estimates on transaction delays.
5.3.2. Identifying Bottlenecks
Congested network links manifest as high betweenness centrality edges in transaction graphs. Alleviating such bottlenecks using solutions like off-chain payment channels improves throughput [82].
Figure 16 visualization demonstrates how graph analysis, particularly edge betweenness centrality, can be used to identify critical links in a blockchain network that leads to bottlenecks. Addressing congestion on these links, perhaps through off-chain payment channels or other scaling solutions, can potentially improve overall network throughput and efficiency. Nodes represent entities in the blockchain network. Edges represent transaction links between these entities. Edges with high betweenness centrality are highlighted in red. These edges are potential network bottlenecks, as they participate in a large number of shortest paths that experience high traffic and congestion. Other edges are shown in grey and dashed, indicating normal transaction links with less centrality and, presumably, less congestion.
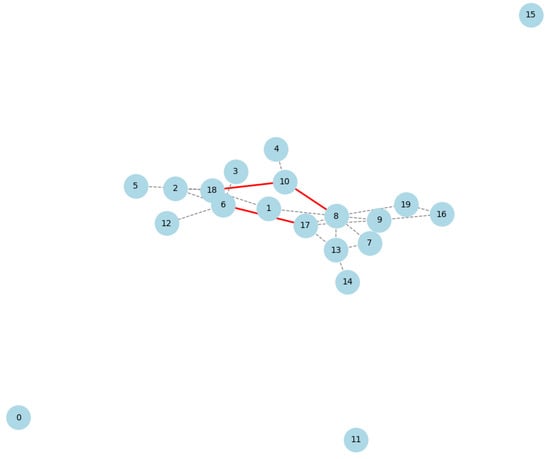
Figure 16.
Identifying bottlenecks.
Assumption 15.
- The blockchain network is modeled as a transaction graph with edges having capacities .
- Transaction throughput is limited by congested edges.
Application Statement 15.
- Edges with high betweenness centrality in the blockchain transaction graph correspond to network bottlenecks limiting throughput. Offloading transactions along these edges to payment channels can improve capacity.
Proof.
- (a)
- Compute edge betweenness centrality in graph G.
- (b)
- Edges with the highest participate in the largest number of shortest paths.
- (c)
- Congestion manifests as transaction backlogs along these top betweenness edges, reducing throughput.
- (d)
- Off-chain payment channels ease congestion along top bottleneck edges, improving network capacity.
□
Graph centrality metrics identify network bottlenecks while payment channels help mitigate congestion and transaction delays on blockchain platforms. This demonstrates a graph analysis-based approach to pinpoint and alleviate congestion bottlenecks limiting blockchain transaction throughput using concepts like betweenness centrality and off-chain scaling solutions.
5.3.3. Sharding Blockchains
Large networks can be partitioned into zones of dense intra-cluster and sparse inter-cluster connections via graph clustering methods. Transactions within shards process faster, enhancing capacity [83]. Figure 17 presents partitioning the network into shards like this, allowing transactions within each shard to be processed more quickly and efficiently, potentially enhancing the overall capacity and speed of the blockchain network. This graph-theoretical approach to sharding aims to improve blockchain scalability by optimizing the processing of transactions within densely connected communities. Nodes represent entities in the blockchain network. Edges represent transaction links between these entities. Different colors indicate different clusters or shards identified using graph clustering methods. Each color represents a different shard, nodes within the same shard (same color) are densely connected, indicating a high density of within-community transactions. Inter-cluster (inter-shard) connections are sparser, indicating less frequent transactions between different shards.
Figure 17.
Sharding blockchains.
Assumption 16.
- is a connected, undirected graph.
- is the set of clusters identified within G, where each is a subset of V, representing a shard.
Application Statement 16.
- Partitioning G into k shards such that transactions within each shard are processed more quickly and efficiently, thereby enhancing the overall capacity and speed of the blockchain network.
Proof.
Given a blockchain network modeled as a transaction graph , where V represents the set of nodes (entities in the blockchain network) and E represents the set of edges (transaction links between entities), our objective is to partition G into subgraphs () that represent shards. This partitioning aims to maximize the density of intra-cluster transactions while minimizing the inter-cluster transactions, enhancing overall network throughput.
- (a)
- Cluster Identification: Apply a graph clustering algorithm, such as modularity optimization, to partition G into k clusters. The modularity Q of a partition is given by:where m is the total number of edges, is the adjacency matrix of G, and are the degrees of nodes i and j, and is the Kronecker delta function, indicating if nodes i and j are in the same cluster. The goal is to maximize Q, which indicates a strong community structure with dense intra-cluster and sparse inter-cluster connections.
- (b)
- Shard Assignment: Each node is assigned to a shard based on its cluster membership determined in step 1. Formally, if , then v belongs to shard i.
- (c)
- Transaction Routing: Intra-shard transactions (those occurring between nodes within the same cluster) are routed internally within . This minimizes the path length and, by extension, the processing time for these transactions. Inter-shard transactions are minimized but when necessary, are processed through designated gateway nodes that facilitate communication between shards.
- (d)
- Throughput Enhancement: By confining the majority of transactions to densely connected clusters, each shard can independently process transactions in parallel, significantly increasing the network’s throughput. The reduction in inter-shard transactions decreases the overall network load, further contributing to speed improvements.
□
The application of graph clustering algorithms to partition a blockchain network into shards effectively segregates transactions into densely connected communities. This method enhances throughput by enabling parallel processing within shards and minimizing the load on the network, thereby increasing the capacity and speed of blockchain transactions. The formalization and optimization of such partitioning through graph-theoretical methods are crucial for realizing scalable and efficient blockchain architectures.
5.3.4. Shaping Peer Networks
Analyzing degree distributions and connectivity trends between node pairs allows configuring P2P topology for efficient resolvability of transactions [84]. Figure 18 infinite average path length suggests that there are isolated nodes or small disconnected components, highlighting areas for potential improvement in the network’s connectivity. This visualization and the calculated metrics demonstrate how analyzing the degree distribution and connectivity patterns in a P2P network can help in configuring the network structure for efficient transaction propagation. Adjustments to the network (like adding or removing edges) would be made to optimize these metrics. The goal is to achieve a network topology that ensures fast and reliable dissemination of transactions, which is crucial for the efficiency of blockchain systems. Nodes represent peers in the P2P network. Edges depict connections between these peers.
Figure 18.
Shaping peer networks.
Assumption 17.
- The P2P network is modeled as a graph where nodes are peers and edges depict connections.
- Efficient propagation of transactions requires optimal P2P topology.
Application Statement 17.
- Analyzing degree distribution and connectivity patterns in the P2P topology graph allows for configuring the network structure for fast and reliable transaction dissemination.
Proof.
- (a)
- Measure degree distribution and avg degrees of peer nodes in G.
- (b)
- Evaluate Giant connected component size and avg path lengths .
- (c)
- Configure graph via adding/removing edges and nodes to tailor , , and to optimal values.
- (d)
- This shapes the P2P topology for efficient and resolvable transaction propagation.
□
Applying graph metrics facilitates engineering blockchain P2P networks’ structure and connectivity patterns for reliable transaction dissemination.
Overall graph algorithms facilitate systematic tracing of performance issues while graph partitioning enables technical remedies.
5.4. Simulating Blockchain Networks
Often, new consensus protocols, computational models and attack strategies need evaluation before deployment on production systems [85]. Graph frameworks help simulate blockchain networks for such testing [86].
5.4.1. Sybil Attacks
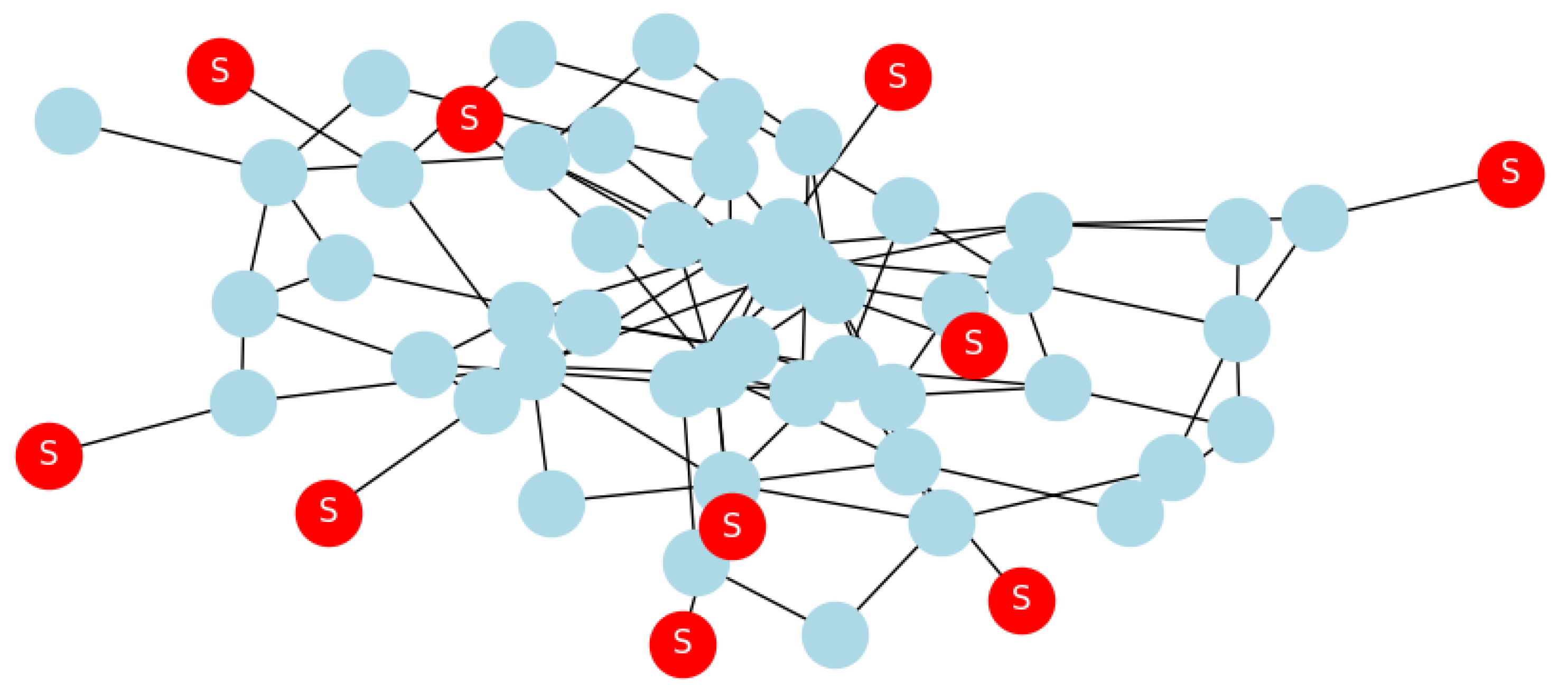
Adding fake identities to subvert consensus is a known risk. Operating Sybil attacks on modeled transaction graphs measures the effectiveness of detection mechanisms [87]. Figure 19 presents a graph-based network modeling and simulation, we can analyze the resilience of blockchain consensus systems against illicit Sybil attacks and benchmark the effectiveness of Sybil detection mechanisms designed to secure network consensus. Light Blue Nodes represent legitimate peers in the blockchain network. Red Nodes represent Sybil nodes inserted into the network by an adversary. These are labeled with ’S’ to indicate their Sybil status. Edges’ connections between nodes in the network, including those between legitimate peers and Sybil nodes, illustrate how Sybil nodes integrate into the network to subvert consensus mechanisms
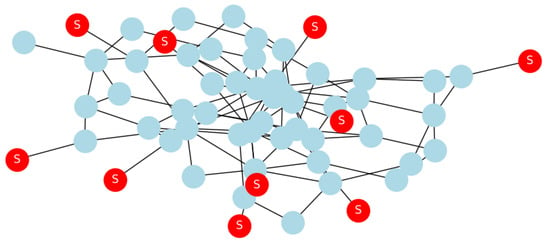
Figure 19.
Sybil attacks.
Assumption 18.
- represents the transaction or interaction graph of a blockchain network.
- represents the set of Sybil nodes inserted by an adversary.
- represents the set of legitimate nodes in the network.
Application Statement 18.
- Simulating Sybil attacks by introducing pseudo-nodes (S) into the modeled blockchain transaction graph G allows for the quantitative evaluation of the effectiveness of Sybil detection mechanisms designed to secure network consensus.
Proof.
Given a blockchain peer network modeled as an interaction graph , where V represents the set of nodes in the network, including both legitimate peers and Sybil nodes, and E represents the set of edges indicating connections between these nodes, our objective is to simulate Sybil attacks and evaluate the effectiveness of Sybil detection mechanisms.
- (a)
- Interaction Graph modelling: Define as the interaction graph of the blockchain network, where nodes represent peers (legitimate and Sybil) and edges represent connections or transactions between these peers.
- (b)
- Sybil Node Insertion: An adversary introduces n Sybil nodes into G, resulting in the updated graph , where and includes edges connecting Sybil nodes to legitimate nodes. Mathematically, for each Sybil node , connect s to at least one via edge .
- (c)
- Community Detection and Sybil Identification: Apply a community detection algorithm to aiming to partition into disjointed subsets where each subset represents a tightly knit community. Formally, identify partitions such that and for . Detect Sybil groups by analyzing community structures; communities with unusually high edge densities to specific external nodes (potential gateways) are flagged as Sybil.
- (d)
- Sybil Detection Algorithm Performance: Evaluate the detection algorithm by calculating the True Positive Rate (TPR) and False Positive Rate (FPR) based on the algorithm’s ability to accurately identify inserted Sybil nodes. Define TPR as and FPR as , where is true positives, is false negatives, is false positives, and is true negatives.
- (e)
- Benchmarking: Benchmark the Sybil detection algorithm’s performance across various network topologies and Sybil attack scenarios by varying the number of Sybil nodes (n) and their connection patterns within .
□
In this modeling of the blockchain network as an interaction graph and simulating Sybil attacks, we quantitatively evaluate the effectiveness of detection mechanisms against such attacks. The mathematical framework and community detection approach provides a systematic method for identifying Sybil nodes and assessing the resilience of blockchain consensus systems to illicit activities, ultimately benchmarking Sybil detection schemes on empirically modeled blockchain topologies.
5.4.2. Stress Testing
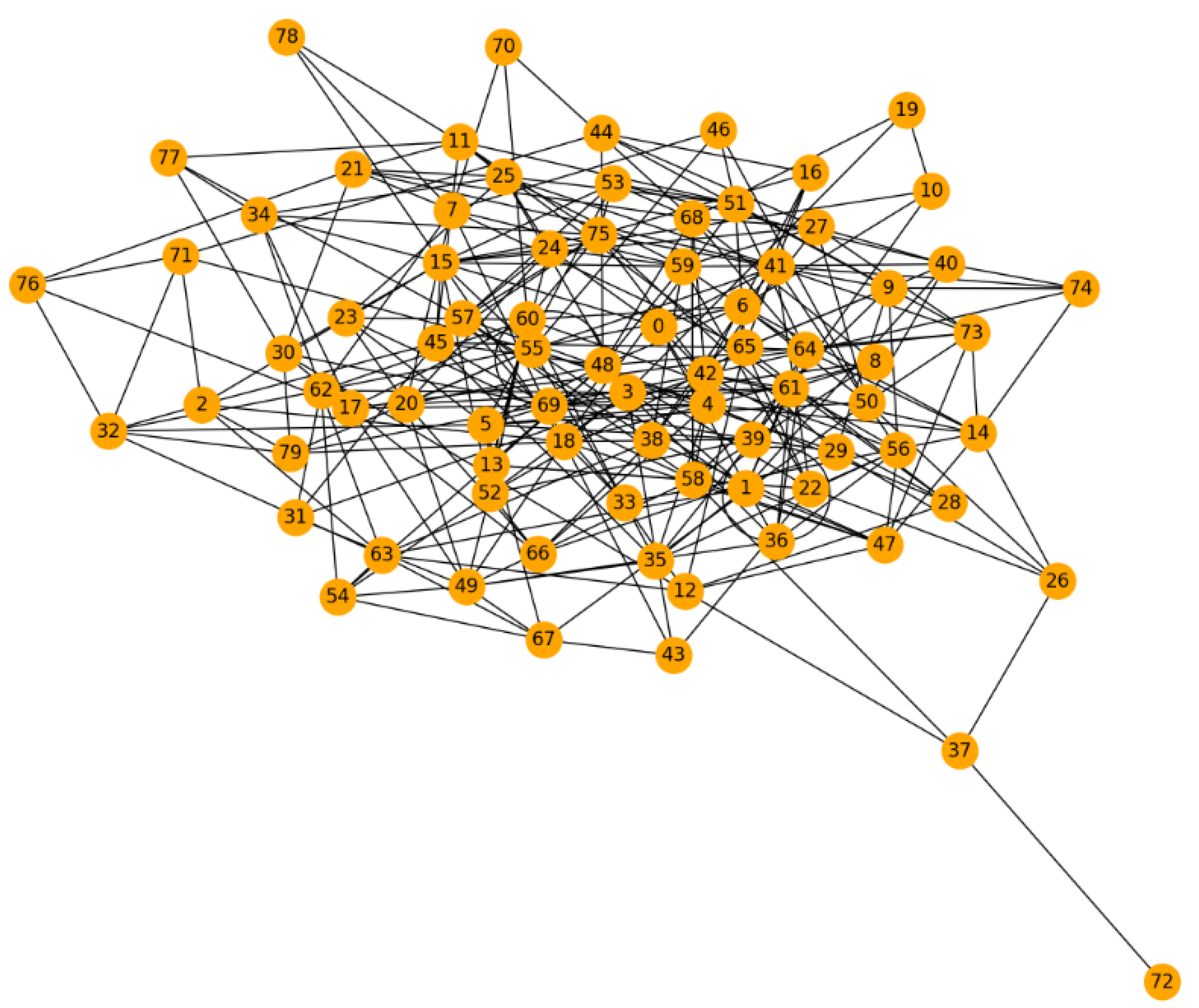
Simulating sudden surges in peak transaction loads on scaled versions of existing graphs examines system robustness. Mining inequality metrics on resultant graphs quantify capacity margins [88]. Figure 20 simulation demonstrates how scaling the blockchain network and introducing surges in transactions can affect network characteristics, such as mining power distribution, indicated by changes in average degree centrality. The increase in average degree centrality from the baseline to the scaled network under peak load suggests a shift in the network’s mining power distribution, potentially pointing towards emerging bottlenecks or capacity margins. Orange Nodes represent nodes in the scaled blockchain network. Edges indicate transactions between nodes, with an increased number of transactions to simulate a surge and examine network robustness under stress.
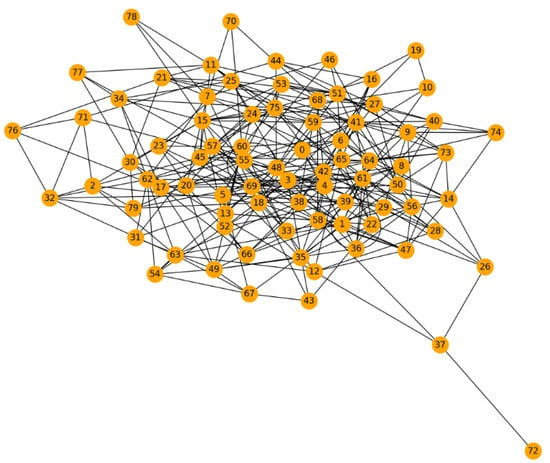
Figure 20.
Stress testing.
Assumption 19.
- The blockchain network is modeled as a transaction graph .
- Network robustness is evaluated under simulated peak traffic.
Application Statement 19.
- Subjecting scaled blockchain transaction graphs to simulated peak traffic loads reveals system capacity margins and bottlenecks via quantitative mining inequality metrics.
Proof.
- (a)
- Model baseline blockchain transaction network as graph . Obtain baseline mining power distribution.
- (b)
- Create scaled synthetic network with amplified transaction and mining traffic based on G.
- (c)
- Simulate surges and analyze emergent mining inequality and centralization metrics on the stressed graph.
□
This examines the robustness of the margins relative to baseline network inequality. Graph-based blockchain simulations under peak projected loads determine capacity headrooms and reliability weaknesses before real-world deployments.
5.4.3. Protocol Testing
Analyzing consensus propagation across node communication graphs under various conditions vets the performance of experimental protocols before finalization [89]. Figure 21 represents a blockchain peer network graph, which serves as a basis for protocol testing of consensus algorithms where nodes represent peers in the blockchain network. Edges depict the communication links between these peers.
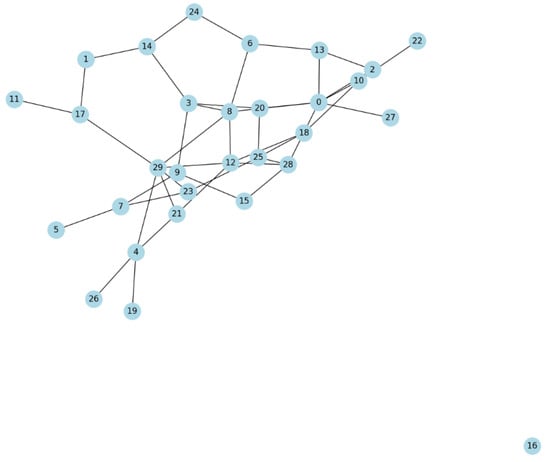
Figure 21.
Protocol testing.
Assumption 20.
- The blockchain peer network is modeled as a communication graph .
- Consensus requires agreement propagation among peers.
Application Statement 20.
- Simulating consensus algorithms on graph models of blockchain peer networks under various conditions facilitates the performance evaluation of proposed protocols before finalization.
Proof.
- (a)
- Model peer network as graph , capturing node connections.
- (b)
- Implement consensus protocol logic for state transitions of G’s nodes and edges.
- (c)
- Test consensus algorithm on G under different conditions of failures, delays and partitions.
- (d)
- Compare simulation metrics like agreement times, message complexity and partitions tolerated to analyze protocol progress and limitations.
□
This allows comprehensive benchmarking of any consensus mechanism under realistic scenarios. Graph-based blockchain network simulations enable the systematic testing of consensus protocols for standardization and live deployment.
5.4.4. Forecasting Trends
Evolving synthetic graphs by adding projected nodes and edges predicts emerging usage patterns and helps plan node additions and infrastructure upgrades [90]. Figure 22 represents an evolved synthetic blockchain network, developed for forecasting future trends in network growth and usage patterns. This network has been expanded based on projected increases in nodes and edges, simulating expected expansion and enabling predictions for emerging usage patterns and infrastructure requirements. The network starts with a historical state and evolves by adding a projected number of new nodes and edges, reflecting the anticipated growth. The orange nodes represent both historical and newly added nodes in the synthetic graph, showcasing the network’s expansion. Edges indicate transaction links, increased according to growth predictions.

Figure 22.
Forecasting trends.
Assumption 21.
- The historical blockchain network is modeled as transaction graph .
- Future growth and usage patterns need estimation.
Application Statement 21.
- Extrapolating synthetic blockchain network graphs based on adding projected nodes and edges to model expected expansion enables predicting emerging usage patterns and required infrastructure upgrades.
Proof.
- (a)
- Analyze historical transaction graph to develop blockchain adoption forecast models.
- (b)
- Initialize synthetic graph matching the latest state of G.
- (c)
- Evolve by adding nodes/edges based on growth predictions.
- (d)
- Analyze properties of the simulated expanded graph across multiple periods.
- (e)
- This forecasts transaction volumes and infrastructure demands to plan upgrades.
□
Generating synthetic blockchain graphs helps estimate future adoption trends for capacity planning.
All the above theorems and proofs using the graph theory model can enable modeling attack scenarios, simulations, forecasting and vetting decisions before modifying production systems. Graph theory can be used as a tool for blockchain simulation models and facilitate safer innovation.
5.5. NFT Manipulation Mapping
Graph theory can be effectively used to represent and analyze activities like buying and selling NFTs (Non-Fungible Tokens) to create fake volume, among other manipulative trading strategies [91]. In a graph-theoretical model, these activities can be mapped in a way that highlights the relationships and transactions between accounts or entities, making it easier to identify patterns indicative of such practices [63]. Various avenues on how graph theory can be applied to the specific activities are as follows:
5.5.1. Buying and Selling NFTs to Create Fake Volume (Wash Trading)
Identifying cycles where an NFT is repeatedly traded between the same set of accounts within a short time frame can indicate wash trading. High transaction volumes with minimal change in ownership could be flagged for further investigation Hasan et al. [92]. Wash trading in the NFT market is a significant concern that requires attention and monitoring to maintain market integrity [93]. Suspicious trading activities, such as wash trading, have been observed in the NFT ecosystem, emphasizing the need for robust detection mechanisms. By characterizing wash trading behaviors through graph theory analysis, it becomes possible to pinpoint irregularities and potential fraudulent activities in NFT transactions [94]. Victor von et al. [95] provides a lower bound estimation for suspicious trading behaviour on NFT markets.
Assumption 22.
- Graph Model: The blockchain transaction network is modeled as a directed graph where:
- −
- V is a set of vertices representing accounts participating in the NFT market.
- −
- E is a set of directed edges representing transactions of NFTs between accounts. Each edge from vertex i to vertex j represents a transaction and is associated with attributes such as transaction value , timestamp , and the specific NFT involved.
- C is a set of cycles within G, where each cycle represents a sequence of transactions returning to the original account.
- A short time frame T is defined to identify rapid trading cycles indicative of wash trading.
- The transaction volume for a cycle C is the sum of the transaction values for all edges in C.
Application Statement 22.
- For a given NFT marketplace transaction graph G, cycles that complete within a short time frame T and exhibit high transaction volumes relative to the network average are indicative of wash trading.
Proof.
- (a)
- Cycle Detection. Detect all cycles C in G, utilizing a depth-first search or other graph traversal algorithms capable of identifying cycles.
- (b)
- Temporal Analysis. For each cycle C, calculate the duration asfor all . Identify cycles where .
- (c)
- Volume Analysis. Calculate the transaction volume for each cycle C identified in step b as
- (d)
- Benchmarking. Define the network’s average transaction volume and compare for each cycle C against . Cycles with are scrutinized for wash trading.
- (e)
- Ownership Consistency. Verify the change in ownership for NFTs involved in cycles C. Minimal change in ownership despite high reinforces the wash trading hypothesis.
□
Figure 23 directed graph modeling of the NFT marketplace transactions. In this graph, Nodes (in skyblue) represent accounts participating in the NFT market. Directed edges (in black) symbolize transactions of NFTs between these accounts. Each NFT involved in a transaction is denoted by labels on the edges (in red). From this graph representation, we detected 37 cycles, which could potentially indicate wash trading activities where NFTs are repeatedly traded between the same set of accounts within a short timeframe.
Figure 23.
NFT marketplace transactions.
Through the mathematical formulation of detecting cycles C within a transaction graph G, analyzing these cycles for short-duration and abnormally high transaction volumes , and scrutinizing the consistency of ownership, we can effectively identify and quantify wash trading activities in the NFT marketplace. This methodological approach enhances our ability to maintain the integrity of blockchain platforms by pinpointing manipulative trading behaviors, thereby ensuring a more transparent and trustworthy NFT ecosystem.
5.5.2. Coordinated Trading
By examining the timestamps and correlation of transactions among a subset of nodes, one can detect abnormal spikes in activity that suggest coordination. Clustering algorithms can help identify groups with unusually synchronized trading patterns [96].
Assumption 23.
- Let be a directed graph where
- −
- V represents traders in the NFT market, and
- −
- E represents transactions of NFTs between traders. Each transaction from trader i to trader j is associated with attributes like transaction value , timestamp , and the specific NFT involved.
- −
- Define a subset where traders are involved in coordinated trading, engaging in transactions within a narrowly defined time frame T.
Application Statement 23.
- In the NFT marketplace represented by graph G, the subset S of traders engaging in coordinated trading activities can be identified by analyzing the temporal clustering of transactions within T, which leads to an abnormal surge in trading volume and price movement for the involved NFTs.
Proof.
- (a)
- Temporal Clustering. For each NFT involved in transactions within the subset S, cluster transactions based on their timestamps . Identify clusters where the number of transactions exceeds a threshold within time frame T, indicative of coordinated trading.
- (b)
- Volume and Price Analysis. Calculate the total transaction volume and average price change for NFTs involved in identified clusters. Compare and with the network-wide averages and to identify significant deviations.
- (c)
- Statistical Significance. Use statistical tests to evaluate the likelihood that observed surges in volume and price movement are due to chance. Significant deviations from the averages suggest the presence of coordinated trading.
□
Figure 24 visualization represents a directed graph of NFT market transactions, highlighting the dynamics of coordinated trading. In the graph, Skyblue Nodes represent all traders participating in the NFT market. Red Nodes indicate the subset of traders involved in coordinated trading within a defined time frame, showcasing potential collusion to manipulate market perception. Edges symbolize transactions between traders, annotated with NFT identifiers, transaction values, and timestamps, providing a comprehensive view of market activity. This model allows us to identify clusters of coordinated trading activity (red nodes) and analyze the temporal clustering of transactions within the narrowly defined time frame T. By examining these patterns and comparing the transaction volume and price changes of involved NFTs to network-wide averages, we can effectively detect and quantify instances of market manipulation.
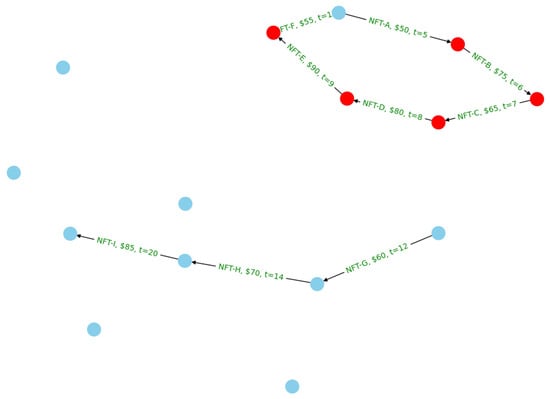
Figure 24.
Coordinated Trading Visualization.
The ability to visualize and mathematically analyze such trading activities highlights the importance of graph-based analysis in enhancing market transparency, integrity, and fairness. Through these methodologies, stakeholders can better understand market dynamics, implement measures to mitigate manipulative practices and foster a more trustworthy NFT ecosystem.
5.5.3. Cross Trading
Cross-referencing transactions involving the same NFTs across different graphs can reveal cross-trading activities. Matching transactions by time, NFT, and price across platforms would highlight potential cross-trading schemes [97].This approach enables the detection of coordinated trading practices that span multiple platforms, contributing to a more comprehensive understanding of market activities and potentially manipulative behaviors.
Assumption 24.
- Let us consider a collection of directed graphs where each graph represents a transaction network on a distinct NFT trading platform k. In each graph:
- −
- is a set of vertices representing traders on platform k.
- −
- is a set of directed edges representing transactions of NFTs between traders on platform k, with each edge from trader i to trader j associated with attributes like transaction value , timestamp , and the specific NFT involved.
Cross-trading is characterized by transactions involving the same set of traders and NFTs across different platforms .
Application Statement 24.
- In a multi-platform NFT marketplace represented by a collection of graphs , the presence of identical subsets of traders engaging in transactions involving the same NFTs across these platforms is indicative of the cross-trading aimed at artificially inflating perceived demand and price.
Proof.
- (a)
- Identification of Common Traders Across Platforms. Identify subsets of traders S who are active across multiple platforms, i.e., .
- (b)
- Transaction Matching. For each trader and for each pair of platforms , match transactions based on NFT identifiers and approximate timestamps. That is, find pairs of transactions where and is minimal, suggesting a deliberate attempt to show activity on multiple platforms.
- (c)
- Volume and Price Analysis. Calculate the aggregated transaction volume and average price for matched transactions across platforms. Compare these with platform-specific and network-wide averages to identify significant deviations.
- (d)
- Statistical Significance. Employ statistical methods to assess whether the observed patterns of cross-platform trading deviate significantly from expected distribution under normal market conditions.
□
Figure 25 visualization illustrates the concept of cross-trading across two distinct NFT trading platforms, represented as directed graphs for platforms G1 represented in blue nodes and G2 represented in green nodes. Nodes represent traders participating in the NFT market on each platform. Directed edges symbolize transactions of NFTs between traders. This model enables the identification of cross-trading activities by analyzing transactions involving the same NFTs by the same group of traders across different platforms. By leveraging graph theory, stakeholders can better safeguard the ecosystem against such deceptive strategies, ensuring a more transparent and fair market environment.
Figure 25.
Cross trading.
5.5.4. Self-Trading
Detecting self-trading involves identifying subgraphs where transactions form closed loops back to the original node, potentially through multiple intermediary nodes, indicating self-trading activity Das et al. [98]. By examining these closed loops within the transaction graph, irregularities suggestive of self-trading can be uncovered, enabling the identification of such manipulative behaviors in NFT transactions. This type of wash trade can be detected by finding Strongly Connected Components (SCCs) in the transaction graph.
Assumption 25.
- Graph Representation. The NFT marketplace is modeled as a directed graph , where
- V represents individual trading accounts and
- E represents transactions between these accounts. Each transaction from account i to account j is associated with attributes such as transaction value , timestamp , and the specific NFT involved.
Account Linkage. A set of accounts A is controlled by a single entity engaging in self-trading. These accounts may engage in transactions amongst themselves to simulate genuine trading activity.
Transaction Analysis. Transactions that contribute to self-trading are characterized by the transfer of NFTs within set A without introducing external market participants.
Application Statement 25.
- Self-trading in the NFT marketplace can be identified by analyzing graph G for closed transaction loops within the subset of accounts A, indicating artificial trading activity aimed at inflating perceived market activity and NFT prices.
Proof.
- (a)
- Identify Linked Accounts. Utilize community detection algorithms or heuristic analysis to identify subsets of accounts that exhibit patterns of closed-loop transactions indicative of single-entity control.
- (b)
- Detect Closed Transaction Loops. For each account , trace outgoing transactions where , forming closed loops that start and end at the same account or within A.
- (c)
- Analyze Transaction Attributes. Examine attributes , , and of transactions within closed loops for patterns such as repetitive trading of the same NFT, closely timed buy-sell actions, and transaction values inconsistent with market norms.
- (d)
- Quantify Artificial Activity. Aggregate the volume of transactions and the frequency of NFT trades within A to quantify the scale of self-trading activity.
- (e)
- Statistical Significance. Assess the statistical deviation of transaction patterns within A from those of the broader market to confirm the non-random nature of self-trading behavior.
□
Figure 26 visualization represents a directed graph simulating self-trading within the NFT marketplace. Nodes (in skyblue) correspond to individual trading accounts within the marketplace. A subset of these accounts (A = 1, 2, 3) is controlled by a single entity engaged in self-trading to simulate genuine trading activity. Directed edges symbolize transactions of NFTs between these controlled accounts. The edges are labeled with the specific NFT involved in the transaction, illustrating the artificial circulation of NFTs within the subset A. This model effectively demonstrates how self-trading can be identified through the analysis of closed transaction loops among linked accounts, thereby artificially inflating trading volume and NFT prices. Through the application of graph theory, the phenomenon of self-trading in the NFT marketplace can be effectively detected and quantified. By modeling the marketplace as a directed graph and identifying patterns of closed transaction loops among linked accounts, it is possible to uncover attempts to artificially inflate trading volume and NFT.
Figure 26.
Self-trading simulation.
Applying graph theory in the analysis of NFT trading activities not only aids in detecting manipulative practices but also contributes to enhancing market transparency and integrity. By leveraging graph-based models to map out transactions and relationships, researchers and regulators can gain valuable insights into fraudulent behaviors and develop effective monitoring tools to safeguard the NFT market.
6. Discussion
This paper demonstrates how graph algorithms analyze blockchain infrastructure across multiple facets—decentralization trends, security hazards, scalability issues and simulation testing. Translating ecosystem dynamics into graphical constructs provides actionable intelligence regarding vulnerabilities. Graph techniques also pinpoint inefficiencies while also assessing resilience to combat external threats or internal performance degradations. Network analysis and predictive modeling further enable smoother technology management ensuring sound innovations.
We explored the multifaceted applications of graph theory and network analysis within the context of blockchain platforms, illustrating how these mathematical tools can unravel the complex dynamics and structural properties inherent to blockchain technology. By translating the intricate web of transactions, consensus mechanisms, and user interactions into graph-based models, we unlocked nuanced insights into the blockchain’s operational efficiency, security posture, and scalability challenges.
The use of graph properties and metrics enriches our understanding of blockchain networks beyond mere transactional throughput or token distribution. It allows for a deeper investigation into the essence of decentralization, revealing how power and control are concentrated across nodes or how resilient the network is to adversarial attacks. This granular view not only highlights current strengths and vulnerabilities but also provides a blueprint for mitigating risks and enhancing system robustness.
Security assessments, through the lens of graph theory, illuminate the pathways through which malicious entities can compromise network integrity. Whether it is through Sybil attacks, double-spending, or other forms of manipulation, graph models help in devising countermeasures that are both precise and effective. Similarly, the examination of network performance under varying loads and conditions offers actionable intelligence for optimizing transaction flow and reducing latency, thereby ensuring a seamless user experience.
Graph theory can also be applied to detect and prevent fraudulent activities in the NFT market, such as wash trading, coordinated trading, cross trading, and self trading. These activities involve manipulating the market by creating artificial demand and inflating prices through coordinated buying and selling of NFTs among a group of users or by a single user using multiple accounts. Graph analysis techniques can identify suspicious trading patterns and clusters of users engaged in these activities by examining the relationships between buyers, sellers, and NFTs in the transaction graph.
The adoption of graph-based approaches for blockchain analysis is not without its challenges. The dynamic nature of blockchain networks, coupled with the ever-increasing scale of transactions, demands the continuous refinement of graph algorithms and modeling techniques. Additionally, privacy considerations and the need for anonymization in graph data pose significant hurdles that must be navigated carefully to preserve user confidentiality while still deriving valuable insights.
7. Conclusions
Throughout this paper, we demonstrated the instrumental role of graph theory and network analysis in enhancing our comprehension and management of blockchain platforms. By representing decentralized digital ledgers and associated interactions within blockchain systems as graph models, this paper illustrates how mathematical abstractions enable advanced evaluations regarding topological structure, operational dynamics and simulated workloads. The multifaceted insights gleaned through graph network analytics empower data-driven decision support to govern blockchain platforms. Graph techniques unveil trends obscuring system transparency, diagnose performance inefficiencies, strengthen network robustness and accelerate innovation cycles—contributing to the continuous evolution of blockchain technology.
As we look to the future, the continued advancement and the increasing sophistication of modeling techniques promise to further bolster the utility of graph-based approaches in blockchain analysis.
8. Limitations and Future Work
While this study provides valuable insights into the application of graph theory in blockchain analysis, it is important to acknowledge its limitations and potential avenues for future research.
One limitation of this work is its primary focus on graph theory, with only a light touch on network science. Although graph theory and network science are closely related and often used in conjunction, this study concentrates mainly on the mathematical aspects of graph theory and its applications in modeling blockchain systems. The thin line separating graph theory and network science is not extensively explored, and a more comprehensive integration of both fields could yield additional insights and opportunities for blockchain analysis.
Another limitation is the absence of real-time blockchain scalability analysis. The scope of this study is limited to theoretical proofs and simulations, demonstrating the potential role of graph theory in modeling and optimizing blockchain networks. However, the application of these concepts to real-time blockchain datasets is not included. Future research could focus on implementing graph-based techniques in live blockchain environments to validate their effectiveness and scalability in handling large-scale, dynamic networks.
It is important to emphasize that this study serves as a theoretical foundation, proving the significance of graph theory in blockchain modeling and optimization. The aim is to showcase how graph theory can be effectively used to model real-world problems in the context of blockchain and provide optimal solutions. However, the practical implementation and evaluation of these techniques in real-time blockchain systems remain open challenges for future work.
Future research could explore several directions to build upon the findings of this study. One avenue is to delve deeper into the integration of graph theory and network science, leveraging the strengths of both fields to develop more comprehensive and robust models for blockchain analysis. This could involve incorporating network science concepts such as network dynamics, community detection, and information propagation into graph-based approaches.
Another direction for future work is to apply graph theory to real-time blockchain datasets, testing the scalability and efficiency of the proposed techniques in handling large-scale, dynamic networks. This could involve collaborating with blockchain platforms or accessing public blockchain data to validate the performance of graph-based algorithms in real-world scenarios.
Additionally, future research could explore the application of graph theory to specific blockchain use cases, such as supply chain management, decentralized finance (DeFi), or identity verification. By focusing on domain-specific challenges and requirements, researchers can develop tailored graph-based solutions that address the unique needs of each application area.
Furthermore, the integration of machine learning and deep learning techniques with graph theory could open up new possibilities for blockchain analysis. Graph neural networks, for example, have shown promise in tasks such as node classification, link prediction, and anomaly detection. Combining these advanced learning algorithms with graph-based representations of blockchain data could lead to more accurate and efficient analysis tools.
This study provides a solid theoretical foundation for the application of graph theory in blockchain analysis, there is ample room for future research to build upon these findings. By addressing the limitations, exploring new directions, and leveraging the power of graph theory in conjunction with other fields, researchers can continue to advance the understanding and optimization of blockchain networks, ultimately contributing to the development of more secure, scalable, and efficient decentralized systems.
Author Contributions
Conceptualization, G.J., K.L.B. and C.P.; methodology, K.L.B.; simulation, G.J.; validation, C.P., K.L.B. and G.J.; formal analysis, K.L.B.; investigation, C.P.; resources, G.J.; data curation, K.L.B.; writing—original draft preparation, G.J.; writing—review and editing, C.P. and K.L.B.; visualization, G.J.; supervision, G.J. and C.P.; project administration, K.L.B.; funding acquisition, G.J., K.L.B. and C.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yli-Huumo, J.; Ko, D.; Choi, S.; Park, S.; Smolander, K. Where is current research on blockchain technology?—A systematic review. PLoS ONE 2016, 11, e0163477. [Google Scholar] [CrossRef] [PubMed]
- Sanka, A.; Cheung, R. A systematic review of blockchain scalability: Issues, solutions, analysis and future research. J. Netw. Comput. Appl. 2021, 195, 103232. [Google Scholar] [CrossRef]
- Barabási, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Easley, D.; Kleinberg, J. Networks, Crowds, and Markets: Reasoning about a Highly Connected World; Cambridge University Press: Cambridge, UK, 2010; Volume 1. [Google Scholar]
- Gangrade, A.; Agrawal, B.; Kumar, S.; Mansuri, A. A study of applications of graph colouring in various fields. Int. J. Stat. Appl. Math. 2022, 7, 2022. [Google Scholar] [CrossRef]
- Majeed, A.; Rauf, I. Graph theory: A comprehensive survey about graph theory applications in computer science and social networks. Inventions 2020, 5, 10. [Google Scholar] [CrossRef]
- Raza, H.; Sharma, S.K.; Azeem, M. On Domatic Number of Some Rotationally Symmetric Graphs. J. Math. 2023, 2023, 3816772. [Google Scholar] [CrossRef]
- Ahmad, A.; Hasni, R.; Akhter, N.; Elahi, K. Analysis of distance-based topological polynomials associated with zero-divisor graphs. Comput. Mater. Contin. 2022, 70, 2898–2904. [Google Scholar] [CrossRef]
- Holmes, T.D.; Rothman, R.H.; Zimmerman, W.B. Graph theory applied to plasma chemical reaction engineering. Plasma Chem. Plasma Process. 2021, 41, 531–557. [Google Scholar] [CrossRef]
- El-Mesady, A.; Bazighifan, O. Construction of mutually orthogonal graph squares using novel product techniques. J. Math. 2022, 2022, 9722983. [Google Scholar] [CrossRef]
- Nithin, G.; Aslam, S.; Sathidevi, P.; Ameer, P.; Gopinath, S.; Radhakrishnan, K.; Parasuram, H. Localization of Epileptogenic Zone: A Graph Theoretical Approach. In Proceedings of the 2nd International Conference on Vision, Image and Signal Processing, Las Vegas, NV, USA, 27–29 August 2018; pp. 1–5. [Google Scholar]
- Nayana, P.; Iyer, R.R. An algorithm to find a dominating set that secures any connected graph G. In Proceedings of the 2022 IEEE 4th Ph.D. Colloquium on Emerging Domain Innovation and Technology for Society (Ph.D. EDITS), Bangalore, India, 4–5 November 2022; pp. 1–2. [Google Scholar]
- Thushara, A.; Amma, C.U.; John, A. Graph Theory-Based Brain Network Connectivity Analysis and Classification of Alzheimer’s Disease. Int. J. Image Graph. 2023, 23, 2240006. [Google Scholar] [CrossRef]
- Jose, G.M.; N, G.K. A Contemporary Technique to Place PMU in an Electrical Power Network using Graph Theory. In Proceedings of the 2023 Fifteenth International Conference on Contemporary Computing, Noida, India, 3–5 August 2023; pp. 598–602. [Google Scholar]
- Nabiyev, V.; Çakiroğlu, Ü.; Karal, H.; Erümit, A.K.; Ayça, Ç. Application of graph theory in an intelligent tutoring system for solving mathematical word problems. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 687–701. [Google Scholar]
- Wan, J.; Chen, H.; Li, T.; Sang, B.; Yuan, Z. Feature grouping and selection with graph theory in robust fuzzy rough approximation space. IEEE Trans. Fuzzy Syst. 2022, 31, 213–225. [Google Scholar] [CrossRef]
- Toppi, J.; Ciaramidaro, A.; Vogel, P.; Mattia, D.; Babiloni, F.; Siniatchkin, M.; Astolfi, L. Graph theory in brain-to-brain connectivity: A simulation study and an application to an EEG hyperscanning experiment. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 2211–2214. [Google Scholar]
- Kisku, D.R.; Gupta, P.; Sing, J.K. Applications of Graph Theory in Face Biometrics. In International Conference on Business Administration and Information Processing, Proceedings of the BAIP 2010: Information Processing and Management, Trivandrum, Kerala, India, 26–27 March 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 28–33. [Google Scholar]
- Bhattacharya, S.; Poray, J. Application of graph theory in bigdata environment. In Proceedings of the 2016 International Conference on Computer, Electrical & Communication Engineering (ICCECE), Kolkata, India, 16–17 December 2016; pp. 1–8. [Google Scholar]
- Yan, S.; Wei, W.; Rui, W.; Zhengyi, W. Application of Matrix Algorithm Based on Graph Theory in Real-time Fault Diagnosis Knowledge Perfection Detection of Spacecraft Telemetry Data. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 25–27 October 2022; pp. 1–6. [Google Scholar]
- Priyadarsini, P. A survey on some applications of graph theory in cryptography. J. Discret. Math. Sci. Cryptogr. 2015, 18, 209–217. [Google Scholar] [CrossRef]
- Lahby, M. Enhancing modeling for network selection using graph theory in beyond 4g networks. Int. J. Bus. Data Commun. Netw. 2020, 16, 48–69. [Google Scholar] [CrossRef]
- Schizas, C.; Evans, F. APL and graph theory in dynamic systems analysis. IEE Proc.-Control Theory Appl. 1981, 3, 85–92. [Google Scholar] [CrossRef]
- Jovanović, N.; Zakić, A. Network simulation tools and spectral graph theory in teaching computer network. Comput. Appl. Eng. Educ. 2018, 26, 2084–2091. [Google Scholar] [CrossRef]
- Andrews, M.; Bhatnagar, S. Graph theory in microprogramming: An alternate approach to designing micro-code for microprocessing. Comput. Electr. Eng. 1980, 7, 175–183. [Google Scholar] [CrossRef]
- Yang, Z.X.; Ning, H.y.; Sun, J.Q.; Yang, J.B. Service portfolio optimization algorithm based on value model and graph theory in SOA. In Proceedings of the 2013 IEEE 4th International Conference on Software Engineering and Service Science, Beijing, China, 23–25 May 2013; pp. 64–67. [Google Scholar]
- Riaz, F.; Ali, K.M. Applications of graph theory in computer science. In Proceedings of the 2011 Third International Conference on Computational Intelligence, Communication Systems and Networks, Bali, Indonesia, 26–28 July 2011; pp. 142–145. [Google Scholar]
- Pavlova, N. Several Outlines of Graph Theory in Framework of MDA. In Advances in Information Systems Development: New Methods and Practice for the Networked Society; Springer: Berlin/Heidelberg, Germany, 2007; pp. 25–36. [Google Scholar]
- Chatain, J.; Varga, R.; Fayolle, V.; Kapur, M.; Sumner, R.W. Grounding graph theory in embodied concreteness with virtual reality. In Proceedings of the Seventeenth International Conference on Tangible, Embedded, and Embodied Interaction, Warsaw, Poland, 26 February–1 March 2023; pp. 1–13. [Google Scholar]
- Coufal, P.; Hubálovskỳ, Š.; Hubálovská, M. Application of basic graph theory in autonomous motion of robots. Mathematics 2021, 9, 919. [Google Scholar] [CrossRef]
- Doczkal, C.; Pous, D. Graph theory in Coq: Minors, treewidth, and isomorphisms. J. Autom. Reason. 2020, 64, 795–825. [Google Scholar] [CrossRef]
- Bowie, W.S. Applications of graph theory in computer systems. Int. J. Comput. Inf. Sci. 1976, 5, 9–31. [Google Scholar] [CrossRef]
- Erumit, A.K.; Nabiyev, V.; Cebi, A. Modeling of motion problems based on graph theory in maths. In Proceedings of the 2012 IV International Conference Problems of Cybernetics and Informatics (PCI), Baku, Azerbaijan, 12–14 September 2012; pp. 1–3. [Google Scholar]
- An, P.T.; Hai, N.N.; Van Hoai, T. The Role of Graph Theory in Solving Euclidean Shortest Path Problems in 2D and 3D. In Advances in Computer Science and Its Applications: CSA 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 179–184. [Google Scholar]
- Qu, C.; Tao, M.; Yuan, R. A hypergraph-based blockchain model and application in internet of things-enabled smart homes. Sensors 2018, 18, 2784. [Google Scholar] [CrossRef] [PubMed]
- Tsoulias, K.; Palaiokrassas, G.; Fragkos, G.; Litke, A.; Varvarigou, T.A. A graph model based blockchain implementation for increasing performance and security in decentralized ledger systems. IEEE Access 2020, 8, 130952–130965. [Google Scholar] [CrossRef]
- Abay, N.C.; Akcora, C.G.; Gel, Y.R.; Kantarcioglu, M.; Islambekov, U.D.; Tian, Y.; Thuraisingham, B. Chainnet: Learning on blockchain graphs with topological features. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 946–951. [Google Scholar]
- Shen, M.; Zhang, J.; Zhu, L.; Xu, K.; Du, X. Accurate decentralized application identification via encrypted traffic analysis using graph neural networks. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2367–2380. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Z.; Li, P.; Guo, S.; Fan, X.; Zhang, J. A graph learning based approach for identity inference in dapp platform blockchain. IEEE Trans. Emerg. Top. Comput. 2020, 10, 438–449. [Google Scholar] [CrossRef]
- Chung, F.R. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997; Volume 92. [Google Scholar]
- Wang, X.; Zha, X.; Ni, W.; Liu, R.P.; Guo, Y.J.; Niu, X.; Zheng, K. Survey on blockchain for Internet of Things. Comput. Commun. 2019, 136, 10–29. [Google Scholar] [CrossRef]
- Jayabalasamy, G.; Koppu, S. High-performance Edwards curve aggregate signature (HECAS) for nonrepudiation in IoT-based applications built on the blockchain ecosystem. J. King Saud. Univ. Comput. Inf. Sci. 2022, 34, 9677–9687. [Google Scholar] [CrossRef]
- Guruprakash, J.; Koppu, S. EC-ElGamal and Genetic algorithm-based enhancement for lightweight scalable blockchain in IoT domain. IEEE Access 2020, 8, 141269–141281. [Google Scholar] [CrossRef]
- Khan, D.; Jung, L.T.; Hashmani, M.A. Systematic literature review of challenges in blockchain scalability. Appl. Sci. 2021, 11, 9372. [Google Scholar] [CrossRef]
- Gochhayat, S.; Shetty, S.; Mukkamala, R.; Foytik, P.; Kamhoua, G.; Njilla, L. Measuring decentrality in blockchain based systems. IEEE Access 2020, 8, 178372–178390. [Google Scholar] [CrossRef]
- Madine, M.; Salah, K.; Jayaraman, R.; Al-Hammadi, Y.; Arshad, J.; Yaqoob, I. appxchain: Application-level interoperability for blockchain networks. IEEE Access 2021, 9, 87777–87791. [Google Scholar] [CrossRef]
- Hu, X.; Islam, A.; Britz, T. Bounds on the closeness centrality of a graph. arXiv 2022, arXiv:2204.11283. [Google Scholar]
- Bazari, A.S.; Aggarwal, A.; Asif, W.; Lestas, M.; Rajarajan, M. Node criticality assessment in a blockchain network. In Proceedings of the 2nd Workshop on Blockchain-Enabled Networked Sensor, New York, NY, USA, 10 November 2019; pp. 22–27. [Google Scholar]
- Shahsavari, Y.; Zhang, K.; Talhi, C. Toward quantifying decentralization of blockchain networks with relay nodes. Front. Blockchain 2022, 5, 812957. [Google Scholar] [CrossRef]
- Bhavadharini, R.; Karthik, S. Blockchain enabled metaheuristic cluster based routing model for wireless networks. Comput. Syst. Sci. Eng. 2023, 44, 1233–1250. [Google Scholar] [CrossRef]
- Ezeh, C.; Ren, T.; Li, Z.; Yiqun, W.; Qu, Y. Multi-type node detection in network communities. Entropy 2019, 21, 1237. [Google Scholar] [CrossRef]
- Devillers, R. Articulation of transition systems and its application to Petri net synthesis. In Application and Theory of Petri Nets and Concurrency, Proceedings of the 40th International Conference, PETRI NETS 2019, Aachen, Germany, 23–28 June 2019; Proceedings 40; Springer: Berlin/Heidelberg, Germany, 2019; pp. 113–126. [Google Scholar]
- Chen, L.; Shan, S. Optimization of the trust propagation on supply chain network based on blockchain plus. J. Intell. Manag. Decis. 2022, 1, 17–27. [Google Scholar] [CrossRef]
- Giuntini, F.; Moraes, K.; Cazzolato, M.; Kirchner, L.; Reis, M.; Traina, A.; Campbell, A.; Ueyama, J. Modeling and assessing the temporal behavior of emotional and depressive user interactions on social networks. IEEE Access 2021, 9, 93182–93194. [Google Scholar] [CrossRef]
- Serrano, W. The blockchain random neural network in cybersecurity and the Internet of Things. In Artificial Intelligence Applications and Innovations, Proceedings of the 15th IFIP WG 12.5 International Conference, AIAI 2019, Hersonissos, Crete, Greece, 24–26 May 2019; Proceedings 15; Springer: Berlin/Heidelberg, Germany, 2019; pp. 50–63. [Google Scholar]
- Lahmadi, A.; Bertin, E.; Li, R. Brains 2020 special issue: Blockchain research and applications for innovative networks and services. Int. J. Netw. Manag. 2021, 32. [Google Scholar] [CrossRef]
- Li, C.; Palanisamy, B. Comparison of decentralization in dpos and pow blockchains. In Proceedings of the Blockchain, ICBC 2020, Honolulu, HI, USA, 18–20 September 2020; pp. 18–32. [Google Scholar] [CrossRef]
- Furno, A.; Faouzi, N.E.; Sharma, R.; Zimeo, E. Graph-based ahead monitoring of vulnerabilities in large dynamic transportation networks. PLoS ONE 2021, 16, e0248764. [Google Scholar] [CrossRef]
- Shinkar, S.V.; Thankachan, D. Scmbqa: Design of a customised scm-aware sidechaining model for qos enhancement under attack scenarios. Int. J. Recent Innov. Trends Comput. Commun. 2022, 10, 200–212. [Google Scholar] [CrossRef]
- Hashim, F.; Shuaib, K.; Sallabi, F. Medshard: Electronic health record sharing using blockchain sharding. Sustainability 2021, 13, 5889. [Google Scholar] [CrossRef]
- Casale-Brunet, S.; Ribeca, P.; Doyle, P.; Mattavelli, M. Networks of Ethereum Non-Fungible Tokens: A graph-based analysis of the ERC-721 ecosystem. In Proceedings of the 2021 IEEE International Conference on Blockchain (Blockchain), Melbourne, Australia, 6–8 December 2021; pp. 188–195. [Google Scholar]
- Tan, Y.; Wu, Z.; Liu, J.; Wu, J.; Zheng, Z.; Chen, T. Bubble or Not: Measurements, Analyses, and Findings on the Ethereum ERC721 and ERC1155 Non-fungible Token Ecosystem. arXiv 2023, arXiv:2301.01991. [Google Scholar]
- Kim, H.; Cui, J.; Jang, E.; Lee, C.; Lee, Y.; Chung, J.W.; Shin, S. DRAINCLoG: Detecting Rogue Accounts with Illegally-obtained NFTs using Classifiers Learned on Graphs. arXiv 2023, arXiv:2301.13577. [Google Scholar]
- Bustamante, P.; Cai, M.; Gomez, M.; Harris, C.; Krishnamurthy, P.; Law, W.; Madison, M.; Murtazashvili, I.; Murtazashvili, J.; Mylovanov, T.; et al. Government by code? blockchain applications to public sector governance. Front. Blockchain 2022, 5, 869665. [Google Scholar] [CrossRef]
- Leonardos, N.; Leonardos, S.; Piliouras, G. Oceanic games: Centralization risks and incentives in blockchain mining. In Mathematical Research for Blockchain Economy, Proceedings of the 1st International Conference MARBLE 2019, Santorini, Greece, 6–9 May 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 183–199. [Google Scholar] [CrossRef]
- Takaishi, T. Statistical properties and multifractality of Bitcoin. Phys. Stat. Mech. Its Appl. 2018, 506, 507–519. [Google Scholar] [CrossRef]
- Gilad, Y.; Hemo, R.; Micali, S.; Vlachos, G.; Zeldovich, N. Algorand: Scaling byzantine agreements for cryptocurrencies. In Proceedings of the 26th Symposium on Operating Systems Principles, Shanghai, China, 28–31 October 2017; pp. 51–68. [Google Scholar]
- Tao, B.; Ho, I.W.H.; Dai, H.N. Complex network analysis of the bitcoin blockchain network. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021; pp. 1–5. [Google Scholar]
- Bock, T. Measuring and modeling group dynamics in open-source software development: A tensor decomposition approach. ACM Trans. Softw. Eng. Methodol. 2021, 31, 1–50. [Google Scholar] [CrossRef]
- Aslam, S.; Tošić, A.; Mrissa, M. Secure and privacy-aware blockchain design: Requirements, challenges and solutions. J. Cybersecur. Priv. 2021, 1, 164–194. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, N.; Lou, W.; Hou, Y.T. A survey of distributed consensus protocols for blockchain networks. IEEE Commun. Surv. Tutor. 2020, 22, 1432–1465. [Google Scholar] [CrossRef]
- Cheng, J.; Xie, L.; Tang, X.; Xiong, N.; Liu, B. A survey of security threats and defense on Blockchain. Multimed. Tools Appl. 2021, 80, 30623–30652. [Google Scholar] [CrossRef]
- Averin, A.; Averina, O. Review of blockchain technology vulnerabilities and blockchain-system attacks. In Proceedings of the 2019 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 1–4 October 2019; pp. 1–6. [Google Scholar]
- Saad, M.; Spaulding, J.; Njilla, L.; Kamhoua, C.; Shetty, S.; Nyang, D.; Mohaisen, D. Exploring the attack surface of blockchain: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 1977–2008. [Google Scholar] [CrossRef]
- Shrivas, M.K.; Dean, T.Y.; Brunda, S.S. The disruptive blockchain security threats and threat categorization. In Proceedings of the 2020 First International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; pp. 327–338. [Google Scholar]
- Choi, J. Inferring the Hidden Cascade Infection over Erdös-Rényi (ER) Random Graph. Electronics 2021, 10, 1894. [Google Scholar] [CrossRef]
- Putz, B.; Pernul, G. Detecting blockchain security threats. In Proceedings of the 2020 IEEE International Conference on Blockchain (Blockchain), Rhodes Island, Greece, 2–6 November 2020; pp. 313–320. [Google Scholar]
- Dorri, A.; Roulin, C.; Pal, S.; Baalbaki, S.; Jurdak, R.; Kanhere, S.S. Device identification in blockchain-based internet of things. IEEE Internet Things J. 2022, 9, 24767–24776. [Google Scholar] [CrossRef]
- Paquet-Clouston, M.; Haslhofer, B.; Dupont, B. Ransomware payments in the bitcoin ecosystem. J. Cybersecur. 2019, 5, tyz003. [Google Scholar] [CrossRef]
- Rožman, N.; Corn, M.; Škulj, G.; Diaci, J.; Podržaj, P. Scalability solutions in blockchain-supported manufacturing: A survey. Stroj. Vestn. J. Mech. Eng. 2022, 68, 585–609. [Google Scholar] [CrossRef]
- Croman, K.; Decker, C.; Eyal, I.; Gencer, A.E.; Juels, A.; Kosba, A.; Miller, A.; Saxena, P.; Shi, E.; Gün Sirer, E.; et al. On Scaling Decentralized Blockchains: (A Position Paper). In International Conference on Financial Cryptography and Data Security, Proceedings of the FC 2016 International Workshops, BITCOIN, VOTING, and WAHC, Christ Church, Barbados, 26 February 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 106–125. [Google Scholar]
- Gervais, A.; Karame, G.O.; Wüst, K.; Glykantzis, V.; Ritzdorf, H.; Capkun, S. On the security and performance of proof of work blockchains. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–26 October 2016; pp. 3–16. [Google Scholar]
- Wang, Q.; Yu, J.; Chen, S.; Xiang, Y. SoK: Diving into DAG-based blockchain systems. arXiv 2020, arXiv:2012.06128. [Google Scholar]
- Maeng, S.; Essaid, M.; Lee, C.; Park, S.; Ju, H. Visualization of ethereum p2p network topology and peer properties. Int. J. Netw. Manag. 2021, 31, e2175. [Google Scholar] [CrossRef]
- Albshri, A.; Alzubaidi, A.; Awaji, B.; Solaiman, E. Blockchain simulators: A systematic mapping study. In Proceedings of the 2022 IEEE International Conference on Services Computing (SCC), Barcelona, Spain, 11–15 July 2022. [Google Scholar] [CrossRef]
- Alharby, M.; Moorsel, A. Blocksim: An extensible simulation tool for blockchain systems. Front. Blockchain 2020, 3, 28. [Google Scholar] [CrossRef]
- Skowroński, R.; Brzeziński, J. Spide: Sybil-proof, incentivized data exchange. Clust. Comput. 2021, 25, 2241–2270. [Google Scholar] [CrossRef]
- Lin, Q.; Li, C.; Zhao, X.; Chen, X. Measuring decentralization in bitcoin and ethereum using multiple metrics and granularities. In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering Workshops (ICDEW), Chania, Greece, 19–22 April 2021; pp. 80–87. [Google Scholar]
- Kang, J.; Xiong, Z.; Niyato, D.; Wang, P.; Ye, D.; Kim, D.I. Incentivizing consensus propagation in proof-of-stake based consortium blockchain networks. IEEE Wirel. Commun. Lett. 2019, 8, 157–160. [Google Scholar] [CrossRef]
- Rosa, E.; D’Angelo, G.; Ferretti, S. Agent-Based Simulation of Blockchains. In Methods and Applications for Modeling and Simulation of Complex Systems, Proceeding of the 19th Asia Simulation Conference, AsiaSim 2019, Singapore, 30 October–1 November 2019; Tan, G., Lehmann, A., Teo, Y.M., Cai, W., Eds.; Springer: Singapore, 2019; pp. 115–126. [Google Scholar]
- Liu, D.; Piccoli, F.; Chen, K.; Tang, A.; Fang, V. Nft wash trading detection. arXiv 2023, arXiv:2305.01543. [Google Scholar]
- Hasan, H.R.; Salah, K.; Battah, A.; Madine, M.; Yaqoob, I.; Jayaraman, R.; Omar, M. Incorporating registration, reputation, and incentivization into the nft ecosystem. IEEE Access 2022, 10, 76416–76433. [Google Scholar] [CrossRef]
- Sifat, I.; Tariq, S.A.; van Donselaar, D. Suspicious trading in nonfungible tokens (NFTs). Inf. Manag. 2024, 61, 103898. [Google Scholar] [CrossRef]
- Tariq, S.A.; Sifat, I. Suspicious trading in nonfungible tokens (nfts): Evidence from wash trading. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- von Wachter, V.; Jensen, J.R.; Regner, F.; Ross, O. NFT Wash Trading: Quantifying suspicious behaviour in NFT markets. In International Conference on Financial Cryptography and Data Security, Proceedings of the FC 2022: Financial Cryptography and Data Security. FC 2022 International Workshops, CoDecFin, DeFi, Voting, WTSC, Grenada, Grenada, 6 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 299–311. [Google Scholar]
- Hsieh, Y.; Vergne, J. The future of the web? The coordination and early-stage growth of decentralized platforms. Strateg. Manag. J. 2022, 44, 829–857. [Google Scholar] [CrossRef]
- Chen, Z.; Omote, K. Toward achieving anonymous nft trading. IEEE Access 2022, 10, 130166–130176. [Google Scholar] [CrossRef]
- Das, D.; Bose, P.; Ruaro, N.; Kruegel, C.; Vigna, G. Understanding security issues in the NFT ecosystem. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 667–681. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).