Abstract
In this context, the nonlinear bending investigation of a sector nanoplate on the elastic foundation is carried out with the aid of the nonlocal strain gradient theory. The governing relations of the graphene plate are derived based on the higher-order shear deformation theory (HSDT) and considering von Karman nonlinear strains. Contrary to the first shear deformation theory (FSDT), HSDT offers an acceptable distribution for shear stress along the thickness and removes the defects of FSDT by presenting acceptable precision without a shear correction parameter. Since the governing equations are two-dimensional and partial differential, the extended Kantorovich method (EKM) and differential quadrature (DQM) have been used to solve the equations. Furthermore, the numeric outcomes were compared with a reference, which shows good harmony between them. Eventually, the effects of small-scale parameters, load, boundary conditions, geometric dimensions, and elastic foundations are studied on maximum nondimensional deflection. It can be concluded that small-scale parameters influence the deflection of the sector nanoplate significantly.
MSC:
5Q99
1. Introduction
The emergence of nanotechnology can be described as the beginning of a new era in the world of science. After the discovery of carbon nanotubes, nanostructures have attracted the attention of many researchers. Preliminary studies showed that the mechanical properties of nanostructures are different from those of other materials. Therefore, these special properties have made nanostructures used in many fields, including nanosensors, nanoactuators, nanobearings, electric batteries, nanocomposites, etc. [1,2,3]. Nanostructures include graphene sheets, carbon nanotubes, nanowires, nanorings, and nanorods, which are created by forming graphene sheets [4]. For this reason, the analysis of graphene sheets is the main subject of the study of carbon nanomaterials. The graphene sheet is as thick as a carbon atom, arranged in a hexagonal crystal lattice that has unique mechanical and physical properties, including high flexibility, high tensile strength, high thermal and electrical conductivity, etc. The geometry of sector nanoplates allows for precise tuning of their physical and chemical properties by controlling parameters such as the angle of the sector. These nanoplates can provide inherent directionality in certain applications, such as in optical devices or sensors [5,6]. This directional response can be advantageous for achieving desired functionalities or improving the sensitivity and selectivity of the nanodevices.
Experimental investigations have shown that the mechanical characteristics of structures at the very small scale can be different from those at the macroscale. For this reason, classical continuum mechanics models cannot anticipate the characteristics of nanostructures because of their inability to consider small-scale effects. To overcome these obstacles, nonclassical continuum mechanics models have been developed, including the nonlocal elasticity principle, couple stress principle, strain gradient principle, etc. These models provide a more thorough understanding of the mechanical properties of nanoscale structures and were created to address the shortcomings of classical approaches. To be more specific, Eringen [7] introduced a nonlocal elasticity model that adds nonlocal effects to classical elasticity theory. According to this principle, the stress at a point is affected by the entire material domain. The various behaviors of ultra-small structures have been widely predicted by size-dependent elasticity models, such as nonlocal elasticity. Furthermore, it has been determined that nonlocal effects disappear after a specified length. Researchers recently employed another theory called nonlocal strain gradient theory in their studies to address these shortcomings [8,9]. Using this ultra-small-size theory, stiffness softening as well as hardening can be illustrated.
To take into account the effects of the strain gradient, Mindlin [10] and Aifantis [11] added the strain gradient component to the classical elasticity principle. Furthermore, Toupin [12] proposed the couple stress theory, which includes the impact of internal couple stresses on material behavior, thereby extending the scope of classical elasticity theory. Also, Yang and his colleagues [13] developed the couple stress principle by considering symmetry, rotation, and strain gradients. Moreover, Lam and his coauthors [14] formulated the modified strain gradient principle, which examines the influence of strain gradients including the dilatation gradient, symmetry rotation gradient, and deviatoric stretch gradient. In these theories, the strain gradient influence, or the nonlocal role, is taken into account. To consider both of these effects for nanostructure computations, the nonlocal strain gradient principle was formulated by Lim et al. [15].
On the basis of the nonlocal strain gradient principle, numerous studies have been carried out on the size-dependent mechanical behavior of nanostructures. For instance, using the nonlocal strain gradient model, Gui and Wu [16] conducted research on the buckling of the thermo-magneto-elastic nanocylindrical shell exposed to axial load. They observed that the effect of the nonlocal coefficient on the buckling load of nanocylindrical shells is more significant than that of the strain gradient parameter. Lu and his colleagues [17] proposed a size-dependent classical model to investigate the buckling analysis of rectangular nanoplates. Using the nonlocal strain gradient principle and FSDT, the bending of the sandwich nanoplates with porosity was presented by Arefi et al. [18]. In addition, Farajpour and his colleagues [19] perused the buckling of orthotropic nanoplates exposed to thermal conditions based on a higher-order nonlocal strain gradient principle. They observed that the higher-order nonlocal parameter almost has a decreasing influence on the buckling load. Moreover, the authors of Ref. [20] applied the same theory to study the nonlinear vibration of sandwich nanoplates. They concluded that by enhancing the amplitude of vibrations, the influence of small-scale parameters on the nonlinear frequency becomes more significant. Thai et al. [21] studied the free vibrations of functionally graded circular/annular nanoplates made of magneto-electro-elastic materials via the nonlocal strain gradient principle. They showed that the non-dimensional natural frequencies obtained from circular nanoplates are higher than those predicted for annular types. In another paper, Thai and his coauthors [22] used the nonlocal strain gradient theory, HSDT, and isogeometric analysis technique to study free vibration analysis of functionally graded (FG) magneto-electro-elastic rectangular nanoplates. They concluded that, considering the nonlocal coefficient is equal to or larger than the strain gradient coefficient, the results gained by the classical theory are higher than those predicted by the nonlocal strain gradient theory. Moreover, in the case that the nonlocal parameter is smaller than the strain gradient parameter, the natural frequencies achieved based on the classical theory are lower than those obtained by the nonlocal strain gradient theory. Alghanmi [23] analyzed the deflection of nanoplates with porosity and functionally graded properties based on the nonlocal strain gradient model. They inferred that the deflection of FG nanoplates with even porosities has higher values than the ones with uneven porosities in many cases.
The nonlinear bending analysis of the plate is one of the important topics in the engineering field, which attracts many researchers [24,25,26]. For instance, Liu et al. [27] studied the large deflection of a thin rectangular plate exposed to uniform loads. Gao et al. [28] studied the large deflection of a cantilever beam exposed to tip and distributed loads. Wang and Xiao [29] investigated the bending examination of the rectangular nanolaminates using the Kirchhoff theory and the Gurtin-Murdoch surface elasticity model. They concluded that surface effects decrease the deflections. Krysko et al. [30] investigated the static analysis of nanoplates exposed to local areas and distributed loads using the modified couple stress theory. They observed that for various boundary conditions and types of loads, the stress–strain state reduces stress and deflection by enhancing the size-dependent parameter. Sadeghian et al. [31] studied the nonlinear bending of circular nanoplates based on nonlocal strain gradient theory and HSDT using the one-dimensional DQM. Because HSDTs consider the effects of shear deformation and satisfy the zero transverse shear stresses on the plate’s top and bottom surfaces, a shear correction parameter is not necessary [32]. The HSDT uses similar presumptions as the FSDT, except that the hypothesis on the straightness of the transverse normal after deformation remains. In other words, the transverse normal is no longer inextensible, causing the deformations as a function of the thickness coordinate z.
Mantari et al. [33] studied the static response of functionally graded plates exposed to transverse, distributed, and bi-sinusoidal loads using a novel HSDT via Navier solution. By comparing their results with other references, they noticed good agreement between their theory and other HSDTs. Li and Hu [34] investigated the nonlinear vibration and bending of functionally graded beams based on the nonlocal strain gradient theory. They noticed the FG beam experiences a stiffness-hardening effect. When the nonlocal coefficient is smaller than the material characteristic coefficient. In contrast, the FG beam experiences a stiffness-softening effect when the nonlocal coefficient is larger than the material characteristic coefficient. Li et al. [35] considered the thickness effect on the dynamical and statical investigations of nanobeams. They demonstrated that the stiffness-hardening effect can be seen for the buckling behaviors of silicon nanobeams due to the size-dependent effect of thickness, but the stiffness-softening effect can only be found for the longitudinal dispersion relationship of silicon.
The unique geometry and tunable properties of sector nanoplates offer advantages over other types of nanoplates in various applications, ranging from catalysis and sensing to optics and material science. Therefore, relevant studies investigating sector nanoplates are needed. In this paper, a combination of nonlocal strain gradient theory and HSDT is presented to examine the nonlinear bending of sector nanoplates. In addition, the roles of diverse factors are examined, including the geometry, elastic foundation, bending loads, sector angle, radius, small-scale parameters, and different boundary conditions. Unlike circular/annular analyses, which consider symmetric assumptions resulting in some terms equal to zero (and can be observed in Ref. [31]), investigations related to sector plates are relatively more complicated due to examining two-dimensional solution methods. Since the governing equations are two-dimensional and partial differential, EKM and DQM have been used to solve the equations. It can be noticed that the small-scale coefficients significantly influence the deflection of the sector nanoplate. Also, the strain gradient parameter has a relatively more notable effect at larger angles of the sector nanoplate.
2. The Governing Equations
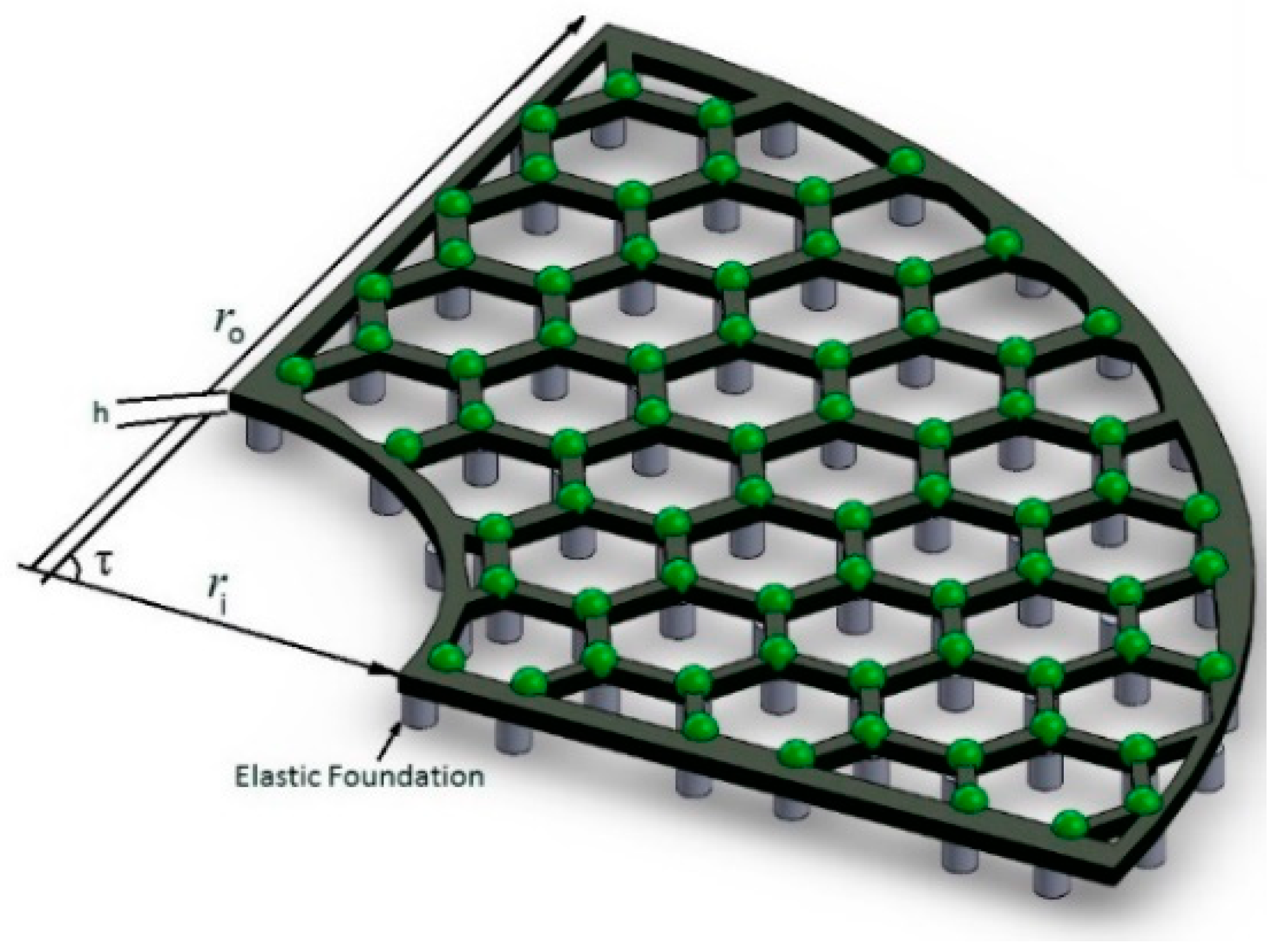
Figure 1 shows the graphene sector plate on the elastic foundation, considering ri and ro as the internal and outer radii, respectively. Additionally, the angle of the sector and the thickness of the plate are defined by and .
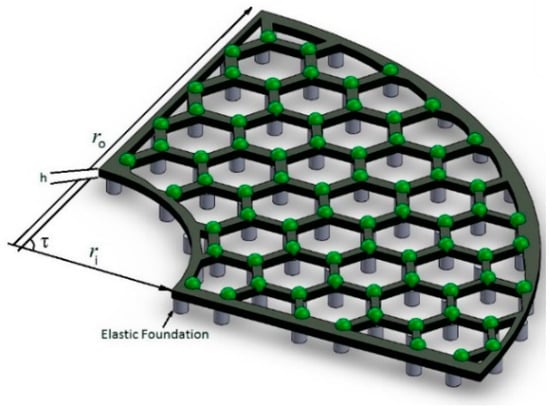
Figure 1.
Graphene annular sector plate on the elastic foundation.
Considering the HSDT with the addition of a special function as , the displacement field can be gained in the r, θ, and z directions (defined by U, V, and W, respectively) as:
Here, u0, v0, and w0 can be regarded as the displacement components of the midplane along , , and axes. Besides, and are the rotation components in the r and θ directions. It is noted that for analyzing the sector plate, the symmetric assumption cannot be considered. So, in Equation (1), has values and also , and are depend on both and (contrary to the circular plate which was analyzed in ref. [31]).
Moreover, the function can be clarified as:
f(z) and y* can be regarded as several functions that have been applied in some references summarized in Table 1. For the better clarification, the Ambartsumian [36] model can be considered as .

Table 1.
Some recommended functions applied in the references.
Based on the presumptions of von Karman, the nonlinear strain components are:
The stress and moment resultants with the nonlocal form () can be written as:
can be defined as the derivative of with respect to the .
The potential energy of the system includes the sum of the strain energy (related to the internal forces work) and the potential energy (related to external forces):
Π can be considered as the potential energy of the whole system, U defines the strain energy of the system. Additionally, Ω is the potential energy of external forces. Considering the principle of minimum potential energy when the system is in equilibrium condition, the variation of the potential energy is equal to zero:
The integral over the volume of the strain energy density is computed in order to write the variations of the system’s strain energy. The following is the strain energy density:
Furthermore, for strain energy variations, the following relation is considered:
Therefore:
Also:
where kw defines the Winkler elastic foundation constant. Therefore:
Considering is equal to zero, the coefficients of , , and should be zero, and the Euler–Lagrange equations are computed in the non-local form (with superscript ) as follows:
It is possible to write Equation (21) as:
The nonlocal strain gradient principle was developed by Lim and his coauthors [15] and is expressed as follows (which can be regarded as the combination of the strain gradient model and nonlocal stresses field):
In Equation (25), the coefficients denoting nonlocal, elastic, and strain gradients (or internal material length scales) are and , respectively. Moreover, the constitutive equation for stress–strain on the nanoscale is shown as [42]:
It is noted that in the above equation, and are the Young modulus along 1 and 2 directions. In addition, and are Poisson’s ratios, also , and are the shear moduli.
The nonlocal form is as:
In the local form, the force and moment resultants are as follows:
The following equations represent the local expression of the equilibrium equations for the sector nanoplate on the elastic foundation:
The following equations represent the local expression of the equilibrium equations for the sector nanoplate on the elastic foundation:
In addition, the boundary conditions can be considered as the following relations:
Simply supported (S):
Clamped (C):
Free (F):
3. The Computational Procedure
One of the most efficient methods for solving partial differential equations is the extended Kantorovich method (EKM), developed in 1968 by Arnold Kerr [43]. In this research, to solve the two-dimensional equations of the sector plate, the extended Kantorovich method was first used, and the two-dimensional equations were converted into one-dimensional form. Then, it is solved by the one-dimensional differential quadratic method. Using the EKM, the bivariate function becomes the product of two univariate functions, as follows:
Moreover, displacement and rotation functions can be written as:
By placing the above relationships in equilibrium relations, differential equations with partial derivatives become ordinary differential relations. With the arbitrary initial choice of the functions , the equilibrium relations will be obtained based on the weighted Galperin residual method. In this method, the governing equations should be multiplied by a suitable function in terms of , and after integration in terms of , ordinary differential equations will only be obtained, which will be a function of . Consequently, by solving the ordinary differential relations and considering the boundary conditions, the functions will be obtained:
where are equilibrium equations.
Each of the equilibrium relations should be multiplied by the suitable function and integrated with the range from 0 to τ with respect to . Therefore, the equilibrium equations (in the partial differential form) are converted into a system of ordinary differential equations in terms of r, which can be solved by taking into account the boundary conditions. By obtaining the functions and placing them in the equilibrium relations, the ordinary differential relations are obtained in terms of , which can be calculated by solving the differential equations.
Using the introduced functions, partial differential equations will be single-variable and become ordinary differential equations. Due to the non-linearity of the governing equations of the plate, numerical methods are used to solve the equations. One of the most efficient and accurate numerical solutions to differential equations is the differential quadrature method.
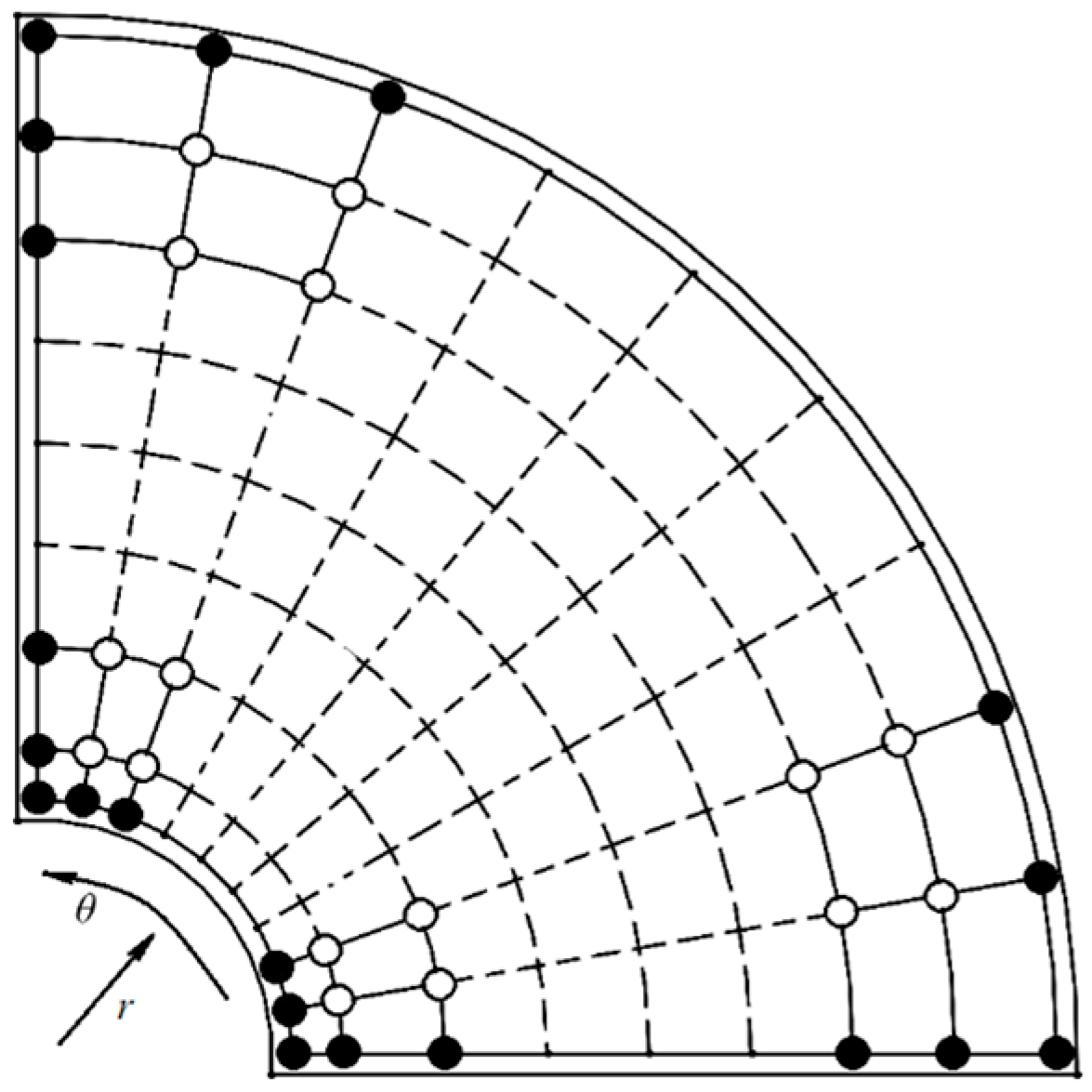
In the two-dimensional analysis, there will be a set of nodes, as shown in Figure 2. Using the Kantorovich method, the calculations are reduced from two directions to one direction, which will cause a noteworthy reduction in the number of calculations. For example, in the two-dimensional analysis, by selecting 9 nodes in each direction, the number of nodes is 81; if using the Kantorovich method, this number is reduced to only 9 points. Reducing the equations from 81 to 9 nonlinear equations will result in a huge reduction in calculations, which is one of the obvious advantages of using the Kantorovich method.
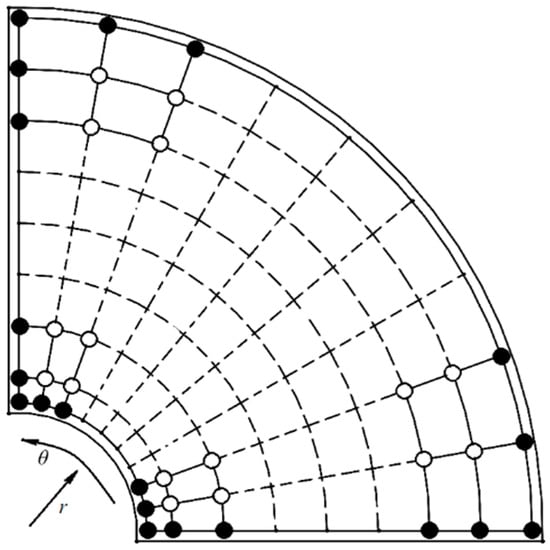
Figure 2.
Distribution of nodes in the geometry of the sector plate.
One of the most efficient and accurate numerical solutions to one-dimensional differential equations is the differential quadratic method. This method is one of the numerical methods with high precession received from the quadratic integration methodology, where the integral at one node in the direction of the domain depends on all the nodes along that direction. It should be noted that weight coefficients determine the dependency value:
where weight coefficients and function values at discrete points can be clarified by and , respectively.
Belman et al. [44] proposed that in quadratic integration, the derivative at a given point in the function domain is dependent upon the function values at every point in the domain through weight coefficients:
Furthermore, with respect to the higher-order derivatives:
The following equations introduce the weighting coefficients for derivatives of the second as well as higher orders:
The grid point distribution used in this paper is on the basis of Chebyshev-Gauss-Lubato points, which speeds up the solution’s convergence and takes the following form:
In Equation (71) the starting and ending points of the function are denoted by and , respectively.
4. Results and Discussions
This section examines various factors based on HSDT and takes the nonlocal strain gradient model into consideration to determine how they affect the deflations of the sector nanoplate via EKM and DQM. Table 2 compares the deflections obtained by the current solution with those reported in the references [45,46], considering the following assumptions:
from which can be seen that the results of this paper are in good agreement with the related references.

Table 2.
The comparison of the deflection gained by this article with references.
By considering the following assumptions:
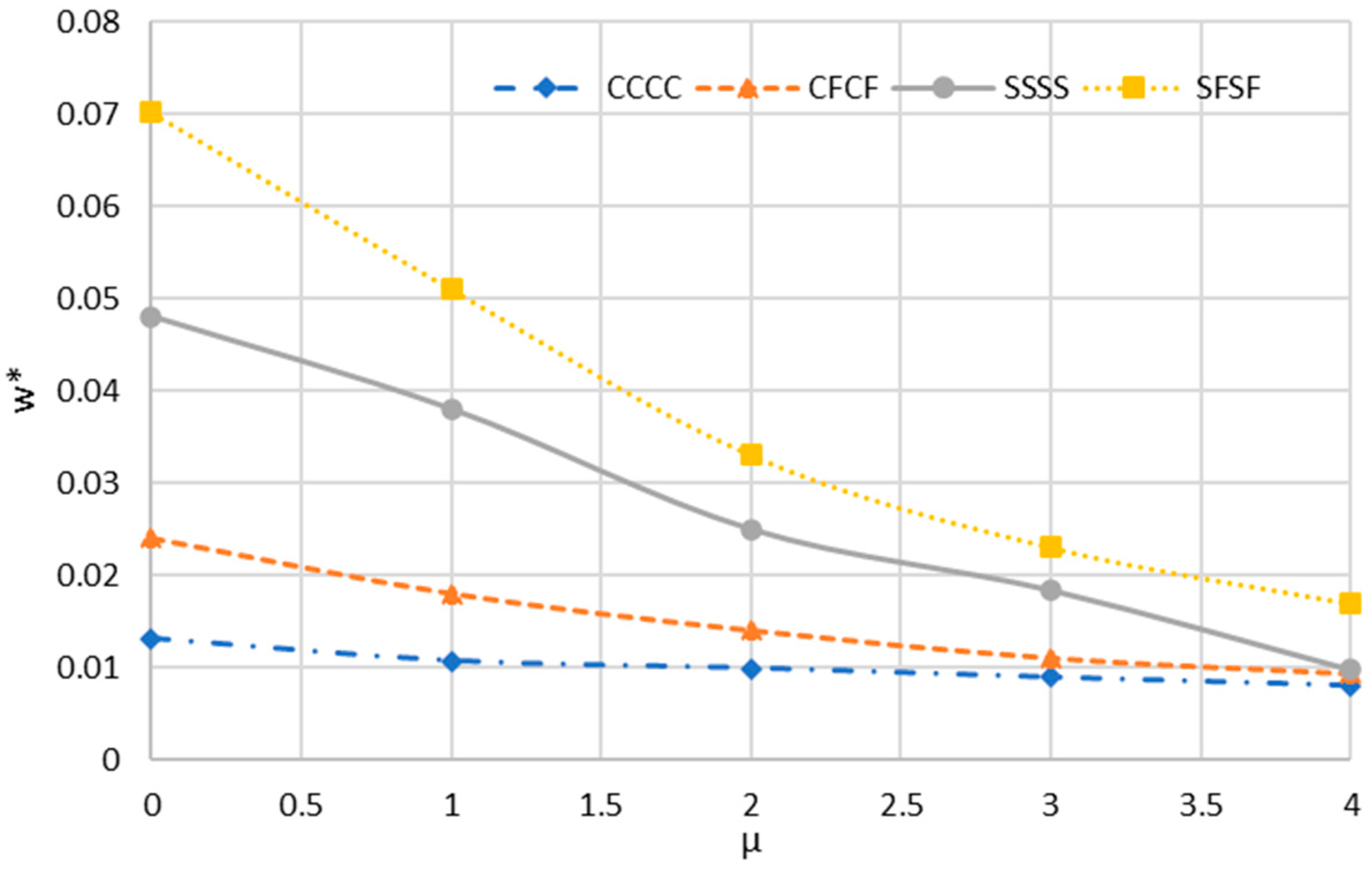
The results of the present study are examined. Also, it is noticed that various functions in Table 1 give similar results [31,47]. Figure 3 reveals the change of nondimensional maximum deflection versus nonlocal parameters for the sector nanoplate for diverse boundary conditions. It can be observed that by increasing the nonlocal parameter, the non-dimensional deflection decreases. This reduction is more noticeable when the boundary conditions are more flexible.
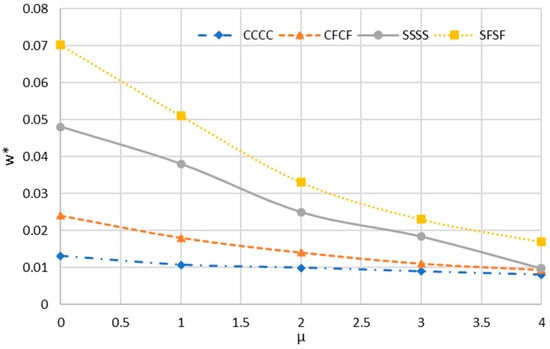
Figure 3.
Changes in dimensionless maximum deflection () versus nonlocal parameter for the sector nanoplate.
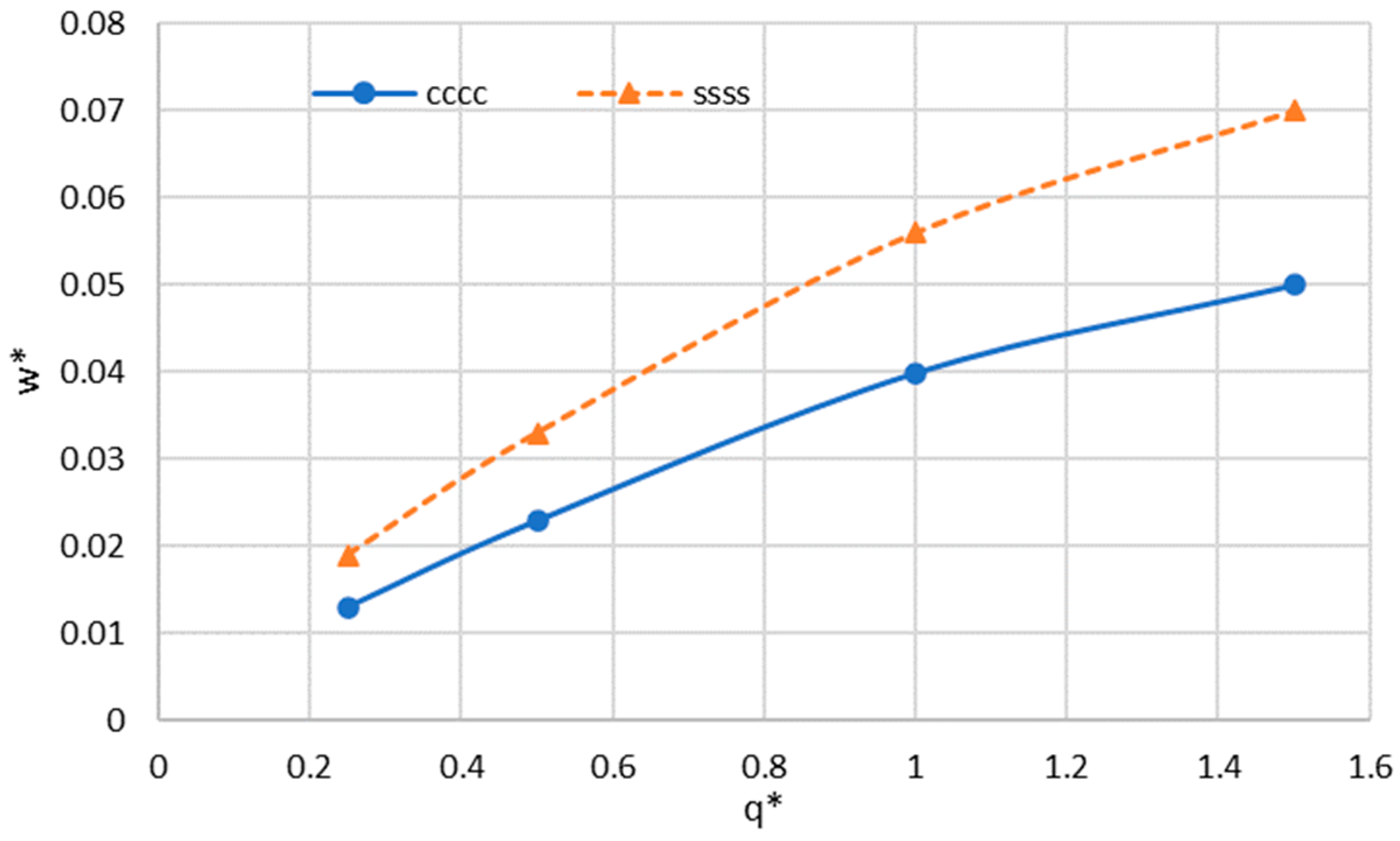
Figure 4 depicts the changes in dimensionless deflection versus bending loads. It is noted that by increasing the deflection, the deflection increases. Moreover, the difference in results between simply supporting boundary conditions and clamped conditions is more significant with the enhancement of the loads.
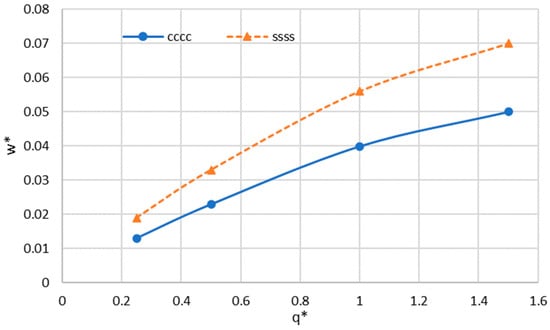
Figure 4.
Changes in dimensionless maximum deflection () versus bending loads for the sector graphene sheet.
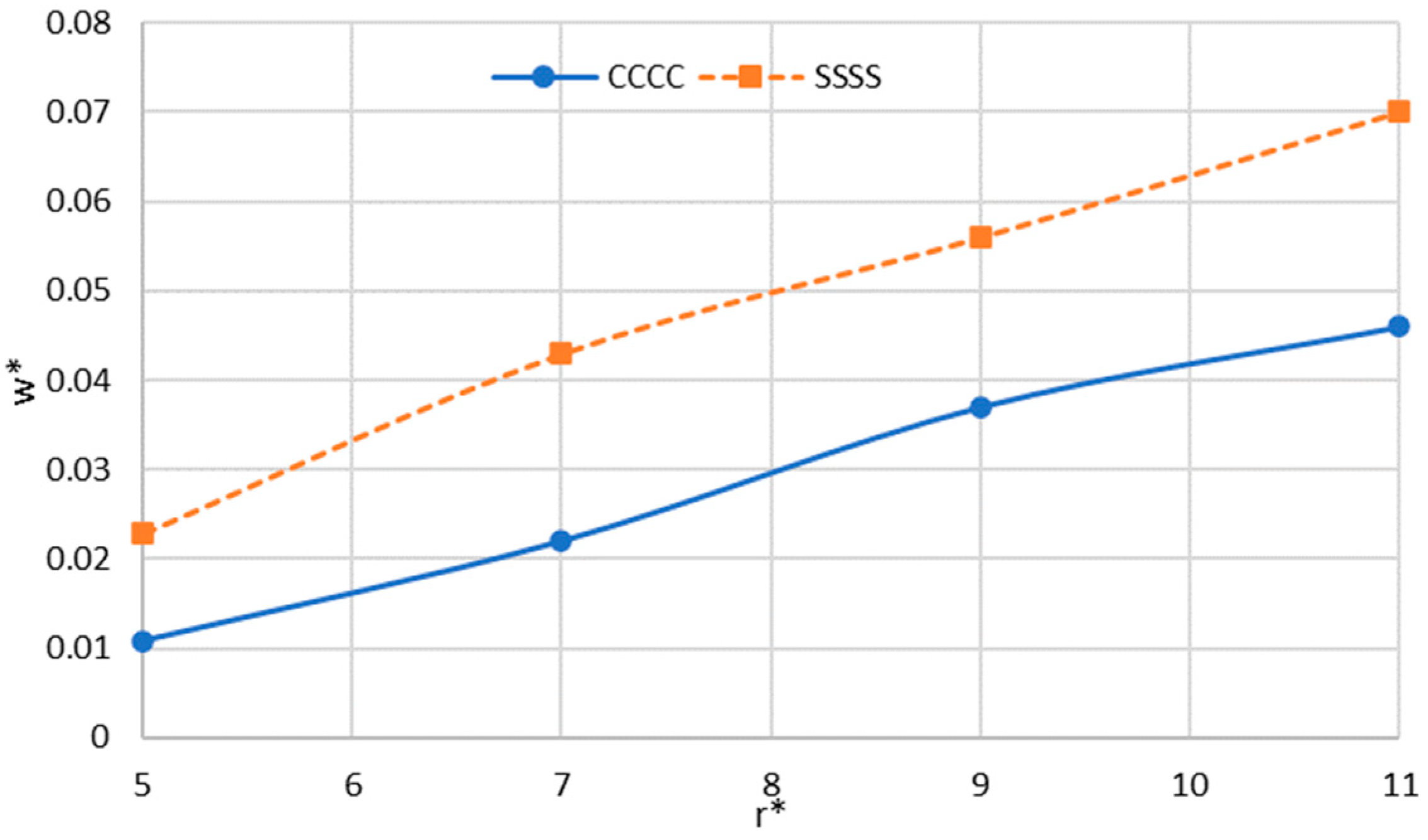
Figure 5 illustrates the changes in dimensionless deflection in terms of nondimensional radius for different boundary conditions. As can be seen, increasing the radius results in an enhancement of the deflection. Furthermore, increasing the radius causes a greater difference between the results of deflection in clamped and simply supported boundary conditions.
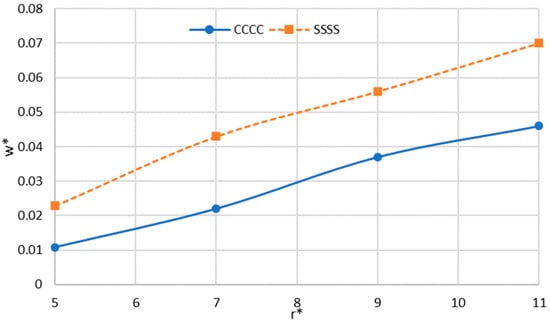
Figure 5.
Changes in dimensionless maximum deflection () versus radius for the sector nanoplate.
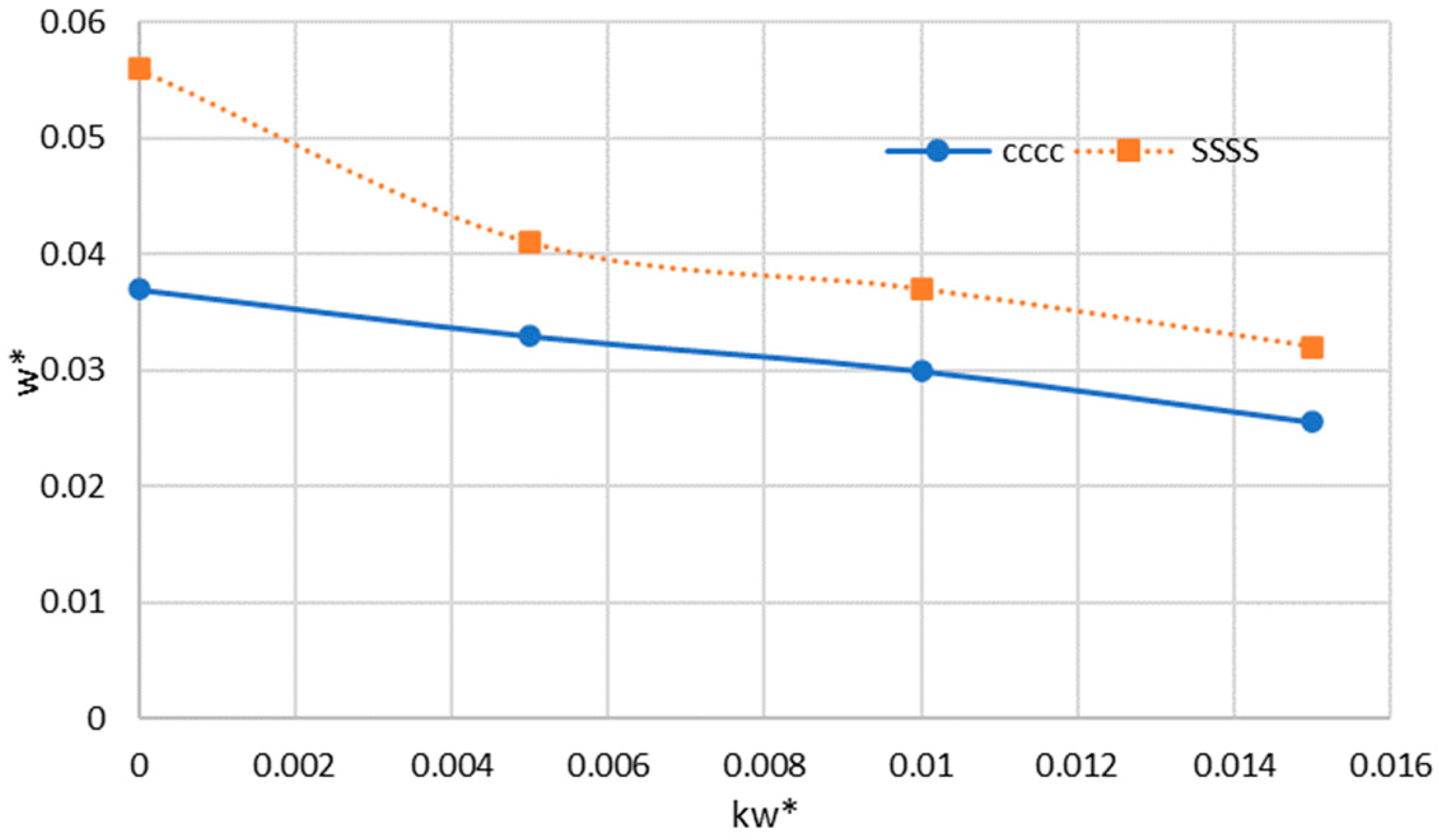
The changes in non-dimension deflection against the elastic foundation can be seen in Figure 6. It can be noticed that increasing the values of the elastic foundation causes a reduction in deflection values. Furthermore, it can be noted that in the higher elastic foundation values, the deflection values for the clamped and simply supported boundary conditions are in close proximity to each other.
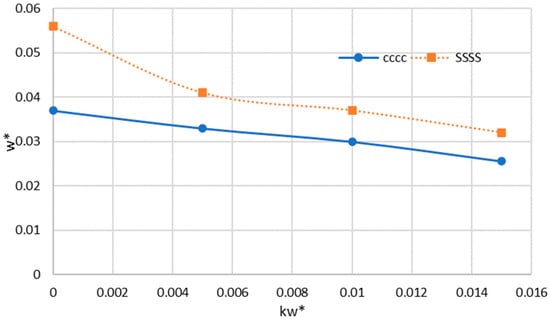
Figure 6.
Influence of the elastic foundation on the non-dimensional maximum deflection of the sector nanoplate.
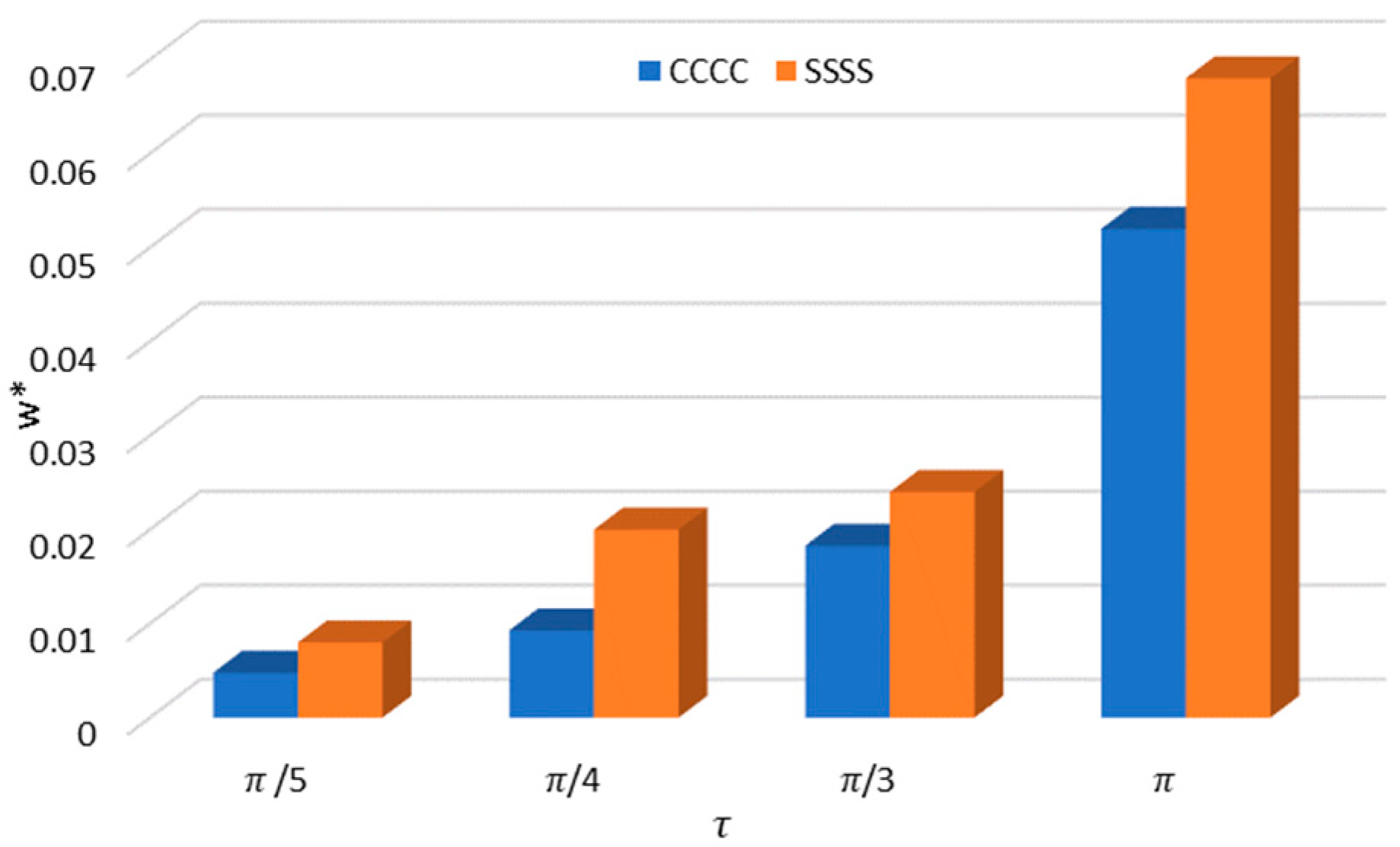
Figure 7 shows the influence of the sector plate angle on the non-dimensional deflection for different boundary conditions. It is noticed that by increasing the sector angle, the deflection increases. Moreover, it can be seen that the difference between the boundary conditions is almost more significant at larger angles.
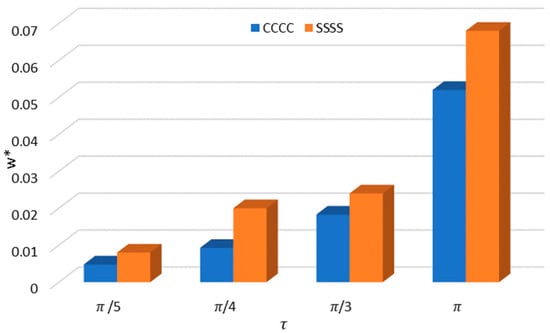
Figure 7.
Effect of the sector angle on nondimensional maximum deflection of the sector nanoplate.
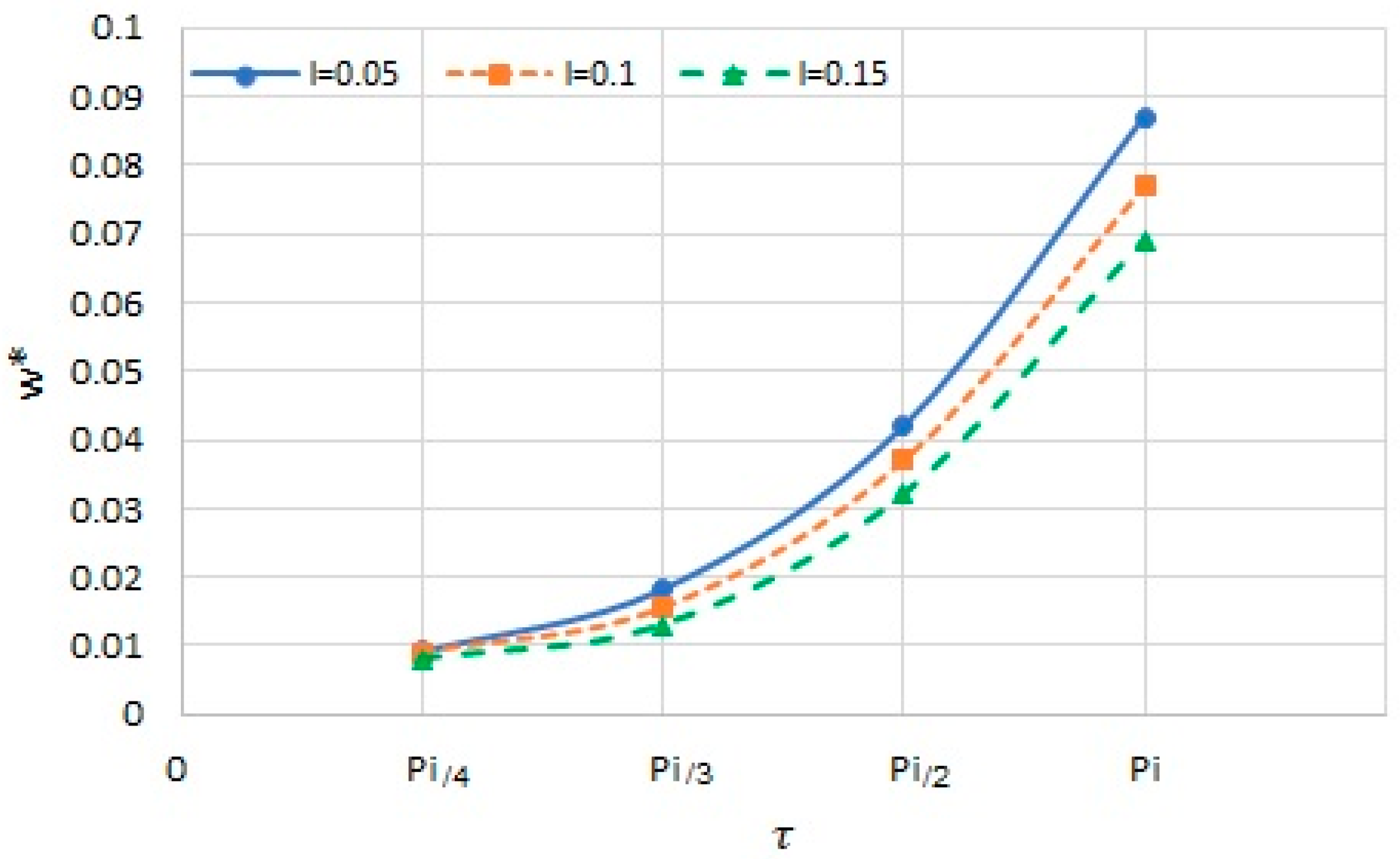
Figure 8 illustrates the influence of the strain gradient parameter with different sector plate angles on the non-dimensional deflection for the clamped boundary conditions. As can be noticed, by increasing the strain gradient parameter, the maximum deflection of the nanoplate decreases (because increasing the strain parameter causes an increase in the stiffness of the nanoplate; therefore, the deflection of the plate decreases). Additionally, a similar result can be found in Ref. [18].
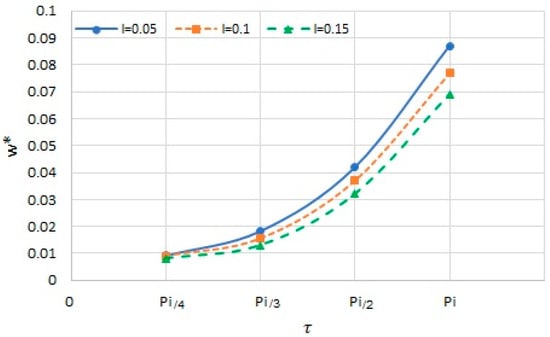
Figure 8.
The nondimensional maximum deflection of the sector nanoplate versus sector angles for different strain gradient parameters.
It can be seen that by increasing the sector angle, the difference among the curves increases. In other words, the strain gradient parameter has a relatively more significant effect at larger sector angles.
5. Conclusions
This paper focuses on the nonlinear bending of the nanoplate with the aid of the nonlocal strain gradient theory with HSDT via DQM. Unlike circular/annular analyses, investigations related to sector plates are relatively more complicated due to the examination of two-dimensional solution methods. Since the governing equations are two-dimensional and partial differential, EKM and DQM have been employed to solve the equations. The results were compared with a reference and showed good harmony. From the results of this paper, it can be noticed that:
- ∗
- Small-scale parameters significantly influence the deflection of the sector nanoplate.
- ∗
- Factors such as radius, flexibility of boundary conditions, load, and sector angle have direct influences on the deflection of the sector plate.
- ∗
- By increasing load, radius, and sector angle, the values of the deflection for different boundary conditions converge.
- ∗
- The strain gradient parameter has a relatively more significant effect at larger angles of the sector nanoplate.
Author Contributions
Conceptualization, M.S. and A.P.; methodology, M.S. and A.P.; software, M.S.; validation, M.S. and A.J.; formal analysis, M.S. and A.J.; investigation, M.S. and V.N.; writing—original draft preparation, M.S. and V.N.; writing—review and editing, A.P. and A.J.; supervision, A.P. and G.J.; funding acquisition, G.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a grant No. S-PD-24-28 from the Research Council of Lithuania (LMTLT).
Data Availability Statement
No data were used for the research described in the article.
Conflicts of Interest
The authors declare that they have no conflicts of interests.
References
- Gupta, R.; Kumar, A.; Biswas, A.; Singh, R.; Gehlot, A.; Akram, S.V.; Verma, A.S. Advances in micro and nano-engineered materials for high-value capacitors for miniaturized electronics. J. Energy Storage 2022, 55, 105591. [Google Scholar] [CrossRef]
- Manolis, G.D.; Dineva, P.S.; Rangelov, T.; Sfyris, D. Mechanical models and numerical simulations in nanomechanics: A review across the scales. Eng. Anal. Bound. Elem. 2021, 128, 149–170. [Google Scholar] [CrossRef]
- Schiavo, L.; Cammarano, A.; Carotenuto, G.; Longo, A.; Palomba, M.; Nicolais, L. An overview of the advanced nanomaterials science. Inorganica Chim. Acta 2024, 559, 121802. [Google Scholar] [CrossRef]
- Farajpour, A.; Mohammadi, M.; Shahidi, A.R.; Mahzoon, M. Axisymmetric buckling of the circular graphene sheets with the nonlocal continuum plate model. Phys. E Low-Dimens. Syst. Nanostructures 2011, 43, 1820–1825. [Google Scholar] [CrossRef]
- Huang, Z.; Shao, G.; Li, L. Micro/nano functional devices fabricated by additive manufacturing. Prog. Mater. Sci. 2023, 131, 101020. [Google Scholar] [CrossRef]
- Collaert, N.; Alian, A.; Arimura, H.; Boccardi, G.; Eneman, G.; Franco, J.; Ivanov, T.; Lin, D.; Loo, R.; Merckling, C.; et al. Ultimate nano-electronics: New materials and device concepts for scaling nano-electronics beyond the Si roadmap. Microelectron. Eng. 2015, 132, 218–225. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Smitt, J. Bending and Vibration Analysis of the FG Circular Nanoplates Subjected to Hygro-Thermo-Electrical Loading Based on Nonlocal Strain Gradient Theory. Int. J. Struct. Stab. Dyn. 2022, 23, 2350017. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M. Axial postbuckling analysis of multilayer functionally graded composite nanoplates reinforced with GPLs based on nonlocal strain gradient theory. Eur. Phys. J. Plus 2017, 132, 490. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Aifantis, E.C. Strain gradient interpretation of size effects. Int. J. Fract. 1999, 95, 299–314. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Gui, Y.; Wu, R. Buckling analysis of embedded thermo-magneto-electro-elastic nano cylindrical shell subjected to axial load with nonlocal strain gradient theory. Mech. Res. Commun. 2023, 128, 104043. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl. Math. Model. 2019, 68, 583–602. [Google Scholar] [CrossRef]
- Arefi, M.; Kiani, M.; Rabczuk, T. Application of nonlocal strain gradient theory to size dependent bending analysis of a sandwich porous nanoplate integrated with piezomagnetic face-sheets. Compos. Part B Eng. 2019, 168, 320–333. [Google Scholar] [CrossRef]
- Farajpour, A.; Yazdi, M.R.H.; Rastgoo, A.; Mohammadi, M. A higher-order nonlocal strain gradient plate model for buckling of orthotropic nanoplates in thermal environment. Acta Mech. 2016, 227, 1849–1867. [Google Scholar] [CrossRef]
- Nematollahi, M.S.; Mohammadi, H. Geometrically nonlinear vibration analysis of sandwich nanoplates based on higher-order nonlocal strain gradient theory. Int. J. Mech. Sci. 2019, 156, 31–45. [Google Scholar] [CrossRef]
- Thai, C.H.; Hung, P.T.; Nguyen-Xuan, H.; Phung-Van, P. A size-dependent meshfree approach for magneto-electro-elastic functionally graded nanoplates based on nonlocal strain gradient theory. Eng. Struct. 2023, 292, 116521. [Google Scholar] [CrossRef]
- Thai, C.H.; Fereira, A.M.J.; Nguyen-Xuan, H.; Hung, P.T.; Phung-Van, P. A nonlocal strain gradient isogeometric model for free vibration analysis of magneto-electro-elastic functionally graded nanoplates. Compos. Struct. 2023, 316, 117005. [Google Scholar] [CrossRef]
- Alghanmi, R.A. Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials 2022, 15, 8601. [Google Scholar] [CrossRef]
- Kumar, D.; Ali, S.F.; Arockiarajan, A. Theoretical and experimental studies on large deflection analysis of double corrugated cantilever structures. Int. J. Solids Struct. 2021, 228, 111126. [Google Scholar] [CrossRef]
- Han, P.; Tian, F.; Babaei, H. Thermally induced large deflection analysis of graphene platelet reinforced nanocomposite cylindrical panels. Structures 2023, 53, 1046–1056. [Google Scholar] [CrossRef]
- Bertóti, E. Primal- and Dual-Mixed Finite Element Models for Geometrically Nonlinear Shear-Deformable Beams—A Comparative Study. Comput. Assist. Methods Eng. Sci. 2020, 27, 285–315. [Google Scholar] [CrossRef]
- Liu, L.; Zhong, X.; Liao, S. Accurate solutions of a thin rectangular plate deflection under large uniform loading. Appl. Math. Model. 2023, 123, 241–258. [Google Scholar] [CrossRef]
- Gao, F.; Liao, W.-H.; Wu, X. Being gradually softened approach for solving large deflection of cantilever beam subjected to distributed and tip loads. Mech. Mach. Theory 2022, 174, 104879. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, J. Analytical solutions of bending analysis and vibration of rectangular nano laminates with surface effects. Appl. Math. Model. 2022, 110, 663–673. [Google Scholar] [CrossRef]
- Krysko, V.A.; Awrejcewicz, J.; Kalutsky, L.A.; Krysko, V.A. Quantification of various reduced order modelling computational methods to study deflection of size-dependent plates. Comput. Math. Appl. 2023, 133, 61–84. [Google Scholar] [CrossRef]
- Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate. Micromachines 2023, 14, 1052. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 96, 165–173. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. Bending response of functionally graded plates by using a new higher order shear deformation theory. Compos. Struct. 2012, 94, 714–723. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Li, L.; Tang, H.; Hu, Y. The effect of thickness on the mechanics of nanobeams. Int. J. Eng. Sci. 2018, 123, 81–91. [Google Scholar] [CrossRef]
- Ambartsumian, S. On the theory of bending plates. Izv. Otd. Tech. Nauk AN SSSR 1958, 5, 69–77. [Google Scholar]
- Ambartsumian, S.A. On the theory of bending of anisotropic plates and shallow shells. J. Appl. Math. Mech. 1960, 24, 500–514. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Reissner, E. On transverse bending of plates, including the effect of transverse shear deformation. Int. J. Solids Struct. 1975, 11, 569–573. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos. Struct. 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. Part B Eng. 2012, 43, 1489–1499. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Chen, X.; Liu, L.; Yu, Y.; Gao, W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler–Pasternak elastic foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- Kerr, A.D.; Alexander, H. An application of the extended Kantorovich method to the stress analysis of a clamped rectangular plate. Acta Mech. 1968, 6, 180–196. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Harik, I.E. Analytical Solution to Orthotropic Sector. J. Eng. Mech. 1984, 110, 554–568. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Tahani, M. Analytical solution for bending of moderately thick radially functionally graded sector plates with general boundary conditions using multi-term extended Kantorovich method. Compos. Part B Eng. 2012, 43, 1405–1416. [Google Scholar] [CrossRef]
- Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlinear Thermal/Mechanical Buckling of Orthotropic Annular/Circular Nanoplate with the Nonlocal Strain Gradient Model. Micromachines 2023, 14, 1790. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).