A Type of Interpolation between Those of Lagrange and Hermite That Uses Nodal Systems Satisfying Some Separation Properties

Abstract

In this paper, we study a method of polynomial interpolation that lies in-between Lagrange and Hermite methods. The novelty is that we use very general nodal systems on the unit circle as well as on the bounded interval only characterized by a separation property. The way in which we interpolate consists in considering all the nodes for the prescribed values and only half for the derivatives. Firstly, we develop the theory on the unit circle, obtaining the main properties of the nodal polynomials and studying the convergence of the interpolation polynomials corresponding to continuous functions with some kind of modulus of continuity and with general conditions on the prescribed values for half of the derivatives. We complete this first part of the paper with the study of the convergence for smooth functions obtaining the rate of convergence, which is slightly slower than that when equidistributed nodal points are considered. The second part of the paper is devoted to solving a similar problem on the bounded interval by using nodal systems having good properties of separation, generalizing the Chebyshev–Lobatto system, and well related to the nodal systems on the unit circle studied before. We obtain an expression of the interpolation polynomials as well as results about their convergence in the case of continuous functions with a convenient modulus of continuity and, particularly, for differentiable functions. Finally, we present some numerical experiments related to the application of the method with the nodal systems dealt with.

1. Introduction

Among the methods of polynomial interpolation most widely studied and used are those corresponding to Lagrange and Hermite interpolation. The problems that have been addressed with them are related to the choice of the nodal systems, the computation of the interpolation polynomials, the analysis of their convergence, and the boundedness of the errors. Although initially developed for bounded intervals of the real line, they were also adapted for application to the unit circle through the Szegő transformation (see [1]) and to the trigonometric interpolation. In addition, all of them have been generalized in different senses.

During the last century, Lagrange interpolation as well as Hermite–Fejér and Hermite interpolations have been developed by using nodal systems related to the zeros of the orthogonal polynomials on the bounded interval, basically Jacobi polynomials, and the zeros of para-orthogonal polynomials on the unit circle. When working with functions, the conditions needed to assure the uniform or the mean convergence of the interpolants to the interpolated function have been widely studied (see [1,2,3,4,5,6,7,8]).

Important extensions of the theory managing to circumvent the link between nodal systems and measures are the normal or strongly normal nodal arrays in the real case (see [9]) and the perturbed roots of the unity in the case of the unit circle (see [10]). In [11] and previous papers, we continued with these ideas, studying the classical Lagrange and Hermite problems and working with nodal distributions characterized by a good property of separation between the nodes, which can be obtained through a perturbation of the uniform distribution.

Some variants in the Hermite method have given rise to other types of interpolation such as Pál-type interpolation (see [12,13]) or Hermite–Birkhoff interpolation. In some recent papers, we considered another variation of the classical methods. Indeed, in [14,15], we studied a problem of interpolation between those of Lagrange and Hermite. There, we use all the nodes for the data values and half of them for the derivative values. The nodal systems that we employ are the roots of complex numbers with modulus 1 on the unit circle and the well-related Chebyshev–Lobatto systems on $[-1,1]$. From the point of view of the behavior of the interpolants in relation to the convergence, this model of interpolation is closer to the Lagrange one. Notice that the Chebyshev–Lobatto systems play an important role in other interpolation methods such as the constrained mock-Chebyshev least squares method (see [16]).

In the present paper, we continue studying the referred intermediate interpolation problem. The novelty is that we use very general nodal systems on the unit circle as well as on the bounded interval, satisfying good properties of separation. If we denote by $\left\{{\alpha }_j\right\}$ and $\left\{x_j\right\}$ the nodes on the unit circle and on the interval, respectively, they are characterized by the following property of separation between two consecutive nodes: the length of the arcs are $\widehat{{\alpha }_{j+1}-{\alpha }_j}=\frac{\pi }{n}+\mathcal{O}\left(\frac{1}{n^2}\right)$ and $arccos{x}_{j+1}-arccos{x}_j=\frac{\pi }{n}+\mathcal{O}\left(\frac{1}{n^2}\right)$, respectively. Hence, these nodal systems could be generated as random perturbations of the roots of a complex number with modulus 1 of the type ${\epsilon }_{jn}\mathcal{O}\left(\frac{1}{n^2}\right)$, where ${\epsilon }_{jn}$ is a random variable with any truncated distribution into $[-1,1]$. Thus, we can say that we work with dynamic systems.

The paper is organized as follows: In Section 2.1, we present the expressions of the interpolation polynomials in terms of the nodal polynomials including the barycentric expressions. Section 2.2 is devoted to describing the nodal systems and to study the properties of nodal polynomials. In Section 2.3, we analyze the convergence of the interpolation polynomials related to continuous functions with an appropriate modulus of continuity and with general conditions on the prescribed values for the derivatives. We dedicate Section 2.4 to the cases of smooth functions on the unit circle. Section 2.5 and Section 2.6 are devoted to studying interpolation problems on $[-1,1]$ with nodal points having good properties of separation and well related to the nodal systems on the unit circle studied before. We obtain both an expression of the interpolation polynomials and results about their convergence in the case of continuous functions with a convenient modulus of continuity. Also, this is particularly for differentiable functions. The results are similar to those obtained in [14] when considering the Chebyshev–Lobatto system. Section 2.7 is devoted to presenting some numerical experiments where distinct nodal systems satisfying the separation property and mechanical models are employed. The results are compared with those obtained by using as nodal systems the roots of para-orthogonal polynomials with respect to a Bernstein–Szegő measure (see [1,17]). When we use the jump function, a Gibbs phenomenon appears. Finally, Section 3 and Section 4 are devoted to Materials, and Discussion and Conclusions.

2. Results

2.1. The Interpolation Polynomials: Expressions

The aim of the present subsection is to study a problem of interpolation on the unit circle, which can be considered an intermediate case between Lagrange and Hermite interpolation problems, the one appearing if we fix the Lagrange values on all the nodal points and we fix the values for the derivatives only on half of the nodes. As usual, when we interpolate on the unit circle $\mathbb{T}=\{z:|z|=1\}$, we work in the space of Laurent polynomials $\mathsf{\Lambda }\left[z\right]=span\{z^k:k\in \mathbb{Z}\}$ because of the density of $\mathsf{\Lambda }\left[z\right]$ in the space of continuous functions on $\mathbb{T}$. Due to the characteristics of the problem, we consider nodal systems with $2n$ nodes that we denote by ${\left\{{\alpha }_{j,2n}\right\}}_{j=1}^{2n},$ where $|{\alpha }_{j,2n}|=1$ for $j=1,\cdots ,2n$ and ${\alpha }_{j,2n}\ne {\alpha }_{k,2n}$ for $j\ne k.$ If we consider two sequences ${\left\{u_{j,2n}\right\}}_{j=1}^{2n}$ and ${\left\{v_{2j-1,n}\right\}}_{j=1}^n$, we pose the following problem:

Compute the Laurent polynomial ${\mathcal{H}}_{-p,q}\left(z\right)$ working in the subspace ${\mathsf{\Lambda }}_{-p,q}\left[z\right]=span\{z^k:-p\le k\le q\},$ with p and q non-negative integers such that $p+q=3n-1$, and satisfying the interpolation conditions

$${\mathcal{H}}_{-p,q}\left({\alpha }_{j,2n}\right)=u_{j,2n},\mathrm{for}j=1,\cdots ,2n,\mathrm{and}{\mathcal{H}}_{-p,q}^{\prime }\left({\alpha }_{2j-1,2n}\right)=v_{2j-1,n},\mathrm{for}j=1,\cdots ,n.$$

For simplicity, we eliminate the second subindex in the notation of the nodal points as well as in the interpolation conditions. Thus, we write ${\left\{{\alpha }_j\right\}}_{j=1}^{2n},$${\left\{u_j\right\}}_{j=1}^{2n}$, and ${\left\{v_{2j-1}\right\}}_{j=1}^n$ instead.

To solve this problem, we decompose it into two separate problems for which we introduce the following notation: We denote by ${\mathcal{HF}}_{-p,q}\left(z\right)$ the Hermite–Fejér-type interpolation polynomial (Hermite–Fejér interpolation polynomial in the sequel) in the Laurent space ${\mathsf{\Lambda }}_{-p,q}$, satisfying the conditions

$${\mathcal{HF}}_{-p,q}\left({\alpha }_j\right)=u_j,j=1,\cdots ,2n,\mathrm{and}{\mathcal{HF}}_{-p,q}^{\prime }\left({\alpha }_{2j-1}\right)=0,j=1,\cdots ,n,$$

(1)

and we denote by ${\mathcal{HD}}_{-p,q}\left(z\right)$ the polynomial in the Laurent space ${\mathsf{\Lambda }}_{-p,q}$, satisfying the conditions

$${\mathcal{HD}}_{-p,q}\left({\alpha }_j\right)=0,j=1,\cdots ,2n,\mathrm{and}{\mathcal{HD}}_{-p,q}^{\prime }\left({\alpha }_{2j-1}\right)=v_{2j-1},j=1,\cdots ,n.$$

(2)

It is clear that

$${\mathcal{H}}_{-p,q}\left(z\right)={\mathcal{HF}}_{-p,q}\left(z\right)+{\mathcal{HD}}_{-p,q}\left(z\right).$$

If F is a function defined on $\mathbb{T}$ and we take $u_j=F\left({\alpha }_j\right)$ for $j=1,\cdots ,2n$, we denote by ${\mathcal{HF}}_{-p,q}(F,z)$ the Hermite–Fejér interpolation polynomial related to F and satisfying (1). If F is a regular function on an open set containing $\mathbb{T}$ and we take $v_{2j-1}=F^{\prime }\left({\alpha }_{2j-1}\right),j=1,\cdots ,n$, we denote the Laurent polynomial satisfying (2) by ${\mathcal{HD}}_{-p,q}(F,z).$ Thus, ${\mathcal{H}}_{-p,q}(F,z)={\mathcal{HF}}_{-p,q}(F,z)+{\mathcal{HD}}_{-p,q}(F,z).$ When $u_j=F\left({\alpha }_j\right)$ for $j=1,\cdots ,2n$ and the values $v_{2j-1}$ for $j=1,\cdots ,n$ are arbitrary, if we denote this vector of values by ${\gamma }_n={\left(v_{2j-1}\right)}_{j=1}^n$, we write ${\mathcal{H}}_{-p,q}(F,{\gamma }_n,z)={\mathcal{HF}}_{-p,q}(F,z)+{\mathcal{HD}}_{-p,q}\left(z\right).$

Our first aim is to obtain the expressions of these interpolation polynomials when we use nodal systems more general than the equally spaced ones. Indeed, the case in which the nodal points are equally spaced was studied in [15]. The novelty of the present paper is that the considered ones are not related to para-orthogonal polynomials on the unit circle, being only characterized by satisfying some suitable separation properties.

Throughout the paper, we denote the nodal polynomials by ${\displaystyle W_{2n}\left(z\right)=\prod _{j=1}^{2n}(z-{\alpha }_j)}$ and we use the factorization $W_{2n}\left(z\right)=Y_n\left(z\right)Z_n\left(z\right)$ with ${\displaystyle Y_n\left(z\right)=\prod _{j=1}^n(z-{\alpha }_{2j-1})}$ and ${\displaystyle Z_n\left(z\right)=\prod _{j=1}^n(z-{\alpha }_{2j}).}$ Now, by taking into account the expressions given in [15], we can state the following result:

Proposition 1.

(i) 

The Hermite–Fejér interpolation polynomial ${\mathcal{HF}}_{-p,q}\left(z\right)$ satisfying (1) has the expression

$${\mathcal{HF}}_{-p,q}\left(z\right)=\sum _{k=1}^n{u}_{2k}{A}_{2k}^{*}\left(z\right)+\sum _{k=1}^n{u}_{2k-1}{A}_{2k-1}^{*}\left(z\right),$$

(3)

where

$$A_{2k}^{*}\left(z\right)=\frac{{\alpha }_{2k}^p{W}_{2n}\left(z\right)Y_n\left(z\right)Z_n^{\prime }\left({\alpha }_{2k}\right)}{z^p(z-{\alpha }_{2k}){\left(W_{2n}^{\prime }\left({\alpha }_{2k}\right)\right)}^2}$$

and

$$\begin{array}{c}\hfill A_{2k-1}^{*}\left(z\right)=\\ \hfill \frac{{\alpha }_{2k-1}^p{W}_{2n}\left(z\right)Y_n\left(z\right)}{z^p{(z-{\alpha }_{2k-1})}^2{W}_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\left(1-(z-{\alpha }_{2k-1})\left(\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}+\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\right)\right)\\ \hfill +\frac{p{\alpha }_{2k-1}^p{W}_{2n}\left(z\right)Y_n\left(z\right)}{z^p(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}.\end{array}$$

(ii) 

The interpolation polynomial ${\mathcal{HD}}_{-p,q}\left(z\right)$ satisfying (2) has the expression

$${\mathcal{HD}}_{-p,q}\left(z\right)=\sum _{k=1}^n{v}_{2k-1}{B}_{2k-1}^{*}\left(z\right),$$

(4)

where

$$B_{2k-1}^{*}\left(z\right)=\frac{{\alpha }_{2k-1}^p{W}_{2n}\left(z\right)Y_n\left(z\right)}{z^p(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}.$$

Proof. 

From [15], we obtain expressions (3) and (4) with $A_{2k}^{*}\left(z\right)=\frac{{\alpha }_{2k}^p}{z^p}{A}_{2k}\left(z\right)$, $A_{2k-1}^{*}\left(z\right)=\frac{{\alpha }_{2k-1}^p}{z^p}{A}_{2k-1}\left(z\right)+\frac{p{\alpha }_{2k-1}^{p-1}}{z^p}{B}_{2k-1}\left(z\right)$ and $B_{2k-1}^{*}\left(z\right)=\frac{{\alpha }_{2k-1}^p}{z^p}{B}_{2k-1}\left(z\right)$, being

$$A_{2k}\left(z\right)=\frac{W_{2n}\left(z\right){\prod }_{j=1}^n(z-{\alpha }_{2j-1})}{(z-{\alpha }_{2k})W_{2n}^{\prime }\left({\alpha }_{2k}\right){\prod }_{j=1}^n({\alpha }_{2k}-{\alpha }_{2j-1})},$$

$$\begin{array}{c}\hfill A_{2k-1}\left(z\right)=\frac{W_{2n}\left(z\right){\prod }_{j=1,j\ne k}^n(z-{\alpha }_{2j-1})}{(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right){\prod }_{j=1,j\ne k}^n({\alpha }_{2k-1}-{\alpha }_{2j-1})}\times \\ \hfill \left[1-(z-{\alpha }_{2k-1})\left(\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}+\frac{{\left({\prod }_{j=1,j\ne k}^n(z-{\alpha }_{2j-1})\right)}_{z={\alpha }_{2k-1}}^{\prime }}{{\prod }_{j=1,j\ne k}^n({\alpha }_{2k-1}-{\alpha }_{2j-1})}\right)\right]\end{array}$$

and

$$B_{2k-1}\left(z\right)=\frac{W_{2n}\left(z\right){\prod }_{j=1,j\ne k}^n(z-{\alpha }_{2j-1})}{W_{2n}^{\prime }\left({\alpha }_{2k-1}\right){\prod }_{j=1,j\ne k}^n({\alpha }_{2k-1}-{\alpha }_{2j-1})}.$$

By doing some computations for the first term, we obtain

$$A_{2k}\left(z\right)=\frac{W_{2n}\left(z\right)Y_n\left(z\right)}{(z-{\alpha }_{2k})W_{2n}^{\prime }\left({\alpha }_{2k}\right)Y_n\left({\alpha }_{2k}\right)}=\frac{W_{2n}\left(z\right)Y_n\left(z\right){\prod }_{j=1,j\ne k}^n({\alpha }_{2k}-{\alpha }_{2j})}{(z-{\alpha }_{2k})W_{2n}^{\prime }\left({\alpha }_{2k}\right)Y_n\left({\alpha }_{2k}\right){\prod }_{j=1,j\ne k}^n({\alpha }_{2k}-{\alpha }_{2j})}=$$

$$\frac{W_{2n}\left(z\right)Y_n\left(z\right)Z_n^{\prime }\left({\alpha }_{2k}\right)}{(z-{\alpha }_{2k}){\left(W_{2n}^{\prime }\left({\alpha }_{2k}\right)\right)}^2}.$$

Proceeding in the same way for the rest, we obtain

$$\begin{array}{c}\hfill A_{2k-1}\left(z\right)=\frac{W_{2n}\left(z\right)Y_n\left(z\right)}{{(z-{\alpha }_{2k-1})}^2{W}_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\times \\ \hfill \left(1-(z-{\alpha }_{2k-1})\left(\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}+\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\right)\right),\end{array}$$

and

$$\begin{array}{c}\hfill B_{2k-1}\left(z\right)=\frac{W_{2n}\left(z\right)(z-{\alpha }_{2k-1}){\prod }_{j=1,j\ne k}^n(z-{\alpha }_{2j-1})}{W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)(z-{\alpha }_{2k-1}){\prod }_{j=1,j\ne k}^n({\alpha }_{2k-1}-{\alpha }_{2j-1})}=\\ \hfill \frac{W_{2n}\left(z\right)Y_n\left(z\right)}{W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)(z-{\alpha }_{2k-1})Y_n^{\prime }\left({\alpha }_{2k-1}\right)}.\end{array}$$

Hence, we obtain the expressions for $A_{2k}^{*},A_{2k-1}^{*}$, and $B_{2k-1}^{*}$. □

The barycentric expressions of these interpolation polynomials are given below. They are very convenient for practical or numerical purposes (see [18]).

Corollary 1.

(i) The Hermite–Fejér interpolation polynomial ${\mathcal{HF}}_{-p,q}\left(z\right)$ satisfying (1) has the barycentric expression

$$\frac{{\displaystyle \sum _{k=1}^n}\frac{{\alpha }_{2k}^p{Z}_n^{\prime }\left({\alpha }_{2k}\right)u_{2k}}{(z-{\alpha }_{2k}){\left(W_{2n}^{\prime }\left({\alpha }_{2k}\right)\right)}^2}+\frac{{\alpha }_{2k-1}^p}{(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\left(\frac{1}{z-{\alpha }_{2k-1}}-\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}-\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}+p\right)u_{2k-1}}{{\displaystyle \sum _{k=1}^n}\frac{{\alpha }_{2k}^p{Z}_n^{\prime }\left({\alpha }_{2k}\right)}{(z-{\alpha }_{2k}){\left(W_{2n}^{\prime }\left({\alpha }_{2k}\right)\right)}^2}+\frac{{\alpha }_{2k-1}^p}{(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\left(\frac{1}{z-{\alpha }_{2k-1}}-\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}-\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}+p\right)}$$

(5)

(ii) The interpolation polynomial ${\mathcal{HD}}_{-p,q}\left(z\right)$ satisfying (2) has the barycentric expression

$$\frac{{\displaystyle \sum _{k=1}^n}\frac{{\alpha }_{2k-1}^p}{(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}{v}_{2k-1}}{{\displaystyle \sum _{k=1}^n}\frac{{\alpha }_{2k}^p{Z}_n^{\prime }\left({\alpha }_{2k}\right)}{(z-{\alpha }_{2k}){\left(W_{2n}^{\prime }\left({\alpha }_{2k}\right)\right)}^2}+\frac{{\alpha }_{2k-1}^p}{(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\left(\frac{1}{z-{\alpha }_{2k-1}}-\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}-\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}+p\right)}$$

(6)

Proof. 

(i) It is obtained in the usual way, that is, by simplifying the common factors after dividing the expression of ${\mathcal{HF}}_{-p,q}\left(z\right)$, given in Proposition 1, by the interpolation polynomial ${\mathcal{H}}_{-p,q}(1,z)$, which corresponds to constant function 1.

(ii) Proceeding in the same manner with ${\mathcal{HD}}_{-p,q}\left(z\right)$ leads to it. □

Remark 1.

Since it is usual to choose the subspaces of Laurent polynomials in a balanced way, we take $p=E\left[\frac{3n}{2}\right]$ and $q=E\left[\frac{3n-1}{2}\right]$. Thus, for n being even, we take $p=\frac{3n}{2}$ along with $q=\frac{3n}{2}-1$ and for n being odd, we take $p=\frac{3n-1}{2}$ together with $q=\frac{3n-1}{2}.$ Without loss of generality, in what follows, we consider and develop the case in which n is even and thus we work in the space ${\mathsf{\Lambda }}_{-\frac{3n}{2},\frac{3n}{2}-1}\left[z\right]$.

2.2. Nodal Systems: Properties and Auxiliary Results

We consider nodal systems ${\left\{{\alpha }_j\right\}}_{j=1}^{2n}$ fulfilling the following separation property: there exists $A>0$ such that for $2n>\frac{A}{\pi }$, the length of the shortest arc between two consecutive nodes ${\alpha }_j$ and ${\alpha }_{j+1}$, that we denote by $\widehat{{\alpha }_j-{\alpha }_{j+1}},$ satisfies

$$\widehat{{\alpha }_j-{\alpha }_{j+1}}=\frac{2\pi }{2n}+\frac{A\left(j\right)}{{\left(2n\right)}^2}=\frac{\pi }{n}+\frac{A\left(j\right)}{4n^2}\mathrm{with}|A\left(j\right)|\le A,j=1,\cdots ,2n,$$

(7)

where ${\alpha }_{2n+1}={\alpha }_1$. We assume that the nodes are numbered in clockwise order. We use Landau’s notation for complex sequences, writing that $a_n=\mathcal{O}\left(b_n\right)$ if $|\frac{a_n}{b_n}|$ is bounded. Thus, we write $\widehat{{\alpha }_j-{\alpha }_{j+1}}=\frac{\pi }{n}+\mathcal{O}\left(\frac{1}{4n^2}\right)$. We will use the same $\mathcal{O}$ to denote different sequences. Unless otherwise mentioned explicitly, the limits we obtain from (7) will be uniform.

So as to study the convergence behavior of the interpolation polynomials, we present below, in several lemmas, some properties related to the nodal system. Most of these properties are based on the following well-known relation between arcs and strings linked to the convex nature of the arcsin function:

For $z_1,z_2\in \mathbb{T}$, it holds that

$$\frac{2}{\pi }\left(\widehat{z_1-z_2}\right)\le |z_1-z_2|\le \left(\widehat{z_1-z_2}\right).$$

Lemma 1.

Let ${\displaystyle W_{2n}\left(z\right)=\prod _{j=1}^{2n}(z-{\alpha }_j)}$ with ${\left\{{\alpha }_j\right\}}_{j=1}^{2n}$ satisfying separation property (7). Then,

(i) 

It holds that

$$|W_{2n}\left(z\right)|<2e^A,\frac{|W_{2n}^{\prime }\left(z\right)|}{2n}<2e^A and \frac{|W_{2n}^{″}\left(z\right)|}{4n^2}<2e^A,\forall z\in \mathbb{T}.$$

(ii) 

There exists a positive constant $B>0$ such that for n large enough,

$$\frac{|W_{2n}^{\prime }\left({\alpha }_j\right)|}{2n}>B,\forall j.$$

(8)

(iii) 

Let us assume that z is not a nodal point and ${\alpha }_1$ and ${\alpha }_{2n}$ are the nodal points nearest to z. Then, there exist positive constants K and E such that

$$\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_1|}<2nKand\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_{2n}|}<2nK$$

and

$$\frac{1}{|z-{\alpha }_j|}<\frac{nE}{j-1},forj>1,and\frac{1}{|z-{\alpha }_{2n-j}|}<\frac{nE}{j},forj\ge 1.$$

Proof. 

(i) and (ii) See Proposition 1 in [11].

(iii) It suffices to apply separation property (7) and the mean value theorem. Notice that the result is valid for every z, which is not a nodal point. It suffices to renumber the nodes in such a way that ${\alpha }_1$ and ${\alpha }_{2n}$ are the nodal points nearest to z. □

As an immediate consequence of the preceding lemma, we obtain certain properties for the polynomials $Y_n\left(z\right)$ and $Z_n\left(z\right)$. They are similar to the former ones. Since $Y_n\left(z\right)={\prod }_{j=1}^n(z-{\alpha }_{2j-1})$ and $Z_n\left(z\right)={\prod }_{j=1}^n(z-{\alpha }_{2j})$,

$$\begin{array}{c}\hfill \widehat{{\alpha }_{2j-1}-{\alpha }_{2j+1}}=\frac{2\pi }{n}+\frac{A(2j-1)+A\left(2j\right)}{4n^2}=\frac{2\pi }{n}+\frac{A_1(2j-1)}{n^2}\mathrm{with}\\ \hfill |A_1(2j-1)|=\frac{|A(2j-1)+A(2j)|}{4}\le \frac{A}{2},j=1,\cdots ,n,\end{array}$$

(9)

and

$$\begin{array}{c}\hfill \widehat{{\alpha }_{2j}-{\alpha }_{2j+2}}=\frac{2\pi }{n}+\frac{A\left(2j\right)+A(2j+1)}{4n^2}=\frac{2\pi }{n}+\frac{A_1\left(2j\right)}{n^2}\mathrm{with}\\ \hfill |A_1\left(2j\right)|=\frac{|A(2j)+A(2j+1)|}{4}\le \frac{A}{2},j=1,\cdots ,n.\end{array}$$

(10)

Therefore, from Lemma 1, we obtain the following lemma:

Lemma 2.

(i) 

It holds that

$$|Y_n\left(z\right)|<2e^{A/2},\frac{|Y_n^{\prime }\left(z\right)|}{n}<2e^{A/2}and\frac{|Y_n^{″}\left(z\right)|}{n^2}<2e^{A/2},\forall z\in \mathbb{T},and$$

$$|Z_n\left(z\right)|<2e^{A/2},\frac{|Z_n^{\prime }\left(z\right)|}{n}<2e^{A/2}and\frac{|Z_n^{″}\left(z\right)|}{n^2}<2e^{A/2},\forall z\in \mathbb{T}.$$

(ii) 

There exists a positive constant $B_1$ such that for n large enough,

$$\frac{|Y_n^{\prime }\left({\alpha }_{2j-1}\right)|}{n}>B_1,\forall j,and$$

$$\frac{|Z_n^{\prime }\left({\alpha }_{2j}\right)|}{n}>B_1,\forall j.$$

(iii) 

If we assume that z is not a nodal point and ${\alpha }_1$ and ${\alpha }_{2n}$ are the nodal points nearest to z, then there exists a positive constant K such that

$$\frac{|Y_n\left(z\right)|}{|z-{\alpha }_1|}<nKand\frac{|Z_n\left(z\right)|}{|z-{\alpha }_{2n}|}<nK.$$

Proof. 

(i) and (ii) are obtained from Lemma 1 by using separation properties (9) and (10).

(iii) By applying the mean value theorem and (i), we have

$$\begin{array}{r}|Y_n\left(z\right)|=|Y_n\left(z\right)-Y_n\left({\alpha }_1\right)|=|Y_n\left(e^{i\theta }\right)-Y_n\left(e^{i{\theta }_1}\right)|\le \\ \underset{z\in \mathbb{T}}{max}|Y_n^{\prime }\left(z\right)|\frac{\pi }{2}|z-{\alpha }_1|\le e^{A/2}\pi n|z-{\alpha }_1|\le Kn|z-{\alpha }_1|.\end{array}$$

We obtain the second inequality proceeding in a similar manner. □

We finish this subsection with some properties, which play an important role in the study of the convergence of the interpolation polynomials.

Lemma 3.

There exists a positive constant $\mathcal{D}$ such that for every n and for every $z\in \mathbb{T}$, it holds that

(i) 

$$\frac{|W_{2n}{\left(z\right)|}^p}{n^p}\sum _{j=1}^{2n}\frac{1}{|z-{\alpha }_j{|}^p}<\left\{\begin{array}{c}\mathcal{D}(1+lnn),p=1,\\ \mathcal{D},p>1.\end{array}\right.$$

(11)

(ii) 

$$\frac{|Y_n{\left(z\right)|}^p}{n^p}\sum _{j=1}^n\frac{1}{|z-{\alpha }_{2j-1}{|}^p}<\left\{\begin{array}{c}\mathcal{D}(1+lnn),p=1,\\ \mathcal{D},p>1.\end{array}\right.$$

Proof. 

(i) By applying Lemma 1, we have

$$\begin{array}{c}\hfill \frac{|W_{2n}{\left(z\right)|}^p}{n^p}\sum _{j=1}^{2n}\frac{1}{|z-{\alpha }_j{|}^p}=\\ \hfill \frac{1}{n^p}\frac{|W_{2n}{\left(z\right)|}^p}{|z-{\alpha }_1{|}^p}+\frac{|W_{2n}{\left(z\right)|}^p}{n^p}\left(\sum _{j=2}^n\frac{1}{|z-{\alpha }_j{|}^p}+\sum _{j=1}^{n-1}\frac{1}{|z-{\alpha }_{2n-j}{|}^p}\right)+\frac{1}{n^p}\frac{|W_{2n}{\left(z\right)|}^p}{|z-{\alpha }_{2n}{|}^p}\le \\ \hfill 2^{p+1}{K}^p+2^p{e}^{Ap}\left(\sum _{j=2}^n\frac{E^p}{{(j-1)}^p}+\sum _{j=1}^{n-1}\frac{E^p}{j^p}\right)=2^{p+1}{K}^p+2^{p+1}{e}^{Ap}{E}^p{H}_{n-1,p},\end{array}$$

where $H_{n-1,p}$ is the $(n-1)$-partial sum of the harmonic series ${\sum }_{j=1}^{\infty }\frac{1}{j^p}$.

Hence,

$$2^{p+1}{K}^p+2^{p+1}{e}^{Ap}{E}^p{H}_{n-1,p}<\left\{\begin{array}{c}\mathcal{D}(1+lnn),p=1,\\ \mathcal{D},p>1.\end{array}\right.$$

(ii) It can be obtained in the same way as (i). To simplify the notation, we consider n as even. Indeed, if we do the same, applying Lemmas 1 and 2, we obtain

$$\begin{array}{c}\hfill \frac{|Y_n{\left(z\right)|}^p}{n^p}\sum _{j=1}^n\frac{1}{|z-{\alpha }_{2j-1}{|}^p}=\frac{1}{n^p}\frac{|Y_n{\left(z\right)|}^p}{|z-{\alpha }_1{|}^p}+\frac{|Y_n{\left(z\right)|}^p}{n^p}\sum _{j=2}^n\frac{1}{|z-{\alpha }_{2j-1}{|}^p}\le \\ \hfill K^p+2^p{e}^{\frac{A}{2}p}\frac{1}{n^p}\sum _{j=2}^n\frac{1}{|z-{\alpha }_{2j-1}{|}^p}=\\ \hfill K^p+2^p{e}^{\frac{A}{2}p}\frac{1}{n^p}\left(\sum _{j=2}^{\frac{n}{2}}\frac{1}{|z-{\alpha }_{2j-1}{|}^p}+\sum _{j=\frac{n}{2}+1}^n\frac{1}{|z-{\alpha }_{2j-1}{|}^p}\right)=\end{array}$$

$$\begin{array}{c}\hfill K^p+2^p{e}^{\frac{A}{2}p}\frac{1}{n^p}\left(\sum _{j=2}^{\frac{n}{2}}\frac{1}{|z-{\alpha }_{2j-1}{|}^p}+\sum _{j=1}^{\frac{n}{2}}\frac{1}{|z-{\alpha }_{2n-(2j-1)}{|}^p}\right)\le \\ \hfill K^p+2^p{e}^{\frac{A}{2}p}{E}^p\left(\sum _{j=2}^{\frac{n}{2}}\frac{1}{{(2j-2)}^p}+\sum _{j=1}^{\frac{n}{2}}\frac{1}{{(2j-1)}^p}\right)=K^p+2^p{e}^{\frac{A}{2}p}{E}^p\sum _{j=1}^{n-1}\frac{1}{j^p}=\\ \hfill K^p+2^p{e}^{\frac{A}{2}p}{E}^p{H}_{n-1,p}<\left\{\begin{array}{c}\mathcal{D}(1+lnn),p=1,\\ \mathcal{D},p>1.\end{array}\right.\end{array}$$

□

In what follows, we bound $2e^A$ and $2e^{\frac{A}{2}}$ by $\mathcal{A}$ and we denote $\mathcal{B}=min\{B,B_1\}$, where A, B, and $B_1$ are the constants appearing in Lemmas 1 and 2.

Remark 2.

In [17], it was proved property (11) when considering as nodal polynomials the para-orthogonal polynomials related to measures in the Szegő class with the Szegő function having analytic extension outside the unit disk (see [1,19]). Here, we have proved it by using only the separation properties satisfied by the nodal points. It is clear that those para-orthogonal polynomials in [17] also hold separation property (7).

2.3. Convergence of Hermite–Fejér and Hermite Interpolation in the Case of Continuous Functions

Proposition 2.

There exists a positive constant $L>0$ such that for every function F bounded on $\mathbb{T}$, it holds that

$$|{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}{(F,z)|\le L\Vert F\Vert }_{\infty }lnn$$

for every $z\in \mathbb{T}$.

Proof. 

The result can be obtained in a more general situation, that is, with p and q such that $p+q=3n-1$, with $p=\mathcal{O}\left(n\right)$. Thus, we begin the proof in this general situation. It is clear that

$$|{\mathcal{HF}}_{-p,q}(F,z)|\le \sum _{k=1}^n|F\left({\alpha }_{2k}\right)A_{2k}^{*}\left(z\right)|+\sum _{k=1}^n|F\left({\alpha }_{2k-1}\right)A_{2k-1}^{*}\left(z\right)|.$$

By applying the preceding lemmas to the first summation, it holds that

$$\begin{array}{c}\hfill \sum _{k=1}^n|F\left({\alpha }_{2k}\right)A_{2k}^{*}\left(z\right)|=\sum _{k=1}^n|F\left({\alpha }_{2k}\right)|\frac{|{\alpha }_{2k}^p{W}_{2n}\left(z\right)Y_n\left(z\right)Z_n^{\prime }\left({\alpha }_{2k}\right)|}{|z^p(z-{\alpha }_{2k})||W_{2n}^{\prime }\left({\alpha }_{2k}\right){|}^2}\le \\ \hfill \sum _{k=1}^n{\Vert F\Vert }_{\infty }\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_{2k}|}\frac{{\mathcal{A}}^{2}n}{{\mathcal{B}}^2{n}^2}\le {\Vert F\Vert }_{\infty }\frac{{\mathcal{A}}^2}{{\mathcal{B}}^2}\mathcal{D}(1+lnn).\end{array}$$

(12)

Proceeding in the same way for the second one, it holds that

$$\begin{array}{c}\hfill \sum _{k=1}^n|F\left({\alpha }_{2k-1}\right)A_{2k-1}^{*}\left(z\right){|\le \Vert F\Vert }_{\infty }\times \\ \hfill \sum _{k=1}^n\left|\frac{{\alpha }_{2k-1}^p{W}_{2n}\left(z\right)Y_n\left(z\right)}{z^p{(z-{\alpha }_{2k-1})}^2{W}_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\left(1-(z-{\alpha }_{2k-1})\left(\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}+\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\right)\right)\right|+\\ \hfill {\Vert F\Vert }_{\infty }p\sum _{k=1}^n\left|\frac{{\alpha }_{2k-1}^p{W}_{2n}\left(z\right)Y_n\left(z\right)}{z^p(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}\right|\le \end{array}$$

$$\begin{array}{c}\hfill {\Vert F\Vert }_{\infty }\times \\ \hfill \sum _{k=1}^n\frac{|W_{2n}\left(z\right)Y_n\left(z\right)|}{|z-{\alpha }_{2k-1}{|}^2|W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)|}\left[1+|z-{\alpha }_{2k-1}|\left(|\frac{W_{2n}^{″}\left({\alpha }_{2k-1}\right)}{2W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)}|+|\frac{Y_n^{″}\left({\alpha }_{2k-1}\right)}{2Y_n^{\prime }\left({\alpha }_{2k-1}\right)}|\right)\right]+\\ \hfill {\Vert F\Vert }_{\infty }p\sum _{k=1}^n\frac{|W_{2n}\left(z\right)Y_n\left(z\right)|}{|z-{\alpha }_{2k-1}||W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)|}\le \\ \hfill {\Vert F\Vert }_{\infty }\frac{1}{2n^2{\mathcal{B}}^2}\sum _{k=1}^n\frac{|W_{2n}\left(z\right)||Y_n\left(z\right)|}{|z-{\alpha }_{2k-1}{|}^2}\left(1+|z-{\alpha }_{2k-1}|\frac{3e^{A}n}{\mathcal{B}}\right)+{\Vert F\Vert }_{\infty }\frac{p{e}^{A/2}}{n^2{\mathcal{B}}^2}\sum _{k=1}^n\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_{2k-1}|}=\\ \hfill {\Vert F\Vert }_{\infty }\frac{|Z_n\left(z\right)|}{2n^2{\mathcal{B}}^2}\sum _{k=1}^n\frac{|Y_n{\left(z\right)|}^2}{|z-{\alpha }_{2k-1}{|}^2}+{\Vert F\Vert }_{\infty }\frac{3e^A}{2n{\mathcal{B}}^3}|W_{2n}\left(z\right)|\sum _{k=1}^n\frac{|Y_n\left(z\right)|}{|z-{\alpha }_{2k-1}|}+\\ \hfill {\Vert F\Vert }_{\infty }\frac{p{e}^{A/2}}{n^2{\mathcal{B}}^2}|\sum _{k=1}^n\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_{2k-1}|}.\end{array}$$

For simplicity, now we take $p=\frac{3n}{2}$ and apply Lemma 3, obtaining

$$\begin{array}{c}\hfill \sum _{k=1}^n|F\left({\alpha }_{2k-1}\right)A_{2k-1}^{*}\left(z\right){|\le \Vert F\Vert }_{\infty }\left[\frac{\mathcal{A}\mathcal{D}}{{\mathcal{B}}^2}+\frac{3{\mathcal{A}}^2\mathcal{D}}{{\mathcal{B}}^3}(1+lnn)+\frac{3\mathcal{A}\mathcal{D}}{2{\mathcal{B}}^2}(1+lnn)\right]\le \\ \hfill {\Vert F\Vert }_{\infty }\frac{\mathcal{D}}{{\mathcal{B}}^2}\mathcal{K}(1+lnn)\end{array}$$

(13)

for some positive constant $\mathcal{K}$. Hence, from (12) and (13), we obtain that there exists L such that

$$|{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}{(F,z)|\le L\Vert F\Vert }_{\infty }lnn.$$

□

In order to prove convergence of the Hermite–Fejér interpolation polynomials related to some continuous functions, first, we recall the following definition and we present an auxiliary result.

The modulus of continuity $w(F,\delta )$ of a given function $F\left(z\right)$ continuous in a subset A of $\mathbb{C}$ is $w(F,\delta )=\underset{z_1,z_2\in A,|z_1-z_2|<\delta }{sup}|F\left(z_1\right)-F\left(z_2\right)|$.

Lemma 4.

Let F be a continuous function on $\mathbb{T}$ with the modulus of continuity $w(F,\delta )=o(|ln\delta {|}^{-1})$ when $\delta \to 0$. Then, for each natural number N, there exists a Laurent polynomial $P_N\in {\mathsf{\Lambda }}_{-N,N}$ and there exists ${\epsilon }_N>0$ with $\left\{{\epsilon }_N\right\}\to 0$ such that $\Vert F-P_N{\Vert }_{\infty }<\frac{{\epsilon }_N}{lnN}.$

Proof. 

This result is a consequence of Jackson’s theorem and the proof can be seen in Lemma 2 of [15]. □

Proposition 3.

Let F be a continuous function on $\mathbb{T}$ with the modulus of continuity $w(F,\delta )=o(|ln\delta {|}^{-1})$ when $\delta \to 0$. Then, ${\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ converges to F uniformly on $\mathbb{T}$.

Proof. 

Let n be large enough and $N=E\left[\sqrt[4]{n}\right]$. Then, it holds that $-\frac{3n}{2}<-N$ and $N<\frac{3n}{2}-1$. By the preceding lemma, we know that there exists $P_N\in {\mathsf{\Lambda }}_{-N,N}\subset {\mathsf{\Lambda }}_{-\frac{3n}{2},\frac{3n}{2}-1}$ such that $\Vert F-P_N{\Vert }_{\infty }<\frac{{\epsilon }_N}{lnN},$ with $\left\{{\epsilon }_N\right\}\to 0$. Then,

$$\begin{array}{c}\hfill \Vert F-{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}{(F,)\Vert }_{\infty }\le \Vert F-P_N{\Vert }_{\infty }+{\Vert P_N-{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,)\Vert }_{\infty }+\\ \hfill \Vert {\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,)-{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,){\Vert }_{\infty }.\end{array}$$

If we now apply Proposition 2, it holds that

$$\begin{array}{c}\hfill \Vert {\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,)-{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,){\Vert }_{\infty }={\Vert {\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N-F,)\Vert }_{\infty }\le \\ \hfill L\Vert P_N{-F\Vert }_{\infty }lnn\le L\frac{{\epsilon }_N}{lnN}lnn\le L_1{\epsilon }_N\end{array}$$

for some constant $L_1$. The last inequality follows from the fact that the sequence $\left\{\frac{lnn}{lnN}\right\}$ is bounded.

On the other hand,

$$\Vert P_N-{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,){\Vert }_{\infty }=\Vert P_N-P_N+{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,){\Vert }_{\infty }={\Vert {\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,)\Vert }_{\infty .}$$

By applying (4) and the generalization of Markov’s inequality (see [20]),

$$\Vert P^{\prime }{\Vert }_{\infty }\le (2r+q){\Vert P\Vert }_{\infty },\mathrm{for}P\in {\mathsf{\Lambda }}_{-r,q},$$

and we have, for $z\in \mathbb{T}$,

$$\begin{array}{c}\hfill |{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,)|=|\sum _{k=1}^n\frac{{\alpha }_{2k-1}^p{W}_{2n}\left(z\right)Y_n\left(z\right)P_N^{\prime }\left({\alpha }_{2k-1}\right)}{z^p(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}|\le \\ \hfill \sum _{k=1}^n\frac{2e^{A/2}|W_{2n}\left(z\right)P_N^{\prime }\left({\alpha }_{2k-1}\right)|}{2n^2{B}_{1}B|z-{\alpha }_{2k-1}|}<\sum _{k=1}^n\frac{\mathcal{A}\Vert P_N^{\prime }{\Vert }_{\infty }}{2n^2{\mathcal{B}}^2}\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_{2k-1}|}=\\ \hfill \frac{\mathcal{A}\Vert P_N^{\prime }{\Vert }_{\infty }}{2n{\mathcal{B}}^2}\frac{1}{n}\sum _{k=1}^n\frac{|W_{2n}\left(z\right)|}{|z-{\alpha }_{2k-1}|}<\frac{\mathcal{A}\Vert P_N^{\prime }{\Vert }_{\infty }}{2n{\mathcal{B}}^2}\mathcal{D}(1+lnn)\le \\ \hfill \frac{\mathcal{A}}{2{\mathcal{B}}^2}\frac{3N\Vert P_N{\Vert }_{\infty }}{n}\mathcal{D}(1+lnn)\le L_2\frac{N}{n}{\Vert P_N\Vert }_{\infty }(1+lnn)\end{array}$$

and for some constant $L_2$ and since $\Vert P_N{\Vert }_{\infty }\le \frac{{\epsilon }_N}{lnN}+{\Vert F\Vert }_{\infty },$ we obtain

$$\begin{array}{c}\hfill \Vert {\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(P_N,){\Vert }_{\infty }\le L_2\frac{N}{n}\left(\frac{{\epsilon }_N}{lnN}+{\Vert F\Vert }_{\infty }\right)(1+lnn)\le \\ \hfill L_2\frac{1}{n^{\frac{3}{4}}}\left(\frac{{\epsilon }_N}{lnN}+{\Vert F\Vert }_{\infty }\right)(1+lnn)\le L_3\frac{(1+lnn)}{n^{\frac{3}{4}}}\end{array}$$

for some positive constant $L_3.$ Therefore, it goes to zero. □

Next, we study the complete problem, that is, the Hermite interpolation problem with nonvanishing conditions for the derivatives. In [17], under suitable conditions for the nodal systems, it was given a sufficient condition on the derivatives, which cannot be improved, in order to obtain convergence for continuous functions. Now, we prove that other similar conditions work.

Proposition 4.

Let F be a continuous function on $\mathbb{T}$ with the modulus of continuity $w(F,\delta )=o(|ln\delta {|}^{-1})$ when $\delta \to 0$ and let ${\gamma }_n={\left(v_{2j-1}\right)}_{j=1}^n$. Then,

(i) 

If $\Vert {\gamma }_n{\Vert }_q=o\left(n\right)$ for some q, $1\le q<\infty$, then ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n,z)$ converges to F uniformly on $\mathbb{T}$.

(ii) 

If $\Vert {\gamma }_n{\Vert }_{\infty }=o\left(\frac{n}{lnn}\right),$ then ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n,z)$ converges to F uniformly on $\mathbb{T}$.

Proof. 

(i) If we apply expression (4), we obtain

$$\begin{array}{c}\hfill |{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)|=|\sum _{k=1}^n\frac{{\alpha }_{2k-1}^{\frac{3n}{2}}{W}_{2n}\left(z\right)Y_n\left(z\right)}{z^{\frac{3n}{2}}(z-{\alpha }_{2k-1})W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)Y_n^{\prime }\left({\alpha }_{2k-1}\right)}{v}_{2k-1}|\le \\ \hfill \sum _{k=1}^n\frac{|W_{2n}\left(z\right)||Y_n\left(z\right)|}{|W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)||Y_n^{\prime }\left({\alpha }_{2k-1}\right)||z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \frac{\mathcal{A}}{2{\mathcal{B}}^{2}n}\sum _{k=1}^n\frac{|W_{2n}\left(z\right)|}{n|z-{\alpha }_{2k-1}|}|v_{2k-1}|.\end{array}$$

Firstly, we assume that $q>1$. In this case, we take $p>1$ such that $\frac{1}{p}+\frac{1}{q}=1$ and apply Lemma 3. Then, we obtain

$$\begin{array}{c}\hfill \frac{\mathcal{A}}{2{\mathcal{B}}^{2}n}\sum _{k=1}^n\frac{|W_{2n}\left(z\right)|}{n|z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \\ \hfill \le \frac{\mathcal{A}}{2{\mathcal{B}}^{2}n}{\left(\frac{|W_{2n}{\left(z\right)|}^p}{n^p}\sum _{k=1}^n\frac{1}{|z-{\alpha }_{2k-1}{|}^p}\right)}^{\frac{1}{p}}{\left(\sum _{k=1}^n{|v_{2k-1}|}^q\right)}^{\frac{1}{q}}\le \frac{\mathcal{A}}{2{\mathcal{B}}^2}\mathcal{D}\frac{\Vert {\gamma }_n{\Vert }_q}{n}.\end{array}$$

Secondly, we assume that $q=1$. If we apply Lemmas 1 and 2, we have

$$\begin{array}{c}\hfill |{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)|\le \sum _{k=1}^n\frac{|W_{2n}\left(z\right)||Y_n\left(z\right)|}{|W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)||Y_n^{\prime }\left({\alpha }_{2k-1}\right)||z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \\ \hfill \frac{\mathcal{A}}{2{\mathcal{B}}^{2}n}\sum _{k=1}^n\frac{|Y_n\left(z\right)|}{n|z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \frac{\mathcal{A}}{2{\mathcal{B}}^{2}n}\frac{|Y_n\left(z\right)|}{n|z-{\alpha }_1|}|v_1|+\frac{{\mathcal{A}}^2}{2{\mathcal{B}}^{2}n}\sum _{k=2}^n\frac{1}{n|z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \\ \hfill \frac{\mathcal{A}K}{2{\mathcal{B}}^{2}n}|v_1|+\frac{{\mathcal{A}}^{2}E}{2{\mathcal{B}}^{2}n}\sum _{k=2}^n|v_{2k-1}|\le L_4\frac{\Vert {\gamma }_n{\Vert }_1}{n}\end{array}$$

for some positive constant $L_4$.

Hence, if we take into account the expression ${\mathcal{H}}_{-n,n-1}(F,{\gamma }_n,z)={\mathcal{HF}}_{-n,n-1}(F,z)+{\mathcal{HD}}_{-n,n-1}\left(z\right)$ and Proposition 3, then the result is proven.

(ii) Proceeding in a similar way, we obtain

$$\begin{array}{c}\hfill |{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)|\le \sum _{k=1}^n\frac{|W_{2n}\left(z\right)||Y_n\left(z\right)|}{|W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)||Y_n^{\prime }\left({\alpha }_{2k-1}\right)||z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \\ \hfill \frac{\mathcal{A}}{2{\mathcal{B}}^2{n}^2}\sum _{k=1}^n\frac{|Y_n\left(z\right)|}{|z-{\alpha }_{2k-1}|}|v_{2k-1}|\le \frac{\mathcal{A}}{2{\mathcal{B}}^2}\frac{\Vert {\gamma }_n{\Vert }_{\infty }}{n}\frac{|Y_n\left(z\right)|}{n}\sum _{k=1}^n\frac{1}{|z-{\alpha }_{2k-1}|}\le \\ \hfill \frac{\mathcal{A}}{2{\mathcal{B}}^2}\frac{\Vert {\gamma }_n{\Vert }_{\infty }}{n}\mathcal{D}(1+lnn)\le \frac{\mathcal{A}\mathcal{D}}{{\mathcal{B}}^2}\frac{\Vert {\gamma }_n{\Vert }_{\infty }}{n}lnn\end{array}$$

and taking into consideration our hypothesis, the result is proven. □

2.4. Interpolation of Smooth Functions: Convergence of the Interpolation Polynomials

Proposition 5.

If F is an analytic function in an open annulus containing $\mathbb{T}$, then ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ uniformly converges to F on $\mathbb{T}$ and the order of convergence is $\mathcal{O}(r^{\frac{3n}{2}}lnn),$ for some r such that $0<r<1.$

Proof. 

We assume that $F\left(z\right)={\sum }_{k=-\infty }^{\infty }{a}_k{z}^k$ with $|a_k|\le P{r}^{|k|}$ for some positive constant P and $0<r<1$. Thus, F can be expressed as $F\left(z\right)=F_{1,n}\left(z\right)+F_{2,n}\left(z\right)+F_{3,n}\left(z\right)$, where

$${\displaystyle F_{1,n}\left(z\right)=\sum _{k=-\frac{3n}{2}}^{\frac{3n}{2}-1}{a}_k{z}^k,F_{2,n}\left(z\right)=\sum _{k=\frac{3n}{2}}^{\infty }{a}_k{z}^k\mathrm{and}{F}_{3,n}\left(z\right)=\sum _{k=-\infty }^{-\frac{3n}{2}-1}{a}_k{z}^k.}$$

(14)

Since ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{1,n},z)=F_{1,n}\left(z\right)$,

$$\begin{array}{c}\hfill |{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)-F\left(z\right)|=|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)+{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{3,n},z)-F_{2,n}\left(z\right)-F_{3,n}\left(z\right)|\le \\ \hfill |{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)-F_{2,n}\left(z\right)|+|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{3,n},z)-F_{3,n}\left(z\right)|.\end{array}$$

In this way, we have to study both absolute differences, that is, $|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{i,n},z)-F_{i,n}\left(z\right)|$ for $i=2,3.$ For simplicity, we develop the case $i=2$.

Note that ${\displaystyle |F_{2,n}\left(z\right)|\le \sum _{k=\frac{3n}{2}}^{\infty }|a_k{z}^k|\le \sum _{k=\frac{3n}{2}}^{\infty }P{r}^k=P\frac{r^{\frac{3n}{2}}}{1-r},}$ which goes to zero uniformly on $\mathbb{T}$.

In order to obtain ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z),$ first, we compute

$${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z)={\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z)+{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z).$$

On the one hand, by taking into account Proposition 2, we obtain $|{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z)|\le Llnn.$ On the other hand, since ${\displaystyle {\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z)=\sum _{k=1}^{n}j{\alpha }_{2k-1}^{j-1}{B}_{2k-1}^{*}\left(z\right)}$ according to (4), by applying (8) and Lemmas 2 and 3, it follows that

$$\begin{array}{c}\hfill {\displaystyle |{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z)|\le \sum _{k=1}^{n}j|B_{2k-1}^{*}\left(z\right)|=\sum _{k=1}^{n}j\frac{|W_{2n}\left(z\right)||Y_n\left(z\right)|}{|z-{\alpha }_{2k-1}||W_{2n}^{\prime }\left({\alpha }_{2k-1}\right)||Y_n^{\prime }\left({\alpha }_{2k-1}\right)|}\le }\\ \hfill \frac{j\mathcal{A}}{2{\mathcal{B}}^{2}n}\frac{|W_{2n}\left(z\right)|}{n}\sum _{k=1}^n\frac{1}{|z-{\alpha }_{2k-1}|}<\frac{j\mathcal{A}}{2{\mathcal{B}}^{2}n}\mathcal{D}(1+lnn).\end{array}$$

Hence,

$$|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^j,z)|\le Llnn+\frac{j\mathcal{A}\mathcal{D}}{2{\mathcal{B}}^{2}n}(1+lnn)\le Q\left(lnn+j\frac{lnn}{n}\right)$$

(15)

and therefore

$$\begin{array}{c}\hfill \left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)\right|=\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left({\displaystyle \sum _{k=\frac{3n}{2}}^{\infty }{a}_k{z}^k,z}\right)\right|=\left|\sum _{k=\frac{3n}{2}}^{\infty }{a}_k{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^k,z)\right|\le \\ \hfill \sum _{k=\frac{3n}{2}}^{\infty }|a_k|\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^k,z)\right|\le \sum _{k=\frac{3n}{2}}^{\infty }|a_k|Q\left(lnn+k\frac{lnn}{n}\right)\le PQlnn\sum _{k=\frac{3n}{2}}^{\infty }{r}^k+PQ\frac{lnn}{n}\sum _{k=\frac{3n}{2}}^{\infty }k{r}^k\end{array}$$

for some positive constant Q.

Taking into account that ${\displaystyle \sum _{k=\frac{3n}{2}}^{\infty }{r}^k=\frac{r^{\frac{3n}{2}}}{1-r}}$ and ${\displaystyle \sum _{k=\frac{3n}{2}}^{\infty }k{r}^k=r^{\frac{3n}{2}}\left(\frac{3n}{2(1-r)}+\frac{r}{{(1-r)}^2}\right),}$ then

$$|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)|\le T{r}^{\frac{3n}{2}}lnn$$

for some positive constant T and thus it goes to zero uniformly on $\mathbb{T}$.

The corresponding result for the absolute difference $|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{3,n},z)-F_{3,n}\left(z\right)|$ can be obtained in a similar way. □

Proposition 6.

If ${\displaystyle F\left(z\right)=\sum _{k=-\infty }^{\infty }{a}_k{z}^k}$ is a function defined on $\mathbb{T}$ with $|a_k|\le K\frac{1}{{|k|}^s},$ for some positive constant $K,k\ne 0$ and $s>2$, then ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ converges to $F\left(z\right)$ uniformly on $\mathbb{T}$. Moreover, the order of convergence is $\mathcal{O}\left(\frac{lnn}{{\left(\frac{3n}{2}\right)}^{s-2}}\right)$.

Proof. 

As we proceed as in the previous proposition, we write $F\left(z\right)=F_{1,n}\left(z\right)+F_{2,n}\left(z\right)+F_{3,n}\left(z\right)$, where $F_{1,n}\left(z\right),F_{2,n}\left(z\right)$, and $F_{3,n}\left(z\right)$ are those given in (14). Since ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{1,n},z)=F_{1,n}\left(z\right),$

$$|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)-F\left(z\right)|\le |{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)-F_{2,n}\left(z\right)|+|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{3,n},z)-F_{3,n}\left(z\right)|.$$

Thus, we have to study the behavior of $|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{i,n},z)-F_{i,n}\left(z\right)|$ for $i=2,3$ to obtain the uniform convergence of ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ to F.

Indeed, if $z\in \mathbb{T}$,

$$\begin{array}{c}\hfill |{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)-F_{2,n}\left(z\right)|\le |{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)|+|F_{2,n}\left(z\right)|\end{array}$$

and, by applying the integral test, it holds that

$$\begin{array}{c}\hfill |F_{2,n}\left(z\right)|=|\sum _{k=\frac{3n}{2}}^{\infty }{a}_k{z}^k|\le \sum _{k=\frac{3n}{2}}^{\infty }|a_k|\le K\sum _{k=\frac{3n}{2}}^{\infty }\frac{1}{k^s}\le \frac{K}{s-1}\frac{1}{{(\frac{3n}{2}-1)}^{s-1}}=\mathcal{O}\left(\frac{1}{{\left(\frac{3n}{2}\right)}^{s-1}}\right).\end{array}$$

By taking into account (15), we have

$$\begin{array}{c}\hfill \left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)\right|=\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left({\displaystyle \sum _{k=\frac{3n}{2}}^{\infty }{a}_k{z}^k,z}\right)\right|=\\ \hfill {\displaystyle \left|\sum _{k=\frac{3n}{2}}^{\infty }{a}_k{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^k,z)\right|\le \sum _{k=\frac{3n}{2}}^{\infty }|a_k|\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(z^k,z)\right|\le }\\ \hfill {\displaystyle \sum _{k=\frac{3n}{2}}^{\infty }\frac{KQ}{k^s}lnn\left(1+\frac{k}{n}\right)=KQlnn\left({\displaystyle \sum _{k=\frac{3n}{2}}^{\infty }\frac{1}{k^s}+\frac{1}{n}\sum _{k=\frac{3n}{2}}^{\infty }\frac{1}{k^{s-1}}}\right)\le }\\ \hfill {\displaystyle KQlnn\left(1+\frac{1}{n}\right)\sum _{k=\frac{3n}{2}}^{\infty }\frac{1}{k^{s-1}}.}\end{array}$$

By applying the integral test again, we obtain

$$\begin{array}{c}\hfill |{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)|\le KQlnn\left(1+\frac{1}{n}\right)\frac{1}{s-2}\frac{1}{{(\frac{3n}{2}-1)}^{s-2}}=\mathcal{O}\left(\frac{lnn}{{(\frac{3n}{2}-1)}^{s-2}}\right).\end{array}$$

Hence, $\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{2,n},z)-F_{2,n}\left(z\right)\right|$ goes to zero and the order of convergence is $\mathcal{O}\left(\frac{lnn}{{\left(\frac{3n}{2}\right)}^{s-2}}\right)$. The term $\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F_{3,n},z)-F_{3,n}\left(z\right)\right|$ can be studied in a similar manner and finally the result follows. □

Remark 3.

In [15], when considering the roots of unimodular complex numbers as nodal systems, we obtained similar results to those given in Propositions 5 and 6 although the order of convergence given in [15] is better than those.

2.5. The Case of the Bounded Interval

In this subsection, we consider very general nodal systems in the interval $[-1,1]$.

Let n be even and let ${\left\{x_j\right\}}_{j=1}^{n+1}$ be a nodal system ordered as follows: $x_{n+1}<x_n<\cdots <x_2<x_1$ with $x_{n+1}=-1$ and $x_1=1$. We also assume that the nodal points satisfy the separation property

$$arccos{x}_{j+1}-arccos{x}_j=\frac{\pi }{n}+\frac{a\left(j\right)}{n^2},\mathrm{being}|a\left(j\right)|\le a,j=1,\cdots ,n,$$

(16)

with a being a positive constant such that $\frac{2a}{\pi }<n.$

Now, our aim is to solve the following interpolation problem, intermediate between those of Lagrange and Hermite on the interval $[-1,1]$:

Given two sequences of real numbers ${\left\{q_j\right\}}_{j=1}^{n+1}$ and ${\left\{v_{2j-1}\right\}}_{j=1}^{\frac{n}{2}+1}$, find an algebraic polynomial $h_{\frac{3n}{2}+1}\left(x\right)\in {\mathbb{P}}_{\frac{3n}{2}+1}\left[x\right]$ satisfying

$$\begin{array}{c}\hfill h_{\frac{3n}{2}+1}\left(x_j\right)=q_j,j=1,\cdots ,n+1,\mathrm{and}\\ \hfill h_{\frac{3n}{2}+1}^{\prime }\left(x_{2j-1}\right)=v_{2j-1},j=1,\cdots ,\frac{n}{2}+1.\end{array}$$

(17)

When $q_j=f\left(x_j\right)$ for $j=1,\cdots ,n+1$, with f being a function defined on $[-1,1]$, and $V_{\frac{n}{2}+1}={\left(v_{2j-1}\right)}_{j=1}^{\frac{n}{2}+1}$ being arbitrary, we denote the interpolation polynomial satisfying (17) by $h_{\frac{3n}{2}+1}(f,V_{\frac{n}{2}+1},x)$. When $q_j=f\left(x_j\right)$ for $j=1,\cdots ,n+1$ and $v_{2j-1}=f^{\prime }\left(x_{2j-1}\right)$ for $j=1,\cdots ,\frac{n}{2}+1$, f being a differentiable function on $[-1,1]$, we denote the corresponding interpolation polynomial by $h_{\frac{3n}{2}+1}(f,x)$.

To obtain the expression of the polynomial $h_{\frac{3n}{2}+1}\left(x\right)$ satisfying (17), first, we study the corresponding problem on $\mathbb{T}$ obtained through the Szegő transformation. By this transformation between $[-1,1]$ and $\mathbb{T}$, which is ${\displaystyle x=\frac{z+\frac{1}{z}}{2},}$ our real nodal system becomes ${\left\{{\alpha }_j\right\}}_{j=1}^{2n}$, where ${\alpha }_1=1$ and ${\alpha }_{n+1}=-1,$ that is, ${\left\{{\alpha }_j\right\}}_{j=1}^{2n}=\{-1,1\}\cup {\left\{{\alpha }_j\right\}}_{j=2}^n\cup {\left\{\overline{{\alpha }_j}\right\}}_{j=2}^n$. According to what was said, we will denote the corresponding nodal polynomial by $W_{2n}\left(z\right)$. Furthermore, since for $j=1,\cdots ,n+1$, ${\alpha }_j=x_j+ı\sqrt{1-x_j^2},$ that is, ${\alpha }_j=e^{ı arccos x_j}$, we have

$$\widehat{{\alpha }_j-{\alpha }_{j+1}}=arccos{x}_{j+1}-arccos{x}_j=\frac{\pi }{n}+\frac{a\left(j\right)}{n^2},j=1,\cdots ,n.$$

Clearly, ${\left\{{\alpha }_j\right\}}_{j=1}^{2n}$ satisfies relation (7) with $A\left(j\right)=4a\left(j\right)$, $A=4a$, and $2n>\frac{A}{\pi }.$

Thus, the transformed problem is that of finding a polynomial ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)$ in the space ${\mathsf{\Lambda }}_{-\frac{3n}{2},\frac{3n}{2}-1}\left[z\right]$ such that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left({\alpha }_1\right)=q_1,{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left({\alpha }_{n+1}\right)=q_{n+1},\\ \hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left({\alpha }_j\right)={\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(\overline{{\alpha }_j}\right)=q_j,\mathrm{for}j=2,\cdots ,n,\\ \hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left({\alpha }_1\right)=0,{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left({\alpha }_{n+1}\right)=0\mathrm{and}\\ \hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left({\alpha }_{2j-1}\right)=\overline{{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(\overline{{\alpha }_{2j-1}}\right)}=ıv_{2j-1}\overline{{\alpha }_{2j-1}}\sqrt{1-x_{2j-1}^2},\mathrm{for}j=2,\cdots ,\frac{n}{2}.\end{array}\end{array}$$

(18)

In Proposition 1, we have given the expressions to compute the polynomial ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)$ satisfying (18). Indeed, by taking into account that the nodal points are conjugated, the expressions can be simplified and it is immediate seeing that ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)$ has real coefficients. Thus, if we define

$$p_{\frac{3n}{2}}\left(x\right)=\frac{1}{2}\left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)+{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(\frac{1}{z}\right)\right)$$

for $x=\frac{z+\frac{1}{z}}{2}$ and $z\in \mathbb{T}$, then $p_{\frac{3n}{2}}\left(x\right)$ fulfills that $p_{\frac{3n}{2}}\left(x_j\right)=q_j$ for $j=1,\cdots ,n+1.$

Since

$$p_{\frac{3n}{2}}^{\prime }\left(x\right)=\frac{1}{2}\left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(z\right)+{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(\frac{1}{z}\right)\left(-\frac{1}{z^2}\right)\right)\frac{dz}{dx}$$

and $\frac{dz}{dx}=\frac{2z^2}{z^2-1}$,

$$p_{\frac{3n}{2}}^{\prime }\left(x\right)=\frac{1}{z^2-1}\left(z^2{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(z\right)-{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(\frac{1}{z}\right)\right)$$

and therefore $p_{\frac{3n}{2}}^{\prime }\left(x_{2j-1}\right)=\frac{1}{{{\alpha }_{2j-1}}^2-1}2ıv_{2j-1}{\alpha }_{2j-1}\sqrt{1-x_{2j-1}^2}=v_{2j-1},$ where the last equality comes from the fact that $\frac{z^2-1}{z}=2ı\sqrt{1-x^2}$.

Since ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(1\right)={\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }(-1)=0$, taking into account that

$${\displaystyle p_{\frac{3n}{2}}^{\prime }\left(1\right)=\underset{x\to 1}{lim}{p}_{\frac{3n}{2}}^{\prime }\left(x\right)=\underset{z\to 1}{lim}\frac{z^2{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(z\right)-{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }\left(\frac{1}{z}\right)}{z^2-1}}$$

and applying L’Hôpital’s rule, we obtain that $p_{\frac{3n}{2}}^{\prime }\left(1\right)={\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}\left(1\right)$. Proceeding in a similar way, we also obtain that $p_{\frac{3n}{2}}^{\prime }(-1)=-{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}(-1)$.

Since we cannot assure that $p_{\frac{3n}{2}}^{\prime }\left(1\right)$ and $p_{\frac{3n}{2}}^{\prime }(-1)$ are equal to $v_1$ and $v_{n+1}$, respectively, we modify $p_{\frac{3n}{2}}\left(x\right)$ by adding two auxiliary polynomials to adjust the values in 1 and $-1$. Thus, to obtain the polynomial $h_{\frac{3n}{2}+1}\left(x\right)$ satisfying (17), we consider the polynomials $Q_{\frac{3n}{2}+1}\left(x\right)$ and $R_{\frac{3n}{2}+1}\left(x\right)$ satisfying the conditions

$$Q_{\frac{3n}{2}+1}\left(x_j\right)=0,j=1,\cdots ,n+1;Q_{\frac{3n}{2}+1}^{\prime }\left(1\right)=1\mathrm{and}{Q}_{\frac{3n}{2}+1}^{\prime }\left(x_{2j-1}\right)=0,j=2,\cdots ,\frac{n}{2}+1$$

and

$$R_{\frac{3n}{2}+1}\left(x_j\right)=0,j=1,\cdots ,n+1;R_{\frac{3n}{2}+1}^{\prime }(-1)=1\mathrm{and}{R}_{\frac{3n}{2}+1}^{\prime }\left(x_{2j-1}\right)=0,j=1,\cdots ,\frac{n}{2},$$

that is,

$$Q_{\frac{3n}{2}+1}\left(x\right)=\frac{{\displaystyle \prod _{j=1}^{n+1}}(x-x_j){\displaystyle \prod _{j=2}^{\frac{n}{2}+1}}(x-x_{2j-1})}{{\displaystyle \prod _{j=2}^{n+1}}(1-x_j){\displaystyle \prod _{j=2}^{\frac{n}{2}+1}}(1-x_{2j-1})};R_{\frac{3n}{2}+1}\left(x\right)=\frac{{\displaystyle \prod _{j=1}^{n+1}}(x-x_j){\displaystyle \prod _{j=1}^{\frac{n}{2}}}(x-x_{2j-1})}{{(-1)}^{\frac{3n}{2}}{\displaystyle \prod _{j=1}^n}(1+x_j){\prod }_{j=1}^{\frac{n}{2}}(1+x_{2j-1})}.$$

Hence, we obtain that the polynomial $h_{\frac{3n}{2}+1}\left(x\right)$ fulfilling (17) has the expression

$$h_{\frac{3n}{2}+1}\left(x\right)=p_{\frac{3n}{2}}\left(x\right)+(v_1-p_{\frac{3n}{2}}^{\prime }\left(1\right))Q_{\frac{3n}{2}+1}\left(x\right)+(v_{n+1}-p_{\frac{3n}{2}}^{\prime }(-1))R_{\frac{3n}{2}+1}\left(x\right).$$

(19)

Our next step is to study some convergence problems by applying the results obtained in the previous subsections. Thus, we have to transform the expression of the polynomial $h_{\frac{3n}{2}+1}\left(x\right)$ given above, for which purpose we begin by transforming $Q_{\frac{3n}{2}+1}\left(x\right)$ and $R_{\frac{3n}{2}+1}\left(x\right)$ here.

Indeed, if we take into account that $x=\frac{z+\frac{1}{z}}{2}$ for $x\in [-1,1]$ and $z\in \mathbb{T}$, then $x-x_j=\frac{1}{2z}(z-{\alpha }_j)(z-\overline{{\alpha }_j})$ for $j=1,\cdots ,n+1$, and, in particular, for $j=1$ and $j=n+1$, it holds that $x-1=\frac{1}{2z}{(z-1)}^2$ and $x+1=\frac{1}{2z}{(z+1)}^2$, respectively.

Moreover, if $x=1$, then $1-x_j=\frac{1}{2}(1-{\alpha }_j)(1-\overline{{\alpha }_j})$ for $j=2,\cdots ,n,$ and if $x=-1,$ then $1+x_j=-\frac{1}{2}(1+{\alpha }_j)(1+\overline{{\alpha }_j})$ for $j=2,\cdots ,n.$

To relate these expressions to the nodal polynomials, we recall that

$$W_{2n}\left(z\right)=(z-1)(z+1)\prod _{j=2}^n(z-{\alpha }_j)(z-\overline{{\alpha }_j}),$$

which implies that

$$W_{2n}^{\prime }\left(1\right)=2\prod _{j=2}^n(1-{\alpha }_j)(1-\overline{{\alpha }_j})\mathrm{and}{W}_{2n}^{\prime }(-1)=-2\prod _{j=2}^n(1+{\alpha }_j)(1+\overline{{\alpha }_j}),$$

and

$$Y_n\left(z\right)=(z-1)(z+1)\prod _{j=2}^{\frac{n}{2}}(z-{\alpha }_{2j-1})(z-\overline{{\alpha }_{2j-1}}),$$

which implies that

$$Y_n^{\prime }\left(1\right)=2\prod _{j=2}^{\frac{n}{2}}(1-{\alpha }_{2j-1})(1-\overline{{\alpha }_{2j-1}})\mathrm{and}{Y}_n^{\prime }(-1)=-2\prod _{j=2}^{\frac{n}{2}}(1+{\alpha }_{2j-1})(1+\overline{{\alpha }_{2j-1}}).$$

Hence, we obtain

(i)

${\displaystyle \prod _{j=2}^n(x-x_j)=\frac{1}{2^{n-1}{z}^{n-1}}\prod _{j=2}^n(z-{\alpha }_j)(z-\overline{{\alpha }_j})=\frac{1}{2^{n-1}{z}^{n-1}}\frac{W_{2n}\left(z\right)}{(z-1)(z+1)}.}$

(ii)

${\displaystyle \prod _{j=2}^{\frac{n}{2}}(x-x_{2j-1})=\frac{1}{2^{\frac{n}{2}-1}{z}^{\frac{n}{2}-1}}\prod _{j=2}^{\frac{n}{2}}(z-{\alpha }_{2j-1})(z-\overline{{\alpha }_{2j-1}})=\frac{1}{2^{\frac{n}{2}-1}{z}^{\frac{n}{2}-1}}\frac{Y_n\left(z\right)}{(z-1)(z+1)}.}$

(iii)

${\displaystyle \prod _{j=2}^n(1-x_j)=\frac{1}{2^{n-1}}\prod _{j=2}^n(1-{\alpha }_j)(1-\overline{{\alpha }_j})=\frac{W_{2n}^{\prime }\left(1\right)}{2^n}.}$

(iv)

${\displaystyle \prod _{j=2}^{\frac{n}{2}}(1-x_{2j-1})=\frac{1}{2^{\frac{n}{2}-1}}\prod _{j=2}^{\frac{n}{2}}(1-{\alpha }_{2j-1})(1-\overline{{\alpha }_{2j-1}})=\frac{Y_n^{\prime }\left(1\right)}{2^{\frac{n}{2}}}.}$

(v)

${\displaystyle \prod _{j=2}^n(1+x_j)=\frac{{(-1)}^{n-1}}{2^{n-1}}\prod _{j=2}^n(1+{\alpha }_j)(1+\overline{{\alpha }_j})=\frac{{(-1)}^n{W}_{2n}^{\prime }(-1)}{2^n}.}$

(vi)

${\displaystyle \prod _{j=2}^{\frac{n}{2}}(1+x_{2j-1})=\frac{{(-1)}^{\frac{n}{2}-1}}{2^{\frac{n}{2}-1}}\prod _{j=2}^{\frac{n}{2}}(1+{\alpha }_{2j-1})(1+\overline{{\alpha }_{2j-1}})=\frac{{(-1)}^{\frac{n}{2}}{Y}_n^{\prime }(-1)}{2^{\frac{n}{2}}}.}$

Therefore,

$$Q_{\frac{3n}{2}+1}\left(x\right)=\frac{{(z+1)}^2{W}_{2n}\left(z\right)Y_n\left(z\right)}{2^3{z}^{\frac{3n}{2}+1}{W}_{2n}^{\prime }\left(1\right)Y_n^{\prime }\left(1\right)}$$

(20)

and

$$R_{\frac{3n}{2}+1}\left(x\right)=\frac{{(z-1)}^2{W}_{2n}\left(z\right)Y_n\left(z\right)}{2^3{(-1)}^n{z}^{\frac{3n}{2}+1}{W}_{2n}^{\prime }(-1)Y_n^{\prime }(-1)}.$$

(21)

Proposition 7.

Let f be a continuous function on $[-1,1]$ with $\omega (f,\delta )=o(|ln\delta {|}^{-1})$ when $\delta \to 0$ and let $h_{\frac{3n}{2}+1}(f,V_{\frac{n}{2}+1},x)\in {\mathbb{P}}_{\frac{3n}{2}+1}$ be the interpolation polynomial satisfying (17) with $V_{\frac{n}{2}+1}={\left(v_{2j-1}\right)}_{j=1}^{\frac{n}{2}+1}.$ If $\Vert V_{\frac{n}{2}+1}{\Vert }_{\infty }=o\left(\frac{n}{lnn}\right)$ or $\Vert V_{\frac{n}{2}+1}{\Vert }_q=o\left(n\right)$ for some q such that $1\le q<\infty$, then the sequence $h_{\frac{3n}{2}+1}(f,V_{\frac{n}{2}+1},x)$ uniformly converges to f on $[-1,1].$

Proof. 

By using the Szegő transformation, we define a function F on $\mathbb{T}$ by means of $F\left(z\right)=F\left(\overline{z}\right)=f\left(x\right)$ for $z\in \mathbb{T}$.

Let us write

$$\begin{array}{l}{\gamma }_n^{*}=\\ (0,ıv_3\sqrt{1-x_3^2}\overline{{\alpha }_3},\cdots ,ıv_{n-1}\sqrt{1-x_{n-1}^2}\overline{{\alpha }_{n-1}},0,-ıv_{n-1}\sqrt{1-x_{n-1}^2}{\alpha }_{n-1},\cdots ,-ıv_3\sqrt{1-x_3^2}{\alpha }_3)\end{array}$$

and denote by ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},z)$ the interpolation polynomial satisfying the conditions

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},{\alpha }_1)=f\left(x_1\right),{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},{\alpha }_{n+1})=f\left(x_{n+1}\right),\\ \hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},{\alpha }_j)=\overline{{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},\overline{{\alpha }_j})}=f\left(x_j\right)\mathrm{for}j=2,\cdots ,n,\\ \hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }(F,{\gamma }_n^{*},{\alpha }_1)=0,{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }(F,{\gamma }_n^{*},{\alpha }_{n+1})=0\mathrm{and}\\ \hfill {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }(F,{\gamma }_n^{*},{\alpha }_{2j-1})=\overline{{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{\prime }(F,{\gamma }_n^{*},\overline{{\alpha }_{2j-1}})}=ıv_{2j-1}\overline{{\alpha }_{2j-1}}\sqrt{1-x_{2j-1}^2}\mathrm{for}j=2,\cdots ,\frac{n}{2}.\end{array}\end{array}$$

If we write $p_{\frac{3n}{2}}(f,{\gamma }_n^{*},x)=\frac{{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},z)+{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},\frac{1}{z})}{2}$ and we take into account expression (19), we obtain

$$h_{\frac{3n}{2}+1}(f,V_{\frac{n}{2}+1},x)=p_{\frac{3n}{2}}(f,{\gamma }_n^{*},x)+(v_1-p_{\frac{3n}{2}}^{\prime }\left(1\right))Q_{\frac{3n}{2}+1}\left(x\right)+(v_{n+1}-p_{\frac{3n}{2}}^{\prime }(-1))R_{\frac{3n}{2}+1}\left(x\right).$$

Hence,

$$\begin{array}{c}\hfill \left|h_{\frac{3n}{2}+1}\left(f,V_{\frac{n}{2}+1},x\right)-f\left(x\right)\right|=\\ \hfill \left|p_{\frac{3n}{2}}(f,{\gamma }_n^{*},x)-f\left(x\right)+\left(v_1-p_{\frac{3n}{2}}^{\prime }\left(1\right)\right)Q_{\frac{3n}{2}+1}\left(x\right)+\left(v_{n+1}-p_{\frac{3n}{2}}^{\prime }(-1)\right)R_{\frac{3n}{2}+1}\left(x\right)\right|=\\ \hfill |\frac{{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},z)+{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},\frac{1}{z})}{2}-\frac{F\left(z\right)+F\left(\frac{1}{z}\right)}{2}+\\ \hfill \left(v_1-p_{\frac{3n}{2}}^{\prime }\left(1\right)\right)Q_{\frac{3n}{2}+1}\left(x\right)+\left(v_{n+1}-p_{\frac{3n}{2}}^{\prime }(-1)\right)R_{\frac{3n}{2}+1}\left(x\right)|\le \\ \hfill \frac{1}{2}\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},z)-F\left(z\right)\right|+\frac{1}{2}\left|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(F,{\gamma }_n^{*},\frac{1}{z}\right)-F\left(\frac{1}{z}\right)\right|+\\ \hfill \left|v_1-p_{\frac{3n}{2}}^{\prime }\left(1\right)\right|\left|Q_{\frac{3n}{2}+1}\left(x\right)\right|+\left|v_{n+1}-p_{\frac{3n}{2}}^{\prime }(-1)\right|\left|R_{\frac{3n}{2}+1}\left(x\right)\right|.\end{array}$$

We study the behaviour of the first two terms in the last expression by applying Proposition 4. To carry this out, we take into account that $\Vert {\gamma }_n^{*}{\Vert }_q\le 2^{\frac{1}{q}}{\Vert V_{\frac{n}{2}+1}\Vert }_q$ and $\Vert {\gamma }_n^{*}{\Vert }_{\infty }\le {\Vert V_{\frac{n}{2}+1}\Vert }_{\infty }$. Hence, under our hypothesis, we have $\epsilon >0$ and then $\Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},){-F\Vert }_{\infty }<\epsilon$ for every $z\in \mathbb{T}$ and n large enough.

To study the last two terms, we take into account the following facts:

(i)

$|v_1|\le \Vert V_{\frac{n}{2}+1}{\Vert }_q$ and $|v_{n+1}|\le \Vert V_{\frac{n}{2}+1}{\Vert }_q$ for q such that $1\le q\le \infty$.

(ii)

By applying Lemmas 1 and 2, we obtain that the polynomials $Q_{\frac{3n}{2}+1}\left(x\right)$ and $R_{\frac{3n}{2}+1}\left(x\right)$ given in (20) and (21) can be bounded for every $x\in [-1,1]$, as

$$\begin{array}{c}\hfill |Q_{\frac{3n}{2}+1}\left(x\right)|\le \frac{{\mathcal{A}}^2}{{\mathcal{B}}^2}\frac{1}{n^2}\mathrm{and}|R_{\frac{3n}{2}+1}\left(x\right)|\le \frac{{\mathcal{A}}^2}{{\mathcal{B}}^2}\frac{1}{n^2}.\end{array}$$

Therefore, it is immediate that $|v_1{Q}_{\frac{3n}{2}+1}\left(x\right)|$ and $|v_{n+1}{R}_{\frac{3n}{2}+1}\left(x\right)|$ go to zero when n goes to ∞.

Finally, we use the same arguments as those of Theorem 6 in [14] in the following way: We know that for an n large enough, there exists $N=E\left[\sqrt{n}\right]$ such that $N^2\le n\le {(N+1)}^2$ and there exists $P_N\in {\mathsf{\Lambda }}_{-N,N}$ satisfying $\Vert F-P_N{\Vert }_{\infty }<\frac{{ϵ}_N}{lnN}$ with $\left\{{\epsilon }_N\right\}\to 0$. Therefore, $\Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},)-P_N{\Vert }_{\infty }<\epsilon +\frac{{\epsilon }_N}{lnN}$. Notice that for an n large enough, ${\mathsf{\Lambda }}_{-N,N}\subset {\mathsf{\Lambda }}_{-\frac{3n}{2},\frac{3n}{2}-1}$.

On the one hand, by applying twice the mentioned Markov’s inequalities, we obtain

$$\begin{array}{c}\hfill \Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}(F,{\gamma }_n^{*},)-P_N^{″}{\Vert }_{\infty }\le \left(\frac{9n}{2}-1\right)\frac{9n}{2}{\Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},)-P_N\Vert }_{\infty }\le \\ \hfill \frac{81n^2}{4}\left(\epsilon +\frac{{\epsilon }_N}{lnN}\right).\end{array}$$

Hence, $\Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}(F,{\gamma }_n^{*},){\Vert }_{\infty }\le {\Vert P_N^{″}\Vert }_{\infty }+\frac{81n^2}{4}\left(\epsilon +\frac{{\epsilon }_N}{lnN}\right).$

On the other hand, applying Markov’s inequality again, we obtain

$$\Vert P_N^{″}{\Vert }_{\infty }\le (9N^2+N){\Vert P\Vert }_{\infty }\le 10n\left({\Vert F\Vert }_{\infty }+\frac{{\epsilon }_N}{lnN}\right)$$

and therefore

$$\Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}(F,{\gamma }_n^{*},){\Vert }_{\infty }\le 10n\left({\Vert F\Vert }_{\infty }+\frac{{\epsilon }_N}{lnN}\right)+\frac{81n^2}{4}\left(\epsilon +\frac{{\epsilon }_N}{lnN}\right),$$

from which we deduce $|p_{\frac{3n}{2}}^{\prime }\left(1\right)||Q_{\frac{3n}{2}+1}\left(x\right)|\le \left({10n(\Vert F\Vert }_{\infty }+\frac{{\epsilon }_N}{lnN})+\frac{81n^2}{4}(\epsilon +\frac{{\epsilon }_N}{lnN})\right)\frac{{\mathcal{A}}^2}{n^2}$ and the same inequality for $|p_{\frac{3n}{2}}^{\prime }(-1)||R_{\frac{3n}{2}+1}\left(x\right)|$. □

2.6. Interpolation of Smooth Functions: Convergence

Now, our objective is to study the rate of convergence for the interpolation polynomials related to smooth functions in the sense given in [21]. Thus, first, we assume that f is a function defined on $[-1,1]$ that can be written as $f\left(x\right)={\sum }_{l=0}^{\infty }{a}_l{T}_l\left(x\right)$, where $|a_l|\le \frac{C}{l^t}$ for some positive constant C and a natural number t. In the expression, $T_l\left(x\right)$ denotes the Chebyshev polynomial of the first kind of degree l.

To obtain the interpolation polynomial $h_{\frac{3n}{2}+1}(f,x)$ satisfying (17) with the nodal system fulfilling (16), we decompose f as follows: $f=f_{1,n}+f_{2,n},$ where $f_{1,n}\left(x\right)={\sum }_{l=0}^{\frac{3n}{2}+1}{a}_l{T}_l\left(x\right)$ and $f_{2,n}\left(x\right)={\sum }_{l=\frac{3n}{2}+2}^{\infty }{a}_l{T}_l\left(x\right).$ Since $h_{\frac{3n}{2}+1}(f_{1,n},x)=f_{1,n}\left(x\right)$, we only need to compute $h_{\frac{3n}{2}+1}(T_l,x)$ for $l\ge \frac{3n}{2}+2$ to obtain $h_{\frac{3n}{2}+1}(f_{2,n},x)$.

Lemma 5.

There exist positive constants ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$ such that for every natural number l,

$$|h_{\frac{3n}{2}+1}(T_l,x)|\le {\mathcal{K}}_1\left(lnn+\frac{llnn}{n}\right)+{\mathcal{K}}_2\frac{l^2}{n^2}.$$

Proof. 

We define a function F on $\mathbb{T}$ by $F\left(z\right)=F\left(\overline{z}\right)=\frac{z^l+z^{-l}}{2}=T_l\left(x\right)$ and we compute the interpolation polynomial ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,{\gamma }_n^{*},z),$ where

$$\begin{array}{l}{\gamma }_n^{*}=(0,ıv_3\sqrt{1-x_3^2}\overline{{\alpha }_3},\cdots ,ıv_{n-1}\sqrt{1-x_{n-1}^2}\overline{{\alpha }_{n-1}},0,-ıv_{n-1}\sqrt{1-x_{n-1}^2}{\alpha }_{n-1},\cdots ,\\ -ıv_3\sqrt{1-x_3^2}{\alpha }_3),\end{array}$$

being $x_{2j-1}=\frac{{\alpha }_{2j-1}+\overline{{\alpha }_{2j-1}}}{2}$ and $v_{2j-1}=T_l^{\prime }\left(x_{2j-1}\right)$.

Thus, we obtain that $ıv_{2j-1}\sqrt{1-x_{2j-1}^2}\overline{{\alpha }_{2j-1}}=\frac{l}{2}\overline{{\alpha }_{2j-1}}({\alpha }_{2j-1}^l-{\overline{{\alpha }_{2j-1}}}^l)$ and therefore $-ıv_{2j-1}\sqrt{1-x_{2j-1}^2}{\alpha }_{2j-1}=-\frac{l}{2}{\alpha }_{2j-1}({\alpha }_{2j-1}^l-{\overline{{\alpha }_{2j-1}}}^l).$

By applying (19) and taking into account that $T_l^{\prime }\left(1\right)=l^2$ and $T_l^{\prime }(-1)={(-1)}^{l-1}{l}^2$, we have

$$h_{\frac{3n}{2}+1}(T_l,x)=p_{\frac{3n}{2}}\left(x\right)+(l^2-p_{\frac{3n}{2}}^{\prime }\left(1\right))Q_{\frac{3n}{2}+1}\left(x\right)+({(-1)}^{l-1}{l}^2-p_{\frac{3n}{2}}^{\prime }(-1))R_{\frac{3n}{2}+1}\left(x\right),$$

where $p_{\frac{3n}{2}}\left(x\right)={\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(\frac{z^l+z^{-l}}{2},{\gamma }_n^{*},z)={\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(\frac{z^l+z^{-l}}{2},z)+{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right).$

From Proposition 2, we know that $|{\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(\frac{z^l+z^{-l}}{2},z)|\le Llnn$. Furthermore, we are in conditions to apply Proposition 4 since $\omega (\frac{z^l+z^{-l}}{2},\delta )={o(|ln\delta |}^{-1})$ and $\Vert {\gamma }_n^{*}{\Vert }_{\infty }\le l=o\left(\frac{n}{lnn}\right)$. Hence, $|{\mathcal{HD}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(z\right)|\le \frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}$.

Therefore, $|p_{\frac{3n}{2}}\left(x\right)|=|{\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(\frac{z^l+z^{-l}}{2},{\gamma }_n^{*},z)|\le Llnn+\frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}.$

Now, we take into account that $p_{\frac{3n}{2}}^{\prime }\left(1\right)={\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}\left(\frac{z^l+z^{-l}}{2},{\gamma }_n^{*},1\right).$ By applying the aforementioned Markov’s inequality twice, we obtain that

$$\begin{array}{c}\hfill \Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}^{″}\left(\frac{z^l+z^{-l}}{2},{\gamma }_n^{*},\right){\Vert }_{\infty }\le \frac{81n^2}{4}{\Vert {\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}\left(\frac{z^l+z^{-l}}{2},{\gamma }_n^{*},\right)\Vert }_{\infty }\le \\ \hfill \frac{81n^2}{4}\left(Llnn+\frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}\right),\end{array}$$

and therefore $|p_{\frac{3n}{2}}^{\prime }\left(1\right)|\le \frac{81n^2}{4}(Llnn+\frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}).$ An analogous expression can be deduced for $|p_{\frac{3n}{2}}^{\prime }(-1)|$.

Hence,

$$\begin{array}{c}\hfill |h_{\frac{3n}{2}+1}(T_l,x)|\le Llnn+\frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}+\frac{{\mathcal{A}}^2}{{\mathcal{B}}^2}\left(2l^2+\frac{81n^2}{2}\left(Llnn+\frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}\right)\right)\frac{1}{n^2}=\\ \hfill \left(1+\frac{81{\mathcal{A}}^2}{2{\mathcal{B}}^2}\right)\left(Llnn+\frac{\mathcal{AD}}{{\mathcal{B}}^2}\frac{llnn}{n}\right)+\frac{2{\mathcal{A}}^2{l}^2}{{\mathcal{B}}^2{n}^2}\le {\mathcal{K}}_1\left(lnn+\frac{llnn}{n}\right)+{\mathcal{K}}_2\frac{l^2}{n^2},\end{array}$$

from which the result follows. □

Proposition 8.

Let f be a function defined on $[-1,1]$ by $f\left(x\right)={\displaystyle \sum _{l=0}^{\infty }}{a}_l{T}_l\left(x\right)$ with $|a_l|\le \frac{C}{l^t}$ for some positive constant C and a real number t such that $t>3$. Then, $h_{\frac{3n}{2}+1}(f,x)$ converges to f uniformly on $[-1,1]$ and the order of convergence is $\mathcal{O}\left(\frac{lnn}{{\left(\frac{3n}{2}\right)}^{t-1}}\right)$.

Proof. 

By using the decomposition of f, given at the beginning of this subsection, we have $|f\left(x\right)-h_{\frac{3n}{2}+1}(f,x)|=|f_{2,n}\left(x\right)-h_{\frac{3n}{2}+1}(f_{2,n},x)|.$

On the one hand, we have $|f_{2,n}\left(x\right)|\le {\displaystyle \sum _{l=\frac{3n}{2}+2}^{\infty }}|a_l||T_l\left(x\right)|\le C{\displaystyle \sum _{l=\frac{3n}{2}+2}^{\infty }}\frac{1}{l^t}\le C\frac{1}{(t-1)}\frac{1}{{\left(\frac{3n}{2}\right)}^{t-1}},$ which goes to 0 uniformly when n tends to ∞.

On the other hand, by applying Lemma 5, we obtain

$$\begin{array}{c}\hfill \begin{array}{c}\hfill |h_{\frac{3n}{2}+1}(f_{2,n},x)|\le \sum _{l=\frac{3n}{2}+2}^{\infty }|a_l||h_{\frac{3n}{2}+1}(T_l,x)|\le C\sum _{l=\frac{3n}{2}+2}^{\infty }\frac{1}{l^t}|h_{\frac{3n}{2}+1}(T_l,x)|\le \\ \hfill C\sum _{l=\frac{3n}{2}+2}^{\infty }\frac{1}{l^t}\left({\mathcal{K}}_1\left(lnn+\frac{llnn}{n}\right)+{\mathcal{K}}_2\frac{l^2}{n^2}\right)=\\ \hfill C{\mathcal{K}}_{1}lnn\sum _{l=\frac{3n}{2}+2}^{\infty }\frac{1}{l^t}+C{\mathcal{K}}_1\frac{lnn}{n}\sum _{l=\frac{3n}{2}+2}^{\infty }\frac{1}{l^{t-1}}+C{\mathcal{K}}_2\frac{1}{n^2}\sum _{l=\frac{3n}{2}+2}^{\infty }\frac{1}{l^{t-2}}.\end{array}\end{array}$$

By using the fact that ${\displaystyle \sum _{l=\frac{3n}{2}+2}^{\infty }}\frac{1}{l^t}\le \frac{1}{t-1}\frac{1}{{\left(\frac{3n}{2}\right)}^{t-1}}$ again, we obtain

$$\begin{array}{c}\hfill |h_{\frac{3n}{2}+1}(f_{2,n},x)|\le \frac{C{\mathcal{K}}_1}{t-1}\frac{lnn}{{\left(\frac{3n}{2}\right)}^{t-1}}+\frac{C{\mathcal{K}}_1}{t-2}\frac{lnn}{n}\frac{1}{{\left(\frac{3n}{2}\right)}^{t-2}}+\frac{C{\mathcal{K}}_2}{t-3}\frac{1}{n^2}\frac{1}{{\left(\frac{3n}{2}\right)}^{t-3}},\end{array}$$

which converges to 0 when n tends to $\infty .$ □

Finally, we treat the case of analytic functions.

Proposition 9.

Let f be an analytic function on $[-1,1]$ that can be written as $f\left(x\right)={\sum }_{l=0}^{\infty }{a}_l{T}_l\left(x\right)$, where $|a_l|\le K{r}^l$ for some constant $K>0$ and $0<r<1$. Then, $h_{\frac{3n}{2}+1}(f,x)$ converges to f uniformly on $[-1,1]$ and the order of convergence is $\mathcal{O}(r^{\frac{3n}{2}}lnn)$.

Proof. 

We write $f=f_{1,n}+f_{2,n}$, with $f_{1,n}$ and $f_{2,n}$ having the expressions given at the beginning of this subsection. Since $h_{\frac{3n}{2}+1}(f_{1,n},)=f_{1,n},$ we have

$$|f-h_{\frac{3n}{2}+1}(f,)|=|f_{2,n}-h_{\frac{3n}{2}+1}(f_{2,n},)|\le |f_{2,n}|+|h_{\frac{3n}{2}+1}(f_{2,n},)|.$$

On the one hand,

$$|f_{2,n}|=|\sum _{l=\frac{3n}{2}+2}^{\infty }{a}_l{T}_l|\le \sum _{l=\frac{3n}{2}+2}^{\infty }K{r}^l=K\frac{r^{\frac{3n}{2}+2}}{1-r}.$$

On the other hand, by applying Lemma 5, we obtain

$$\begin{array}{c}\hfill |h_{\frac{3n}{2}+1}(f_{2,n},)|=|h_{\frac{3n}{2}+1}(\sum _{l=\frac{3n}{2}+2}^{\infty }{a}_l{T}_l,)|\le \sum _{l=\frac{3n}{2}+2}^{\infty }|a_l||h_{\frac{3n}{2}+1}(T_l,)|\le K\sum _{l=\frac{3n}{2}+2}^{\infty }{r}^l|h_{\frac{3n}{2}+1}(T_l,)|\le \\ \hfill K\sum _{l=\frac{3n}{2}+2}^{\infty }\left({\mathcal{K}}_{1}lnn{r}^l+{\mathcal{K}}_{1}l\frac{lnn}{n}{r}^l+{\mathcal{K}}_2\frac{l^2}{n^2}{r}^l\right)=K{\mathcal{K}}_{1}lnn\frac{r^{\frac{3n}{2}+2}}{1-r}+\\ \hfill K{\mathcal{K}}_1\frac{lnn}{n}\left(\frac{(\frac{3n}{2}+2)r^{\frac{3n}{2}+2}}{1-r}+\frac{r^{\frac{3n}{2}+3}}{{(1-r)}^2}\right)+\frac{K{\mathcal{K}}_2}{n^2}\left(\frac{{(\frac{3n}{2}+2)}^2}{1-r}+\frac{(3n+5)r-3(n+1)r^2}{{(1-r)}^3}\right)r^{\frac{3n}{2}+2},\end{array}$$

which goes to zero when n tends to ∞. □

Remark 4.

The last results are similar to those given in [14], where we use the Chebyshev–Lobatto points as a nodal system. In that particular situation, the order of convergence is faster than those obtained in the present propositions, Propositions 8 and 9.

2.7. Numerical Experiments

This subsection is devoted to presenting some graphs related to the application of the method with the nodal systems dealt with. Actually, we have been interested in these types of nodal systems for some years. Notice that the different theories of interpolation have been developed based, in many cases, upon the roots of orthogonal polynomials; but this is a quite theoretical situation outside the equispaced nodal systems on $\mathbb{T}$ (closely connected with the four Chebyshev families on the bounded interval). Indeed, the separation property stated in (7) was obtained as a result of the study of the roots of para-orthogonal polynomials with respect to a measure that is an analytical modification of the Lebesgue measure on the unit circle. But we can obtain a lot of nodal systems with the same property using mechanical models.

So, all our examples are related to nodal systems on $\mathbb{T}$ satisfying the separation property because of different origins and particular functions, which are interpolated using barycentric expressions (5) and (6). We use distinct nodal systems presented in two different papers, where they were studied in detail. We also use the parameters considered there. Next, we list the nodal systems and the functions that will be employed.

• Our first example uses a measuring instrument based on a Cardan device. The full description of the nodal system and the proof that the system satisfies, (7), can be found in [11]. We choose $F\left(z\right)={\displaystyle \sum _{k=1}^{\infty }}\frac{1}{k^6}(z^k+z^{-k})$ as the test function.
• Our second example uses a measuring device based on a countdown process. The full description of the nodal system and the proof that it satisfies, (7), can be found in [11]. As the test function, we take $F\left(z\right)=\frac{z+\frac{1}{z}}{2}sin\frac{2}{z+\frac{1}{z}}$.
• The third example is based on the analysis of certain positions of a natural satellite orbiting its planet. A detail description of the nodal system and the proof that (7) is satisfied can be found in [11]. We choose $F\left(z\right)=e^z+e^{\frac{1}{z}}$ as the test function.
• Finally, we present an example that uses a nodal system constituted by the roots of a para-orthogonal polynomial with respect to a Bernstein–Szegő measure. The full description of the nodal system and the proof that it satisfies, (7), can be found in [19]. We select a jump function as the function to be approximated through interpolation.

In order to obtain a simple graphical representation, we always use a real-valued function $F\left(z\right)$ with $z=e^{i\theta }$. All the graphs depict $F\left(e^{i\theta }\right)$ and the real part of the interpolation polynomial, the only component which has interest as a consequence of this piece of work. Thus, when considering ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ with $z=e^{i\theta }$, all the graphs represent $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$. In this case, it is easy to prove that the original interpolation conditions lead to zeroth-order contact points where the derivatives are not prescribed and first-order contact points where the derivatives are prescribed. In some cases, we use the Hermite–Fejér polynomial ${\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })$. In a similar way, the original interpolation conditions originate zeroth-order contact points where the derivatives are not prescribed and zeroth-order contact points where null values for the derivatives are prescribed. At these last nodes, $\Re \left({\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ will necessarily have a horizontal tangent.

Example 1.

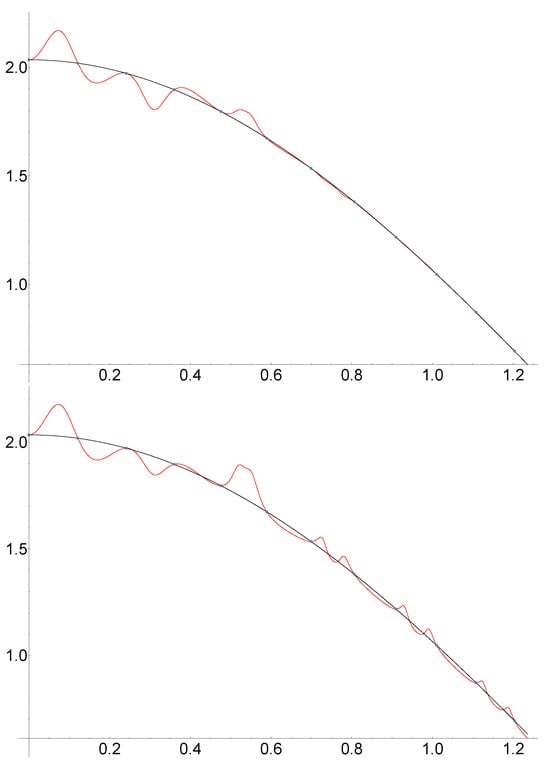
Our first example presents, in a graphical way, the peculiarities of ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ and ${\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$. We use a nodal system with $2n$ nodes and $n=30$. The objective function is $F\left(z\right)={\displaystyle \sum _{k=1}^{\infty }}\frac{1}{k^6}(z^k+z^{-k})$. In Figure 1 below, $F\left(e^{i\theta }\right)$ is depicted in black and $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ in red. We added the interpolation points in blue; notice that the region contains only 12 nodes. The only change below is that we represent $\Re \left({\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ instead of $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$.

Figure 1. Representation of $F\left(z\right)={\displaystyle \sum _{k=1}^{\infty }}\frac{1}{k^6}(z^k+z^{-k})$ in black and the real parts of the interpolation polynomials in red. Above with $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ and below with $\Re \left({\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$.

The more relevant facts are

1. 

The set of contact points between the objetive function and $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ is a mix of zeroth-order contact points (even nodes, numbering in increasing order for the arguments, that is, starting from $\theta =0$) and first-order contact points (odd nodes, numbering in the same way).

2. 

In a similar way, the contact points between the function and the real part of the Hermite–Fejér interpolant, which is $\Re \left({\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$, are zero-order contact ones. But at the odd nodes, it has a horizontal tangent.

Example 2.

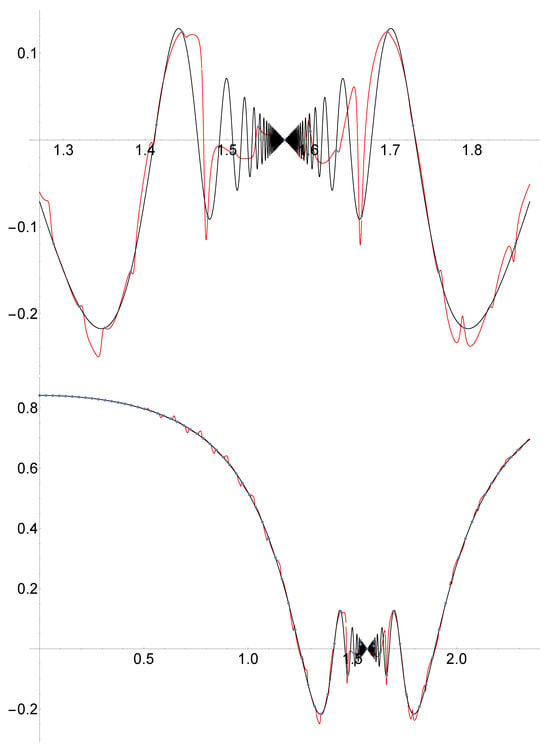
Our second example is included to show the convergence of the Hermite–Fejér interpolant ${\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ and the interpolant ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$, taking derivatives, and allowing us to satisfy the hypothesis of Proposition 4. We employ a nodal system with $2n$ nodes and $n=100$. The objective function is $F\left(z\right)=\frac{z+\frac{1}{z}}{2}sin\frac{2}{z+\frac{1}{z}}$, a quite variable function near $\frac{\pi }{2}$ and $\frac{3\pi }{2}$ ($\pm i$). In Figure 2 below, the function $F\left(e^{i\theta }\right)$ with $\theta \in [\frac{\pi }{2}-0.3,\frac{\pi }{2}+0.3]$, which is close to $\frac{\pi }{2}$, is depicted in black. Furthermore, $\Re \left({\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ is depicted in red. We added the interpolation points in blue. Below, we represent, in a greater interval, $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ and the function for $\theta \in [0,\frac{\pi }{2}+0.3]$. Near $\frac{\pi }{2}$ and $\frac{3\pi }{2}$, we take null values for the derivatives and far from both points, we use the derivatives of the function, allowing the hypothesis of Proposition 4 to be satisfied.

Figure 2. Representation of $F\left(z\right)=\frac{z+\frac{1}{z}}{2}sin\frac{2}{z+\frac{1}{z}}$ in black along with the real parts of the interpolation polynomials in red. Above, $\Re \left({\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$. Below, $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ using a subset of derivatives.

Example 3.

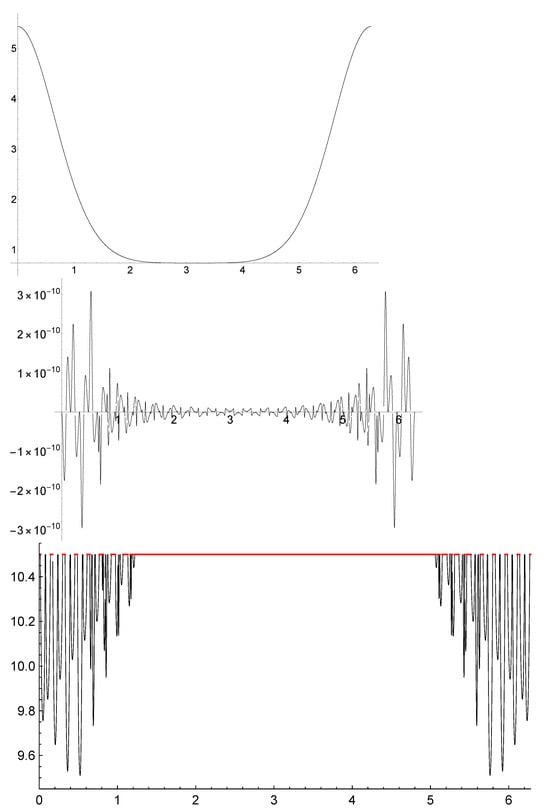
This example is considered to represent the convergence of ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ corresponding to an analytical function on an open annulus containing $\mathbb{T}$. We use a nodal system with $2n$ nodes and $n=40$. The objective function is $F\left(z\right)=e^z+e^{\frac{1}{z}}$. In Figure 3, at the top, the function $F\left(e^{i\theta }\right)$ with $\theta \in [0,2\pi ]$ is depicted in black and $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ is depicted in red. The relevant fact is that both functions are indistinguishable. In the middle, we represent the difference between both functions to observe the accuracy. Finally, at the bottom, $-{log}_{10}|\Re ({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta }))|$ is represented in black when this value is less than or equal to $10.5$, and in red for $10.5$ or in other cases; this gives a clear idea of the order of the error.

Figure 3. At the top, representation of $F\left(e^{i\theta }\right)$ (where $F\left(z\right)=e^z+e^{\frac{1}{z}}$) in black together with $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ in red. In the middle, representation of the difference between the functions. At the bottom, in black, $-{log}_{10}|\Re ({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta }))|$ when this value is less than or equal to $10.5$, and in red for $10.5$ or in other cases; this gives a clear idea of the order of the error.

Example 4.

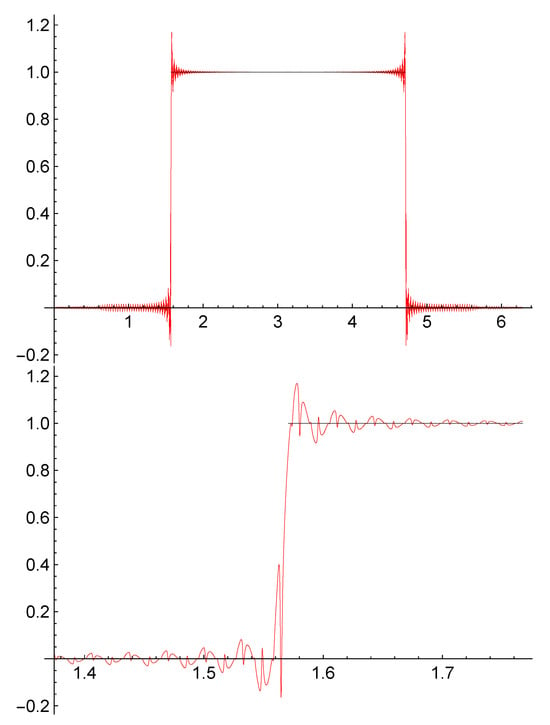
Our last example is included to present ${\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ and ${\mathcal{HF}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,z)$ when $F\left(z\right)=\left\{\begin{array}{ccc}0\hfill & if& \Re \left(z\right)\ge 0\\ 1\hfill & if& \Re \left(z\right)<0\end{array}\right.$ is the interpolated function, in which case they are equal. We use a 2n-node system with $n=400$.

Note that the function is discontinuous and we have not developed a theory for these types of functions. Observing Figure 4, the more relevant facts are

Figure 4. Above, representation of the jump function $F\left(e^{i\theta }\right)$ in black together with $\Re \left({\mathcal{H}}_{-\frac{3n}{2},\frac{3n}{2}-1}(F,e^{i\theta })\right)$ in red. Below, detail near one jump.

1. 

Far from $\pm i$, we can intuit convergence.

2. 

Near $\pm i$, a phenomenon similar to a Gibbs phenomenon with a singular aspect appears.

3. Materials

To perform the numerical experiments included in this piece of work, we created four variants of a common program (root1.nb, root2.nb, root3.nb, and root4.nb), which can be obtained at the url https://github.com/eberriochoa/slhseparationproperties (accessed on 31 January 2024), which enlists different programs. The notation and formulae are included in the paper. These files are the text of notebooks elaborated on with Mathematica^® 14.0. These programs (notebooks) should run correctly with recent previous versions and future versions because we use only simple commands. It is possible that minimal adaptations can be needed. Furthermore, we do not use compiled routines.

4. Discussion and Conclusions

In this paper, we have developed a theory working around two topics, namely, nodal systems on the unit circle not related with measures and an interpolation method between Lagrange and Hermite methods.

(i)

Nodal systems on the unit circle not related with measures.

In [11] and previous papers, we established a new type of nodal system on the unit circumference addressed to the classical interpolation methods of Lagrange and Hermite. Indeed, we characterized the nodal arrays by satisfying only a property of separation generalizing the uniform separation. With the goal of using these nodal systems in a new method of interpolation introduced in [15], in the present work, we carried out an important advance in the type of nodal system used. Although this property of separation is the one satisfied by the nodal points corresponding to the roots of para-orthogonal polynomials with respect to measures in the Szegő class with analytic extension outside the unit disk, we develop our work without using any measure. Thus, our results are rather general. We also highlight the importance of these nodal systems due to the large number of applications and their relevance. Examples of nodal systems treated in this work appear in some situations that are studied in Applied Physics such as celestial mechanics and mechanical applications. Thus, our results allow us to interpolate functional values in applied sciences. In addition, these systems originate others in the interval with identical separation properties. Thus, the first important conclusion is that we can use different interpolation methods based on nodal systems, which are not related with measures, and we can use these methods confidently. This conclusion is fully supported in the article and the previous cited papers.

(ii)

An interpolation method between Lagrange and Hermite methods.

An important conclusion is related with the use or not of supplementary information that we could have in some interpolation problems. At least, when the supplementary information is related with derivatives in a relevant part of the nodal system regularly distributed and we approximate or reconstruct a smooth function, we must conjecture that we must use the information. Indeed, if we interpolate a smooth function by using our nodal systems, the accuracy obtained using this intermediate method of interpolation is better than that obtained using Lagrange interpolation. This conjecture is supported in Section 2.4 and Section 2.6 and we must point out that smooth functions are in many cases the object of interpolation methods.

A future research direction could be the analysis of the Gibbs–Wilbraham phenomenon associated with this intermediate interpolation method with our nodal system.